A Nonlinear Disturbance Observer Based Virtual Negative Inductor Stabilizing Strategy for DC Microgrid with Constant Power Loads
Abstract
1. Introduction
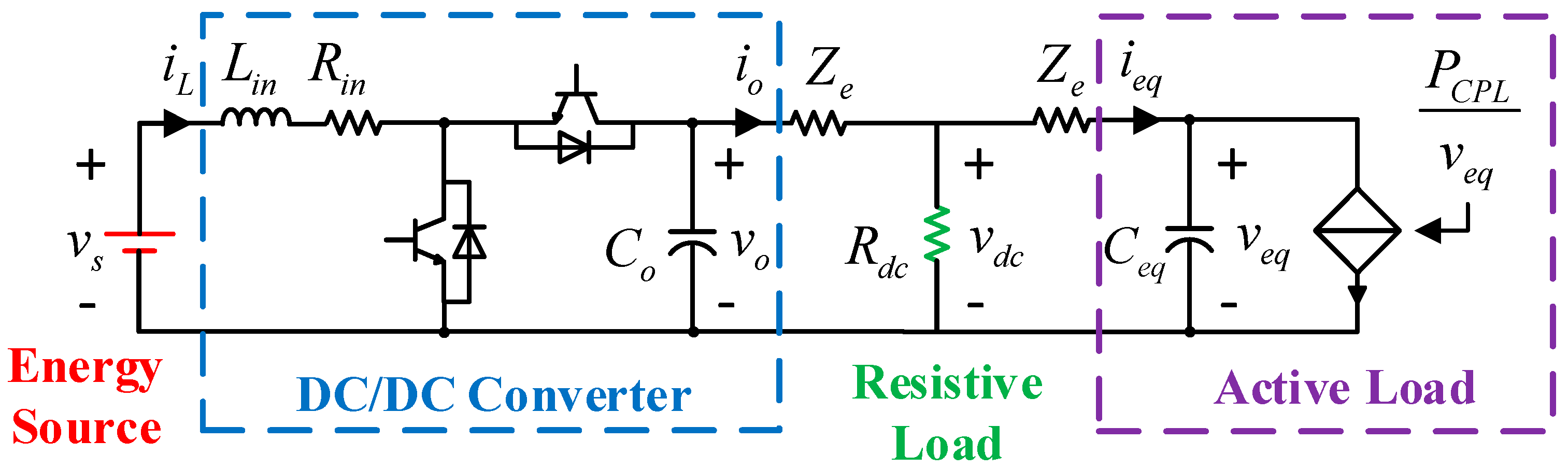
2. Problem Formulation
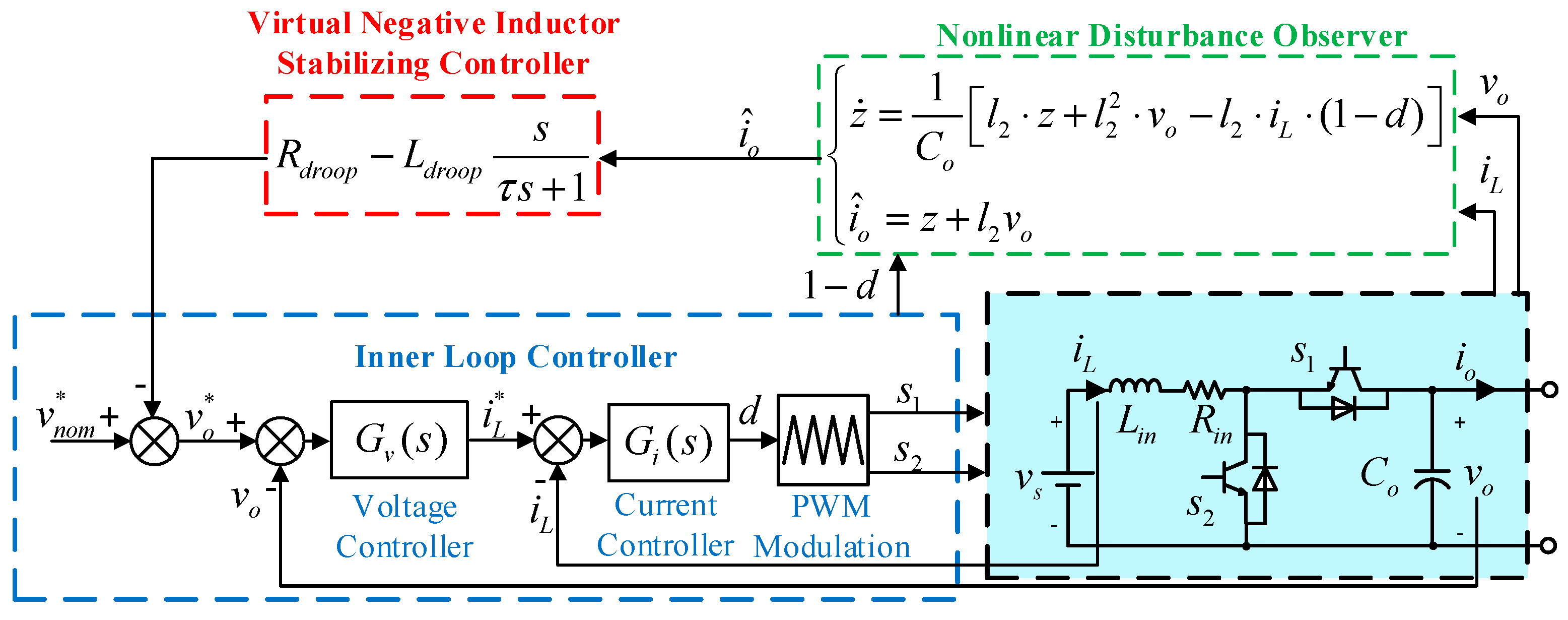
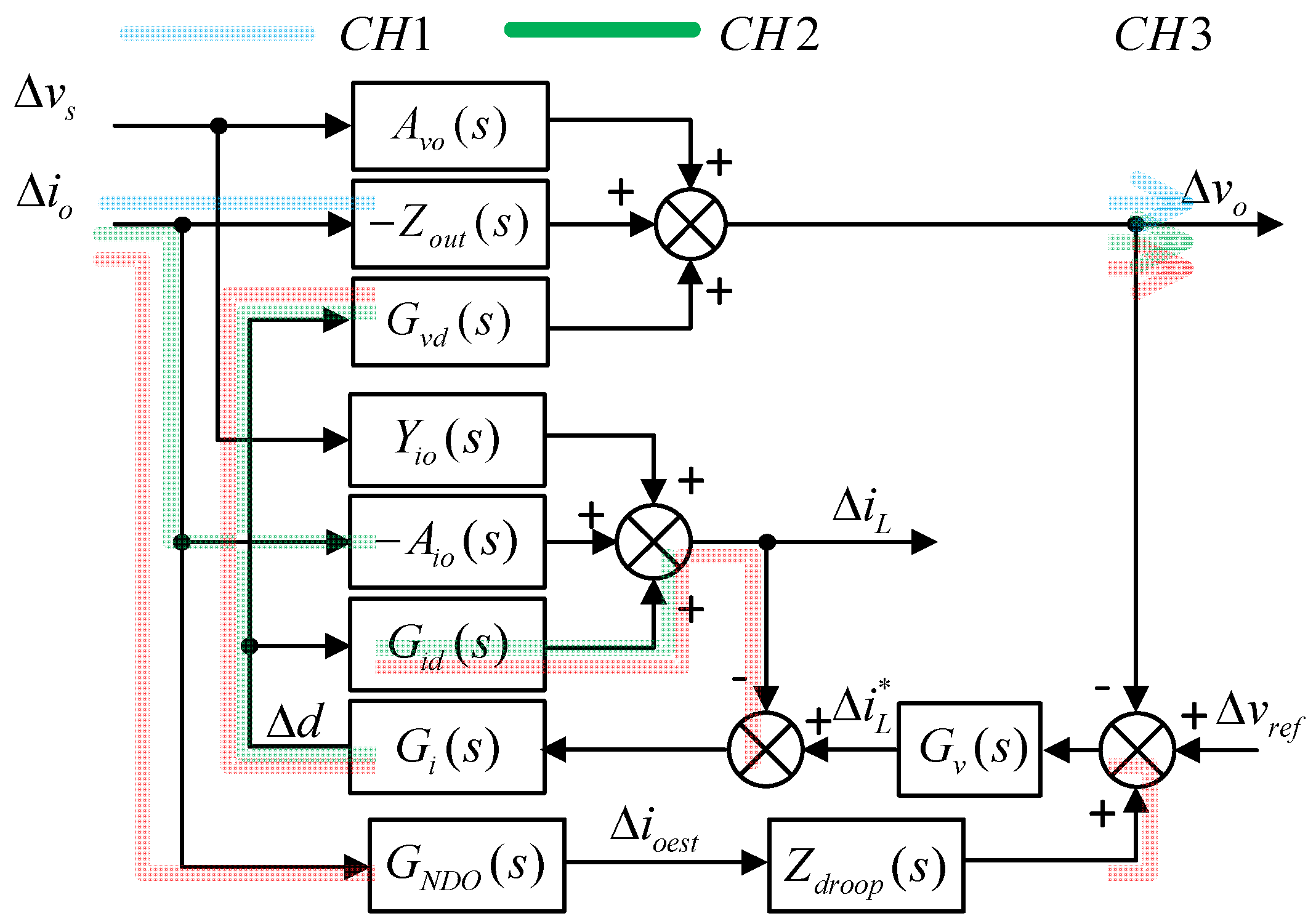
3. NDO Based VNI Stabilizing Strategy
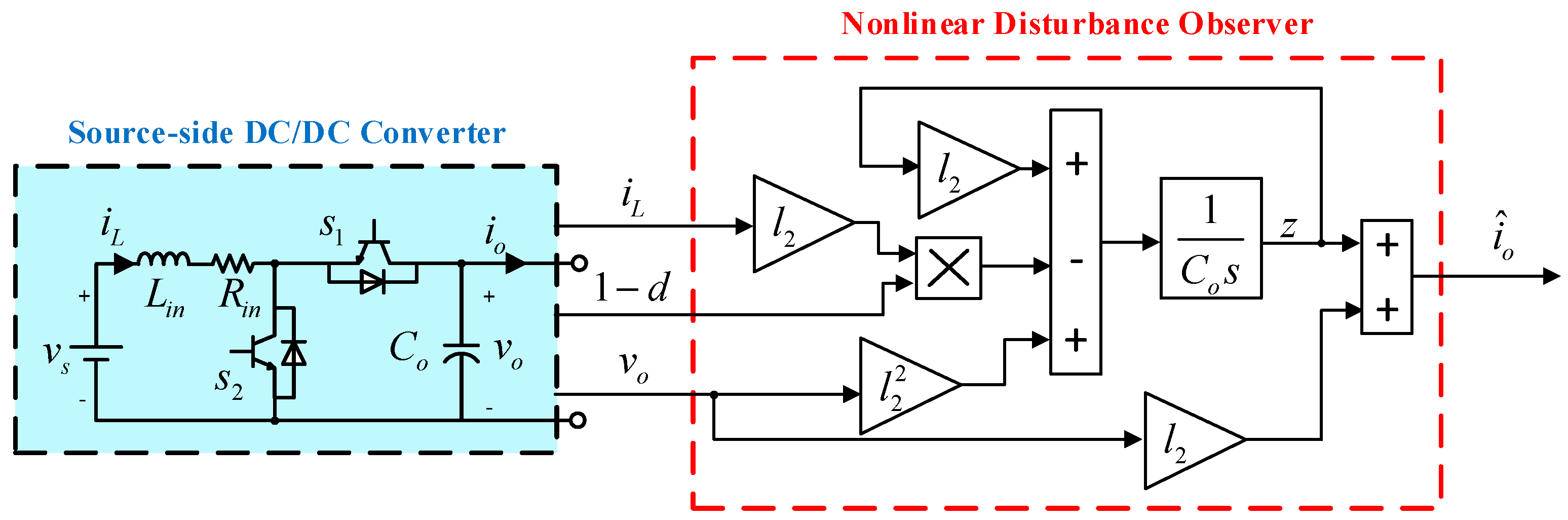
3.1. DC/DC Converter Modeling and Inner Loop Controller
3.2. Virtual Negative Inductor Stabilizing Strategy
3.3. Nonlinear Disturbance Observer
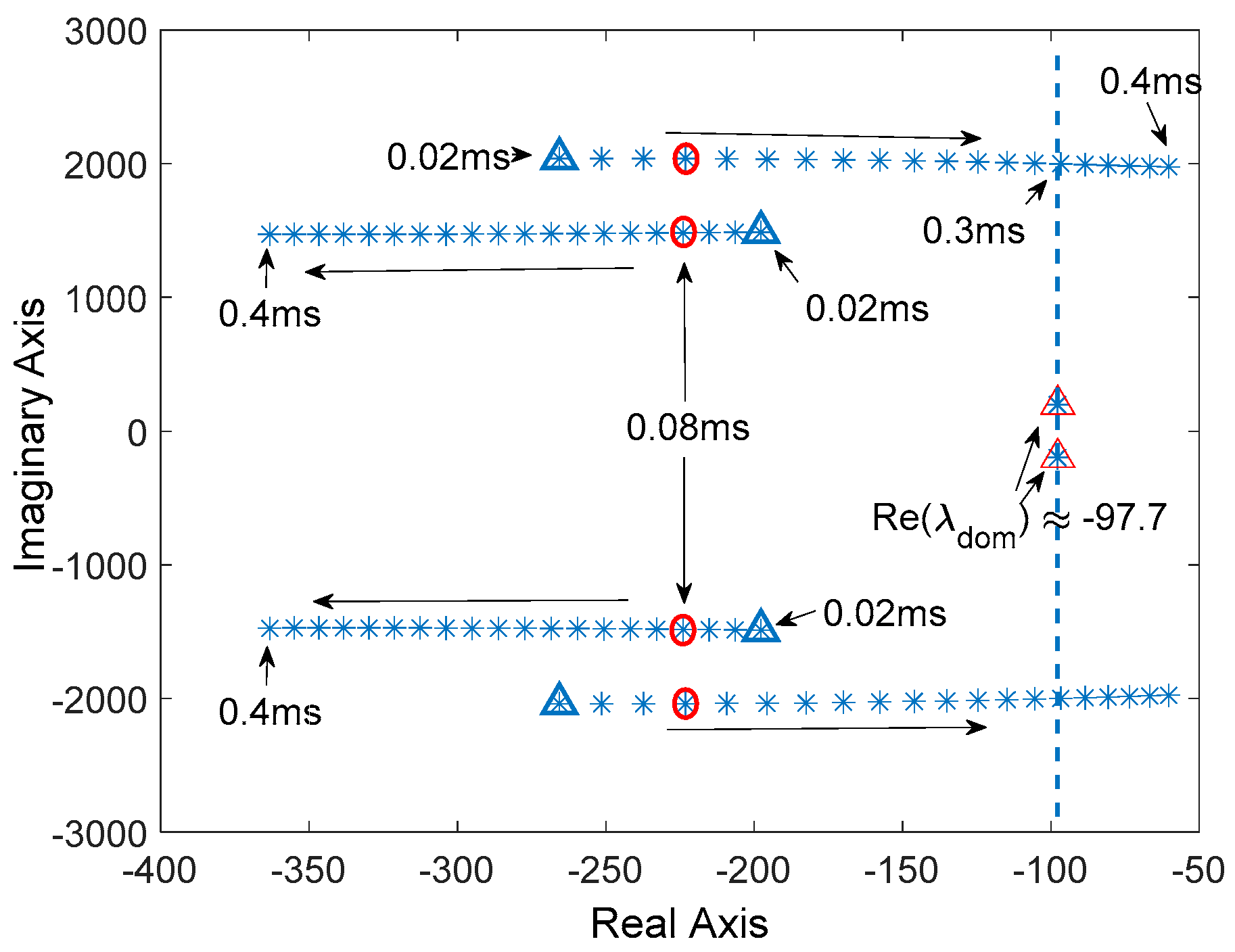
3.4. Parameter Designing
4. Stability Analysis
4.1. Output Impedance Model of the DC/DC Converter
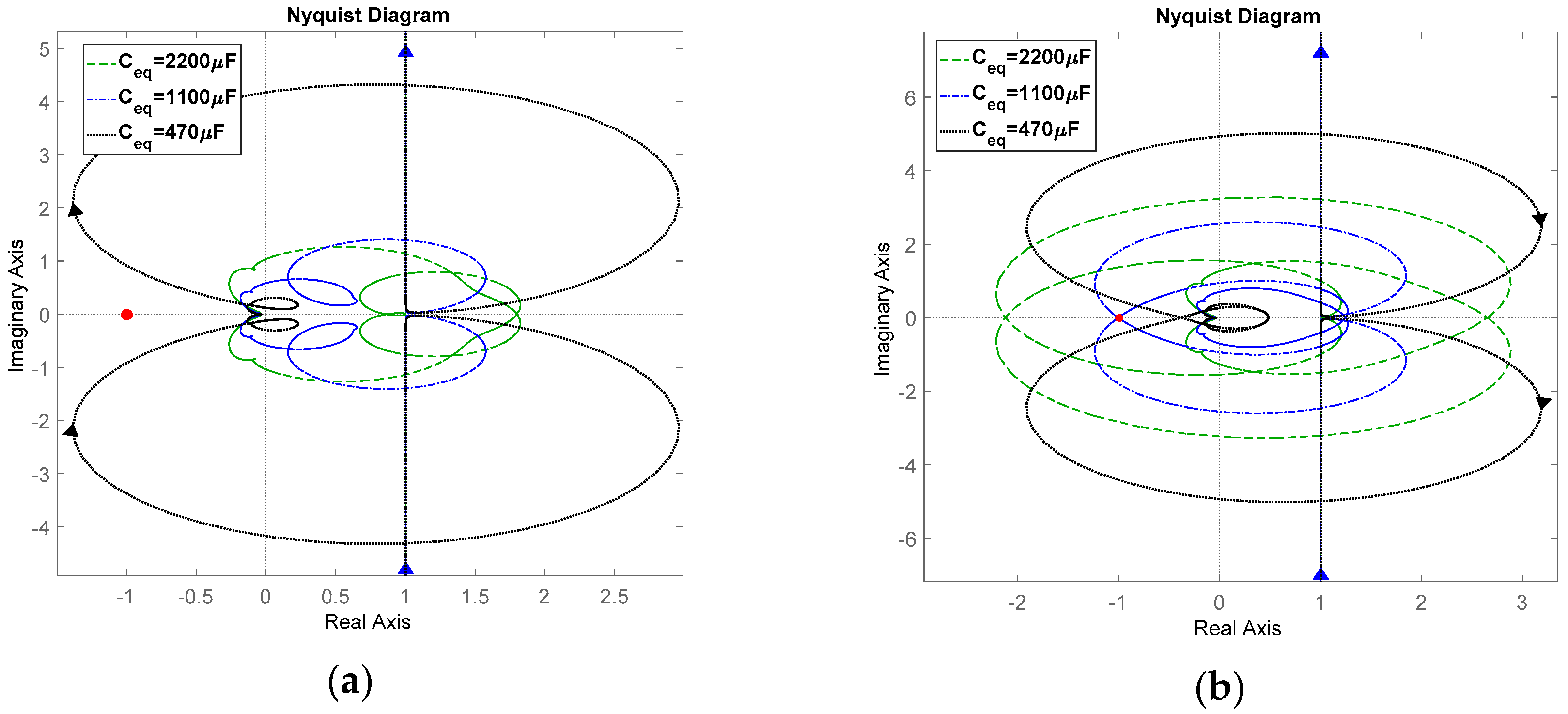
4.2. Nyquist Stability Criterion
- (a)
- If equals to zero, the system will be stable;
- (b)
- Or else, the system will be unstable.
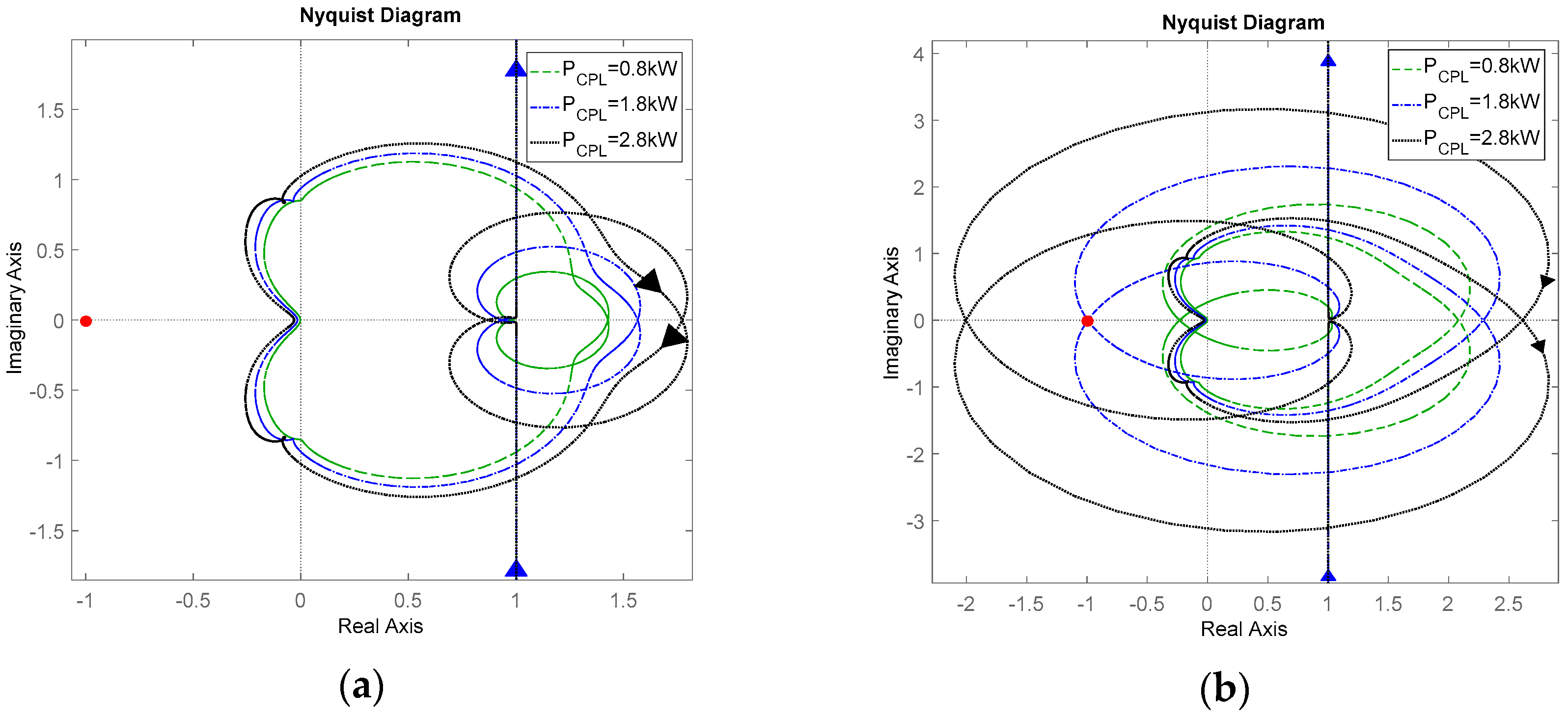
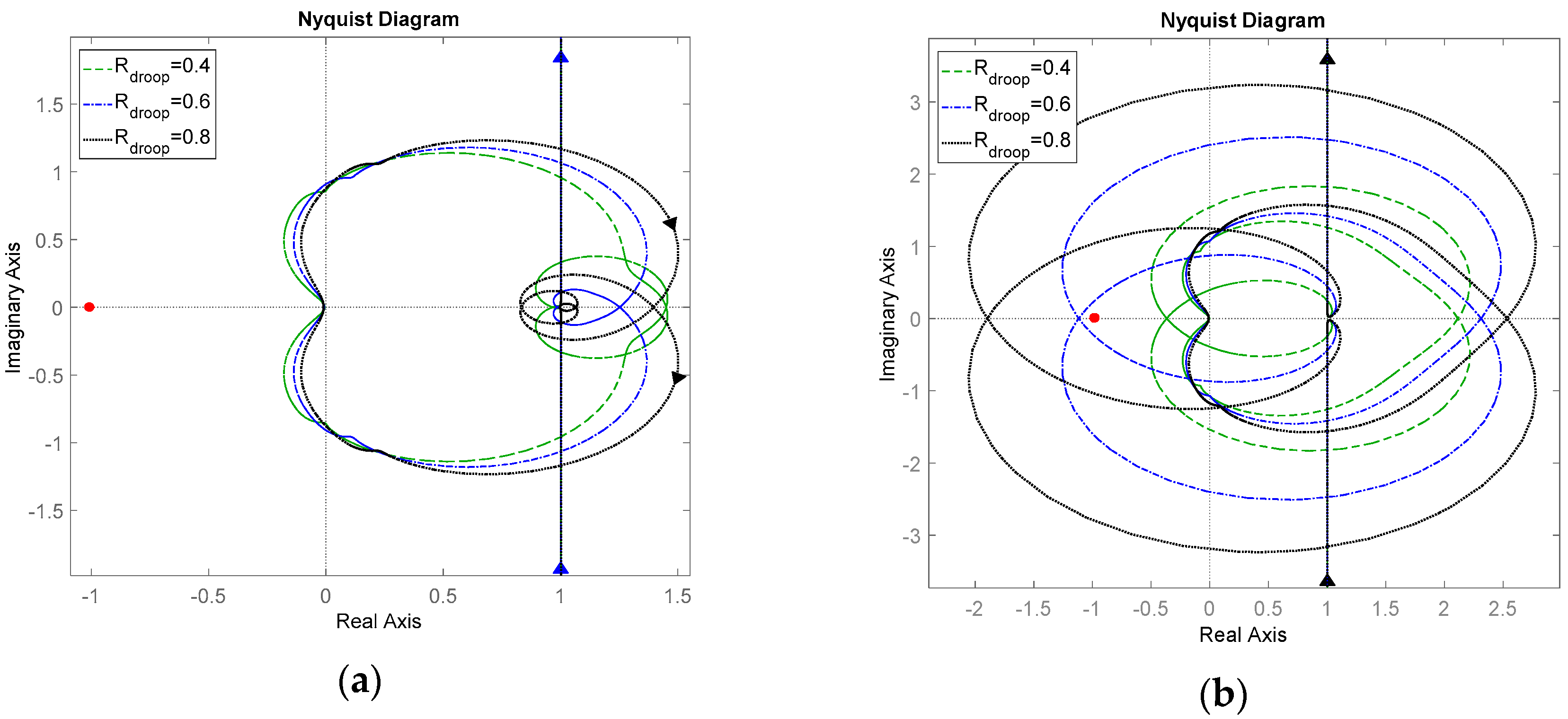
4.3. Comparative Stability Analysis
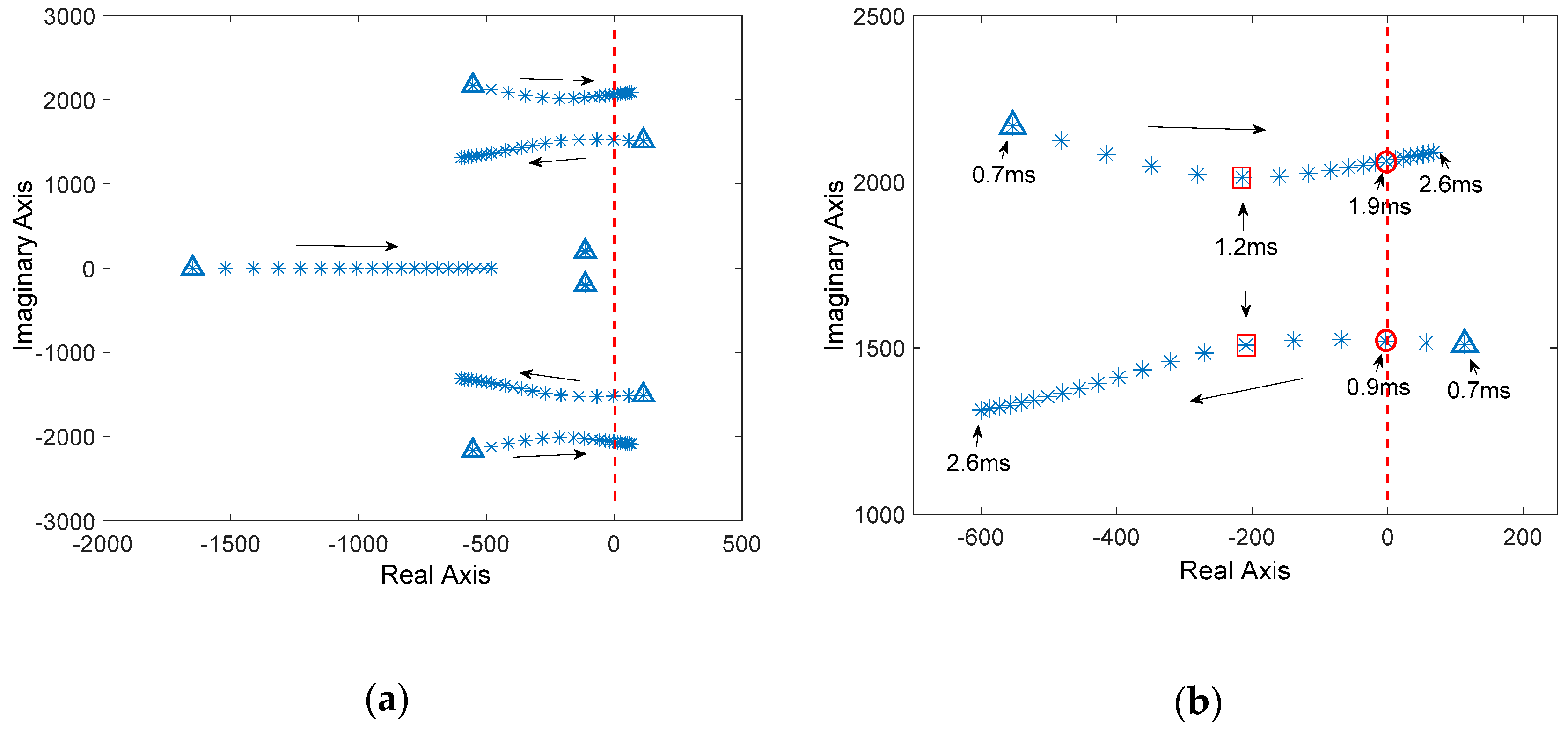
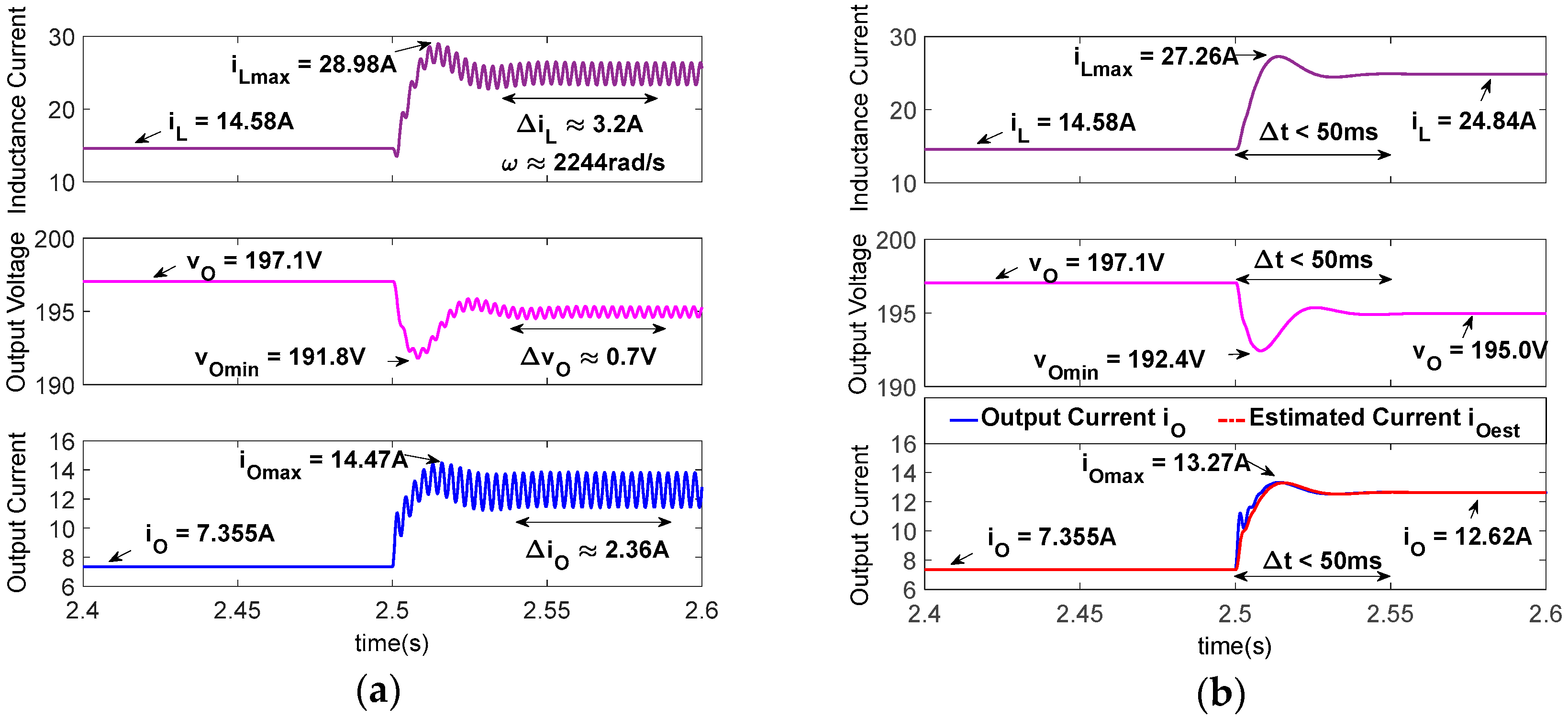
4.3.1. Case 1: CPL Power Change
4.3.2. Case 2: Droop Coefficient Variation
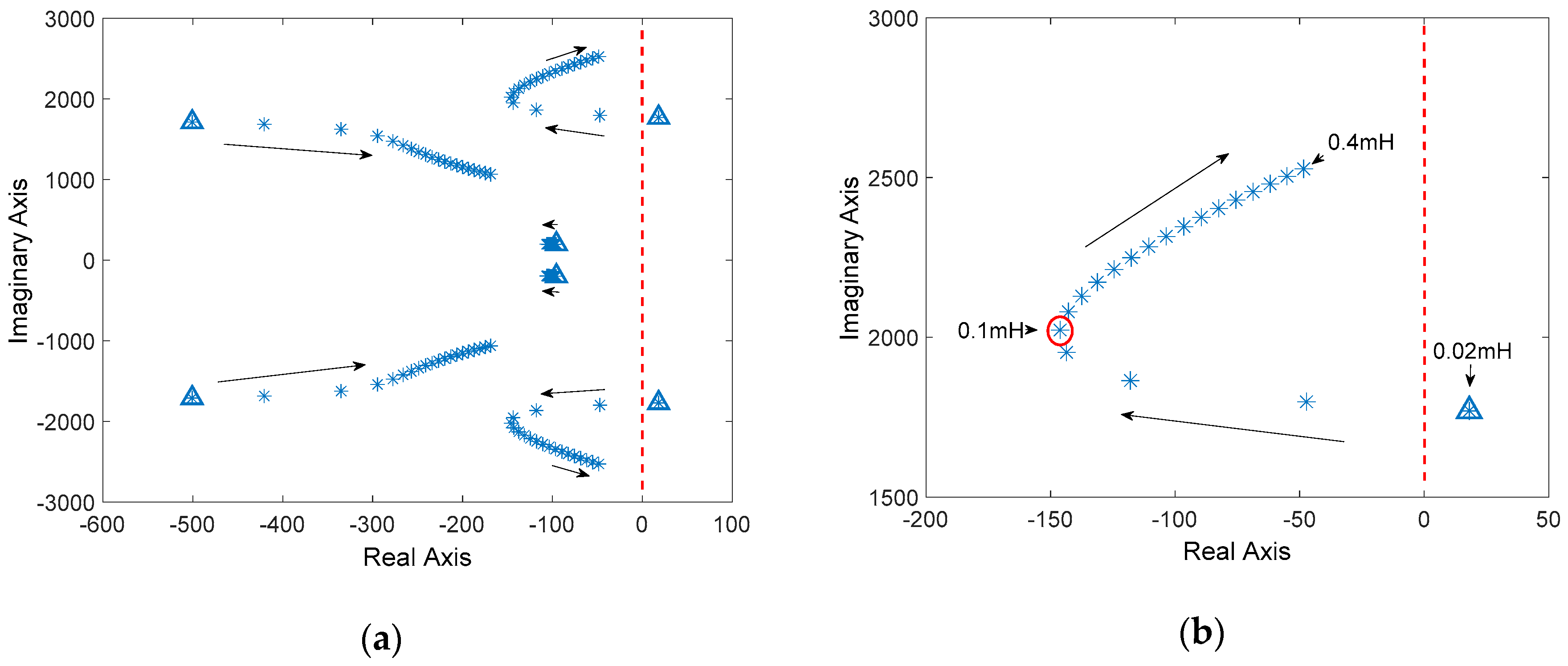
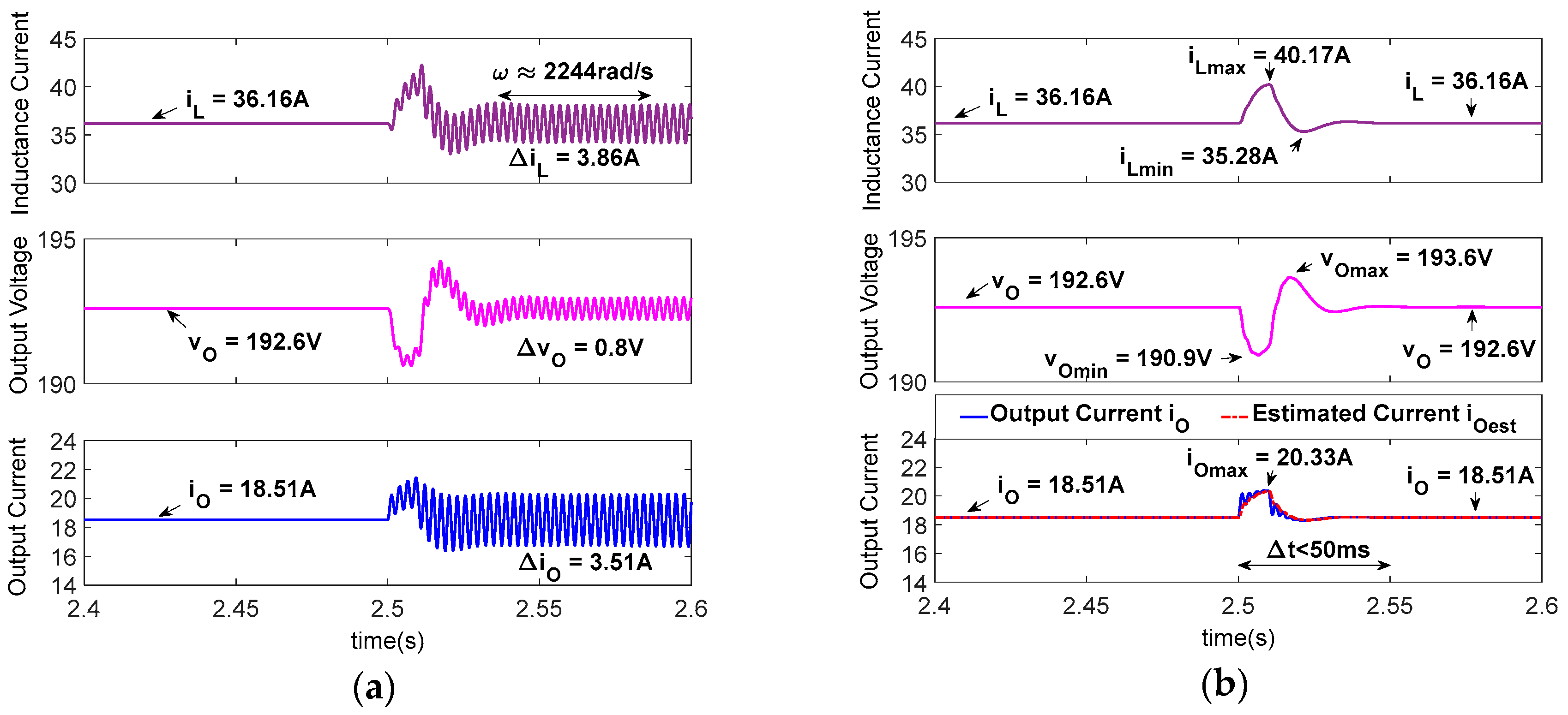
4.3.3. Case 3: CPL-side Capacitance Perturbation
5. Numerical Simulations
5.1. Effectiveness Validation
5.2. Test of Droop Coefficient Variation
5.3. Test of CPL-Side Capacitance Variations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (a)
- the NDO observer gain satisfies
- (b)
- and the disturbance signal tends to be constant as the time goes to the infinitythe NDO estimation error shown in (A8) will have a ultimate asymptotically stable point at , which means that the estimated current will eventually converge to the real one .
Appendix B
References
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part II: A Review of Power Architectures, Applications, and Standardization Issues. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y.W.; Tian, H.; Wu, X. Energy Management Strategy of Multiple Supercapacitors in a DC Microgrid Using Adaptive Virtual Impedance. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1174–1185. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An Improved Droop Control Method for DC Microgrids Based on Low Bandwidth Communication with DC Bus Voltage Restoration and Enhanced Current Sharing Accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1812. [Google Scholar] [CrossRef]
- Gu, Y.; Xiang, X.; Li, W.; He, X. Mode-Adaptive Decentralized Control for Renewable DC Microgrid with Enhanced Reliability and Flexibility. IEEE Trans. Power Electron. 2014, 29, 5072–5080. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G.; Guerrero, J.M. Distributed Control to Ensure Proportional Load Sharing and Improve Voltage Regulation in Low-Voltage DC Microgrids. IEEE Trans. Power Electron. 2013, 28, 1900–1913. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.-R.I. Assessment and Mitigation of Interaction Dynamics in Hybrid AC/DC Distribution Generation Systems. IEEE Trans. Smart Grid 2012, 3, 1382–1393. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Garci de Vicuna, L.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids-A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Liu, S.; Su, P.; Zhang, L. A Virtual Negative Inductor Stabilizing Strategy for DC Microgrid with Constant Power Loads. IEEE Access 2018, 6, 59728–59741. [Google Scholar] [CrossRef]
- Singh, S.; Gautam, A.R.; Fulwani, D. Constant power loads and their effects in DC distributed power systems: A review. Renew. Sustain. Energy Rev. 2017, 72, 407–421. [Google Scholar] [CrossRef]
- Hossain, E.; Perez, R.; Padmanaban, S.; Siano, P. Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids. Energies 2017, 10, 1086. [Google Scholar] [CrossRef]
- Al-Nussairi, M.K.; Bayindir, R.; Padmanaban, S.; Mihet-Popa, L.; Siano, P. Constant Power Loads (CPL) with Microgrids: Problem Definition, Stability Analysis and Compensation Techniques. Energies 2017, 10, 1656. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L.; Wang, J. Stability Enhancement Based on Virtual Impedance for DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2015, 6, 2770–2783. [Google Scholar] [CrossRef]
- Cespedes, M.; Xing, L.; Sun, J. Constant-Power Load System Stabilization by Passive Damping. IEEE Trans. Power Electron. 2011, 26, 1832–1836. [Google Scholar] [CrossRef]
- Kwasinski, A.; Onwuchekwa, C.N. Dynamic Behavior and Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2011, 26, 822–834. [Google Scholar] [CrossRef]
- Mohamed, Y.A.-R.I.; Radwan, A.A.A.; Lee, T.K. Decoupled Reference-Voltage-Based Active DC-Link Stabilization for PMSM Drives with Tight-Speed Regulation. IEEE Trans. Ind. Electron. 2012, 59, 4523–4536. [Google Scholar] [CrossRef]
- Huddy, S.R.; Skufca, J.D. Amplitude Death Solutions for Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2013, 28, 247–253. [Google Scholar] [CrossRef]
- Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S. Active Stabilization of DC Microgrids Without Remote Sensors for More Electric Aircraft. IEEE Trans. Ind. Appl. 2013, 49. [Google Scholar] [CrossRef]
- Lee, W.-J.; Sul, S.-K. DC-Link Voltage Stabilization for Reduced DC-Link Capacitor Inverter. IEEE Trans. Ind. Appl. 2014, 50, 404–414. [Google Scholar] [CrossRef]
- Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S. Dynamic Consideration of DC Microgrids with Constant Power Loads and Active Damping System-A Design Method for Fault-Tolerant Stabilizing System. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 562–570. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Guo, L.; Li, Y.W. A Nonlinear-Disturbance-Observer-Based DC-Bus Voltage Control for a Hybrid AC/DC Microgrid. IEEE Trans. Power Electron. 2014, 29, 6162–6177. [Google Scholar] [CrossRef]
- Solsona, J.A.; Gomez Jorge, S.; Busada, C.A. Nonlinear Control of a Buck Converter Which Feeds a Constant Power Load. IEEE Trans. Power Electron. 2015, 30, 7193–7201. [Google Scholar] [CrossRef]
- Zadeh, M.K.; Gavagsaz-Ghoachani, R.; Pierfederici, S.; Nahid-Mobarakeh, B.; Molinas, M. Stability Analysis and Dynamic Performance Evaluation of a Power Electronics-Based DC Distribution System with Active Stabilizer. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 93–102. [Google Scholar] [CrossRef]
- Gao, F.; Bozhko, S.; Costabeber, A.; Asher, G.; Wheeler, P. Control Design and Voltage Stability Analysis of a Droop-Controlled Electrical Power System for More Electric Aircraft. IEEE Trans. Ind. Electron. 2017, 64, 9271–9281. [Google Scholar] [CrossRef]
- Gao, F.; Bozhko, S.; Costabeber, A.; Patel, C.; Wheeler, P.; Hill, C.I.; Asher, G. Comparative Stability Analysis of Droop Control Approaches in Voltage-Source-Converter-Based DC Microgrids. IEEE Trans. Power Electron. 2017, 32, 2395–2415. [Google Scholar] [CrossRef]
- Hosseinipour, A.; Hojabri, H. Virtual inertia control of PV systems for dynamic performance and damping enhancement of DC microgrids with constant power loads. IET Renew. Power Gener. 2018, 12, 430–438. [Google Scholar] [CrossRef]
- Huangfu, Y.; Pang, S.; Nahid-Mobarakeh, B.; Guo, L.; Rathore, A.K.; Gao, F. Stability Analysis and Active Stabilization of On-board DC Power Converter System with Input Filter. IEEE Trans. Ind. Electron. 2018, 65, 790–799. [Google Scholar] [CrossRef]
- Rahimi, A.M.; Emadi, A. Active Damping in DC/DC Power Electronic Converters: A Novel Method to Overcome the Problems of Constant Power Loads. IEEE Trans. Ind. Electron. 2009, 56, 1428–1439. [Google Scholar] [CrossRef]
- Liutanakul, P.; Awan, A.-B.; Pierfederici, S.; Nahid-Mobarakeh, B.; Meibody-Tabar, F. Linear Stabilization of a DC Bus Supplying a Constant Power Load: A General Design Approach. IEEE Trans. Power Electron. 2010, 25, 475–488. [Google Scholar] [CrossRef]
- Magne, P.; Marx, D.; Nahid-Mobarakeh, B.; Pierfederici, S. Large-Signal Stabilization of a DC-Link Supplying a Constant Power Load Using a Virtual Capacitor: Impact on the Domain of Attraction. IEEE Trans. Ind. Appl. 2012, 48, 878–887. [Google Scholar] [CrossRef]
- Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S. General Active Global Stabilization of Multiloads DC-Power Networks. IEEE Trans. Power Electron. 2012, 27, 1788–1798. [Google Scholar] [CrossRef]
- Maheshwari, R.; Munk-Nielsen, S.; Lu, K. An Active Damping Technique for Small DC-Link Capacitor Based Drive System. IEEE Trans. Ind. Inform. 2013, 9, 848–858. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Ha, D. A Sliding-Mode Duty-Ratio Controller for DC/DC Buck Converters with Constant Power Loads. IEEE Trans. Ind. Appl. 2014, 50, 1448–1458. [Google Scholar] [CrossRef]
- Hossain, E.; Perez, R.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Ramachandaramurthy, V.K. Sliding Mode Controller and Lyapunov Redesign Controller to Improve Microgrid Stability: A Comparative Analysis with CPL Power Variation. Energies 2017, 10, 1959. [Google Scholar] [CrossRef]
- Zhang, X.; Vilathgamuwa, D.M.; Tseng, K.-J.; Bhangu, B.S.; Gajanayake, C.J. Power Buffer with Model Predictive Control for Stability of Vehicular Power Systems with Constant Power Loads. IEEE Trans. Power Electron. 2013, 28, 5804–5812. [Google Scholar] [CrossRef]
- Sulligoi, G.; Bosich, D.; Giadrossi, G.; Zhu, L.; Cupelli, M.; Monti, A. Multiconverter Medium Voltage DC Power Systems on Ships: Constant-Power Loads Instability Solution Using Linearization via State Feedback Control. IEEE Trans. Smart Grid 2014, 5, 2543–2552. [Google Scholar] [CrossRef]
- Rahimi, A.M.; Williamson, G.A.; Emadi, A. Loop-Cancellation Technique: A Novel Nonlinear Feedback to Overcome the Destabilizing Effect of Constant-Power Loads. IEEE Trans. Veh. Technol. 2010, 59, 650–661. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtual-Impedance-Based Control for Voltage-Source and Current-Source Converters. IEEE Trans. Power Electron. 2015, 30, 7019–7037. [Google Scholar] [CrossRef]
- Wu, M.; Lu, D.D.-C. A Novel Stabilization Method of LC Input Filter with Constant Power Loads Without Load Performance Compromise in DC Microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4552–4562. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, X.; Tse, C.K. Impedance-Based Local Stability Criterion for DC Distributed Power Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 916–925. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, S.; Li, X.; Li, Y.W.; Wang, C.; Feng, Y. Stability Analysis and Damping Enhancement Based on Frequency-Dependent Virtual Impedance for DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 338–350. [Google Scholar] [CrossRef]
- Prabhakaran, P.; Goyal, Y.; Agarwal, V. Novel Nonlinear Droop Control Techniques to Overcome the Load Sharing and Voltage Regulation Issues in DC Microgrid. IEEE Trans. Power Electron. 2018, 33, 4477–4487. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, G.; Xu, D.; Xiao, D. An Active Damping Control Method for Reduced DC-Link Capacitance IPMSM Drives. IEEE Trans. Ind. Electron. 2018, 65, 2057–2068. [Google Scholar] [CrossRef]
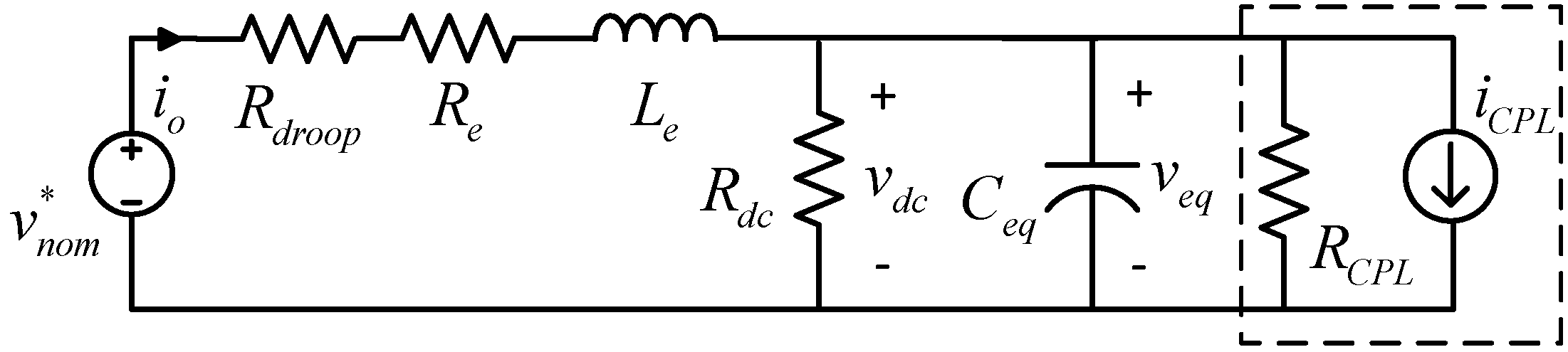

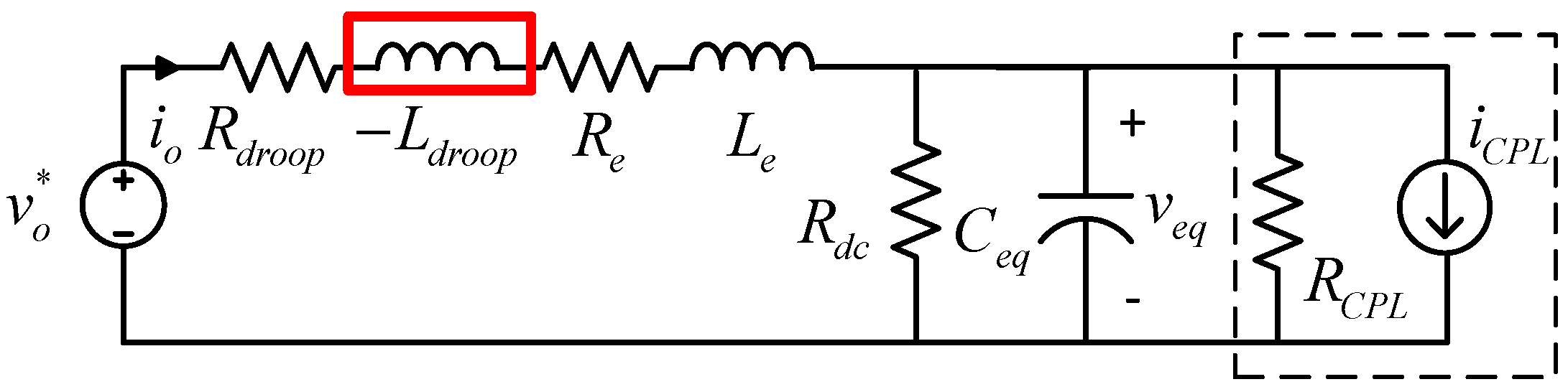
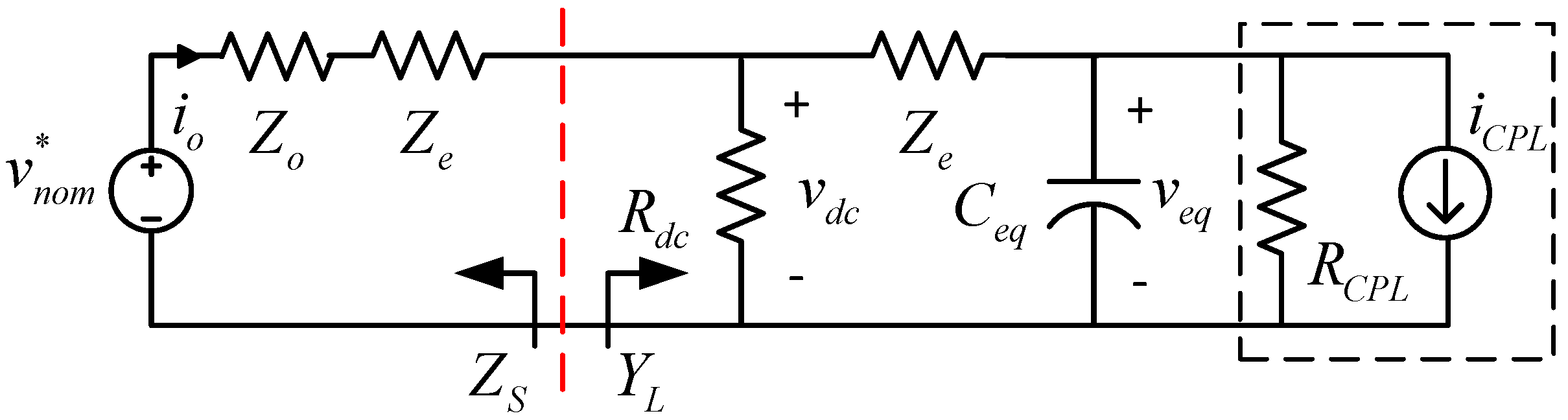


| Variables | Description | Value |
|---|---|---|
| source voltage | 100 V | |
| dc bus nominal voltage | 200 V | |
| source converter input inductance | 2 mH | |
| source converter input resistance | 0.04 | |
| source converter output capacitance | 2200 | |
| line resistance | 0.1 | |
| line inductance | 0.1 mH | |
| CPL-side capacitance | 2200 | |
| resistive load | 60 | |
| nominal power of dc/dc converter | 5 kW | |
| switching frequency | 10 kHz | |
| natural frequency of the inductance current loop | 2000 rad/s | |
| natural frequency of the output voltage loop | 400 rad/s | |
| damping ratio of the inductance current loop | 0.5 | |
| damping ratio of the output voltage loop | 0.5 | |
| proportional coefficient of the inductance current controller | 0.02 | |
| integral coefficient of the inductance current controller | 40 | |
| proportional coefficient of the output voltage controller | 1.76 | |
| integral coefficient of the output voltage controller | 704 |
| Variables | Description | Value |
|---|---|---|
| Droop coefficient for the source converter | 0.4 | |
| Optimal value of the virtual negative inductor | 0.1 mH | |
| Optimal value of the NDO time constant | 1.2 ms | |
| Optimal value of the low pass filter time constant | 0.08 ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Su, P.; Zhang, L. A Nonlinear Disturbance Observer Based Virtual Negative Inductor Stabilizing Strategy for DC Microgrid with Constant Power Loads. Energies 2018, 11, 3174. https://doi.org/10.3390/en11113174
Liu S, Su P, Zhang L. A Nonlinear Disturbance Observer Based Virtual Negative Inductor Stabilizing Strategy for DC Microgrid with Constant Power Loads. Energies. 2018; 11(11):3174. https://doi.org/10.3390/en11113174
Chicago/Turabian StyleLiu, Sheng, Peng Su, and Lanyong Zhang. 2018. "A Nonlinear Disturbance Observer Based Virtual Negative Inductor Stabilizing Strategy for DC Microgrid with Constant Power Loads" Energies 11, no. 11: 3174. https://doi.org/10.3390/en11113174
APA StyleLiu, S., Su, P., & Zhang, L. (2018). A Nonlinear Disturbance Observer Based Virtual Negative Inductor Stabilizing Strategy for DC Microgrid with Constant Power Loads. Energies, 11(11), 3174. https://doi.org/10.3390/en11113174





