Numerical Investigation of Gas-Liquid Two-Phase Flow inside PEMFC Gas Channels with Rectangular and Trapezoidal Cross Sections
Abstract
:1. Introduction
2. Model Formulation
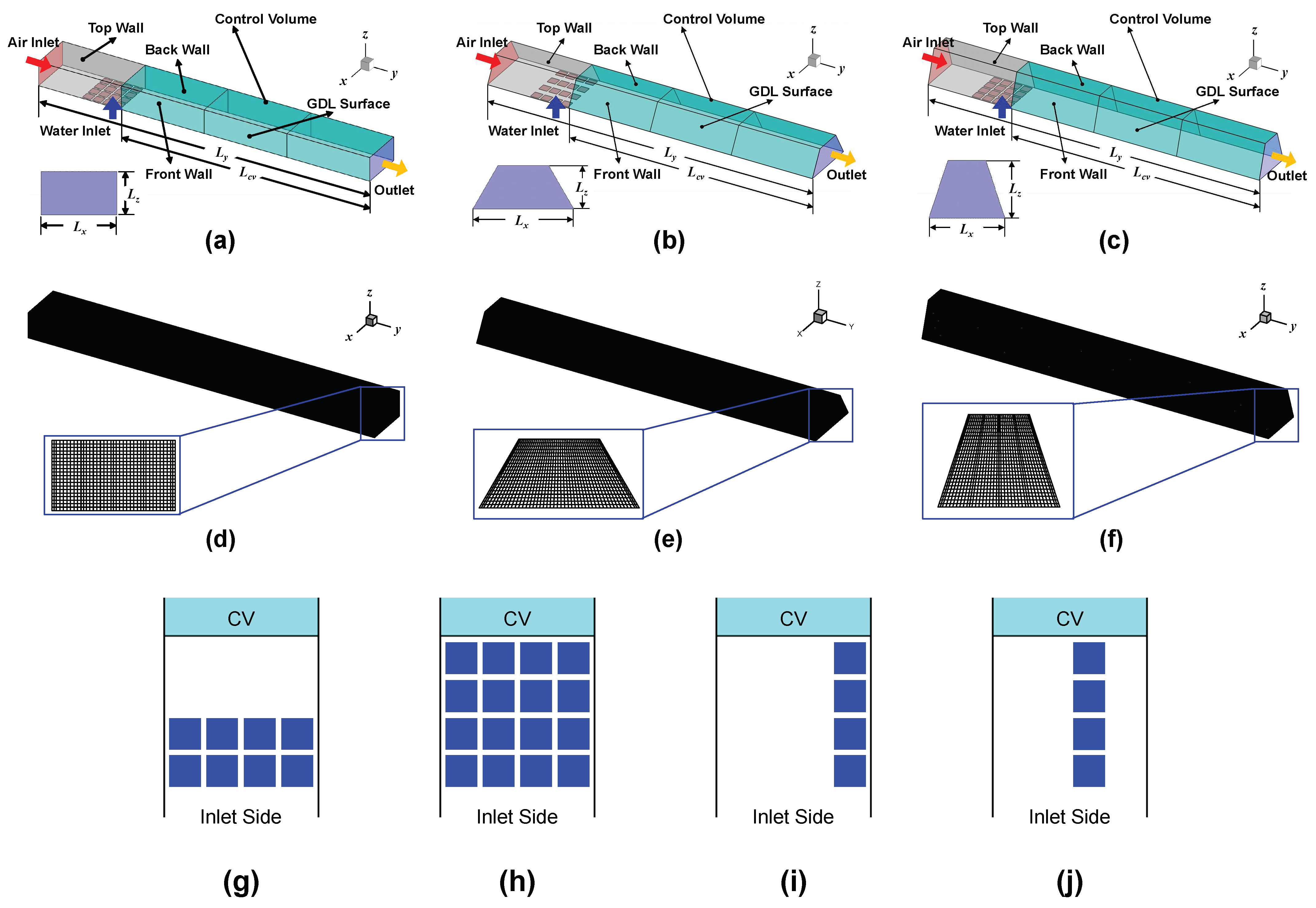
2.1. Computational Domain
2.2. Numerical Method
2.3. Boundary, Initial, and Operating Conditions
3. Results and Discussion
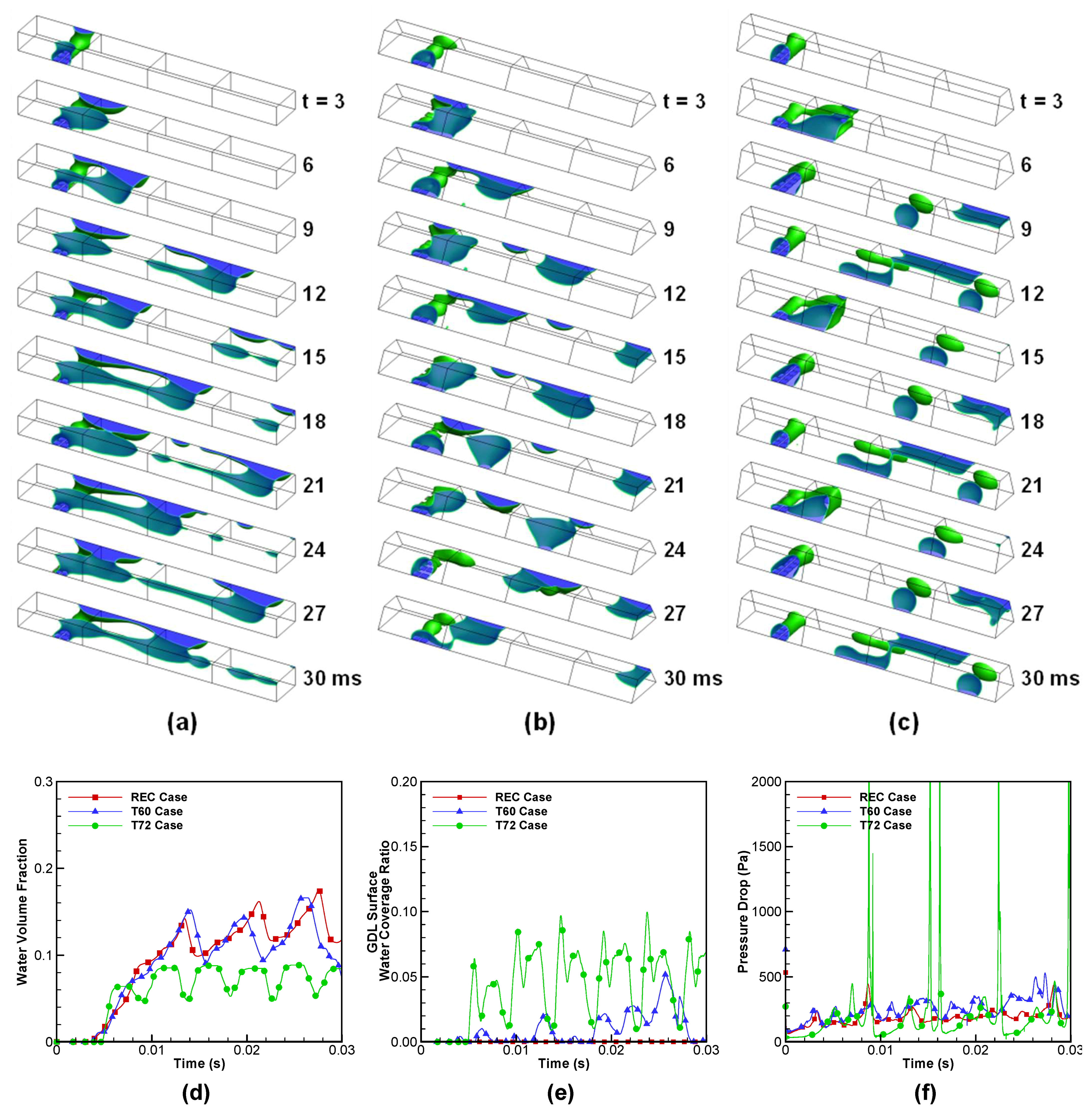
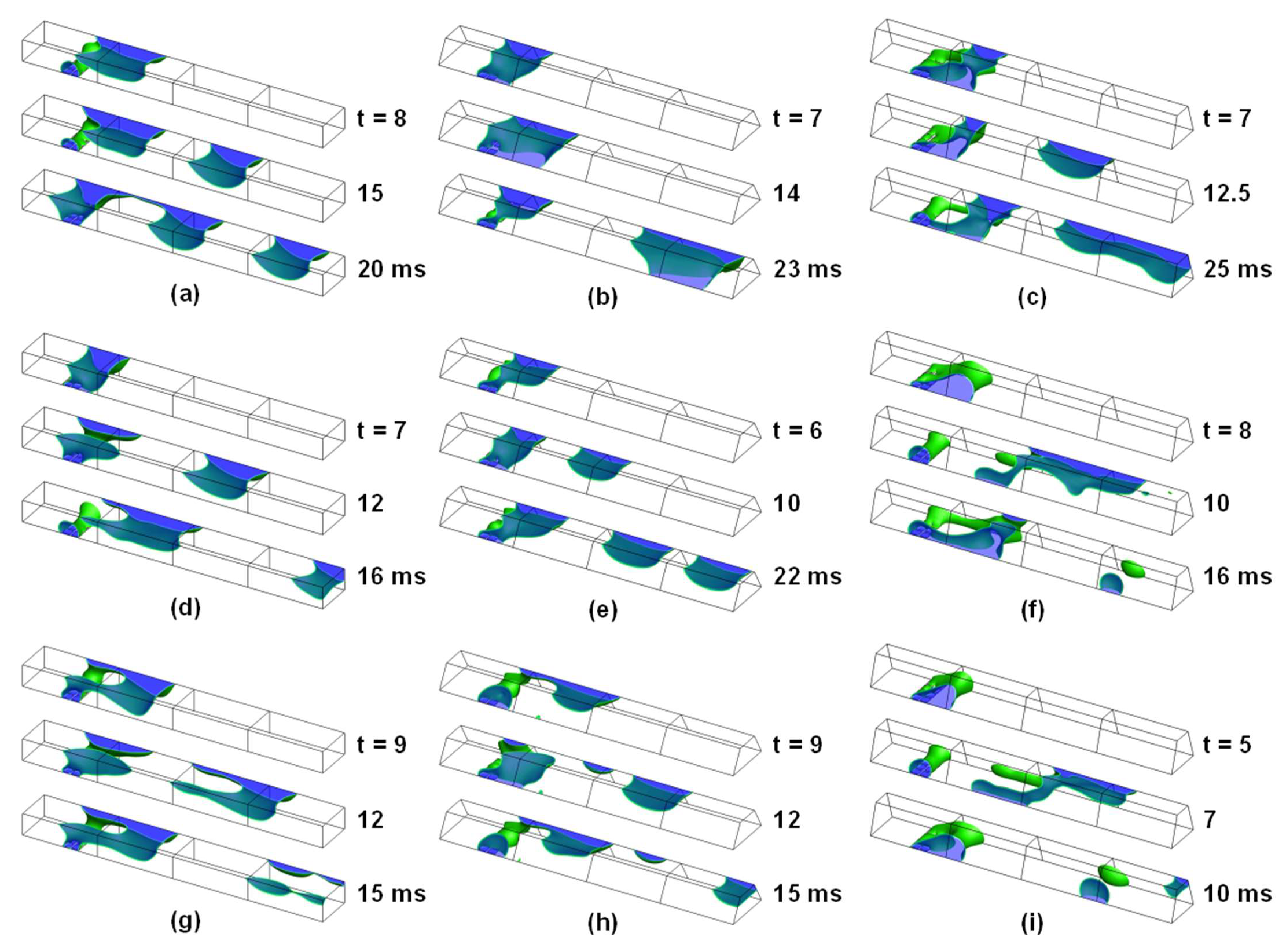
3.1. Temporal Evolution of Gas-Liquid Two-Phase Flow Pattern
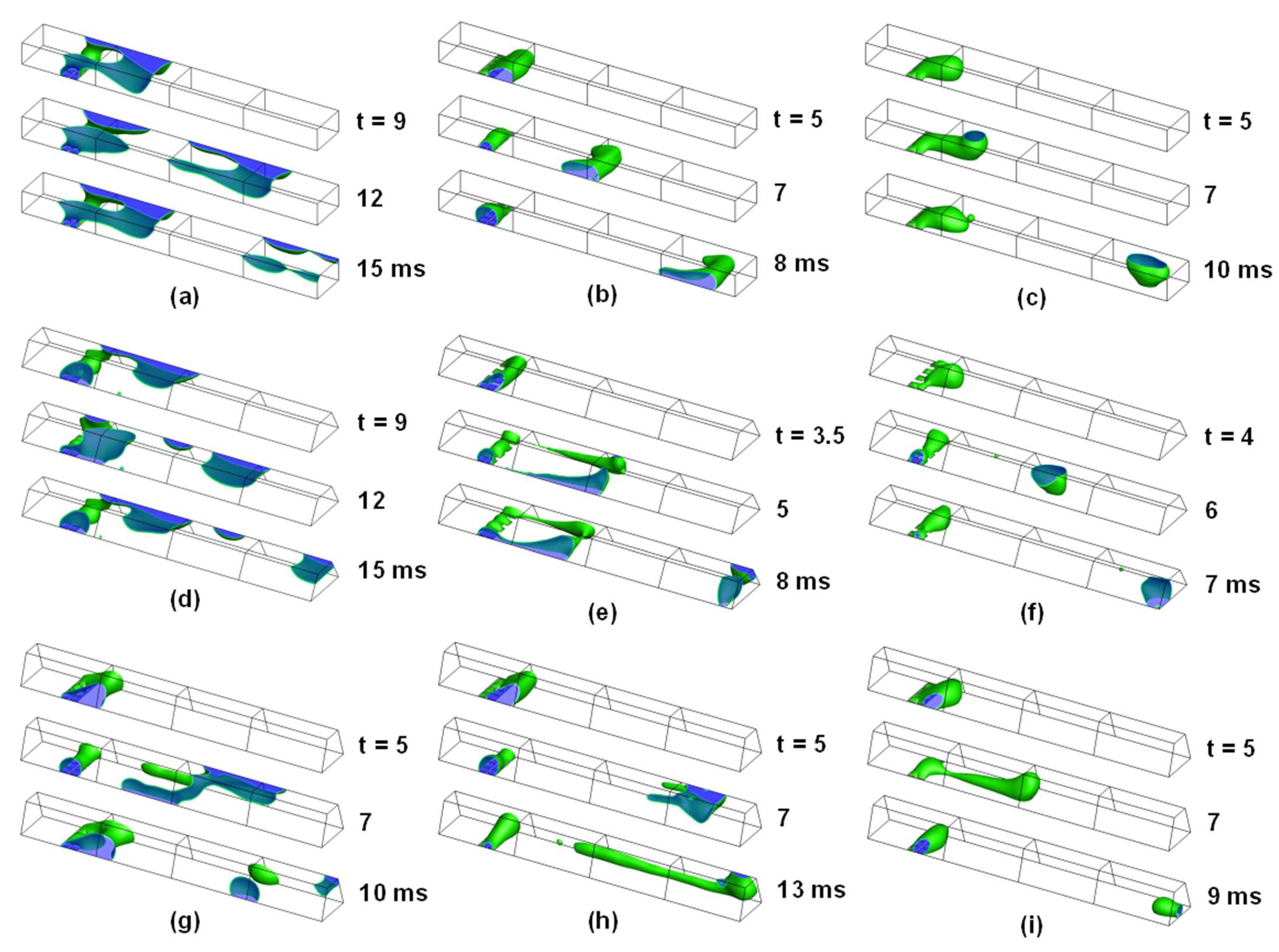
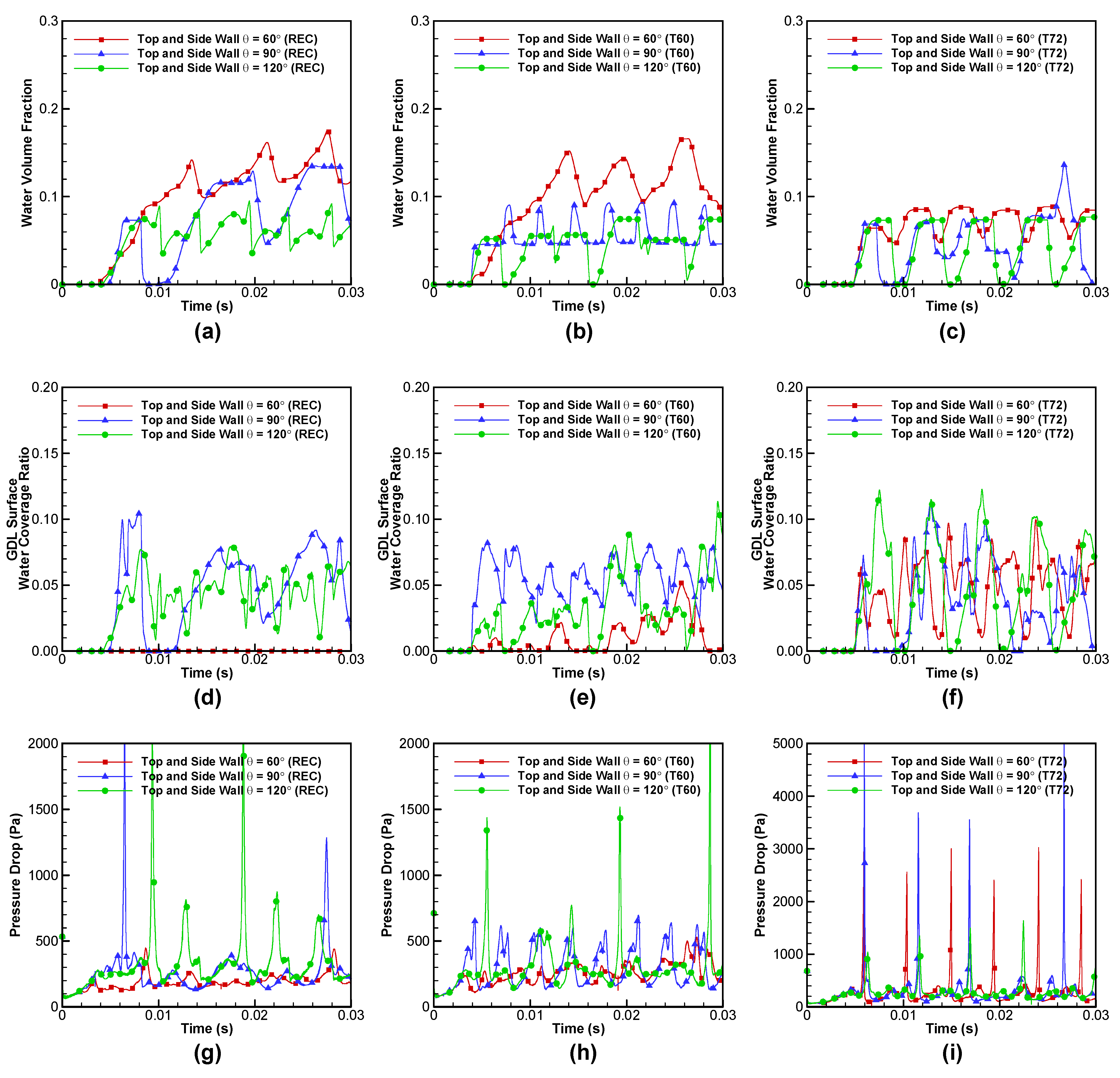
3.2. Effect of Surface Contact Angle of Top and Side Walls
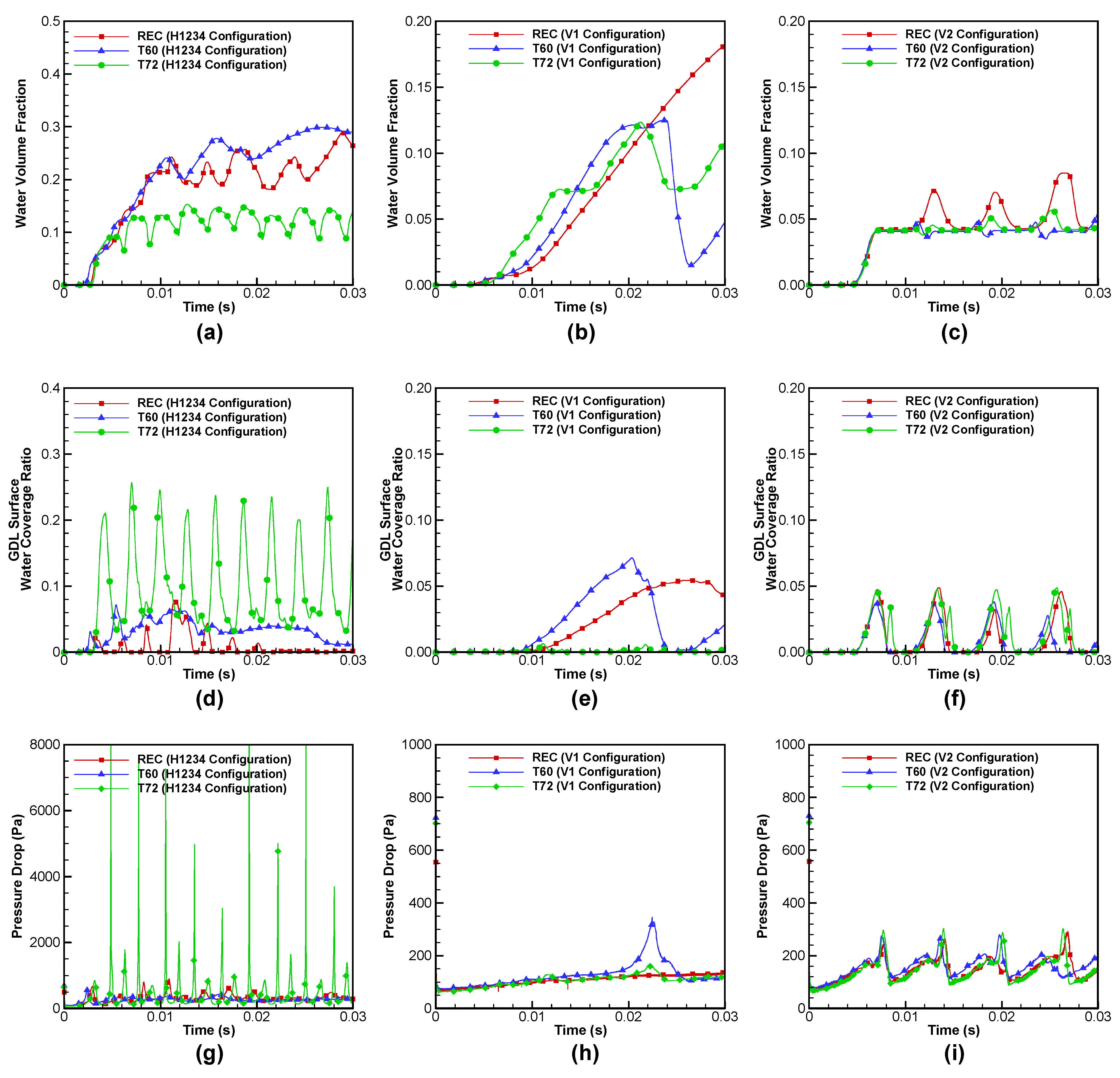
3.3. Effect of Water Inlet Configuration
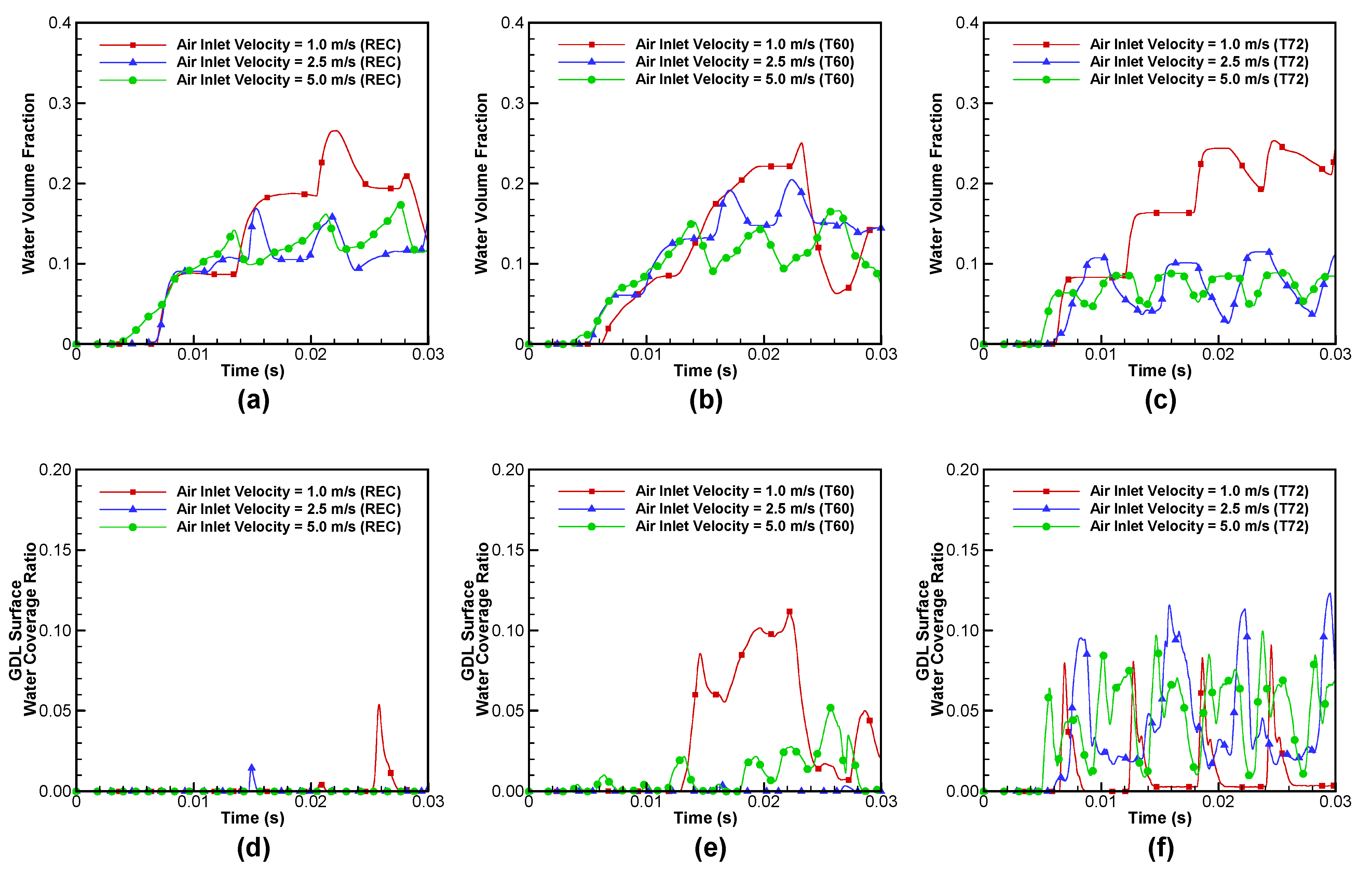
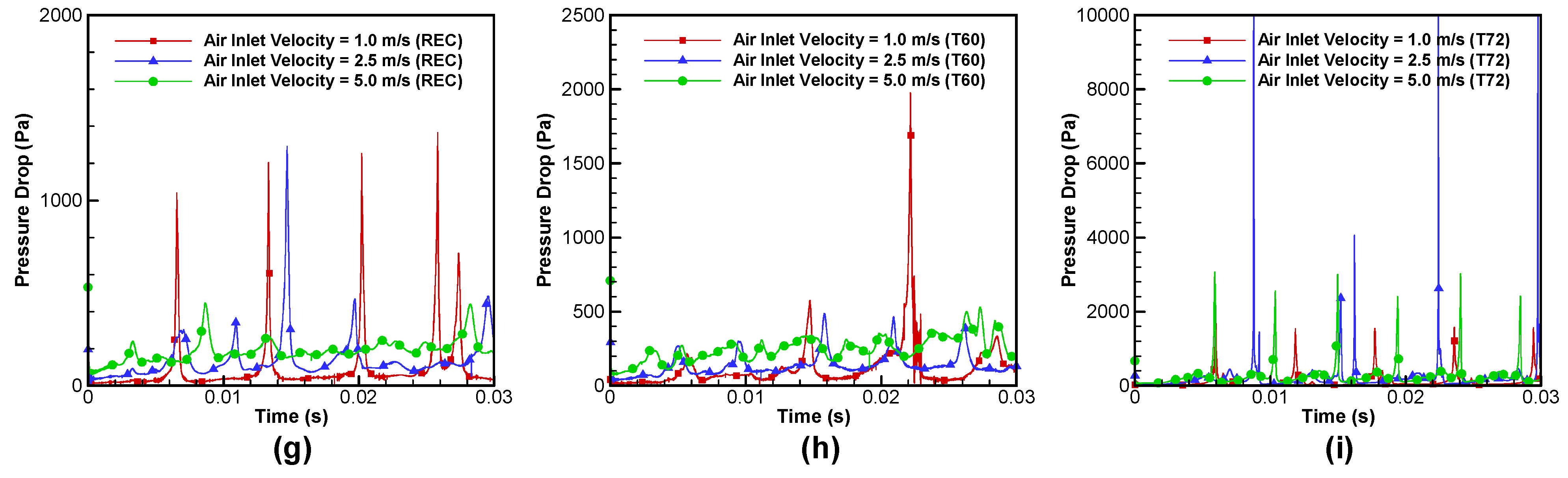
3.4. Effect of Air Inlet Velocity
4. Conclusions
- (1)
- For the hydrophobic GDL surface and the hydrophilic top and side walls, the trapezoidal channel with open angles of 72° provides the lowest water volume fraction and the water coverage ratio of the GDL surface around 7% due to the action of periodic pressure spikes. The other two cases show a higher water volume fraction and a lower water coverage ratio of the GDL surface as most of liquid water moves along the channel while attached to the top wall.
- (2)
- As the contact angle of top and side walls increases from 60° to 120°, the patterns of liquid water dynamics become similar for all the three cross-sectional shapes. In particular, the trapezoidal cross section with open angles of 72° produces similar results irrespective of the contact angle of top and side walls.
- (3)
- When the liquid water emergence is concentrated along the side wall, the trapezoidal cross section with open angles of 72° shows the best water removal characteristics.
- (4)
- For all the three channel cross-sectional shapes, water slugs move faster and have smaller sizes as the air inlet velocity increases.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Co | Courant number |
| Momentum source term related to surface tension, N·m−3 | |
| Gravitational acceleration vector, m·s−2 | |
| GC | Gas channel |
| GDL | Gas diffusion layer |
| GWCR | Water coverage ratio at the GDL surface |
| Unit normal vector at the interface | |
| Static pressure, N·m−2 | |
| PEM | Polymer electrolyte membrane |
| Re | Reynolds number |
| Reair | Reynolds number at the air inlet |
| Rewater | Reynolds number at the water inlet pore |
| REC | Rectangular channel cross section |
| s | Standard deviation |
| t | Time, s |
| T60 | Trapezoidal channel cross section with open angles of 60 degrees |
| T72 | Trapezoidal channel cross section with open angles of 72 degrees |
| Velocity vector, m·s−1 | |
| Velocity vector of the liquid phase, m·s−1 | |
| Air inlet velocity, m·s−1 | |
| Water inlet velocity, m·s−1 | |
| WCR | Water coverage ratio |
| WVF | Water volume fraction |
| Position vector, m | |
| Greek Symbols | |
| Volume fraction of the gas phase | |
| Volume fraction of the liquid phase | |
| Volume fraction of qth fluid | |
| Gas-liquid interface | |
| Three-dimensional Dirac delta function | |
| Surface curvature of the gas-liquid phase | |
| θ | Contact angle, degrees |
| Contact angle at the GDL surface, degrees | |
| Contact angle at the top and side wall surfaces, degrees | |
| Dynamic viscosity of the mixture, N·s·m−2 | |
| Dynamic viscosity of the gas phase, N·s·m−2 | |
| Dynamic viscosity of the liquid phase, N·s·m−2 | |
| Density of the mixture, kg·m−3 | |
| Density of the gas phase, kg·m−3 | |
| Density of the liquid phase, kg·m−3 | |
| Surface tension coefficient, N·m−1 | |
| Subscripts | |
| 1 | Gas phase |
| 2 | Liquid phase |
| g | GDL surface |
| in,air | Air inlet |
| in,water | Water inlet |
| q | Index for qth fluid |
| ts | Top and side wall surfaces |
References
- Byun, S.-J.; Wang, Z.H.; Son, J.; Kwak, D.-K.; Kwon, Y.-C. Experimental study on improvement of performance by wave form cathode channels in a PEM fuel cell. Energies 2018, 11, 319. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, X.; Chen, R.; Shangguan, X. Water transport and removal in PEMFC gas flow channel with various water droplet locations and channel surface wettability. Energies 2018, 11, 880. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Peng, L.; Zhang, J.; Shao, Z.; Huang, J.; Sun, C.; Ouyang, M.; He, X. Recent progress on the key materials and components for proton exchange membrane fuel cells in vehicle applications. Energies 2016, 9, 603. [Google Scholar] [CrossRef]
- Vinh, N.D.; Kim, H.-M. Comparison of numerical and experimental studies for flow-field optimization based on under-rib convection in polymer electrolyte membrane fuel cells. Energies 2016, 9, 844. [Google Scholar] [CrossRef]
- Anderson, R.; Zhang, L.; Ding, Y.; Blanco, M.; Bi, X.; Wilkinson, D.P. A critical review of two-phase flow in gas flow channels of proton exchange membrane fuel cells. J. Power Sources 2010, 195, 4531–4553. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Lorenzini-Gutierrez, D.; Kandlikar, S.G.; Hernandez-Guerrero, A.; Elizalde-Blancas, F. Residence time of water film and slug flow features in fuel cell gas channels and their effect on instantaneous area coverage ratio. J. Power Sources 2015, 279, 567–580. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, G.G.; Kim, W.T. Comparison of liquid water dynamics in bent gas channels of a polymer electrolyte membrane fuel cell with different channel cross sections in a channel flooding situation. Energies 2017, 10, 748. [Google Scholar] [CrossRef]
- Liu, X.; Guo, H.; Ye, F.; Ma, C.F. Water flooding and pressure drop characteristics in flow channels of proton exchange membrane fuel cells. Electrochim. Acta 2007, 52, 3607–3614. [Google Scholar] [CrossRef]
- Grimm, M.; See, E.J.; Kandlikar, S.G. Modeling gas flow in PEMFC channels: Part I—Flow pattern transitions and pressure drop in a simulated ex situ channel with uniform water injection through the GDL. Int. J. Hydrogen Energy 2012, 37, 12489–12503. [Google Scholar] [CrossRef]
- Bazylak, A. Liquid water visualization in PEM fuel cells: A review. Int. J. Hydrogen Energy 2009, 34, 3845–3857. [Google Scholar] [CrossRef]
- Ferreira, R.B.; Falcão, D.S.; Oliveira, V.B.; Pinto, A.M.F.R. Numerical simulations of two-phase flow in proton exchange membrane fuel cells using the volume of fluid method: A review. J. Power Sources 2015, 277, 329–342. [Google Scholar] [CrossRef]
- Molaeimanesh, G.R.; Googarchin, H.S.; Mqaddam, A.Q. Lattice Boltzmann simulation of proton exchange membrane fuel cells—A review on opportunities and challenges. Int. J. Hydrogen Energy 2016, 41, 22221–22245. [Google Scholar] [CrossRef]
- Manso, A.P.; Marzo, F.F.; Barranco, J.; Garikano, X.; Mujika, M.G. Influence of geometric parameters of the flow fields on the performance of a PEM fuel cell. A review. Int. J. Hydrogen Energy 2012, 37, 15256–15287. [Google Scholar] [CrossRef]
- Owejan, J.P.; Trabold, T.A.; Jacobson, D.L.; Arif, M.; Kandlikar, S.G. Effects of flow field and diffusion layer properties on water accumulation in a PEM fuel cell. Int. J. Hydrogen Energy 2007, 32, 4489–4502. [Google Scholar] [CrossRef]
- Zhu, X.; Liao, Q.; Sui, P.C.; Djilali, N. Numerical investigation of water droplet dynamics in a low-temperature fuel cell microchannel: Effect of channel geometry. J. Power Sources 2010, 195, 801–812. [Google Scholar] [CrossRef]
- Lu, Z.; Rath, C.; Zhang, G.; Kandlikar, S.G. Water management studies in PEM fuel cells, part IV: Effects of channel surface wettability, geometry and orientation on the two-phase flow in parallel gas channels. Int. J. Hydrogen Energy 2011, 36, 9864–9875. [Google Scholar] [CrossRef]
- Gopalan, P.; Kandlikar, S.G. Effect of channel materials and trapezoidal corner angles on emerging droplet behavior in proton exchange membrane fuel cell gas channels. J. Power Sources 2014, 248, 230–238. [Google Scholar] [CrossRef]
- Owejan, J.P.; Gagliardo, J.J.; Sergi, J.M.; Kandlikar, S.G. Water management studies in PEM fuel cells, Part I: Fuel cell design and in situ water distributions. Int. J. Hydrogen Energy 2009, 34, 3436–3444. [Google Scholar] [CrossRef]
- Ding, Y.; Bi, H.T.; Wilkinson, D.P. Three-dimensional numerical simulation of water droplet emerging from a gas diffusion layer surface in micro-channels. J. Power Sources 2010, 195, 7278–7288. [Google Scholar] [CrossRef]
- Jo, J.H.; Kim, W.T. Numerical simulation of water droplet dynamics in a right angle gas channel of a polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2015, 40, 8368–8383. [Google Scholar] [CrossRef]
- Gopala, V.R.; van Wachem, B.G.M. Volume of fluid methods for immiscible-fluid and free-surface flows. Chem. Eng. J. 2008, 141, 204–221. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. OpenFOAM v4 User Guide; OpenFOAM Foundation: London, UK, 2017. [Google Scholar]
- Deshpande, S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Francois, M.M.; Cummins, S.J.; Dendy, E.D.; Kothe, D.B.; Sicilian, J.M.; Williams, M.W. A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework. J. Comput. Phys. 2006, 213, 141–173. [Google Scholar] [CrossRef]
- Deshpande, S.; Trujillo, M.F.; Wu, X.; Chahine, G. Computational and experimental characterization of a liquid jet plunging into a quiescent pool at shallow inclination. Int. J. Heat Fluid Flow 2012, 34, 1–14. [Google Scholar] [CrossRef]
- Holzmann, T. SIMPLE, PISO and PIMPLE algorithm. In Mathematics, Numerics, Derivations and OpenFOAM, 4th ed.; Holzmann CFD: Leoben, Austria, 2017. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zamach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.-W.; Popov, B.N. A review of gas diffusion layer in PEM fuel cells: Materials and designs. Int. J. Hydrogen Energy 2012, 37, 5850–5865. [Google Scholar] [CrossRef]
- Gurau, V.; Bluemle, M.J.; De Castro, E.S.; Tsou, Y.-M.; Mann, J.A., Jr.; Zawodzinski, T.A., Jr. Characterization of transport properties in gas diffusion layers for proton exchange membrane fuel cells 1. Wettability (internal contact angle to water and surface energy of GDL fibers). J. Power Sources 2006, 160, 1156–1162. [Google Scholar] [CrossRef]
- Enz, S.; Dao, T.A.; Messerschmidt, M.; Scholta, J. Investigation of degradation effects in polymer electrolyte fuel cells under automotive-related operating conditions. J. Power Sources 2015, 274, 521–535. [Google Scholar] [CrossRef]
- Hossain, M.; Islam, S.Z.; Colley-Davies, A.; Adom, E. Water dynamics inside a cathode channel of a polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2013, 50, 763–779. [Google Scholar] [CrossRef]
- Quan, P.; Lai, M.-C. Numerical study of water management in the air flow channel of a PEM fuel cell cathode. J. Power Sources 2007, 164, 222–237. [Google Scholar] [CrossRef]
- Turhan, A.; Kim, S.; Hatzell, M.; Mench, M.M. Impact of channel wall hydrophobicity on through-plane water distribution and flooding behavior in a polymer electrolyte fuel cell. Electrochim. Acta 2010, 55, 2734–2745. [Google Scholar] [CrossRef]

| Reference and Published Year | GC Cross Sectional Shape | GC Flow Field Geometry | Water Introduction | Numerical Method (Software) |
|---|---|---|---|---|
| Zhu et al. [16] (2010) | Rectangle, Trapezoid, Upside-down Trapezoid, Triangle, Rectangle with a Curved Bottom Wall, Semicircle (Width 177–790 m, Height 79–354 m) | Straight GC (Length 1000 m) | Continuous water injection through a single micropore on the GDL | VOF (FLUENT 6.3.26) |
| Ding et al. [20] (2010) | Rectangle (250 m 250 m) | Straight GC (Length 1250 m) | Continuous water injection through 1–64 micropores on the GDL | VOF (FLUENT 6.3.26) |
| Lorenzini-Gutierrez et al. [7] (2015) | Rectangle, Trapezoid with open angle of 40°, Trapezoid with open angle of 50°, Trapezoid with open angle of 60°, Semi-circle (Width 700–1177 m, Height 400–422 m) | Straight GC (Length 30,000 m) | Hexahedral water slug in the GC at the start of the calculation | VOF (FLUENT 14.0) |
| Kim et al. [8] (2017) | Rectangle, Trapezoid with open angle of 50°, Trapezoid with open angle of 60° (Width 700–1036 m, Height 400 m) | Bent GC (Length 20,000 m) | Hexahedral water slug in the GC at the start of the calculation | VOF (FLUENT 14.0) |
| Present (2018) | Rectangle, Trapezoid with open angle of 60°, Trapezoid with open angle of 72° (Width 700–931 m, Height 400–533 m) | Straight GC (Length 5000 m) | Continuous water injection through 4–16 micropores on the GDL | VOF (OpenFOAM 4.1, interFoam) |
| Boundary Type | Momentum Equation | Pressure Equation | Volume Fraction Equation |
|---|---|---|---|
| Air Inlet | A fully developed laminar velocity profile (mean 5.0/2.5/1.0 m·s−1) | Fixed flux pressure condition | Constant = 0.0 |
| Water Inlet | A uniform velocity profile ( m·s−1) | Zero gradient | Constant = 1.0 |
| Outlet | Zero velocity gradient | Fixed pressure value (1 atm.) | Internal field condition |
| Wall | No slip | Fixed flux pressure condition | Constant contact angle ( = 60°/90°/120°, = 130°) |
| Air Temperature | 303.15 K | ||
| Water Temperature | 353.15 K | ||
| Dynamic Viscosity of Air | 1.86 × 10−5 N·s·m−2 | ||
| Air-water Surface Tension Coefficient | 0.0626 N·m−1 | ||
| Case | WVF | GWCR | Pressure Drop (Pa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Mean | Mean | |||||||
| REC, H12 | 0.095 | 0.051 | 0.176 | 0.000 | 0.000 | 0.001 | 191 | 60 | 534 |
| T60, H12 | 0.092 | 0.048 | 0.166 | 0.009 | 0.012 | 0.052 | 257 | 81 | 711 |
| T72, H12 | 0.060 | 0.028 | 0.089 | 0.041 | 0.028 | 0.100 | 356 | 472 | 3067 |
| REC, H1234 | 0.182 | 0.076 | 0.290 | 0.007 | 0.015 | 0.077 | 339 | 137 | 897 |
| T60, H1234 | 0.208 | 0.090 | 0.299 | 0.032 | 0.017 | 0.072 | 276 | 67 | 686 |
| T72, H1234 | 0.105 | 0.038 | 0.153 | 0.078 | 0.056 | 0.256 | 782 | 1295 | 14,855 |
| REC, V1 | 0.069 | 0.060 | 0.182 | 0.023 | 0.022 | 0.055 | 108 | 19 | 555 |
| T60, V1 | 0.051 | 0.045 | 0.125 | 0.020 | 0.022 | 0.071 | 128 | 49 | 723 |
| T72, V1 | 0.061 | 0.039 | 0.124 | 0.001 | 0.001 | 0.007 | 107 | 22 | 702 |
| REC, V2 | 0.042 | 0.023 | 0.085 | 0.009 | 0.014 | 0.049 | 150 | 41 | 558 |
| T60, V2 | 0.034 | 0.016 | 0.056 | 0.008 | 0.011 | 0.038 | 161 | 40 | 730 |
| T72, V2 | 0.035 | 0.016 | 0.057 | 0.012 | 0.015 | 0.049 | 147 | 50 | 705 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.H.; Kim, W.T. Numerical Investigation of Gas-Liquid Two-Phase Flow inside PEMFC Gas Channels with Rectangular and Trapezoidal Cross Sections. Energies 2018, 11, 1403. https://doi.org/10.3390/en11061403
Kim JH, Kim WT. Numerical Investigation of Gas-Liquid Two-Phase Flow inside PEMFC Gas Channels with Rectangular and Trapezoidal Cross Sections. Energies. 2018; 11(6):1403. https://doi.org/10.3390/en11061403
Chicago/Turabian StyleKim, Jin Hyun, and Woo Tae Kim. 2018. "Numerical Investigation of Gas-Liquid Two-Phase Flow inside PEMFC Gas Channels with Rectangular and Trapezoidal Cross Sections" Energies 11, no. 6: 1403. https://doi.org/10.3390/en11061403






