Control Oriented Prediction of Driver Brake Intention and Intensity Using a Composite Machine Learning Approach
Abstract
:1. Introduction
2. Experimental Data Collection
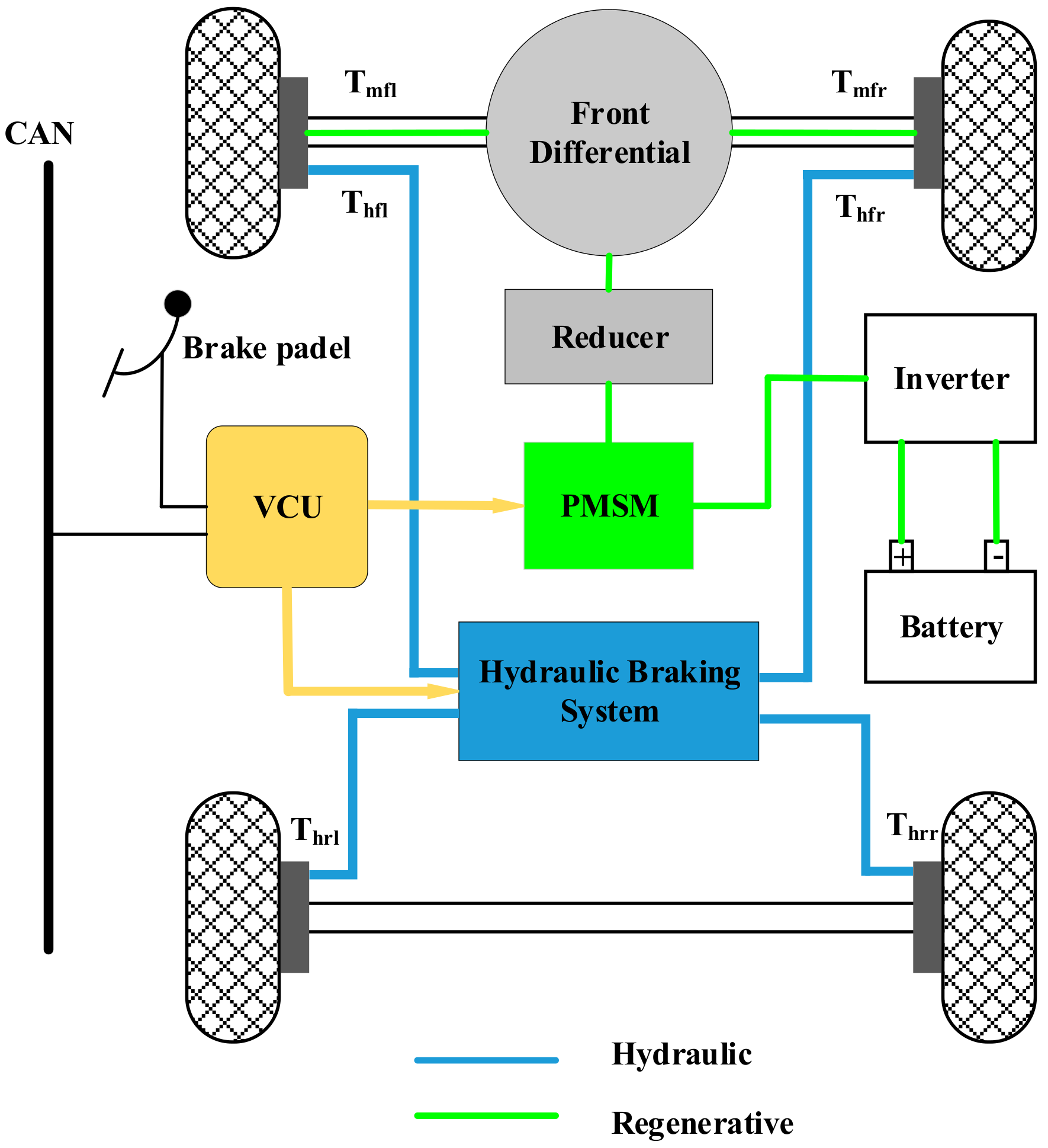
2.1. Test Vehicle and Its Braking System
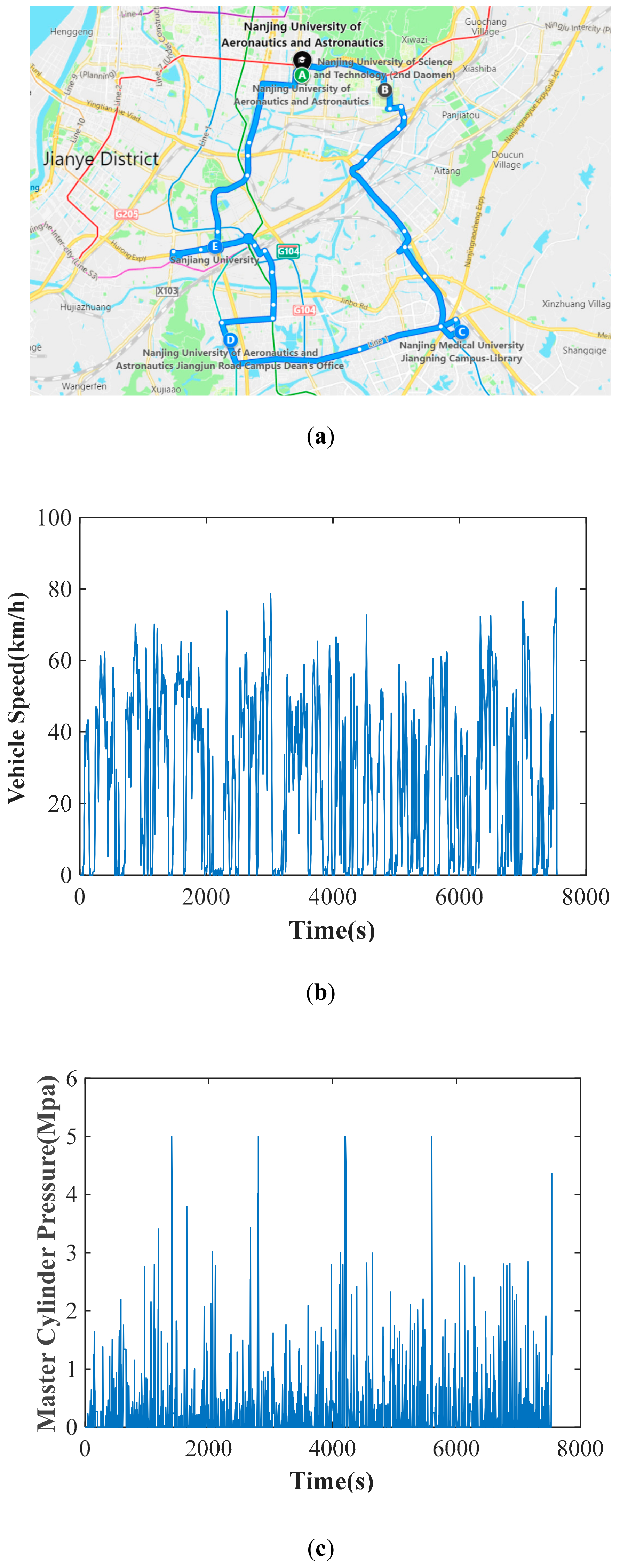
2.2. Data Collection
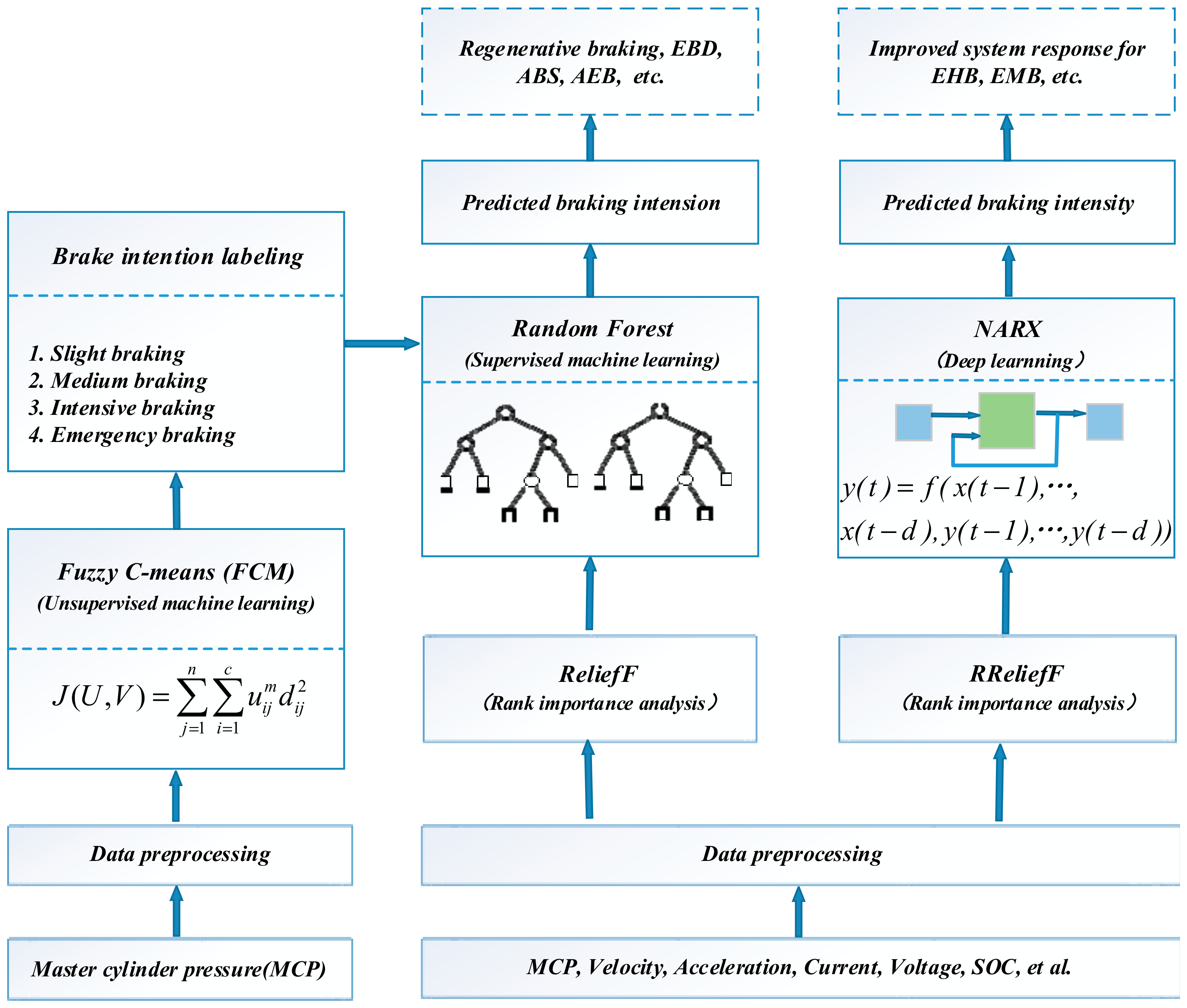
3. Hybrid Machine Learning Framework
4. Brake Intension Prediction
4.1. FCM-Based Brake Intention Labeling
4.1.1. Fuzzy C-means Clustering Algorithm
- (1)
- Randomly initialize the cluster membership values, uij.
- (2)
- Calculate the cluster centers:
- (3)
- Update uij according to the following:
- (4)
- Calculate the objective function, Jm.
- (5)
- Repeat steps 2–4 until Jm improves by less than a specified minimum threshold or until after a specified maximum number of iterations.
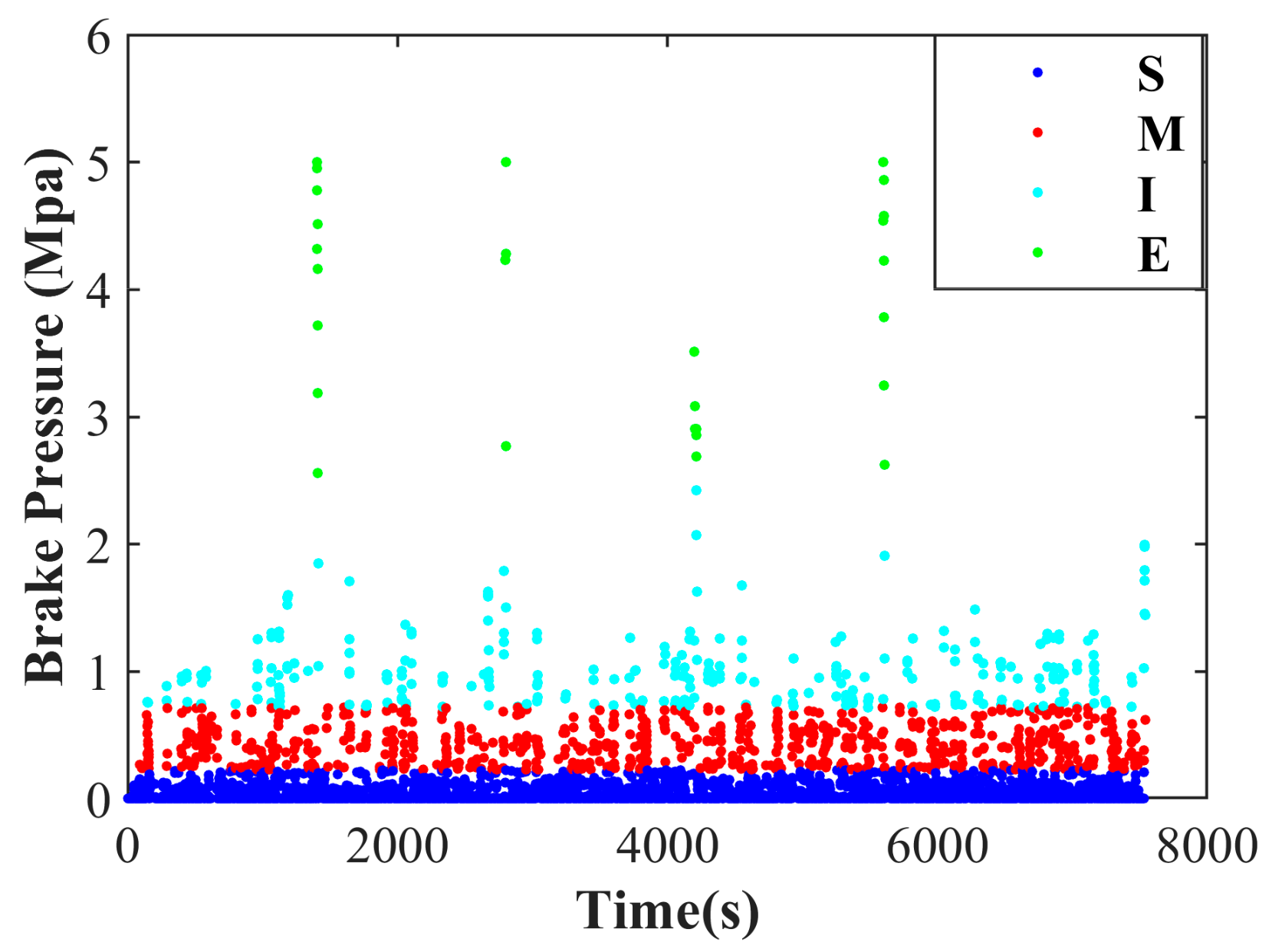
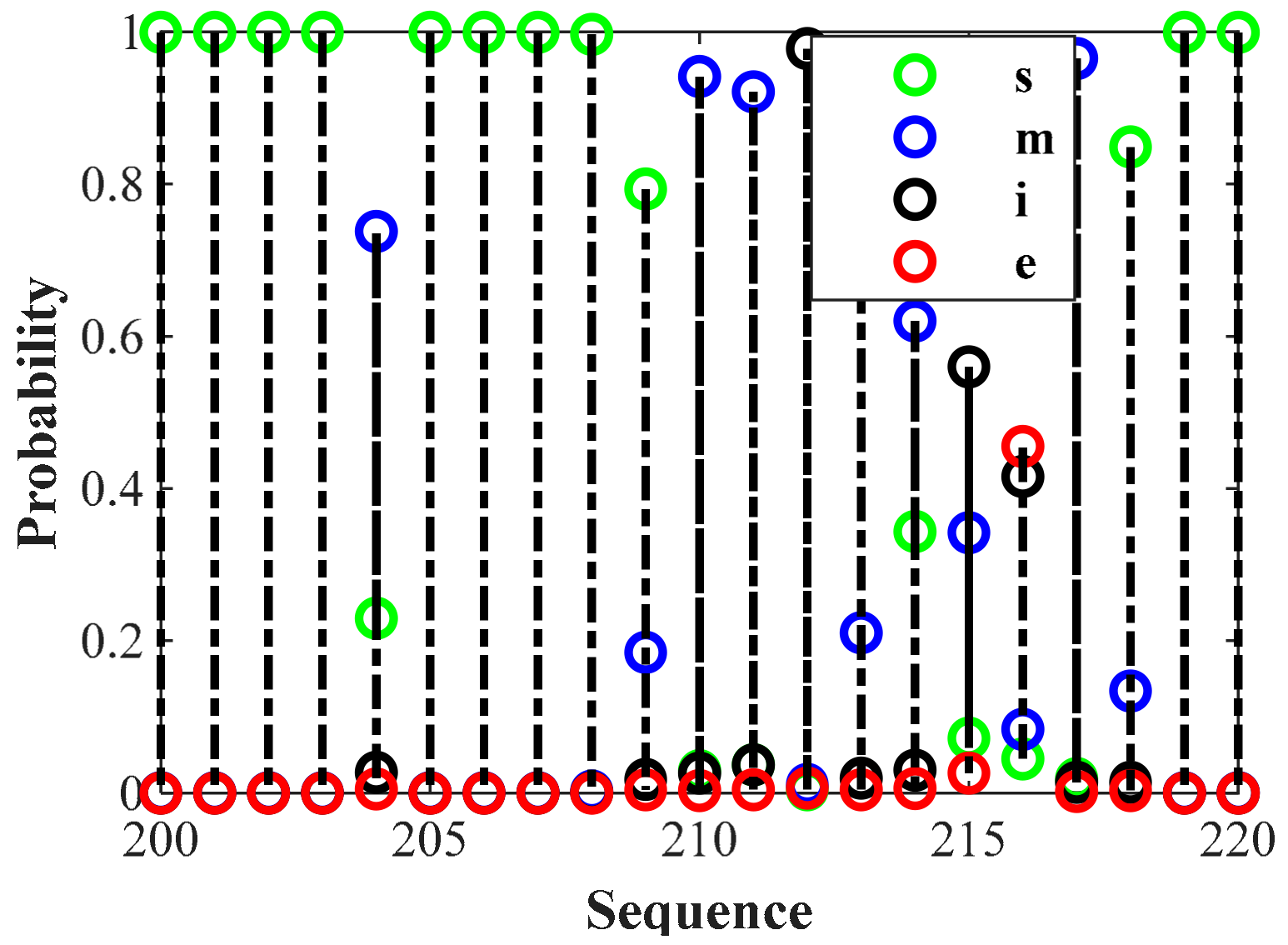
4.1.2. Brake Intention Labeling Results
4.2. ReliefF Rank Importance Analysis
4.3. RF Based Brake Intention Prediction
4.3.1. Random Forest Classification Algorithm
- (1)
- The bootstrap sampling method is used to get n of training samples from the original training samples.
- (2)
- Each training sample is trained to generate a single decision tree, and the features of the decision tree are randomly selected. The splitting rule of the decision trees is according to the CART (Classification and Regression Tree) algorithm and the minimum principle of the Gini coefficient. The Gini coefficient can be expressed as follow:where Pk is the probability of occurrence of category k.
- (3)
- Each decision tree is trained to generate a prediction result according to the randomly selected characteristics of the sample, which reduces the effects of overfitting and improves generalization.
- (4)
- All of the predicted results of the decision tree are gathered to determine the final predicted results by voting.
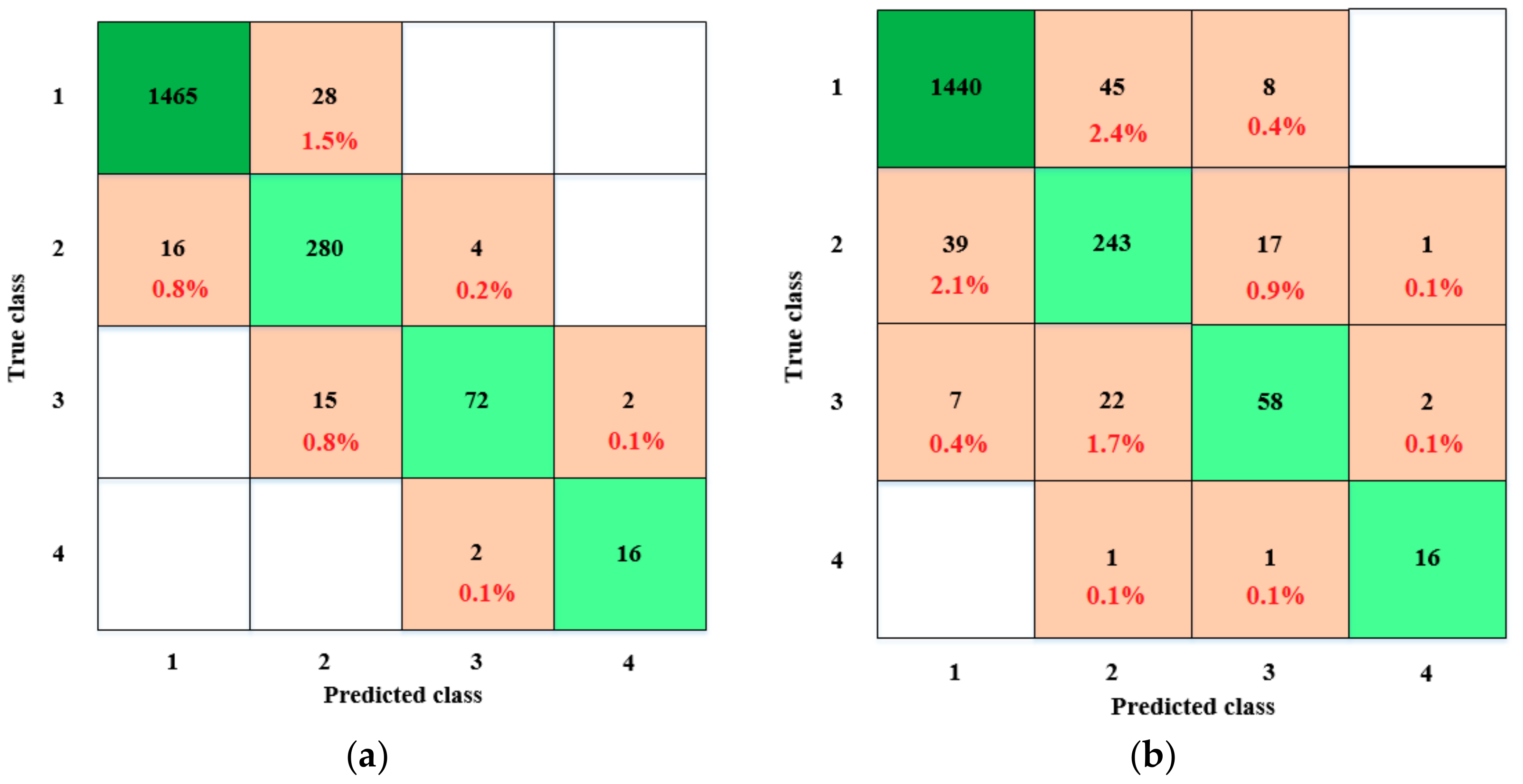
4.3.2. Performance Analysis of Brake Intention Prediction
5. Brake Intensity Prediction
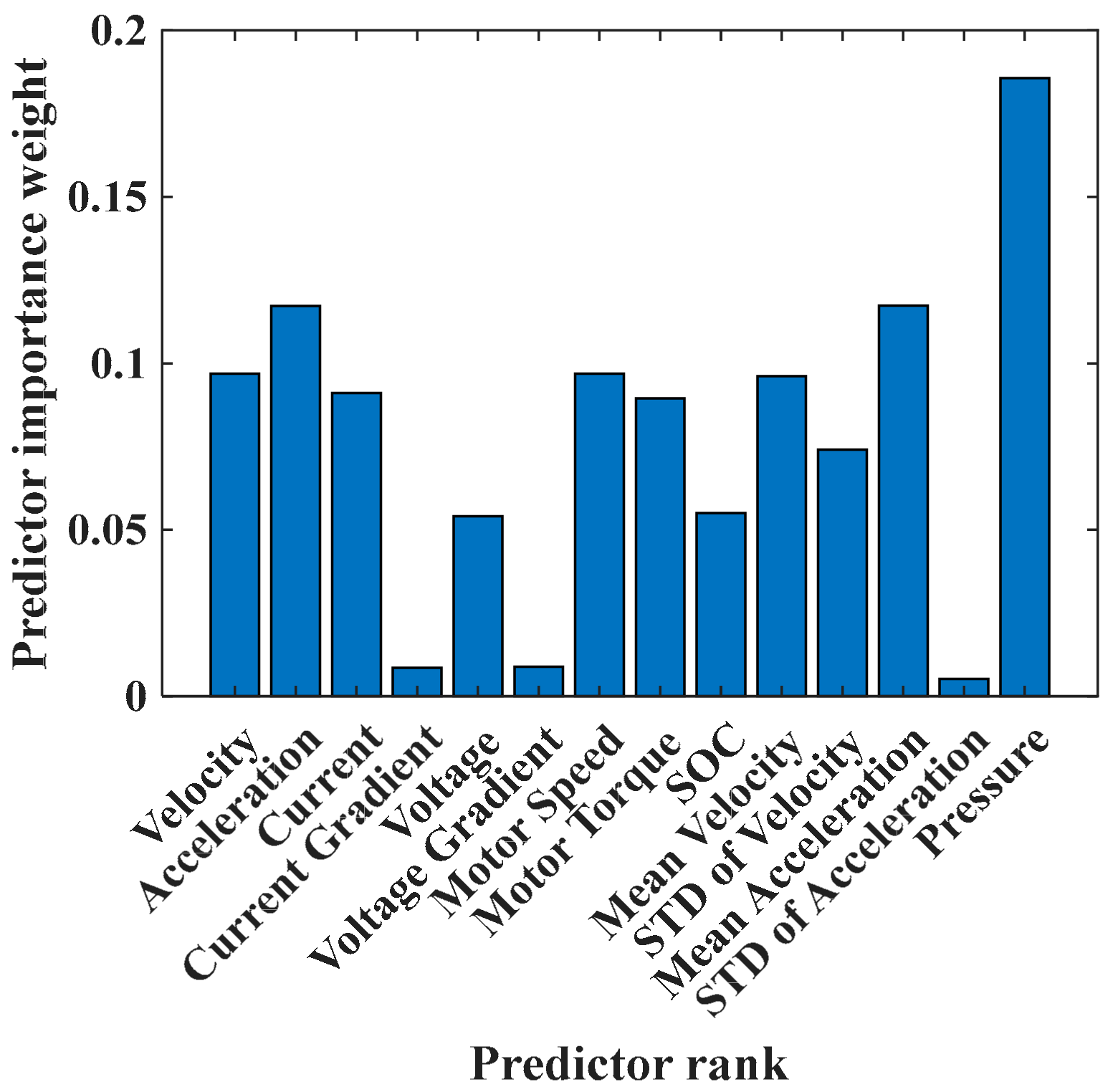
5.1. RReliefF-Based Rank Importance Analysis
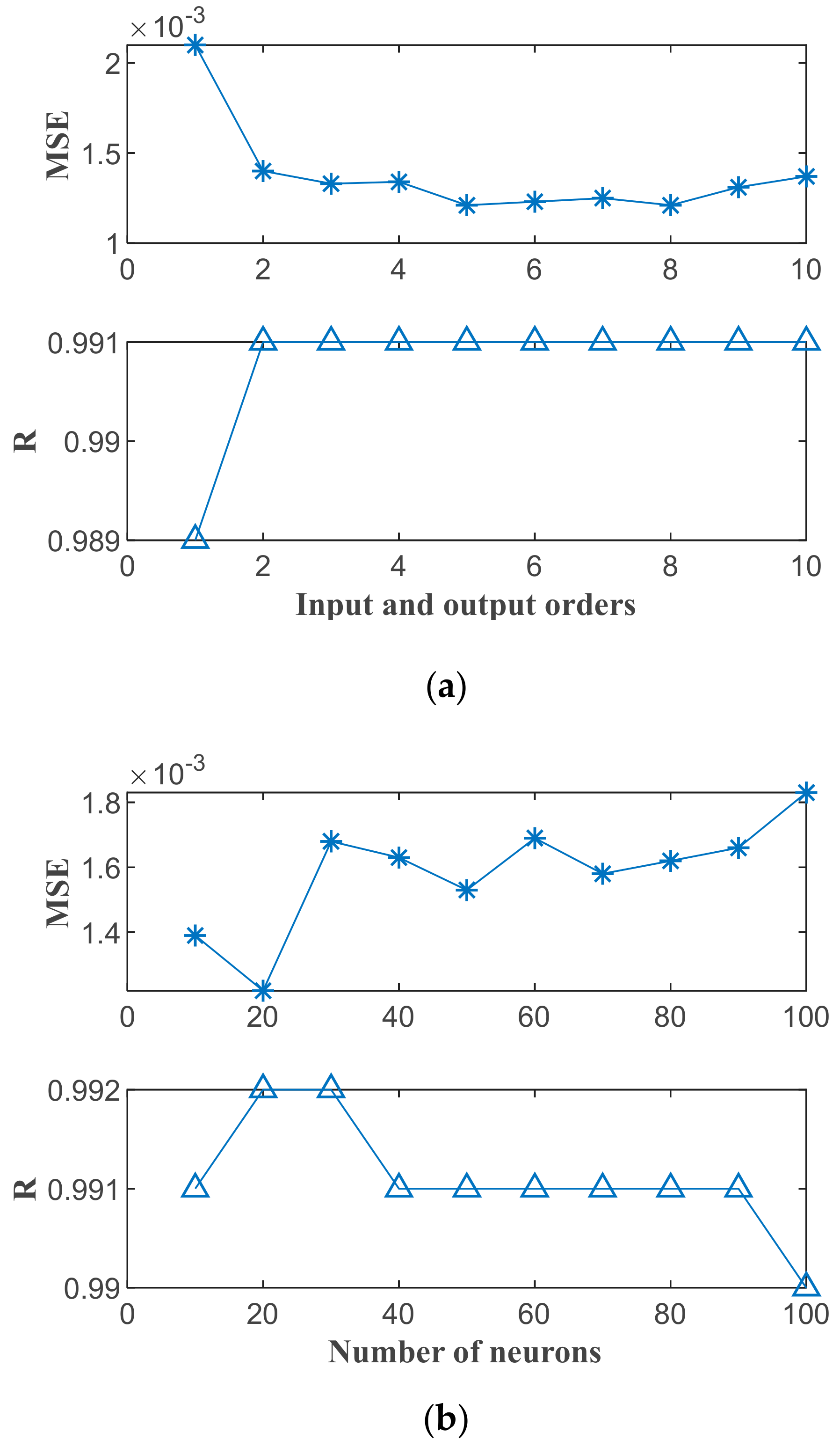
5.2. NARX Network-Based Brake Intensity Prediction
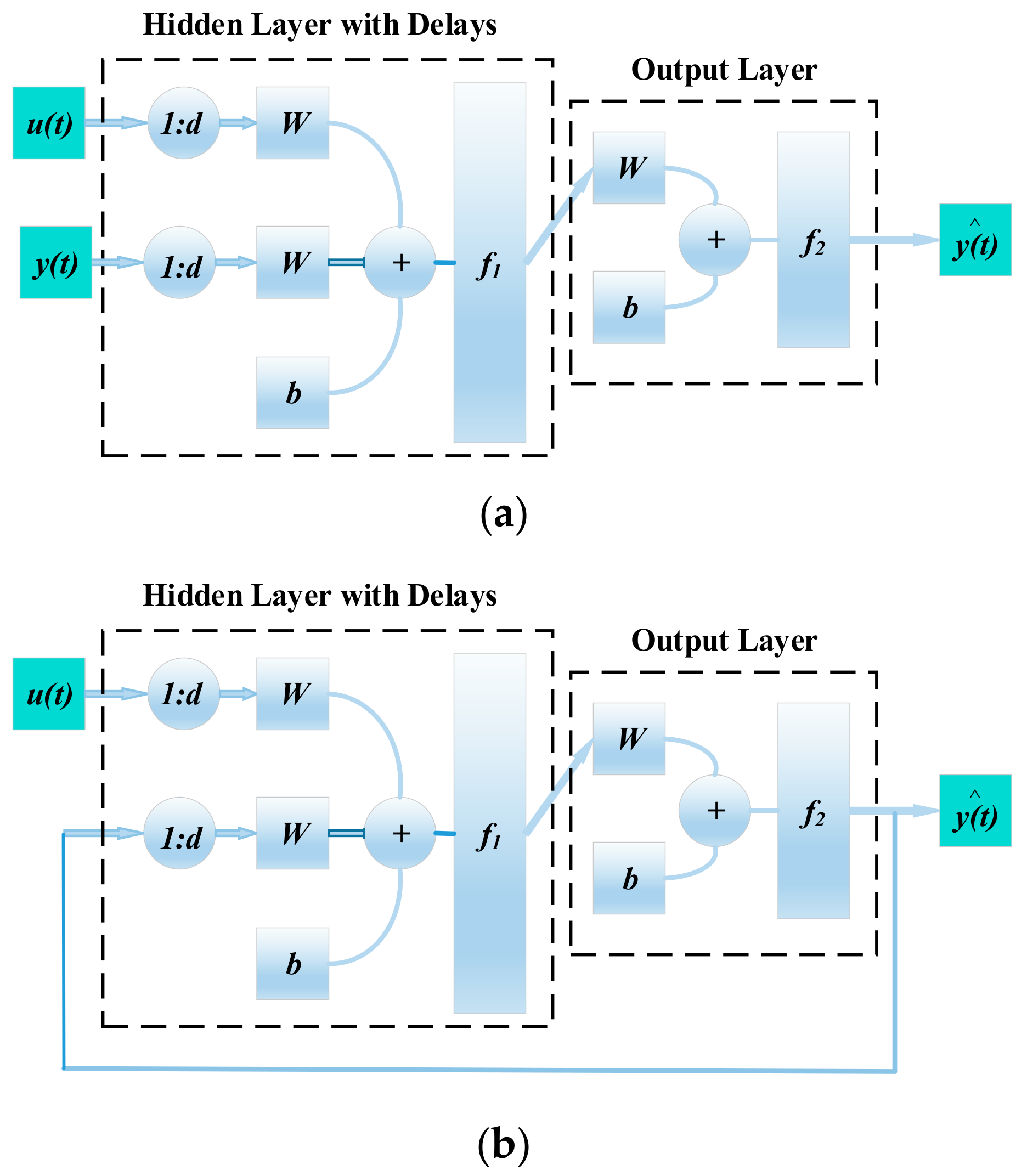
5.2.1. NARX Network
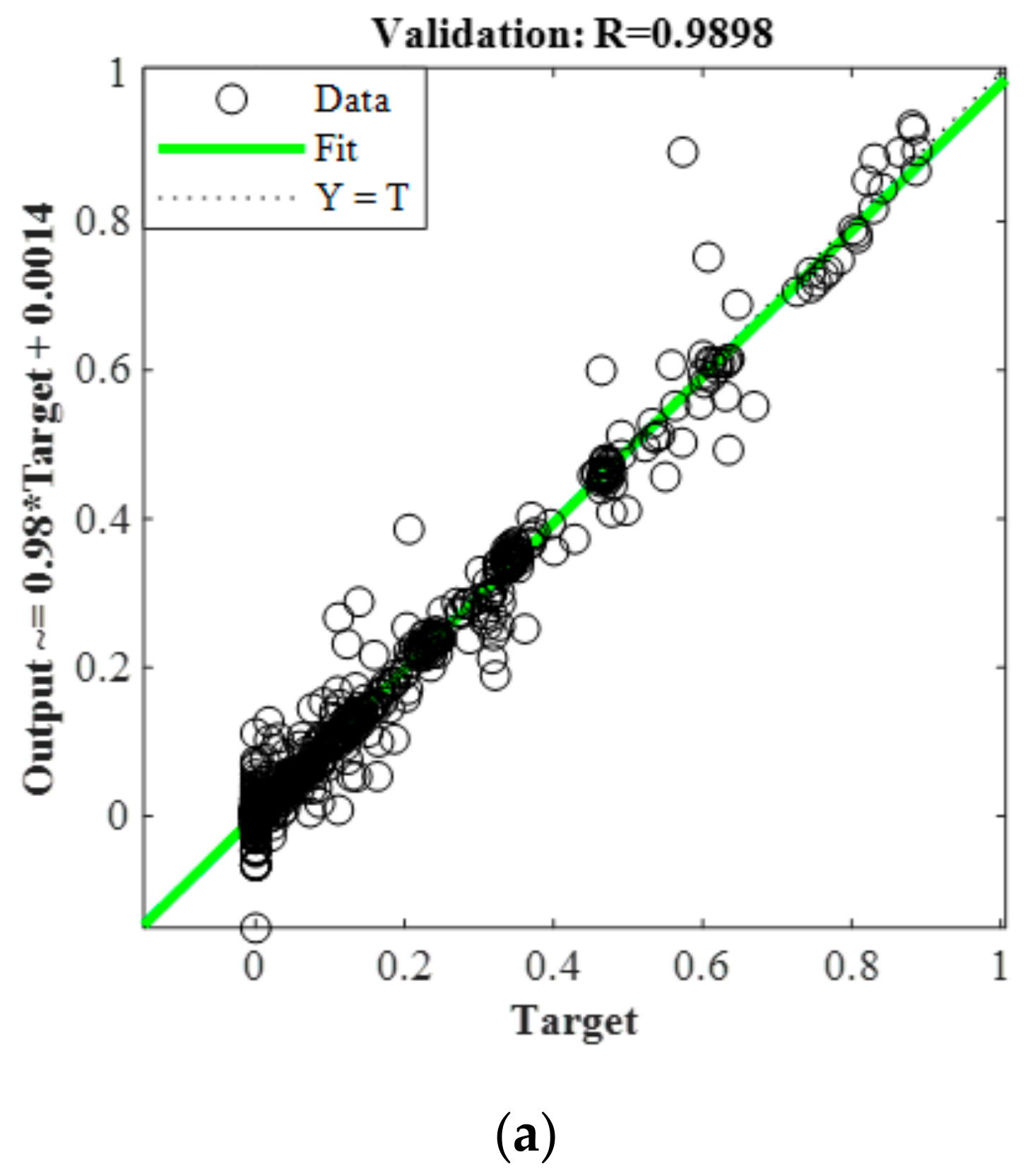
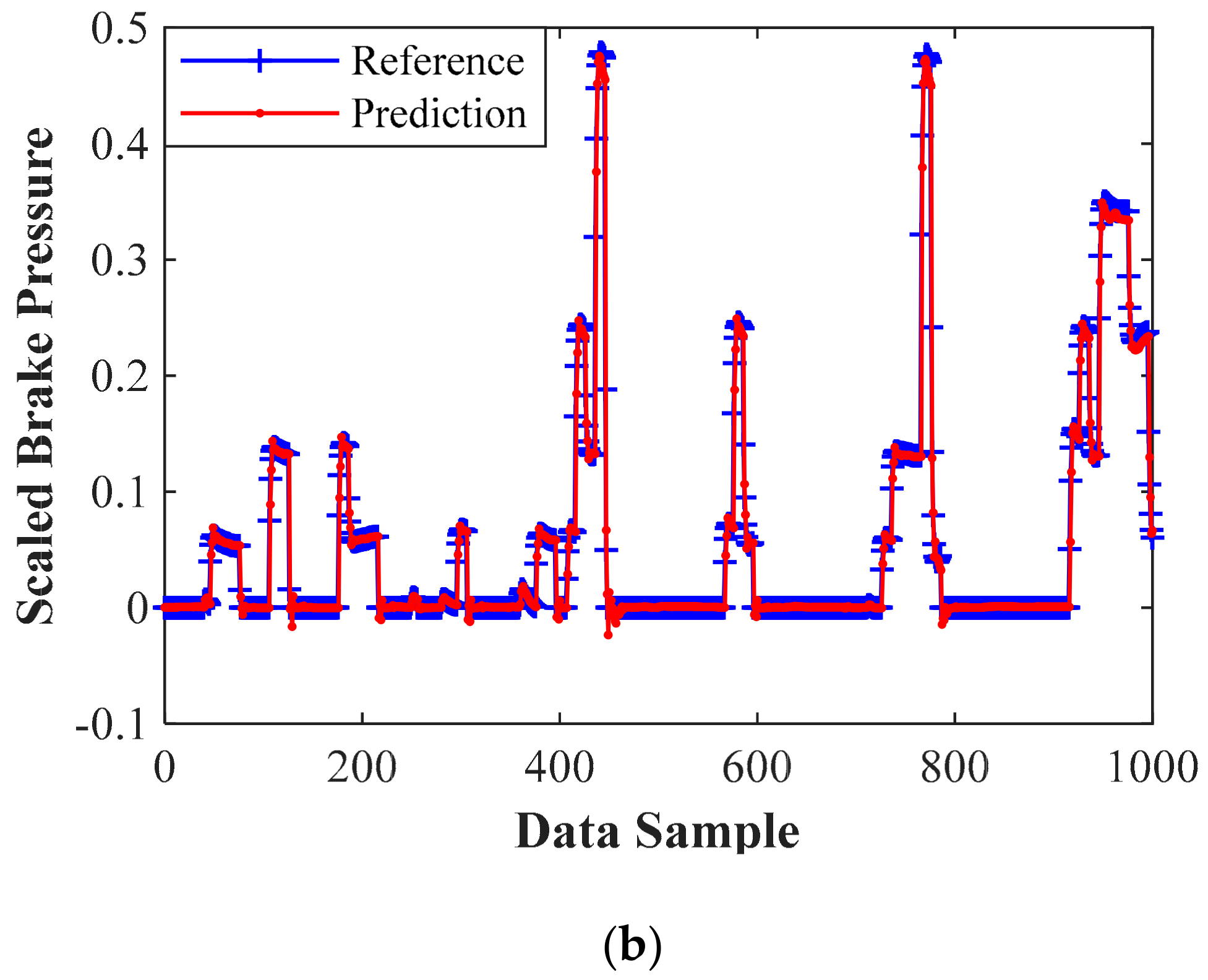
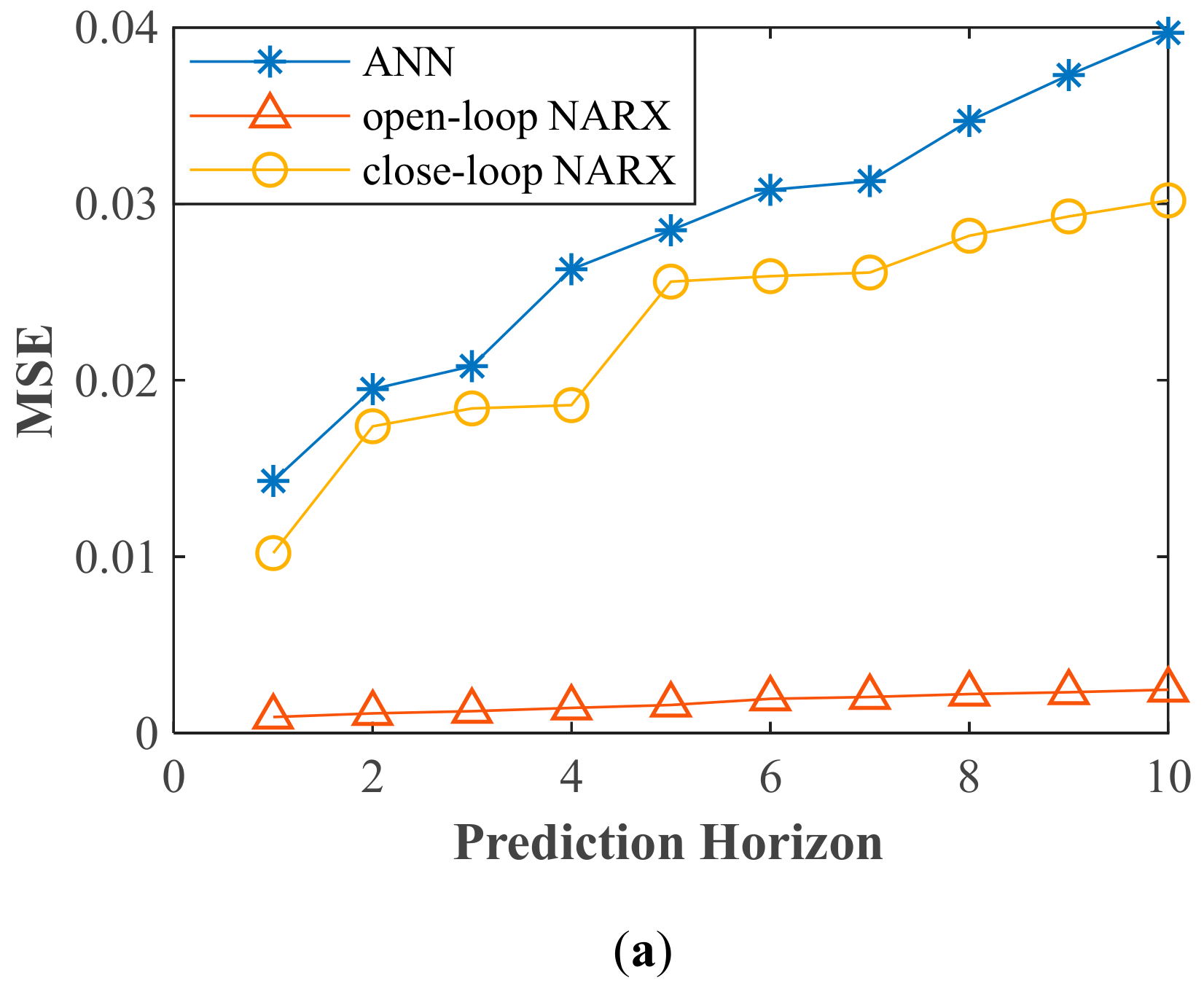
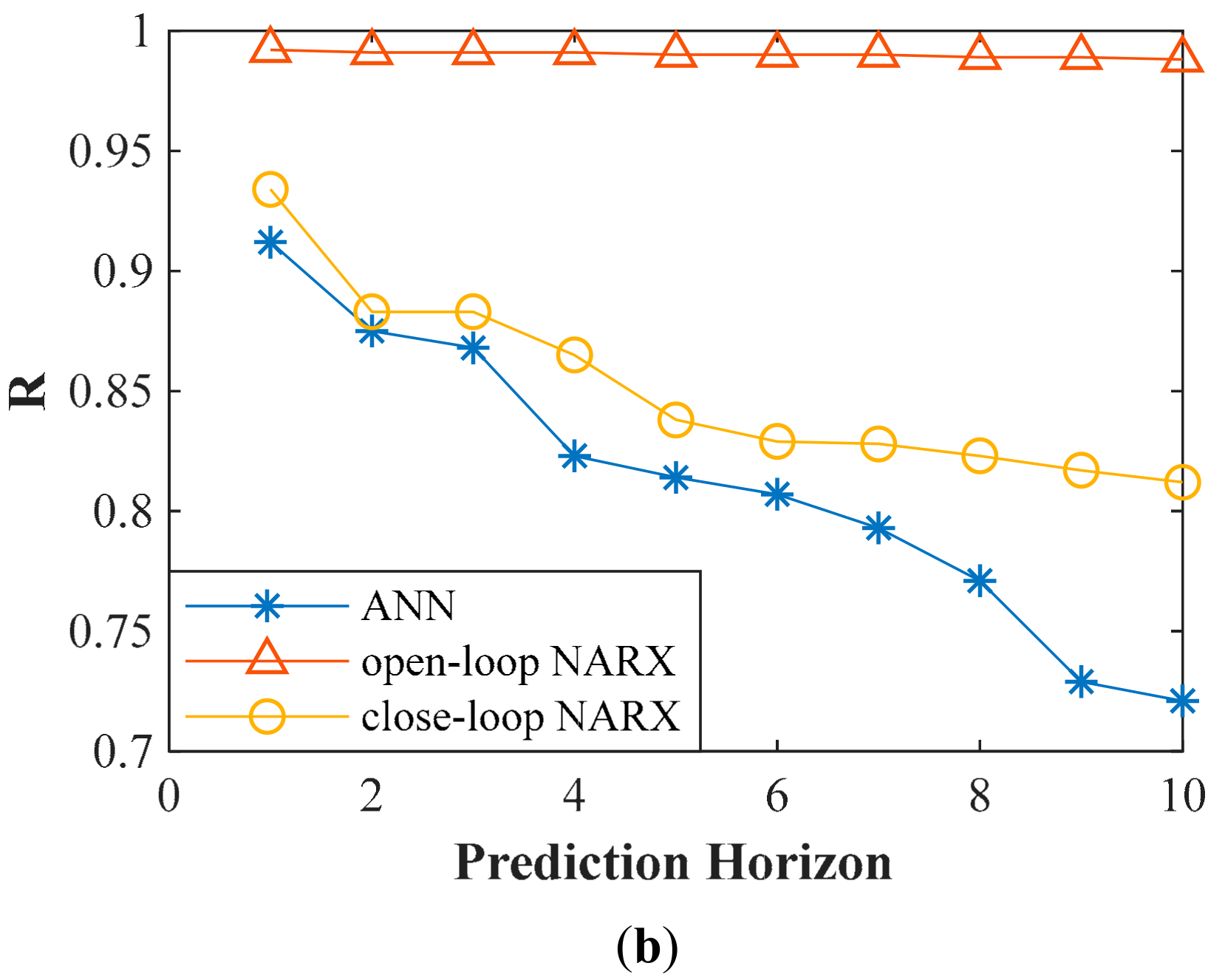
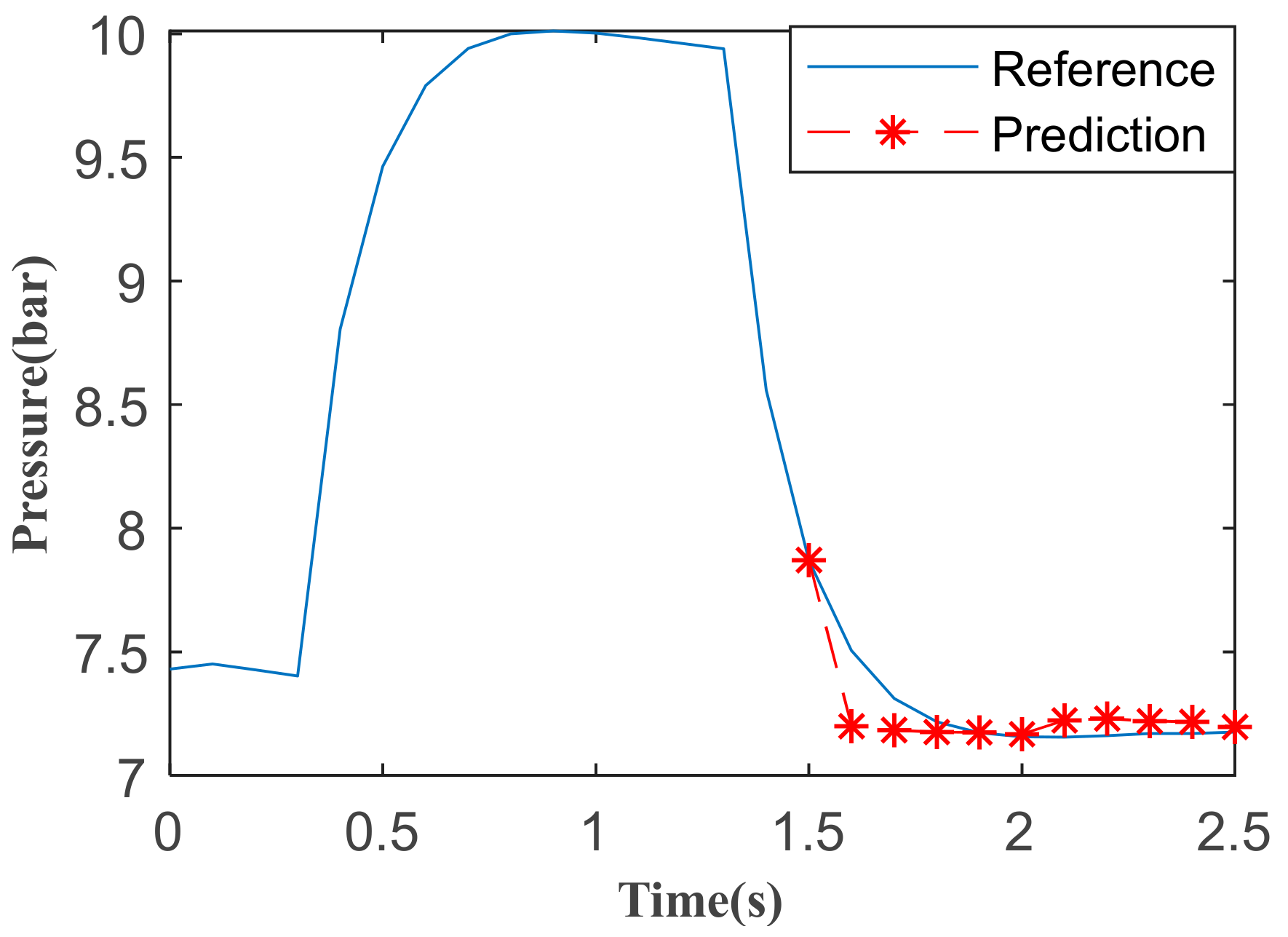
5.2.2. Performance Analysis of Brake Intensity Prediction
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bärgman, J.; Boda, C.N.; Dozza, M. Counterfactual simulations applied to SHRP2 crashes: The effect of driver behavior models on safety benefit estimations of intelligent safety systems. Accid. Anal. Prev. 2017, 102, 165–180. [Google Scholar] [CrossRef]
- Dumitru, A.I.; Girbacia, T.; Boboc, R.G.; Cristian, P.; Leonte, M. Effects of smartphone based advanced driver assistance system on distracted driving behavior: A simulator study. Comput. Hum. Behav. 2018, 83, 1–7. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Cao, B. Regenerative braking strategy for electric vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 864–868. [Google Scholar]
- Song, C.; Li, S.; Zong, C. Fuzzy logic control method of EHB system based on braking intention pattern identification. In Proceedings of the IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009; pp. 1243–1247. [Google Scholar]
- Li, W.; Du, H.; Li, W. Driver intention based coordinate control of regenerative and plugging braking for electric vehicles with in-wheel PMSMs. IET Intell. Transp. Syst. 2018, 12, 1300–1311. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, M. Regenerative braking algorithm for the electric vehicle with a seamless two-speed transmission. J. Automob. Eng. 2019, 233, 905–916. [Google Scholar] [CrossRef]
- Paul, D.; Velenis, E.; Cao, D. Optimal μ—Estimation-Based Regenerative Braking Strategy for an AWD HEV. IEEE Trans. Transp. Electrif. 2016, 3, 249–258. [Google Scholar] [CrossRef]
- Imamura, T.; Ogi, T.; Zhang, Z.; Tetsuo, M. Study of Induction and Estimation Method for Driver’s Intention by Using a Driving Simulator. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 3322–3326. [Google Scholar]
- Kost, F.; Schuh, J.; Koch-Dücker, H.J. Electronic Stability Program; ESP: Taunton, MA, USA, 2015. [Google Scholar]
- Alonso, M.; Vega, M.H.; Martín, O. Driving simulation study for the analysis of distraction effects in longitudinal driving behaviour. Cogn. Technol. Work 2012, 14, 283–297. [Google Scholar] [CrossRef]
- Fenzhu, J.I.; Farong, D.U.; Wenbo, Z. Electric vehicle energy economy based on braking intention identification. J. Beijing Univ. Aeronaut. Astronaut. 2016. [Google Scholar] [CrossRef]
- Hernández, L.G.; Mozos, O.M.; Ferrández, J.M.; Antelis, J.M. EEG-based detection of braking intention under different car driving conditions. Front. Neuroinform. 2018, 12, 29. [Google Scholar] [CrossRef] [PubMed]
- Haufe, S.; Kim, J.W.; Kim, I.H.; Sonnleitner, A.; Schrauf, M.; Curio, G.; Blankertz, B. Electrophysiology-based detection of emergency braking intention in real-world driving. J. Neural Eng. 2014, 11, 056011. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.H.; Bong, J.H.; Park, J.; Park, S. Prediction of driver’s intention of lane change by augmenting sensor information using machine learning techniques. Sensors 2017, 17, 1350. [Google Scholar] [CrossRef]
- Li, F.; Wang, W.; Feng, G. Driving intention inference based on dynamic Bayesian networks. In Practical Applications of Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1109–1119. [Google Scholar]
- Zeng, X.; Wang, J. A stochastic driver pedal behavior model incorporating road information. IEEE Trans. Hum. -Mach. Syst. 2017, 47, 614–624. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, S.; Ye, Y.; Man, Y.; Wang, G. Composite braking AMT shift strategy for extended-range heavy commercial electric vehicle based on LHMM/ANFIS braking intention identification. Clust. Comput. 2018, 1–16. [Google Scholar] [CrossRef]
- Xing, Y.; Lv, C.; Wang, H.; Xao, D. Recognizing driver braking intention with vehicle data using unsupervised learning methods. SAE 2017. [Google Scholar] [CrossRef]
- Lv, C.; Xing, Y.; Lu, C.; Xao, D.; Gao, H.; Guo, H. Hybrid-learning-based classification and quantitative inference of driver braking intensity of an electrified vehicle. IEEE Trans. Veh. Technol. 2018, 67, 5718–5729. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, S.; Ma, J.; Gao, Y.; Man, Y. Identification of driver’s braking intention based on a hybrid model of GHMM and GGAP-RBFNN. Neural Comput. Appl. 2018, 31, 1–14. [Google Scholar] [CrossRef]
- Ding, N.; Yu, G.; Wang, W. Estimation of brake pressure and tyre–road friction during ABS activation. Int. J. Veh. Des. 2012, 58, 33–45. [Google Scholar] [CrossRef]
- Ho, L.M.; Satzger, C.; de Castro, R. Fault-tolerant control of an electrohydraulic brake using virtual pressure sensor. In Proceedings of the International Conference on Robotics and Automation Sciences (ICRAS), Hong Kong, China, 26–29 August 2017; pp. 76–82. [Google Scholar]
- Lv, C.; Xing, Y.; Zhang, J.; Na, X.; Li, Y.; Liu, T. Levenberg–Marquardt backpropagation training of multilayer neural networks for state estimation of a safety-critical cyber-physical system. IEEE Trans. Ind. Inform. 2017, 14, 3436–3446. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, I.H.; Lee, S.W. Detection of braking intention during simulated driving based on EEG analysis: Online study. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Kowloon, China, 9–12 October 2015; pp. 887–891. [Google Scholar]
- Kim, I.H.; Kim, J.W.; Haufe, S.; Lee, S.W. Detection of braking intention in diverse situations during simulated driving based on EEG feature combination. J. Neural Eng. 2014, 12, 016001. [Google Scholar] [CrossRef]
- Kumar, M.; Thenmozhi, M. Forecasting stock index movement: A comparison of support vector machines and random forest. In Proceedings of the Indian Institute of Capital Markets 9th Capital Markets Conference Paper, Mumbai, India, 24 January 2006. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Peker, M.; Arslan, A.; Sen, B.; Celebi, F.V.; But, A. A novel hybrid method for determining the depth of anesthesia level: Combining ReliefF feature selection and random forest algorithm (ReliefF+RF). In Proceedings of the International Symposium on Innovations in Intelligent SysTems and Applications (INISTA), Udaipur, Rajasthan, India, 18–20 September 2015; pp. 1–8. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Menezes, J.M.P., Jr.; Barreto, G.A. Long-term time series prediction with the NARX network: An empirical evaluation. Neurocomputing 2008, 71, 3335–3343. [Google Scholar] [CrossRef]
- Hochreiter, S.; Bengio, Y.; Frasconi, P. Gradient Flow in Recurrent Nets: The Difficulty of Learning Long-Term Dependencies; Wiley-IEEE Press: New York, NY, USA, 2001. [Google Scholar]
- Siegelmann, H.T.; Horne, B.G.; Giles, C.L. Computational capabilities of recurrent NARX neural networks. Ieee Trans. Syst. ManCybern. 1997, 27, 208–215. [Google Scholar] [CrossRef] [Green Version]
- Chetouani, Y. Using ARX and NARX approaches for modeling and prediction of the process behavior: Application to a reactor-exchanger. Asia-Pac. J. Chem. Eng. 2008, 3, 597–605. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Xie, H.; Tang, H.; Liao, Y.H. Time series prediction based on NARX neural networks: An advanced approach. In Proceedings of the International conference on machine learning and cybernetics, Hebei, China, 12–15 July 2009; pp. 1275–1279. [Google Scholar]
- Capraro, F.; Patino, D.; Tosetti, S.; Schugurensky, C. Neural network-based irrigation control for precision agriculture. In Proceedings of the IEEE International Conference on Networking, Sensing and Control, Sanya, China, 6–8 April 2008; pp. 357–362. [Google Scholar]
- Giles, C.L.; Lin, T.; Horne, B.G. Remembering the past: The role of embedded memory in recurrent neural network architectures. In Proceedings of the Neural Networks for Signal Processing VII. Proceedings of the 1997 IEEE Signal Processing Society Workshop, Amelia Island, FL, USA, 24–26 September 1997; pp. 34–43. [Google Scholar]

| No. | Predictors | No. | Predictors |
|---|---|---|---|
| 1 | Velocity (km/h) | 8 | Battery current gradient (A/s) |
| 2 | Mean velocity (km/h) | 9 | Battery voltage (V) |
| 3 | Standard deviation of velocity (km/h) | 10 | Battery volatge gradient (A/s) |
| 4 | Acceleration (m/s2) | 11 | State of Charge (SOC) (%) |
| 5 | Mean acceleration (m/s2) | 12 | Motor torque (N.m) |
| 6 | Standard deviation of acceleration (m/s2) | 13 | Motor speed (rpm) |
| 7 | Battery current (A) | 14 | Master cylinder pressure (MPa) |
| Classification Algorithm | Accuracy (%) | Training Time(s) |
|---|---|---|
| Support Vector Machine(SVM) | 93.10 | 23.08 |
| K nearest neighbors (KNN) | 91.40 | 7.13 |
| Decision Tree | 94.80 | 9.65 |
| AdaBoost Trees | 94.10 | 17.84 |
| Random Forest | 97.30 | 11.26 |
| Training Algorithms | Mean Square Error | R | Training Time (s) |
|---|---|---|---|
| Scaled Conjugate Gradient (SCG) | 0.003126 | 0.981 | 9 |
| One-step Secant (OSS) | 0.003779 | 0.979 | 25 |
| Quasi-Newton (QN) | 0.001714 | 0.988 | 10 |
| gradient descent with momentum (GDM) | 0.126163 | 0.925 | 5 |
| Levenberg-Marquardt (LM) | 0.001408 | 0.991 | 19 |
| Bayesian Regularization (BR) | 0.001248 | 0.992 | 37 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Sun, J.; He, L.; Ding, Y.; Cao, H.; Zhao, W. Control Oriented Prediction of Driver Brake Intention and Intensity Using a Composite Machine Learning Approach. Energies 2019, 12, 2483. https://doi.org/10.3390/en12132483
Zhou J, Sun J, He L, Ding Y, Cao H, Zhao W. Control Oriented Prediction of Driver Brake Intention and Intensity Using a Composite Machine Learning Approach. Energies. 2019; 12(13):2483. https://doi.org/10.3390/en12132483
Chicago/Turabian StyleZhou, Jianhao, Jing Sun, Longqiang He, Yi Ding, Hanzhang Cao, and Wanzhong Zhao. 2019. "Control Oriented Prediction of Driver Brake Intention and Intensity Using a Composite Machine Learning Approach" Energies 12, no. 13: 2483. https://doi.org/10.3390/en12132483
APA StyleZhou, J., Sun, J., He, L., Ding, Y., Cao, H., & Zhao, W. (2019). Control Oriented Prediction of Driver Brake Intention and Intensity Using a Composite Machine Learning Approach. Energies, 12(13), 2483. https://doi.org/10.3390/en12132483




