Numerical Study of Highly Viscous Fluid Sloshing in the Real-Scale Membrane-Type Tank
Abstract
:1. Introduction
2. Numerical Methodology
3. Model Validations
3.1. Validation of Sloshing of Glycerin under Surge Excitation
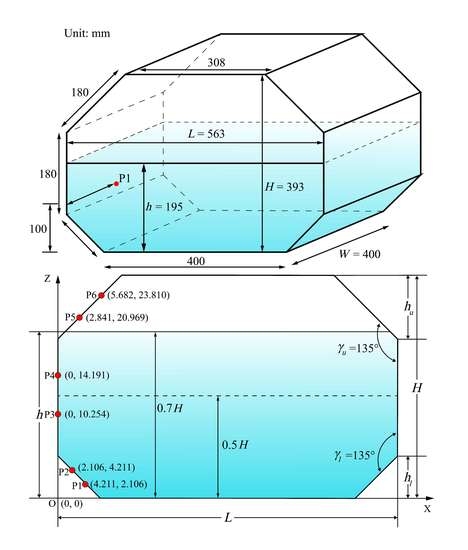
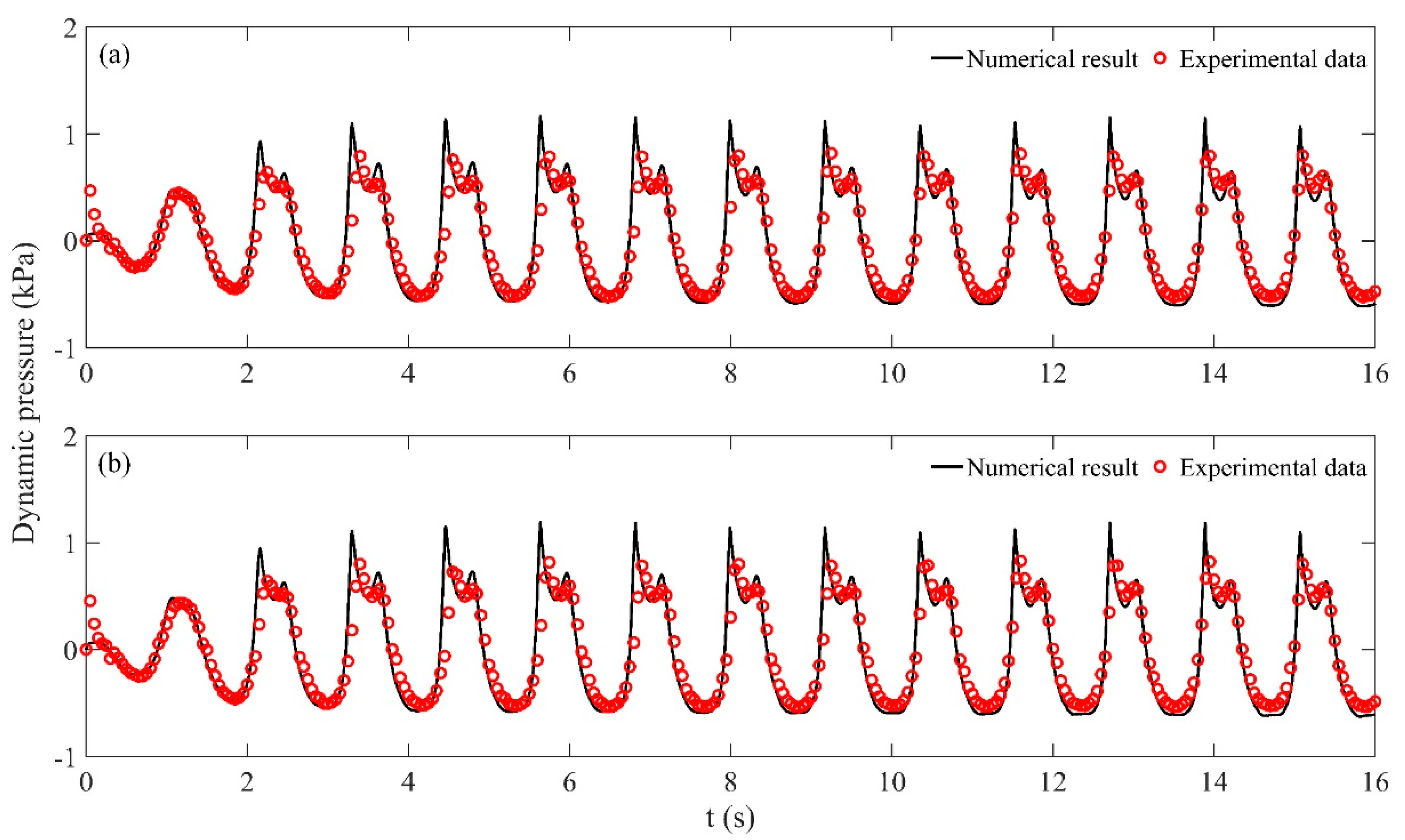
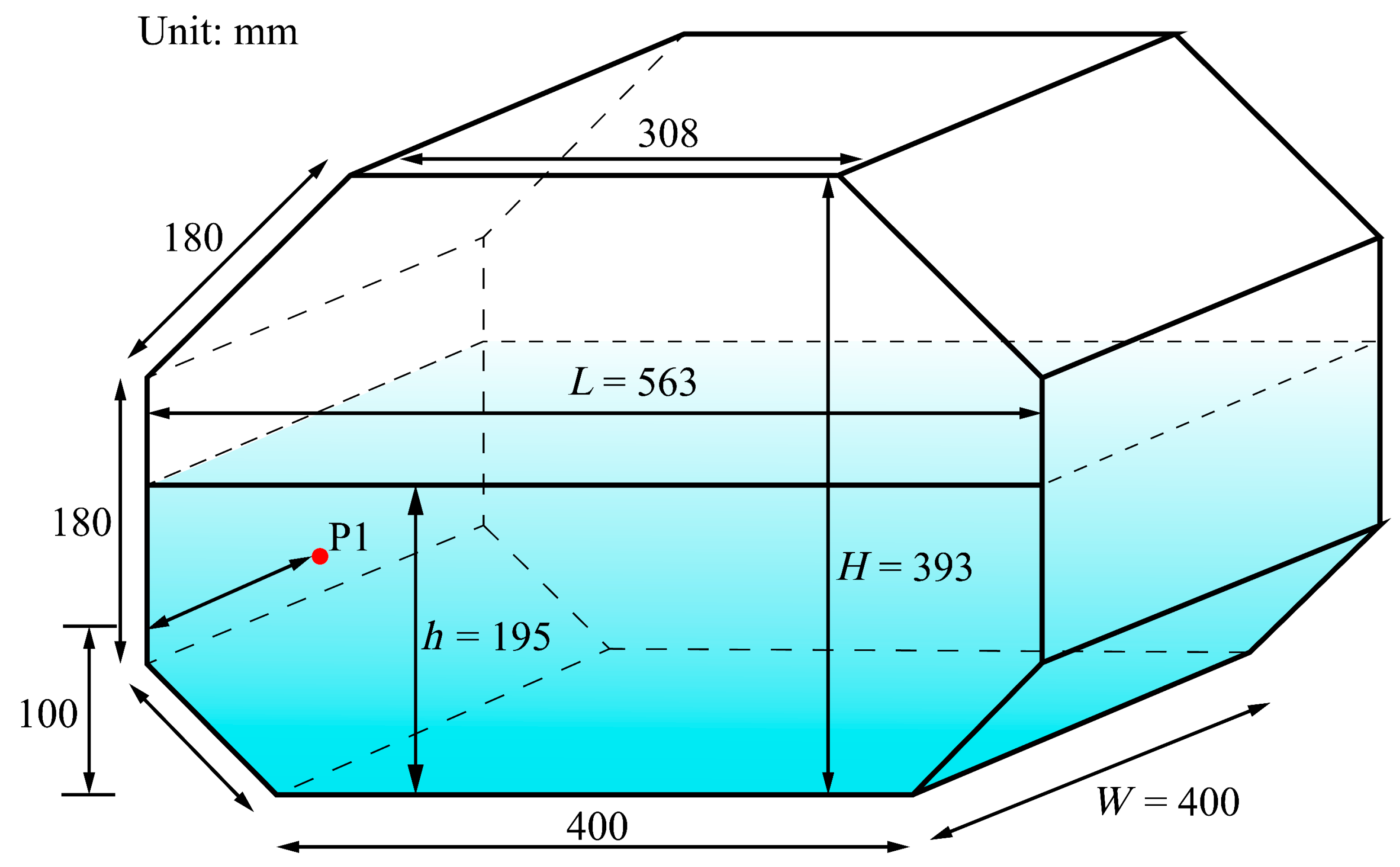
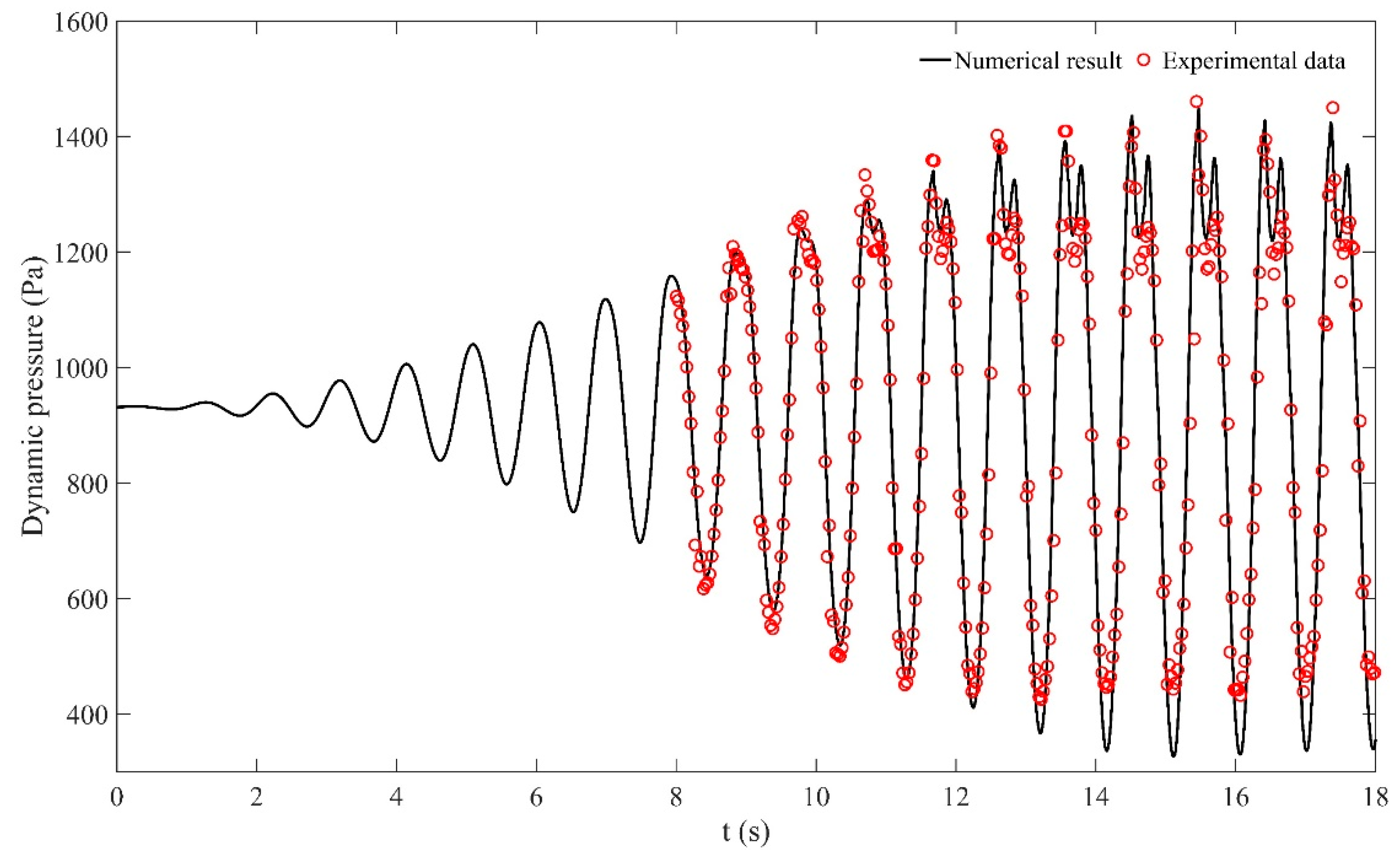
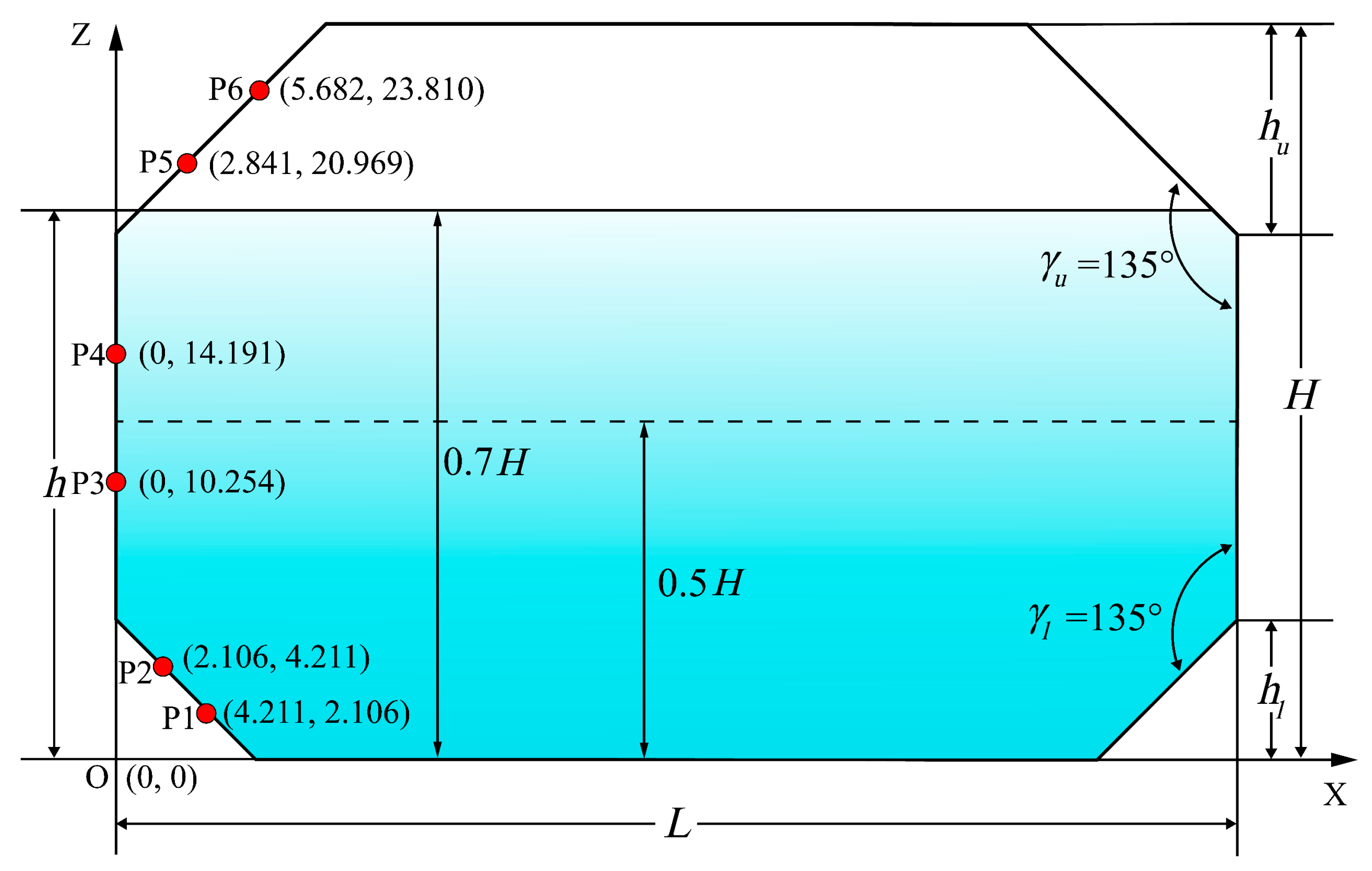
3.2. Validation of Membrane-Type Tank Sloshing under Roll Excitation
4. Results and Discussion
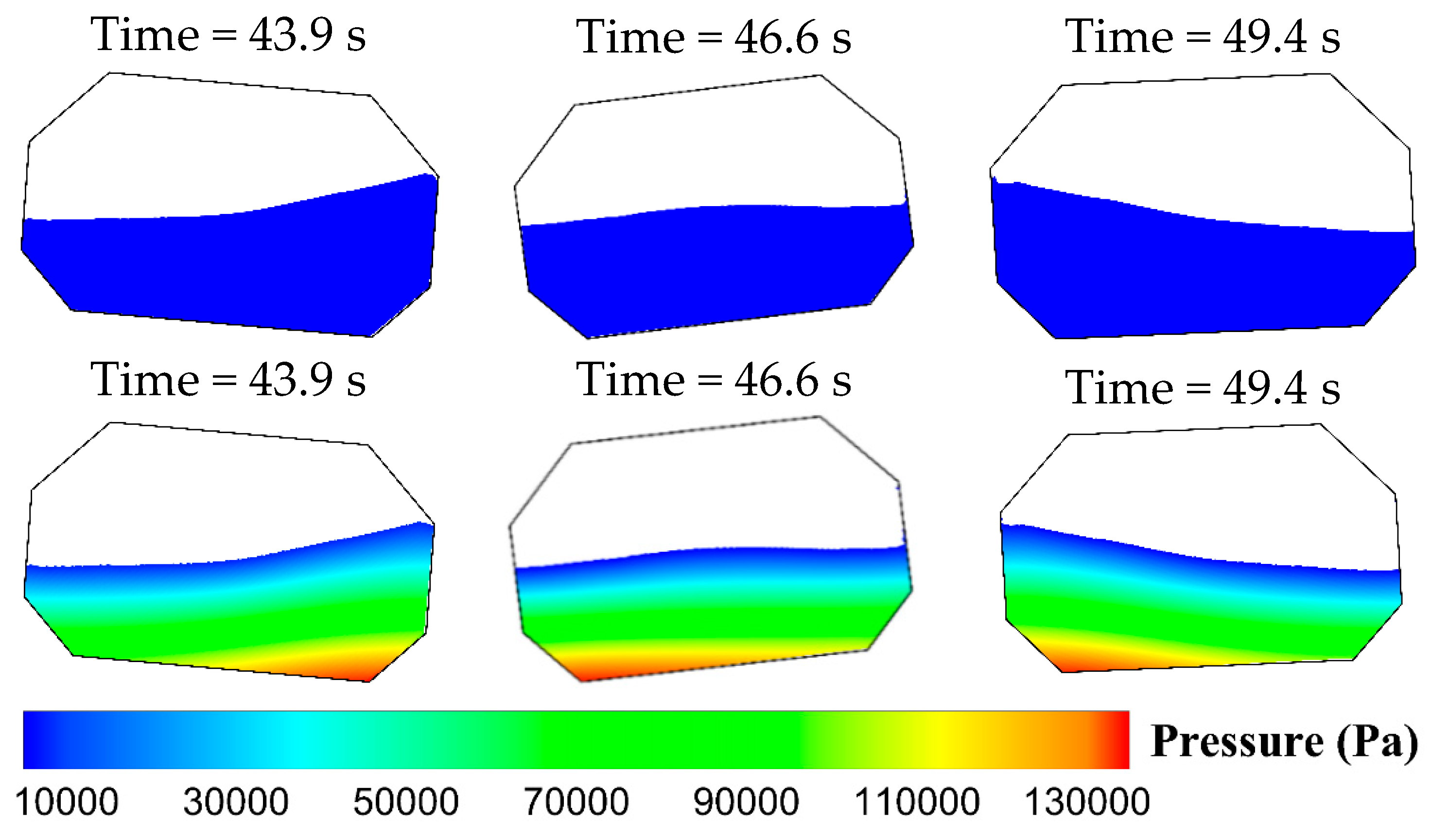
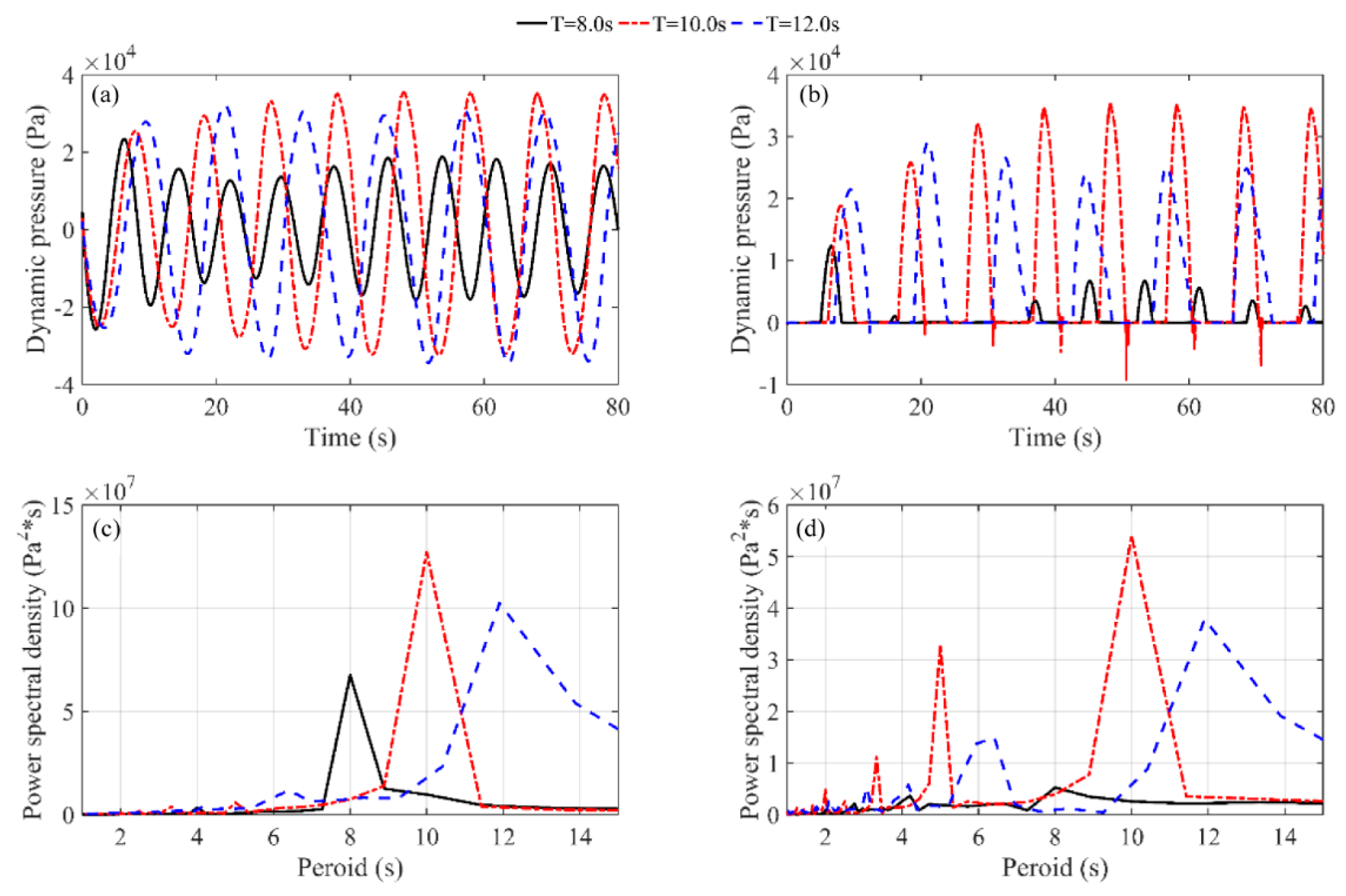
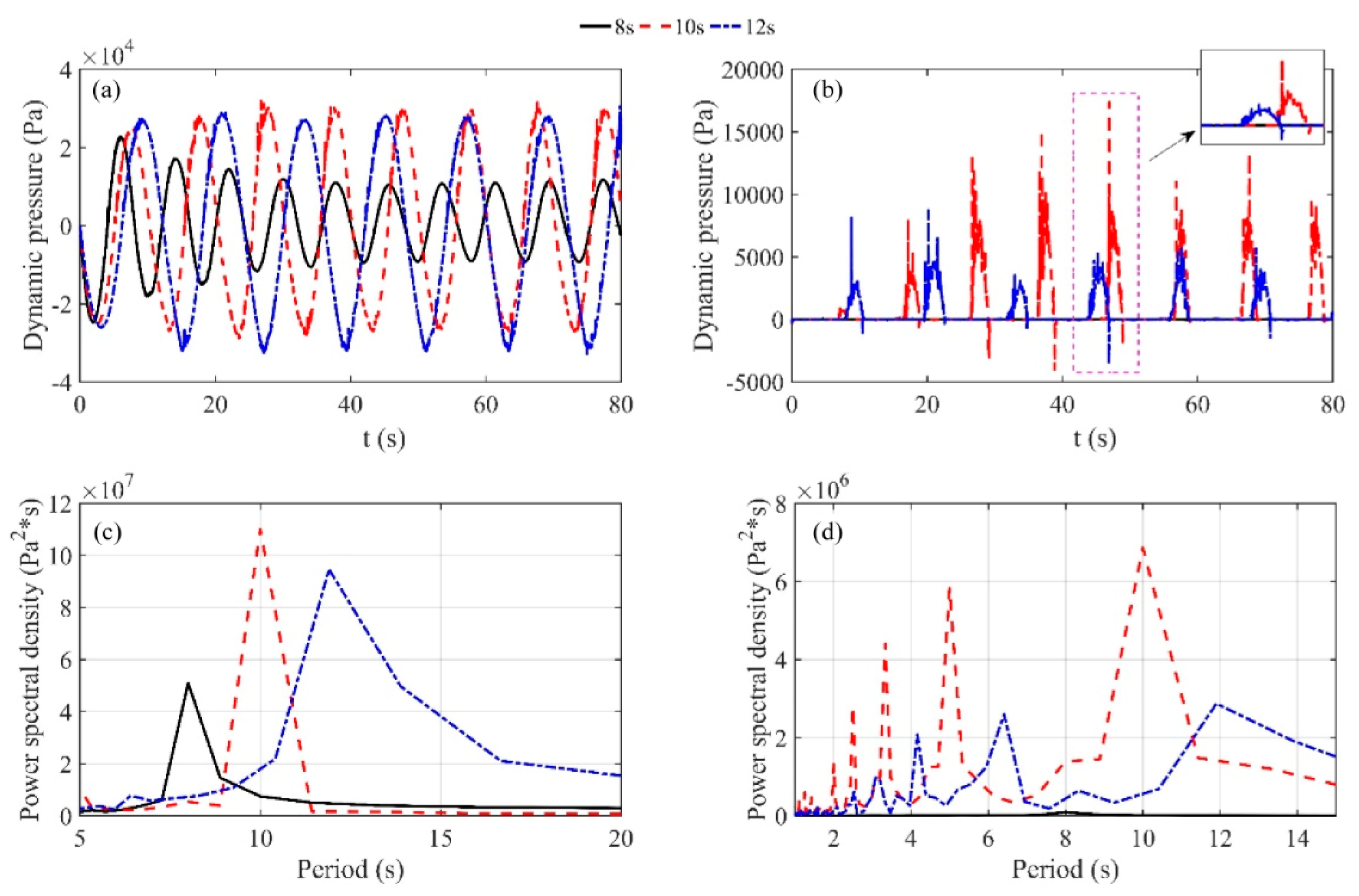
4.1. Sloshing Responses of Lower Filling Level 50% of Tank Height
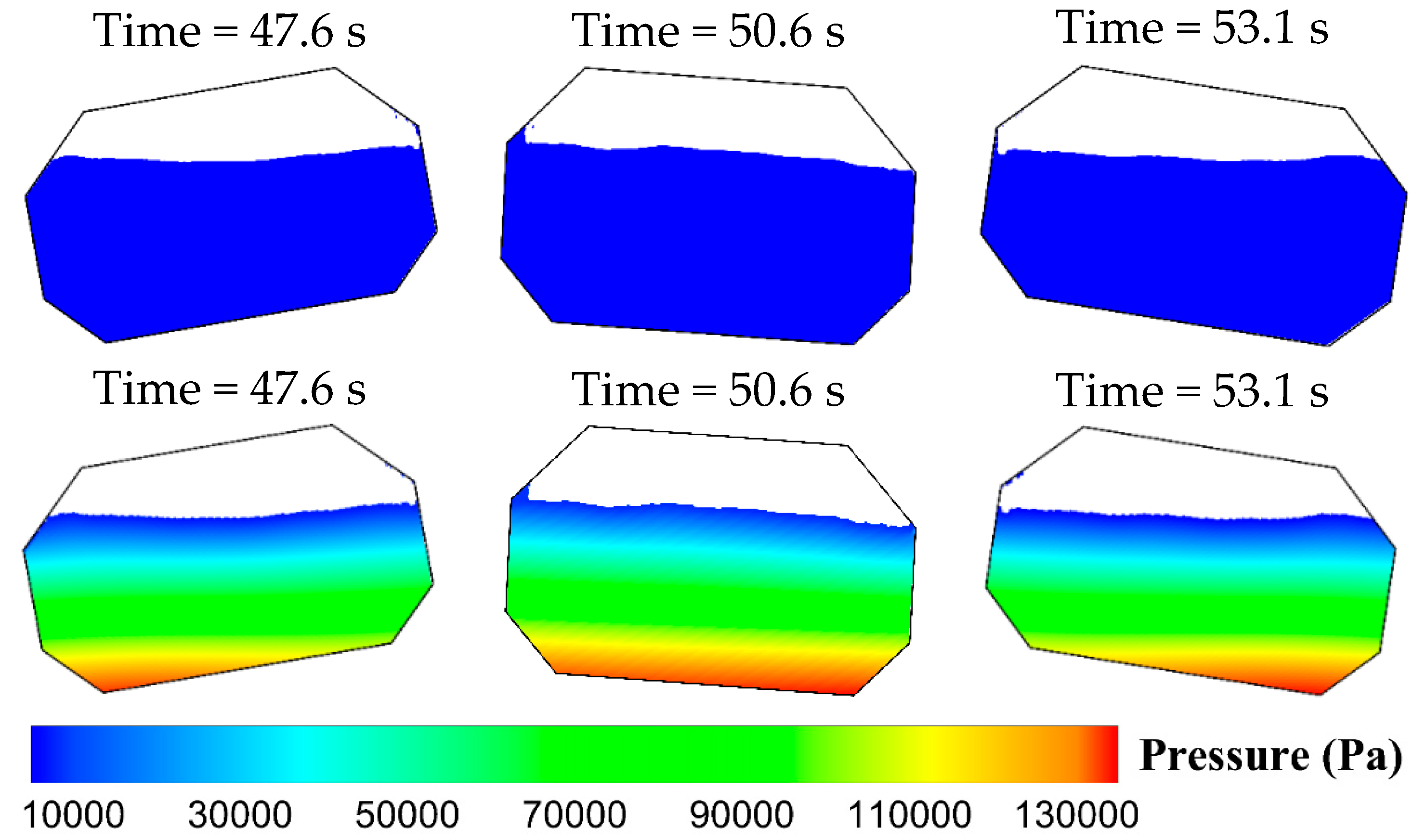
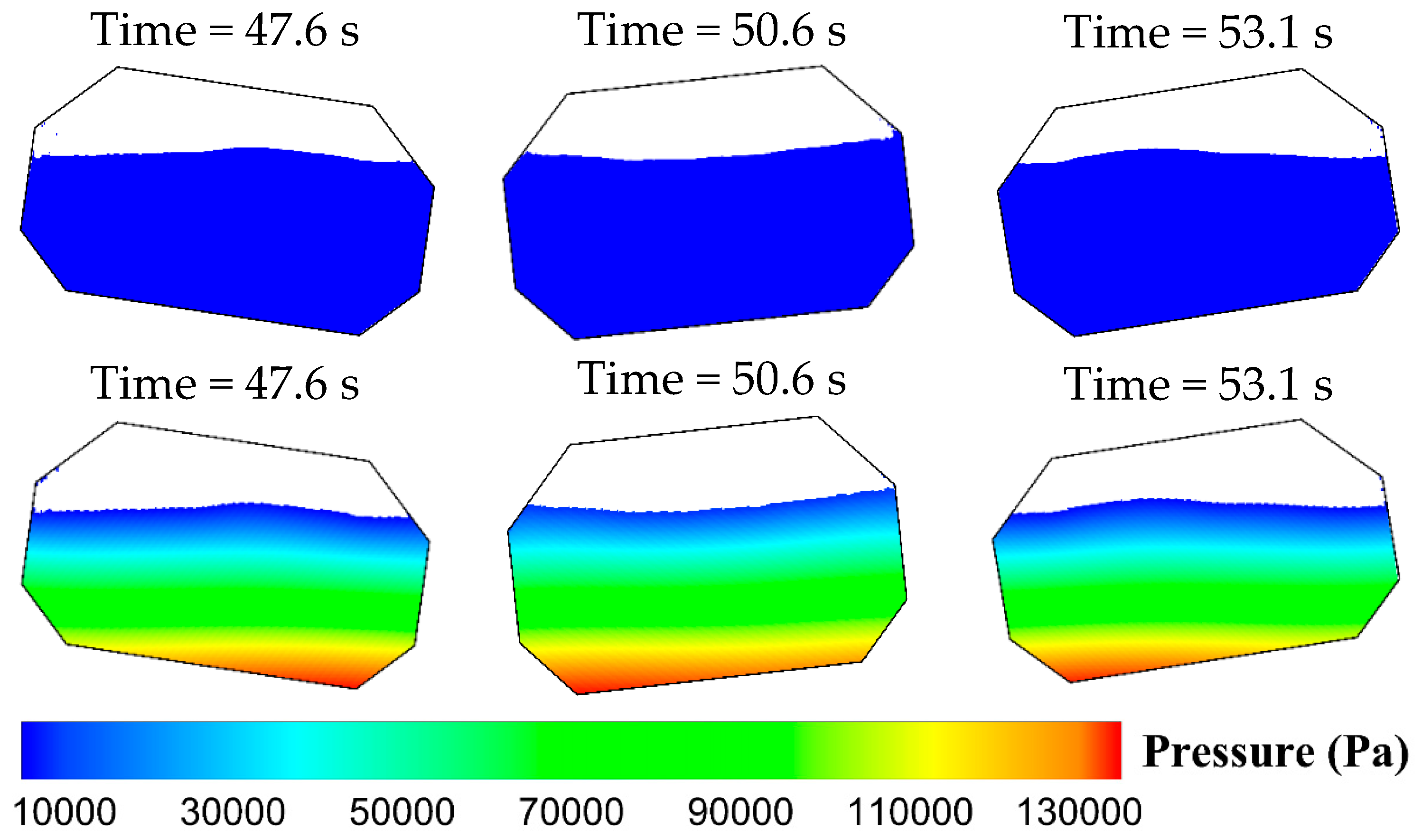
4.2. Sloshing Responses of Higher Filling Level 70% of Tank Height
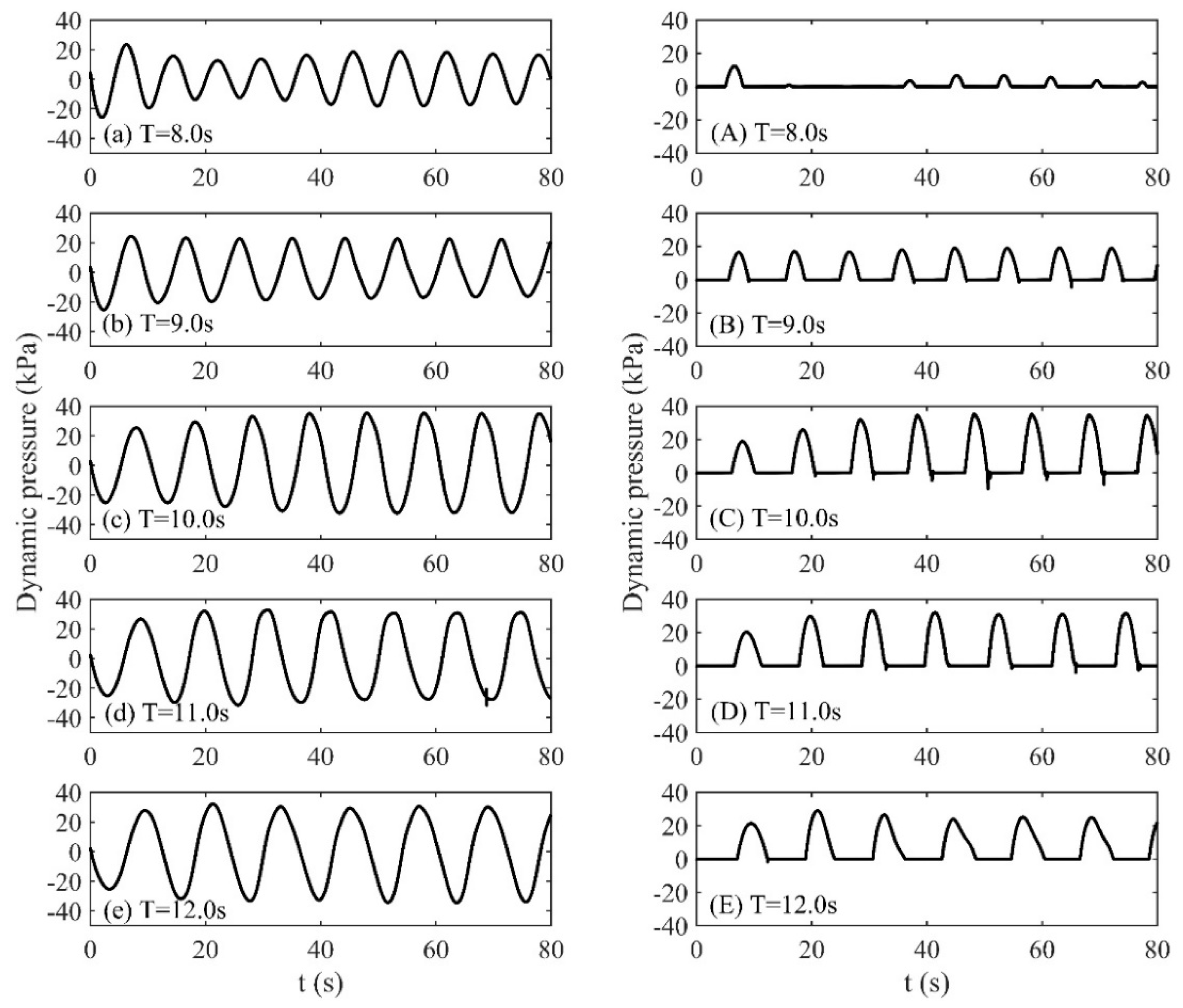
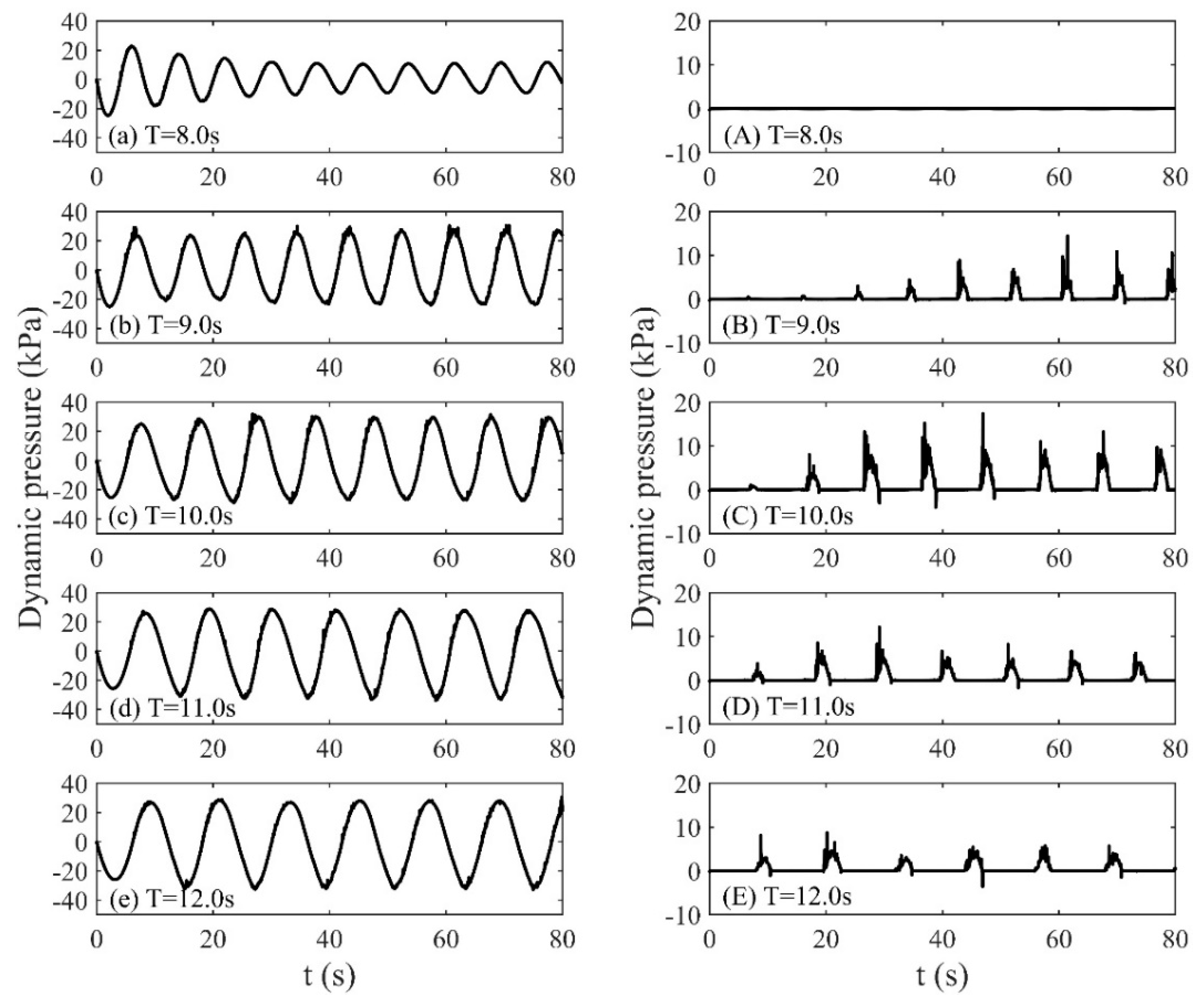
4.3. Frequency Responses of the Sloshing
5. Conclusions
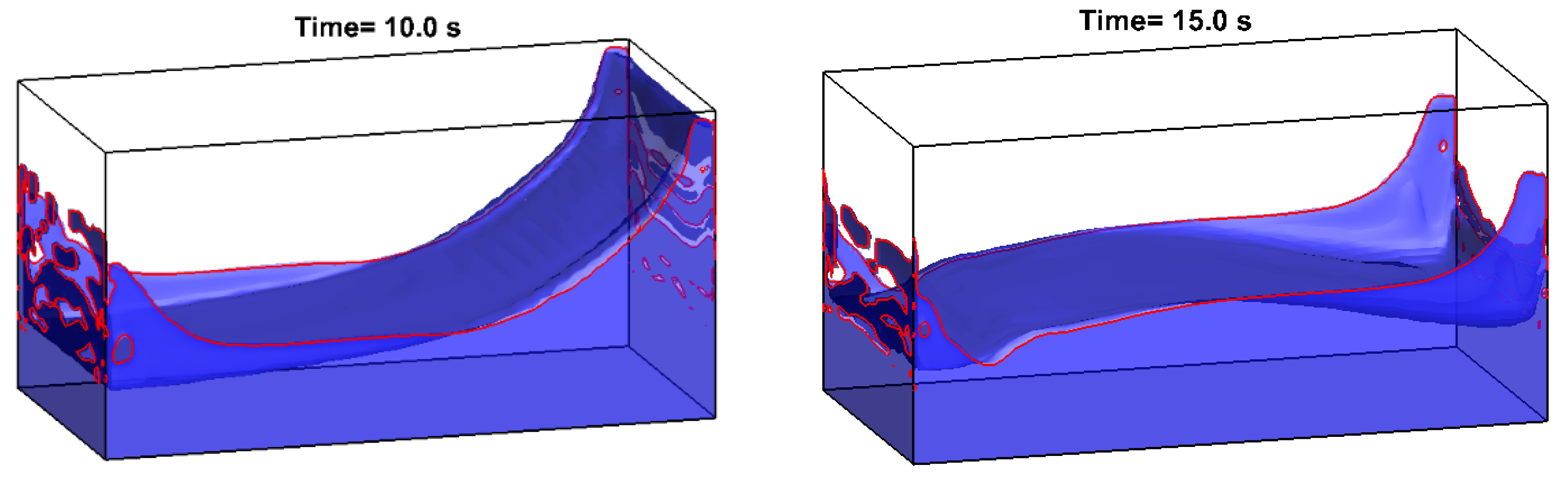
- The responses of dynamic pressures of the 50% filling height of the tank length behave larger values than that of the 70% filling height of the tank length for the same forcing period. The sloshing of the lower filling level behaves like a traveling wave and the sloshing of the higher filling level generally moves like a standing wave.
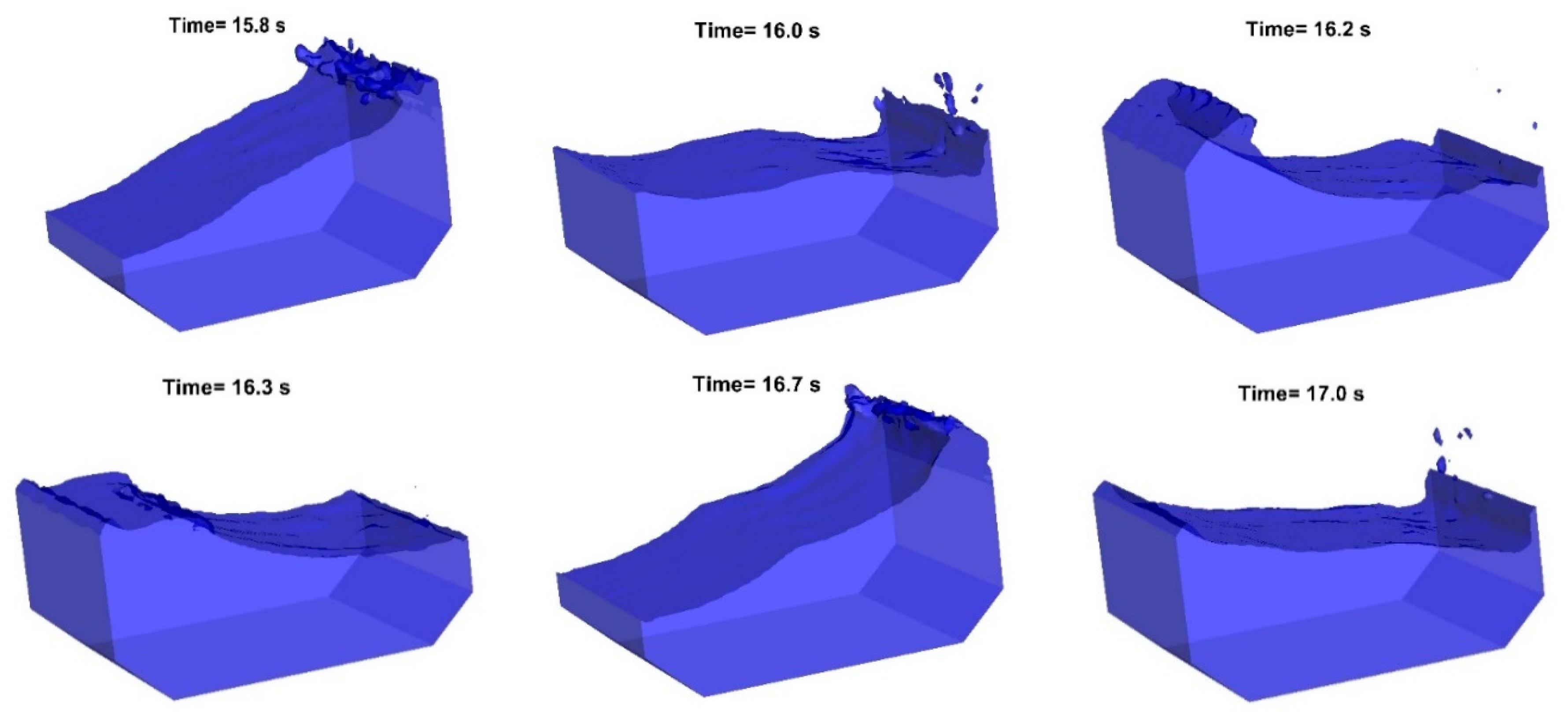
- The free surface of the 70% filling case is more breaking than the lower filling case. There exist several peaks in the crests of the dynamic pressures for the 70% filling case, and the time intervals between peaks are very shot, which also reveals that the slamming effect is more obvious than the lower filling case.
- Due to viscous effects, the nonlinearity is largely reduced compared to that of water but also exists by recalling the existence of the combinations of various frequencies. The dominant response frequencies of glycerin sloshing turn from the forcing period and lowest natural period to the forcing period and score times of the forcing period.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bass, R.L.; Bowles, E.B.; Trudell, R.W.; Navickas, J.; Peck, J.C.; Yoshimura, N.; Endo, S.; Pots, B.F.M. Modeling Criteria for Scaled LNG Sloshing Experiments. J. Fluid Eng. 1985, 107. [Google Scholar] [CrossRef]
- Kim, Y.; Shin, Y.-S.; Lee, K.H. Numerical study on slosh-induced impact pressures on three-dimensional prismatic tanks. Appl. Ocean Res. 2004, 26, 213–226. [Google Scholar] [CrossRef]
- Zou, C.-F.; Wang, D.-Y.; Cai, Z.-H.; Li, Z. The effect of liquid viscosity on sloshing characteristics. J. Mar. Sci. Technol. 2015, 20, 765–775. [Google Scholar] [CrossRef]
- Baudry, V.; Rousset, J.-M. Experimental Study of Viscous Cargo Behaviour and Investigation on Global Loads Exerted on Ship Tanks. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; p. V07BT06A015. [Google Scholar]
- Faitinsen, O.M. A numerical nonlinear method of sloshing in tanks with two-dimensional flow. J. Ship Res. 1978, 22, 193–202. [Google Scholar]
- Faltinsen, O.M.; Rognebakke, O.F.; Lukovsky, I.A.; Timokha, A.N. Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth. J. Fluid Mech. 2000, 407, 201–234. [Google Scholar] [CrossRef]
- Hill, D.F. Transient and steady-state amplitudes of forced waves in rectangular basins. Phys. Fluids 2003, 15, 1576–1587. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. Resonant three-dimensional nonlinear sloshing in a square-base basin. Part 4. Oblique forcing and linear viscous damping. J. Fluid Mech. 2017, 822, 139–169. [Google Scholar] [CrossRef]
- Wu, G.; Taylor, R.E.; Greaves, D.J.J.o.E.M. The effect of viscosity on the transient free-surface waves in a two-dimensional tank. J. Eng. Math. 2001, 40, 77–90. [Google Scholar] [CrossRef]
- Rudman, M.; Cleary, P.W.; Prakash, M. Simulation of liquid sloshing in model LNG tank using smoothed particle hydrodynamics. Int. J. Offshore Polar Eng. 2009, 19, 286–294. [Google Scholar]
- Luo, M.; Koh, C.; Bai, W.J.O.E. A three-dimensional particle method for violent sloshing under regular and irregular excitations. Ocean Eng. 2016, 120, 52–63. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, H.-C.J.O.E. Numerical simulation of 3D sloshing flow in partially filled LNG tank using a coupled level-set and volume-of-fluid method. Ocean Eng. 2015, 104, 10–30. [Google Scholar] [CrossRef]
- Kim, J.K.W.; Shin, Y.; Sim, I.; Kim, Y.; Bai, K. Three-Dimensional Finite-Element Computation for the Sloshing Impact Pressure In LNG Tank. In Proceedings of the Thirteenth International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003. [Google Scholar]
- Jin, X.; Lin, P. Viscous effects on liquid sloshing under external excitations. Ocean Eng. 2019, 171, 695–707. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Lin, P.; Li, C. Wave–current interaction with a vertical square cylinder. Ocean Eng. 2003, 30, 855–876. [Google Scholar] [CrossRef]
- Dongming, L. Numerical Modeling of Three-Dimensional Water Waves and Their Interaction with Structures; National University of Singapore: Singapore, 2008. [Google Scholar]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Gueyffier, D.; Li, J.; Nadim, A.; Scardovelli, R.; Zaleski, S.J.J.o.C.p. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows. J. Comput. Phys. 1999, 152, 423–456. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.-A.; Zheng, J. Experimental study of vertical slat screens effects on reducing shallow water sloshing in a tank under horizontal excitation with a wide frequency range. Ocean Eng. 2019, 173, 131–141. [Google Scholar] [CrossRef]
- Register, L. Guidance on the Operation of Membrane LNG Ships to Reduce the Risk of Damage Due to Sloshing; Technical report; Lloyds Register: London, UK, 2008. [Google Scholar]
- Cai, Z.-h.; Wang, D.-y.; Li, Z. Influence of excitation frequency on slosh-induced impact pressures of liquefied natural gas tanks. J. Shanghai Jiao Tong Univ. 2011, 16, 124–128. [Google Scholar] [CrossRef]
- Toba, Y.; Iida, N.; Kawamura, H.; Ebuchi, N.; Jones, I.S. Wave dependence of sea-surface wind stress. J. Phys. Oceanogr. 1990, 20, 705–721. [Google Scholar] [CrossRef]
- Earle, M.D. Extreme wave conditions during Hurricane Camille. J. Geophys. Res. 1975, 80, 377–379. [Google Scholar] [CrossRef]
- Pickrill, R.; Mitchell, J. Ocean wave characteristics around New Zealand. N. Zeal. J. Mar. Fresh 1979, 13, 501–520. [Google Scholar] [CrossRef] [Green Version]
- Araújo, C.E.; Franco, D.; MELO, E.; Pimenta, F. Wave regime characteristics of the southern Brazilian coast. In Proceedings of the Sixth International Conference on Coastal and Port Engineering in Developing Countries, COPEDEC VI, Colombo, Sri Lanka, 5–19 September 2003; p. 15. [Google Scholar]
- Biswal, K.; Bhattacharyya, S.; Sinha, P. Free-vibration analysis of liquid-filled tank with baffles. J. Sound Vib. 2003, 259, 177–192. [Google Scholar] [CrossRef]
- Xue, M.-A.; Lin, P. Numerical study of ring baffle effects on reducing violent liquid sloshing. Comput. Fluids 2011, 52, 116–129. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, S.; Huang, Z.; Jin, X.; Tabatabaei Malazi, M.; Liu, M. Numerical Study of Highly Viscous Fluid Sloshing in the Real-Scale Membrane-Type Tank. Energies 2019, 12, 4244. https://doi.org/10.3390/en12224244
Mi S, Huang Z, Jin X, Tabatabaei Malazi M, Liu M. Numerical Study of Highly Viscous Fluid Sloshing in the Real-Scale Membrane-Type Tank. Energies. 2019; 12(22):4244. https://doi.org/10.3390/en12224244
Chicago/Turabian StyleMi, Shuo, Zongliu Huang, Xin Jin, Mahdi Tabatabaei Malazi, and Mingming Liu. 2019. "Numerical Study of Highly Viscous Fluid Sloshing in the Real-Scale Membrane-Type Tank" Energies 12, no. 22: 4244. https://doi.org/10.3390/en12224244
APA StyleMi, S., Huang, Z., Jin, X., Tabatabaei Malazi, M., & Liu, M. (2019). Numerical Study of Highly Viscous Fluid Sloshing in the Real-Scale Membrane-Type Tank. Energies, 12(22), 4244. https://doi.org/10.3390/en12224244