Why PV Modules Should Preferably No Longer Be Oriented to the South in the Near Future
Abstract
1. Introduction
2. Methodology
3. PV System Output Calculation
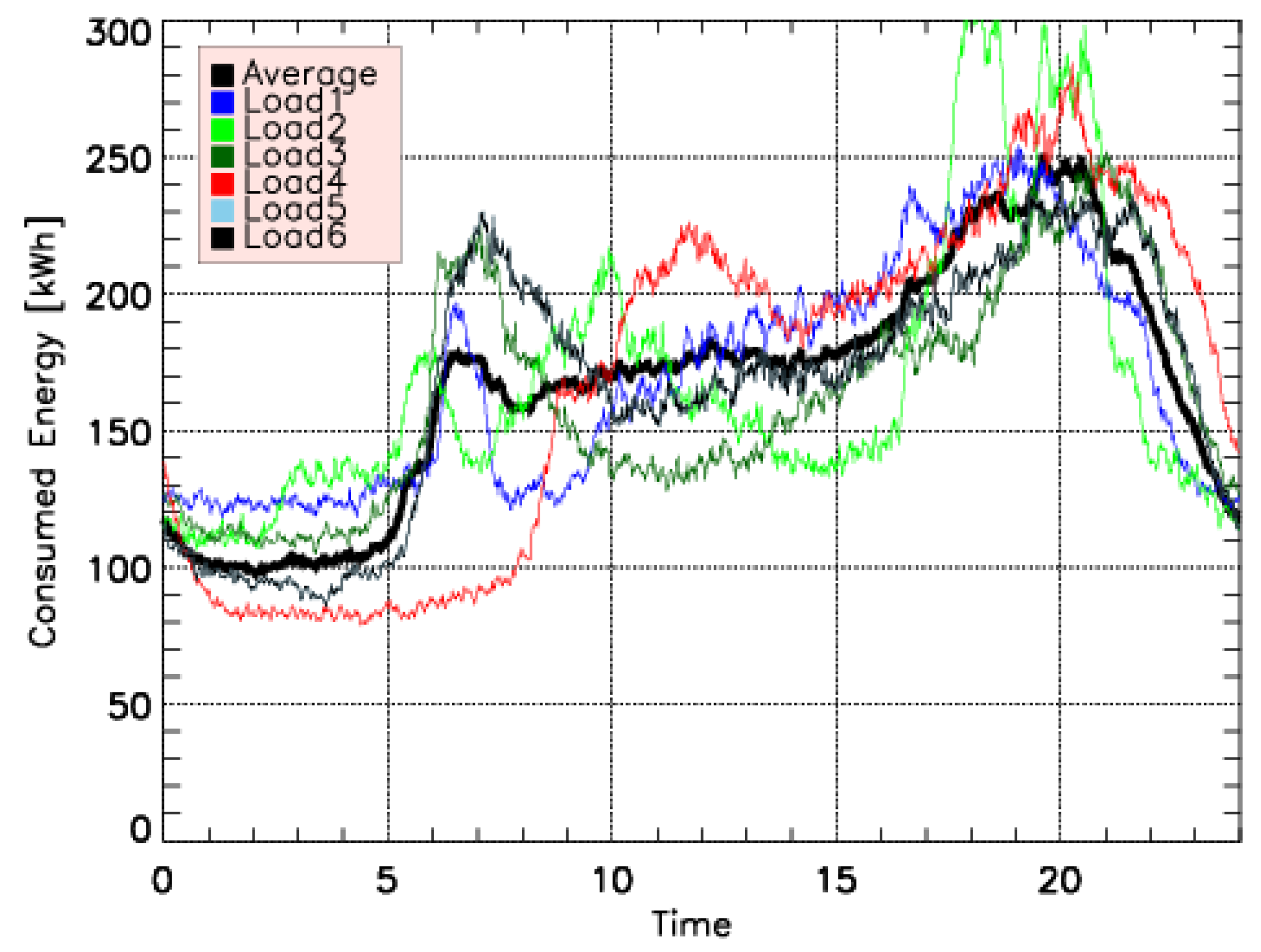
3.1. Load Profile
3.2. Economic Parameters
3.3. PV Software
4. Results and Discussion
4.1. Production and Consumption under Different Weather Conditions
4.2. Annual Insolation
4.3. Effects of the Changing Feed-In Tariffs
4.4. Comparison with PV Software
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| SC | Self-consumption |
| AD | Degree of autarky |
| Power output of the PV system | |
| Rated PV system power | |
| Measured solar irradiance | |
| Solar irradiance at STC (1000 W/m2) | |
| Sensor temperature | |
| γ | Power temperature coefficient |
| Pdu | PV directly used energy |
| PLF | Power loss factor |
| φ | Geographical latitude φ |
| PVg | Total PV generated energy |
| Pe | Electricity price |
| PG | Grid electricity price |
| Pfi, FIT | Feed-in tariff |
| LC | Levelized coast of PV energy |
References
- Jäger-Waldau, A. Snapshot of Photovoltaics 2018. EPJ Photovolt. 2018, 9, 6. [Google Scholar] [CrossRef]
- Ginley, D.; Green, M.A.; Collins, R. Solar energy conversion toward 1 TW. MRS Bull. 2008, 33, 355–364. [Google Scholar] [CrossRef]
- Vartiainen, E.; Breyer, C.; Moser, D.; Medina, E.R. Impact of weighted average cost of capital, capital expenditure, and other parameters on future utility-scale PV levelised cost of electricity. Prog. Photovolt. Res. Appl. 2019, 1–15. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Statistics 2018, The International Renewable Energy Agency. Available online: https://www.irena.org//media/Files/IRENA/Agency/Publication/2019/Mar/RE_capacity_highlights_2019 pdf?la=en&hash=BA9D38354390B001DC0CC9BE03EEE559C280013F (accessed on 26 October 2019).
- Khoo, Y.S.; Nobre, A.; Malhotra, R.; Yang, D.; Ruther, R.; Reindl, T.; Aberle, A.G. Optimal orientation and tilt angle for maximizing in-plane solar irradiation for PV applications in Singapore. IEEE J. Photovolt. 2014, 4, 647–653. [Google Scholar] [CrossRef]
- Hartner, M.; Ortner, A.; Heisl, A.; Haas, R. East to west—The optimal tilt angle and orientation of photovoltaic panels from an electricity system perspective. Appl. Energy 2015, 160, 94–107. [Google Scholar] [CrossRef]
- Seme, S.; Krawczyk, A.; Łada, E.; Tondyra, Š.B.; Hadžiselimović, M. The Efficiency of Different Orientations of Photovoltaic Systems. Przegląd Elektrotechniczny 2017, 93, 201–204. [Google Scholar] [CrossRef][Green Version]
- Ghazi, S.; Ip, K. The effect of weather conditions on the efficiency of PV panels in southeast of UK. Renew. Energy 2014, 69, 50–59. [Google Scholar] [CrossRef]
- Colli, A.; Zaaiman, W.J. Maximum-power-based PV performance validation method: Application to single-axis tracking and Fixed-Tilt c-Si systems in the Italian Alpine region. IEEE J. Photovolt 2012, 2, 555–563. [Google Scholar] [CrossRef]
- Bakirci, K. General models for optimum tilt angles of solar panels: Turkey case study. Renew. Sustain. Energy Rev. 2012, 16, 6149–6159. [Google Scholar] [CrossRef]
- Yan, R.; Saha, T.K.; Meredith, P.; Goodwin, S. Analysis of yearlong performance of differently tilted photovoltaic systems in Brisbane, Australia. Energy Convers. Manag. 2013, 74, 102–108. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J. Optimum fixed orientations and benefits of tracking for capturing solar radiation in the continental United States. Renew. Energy 2011, 36, 1145–1152. [Google Scholar] [CrossRef]
- Agarwal, A.; Vashishtha, V.K.; Mishra, S.N. Comparative approach for the optimization of tilt angle to receive maximum radiation. Int. J. Eng. Res. Technol. 2012, 1, 1–9. [Google Scholar]
- Tang, R.; Wu, T. Optim. tilt-angles for solar collectors used in China. Appl. Energy 2004, 79, 239–248. [Google Scholar] [CrossRef]
- Uba, F.A.; Sarsah, E.A. Optimization of tilt angle for solar collectors in WA, Ghana, Pelagia Research Library. Adv. Appl. Sci. Res. 2013, 4, 108–114. [Google Scholar]
- Huld, T.; Šúri, M.; Dunlop, E.D. Comparison of potential solar electricity output from fixed-inclined and two-axis tracking photovoltaic modules in Europe. Prog. Photovolt. Res. Appl. 2008, 16, 47–59, ISSN 1099-159X. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Quinn, S.W.; Lehman, B.A. Simple formula for the optimum tilt angles of photovoltaic panels. In Proceedings of the IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), Salt Lake City, UT, USA, 23–26 June 2013; pp. 1–8. [Google Scholar]
- Beringer, S.; Schilke, H.; Lohse, I.; Seckmeyer, G. Case study showing that the tilt angle of photovoltaic plants is nearly irrelevant. Sol. Energy 2011, 85, 470–476. [Google Scholar] [CrossRef]
- Bodis, K.; Kougias, I.; Jäger-Waldau, A.; Taylor, N.; Szabo, S. A high-resolution geospatial assessment of the rooftop solar photovoltaic potential in the European Union. Renew. Sustain. Energy Rev. 2019, 114, 109309. [Google Scholar] [CrossRef]
- Mertens, K. Photovoltaics: Fundamentals, Technology and Practice, 1st ed.; John Wiley & Sons, Ltd. Published: Hoboken, NJ, USA, 2014. [Google Scholar]
- Luthander, R. Photovoltaic System Layout for Optimized Self-Consumption. Uppsala Universitet. 2013. Available online: http://www.diva-portal.org/smash/get/diva2:637625/FULLTEXT01.pdf (accessed on 26 November 2019).
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the influence of the temporal resolution of electrical load and PV generation profiles on self-consumption and sizing of PV-battery systems. Appl. Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Luthander, R.; Widen, J.; Nilsson, D.; Palm, J. Photovoltaic self consumprion in buidings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Leicester, P.A.; Rowley, P.N.; Goodier, C.I. Probabilistic analysis of solar photovoltaic self-consumption using Bayesian network models. IET Renew. Power Gener. 2016, 10, 448–455. [Google Scholar] [CrossRef]
- Martín, A.M.; Domínguez, J.; Amador, J. Applying LIDAR datasets and GIS based model to evaluate solar potential over roofs: A review. AIMS Energy 2015, 3, 326–343. [Google Scholar] [CrossRef]
- PVSOL. PV*SOL Online—A Free Tool Forsolar Power (PV) Systems. 2019. Available online: http://pvsol-online.valentin-software.com/#/ (accessed on 6 May 2019).
- PVSyst, Version, 6.79; [Computer Software]; University of Geneva: Geneva, Switzerland, 2019.
- DGS. EnergyMap.info; Deutsche Gesellschaft für Sonnenenergie e.V.: Berlin, Germany, 2015. [Google Scholar]
- PVGIS. Overview of PVGIS data sources and calculation methods. European Commission. Available online: http://re.jrc.ec.europa.eu/pvg_static/methods.html (accessed on 26 November 2019).
- Idoko, L.; Anaya-Lara, O.; McDonald, A. Enhancing PV modules efficiency and power output using multi-concept cooling technique. Energy Rep. 2018, 4, 357–369. [Google Scholar] [CrossRef]
- Tjaden, T.; Bergner, J.; Weniger, J.; Quaschning, V. Repräsentative elektrische Lastprofile für Wohngebäude in Deutschland auf 1-sekündiger Datenbasis. Technical report, Berlin, Germany. Hochschule für Technik und Wirtschaft HTW Berlin. Available online: https://pvspeicher.htw-berlin.de/wp-content/uploads/2017/05/HTW-BERLIN-2015-Repr%C3%A4sentative-elektrische-Lastprofile-f%C3%BCr-Wohngeb%C3%A4ude-in-Deutschland-auf-1-sek%C3%BCndiger-Datenbasis.pdf (accessed on 26 November 2019).
- Haysom, J.E.; Hinzer, K.; Wright, D. Impact of electricity tariffs on optimal orientation of photovoltaic modules. Prog. Photovolt. Res. Appl. 2015, 24, 253–260. [Google Scholar] [CrossRef]
- Jager-Waldau, A.; Bucher, C.; Frederiksen, K.H.B.; Guerro-Lemus, R.; Mason, G.; Mather, B.; Mayr, C.; Moneta, D.; Nikoletatos, J.; Roberts, M.B. Self-consumption of electricity produced from PV systems in apartment buildings—Comparison of the situation in Australia, Austria, Denmark, Germany, Greece, Italy, Spain, Switzerland and the USA. In Proceedings of the 2018 IEEE 7th World Conf. Photovolt. Energy Conversion, WCPEC 2018—A Jt. Conf. 45th IEEE PVSC, 28th PVSEC 34th EU PVSEC 1424–1430, Waikoloa Village, HI, USA, 10–15 June 2018. [Google Scholar] [CrossRef]
- Mojonero, D.H.; Villacorta, A.R.; Kuong, J.L. Impact assessment of net metering for residential photovoltaic distributed generation in Peru. Int. J. Renew. Energy Res. 2018, 8, 1200–1207. [Google Scholar]
- Pereira da Silva, P.; Dantas, G.; Pereira, G.I.; Câmara, L.; De Castro, N.J. Photovoltaic distributed generation—An international review on diffusion, support policies, and electricity sector regulatory adaptation. Renew. Sustain. Energy Rev. 2019, 103, 30–39. [Google Scholar] [CrossRef]
- BDEW. BDEW-Strompreisanalyse (Haushalte und Industrie). Available online: https://www.bdew.de/me-dia/documents/190115_BDEW-Strompreisanalyse_Januar-2019.pdf (accessed on 28 January 2019).
- Fraunhofer Institute for Solar Energy Systems (ISE). Levelized Cost of Electricity Renewable Energy Technologies; Fraunhofer Institute for Solar Energy Systems (ISE): Freiburg, Germany, 2018. [Google Scholar]
- Stenzel, P.; Linssen, J.; Fleer, J.; Busch, F. Impact of temporal resolution of supply and demand profiles on the design of photovoltaic battery systems for increased self-consumption. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar]
- Talavera, D.L.; Nofuentes, G.; Aguilera, J. The Internal Rate of Return of Photovoltaic Grid-Connected Systems: A Comprehensive Sensitivity. Renew. Energy 2010, 35, 101–111. [Google Scholar] [CrossRef]
- Tapia, M. Evaluation of Performance Models against Actual Performance of Grid Connected PV Systems. Master’s Thesis, Carl von Ossietzky Universität, Oldenburg, Germany, 2014. [Google Scholar]
- Fraunhofer ISE. Recent Facts about Photovoltaics in Germany; Fraunhofer Institute for Solar Energy Systems ISE: Freiburg, Gemmary, 2019. [Google Scholar]
- Obane, H.; Okajima, K. Extracting issues significant to valuing electricity from small photovoltaic systems using quantitative content analysis. Electr. J. 2019, 32, 106673. [Google Scholar] [CrossRef]
- Solar Power Europe. Global Market Outlook for Solar Power 2018–2022; Solar Power Europe: Brussels, Belgium, 2018. [Google Scholar]
- Mubarak, R.; Hofmann, M.; Riechelmann, S.; Seckmeyer, G. Comparison of modelled and measured tilted solar irradiance for photovoltaic applications. Energies 2017, 10, 1688. [Google Scholar] [CrossRef]
- Hofmann, M.; Seckmeyer, G. Influence of various irradiance models and their combination on simulation results of photovoltaic systems. Energies 2017, 10, 1495. [Google Scholar] [CrossRef]
- Hofmann, M.; Seckmeyer, G. A New Model for Estimating the Diffuse Fraction of Solar Irradiance for PV System Simulations. Energies 2017, 10, 248. [Google Scholar] [CrossRef]
- Seckmeyer, G.; Lagos Rivas, L.; Gaetani, C.; Heinzel, J.W.; Schrempf, M. Biologische und medizinische Wirkungen solarer Strahlung (Biological and medical effects of solar radiation). In Promet, Heft 100 Strahlungsbilanzen; Chapter 13; Deutscher Wetterdienst (DWD): Offenbach am Main, Germany, 2018. [Google Scholar]
- Riechelmann, S.; Schrempf, M.; Seckmeyer, G. Simultaneous measurement of spectral sky radiance by a non-scanning multidirectional spectroradiometer (MUDIS). Meas. Sci. Technol. 2013, 24, 125501. [Google Scholar] [CrossRef]







| East | ← | Azimuth | → | West | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tilt | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| 0 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | 86 |
| 10 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 92 | 93 | 93 | 93 | 92 | 92 | 91 | 90 | 89 | 88 | 87 | 86 |
| 20 | 84 | 86 | 88 | 90 | 92 | 94 | 95 | 96 | 97 | 97 | 97 | 96 | 96 | 94 | 93 | 91 | 89 | 87 | 84 |
| 30 | 81 | 84 | 87 | 90 | 93 | 95 | 97 | 98 | 99 | 99 | 99 | 98 | 97 | 96 | 93 | 91 | 88 | 85 | 81 |
| 40 | 78 | 82 | 85 | 89 | 92 | 94 | 96 | 98 | 99 | 100 | 99 | 98 | 97 | 95 | 92 | 89 | 86 | 82 | 78 |
| 50 | 74 | 78 | 82 | 86 | 89 | 92 | 94 | 96 | 97 | 97 | 97 | 96 | 95 | 92 | 90 | 87 | 83 | 79 | 74 |
| 60 | 70 | 74 | 78 | 82 | 85 | 88 | 90 | 92 | 93 | 93 | 93 | 92 | 91 | 89 | 86 | 82 | 79 | 74 | 70 |
| 70 | 65 | 69 | 73 | 76 | 80 | 82 | 84 | 86 | 87 | 87 | 87 | 86 | 85 | 83 | 80 | 77 | 73 | 69 | 65 |
| 80 | 59 | 63 | 67 | 70 | 73 | 75 | 77 | 78 | 79 | 80 | 79 | 79 | 78 | 76 | 73 | 70 | 67 | 64 | 60 |
| 90 | 53 | 57 | 60 | 63 | 65 | 67 | 69 | 69 | 70 | 70 | 70 | 70 | 69 | 68 | 66 | 63 | 60 | 57 | 54 |
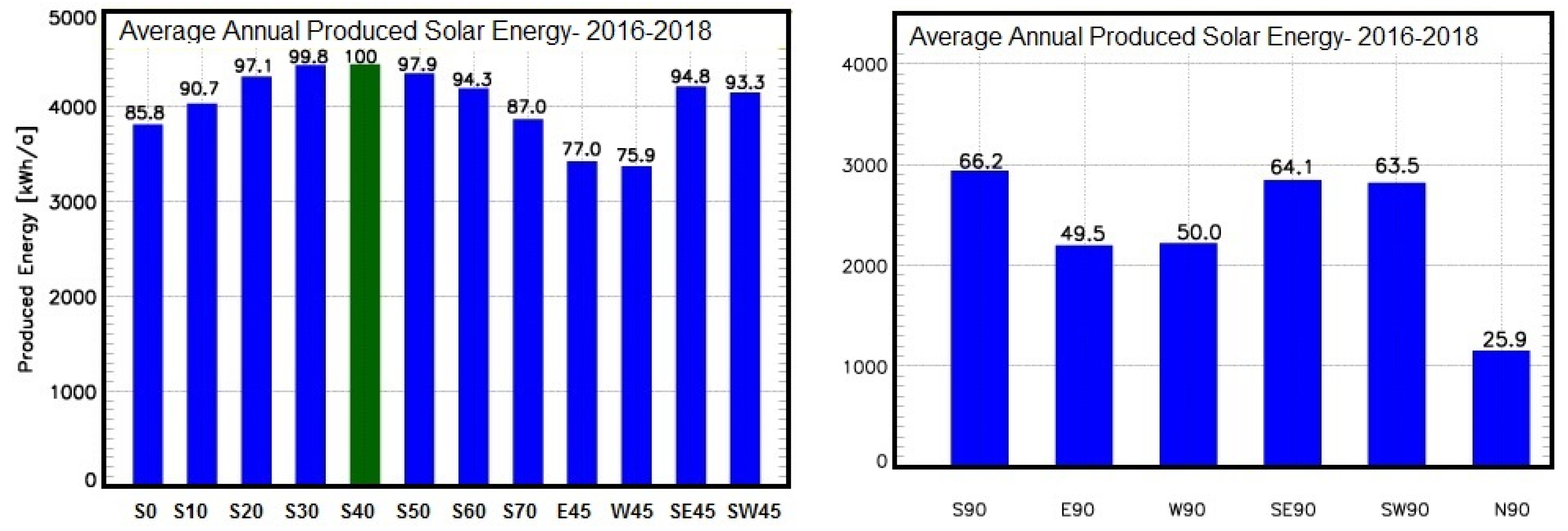
| Orientation | S45 | E45 | W45 | E45+W45 | SE45 | SW45 | SE45 + SW45 | S90 | E90 | W90 | SE90 | SW90 | N90 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Percentage of SS45 (%) | 100 | 76.2 | 75.0 | 75.6 | 94.6 | 93.1 | 93.8 | 66.8 | 49.8 | 50.3 | 64.6 | 64.4 | 25.8 | |
| Annual PV Generation (kWh/a) | 4145 | 3157 | 3111 | 3134 | 3921 | 3859 | 3890 | 2769 | 2064 | 2046 | 2678 | 2655 | 1069 | |
| SC rate (%) | 37.9 | 44.9 | 47.9 | 51.4 | 38.6 | 40.7 | 41.9 | 50.9 | 57.4 | 66.2 | 50.0 | 55.4 | 95.1 | |
| Autarky (%) | 39.2 | 35.4 | 37.2 | 40.3 | 37.8 | 39.2 | 40.7 | 35.2 | 29.6 | 34.5 | 33.4 | 36.7 | 25.4 | |
| Cost Ct/kWh | No FIT | 29.5 | 30.7 | 30.1 | 29.2 | 30.5 | 29.5 | 29.1 | 30.9 | 32.7 | 31.1 | 31.4 | 30.4 | 34.0 |
| With FIT | 22.0 | 25.6 | 25.3 | 24.7 | 23.0 | 22.8 | 22.5 | 27.0 | 30.2 | 29.1 | 27.6 | 27.1 | 33.9 | |
| IRR % Over 20 ys | No FIT | 1.59 | 0.20 | 0.84 | 1.90 | 1.10 | 1.57 | 2.09 | 0.13 | −2.15 | −0.19 | −0.53 | 0.70 | −4.23 |
| With FIT | 7.05 | 4.13 | 4.42 | 5.14 | 6.29 | 6.45 | 6.82 | 3.23 | 0.12 | 1.45 | 2.61 | 3.33 | −4.10 | |
| Parameter | Model (PVSol, PVSyst) |
|---|---|
| Modules | 4.8 kWp, mono, 24 modules |
| Inverter | ABB, 4.6 kW |
| Climate data | Meteonorm 7.2 |
| Transposition model | Perez-Ineichen model |
| Diffuse radiation model | Perez model |
| Orientation | S45 | E45 | W45 | E45 + W45 | SE45 | SW45 | SE45 + SW45 | S90 | E90 | W90 | SE90 | SW90 | NN90 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PVsyst | |||||||||||||
| Annual PV (kWh) | 4457 | 3596 | 3531 | 3564 | 4250 | 4174 | 4212 | 3161 | 2439 | 2362 | 3053 | 2938 | 1148 |
| Percentage of the max (%) | 100 | 79.5 | 79.3 | 78.7 | 94.8 | 94.1 | 93.9 | 71.0 | 55.1 | 54.6 | 68.4 | 67.2 | 26.0 |
| SC (%) | 32.9 | 40.7 | 38.9 | 43.1 | 34.9 | 33.9 | 36.1 | 40.7 | 49.5 | 46.6 | 42.3 | 40.9 | 85.7 |
| AD (%) | 36.2 | 35.6 | 34.0 | 37.4 | 36.4 | 35.1 | 37.3 | 31.8 | 30.1 | 28.0 | 31.9 | 30.3 | 24.6 |
| PVSOL | |||||||||||||
| Annual PV (kWh) | 4330 | 3425 | 3046 | 3148 | 4160 | 3857 | 3920 | 3012 | 2289 | 1975 | 2945 | 2629 | 1115 |
| Percentage of the max (%) | 100 | 77.8 | 68.7 | 71.3 | 95.9 | 88.3 | 90.1 | 69.9 | 53.1 | 45.9 | 68.4 | 61.1 | 25.8 |
| SC (%) | 32.3 | 39.9 | 43.1 | 44.5 | 33.4 | 35.6 | 35.6 | 40.7 | 50.4 | 57.0 | 41.5 | 45.6 | 89.0 |
| AD (%) | 34.7 | 33.4 | 31.9 | 34.1 | 34.5 | 33.8 | 34.5 | 30.6 | 28.8 | 28.1 | 30.5 | 29.9 | 24.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mubarak, R.; Weide Luiz, E.; Seckmeyer, G. Why PV Modules Should Preferably No Longer Be Oriented to the South in the Near Future. Energies 2019, 12, 4528. https://doi.org/10.3390/en12234528
Mubarak R, Weide Luiz E, Seckmeyer G. Why PV Modules Should Preferably No Longer Be Oriented to the South in the Near Future. Energies. 2019; 12(23):4528. https://doi.org/10.3390/en12234528
Chicago/Turabian StyleMubarak, Riyad, Eduardo Weide Luiz, and Gunther Seckmeyer. 2019. "Why PV Modules Should Preferably No Longer Be Oriented to the South in the Near Future" Energies 12, no. 23: 4528. https://doi.org/10.3390/en12234528
APA StyleMubarak, R., Weide Luiz, E., & Seckmeyer, G. (2019). Why PV Modules Should Preferably No Longer Be Oriented to the South in the Near Future. Energies, 12(23), 4528. https://doi.org/10.3390/en12234528





