Simulation of the Dynamic Characteristics of a PEMFC System in Fluctuating Operating Conditions
Abstract
1. Introduction
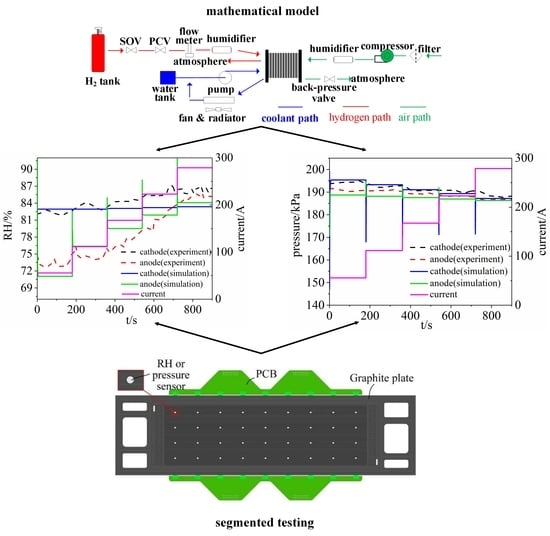
2. Mathematical Model and Experimental Platform
- (a)
- The gas dynamics follow the ideal gas equation of state (EoS).
- (b)
- Temperature, pressure and humidity distributed uniformly.
- (c)
- The stack operated well during the calculating period, local clogging, flooding and their influence on the stack state were not considered in this paper.
- (d)
- The water management was not considered in the model of water dynamics.
2.1. Operational Voltage
2.2. Fluid Physics
2.2.1. Gas Flow into the Stack
2.2.2. Humidifier
2.2.3. Supply Manifolds
2.2.4. Cathode Channel
2.2.5. Anode Channel
2.2.6. Cathode Exhaust Manifolds
2.2.7. Anode Exhaust Manifolds
2.2.8. Back-Pressure Valve
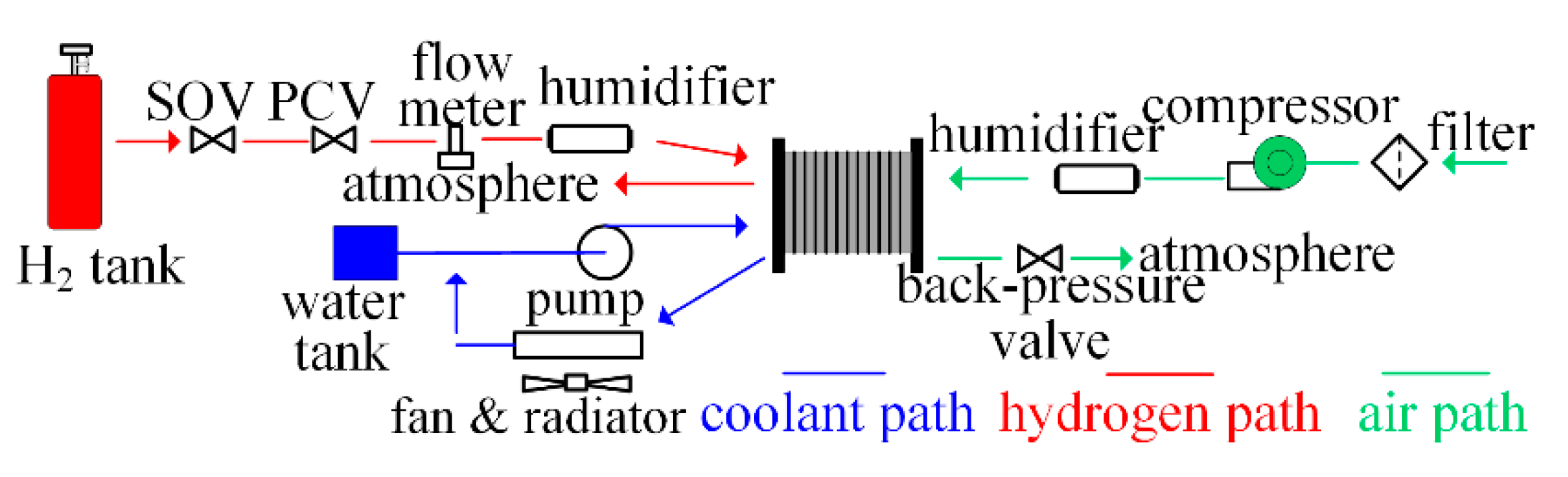
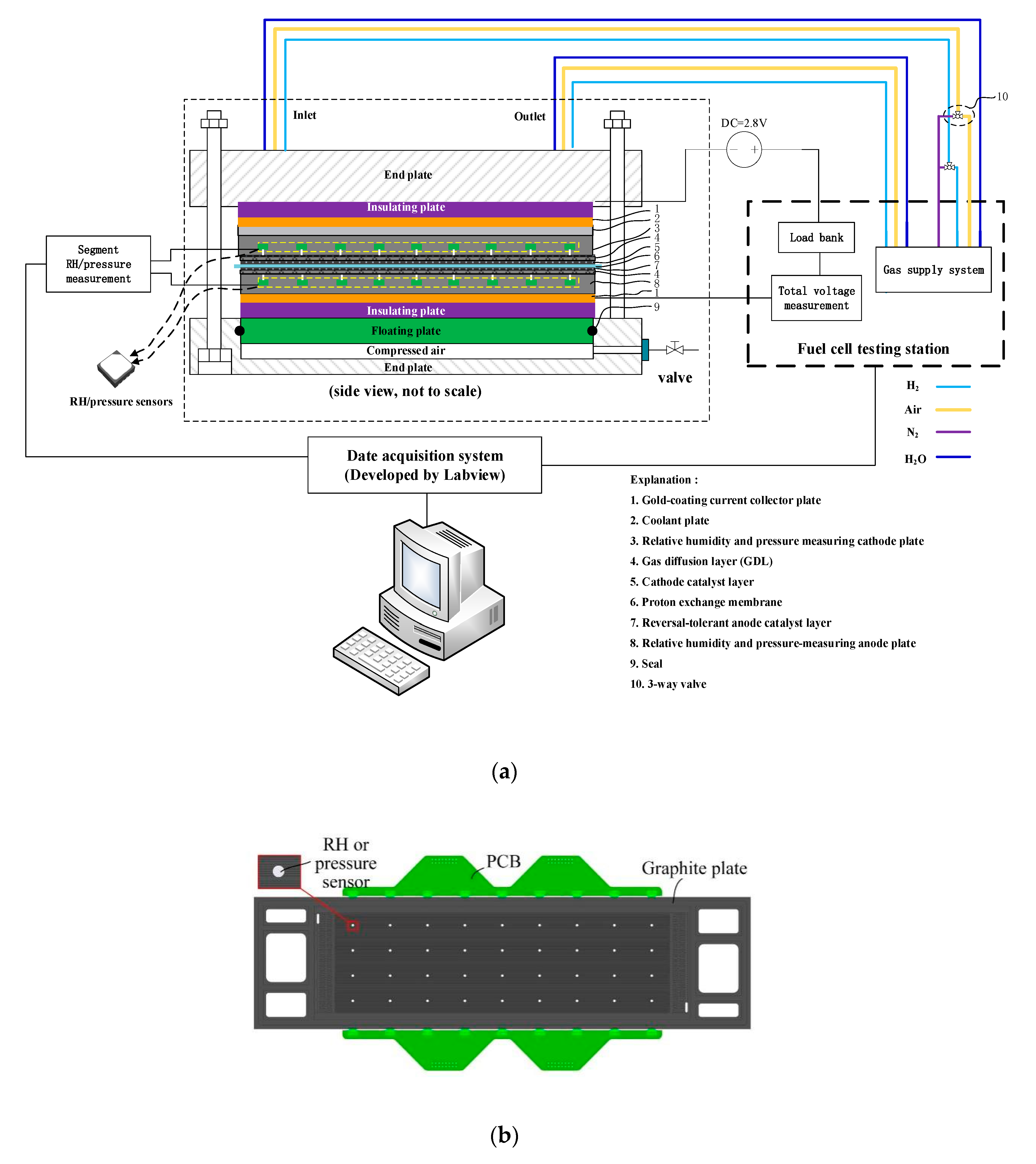
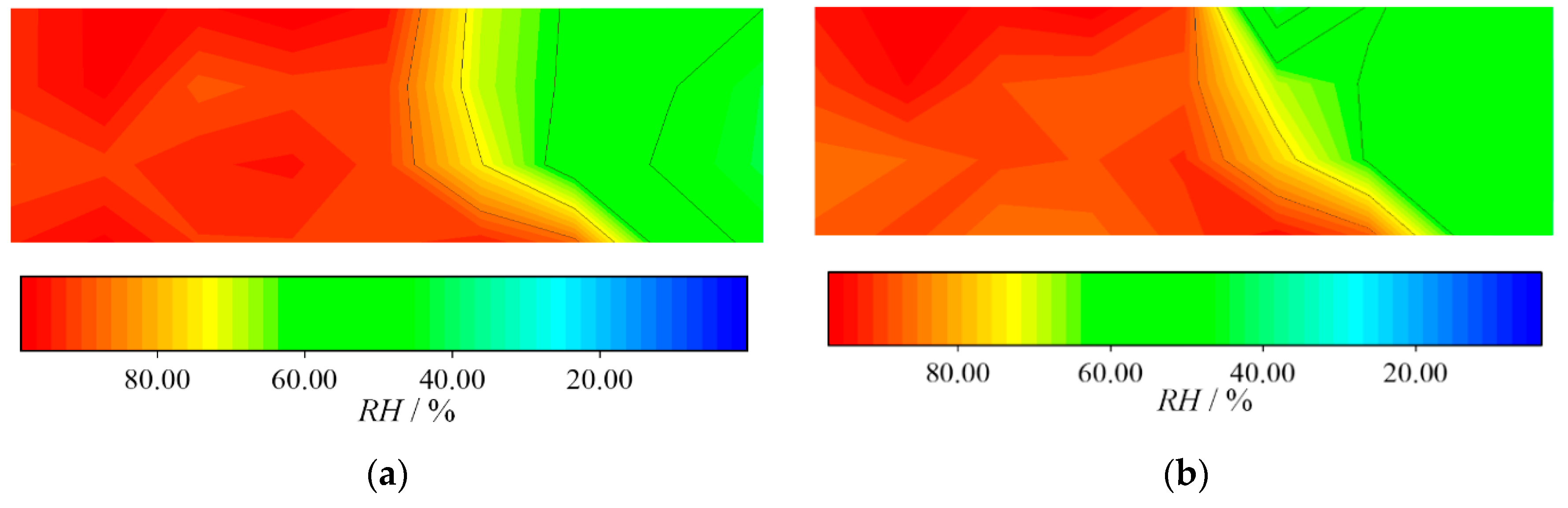
2.3. Segmented Cell Testing Experiment to Verify the Model
2.4. Calculations and Experimental Conditions
3. Results and Model Verification
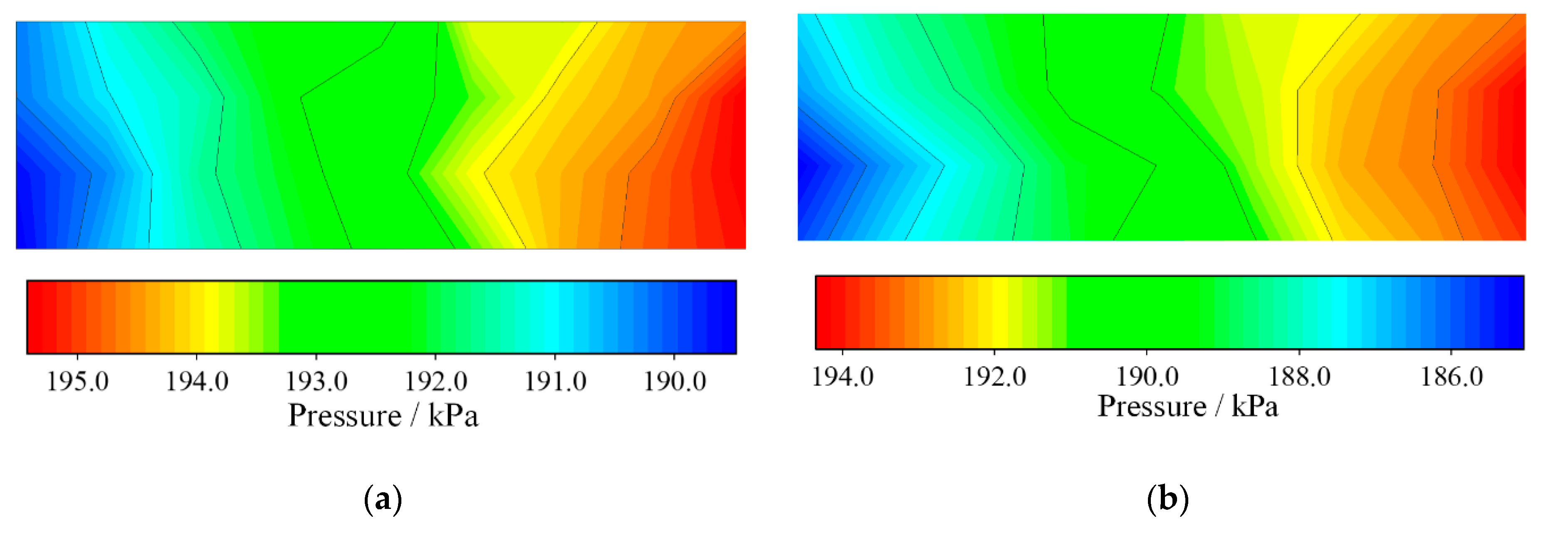
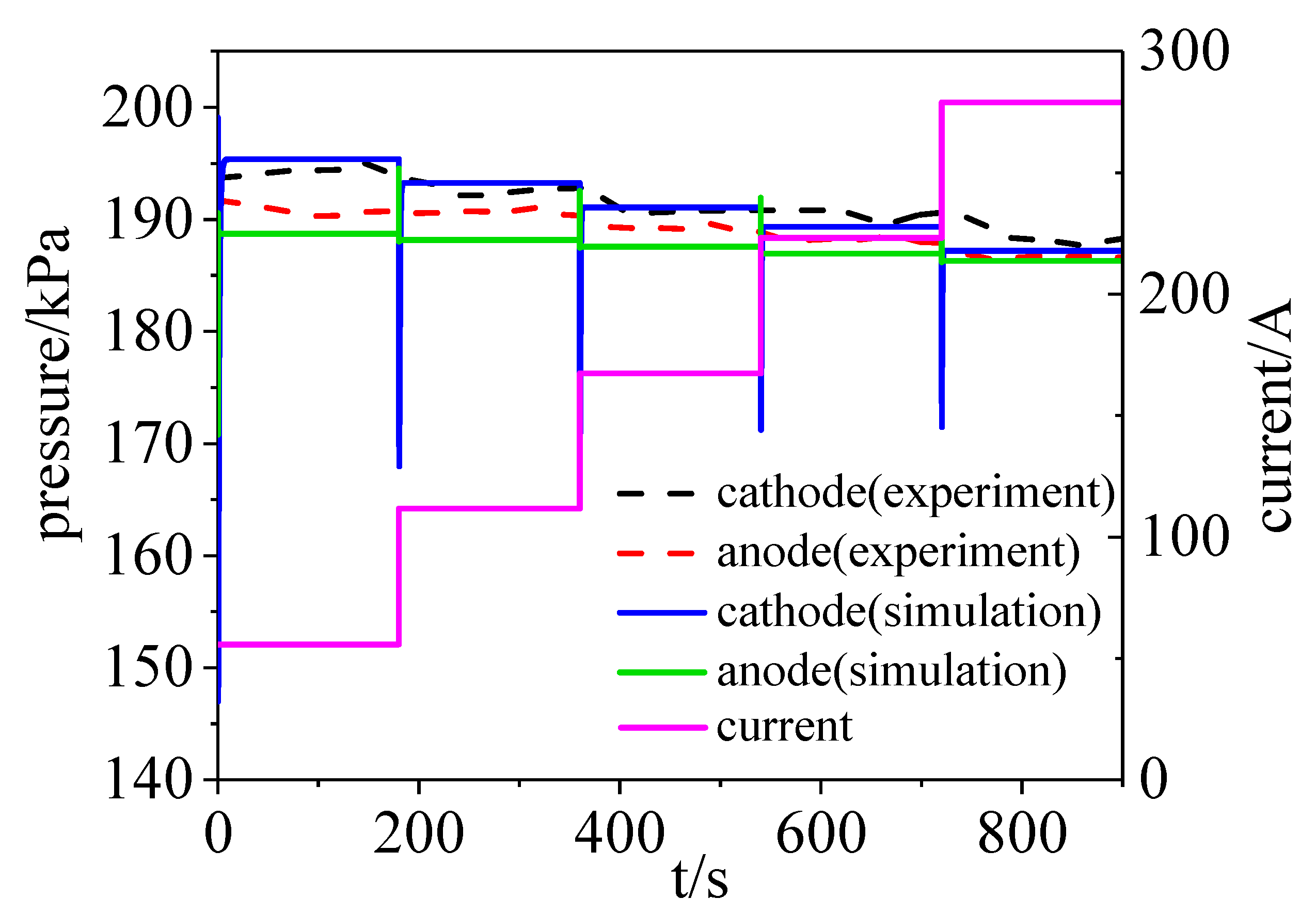
3.1. Pressure Dynamics
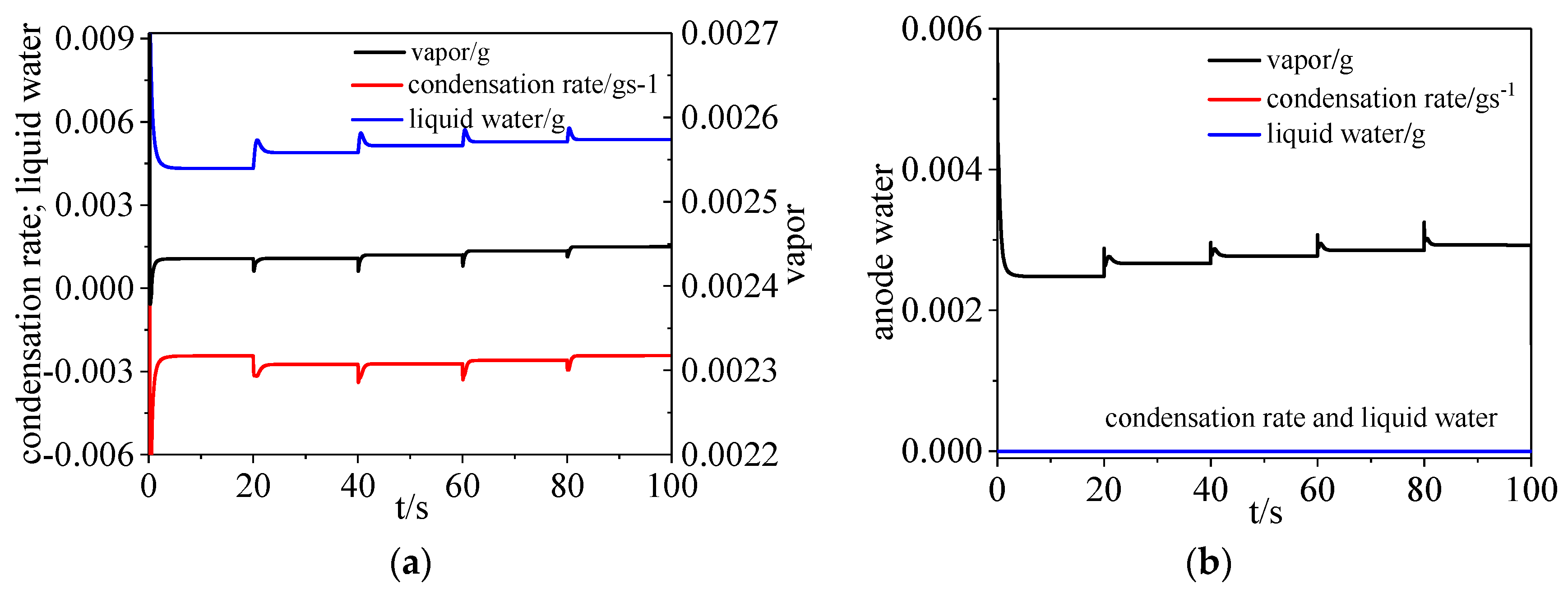
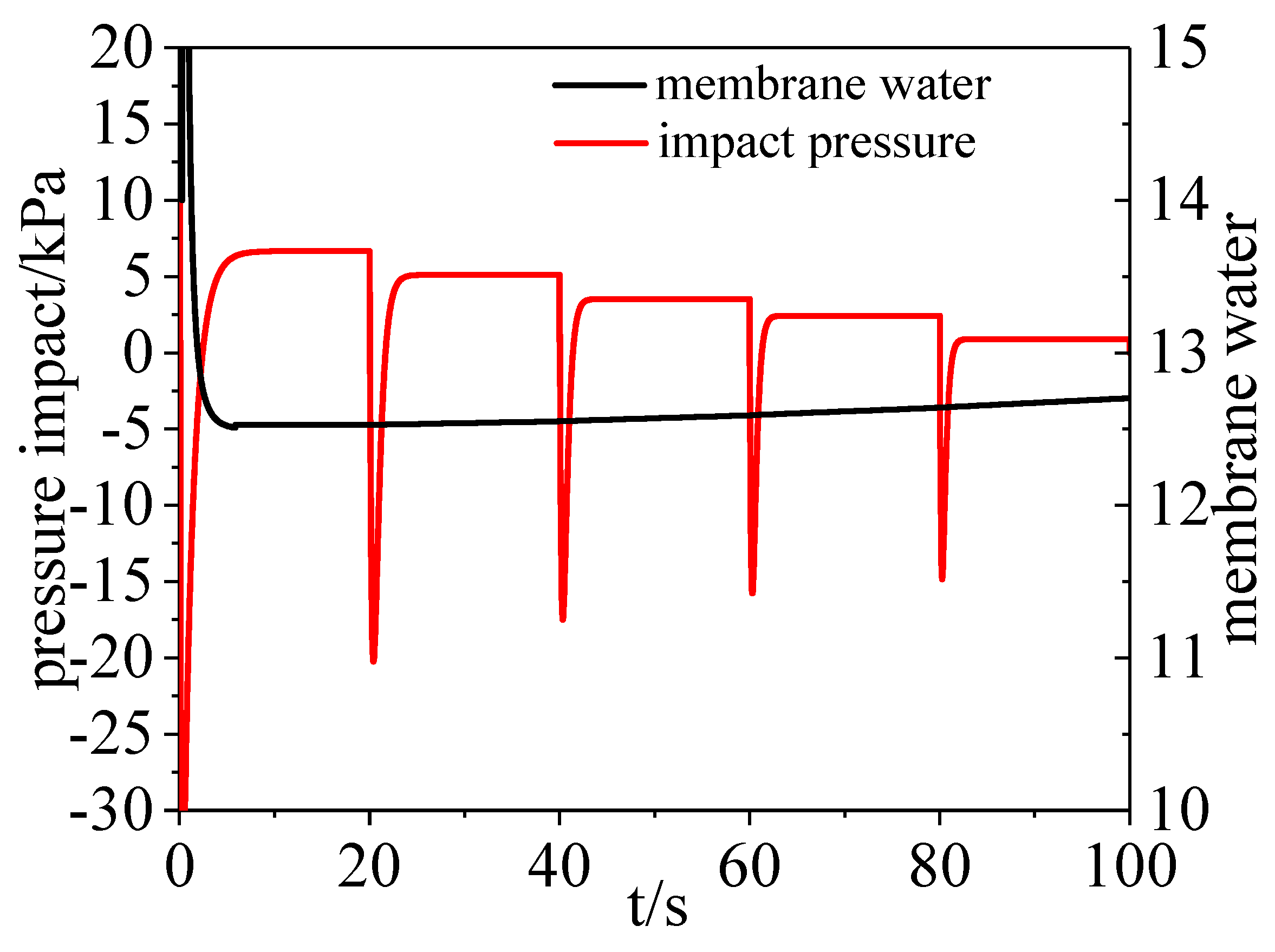
3.2. Water Dynamics
4. Discussion
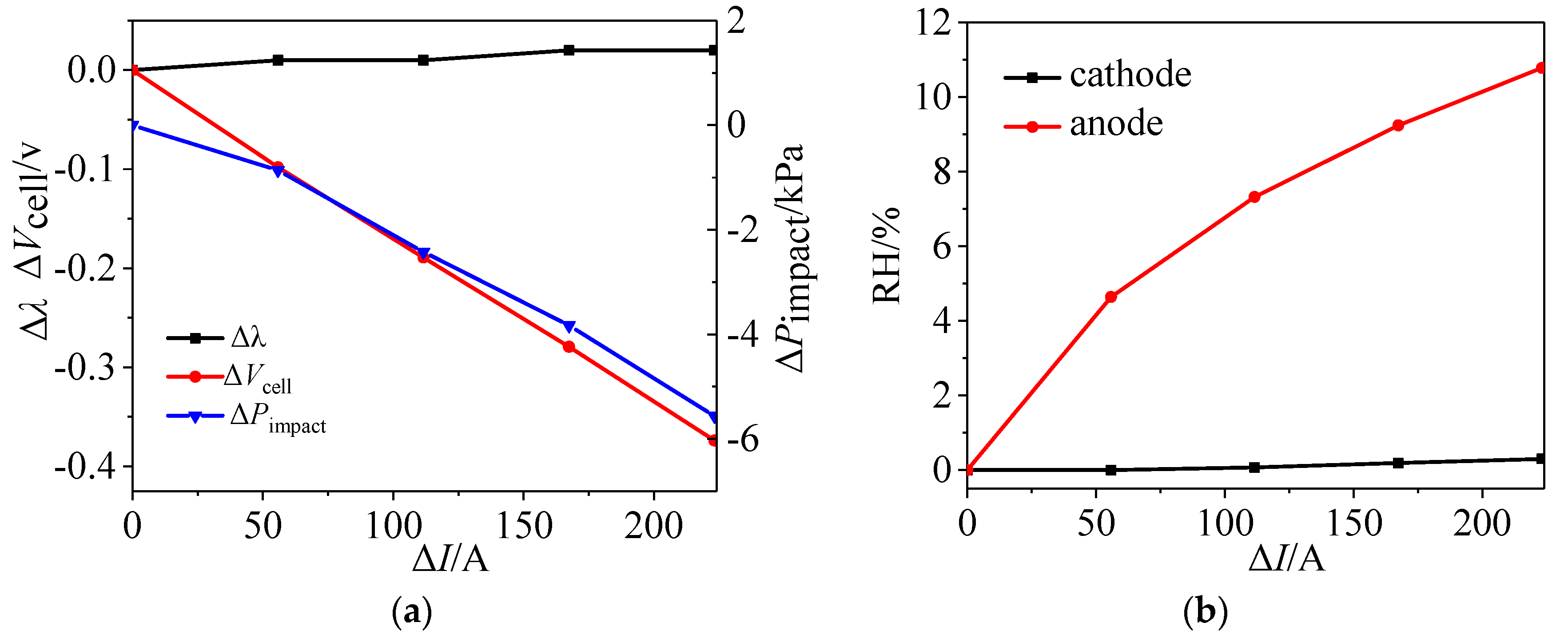
4.1. Role of Load Change Magnitude
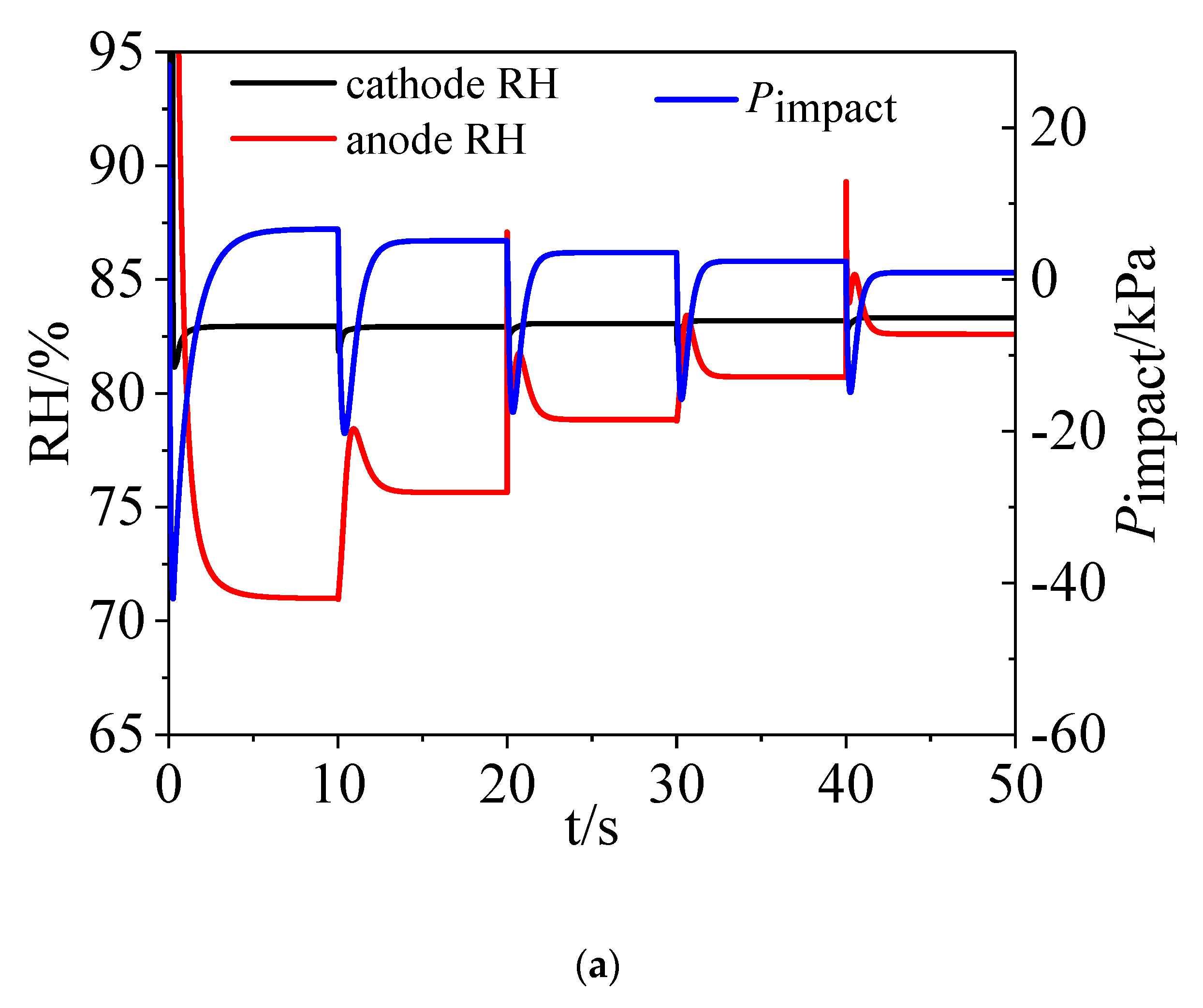
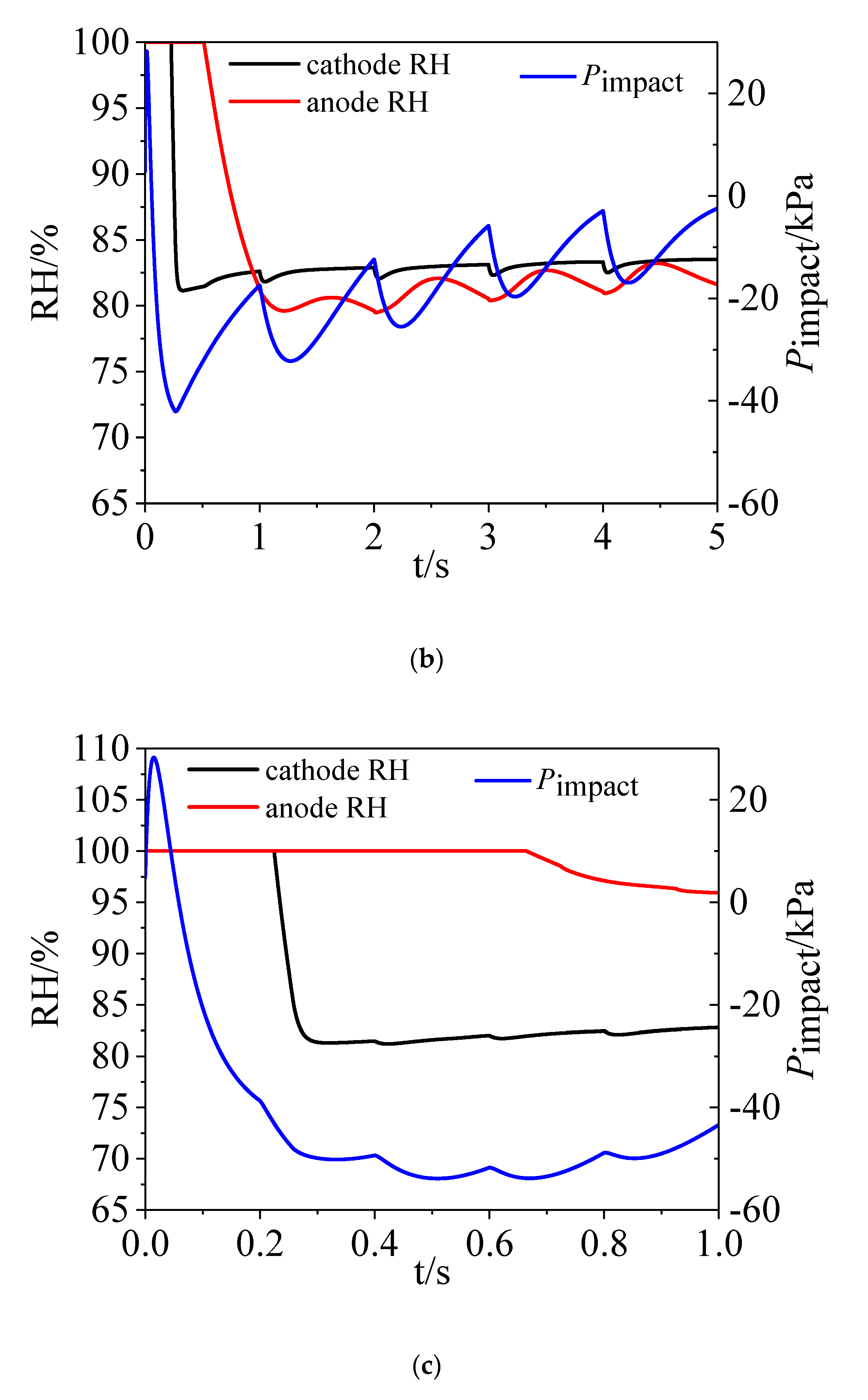
4.2. Role of Time Interval of Load Change
5. Conclusions
- A complete model involving a PEMFC stack and its accessories was built in this paper, and it was verified to some extent by a segmented testing experiment. This model can be used to simulate the dynamic state inside the stack.
- The pressure in the channels, and exhaust manifolds declined with increasing current. The transient pressure difference between the cathode and anode sides had a huge impact on the MEA.
- On the cathode side, the vapor and liquid water increased when the load current increased. On the anode side, water vapor increased with time while there was hardly any liquid water and water condensation existing in the channel.
- Changes in the outside load definitely influenced the stack’s stability in terms of pressure, water, and voltage. When the magnitude of the current change increased, the stack state underwent greater fluctuation. If the load varied in a short enough time, the stack components and physical processes could not reach equilibrium.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aaldering, L.J.; Song, C.H. Tracing the technological development trajectory in post-lithium-ion battery technologies: A patent-based approach. J. Clean. Prod. 2019, 241, 1–18. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Available online: https://www.energy.gov/eere/fuelcells/hydrogen-and-fuel-cells-annual-progress-reports (accessed on 1 April 2019).
- China Nengyuan.com. Available online: http://www.china-nengyuan.com/news/141562.html (accessed on 2 July 2019).
- Bao, C.; Ouyang, M.; Yi, B. Modeling and control of air stream and hydrogen flow with recirculation in a PEM fuel cell system—I. control-oriented modeling. Int. J. Hydrog. Energy 2006, 31, 1879–1896. [Google Scholar] [CrossRef]
- Springe, T.E.; Zawodzinski, T.; Gottesfeld, A.S. Polymer electrolyte fuel cell model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Xu, L.; Fang, C.; Hu, J. Parameter extraction and uncertainty analysis of a proton exchange membrane fuel cell system based on Monte Carlo simulation. Int. J. Hydrog. Energy 2017, 42, 2309–2326. [Google Scholar] [CrossRef]
- Peron, J.; Mani, A.; Zhao, X. Properties of Nafion® NR-211 membranes for PEMFCs. J. Membr. Sci. 2010, 356, 44–51. [Google Scholar] [CrossRef]
- Deevanhxay, P.; Sasabe, T.; Tsushima, S.; Hirai, S. In situ diagnostic of liquid water distribution in cathode catalyst layer in an operating PEMFC by high-resolution soft X-ray radiography. Electrochem. Commun. 2012, 22, 33–36. [Google Scholar] [CrossRef]
- Deevanhxay, P.; Tsushima, S.; Hirai, S. Investigation on the effect of microstructure of proton exchange membrane fuel cell porous layers on liquid water behavior by soft X-ray radiography. J. Power Sources 2011, 196, 8197–8206. [Google Scholar]
- Suzuki, T.; Tabuchi, Y.; Tsushima, S. Measurement of water content distribution in catalyst coated membranes under water permeation conditions by magnetic resonance imaging. Int. J. Hydrog. Energy 2011, 36, 5479–5486. [Google Scholar] [CrossRef]
- Jay, B. Fan the flame with water: Current ignition, front propagation and multiple steady states in polymer electrolyte membrane fuel cells. AICHE J. 2009, 55, 3034–3040. [Google Scholar]
- Erin, K.; Tamara, W.; Yannis, K.; Jay, B. Drops, slugs, and flooding in polymer electrolyte membrane fuel cells. AICHE J. 2008, 54, 1313–1320. [Google Scholar]
- Luna, J.; Jemei, S.; Yousfifi-Steiner, N.; Husar, A.; Serra, M. Nonlinear predictive control for durability enhancement and efficiency improvement in a fuel cell power system. J. Power Sources 2016, 328, 250–261. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cell: Theory and Practice, 2nd ed.; Elsevier Press: Amsterdam, The Netherlands, 2012; p. 25. [Google Scholar]
- Fang, C. Fuel Cell Engine Control Based on Reduced Dimension Model. Ph.D. Thesis, Tsinghua University, Beijing, China, 2017. [Google Scholar]
- Hua, J.; Li, J.; Ouyang, M. Proton exchange membrane fuel cell system diagnosis based on the multivariate statistical method. Int. J. Hydrog. Energy 2011, 36, 9896–9905. [Google Scholar] [CrossRef]
- Hong, P.; Xu, L.; Li, J. Modeling and analysis of internal water transfer behavior of PEM fuel cell of large surface area. Int. J. Hydrog. Energy 2017, 42, 18540–18550. [Google Scholar] [CrossRef]
- Sui, P.; Zhu, X.; Djilali, N. Modeling of PEM fuel cell catalyst layers: Status and outlook. Electrochem. Energy Rev. 2019, 2, 428–466. [Google Scholar] [CrossRef]
- Tian, N.; Lu, B.; Yang, X. Rational design and synthesis of low-temperature fuel cell electrocatalysts. Electrochem. Energy Rev. 2018, 1, 54–83. [Google Scholar] [CrossRef]
- Xu, L.; Fang, C.; Hu, J. Self-humidification of a polymer electrolyte membrane fuel cell system with cathodic exhaust gas recirculation. J. Electrochem. Energy Convers. Storage 2018, 15, 1–18. [Google Scholar] [CrossRef]
- Hong, P.; Xu, L.; Li, J. Modeling of membrane electrode assembly of PEM fuel cell to analyze voltage losses inside. Energy 2017, 139, 277–288. [Google Scholar] [CrossRef]
- Xu, L.; Fang, C.; Li, J. Nonlinear dynamic mechanism modeling of a polymer electrolyte membrane fuel cell with dead-ended anode considering mass transport and actuator properties. Appl. Energy 2018, 230, 106–121. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, L.; Li, J. Performance prediction of proton exchange membrane fuel cell engine thermal management system using 1D and 3D integrating numerical simulation. Int. J. Hydrog. Energy 2018, 43, 1736–1748. [Google Scholar] [CrossRef]
- Pasaogullari, U.; Mukherjee, P.; Wang, C.; Chen, K. Anisotropie heat and water transport in a PEFC cathode gas diffusion layer. J. Electrochem. Soc. 2007, 154, B823. [Google Scholar] [CrossRef]
- Vladimir, G.; Adin, M. A critical overview of computational fluid dynamics multiphase models for proton exchange membrane fuel cells. SIAM J. Appl. Math 2009, 70, 410–454. [Google Scholar]
- Lin, R.; Lin, X.; Weng, Y. Evolution of thermal drifting during and after cold start of proton exchange membrane fuel cell by segmented cell technology. Int. J. Hydrog. Energy 2015, 40, 7370–7381. [Google Scholar] [CrossRef]
- Lin, R.; Weng, Y.; Li, Y. Internal behavior of segmented fuel cell during cold start. Int. J. Hydrog. Energy 2014, 39, 16025–16035. [Google Scholar] [CrossRef]
- Pei, H.; Liu, Z.; Zhang, H. In situ measurement of temperature distribution in proton exchange membrane fuel cell I a hydrogeneair stack. J. Power Sources 2013, 227, 72–79. [Google Scholar] [CrossRef]
- Lin, R.; Cui, X.; Shan, J. Investigating the effect of start-up and shut-down cycles on the performance of the proton exchange membrane fuel cell by segmented cell technology. Int. J. Hydrog. Energy 2015, 40, 14952–14962. [Google Scholar] [CrossRef]
- Lin, R.; Xiong, F.; Tang, W. Investigation of dynamic driving cycle effect on the degradation of roton exchange membrane fuel cell by segmented cell technology. J. Power Sources 2014, 260, 150–158. [Google Scholar] [CrossRef]
- Dutta, S.; Shimpalee, S.; Zee, J. Numerical prediction of mass-exchange between cathode and anode channels in a PEM fuel cell. Int. J. Heat Mass Transf. 2001, 44, 2029–2042. [Google Scholar] [CrossRef]
- May, C.; Ioannis, K.; Jay, B. Water slug formation and motion in gas flow channels: The effects of geometry, surface wettability, and gravity. Langmuir 2013, 29, 9918–9934. [Google Scholar]
- Wensheng, H.; Jung, S.; Trung, N. Two-phase flow model of the cathode of PEM fuel cells using interdigitated flow fields. AIChE J. 2000, 46, 2053–2060. [Google Scholar]
- Dilip, N.; Trung, N. A two-dimensional, two-phase, multicomponent, transient model for the cathode of a proton exchange membrane fuel cell using conventional gas distributors. J. Electrochem. Soc. 2001, 48, 1324–1335. [Google Scholar]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| cathode channel volume, vca/cm3 | 5.088 (stack parameter) | cell internal current due to fuel crossover, In/A | 3 (stack parameter) |
| cathode exhaust volume, vem,ca/cm3 | 0.15 (stack parameter) | cell nozzle orifice coefficient, kca/gPa−1s−1 | 3.71 × 10−5 (adjusted) |
| anode channel volume, van/cm3 | 2.387 (stack parameter) | cell nozzle orifice coefficient, ksm,ca/gPa−1s−1 | 2.199 × 10−5 (adjusted) |
| anode exhaust manifold volume, vem,an/cm3 | 0.07 (stack parameter) | cell nozzle orifice coefficient, kan/gPa−1s−1 | 1.51 × 10−6 (adjusted) |
| drag coefficient, nd | 2.5λ/22 [5] | cell nozzle orifice coefficient, ksm,an/gPa−1s−1 | 2.28 × 10−6 (adjusted) |
| steam condensation rate, kc/s−1 | 100 [33] | cell nozzle orifice coefficient, kem,an/gPa−1s−1 | 5.08 × 10−8 (adjusted) |
| evaporation rate of liquid water, ke/atms−1 | 1 [34] | membrane thickness, lm/μm | 25 (stack parameter) |
| liquid water coefficient, kliq/s−1 | 100 (ajusted) | effective area of each cell, Acell/cm2 | 186 (stack parameter) |
| cell exchange current, I0/A | 0.0008 (stack parameter) | cell contact resistance, R0/mΩ | 1 (stack parameter) |
| reversible cell potential at standard pressure, V0/V | 1.229 (stack parameter) | cell limiting current, I1/A | 320 (stack parameter) |
| Time (s) | 0–20 | 20–40 | 40–60 | 60–80 | 80–100 |
|---|---|---|---|---|---|
| Current (A) | 55.8 | 111.6 | 167.4 | 223.2 | 279 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Zhou, C.; Rong, Z.; Wang, H.; Li, H.; Hu, X. Simulation of the Dynamic Characteristics of a PEMFC System in Fluctuating Operating Conditions. Energies 2020, 13, 3596. https://doi.org/10.3390/en13143596
Yan J, Zhou C, Rong Z, Wang H, Li H, Hu X. Simulation of the Dynamic Characteristics of a PEMFC System in Fluctuating Operating Conditions. Energies. 2020; 13(14):3596. https://doi.org/10.3390/en13143596
Chicago/Turabian StyleYan, Jiangyan, Chang Zhou, Zhihai Rong, Haijiang Wang, Hui Li, and Xuejiao Hu. 2020. "Simulation of the Dynamic Characteristics of a PEMFC System in Fluctuating Operating Conditions" Energies 13, no. 14: 3596. https://doi.org/10.3390/en13143596
APA StyleYan, J., Zhou, C., Rong, Z., Wang, H., Li, H., & Hu, X. (2020). Simulation of the Dynamic Characteristics of a PEMFC System in Fluctuating Operating Conditions. Energies, 13(14), 3596. https://doi.org/10.3390/en13143596