Cost-Effective Placement of Phasor Measurement Units to Defend against False Data Injection Attacks on Power Grid
Abstract
:1. Introduction
2. Related Works
3. Preliminaries
3.1. System Assumptions
- Given power grids consist of active power flow measurements at all branches on both ends;
- A simplified linearized approximation model is considered;
- A PMU placed at a given bus can measure both the voltage and current phasor at all branches present at that bus;
- The measurements obtained by the PMUs are secure since the PMU networked system has been designed for secure data transfer.
3.2. Active Power Flow Model
3.3. State Estimation
3.4. False Data Injection Attacks: Basic Principle
4. Identification of Vulnerable Locations to False data Injection Attacks
4.1. Identification Method of Vulnerable Locations
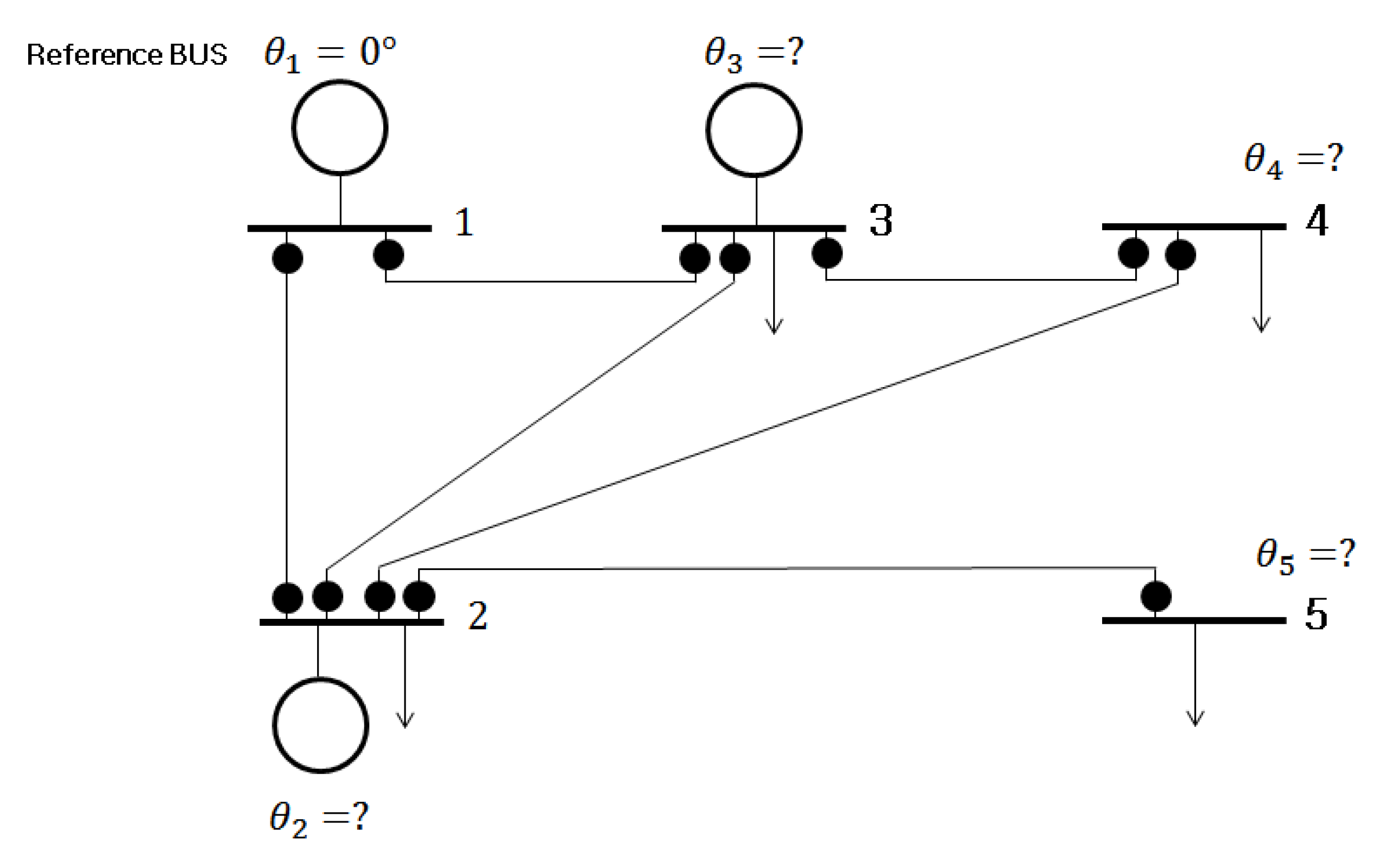
Example 5-bus System
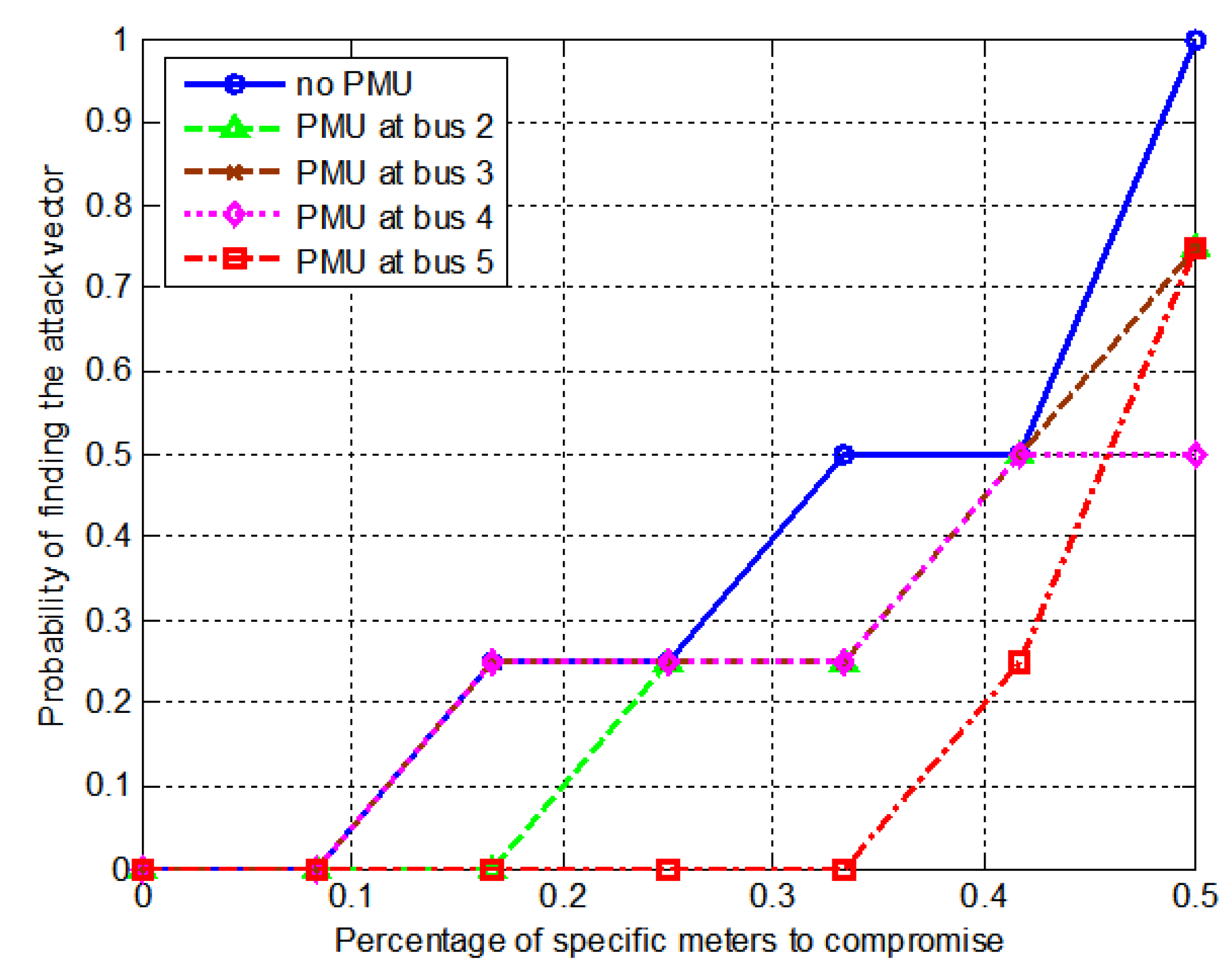
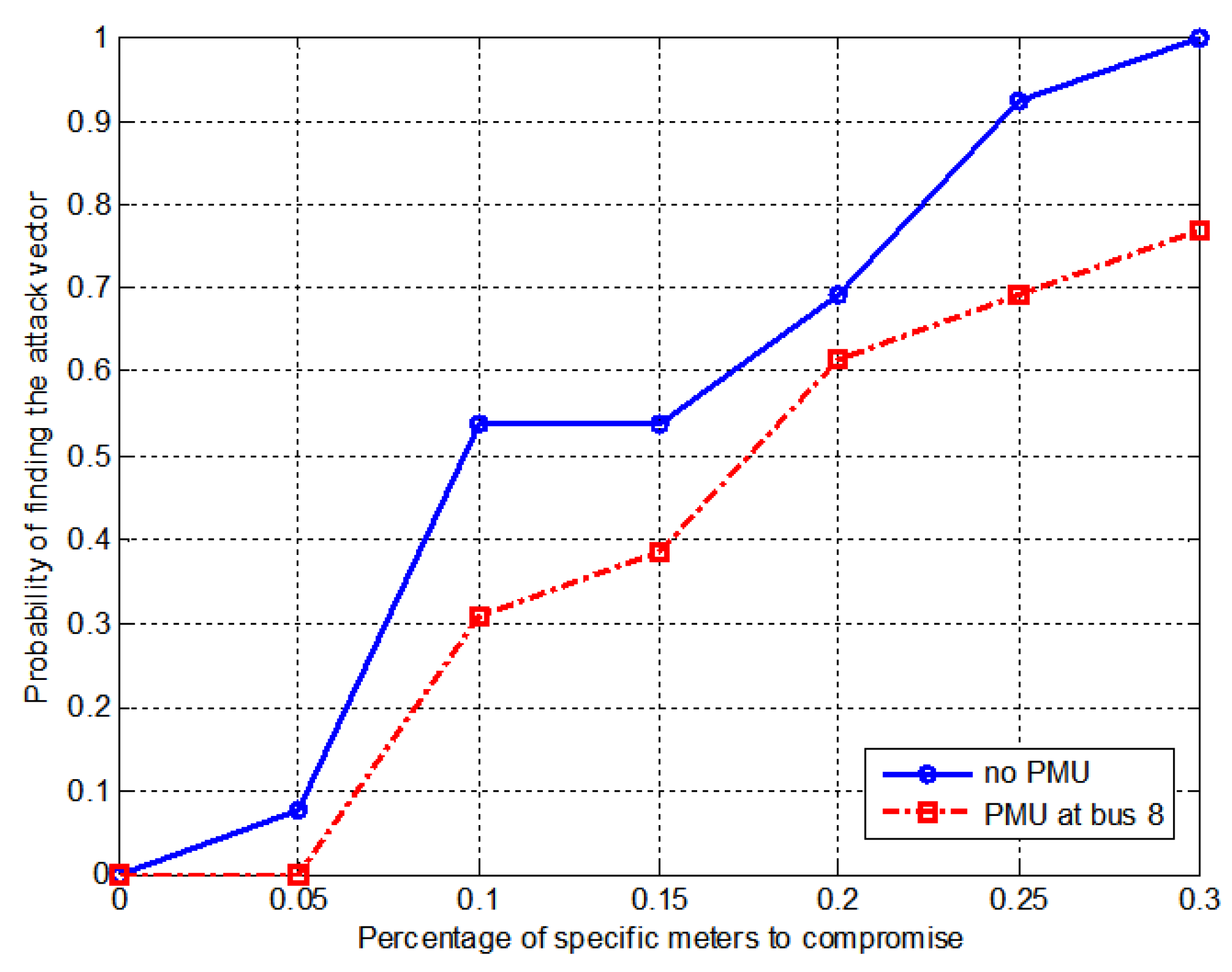
4.2. Impacts of Adding a PMU on Power Grid
5. Proposed PMU Placement Algorithm Considering Cyber Security Constraint
- : total number of buses;
- : vector whose entries are all equal to 1;
- : binary information matrix of connectivity between all buses with/without conventional meters;
- : binary information matrix of connectivity between vulnerable buses identified by the matrix ;
- : binary (0/1) vector.
- (1)
- Identify rows of in the matrix ;
- (2)
- Identify if and only if ;
- (3)
- Find the full observability constraint;
- (4)
- Find the cyber security constraint; the cyber security constraint in the proposed ILP algorithm is modified by determined vulnerable locations;
- (5)
- The total solution is obtained by the proposed ILP algorithm.
6. Simulation Results
6.1. IEEE 14-Bus System
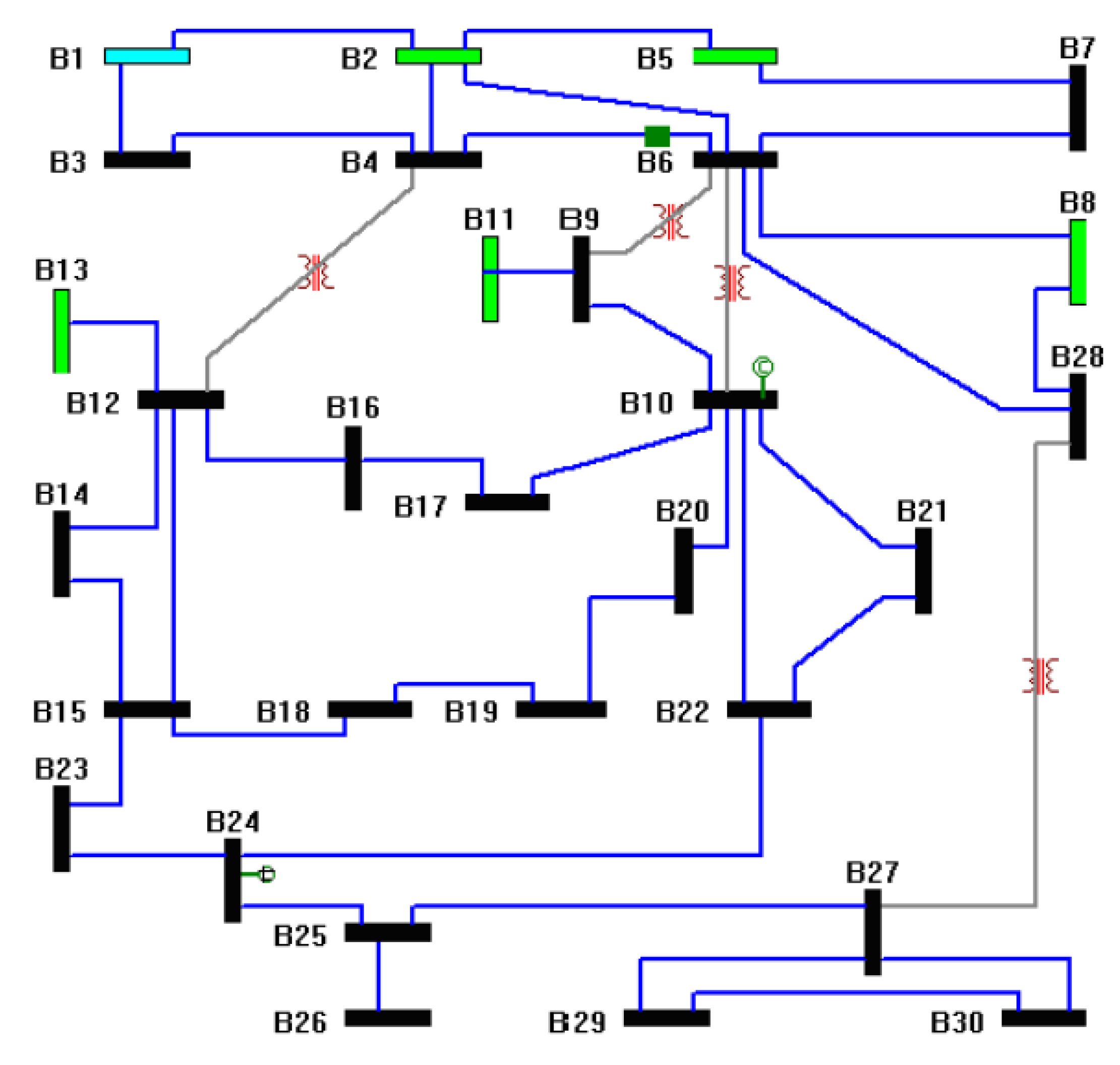
6.2. IEEE 30-Bus System
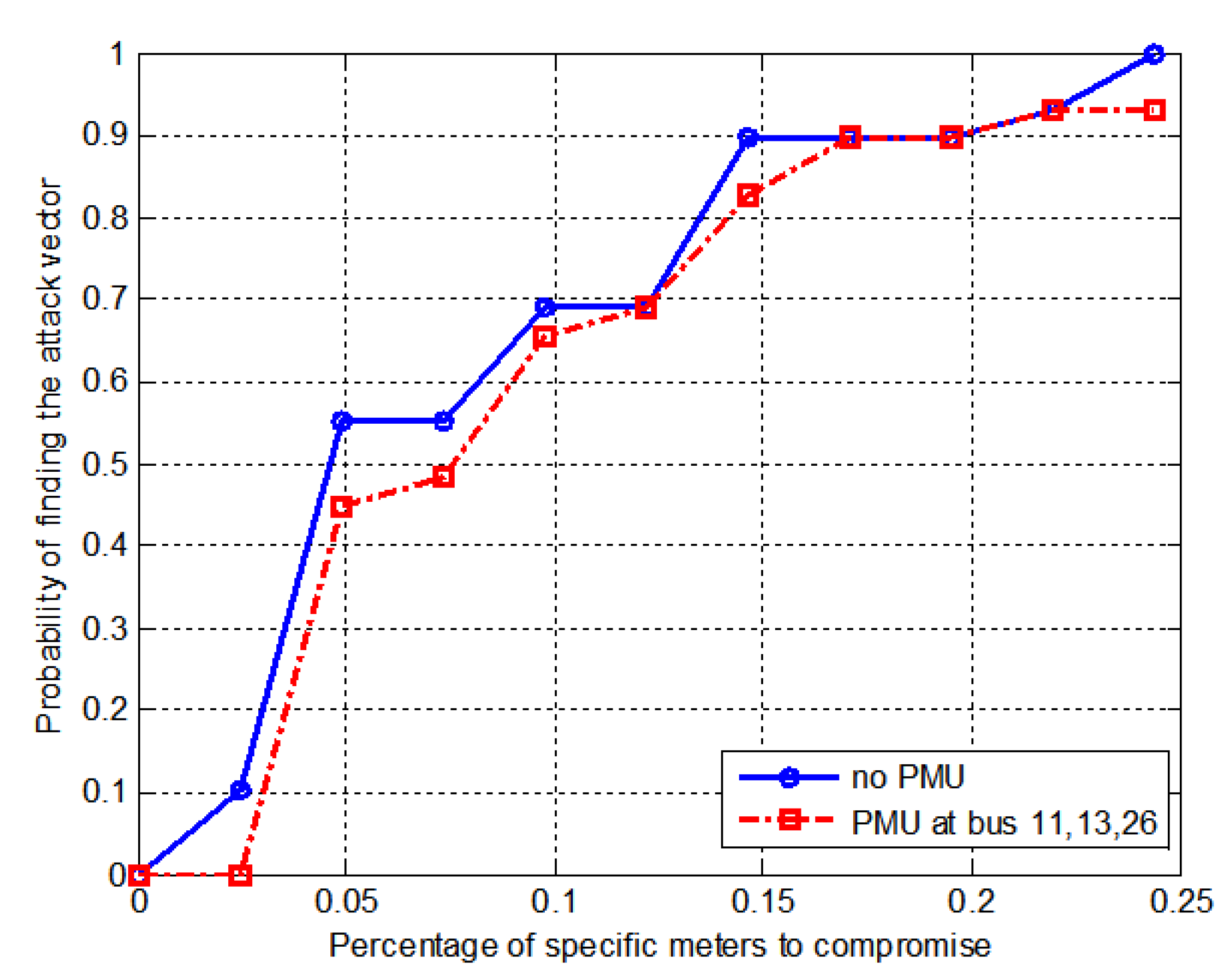
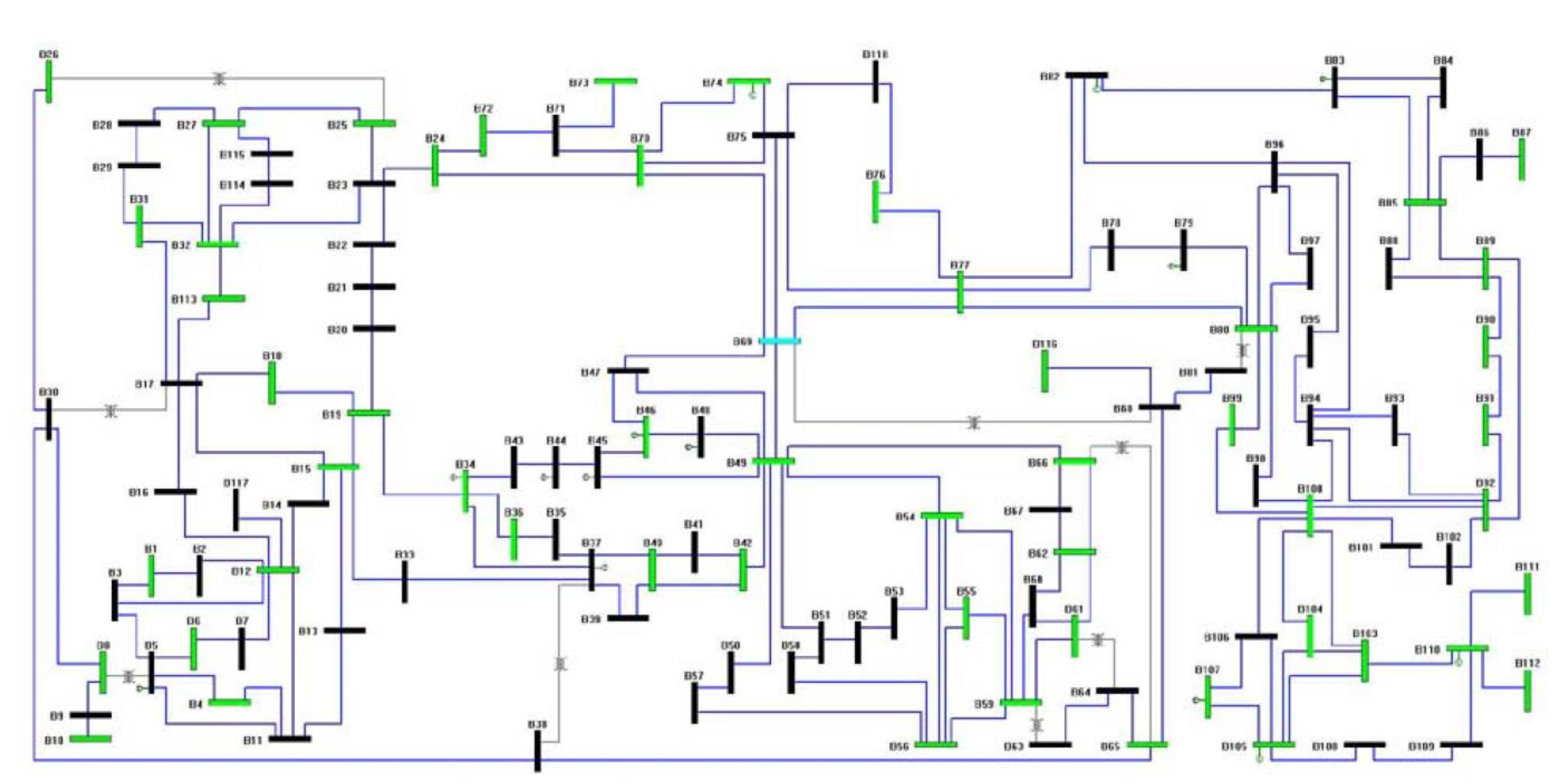
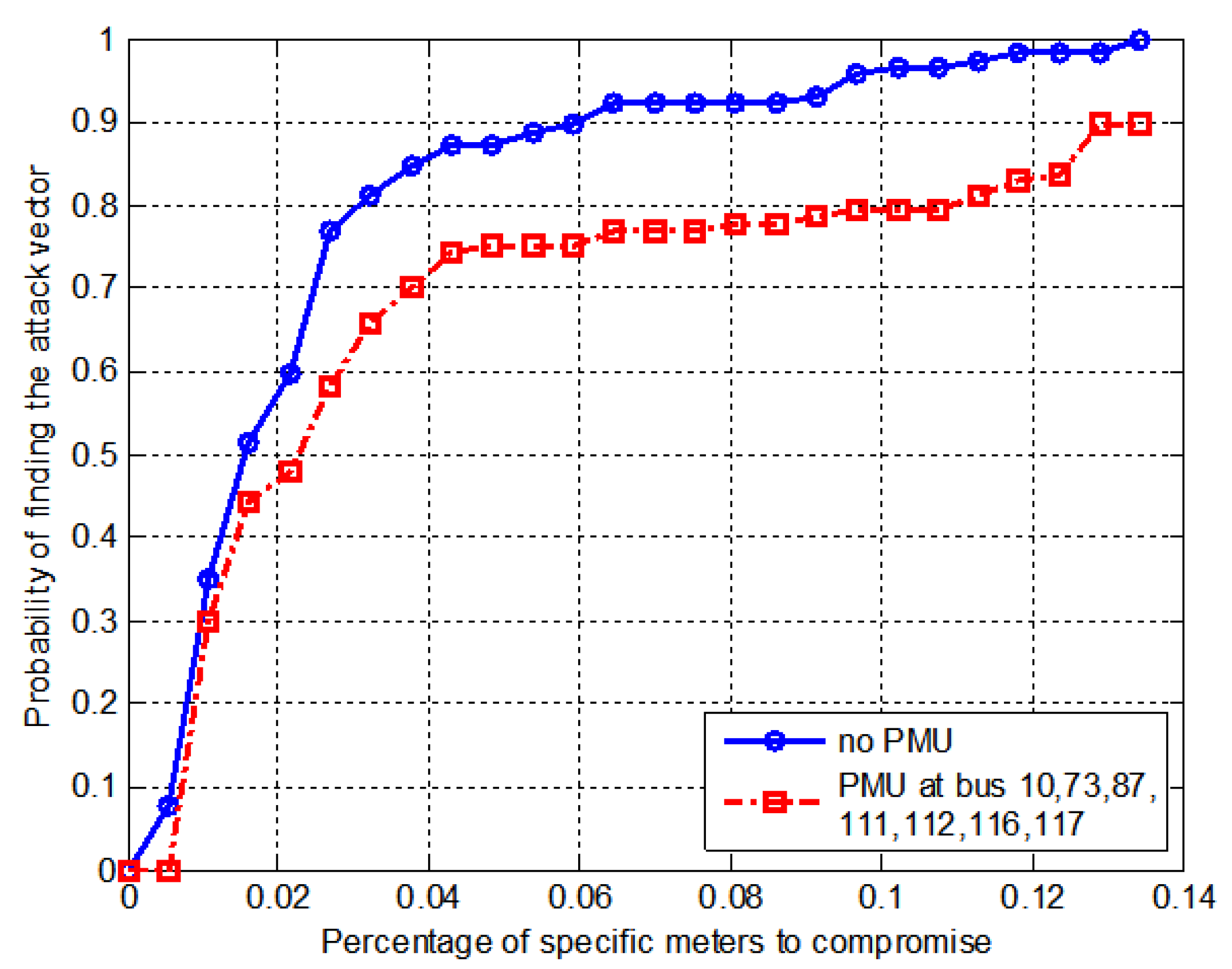
6.3. IEEE 118-Bus System
7. Conclusions
- (1)
- Identification of vulnerable locations when an attacker has perfect or imperfect knowledge about the topology of power grid;
- (2)
- Suggestion of evaluation metrics to prove vulnerable locations;
- (3)
- Development of an integer linear programming-based algorithm considering both full observability and cyber security constraints.
Funding
Acknowledgments
Conflicts of Interest
References
- Teixeira, A.; Amin, S.; Sandberg, H.; Johansson, K.H.; Sastry, S.S. Cyber-security analysis of state estimators in electric power systems. In Proceedings of the IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5991–5998. [Google Scholar]
- Liang, G.; Weller, S.R.; Zhao, J.; Luo, F.; Dong, Z.Y. The 2015 Ukraine Blackout: Implications for False Data Injection Attacks. IEEE Trans. Power Syst. 2017, 32, 3317–3318. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N.; Georgilakis, P.S. Taxonomy of PMU placement methodologies. IEEE Trans. Power Syst. 2012, 27, 1070–1077. [Google Scholar] [CrossRef]
- Chen, J.; Abur, A. Placement of PMUs to enable bad data detection in state estimation. IEEE Trans. Power Syst. 2006, 21, 1608–1615. [Google Scholar] [CrossRef]
- Ree, J.; Centeno, V.; Thorp, J.S.; Phadke, A.G. Synchronized phasor measurement applications in power systems. IEEE Trans. Smart Grid 2010, 1, 20–27. [Google Scholar]
- Gou, B. Generalized integer linear programming formulation for optimal PMU placement. IEEE Trans. Power Syst. 2008, 23, 1099–1104. [Google Scholar] [CrossRef]
- Chakra barti, S.; Kyriakides, E.; Eliades, D.G. Placement of synchronized measurements for power system observability. IEEE Trans. Power Del. 2009, 24, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Abbasy, N.H.; Ismail, H.M. A unified approach for the optimal PMU location for power system state estimation. IEEE Trans. Power Syst. 2009, 24, 806–813. [Google Scholar] [CrossRef]
- Aminifar, F.; Khodaei, A.; Fotuhi-Firuzabad, M.; Shahidehpour, M. Contingency-constrained PMU placement in power networks. IEEE Trans. Power Syst. 2010, 25, 516–523. [Google Scholar] [CrossRef]
- Wells, C.; Moore, A.; Tjader, K.; Isaacs, W. Cyber secure synchrophasor platform. In Proceedings of the IEEE PES Power Systems Conference & Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–4. [Google Scholar]
- Phadke, A.G.; Thorp, J.S.; Nuqui, R.F.; Zhou, M. Recent developments state estimation with phasor measurements. In Proceedings of the IEEE PES Power Systems Conference & Exposition, Seattle, DC, USA, 15–18 March 2009; pp. 1–7. [Google Scholar]
- Ahmadi, A.; Alinejad-Beromi, Y.; Moradi, M. Optimal PMU placement for power system observability using binary particle swarm optimization and considering measurement redundancy. Expert Syst. Appl. 2011, 38, 7263–7269. [Google Scholar] [CrossRef]
- Emami, R.; Abur, A. Robust measurement design by placing synchronized phasor measurements on network branches. IEEE Trans. Power Syst. 2010, 25, 38–43. [Google Scholar] [CrossRef]
- Korkali, M.; Abur, A. Impact of network sparsity on strategic placement of phasor measurement units with fixed channel capacity. In Proceedings of the IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 3445–3448. [Google Scholar]
- Giani, A.; Sastry, S.S.; Johansson, K.H.; Sandberg, H. The VIKING Project: An initiative on resilient control of power networks. In Proceedings of the 2nd International Symposium on Resilient Control Systems, Idaho Falls, Idaho, 11–13 August 2009. [Google Scholar]
- Mo, Y.; Sinopoli, B. Secure control against replay attack. In Proceedings of the 47th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 30 September–2 October 2009. [Google Scholar]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. In Proceedings of the 16th of ACM Conference on Computer and Communications Security, Chicago, IL, USA, 30 September–2 October 2009. [Google Scholar]
- Kosut, O.; Jia, L.; Thomas, R.; Tong, L. Malicious data attacks on smart grid state estimation: Attack strategies and countermeasures. In Proceedings of the IEEE Conference on Smart Grid Communications, Gathersburg, MD, USA, 4–6 October 2010. [Google Scholar]
- Huang, Y.; Li, H.; Campbell, K.A.; Han, Z. Defending false data injection attack on smart grid network using adaptive cusum test. In Proceedings of the IEEE Conference on Information Sciences and Systems, Baltimore, MD, USA, 23–25 March 2011. [Google Scholar]
- Bobba, R.; Rogers, K.; Wang, Q.; Khurana, H.; Nahrstedt, K.; Overbye, T. Detecting False Data Injection Attacks on DC State Estimation. In Proceedings of the 1st Workshop on Secure Control Systems (SCS 2010), Stockholm, Switzerland, 12 April 2010. [Google Scholar]
- Kim, T.T.; Poor, H.V. Strategy protection against data injection attacks on power grids. IEEE Trans. Smart Grid. 2011, 3, 326–333. [Google Scholar] [CrossRef]
- Hug, G.; Giampapa, J.A. Vulnerability assessment of AC state estimation with respect to false data injection cyber-attacks. IEEE Trans. Smart Grid. 2012, 3, 1362–1370. [Google Scholar] [CrossRef] [Green Version]
- Ganjkhani, M.; Fallah, S.N.; Badakhshan, S.; Shamshirband, S.; Chau, K. A novel detection algorithm to identify false data injection attacks on power system state estimation. Energies 2019, 12, 2209. [Google Scholar] [CrossRef] [Green Version]
- Abur, A.; Exposito, A.G. Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Bae, J.; Lee, S.; Kim, Y.W.; Kim, J.H. Protection strategies against false data injection attacks with uncertain information on electric power grids. J. Electr. Eng. Technol. 2017, 12, 19–28. [Google Scholar] [CrossRef] [Green Version]
- MATPOWER, A MATLAB Power System Simulation Package [Online]. Available online: http://www.pserc.cornell.edu/matpower/ (accessed on 20 June 2019).

| Given Topology | Number of Required PMU | PMU Placement |
|---|---|---|
| Without Meters | 4 | B2, B6, B7, B9 |
| With Meters | 1 | B8 |
| Given Topology | Number of Required PMU | PMU Placement |
|---|---|---|
| Without meters | 10 | B1, B7, B9, B10, B12, B18, B24, B25, B27, B28 |
| With meters | 3 | B11, B13, B26 |
| Given Topology | Number of Required PMU | PMU Placement |
|---|---|---|
| Without meters | 32 | B2, B5, B9, B11, B12, B17, B21, B24, B25, B28, B34, B37, B40, B45, B49, B52, B56, B62, B63, B68, B73, B75, B77, B80, B85, B86, B90, B94, B101, B105, B110, B114 |
| With meters | 7 | B10, B73, B87, B111, B112, B116, B117 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, J. Cost-Effective Placement of Phasor Measurement Units to Defend against False Data Injection Attacks on Power Grid. Energies 2020, 13, 3862. https://doi.org/10.3390/en13153862
Bae J. Cost-Effective Placement of Phasor Measurement Units to Defend against False Data Injection Attacks on Power Grid. Energies. 2020; 13(15):3862. https://doi.org/10.3390/en13153862
Chicago/Turabian StyleBae, Junhyung. 2020. "Cost-Effective Placement of Phasor Measurement Units to Defend against False Data Injection Attacks on Power Grid" Energies 13, no. 15: 3862. https://doi.org/10.3390/en13153862
APA StyleBae, J. (2020). Cost-Effective Placement of Phasor Measurement Units to Defend against False Data Injection Attacks on Power Grid. Energies, 13(15), 3862. https://doi.org/10.3390/en13153862




