Validation of the Transient Liquid Crystal Thermography Technique for Heat Transfer Measurements on a Rotating Cooling Passage
Abstract
1. Introduction
2. Experimental Setups and Methodologies
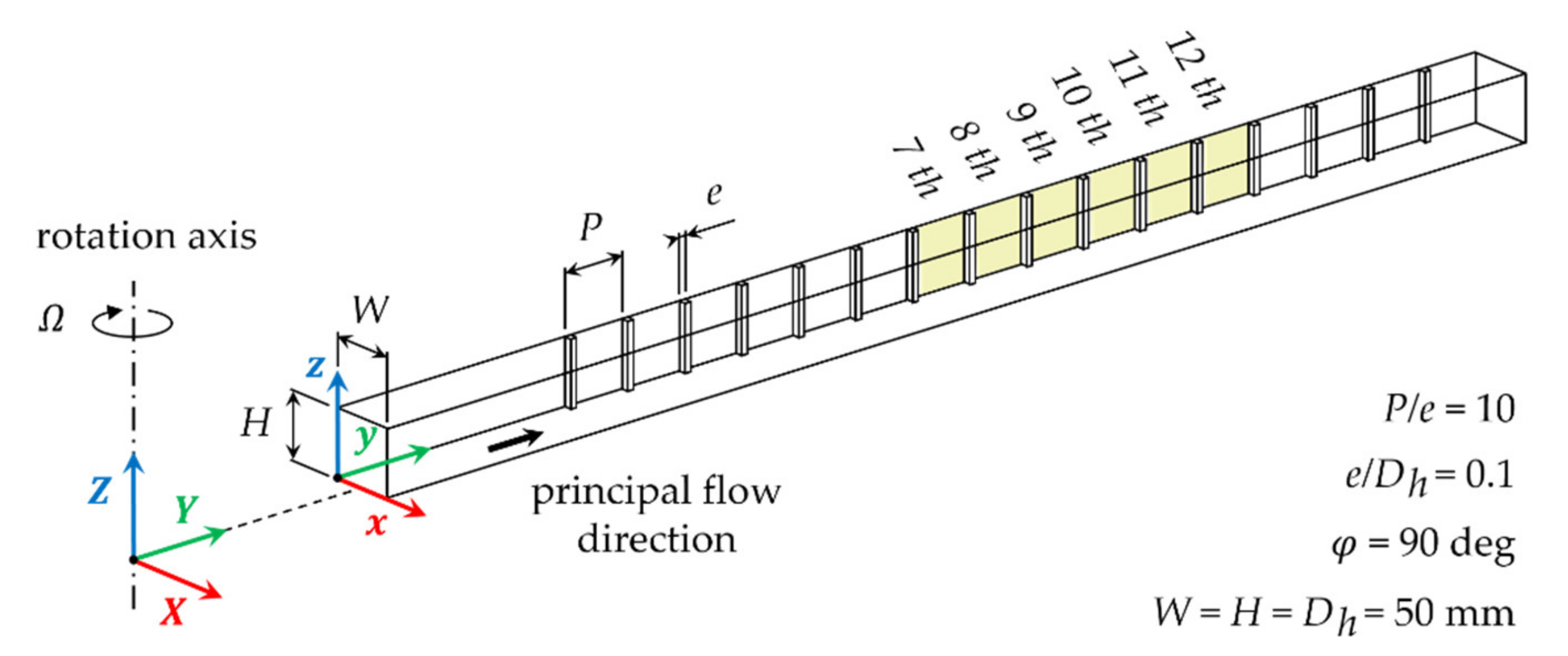
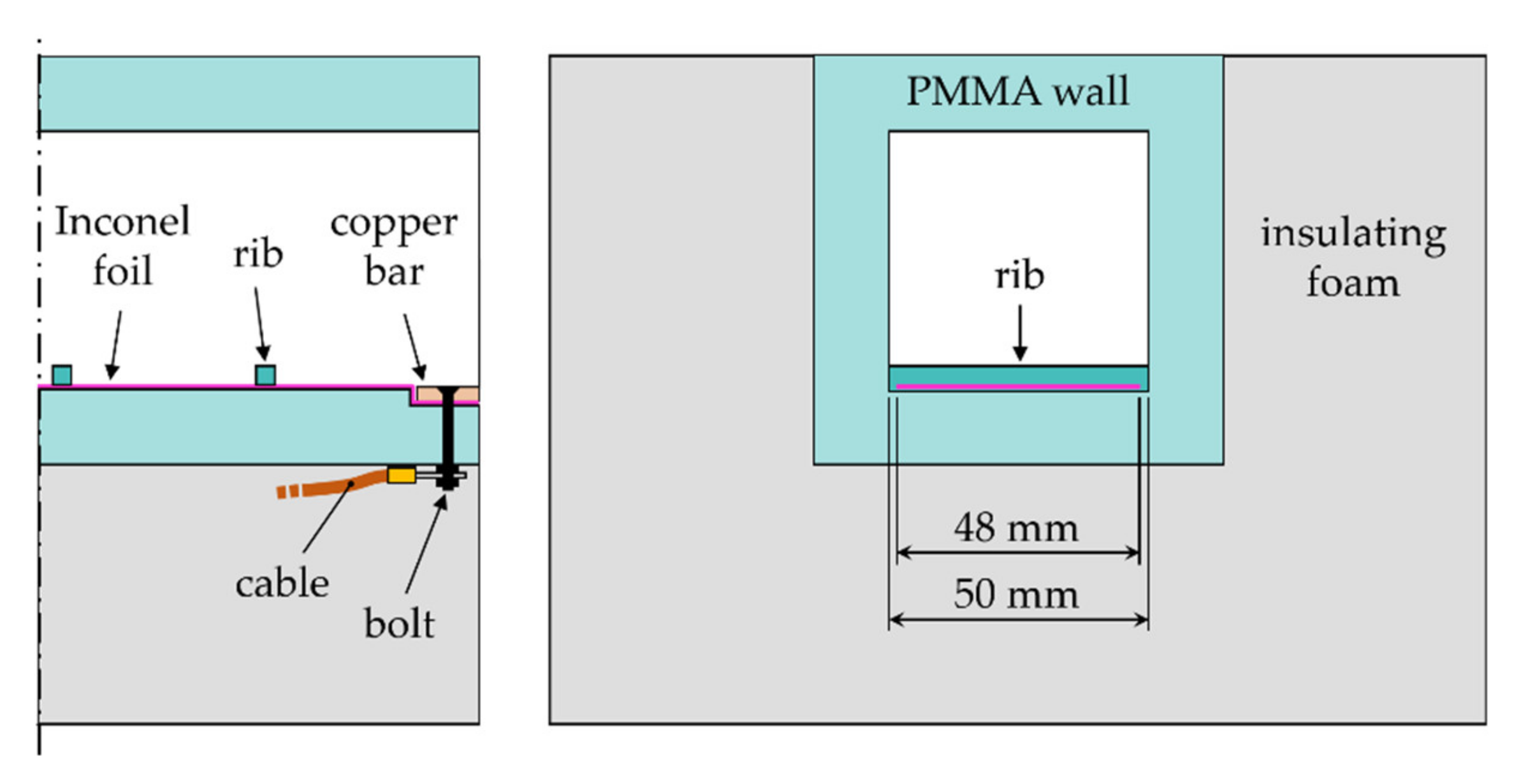
2.1. Channel Geometry and Test Conditions
2.2. Rotating Channel Facility
2.3. Steady-State Liquid Crystals Thermography
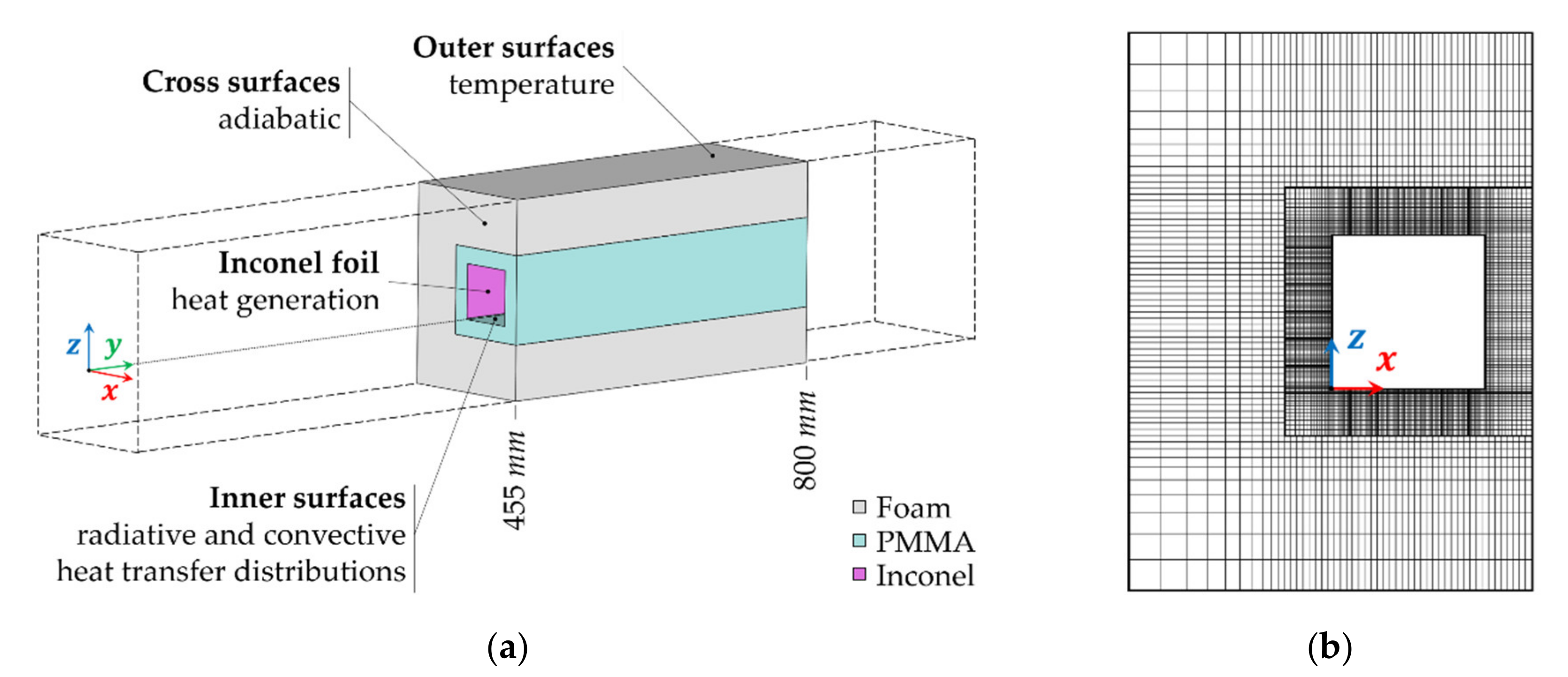
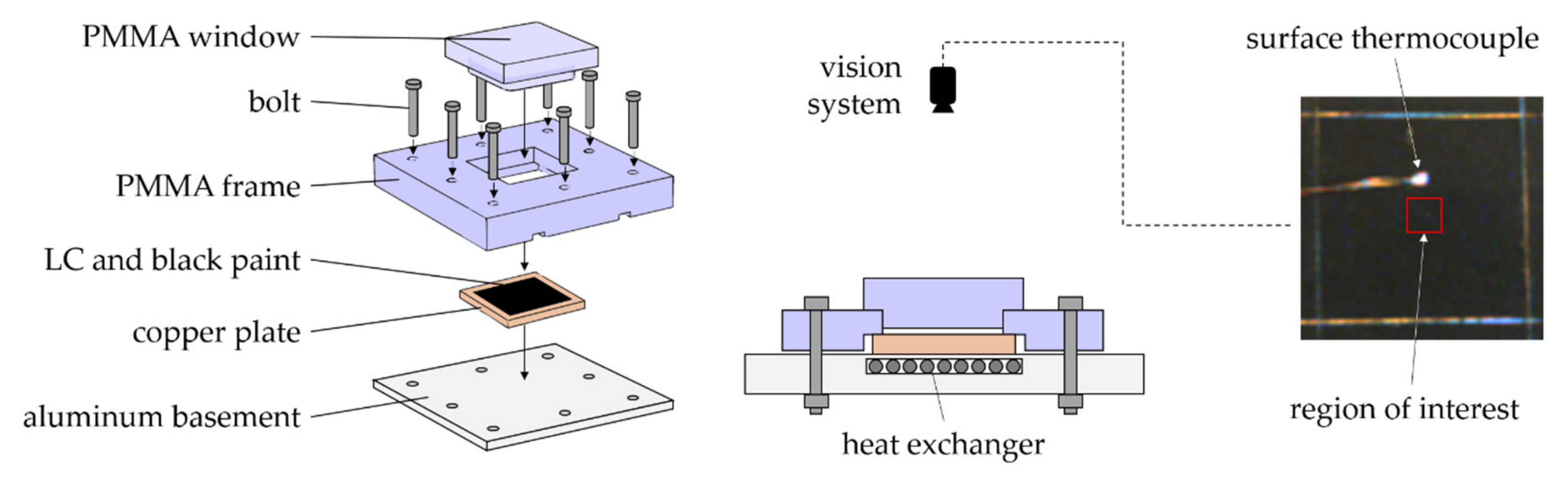
2.4. Transient Liquid Crystals Thermography
- the wall temperature indicated by the LC activation (i.e., a specific temperature is matched to the full intensity of the green colour, as it will be explained in the calibration procedure described in the next subsection);
- the LC activation time (i.e., the elapsed time between the start of the test and the instant at which the green peak is reached);
- the thermo-physical properties of the wall material ;
- the flow-temperature evolution in the entire domain.
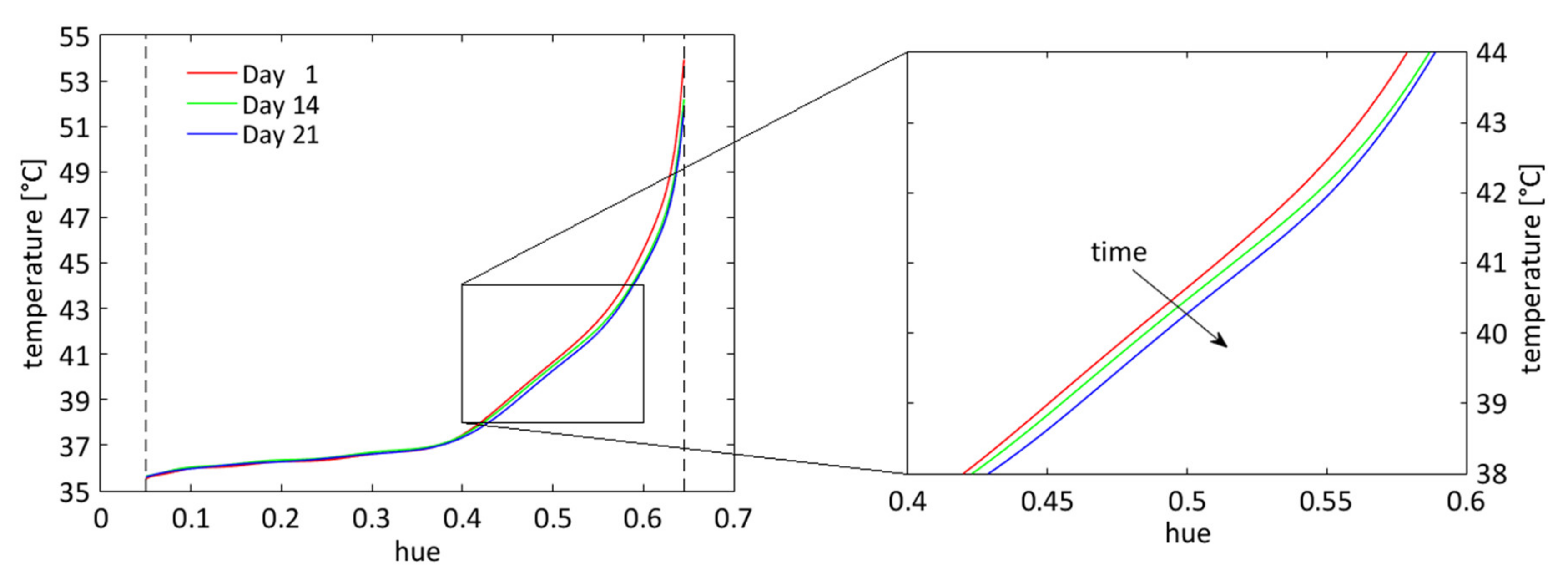
2.5. Liquid Crystals Calibration
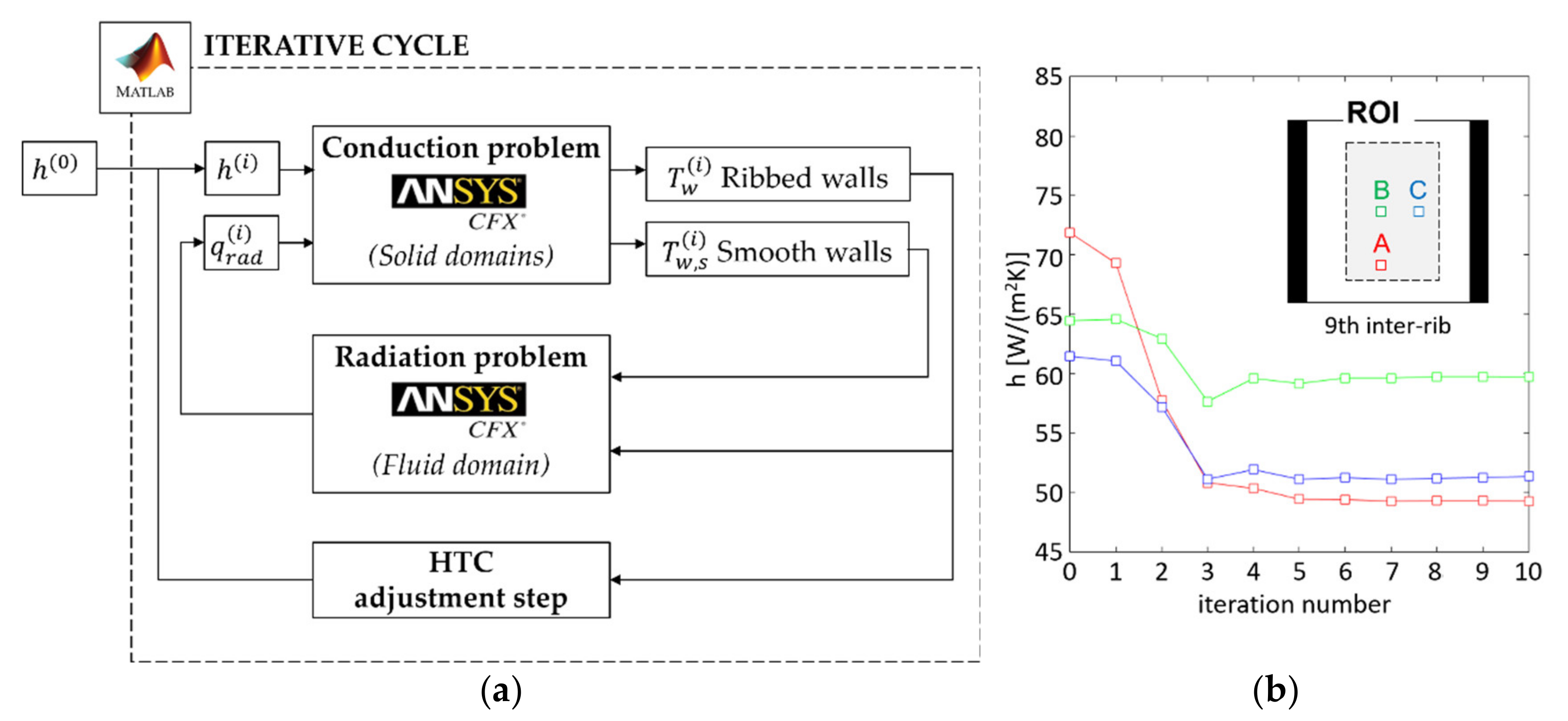
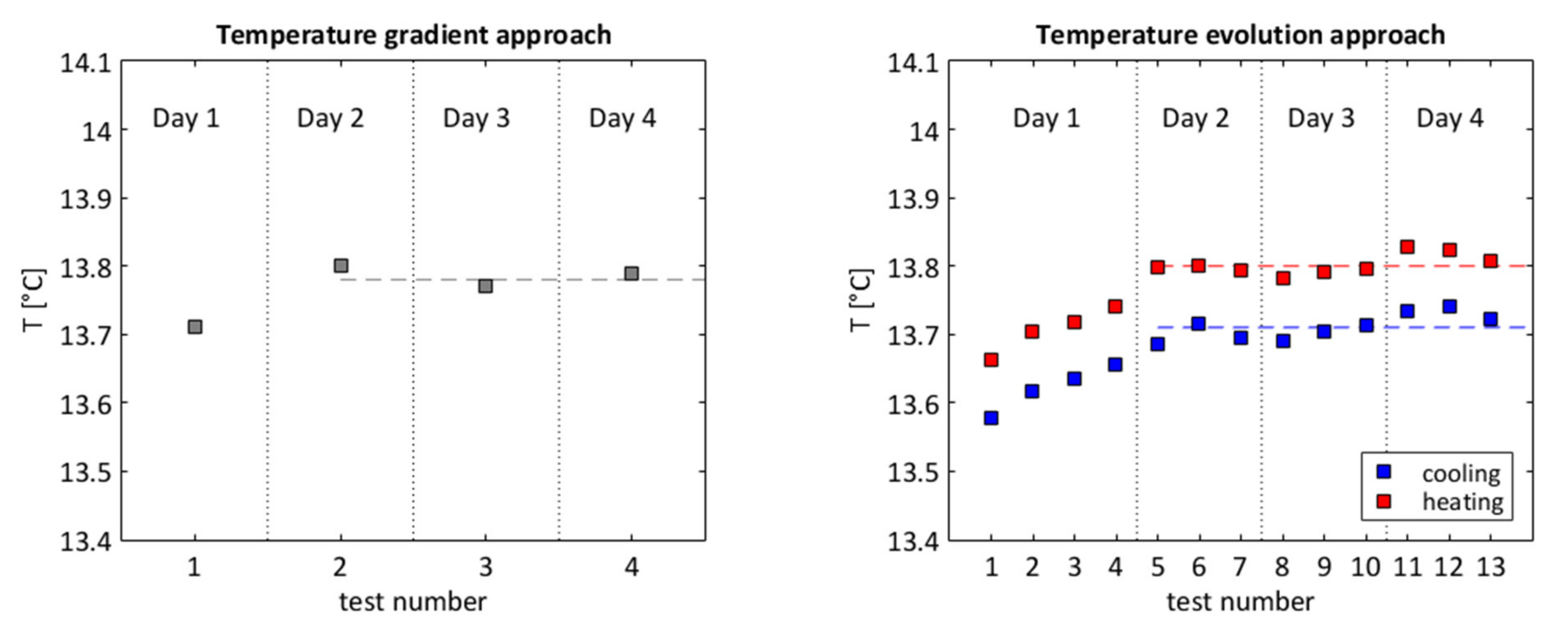
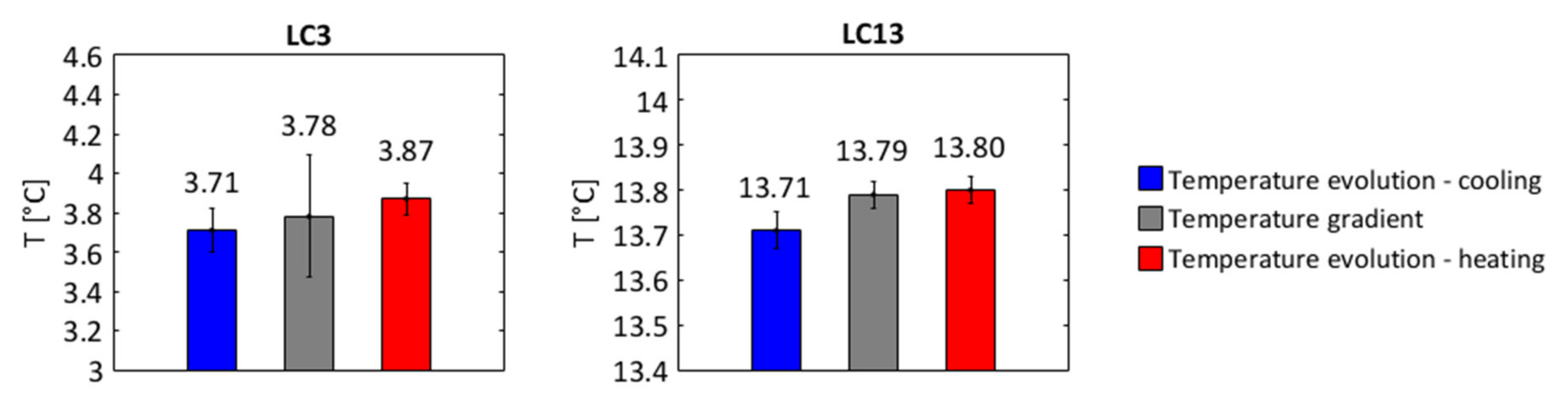
2.6. Uncertainty Analysis
3. Results
3.1. Liquid Crystals Calibrations
3.2. Heat-Transfer Measurements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ireland, P.T.; Jones, T.V. Liquid crystal measurements of heat transfer and surface shear stress. Meas. Sci. Technol. 2000, 11, 969–986. [Google Scholar] [CrossRef]
- Rau, G.; Çakan, M.; Moeller, D.; Arts, T. The effect of periodic ribs on the local aerodynamic and heat transfer performance of a straight cooling channel. J. Turbomach. 1998, 120, 368–375. [Google Scholar] [CrossRef]
- Shiau, C.C.; Chen, A.F.; Han, J.C.; Krewinkel, R. Detailed Heat Transfer Coefficient Measurements on a Scaled Realistic Turbine Blade Internal Cooling System. J. Therm. Sci. Eng. Appl. 2019, 12, 31015. [Google Scholar] [CrossRef]
- Pountney, O.; Cho, G.; Lock, G.D.; Owen, J.M. Solutions of Fourier’s equation appropriate for experiments using thermochromic liquid crystal. Int. J. Heat Mass Transf. 2012, 55, 5908–5915. [Google Scholar] [CrossRef]
- Schultz, D.L.; Jones, T.V. Heat Transfer Measurements in Short-Duration Hypersonic Facilities, 1st ed.; North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development: London, UK, 1973. [Google Scholar]
- Buttsworth, D.R.; Jones, T.V. Radial conduction effects in transient heat transfer experiments. Aeronaut. J. 1997, 101, 209–212. [Google Scholar]
- Wagner, G.; Kotulla, M.; Ott, P.; Weigand, B.; von Wolfersdorf, J. The transient liquid crystal technique: Influence of surface curvature and finite wall thickness. J. Turbomach. 2005, 127, 175–182. [Google Scholar] [CrossRef]
- Von Wolfersdorf, J. Influence of lateral conduction due to flow temperature variations in transient heat transfer measurements. Int. J. Heat Mass Transf. 2007, 50, 1122–1127. [Google Scholar] [CrossRef]
- Kingsley-Rowe, J.R.; Lock, G.D.; Owen, J.M. Transient heat transfer measurements using thermochromic liquid crystal: Lateral-conduction error. Int. J. Heat Fluid Flow 2005, 26, 256–263. [Google Scholar] [CrossRef]
- Ahmed, S.; Singh, P.; Ekkad, S.V. Three-Dimensional transient heat conduction equation solution for accurate determination of heat transfer coefficient. J. Heat Transf. 2020, 142, 51302. [Google Scholar] [CrossRef]
- Waidmann, C.; Poser, R.; von Wolfersdorf, J.; Fois, M.; Semmler, K. Investigations of heat transfer and pressure loss in an engine-similar two-pass internal blade cooling configuration. In Proceedings of the 10th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Lappeenranta, Finland, 15–19 April 2013. [Google Scholar]
- Domaschke, N.; von Wolfersdorf, J.; Semmler, K. Heat transfer and pressure drop measurements in a rib roughened leading edge cooling channel. J. Turbomach. 2012, 134, 61006. [Google Scholar] [CrossRef]
- Kunstmann, S.; von Wolfersdorf, J.; Ruedel, U. Heat transfer and pressure loss in rectangular one-side-ribbed channels with different aspect ratios. J. Turbomach. 2012, 135, 31004. [Google Scholar] [CrossRef]
- Pagnacco, F.; Furlani, L.; Armellini, A.; Casarsa, L. Gas turbine blades internal cooling: Design, development and validation of a new rig for heat transfer measurements under rotation. In Proceedings of the 12th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Lamont, J.A.; Ekkad, S.V.; Alvin, M.A. Detailed Heat Transfer Measurements Inside Rotating Ribbed Channels Using the Transient Liquid Crystal Technique. J. Therm. Sci. Eng. Appl. 2012, 4, 11002. [Google Scholar] [CrossRef]
- Singh, P.; Li, W.; Ekkad, S.V.; Ren, J. A new cooling design for rib roughened two-pass channel having positive effects of rotation on heat transfer enhancement on both pressure and suction side internal walls of a gas turbine blade. Int. J. Heat Mass Transf. 2017, 115, 6–20. [Google Scholar] [CrossRef]
- Singh, P.; Ekkad, S.V. Experimental investigation of rotating rib roughened two-pass square duct with two different channel orientations. In Proceedings of the ASME Turbo Expo, Charlotte, CA, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Singh, P.; Ji, Y.; Ekkad, S.V. Multipass Serpentine Cooling Designs for Negating Coriolis Force Effect on Heat Transfer: 45-deg Angled Rib Turbulated Channels. J. Turbomach. 2019, 141, 71003. [Google Scholar] [CrossRef]
- Singh, P.; Ji, Y.; Ekkad, S.V. Multi-Pass Serpentine Cooling Designs for Negating Coriolis Force Effect on Heat Transfer: Smooth Channels. J. Turbomach. 2019, 141, 71001. [Google Scholar] [CrossRef]
- Waidmann, C.; Poser, R.; Nieland, S.; Von Wolfersdorf, J. Design of a rotating test rig for transient thermochromic liquid crystal heat transfer experiments. In Proceedings of the Open archives of the 16th ISROMAC 2016, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- Mayo, I.; Lahalle, A.; Gori, G.L.; Arts, T. Aerothermal characterization of a rotating ribbed channel at engine representative conditions-part II: Detailed liquid crystal thermography measurements. J. Turbomach. 2016, 138, 101009. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Han, J.-C. Detailed heat transfer distributions in two-pass square channels with rib turbulators. Int. J. Heat Fluid Flow 1997, 40, 2525–2537. [Google Scholar] [CrossRef]
- Mayo, I.; Arts, T.; El-Habib, A.; Parres, B. Two-Dimensional Heat Transfer Distribution of a Rotating Ribbed Channel at Different Reynolds Numbers. J. Turbomach. 2014, 137, 31002. [Google Scholar] [CrossRef]
- Abdullah, N.; Abu Talib, A.R.; Mohd Saiah, H.R.; Jaafar, A.A.; Mohd Salleh, M.A. Film thickness effects on calibrations of a narrowband thermochromic liquid crystal. Exp. Therm. Fluid Sci. 2009, 33, 561–578. [Google Scholar] [CrossRef]
- Anderson, M.R.; Baughn, J.W. Hysteresis in liquid crystal thermography. J. Heat Transf. 2004, 126, 339–346. [Google Scholar] [CrossRef]
- Kakade, V.U.; Lock, G.D.; Wilson, M.; Owen, J.M.; Mayhew, J.E. Accurate heat transfer measurements using thermochromic liquid crystal. Part 1: Calibration and characteristics of crystals. Int. J. Heat Fluid Flow 2009, 30, 939–949. [Google Scholar] [CrossRef]
- Pagnacco, F.; Furlani, L.; Armellini, A.; Casarsa, L.; Davis, A. Rotating heat transfer measurements on a multi-pass internal cooling channel-I rig development. In Proceedings of the ASME TE16, Seoul, Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross−Section Conduits Running Full–Part 2: Orifice Plates. ISO 5167-2. 2003. Available online: https://www.iso.org/standard/30190.html (accessed on 11 September 2020).
- Farina, D.J.; Hacker, J.M.; Moffat, R.J.; Eaton, J.K. Illuminant invariant calibration of thermochromic liquid crystals. Exp. Therm. Fluid Sci. 1994, 9, 1–12. [Google Scholar] [CrossRef]
- Lucas, M.L.; Ireland, P.T.; Wang, Z.; Jones, T.V. Fundamental Studies of Impingement Cooling Thermal Boundary Conditions. In Proceedings of the 80th Propulsion and Energetics Panel Symposium AGARD, Antalya, Turkey, 12–16 October 1992. [Google Scholar]
- Çakan, M. Aero-Thermal Investigation of Fixed Rib-Roughened Internal Cooling Passages. Ph.D. Thesis, Université Catholique de Louvain and von Karman Institute for Fluid Dynamics, Louvain, Belgium, 2000. [Google Scholar]
- Scienza e Tecnologia dei Materiali. Available online: http://www.nanofun.net/ (accessed on 24 July 2020).
- Poser, R.; von Wolfersdorf, J.; Lutum, E. Advanced evaluation of transient heat transfer experiments using thermochromic liquid crystals. In Proceedings of the 7th ETC, Athens, Greece, 5–9 March 2007. [Google Scholar]
- Yan, Y.; Owen, J.M. Uncertainties in transient heat transfer measurements with liquid crystal. Int. J. Heat Fluid Flow 2002, 23, 29–35. [Google Scholar] [CrossRef]
- Metzger, D.E.; Larson, D.E. Use of melting point surface coatings for local convection heat transfer measurements in rectangular channel flows with 90-deg turns. J. Heat Transf. 1986, 108, 48–54. [Google Scholar] [CrossRef]
- Cukurel, B.; Selcan, C.; Arts, T. Color theory perception of steady wide band liquid crystal thermometry. Exp. Therm. Fluid Sci. 2012, 39, 112–122. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Wiberg, R.; Lior, N. Errors in thermochromic liquid crystal thermometry. Rev. Sci. Instrum. 2004, 75, 2985–2994. [Google Scholar] [CrossRef]
- Coletti, F.; Jacono, D.L.; Cresci, I.; Arts, T. Turbulent flow in rib-roughened channel under the effect of Coriolis and rotational buoyancy forces. Phys. Fluids 2014, 26, 45111. [Google Scholar] [CrossRef]
- Pascotto, M.; Armellini, A.; Mucignat, C.; Casarsa, L. Coriolis effects on the flow field inside a rotating triangular channel for leading edge cooling. J. Turbomach. 2013, 136, 31019. [Google Scholar] [CrossRef]



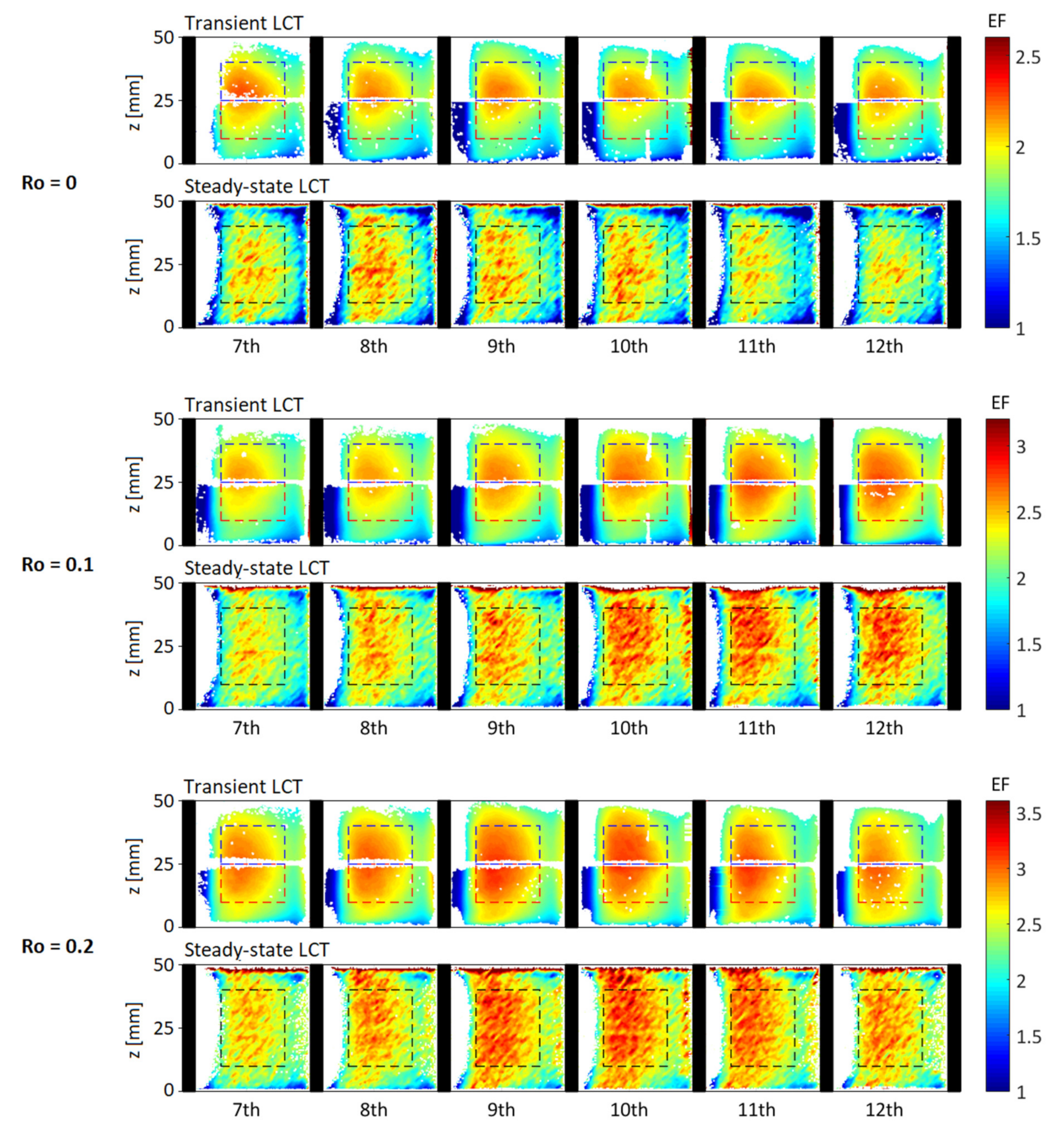
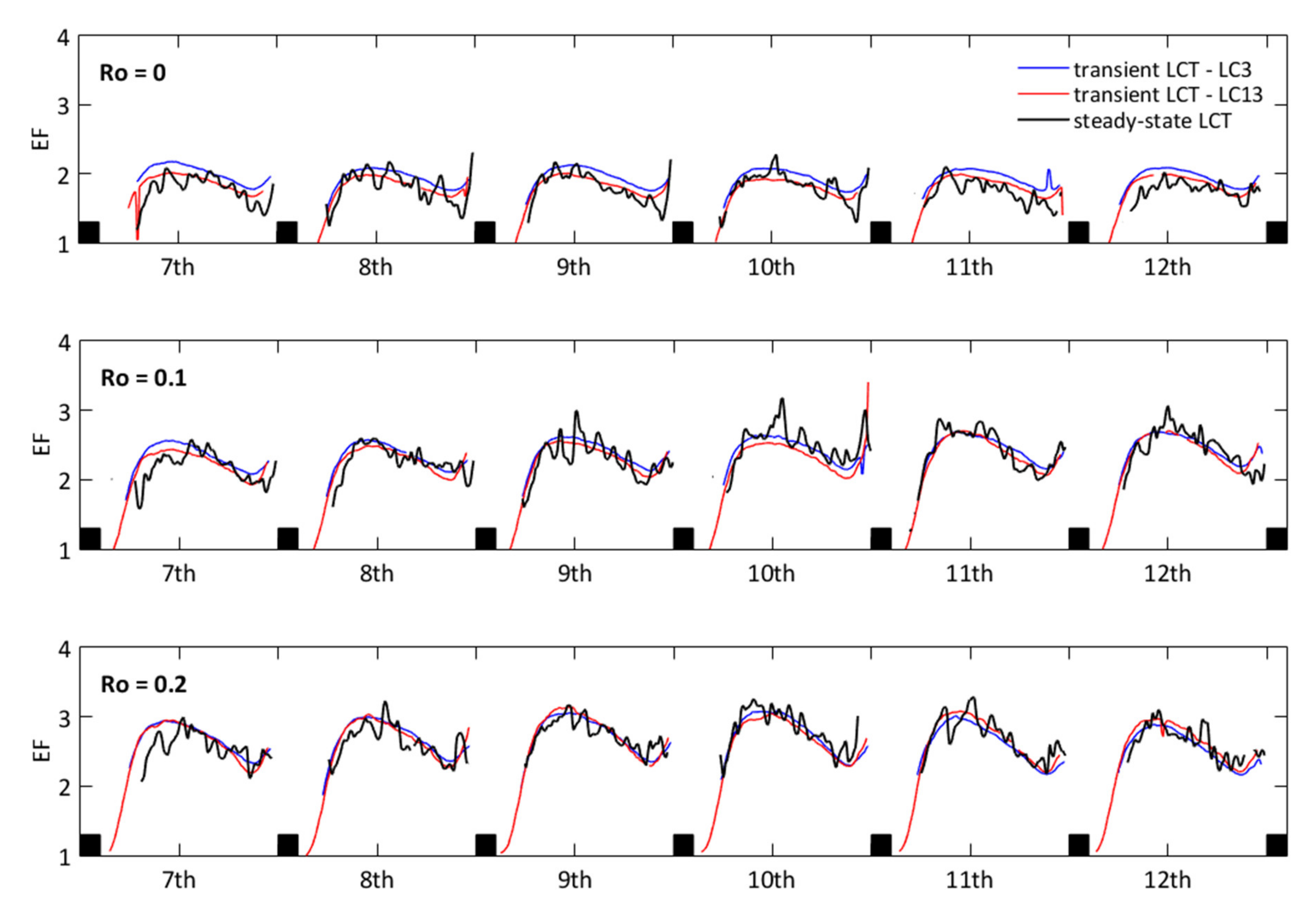
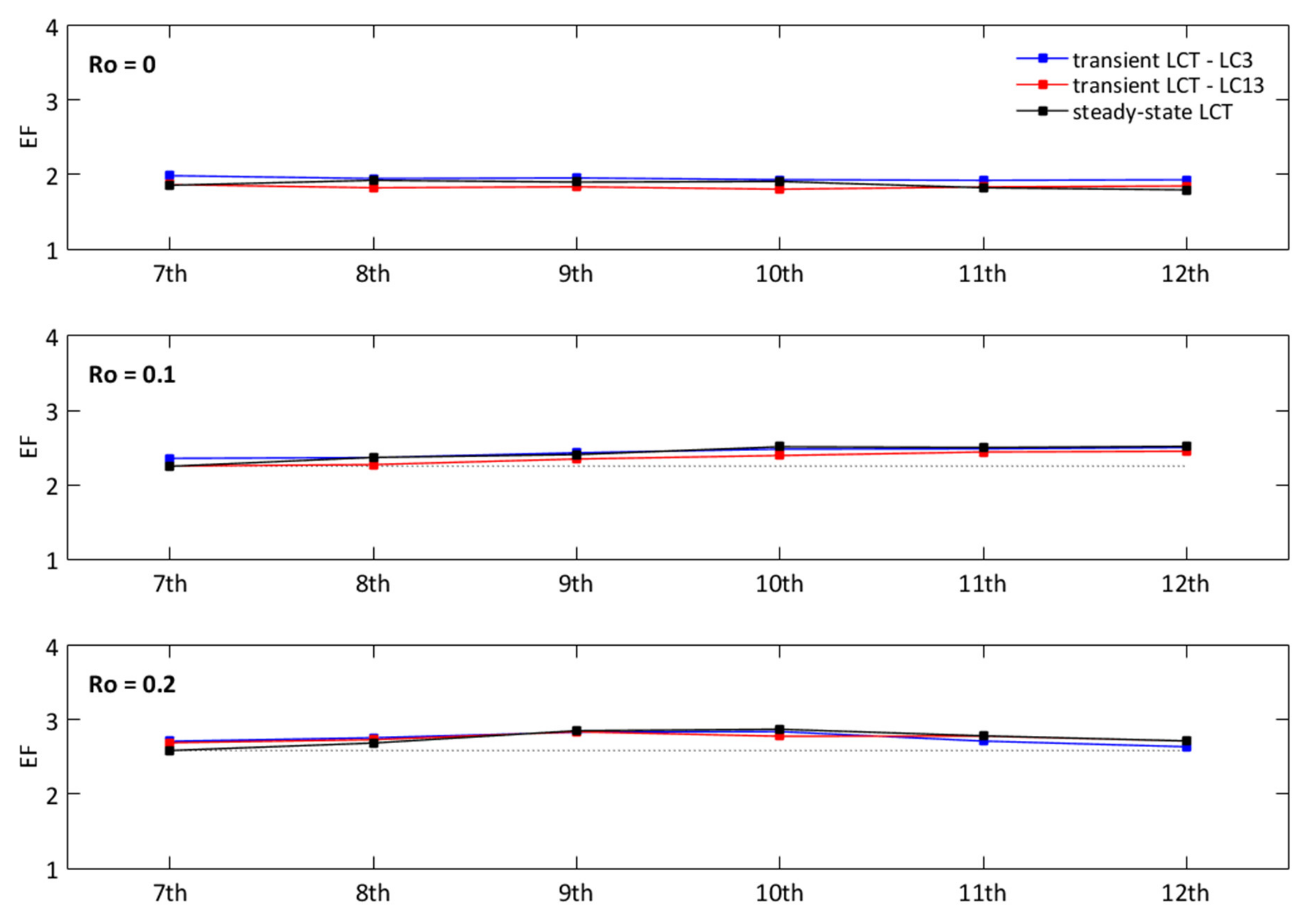
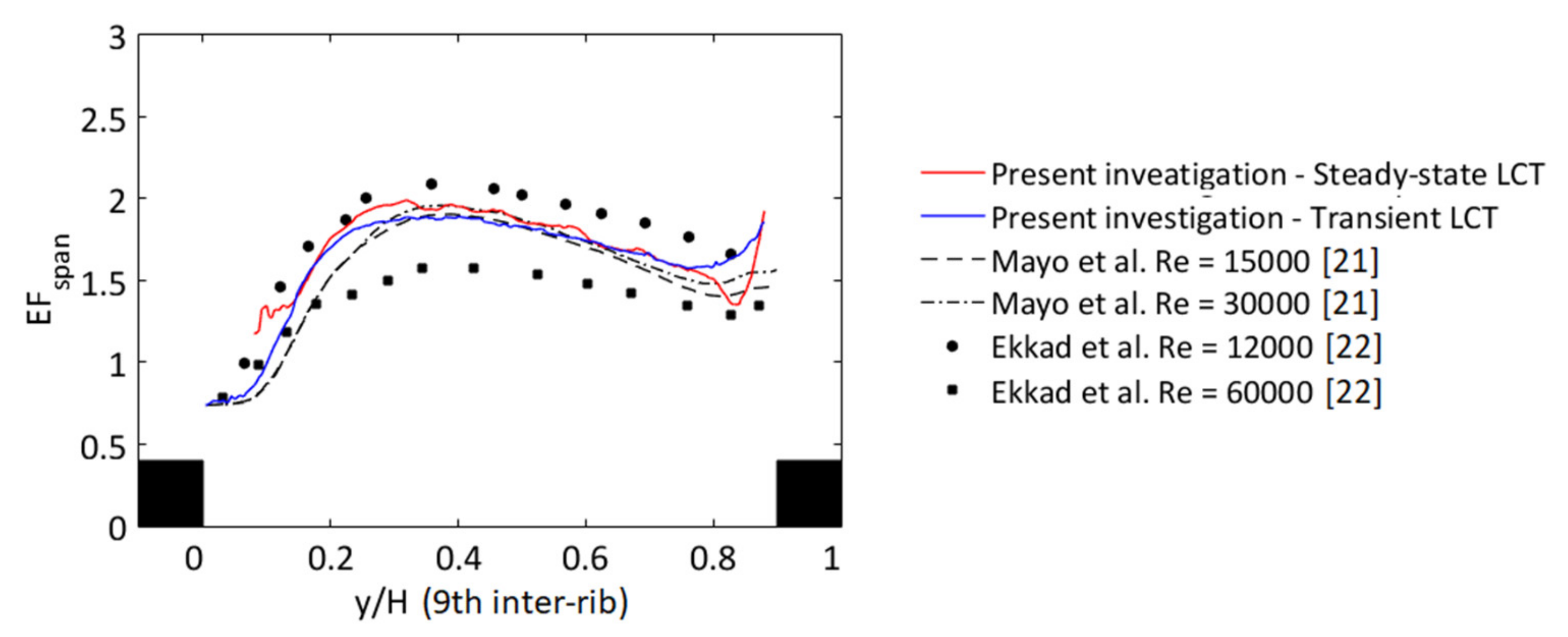
| Steady-State LCT | Transient LCT–LC3 | Transient LCT–LC13 | |||||
|---|---|---|---|---|---|---|---|
| 7th | 12th | 7th | 12th | 7th | 12th | ||
| 20,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20,000 | 0.10 | 0.010 | 0.012 | 0.011 | 0.013 | 0.011 | 0.009 |
| 20,000 | 0.20 | 0.039 | 0.050 | 0.036 | 0.048 | 0.038 | 0.046 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lorenzon, A.; Casarsa, L. Validation of the Transient Liquid Crystal Thermography Technique for Heat Transfer Measurements on a Rotating Cooling Passage. Energies 2020, 13, 4759. https://doi.org/10.3390/en13184759
Lorenzon A, Casarsa L. Validation of the Transient Liquid Crystal Thermography Technique for Heat Transfer Measurements on a Rotating Cooling Passage. Energies. 2020; 13(18):4759. https://doi.org/10.3390/en13184759
Chicago/Turabian StyleLorenzon, Andrea, and Luca Casarsa. 2020. "Validation of the Transient Liquid Crystal Thermography Technique for Heat Transfer Measurements on a Rotating Cooling Passage" Energies 13, no. 18: 4759. https://doi.org/10.3390/en13184759
APA StyleLorenzon, A., & Casarsa, L. (2020). Validation of the Transient Liquid Crystal Thermography Technique for Heat Transfer Measurements on a Rotating Cooling Passage. Energies, 13(18), 4759. https://doi.org/10.3390/en13184759




