Modeling and Evaluation of Energy Efficiency of New Hybrid Turning-Burnishing Process in Terms of Surface Properties
Abstract
:1. Introduction
2. Development of a New Hybrid Turning-Burnishing Tool
3. Optimization Framework
3.1. Optimization Issues
3.2. Optimization Approach
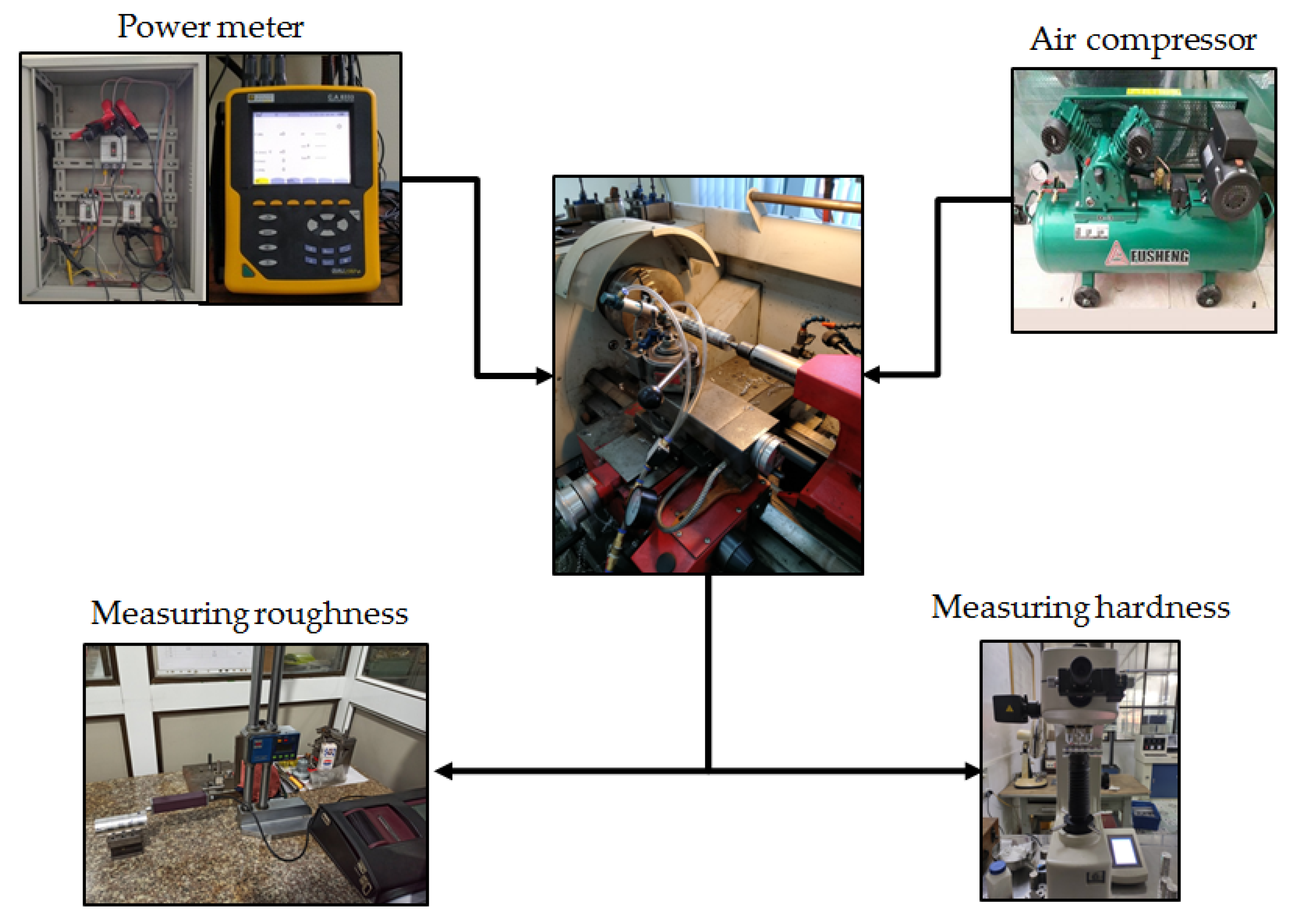
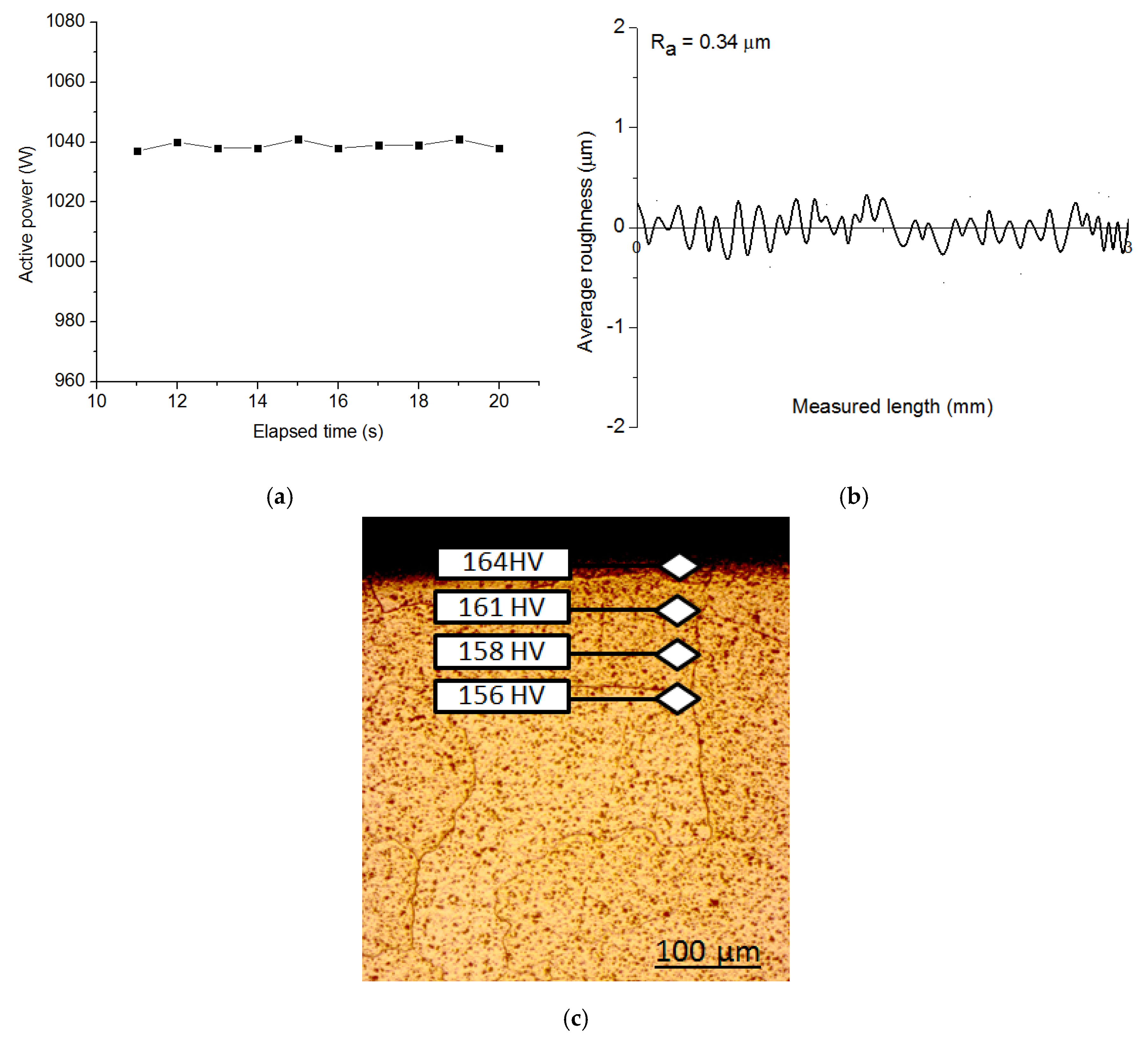
4. Experiments and Measurements
5. Results and Discussion
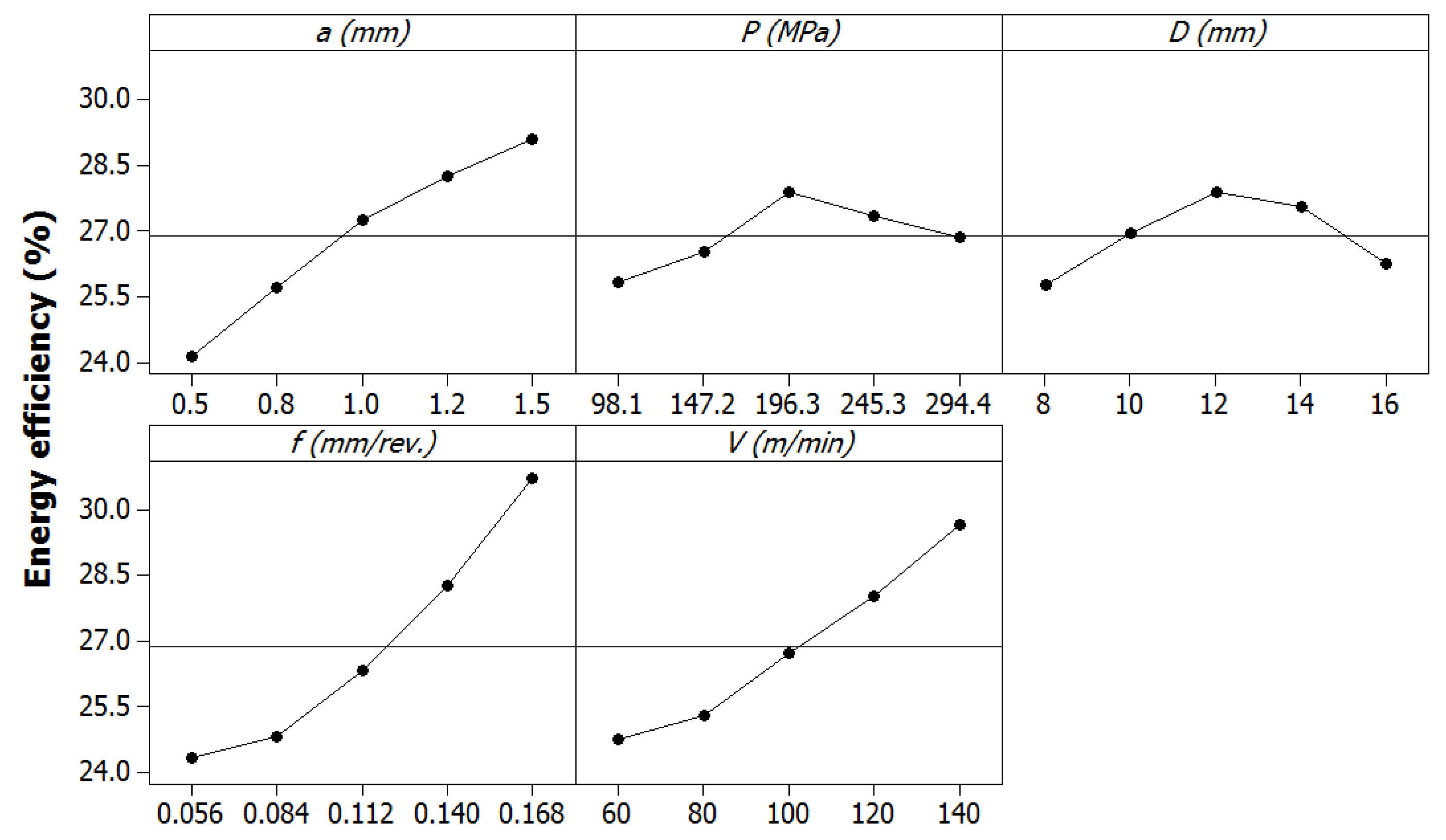
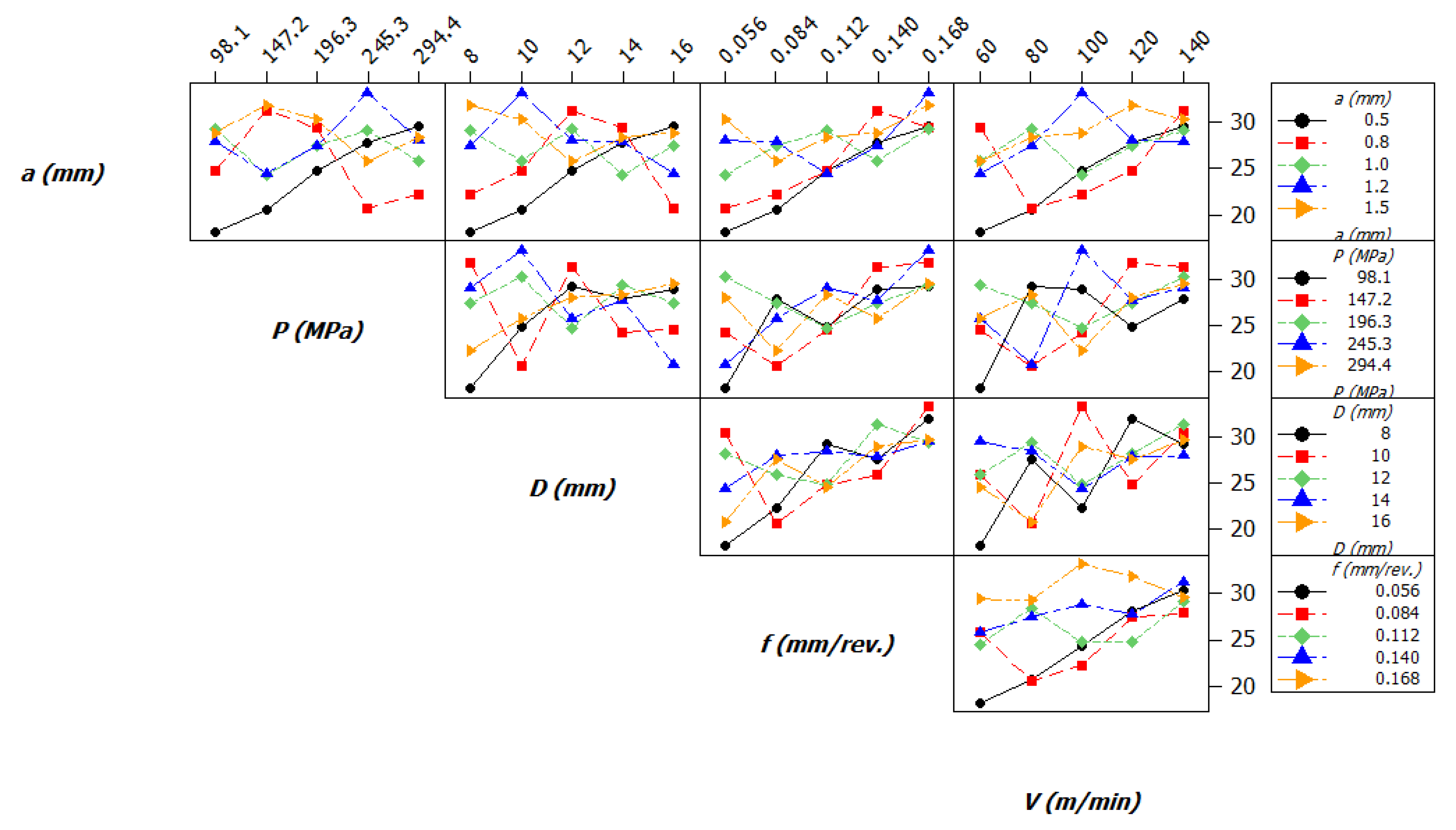
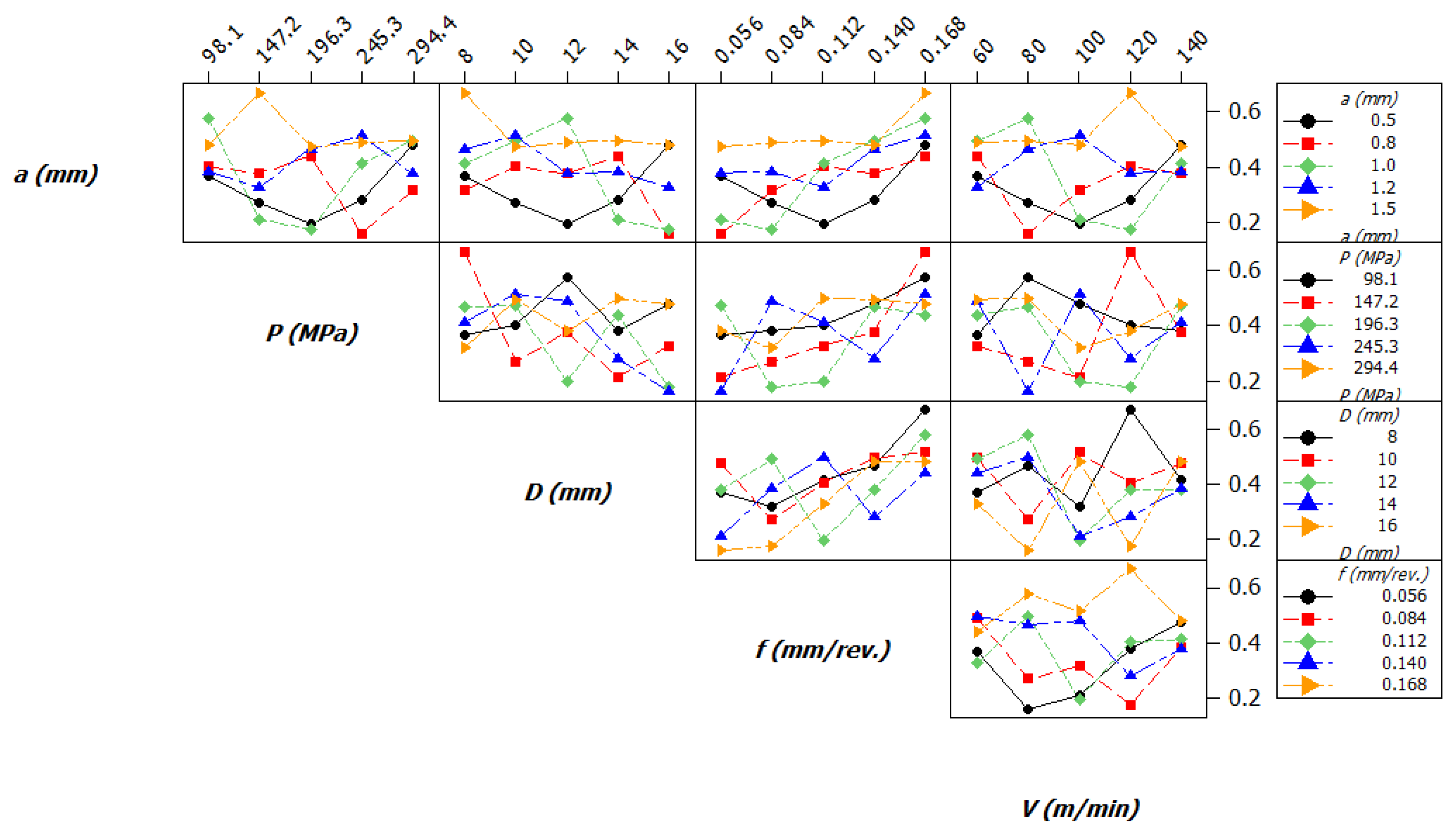
5.1. Parametric Effects
5.2. Optimization Results
6. Conclusions
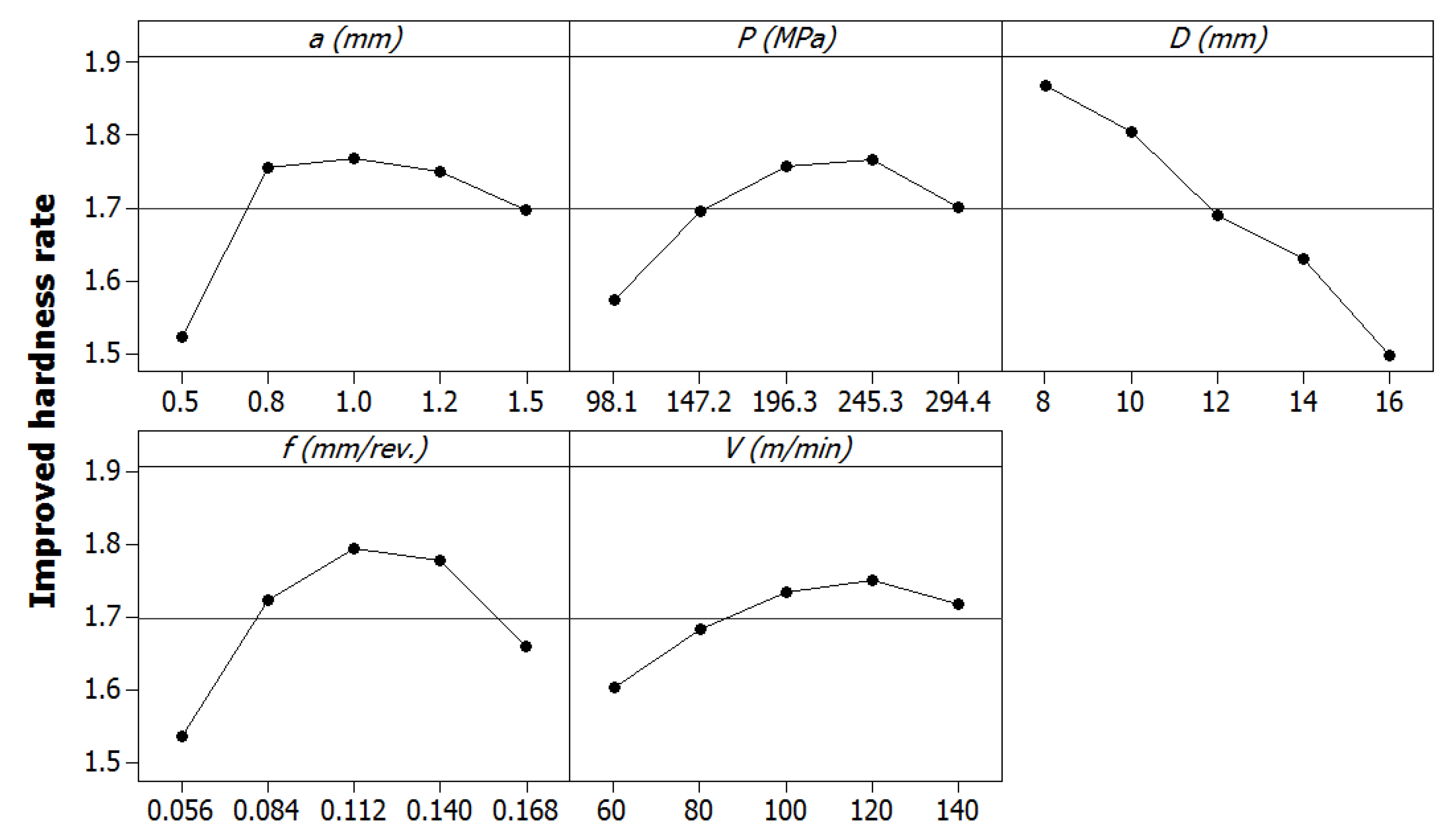
- The highest values of the depth of cut, feed rate, and turning speed cause an increased energy efficiency, while the middle levels of the diameter and burnishing pressure can be used to obtain higher energy efficiency. The lowest levels of the depth of cut and feed are recommended to decrease roughness, while the larger diameter is used to achieve a smooth surface. The middle values of the burnishing pressure and speed can be employed to enhance the machined quality. Higher hardness is obtained with an increment in the depth of cut, burnishing pressure, and turning speed. A low diameter can be employed to obtain a higher hardness, while the middle value of the feed can be applied to improve hardness.
- The optimal factors setting obtained by TOPSIS of the depth of cut, burnishing pressure, ball diameter, feed rate, and turning speed were 1.00 mm, 0.4 MPa, 16.0 mm, 0.084 mm/rev, and 100 m/min. The EF and IHR were enhanced by 20.75% and 8.23%, while the DRR was decreased by 19.05%. Additionally, the outcomes can be considered as technical solutions for improvements in energy efficiency and machined quality of the turning-burnishing processes.
- The hybrid approach, including the Taguchi method, WPCA, and TOPSIS, can extensively support the optimization of the hybrid operation when the responses have contradictory impacts. The proposed method was employed to save machining costs and efforts due to the lesser number of experiments. The WPCA was used to identify the weight for each objective, without the maker ‘subjective choice’. Therefore, the hybrid approach is multi-purposeful and can be applied to different manufacturing operations.
- It is difficult to apply the new turning-burnishing tool to machine difficult-to-cut material and/or hardened steels. The proper materials for the hybrid process are aluminum, copper, and brass. Moreover, an increase in the burnishing head and pneumatic cylinder can be used to enhance the machined quality.
- This work addressed the three machining responses, including energy efficiency, roughness, and hardness, that were considered as the outputs. Other responses such as residual stress and the depth of the hardened layer should be studied in order to holistically optimize the turning-burnishing process.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| No. | a (mm) | p (MPa) | d (mm) | f (mm/rev.) | v mm/min | EF (%) | RTB µm | HTB HV | DDR | IHR |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.2 | 8 | 0.056 | 60 | 18.11 | 0.72 | 126 | 0.37 | 1.32 |
| 2 | 0.5 | 0.3 | 10 | 0.084 | 80 | 20.52 | 0.53 | 154 | 0.27 | 1.60 |
| 3 | 0.5 | 0.4 | 12 | 0.112 | 100 | 24.73 | 0.38 | 168 | 0.19 | 1.75 |
| 4 | 0.5 | 0.5 | 14 | 0.14 | 120 | 27.75 | 0.55 | 157 | 0.28 | 1.64 |
| 5 | 0.5 | 0.6 | 16 | 0.168 | 140 | 29.58 | 0.94 | 125 | 0.48 | 1.31 |
| 6 | 0.8 | 0.2 | 10 | 0.112 | 120 | 24.79 | 0.79 | 181 | 0.40 | 1.89 |
| 7 | 0.8 | 0.3 | 12 | 0.14 | 140 | 31.37 | 0.74 | 178 | 0.38 | 1.85 |
| 8 | 0.8 | 0.4 | 14 | 0.168 | 60 | 29.42 | 0.86 | 152 | 0.44 | 1.58 |
| 9 | 0.8 | 0.5 | 16 | 0.056 | 80 | 20.71 | 0.31 | 143 | 0.16 | 1.49 |
| 10 | 0.8 | 0.6 | 8 | 0.084 | 100 | 22.24 | 0.62 | 189 | 0.32 | 1.97 |
| 11 | 1 | 0.2 | 12 | 0.168 | 80 | 29.37 | 1.13 | 150 | 0.58 | 1.56 |
| 12 | 1 | 0.3 | 14 | 0.056 | 100 | 24.30 | 0.41 | 151 | 0.21 | 1.57 |
| 13 | 1 | 0.4 | 16 | 0.084 | 120 | 27.52 | 0.34 | 164 | 0.17 | 1.71 |
| 14 | 1 | 0.5 | 8 | 0.112 | 140 | 29.16 | 0.81 | 201 | 0.41 | 2.09 |
| 15 | 1 | 0.6 | 10 | 0.14 | 60 | 25.84 | 0.97 | 183 | 0.50 | 1.91 |
| 16 | 1.2 | 0.2 | 14 | 0.084 | 140 | 27.90 | 0.75 | 158 | 0.38 | 1.65 |
| 17 | 1.2 | 0.3 | 16 | 0.112 | 60 | 24.53 | 0.64 | 147 | 0.33 | 1.53 |
| 18 | 1.2 | 0.4 | 8 | 0.14 | 80 | 27.45 | 0.92 | 196 | 0.47 | 2.04 |
| 19 | 1.2 | 0.5 | 10 | 0.168 | 100 | 33.29 | 1.01 | 185 | 0.52 | 1.93 |
| 20 | 1.2 | 0.6 | 12 | 0.056 | 120 | 28.13 | 0.74 | 154 | 0.38 | 1.60 |
| 21 | 1.5 | 0.2 | 16 | 0.14 | 100 | 28.95 | 0.94 | 140 | 0.48 | 1.46 |
| 22 | 1.5 | 0.3 | 8 | 0.168 | 120 | 31.95 | 1.32 | 185 | 0.67 | 1.92 |
| 23 | 1.5 | 0.4 | 10 | 0.056 | 140 | 30.34 | 0.93 | 163 | 0.47 | 1.70 |
| 24 | 1.5 | 0.5 | 12 | 0.084 | 60 | 25.78 | 0.96 | 162 | 0.49 | 1.69 |
| 25 | 1.5 | 0.6 | 14 | 0.112 | 80 | 28.42 | 0.98 | 165 | 0.50 | 1.72 |
References
- Rech, J.; Hamdi, H.; Valette, S. Workpiece Surface Integrity. In Machining; Springer: London, UK, 2008. [Google Scholar] [CrossRef]
- Frăţilă, D.; Caizar, C. Investigation of the Influence of Process Parameters and Cooling Method on the Surface Quality of AISI-1045 during Turning. Mater. Manuf. Process. 2012, 27, 1123–1128. [Google Scholar] [CrossRef]
- Jafarian, F.; Amirabadi, H.; Sadri, J.; Banooie, H.R. Simultaneous Optimizing Residual Stress and Surface Roughness in Turning of Inconel718 Superalloy. Mater. Manuf. Process. 2014, 29, 337–343. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, D.; Ren, J. Optimization of Process Parameters for Surface Roughness and Microhardness in Dry Milling of Magnesium Alloy Using Taguchi with Grey Relational Analysis. Int. J. Adv. Manuf. Technol. 2015, 81, 645–651. [Google Scholar] [CrossRef]
- Bhopale, N.N.; Pawade, R.S.; Joshi, S.S. Surface Quality Analysis in Ball End Milling of Inconel 718 Cantilevers by Response Surface Methodology. Proc. Inst. Mech. Eng. B 2015, 231, 628–640. [Google Scholar] [CrossRef]
- Da Silva, L.R.; Couto, D.A.; dos Santo, F.V.; Duarte, F.J.; Mazzaro, R.S.; Veloso, G.V. Evaluation of Machined Surface of the Hardened AISI 4340 Steel Through Roughness and Residual Stress Parameters in Turning and Grinding. Int. J. Adv. Manuf. Technol. 2020, 107, 791–803. [Google Scholar] [CrossRef]
- Duo, L.; Xiangqian, J.; Zhen, T.; Liam, B. Development and Application of Interferometric On-Machine Surface Measurement for Ultraprecision Turning Process. J. Manuf. Sci. Eng. 2019, 141, 014502. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Wang, B.; Qiao, Z.; Jiang, X. Ultraprecision machining of microlens arrays with integrated on-machine surface metrology. Opt. Express 2019, 27, 212–224. [Google Scholar] [CrossRef]
- Yao, C.; Ma, L.; Du, Y.; Ren, J.; Zhang, D. Surface Integrity and Fatigue Behavior in Shot-Peening for High-Speed Milled 7055 Aluminum Alloy. Proc. Inst. Mech. Eng. B 2017, 231, 243–256. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Cao, L.H.; Nguyen, T.A.; Dang, X.P. Multi-response optimization of the roller burnishing process in terms of energy consumption and product quality. J. Clean. Prod. 2020, 245, 119328. [Google Scholar] [CrossRef]
- Amdouni, H.; Bouzaiene, H.; Montagne, A.; Nasri, M.; Iost, A. Experimental study of a six new ball-burnishing strategies effects on the Al-alloy flat surfaces integrity enhancement. Int. J. Adv. Manuf. Tech. 2017, 90, 2271–2282. [Google Scholar] [CrossRef] [Green Version]
- John, M.R.S.; Banerjee, N.; Shrivastava, K.; Vinayagam, B.K. Optimization of Roller Burnishing Process on EN-9 Grade Alloy Steel using Response Surface Methodology. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3089–3101. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Le, X.B. Optimization of Interior Roller Burnishing Process for Improving Surface Quality. Mater. Manuf. Process. 2018, 33, 1233–1241. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Le, X.B. Optimization of roller burnishing process using Kriging model to improve surface properties. Proc. Inst. Mech. Eng. B 2019, 233, 2264–2282. [Google Scholar] [CrossRef]
- Sachin, B.; Narendranath, S.; Chakradhar, D. Selection of Optimal Process Parameters in Sustainable Diamond Burnishing of 17-4 PH Stainless Steel. Proc. Inst. Mech. Eng. B 2019, 41, 219. [Google Scholar] [CrossRef]
- Świrad, S.; Wydrzynski, D.; Nieslony, P.; Krolczyk, G.M. Influence of Hydrostatic Burnishing Strategy on the Surface Topography of Martensitic Steel. Measurement 2019, 138, 590–601. [Google Scholar] [CrossRef]
- Grzesik, W.; Krzysztof, Ż. Modification of surface finish produced by hard turning using superfinishing and burnishing operations. J. Mater. Process. Technol. 2012, 212, 315–322. [Google Scholar] [CrossRef]
- Axinte, D.A.; Gindy, N. Turning assisted with deep cold rolling-a cost efficient hybrid process for workpiece surface quality enhancement. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2004, 218, 807–811. [Google Scholar] [CrossRef]
- Mezlini, S.; Mzali, S.; Sghaier, S.; Braham, C.; Kapsa, P. Effect of a combined machining/burnishing tool on the roughness and mechanical properties. Lubr. Sci. 2014, 26. [Google Scholar] [CrossRef] [Green Version]
- Rami, A.; Kallel, A.; Djemaa, S.; Mabrouki, T.; Sghaier, S.; Hamdi, H. Numerical assessment of residual stresses induced by combining turning-burnishing (cotub) process of aisi 4140 steel using 3d simulation based on a mixed approach. Int. J. Adv. Manuf. Technol. 2018, 97, 1897–1912. [Google Scholar] [CrossRef]
- Rami, A.; Gharbi, F.; Sghaier, S.; Hamdi, H. Some Insights on Combined Turning-Burnishing (CoTuB) Process on Workpiece Surface Integrity. Int. J. Precis. Eng. Manuf. 2018, 19, 67–78. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, T.; Trinh, Q. Optimization of Milling Parameters for Energy Savings and Surface Quality. Arab. J. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Duong, Q.-D.; Mia, M. Sustainability-Based Optimization of the Rotary Turning of the Hardened Steel. Metals 2020, 10, 939. [Google Scholar] [CrossRef]
- Swirad, S.; Pawlus, P. The Effect of Ball Burnishing on Tribological Performance of 42CrMo4 Steel under Dry Sliding Conditions. Materials 2020, 13, 2127. [Google Scholar] [CrossRef] [PubMed]
- Jerez-Mesa, R.; Plana-García, V.; Llumà, J.; Travieso-Rodriguez, J.A. Enhancing Surface Topology of Udimet®720 Superalloy through Ultrasonic Vibration-Assisted Ball Burnishing. Metals 2020, 10, 915. [Google Scholar] [CrossRef]
- Amini, C.; Jerez-Mesa, R.; Travieso-Rodriguez, J.A.; Llumà, J.; Estevez-Urra, A. Finite Element Analysis of Ball Burnishing on Ball-End Milled Surfaces Considering Their Original Topology and Residual Stress. Metals 2020, 10, 638. [Google Scholar] [CrossRef]
- Paiva, A.P.; Costa, S.C.; Paiva, E.J.; Balestrassi, P.P.; Ferreira, J.R. Multi-objective optimization of pulsed gas metal arc welding process based on weighted principal component scores. Int. J. Adv. Manuf. Technol. 2010, 50, 113–125. [Google Scholar] [CrossRef]
- Costa, D.M.D.; Belinato, G.; Brito, T.G.; Paiva, A.P.; Ferreira, J.R.; Balestrassi, P.P. Weighted principal component analysis combined with Taguchi’s signal-to-noise ratio to the multiobjective optimization of dry end milling process: A comparative study. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1663–1681. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Cao, L.H.; Dang, X.P.; Nguyen, T.A.; Trinh, Q.H. Multi-objective optimization of the flat burnishing process for energy efficiency and surface characteristics. Mater. Manuf. Process. 2019, 34, 1888–1901. [Google Scholar] [CrossRef]
- Park, H.; Nguyen, T.; Dang, X. Multi-objective optimization of turning process of hardened material for energy efficiency. Int. J. Precis. Eng. Manuf. 2016, 17, 1623–1631. [Google Scholar] [CrossRef]
- Ning, J.; Nguyen, V.; Huang, Y.; Karl, T.H.; Steven, Y.L. Constitutive modeling of ultra-fine-grained titanium flow stress for machining temperature prediction. Bio-Des. Manuf. 2019, 2, 153–160. [Google Scholar] [CrossRef]
- Ning, J.; Nguyen, V.; Liang, S.Y. Analytical modeling of machining forces of ultra-fine-grained titanium. Int. J. Adv. Manuf. Technol. 2019, 101, 627–636. [Google Scholar] [CrossRef]





| Year | Authors [Ref.] | Actuator | Responses | Outcomes |
|---|---|---|---|---|
| 2004 | Axinte and Gindy [18] | Hydraulic unit | Roughness | 68% decreased roughness |
| Thickness of the depth layer | 300 μm of the depth of layer | |||
| 2014 | Mezlini et al. [19] | Mechanical unit | Roughness | 77% decreased roughness |
| Total machining time | 51% decreased total time | |||
| 2018 | Rami et al. [20] | Mechanical tool | Prediction of the compressive stress | Acceptable accuracy for prediction |
| 2018 | Rami et al. [21] | Mechanical tool | Roughness | 70% decreased roughness |
| Hardness | Enhanced hardness | |||
| Compressive stress | Enhanced compressive stress |
| Symbol | Parameters | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| a | Depth of cut (mm) | 0.50 | 0.80 | 1.00 | 1.20 | 1.50 |
| p | Burnishing pressure (MPa) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| d | Diameter (mm) | 8 | 10 | 12 | 14 | 16 |
| f | Feed rate (mm/rev.) | 0.056 | 0.084 | 0.112 | 0.140 | 0.168 |
| v | Turning speed (m/min) | 60 | 80 | 100 | 120 | 140 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value | Remark | Contribution |
|---|---|---|---|---|---|---|
| Model | 579.5436 | 28.9772 | 77.5620 | <0.0001 | Significant | |
| a | 71.8055 | 71.8055 | 192.1987 | <0.0001 | Significant | 12.39 |
| p | 34.8885 | 34.8885 | 93.3847 | <0.0001 | Significant | 6.02 |
| d | 22.8920 | 22.8920 | 61.2740 | <0.0001 | Significant | 3.95 |
| f | 104.2019 | 104.2019 | 278.9131 | <0.0001 | Significant | 17.98 |
| v | 83.8600 | 83.8600 | 224.4646 | <0.0001 | Significant | 14.47 |
| ap | 12.1125 | 12.1125 | 32.4209 | 0.0254 | Significant | 2.09 |
| ad | 10.3738 | 10.3738 | 27.7672 | 0.0385 | Significant | 1.79 |
| af | 14.1988 | 14.1988 | 38.0054 | 0.0214 | Significant | 2.45 |
| av | 8.2875 | 8.2875 | 22.1827 | 0.0416 | Significant | 1.43 |
| pd | 7.0125 | 7.0125 | 18.7700 | 0.0422 | Significant | 1.21 |
| pf | 6.3170 | 6.3170 | 16.9085 | 0.0486 | Significant | 1.09 |
| pv | 0.1159 | 0.1159 | 0.3102 | 1.0000 | Insignificant | 0.02 |
| df | 10.2579 | 10.2579 | 27.4570 | 0.0394 | Significant | 1.77 |
| dv | 10.5477 | 10.5477 | 28.2326 | 0.0383 | Significant | 1.82 |
| fv | 19.1249 | 19.1249 | 51.1909 | 0.0167 | Significant | 3.30 |
| a2 | 15.4738 | 15.4738 | 41.4181 | 0.0204 | Significant | 2.67 |
| p2 | 51.9851 | 51.9851 | 139.1463 | <0.0001 | Significant | 8.97 |
| d2 | 51.1157 | 51.1157 | 136.8194 | <0.0001 | Significant | 8.82 |
| f2 | 29.6726 | 29.6726 | 79.4235 | 0.0059 | Significant | 5.12 |
| v2 | 15.3000 | 15.3000 | 40.9528 | 0.0224 | Significant | 2.64 |
| Error | 7.4714 | 0.3736 | ||||
| Total | 587.0150 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value | Remark | Contribution |
|---|---|---|---|---|---|---|
| Model | 0.5574 | 0.0279 | 53.7928 | <0.0001 | Significant | |
| a | 0.0865 | 0.0865 | 173.0485 | <0.0001 | Significant | 16.63 |
| p | 0.0130 | 0.0130 | 26.0145 | 0.0097 | Significant | 2.50 |
| d | 0.0523 | 0.0523 | 104.5783 | <0.0001 | Significant | 10.05 |
| f | 0.0829 | 0.0829 | 165.8685 | <0.0001 | Significant | 15.94 |
| v | 0.0088 | 0.0088 | 17.6899 | 0.0468 | Significant | 1.70 |
| ap | 0.0003 | 0.0003 | 0.5203 | 0.9119 | Insignificant | 0.05 |
| ad | 0.0019 | 0.0019 | 3.8501 | 0.8249 | Insignificant | 0.37 |
| af | 0.0271 | 0.0271 | 54.2142 | 0.0053 | Significant | 5.21 |
| av | 0.0089 | 0.0089 | 17.8980 | 0.047 | Significant | 1.72 |
| pd | 0.0243 | 0.0243 | 48.5951 | 0.0110 | Significant | 4.67 |
| pf | 0.0097 | 0.0097 | 19.4588 | 0.0446 | Significant | 1.87 |
| pv | 0.0000 | 0.0000 | 0.0000 | 1.0000 | Insignificant | 0 |
| df | 0.0010 | 0.0010 | 1.9771 | 0.9119 | Insignificant | 0.19 |
| dv | 0.0048 | 0.0048 | 9.6774 | 0.5814 | Insignificant | 0.93 |
| fv | 0.0000 | 0.0000 | 0.0000 | 1.0000 | Insignificant | 0 |
| a2 | 0.0309 | 0.0309 | 61.7064 | 0.0049 | Significant | 5.93 |
| p2 | 0.0691 | 0.0691 | 138.1890 | <0.0001 | Significant | 13.28 |
| d2 | 0.0051 | 0.0051 | 10.1977 | 0.6106 | Insignificant | 0.98 |
| f2 | 0.0488 | 0.0488 | 97.5024 | <0.0001 | Significant | 9.37 |
| v2 | 0.0448 | 0.0448 | 89.5939 | 0.0002 | Significant | 8.61 |
| Error | 0.0104 | 0.0005 | ||||
| Total | 0.5677 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value | Remark | Contribution |
|---|---|---|---|---|---|---|
| Model | 1.0484 | 0.0524 | 74.8865 | <0.0001 | Significant | |
| a | 0.0786 | 0.0786 | 112.3298 | <0.0001 | Significant | 7.50 |
| p | 0.0028 | 0.0028 | 4.0439 | 0.9864 | Insignificant | 0.27 |
| d | 0.1578 | 0.1578 | 225.4085 | <0.0001 | Significant | 15.05 |
| f | 0.0482 | 0.0482 | 68.8956 | <0.0001 | Significant | 4.60 |
| v | 0.0713 | 0.0713 | 101.8457 | <0.0001 | Significant | 6.80 |
| ap | 0.0561 | 0.0561 | 80.1286 | <0.0001 | Significant | 5.35 |
| ad | 0.0029 | 0.0029 | 4.1936 | 0.7888 | Insignificant | 0.28 |
| af | 0.0095 | 0.0095 | 13.6293 | 0.3849 | Insignificant | 0.91 |
| av | 0.0791 | 0.0791 | 112.9289 | 0.0032 | Significant | 7.54 |
| pd | 0.0047 | 0.0047 | 6.7398 | 0.6657 | Insignificant | 0.45 |
| pf | 0.0000 | 0.0000 | 0.0000 | 1.0000 | Insignificant | 0 |
| pv | 0.0000 | 0.0000 | 0.0000 | 1.0000 | Insignificant | 0 |
| df | 0.0018 | 0.0018 | 2.5461 | 0.8707 | Insignificant | 0.17 |
| dv | 0.0061 | 0.0061 | 8.6868 | 0.5765 | Insignificant | 0.58 |
| fv | 0.0021 | 0.0021 | 2.9955 | 0.8455 | Insignificant | 0.20 |
| a2 | 0.1489 | 0.1489 | 212.6777 | <0.0001 | Significant | 14.20 |
| p2 | 0.1321 | 0.1321 | 188.7141 | <0.0001 | Significant | 12.60 |
| d2 | 0.1286 | 0.1286 | 183.7715 | <0.0001 | Significant | 12.27 |
| f2 | 0.0277 | 0.0277 | 39.5401 | 0.0098 | Significant | 2.64 |
| v2 | 0.0901 | 0.0901 | 128.6551 | <0.0001 | Significant | 8.59 |
| Error | 0.0140 | 0.0007 | ||||
| Total | 1.1635 |
| No. | EF | DDR | IHR |
|---|---|---|---|
| 1 | 1.0000 | 0.4324 | 0.9924 |
| 2 | 0.8826 | 0.5926 | 0.8188 |
| 3 | 0.7323 | 0.8421 | 0.7486 |
| 4 | 0.6526 | 0.5714 | 0.7988 |
| 5 | 0.6122 | 0.3333 | 1.0000 |
| 6 | 0.7305 | 0.4000 | 0.6931 |
| 7 | 0.5773 | 0.4211 | 0.7081 |
| 8 | 0.6156 | 0.3636 | 0.8291 |
| 9 | 0.8745 | 1.0000 | 0.8792 |
| 10 | 0.8143 | 0.5000 | 0.6650 |
| 11 | 0.6166 | 0.2759 | 0.8397 |
| 12 | 0.7453 | 0.7619 | 0.8344 |
| 13 | 0.6581 | 0.9412 | 0.7661 |
| 14 | 0.6211 | 0.3902 | 0.6268 |
| 15 | 0.7009 | 0.3200 | 0.6859 |
| 16 | 0.6491 | 0.4211 | 0.7939 |
| 17 | 0.7383 | 0.4848 | 0.8562 |
| 18 | 0.6597 | 0.3404 | 0.6422 |
| 19 | 0.5440 | 0.3077 | 0.6788 |
| 20 | 0.6438 | 0.4211 | 0.8188 |
| 21 | 0.6256 | 0.3333 | 0.8973 |
| 22 | 0.5668 | 0.2388 | 0.6823 |
| 23 | 0.5969 | 0.3404 | 0.7706 |
| 24 | 0.7025 | 0.3265 | 0.7751 |
| 25 | 0.6372 | 0.3200 | 0.7616 |
| Principal Component | Eigenvalues | Proportion (%) |
|---|---|---|
| First | 1.9759 | 71.90 |
| Second | 1.1456 | 26.40 |
| Third | 0.1784 | 1.70 |
| Characteristics | Eigenvectors | Contribution (%) | ||
|---|---|---|---|---|
| PC1 | PC2 | PC3 | ||
| EF | 0.659 | 0.08 | 0.749 | 0.22 |
| DDR | 0.57 | 0.60 | 0.561 | 0.34 |
| IHR | 0.491 | 0.80 | 0.352 | 0.44 |
| No. | EF | DDR | IHR |
|---|---|---|---|
| 1 | 0.0294 | 0.0608 | 0.0679 |
| 2 | 0.0333 | 0.0443 | 0.0823 |
| 3 | 0.0401 | 0.0312 | 0.0900 |
| 4 | 0.0450 | 0.0460 | 0.0843 |
| 5 | 0.0480 | 0.0788 | 0.0674 |
| 6 | 0.0402 | 0.0657 | 0.0972 |
| 7 | 0.0509 | 0.0624 | 0.0951 |
| 8 | 0.0477 | 0.0722 | 0.0812 |
| 9 | 0.0336 | 0.0263 | 0.0766 |
| 10 | 0.0361 | 0.0525 | 0.1013 |
| 11 | 0.0476 | 0.0952 | 0.0802 |
| 12 | 0.0394 | 0.0345 | 0.0807 |
| 13 | 0.0446 | 0.0279 | 0.0879 |
| 14 | 0.0473 | 0.0673 | 0.1075 |
| 15 | 0.0419 | 0.0821 | 0.0982 |
| 16 | 0.0452 | 0.0624 | 0.0848 |
| 17 | 0.0398 | 0.0542 | 0.0787 |
| 18 | 0.0445 | 0.0772 | 0.1049 |
| 19 | 0.0540 | 0.0854 | 0.0992 |
| 20 | 0.0456 | 0.0624 | 0.0823 |
| 21 | 0.0469 | 0.0788 | 0.0751 |
| 22 | 0.0518 | 0.1100 | 0.0987 |
| 23 | 0.0492 | 0.0772 | 0.0874 |
| 24 | 0.0418 | 0.0805 | 0.0869 |
| 25 | 0.0461 | 0.0821 | 0.0884 |
| No. | S+ | S- | D | Ranking |
|---|---|---|---|---|
| 1 | 0.0580 | 0.0492 | 0.9360 | 16 |
| 2 | 0.0373 | 0.0674 | 0.9798 | 7 |
| 3 | 0.0229 | 0.0827 | 0.9937 | 2 |
| 4 | 0.0317 | 0.0680 | 0.9854 | 4 |
| 5 | 0.0664 | 0.0363 | 0.8917 | 23 |
| 6 | 0.0430 | 0.0545 | 0.9672 | 11 |
| 7 | 0.0383 | 0.0591 | 0.9758 | 8 |
| 8 | 0.0533 | 0.0442 | 0.9396 | 15 |
| 9 | 0.0370 | 0.0843 | 0.9840 | 6 |
| 10 | 0.0324 | 0.0670 | 0.9846 | 5 |
| 11 | 0.0744 | 0.0267 | 0.8283 | 25 |
| 12 | 0.0316 | 0.0773 | 0.9873 | 3 |
| 13 | 0.0218 | 0.0860 | 0.9945 | 1 |
| 14 | 0.0416 | 0.0612 | 0.9725 | 9 |
| 15 | 0.0579 | 0.0434 | 0.9284 | 19 |
| 16 | 0.0435 | 0.0531 | 0.9656 | 12 |
| 17 | 0.0426 | 0.0579 | 0.9697 | 10 |
| 18 | 0.0518 | 0.0521 | 0.9510 | 14 |
| 19 | 0.0597 | 0.0472 | 0.9298 | 18 |
| 20 | 0.0448 | 0.0524 | 0.9631 | 13 |
| 21 | 0.0621 | 0.0366 | 0.9046 | 22 |
| 22 | 0.0842 | 0.0385 | 0.8445 | 24 |
| 23 | 0.0549 | 0.0432 | 0.9348 | 17 |
| 24 | 0.0592 | 0.0375 | 0.9145 | 2210 |
| 25 | 0.0595 | 0.0387 | 0.9162 | 20 |
| Method | a (mm) | p (MPa) | d (mm) | f (mm/rev) | v mm/min | EF (%) | RTB µm | HTB HV | DDR | IHR |
|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 0.75 | 0.3 | 12 | 0.090 | 90 | 21.81 | 0.42 | 152 | 0.21 | 1.58 |
| Optimal | 1.00 | 0.4 | 16 | 0.084 | 120 | 27.52 | 0.34 | 164 | 0.17 | 1.71 |
| Improvement (%) | 20.75 | −19.05 | 8.23 | |||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-T.; Mia, M. Modeling and Evaluation of Energy Efficiency of New Hybrid Turning-Burnishing Process in Terms of Surface Properties. Energies 2020, 13, 4929. https://doi.org/10.3390/en13184929
Nguyen T-T, Mia M. Modeling and Evaluation of Energy Efficiency of New Hybrid Turning-Burnishing Process in Terms of Surface Properties. Energies. 2020; 13(18):4929. https://doi.org/10.3390/en13184929
Chicago/Turabian StyleNguyen, Trung-Thanh, and Mozammel Mia. 2020. "Modeling and Evaluation of Energy Efficiency of New Hybrid Turning-Burnishing Process in Terms of Surface Properties" Energies 13, no. 18: 4929. https://doi.org/10.3390/en13184929






