Digital Luminaire Design Using LED Digital Twins—Accuracy and Reduced Computation Time: A Delphi4LED Methodology
Abstract
:1. Introduction
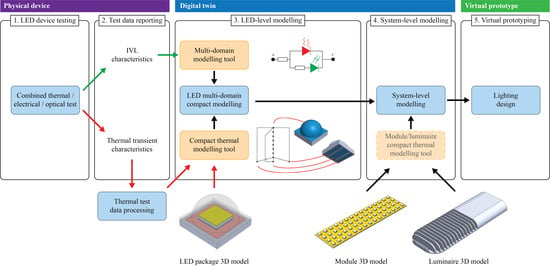
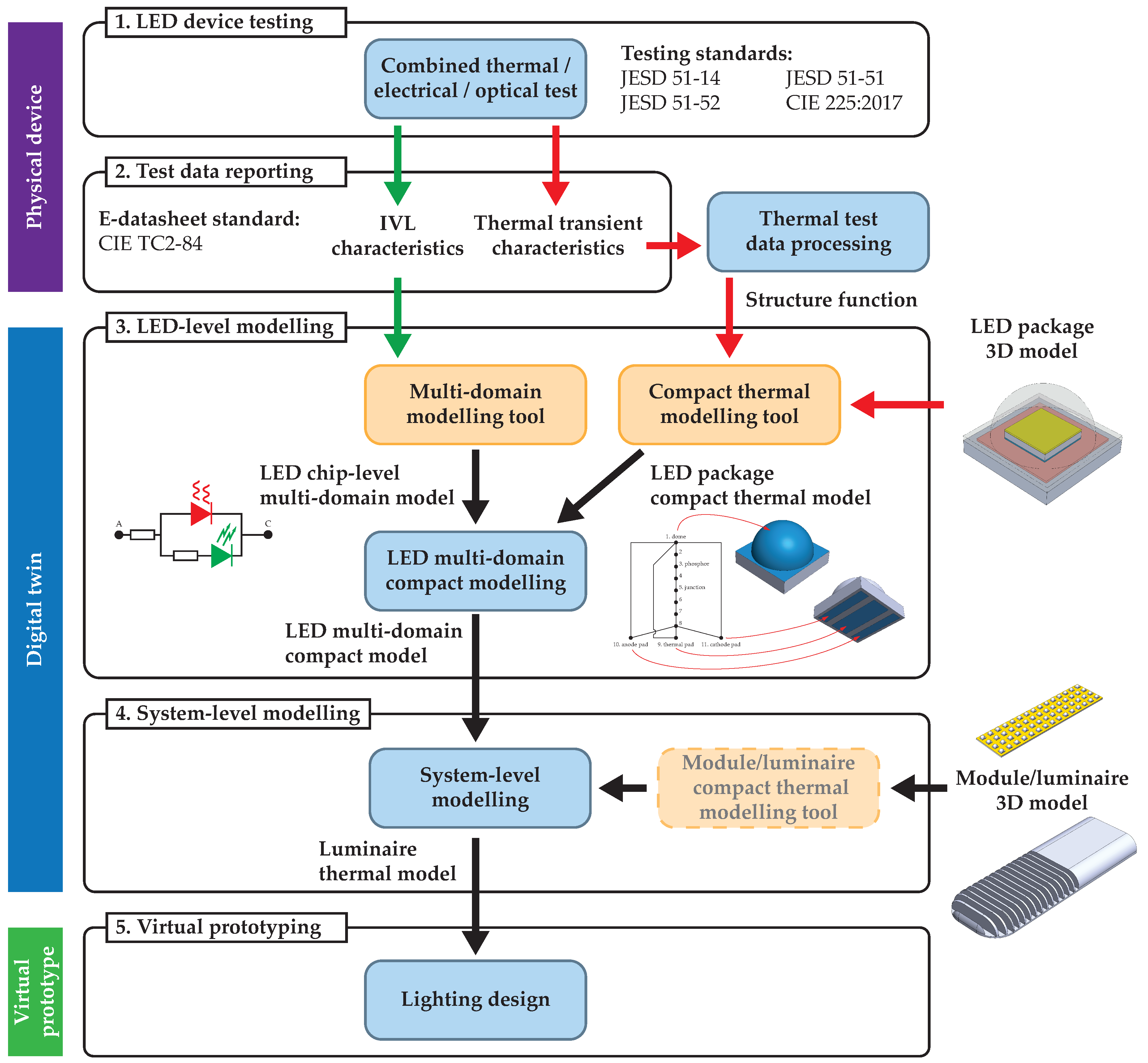
2. Materials and Methods
2.1. LED Device Testing
2.2. LED-Level Modelling
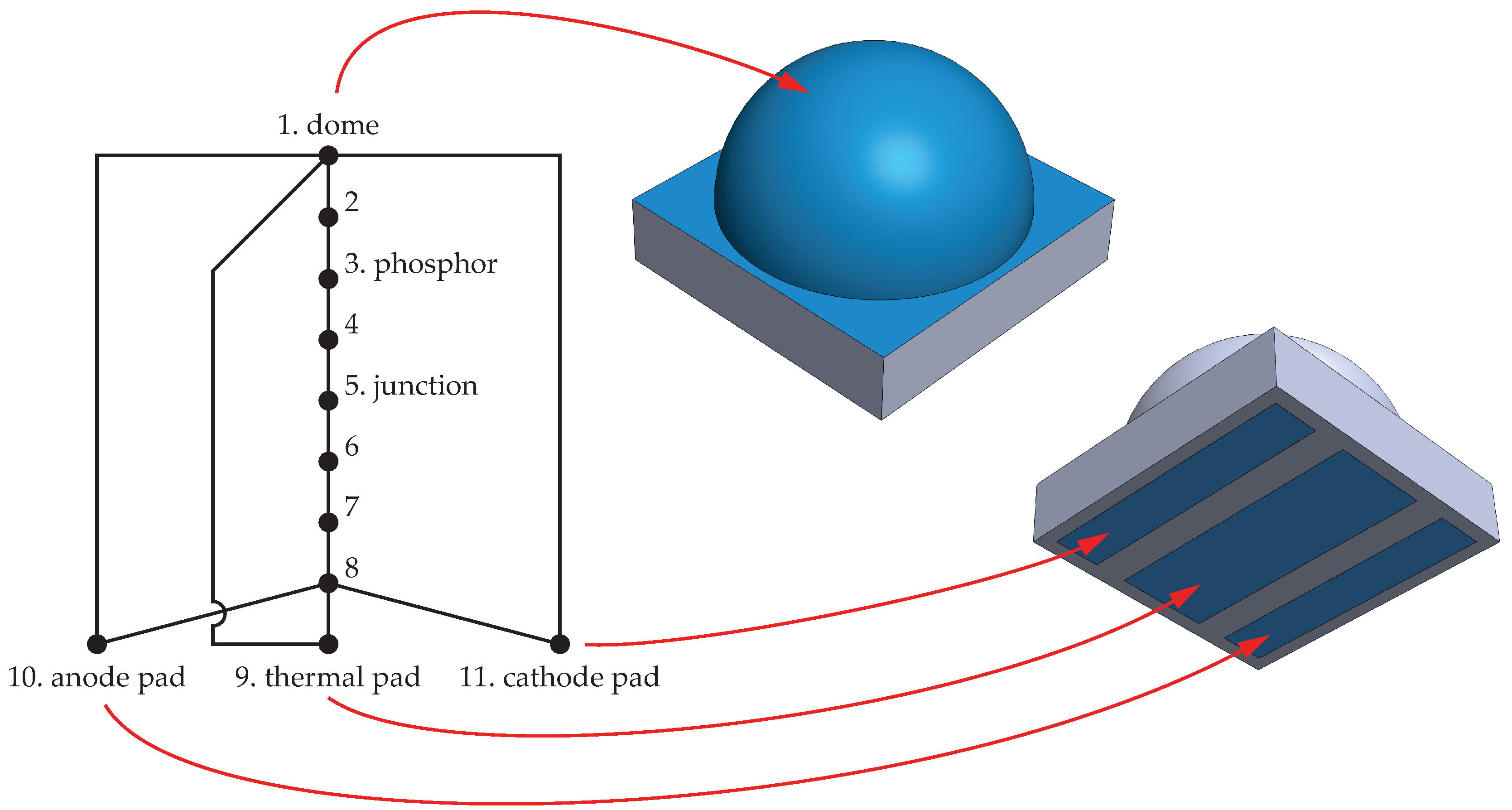
2.2.1. LED Detailed Model
2.2.2. LED CTM
2.3. System-Level Modelling
2.3.1. LED Module-Level Model
2.3.2. LED Luminaire-Level Model
3. Results
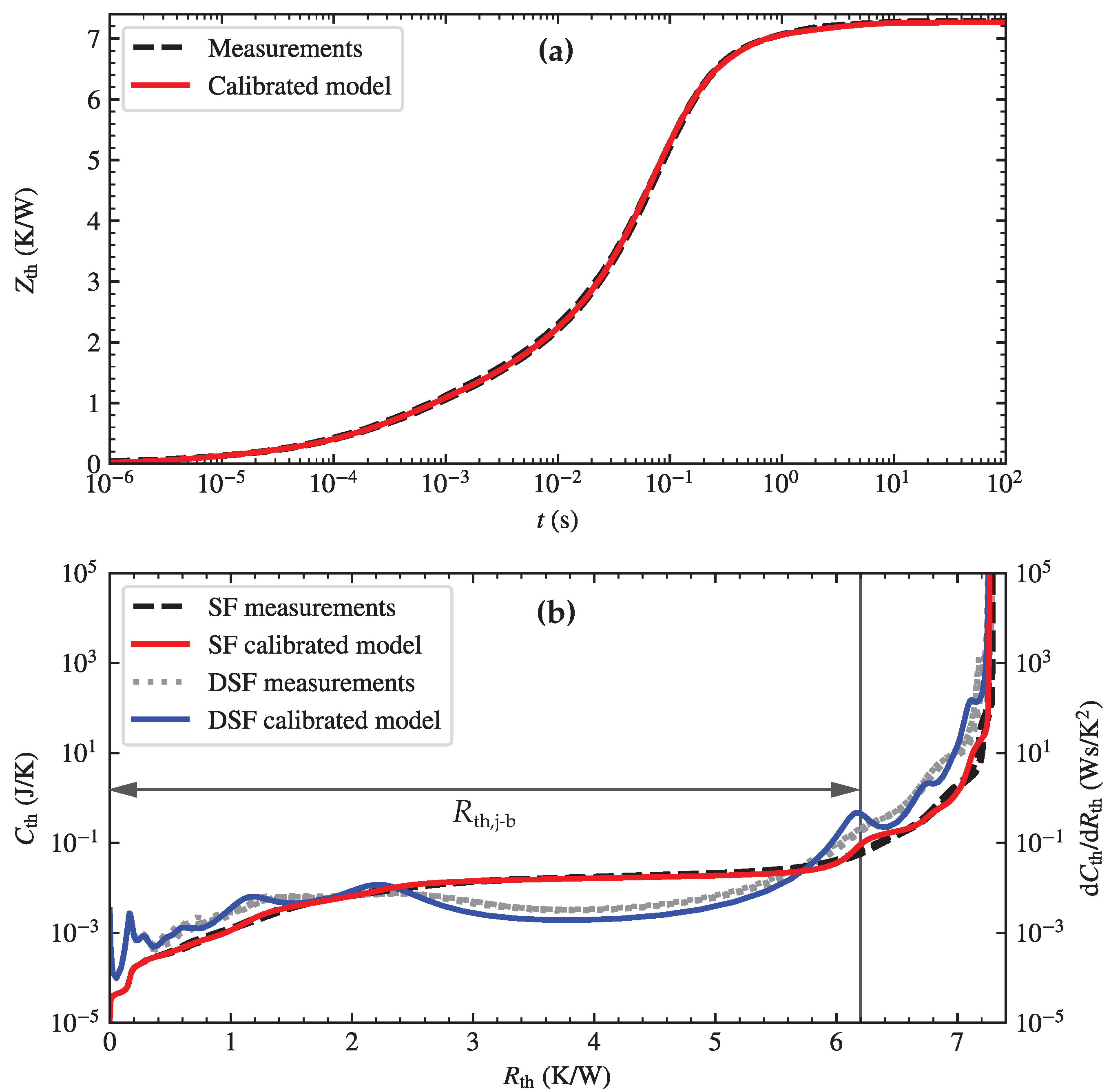
3.1. LED Device Testing Results
3.2. LED-Level Modelling Results
3.3. LED Module-Level Model
3.4. LED Luminaire-Level Model
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BCI | boundary condition independent |
| CCT | correlated color temperature |
| CFD | computational fluid dynamics |
| CPU | central processing unit |
| CRI | color rendering index |
| CTM | compact thermal model |
| DSF | differential structure function |
| DUT | device under test |
| HTC | heat transfer coefficient |
| IMS | insulated metal substrate |
| IR | infrared |
| LED | light-emitting diode |
| PCB | printed circuit board |
| MDCM | multi-domain compact model |
| ROM | reduced order model |
| SF | structure function |
References
- Delphi4LED Project Website. Available online: https://delphi4led.org (accessed on 27 March 2019).
- Bornoff, R.; Hildenbrand, V.; Lugten, S.; Martin, G.; Marty, C.; Poppe, A.; Rencz, M.; Schilders, W.H.; Yu, J. Delphi4LED—From measurements to standardized multi-domain compact models of LED: A new European R&D project for predictive and efficient multi-domain modeling and simulation of LEDs at all integration levels along the SSL supply chain. In Proceedings of the 2016 22nd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Budapest, Hungary, 21–23 September 2016; pp. 174–180. [Google Scholar] [CrossRef]
- Martin, G.; Marty, C.; Bornoff, R.; Poppe, A.; Onushkin, G.; Rencz, M.; Yu, J. Luminaire Digital Design Flow with Multi-Domain Digital Twins of LEDs. Energies 2019, 12, 2389. [Google Scholar] [CrossRef] [Green Version]
- Bein, M.C.; Hegedus, J.; Hantos, G.; Gaal, L.; Farkas, G.; Rencz, M.; Poppe, A. Comparison of two alternative junction temperature setting methods aimed for thermal and optical testing of high power LEDs. In Proceedings of the 2017 23rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Amsterdam, The Netherlands, 27–29 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Hantos, G.; Hegedus, J.; Bein, M.C.; Gaal, L.; Farkas, G.; Sarkany, Z.; Ress, S.; Poppe, A.; Rencz, M. Measurement issues in LED characterization for Delphi4LED style combined electrical-optical-thermal LED modeling. In Proceedings of the 2017 IEEE 19th Electronics Packaging Technology Conference (EPTC), Singapore, 6–9 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Onushkin, G.A.; Bosschaart, K.J.; Yu, J.; van Aalderen, H.J.; Joly, J.; Martin, G.; Poppe, A. Assessment of isothermal electro-optical-thermal measurement procedures for LEDs. In Proceedings of the 2017 23rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Amsterdam, The Netherlands, 27–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Farkas, G.; Gaal, L.; Bein, M.; Poppe, A.; Ress, S.; Rencz, M. LED Characterization Within the Delphi4LED Project. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 29 May–1 June 2018; pp. 262–270. [Google Scholar] [CrossRef]
- JEDEC JESD51-14: Transient Dual Interface Test Method for the Measurement of the Thermal Resistance Junction to Case of Semiconductor Devices with Heat Flow Trough a Single Path; Technical Report; JEDEC Solid State Technology Association: Arlington, VA, USA, 2010.
- JEDEC JESD51-51: Implementation of the Electrical Test Method for the Measurement of Real Thermal Resistance and Impedance of Light-Emitting Diodes with Exposed Cooling; Technical Report; JEDEC Solid State Technology Association: Arlington, VA, USA, 2012.
- JEDEC JESD51-52: Guidelines for Combining CIE 127-2007 Total Flux Measurements with Thermal Measurements of LEDs with Exposed Cooling Surface; Technical Report; JEDEC Solid State Technology Association: Arlington, VA, USA, 2012.
- Zong, Y.; Chou, P.; Dekker, P.; Distl, R.; Godo, K.; Hanselaer, P.; Heidel, G.; Hulett, J.; Oshima, K.; Poppe, A.; et al. CIE 225:2017 Optical Measurement of High-Power LEDs; Technical Report; International Commission on Illumination: Vienna, Austria, 2017. [Google Scholar] [CrossRef]
- Martin, G.; Marty, C.; Bornoff, R.; Vaumorin, E.; Kleij, A.; Onushkin, G.; Poppe, A. From Measurements to Standardised Multi-Domain Compact Models of LEDs using LED E-Datasheets. In Proceedings of the 29th Quadrennial Session of the CIE. International Commission on Illumination, Washington, DC, USA, 14–22 June 2019; CIE: Vienna, Austria, 2019; pp. 379–386. [Google Scholar] [CrossRef]
- Poppe, A. Multi-domain compact modeling of LEDs: An overview of models and experimental data. Microelectron. J. 2015, 46, 1138–1151. [Google Scholar] [CrossRef]
- Poppe, A.; Farkas, G.; Gaál, L.; Hantos, G.; Hegedüs, J.; Rencz, M. Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires. Energies 2019, 12, 1909. [Google Scholar] [CrossRef] [Green Version]
- Bornoff, R.; Farkas, G.; Gaal, L.; Rencz, M.; Poppe, A. LED 3D thermal model calibration against measurement. In Proceedings of the 2018 19th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Toulouse, France, 15–18 April 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Bornoff, R. Extraction of Boundary Condition Independent Dynamic Compact Thermal Models of LEDs—A Delphi4LED Methodology. Energies 2019, 12, 1628. [Google Scholar] [CrossRef] [Green Version]
- Poppe, A.; Hegedus, J.; Szalai, A.; Bornoff, R.; Dyson, J. Creating multi-port thermal network models of LED luminaires for application in system level multi-domain simulation using spice-like solvers. In Proceedings of the 2016 32nd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 14–17 March 2016; pp. 44–49. [Google Scholar] [CrossRef]
- Poppe, A. Simulation of LED based luminaires by using multi-domain compact models of LEDs and compact thermal models of their thermal environment. Microelectron. Reliab. 2017, 72, 65–74. [Google Scholar] [CrossRef]
- Marty, C.; Yu, J.; Martin, G.; Bornoff, R.; Poppe, A.; Fournier, D.; Fournier, D. Design flow for the development of optimized LED luminaires using multi-domain compact model simulations. In Proceedings of the 2018 24rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Stockholm, Sweden, 26–28 September 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Codecasa, L. A novel approach for generating boundary condition independent compact dynamic thermal networks of packages. IEEE Trans. Components Packag. Technol. 2005, 28, 593–604. [Google Scholar] [CrossRef]
- Codecasa, L.; D’Alessandro, V.; Magnani, A.; Rinaldi, N.; Zampardi, P.J. Fast novel thermal analysis simulation tool for integrated circuits (FANTASTIC). In Proceedings of the THERMINIC 2014—20th International Workshop on Thermal Investigations of ICs and Systems, London, UK, 24–26 September 2014; Volume 2014, pp. 1–6. [Google Scholar] [CrossRef]
- Codecasa, L.; Magnani, A.; D’Alessandro, V.; Rinaldi, N.; Metzger, A.G.; Bornoff, R.; Parry, J. Novel MOR approach for extracting dynamic compact thermal models with massive numbers of heat sources. In Proceedings of the 2016 32nd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 14–17 March 2016; pp. 218–223. [Google Scholar] [CrossRef]
- Lungten, S.; Bornoff, R.; Dyson, J.; Maubach, J.M.L.; Schilders, W.H.A.; Warner, M. Dynamic compact thermal model extraction for LED packages using model order reduction techniques. In Proceedings of the 2017 23rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Amsterdam, The Netherlands, 27–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Martin, G.; Yu, J.; Zuidema, P.; van der Schans, M. Luminaire Digital Design Flow with Delphi4LED LEDs Multi-Domain Compact Model. In Proceedings of the 2019 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019; Volume 2019, pp. 1–5. [Google Scholar] [CrossRef]
- Farkas, G.; Vader, Q.; Poppe, A.; Bognar, G. Thermal investigation of high power Optical Devices by transient testing. IEEE Trans. Components Packag. Technol. 2005, 28, 45–50. [Google Scholar] [CrossRef]
- Farkas, G.; Hara, T.; Rencz, M. Thermal transient testing. In Wide Bandgap Power Semiconductor Packaging; Elsevier: Amsterdam, The Netherlands, 2018; pp. 127–153. [Google Scholar] [CrossRef]
- Alexeev, A.; Onushkin, G.; Linnartz, J.P.; Martin, G. Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs. Energies 2019, 12, 1860. [Google Scholar] [CrossRef] [Green Version]
- Bornoff, R.; Gaal, L. Comparison of Model Order Reduction and Thermal Network Approaches in the Extraction of Dynamic Compact Thermal Models of LEDs. In Proceedings of the 2019 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019; Volume 2019, pp. 1–7. [Google Scholar] [CrossRef]
- Schweitzer, D. Generation of multisource dynamic compact thermal models by RC-network optimization. In Proceedings of the 29th IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 17–21 March 2013; pp. 116–123. [Google Scholar] [CrossRef]
- Powell, M.J.D. The BOBYQA Algorithm for Bound Constrained Optimization without Derivatives (NA2009/06); Technical Report; Department of Applied Mathematics and Theoretical Physics, University of Cambridge: Cambridge, UK, 2009. [Google Scholar]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. Available online: http://github.com/stevengj/nlopt (accessed on 28 January 2020).
- Lungten, S.; Alexeev, A.; Onushkin, G. Delphi4LED D1.1—Report on End-User Specifications. Available online: https://delphi4led.org/pydio/public/b610a0 (accessed on 15 April 2019).
- Lasance, C.J.M. Ten Years of Boundary-Condition- Independent Compact Thermal Modeling of Electronic Parts: A Review. Heat Transf. Eng. 2008, 29, 149–168. [Google Scholar] [CrossRef]
- Lasance, C.; Den Hertog, D.; Stehouwer, P. Creation and evaluation of compact models for thermal characterisation using dedicated optimisation software. In Proceedings of the Fifteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium, San Diego, CA, USA, 9–11 March 1999; pp. 189–200. [Google Scholar] [CrossRef]
- Lasance, C.J. The conceivable accuracy of experimental and numerical thermal analyses of electronic systems. IEEE Trans. Components Packag. Technol. 2002, 25, 366–382. [Google Scholar] [CrossRef]
- Kusama, H.; Sovers, O.J.; Yoshioka, T. Line Shift Method for Phosphor Temperature Measurements. Jpn. J. Appl. Phys. 1976, 15, 2349–2358. [Google Scholar] [CrossRef]
- Yang, T.H.; Huang, H.Y.; Sun, C.C.; Glorieux, B.; Lee, X.H.; Yu, Y.W.; Chung, T.Y. Noncontact and instant detection of phosphor temperature in phosphor-converted white LEDs. Sci. Rep. 2018, 8, 296. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Sun, Y.; Su, R.; Wei, K.; Gan, Y.; Ye, N.; Zou, C.; Liu, W. The phosphor temperature measurement of white light-emitting diodes based on magnetic nanoparticle thermometer. Rev. Sci. Instruments 2018, 89, 94901. [Google Scholar] [CrossRef] [PubMed]
- Hegedüs, J.; Hantos, G.; Poppe, A. Lifetime Modelling Issues of Power Light Emitting Diodes. Energies 2020, 13, 3370. [Google Scholar] [CrossRef]








| Set | HTC | ||
|---|---|---|---|
| Anode/Cathode Pad | Thermal Pad | Dome | |
| 1 | 10,000 | 25,000 | 10 |
| 2 | 3000 | 75,000 | 20 |
| 3 | 1500 | 20,000 | 100 |
| 4 | 50,000 | 10,000 | 5 |
| Set | HTC | ||
|---|---|---|---|
| Anode/Cathode Pad | Thermal Pad | Dome | |
| 1 | 42,725 | 13,250 | 66.75 |
| 2 | 1500 | 58,750 | 71.5 |
| 3 | 18,475 | 49,000 | 100 |
| 4 | 37,875 | 36,000 | 95.25 |
| 5 | 50,000 | 45,750 | 62 |
| 6 | 20,900 | 71,750 | 76.25 |
| 7 | 40,300 | 65,250 | 90.5 |
| 8 | 30,600 | 32,750 | 5 |
| 9 | 28,175 | 10,000 | 33.5 |
| 10 | 47,575 | 23,000 | 28.75 |
| 11 | 23,325 | 19,750 | 81 |
| 12 | 16,050 | 42,500 | 57.25 |
| 13 | 8775 | 16,500 | 47.75 |
| 14 | 35,450 | 68,500 | 52.5 |
| 15 | 6350 | 52,250 | 24 |
| 16 | 33,025 | 39,250 | 43 |
| 17 | 13,625 | 75,000 | 38.25 |
| 18 | 45,150 | 55,500 | 19.25 |
| 19 | 25,750 | 62,000 | 14.5 |
| 20 | 3925 | 29,500 | 85.75 |
| C () | R () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 1 | 8.533 × 10−4 | |||||||||||
| 2 | 9.906 × 10−3 | 222.6 | ||||||||||
| 3 | 1.157 × 10−4 | 291.4 | ||||||||||
| 4 | 2.793 × 10−4 | 7.707 | ||||||||||
| 5 | 5.306 × 10−5 | 8.563 | ||||||||||
| 6 | 2.365 × 10−4 | 0.299 | ||||||||||
| 7 | 2.567 × 10−3 | 1.350 | ||||||||||
| 8 | 9.209 × 10−3 | 0.096 | ||||||||||
| 9 | 1.113 × 10−4 | 1268 | 1.822 | |||||||||
| 10 | 4.374 × 10−4 | 1645 | 4.911 | |||||||||
| 11 | 4.374 × 10−4 | 1645 | 4.911 | |||||||||
| LED Module | (K) | Rel. Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Detailed Model | CTM | ||||||||
| Min. | Avg. | Max. | Min. | Avg. | Max. | Min. | Avg. | Max. | |
| 1 | 118.8 | 121.1 | 122.2 | 118.2 | 120.3 | 121.7 | 0.4 | 0.7 | 0.9 |
| 2 | 118.9 | 121.1 | 122.2 | 118.3 | 120.3 | 121.6 | 0.5 | 0.7 | 0.9 |
| 3 | 100.7 | 113.2 | 120.7 | 99.8 | 112.2 | 119.4 | 0.5 | 0.9 | 1.1 |
| 4 | 101.5 | 114.3 | 121.8 | 100.8 | 113.6 | 120.7 | 0.3 | 0.7 | 0.9 |
| 5 | 100.7 | 113.2 | 120.7 | 99.8 | 112.2 | 119.4 | 0.5 | 0.9 | 1.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
van der Schans, M.; Yu, J.; Martin, G. Digital Luminaire Design Using LED Digital Twins—Accuracy and Reduced Computation Time: A Delphi4LED Methodology. Energies 2020, 13, 4979. https://doi.org/10.3390/en13184979
van der Schans M, Yu J, Martin G. Digital Luminaire Design Using LED Digital Twins—Accuracy and Reduced Computation Time: A Delphi4LED Methodology. Energies. 2020; 13(18):4979. https://doi.org/10.3390/en13184979
Chicago/Turabian Stylevan der Schans, Marc, Joan Yu, and Genevieve Martin. 2020. "Digital Luminaire Design Using LED Digital Twins—Accuracy and Reduced Computation Time: A Delphi4LED Methodology" Energies 13, no. 18: 4979. https://doi.org/10.3390/en13184979
APA Stylevan der Schans, M., Yu, J., & Martin, G. (2020). Digital Luminaire Design Using LED Digital Twins—Accuracy and Reduced Computation Time: A Delphi4LED Methodology. Energies, 13(18), 4979. https://doi.org/10.3390/en13184979