Experimental and Numerical Investigation of the Behavior of Automotive Battery Busbars under Varying Mechanical Loads
Abstract
:1. Introduction
2. Materials and Methods
2.1. Busbar Materials
2.2. Experimental Setup
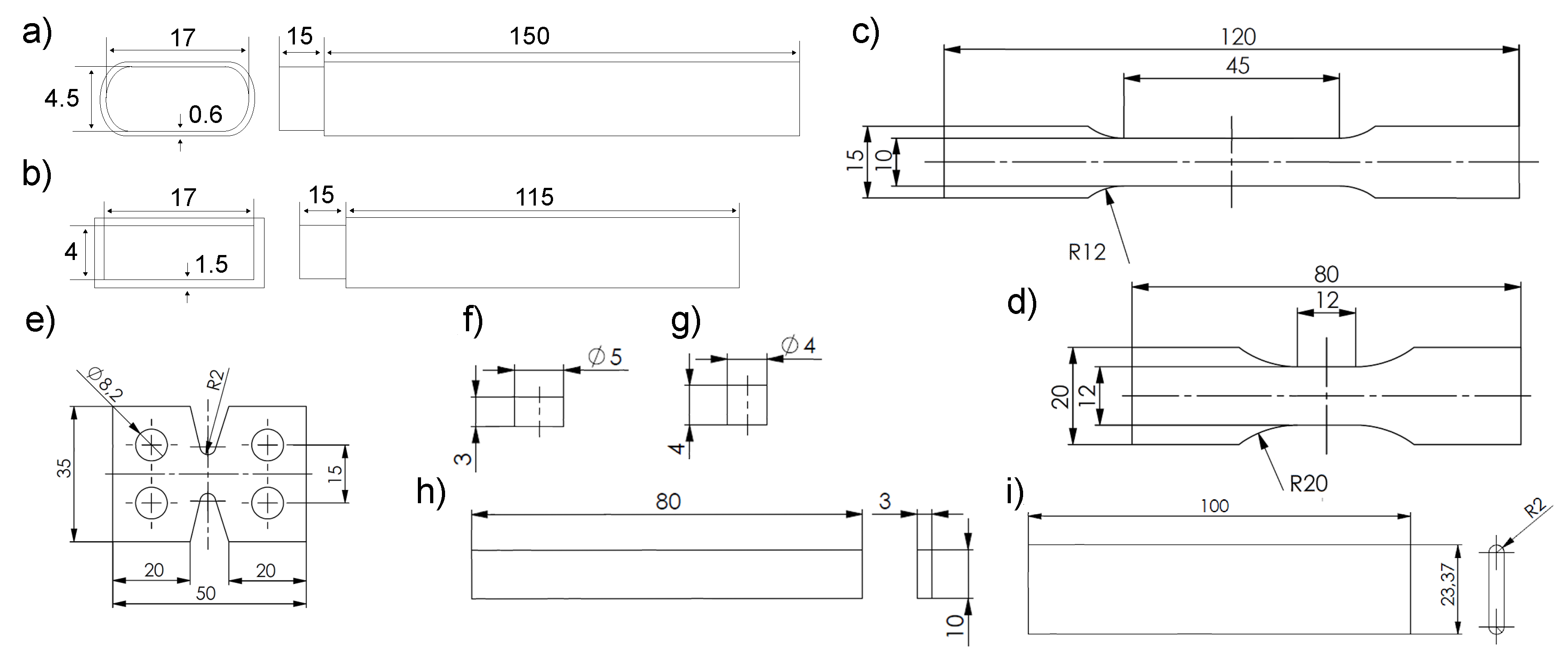
2.3. Specimen Geometry
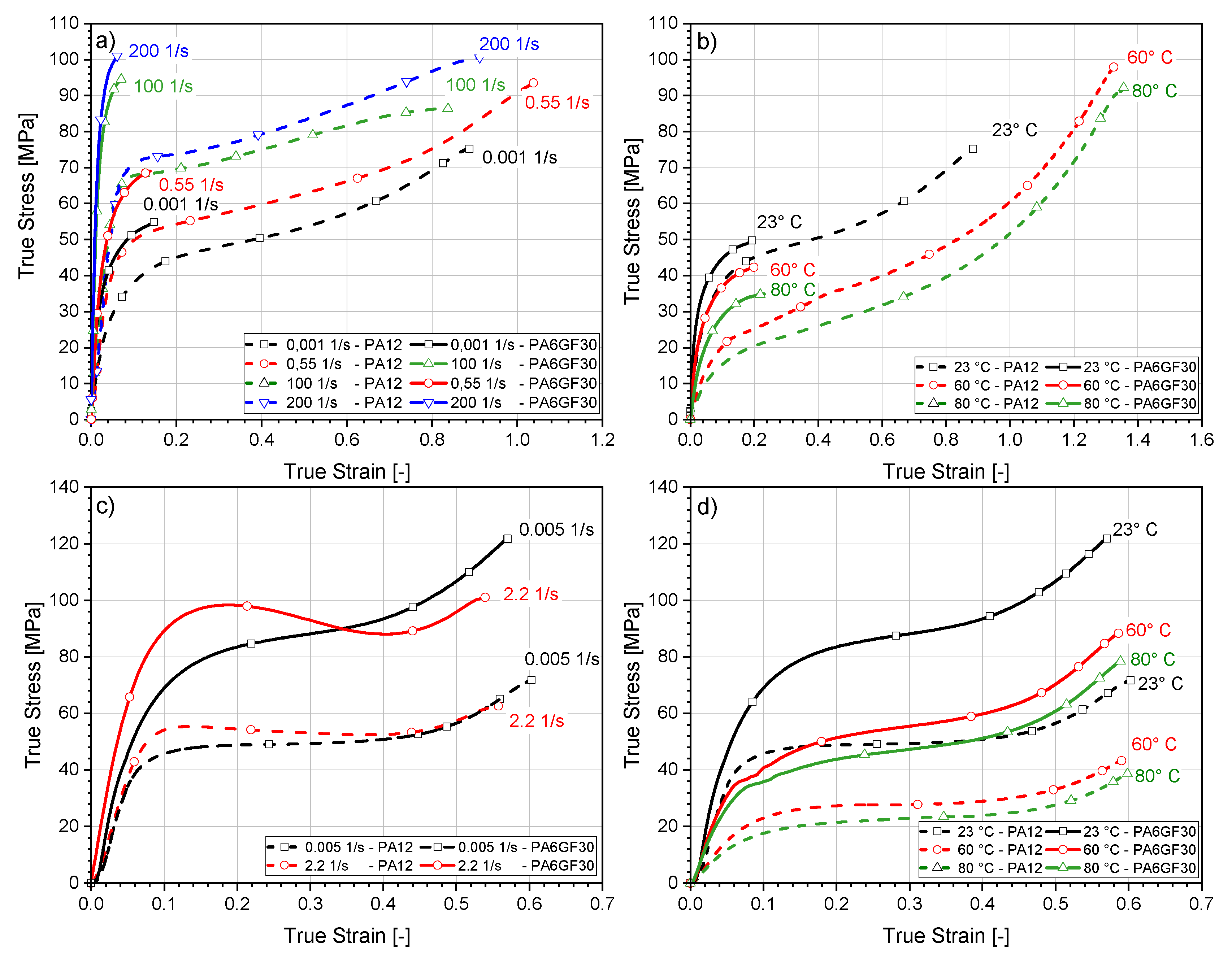
3. Experimental Material Characterization
4. Material Modeling
4.1. Selection of Material Models
4.2. Material Model Optimization Procedure
4.3. Generalized Incremental Stress State Dependent Model (GISSMO)—Damage Modeling
4.4. Results
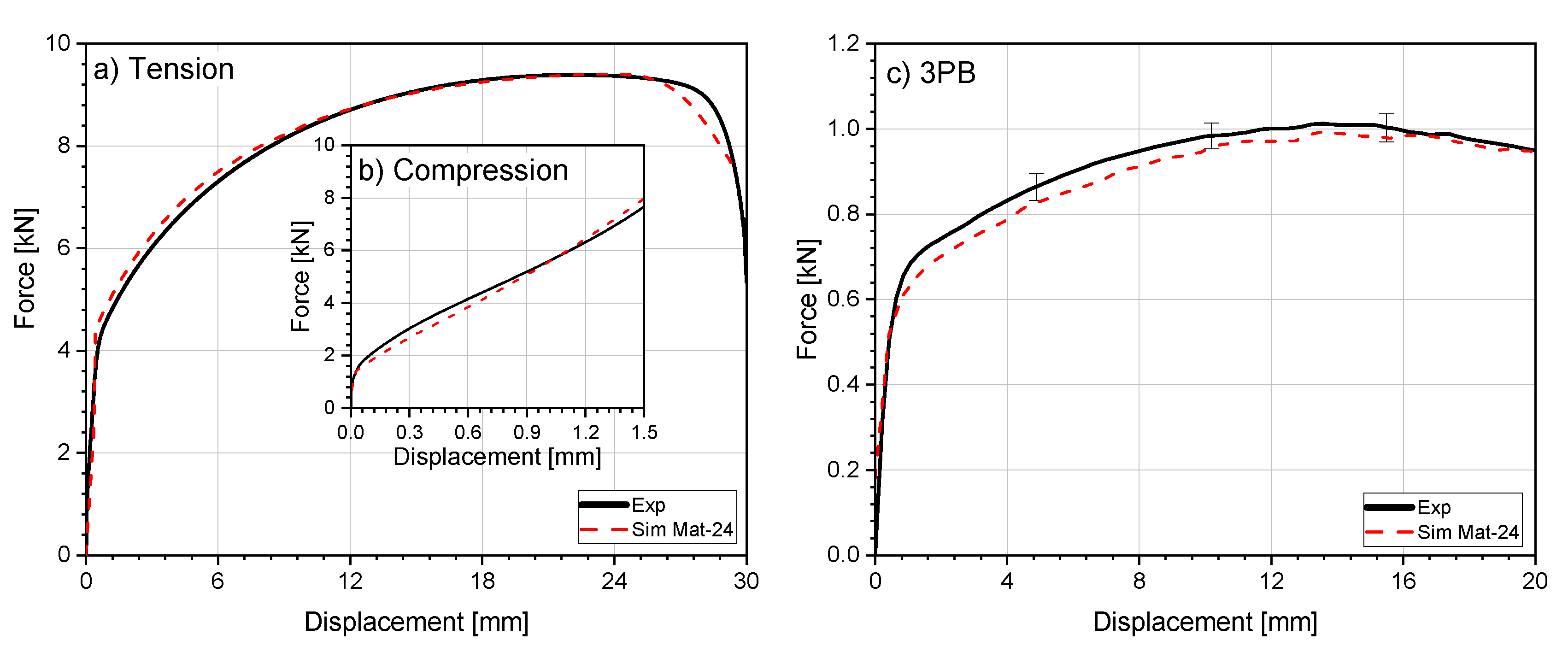
4.4.1. Tensile and Compression Test
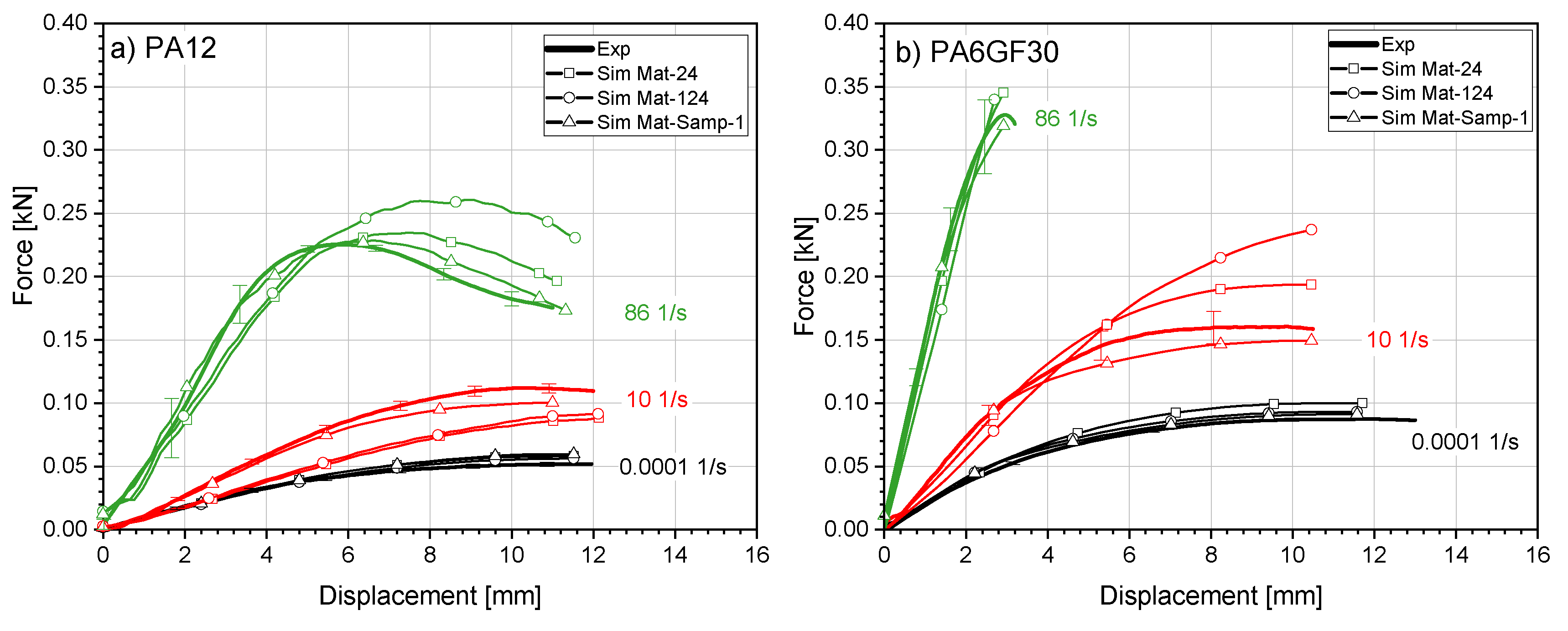
4.4.2. Prevalidation—Three-Point-Bending of Polyamides and Copper
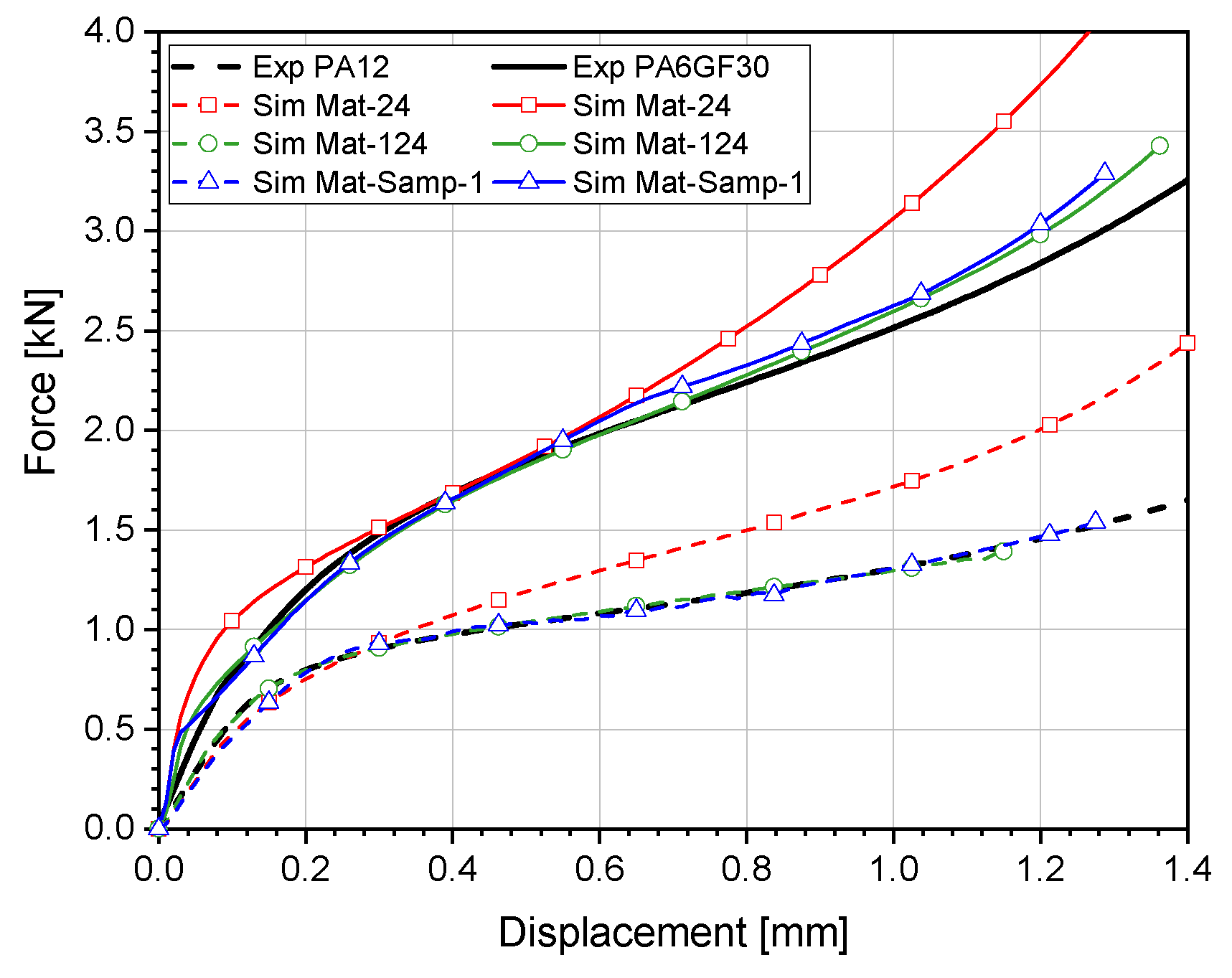
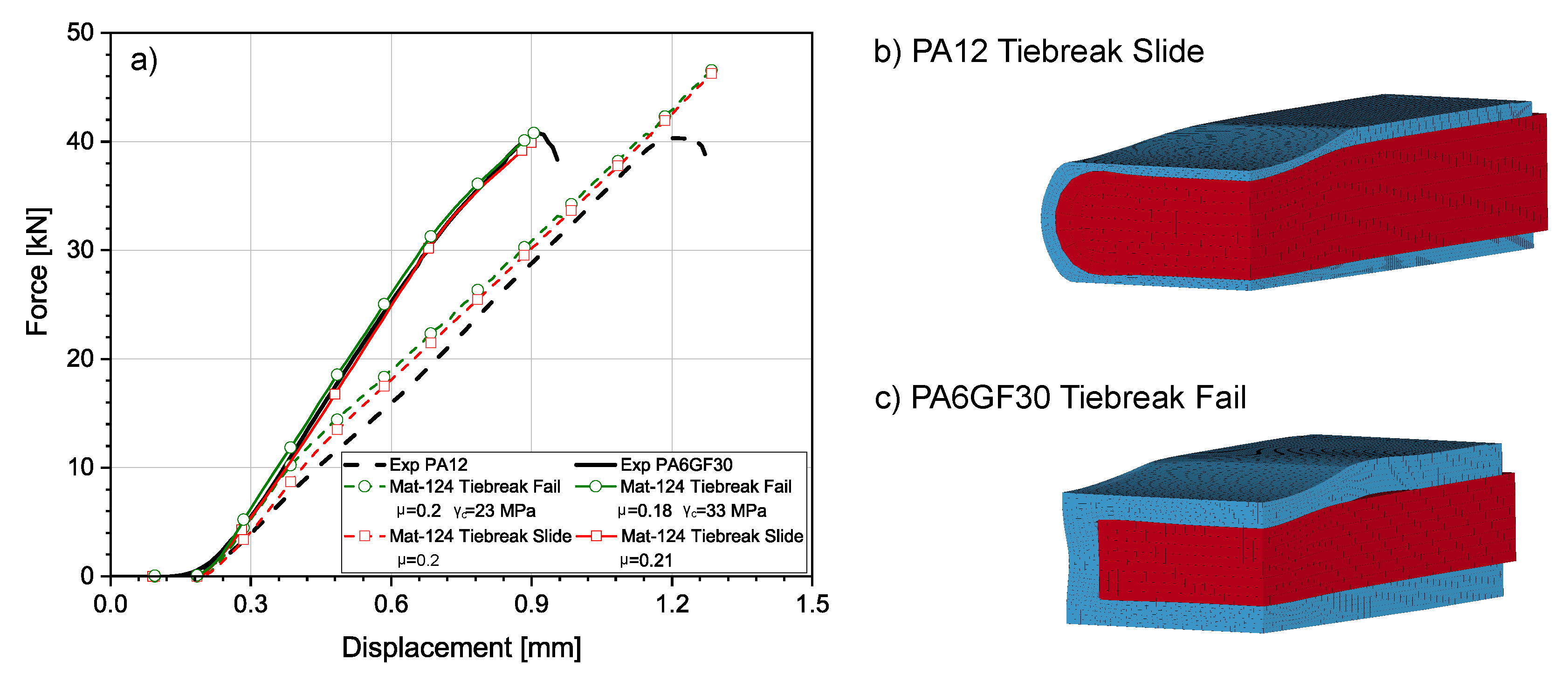
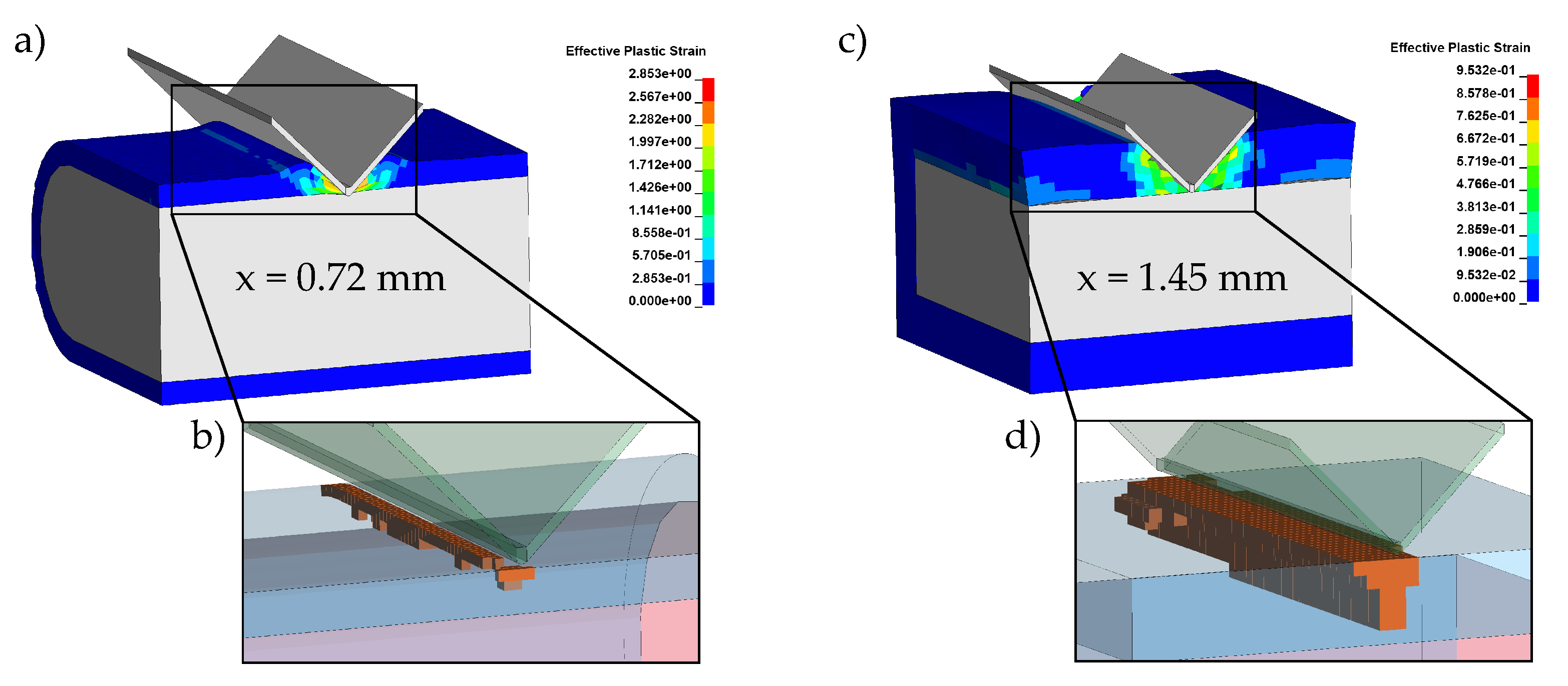
4.4.3. Component Validation
4.4.4. Interface Optimization
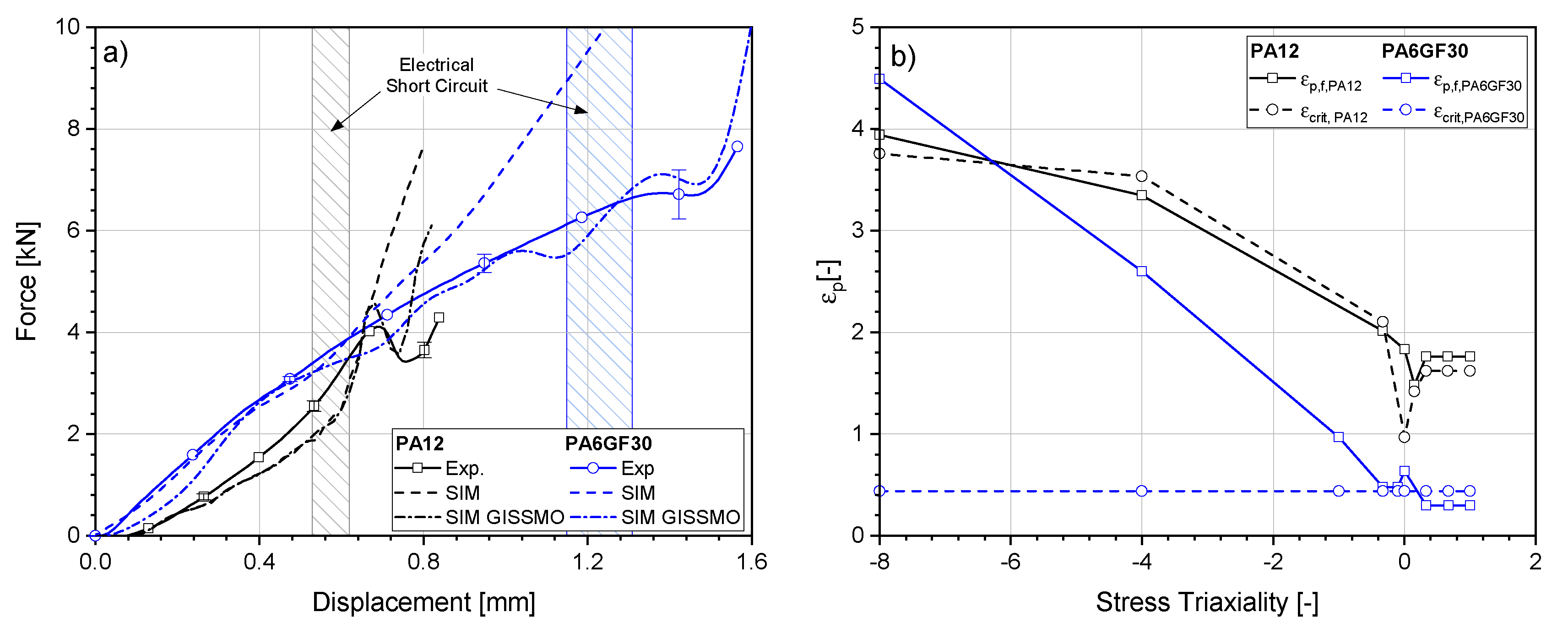
4.4.5. GISSMO—Parameter Identification
5. Discussion and Conclusions
- Busbars should be designed with vehicle safety and possible deformations of the battery pack in mind;
- Possible mechanical loads should be analyzed in the early development, using a material model that allows for tension–compression anisotropy;
- The contact modeling of the busbar has a great influence on the simulation results;
- The insulation material and its thickness should be chosen in accordance with possible mechanical loads and electrical properties;
- A ductile unreinforced insulation material is recommended for possible bending loads;
- A fiber reinforced insulation material should be used if compressive loads or penetrating objects can occur.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GISSMO | Generalized Incremental Stress State dependent MOdel |
| ETP | Electrolytic-Tough-Pitch |
| HV | High-voltage |
| TR | Thermal Runaway |
| FE | Finite Element |
| 3PB | Three-Point-Bending |
References
- IEA, Global EV Outlook 2019. Available online: https://www.iea.org/reports/global-ev-outlook-2019 (accessed on 12 October 2019).
- Hendricks, C.; Williard, N.; Mathew, S.; Pecht, M. A failure modes, mechanisms, and effects analysis (FMMEA) of lithium-ion batteries. J. Power Sources 2015, 297, 113–120. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Jia, Y.; Yuan, C.; Wang, L.; Gao, X.; Yin, S.; Xu, J. Safety issues and mechanisms of lithium-ion battery cell upon mechanical abusive loading: A review. Energy Storage Mater. 2020, 24, 85–112. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Bubbico, R.; Greco, V.; Menale, C. Hazardous scenarios identification for Li-ion secondary batteries. Saf. Sci. 2018, 108, 72–88. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Abaza, A.; Ferrari, S.; Wong, H.K.; Lyness, C.; Moore, A.; Weaving, J.; Blanco-Martin, M.; Dashwood, R.; Bhagat, R. Experimental study of internal and external short circuits of commercial automotive pouch lithium-ion cells. J. Energy Storage 2018, 16, 211–217. [Google Scholar] [CrossRef]
- Khan, M.; Magne, P.; Bilgin, B.; Wirasingha, S.; Emadi, A. Laminated busbar design criteria in power converters for electrified powertrain applications. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 15–18 June 2014. [Google Scholar]
- Bao, Y.J.; Cheng, K.W.E.; Ding, K.; Wang, D.H. The study on the busbar system and its fault analysis. In Proceedings of the 5th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 11–13 December 2013. [Google Scholar]
- Yang, S.; Wang, W.; Lin, C.; Shen, W.; Li, Y. Investigation of Internal Short Circuits of Lithium-Ion Batteries under Mechanical Abusive Conditions. Energies 2019, 10, 1885. [Google Scholar] [CrossRef] [Green Version]
- Sahraei, E.; Campbell, J.; Wierzbicki, T. Modeling and short circuit detection of 18650 Li-ion cells under mechanical abuse conditions. J. Power Sources 2012, 220, 360–372. [Google Scholar] [CrossRef]
- Werling, T.; Geuting, P.; Höschele, P.; Ellersdorfer, C.; Sinz, W. Investigation of the electro-mechanical behavior of automotive high voltage busbars under combined electrical load with varying indenter geometry and environmental conditions. J. Energy Storage 2020, 32, 101861. [Google Scholar] [CrossRef]
- Xia, Y.; Wierzbicki, T.; Sahraei, E.; Zhang, X. Damage of cells and battery packs due to ground impact. J. Power Sources 2014, 267, 78–97. [Google Scholar] [CrossRef]
- Kukreja, J.; Nguyen, T.; Siegmund, T.; Chen, W.; Tsutsui, W.; Balakrishnan, K.; Liao, H.; Parab, N. Crash analysis of a conceptual electric vehicle with a damage tolerant battery pack. Extrem. Mech. Lett. 2016, 9, 371–378. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Chen, G.; Zhou, Q.; Shi, X.; Shi, F. Failure behaviours of 100% SOC lithium-ion battery modules under different impact loading conditions. Eng. Fail. Anal. 2017, 82, 149–160. [Google Scholar] [CrossRef]
- Cu-OFE. Available online: https://www.matthey.ch/fileadmin/user_upload/downloads/fichetechnique/DE/Cu-OFE_C.pdf (accessed on 28 October 2020).
- Grilamid XE 3817. Available online: https://www.campusplastics.com/campus/de/datasheet/Grilamid+XE+3817 (accessed on 28 October 2020).
- Grilon BG-30 FR. Available online: https://www.campusplastics.com/campus/de/datasheet/Grilon+BG-30+FR (accessed on 28 October 2020).
- ISO 6892–1:2019. Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature; ISO: Geneva, Switzerland, 2020. [Google Scholar]
- DIN EN 50106:2016-11. Testing of Metallic Materials—Compression Test at Room Temperature; DIN: Berlin, Germany, 2016. [Google Scholar]
- ISO 527–2:2012. Plastics—Determination of Tensile Properties—Part 1: Test Conditions for Moulding and Extrsion Plastics; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- ISO 604:2002. Plastics—Determination of Compressive Properties; ISO: Geneva, Switzerland, 2002. [Google Scholar]
- ISO 178:2010. Plastics—Determination of Flexural Properties; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- ISO 527–1:2019. Plastics—Determination of Tensile Properties—Part 1: General Principles; ISO: Geneva, Switzerland, 2019. [Google Scholar]
- Becker, F. Entwicklung einer Beschreibungsmethodik für das mechanische Verhalten unverstärkter Thermoplaste bei hohen Deformationsgeschindigkeiten. Ph.D. Thesis, Universisty Halle-Wittenberg, Halle-Wittenberg, Germany, 2009. [Google Scholar]
- Becker, F.; Kraatz, A.; Moneke, M. Determination of the mechanical properties of oriented short fibre reinforced thermoplastics under different stress states. In Proceedings of the 6th LS-DYNA Users Conference, Gothenburg, Germany, 28–30 May 2007. [Google Scholar]
- Goldberg, N.; Arcan, A.; Nicolau, N.; Goldenberg, N. On the most suitable specimen shape for testing shear strength of plastics. ASTM Spec. Techn. Publ. 1959, 247, 115–121. [Google Scholar]
- ISO 1110:2019. Plastics–Polyamides–Accelerated Conditioning of Test Specimens; ISO: Geneva, Switzerland, 2019. [Google Scholar]
- Bonten, C. Plastics Technology: Introduction and Fundamentals; Hanser Publishers: Munich, Germany, 2019; pp. 48–60. [Google Scholar]
- Junginger, M. Charakterisierung und Modellierung unverstärkter thermoplastischer Kunststoffe zur numerischen Simulation von Crashvorgängen. Ph.D. Thesis, Technical University Munich, Munich, Germany, 2004. [Google Scholar]
- Reithofer, P.; Fertschej, A.; Hirschmann, B. Material Models for Thermoplastics in LS-DYNA: From Deformation To Failure. In Proceedings of the 15th International LS-DYNA Users Conference, Dearborn, MI, USA, 13–14 June 2018. [Google Scholar]
- Hallquist, J. LS-DYNA Keyword User’s Manual: Volume II - Material Models; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2020. [Google Scholar]
- Hallquist, J. LS-DYNA Theory Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2019. [Google Scholar]
- Arriaga, A.; Pagaldai, R.; Zaldua, A.M.; Chrysostomou, A.; O’Brien, M. Impact testing and simulation of a polypropylene component. Correlation with strain rate sensitive constitutive models in ANSYS and LS-DYNA. Polym. Test. 2010, 29, 170–180. [Google Scholar] [CrossRef]
- Myers, E.C.; Shanmugam, M. Evaluation of Thermoplastic SMA Material Models for Predicting Crashworthiness for Automotive Applications. In SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2002. [Google Scholar]
- Kolling, S.; Haufe, A.; Feucht, M.; Du Bois, P.A. SAMP-1: A Semi-Analytical Model for the Simulation of Polymers. In Proceedings of the 4th LS-DYNA User Conference, Bamberg, Germany, 20–21 October 2005. [Google Scholar]
- Koukal, A. Crash- und Bruchverhalten von Kunststoffen im Fußgängerschutz von Fahrzeugen. Ph.D. Thesis, Technical University Munich, Munich, Germany, 2014. [Google Scholar]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin, Germany, 1909. [Google Scholar]
- Hollomon, J.H. Tensile Deformation. AIME 1945, 162, 268–290. [Google Scholar]
- Gomeringer, R. Mechanical and Metal Trades Handbook; Europa-Technical Book Series for the Metalworking Trades, 4th ed.; Verlag Europa-Lehrmittel: Haan-Gruiten, Germany, 2018. [Google Scholar]
- Neukamm, F.; Feucht, M.; Haufe, A. Considering damage history in crashworthiness simulations. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009. [Google Scholar]
- Althammer, F.; Moncayo, D.; Mittendorf, P. Approach for modeling of thermoplastic generative designed parts. In Proceedings of the 12th European LS-DYNA Conference, Koblenz, Germany, 14-16 May 2019. [Google Scholar]
- Tabacu, S.; Ducu, C. Numerical investigations of 3D printed structures under compressive loads using damage and fracture criterion: Experiments, parameter identification, and validation. Extr. Mech. Lett. 2020, 39, 100775. [Google Scholar] [CrossRef]
- Effelsberg, J.; Haufe, A.; Feucht, M.; Neukamm, F.; Du Bois, P. On parameter identification for the GISSMO damage model. In Proceedings of the 12th International LS-DYNA User Conference, Dearborn, MI, USA, 3–5 June 2012. [Google Scholar]
- Andrade, F.X.C.; Feucht, M.; Haufe, A.; Neukamm, F. An incremental stress state dependent damage model for ductile failure prediction. Int. J. Fract. 2016, 200, 127. [Google Scholar] [CrossRef]







| Properties | Cu-OFE R200 | PA12 | PA6GF30 |
|---|---|---|---|
| Density [g/cm] | 8.94 | 1.01 | 1.39 |
| E-Modulus [GPa] | 127 | 1.2 | 4.5 |
| Yield Strength [MPa] | 140 | 40 | 60 |
| Water Absorption [%] | - | 1.5 | 7 |
| Material | Test | Strain Rate [1/s] | Temp. [°C] | Repetitions |
|---|---|---|---|---|
| PA12 / PA6GF30 | Tension | 0.001 | 23, 60, 80 | 5 |
| 0.55, 100, 200 | 23 | 5 | ||
| Compression | 0.005 | 23, 60, 80 | 5 | |
| 2.2 | 23 | 5 | ||
| 3PB | 0.0001 | 23, 60, 80 | 5 | |
| 10, 86 | 23 | 5 | ||
| Cu-OFE R200 | Tension | 0.0002 | 23 | 3 |
| Compression | 0.0002 | 23 | 3 | |
| 3PB | 0.0008 | 23 | 3 | |
| Busbar | 3PB | 0.0001 | 23 | 5 |
| Compression | 0.001 | 23 | 5 |
| Model | Yield Surface | Visco Elasticity | Visco Plasticity | Stress State | Volume |
|---|---|---|---|---|---|
| Mat-24 | von Mises | × | ✓ | Tension | constant |
| Mat-124 | von Mises Drucker-Prager | ✓ | ✓ | Tension Compression | constant |
| Samp-1 | von Mises Drucker-Prager Parabolic | ✓ | ✓ | Tension Compression Shear | compressible |
| 0.0–0.14 | 0.16 | 0.18 | 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 | 0.32 | 0.34 | 0.36 | 0.38–0.8 | |
| 0.26 | 0.27 | 0.28 | 0.29 | 0.3 | 0.32 | 0.34 | 0.36 | 0.38 | 0.40 | 0.44 | 0.48 | 0.5 |
| Model | PA12 | PA6GF30 | ||
|---|---|---|---|---|
| 3PB | Compression | 3PB | Compression | |
| Mat-24 | - | - | - | - |
| Mat-124 | + 5% | + 12% | + 8% | + 15% |
| Samp-1 | + 45% | + 101% | + 151% | + 139% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Werling, T.; Sprenger, M.; Ellersdorfer, C.; Sinz, W. Experimental and Numerical Investigation of the Behavior of Automotive Battery Busbars under Varying Mechanical Loads. Energies 2020, 13, 6572. https://doi.org/10.3390/en13246572
Werling T, Sprenger M, Ellersdorfer C, Sinz W. Experimental and Numerical Investigation of the Behavior of Automotive Battery Busbars under Varying Mechanical Loads. Energies. 2020; 13(24):6572. https://doi.org/10.3390/en13246572
Chicago/Turabian StyleWerling, Tobias, Marvin Sprenger, Christian Ellersdorfer, and Wolfgang Sinz. 2020. "Experimental and Numerical Investigation of the Behavior of Automotive Battery Busbars under Varying Mechanical Loads" Energies 13, no. 24: 6572. https://doi.org/10.3390/en13246572








