Author Contributions
Conceptualization, D.H. and M.K.; methodology, D.H. and M.K.; software, D.H.; validation, D.H. and M.K.; formal analysis, D.H. and M.K.; investigation, D.H.; resources, D.H.; data curation, M.K.; writing—original draft preparation, D.H.; writing—review and editing, M.K.; visualization, D.H.; supervision, M.K.; project administration, D.H.; funding acquisition, D.H. All authors have read and agreed to the published version of the manuscript.
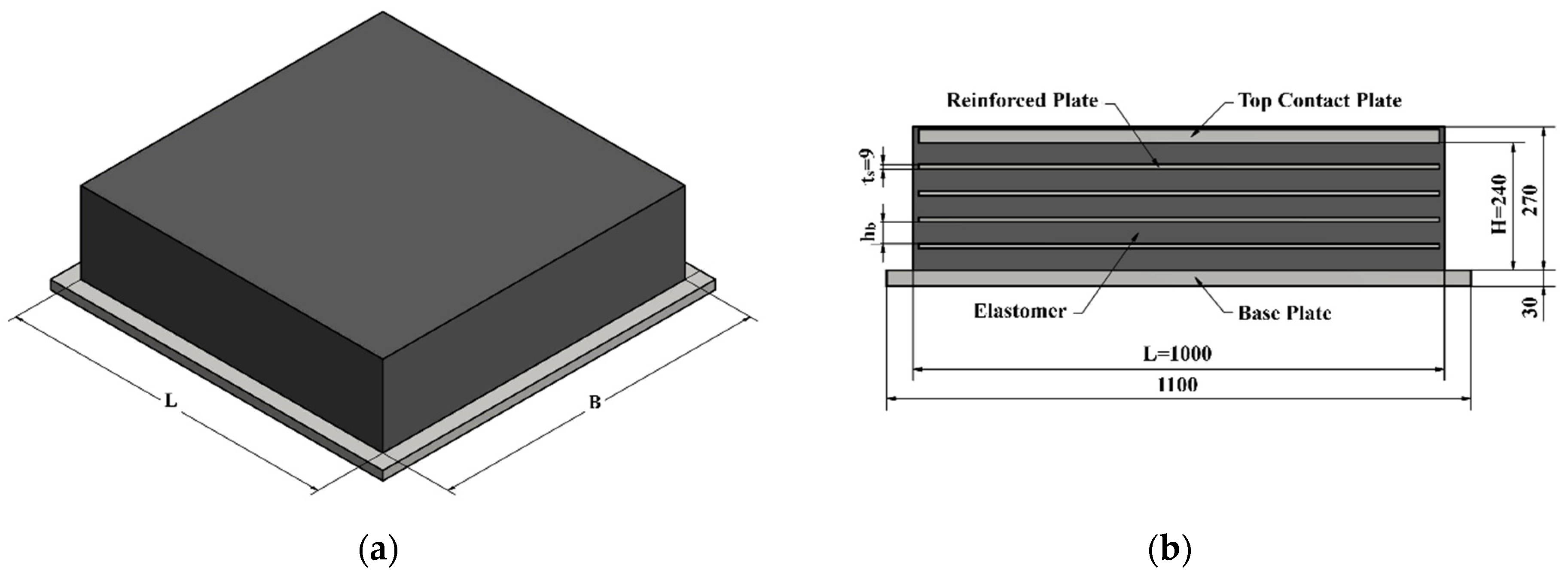
Figure 1.
This is a figure of the schematics of an offshore elastomeric bearing pad: (a) 3D Model of elastomeric bearing for offshore plants; (b) Schematics of elastomeric bearing.
Figure 1.
This is a figure of the schematics of an offshore elastomeric bearing pad: (a) 3D Model of elastomeric bearing for offshore plants; (b) Schematics of elastomeric bearing.
Figure 2.
This is a figure of the half-domain finite element model for Analysis: (a) without reinforcing plate; (b) with 4-rows reinforcing plate; (c) with 8-rows reinforcing plate.
Figure 2.
This is a figure of the half-domain finite element model for Analysis: (a) without reinforcing plate; (b) with 4-rows reinforcing plate; (c) with 8-rows reinforcing plate.
Figure 3.
This is a figure of the loads and boundary conditions for analysis: (a) Compression; (b) Shear; (c) Bending.
Figure 3.
This is a figure of the loads and boundary conditions for analysis: (a) Compression; (b) Shear; (c) Bending.
Figure 4.
This is a figure of the stress distribution of two bearing models with 4-row (left figure) and with 8-row reinforcing plate (right figure): (a) Compression (when vertical displacement is 3 mm); (b) Shear (when horizontal displacement is 50 mm); (c) Bending (when rotation angle is 0.005 rad).
Figure 4.
This is a figure of the stress distribution of two bearing models with 4-row (left figure) and with 8-row reinforcing plate (right figure): (a) Compression (when vertical displacement is 3 mm); (b) Shear (when horizontal displacement is 50 mm); (c) Bending (when rotation angle is 0.005 rad).
Figure 5.
This is a figure of the Elastic modulus ratio of elastomeric bearing according to the number of reinforcing plates.
Figure 5.
This is a figure of the Elastic modulus ratio of elastomeric bearing according to the number of reinforcing plates.
Figure 6.
This is a figure demonstrating the compression coefficient of elastomeric bearing according to each elastomer height.
Figure 6.
This is a figure demonstrating the compression coefficient of elastomeric bearing according to each elastomer height.
Figure 7.
This is a figure of the Shear modulus ratio of elastomeric bearing according to the number of reinforcing plates when vertical displacement of 3 mm and horizontal displacement of 50 mm are imposed.
Figure 7.
This is a figure of the Shear modulus ratio of elastomeric bearing according to the number of reinforcing plates when vertical displacement of 3 mm and horizontal displacement of 50 mm are imposed.
Figure 8.
This is a figure demonstrating the bending modulus ratio of elastomeric bearing according to the number of reinforcing plates when the rotation angle is 0.005 rad.
Figure 8.
This is a figure demonstrating the bending modulus ratio of elastomeric bearing according to the number of reinforcing plates when the rotation angle is 0.005 rad.
Figure 9.
This is a figure demonstrating the stiffness ratios of bearing as a function of the number of reinforcing plates: (a) compression condition; (b) shear condition; (c) bending condition.
Figure 9.
This is a figure demonstrating the stiffness ratios of bearing as a function of the number of reinforcing plates: (a) compression condition; (b) shear condition; (c) bending condition.
Figure 10.
This is a figure showing the FPSO global axis system.
Figure 10.
This is a figure showing the FPSO global axis system.
Figure 11.
This is a figure showing the half-domain finite element model of vertical elastomeric bearing for FPSO.
Figure 11.
This is a figure showing the half-domain finite element model of vertical elastomeric bearing for FPSO.
Figure 12.
This is a figure showing the stress distribution for steel plate (left figure) and elastomers (right figure) of vertical bearing under compression: (a) SLS load condition; (b) ULS load condition; (c) ALS load condition.
Figure 12.
This is a figure showing the stress distribution for steel plate (left figure) and elastomers (right figure) of vertical bearing under compression: (a) SLS load condition; (b) ULS load condition; (c) ALS load condition.
Table 1.
This is a table, Mechanical properties for S355 structural steel (EN 10025-2).
Table 1.
This is a table, Mechanical properties for S355 structural steel (EN 10025-2).
| Items | Sign | Unit | Value |
|---|
| Young’s Modulus | E | GPa | 200 |
| Poisson’s Ratio | N | - | 0.29 |
| Yield Strength | σY | Mpa | 355 |
| Ultimate Strength | σU | Mpa | 510–680 |
Table 2.
This is a table of the mechanical properties for Neoprene sheet (Shore hardness 50–60 A).
Table 2.
This is a table of the mechanical properties for Neoprene sheet (Shore hardness 50–60 A).
| Items | Sign | Unit | Value |
|---|
| Mooney–Rivlin Constants | C10 | Mpa | 0.382 |
| C1 | Mpa | 0.096 |
| Poisson’s Ratio | ν | - | 0.49 |
| Tensile (Ultimate) Strength | σU | Mpa | 15.0 |
Table 3.
This is a table illustrating the maximum stress for reinforcing steel plate of bearing according to the number of plates under a compression load (unit: MPa).
Table 3.
This is a table illustrating the maximum stress for reinforcing steel plate of bearing according to the number of plates under a compression load (unit: MPa).
| Vertical Disp. (Dz) | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 mm | N/A | 4.4 | 7.3 | 11.0 | 15.5 | 21.3 | 28.4 | 37.4 | 48.8 |
| 2 mm | N/A | 8.9 | 14.6 | 22.1 | 31.3 | 42.9 | 57.3 | 75.5 | 98.5 |
| 3 mm | N/A | 13.3 | 22.1 | 33.4 | 47.3 | 64.8 | 86.6 | 114.2 | 149.2 |
| 4 mm | N/A | 17.8 | 29.7 | 44.8 | 63.5 | 87.0 | 116.5 | 153.7 | 200.9 |
| 5 mm | N/A | 22.4 | 37.4 | 56.3 | 79.9 | 109.6 | 146.9 | 194.0 | 253.8 |
Table 4.
This is a table of the maximum stress for elastomer of bearing according to the number of plates under the compression load (unit: MPa).
Table 4.
This is a table of the maximum stress for elastomer of bearing according to the number of plates under the compression load (unit: MPa).
| Vertical Disp. (Dz) | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 mm | 0.06 | 0.08 | 0.13 | 0.19 | 0.26 | 0.34 | 0.44 | 0.55 | 0.69 |
| 2 mm | 0.11 | 0.17 | 0.27 | 0.39 | 0.53 | 0.70 | 0.90 | 1.15 | 1.47 |
| 3 mm | 0.17 | 0.25 | 0.40 | 0.59 | 0.81 | 1.08 | 1.41 | 1.85 | 2.42 |
| 4 mm | 0.22 | 0.33 | 0.54 | 0.79 | 1.10 | 1.49 | 2.00 | 2.67 | 3.59 |
| 5 mm | 0.28 | 0.42 | 0.69 | 1.01 | 1.42 | 1.95 | 2.67 | 3.65 | 5.02 |
Table 5.
This is a table of the safety factor for reinforcing steel plate of bearing according to the number of plates under the compression load.
Table 5.
This is a table of the safety factor for reinforcing steel plate of bearing according to the number of plates under the compression load.
| Vertical Disp. (Dz) | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 mm | N/A | 80.5 | 48.8 | 32.3 | 22.8 | 16.7 | 12.5 | 9.5 | 7.3 |
| 2 mm | N/A | 40.1 | 24.2 | 16.0 | 11.3 | 8.3 | 6.2 | 4.7 | 3.6 |
| 3 mm | N/A | 26.7 | 16.1 | 10.6 | 7.5 | 5.5 | 4.1 | 3.1 | 2.4 |
| 4 mm | N/A | 19.9 | 12.0 | 7.9 | 5.6 | 4.1 | 3.0 | 2.3 | 1.8 |
| 5 mm | N/A | 15.9 | 9.5 | 6.3 | 4.4 | 3.2 | 2.4 | 1.8 | 1.4 |
Table 6.
This is a table of the safety factor for elastomer of bearing according to the number of plates under the compression load.
Table 6.
This is a table of the safety factor for elastomer of bearing according to the number of plates under the compression load.
| Vertical Disp. (Dz) | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 mm | 272.2 | 182.5 | 113.0 | 78.3 | 57.5 | 43.9 | 34.3 | 27.2 | 21.8 |
| 2 mm | 135.6 | 90.9 | 56.2 | 38.9 | 28.5 | 21.5 | 16.6 | 13.0 | 10.2 |
| 3 mm | 90.2 | 60.3 | 37.1 | 25.6 | 18.6 | 13.9 | 10.6 | 8.1 | 6.2 |
| 4 mm | 67.6 | 45.0 | 27.6 | 18.9 | 13.6 | 10.1 | 7.5 | 5.6 | 4.2 |
| 5 mm | 53.8 | 35.8 | 21.8 | 14.8 | 10.6 | 7.7 | 5.6 | 4.1 | 3.0 |
Table 7.
This is a table illustrating the vertical forces (Fz) of elastomeric bearing according to the number of reinforcing plates (unit: MN).
Table 7.
This is a table illustrating the vertical forces (Fz) of elastomeric bearing according to the number of reinforcing plates (unit: MN).
| Vertical Disp. (Dz) | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 mm | 0.04 | 0.19 | 0.45 | 0.89 | 1.57 | 2.55 | 3.96 | 5.94 | 8.69 |
| 2 mm | 0.09 | 0.38 | 0.92 | 1.81 | 3.18 | 5.19 | 8.07 | 12.11 | 17.72 |
| 3 mm | 0.13 | 0.58 | 1.40 | 2.76 | 4.85 | 7.92 | 12.31 | 18.50 | 27.10 |
| 4 mm | 0.18 | 0.79 | 1.89 | 3.74 | 6.57 | 10.74 | 16.71 | 25.13 | 36.86 |
| 5 mm | 0.22 | 1.00 | 2.40 | 4.74 | 8.34 | 13.65 | 21.28 | 32.03 | 47.03 |
Table 8.
This is a table showing the compression stiffness (Kc) of elastomeric bearing according to the number of reinforcing plates (unit: kN/mm).
Table 8.
This is a table showing the compression stiffness (Kc) of elastomeric bearing according to the number of reinforcing plates (unit: kN/mm).
| Vertical Disp. (Dz) | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 mm | 43 | 190 | 454 | 893 | 1566 | 2554 | 3965 | 5944 | 8689 |
| 2 mm | 43 | 192 | 461 | 907 | 1591 | 2597 | 4034 | 6053 | 8859 |
| 3 mm | 44 | 194 | 467 | 920 | 1616 | 2640 | 4105 | 6166 | 9033 |
| 4 mm | 44 | 197 | 474 | 934 | 1642 | 2685 | 4179 | 6284 | 9216 |
| 5 mm | 44 | 199 | 480 | 948 | 1669 | 2731 | 4255 | 6407 | 9407 |
Table 9.
This is a table showing the compression resultant of elastomeric bearing according to the number of reinforcing plates.
Table 9.
This is a table showing the compression resultant of elastomeric bearing according to the number of reinforcing plates.
| Compression Resultant | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| Hb (mm) | 240 | 231 | 222 | 213 | 204 | 195 | 186 | 177 | 168 |
| hb (mm) | 240 | 115.5 | 74.0 | 53.3 | 40.8 | 32.5 | 26.6 | 22.1 | 18.7 |
| Kc (kN/mm) | 44 | 194 | 467 | 920 | 1616 | 2640 | 4105 | 6166 | 9033 |
| RKc (-) | 1.0 | 4.4 | 10.6 | 20.9 | 36.7 | 60.0 | 93.3 | 140.1 | 205.3 |
| Ec (MPa) | 10.6 | 44.8 | 103.7 | 196.0 | 329.7 | 514.8 | 763.5 | 1091.4 | 1517.5 |
| Rc (-) | 1.0 | 4.2 | 9.8 | 18.6 | 31.2 | 48.8 | 72.3 | 103.4 | 143.7 |
Table 10.
This is a table showing the Shear resultant of elastomeric bearing according to the number of reinforcing plates when horizontal displacement of 50 mm and vertical displacement of 3 mm are imposed (unit: kN).
Table 10.
This is a table showing the Shear resultant of elastomeric bearing according to the number of reinforcing plates when horizontal displacement of 50 mm and vertical displacement of 3 mm are imposed (unit: kN).
| Shear Resultant | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| Fx (kN) | 190.5 | 196.0 | 203.2 | 210.6 | 218.0 | 225.3 | 232.2 | 238.4 | 243.4 |
| Ks (kN/mm) | 3.81 | 3.92 | 4.06 | 4.21 | 4.36 | 4.51 | 4.64 | 4.77 | 4.87 |
| RKs (-) | 1.00 | 1.03 | 1.07 | 1.10 | 1.14 | 1.18 | 1.22 | 1.25 | 1.28 |
| G (MPa) | 0.91 | 0.91 | 0.90 | 0.90 | 0.89 | 0.88 | 0.86 | 0.84 | 0.82 |
| Rs (-) | 1.00 | 1.00 | 0.99 | 0.99 | 0.98 | 0.97 | 0.95 | 0.92 | 0.90 |
Table 11.
This is a table showing the bending resultant of elastomeric bearing according to the number of reinforcing plates when the rotation angle is 0.005 rad.
Table 11.
This is a table showing the bending resultant of elastomeric bearing according to the number of reinforcing plates when the rotation angle is 0.005 rad.
| Bending Resultant | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| My (kN-m) | 10.1 | 25.7 | 45.7 | 68.2 | 91.9 | 177.1 | 145.2 | 177.4 | 215.6 |
| Kb (kN-m/rad) | 2025 | 5139 | 9131 | 13,630 | 18,373 | 23,429 | 29,031 | 35,483 | 43,128 |
| RKb (-) | 1.0 | 2.5 | 4.5 | 6.7 | 9.1 | 11.6 | 14.3 | 17.5 | 21.3 |
| Eb (MPa) | 5.8 | 14.2 | 24.3 | 34.8 | 45.0 | 54.8 | 64.8 | 75.4 | 86.9 |
| Rb (-) | 1.0 | 2.4 | 4.2 | 6.0 | 7.7 | 9.4 | 11.1 | 12.9 | 14.9 |
Table 12.
This is a table of the compressive, shear, and bending stiffness of elastomeric bearing according to the number of reinforcing plates.
Table 12.
This is a table of the compressive, shear, and bending stiffness of elastomeric bearing according to the number of reinforcing plates.
| Stiffness | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| Kc (kN/mm) | 44 | 194 | 467 | 920 | 1616 | 2640 | 4105 | 6166 | 9033 |
| Ks (kN/mm) | 3.81 | 3.92 | 4.06 | 4.21 | 4.36 | 4.51 | 4.64 | 4.77 | 4.87 |
| Kb (kN-m/rad) | 2025 | 5139 | 9131 | 13,630 | 18,373 | 23,429 | 29,031 | 35,483 | 43,128 |
Table 13.
This is a table showing the stiffness ratio of elastomeric bearing according to the number of reinforcing plates.
Table 13.
This is a table showing the stiffness ratio of elastomeric bearing according to the number of reinforcing plates.
| Stiffness Ratio | Number of Reinforcing Plate (Ns) |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| RKc = Kc/Kc0 | 1.0 | 4.4 | 10.6 | 20.9 | 36.7 | 60.0 | 93.3 | 140.1 | 205.3 |
| RKs = Ks/Ks0 | 1.00 | 1.03 | 1.07 | 1.10 | 1.14 | 1.18 | 1.22 | 1.25 | 1.28 |
| RKb = Kb/Kb0 | 1.0 | 2.5 | 4.5 | 6.7 | 9.1 | 11.6 | 14.3 | 17.5 | 21.3 |
Table 14.
This is a table showing the LRFD combinations.
Table 14.
This is a table showing the LRFD combinations.
| Items | Load Combinations | Load Conditions | Safety Factor |
|---|
| Ultimate Limit States (ULS) | 1.3 × Permanent Loads + 0.7 × Environmental Loads | Transit (Tow)
100-yr Extreme | >1.67 |
| Accidental Limit States (ALS) | 1.0 × Permanent Loads + 1.0 × Environmental Loads | 10,000-yr Abnormal
1-yr Damaged | >1.33 |
| Serviceability Limit States (SLS) | 1.0 × Permanent Loads + 1.0 × Environmental Loads | 1-yr Operating | >3.0 * |
Table 15.
This is a table showing the load and displacement conditions applied to elastomeric bearing for FPSO.
Table 15.
This is a table showing the load and displacement conditions applied to elastomeric bearing for FPSO.
| Load Conditions | Fx (kN) | Fy (kN) | Fz (kN) | Dx (mm) | θy (rad) |
|---|
| ULS | Transit (Tow) | 3055 | 5460 | 16,523 | 20 | 0.003 |
| 100-yr Extreme | 5991 | 8160 | 21,820 | 26 | 0.005 |
| ALS | 10000-yr Abnormal | 7778 | 11,664 | 24,877 | 33 | 0.007 |
| 1-yr Damage | 6124 | 9671 | 22,839 | 27 | N/A |
| SLS | 1-yr Operating | 4244 | 5009 | 18,323 | 19 | 0.002 |
| | | Compression | Shear | Bending |
Table 16.
This is a table of the dimensions for the analytic model.
Table 16.
This is a table of the dimensions for the analytic model.
| Items | Dimensions |
|---|
| Overall Size | 1100 × 1100 × 300 mm |
| Base Plate | 1100 × 1100 × 30 mm |
| Elastomeric Bearing | 1000 × 1000 × 270 mm |
| Top Contact Plate | 980 × 980 × 25 mm |
| Reinforcing Plate | 980 × 980 × 9 mm (7-rows) |
Table 17.
This is a table shoing the maximum stresses and safety factors of vertical bearing under compression and shear load.
Table 17.
This is a table shoing the maximum stresses and safety factors of vertical bearing under compression and shear load.
| Items | Reinforcing Steel Plate | Elastomer | Remarks (Safety Factor) |
|---|
| Stresses (MPa) | Safety Factor | Stresses (Mpa) | Safety Factor |
|---|
| Compression | SLS | 113.4 | 3.13 | 2.42 | 6.20 | >3.0 |
| ULS | 133.9 | 2.35 | 3.24 | 4.63 | >1.67 |
| ALS | 151.6 | 2.34 | 4.12 | 3.64 | >1.33 |
| Shear | SLS | 113.4 | 3.13 | 2.42 | 6.20 | >3.0 |
| ULS | 133.9 | 2.65 | 3.24 | 4.63 | >1.67 |
| ALS | 151.6 | 2.34 | 4.12 | 3.64 | >1.33 |
| Bending | SLS | 51.9 | 6.84 | 0.17 | 88.8 | >3.0 |
| ULS | 130.2 | 2.73 | 0.43 | 34.9 | >1.67 |
| ALS | 182.6 | 1.94 | 0.61 | 24.7 | >1.33 |
Table 18.
This is a table showing the stiffness of vertical bearing according to load conditions.
Table 18.
This is a table showing the stiffness of vertical bearing according to load conditions.
| Load Conditions | Max. Load | Displacement | Stiffness |
|---|
| Compression | SLS | 18,323 kN | 2.98 mm | 6149 kN/mm |
| ULS | 21,850 kN | 3.51 mm | 6225 kN/mm |
| ALS | 24,877 kN | 3.96 mm | 6282 kN/mm |
| Shear | SLS | 90 kN | 19 mm | 4.74 kN/mm |
| ULS | 120 kN | 26 mm | 4.62 kN/mm |
| ALS | 148 kN | 33 mm | 4.49 kN/mm |
| Bending | SLS | 70.8 kN-m | 0.002 rad | 35,390 kN-m/rad |
| ULS | 177.4 kN-m | 0.005 rad | 35,483 kN-m/rad |
| ALS | 249.1 kN-m | 0.007 rad | 35,589 kN-m/rad |