Investigating the System Behaviors of a 10 kW Organic Rankine Cycle (ORC) Prototype Using Plunger Pump and Centrifugal Pump
Abstract
:1. Introduction
2. Experimental Setup Description
2.1. System Design and Operating Method
2.2. Plunger Pump and Centrifugal Pump
3. Measuring Device and Thermodynamic Analysis
4. Results and Discussion
4.1. Basic Operating Parameters
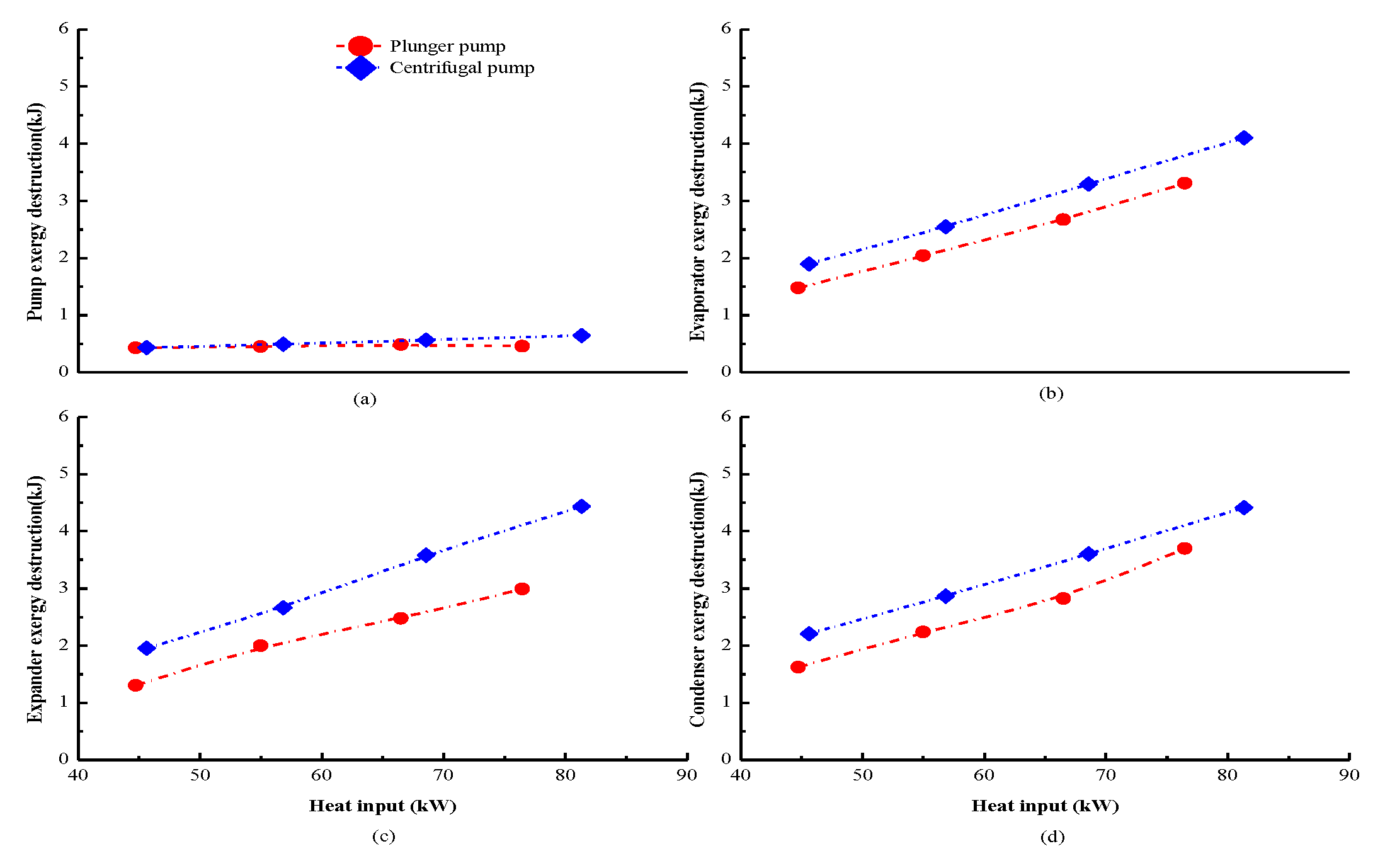
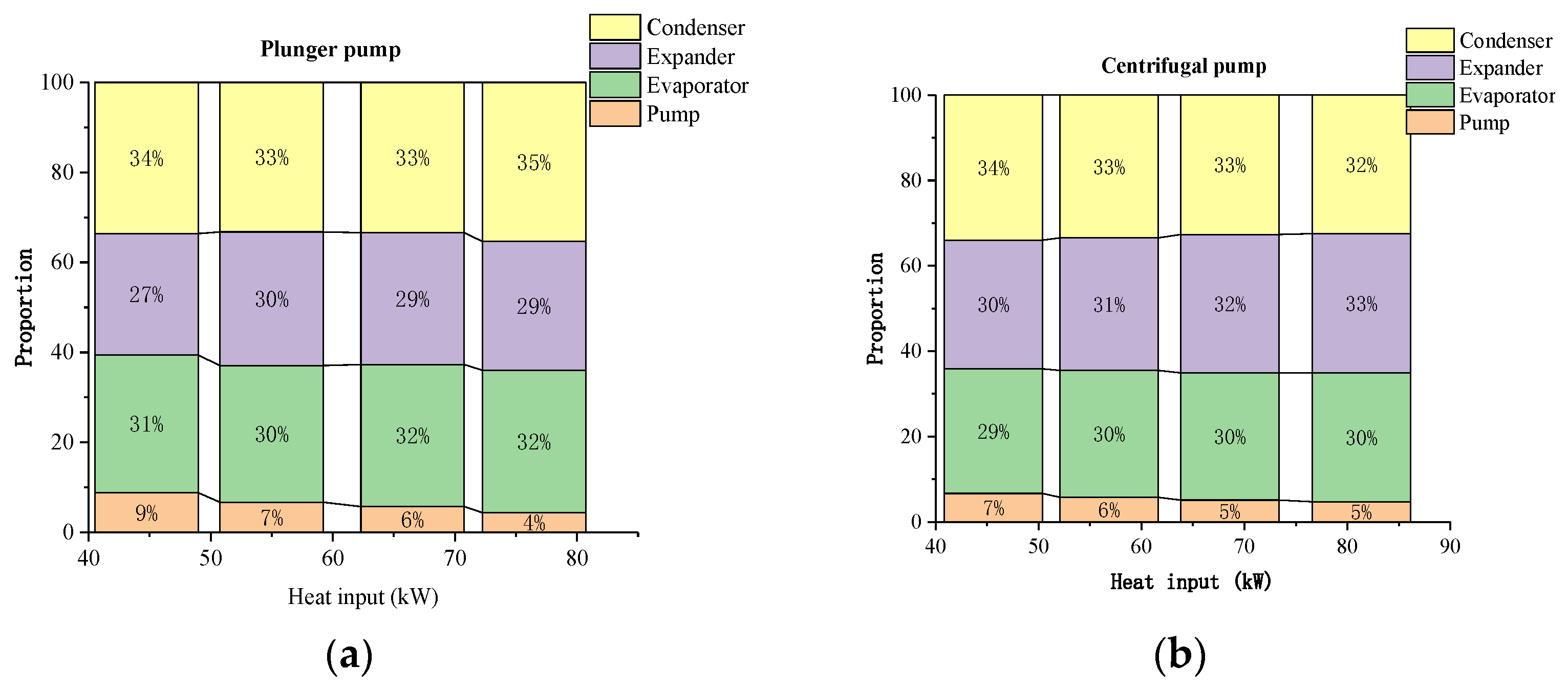
4.2. Detailed Components’ Behavior
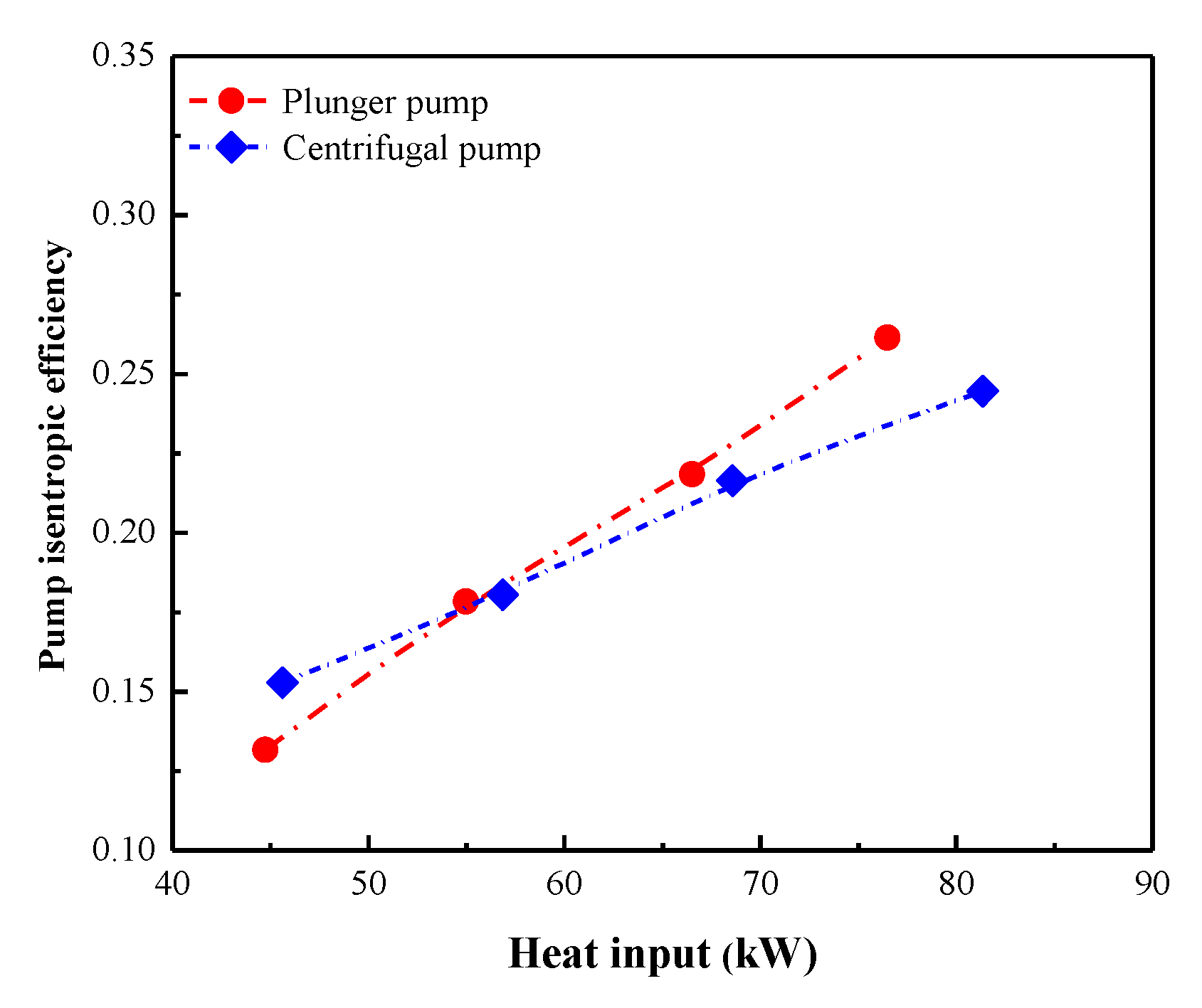
4.2.1. Pump Behavior
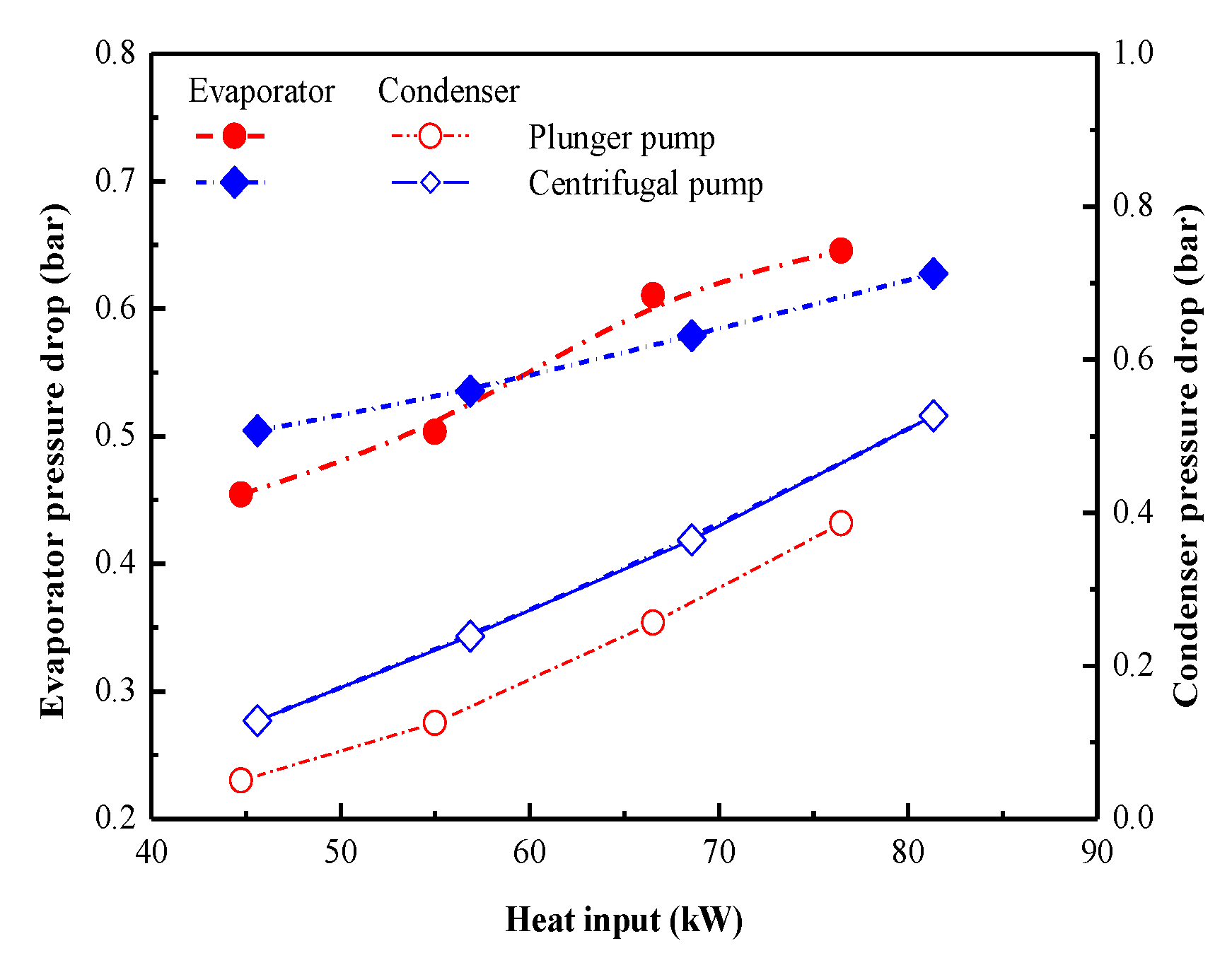
4.2.2. Heat Exchanger Behavior
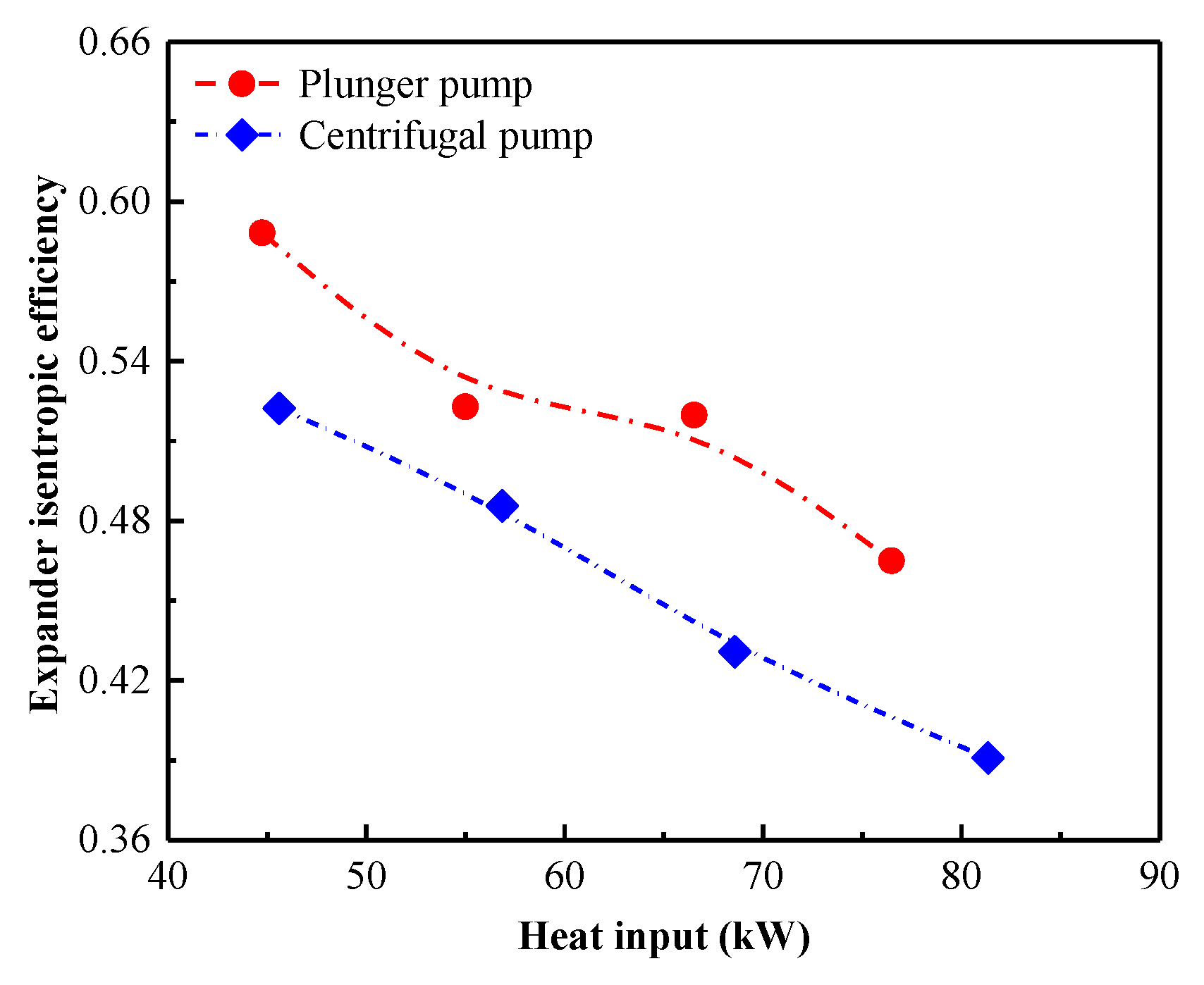
4.2.3. Expander Behavior
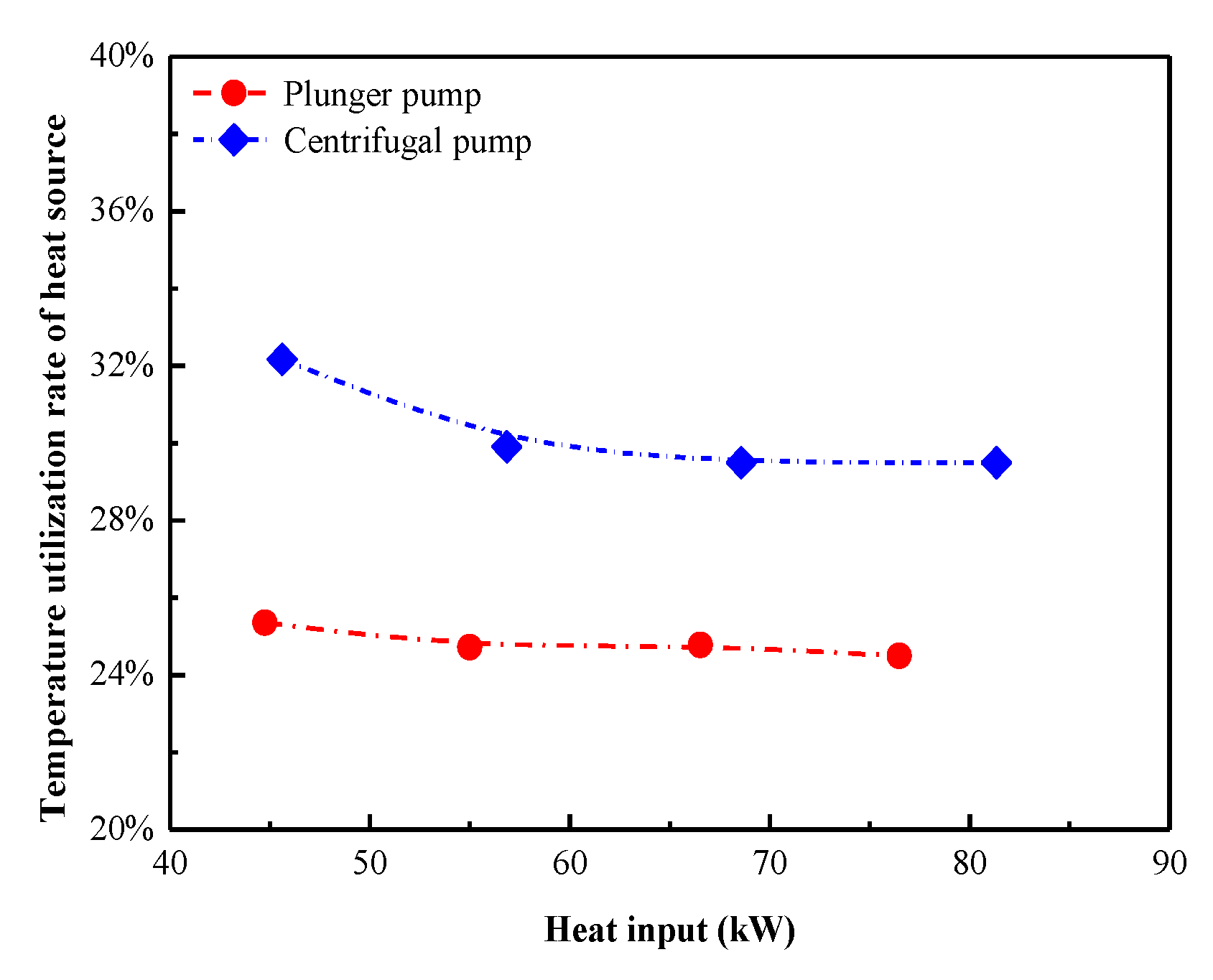
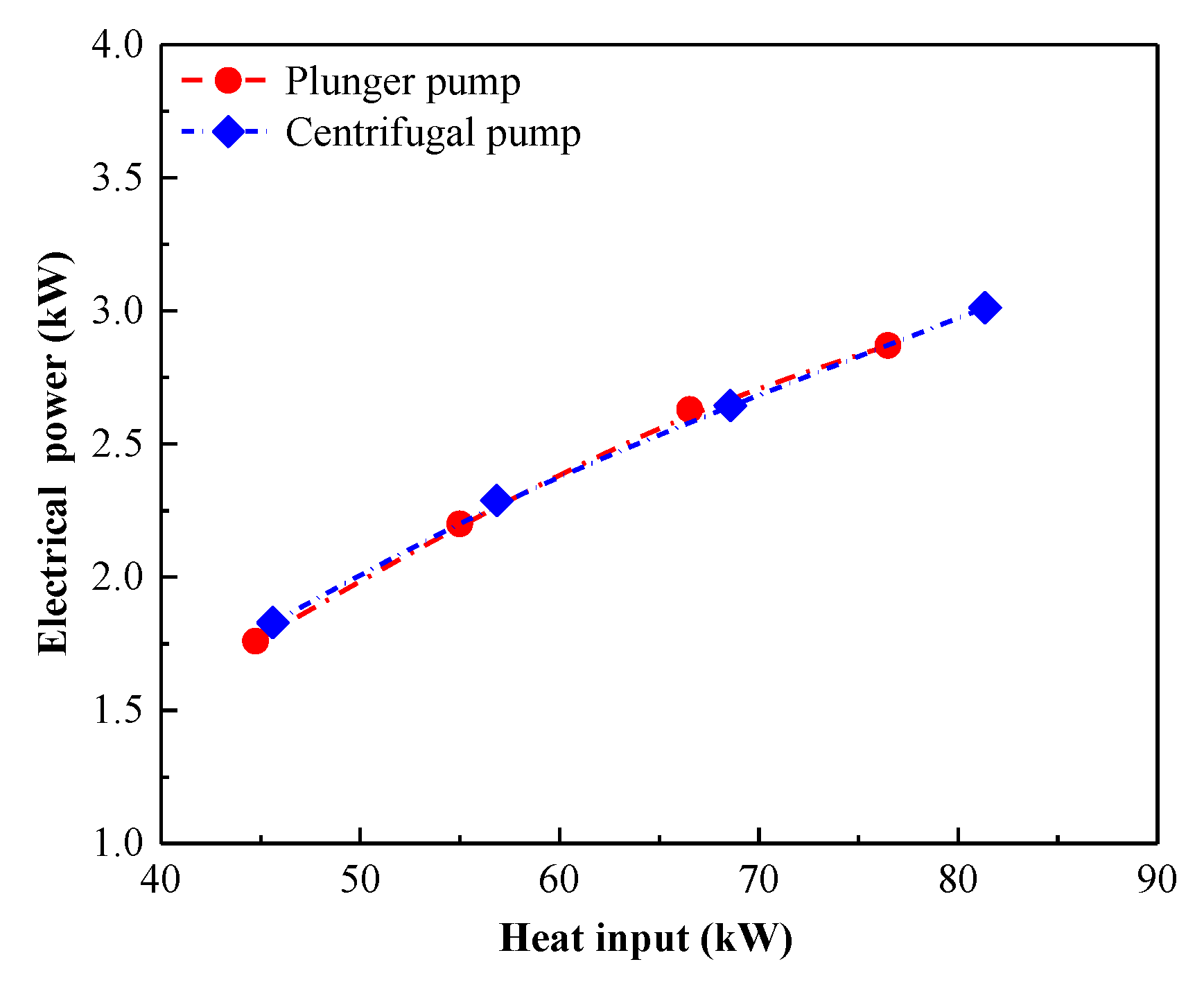
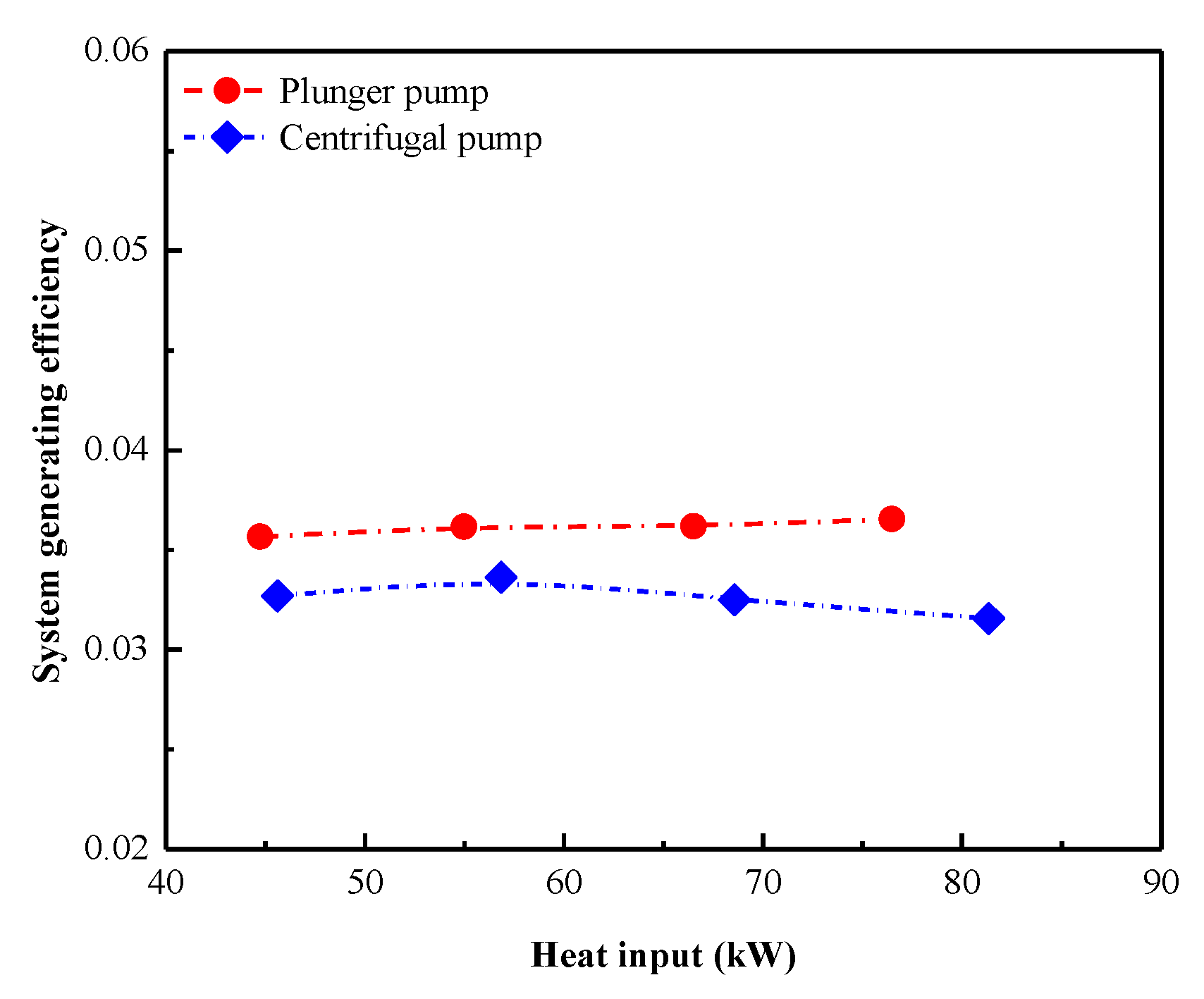
4.3. Overall System Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Johnson, I.; Choate, W.T.; Davidson, A. Waste Heat Recovery: Technology and Opportunities in U.S. Industry; BCS, lnc.: Laurel, MD, USA, 2008. [Google Scholar]
- Feng, Y.Y.; Zhang, Y.Y.; Li, B.B.; Yang, J.J.; Shi, Y. Comparison between regenerative organic Rankine cycle (RORC) and basic organic Rankine cycle (BORC) based on thermoeconomic multi-objective optimization considering exergy efficiency and levelized energy cost (LEC). Energy Convers. Manag. 2015, 96, 58–71. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Hung, T.C.; Greg, K.; Zhang, Y.Y.; Li, B.B.; Yang, J.F. Thermoeconomic comparison between pure and mixture working fluids for low-grade organic Rankine cycles (ORCs). Energy Convers. Manag. 2015, 106, 859–872. [Google Scholar] [CrossRef]
- Peris, B.; Navarro-Esbr, J.; Moles, F.; Martí, J.J.; Mota-Babiloni, A. Experimental characterization of an Organic Rankine Cycle (ORC) for micro-scale CHP applications. Appl. Ther. Eng. 2015, 79, 1–8. [Google Scholar] [CrossRef]
- Capata, R.; Toro, C. Feasibility analysis of a small-scale ORC energy recovery system for vehicular application. Energy Convers. Manag. 2014, 86, 1078–1090. [Google Scholar] [CrossRef]
- Freeman, J.; Hellgardt, K.; Markides, C.N. An assessment of solar-powered organic Rankine cycle systems for combined heating and power in UK domestic applications. Appl. Energy 2015, 138, 605–620. [Google Scholar] [CrossRef] [Green Version]
- Pantano, F.; Capata, R. Expander selection for an on board ORC energy recovery system. Energy 2017, 141, 1084–1096. [Google Scholar] [CrossRef] [Green Version]
- Atiz, A.; Karakilcik, H.; Erden, M.; Karakilcik, M. Investigation energy, exergy and electricity production performance of an integrated system based on a low-temperature geothermal resource and solar energy. Energy Convers. Manag. 2019, 195, 798–809. [Google Scholar] [CrossRef]
- Mathias, J.J.; Johnston, J.J.; Cao, J.J.; Priedeman, D.D.; Christensen, R.N. Experimental testing of gerotor and scroll expanders used in, and energetic and exergetic modeling of, an organic Rankine cycle. J. Energy Res. Technol. Trans. ASME 2009, 131, 21–24. [Google Scholar] [CrossRef]
- Lei, B.; Wang, J.-F.; Wu, Y.-T.; Ma, C.-F.; Wang, W.; Zhang, L.; Li, J.-Y. Experimental study and theoretical analysis of a Roto-Jet pump in small scale organic Rankine cycles. Energy Convers. Manag. 2016, 111, 198–204. [Google Scholar] [CrossRef]
- Bianchi, G.; Fatigati, F.; Murgia, S.; Cipollone, R.; Contaldi, G. Modeling and experimental activities on a small-scale sliding vane pump for ORC-based waste heat recovery applications. Energy Procedia 2016, 101, 1240–1247. [Google Scholar] [CrossRef]
- Villani, M.; Tribioli, L. Comparison of different layouts for the integration of an organic Rankine cycle unit in electrified powertrains of heavy duty Diesel trucks. Energy Convers. Manag. 2019, 187, 248–261. [Google Scholar] [CrossRef]
- Zeleny, Z.; Vodicka, V.; Novotny, V.; Mascuch, J. Gear pump for low power output ORC—An efficiency analysis. Energy Procedia 2017, 129, 1002–1009. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, J.J.; Zhao, L.; Deng, S.; Zhang, Y. Novel experimental research on the compression process in organic Rankine cycle (ORC). Energy Convers. Manag. 2017, 137, 1–11. [Google Scholar] [CrossRef]
- Carraro, G.; Pallis, P.; Leontaritis, A.D.; Karellas, S.; Vourliotis, P.; Rech, S.; Lazzaretto, A. Experimental performance evaluation of a multi-diaphragm pump of a micro-ORC system. Energy Procedia 2017, 129, 1018–1025. [Google Scholar] [CrossRef]
- Bianchi, M.; Branchini, L.; Casari, N.; Pascale, D.; Melino, F.; Ottaviano, S.; Pinelli, M.; Spina, P.; Suman, A. Experimental analysis of a micro-ORC driven by piston expander for low-grade heat recovery. Appl. Ther. Eng. 2019, 148, 1278–1291. [Google Scholar] [CrossRef]
- Zhang, H.H.; Xi, H.; He, Y.Y.; Zhang, Y.Y.; Ning, B. Experimental study of the organic rankine cycle under different heat and cooling conditions. Energy 2019, 180, 678–688. [Google Scholar] [CrossRef]
- Xi, H.; He, Y.Y.; Wang, J.J.; Huang, Z.H. Transient response of waste heat recovery system for hydrogen production and other renewable energy utilization. Int. J. Hydrogen Energy 2019, 44, 15985–15996. [Google Scholar] [CrossRef]
- Abam, F.F.; Ekwe, E.E.; Effiom, S.S.; Ndukwu, M.M.; Briggs, T.T.; Kadurumba, C.H. Optimum exergetic performance parameters and thermo-sustainability indicators of low-temperature modified organic Rankine cycles (ORCs). Sustain. Energy Technol. Assess. 2018, 30, 91–104. [Google Scholar] [CrossRef]
- Aleksandra, B.-G. Pumping work in the organic Rankine cycle. Appl. Ther. Eng. 2013, 51, 781–786. [Google Scholar]
- Wu, T.T.; Liu, J.J.; Zhang, L.; Xu, X.J. Experimental study on multi-stage gas-liquid booster pump for working fluid pressurization. Appl. Ther. Eng. 2017, 126, 9–16. [Google Scholar] [CrossRef]
- Meng, F.F.; Zhang, H.H.; Yang, F.F.; Hou, X.X.; Lei, B.; Zhang, L. Study of efficiency of a multistage centrifugal pump used in engine waste heat recovery application. Appl. Ther. Eng. 2017, 110, 779–786. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Zhang, H.H.; Xu, Y.Y.; Yang, F.B.; Wu, Y.Y.; Lei, B. Matching and operating characteristics of working fluid pumps with organic Rankine cycle system. Appl. Ther. Eng. 2018, 142, 622–631. [Google Scholar] [CrossRef]
- Sun, H.H.; Qin, J.; Hung, T.C.; Hua, H.H.; Ya, P.P.; Lin, C.H. Effect of flow losses in heat exchangers on the performance of organic Rankine cycle. Energy 2019, 172, 391–400. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Hung, T.C.; He, Y.Y.; Wang, Q.; Wang, S.; Li, B.B.; Lin, J.J.; Zhang, W.P. Operation characteristic and performance comparison of organic Rankine cycle (ORC) for low-grade waste heat using R245fa, R123 and their mixtures. Energy Convers. Manag. 2017, 144, 153–163. [Google Scholar] [CrossRef]
- Feng, Y.Q.; Hung, T.C.; Wu, S.S.; Lin, C.C.; Li, B.B.; Huang, K.K.; Qin, J. Operation characteristic of a R123-based organic Rankine cycle depending on working fluid mass flow rates and heat source temperature. Energy Convers. Manag. 2017, 131, 55–68. [Google Scholar] [CrossRef]
- Yang, S.S.; Hung, T.C.; Feng, Y.Y.; Wu, C.C.; Wong, K.K.; Huang, K.C. Experimental investigation on a 3 kW organic Rankine cycle for low grade waste heat under different operation parameters. Appl. Ther. Eng. 2017, 113, 756–764. [Google Scholar] [CrossRef]
- D’Amico, F.; Pallis, P.; Leontaritis, A.D.; Karellas, S.; Kakalis, N.M.; Rech, S.; Lazzaretto, A. Semi-empirical model of a multi-diaphragm pump in an Organic Rankine Cycle (ORC) experimental unit. Energy 2018, 143, 1056–1071. [Google Scholar] [CrossRef]
- Liu, L.L.; Zhu, T.; Wang, T.T.; Gao, N.P. Experimental investigation on the effect of working fluid charge in a small-scale Organic Rankine Cycle under off-design conditions. Energy 2019, 174, 664–677. [Google Scholar] [CrossRef]
- Yang, X.X.; Xu, J.J.; Miao, Z.; Zou, J.J.; Yu, C. Operation of an organic Rankine cycle dependent on pumping flow rates and expander torques. Energy 2015, 90, 864–878. [Google Scholar] [CrossRef]
- Pei, G.; Li, J.; Li, Y.Y.; Wang, D.D.; Ji, J. Construction and dynamic test of a small-scale organic rankine cycle. Energy 2011, 36, 3215–3223. [Google Scholar] [CrossRef]
- Galindo, J.; Ruiz, S.; Dolz, V.; Royo-Pascual, L.; Haller, R.; Nicolas, B.; Glavatskaya, Y. Experimental and thermodynamic analysis of a bottoming Organic Rankine Cycle (ORC) of gasoline engine using swash-plate expander. Energy Convers. Manag. 2015, 103, 519–532. [Google Scholar] [CrossRef]
- Dumont, O.; Quoilin, S.; Lemort, V. Experimental investigation of a reversible heat pump/organic Rankine cycle unit designed to be coupled with a passive house to get a Net Zero Energy Building. Int. J. Refrig. 2015, 54, 190–203. [Google Scholar] [CrossRef]
- Gao, P.; Wang, Z.Z.; Wang, L.L.; Lu, H.T. Technical feasibility of a gravity-type pumpless ORC system with one evaporator and two condensers. Appl. Ther. Eng. 2018, 145, 569–575. [Google Scholar] [CrossRef]
- Bao, H.H.; Ma, Z.Z.; Roskilly, A.P. Chemisorption power generation driven by low grade heat – Theoretical analysis and comparison with pumpless ORC. Appl. Energy 2017, 186, 282–290. [Google Scholar] [CrossRef]
- Jiang, L.; Lu, H.H.; Wang, R.R.; Wang, L.L.; Gong, L.L.; Lu, Y.Y.; Roskilly, A.P. Investigation on an innovative cascading cycle for power and refrigeration cogeneration. Energy Convers. Manag. 2017, 145, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.Y.; Hung, T.C.; Su, T.T.; Wang, S.; Wang, Q.; Yang, S.S.; Lin, J.J.; Lin, C.H. Experimental investigation of a R245fa-based organic Rankine cycle adapting two operation strategies: Stand alone and grid connect. Energy 2017, 141, 1239–1253. [Google Scholar] [CrossRef]
- Sun, H.H.; Qin, J.; Hung, T.C.; Lin, C.C.; Lin, Y.F. Performance comparison of organic Rankine cycle with expansion from superheated zone or two-phase zone based on temperature utilization rate of heat source. Energy 2018, 149, 566–576. [Google Scholar] [CrossRef]



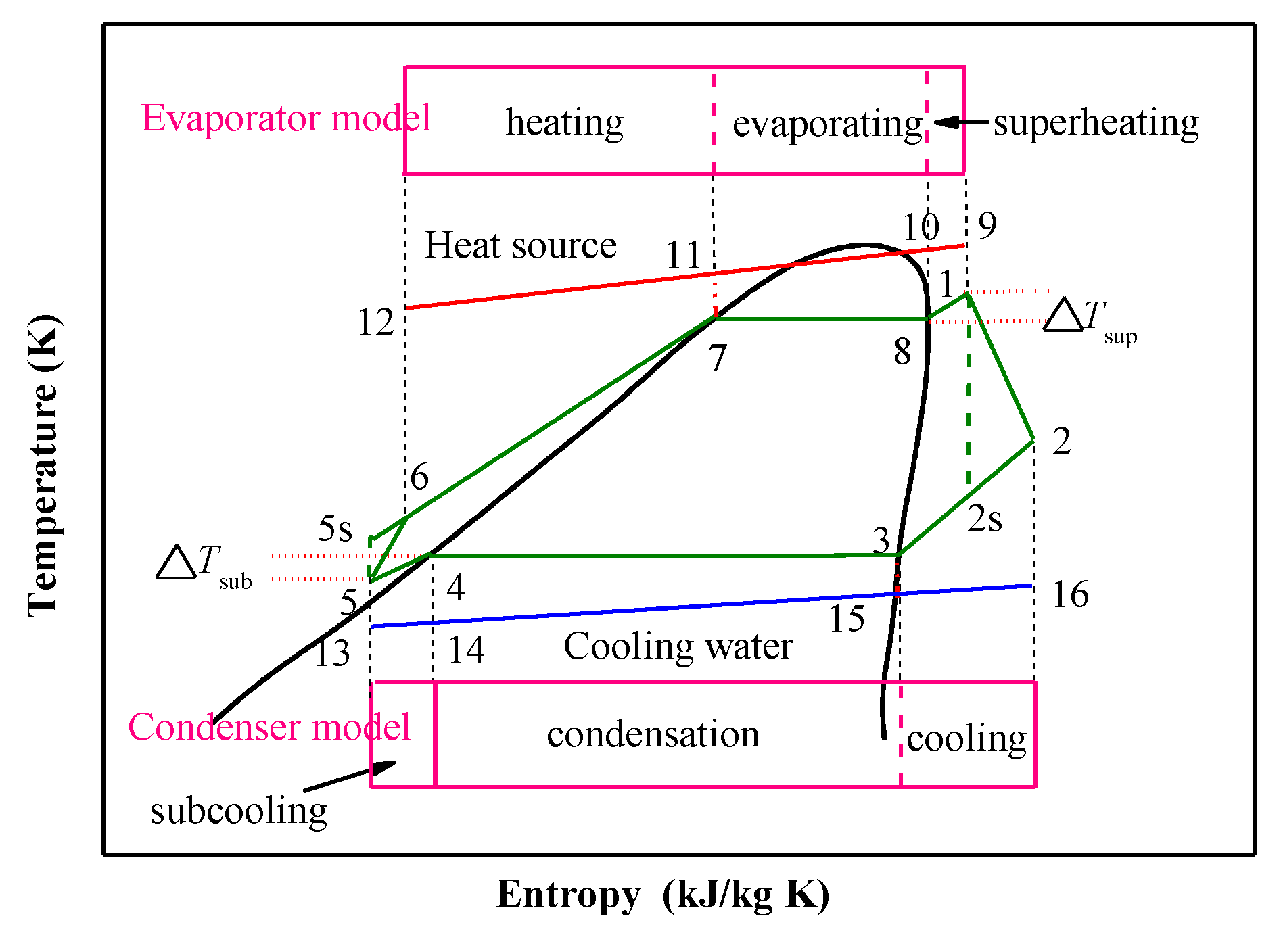
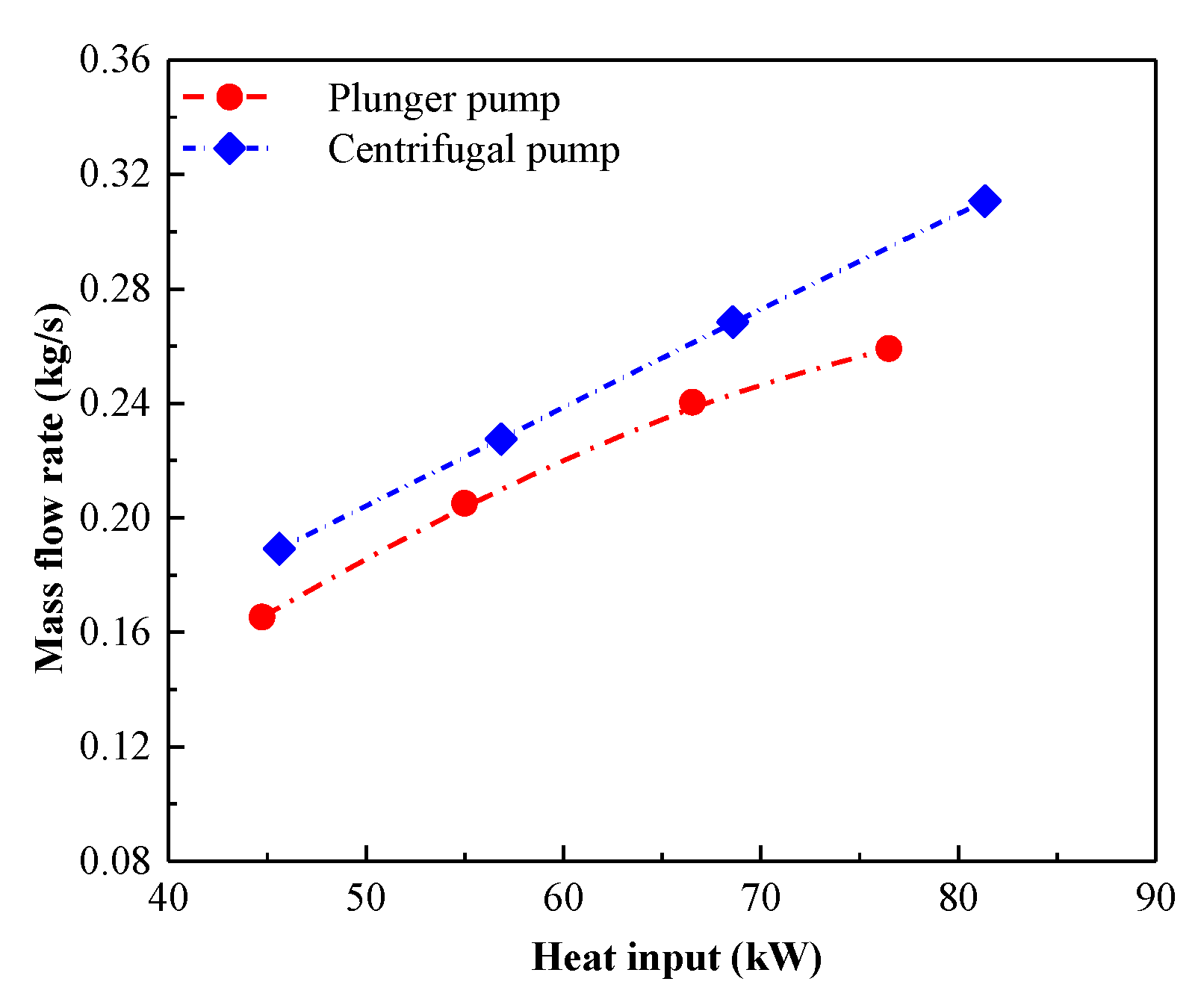
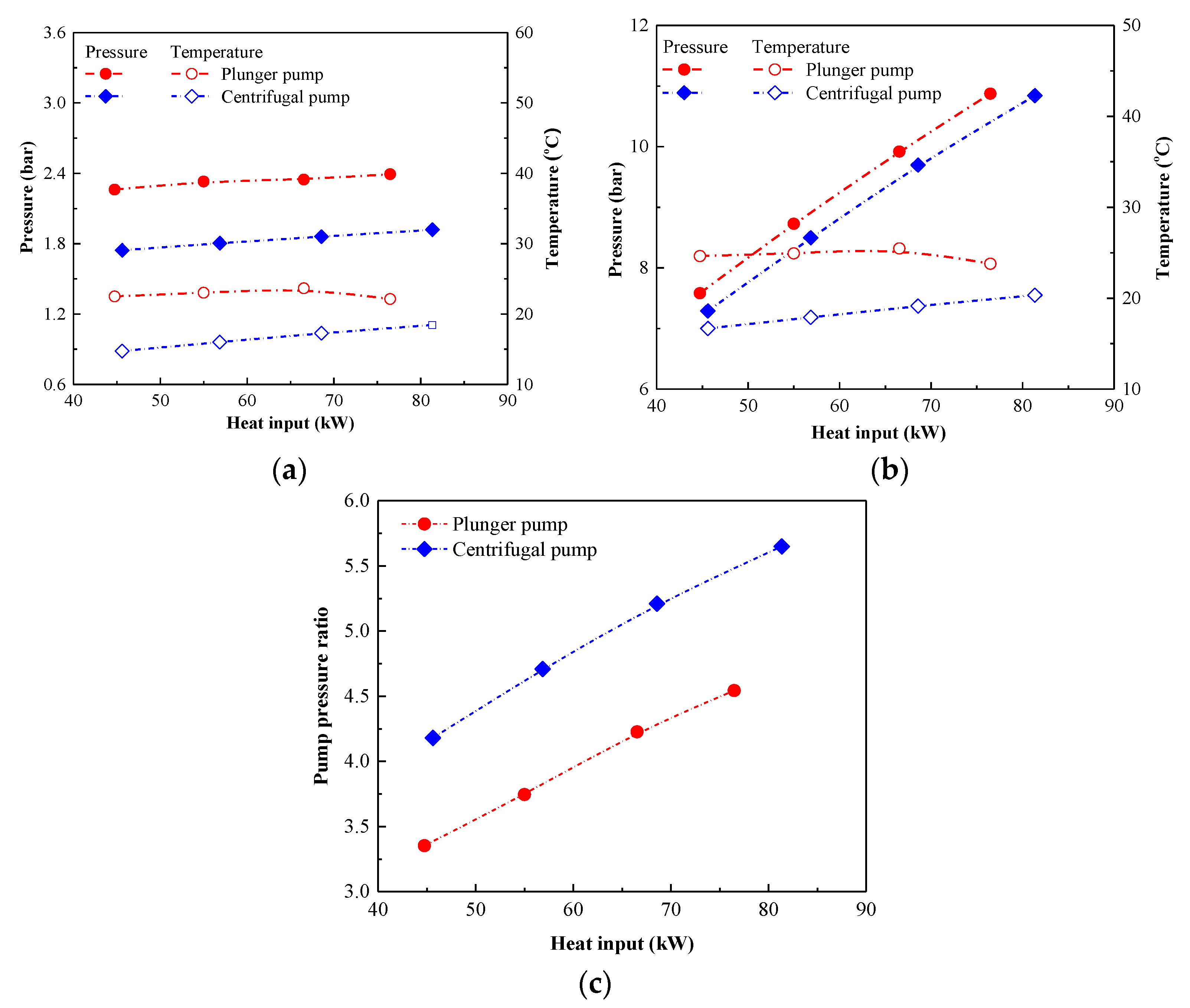
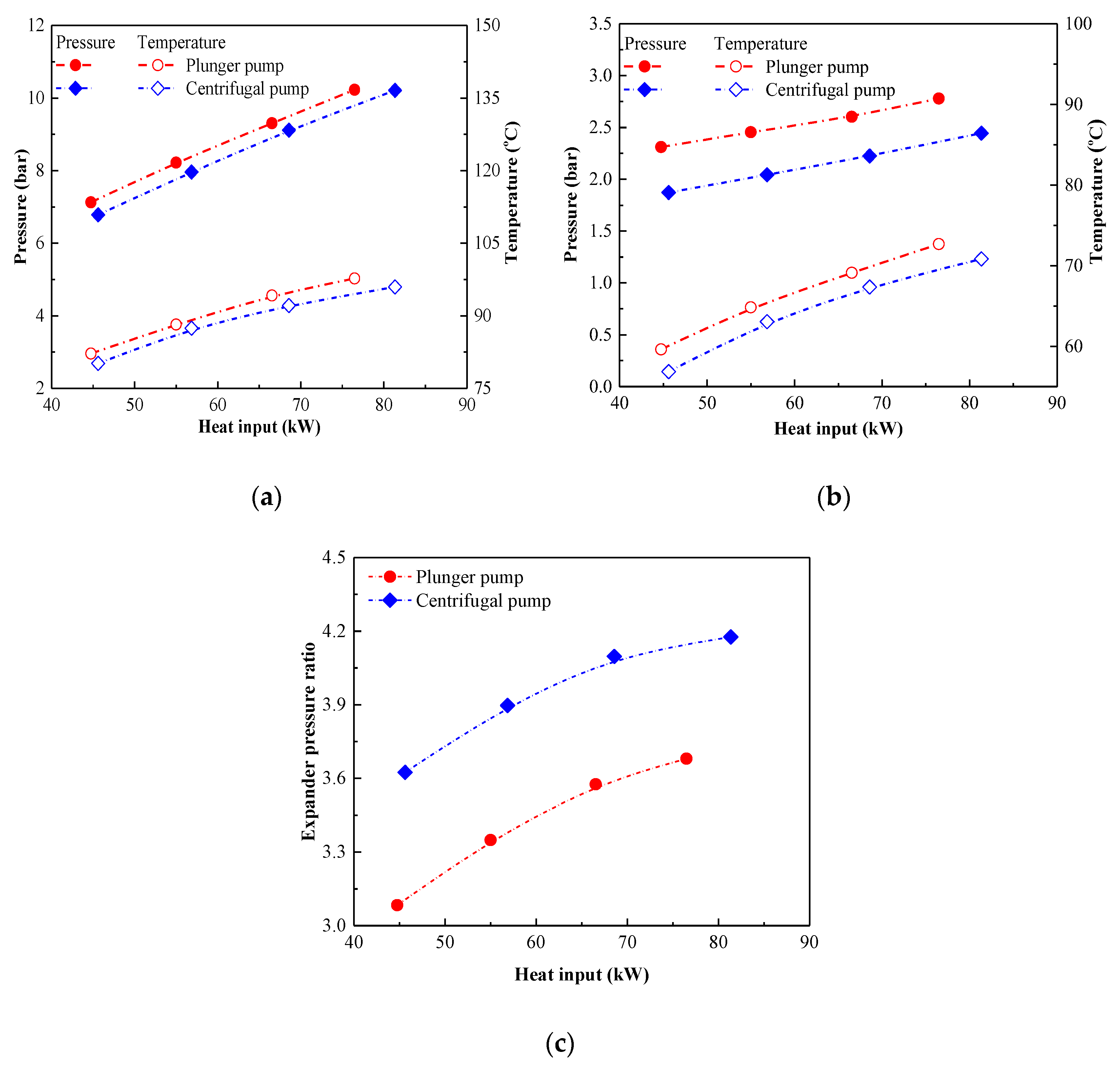


| Component | Maximum Temperature | Total Volume | Total Heat Transfer Area | Maximum Pressure |
|---|---|---|---|---|
| Heat exchanger | 200 °C | 8.848 L | 4.175 m2 | 30 bar |
| Component | Volume Ratio | Inspiratory Volume | Gear Height | Basic Circle Radius |
|---|---|---|---|---|
| Scroll expander | 2.95 | 23.56 m3/hr | 48.2 mm | 4.456 mm |
| Components | Maximum Pressure(bar) | Maximum Flow(L/min) | Temperature Resistance (°C) | Nominal Speed (RPM) |
|---|---|---|---|---|
| Plunger pump | 20 | 15.5 | 40 | 850 |
| Centrifugal pump | 25 | 36.7 | 120 | 3500 |
| Item | Type | Measurement Range | Device Uncertainty |
|---|---|---|---|
| Temperature | T-type | 0–623.15 K | ±0.3 K |
| Pressure | JPT-131S | 0–30 bar | ±0.5% F.S |
| Flow rate | GPI S050 | 1.9–37.9 L/min | ±3% L/min |
| Rotation speed | UT-372 | 10–99,999 rpm | ±3% rpm |
| Electrical power | PA310 | 0.5% | |
| Pump shaft power | 3.9% | ||
| Pump isentropic efficiency | 4.5% | ||
| Evaporator heat transfer coefficient | 1.9% | ||
| Condenser heat transfer coefficient | 2.2% | ||
| Expander isentropic efficiency | 4.7% | ||
| System generating efficiency | 1.2% |
| Heat input (kW) | 38.7 | 48.8 | 58.2 | 63.8 |
| Environment temperature (°C) | 23.5 | 23.5 | 24.0 | 21.5 |
| Heat input (kW) | 46.0 | 56.2 | 66.6 | 77.3 |
| Environment temperature (°C) | 17.5 | 17.3 | 18.9 | 18.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Feng, Y.-q.; Hung, T.-C.; He, Z.-x.; Lin, C.-H.; Sultan, M. Investigating the System Behaviors of a 10 kW Organic Rankine Cycle (ORC) Prototype Using Plunger Pump and Centrifugal Pump. Energies 2020, 13, 1141. https://doi.org/10.3390/en13051141
Wang X, Feng Y-q, Hung T-C, He Z-x, Lin C-H, Sultan M. Investigating the System Behaviors of a 10 kW Organic Rankine Cycle (ORC) Prototype Using Plunger Pump and Centrifugal Pump. Energies. 2020; 13(5):1141. https://doi.org/10.3390/en13051141
Chicago/Turabian StyleWang, Xin, Yong-qiang Feng, Tzu-Chen Hung, Zhi-xia He, Chih-Hung Lin, and Muhammad Sultan. 2020. "Investigating the System Behaviors of a 10 kW Organic Rankine Cycle (ORC) Prototype Using Plunger Pump and Centrifugal Pump" Energies 13, no. 5: 1141. https://doi.org/10.3390/en13051141
APA StyleWang, X., Feng, Y.-q., Hung, T.-C., He, Z.-x., Lin, C.-H., & Sultan, M. (2020). Investigating the System Behaviors of a 10 kW Organic Rankine Cycle (ORC) Prototype Using Plunger Pump and Centrifugal Pump. Energies, 13(5), 1141. https://doi.org/10.3390/en13051141








