Optimal Design for a Shared Swap Charging System Considering the Electric Vehicle Battery Charging Rate
Abstract
:1. Introduction
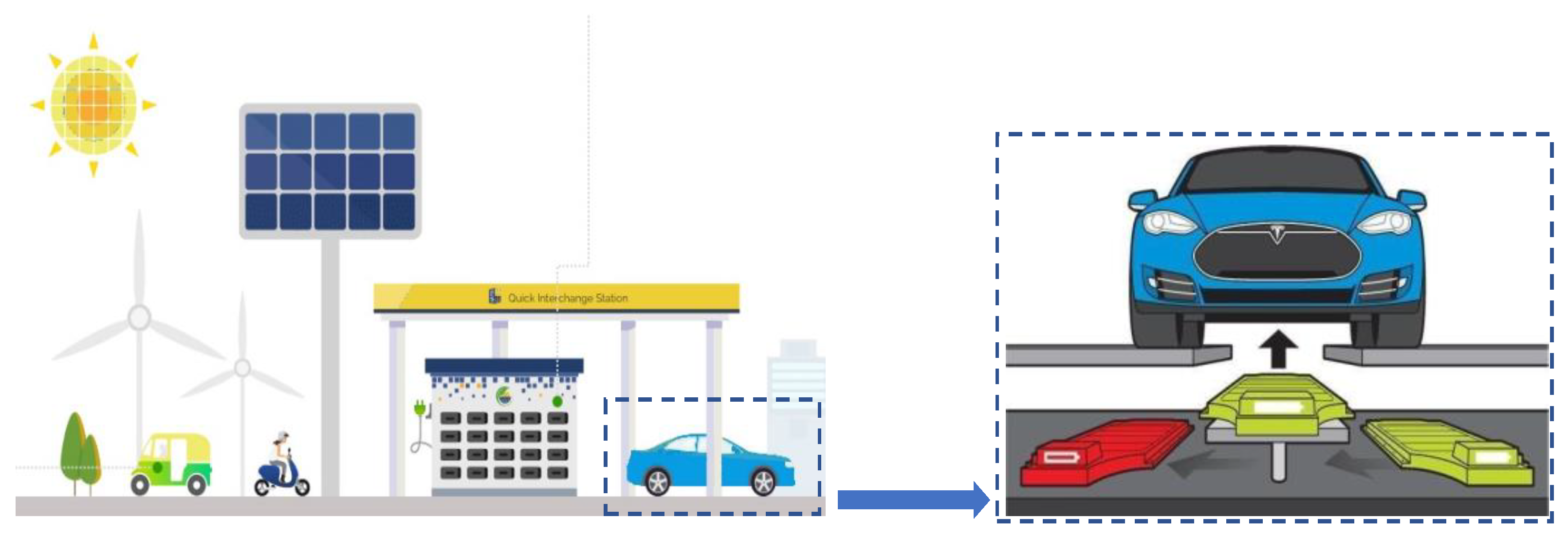
- Reserved charging demand: This feature differs this system from the regular SCS, which can supply service on a come and served basis, as the newly proposed SSCS requires online reservations in advance. All vehicle service strategies (e.g., routing and swapping battery types) can be calculated according to their origins and destinations (ODs), their initial battery power level, etc.
- Multi-type battery supplied: The SCS can only provide fully charged batteries [29], while the SSCS can provide online reservations and allow the BSS to optimally deploy their state of charge (SOC) battery.
- Accurate cost calculated: Different from a regular SCS, where the economic essence is battery leasing, the SSCS conducts energy leasing. In the pricing strategy, the SCS sets a price for each battery, while the SSCS sets a price for the process of recharging the depleted battery to the same power level as the new battery.
- Charging rate considered: In this proposed system, the recharge cost of depleted batteries is calculated by considering the battery charging rate curve. The SSCS can help achieve an optimal charging strategy and improve energy usage efficiency.
1.1. Literature Review
- The battery charging dispatch model was set up from the grid side to minimize the total cost (e.g., infrastructure deployment cost [4] and sequential decision cost [26]) while satisfying various physical constraints. Later, an increasing number of researchers began focusing on the transportation side due to the massive traffic issue and then dealt with this SCS as a vehicle routing problem (VRP) [27,36,37], location routing problem (LRP) [3,24,38], or battery dispatch management problem [15,26,29,32,39,40]. In this paper, we propose vehicle routing and battery dispatching as two vital indices for optimizing an SSCS.
- Due to technological or application limitations (i.e., an internet-based booking platform; BSS operation information processing center (IPC); centralized vehicle introduction systems) over the past few years, there are only a limited number of recent studies [27] on the BSS online reservation system that focused on various vehicle demands. This study proposes a new operational mode under a new information system (i.e., vehicles require advanced reservations and the IPC gives various service strategies).
- Most previous studies provided only a single battery type (i.e., fully charged battery) [4,36,40], and they only allow depleted batteries to be replaced by a standard SOC battery. However, some researchers have considered providing multi-type batteries, as stated in the references [15,27,29], and the introduction of varying SOC batteries gives more flexibility in optimal applications. Since our SSCS model is based on the battery charging rate, we propose an optimal operation strategy, deploying multi-type batteries simultaneously.
1.2. Contributions
- First, we propose an innovative binary programming SSCS model to balance the tradeoff between the vehicle travel cost and battery dispatching cost. This model is a linear integer problem that solves exact solutions by off-the-shelf commercial solvers (e.g., Gurobi).
- Second, we propose an optimal operation strategy for deploying multi-type batteries and simultaneously consider the charging process. In this process, a large number of various charging requests with various initial battery power levels are given various charging strategies (i.e., optimal routes to BSS and battery types). These charging strategies can help improve charging efficiency and minimize the overall system operational cost.
- Finally, a numerical example with real-world freeway data from Guangdong Province, China is conducted to demonstrate the applicability of the proposed model and its effectiveness in reducing construction costs. Overall, this paper provides valuable insights into the future integration of BSSs into long-distance freeway services and offers a numerical method for designing an optimal operational plan for this integrated system.
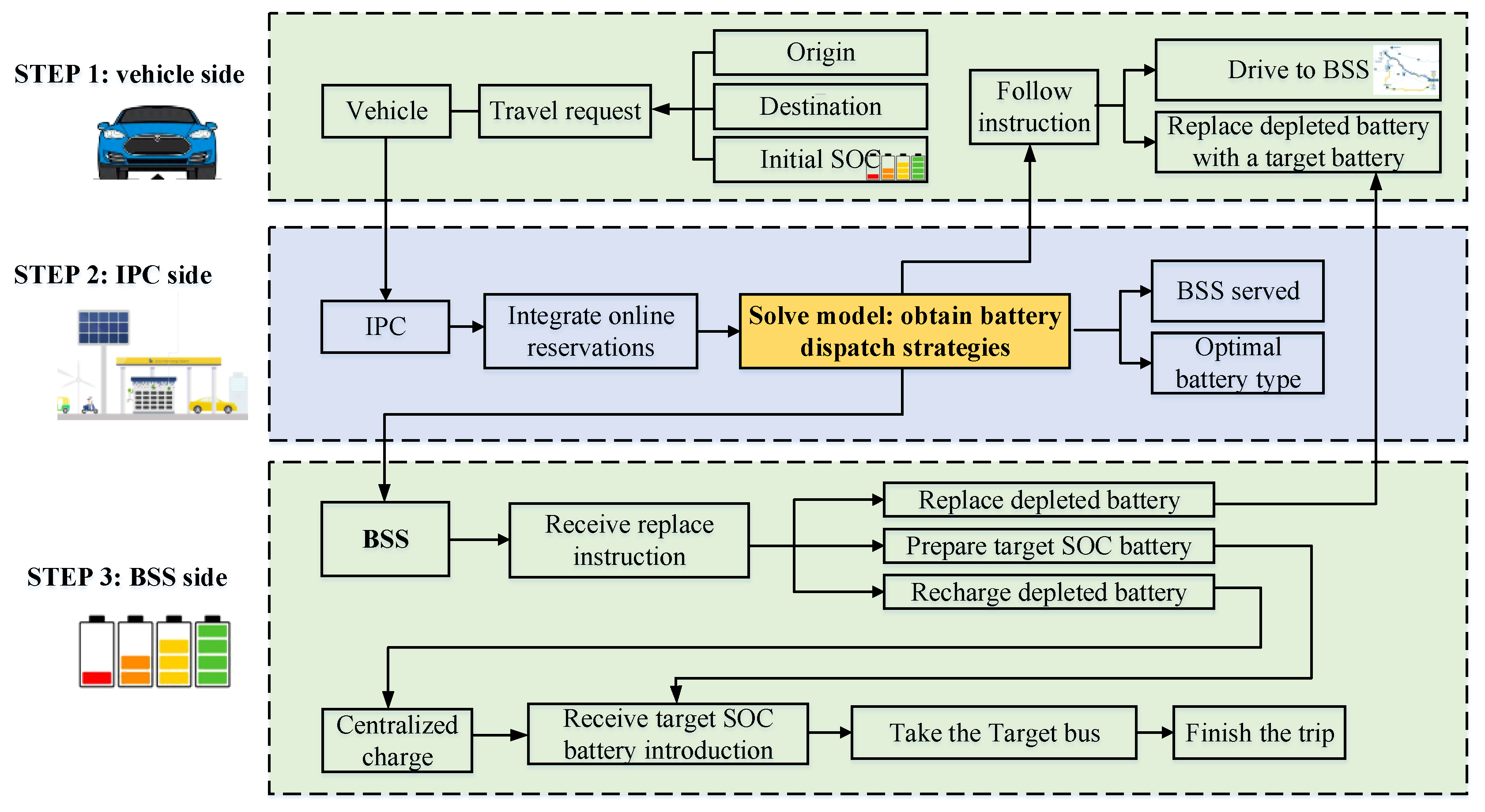
2. Model Description
3. Model Formulation
3.1. Objective Function
3.2. Constraints
3.3. Alternative Systems
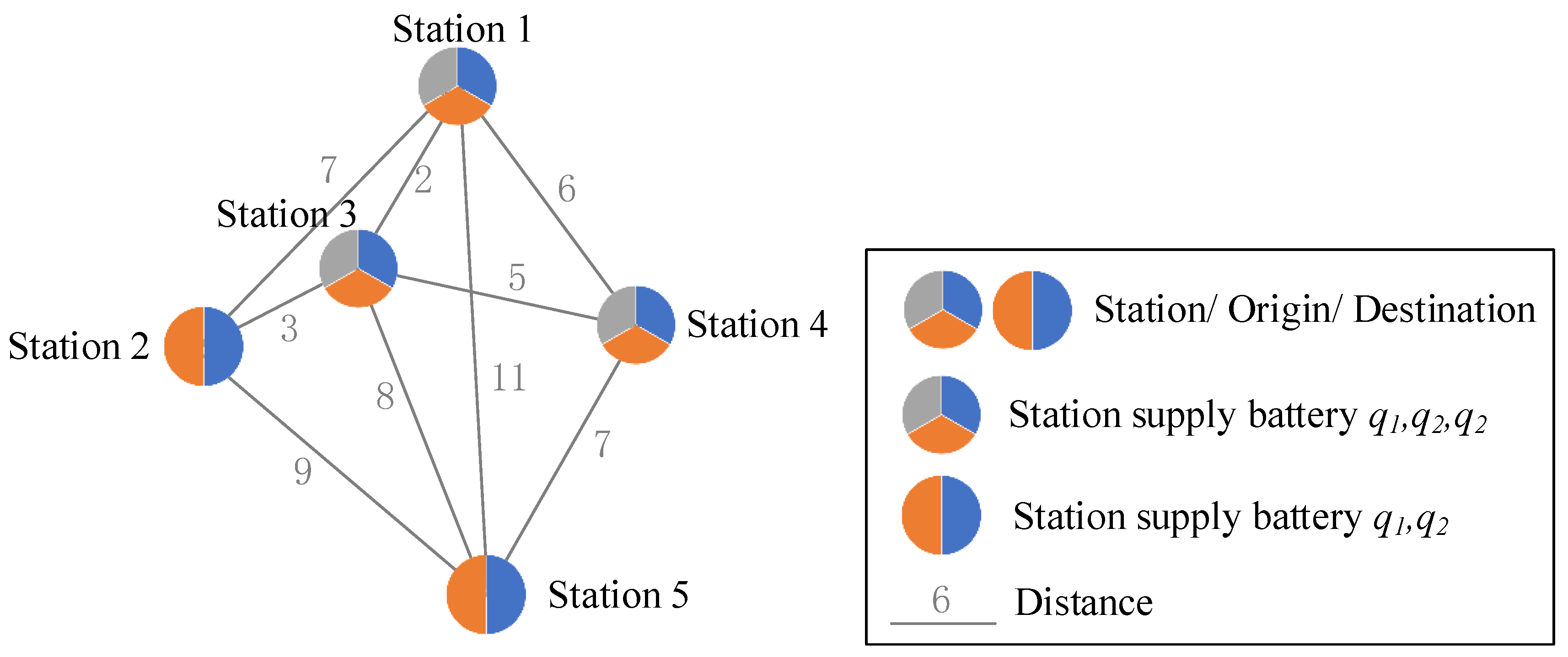
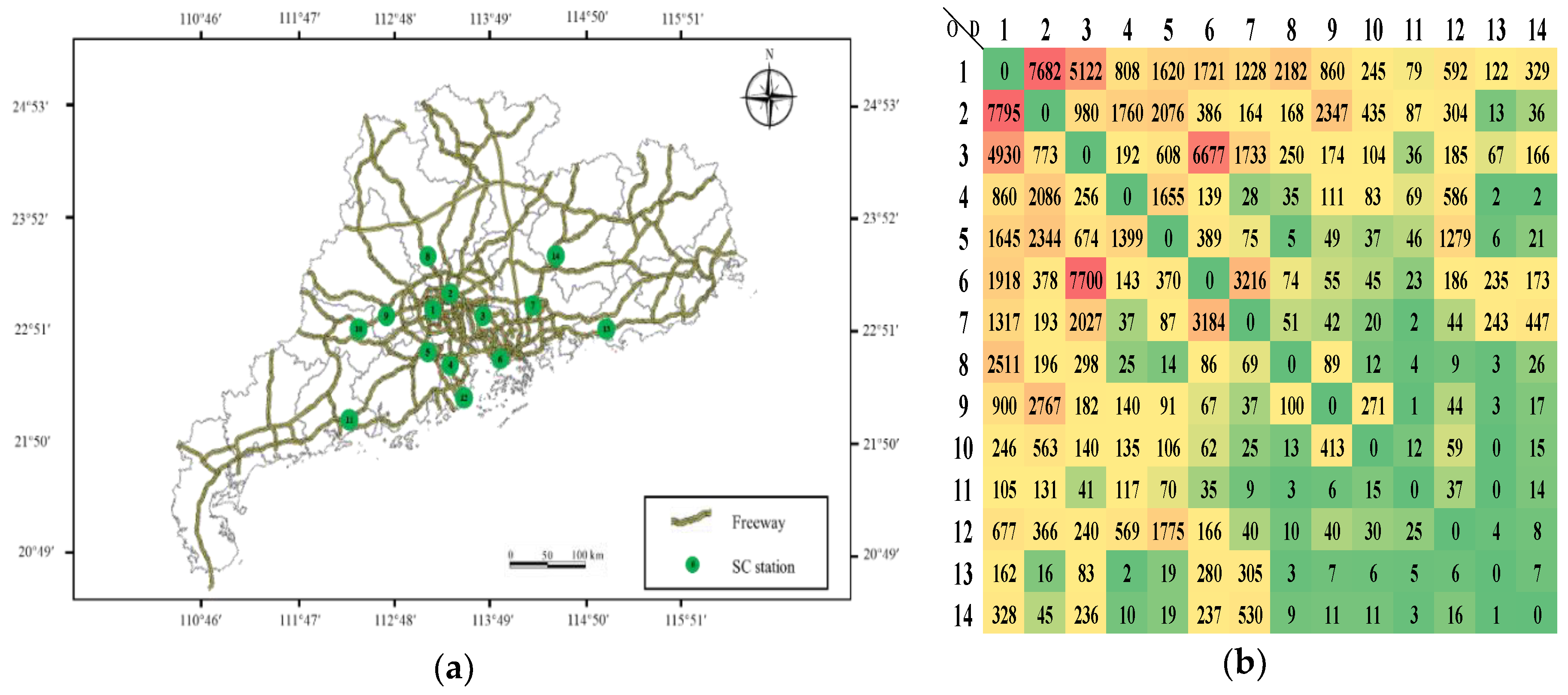
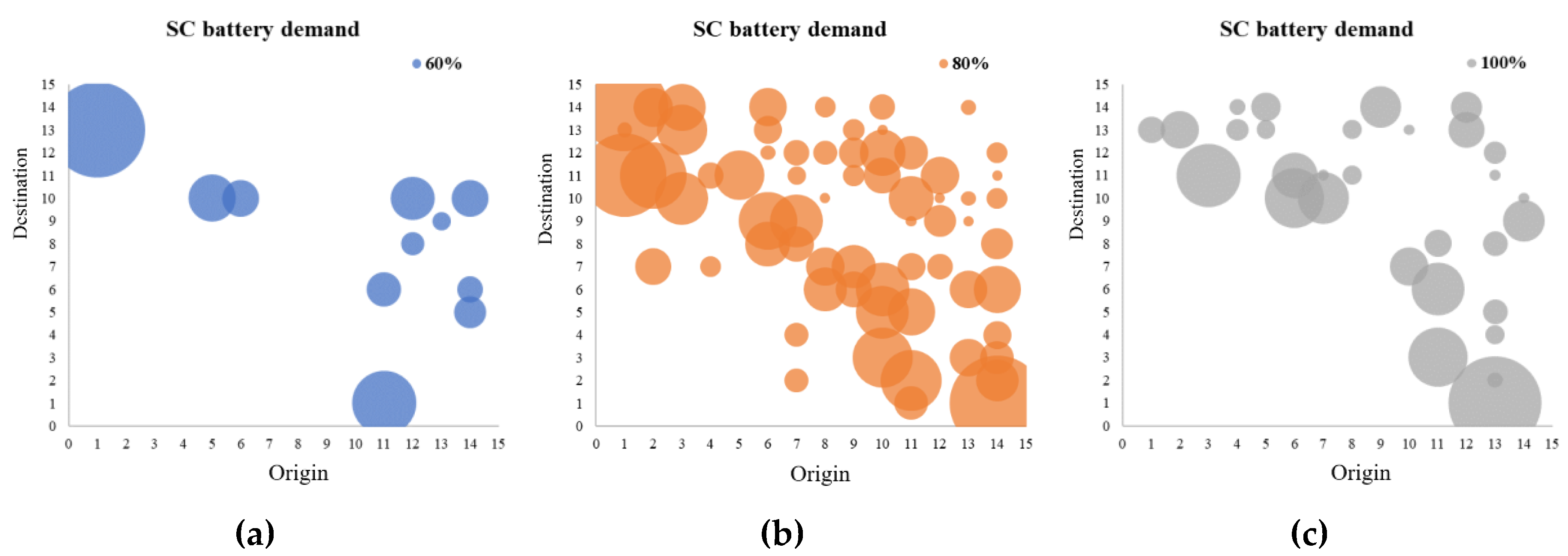
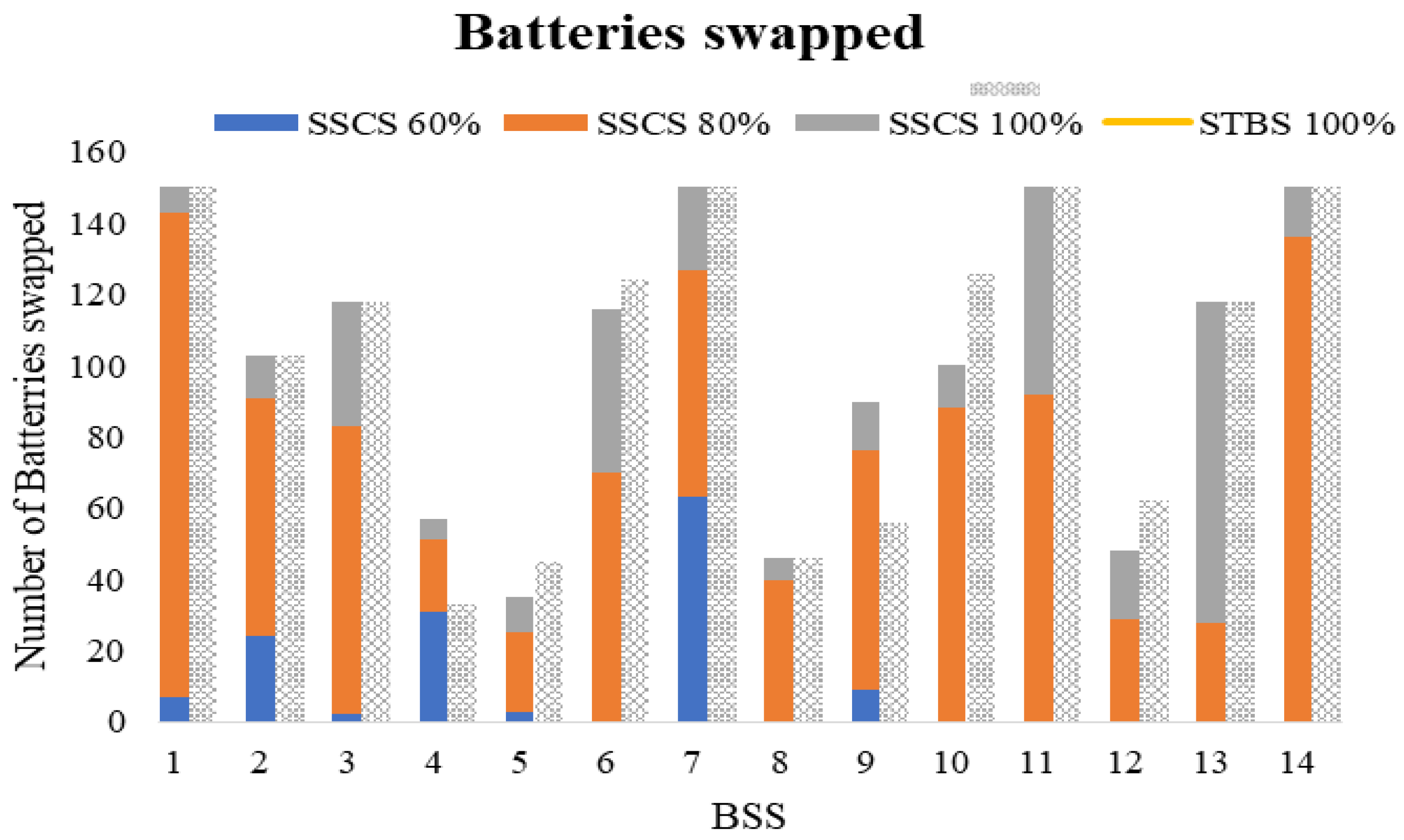
4. Numerical Example
4.1. Input Parameters
4.2. Optimal Location Result
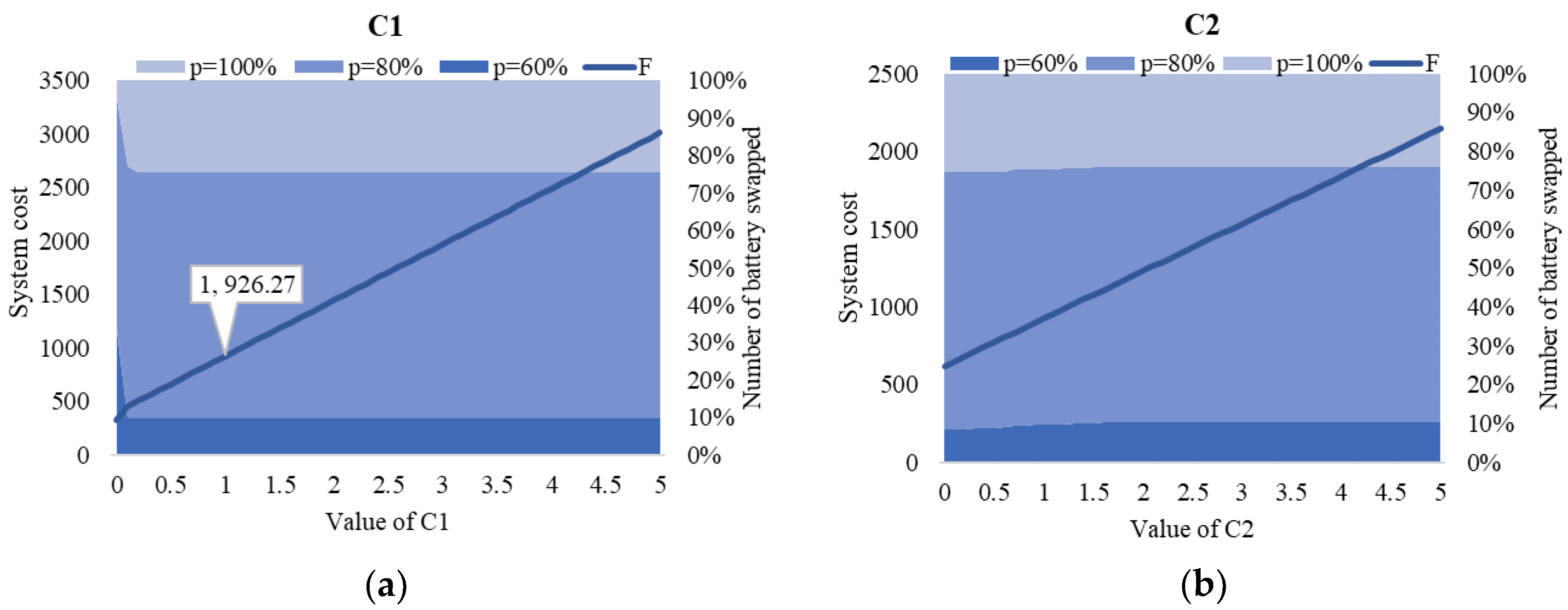
4.3. Sensitivity Analysis
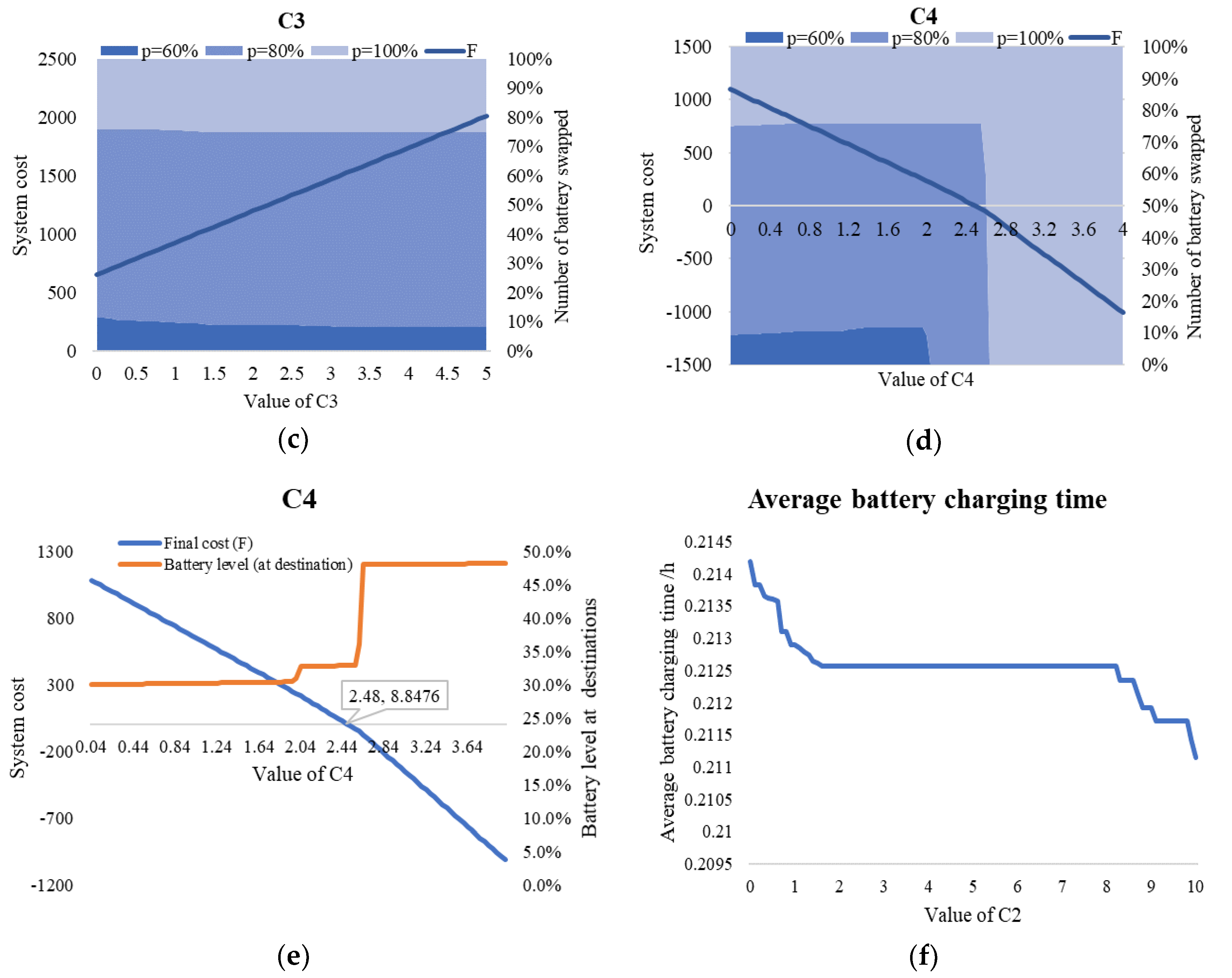
- We perform a regression analysis of , , , and with the system operational cost (simplified as ), as shown in Figure 8a–d and obtain with . This result reveals a high linear correlation with all four critical parameters.
- The optimal result of battery type performance stability with varying values of , , and is shown in Figure 8. The varying value of can change the optimal strategy significantly, as shown in Figure 8d,e. The increased value of would result in an increased number of vehicles holding more residual energy at the destination.
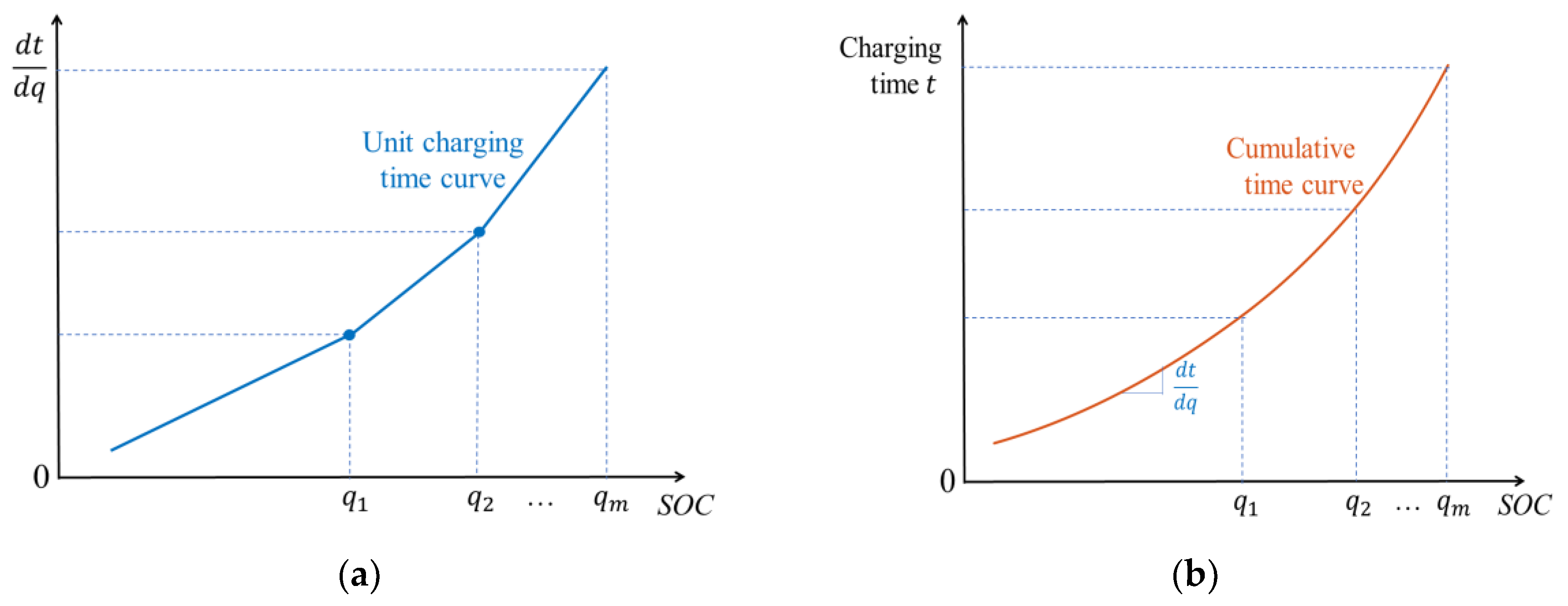
- Figure 8f shows the performance of the average battery charging time with varying . We learn that is related to the unit time cost for the battery charging process, and it reaches a plateau period when the value of is over 1.5.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, Y.; Dong, Z.Y.; Xu, Y.; Meng, K.; Zhao, J.H.; Qiu, J. Electric vehicle battery charging/swap stations in distribution systems: Comparison study and optimal planning. IEEE Trans. Power Syst. 2014, 29, 221–229. [Google Scholar] [CrossRef]
- Mechthild Wörsdörfer. Global EV Outlook 2019; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Mak, H.Y.; Rong, Y.; Shen, Z.J.M. Infrastructure planning for electric vehicles with battery swapping. Manag. Sci. 2013, 59, 1557–1575. [Google Scholar] [CrossRef] [Green Version]
- Sierzchula, W.; Bakker, S.; Maat, K.; Van Wee, B. The influence of financial incentives and other socio-economic factors on electric vehicle adoption. Energy Policy 2014, 68, 183–194. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, Z.; Chootinan, P.; Ryu, S.; Yang, C.; Wong, S.C. Transport Network Design Problem under Uncertainty: A Review and New Developments. Transp. Rev. 2011, 31, 743–768. [Google Scholar] [CrossRef] [Green Version]
- Nie, Y.; Ghamami, M. A corridor-centric approach to planning electric vehicle charging infrastructure. Transp. Res. Part B Methodol. 2013, 57, 172–190. [Google Scholar] [CrossRef]
- Deflorio, F.; Guglielmi, P.; Pinna, I.; Castello, L.; Marfull, S. Modeling and analysis of wireless “charge while driving” operations for fully electric vehicles. Transp. Res. Procedia 2015, 5, 161–174. [Google Scholar] [CrossRef] [Green Version]
- Mouhrim, N.; El Hilali Alaoui, A.; Boukachour, J. Optimal allocation of wireless power transfer system for electric vehicles in a multipath environment. In Proceedings of the 2016 3rd International Conference on Logistics Operations Management (GOL), Fez, Morocco, 23–25 May 2016. [Google Scholar]
- Liu, Z.; Song, Z. Robust planning of dynamic wireless charging infrastructure for battery electric buses. Transp. Res. Part C Emerg. Technol. 2017, 83, 77–103. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Yin, J.; Cui, J.; Yang, L.; An, S. An integrated framework for electric vehicle rebalancing and staff relocation in one-way carsharing systems: Model formulation and Lagrangian relaxation-based solution approach. Transp. Res. Part B Methodol. 2018, 117, 542–572. [Google Scholar] [CrossRef]
- Ko, Y.D.; Jang, Y.J.; Lee, M.S. The optimal economic design of the wireless powered intelligent transportation system using genetic algorithm considering nonlinear cost function. Comput. Ind. Eng. 2015, 89, 67–79. [Google Scholar] [CrossRef]
- Yatnalkar, G.; Narman, H. Survey on Wireless Charging and Placement of Stations for Electric Vehicles. In Proceedings of the 2018 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Louisville, KY, USA, 6–8 December2018; pp. 526–531. [Google Scholar]
- Chen, Z.; He, F.; Yin, Y. Optimal deployment of charging lanes for electric vehicles in transportation networks. Transp. Res. Part B Methodol. 2016, 91, 344–365. [Google Scholar] [CrossRef] [Green Version]
- Sepetanc, K.; Pandzic, H. A Cluster-Based Operation Model of Aggregated Battery Swapping Stations. IEEE Trans. Power Syst. 2020, 1, 249–260. [Google Scholar] [CrossRef]
- Bansal, P. Charging of Electric Vehicles: Technology and Policy Implications. J. Sci. Policy Gov. 2015, 6, 1–20. [Google Scholar]
- Machura, P.; Li, Q. A critical review on wireless charging for electric vehicles. Renew. Sustain. Energy Rev. 2019, 104, 209–234. [Google Scholar] [CrossRef] [Green Version]
- Jang, Y.J. Survey of the operation and system study on wireless charging electric vehicle systems. Transp. Res. Part C Emerg. Technol. 2018, 95, 844–866. [Google Scholar] [CrossRef]
- Yang, J.; Guo, F.; Zhang, M. Optimal planning of swapping/charging station network with customer satisfaction. Transp. Res. Part E Logist. Transp. Rev. 2017, 103, 174–197. [Google Scholar] [CrossRef]
- Schneider, F.; Thonemann, U.W.; Klabjan, D. Optimization of battery charging and purchasing at electric vehicle battery swap stations. Transp. Sci. 2018, 52, 1211–1234. [Google Scholar] [CrossRef]
- Du, J.; Ouyang, M. Review of electric vehicle technologies progress and development prospect in China. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–8. [Google Scholar]
- Pérez, J.M.G. Emerging Technologies for Electric and Hybrid Vehicles; MDPI: Basel, Switzerland, 2018; ISBN 3038971901. [Google Scholar]
- Mohamed, A.A.S.; Meintz, A.; Zhu, L. System Design and Optimization of In-Route Wireless Charging Infrastructure for Shared Automated Electric Vehicles. IEEE Access 2019, 7, 79968–79979. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transp. Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Hosny, M.; Demir, E.; Genikomsakis, K.N.; Cheikhrouhou, N. The dial-a-ride problem with electric vehicles and battery swapping stations. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 392–420. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Yao, J.; Kang, T.; Zhu, X. Dynamic operation model of the battery swapping station for EV (electric vehicle) in electricity market. Energy 2014, 65, 544–549. [Google Scholar] [CrossRef]
- Adler, J.D.; Mirchandani, P.B. Online routing and battery reservations for electric vehicles with swappable batteries. Transp. Res. Part B Methodol. 2014, 70, 285–302. [Google Scholar] [CrossRef]
- Adegbohun, F.; von Jouanne, A.; Lee, K.Y. Autonomous battery swapping system and methodologies of electric vehicles. Energies 2019, 12, 667. [Google Scholar] [CrossRef] [Green Version]
- Ding, T.; Bai, J.; Du, P.; Qin, B.; Li, F.; Ma, J.; Dong, Z. Rectangle packing problem for battery charging dispatch considering uninterrupted discrete charging rate. IEEE Trans. Power Syst. 2019, 34, 2472–2475. [Google Scholar] [CrossRef]
- Kang, Q.; Wang, J.; Zhou, M.; Ammari, A.C. Centralized Charging Strategy and Scheduling Algorithm for Electric Vehicles under a Battery Swapping Scenario. IEEE Trans. Intell. Transp. Syst. 2016, 17, 659–669. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Ma, K.; Yang, B. Optimal Dispatching Strategy for Shared Battery Station of Electric Vehicle by Divisional Battery Control. IEEE Access 2019, 7, 38224–38235. [Google Scholar] [CrossRef]
- Sun, B.; Sun, X.; Tsang, D.H.K.; Whitt, W. Optimal battery purchasing and charging strategy at electric vehicle battery swap stations. Eur. J. Oper. Res. 2019, 279, 524–539. [Google Scholar] [CrossRef]
- He, F.; Yin, Y.; Lawphongpanich, S. Network equilibrium models with battery electric vehicles. Transp. Res. Part B Methodol. 2014, 67, 306–319. [Google Scholar] [CrossRef]
- He, F.; Wu, D.; Yin, Y.; Guan, Y. Optimal deployment of public charging stations for plug-in hybrid electric vehicles. Transp. Res. Part B Methodol. 2013, 47, 87–101. [Google Scholar] [CrossRef]
- Worley, O.; Klabjan, D. Optimization of battery charging and purchasing at electric vehicle battery swap stations. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–4. [Google Scholar]
- Jie, W.; Yang, J.; Zhang, M.; Huang, Y. The two-echelon capacitated electric vehicle routing problem with battery swapping stations: Formulation and efficient methodology. Eur. J. Oper. Res. 2019, 272, 879–904. [Google Scholar] [CrossRef]
- Chen, J.; Qi, M.; Miao, L. The Electric Vehicle Routing Problem with Time Windows and Battery Swapping Stations. IEEE Int. Conf. Ind. Eng. Eng. Manag. 2016, 2016, 712–716. [Google Scholar]
- Amiri, S.S.; Jadid, S.; Saboori, H. Multi-objective optimum charging management of electric vehicles through battery swapping stations. Energy 2018, 165, 549–562. [Google Scholar] [CrossRef]
- Widrick, R.S.; Nurre, S.G.; Robbins, M.J. Optimal policies for the management of an electric vehicle battery swap station. Transp. Sci. 2018, 52, 59–79. [Google Scholar] [CrossRef]
- Infante, W.; Ma, J.; Han, X.; Liebman, A. Optimal Recourse Strategy for Battery Swapping Stations Considering Electric Vehicle Uncertainty. IEEE Trans. Intell. Transp. Syst. 2019, 1–11. [Google Scholar] [CrossRef]
- Ouyang, D.; Chen, M.; Liu, J.; Wei, R.; Weng, J.; Wang, J. Investigation of a commercial lithium-ion battery under overcharge/over-discharge failure conditions. RSC Adv. 2018, 8, 33414–33424. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Liu, W.; Yin, Y. Deployment of stationary and dynamic charging infrastructure for electric vehicles along traffic corridors. Transp. Res. Part C Emerg. Technol. 2017, 77, 185–206. [Google Scholar] [CrossRef] [Green Version]
- Koç, Ç.; Jabali, O.; Mendoza, J.E.; Laporte, G. The electric vehicle routing problem with shared charging stations. Int. Trans. Oper. Res. 2019, 26, 1211–1243. [Google Scholar] [CrossRef]
- Wu, X.; Freese, D.; Cabrera, A.; Kitch, W.A. Electric vehicles’ energy consumption measurement and estimation. Transp. Res. Part D Transp. Environ. 2015, 34, 52–67. [Google Scholar] [CrossRef]
- Smith, O.J.; Boland, N.; Waterer, H. Solving shortest path problems with a weight constraint and replenishment arcs. Comput. Oper. Res. 2012, 39, 964–984. [Google Scholar] [CrossRef] [Green Version]
- Laporte, G.; Pascoal, M.M.B. Minimum cost path problems with relays. Comput. Oper. Res. 2011, 38, 165–173. [Google Scholar] [CrossRef]
- Hwang, I.; Jang, Y.J.; Ko, Y.D.; Lee, M.S. System Optimization for Dynamic Wireless Charging Electric Vehicles Operating in a Multiple-Route Environment. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1709–1726. [Google Scholar] [CrossRef]
- Cochran, J.J.; Cox, L.A.; Keskinocak, P.; Kharoufeh, J.P.; Smith, J.C.; Linderoth, J.T.; Lodi, A. MILP Software. In Wiley Encyclopedia of Operations Research and Management Science; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, Y.; D’Ariano, A.; He, B.; Peng, Q. Microscopic optimization model and algorithm for integrating train timetabling and track maintenance task scheduling. Transp. Res. Part B Methodol. 2019, 127, 237–278. [Google Scholar] [CrossRef]
- Fuentes, M.; Cadarso, L.; Marín, Á. A hybrid model for crew scheduling in rail rapid transit networks. Transp. Res. Part B Methodol. 2019, 125, 248–265. [Google Scholar] [CrossRef]
| EV Type | Charging Mode | Power Refill Rate * | Infrastructure Cost | Operation Cost | Usage Scenarios ** | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| PEV | Slow charging | 30–75 miles/h | L | L | Home/workplace | Cheap and safe | Long charging time |
| Rapid charging | 180 miles/h | H | M | Public charging stations | Charge rapidly; not very expensive | Long charging time; powerful cooling systems required | |
| WCEV | Dynamic charging | − | VH | VH | Designed to use on heavy load traffic corridor/ freeway | Charging while moving; without range anxiety | Extremely high investment cost |
| Static charging | 20 to 100 miles/h | H | H | Public charging stations | Wireless | Long charging time | |
| SCEV | Centralized battery charging | Swap time can be less than a minute | M | M | Public swap charging stations | Shorten charge time sharply; centralized charging | Battery ownership, purchase cost, standardization, and safety issues in the swap and charge process |
| EV Type | System Mode | Operation Mode | Battery Type ** | Average SC Cost | Charging Rate | Average Charging Cost | Residual Value | Capacity of BSS |
|---|---|---|---|---|---|---|---|---|
| SCEV | SCS | Come and served | Single | M | − | M | − | − |
| SSCS (this paper) | Reserved online in advance | Multiple | L | • | L | • | • |
| Authors | Objective Function | Decision Variable | Battery Type | Online Reservation | Various Demands | Battery Charging Rate | Capacity of BSS | Model Approach |
|---|---|---|---|---|---|---|---|---|
| Mak et al. (2013) [4] | Building and operating costs | Infrastructure deployment | S | − | − | − | − | MISOCP |
| Adler and Mirchandani (2014) [27] | Average delay | VRP and battery dispatch | S | • | − | − | • | DP |
| Yang et al. (2014) [26] | Battery management | Sequential decision | M | − | − | − | − | Simulation |
| Yang and Sun (2015) [3] | Construction and routing cost | LRP | S | − | − | − | − | MIP |
| Chen et al. (2017) [37] | Travel distance | VRP | S | − | − | − | − | MIP |
| Hof et al. (2017) [24] | Construction and routing cost | LRP | S | − | − | − | − | MIP |
| Amiri et al. (2018) [38] | Total charging cost | LRP | S | − | − | − | • | MINLP |
| Widrick et al. (2018) [39] | Total reward | Battery dispatch | S | − | − | − | • | DP |
| Ding et al. (2019) [29] | Total profit | Battery dispatch | M | − | − | • | • | MIP |
| Jie et al. (2019) [36] | System cost | VRP | S | − | − | − | − | IP |
| Infante et al. (2019) [40] | Minimum recourse | Battery dispatch | S | − | − | − | • | MILP |
| Sun et al. (2019) [32] | Battery investment and operating cost | Battery dispatch | S | − | − | − | • | Fluid model |
| Šepetanc and Pandžić (2020) [15] | Total profit | Battery dispatch and pricing | M | − | − | − | • | MILP |
| This paper | System operational cost | VRP and battery dispatch | M | • | • | • | • | IP |
| Sets | |
| Set of the vehicle trip characteristic index, | |
| Set of vehicle stations (i.e., origin stations and destinations), | |
| Set of the shared BSS index, | |
| Set of varying SOCs that shared the BSS provided, | |
| Parameters | |
| Index of the vehicle trip characteristics, | |
| Shared BSS index, | |
| Origin for vehicle trip characteristic index | |
| Destination for vehicle trip characteristic index | |
| Initial battery SOC for vehicle trip characteristic index | |
| Battery SOC that shared the BSS provided, | |
| Battery capacity of the shared BSS provided for the vehicle trip characteristic index . | |
| Travel distance between station to station | |
| Distance for charging detour, | |
| Unit detour cost, Yuan/km | |
| Unit time cost for battery charging process, Yuan/min | |
| Unit power cost for battery charging process, Yuan/kW | |
| Unit power salvage value in the battery, Yuan/kW | |
| Unit energy consumption per kilometer, kW/km | |
| Formula of the battery charging time rate with varying SOC | |
| Lower band of the battery SOC | |
| Swapping battery supplement at station , with battery SOC | |
| Decision variables | |
| Binary variables, when vehicle goes to power station and the battery is replaced by a new battery with power quantity ; otherwise | |
| Parameter | Description | Value | Data Source |
|---|---|---|---|
| Unit detour cost | 1 Yuan/km | EV travel cost (https://afdc.energy.gov/fuels/) | |
| Unit time cost | 1 Yuan/h | Guangzhou Municipal Human Resources and Social Security Bureau reports in 2019 (http://gzrsj.hrssgz.gov.cn/english/) | |
| Unit power cost | 1 Yuan/kW | Electricity price in China (https://www.ceicdata.com/china/electricity-price) | |
| Unit power salvage value | 0.4 Yuan/kW | Related to the PEV charging price (https://afdc.energy.gov/fuels/electricity_charging) | |
| Unit energy consumption/km | 0.25%/km | Most EVs are currently capable of approximately 100–250 miles of driving before they need to charge (Data source: UC Davis; https://phev.ucdavis.edu/) | |
| Average vehicle travel speed in km/h | 100 km/h | The operating speed of EVs on the freeway (http://www.0512s.com/lukuang/G94.html) | |
| Lower battery power limit | 20% | Safety suggestion from EV enterprises (e.g., Beijing Automotive Group Co., etc.) |
| SSCS | STBS | |||
|---|---|---|---|---|
| Evaluation Criteria | SOC | Multi-Type | Rate ** | |
| 60% | 139 | − | − |
| 80% | 940 | − | − | |
| 100% | 352 | 1431 | − | |
| 32.1% | 65% | 2.025 | |
| 83.0% | 100% | 1.205 | |
| 50.9% | 35% | 0.687 | |
| 30.0% | 46% | 1.533 | |
| 53% | 54% | 1.019 | |
| 926.3 | 1428.9 | 1.543 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, L.; Pei, M. Optimal Design for a Shared Swap Charging System Considering the Electric Vehicle Battery Charging Rate. Energies 2020, 13, 1213. https://doi.org/10.3390/en13051213
Zhong L, Pei M. Optimal Design for a Shared Swap Charging System Considering the Electric Vehicle Battery Charging Rate. Energies. 2020; 13(5):1213. https://doi.org/10.3390/en13051213
Chicago/Turabian StyleZhong, Lingshu, and Mingyang Pei. 2020. "Optimal Design for a Shared Swap Charging System Considering the Electric Vehicle Battery Charging Rate" Energies 13, no. 5: 1213. https://doi.org/10.3390/en13051213
APA StyleZhong, L., & Pei, M. (2020). Optimal Design for a Shared Swap Charging System Considering the Electric Vehicle Battery Charging Rate. Energies, 13(5), 1213. https://doi.org/10.3390/en13051213






