Analysis of Approaches for Modeling the Low Frequency Emission of LED Lamps
Abstract
:1. Introduction
2. Rationale of the Development and Evaluation of Time and Frequency Domain Models
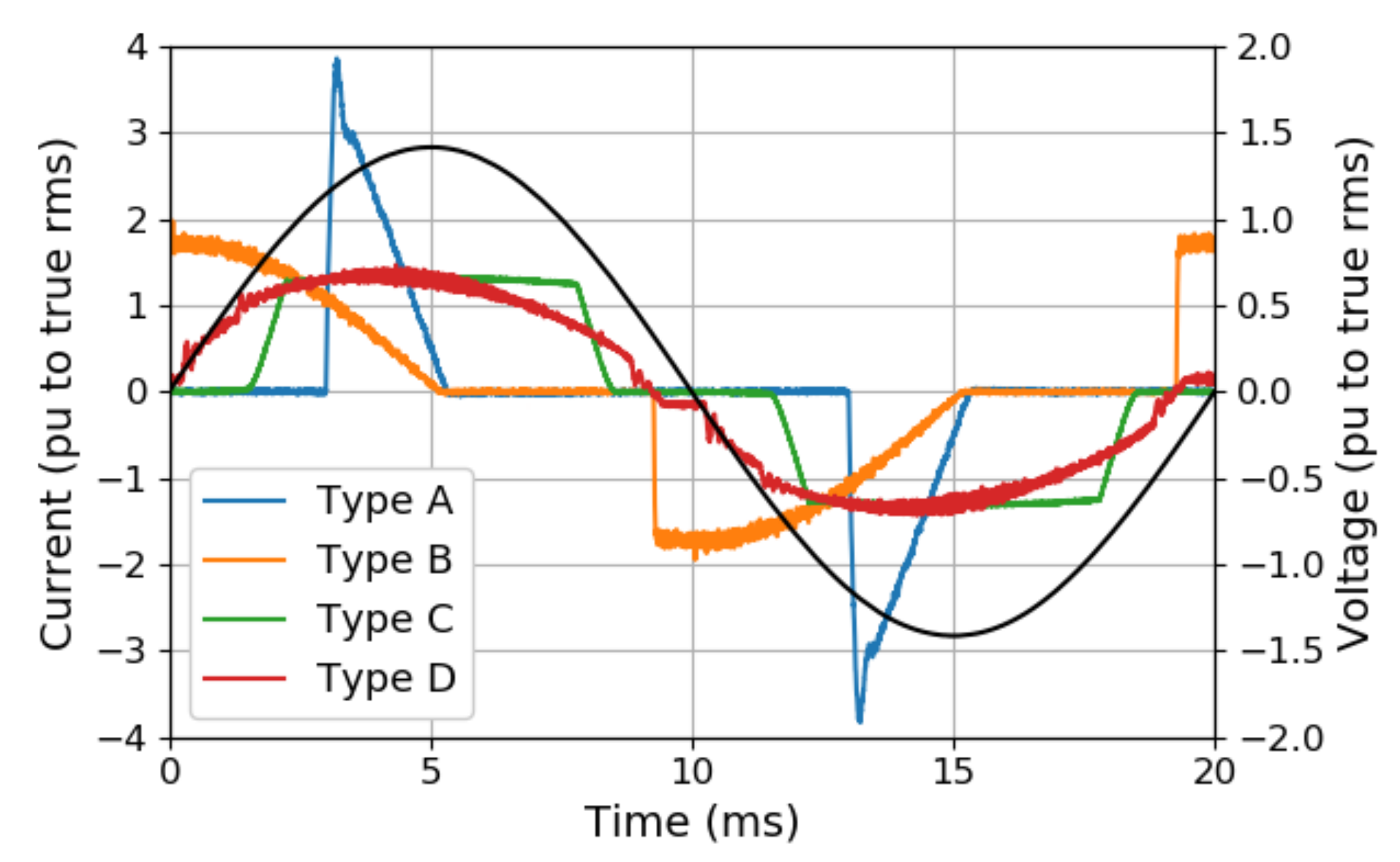
2.1. LED Lamp Set
- Type A: consists of a full-wave rectifier with bulk smoothing capacitor and DC-DC switch-mode converter;
- Type B: consists of a simple capacitor divider formed across a full-wave rectifier circuit;
- Type C: consists of a full-wave rectifier loaded by a constant current regulator (CCR);
- Type D: includes a switch-mode driver circuit with active power factor correction (aPFC), which can be either a single-stage or a double-stage converter.
2.2. Characteristic Voltage Waveforms for Test Points Definition
2.3. Model Performance Evaluation
3. Time Domain Models
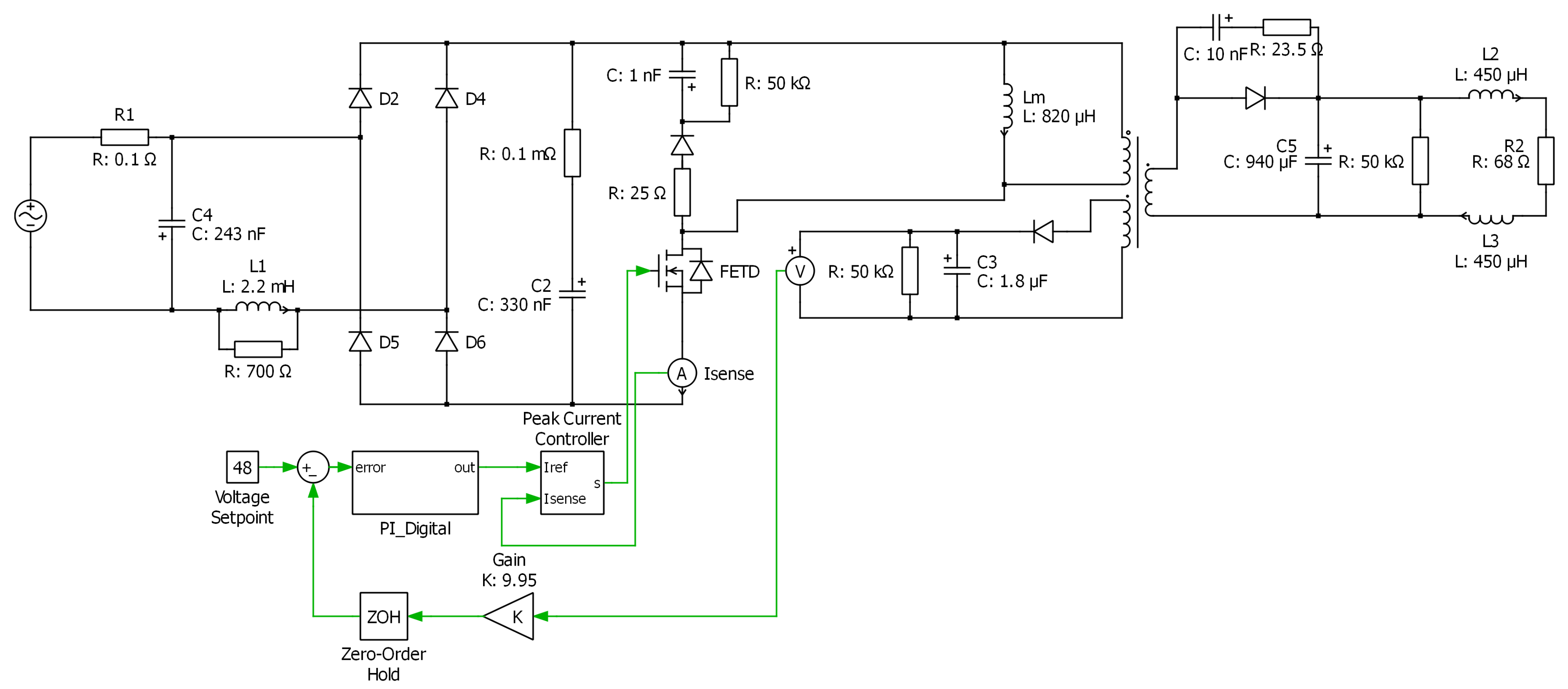
3.1. Time Domain Model Development
- In the first stage, the key components of the topology and functionality of the circuit should be identified. This can be achieved by reverse engineering of the lamp or using a priori knowledge of the relationship between current waveform shape and specific circuitry;
- In the second stage, values for the key components should be obtained. This can be performed either by reverse engineering of the lamp or by a parameter estimation technique.
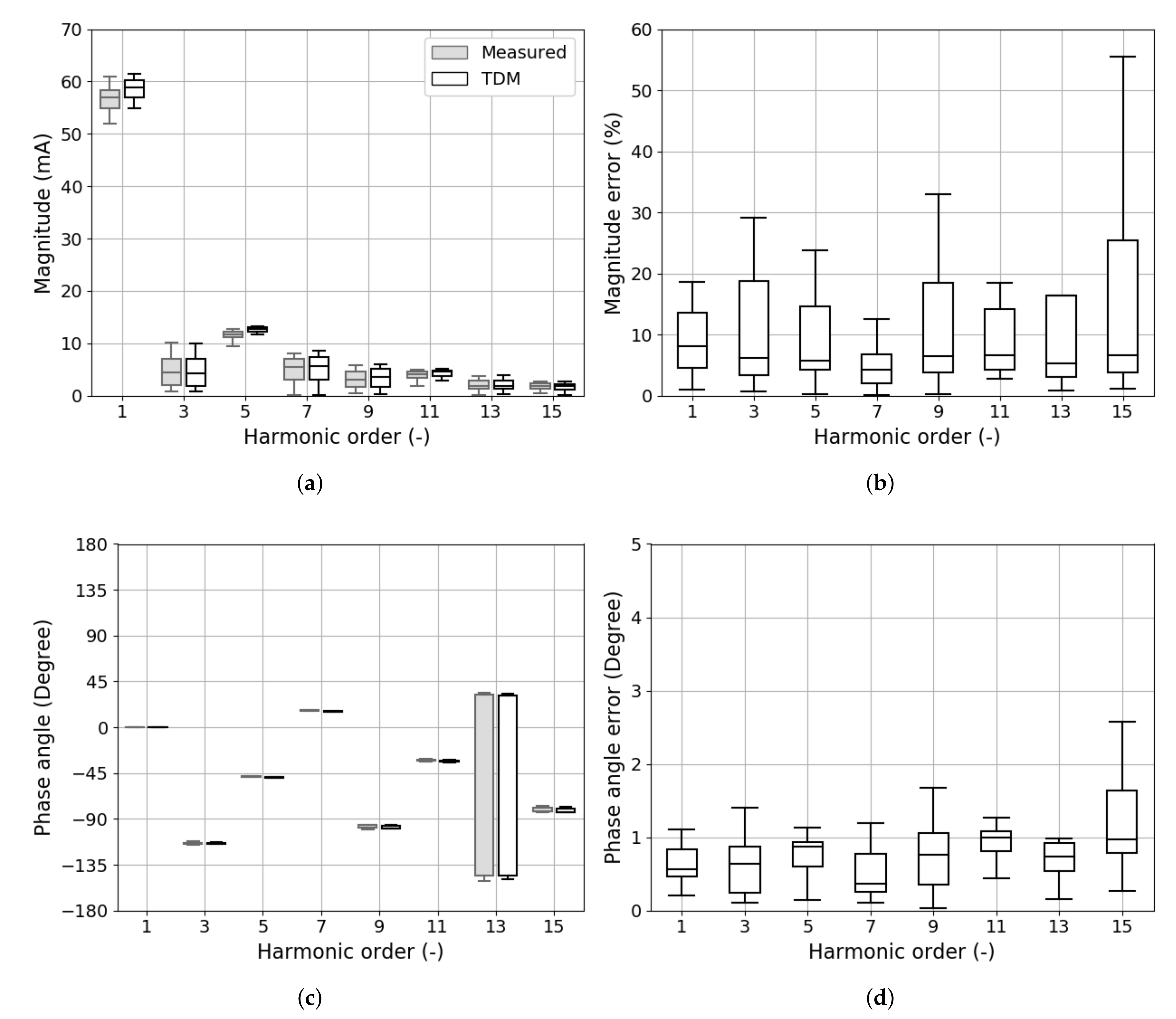
3.2. Time Domain Model Evaluation
3.3. Results
3.3.1. Type A
3.3.2. Type B
3.3.3. Type C
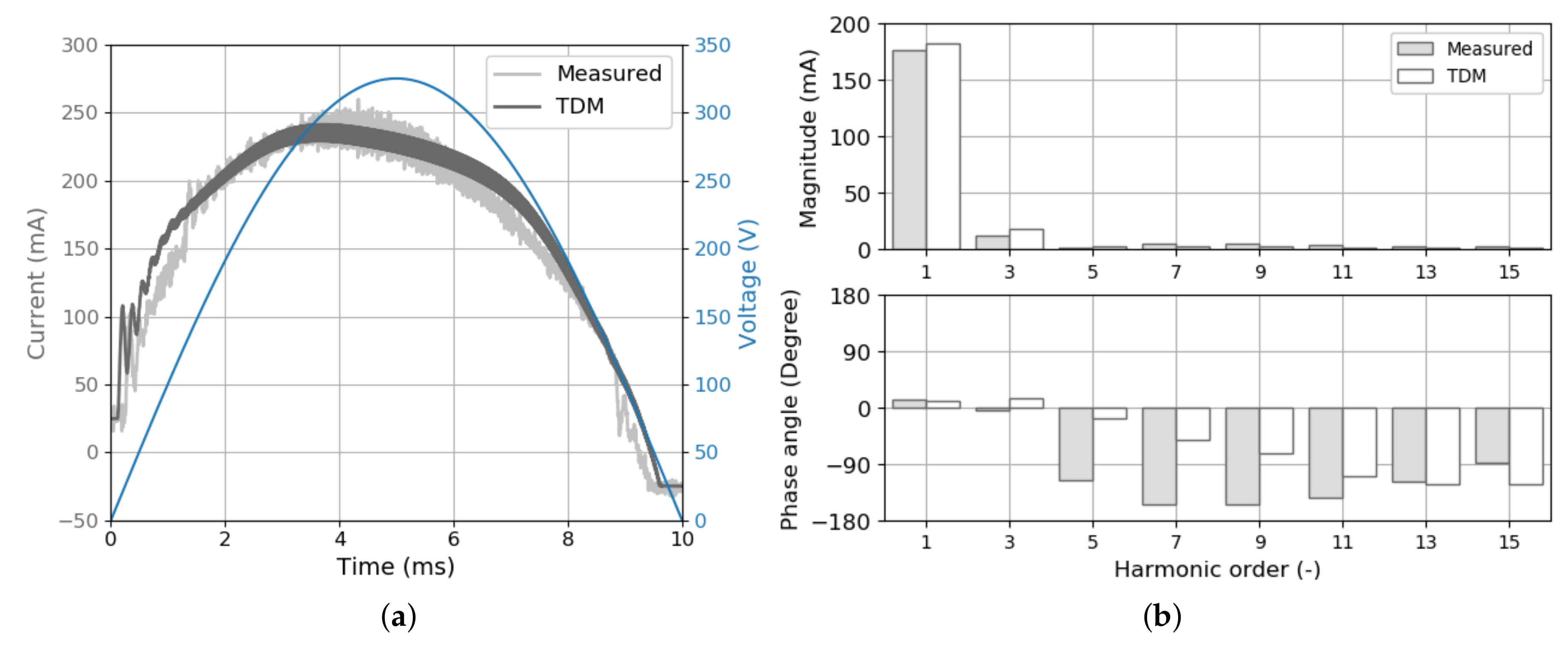
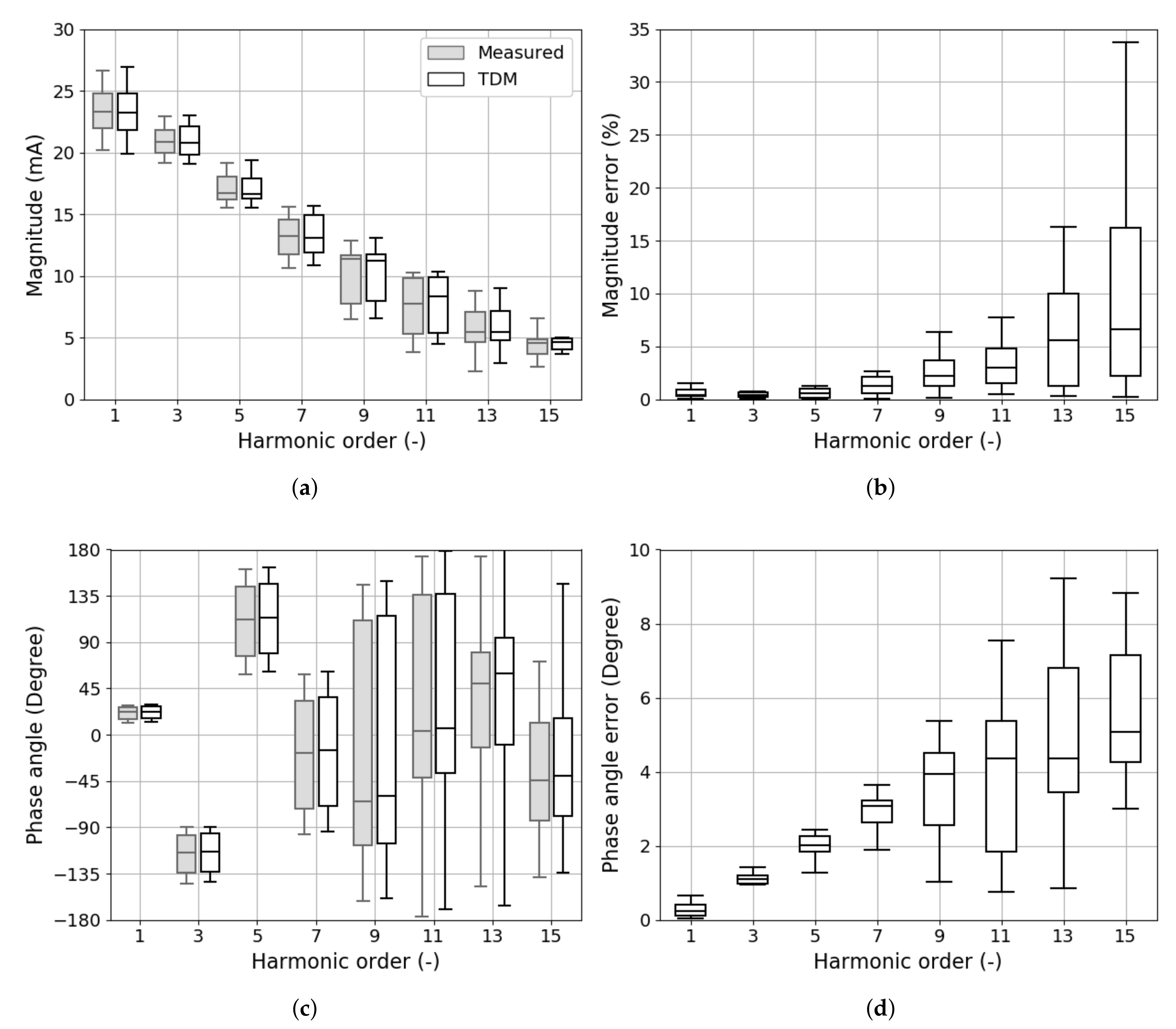
3.3.4. Type D
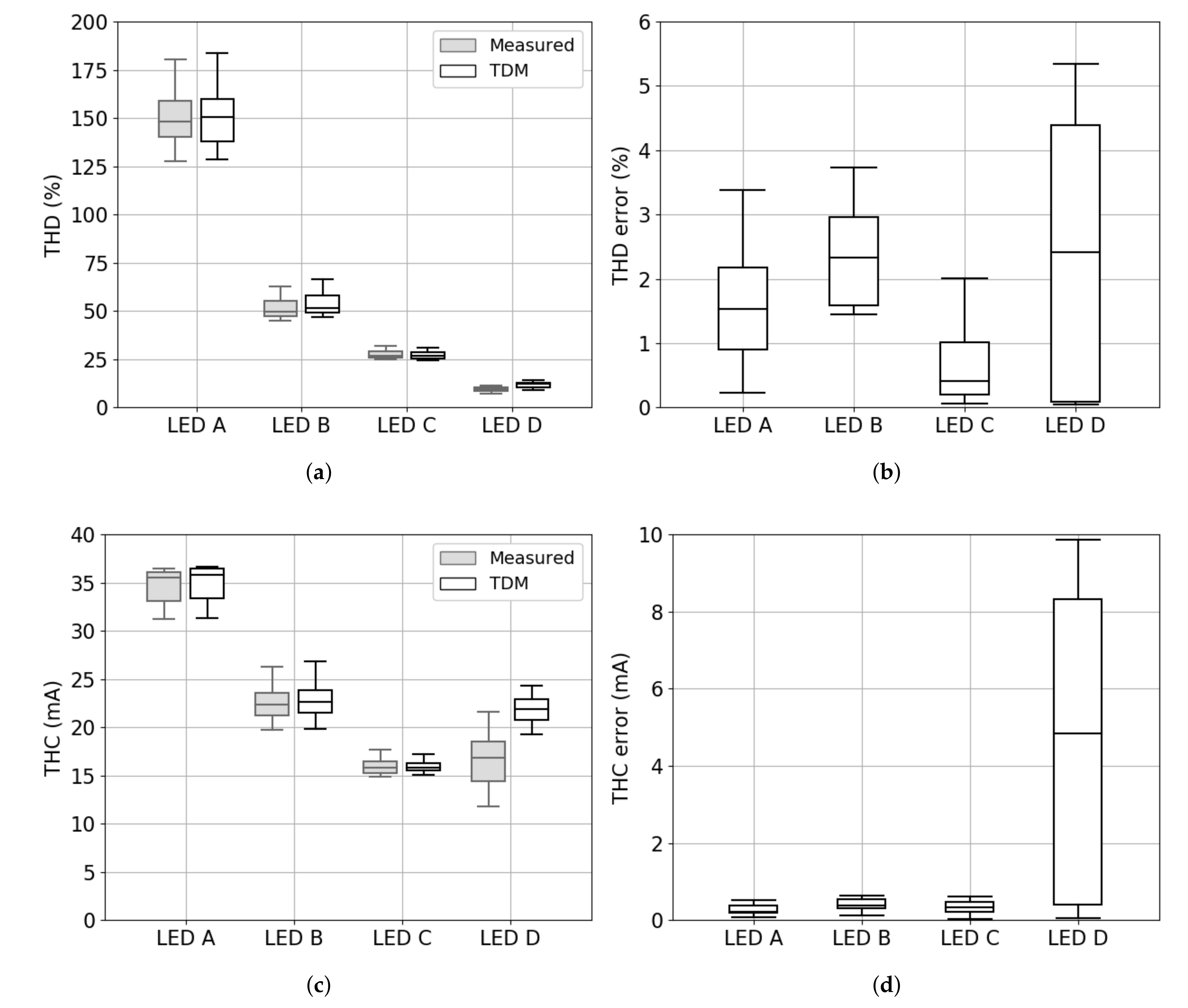
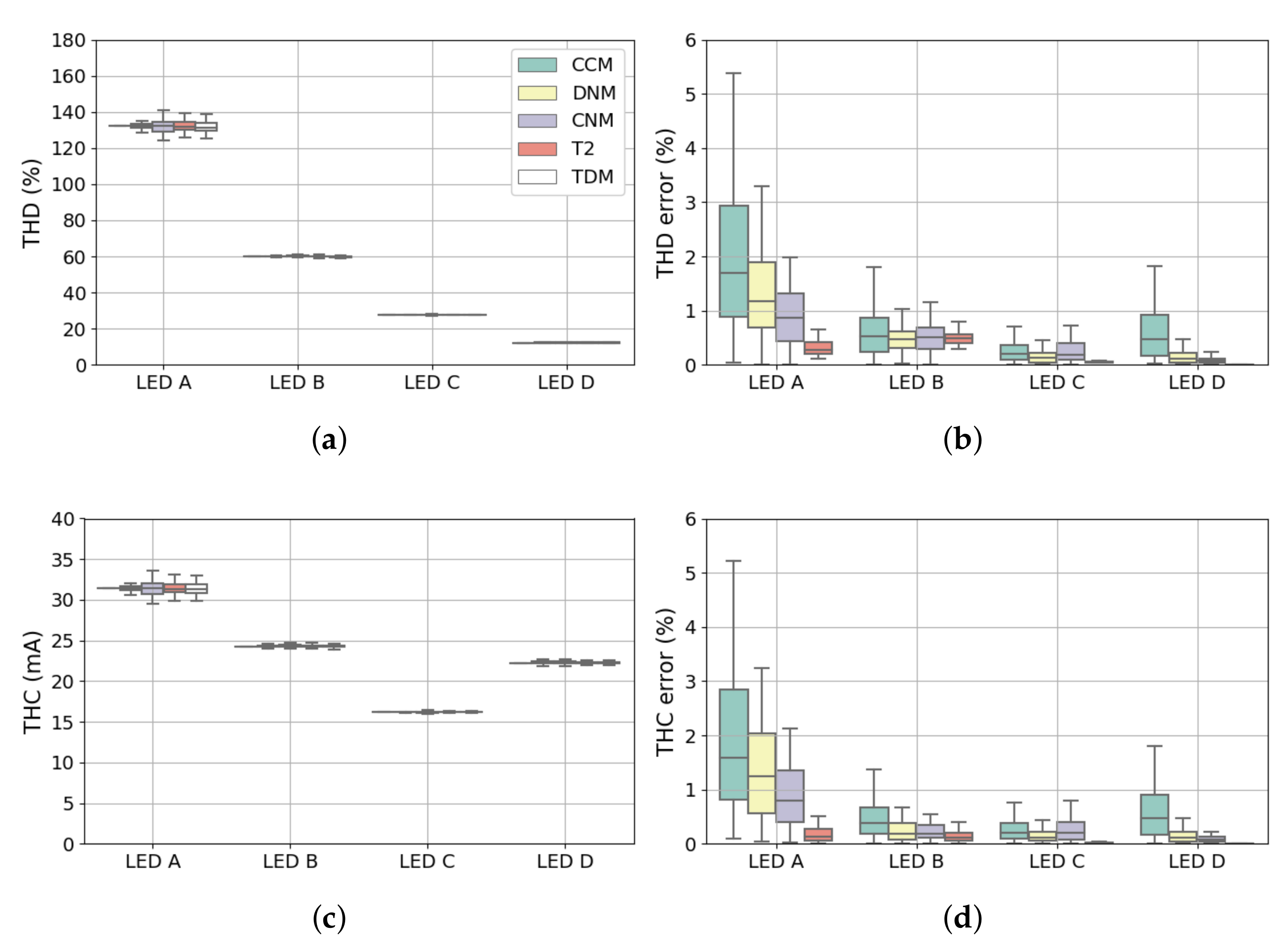
3.4. Total Distortion Indices
4. Frequency Domain Modeling
4.1. Frequency Domain Model Development
4.2. Frequency Domain Model Assessment
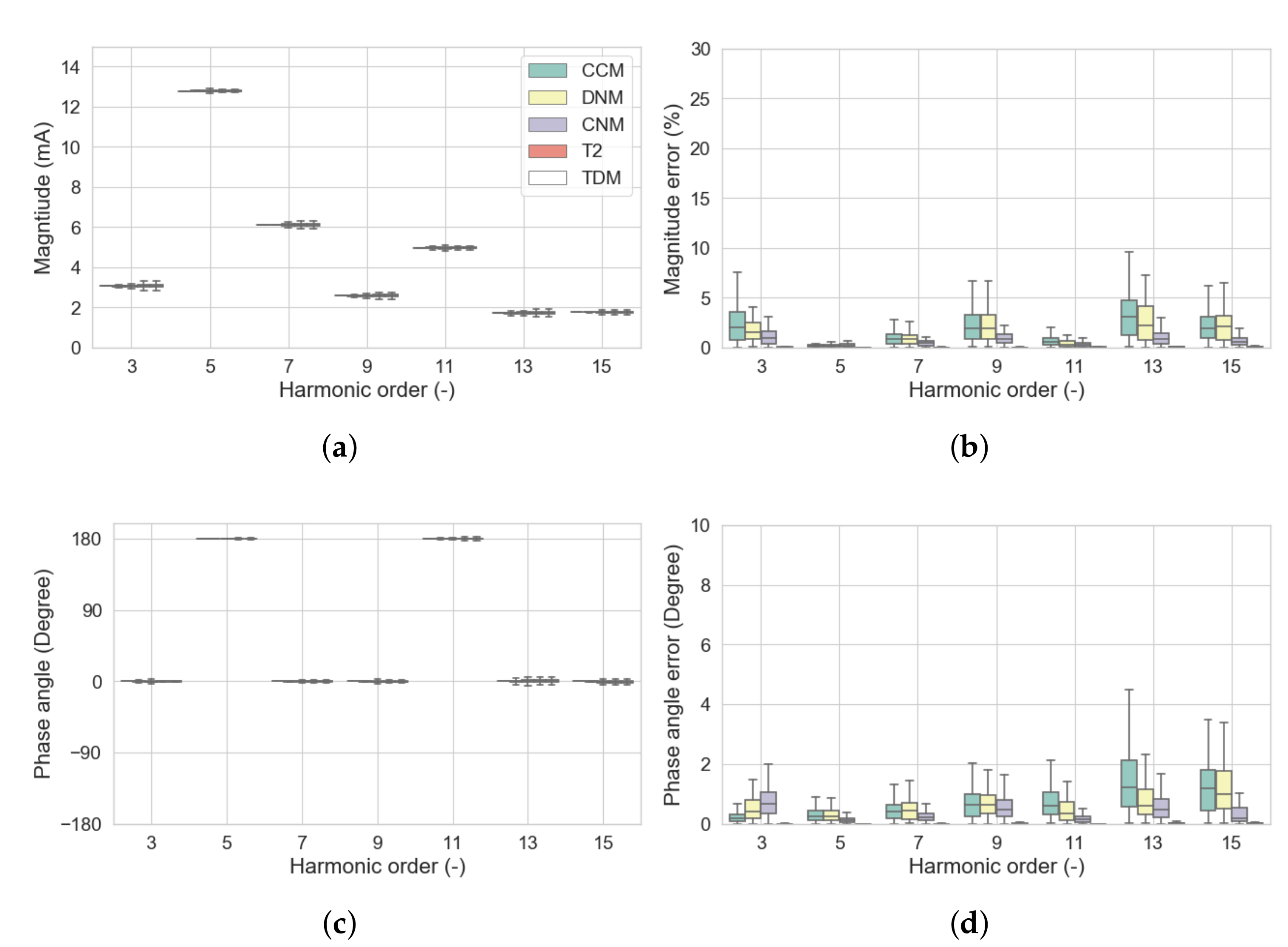
4.3. Results
- the T2 model is always more accurate, as it takes into account both and ;
- the CCM is as accurate as the other FDMs if the values of the and matrices are negligible;
- the DNM performance is comparable with the CNM and the T2 model if the off-diagonal elements of and of matrices are negligible; and
- the CNM performance is comparable with the T2 model if the matrix values tend to zero.
4.3.1. Type A
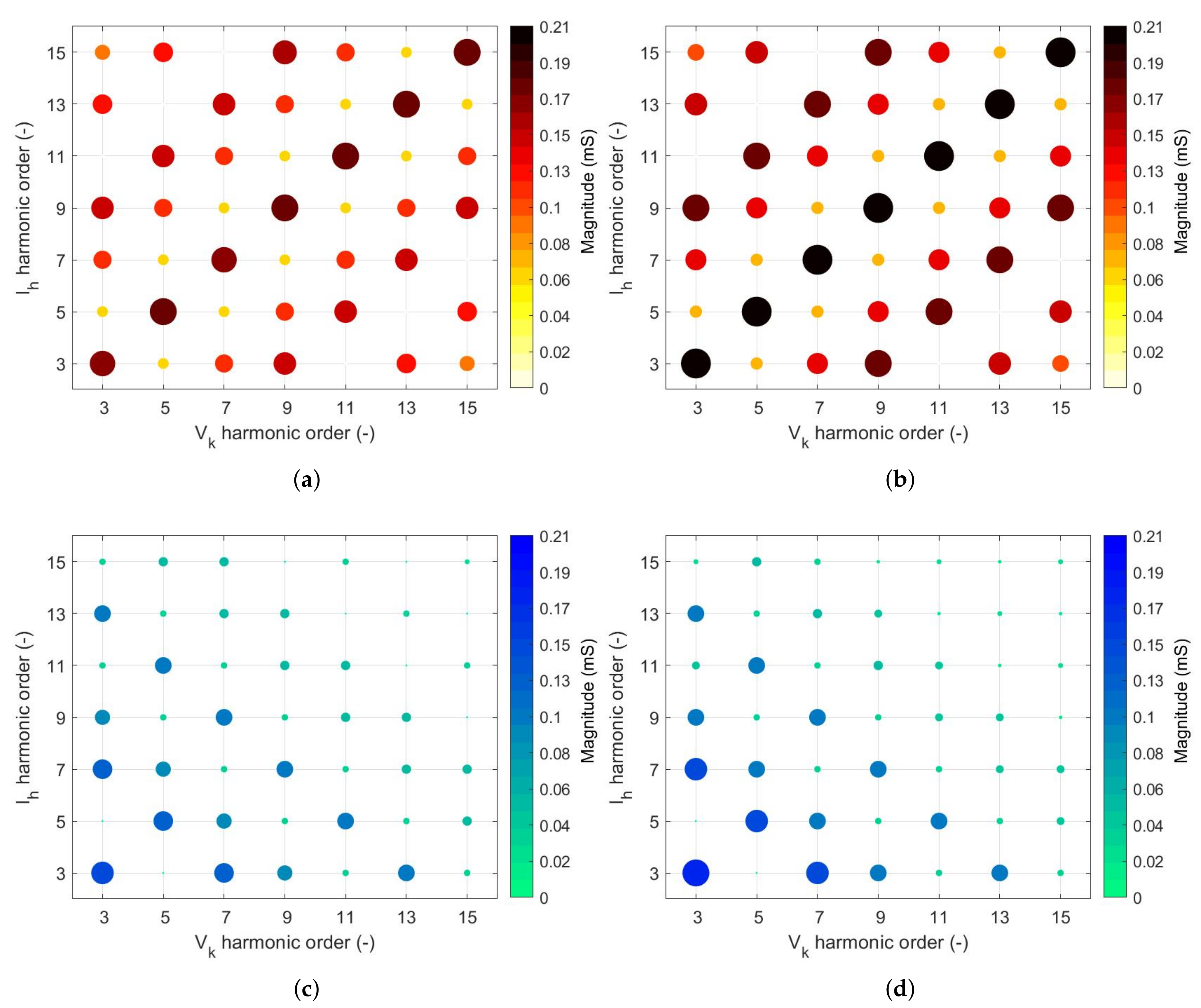
- the CNM and the T2 model perform noticeably better than the CCM and the DNM for both flat-top and peak-top voltage waveforms. This can be explained by the presence of non-negligible off-diagonal elements in both matrices (see Figure 11a,b);
- the T2 model performs significantly better than the CNM due to the non-negligible magnitudes of the elements of the matrices (see Figure 11c,d), although the magnitudes are about six times lower than the corresponding values of for both FT and PT;
- looking at Figure 11a,b, it is evident that in the case of PT supply condition the magnitudes of the elements of are smaller by a factor 3 compared to the FT supply condition; and
- the same considerations apply for phase angles. It should be noted that the phase angles returned by the FDMs are with respect to the cosine of the voltage waveform, rather than the sinusoid used in the TDM, so the angles presented here (and for the FDMs of other LED lamp types) cannot be directly compared with those in Section 3, but allow for a comparison between FDMs.
4.3.2. Type B
- approaches a diagonal matrix, indicating that the most pronounced coupling exists between same order harmonics (e.g., between 11th and 11th) and between them and their nearest neighbors (e.g., between 11th and 9th and 13th), as can be seen in Figure 14a,b;
- for this LED lamp, the CNM and the T2 model perform noticeably better than the CCM and the DNM for both FT and PT voltage waveforms, even if only a few off-diagonal elements of have non-zero values;
- although of similar magnitudes, the values of the for the PT voltage wavefom are generally higher than those present in the for the FT voltage waveform, as demonstrated by the different level of accuracy between CNM and T2 in FT supply conditions in Figure 12c,d and in PT supply conditions in Figure 13c,d; and
- the same considerations apply for phase angles.
4.3.3. Type C
- the ’patterns’ of both and are almost identical for both voltage waveforms, even if they have very small magnitudes compared with the other lamps;
- off-diagonal elements each two harmonic orders of are, in both cases, of the same order of magnitude of diagonal elements as evidenced by the great difference of performances between CCM and DNM versus CNM and T2; and
- the performance of the T2 model is significantly better than the other methods due to the order of magnitude of the elements of , which are the same as .
4.3.4. Type D
- All FDMS, with the exception of the CCM, exhibit similar accuracy. This can be explained by analyzing in Figure 20 which is a diagonal matrix, indicating that the LED lamp behaves as a linear load and only direct coupling between same order harmonics exists;
- are practically identical for both voltage waveforms;
- the aforementioned linear behavior can be modeled, for each harmonic, by a simple Norton equivalent constituted by a parallel RC circuit in parallel with a constant current source;
- demonstrates that the sensitivity to the phase angle of the lower order harmonics is more pronounced, however, the values are generally two orders of magnitude lower than ; and
- for the PT voltage waveform, the magnitudes of the matrix are negligible for the 11th order harmonic current, which is reflected in the results in Figure 18 and Figure 19, respectively, where the errors of the 11th harmonic are noticeably lower for the PT voltage waveform than the FT voltage waveform.
4.3.5. Total Distortion Indices
5. Conclusions
- The TDMs, which in this paper were validated using experimental measurements, demonstrate that it is possible to achieve excellent levels of accuracy for certain types of LED lamps, i.e., Type A and B, in which control is either not present or can be emulated using an equivalent circuit form. For LED lamps that require specific representation of the control logic, i.e., Type C and Type D, new models were presented, for the first time, in this paper. For the Type C LED lamp example, the accuracy of the TDM is lower than Type A and Type B, but the median values are still very low with respect to measurements ( < 10%). Higher magnitude errors are observed for the Type D LED lamp model but, in absolute terms, their values are very low. Areas of possible further improvement, e.g., by fine tuning the settings of the control algorithms, were discussed.
- The FDMs, which in this paper were derived from and compared against the TDMs, clearly show that the simulation error is significantly influenced by both the LED lamp type and the background voltage distortion. As expected, the overall errors reduce when increasing the model complexity; the magnitude errors obtained with the most complex model (i.e., the tensor based model T2) are always below 10%, and generally considerably lower (with median values of around a few percent or less), while the phase errors are always less than 5°, highlighting the value of including the phase dependency in the model formulation.
- The presented models and the quantitative results about their accuracy allow probabilistic harmonic penetration studies, such as the assessment of voltage distortion in LV networks and their future evolution, to be approached with the knowledge of the accuracy levels that can be obtained using different types of FDM.
- TDM parameter values were also reported in Appendix A for use by the community. From the presented TDMs, the FDMs analyzed in this paper can be obtained. Alternatively, the authors are happy to provide the parameters of the FDMs upon request.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Time Domain Models and Parameters
Appendix A.1. Type A LED Lamp


Appendix A.2. Type B LED Lamp


Appendix A.3. Type C LED Lamp


Appendix A.4. Type D LED Lamp
| Kp | Ki | Ts | Usat | n | trd |
|---|---|---|---|---|---|
| 0.0001 | 1/0.1 | 1e-6 | 10 | 7 | 0.002 |
| fs (kHz) | Min Duty Cycle (%) | Max Duty Cycle (%) | Slope Compensation (A) | Time Delay (s) |
|---|---|---|---|---|
| 60 | 1 | 33 | 10 | 0 |
| Windings | Turns | Polarity | Magnetization Inductance (H) | Initial Magnetization Current (A) |
|---|---|---|---|---|
| [2 1] | [120 -4 -36 ] | + | Inf | 0 |
References
- Gil-De-Castro, A.; Medina Gracia, R.; Ronnberg, S.K.; Blanco Castaneda, A.; Meyer, J. Differences in the performance between CFL and LED lamps under different voltage distortions. In Proceedings of the 18th IEEE International Conference on Harmonics and Quality of Power, Ljubljana, Slovenia, 13–16 May 2018. [Google Scholar]
- Collin, A.J.; Delle Femine, A.; Landi, C.; Langella, R.; Luiso, M.; Testa, A. Assessment of the high frequency emissions of low-voltage electronic equipment under different supply conditions. In Proceedings of the 10th IEEE International Workshop on Applied Measurements for Power Systems, Aachen, Germany, 25–27 September 2019. [Google Scholar]
- Medina, A.; Segundo-Ramirez, J.; Ribeiro, P.; Xu, W.; Lian, K.L.; Chang, G.W.; Dinavahi, V.; Watson, N.R. Harmonic analysis in frequency and time domain. IEEE Trans. Power Del. 2013, 28, 1813–1821. [Google Scholar] [CrossRef]
- Yanchenko, S.; Meyer, J. Harmonic emission of household devices in presence of typical voltage distortions. In Proceedings of the IEEE PowerTech Conference, Eindhoven, Holland, 29 June–2 July 2015. [Google Scholar]
- Blanco, A.M.; Yanchenko, S.; Meyer, J. Impact of supply voltage distortion on the harmonic emission of electronic household equipment. In Proceedings of the 2013 VII Simposio Internacional sobre la Calidad de la Energía Eléctrica—SICEL, Medellín, Colombia, 27–29 November 2013. [Google Scholar]
- Xu, X.; Collin, A.J.; Djokic, S.Z.; Yanchenko, S.; Moller, F.; Meyer, J.; Langella, R.; Testa, A. Analysis and modeling of power-dependent harmonic characteristics of modern PE devices in LV networks. IEEE Trans. Power Del. 2017, 32, 1014–1023. [Google Scholar]
- Cresswell, C. Steady State Load Models for Power System Analysis. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2009. [Google Scholar]
- Rylander, M.; Grady, W.M.; Arapostathis, A.; Powers, E.J. Power Electronic Transient Load Model for Use in Stability Studies of Electric Power Grids. IEEE Trans. Power Syst. 2010, 25, 914–921. [Google Scholar] [CrossRef]
- Du, Y.; Lu, D.D.-C.; James, G.; Cornforth, D.J. Modeling and analysis of current harmonic distortion from grid connected PV inverters under different operating conditions. Sol. Energy 2013, 94, 182–194. [Google Scholar] [CrossRef]
- Kukacka, L.; Dupuis, P.; Simanjuntak, R.; Zissis, G. Simplified models of LED ballasts for spice. In Proceedings of the 2014 IEEE Industry Application Society Annual Meeting, Vancouver, BC, Canada, 5–9 October 2014; pp. 1–5. [Google Scholar]
- Arrillaga, J.; Smith, B.C.; Watson, N.R.; Wood, A.R. Power System Harmonic Analysis; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Caicedo, J.E.; Romero, A.A.; Zini, H.C.; Langella, R.; Meyer, J.; Watson, N.R. Impact of Reference Conditions on the Frequency Coupling Matrix of a Plug-in Electric Vehicle Charger. In Proceedings of the 18th IEEE International Conference on Harmonics and Quality of Power, Ljubljana, Slovenia, 13–16 May 2018. [Google Scholar]
- Ramirez, A.; Rico, J.J. Harmonic/State Model-Order Reduction of Nonlinear Networks. IEEE Trans. Power Del. 2016, 31, 1379–1387. [Google Scholar] [CrossRef]
- Kwon, J.B.; Wang, X.; Blaabjerg, F.; Bak, C.L.; Wood, A.R.; Watson, N.R. Harmonic Instability Analysis of a Single-Phase Grid-Connected Converter Using a Harmonic State-Space Modeling Method. IEEE Trans. Ind. Appl. 2016, 52, 4188–4200. [Google Scholar] [CrossRef]
- Kwon, J.B.; Wang, X.; Blaabjerg, F.; Bak, C.L.; Sularea, V.S.; Busca, C. Harmonic Interaction Analysis in a Grid-Connected Converter Using Harmonic State-Space (HSS) Modelling. IEEE Trans. Power Electron. 2017, 32, 6823–6835. [Google Scholar] [CrossRef] [Green Version]
- Larsen, E.; Baker, D.; McIver, J. Low-order harmonic interactions on ac/dc systems. IEEE Trans. Power Del. 1989, 4, 493–5019. [Google Scholar] [CrossRef]
- Fauri, M. Harmonic modeling of non-linear load by means of crossed frequency admittance matrix. IEEE Trans. Power Syst. 1997, 12, 1632–16387. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, G.; Xu, W.; Mayordomo, J.G. A harmonically coupled admittance matrix model for AC/DC converters. IEEE Trans. Power Syst. 2007, 22, 1574–1582. [Google Scholar] [CrossRef]
- Lehn, P.W.; Lian, K.L. Frequency coupling matrix of a voltage source converter derived from piecewise linear differential equations. IEEE Trans. Power Del. 2007, 22, 1603–1612. [Google Scholar] [CrossRef]
- Smith, B.C.; Watson, N.R.; Wood, A.R.; Arrillaga, J. Harmonic tensor linearisation of HVDC converters. IEEE Trans. Power Del. 1998, 13, 1244–1250. [Google Scholar] [CrossRef]
- Watson, N.R.; Scott, T.L.; Hirsch, S.J.J. Implications for distribution networks of high penetration of compact fluorescent lamps. IEEE Trans. Power Del. 2009, 24, 1521–1528. [Google Scholar] [CrossRef]
- Yong, J.; Chen, L.; Nassif, A.B.; Xu, W. A frequency-domain harmonic model for compact fluorescent lamps. IEEE Trans. Power Del. 2010, 25, 1182–1189. [Google Scholar] [CrossRef]
- Molina, J.; Sainz, L. Model of electronic ballast compact fluorescent lamps. IEEE Trans. Power Del. 2014, 29, 1363–1371. [Google Scholar] [CrossRef]
- Molina, J.; Mesas, J.J.; Mesbahi, N.; Sainz, L. LED lamp modeling for harmonic studies in distribution systems. IET Gen. Trans. Distrib. 2017, 11, 1063–1071. [Google Scholar] [CrossRef]
- Guo, Z.; Djokic, S.Z.; Xu, X.; Collin, A.J.; Langella, R.; Testa, A. Parameterised component-based models for harmonic analysis of aggregate LED lamp loads. In Proceedings of the 19th IEEE International Conference on Harmonics and Quality of Power, Dubai, UAE, 22–25 March 2020. [Google Scholar]
- Collin, A.J.; Drapela, J.; Langella, R.; Testa, A.; Djokic, S.Z.; Watson, N.R. Harmonic modeling of LED lamps by means of admittance frequency coupling matrices. In Proceedings of the IEEE PowerTech Conference, Milan, Italy, 23–27 June 2019. [Google Scholar]
- Blanco, A.M.; Parra, E.E. Effects of high penetration of CFLs and LEDs on the distribution networks. In Proceedings of the 14th IEEE International Conference on Harmonics and Quality of Power, Bergamo, Italy, 26–29 September 2010. [Google Scholar]
- Xu, X.; Collin, A.; Djokic, S.Z.; Langella, R.; Testa, A.; Drapela, J. Experimental evaluation and classification of LED lamps for typical residential applications. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017. [Google Scholar]
- Collin, A.; Djokic, S.; Drapela, J.; Langella, R.; Testa, A. Light flicker and power factor labels for comparing LED lamp performance. IEEE Trans. Ind. Appl. 2019, 55, 7062–7070. [Google Scholar] [CrossRef] [Green Version]
- Arias, M.; Vazquez, A.; Sebastian, J. An overview of the AC-DC and DC-DC converters for LED lighting applications. Automatika 2012, 53, 156–172. [Google Scholar] [CrossRef] [Green Version]
- Electromagnetic Compatibility (EMC)—Part 4-13: Testing and Measurement Techniques—Harmonics and Interharmonics Including Mains Signalling at a.c. Power Port, Low Frequency Immunity Tests; IEC 61000-4-13:2002 + AMD1:2009 + AMD2:2015; CEI-IEC: Geneva, Switzerland, 2015.
- Xu, X. Harmonic Modeling and Characterisation of Modern Power Electronic Devices in Low Voltage Networks. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2018. [Google Scholar]
- Xu, X.; Gunda, J.; Fang, D. Modelling and aggregation of LED lamps for network harmonic analysis. In Proceedings of the Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Testing and Measurement Techniques – General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto; IEC 61000-4-7, 2002 + A1:2009; CEI-IEC: Geneva, Switzerland, 2009.
- Gallo, D.; Langella, R.; Luiso, M.; Testa, A.; Watson, N.R. A new test procedure to measure power electronic devices’ frequency coupling admittance. IEEE Trans. Instrum. Meas. 2018, 67, 2401–2409. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Caicedo, J.E.; Romero, A.A.; Zini, H.C.; Meyer, J.; Watson, N.R. On the use of fourier descriptors for the assessment of frequency coupling matrices of power electronic devices. In Proceedings of the 18th IEEE International Conference on Harmonics and Quality of Power, Ljubljana, Slovenia, 13–16 May 2018. [Google Scholar]
- Frater, L. Light Flicker and Harmonic Modeling of Electrical Lighting. Ph.D. Thesis, University of Canterbury, Canterbury, New Zealand, 2015. [Google Scholar]
- Voltage Characteristics of Electricity Supplied by Public Distribution Networks; CENELEC, Standard EN 50160; CENELEC: Brussels, Belgium, 2013.
- Guo, Z. Harmonic Load Modeling of Residential Customers in Low-Voltage Networks. Master’s Thesis, University of Edinburgh, Edinburgh, UK, 2019. [Google Scholar]
Sample Availability: All of the models are available upon request from the authors. |















| Type (-) | Power (W) | PF1 (-) | THD (%) | THC (mA) |
|---|---|---|---|---|
| A | 5 | 0.93 | 139 | 32.3 |
| B | 4.5 | 0.44 | 49 | 21.6 |
| C | 13.6 | 1.00 | 28 | 16.4 |
| D | 40 | 0.98 | 8 | 14.4 |
| k | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
|---|---|---|---|---|---|---|---|
| Limit (%) | 5 | 6 | 5 | 1.5 | 3.5 | 3 | 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collin, A.J.; Z. Djokic, S.; Drapela, J.; Guo, Z.; Langella, R.; Testa, A.; Watson, N.R. Analysis of Approaches for Modeling the Low Frequency Emission of LED Lamps. Energies 2020, 13, 1571. https://doi.org/10.3390/en13071571
Collin AJ, Z. Djokic S, Drapela J, Guo Z, Langella R, Testa A, Watson NR. Analysis of Approaches for Modeling the Low Frequency Emission of LED Lamps. Energies. 2020; 13(7):1571. https://doi.org/10.3390/en13071571
Chicago/Turabian StyleCollin, Adam J., Sasa Z. Djokic, Jiri Drapela, Zekun Guo, Roberto Langella, Alfredo Testa, and Neville R. Watson. 2020. "Analysis of Approaches for Modeling the Low Frequency Emission of LED Lamps" Energies 13, no. 7: 1571. https://doi.org/10.3390/en13071571
APA StyleCollin, A. J., Z. Djokic, S., Drapela, J., Guo, Z., Langella, R., Testa, A., & Watson, N. R. (2020). Analysis of Approaches for Modeling the Low Frequency Emission of LED Lamps. Energies, 13(7), 1571. https://doi.org/10.3390/en13071571








