Heat Transport Analysis in Rectangular Shields Using the Laplace and Poisson Equations †
Abstract
1. Introduction
- I.
- Because of the boundary conditions:First, second and third conditions. Fourth type.
- II.
- Due to cyclical boundary conditions [12]:Temperature, solar radiation
- III.
- Single-material, multi-layer.
- IV.
- Due to the type of impulse:Dirac delta, step Heaviside function.
2. Materials and Methods
2.1. Governing Equation
- symmetry–symmetry SS (x and y even),
- symmetry–antisymmetry SA (x even, y odd),
- antisymmetry–symmetry AS (x odd, y even),
- antisymmetry–antisymmetry AA (x and y odd).
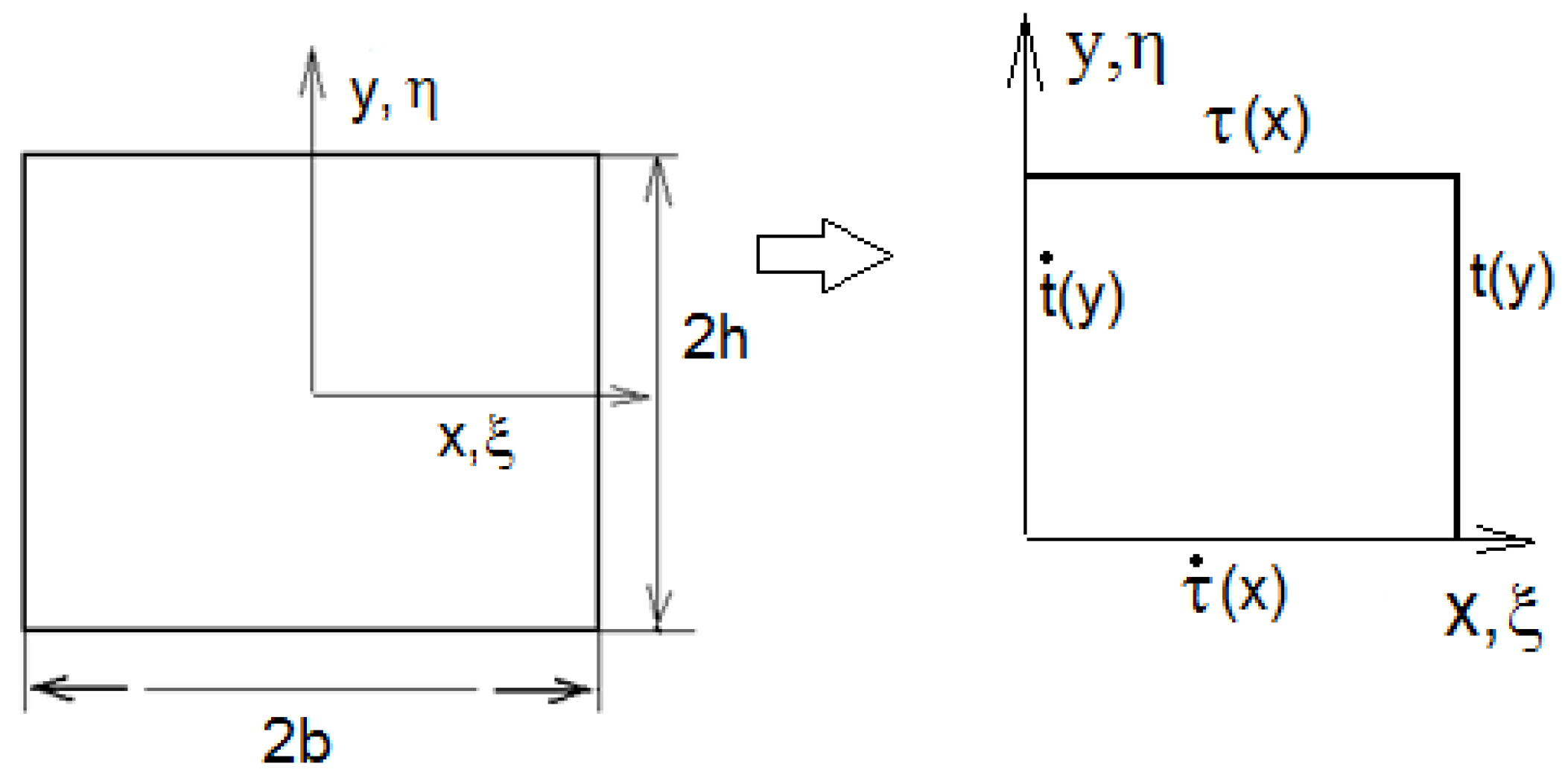
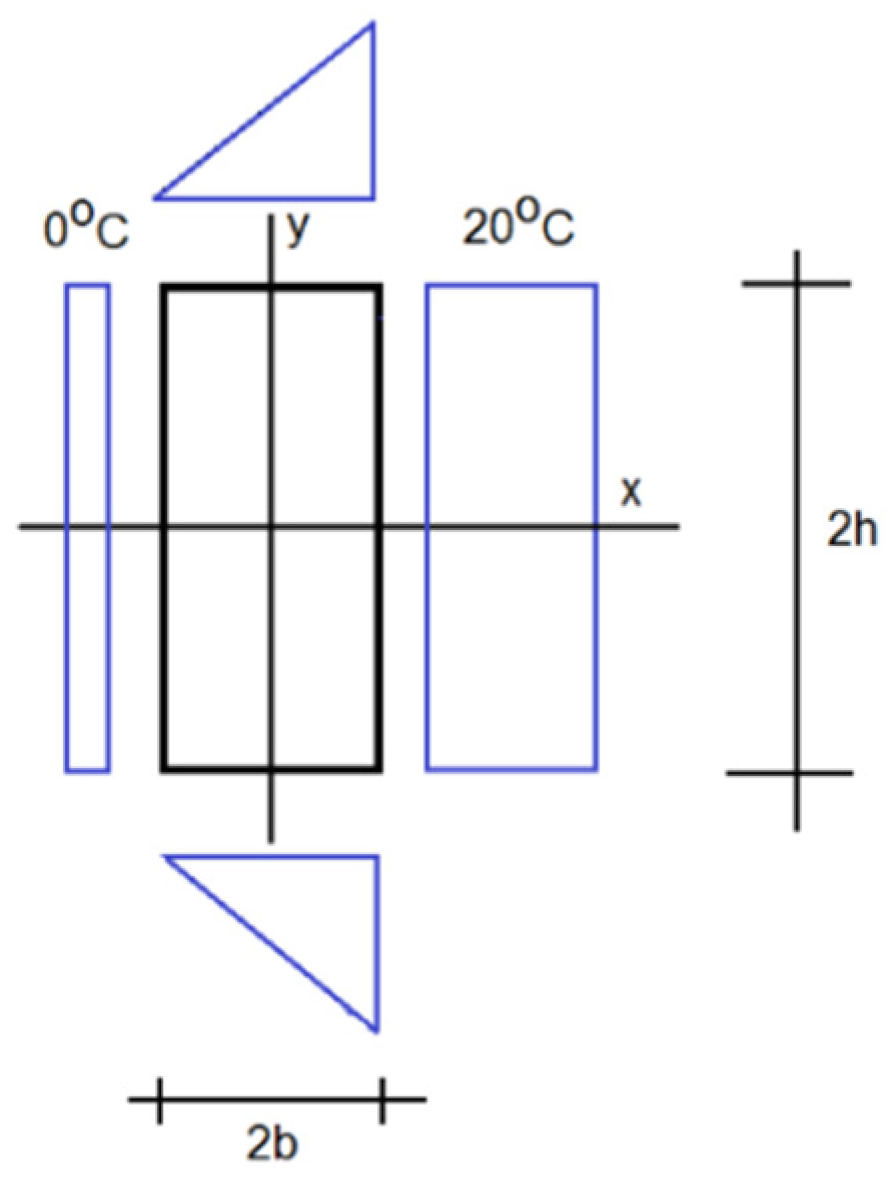
2.2. Boundary Conditions
2.3. Solution of the Area Problem in Steady State
2.4. Expressions on Temperature in Case of Limitation to the First Consecutive Polynomials of Rank 10
3. Results and Discussion
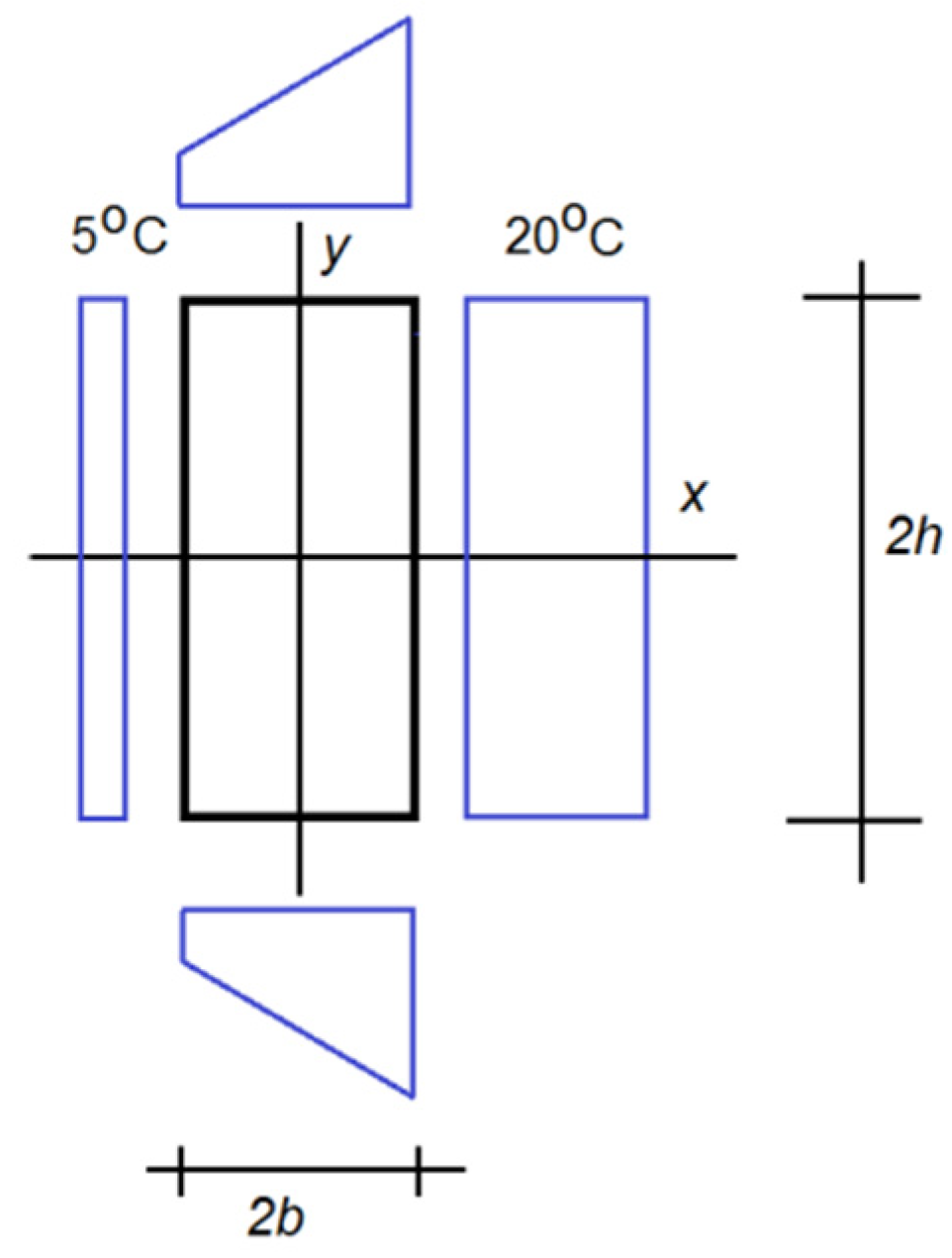
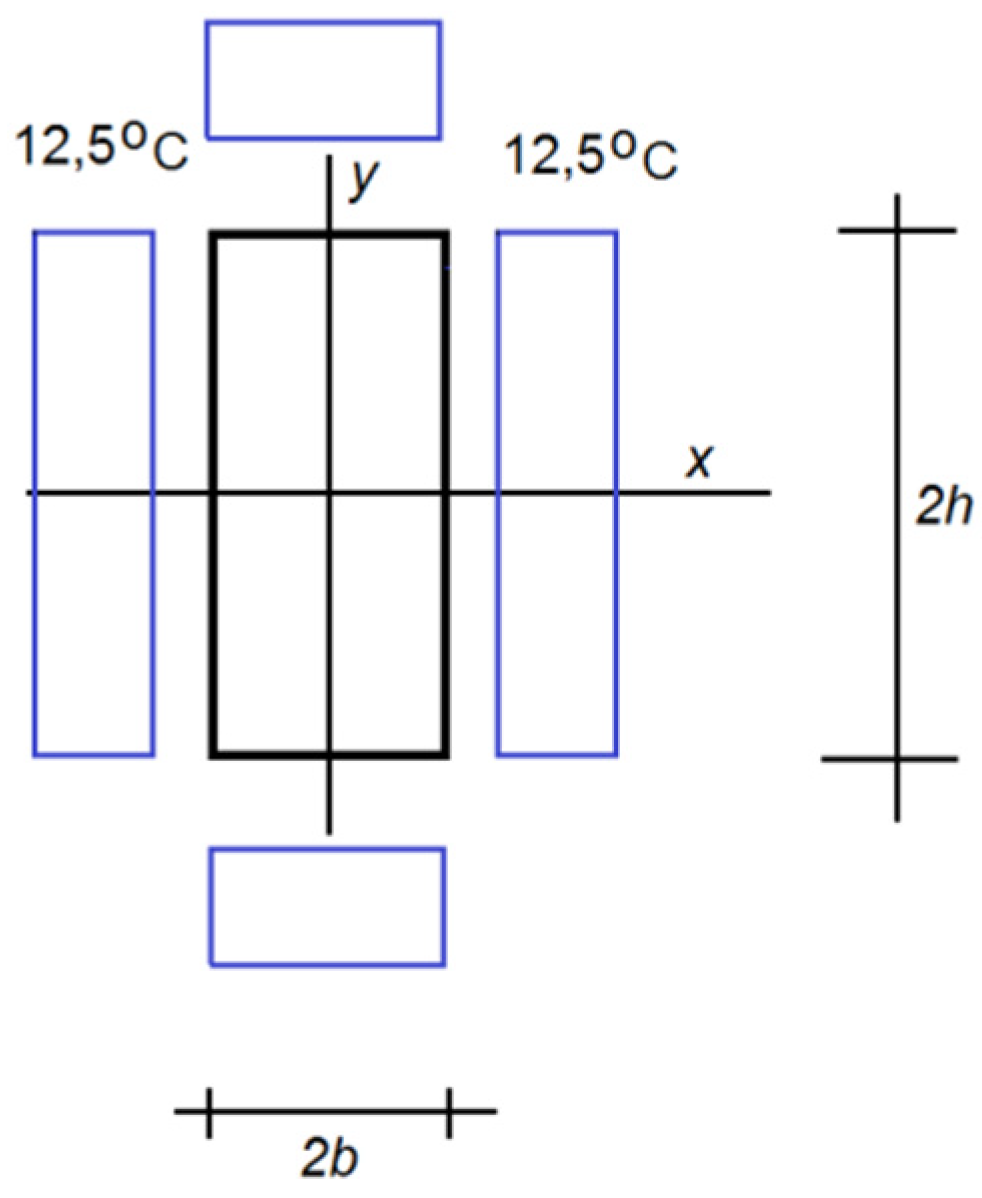
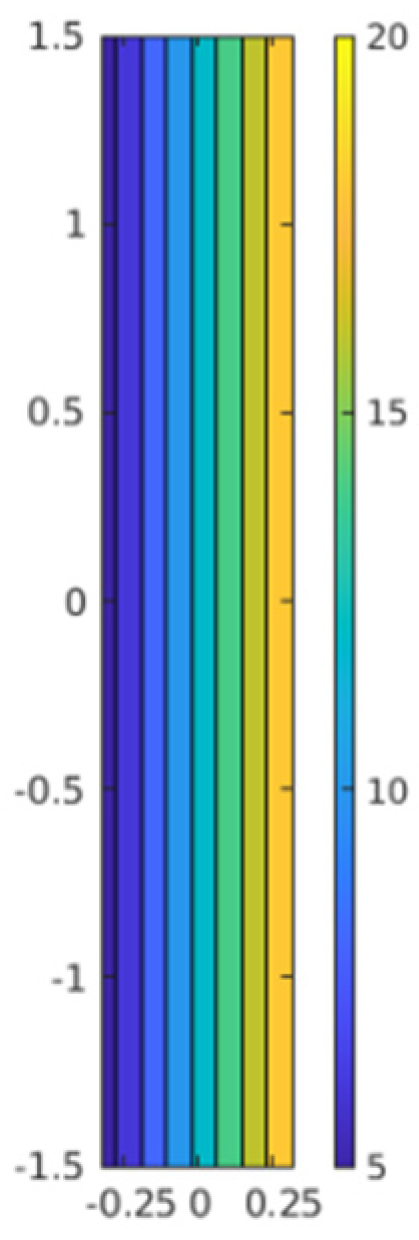
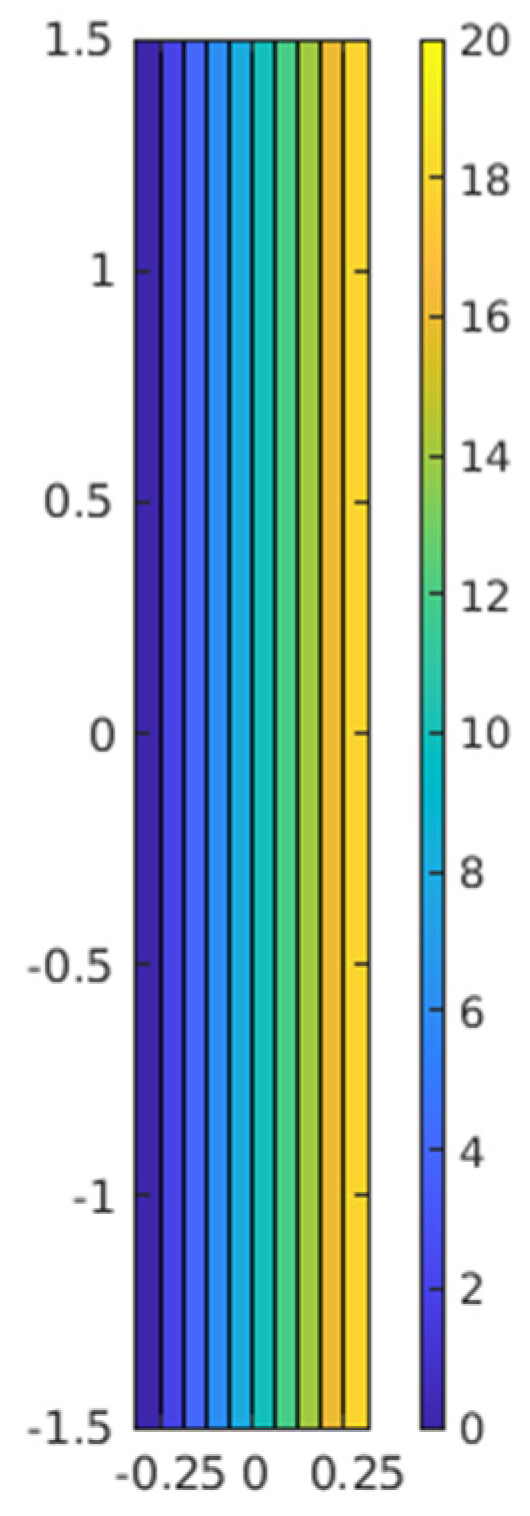
3.1. Solution to the Example Formulated in Point 2
3.2. Area Solution for Transient State
3.2.1. Task Formulation
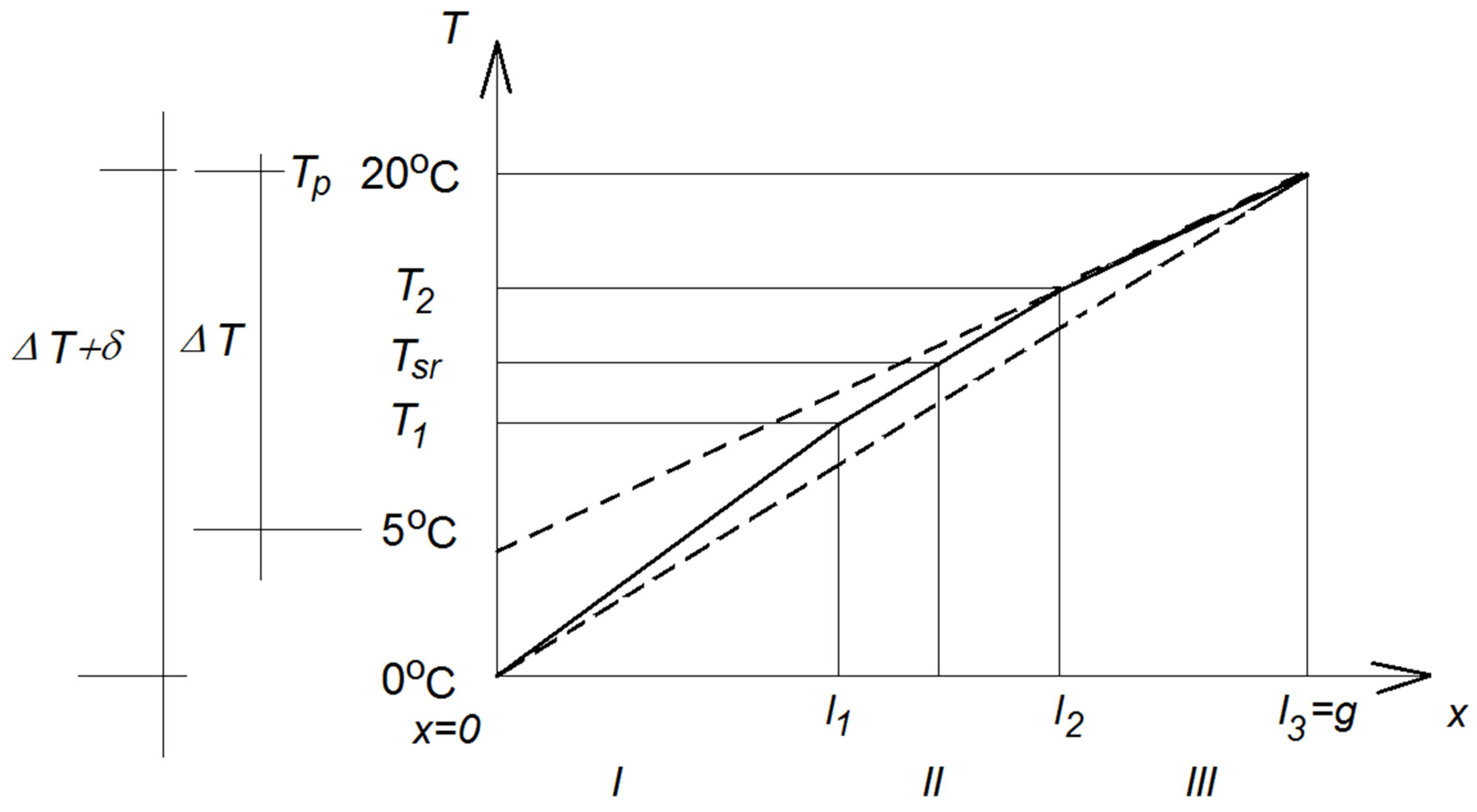
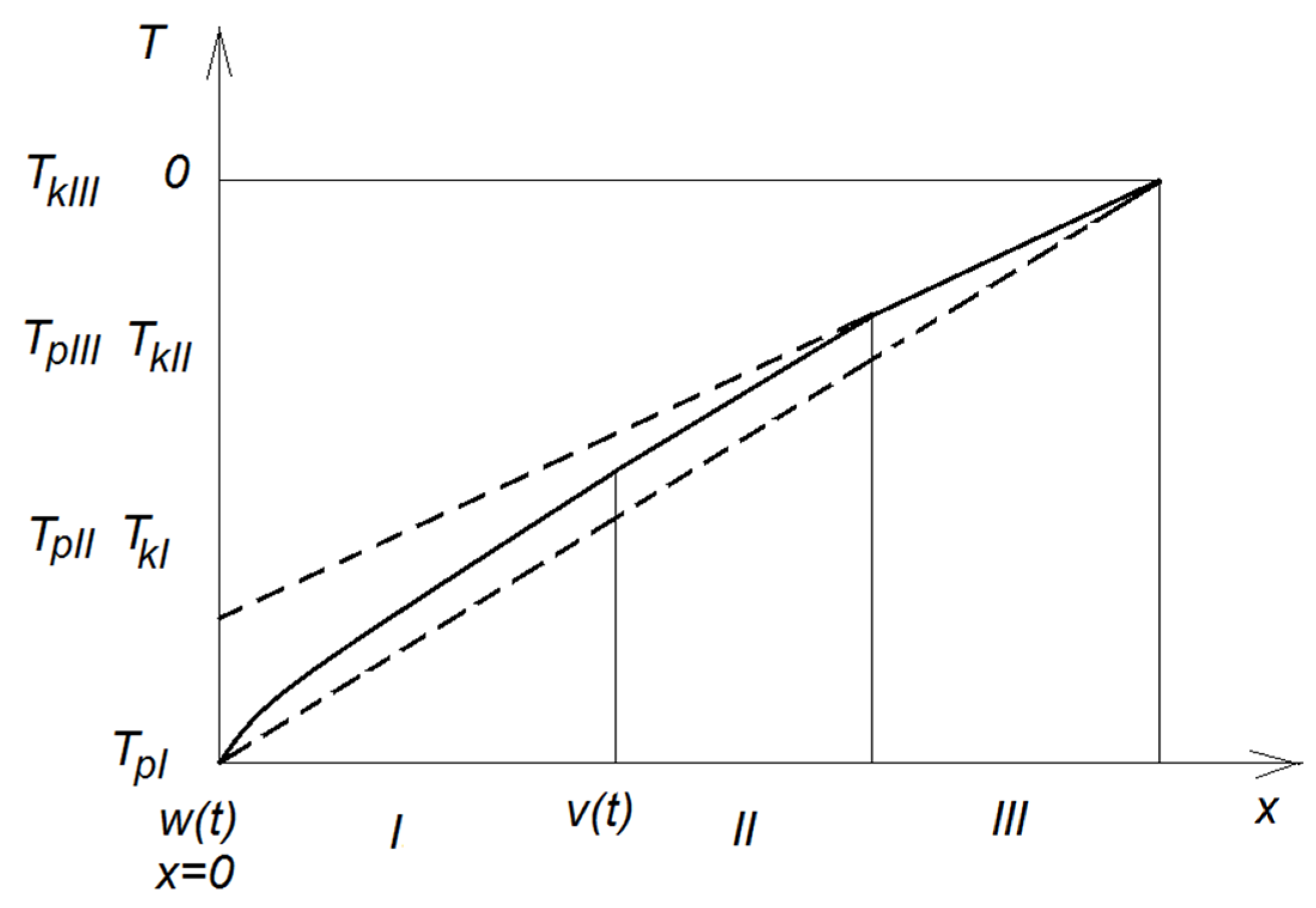
3.2.2. Description of the Temperature Effect Caused by the Pulse on the Left Bank
3.2.3. Description of the Integral Heat Balance Method on the Example of One-Dimensional Transient Heat Conduction
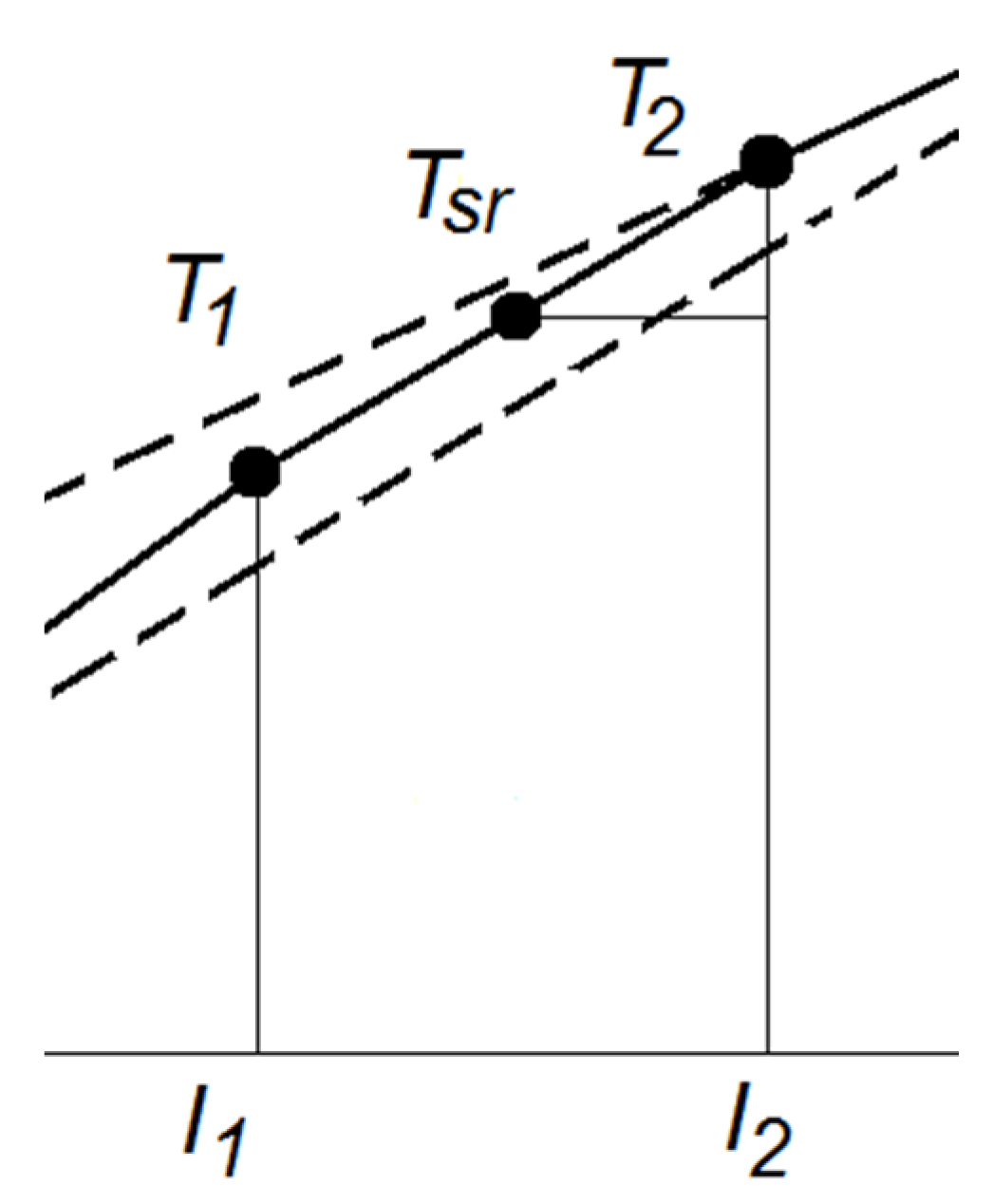
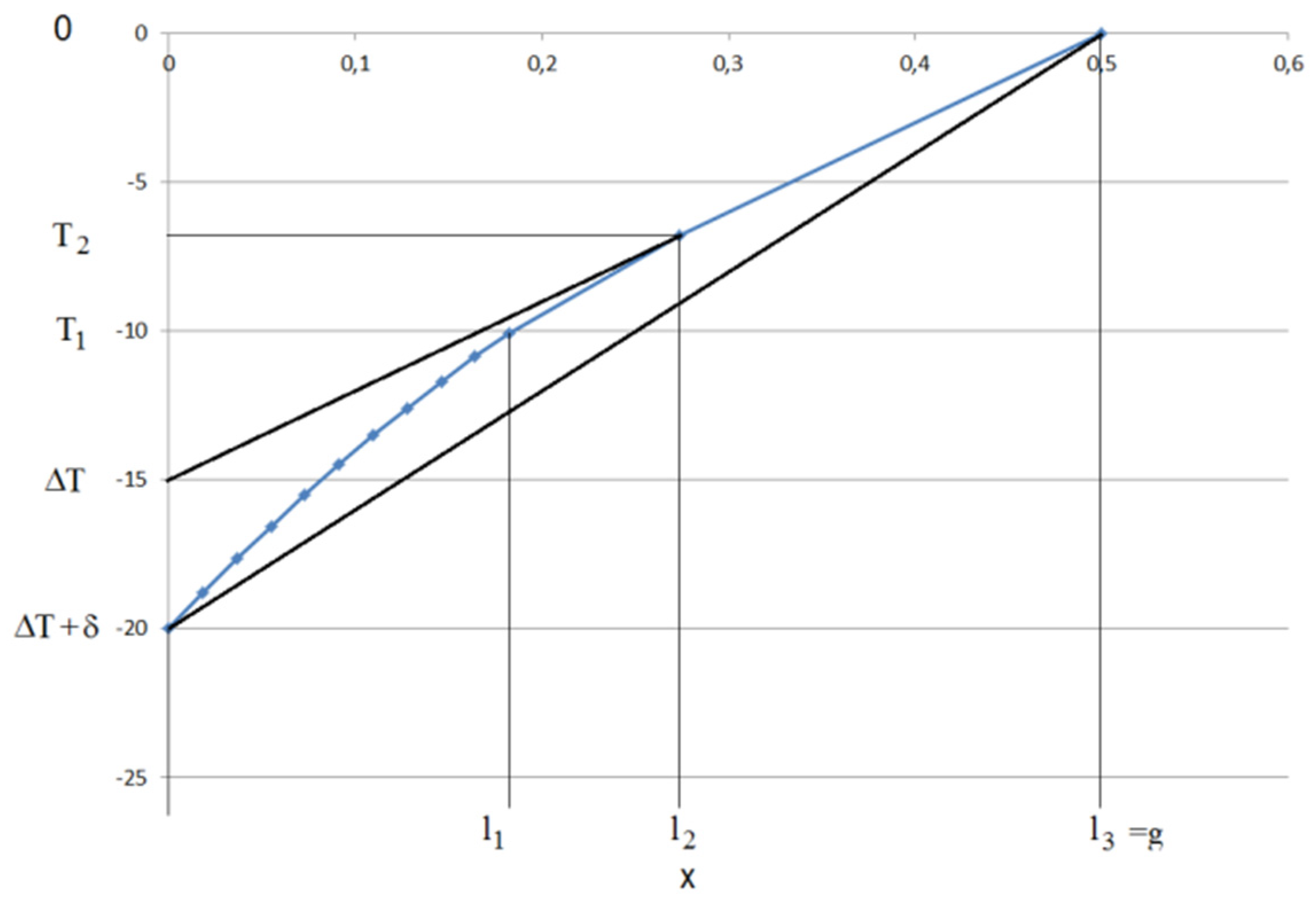
3.2.4. Example of Determining the Slope Coefficient of Straight Lines in Three Intervals
4. Conclusions
- Solution classes (polynomial solutions);
- Breaking down the task into smaller ones with fewer constants (expressiveness of the task);
- Forms of description of boundary tasks (number of conditions on the edges);
- Simplicity of the form of solutions received.
Author Contributions
Funding
Conflicts of Interest
References
- Balaras, C.A. The role of thermal mass on the cooling load of buildings: An overview of computational methods. Energy Build. 1996, 24, 1–10. [Google Scholar] [CrossRef]
- Levinskytė, A.; Bliūdžius, R.; Burlingis, A.; Makaveckas, T. Dependencies of heat transmittance through the ventilated wall system on thermal conductivity of connectors crossing thermal insulation layer. MATEC Web Conf. 2019, 282, 2089. [Google Scholar] [CrossRef][Green Version]
- Medved, I.; Kalvoda, L.; Vejmelkova, E.; Vratislav, S.; Černy, R. Transport of gadolinium in a cement composite. MATEC Web Conf. 2019, 282, 2105. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Method of initial functions in problems of the theory of elasticity. Bull. USSR Acad. Sci. 1955, 7, 49–69. (In Russian) [Google Scholar]
- Lur’e, A.I. Three Dimensional Problems of the Theory of Elasticity; Gostehizdat: Moscow, Russia, 1955. (In Russian) [Google Scholar]
- Owczarek, S. Wielomianowa Postać Rozwiązania Zagadnień Statyki Sprężystych Tarcz Prostokątnych; IFTR Reports nr 17; Institute of Fundamnetal Technological Research PAS: Warsaw, Poland, 1984. (In Polish) [Google Scholar]
- Patel, R.; Dubey, S.K.; Pathak, K.K. Infilled reinforced concrete beams for sustainable construction. J. Civ. Eng. Archit. 2013, 7. [Google Scholar] [CrossRef]
- Patel, R.; Dubey, S.K.; Pathak, K.K. Analysis of RC brick filled composite beams using MIF. Procedia Eng. 2013, 51. [Google Scholar] [CrossRef][Green Version]
- Aste, N.; Angelotti, A.; Buzzetti, M. The influence of the external walls thermal inertia on the energy performance of well insulated buildings. Energy Build. 2009, 41, 1181–1187. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Thermal Performance of Buildings–Transmission and Ventilation Heat Transfer Coefficients—Calculation Method; ISO 13789; International Organization for Standardization (ISO): Geneva, Switzerland, 2017. [Google Scholar]
- International Organization for Standardization (ISO). Thermal Performance of Building Components—Dynamic Thermal Characteristics—Calculation Methods; ISO 13786; International Organization for Standardization (ISO): Geneva, Switzerland, 2017. [Google Scholar]
- Ma, P.; Wang, L.-S. Effective heat capacity of interior planar thermal mass (iPTM) subject to periodic heating and cooling. Energy Build. 2012, 47, 44–52. [Google Scholar] [CrossRef]
- Kossecka, E.; Kosny, J. Influence of insulation configuration on heating and cooling loads in a continuously used building. Energy Build. 2002, 34, 321–331. [Google Scholar] [CrossRef]
- Collet, F.; Serres, L.; Miriel, J.; Bart, M. Study of thermal behaviour of clay wall facing south. Build. Environ. 2006, 41, 307–315. [Google Scholar] [CrossRef]
- Stazi, F.; Tomassoni, F.; Veglio, A.; Di Perna, C. Experimental evaluation of ventilated walls with an external clay cladding. Renew. Energy 2011, 36, 3373–3385. [Google Scholar] [CrossRef]
- Pogorzelski, J.A. Fizyka Cieplna Budowli; Polish Scientific Publishers (PWN): Warsaw, Poland, 1976. (In Polish) [Google Scholar]
- Taler, J.; Duda, P. Rozwiązywanie Prostych i Odwrotnych Zagadanień Przewidzenia Ciepła; Wydawnictwa Naukowo-Techniczne (WNT): Warsaw, Poland, 2003. (In Polish) [Google Scholar]



| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| j(n) | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| J(n) | 1 | 0 | −1 | 0 | 1 | 0 | −1 |
| j(n + 1) | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| J(n + 1) | 0 | −1 | 0 | 1 | 0 | −1 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owczarek, S.; Owczarek, M. Heat Transport Analysis in Rectangular Shields Using the Laplace and Poisson Equations. Energies 2020, 13, 1714. https://doi.org/10.3390/en13071714
Owczarek S, Owczarek M. Heat Transport Analysis in Rectangular Shields Using the Laplace and Poisson Equations. Energies. 2020; 13(7):1714. https://doi.org/10.3390/en13071714
Chicago/Turabian StyleOwczarek, Stefan, and Mariusz Owczarek. 2020. "Heat Transport Analysis in Rectangular Shields Using the Laplace and Poisson Equations" Energies 13, no. 7: 1714. https://doi.org/10.3390/en13071714
APA StyleOwczarek, S., & Owczarek, M. (2020). Heat Transport Analysis in Rectangular Shields Using the Laplace and Poisson Equations. Energies, 13(7), 1714. https://doi.org/10.3390/en13071714




