Use of Available Daylight to Improve Short-Term Load Forecasting Accuracy
Abstract
1. Introduction
- -
- The relation between sunrise and sunset times and hourly load is modeled.
- -
- A valid linearization for this relation is presented so that it can be included in both linear or non-linear models is presented.
- -
- This new input is included in both types of models to reduce the forecasting error on sunrise and sunset times, especially when sunrise and sunset times vary faster and when DST time-shifts are implemented.
2. Materials and Methods
2.1. Model Structure
2.2. Data Analysis
2.2.1. Load Data
- -
- Long-term trend: Economic growth is the main driver for long-term trends in electricity demand in Spain. The base model uses a quadratic polynomial of time to model these trends, but when larger periods of data are used for training this approach is no longer valid. In order to use more training years, the linear and quadratic terms are substituted by a 52-week moving average of the load.
- -
- Recent trend: Load series are highly autocorrelated. Therefore, even if the most relevant predictors are used, a recent value of the series has hidden information from which accuracy of the model may benefit. To this end, the base model includes the most recent known value at the time of the forecast as an input. Nevertheless, this value will not be used in the design stage of our model because it may cover up part of the effect of the variables to be analyzed.
2.2.2. Temperature Data
2.2.3. Calendar Data
2.2.4. Daylight
2.3. Linearization of Daylight Variables
2.3.1. Piecewise Linearization
2.3.2. Sigmoid Linearization
2.3.3. Validation of Linearized Variables
2.3.4. Other Modeling Improvements
2.4. Description of Tests
3. Results
3.1. Design Results
- -
- Midday and midnight hours are not improved significantly by the addition of available daylight information other than the month information. Midday and midnight modeling errors vary in a range of barely 0.07 percentage points.
- -
- Sunrise hours are improved from 1.92% to 1.83%.
- -
- Sunset hours are more significantly improved, going from 2.14% to 1.96% in out-of-sample test.
3.2. Assessment Results
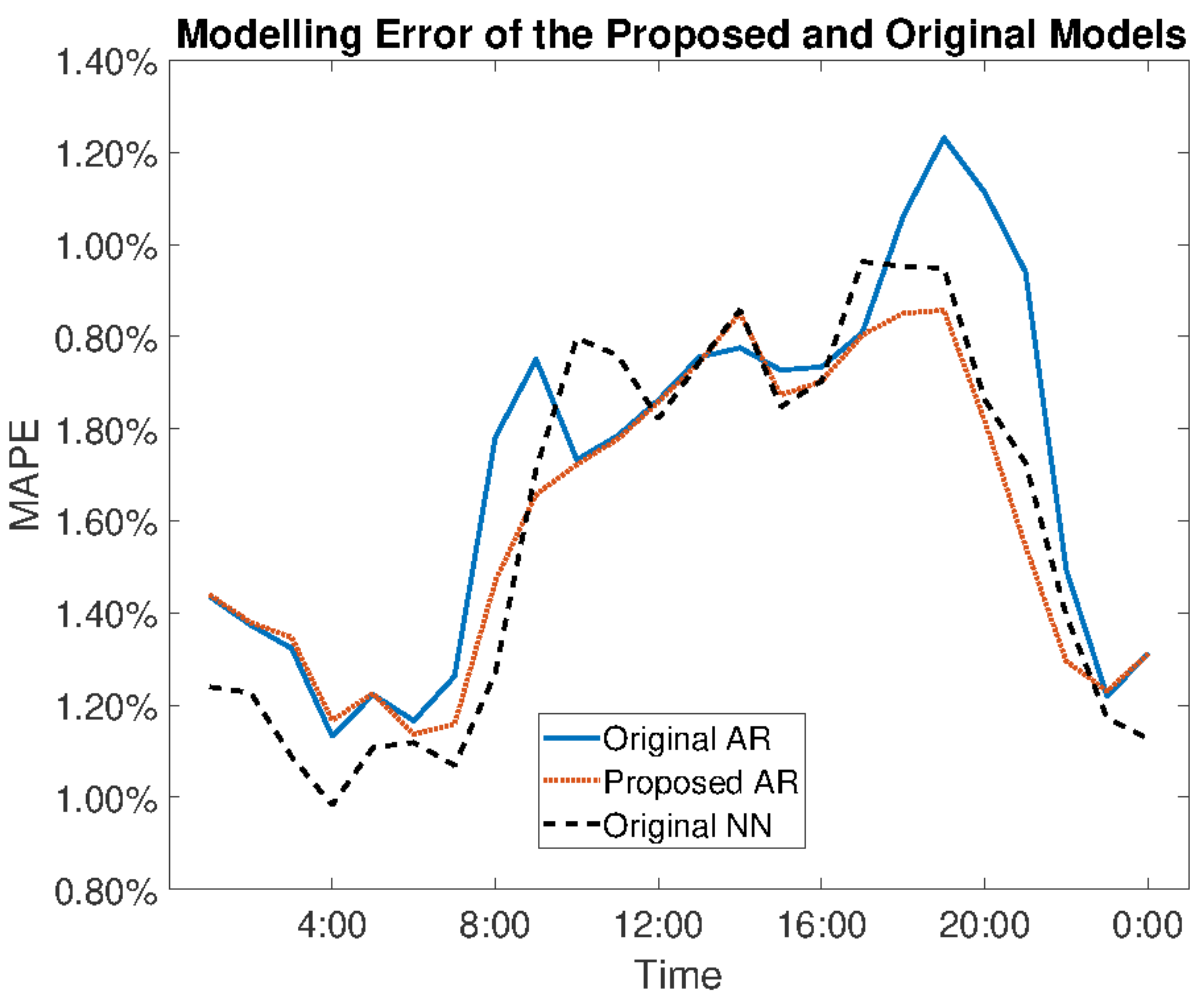
Proposed Model vs. NN
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chamandoust, H.; Derakhshan, G.; Hakimi, S.M.; Bahramara, S. Tri-Objective Optimal Scheduling of Smart Energy Hub System with Schedulable Loads. J. Clean. Prod. 2019, 236, 117584. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural Networks for Short-Term Load Forecasting: A Review and Evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Lopez Garcia, M.; Valero, S.; Senabre, C.; Gabaldon Marin, A. Short-Term Predictability of Load Series: Characterization of Load Data Bases. IEEE Trans. Power Syst. 2013, 28, 2466–2474. [Google Scholar] [CrossRef]
- Hernandez, L.; Baladron, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J.; Massana, J. A Survey on Electric Power Demand Forecasting: Future Trends in Smart Grids, Microgrids and Smart Buildings. IEEE Commun. Surv. Tutor. 2014, 16, 1460–1495. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical Load Forecasting Models: A Critical Systematic Review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Rodriguez, A.; Veiras, I.; Senabre, C. New Online Load Forecasting System for the Spanish Transport System Operator. Electr. Power Syst. Res. 2018, 154, 401–412. [Google Scholar] [CrossRef]
- Charlton, N.; Singleton, C. A Refined Parametric Model for Short Term Load Forecasting. Int. J. Forecast. 2014, 30, 364–368. [Google Scholar] [CrossRef]
- Wang, P.; Liu, B.; Hong, T. Electric Load Forecasting with Recency Effect: A Big Data Approach. Int. J. Forecast. 2016, 32, 585–597. [Google Scholar] [CrossRef]
- Yun, Z.; Quan, Z.; Caixin, S.; Shaolan, L.; Yuming, L.; Yang, S. RBF Neural Network and ANFIS-Based Short-Term Load Forecasting Approach in Real-Time Price Environment. IEEE Trans. Power Syst. 2008, 23, 853–858. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Senabre, C.; Aparicio, J.; Gabaldon, A. Application of SOM Neural Networks to Short-Term Load Forecasting: The Spanish Electricity Market Case Study. Electr. Power Syst. Res. 2012, 91, 18–27. [Google Scholar] [CrossRef]
- Hinojosa, V.H.; Hoese, A. Short-Term Load Forecasting Using Fuzzy Inductive Reasoning and Evolutionary Algorithms. IEEE Trans. Power Syst. 2010, 25, 565–574. [Google Scholar] [CrossRef]
- Wang, J.; Jin, S.; Qin, S.; Jiang, H. Swarm Intelligence-Based Hybrid Models for Short-Term Power Load Prediction. Math. Probl. Eng. 2014, 2014, 17. [Google Scholar] [CrossRef]
- Bashir, Z.A.; El-Hawary, M.E. Applying Wavelets to Short-Term Load Forecasting Using PSO-Based Neural Networks. IEEE Trans. Power Syst. 2009, 24, 20–27. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Short-Term Load Forecasting of Power Systems by Combination of Wavelet Transform and Neuro-Evolutionary Algorithm. Energy 2009, 34, 46–57. [Google Scholar] [CrossRef]
- Ghadimi, N.; Akbarimajd, A.; Shayeghi, H.; Abedinia, O. Two Stage Forecast Engine with Feature Selection Technique and Improved Meta-Heuristic Algorithm for Electricity Load Forecasting. Energy 2018, 161, 130–142. [Google Scholar] [CrossRef]
- Gao, W.; Darvishan, A.; Toghani, M.; Mohammadi, M.; Abedinia, O.; Ghadimi, N. Different States of Multi-Block Based Forecast Engine for Price and Load Prediction. Int. J. Electr. Power Energy Syst. 2019, 104, 423–435. [Google Scholar] [CrossRef]
- Motepe, S.; Hasan, A.N.; Stopforth, R. Improving Load Forecasting Process for a Power Distribution Network Using Hybrid AI and Deep Learning Algorithms. IEEE Access 2019, 7, 82584–82598. [Google Scholar] [CrossRef]
- Ryu, S.; Noh, J.; Kim, H. Deep Neural Network Based Demand Side Short Term Load Forecasting. Energies 2016, 10, 3. [Google Scholar] [CrossRef]
- Yin, L.; Sun, Z.; Gao, F.; Liu, H. Deep Forest Regression for Short-Term Load Forecasting of Power Systems. IEEE Access 2020, 8, 49090–49099. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-Term Load Forecasting With Deep Residual Networks. IEEE Trans. Smart Grid 2019, 10, 3943–3952. [Google Scholar] [CrossRef]
- Moral-Carcedo, J.; Pérez-García, J. Time of Day Effects of Temperature and Daylight on Short Term Electricity Load. Energy 2019, 174, 169–183. [Google Scholar] [CrossRef]
- Zhang, N.; Li, Z.; Zou, X.; Quiring, S.M. Comparison of Three Short-Term Load Forecast Models in Southern California. Energy 2019, 189, 116358. [Google Scholar] [CrossRef]
- Haben, S.; Giasemidis, G.; Ziel, F.; Arora, S. Short Term Load Forecasting and the Effect of Temperature at the Low Voltage Level. Int. J. Forecast. 2019, 35, 1469–1484. [Google Scholar] [CrossRef]
- Wang, Y.; Bielicki, J.M. Acclimation and the Response of Hourly Electricity Loads to Meteorological Variables. Energy 2018, 142, 473–485. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Senabre, C.; Gabaldón, A. Analysis of the Influence of Meteorological Variables on Real-Time Short-Term Load Forecasting in Balearic Islands. In Proceedings of the 2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 1 May 2017; pp. 10–15. [Google Scholar]
- Fan, S.; Chen, L. Short-Term Load Forecasting Based on an Adaptive Hybrid Method. IEEE Trans. Power Syst. 2006, 21, 392–401. [Google Scholar] [CrossRef]
- Arora, S.; Taylor, J.W. Short-Term Forecasting of Anomalous Load Using Rule-Based Triple Seasonal Methods. IEEE Trans. Power Syst. 2013, 28, 3235–3242. [Google Scholar] [CrossRef]
- López, M.; Sans, C.; Valero, S.; Senabre, C. Classification of Special Days in Short-Term Load Forecasting: The Spanish Case Study. Energies 2019, 12, 1253. [Google Scholar] [CrossRef]
- Rivers, N. Does Daylight Savings Time Save Energy? Evidence from Ontario. Environ. Resour. Econ. 2017. [Google Scholar] [CrossRef]
- Choi, S.; Pellen, A.; Masson, V. How Does Daylight Saving Time Affect Electricity Demand? An Answer Using Aggregate Data from a Natural Experiment in Western Australia. Energy Econ. 2017, 66, 247–260. [Google Scholar] [CrossRef]
- Verdejo, H.; Becker, C.; Echiburu, D.; Escudero, W.; Fucks, E. Impact of Daylight Saving Time on the Chilean Residential Consumption. Energy Policy 2016, 88, 456–464. [Google Scholar] [CrossRef]
- Hill, S.I.; Desobry, F.; Garnsey, E.W.; Chong, Y.-F. The Impact on Energy Consumption of Daylight Saving Clock Changes. Energy Policy 2010, 38, 4955–4965. [Google Scholar] [CrossRef]
- Afshin, M.; Sadeghian, A. PCA-Based Least Squares Support Vector Machines in Week-Ahead Load Forecasting. In Proceedings of the 2007 IEEE/IAS Industrial & Commercial Power Systems Technical Conference, Edmonton, AB, Canada, 6–11 May 2007; pp. 1–6. [Google Scholar]
- Bessec, M.; Fouquau, J. Short-Run Electricity Load Forecasting with Combinations of Stationary Wavelet Transforms. Eur. J. Oper. Res. 2018, 264, 149–164. [Google Scholar] [CrossRef]
- Do, L.P.C.; Lin, K.-H.; Molnár, P. Electricity Consumption Modelling: A Case of Germany. Econ. Model. 2016, 55, 92–101. [Google Scholar] [CrossRef]
- Cancelo, J.R.; Espasa, A.; Grafe, R. Forecasting the Electricity Load from One Day to One Week Ahead for the Spanish System Operator. Int. J. Forecast. 2008, 24, 588–602. [Google Scholar] [CrossRef]
- Caro, E.; Juan, J.; Cara, J. Periodically Correlated Models for Short-Term Electricity Load Forecasting. Appl. Math. Comput. 2020, 364, 124642. [Google Scholar] [CrossRef]
- ESIOS REE-Information System for the Electric System Operator. Available online: https://www.esios.ree.es/es2019 (accessed on 7 July 2019).
- Peng, Y.; Wang, Y.; Lu, X.; Li, H.; Shi, D.; Wang, Z.; Li, J. Short-Term Load Forecasting at Different Aggregation Levels with Predictability Analysis. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3385–3390. [Google Scholar]
- Pincus, S.M. Approximate Entropy: A Complexity Measure for Biological Time Series Data. In Proceedings of the Proceedings of the 1991 IEEE Seventeenth Annual Northeast Bioengineering Conference, Hartford, CT, USA, 4–5 April 1991; pp. 35–36. [Google Scholar]
- AEMET OpenData. 2019. Available online: http://www.aemet.es/es/datos_abiertos (accessed on 15 July 2019).
- Kotchen, M.J.; Grant, L.E. Does Daylight Saving Time Save Energy? Evidence from a Natural Experiment in Indiana. Rev. Econ. Stat. 2011, 93, 1172–1185. [Google Scholar] [CrossRef]
- Kellogg, R.; Wolff, H. Daylight Time and Energy: Evidence from an Australian Experiment. J. Environ. Econ. Manag. 2008, 56, 207–220. [Google Scholar] [CrossRef]
- Mirza, F.M.; Bergland, O. The Impact of Daylight Saving Time on Electricity Consumption: Evidence from Southern Norway and Sweden. Energy Policy 2011, 39, 3558–3571. [Google Scholar] [CrossRef]
- López, M. Daylight Effect on the Electricity Demand in Spain and Assessment of Daylight Saving Time Policies. Energy Policy 2020, 140, 111419. [Google Scholar] [CrossRef]




| Embedded Dimension | 1 | 4 | 8 | 12 | 16 | 20 | 24 |
|---|---|---|---|---|---|---|---|
| ApEn | 1.038 | 0.553 | 0.266 | 0.125 | 0.078 | 0.058 | 0.034 |
| Time delay = 1; radius = 0.2 times the standard deviation of the load series | |||||||
| Lag | MAD | BCN | SEV | ZAR | BIL |
|---|---|---|---|---|---|
| 0 | HDD/CDD | HDD/CDD | HDD/CDD | HDD/CDD | ---/CDD |
| 1 | ---/--- | HDD/CDD | ---/--- | ---/--- | ---/--- |
| 2 | ---/--- | ---/--- | ---/--- | ---/--- | ---/--- |
| Out-of-Sample | 7 a.m. | 8 a.m. | 9 a.m. | Avg. Sunrise | 4 p.m. | 5 p.m. | 6 p.m. | 7 p.m. | 8 p.m. | 9 p.m. | 10 p.m. | Avg. Sunset | Avg. Rest |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| w/o daylight | 2.23% | 2.91% | 2.76% | 2.63% | 2.47% | 2.50% | 2.68% | 3.65% | 3.61% | 3.55% | 2.51% | 2.86% | 2.30% |
| piecewise | 2.21% | 2.52% | 2.62% | 2.45% | 2.47% | 2.49% | 2.50% | 2.44% | 2.37% | 2.24% | 2.09% | 2.40% | 2.30% |
| sigmoid | 2.21% | 2.55% | 2.61% | 2.46% | 2.47% | 2.50% | 2.51% | 2.43% | 2.35% | 2.24% | 2.08% | 2.40% | 2.30% |
| # | Name | Description | Vars. Per Hour | Period |
|---|---|---|---|---|
| 1 | Base w/o month | Original model in which eleven binary variables coding the month are removed. | 87 | 2011–2017 |
| 2 | Base | Original model | 98 | |
| 3 | Base + piecewise | Original model with piecewise linearization (n = 10) | 108 | |
| 4 | Base + sigmoid | Original model with sigmoid linearization | 99 | |
| 5 | Base + piecewise by type of day | Original model with piecewise linearization for each type of day (n = 10). | 138 | |
| 6 | Base + sigmoid by type of day | Original model with sigmoid linearization for each type of day. | 103 |
| Model Nr. | Sunrise (7 a.m.–9 a.m.) | Mid-Day (10 a.m.–5 p.m.) | Sunset (6 p.m.–10 p.m.) | Mid-Night (11 p.m.–6 a.m.) | All Day |
|---|---|---|---|---|---|
| 1 | 2.08% | 2.01% | 2.77% | 1.81% | 2.09% |
| 2 | 1.92% | 2.00% | 2.14% | 1.72% | 1.91% |
| 3 | 1.88% | 2.00% | 2.06% | 1.72% | 1.90% |
| 4 | 1.89% | 2.00% | 2.07% | 1.72% | 1.90% |
| 5 | 1.83% | 1.97% | 1.96% | 1.65% | 1.84% |
| 6 | 1.84% | 1.99% | 1.96% | 1.70% | 1.86% |
| Model | Sunrise (7 a.m.–9 a.m.) | Mid-Day | Sunset (6 p.m.–10 p.m.) | Mid-Night | All Day | |
|---|---|---|---|---|---|---|
| OVERALL | Original AR | 1.33% | 1.45% | 1.56% | 1.17% | 1.35% |
| Proposed AR | 1.21% | 1.45% | 1.38% | 1.17% | 1.30% | |
| Original NN | 1.18% | 1.48% | 1.43% | 1.10% | 1.29% | |
| DST WEEK | Original AR | 1.90% | 1.85% | 2.53% | 1.44% | 1.85% |
| Proposed AR | 1.37% | 1.80% | 2.09% | 1.42% | 1.67% | |
| Original NN[M1] | 1.35% | 1.83% | 2.14% | 1.38% | 1.68% |
| Model | Sunrise (7 a.m.–9 a.m.) | Mid-Day | Sunset (6 p.m.–10 p.m.) | Mid-Night | All Day |
|---|---|---|---|---|---|
| Persistent (7-days) | 4.64% | 5.10% | 5.18% | 3.68% | 4.58% |
| * Cancelo et Al [37] | 1.48% | 1.67% | 1.70% | 1.38% | 1.56% |
| Original AR 37% + NN 63% | 1.12% | 1.36% | 1.37% | 1.04% | 1.21% |
| * Caro et Al [38] | 1.26% | 1.33% | 1.44% | 1.06% | 1.25% |
| Proposed AR 59% + NN 41% | 1.09% | 1.34% | 1.30% | 1.05% | 1.20% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, M.; Valero, S.; Sans, C.; Senabre, C. Use of Available Daylight to Improve Short-Term Load Forecasting Accuracy. Energies 2021, 14, 95. https://doi.org/10.3390/en14010095
López M, Valero S, Sans C, Senabre C. Use of Available Daylight to Improve Short-Term Load Forecasting Accuracy. Energies. 2021; 14(1):95. https://doi.org/10.3390/en14010095
Chicago/Turabian StyleLópez, Miguel, Sergio Valero, Carlos Sans, and Carolina Senabre. 2021. "Use of Available Daylight to Improve Short-Term Load Forecasting Accuracy" Energies 14, no. 1: 95. https://doi.org/10.3390/en14010095
APA StyleLópez, M., Valero, S., Sans, C., & Senabre, C. (2021). Use of Available Daylight to Improve Short-Term Load Forecasting Accuracy. Energies, 14(1), 95. https://doi.org/10.3390/en14010095





