Towards Engineered Hydrochars: Application of Artificial Neural Networks in the Hydrothermal Carbonization of Sewage Sludge
Abstract
1. Introduction
2. Materials and Methods
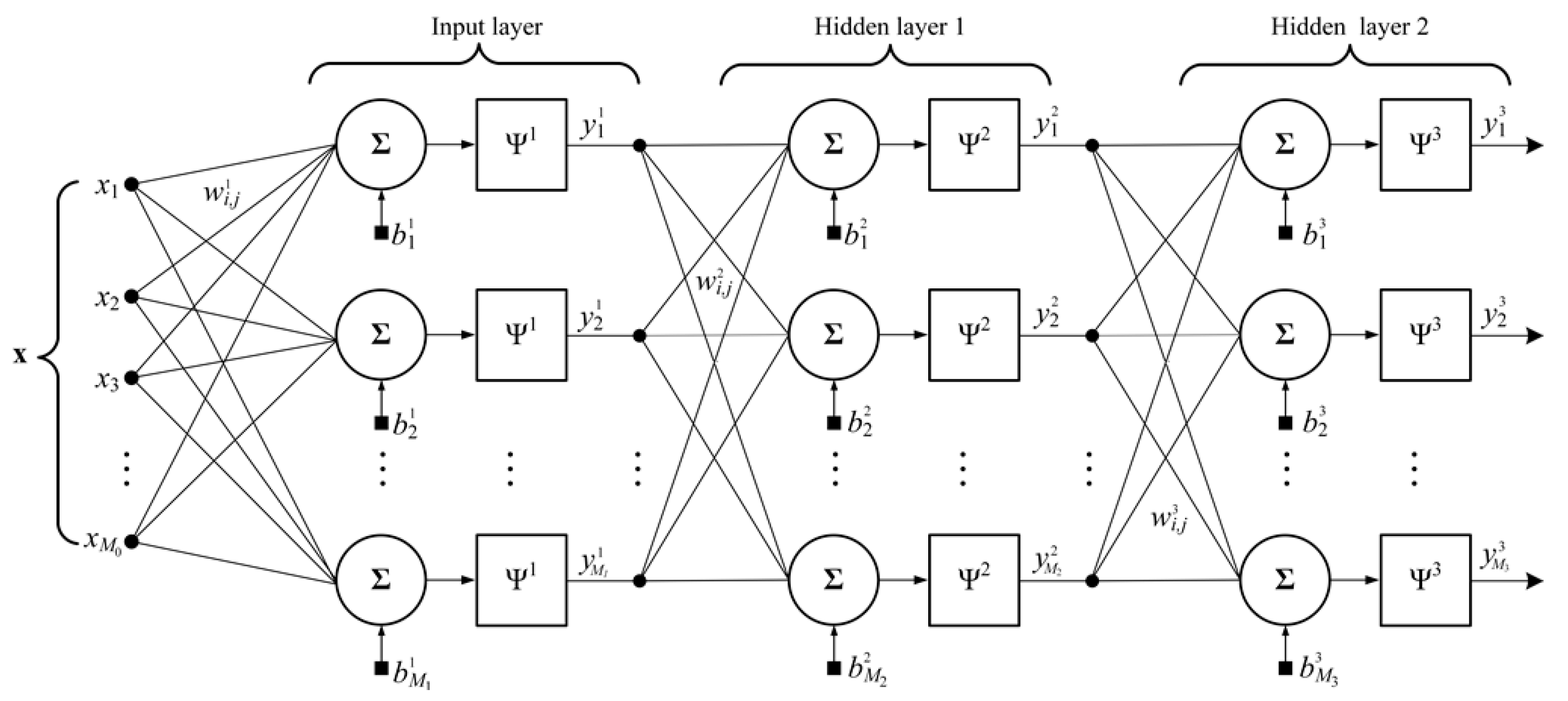
2.1. Artificial Neural Network Architecture
2.2. Pre-Processing of Data
3. Results
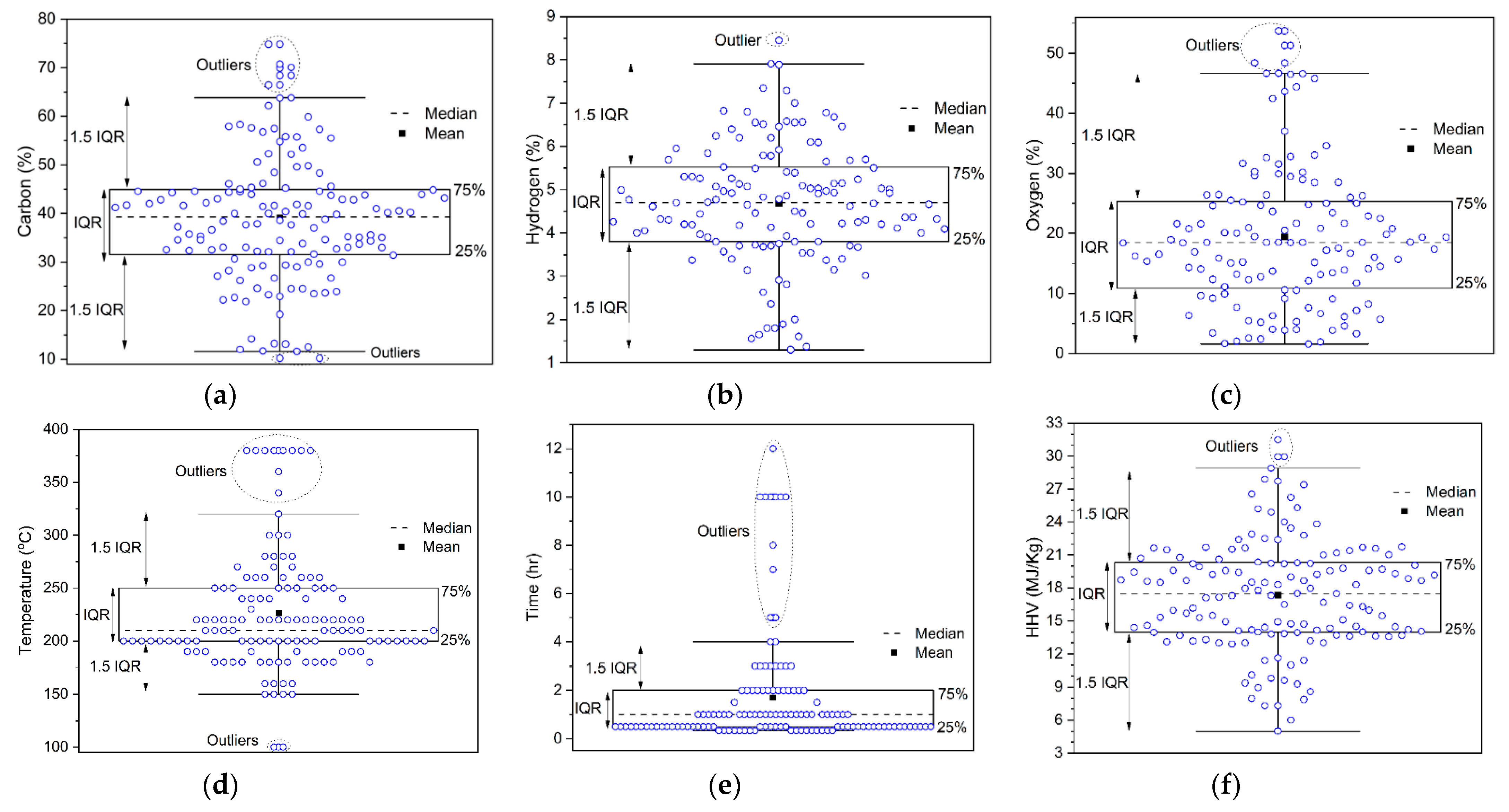
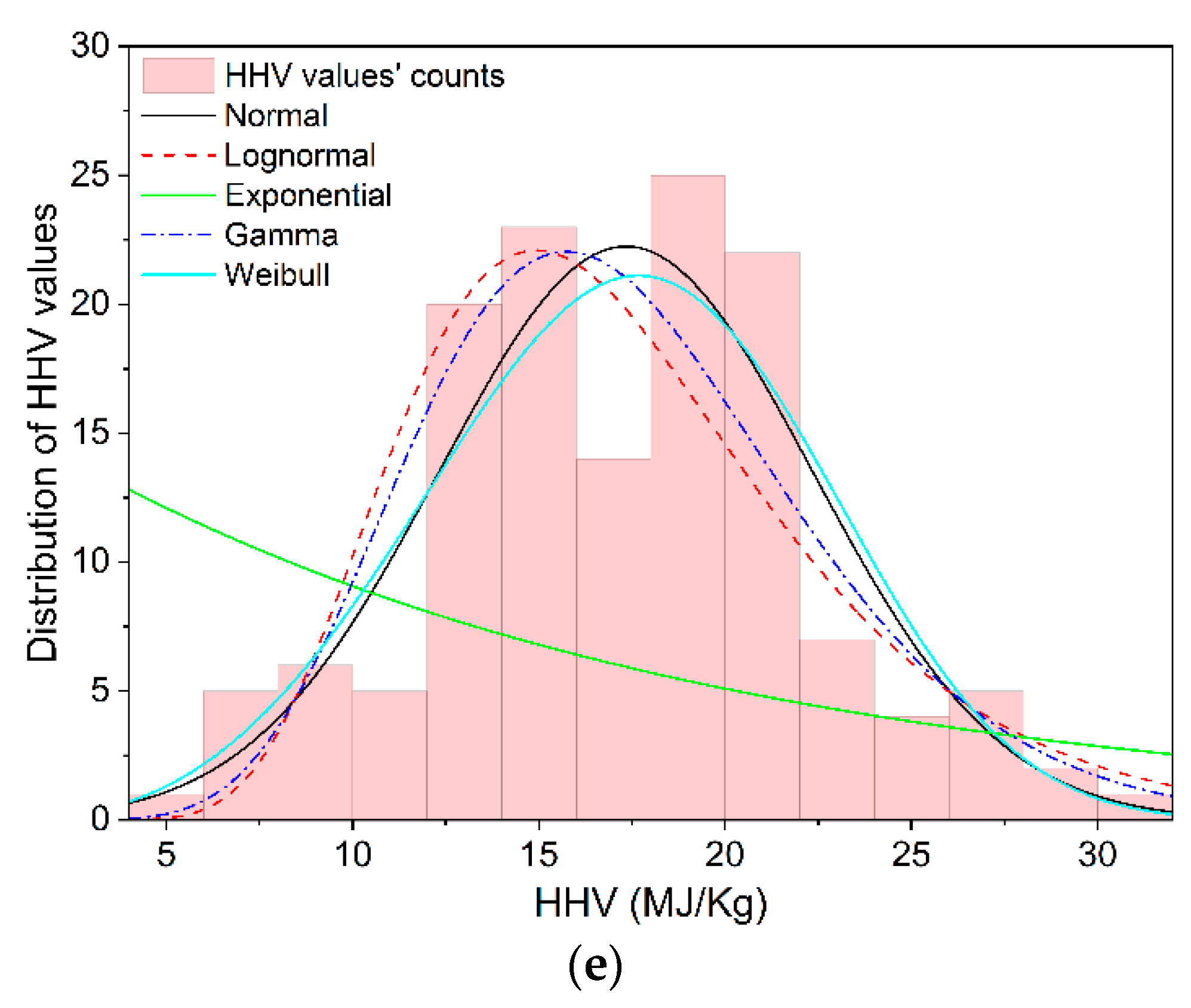
3.1. Hydrochar Properties’ Statistical Analysis
3.2. Correlation Patterns Between Hydrochar Properties
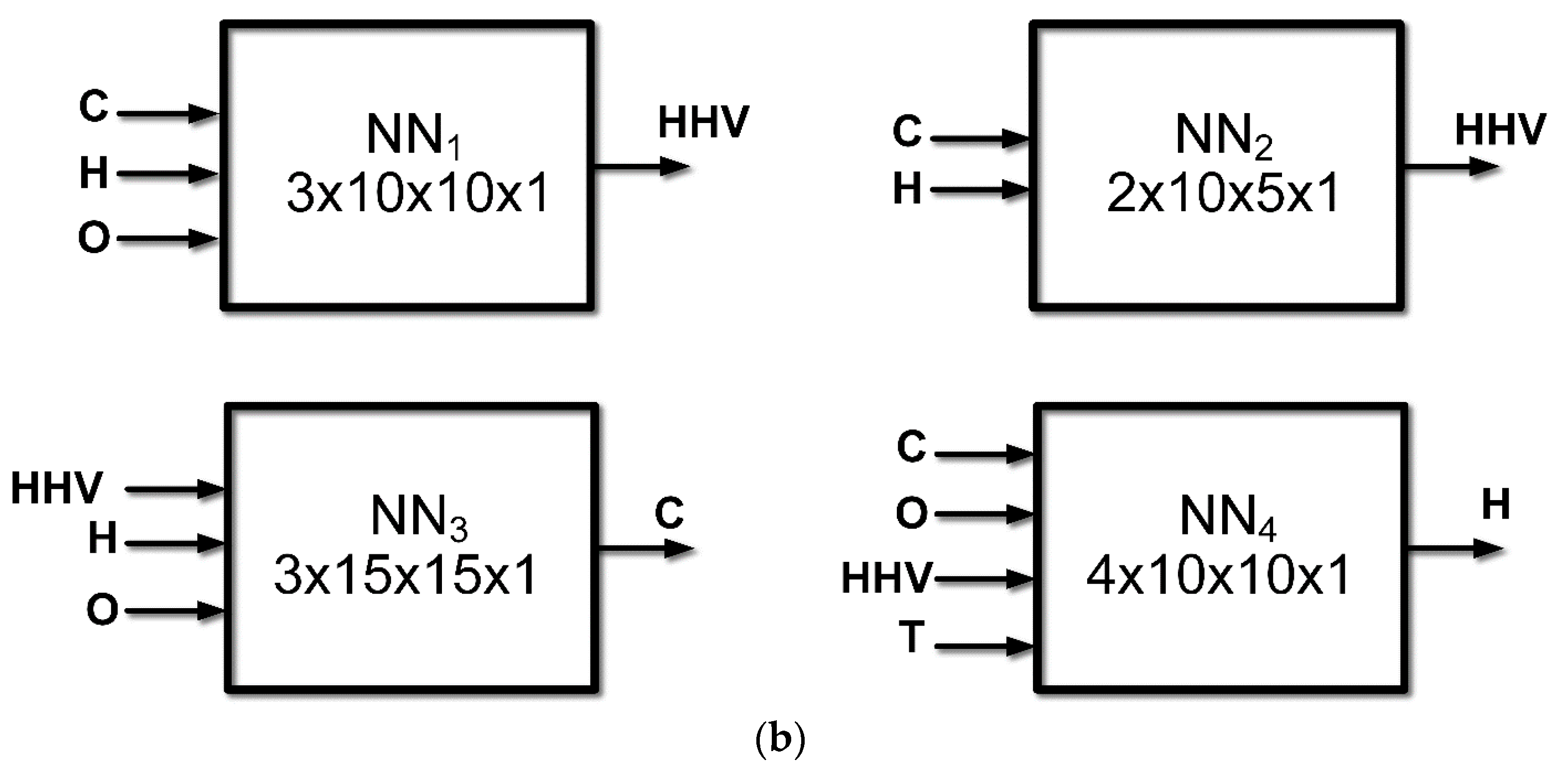
3.3. Artificial Neural Network Modeling
3.4. ANN Models’ Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Libra, J.A.; Ro, K.S.; Kammann, C.; Funke, A.; Berge, N.D.; Neubauer, Y.; Titirici, M.-M.; Fühner, C.; Bens, O.; Kern, J.; et al. Hydrothermal carbonization of biomass residuals: A comparative review of the chemistry, processes and applications of wet and dry pyrolysis. Biofuels 2011, 2, 71–106. [Google Scholar] [CrossRef]
- Heidari, M.; Dutta, A.; Acharya, B.; Mahmud, S. A review of the current knowledge and challenges of hydrothermal carbonization for biomass conversion. J. Energy Inst. 2019, 92, 1779–1799. [Google Scholar] [CrossRef]
- Wang, T.; Zhai, Y.; Zhu, Y.; Li, C.; Zeng, G. A review of the hydrothermal carbonization of biomass waste for hydrochar formation: Process conditions, fundamentals, and physicochemical properties. Renew. Sustain. Energy Rev. 2018, 90, 223–247. [Google Scholar] [CrossRef]
- Vardiambasis, I.O.; Kapetanakis, T.N.; Nikolopoulos, C.D.; Trang, T.K.; Tsubota, T.; Keyikoglu, R.; Khataee, A.; Kalderis, D. Hydrochars as emerging biofuels: Recent advances and application of artificial neural networks for the prediction of heating values. Energies 2020, 13, 4572. [Google Scholar] [CrossRef]
- Li, S.; Zeng, W.; Jia, Z.; Wu, G.; Xu, H.; Peng, Y. Phosphorus species transformation and recovery without apatitein FeCl3-assisted sewage sludge hydrothermal treatment. Chem. Eng. J. 2020, 399, 125735. [Google Scholar] [CrossRef]
- Waldmüller, W.; Herdzik, S.; Gaderer, M. Combined filtration and oxalic acid leaching for recovering phosphorus from hydrothermally carbonized sewage sludge. J. Environ. Chem. Eng. 2021, 9, 104800. [Google Scholar] [CrossRef]
- Medina-Martos, E.; Istrate, I.-R.; Villamil, J.A.; Gálvez-Martos, J.-L.; Dufour, J.; Mohedano, A.F. Techno-economic and life cycle assessment of an integrated hydrothermal carbonization system for sewage sludge. J. Clean. Prod. 2020, 277, 122930. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, X.; Zheng, C.; Huang, T.; Lu, X.; Tian, Y. Co-hydrothermal Carbonization of Water Hyacinth and Sewage Sludge: Effects of Aqueous Phase Recirculation on the Characteristics of Hydrochar. Energy Fuels 2020, 34, 14147–14158. [Google Scholar] [CrossRef]
- Lu, X.; Ma, X.; Chen, X. Co-hydrothermal carbonization of sewage sludge and lignocellulosic biomass: Fuel properties and heavy metal transformation behaviour of hydrochars. Energy 2021, 221, 119896. [Google Scholar] [CrossRef]
- McGaughy, K.; Toufiq Reza, M. Hydrothermal carbonization of food waste: Simplified process simulation model based on experimental results. Biomass Convers. Biorefin. 2018, 8, 283–292. [Google Scholar] [CrossRef]
- Gallifuoco, A. A new approach to kinetic modeling of biomass hydrothermal carbonization. ACS Sustain. Chem. Eng. 2019, 7, 13073–13080. [Google Scholar] [CrossRef]
- Conag, A.T.; Villahermosa, J.E.R.; Cabatingan, L.K.; Go, A.W. Predictive HHV model for raw and torrefied sugarcane residues. Waste Biomass Valorization 2019, 10, 1929–1943. [Google Scholar] [CrossRef]
- Vallejo, F.; Díaz-Robles, L.A.; Vega, R.; Cubillos, F. A novel approach for prediction of mass yield and higher calorific value of hydrothermal carbonization by a robust multilinear model and regression trees. J. Energy Inst. 2020, 93, 1755–1762. [Google Scholar] [CrossRef]
- Akdeniz, F.; Biçil, M.; Karadede, Y.; Özbek, F.E.; Özdemir, G. Application of real valued genetic algorithm on prediction of higher heating values of various lignocellulosic materials using lignin and extractive contents. Energy 2018, 160, 1047–1054. [Google Scholar] [CrossRef]
- Tasca, A.L.; Puccini, M.; Gori, R.; Corsi, I.; Galletti, A.M.R.; Vitolo, S. Hydrothermal carbonization of sewage sludge: A critical analysis of process severity, hydrochar properties and environmental implications. Waste Manag. 2019, 93, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Liodakis, G.; Arvanitis, D.; Vardiambasis, I.O. Neural network based digital receiver for radio communications. WSEAS Trans. Syst. 2004, 3, 3308–3313. [Google Scholar]
- Kapetanakis, T.N.; Vardiambasis, I.O.; Ioannidou, M.P.; Konstantaras, A.I. Recent Trends on Electromagnetic Environmental Effects for Aeronautics and Space Applications; Nikolopoulos, C.D., Ed.; IGI Global: Hershey PA, USA, 2021; Chapter 7; pp. 186–225. [Google Scholar]
- Kapetanakis, T.N.; Vardiambasis, I.O.; Ioannidou, M.P.; Maras, A. Neural network modeling for the solution of the inverse loop antenna radiation problem. IEEE Trans. Antennas Propag. 2018, 66, 6283–6290. [Google Scholar] [CrossRef]
- Kapetanakis, T.N.; Vardiambasis, I.O.; Lourakis, E.I.; Maras, A. Applying neuro-fuzzy soft computing techniques to the circular loop antenna radiation problem. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1673–1676. [Google Scholar] [CrossRef]
- Vardiambasis, I.O.; Tsalamengas, J.L.; Fikioris, J.G. Hybrid wave propagation in circularly shielded microslot lines. IEEE Trans. Microw. Theory Technol. 1995, 43, 1960–1966. [Google Scholar] [CrossRef]
- Vardiambasis, I.O.; Tsalamengas, J.L.; Fikioris, J.G. Plane wave scattering by slots on a ground plane loaded with semicircular dielectric cylinders in case of oblique incidence and arbitrary polarization. IEEE Trans. Antennas Propag. 1998, 46, 1571–1579. [Google Scholar] [CrossRef]
- Adamidis, G.A.; Vardiambasis, I.O.; Ioannidou, M.P.; Kapetanakis, T.N. Design and implementation of single-layer 4× 4 and 8× 8 Butler matrices for multibeam antenna arrays. Int. J. Antennas Propag. 2019, 1645281, 1–12. [Google Scholar] [CrossRef]
- Sergaki, E.; Spiliotis, G.; Vardiambasis, I.O.; Kapetanakis, T.; Krasoudakis, A.; Giakos, G.C.; Zervakis, M.; Polydorou, A. Application of ANN and ANFIS for detection of brain tumors in MRIs by using DWT and GLCM texture analysis. Int. Conf. Imaging Syst. Technol. 2018, 1–6. [Google Scholar] [CrossRef]
- Bhange, V.P.; Bhivgade, U.V.; Vaidya, A.N. Artificial neural network modeling in pretreatment of garden biomass for lignocellulose degradation. Waste Biomass Valorization 2019, 10, 1571–1583. [Google Scholar] [CrossRef]
- Baruah, D.; Baruah, D.C.; Hazarika, M.K. Artificial neural network based modeling of biomass gasification in fixed bed downdraft gasifiers. Biomass Bioenergy 2017, 98, 264–271. [Google Scholar] [CrossRef]
- Nasrudin, N.A.; Jewaratnam, J.; Hossain, M.A.; Ganeson, P.B. Performance comparison of feedforward neural network training algorithms in modelling microwave pyrolysis of oil palm fibre for hydrogen and biochar production. Asia Pac. J. Chem. Eng. 2020, 15. [Google Scholar] [CrossRef]
- Hawthorne, S.B.; Lagadec, A.J.M.; Kalderis, D.; Lilke, A.V.; Miller, D.J. Pilot-scale destruction of TNT, RDX, and HMX on contaminated soils using subcritical water. Environ. Sci. Technol. 2000, 34, 3224–3228. [Google Scholar] [CrossRef]
- Daskalaki, V.M.; Timotheatou, E.S.; Katsaounis, A.; Kalderis, D. Degradation of Reactive Red 120 using hydrogen peroxide in subcritical water. Desalination 2011, 274, 200–205. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, X.; Ok, Y.S. The application of machine learning methods for prediction of metal sorption onto biochars. J. Hazard. Mater. 2019, 378, 120727. [Google Scholar] [CrossRef]
- Li, J.; Pan, L.; Suvarna, M.; Tong, Y.W.; Wang, X. Fuel properties of hydrochar and pyrochar: Prediction and exploration with machine learning. Appl. Energy 2020, 269, 115166. [Google Scholar] [CrossRef]
- Deep Learning Toolbox v12.1 (2019a); MathWorks, The Inc.: Natick, MA, USA, 1999.
- Mazumder, S.; Saha, P.; Reza, M.T. Co-hydrothermal carbonization of coal waste and food waste: Fuel characteristics. Biomass Convers. Biorefin. 2020. [Google Scholar] [CrossRef]
- Mazumder, S.; Saha, P.; McGaughy, K.; Saba, A.; Reza, M.T. Technoeconomic analysis of co-hydrothermal carbonization of coal waste and food waste. Biomass Convers. Biorefin. 2020. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Afzal, M.T. HHV predicting correlations for torrefied biomass using proximate and ultimate analyses. Bioengineering 2017, 4, 7. [Google Scholar] [CrossRef]
- Verleysen, Μ.; François, D.; Simon, G.; Wertz, V. On the effects of dimensionality on data analysis with neural networks. In Proceedings of the 7th International Work-Conference on Artificial & Natural Neural Networks (IWANN 2003), Menorca, Spain, 3–6 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2687, pp. 105–112. [Google Scholar]
- Konstantaras, A. Deep learning and parallel processing spatio-temporal clustering unveil new Ionian distinct seismic zone. Informatics 2020, 7, 39. [Google Scholar] [CrossRef]
- Zheng, X.; Jiang, Z.; Ying, Z.; Song, J.; Chen, W.; Wang, B. Role of feedstock properties and hydrothermal carbonization conditions on fuel properties of sewage sludge-derived hydrochar using multiple linear regression technique. Fuel 2020, 271, 117609. [Google Scholar] [CrossRef]
- Zhao, P.; Shen, Y.; Ge, S.; Yoshikawa, K. Energy recycling from sewage sludge by producing solid biofuel with hydrothermal carbonization. Energy Convers. Manag. 2014, 78, 815–821. [Google Scholar] [CrossRef]
- Wang, L.; Chang, Y.; Li, A. Hydrothermal carbonization for energy-efficient processing of sewage sludge: A review. Renew. Sustain. Energy Rev. 2019, 108, 423–440. [Google Scholar] [CrossRef]
- Teoh, S.K.; Li, L.Y. Feasibility of alternative sewage sludge treatment meth-ods from a lifecycle assessment (LCA) perspective. J. Clean. Prod. 2020, 247, 119495. [Google Scholar] [CrossRef]
- Han, L.; Ro, K.S.; Sun, K.; Sun, H.; Wang, Z.; Libra, J.A.; Xing, B. New evidence for high sorption capacity of hydrochar for hydrophobic organic pollutants. Environ. Sci. Technol. 2016, 50, 13274–13282. [Google Scholar] [CrossRef] [PubMed]
- Tasca, A.L.; Stefanelli, E.; Galletti, A.M.R.; Gori, R.; Mannarino, G.; Vitolo, S.; Puccini, M. Hydrothermal carbonization of sewage sludge: Analysis of process severity and solid content. Chem. Eng. Technol. 2020, 43, 2382–2392. [Google Scholar] [CrossRef]





| Temperature | Time | Carbon | Hydrogen | Oxygen | HHV | Solid Yield | ||
|---|---|---|---|---|---|---|---|---|
| Temperature | r | 1.000 | −0.162 | −0.067 | −0.229 | −0.440 | 0.055 | −0.310 |
| p-value | -- | 0.058 | 0.474 | 0.015 | 0.000 | 0.550 | 0.003 | |
| Time | r | −0.162 | 1.000 | 0.092 | −0.099 | −0.173 | −0.111 | 0.061 |
| p-value | 0.058 | -- | 0.329 | 0.306 | 0.076 | 0.226 | 0.571 | |
| Carbon | r | −0.067 | 0.092 | 1.000 | 0.719 | 0.202 | 0.821 | −0.246 |
| p-value | 0.474 | 0.329 | -- | 0.000 | 0.022 | 0.000 | 0.049 | |
| Hydrogen | r | −0.229 | −0.099 | 0.719 | 1.000 | 0.416 | 0.694 | −0.050 |
| p-value | 0.015 | 0.306 | 0.000 | -- | 0.000 | 0.000 | 0.705 | |
| Oxygen | r | −0.440 | −0.173 | 0.202 | 0.416 | 1.000 | 0.172 | 0.460 |
| p-value | 0.000 | 0.076 | 0.022 | 0.000 | -- | 0.060 | 0.000 | |
| HHV | r | 0.055 | −0.111 | 0.821 | 0.694 | 0.172 | 1.000 | −0.398 |
| p-value | 0.550 | 0.226 | 0.000 | 0.000 | 0.060 | -- | 0.000 | |
| Solid Yield | r | −0.310 | 0.061 | −0.246 | −0.050 | 0.460 | −0.398 | 1.000 |
| p-value | 0.003 | 0.571 | 0.049 | 0.705 | 0.000 | 0.000 | -- | |
| Significance Level | p < 0.05 | Temperature | Time | Carbon | Hydrogen | Oxygen | HHV | Solid Yield |
| H, O, SY | -- | H, O, HHV, SY | T, C, O, HHV | T, C, H, SY | C, H, SY | T, C, O, HHV |
| Table 2. Cont. | MAE | RMSE | RE |
|---|---|---|---|
| NN1 | 0.483 | 0.622 | 0.028 |
| NN2 | 0.189 | 0.622 | 0.033 |
| NN3 | 1.553 | 2.164 | 0.041 |
| NN4 | 0.790 | 1.035 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapetanakis, T.N.; Vardiambasis, I.O.; Nikolopoulos, C.D.; Konstantaras, A.I.; Trang, T.K.; Khuong, D.A.; Tsubota, T.; Keyikoglu, R.; Khataee, A.; Kalderis, D. Towards Engineered Hydrochars: Application of Artificial Neural Networks in the Hydrothermal Carbonization of Sewage Sludge. Energies 2021, 14, 3000. https://doi.org/10.3390/en14113000
Kapetanakis TN, Vardiambasis IO, Nikolopoulos CD, Konstantaras AI, Trang TK, Khuong DA, Tsubota T, Keyikoglu R, Khataee A, Kalderis D. Towards Engineered Hydrochars: Application of Artificial Neural Networks in the Hydrothermal Carbonization of Sewage Sludge. Energies. 2021; 14(11):3000. https://doi.org/10.3390/en14113000
Chicago/Turabian StyleKapetanakis, Theodoros N., Ioannis O. Vardiambasis, Christos D. Nikolopoulos, Antonios I. Konstantaras, Trinh Kieu Trang, Duy Anh Khuong, Toshiki Tsubota, Ramazan Keyikoglu, Alireza Khataee, and Dimitrios Kalderis. 2021. "Towards Engineered Hydrochars: Application of Artificial Neural Networks in the Hydrothermal Carbonization of Sewage Sludge" Energies 14, no. 11: 3000. https://doi.org/10.3390/en14113000
APA StyleKapetanakis, T. N., Vardiambasis, I. O., Nikolopoulos, C. D., Konstantaras, A. I., Trang, T. K., Khuong, D. A., Tsubota, T., Keyikoglu, R., Khataee, A., & Kalderis, D. (2021). Towards Engineered Hydrochars: Application of Artificial Neural Networks in the Hydrothermal Carbonization of Sewage Sludge. Energies, 14(11), 3000. https://doi.org/10.3390/en14113000










