Artificial Neural Network Simulation of Energetic Performance for Sorption Thermal Energy Storage Reactors
Abstract
:1. Introduction
2. Methodology
2.1. Recurrent Neural Network
2.2. Data Processing
3. Results and Discussion
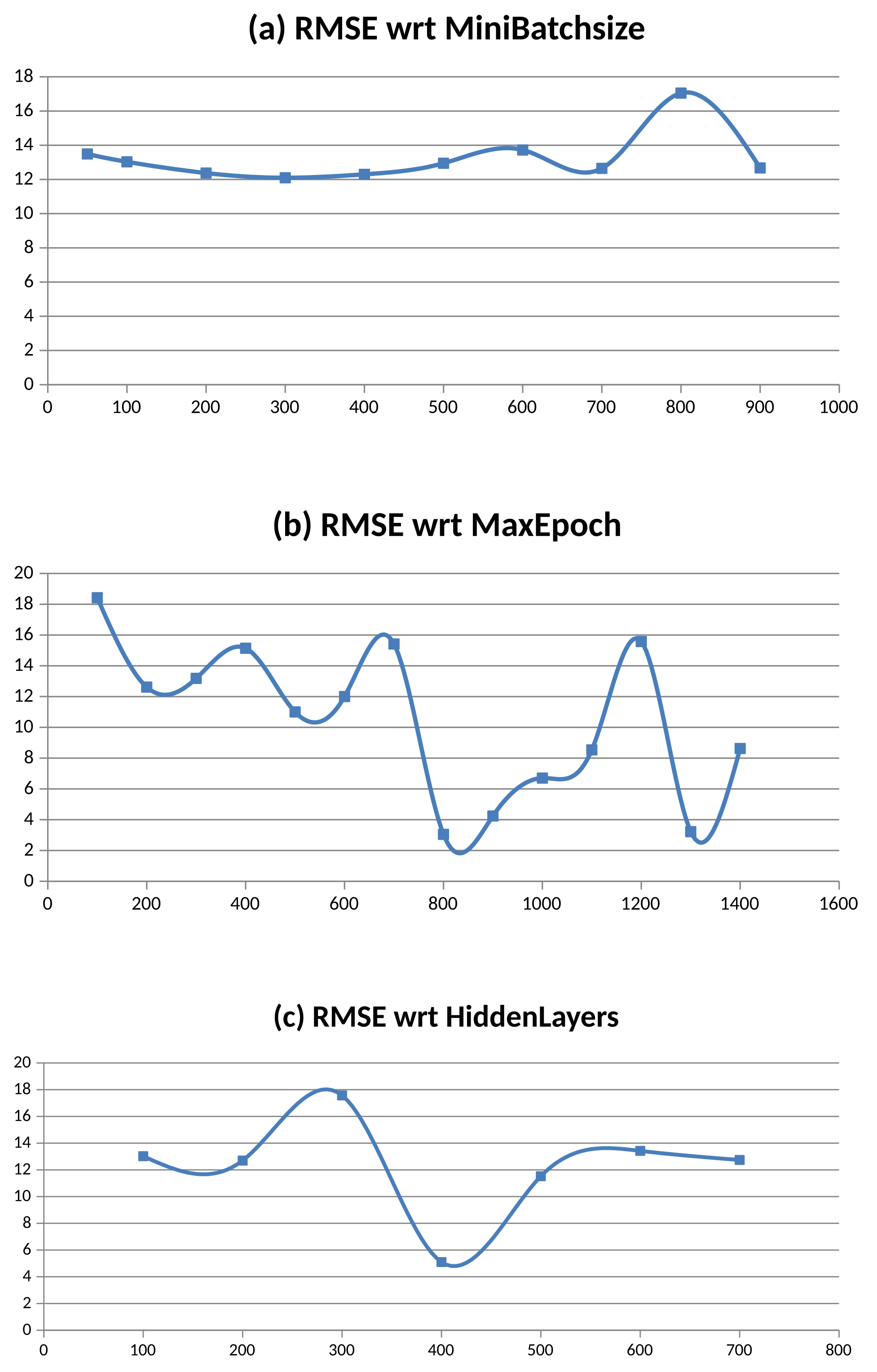
3.1. Determination of the Optimal Rnn Parameters for Training
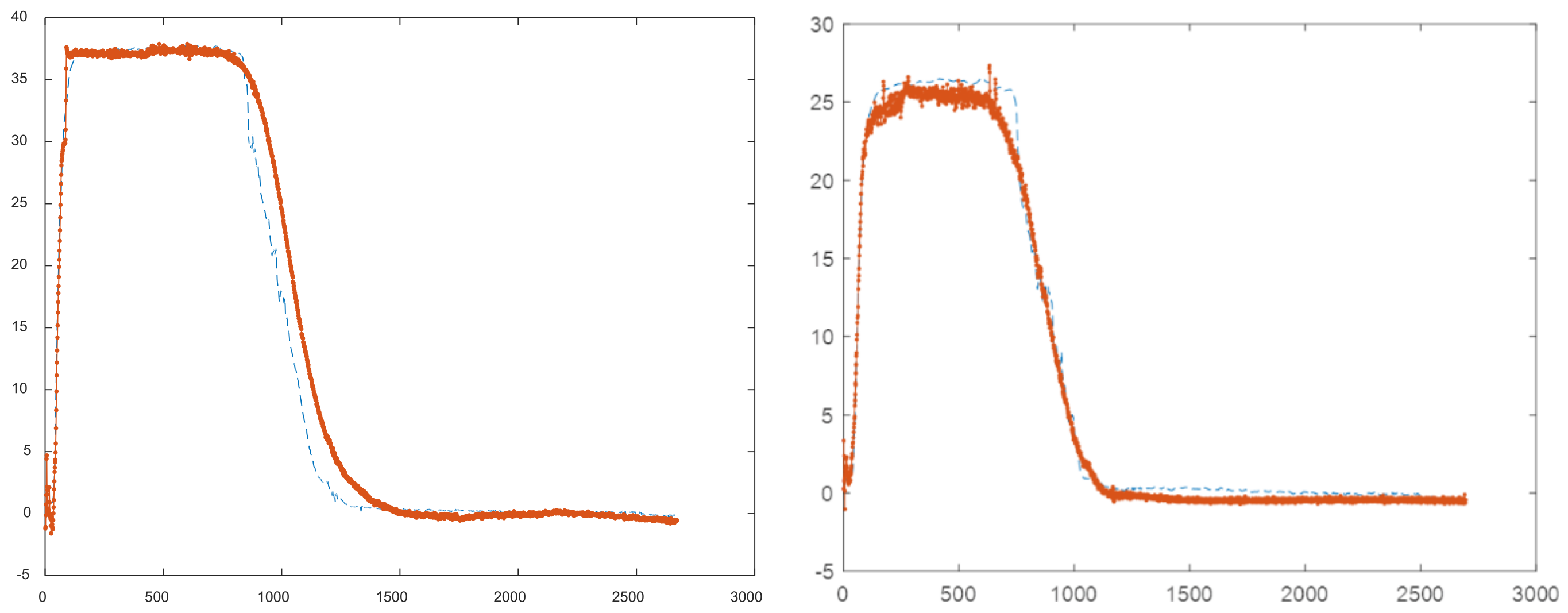
3.2. Validation of the Model with the Same Training and Verification Dataset
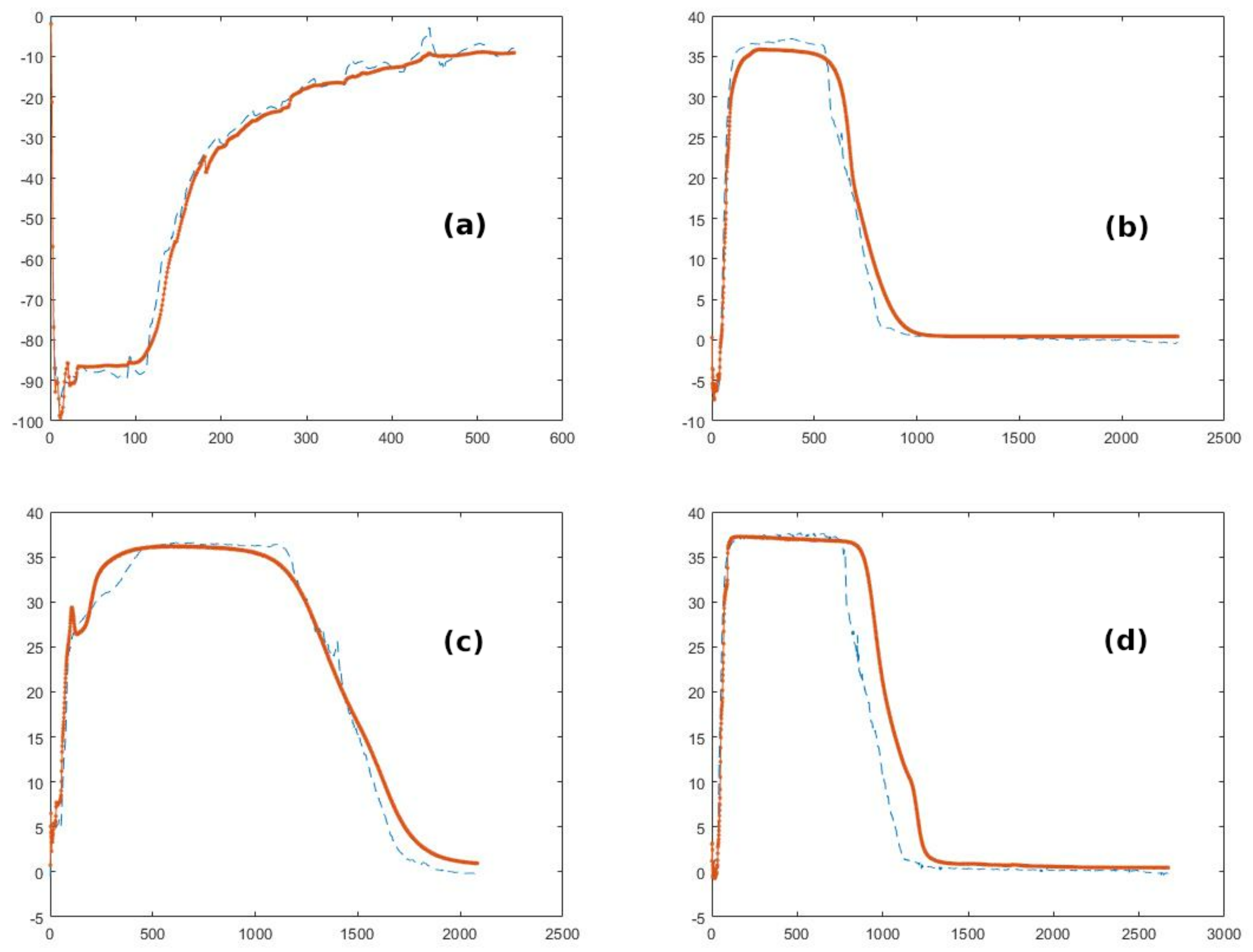
3.3. Validation of the Model with Specific Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Training Code (Matlab)
- %% Create and train a Recurrent Neural Network (RNN)
- %
- % A set of data is used to train the network, where inputs
- % and outputs are known. Another set of data is used to test
- % (validate) the accuracy of the RNN.
- %
- % Graphs for each cycles will be plotted at the end of the
- % program to compare the predicted values with the
- % experimental ones.
- %% Initialisation of the data
- % Load the data from the files
- filenamePredictorsX = fullfile("TrainingX.txt");
- filenamePredictorsY = fullfile("TrainingY.txt");
- % Put the data in matrix XTrain for the inputs and YTrain
- % for the outputs using the prepareData() function
- [XTrain] = prepareData(filenamePredictorsX);
- [YTrain] = prepareData(filenamePredictorsY);
- % Normalise matrix XTrain
- mu = mean([XTrain{:}],2);
- sig = std([XTrain{:}],0,2);
- for i = 1:numel(XTrain)
- XTrain{i} = (XTrain{i} - mu) ./ sig;
- end
- %% Create the Neural Network
- % Neural Network parameters
- miniBatchSize = 100;
- maxEpochs = 200;
- numHiddenUnits = 200;
- % Neural network initialisation
- numResponses = size(YTrain{1},1);
- featureDimension = size(XTrain{1},1);
- layers = [ …
- sequenceInputLayer(featureDimension)
- lstmLayer(numHiddenUnits,’OutputMode’,’sequence’)
- fullyConnectedLayer(50)
- dropoutLayer(0.5)
- fullyConnectedLayer(numResponses)
- regressionLayer];
- options = trainingOptions(’adam’, …
- ’MaxEpochs’,maxEpochs, …
- ’MiniBatchSize’,miniBatchSize, …
- ’InitialLearnRate’,0.01, …
- ’GradientThreshold’,1, …
- ’Shuffle’,’never’, …
- ’Plots’,’training-progress’,…
- ’Verbose’,0);
- %% Train the Neural Network
- net = trainNetwork(XTrain, YTrain, layers, options);
- %% Save the Neural Network to a file
- save ("netsave4","net");
- %% Test the Neural Network
- % Load the text files used to test the neural network and
- % put them in a matrix
- filenameResponsesX = fullfile("HDXValidation.txt");
- filenameResponsesY = fullfile("HDYValidation.txt");
- [XTest] = prepareData(filenameResponsesX);
- [YVerif] = prepareData(filenameResponsesY);
- % Normalise the test matrix
- for i = 1:numel(XTest)
- XTest{i} = (XTest{i} - mu) ./ sig;
- end
- % Predict the outputs of the testing inputs through the
- % neural network
- YTest = predict(net, XTest);
- %% Plot the results predicted with the neural network along
- % with the experimental results using the plotResults()
- % function
- plotResults(XTest, YTest, YVerif)
- %% Validation of the model
- % Compute the RMSE at each cycle
- % RMSE is an indicator of the discrepancy between
- % experimental values and predicted values
- RMSE = zeros(numel(XTest),1);
- for i = 1:numel(XTest)
- RMSE(i)= sqrt(mean((YTest{i} - YVerif{i}).^2));
- end
- RMSE
- %% plotResults() returns a figure for each test set plotting
- %% the predicted values along with the experimental results.
- function []= plotResults(XTest, YTest, YVerif)
- for i = 1:numel(XTest)
- YTestcurrent=YTest{i}’;
- YVerifcurrent=YVerif{i}’;
- figure(i)
- plot(YVerifcurrent,’--’)
- hold on
- plot(YTestcurrent,’.-’)
- off
- end
- end
Appendix B. Data Processing Code (Matlab)
- %% prepareData() returns a cell composed of one matrix per
- %% experimental test data.
- function [XTrain] = prepareData(filenamePredictors)
- dataTrain = dlmread(filenamePredictors);
- numObservations = max(dataTrain(:,1));
- XTrain = cell(numObservations,1);
- for i = 1:numObservations
- idx = dataTrain(:,1) == i;
- X = dataTrain(idx,2:end)’;
- XTrain{i} = X;
- end
- end
Appendix C. Determination of Hyperparameters
| Try | Mini Batchsize | Max Epoch | Hidden Layers | RMSE1 | RMSE2 | RMSE3 | RMSE4 | Mean RMSE |
| 1 | 200 | 100 | 200 | 18.55 | 16.08 | 24.34 | 14.73 | 18.43 |
| 2 | 200 | 200 | 200 | 16.34 | 15.00 | 4.68 | 14.44 | 12.62 |
| 3 | 200 | 300 | 200 | 16.11 | 14.95 | 8.23 | 13.44 | 13.18 |
| 4 | 200 | 400 | 200 | 16.28 | 15.21 | 2.86 | 26.21 | 15.14 |
| 5 | 200 | 500 | 200 | 16.73 | 5.80 | 3.90 | 17.56 | 11.00 |
| 6 | 200 | 600 | 200 | 16.18 | 15.83 | 2.82 | 13.18 | 12.00 |
| 7 | 200 | 700 | 200 | 23.64 | 21.49 | 4.26 | 12.28 | 15.42 |
| 8 | 200 | 800 | 200 | 2.56 | 1.96 | 2.43 | 2.25 | 3.30 |
| 9 | 200 | 900 | 200 | 2.42 | 4.38 | 2.39 | 7.78 | 4.24 |
| 10 | 200 | 1000 | 200 | 4.94 | 2.71 | 5.49 | 13.67 | 6.70 |
| 11 | 200 | 1100 | 200 | 22.92 | 3.17 | 4.37 | 3.68 | 8.54 |
| 12 | 200 | 1200 | 200 | 24.30 | 16.60 | 6.60 | 14.80 | 15.58 |
| 13 | 200 | 1300 | 200 | 3.30 | 2.10 | 4.90 | 2.60 | 3.23 |
| 14 | 200 | 1400 | 200 | 9.00 | 12.00 | 2.80 | 10.70 | 8.63 |
| 15 | 50 | 200 | 200 | 16.15 | 15.07 | 9.14 | 13.61 | 13.49 |
| 16 | 100 | 200 | 200 | 17.41 | 15.63 | 4.76 | 14.33 | 13.03 |
| 17 | 200 | 200 | 200 | 16.50 | 15.10 | 4.40 | 13.50 | 12.38 |
| 18 | 300 | 200 | 200 | 15.60 | 15.10 | 3.50 | 14.20 | 12.10 |
| 19 | 400 | 200 | 200 | 16.60 | 15.10 | 3.40 | 14.10 | 12.30 |
| 20 | 500 | 200 | 200 | 17.00 | 15.40 | 5.30 | 14.10 | 12.95 |
| 21 | 600 | 200 | 200 | 16.20 | 16.00 | 8.50 | 14.20 | 13.73 |
| 22 | 700 | 200 | 200 | 16.20 | 15.70 | 4.60 | 14.10 | 12.65 |
| 23 | 800 | 200 | 200 | 20.30 | 15.20 | 9.70 | 23.00 | 17.05 |
| 24 | 900 | 200 | 200 | 16.30 | 15.20 | 5.30 | 13.90 | 12.68 |
| 25 | 200 | 200 | 100 | 16.10 | 15.60 | 6.20 | 14.20 | 13.03 |
| 26 | 200 | 200 | 200 | 16.80 | 14.80 | 5.40 | 13.80 | 12.70 |
| 27 | 200 | 200 | 300 | 16.50 | 15.20 | 24.50 | 14.10 | 17.58 |
| 28 | 200 | 200 | 400 | 7.80 | 4.60 | 4.10 | 3.90 | 5.10 |
| 29 | 200 | 200 | 500 | 14.00 | 14.50 | 3.50 | 14.10 | 11.53 |
| 30 | 200 | 200 | 600 | 16.28 | 15.68 | 7.87 | 13.86 | 13.42 |
| 31 | 200 | 200 | 700 | 13.44 | 15.37 | 7.19 | 14.97 | 12.74 |
| 32 | 50 | 800 | 400 | 6.76 | 14.82 | 2.89 | 14.25 | 9.68 |
| 33 | 200 | 1300 | 200 | 3.26 | 2.68 | 3.25 | 15.99 | 6.30 |
| 34 | 200 | 800 | 200 | 17.19 | 12.46 | 5.29 | 15.64 | 12.65 |
| 35 | 200 | 900 | 200 | 24.11 | 7.18 | 3.88 | 12.98 | 12.04 |
| 36 | 200 | 1300 | 400 | 2.91 | 2.11 | 2.59 | 1.87 | 2.37 |
References
- Mahon, D.; Claudio, G.; Eames, P. A study of novel high performance and energy dense zeolite composite materials for domestic interseasonal thermochemical energy storage. Energy Procedia 2019, 158, 4489–4494. [Google Scholar] [CrossRef]
- Johannes, K.; Kuznik, F.; Hubert, J.L.; Durier, F.; Obrecht, C. Design and characterisation of a high powered energy dense zeolite thermal energy storage system for buildings. Appl. Energy 2015, 159, 80–86. [Google Scholar] [CrossRef]
- Chen, B.; Kuznik, F.; Horgnies, M.; Johannes, K.; Morin, V.; Gengembre, E. Physicochemical properties of ettringite/meta-ettringite for thermal energy storage: Review. Sol. Energy Mater. Sol. Cells 2019, 193, 320–334. [Google Scholar] [CrossRef]
- Hongois, S.; Kuznik, F.; Stevens, P.; Roux, J.J. Development and characterisation of a new MgSO4–zeolite composite for long-term thermal energy storage. Sol. Energy Mater. Sol. Cells 2011, 95, 1831–1837. [Google Scholar] [CrossRef]
- Scapino, L.; Zondag, H.A.; Diriken, J.; Rindt, C.C.; Van Bael, J.; Sciacovelli, A. Modeling the performance of a sorption thermal energy storage reactor using artificial neural networks. Appl. Energy 2019, 253, 113525. [Google Scholar] [CrossRef]
- Korhammer, K.; Druske, M.M.; Fopah-Lele, A.; Rammelberg, H.U.; Wegscheider, N.; Opel, O.; Osterland, T.; Ruck, W. Sorption and thermal characterization of composite materials based on chlorides for thermal energy storage. Appl. Energy 2016, 162, 1462–1472. [Google Scholar] [CrossRef]
- Fumey, B.; Weber, R.; Baldini, L. Sorption based long-term thermal energy storage—Process classification and analysis of performance limitations: A review. Renew. Sustain. Energy Rev. 2019, 111, 57–74. [Google Scholar] [CrossRef]
- Cabeza, L.; Martorell, I.; Miró, L.; Fernández, A.; Barreneche, C. 1-Introduction to thermal energy storage (TES) systems. In Advances in Thermal Energy Storage Systems; Cabeza, L.F., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2015; pp. 1–28. [Google Scholar] [CrossRef]
- Kuznik, F.; Gondre, D.; Johannes, K.; Obrecht, C.; David, D. Numerical modelling and investigations on a full-scale zeolite 13X open heat storage for buildings. Renew. Energy 2019, 132, 761–772. [Google Scholar] [CrossRef]
- Tatsidjodoung, P.; Le Pierrès, N.; Heintz, J.; Lagre, D.; Luo, L.; Durier, F. Experimental and numerical investigations of a zeolite 13X/water reactor for solar heat storage in buildings. Energy Convers. Manag. 2016, 108, 488–500. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Lawrence, J. Introduction to Neural Networks: Design. In Theory, and Applications; California Scientific Software: Nevada City, CA, USA, 1994. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kuznik, F.; Gondre, D.; Johannes, K.; Obrecht, C.; David, D. Sensitivity analysis of a zeolite energy storage model: Impact of parameters on heat storage density and discharge power density. Renew. Energy 2020, 149, 468–478. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Gold, O.; Sharir, M. Dynamic Time Warping and Geometric Edit Distance: Breaking the Quadratic Barrier. ACM Trans. Algorithms 2018, 14. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Koprinska, I.; Wu, D.; Wang, Z. Convolutional neural networks for energy time series forecasting. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]


| Experiment | min () | max () | min | max | min (·) | max (·) | min () | max () | Volume of Data | Training or Validation |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 series | 19.71 | 20.39 | 0.0067 | 0.0073 | 127.9 | 189.8 | 38.42 | 784 | training | |
| 2 top | 19.38 | 20.48 | 0.0074 | 0.0089 | 49.09 | 90.22 | 37.69 | 2671 | validation | |
| 2 bottom | 19.45 | 20.59 | 0.0074 | 0.0089 | 56.21 | 95.85 | 37.80 | 2671 | training | |
| 4 top | 17.49 | 20.21 | 0.0046 | 0.0050 | 91.49 | 99.83 | 37.18 | 2272 | validation | |
| 4 bottom | 17.31 | 20.26 | 0.0046 | 0.0050 | 85.28 | 92.56 | 37.18 | 2272 | training | |
| 5 top | 16.92 | 20.12 | 0.0038 | 0.0047 | 72.45 | 99.15 | 26.52 | 2695 | training | |
| 5 bottom | 17.09 | 20.18 | 0.0038 | 0.0047 | 17.24 | 92.65 | 26.60 | 2695 | training | |
| 8 top | 18.80 | 19.97 | 0.0025 | 0.0030 | 55.10 | 65.82 | 36.68 | 2083 | training | |
| 8 bottom | 18.85 | 20.18 | 0.0025 | 0.0030 | 52.50 | 62.37 | 36.60 | 2083 | validation |
| Experiment | min () | max () | min | max | min (·) | max (·) | min () | max () | Volume of Data | Training or Validation |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 top | 19.27 | 121.97 | 0.0047 | 0.0111 | 76.69 | 99.82 | 544 | validation | ||
| 4 bottom | 19.41 | 124.28 | 0.0047 | 0.0111 | 69.01 | 87.65 | 544 | training | ||
| 5 top | 18.92 | 123.13 | 0.0048 | 0.0052 | 75.68 | 101.53 | −0.60 | 980 | training | |
| 5 bottom | 18.88 | 126.60 | 0.0048 | 0.0052 | 66.82 | 86.10 | 980 | training |
| RMSE1 | RMSE2 | RMSE3 | RMSE4 | RMSE5 |
| 1.66 | 1.32 | 0.90 | 2.10 | 2.02 |
| RMSE6 | RMSE7 | RMSE8 | RMSE9 | Average |
| 2.02 | 1.11 | 0.99 | 2.31 | 1.60 |
| RMSE1 | RMSE2 | RMSE3 | RMSE4 | Average |
| 2.91 | 2.11 | 2.59 | 1.87 | 2.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delmarre, C.; Resmond, M.-A.; Kuznik, F.; Obrecht, C.; Chen, B.; Johannes, K. Artificial Neural Network Simulation of Energetic Performance for Sorption Thermal Energy Storage Reactors. Energies 2021, 14, 3294. https://doi.org/10.3390/en14113294
Delmarre C, Resmond M-A, Kuznik F, Obrecht C, Chen B, Johannes K. Artificial Neural Network Simulation of Energetic Performance for Sorption Thermal Energy Storage Reactors. Energies. 2021; 14(11):3294. https://doi.org/10.3390/en14113294
Chicago/Turabian StyleDelmarre, Carla, Marie-Anne Resmond, Frédéric Kuznik, Christian Obrecht, Bao Chen, and Kévyn Johannes. 2021. "Artificial Neural Network Simulation of Energetic Performance for Sorption Thermal Energy Storage Reactors" Energies 14, no. 11: 3294. https://doi.org/10.3390/en14113294
APA StyleDelmarre, C., Resmond, M.-A., Kuznik, F., Obrecht, C., Chen, B., & Johannes, K. (2021). Artificial Neural Network Simulation of Energetic Performance for Sorption Thermal Energy Storage Reactors. Energies, 14(11), 3294. https://doi.org/10.3390/en14113294







