Electrodynamics of Reactive Power in the Space of Inter-Substation Zones of AC Electrified Railway Line

Abstract

In railway traction, the definition of “electromagnetic field” is functionally connected to the concept of the reactive power consumed by the electric rolling stock, and characterized by the running and standing electromagnetic waves in the space of the inter-substation zones from the site of the AC traction system. Such a definition is established and theoretically justified by the theory of electromagnetic fields. This article uses the methodology of this theory, in particular, a method for power balance estimation in electromagnetic fields based on Maxwell’s equations, as well as methods for the analysis of running and standing electromagnetic waves based on the theory of reflection, propagation and transmission of plane harmonic waves. The research considers the regularities of standing electromagnetic waves in the space of inter-substation zones of electric traction systems, which occur due to the incomplete reflection of incident waves from the contact wire and metal parts of the roof surface and the frontal part of the body of the electric rolling stock. The flow of electricity to the roof surface and the frontal part of the body of an electric locomotive is considered. The possibility of using existing methods to reduce wave reflections and thereby to effectively compensate for reactive power in the space of inter-substation zones is discussed.

1. Introduction

The fundamental role of reactive power is widely recognized in the electric power industry, and the ambiguity of the concept and formulae for determining reactive power is well known. In five years from now, we will celebrate the 100th anniversary of the “reactive power” concept [1,2], which has brought about a long-lasting discussion that has continued to the present day; let us review some of them.

The works of Constantin J. Budeanu [2] and Stanisław S. Fryze [3,4] were the initial studies at the first stage of the development of the reactive power definition, which lasted until the 1980s. Comprehensive review, classification and analysis of the methods developed during this period, and the names of their authors, are given in monographs by Leszek S. Czarnecki [5] and Volodymyr E. Tonkal [6].

The beginning of the second stage in the development of the power theory was laid in [7,8,9], proved by Hirofumi Akagi et al. in 1982. The main direction in this work is to obtain mathematical relationships and develop algorithms for the control systems of active filters when solving problems of compensating the reactive component of the first harmonic of the current and suppressing its higher harmonics. As a result, the author proposed the so-called “generalized theory of the instantaneous reactive power in three-phase circuits”, which is frequently known as the “p-q theory”. Unfortunately, in this theory, the authors do not explain reactive power’s physical meaning, considering it as a calculated value when analyzing three-phase three-wire systems without a neutral wire. The improved p-q theory was proposed in [10], in which the limitations of its original version were overcome.

As opposed to the p-q theory, based on a plane, the power theory, based on the use of a spatial Cartesian coordinate system, was proposed by Fang Z. Peng et al. in [11] for the three-phase four-wire systems. This theory is applicable for all the following conditions of operation: sinusoidal or non-sinusoidal, as well as balanced or not.

Further development of the previous theory is given in the studies [12,13]. Considering the essence and degree of generalization of the obtained version, the authors proposed calling it the “p-q-r theory”. The supply voltage and consumer currents are converted into rotating rectangular spatial pqr coordinates, where the reactive powers $q_q$ and $q_r$ are calculated as scalar and vector products of voltage and current vectors. A comparative analysis of the considered three power theories is given in the review article [14].

In recent years, the actual publications, including [15,16,17], state the precise physical foundations of the fundamental theory of instantaneous active and reactive power.

Compared with previous power theories, the mathematical relationships of which are intended to determine the instantaneous active and reactive power in three-phase circuits with valve converters, the expressions of instantaneous reactive power in [18,19,20] are proposed together with a physical interpretation. It allowed determining the reactive power in single-phase circuits and individual phases of three-phase systems, including circuits equipped with converters.

From the history of reactive power development, it is seen that the main subject of long-lasting discussions and scientific research is the ambiguity of the concept and formulae for its definition in electrical circuits with non-sinusoidal voltages and currents. From the time of the first work of C. J. Budeanu and up to the 1980s, such ambiguity has already led to the emergence of more than ten methods for determining and calculating reactive power, proposed by many authors. Moreover, in each of these methods, various researchers proposed their approaches to assessing reactive power. For a simple comparison, reactive power was calculated for the DE1 electric locomotive (Ukraine) according to crucial theories. The calculation results are shown in [20] and

Table 1. Comparison of reactive powers calculated by different methods.

No	Active Power $\mathit{P}$ [MW]	Total Power $\mathit{S}$ [MVA]	Reactive Power [Var] by Different Theories
			Budeanu ${\mathit{Q}}_{\mathit{B}}\mathit{·}{10}^4$	Fryze ${\mathit{Q}}_{\mathit{F}}\mathit{·}{10}^6$	Differential ${\mathit{Q}}_{\mathit{d}}\mathit{·}{10}^4$	Integral ${\mathit{Q}}_{\mathit{i}}\mathit{·}{10}^4$	Generalized ${\mathit{Q}}_{\mathit{g}}\mathit{·}{10}^4$
1	1.50	2.58	−1.83	1.60	−5.8	−2.22	6.79
2	2.27	3.59	−4.78	2.24	1.04	−3.67	9.33
3	1.93	3.09	−2.06	1.87	−3.7	−1.73	5.73
4	1.34	2.37	1.35	1.47	−2.7	1.50	4.92
5	1.45	2.56	3.55	1.64	−1.1	2.72	4.77
6	1.55	2.54	2.51	1.47	14.6	5.12	5.67
7	1.63	2.68	3.73	1.59	−1.6	2.86	5.18
8	1.41	2.28	1.73	1.21	4.9	1.20	5.20
9	2.76	4.10	2.88	2.46	22.3	2.66	10.41
10	1.00	1.83	3.00	1.25	4.9	4.06	4.37
11	1.90	3.08	2.84	1.90	2.4	2.39	5.29

. The below theories and expressions were used:

-by C. J. Budeanu

$$Q_B={\displaystyle \sum }_{k=1}^n{Q}^{\left(k\right)}={\displaystyle \sum }_{k=1}^n{U}^{\left(k\right)}{I}^{\left(k\right)}\sin {\phi }^{\left(k\right)},$$

-by S. S. Fryze

$$Q_F=\sqrt{S^2-P^2},$$

-by differential

$$Q_d={\displaystyle \sum }_{k=1}^{n}k{Q}^{\left(k\right)}={\displaystyle \sum }_{k=1}^{n}k{U}^{\left(k\right)}{I}^{\left(k\right)}\sin {\phi }^{\left(k\right)},$$

-by integral

$$Q_i={\displaystyle \sum }_{k=1}^n\frac{Q^{\left(k\right)}}{k}={\displaystyle \sum }_{k=1}^n\frac{1}{k}{U}^{\left(k\right)}{I}^{\left(k\right)}\sin {\phi }^{\left(k\right)},$$

-by generalized

$$Q_g=\sqrt{Q_d{Q}_i},$$

where $U$—pantograph voltage, $I$—locomotive current, $k$—harmonic number, $\phi$—phase shift, $S$—total (apparent) power, $P$—active power, $S$—total (apparent) power, $Q$—reactive (inactive) power, $Q_d$—the sum of the reduced reactive powers of all of the circuit elements whose voltage and current have the same harmonics, $Q_i$—the sum of the reduced reactive powers of all of the circuit elements whose voltage and current have different harmonics (according to O. A. Maevski).

The different values of reactive powers in Table 1, as well as the different signs, show clear evidence of the ambiguity of the reactive power defined by these theories. In our opinion, it has not been excluded because of numerous reasons and, perhaps, the most important of them is a state of the problem of “reactive power”, of which the solution is based on the “circuit” approach, that is, on the theory of electric and magnetic circuits. However, the theory of circuits is known to historically originate from the nucleation and development of a more complex fundamental theory of electromagnetic fields. Many physical concepts, such as the theory of electric and magnetic circuits, like most laws, are based precisely on the formulas and postulates of the field theory. The “circuit” principles for the analysis of processes in electrical devices are widespread, but also provide numerous obligatory assumptions and simplifications of electromagnetic processes, which determine their nature and mechanisms only approximately, and in some cases give erroneous results. Moreover, electric power processes in all electrotechnical devices and systems are the processes of creation, transformation and propagation of electromagnetic fields and the interaction of fields with electric charges. Therefore, to solve electric power problems in electric transport systems, a “field” approach is needed.

This approach is based on the fact that electromagnetic energy is transmitted from traction substations to the electric rolling stock (electric locomotives, electric trains, trams, metro trains) of electric transport systems through the airspace of inter-substation zones, by means of electromagnetic waves (i.e., by the movement of the electromagnetic field) rather than through the traction network (i.e., catenary system [21] and rails [22]). In this case, the amount and direction of the transmitted energy are determined by the Poynting vector $\overrightarrow{S}$, known from the theory of electrical engineering and radio engineering [23], as follows:

$$\overrightarrow{S}=\overrightarrow{E}\times \overrightarrow{H}$$

where $\overrightarrow{E}$ and $\overrightarrow{H}$—the values of the vectors of the strengths of electric and magnetic fields at points within the space of inter-substation zones.

In this case, the incident (direct) running electromagnetic waves fall at the surface of the contact wire, rails and body of the electric rolling stock, and form reverse (reflected) waves, which play a double role in the consumption of active and reactive power. Firstly, the flow of active energy decreases, since it is equal to the difference between the energy fields of the incident and reflected waves. Secondly, when combined with the incident wave under certain conditions, the reflected waves cause the appearance of standing waves, which are a characteristic feature of reactive power.

Classical approaches [23,24,25] describing the processes of the complete reflection of incident waves, and thus the formation of standing waves, which currently prevail in theoretical electrical engineering, are limited to the “circuit” approach (according to the theory of electrical circuits) and mainly to the analysis of the operating modes of a long line in the limiting cases of its load, as follows: idle, short circuit, reactive load, etc. To solve the problem set in this article, a “field” approach must be applied, in which the feeder or substation zones of the electrified section are considered simple conducting systems with special properties for the propagation of electromagnetic waves from traction substations to the electric rolling stock, which is associated with currents flowing in the catenary system and rails and, finally, the charges arising on them.

A review of the existing investigations has shown that there are currently no scientific publications on this issue. Some exceptions are articles [26,27,28,29], which, using elements of the electromagnetic field theory, make a physical explanation for the occurrence of reactive power $Q$ and distortion power $D$ in electrical circuits with nonsinusoidal voltages and currents. They mostly use the well-known expression of the Umov–Poynting theorem in its complex form to express the balance of powers over volume $V$ of the periodic electromagnetic field, and conclude that the real part of this expression describes active power $P$ and the imaginary part describes reactive power $Q$. Finally, the authors obtain expressions for the $E$, $D$, $H$ and $B$ quantities of the electromagnetic field using EMF, voltage and current in an external nonlinear electric circuit. Ultimately, the authors adhere to the concept of C. J. Budeanu that the total power is determined by the following ratio:

$$S=\sqrt{P^2+Q^2+D^2},$$

thus, the processes of wave propagation of energy in the electromagnetic field are not considered in these works.

The need for a physical interpretation of the inactive components of the total power using the Poynting vector is also emphasized by the results of the research presented in [24]. The author correctly describes the mechanism of the flow of electricity that propagates in the dielectric space around the wires of a three-phase power line. According to this research, the electrical energy of running electromagnetic waves, dissipated in the conductors of the supply line, is distributed over the phases of the load or accumulated and returned by inductions or capacitances. The author divides these waves into two groups. The first group consist of waves with a unidirectional flow of energy from source to load. These waves, making oscillations (called “active”), have a nonzero average value of the transferred energy. The waves of the second group, making oscillations (called “inactive”), do not transfer energy. They spread in the dielectric space around the supply line conductors.

As well as in the previous research, research [30] states that a plane electromagnetic wave is characterized by two flows of energy and two, active and reactive, densities. As these energy flows are inseparable at the phase shift angle $\phi \ne 0$. If $\phi =0$, the reactive components of the energy flow will disappear. The author mathematically and physically substantiated the algorithm for separating the active and reactive components of the energies of electromagnetic waves, and expressed them in the following way:

$${\Pi }_a=\frac{A^2}{\left|\rho \right|}{e}^{-2\alpha z}\cos \phi ·{\cos }^2\left(\omega t-\beta z\right)·e_z,$$

$${\Pi }_r=\frac{A^2}{2\left|\rho \right|}{e}^{-2\alpha z}\sin \phi ·\sin \left(2\left(\omega t-\beta z\right)\right)·e_z,$$

where ${\Pi }_a$ and ${\Pi }_r —$active and reactive components of Poynting vector, $A$—power, $\alpha$—attenuation coefficient, $\beta$—phase coefficient, $\omega$—angular frequency, $\rho$—wave impedance, $z$—coordinate in the direction of which the Pointing vector is moved. The importance of such division of the energy of electromagnetic waves is shown by the author in an example of the propagation speed of wave energy in a medium with losses.

Quite an original consideration of the components of the total power and their balance is shown in [31]. This article proves that in order to balance complex power, the following applies:

$$\underset{¯}{S}=P+jQ,$$

that is, the balance of this expression for both sides, time $t-js$ must be considered. This is due to the fact that there cannot exist a balance of reactive energy in the “active” (real) time. This balance must be considered at “reactive” time $t-js$. The authors try to show the stated idea on the example of time-dependent, i.e., parametric, $RLC$ circuits.

The fulfilment of the power balance in the electromagnetic field is also studied in the processes of dissipation and absorption of the energy of electromagnetic waves. In particular, a finite-size coated sphere scatterer is considered in [32], which is illuminated by incident electromagnetic waves. The percentage of absorbed and scattered energies determined by the Poynting vector is analyzed. The study found that the absorbed energy, called active energy, is about 25% of the energy of the incident electromagnetic field. It is stated that the imaginary part of the complex power balance expression is the dissipated power, and its occurrence is due to the phase shift between the incident electromagnetic field and polarization currents. Finally, it concludes that the diffuser must be optimally designed to eliminate the reactive power.

From the above analysis follows that the authors of the publications, recognizing the presence of active and inactive components of the energy of electromagnetic waves, do not consider the processes of wave reflection, and do not associate the physical interpretation of reactive power with the emergence and suppression of standing electromagnetic waves in the dielectric space of the electromagnetic field.

2. Objective of the Article

The article continues and develops the research presented in [33], dedicated to the “field” approach to substantiate the nature and processes of electricity transmission from traction substations (TS) to the electric rolling stock (ERS).

The primary purpose is to establish and provide theoretical grounds for the “field” functional connection between reactive power consumed by the electric rolling stock, and the occurrence and damping of standing electromagnetic waves in the space of inter-substation zones of electric transport systems, based on the electromagnetic field theory.

3. Novelty of Scientific Results of the Article in Relation to Existing Publications

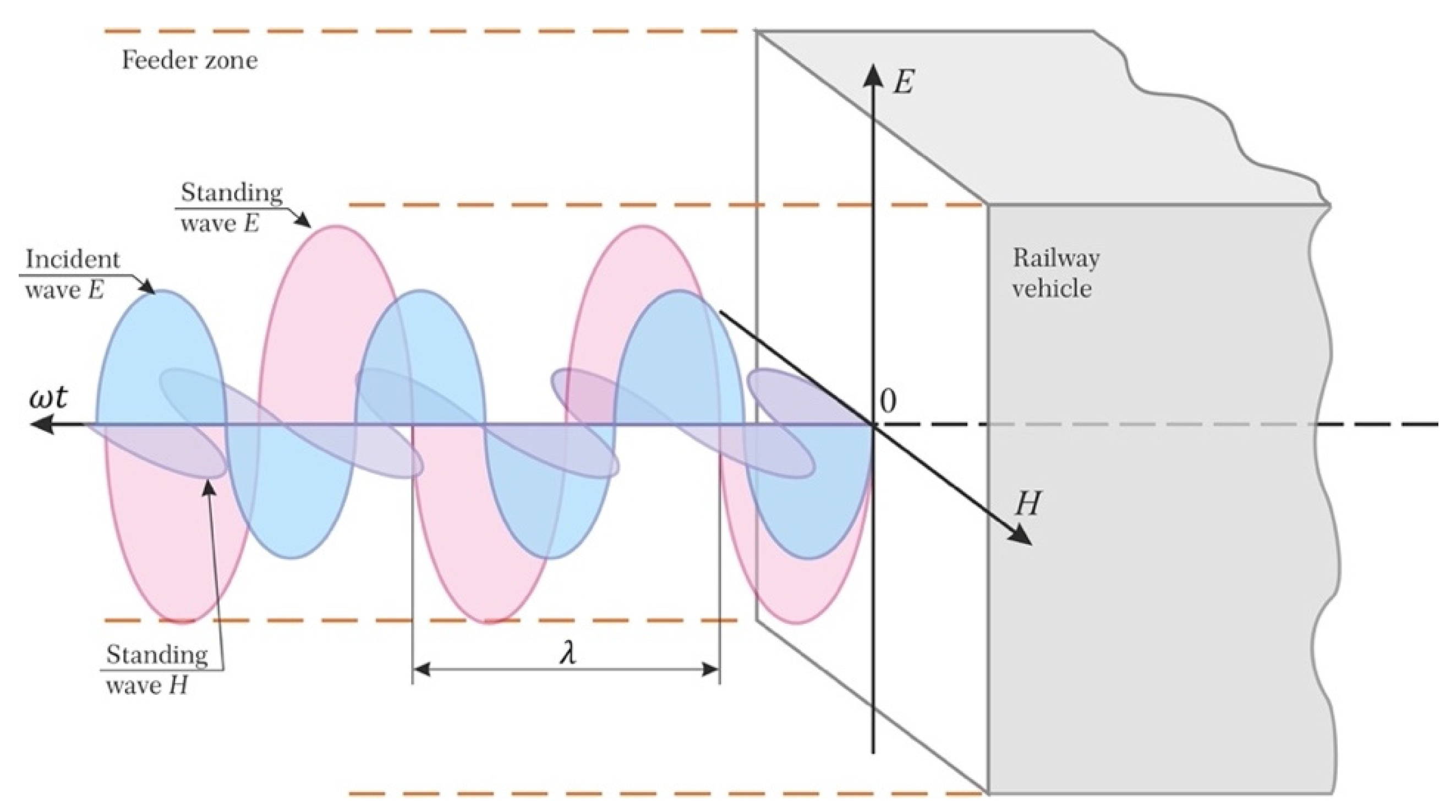
• For the first time in the Ukraine and Europe, a “field” (i.e., based on the electromagnetic field theory) interpretation of functional connectivity of reactive power, transmitted from a traction substation to the electric rolling stock, with occurrence and dissipation processes of standing electromagnetic waves in inter-substation zones of electric transport systems, is hereby proposed and substantiated.
• Dependencies have been found to describe the occurrence of standing waves in the space of inter-substation zones under the incomplete reflection of incident electromagnetic waves from a contact wire, rails, metal and dielectric surfaces of roofs, front and side parts of the body of the ERS.
• For the first time, existing methods for the suppression of standing electromagnetic waves are adapted to compensate the reactive power in electric transport systems by applying single- or multi-layered film coatings, with specific electromagnetic properties, on the surfaces of feeder zone devices.

4. Reactive Power as a Measure of Asymmetry of the Rates of Change of Electric Power in Electrical and Magnetic Fields

Let us consider the starting point of a 560 km long railway line supplied by a 25 kV AC 50 Hz traction power system. Imagine that the space of the specified line assumed to be limited by a traction substation, catenary system, railway vehicle and the rails, has a volume $V$ limited by the enclosing surface $A_v$, as shown in Figure 1. The trains in this section are driven by single-phase AC electric locomotives, types VL80 and VL85 (Ukraine). The locomotives have thyristor power converters supplying the traction motors. The frequency of voltage higher harmonics on the output changes are in the range of 1250 to 1950 Hz, according to [34,35].

Let this space be linear, homogeneous and isotropic with the following electromagnetic properties: permittivity $\epsilon$, conductivity $\sigma$ and permeability $\mu$. Then, the alternating electromagnetic field in this space could be described by Maxwell’s equations in its complex form according to [23], as follows:

$$rot\underset{¯}{\overrightarrow{H}}=\sigma \underset{¯}{\overrightarrow{E}}+j\omega \epsilon \underset{¯}{\overrightarrow{E}}$$

(1)

$$rot\underset{¯}{\overrightarrow{E}}=-j\omega \mu \underset{¯}{\overrightarrow{H}},$$

(2)

where $\underset{¯}{\overrightarrow{E}}$ and $\underset{¯}{\overrightarrow{H}}$ are the vectors of electric and magnetic field tensions in the space of inter-substation zones.

Since both tensions $\underset{¯}{\overrightarrow{E}}$ and $\underset{¯}{\overrightarrow{H}}$ are created by a single energy source, i.e., by a traction substation, electricity is transferred according to Poynting vector $\underset{¯}{S}$, and takes place in one direction from TS to ERS.

Like complex power $\underset{¯}{S}$ in the theory of circuits, we form a complex Poynting vector (Figure 1) as follows:

$$\underset{¯}{\overrightarrow{S}}=\left[\overrightarrow{\underset{¯}{E}}\overrightarrow{\underset{¯}{H}}″\right],$$

(3)

where

$$rot{\underset{¯}{\overrightarrow{H}}}^{″}=\sigma {\underset{¯}{\overrightarrow{E}}}^{″}+j\omega \epsilon {\underset{¯}{\overrightarrow{E}}}^{″}.$$

(4)

Next, let us transform system (1)–(4) as follows: multiply expression (4) by $\underset{¯}{\overrightarrow{E}}$, and (2) by ${\underset{¯}{\overrightarrow{H}}}^{″}$. Then the following expressions could be written:

$$\underset{¯}{\overrightarrow{E}}rot{\underset{¯}{\overrightarrow{H}}}^{″}=\sigma \underset{¯}{\overrightarrow{E}}{\underset{¯}{\overrightarrow{E}}}^{″}+j\omega \epsilon \underset{¯}{\overrightarrow{E}}{\underset{¯}{\overrightarrow{E}}}^{″}$$

(5)

$${\underset{¯}{\overrightarrow{H}}}^{″}rot\underset{¯}{\overrightarrow{E}}=-j\omega \mu \underset{¯}{\overrightarrow{H}}{\underset{¯}{\overrightarrow{H}}}^{″}$$

(6)

Subtracting (6) from (5) and considering that the difference of the left parts of (5) and (6) is equal to $-div\underset{¯}{\overrightarrow{S}}$, we have the following:

$$-div\underset{¯}{\overrightarrow{S}}=\sigma E^2+j\omega \left(\mu H^2-\epsilon E^2\right).$$

(7)

Then the flow of the Pointing vector through the enclosing surface $A_V$ into the volume $V$ of inter-substation zones (Figure 1) will be equal to the following:

$$-\underset{V}{\overset{}{{\displaystyle \int }}}div\underset{¯}{\overrightarrow{S}}dV=\underset{V}{\overset{}{{\displaystyle \int }}}\sigma E^{2}dV+j2\omega \underset{V}{\overset{}{{\displaystyle \int }}}\left(\frac{\mu H^2}{2}-\frac{\epsilon E^2}{2}\right)dV$$

(8)

By analogy with the theory of circuits and according to the Joule–Lenz law in its differential form [23], the first component on the right side of Expression (8) is the average value of heat losses in volume $V$ of inter-substation zones over the period of the supply voltage, and the second component, i.e., the imaginary part, is the average value of reactive power $Q$ entering into volume $V$ through the enclosing surface $A_V$, as follows:

$$Q=2\omega \underset{V}{\overset{}{{\displaystyle \int }}}\left(\frac{\mu H^2}{2}-\frac{\epsilon E^2}{2}\right)dV$$

(9)

where $E$ and $H$ are the effective values of the harmonic tensions.

Given that $\overrightarrow{B}=\mu \overrightarrow{H}$ and $\overrightarrow{D}=\epsilon \overrightarrow{E}$, and considering Formula (9), the expression of the energy of the “field” (by the electromagnetic field vectors) for the representation of reactive power can be written in the following form:

$$Q=2\omega \underset{V}{\overset{}{{\displaystyle \int }}}\left(\frac{\mu H^2}{2}-\frac{\epsilon E^2}{2}\right)dV\approx \underset{V}{\overset{}{{\displaystyle \int }}}\left(\underset{¯}{\overrightarrow{H}}\frac{\partial \underset{¯}{\overrightarrow{B}}}{\partial t}-\underset{¯}{\overrightarrow{E}}\frac{\partial \underset{¯}{\overrightarrow{D}}}{\partial t}\right)dV=\underset{V}{\overset{}{{\displaystyle \int }}}\frac{\partial }{\partial t}\left(\frac{\underset{¯}{\overrightarrow{H}}\underset{¯}{\overrightarrow{B}}}{2}-\frac{\underset{¯}{\overrightarrow{E}}\underset{¯}{\overrightarrow{D}}}{2}\right)dV.$$

(10)

Therefore, reactive power in the space of inter-substation zones by volume $V$ is a measure of the asymmetry of the rates of change in the electric and magnetic components of the energy of the electromagnetic field. Numerically, it is equal to the difference between average energies stored in the magnetic and electric fields in a given volume $V$, multiplied by $2\omega$.

5. Volume of Reactive Power in the Space of Inter-Substation Zones of Electrified Section

Using Expressions (9) and (10), let us consider the reactive power $Q$ spreading in the space of an inter-substation zone consisting of seven sections with a total length of 560 km. Each inter-substation zone has a one-sided power supply via the catenary of PBSM-95+MF-100 type and the rails of R65 type, which could be specified as follows: PBSM-95 catenary wire—bimetal steel copper wire with a cross-section of 95 m²; MF-100 contact wire—solid copper wire with a cross-section of 100 m², R65 rails—carbon steel rails with a specific weight of 64.88 kg/m [36]. The VL85 electric locomotive with a train is moving along the inter-substation zone at 160 km/h and taking power $P=5369$ kW. According to the experimental research of this study, at this speed, the voltage at the pantograph is $U=26.12$ kV, the current in the contact wire and the electric locomotive is $I_c=208.9$ A, and in the rails of the one-side AC traction system is $I_r=83.6$ A.

Let us define the tensions of the electric and magnetic fields in the space of the inter-substation zones.

The tension of the electric field in a dielectric (i.e., in the air) has the following two components: tangential $E_{\tau }$ and normal $E_n$ parts, which are shown in Figure 1. The tangential component $E_{\tau }$ in the air of inter-substation zones, according to the “conductor-dielectric” boundary condition [23], is equal to the tangential component in conductor $E_{\tau c}$, which can be determined from the differential Ohm’s law, as follows:

$$J=\sigma E_{\tau c},$$

(11)

where $J$ is the current density in the equivalent conductor of the catenary system, and $\sigma$ is the specific electrical conductivity of the material of the contact wire.

Given that the cross-section area of an equivalent contact wire is $A=193.3\times {10}^{-6}$ m², with a current of $I_c=208.9$ A, we find that the current density is $J=1.08\times {10}^6$ A/m², assuming that the conductivity of copper is $\sigma =5.8\times {10}^7$ S/m. Then, the tangential component of tension $E_{\tau }$ in the air, according to (11), equals $0.186$ V/m. The distance between the contact wire and the head of the rail usually varies from $h_{min}=5.75$ m to $h_{max}=6.8$ m. Assuming the maximum distance and the above-mentioned voltage $U=26.12$ kV, we find the normal component of the tension, which is equal to $E_n=3841$ V/m. Consequently, as far as $E_n\gg E_{\tau }$, we could find that electric field tension in the airspace of inter-substation zones is $E=E_n=3841$ V/m.

The tension of the magnetic field at any point of the inter-substation space $\overrightarrow{H}$ is defined as the vector sum of the components created by the currents in the contact wire ${\overrightarrow{H}}_c$ and in the rail ${\overrightarrow{H}}_r$, as follows:

$$\overrightarrow{H}={\overrightarrow{H}}_c+{\overrightarrow{H}}_r$$

(12)

Each of these components has to be defined using the law of total currents in catenary $I_c$ and rails $I_r$ (Figure 1), as below:

$$H_c\left(x\right)=\frac{I_c}{2\pi \left(x+r_c\right)}$$

(13)

$$H_r\left(x\right)=\frac{I_r}{2\pi \left(6.8-x\right)}$$

(14)

where $x$ is the wire-to-rail coordinate, which varies from an equivalent contact wire to an equivalent rail and is mostly equal to the distance between them $h=6.8$ m, according to Figure 1; $r_c$ and $r_r$ are the radii of equivalent contact wires and rails, which are equal to $r_c=7.85\times {10}^{-3}$ m and $r_r=72.7\times {10}^{-3}$ m, respectively.

So, we can calculate, according to Formulae (12)–(14), the dependence of the resulting tension of the magnetic field $H$ in the inter-substation space on the $x$ coordinate, i.e., on height $h$. The results are shown in Figure 2 and

Table 2. Calculated physical parameters of the equivalent contact wire and rails.

Element of Feeder Zone	Parameters of Metal
	Electrical Conductivity $\mathit{\sigma }$ [S/M]	Relative Magnetic Permeability $\mathit{\mu }$ [R.U.]	Radii of Rail and Wire, or Sheet Thickness [Mm]
Equivalent contact wire	$3.82\times {10}^7$	10	7.85
Equivalent rails	$8\times {10}^6$	1000	72.7
Electric locomotive, steel sheet	$1.8\times {10}^6$	5200	5

.

Let us calculate the possible reactive power $Q$ in a volume $V$ of the space of the inter-substation zone. The volume could be found using the following data: the total length of the space of the inter-substation zone of 560 km, its width is taken to be the width of the railway track of 1.524 m, and its height of $h=6.8$ m; then, $V=\mathrm{5,803,392}$ m³.

Given that the electric field is uniformly distributed over the inter-substation space and magnetic power is distributed according to Figure 2, the reactive power spreading from TS to ERS is found by specified Formula (10), as follows:

$$Q=2\omega \underset{V}{\overset{}{{\displaystyle \int }}}\left(\frac{{\mu }_0{H}^2\left(h\right)}{2}-\frac{{\epsilon }_0{E}^2}{2}\right)dV\approx 4\pi f{\displaystyle \sum }_{h_i=0.1}^{6.8}\left(\frac{{\mu }_0{H}^2\left(h_i\right)}{2}-\frac{{\epsilon }_0{E}^2}{2}\right)\Delta V_i$$

(15)

Finally, based on Expression (15) and

Table 3. Results of calculations of basic electromagnetic coefficients according to Expression (15).

${\mathit{x}}_{\mathit{i}}$ [m]	${\mathit{H}}_{\mathit{c}}$ [A/m]	${\mathit{H}}_{\mathit{r}}$ [A/m]	$\mathit{H}$ [A/m]	$\frac{{\mathit{\mu }}_0{\mathit{H}}^2}{2}\mathit{·}{10}^{-3}$ [r.u.]	$\left(\frac{{\mathit{\mu }}_0{\mathit{H}}^2}{2}-\frac{{\mathit{\epsilon }}_0{\mathit{E}}^2}{2}\right)\mathit{·}{10}^{-3}$ [r.u.]
0	4237.5	4.9	4242.4	11.3	11.3
0.1	308.43	2.0	310.4	60.5	60.4
0.2	160.0	2.0	162	16.48	16.4
0.3	108.1	2.05	110	8.1	7.6
0.4	81.56	2.08	84	4.13	4.36
0.5	65.5	2.14	68	2.9	2.84
0.7	47.0	2.2	49.5	1.5	1.46
1.0	33	2.3	35.3	0.783	0.17
1.5	22.06	2.5	24.50	0.377	0.311
2.0	16.57	2.8	18.8	0.347	0.28
3.0	11.06	3.5	14.56	0.246	0.18
4.0	8.3	4.8	13	0.255	0.19
5.0	6.642	7.4	14	0.396	0.33
5.5	6.04	10.22	16.2	0.628	0.563
5.8	5.73	13.3	19.0	0.95	0.89
6.0	5.54	16.6	22	1.39	1.33
6.2	5.36	22.2	27.6	2.32	2.26
6.4	5.19	33.3	38.5	4.9	4.84
6.6	5.03	66.5	71.5	2.42	2.25
6.7	4.96	53	58	71.6	5.9
6.8	4.89	183	188	134	134

, we can conclude that an electric locomotive in the specified mode with electrical parameters $U=26.12$ kV, $I_r=208.9$ A, $I_r=83.6$ A, totally could transfer a reactive power of 2930.5 kvar from the feeder zone.

6. Conditions for the Formation of Standing and Mixed Electromagnetic Waves

The alternating electromagnetic field created in the airspace of inter-substation zones is characterized by the harmonic plane running waves of electric and magnetic field tensions that transmit electricity from TS to ERS [23], as follows:

$$E\left(y,t\right)=E_{m in}\sin \left(\omega t-\beta y\right)+E_{m rf}\sin \left(\omega t+\beta y\right)$$

(16)

$$H\left(y,t\right)=H_{m in}\sin \left(\omega t-\beta y\right)+H_{m rf}\sin \left(\omega t+\beta y\right)$$

(17)

Let us rewrite Expressions (16) and (17) in the following complex form:

$$\underset{¯}{E}\left(y\right)=E_{m in}{e}^{-j\beta y}+E_{m rf}{e}^{j\beta y}$$

(18)

$$\underset{¯}{H}\left(y\right)=H_{m in}{e}^{-j\beta y}-H_{m rf}{e}^{j\beta y}$$

(19)

As it is known, a reflected wave will be formed if the incident wave meets another medium (dielectric or conductor) on its way. For a medium with infinite electrical conductivity $\sigma$ (a lossless medium), when $\left|\mathsf{\Gamma }\right|=1$, the amplitude of the reflected wave is equal to the amplitude of the incident wave and, as a result of their adding together, a standing wave is formed. In this regard, given that $E_m=E_{m in}=E_{m rf}$, $H_m=H_{m in}=H_{m rf}$, we obtain the following expressions of standing waves:

$$E\left(y,t\right)=2E_m\cos \left(\beta y\right)\sin \left(\omega t\right)$$

(20)

$$H\left(y,t\right)=-2H_m\sin \left(\beta y\right)\cos \left(\omega t\right)$$

(21)

A graphical representation of the standing waves of electric and magnetic fields reflected from the railway vehicle is shown in Figure 3.

Consequently, it is generally accepted that a necessary condition for the occurrence of standing electromagnetic waves is a complete reflection of the incident waves. Let us analyze this issue, considering [23,25,37,38,39], as follows.

As it is widely recognized, if a plane sinusoidally changing the electromagnetic wave moving in medium 1 (in our case, it is the air), with properties ${\epsilon }_1$, ${\sigma }_1$, ${\mu }_1,$ encounters on its way the interface of another medium 2 (parts and devices of the railway vehicle), with properties ${\epsilon }_2$, ${\sigma }_2$, ${\mu }_2,$ and this wave falls (the incident wave having tensions ${\underset{¯}{\overrightarrow{E}}}_{in}$, ${\underset{¯}{\overrightarrow{H}}}_{in}$) perpendicularly to the boundary of the media, it is partially reflected ${\overrightarrow{\underset{¯}{E}}}_{rf}$, ${\overrightarrow{\underset{¯}{H}}}_{rf}$ with a reflection ratio $\underset{¯}{\mathsf{\Gamma }}.$

$$\underset{¯}{\mathsf{\Gamma }}=\frac{{\underset{¯}{\eta }}_2-{\underset{¯}{\eta }}_1}{{\underset{¯}{\eta }}_2+{\underset{¯}{\eta }}_1}=\frac{1-\underset{¯}{\mathsf{{\rm T}}}}{1+\underset{¯}{\mathsf{{\rm T}}}}$$

(22)

where $\underset{¯}{\mathsf{{\rm T}}}={\underset{¯}{\eta }}_1/{\underset{¯}{\eta }}_2$—running wave coefficient; ${\underset{¯}{\eta }}_1$ and ${\underset{¯}{\eta }}_2$—wave complex resistances of media 1 and 2, defined as follows:

- for dielectrics

$$\eta =\sqrt{\mu /\epsilon }$$

(23)

- for the conducting medium

$$\underset{¯}{\eta }=\sqrt{j\omega \mu /\sigma }$$

(24)

Let us analyze the flow of electricity from the traction substation to the devices of the inter-substation zone.

7. Energy Flow to the Contact Wire

At the boundary of the contact wire, the electromagnetic wave falling from the air of the inter-substation zone is partly reflected from the wire surface and partly penetrates into it (Figure 1). Let us determine the properties of the reflected wave.

For air, medium 1, the wave resistance is ${\eta }_{air}={\eta }_1=376.7 \mathsf{\Omega }$.

Medium 2 is a conductive medium represented by the catenary system of the PBSM-95 + MF − 100 type. The cross-section area of the equivalent contact wire is $193.3\times {10}^{-6}$ m², hence the specific conductivity is ${\sigma }_2={\sigma }_{eq w}=5\times {10}^7$ S/m and the permeability is ${\mu }_{r2}=10$.

The higher harmonics of the feeder current in the normal operating mode have frequencies up to 750–1950 Hz, which will be taken into account too. The wave resistance of the material of the equivalent wire for $f=1950$ Hz is $1.33\mathsf{\Omega }$ according to (24), at the same time for $f=50$ Hz it is equal to $0.212\mathsf{\Omega }$. Then, the reflection ratio on the boundary “air-to-wire” surface, for example, for the current harmonic with a frequency of $f=1950$ Hz is defined as ${\underset{¯}{\mathsf{\Gamma }}}_{12}\approx -1$ according to Expression (22).

Then, according to Expressions (23)–(24), the field tensions of the reflected wave are as follows:

$${\underset{¯}{\overrightarrow{E}}}_{rf1}\approx -{\underset{¯}{\overrightarrow{E}}}_{in1}\mathrm{and}{\underset{¯}{\overrightarrow{H}}}_{rf1}\approx {\underset{¯}{\overrightarrow{H}}}_{in1}$$

that is, the almost completely reflected wave changes the sign of vector $\overrightarrow{E}$, and a similar result is obtained for the rails.

8. Incidence of the Poynting Vector on the ERS Roof

As defined in [33], the electromagnetic energy supplying the ERS comes from the traction network of the power supply system in two ways (Figure 4). The first way is contact wire 2—roof bushing insulator 4—appliances of the high-voltage cabinet 6—traction motors. The second way is rails 3—bottom part of the ERS—traction motors and the high-voltage cabinet 6. A significantly minor amount of the energy of the electromagnetic waves comes from the airspace 1 of the inter-substation zones to any part of the EPS, as follows: metal body 8 and to the glass of the driver’s cabin 7 in (Figure 4).

At the outset, let us analyze the basic stream in which the following components of the Poynting vector carrying this stream can be identified (Figure 4):

• Basic vector $0.5{\overrightarrow{S}}_{basic}$ corresponding to the density of energy flow coming into the elements of the traction power circuit of the ERS (i.e., into the high-voltage cabinet) through the roof bushing porcelain insulator 4. To analyze the electromagnetic waves carrying ${\overrightarrow{S}}_{basic}$, the coefficients of reflection ${\mathsf{\Gamma }}_{14}$ and refraction ${\mathsf{{\rm T}}}_{14}$ (i.e., transmission, penetration) of the incident wave on the “air 1-to-porcelain 4” border have to be defined. For perfect dielectrics like air ${\epsilon }_{r1}=1.0$ and porcelain ${\epsilon }_{r4}=6.0$, so for $\mathsf{\Gamma }$ and $\mathsf{{\rm T}}$ coefficients we will get the following:

$${\mathsf{\Gamma }}_{14}=\frac{\sqrt{{\epsilon }_{r1}}-\sqrt{{\epsilon }_{r4}}}{\sqrt{{\epsilon }_{r1}}+\sqrt{{\epsilon }_{r4}}}=-0.42{\mathrm{and}\mathrm{T}}_{14}^E=\frac{2\sqrt{{\epsilon }_{r1}}}{\sqrt{{\epsilon }_{r1}}+\sqrt{{\epsilon }_{r4}}}=0.58$$

(25)

As we can see, some part of the energy is reflected from the insulator, as follows:

$$E_{rf14}=-0.42E_{in1}{\mathrm{and}\mathrm{T}}_{14}^H=\frac{2\sqrt{{\epsilon }_{r4}}}{\sqrt{{\epsilon }_{r1}}+\sqrt{{\epsilon }_{r4}}}=1.42$$

(26)

$$H_{rf14}=-\left(0.42H_{in1}\right)=0.42H_{in1}$$

$$E_{pn14}=0.58E_{in1}$$

$$H_{pn14}=1.42H_{in1}$$

where $rf$ index denotes the reflected value, $in$ index denotes the incident value, $pn$ index denotes the refracted (penetrated, transmitted) value.

The second stream of ${\overrightarrow{S}}_{basic}$ (Figure 4) penetrates into the high-voltage cabinet of the ERS from the space around rails 3 (i.e., from the bottom of ERS). The wave propagation and power transmission in this space need more in-depth study, which is not provided in this article.

2.

Vector ${\overrightarrow{S}}_{roof}$ is normally pointed to the roof surface (Figure 4). Its material is a sheet structural steel of 2 mm thick, with the properties of $\sigma =7\times {10}^6$ S/m and ${\mu }_r=1000$. The electromagnetic harmonic waves of various frequencies, incident from air 1 on the border with the surface of metal roof 5 (Figure 4), are partially reflected and partially penetrate into it. They are gradually damped, resulting in electric power losses in the metal roof.

The wave resistance of the roof metal ${\eta }_5$, found by Expression (24) in the case of the current harmonic with $f=1950$ Hz, is 1.33 $\mathsf{\Omega }$, and for air it is ${\eta }_1=376.7$ $\mathsf{\Omega }$. Substituting for ${\eta }_1$ and ${\eta }_5$ in (22), the coefficient of wave reflection from the roof surface being ${\mathsf{\Gamma }}_{15}\approx -1$, the refraction (transmission, penetration) coefficient equals ${\mathsf{{\rm T}}}_{15}\approx 0.87\times {10}^{-5}$. A 1950 Hz wave penetrates to the depth of $d_5=0.115$ mm. In the case of basic current harmonic with a frequency of 50 Hz, the wave resistance of the roof metal ${\eta }_5$ is 0.212 $\mathsf{\Omega }$, hence the wave penetrates 0.85 mm deep. The metal sheet of the roof is “impenetrable” for the waves, since they are completely damped out within it without reaching an opposite surface. We obtain similar results for the side surfaces of the ERS body.

9. Incidence of the Waves on the Frontal Part of the Locomotive Body

Electromagnetic waves spread in the middle part of the air space between the contact wire and the rail, and fall on the frontal part of the locomotive body consisting of glass and metallic parts.

The windshield has a thickness of 15 mm and permittivity ${\epsilon }_r=5.5\dots 10$ (let us assume 9.0). At the “air-to-glass” boundary, the waves are partially reflected with a ratio of $\mathsf{\Gamma }=-0.5$, according to the following:

$$\mathsf{\Gamma }=\frac{\sqrt{{\epsilon }_{r1}}-\sqrt{{\epsilon }_r}}{\sqrt{{\epsilon }_{r1}}+\sqrt{{\epsilon }_r}}$$

(27)

The metal part of the lower frontal part of the ERS body is made of structural steel sheets of 7 mm thick, with parameters $\sigma =7\times {10}^6$ S/m and ${\mu }_r=1000$. Then, the wave resistance of this metal body, according to (25), is equal to ${\eta }_{front}={\eta }_2=33.6\times {10}^{-5}$ $\mathsf{\Omega }$. Substituting ${\eta }_{air}={\eta }_1$ and ${\eta }_{front}={\eta }_2$ in (22), the reflection ratio of the waves from the metal part of the body equals ${\mathsf{\Gamma }}_1=-1$.

The performed calculations of the reflection coefficient of electromagnetic waves from electric traction devices (i.e., contact wire, glass, porcelain bushing, as well as metal roofs and sidewalls of the body) show that incomplete reflection of waves from the surfaces of specified parts and devices occurs in the process of electric locomotive operation. Simultaneously, in the space of the inter-substation zone, both active and reactive powers are transferred from TS to ERS. Consequently, there are running and standing waves that superimpose in this space and form mixed electromagnetic waves. Let us show that the necessary condition for standing waves occurrence, namely, the existence of total reflection, is not so strict. The standing waves in the inter-substation space, which characterize the reactive energy [37], are also possible with incomplete reflection, i.e., when the reflection ratio is $0\le \mathsf{\Gamma }<1$.

Given that $E_{m in}/H_{m in}={\eta }_{air}={\eta }_1$, where ${\eta }_{air}$ is a wave resistance of the airspace of inter-substation zones, let us rewrite Expressions (18) and (19) in the following way:

$$\underset{¯}{E}\left(y\right)={\underset{¯}{E}}_{m in}{e}^{-j\beta y}\left(1+\mathsf{\Gamma }{e}^{j2\beta y}\right)$$

(28)

$$\underset{¯}{H}\left(y\right)=\frac{{\underset{¯}{E}}_{m in}}{{\eta }_1}{e}^{-j\beta y}\left(1-\mathsf{\Gamma }{e}^{j2\beta y}\right)$$

(29)

Then, according to the theory of the well-established symbolic method for the analysis of electric circuits, the instantaneous complex values of electric and magnetic field strengths can be found after formal multiplication of Equations (28) and (29) by operator $e^{j\omega t}$, as follows:

$$\underset{¯}{E}\left(y\right)={\underset{¯}{E}}_{m in}\left(1+\mathsf{\Gamma }{e}^{j2\beta y}\right)e^{j\left(\omega t-\beta y\right)}$$

(30)

$$\underset{¯}{H}\left(y\right)=\frac{{\underset{¯}{E}}_{m in}}{{\eta }_1}\left(1-\mathsf{\Gamma }{e}^{j2\beta y}\right)e^{j\left(\omega t-\beta y\right)}$$

(31)

Compared to Expressions (18) and (19), where the fields are represented as the sum of the incident and reflected waves, the form of writing of Expressions (30) and (31) corresponds to only one incident wave with an amplitude varying from the coordinate, as follows:

$${\underset{¯}{E}}_m\left(y\right)={\underset{¯}{E}}_{m in}\left|1+\mathsf{\Gamma }{e}^{j2\beta y}\right|$$

(32)

$${\underset{¯}{H}}_m\left(y\right)=\frac{{\underset{¯}{E}}_{m in}}{{\eta }_1}\left|1-\mathsf{\Gamma }{e}^{j2\beta y}\right|$$

(33)

These functions are periodic in the inter-substation space and acquire maximum values with $\left(1+\mathsf{\Gamma }\right)$, which are much larger than the amplitude of the incident wave at points called “wave antinodes”. Between them, there are “wave nodes”, where the amplitude is minimal and equals $\left(1-\mathsf{\Gamma }\right)$ of the incident wave amplitude. The spatial position of these points does not change over time; therefore, for the expressions described by (30) and (31), the definition of “standing wave” is used [40]. Consequently, in a non-perfect conductor (such as the body of an electric locomotive), the reflected wave has a smaller amplitude than the incident wave. So, a small running wave perpendicular to the conductor surface is superimposed on the standing wave, which compensates for power losses in the conductor.

For more advanced analysis, let us consider the dependence of electromagnetic waves type on the coefficient of running wave $\mathsf{{\rm T}}$. For this, we rewrite the system of Expressions (28) and (29), considering the well-established Euler’s formula and Expression (22), then we obtain the following:

$$\underset{¯}{E}\left(y\right)={\underset{¯}{E}}_{in}·\frac{2}{1+\mathsf{{\rm T}}}·\left(\cos \left(\beta y\right)-j\mathsf{{\rm T}}·\sin \left(\beta \mathrm{y}\right)\right)$$

(34)

$$\underset{¯}{H}\left(y\right)=\frac{{\underset{¯}{E}}_{in}}{{\eta }_1}·\left(2-\frac{1}{\mathsf{{\rm T}}}\right)·\left(\cos \left(\beta y\right)-j\frac{1}{\mathsf{{\rm T}}}·\sin \left(\beta \mathrm{y}\right)\right)$$

(35)

After some simple transformations of Expressions (34) and (35), and a transition into instantaneous quantities, we obtain the following system:

$$E\left(y,t\right)=E_{in}·\frac{4}{1+\mathsf{{\rm T}}}·\left(\sin \left(\omega t-\beta y\right)+E_{in}·\frac{2·\left(1-\mathsf{{\rm T}}\right)}{1+\mathsf{{\rm T}}}·\cos \left(\beta \mathrm{y}\right)·\sin \left(\omega t\right)\right)$$

(36)

$$H\left(y,t\right)=\frac{E_{in}}{{\eta }_1}·\frac{1}{\mathsf{{\rm T}}}·\sin \left(\omega t-\beta y\right)+\frac{E_{in}}{{\eta }_1}·2·\left(1-\frac{1}{\mathsf{{\rm T}}}\right)·\cos \left(\beta \mathrm{y}\right)·\sin \left(\omega t\right)$$

(37)

It follows from Expressions (36) and (37) that the expressions for the electric and magnetic field strengths are the sums of running and standing waves. It follows from them that if the coefficient of wave transmission is $\mathsf{{\rm T}}=1$, i.e., if the air space of the inter-substation zones is consistent with the materials of the contact wire and the body of the electric rolling stock (${\eta }_1={\eta }_2$), then standing waves do not arise in the inter-substation space, since there is no wave reflection. If $\mathsf{{\rm T}}\ne 1$, i.e., space and materials are not consistent (${\eta }_1\ne {\eta }_2$), there is an incomplete reflection and both running and standing waves arise in the inter-substation air space, as a result of which a mixed wave is formed. Incomplete reflection is also indicated by the fact that the metals of both the contact wire and the locomotive body are “real” materials, i.e., they have a finite (and not infinite) conductivity. Therefore, it follows that not all the energy of the incident wave is reflected, and some part of it passes into the metal and dissipates in it as heat.

The above suggests that active energy is transmitted from traction substations to locomotives in the inter-substation airspace by running waves. Thus, the energy exchanged between electric and magnetic fields characterizing the standing waves involves the exchange of reactive power too.

10. Reactive Power Compensation by “Suppression” of Standing Electromagnetic Waves and Discussion of Results

Reactive power consumed by the ERS of different types is quite significant, as in some modes it reaches up to 40–65% of the consumed power [41]. Therefore, the problem of its compensation is significant for electric traction systems. As it follows from the above analysis, this problem has to be solved by “suppression” of standing waves in the space of inter-substation zones. Since standing waves result from reflected waves, reflections of incident waves need to be reduced to compensate for reactive power. Therefore, it is necessary to investigate issues of the suppression of standing waves and how to damp or eliminate reflected waves. As it follows from Expression (22), it is necessary to ensure that wave resistances along both sides of their separation boundary are as close as possible to each other. There are several ways to reduce the reflection coefficient of monochromatic electromagnetic waves [40,42].

The easiest way to reduce reflections is a thin-film method [40]. For the problem solved in this article, this means that a layer of electrically conductive or dielectric coating of certain thickness $d$ with wave resistance ${\eta }_2$ should be applied to the contact wire, rails and the body of the electric rolling stock. In this case, we will get a circuit model consisting of three environments (1, 2, 3), shown in Figure 5, where ${\eta }_1$, ${\eta }_2$ and ${\eta }_3$ are wave resistances of the environments, and $K_1$, $K_2$ and $K_3$ are their wave numbers defined as $K_i=2\pi /{\lambda }_i$ (where $i=1,2,3$).

Air and the contact wire material are considered to be semi-infinite environments, since they are “impermeable” to electromagnetic waves. The incident waves $P_{in1}$ and $P_{in2}$ both meet partial reflections $P_{rf1}$ and $P_{rf2}$, respectively, from the first and the second boundaries; the wave $P_{in3}$ passes into the third environment.

The influence of the coating layer (environment 2 in Figure 5) on the formation of reflected waves is analyzed using analogies of the expressions obtained in the theory of electric circuits with distributed parameters for long lines. These analogies allow us to obtain the reflection coefficient from the first boundary of the environments, i.e., in the air of the inter-substation zone, in the form as below [40]:

$$\underset{¯}{\mathsf{\Gamma }}=\frac{{\eta }_2·\left({\eta }_3-{\eta }_1\right)+j\left({\eta }_2^2-{\eta }_1·{\eta }_3\right)·\tan \left(K_2·d\right)}{{\eta }_2·\left({\eta }_3+{\eta }_1\right)+j\left({\eta }_2^2-{\eta }_1·{\eta }_3\right)·\tan \left(K_2·d\right)}$$

(38)

Let us consider under what conditions the reflection coefficient $\mathsf{\Gamma }$ in Expression (39) disappears, i.e., when there are no reflected and, therefore, standing waves.

According to the first variant, if ${\eta }_1={\eta }_2={\eta }_3,$ then the real and imaginary parts of the numerator in Expression (39) are equal to zero, and hence $\mathsf{\Gamma }=0$. However, such conditions are practically impossible if environment 3 is a contact wire or metal parts of the locomotive body, since ${\eta }_1$ is the wave resistance of the air, ${\eta }_1=$376.7 $\mathsf{\Omega }$, and ${\eta }_3$ is the resistance of the metal, ${\eta }_3=1.33\mathsf{\Omega }$; as a result, ${\eta }_1>{\eta }_3$. At the same time, this condition is feasible for dielectric environment 3, that is, the passage porcelain insulator of the locomotive roof or the glass of its frontal part. However, first, it is necessary to choose the dielectric permittivity of porcelain and glass, equal to the dielectric permittivity of the air. This will provide the following condition: ${\eta }_1={\eta }_3$. Second, the thickness of environment 2 (coating) must be, regardless of its ${\eta }_2$, equal to a multiplication of half the wavelength in this environment ($d=n·{\lambda }_2/2$; $n=1,2,3$). In this case, the reflection coefficient of the waves from the first boundary in Expression (39) is equal to $\tan \left(K_2·d\right)=0$. So, for the first boundary, the following applies:

$${\mathsf{\Gamma }}_1=\frac{{\eta }_2-{\eta }_1}{{\eta }_2+{\eta }_1}$$

and for the second boundary, the following:

$${\mathsf{\Gamma }}_2=\frac{{\eta }_3-{\eta }_2}{{\eta }_3+{\eta }_2}$$

Since ${\eta }_1={\eta }_3$, the coefficients ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ have equal amplitudes, but opposite signs, and therefore opposite phases in the reflection planes. However, the passage of the wave reflected from the second boundary, the distance $d$ “back and forth”, causes an additional incursion of its phase by the value of 2$K_{2}d=2\pi n$. As a result, the waves in the air environment 1, as equal in amplitude, but opposite in phase, cancel out each other and the resulting wave will be absent.

Another way to reduce reflection is based on using the fact that the wave resistance of a non-conductive material is defined as $\eta =\sqrt{\mu /\epsilon }$. By selecting $\mu$ and $\epsilon$, we can get $\eta$ equal to the air resistance. If the hysteresis loops $\mu \left(H\right)$ and $\epsilon \left(E\right)$ are the same, so that for any pair of tensions $H$ and $E$ ratio $\mu /\epsilon$ is the same, then the layer of this absorbing material will be an empty space for the incident wave with a normal incidence.

It is somewhat more complicated to provide a complete or partial reflection of waves from metal parts of the roof and the locomotive body. The most effective way is to make the body with intermediate media with graded or multi-layered (from three to four layers) coatings made of different materials. They could be based on thin films made from metal, magnetodielectric, semiconductor and superplastic materials [40]. In this case, the required value of the reflection coefficient is obtained by a change in thickness of the layers and properties $\epsilon$, $\mu$, $\sigma$ of the material. It is necessary to create such an intermediate coating, either graded or multi-layered, in which wave resistance would change exponentially as ${\eta }_2={\eta }_1{e}^{\beta x}$ [40]. It is always possible to choose such value $\beta$ as to match the impedances of this layer and the air of inter-substation zones. The advantages of multi-layered coatings over single-layered coatings are clear from researches presented in [42,43]. It follows that double-layered coatings have significantly lower reflection $\mathsf{\Gamma }$ (on 12–16%), transmission $\mathsf{{\rm T}}$ (on 37–42%) and absorption $\mathsf{A}$ (on 49–58%) coefficients than single-layered coatings.

It should also be noted that the presented-above calculations show results for basic and higher harmonics created by power converters feeding the traction motors. The higher harmonics can be significantly reduced by appropriate configuration of converters and the application of harmonic filters, which exclude waves created by higher frequencies mentioned above in the article. Such a solution substantially improves power quality and reduces reactive energy transferred by higher harmonics. At the same time, the basic component stills transferer reactive power. So, the proposed multi-layered and composite materials could be applied to compensate this power by the way presented above.

These materials have beneficial reflective properties [44,45,46]. It is also necessary to use the fact that a rough (reflexed, corrugated) metal surface reduces the reflection coefficient [43]. The analogical result could be achieved if the same is done with micro-layered coatings. Nowadays, layered materials are the most advanced and comparatively cheap solution; their design technique is shown in [47]. We have to note that a more elaborated manufacture of the body of the electric rolling stock, by applying multi-layered reflective coatings, will pay back quickly and noticeably. This conclusion is evident due to the large amounts of reactive power exchanged in inter-substation zones and the ever-increasing cost of electricity spent on trains’ electric traction.

In conclusion, it must be added that the presented idea in this article must be continued and added with the more comprehensive analysis of the described-below aspects. First, the article considered the field created by the return current flowing in rails because of the high values of magnetic fields. This current concentrates in rails, but its value equals only 40% of the current taken by locomotive. The other part, known as the stray current, enters to the ground and flows through the metal parts and pipelines. Because of the complexity of the process and difficulties to calculate the values in the nearest underground metal infrastructure [48,49,50,51], this current is not considered in the article. Second, for simplification, the influence of eddy currents in the metal body of the electric locomotive is not considered. In our opinion, this issue is very complex and requires separate special studies. Third, as it was written above, the method is in the conceptual phase and its model must be validated through field tests. To establish the adequacy of the “field” approach for reactive power estimation, one should take the following steps. On the first stage:

• Select an extended electrified railway line with a few sections, with a length longer than 160 km;
• Choose an AC electric locomotive, which will move along this section;
• Perform hourly monitoring of field strengths at the surface of the electric loc motive’s roof using broadband electric and magnetic field strength meter. Simultaneously, record the voltage across the current collector and locomotive current by oscilloscope and define its harmonic spectrum;
• Calculate the volume of reactive energy $Q_1$ according to Formula (15).

At the second stage of the experimental tests, it is necessary to cover the surface of the roof of the electric locomotive with a single-layer or multi-layer coating film and perform the exact step-by-step procedure for determining the reactive power $Q_2$. Finally, after comparing obtained values of the reactive power, if $Q_2>Q_1$, we could conclude that the “field” approach is adequate.

11. Conclusions

• The currently existing methods for analyzing electric power processes in electric traction systems do not consider the fundamental law of the propagation of electromagnetic energy. It does not account accurately the energy spent on train traction;
• Electromagnetic harmonic waves spreading in the space of inter-substation zones from the traction substation to electric rolling stock, incident on the surface of the contact wire, as well as on the frontal, lateral and roof surfaces of the body of electric rolling stock, partially reflected and summing up with the incident waves, form standing waves whose energy is reactive;
• Reactive power in the space of inter-substation zones is a measure of the asymmetry of the rates of change in the electric and magnetic components of the energy of the electromagnetic field existing in that zone. This power is numerically equal to the difference between the average values of the energies stored in the magnetic and electric fields in the volume of the feeder zone, multiplied by $2\omega$;
• To compensate for the reactive power existing in the space of inter-substation zones, it is necessary to “suppress” (damp) standing waves by applying single-layered or multi-layered film coatings with certain electromagnetic properties to particular parts of the surface of the body of the electric rolling stock;
• The stated and theoretically substantiated “field” (based on the theory of the electromagnetic field) approach to the processes of formation, transmission, and “damping” of standing electromagnetic waves, as characteristics of reactive power in inter-substation zones, is applicable to any type of electric locomotives and AC electric traction systems. However, there are no theoretical limitations.