Fast and Accurate 2D Analytical Subdomain Method for Coaxial Magnetic Coupling Analysis
Abstract
:1. Introduction
2. Development and Validation of the 2D Analytical Tool
- End effects are neglected due to the cylindrical geometry.
- Permeability of the back iron is infinite. Hence, the magnetic field is perpendicular to the back iron.
- Relative permeability of the PMs is taken as 1.
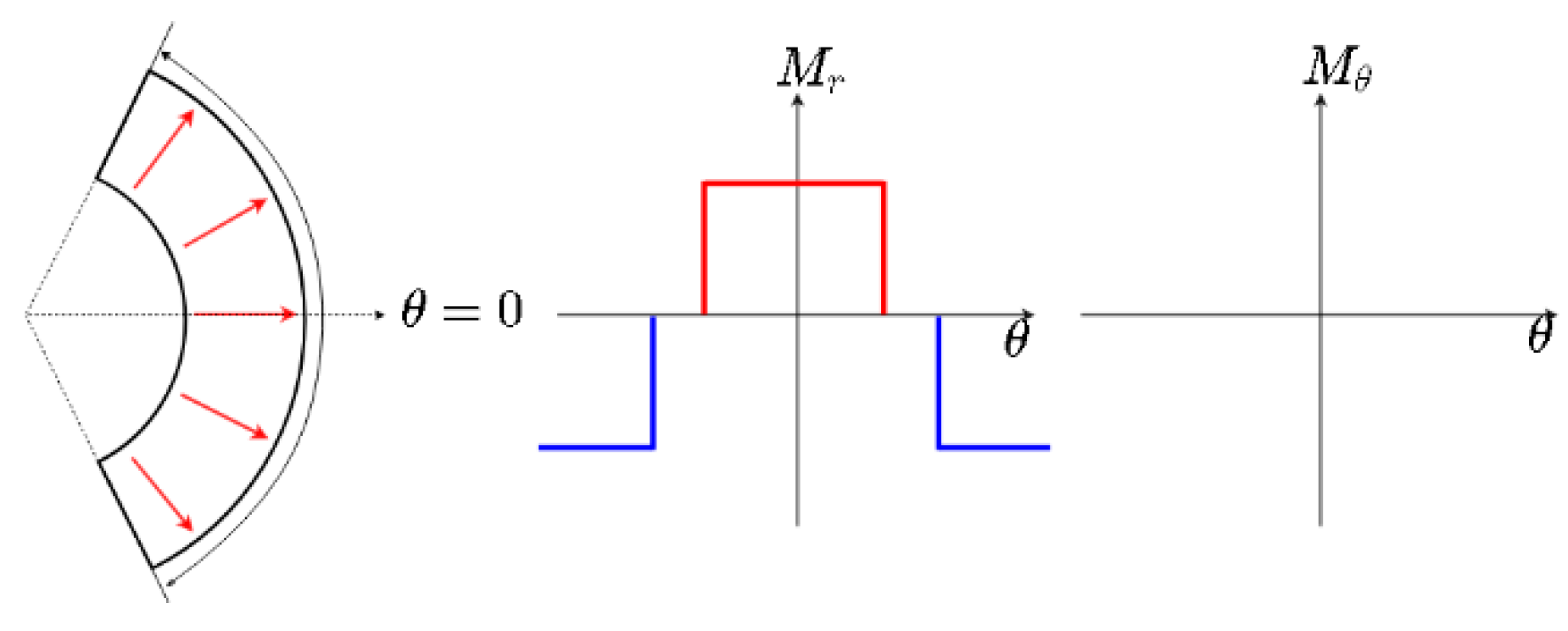
- PMs are radially magnetized.
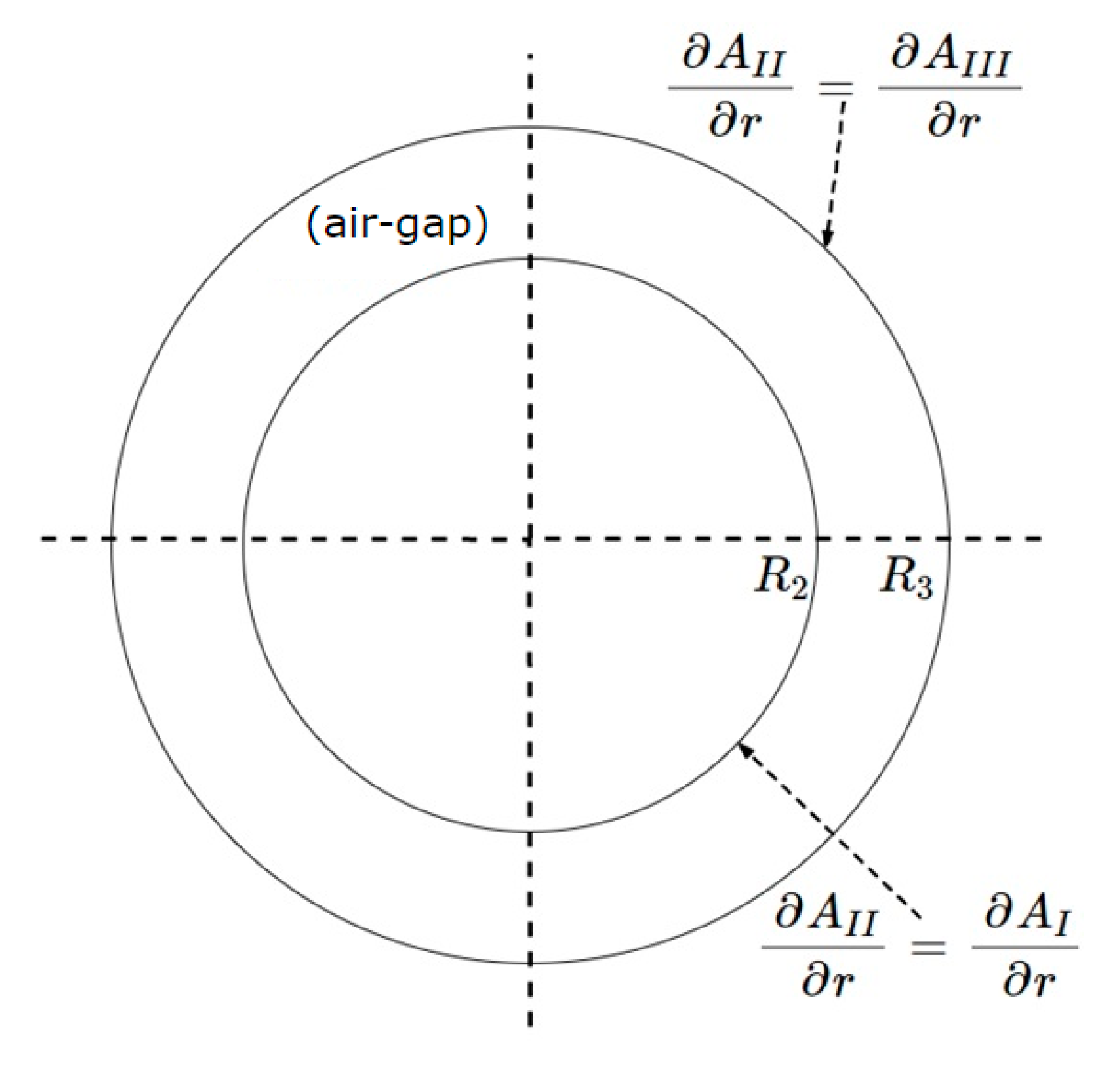
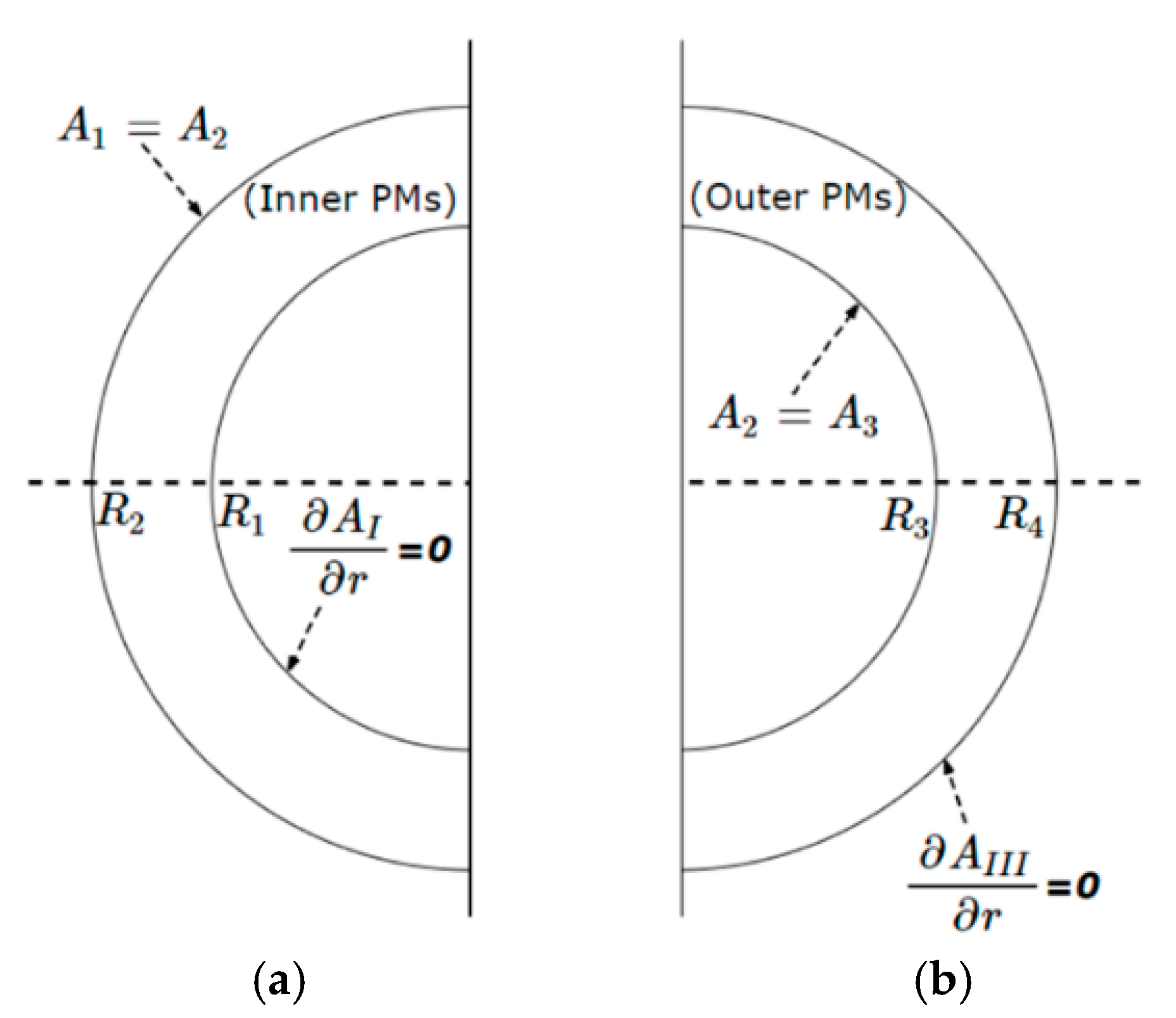
2.1. Potential Functions
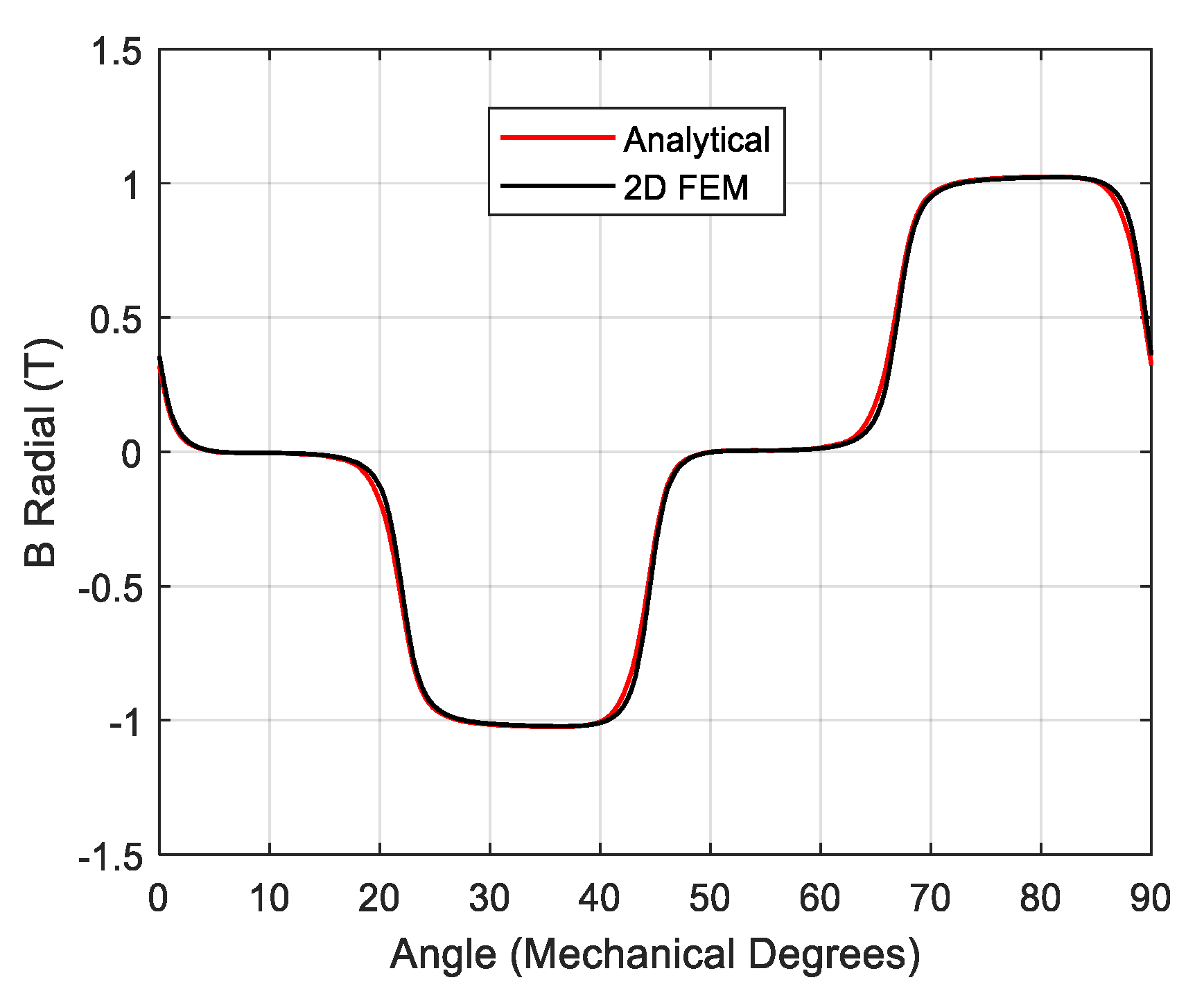
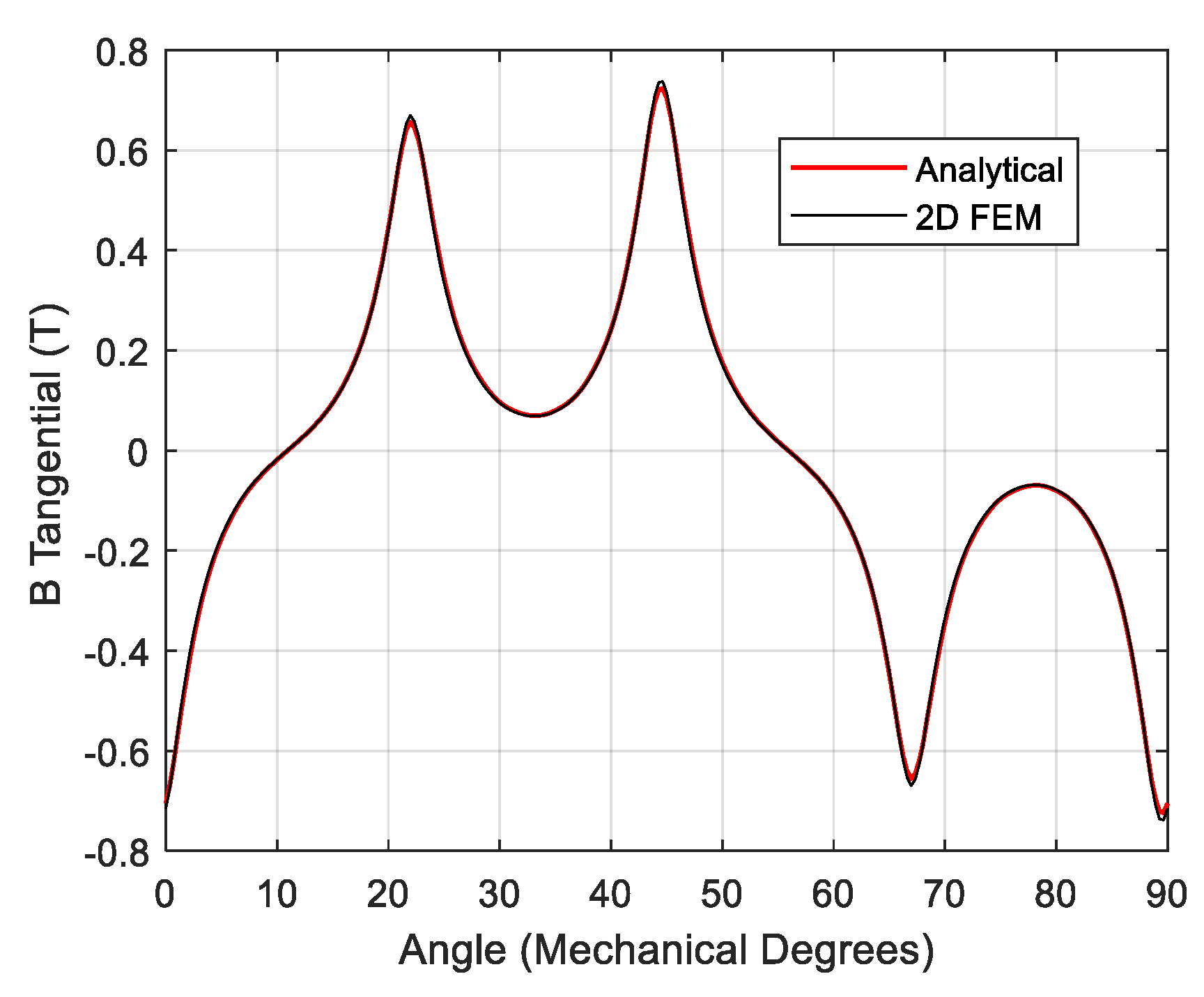
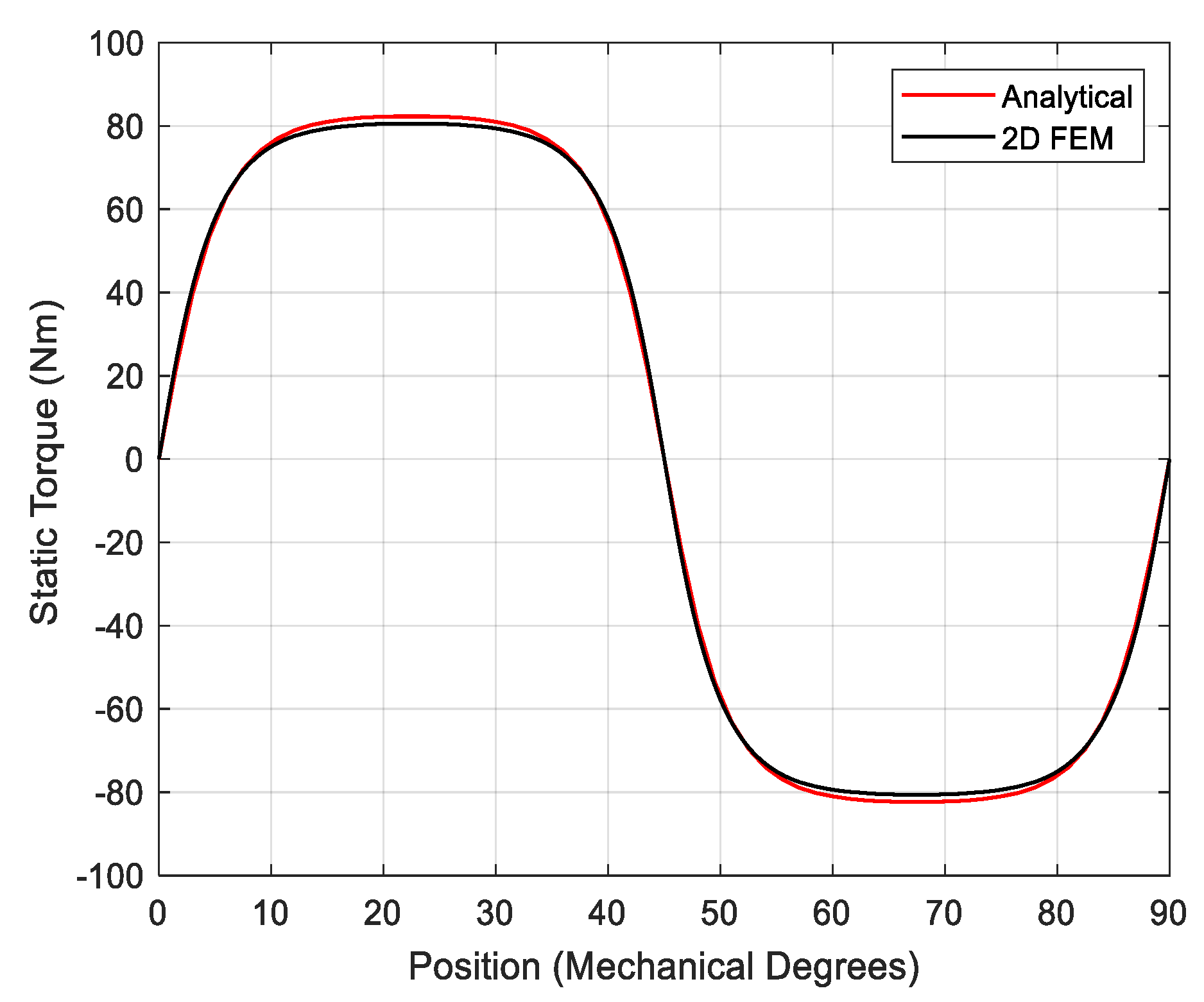
2.2. Flux Density and Static Torque
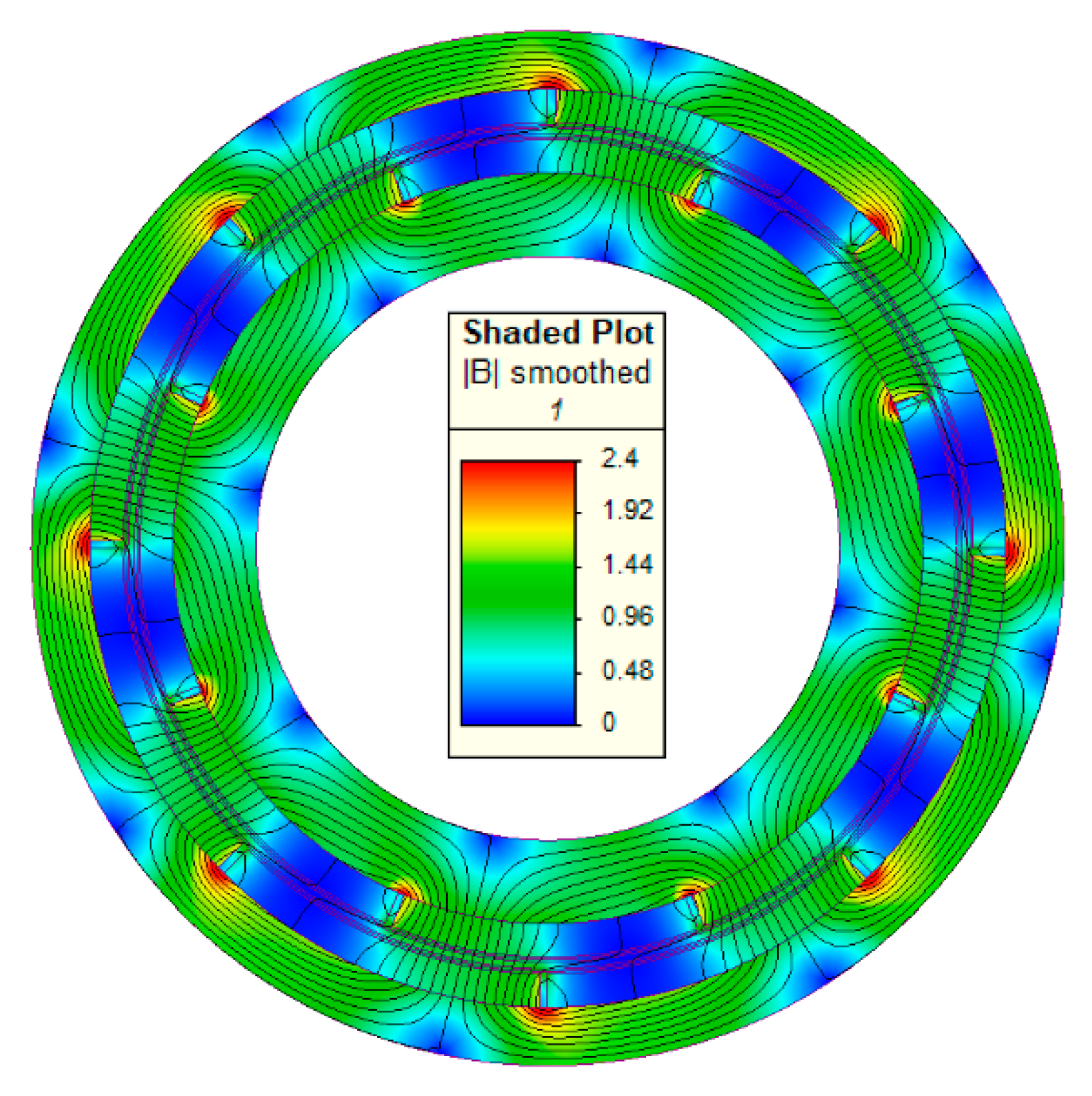
2.3. Validation Exercise
3. Sensitivity Analyses and Computational Time Evaluation
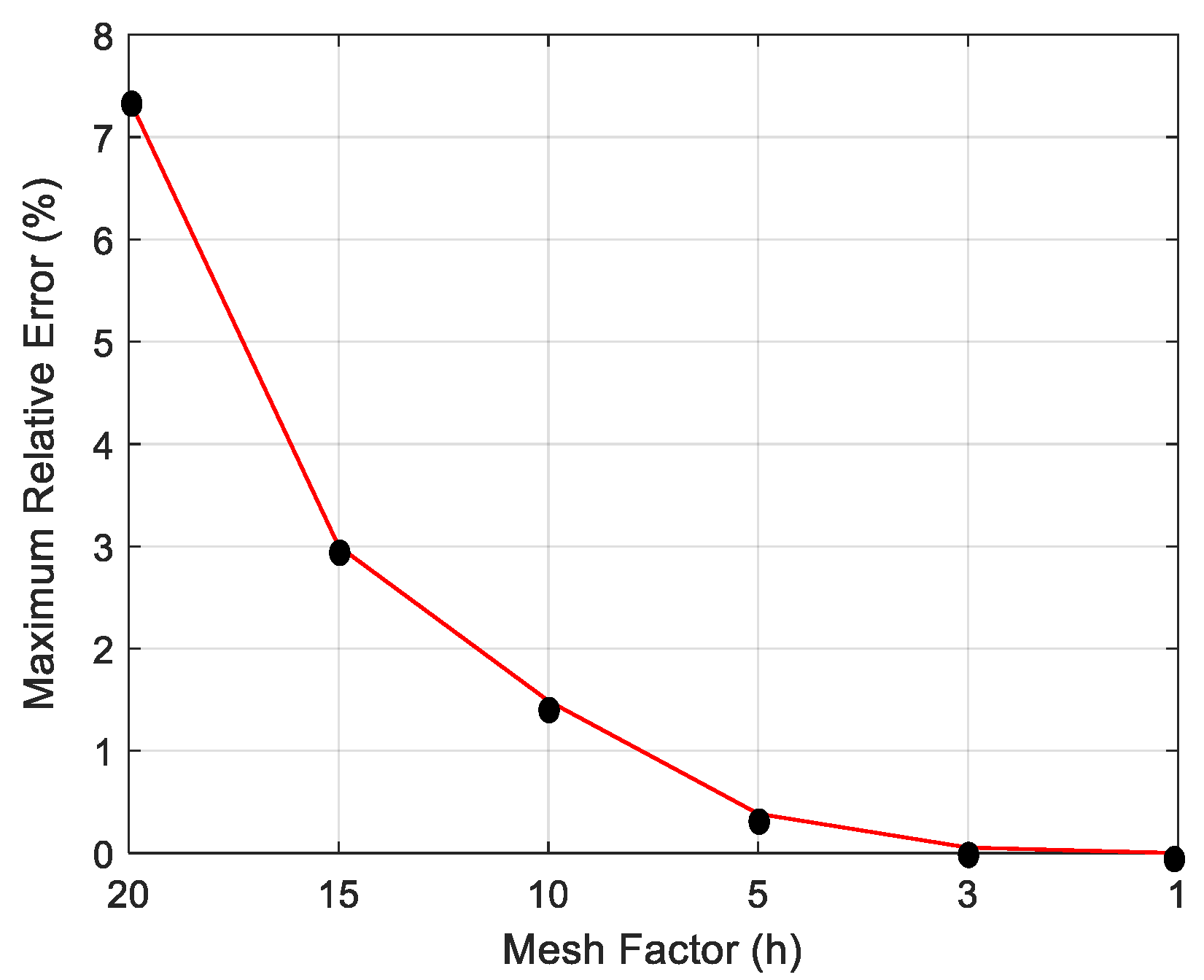
3.1. Mesh Size Selection
3.2. Harmonic Numbers Selection
3.3. Results Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wu, W.; Lovatt, H.; Dunlop, J. Analysis and design optimisation of magnetic couplings using 3D finite element modelling. IEEE Trans. Magn. 1997, 33, 4083–4094. [Google Scholar] [CrossRef]
- Galea, M.; Giangrande, P.; Madonna, V.; Buticchi, G. Reliability-Oriented Design of Electrical Machines: The Design Process for Machines’ Insulation Systems MUST Evolve. IEEE Ind. Electron. Mag. 2020, 14, 20–28. [Google Scholar] [CrossRef]
- Charpentier, J.-F.; Lemarquand, G. Study of permanent-magnet couplings with progressive magnetization using an analytical formulation. IEEE Trans. Magn. 1999, 35, 4206–4217. [Google Scholar] [CrossRef]
- Kim, S.H.; Shin, J.W.; Ishiyama, K. Magnetic Bearings and Synchronous Magnetic Axial Coupling for the Enhancement of the Driving Performance of Magnetic Wireless Pumps. IEEE Trans. Magn. 2013, 50, 1–4. [Google Scholar] [CrossRef]
- Akcay, Y.; Giangrande, P.; Galea, M. A Novel Magnetic Coupling Configuration for Enhancing the Torque Density. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 228–233. [Google Scholar]
- Akcay, Y.; Giangrande, P.; Galea, M. Design, Analysis and Dynamic Performance of Radial Magnetic Coupling. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 222–227. [Google Scholar]
- Ho, S.L.; Niu, S.; Fu, W. Transient Analysis of a Magnetic Gear Integrated Brushless Permanent Magnet Machine Using Circuit-Field-Motion Coupled Time-Stepping Finite Element Method. IEEE Trans. Magn. 2010, 46, 2074–2077. [Google Scholar] [CrossRef]
- Giangrande, P.; Madonna, V.; Nuzzo, S.; Galea, M. Design of Fault-Tolerant Dual Three-Phase Winding PMSM for Helicopter Landing Gear EMA. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018. [Google Scholar]
- Al-Timimy, A.; Degano, M.; Giangrande, P.; Calzo, G.L.; Xu, Z.; Galea, Z.X.M.; Gerada, C.; Zhang, H.; Xia, L. Design and optimization of a high power density machine for flooded industrial pump. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1480–1486. [Google Scholar]
- Giangrande, P.; Cupertino, F.; Pellegrino, G. Modelling of linear motor end-effects for saliency based sensorless control. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3261–3268. [Google Scholar] [CrossRef]
- Karban, P.; Pánek, D.; Orosz, T.; Petrášová, I.; Doležel, I. FEM based robust design optimization with Agros and Ārtap. Comput. Math. Appl. 2021, 81, 618–633. [Google Scholar] [CrossRef]
- Kiss, G.M.; Kaska, J.; Oliveira, R.; Rubanenko, O.; Tóth, B. Performance Analysis of FEM Solvers on Practical Electromagnetic Problems. Period. Polytech. Electr. Eng. Comput. Sci. 2021, 65, 113–122. [Google Scholar] [CrossRef]
- Mezani, S.; Laporte, B.; Takorabet, N. Saturation and space harmonics in the complex finite element computation of induction motors. IEEE Trans. Magn. 2005, 41, 1460–1463. [Google Scholar] [CrossRef]
- Williamson, S.; Lim, L.; Smith, A. Transient analysis of cage-induction motors using finite-elements. IEEE Trans. Magn. 1990, 26, 941–944. [Google Scholar] [CrossRef]
- Williamson, S.; Lim, L.; Robinson, M. Finite-element models for cage induction motor analysis. IEEE Trans. Ind. Appl. 1990, 26, 1007–1017. [Google Scholar] [CrossRef]
- Coulomb, J. A methodology for the determination of global electromechanical quantities from a finite element analysis and its application to the evaluation of magnetic forces, torques and stiffness. IEEE Trans. Magn. 1983, 19, 2514–2519. [Google Scholar] [CrossRef]
- Lukic, M.; Hebala, A.; Giangrande, P.; Klumpner, C.; Nuzzo, S.; Chen, G.; Gerada, C.; Eastwick, C.; Galea, M. State of the Art of Electric Taxiing Systems. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018. [Google Scholar]
- Giangrande, P.; Madonna, V.; Sala, G.; Kladas, A.; Gerada, C.; Galea, M. Design and Testing of PMSM for Aerospace EMA Applications. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 2038–2043. [Google Scholar]
- Davey, K.R. Analytic analysis of single- and three-phase induction motors. IEEE Trans. Magn. 1998, 34, 3721–3727. [Google Scholar] [CrossRef]
- Marcsa, D.; Kuczmann, M. Motion finite element simulation of a single-phase induction motor. Pollack Period. 2009, 4, 57–66. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Simple Analytical Expressions for the Force and Torque of Axial Magnetic Couplings. IEEE Trans. Energy Convers. 2012, 27, 536–546. [Google Scholar] [CrossRef] [Green Version]
- Lubin, T.; Mezani, S.; Rezzoug, A. Steady-state and transient analysis of an axial-field magnetic coupling. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1443–1449. [Google Scholar]
- Lubin, T.; Mezani, S.; Rezzoug, A. Experimental and Theoretical Analyses of Axial Magnetic Coupling Under Steady-State and Transient Operations. IEEE Trans. Ind. Electron. 2013, 61, 4356–4365. [Google Scholar] [CrossRef] [Green Version]
- Lubin, T.; Rezzoug, A. Steady-State and Transient Performance of Axial-Field Eddy-Current Coupling. IEEE Trans. Ind. Electron. 2014, 62, 2287–2296. [Google Scholar] [CrossRef] [Green Version]
- Lubin, T.; Rezzoug, A. 3-D Analytical Model for Axial-Flux Eddy-Current Couplings and Brakes under Steady-State Conditions. IEEE Trans. Magn. 2015, 51, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Nagrial, M. Analysis, design and performance of magnetic couplings. In Proceedings of the 1995 International Conference on Power Electronics and Drive Systems. PEDS 95, Singapore, 21–24 February 1995; Volume 2, pp. 634–638. [Google Scholar]
- Yao, Y.; Huang, D.; Lin, S.; Wang, S. Theoretical computations of the magnetic coupling between magnetic gears. IEEE Trans. Magn. 1996, 32, 710–713. [Google Scholar] [CrossRef]
- Nagrial, M.H. Performance of magnetic couplings using Nd-Fe-B magnets. In Proceedings of the 1996 IEEE IECON. 22nd International Conference on Industrial Electronics, Control, and Instrumentation, Taipei, Taiwan, 9 August 1996; Volume 2, pp. 997–998. [Google Scholar]
- Akcay, Y.; Giangrande, P.; Gerada, C.; Galea, M. Comparative analysis between axial and coaxial magnetic couplings. In Proceedings of the 10th International Conference on Power Electronics, Machines and Drives (PEMD 2020), Online, 15–17 December 2020; pp. 385–390. [Google Scholar]
- Al-Timimy, A.; Giangrande, P.; Degano, M.; Galea, M.; Gerada, C. Comparative study of permanent magnet-synchronous and permanent magnet-flux switching machines for high torque to inertia applications. In Proceedings of the 2017 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Nottingham, UK, 20–21 April 2017; pp. 45–51. [Google Scholar]
- Li, K.; Bird, J. A 3-D analytical model of a Halbach axial magnetic coupling. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1448–1454. [Google Scholar]
- Al-Timimy, A.; Al-Ani, M.; Degano, M.; Giangrande, P.; Gerada, C.; Galea, M. Influence of rotor endcaps on the electromagnetic performance of high-speed PM machine. IET Electr. Power Appl. 2018, 12, 1142–1149. [Google Scholar] [CrossRef]
- Al-Timimy, A.; Degano, M.; Xu, Z.; Calzo, G.L.; Giangrande, P.; Galea, M.; Gerada, C.; Zhang, H.; Xia, L. Trade-off analysis and design of a high power density PM machine for flooded industrial pump. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1749–1754. [Google Scholar]



| Symbol | Parameters | Values |
|---|---|---|
| Back iron inner radius | 35 mm | |
| Inner PM inner radius | 45 mm | |
| Inner PM outer radius | 49 mm | |
| Outer PM inner radius | 51 mm | |
| Outer PM outer radius | 55 mm | |
| Outer back iron outer radius | 62 mm | |
| Air-gap thickness | 2 mm | |
| Number of pole-pairs | 4 | |
| PM thickness | 4 mm | |
| PM openings | 95% | |
| Outer diameter | 50 mm | |
| Active part length | 50 mm | |
| Remanence of PMs | 1.29 T |
| Symbol | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 |
|---|---|---|---|---|---|---|---|
| 35 | 35 | 35 | 35 | 150 | 150 | 35 | |
| 45 | 45 | 45 | 45 | 200 | 200 | 45 | |
| 49 | 49 | 49 | 49 | 220 | 230 | 49 | |
| 51 | 51 | 53 | 57 | 224 | 234 | 51 | |
| 55 | 55 | 61 | 61 | 244 | 264 | 55 | |
| 62 | 62 | 68 | 68 | 294 | 314 | 62 | |
| 2 | 2 | 4 | 8 | 4 | 4 | 2 | |
| 4 | 16 | 8 | 8 | 8 | 8 | 2–30 | |
| 4 | 4 | 4 | 4 | 20 | 30 | 4 | |
| (%) | 95 | 95 | 95 | 95 | 95 | 95 | 95 |
| 50 | 50 | 50 | 50 | 150 | 250 | 50 | |
| 1.29 | 1.29 | 1.29 | 1.29 | 1.29 | 1.29 | 1.29 |
| Region | Mesh Expression (mm) | Mesh Size for h = 1 (mm) |
|---|---|---|
| Air-gap | 0.25 * h | 0.25 |
| PMs | 0.5 * h | 0.5 |
| Back Iron | 1 * h | 1 |
| Mesh (mm) | Case1 (h = 3) | Case 2 (h = 2) | Case 3 (h = 1) | Case 4 (h = 1) | Case 5 (h = 5) | Case 6 (h = 5) | Case 7 (h = 5) |
|---|---|---|---|---|---|---|---|
| Air-gap | 0.75 | 0.5 | 0.25 | 0.25 | 1.25 | 1.25 | 1.25 |
| PMs | 1.5 | 1 | 0.5 | 0.5 | 2.5 | 2.5 | 2.5 |
| Back Iron | 3 | 2 | 1 | 1 | 5 | 5 | 5 |
| Harmonic | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 |
|---|---|---|---|---|---|---|---|
| Fundamental | 4 | 16 | 8 | 8 | 8 | 8 | 2–30 |
| Sum 1 | 12 | 48 | 24 | 24 | 24 | 24 | 6–90 |
| Sum 2 | 20 | 80 | 40 | 40 | 40 | 40 | 10–150 |
| Sum 3 | 28 | 112 | 56 | 56 | 56 | 45 | 14–210 |
| Sum 4 | 36 | 144 | 72 | 72 | 72 | 72 | 18–270 |
| Case Number | Analyt. (Fund.) (s) | Error (Fund.) (%) | Analyt. (Sum. 1) (s) | Error (Sum. 1) (%) | Analyt. (Sum. 2) (s) | Error (Sum. 2) (%) | Analyt. (Sum. 3) (s) | Error (Sum. 3) (%) | Analyt. (Sum. 4) (s) | Error (Sum. 4) (%) | FEM (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 11.54 | 15.8 | 16.36 | 7.3 | 21.87 | 4.2 | 27.51 | 3.4 | 32.8 | 3.1 | 240 |
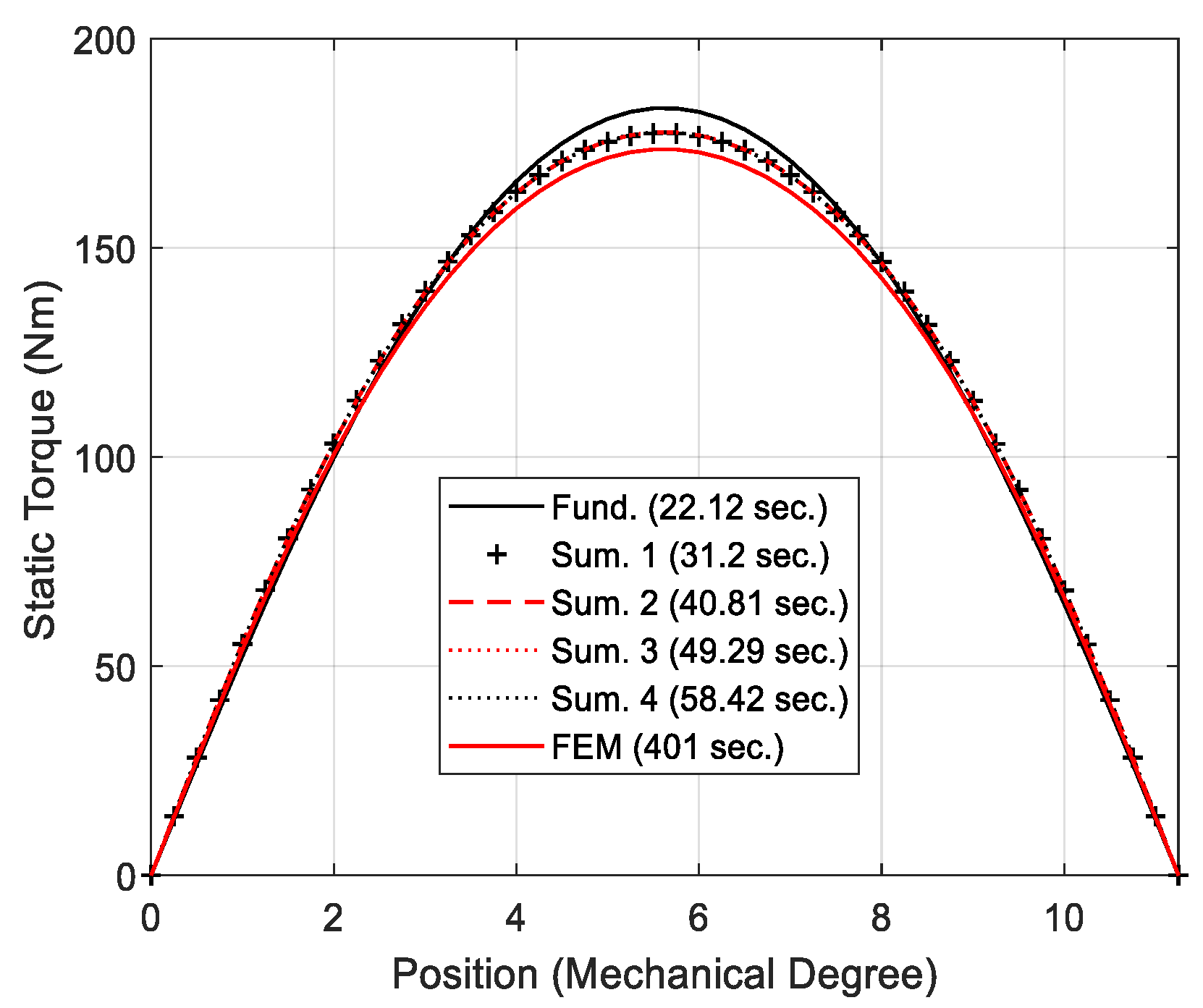
| Case 2 | 22.12 | 5.4 | 31.2 | 3.8 | 40.81 | 4.2 | 49.29 | 4.4 | 58.42 | 4.4 | 401 |
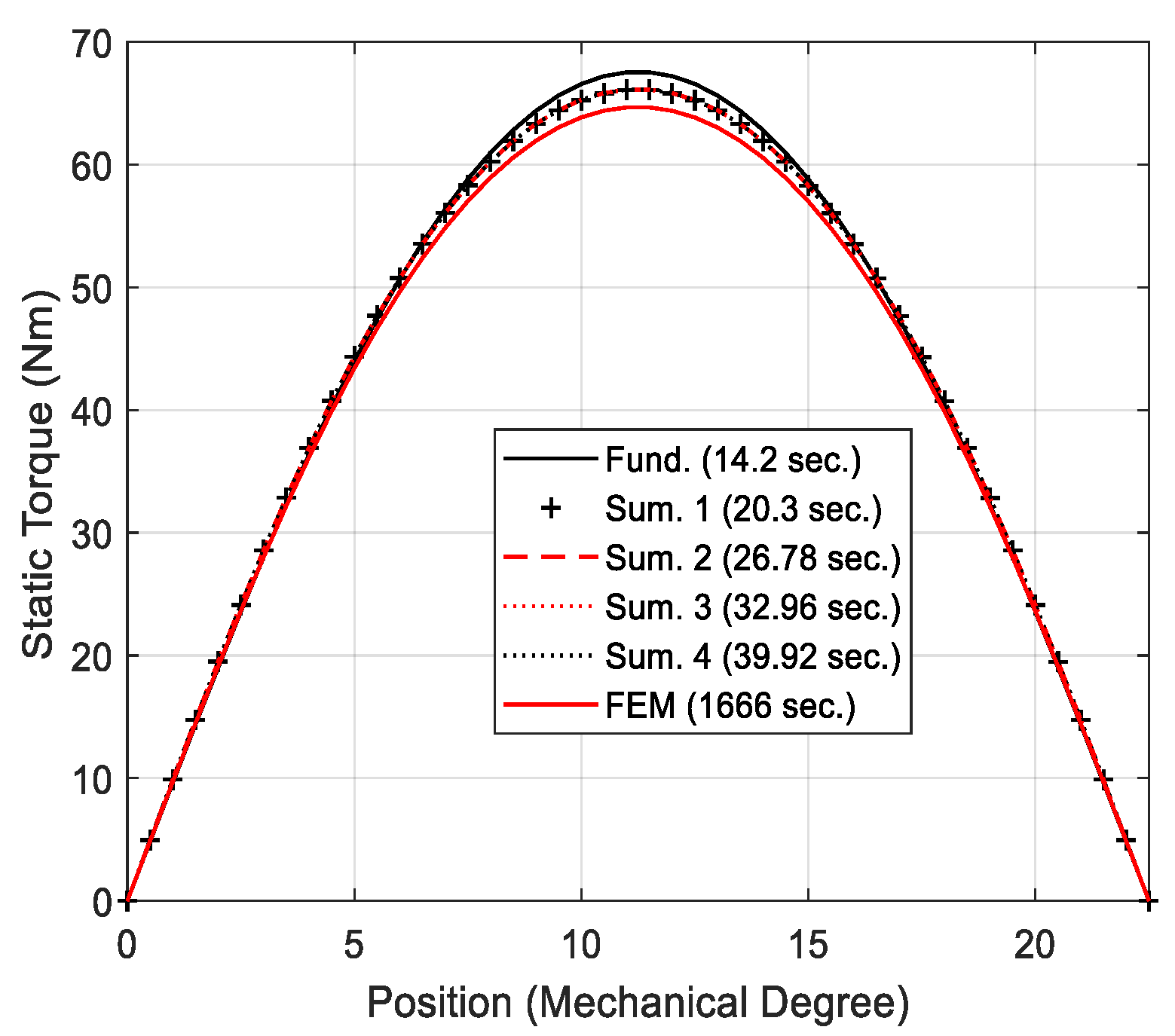
| Case 3 | 14.2 | 6.6 | 20.3 | 3.3 | 26.78 | 2.9 | 32.96 | 2.9 | 39.92 | 2.9 | 665 |
| Case 4 | 14.2 | 4.3 | 20.3 | 3.1 | 26.78 | 3 | 32.96 | 3 | 39.92 | 3 | 1666 |
| Case 5 | 14.2 | 10.5 | 20.3 | 5 | 26.78 | 3.5 | 32.96 | 2.8 | 39.92 | 2.7 | 815 |
| Case 6 | 14.2 | 8.8 | 20.3 | 4.4 | 26.78 | 3.2 | 32.96 | 2.6 | 39.92 | 2.5 | 990 |
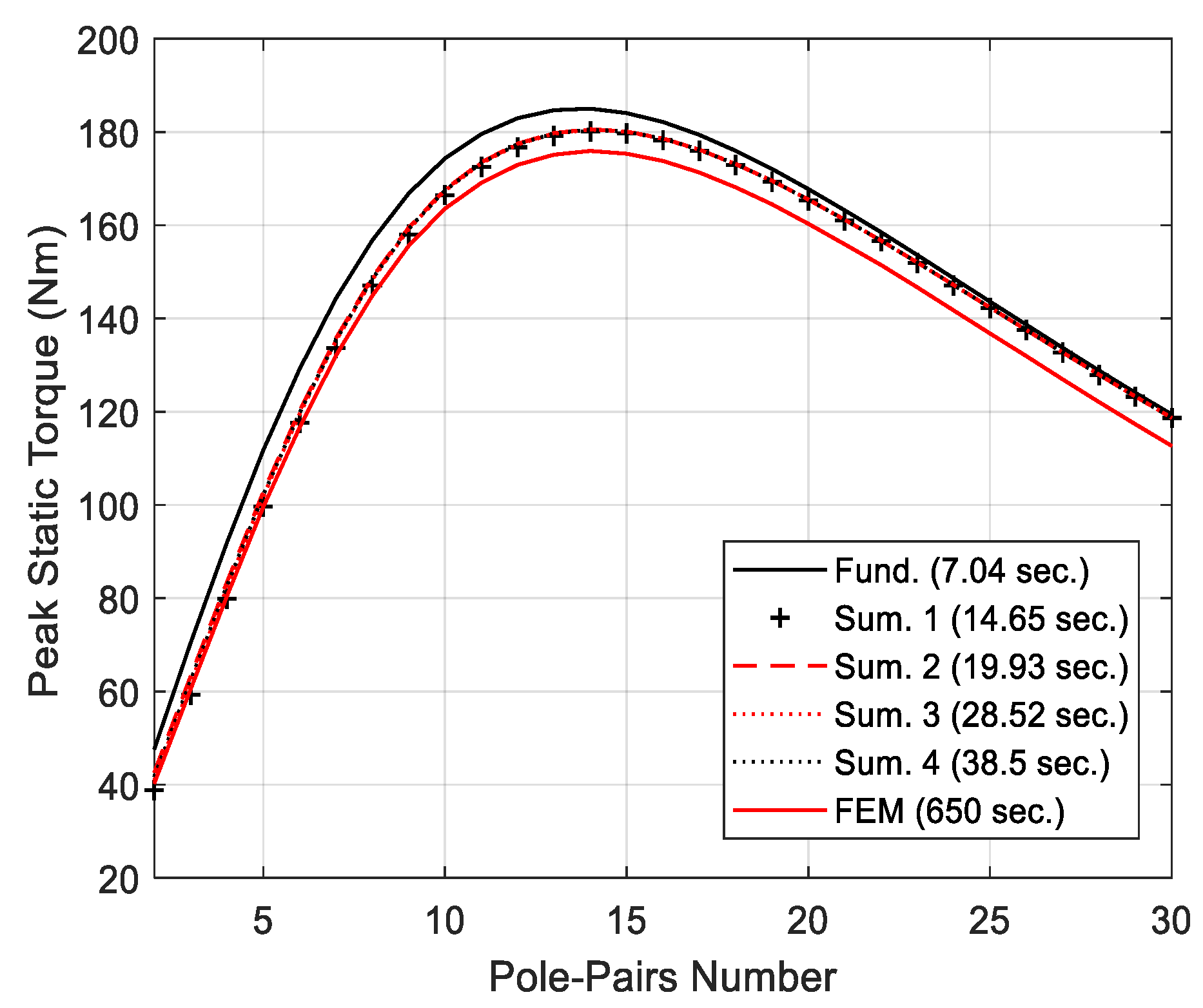
| Case 7 | 7.04 | 20.3 | 14.65 | 6 | 19.93 | 6.5 | 28.52 | 6 | 38.5 | 6 | 650 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akcay, Y.; Giangrande, P.; Tweedy, O.; Galea, M. Fast and Accurate 2D Analytical Subdomain Method for Coaxial Magnetic Coupling Analysis. Energies 2021, 14, 4656. https://doi.org/10.3390/en14154656
Akcay Y, Giangrande P, Tweedy O, Galea M. Fast and Accurate 2D Analytical Subdomain Method for Coaxial Magnetic Coupling Analysis. Energies. 2021; 14(15):4656. https://doi.org/10.3390/en14154656
Chicago/Turabian StyleAkcay, Yusuf, Paolo Giangrande, Oliver Tweedy, and Michael Galea. 2021. "Fast and Accurate 2D Analytical Subdomain Method for Coaxial Magnetic Coupling Analysis" Energies 14, no. 15: 4656. https://doi.org/10.3390/en14154656
APA StyleAkcay, Y., Giangrande, P., Tweedy, O., & Galea, M. (2021). Fast and Accurate 2D Analytical Subdomain Method for Coaxial Magnetic Coupling Analysis. Energies, 14(15), 4656. https://doi.org/10.3390/en14154656







