Numerical Modelling of Heat Transfer in Fine Dispersive Slurry Flow
Abstract
:1. Introduction
- -
- particle size distribution and its shape, elasticity, porosity, degradation, hydrophobicity, averaged solid particle diameter and density;
- -
- carrier liquid viscosity and density;
- -
- type of slurry: Newtonian or non-Newtonian, with or without yield stress;
- -
- type of solid concentration: dilute suspension or highly concentrated;
- -
- type of slurry flow: laminar, transient, turbulent, homogeneous, pseudo-homogeneous, heterogeneous, with steady or moving beds;
- -
- geometry and flow direction: circular or noncircular conduit, one-, two-, or three-dimensional, vertical, horizontal, or inclined conduit;
- -
- boundary conditions for velocity and temperature;
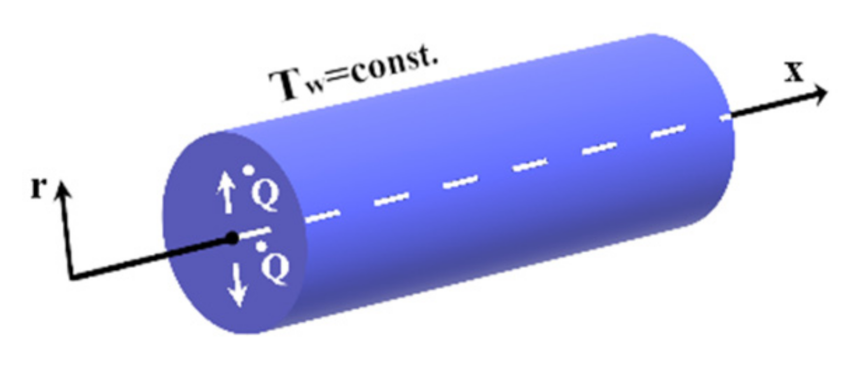
2. Physical Model
- -
- solid particles are round, smooth, rigid, non-hydrophobic, and the influence of such properties on slurry flow is not considered;
- -
- solid particles are sufficiently fine, with a median particle diameter dP ≅ 20 μm, so the damping of turbulence, described by Wilson and Thomas [25], occurs;
- -
- the slurry flows in a straight and smooth horizontal pipeline, which is rigid and its inner diameter is constant;
- -
- -
- the rheological properties of the slurry can be approximated by the Bingham model;
- -
- the flow of the slurry is turbulent, steady, axially symmetric (V = 0) and without circumferential eddies (W = 0);
- -
- the slurry flow is fully developed hydrodynamically, which means that the time-averaged velocity component U does not change in the flow direction (∂U/∂x = 0).
- -
- the wall temperature is steady;
- -
- the heat flux is homogeneous; the heat flux acts from the slurry to the pipe wall; its value is steady, known, and sufficiently small, so the following arbitrarily chosen condition is met: |Tb − Tw|< 7 K;
- -
- the apparent viscosity and specific heat are constant and are determined by the thermal condition at the pipe wall, while the slurry density and conduction coefficient are calculated from the bulk temperature;
- -
- there is no inner heat production in a slurry, and conversion of mechanical energy into internal heat is not considered;
- -
- heat due to radiation and conduction through a pipe wall are negligible;
- -
- the slurry flow is fully developed thermally, which means that the temperature changes linearly in the flow direction ‘ox’ (∂T/∂x = const ≠ 0).
3. Mathematical Model
3.1. Newtonian Liquid
3.2. Non-Newtonian Fine Dispersive Slurry
4. Numerical Procedure
- -
- T(r) = Tw;
- -
- U(r) = Umax[(R − r)/R]1/7, where Umax was arbitrarily chosen;
- -
- k was set up on the basis of the intensity of the assigned turbulence, that is, k(r) = ½ U2(r);
- -
- ε was established based of the relation: ε(r) = 0.093/4 k3/2(r)/L, where L was determined from the Nikuradse formula.
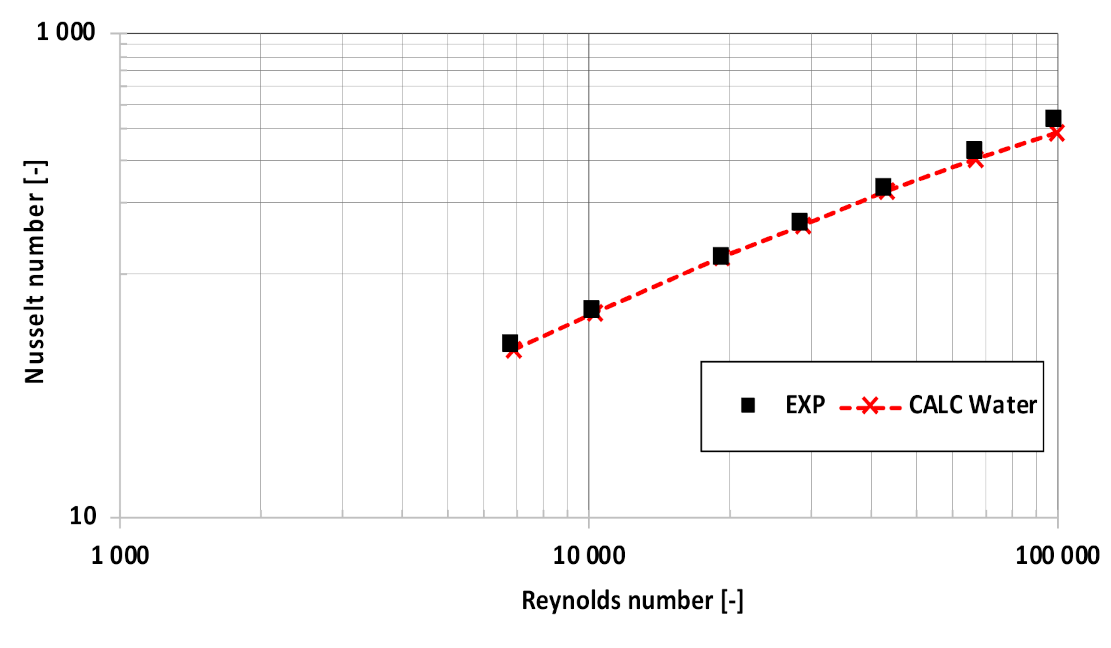
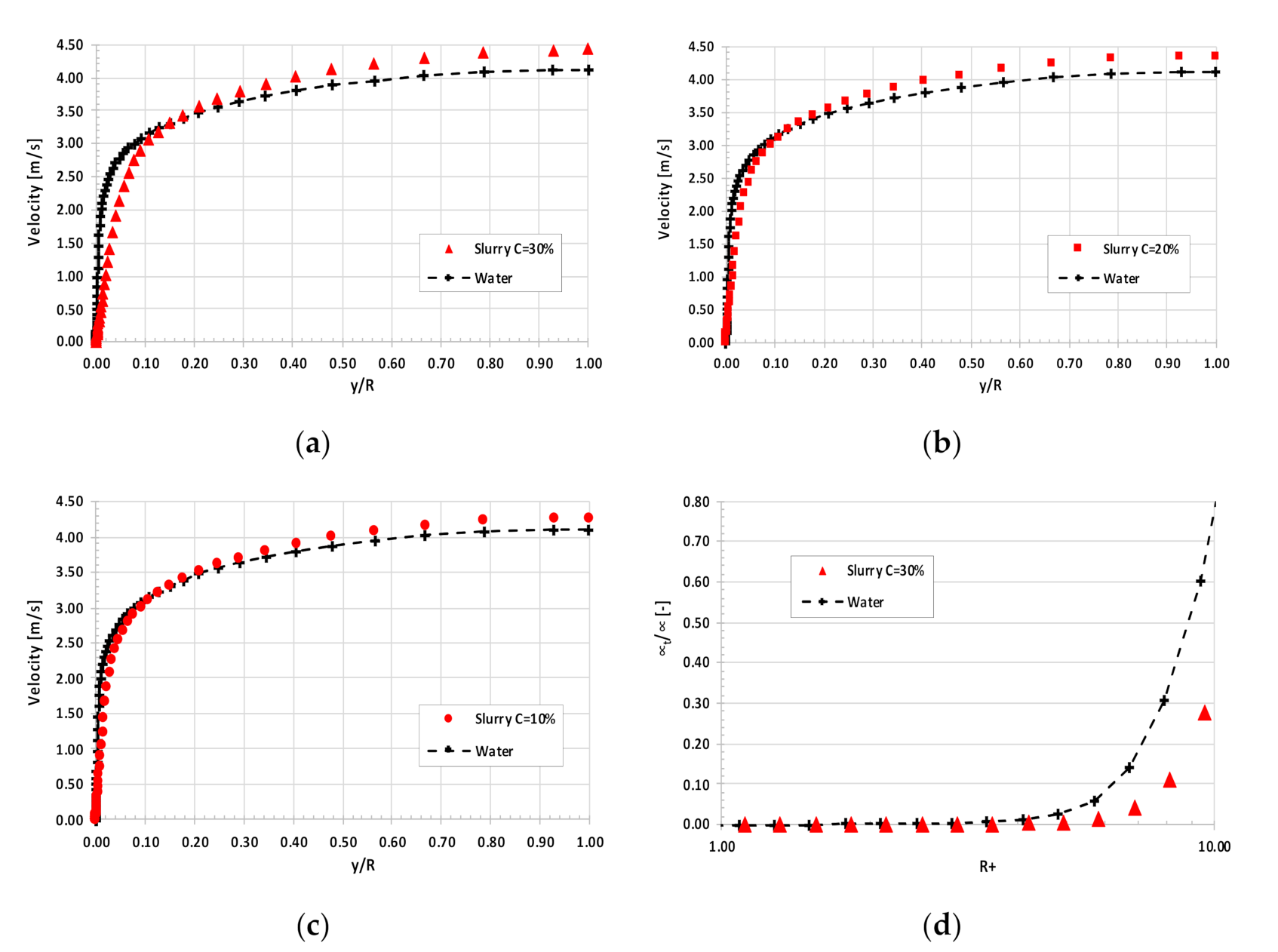
5. Validation of the Mathematical Model
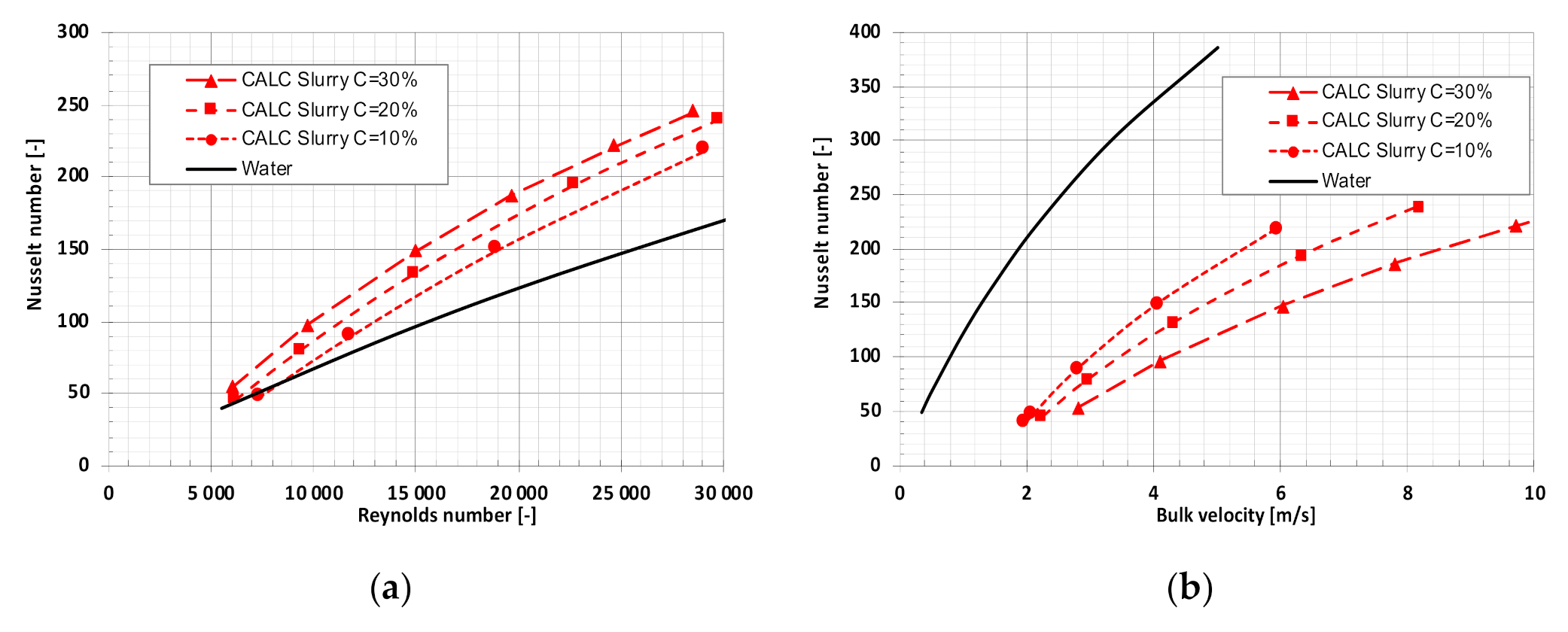
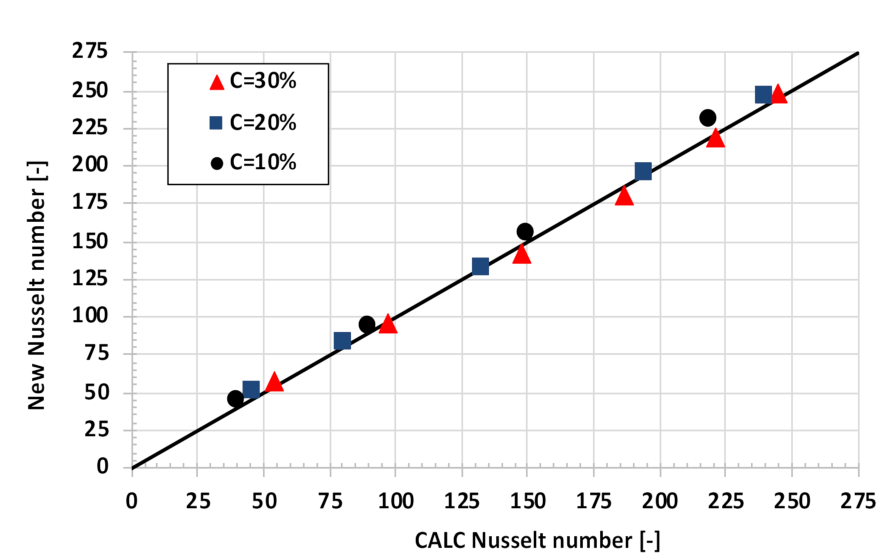
6. Simulation Results
7. Discussion and Conclusions
- The slurry velocity profile substantially influences the heat transfer process. Therefore, it is crucial that the mathematical model be validated for isothermal flow first.
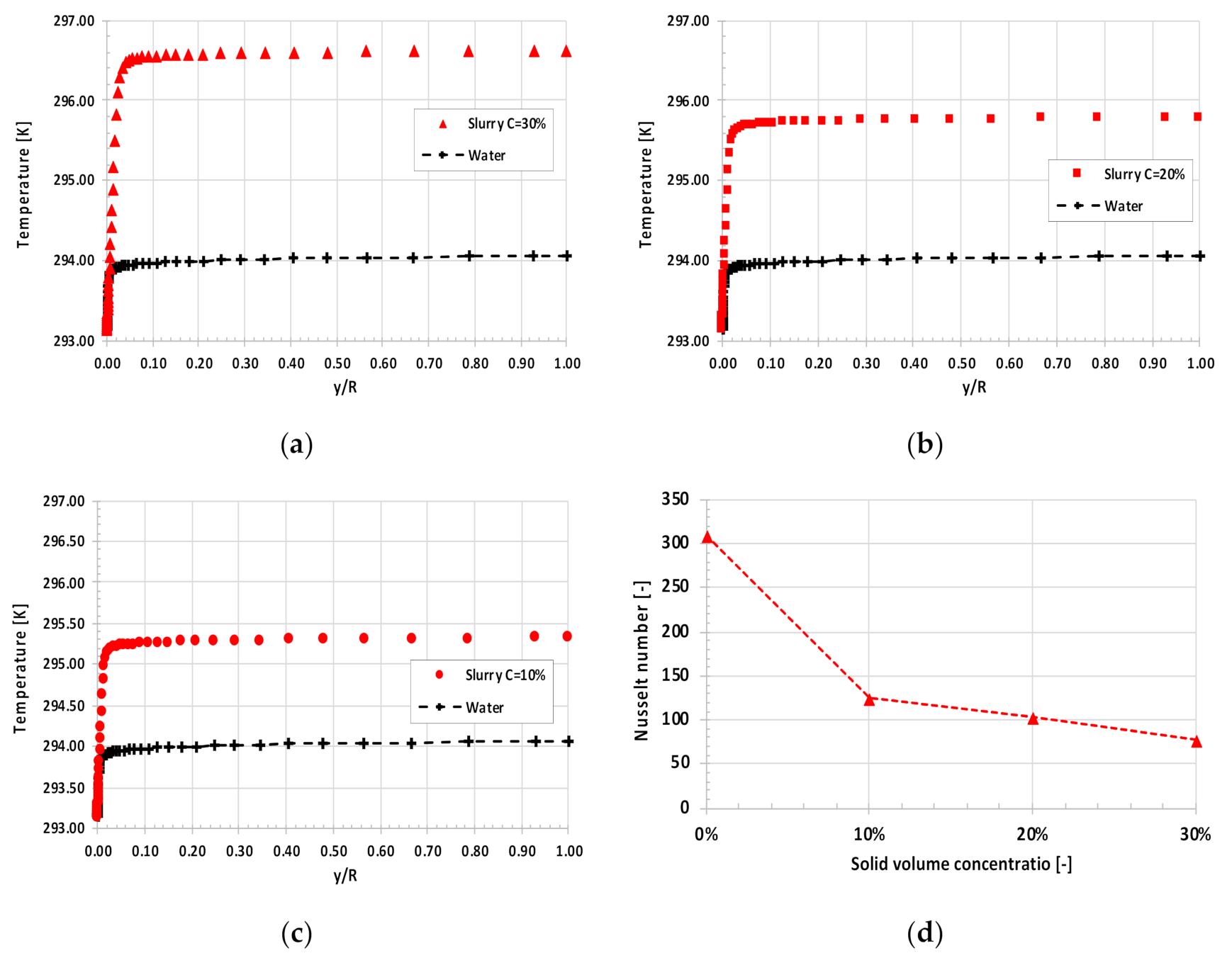
- The increase in the thickness of the viscous sublayer, which exists in fine dispersive slurry, depends on solid concentration and causes an increase in the resistance of the heat flux that acts from the slurry to the pipe wall.
- For the same bulk velocity of the slurry, the Nusselt number decreases with solid volume concentration increase. The highest rate of decrease in the Nusselt number seems to be when 0 < C < 10%.
- The new Nusselt number developed for the parameters studied depends on the solid concentration, the dimensionless yield shear stress, and the Reynolds and Prandtl numbers.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | pipe cross section perpendicular to the symmetry axis (m2) |
| A* | outer surface of a pipe of unit length L (m2) |
| a, b, c | empirical constants in the Taylor expansion (-) |
| Ci | constant in the Launder and Sharma turbulence model, I = 1, 2, (-) |
| C | solid volume concentration (cross sectional solid volume fraction) (%) |
| cp | specific heat at constant pressure [J/(kg K)] |
| D | inner pipe diameter (m) |
| dP | solid particle diameter, (μm) |
| fμ | turbulence damping function at the pipe wall (-) |
| g | gravitational acceleration (m/s2) |
| k | kinetic energy of turbulence (m2/s2) |
| L | unit length of the pipe (m) |
| m | mass flux, (kg/s) |
| Nu | Nusselt number (-) |
| Pr | Prandtl number (-) |
| p | static pressure (Pa) |
| Q | heat flux (W) |
| q | density of heat flux (W/m) |
| R | inner pipe radius (m) |
| r | distance from the symmetry axis (m) |
| Re | Reynolds number (-) |
| T | temperature (K) |
| t’ | fluctuating part of the temperature (K) |
| U | velocity component in the ox direction (m/s) |
| u’ | fluctuating component of velocity in the ox direction (m/s) |
| V | velocity component in or direction (m/s) |
| v’ | fluctuating components of the velocity V in or direction (m/s) |
| W | velocity component in oθ direction (m/s) |
| X | coordinate, main flow direction (m) |
| y | coordinate for oy direction or distance from a pipe wall (m) |
| ¯ | time-averaged quantity |
| Special characters | |
| α | heat transfer coefficient (convective heat transfer) [W/(m2 K)] |
| γ | shear rate (s−1) |
| δij | Kronecker quantity, (-) |
| ε | rate of dissipation of kinetic energy of turbulence [m2/s3] |
| λ | coefficient of heat conduction [W/(m K)] |
| μ | coefficient of dynamic viscosity (Pa∙s) |
| μapp | slurry apparent viscosity (Pa∙s) |
| μPL | plastic viscosity in the Bingham rheological model (Pa∙s) |
| μt | turbulent viscosity (Pa∙s) |
| ν | coefficient of kinematic viscosity (m2/s) |
| ρ | density (kg/m3) |
| σi | diffusion coefficients in the k-ε turbulence model, i = k, ε [-] |
| τ | shear stress [Pa] |
| τo | yield shear stress [Pa] |
| τw | wall shear stress [Pa] |
| Φ | general dependent variable, Φ = U, T, k, ε, λ, ρ, cp |
| Subscript | |
| b | bulk |
| i | ith direction, i = 1, 2, 3 |
| j | jth direction, j = 1, 2, 3 |
| L | liquid |
| S | solid |
| SL | slurry |
| t | turbulent |
| w | wall |
References
- Dai, Y.; Zhang, Y.; Li, X. Numerical and experimental investigations on pipeline internal solid-liquid mixed fluid for deep ocean mining. Ocean. Eng. 2021, 220, 108411. [Google Scholar] [CrossRef]
- Wilson, K.C.; Clift, R.; Sellgren, A. Operating points for pipelines carrying concentrated heterogeneous slurries. Powder Technol. 2002, 123, 19–24. [Google Scholar] [CrossRef]
- Tomareva, I.A.; Kozlovtseva, E.Y.; Perfilov, V.A. Impact of pipeline construction on air environment. IOP Conf. Ser. Mater. Sci. Eng. 2017, 262, 1–7. [Google Scholar] [CrossRef]
- Michaels, A.S.; Bolger, J.C. The plastic flow behavior of flocculated Kaolin suspensions. J. Ind. Eng. Chem. Fundam. 1962, 1, 153–162. [Google Scholar] [CrossRef]
- Roco, M.C.; Shook, C.A. Computational methods for coal slurry pipeline with heterogeneous size distribution. Powder Technol. 1984, 39, 159–176. [Google Scholar] [CrossRef]
- Shook, C.A.; Roco, M.C. Slurry Flow: Principles and Practice; Butterworth−Heinemann: Boston, MA, USA, 1991; Available online: https://www.amazon.com/Slurry-Flow-Principles-Butterworth-Heinemann-Engineering/dp/0750691107 (accessed on 7 August 2021).
- Gillies, R.G.; Schaan, J.; Sumner, R.J.; Mckibben, M.J.; Shook, C.A. Deposition velocities for Newtonian slurries in turbulent flow. Can. J. Chem. Eng. 2000, 78, 704–708. [Google Scholar] [CrossRef]
- Doron, P.; Barnea, D. A three-layer model for solid liquid flow in horizontal pipes. Int. J. Multiph. Flow 1993, 19, 1029–1043. [Google Scholar] [CrossRef]
- El-Nahhas, K.; El-Hak, N.G.; Rayan, M.A.; El-Sawaf, I. Flow behaviour of non-Newtonian clay slurries. In Proceedings of the Ninth International Water Technology Conference, IWTC9 2005, Sharm El-Sheikh, Egypt, 17–20 March 2005; pp. 627–640. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.302.772&rep=rep1&type=pdf (accessed on 7 August 2021).
- Gopaliya, M.K.; Kaushal, D.R. Analysis of effect of grain size on various parameters of slurry flow through pipeline using CFD. Part. Sci. Technol. 2015, 33, 369–384. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. Improvements in the numerical prediction of fully developed slurry flow in horizontal pipes. Powder Technol. 2015, 270, 358–367. [Google Scholar] [CrossRef]
- Silva, R.; Garcia, F.A.P.; Faia, P.M.; Rasteiro, M.G. Settling suspensions flow modelling: A Review. KONA Powder Part. J. 2015, 2015, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Li, M.Z.; He, Y.P.; Liu, Y.D.; Huang, C. Pressure drop model of high-concentration graded particle transport in pipelines. Ocean Eng. 2018, 163, 630–640. [Google Scholar] [CrossRef]
- Vlasák, P.; Matouek, V.; Chára, Z.; Krupicka, J.; Konfrst, J.; Keseley, M. Solid volume concentration distribution and deposition limit of medium-coarse sand-water slurry in inclined pipe. J. Hydrol. Hydromech. 2020, 68, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Shook, C.; Bartosik, A. Particle-wall stresses in vertical slurry flows. Powder Technol. Elsevier Sci. 1994, 81, 117–124. Available online: https://www.sciencedirect.com/science/article/abs/pii/003259109402877X (accessed on 7 August 2021). [CrossRef]
- Wilson, K.C.; Thomas, A.D. Analytic model of laminar-turbulent transition for Bingham plastics. Can. J. Chem. Eng. 2006, 84, 520–526. [Google Scholar] [CrossRef]
- Kelessidis, V.C.; Dalamarinis, P.; Maglione, R. Experimental study and predictions of pressure losses of fluids modeled as Herschel–Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows. J. Pet. Sci. Eng. 2011, 77, 305–312. [Google Scholar] [CrossRef]
- Talmon, A.M. Analytical model for pipe wall friction of pseudo-homogenous sand slurries. Part. Sci. Technol. Int. J. 2013, 31, 264–270. [Google Scholar] [CrossRef]
- Cotas, C.; Asendrych, D. Numerical simulation of turbulent pulp flow: Influence of the non-Newtonian properties of the pulp and of the damping function. In Proceedings of the 8th International Conference for Conveying and Handling of Particulate Solids, Tel-Aviv, Israel, 3–7 May 2015; pp. 1–18. Available online: https://www.researchgate.net/publication/283345241 (accessed on 7 August 2021).
- Cotas, C.; Asendrych, D.; Garcia, F.A.P.; Fala, P.; Rasteiro, M.G. Turbulent flow of concentrated pulp suspensions in a pipe—Numerical study based on a pseudo-homogeneous approach. In Proceedings of the COST Action FP1005 Final Conference, EUROMECH Colloquium 566, Trondheim, Norway, 9–11 June 2015; Available online: https://www.researchgate.net/publication/283342328 (accessed on 7 August 2021).
- Cotas, C.; Silva, R.; Garcia, F.; Faia, P.; Asendrych, D.; Rasteiro, M.G. Application of different low-Reynolds k-ε turbulence models to model the flow of concentrated pulp suspensions in pipes. Procedia Eng. 2015, 102, 1326–1335. [Google Scholar] [CrossRef] [Green Version]
- Rawat, A.; Singh, S.N.; Seshadri, V. Computational methodology for determination of head loss in both laminar and turbulent regimes for the flow of high concentration coal ash slurries through pipeline. Part. Sci. Technol. 2016, 34, 289–300. [Google Scholar] [CrossRef]
- Kumar, N.; Gopaliya, M.K.; Kaushal, D.R. Experimental investigations and CFD modeling for flow of highly concentrated iron ore slurry through horizontal pipeline. Part. Sci. Technol. 2019, 37, 232–250. [Google Scholar] [CrossRef]
- Mehta, D.; Radhakrishnan, A.K.T.; Van Lier, J.B.; Clemens, F.H.L.R. Assessment of numerical methods for estimating the wall shear stress in turbulent Herschel–Bulkley slurries in circular pipes. J. Hydraul. Res. 2020, 58, 196–213. [Google Scholar] [CrossRef]
- Wilson, K.; Thomas, A. A new analysis of the turbulent flow of non-Newtonian fluids. Can. J. Chem. Eng. 1985, 63, 539–546. [Google Scholar] [CrossRef]
- Zisselmar, R.; Molerus, O. Investigation of solid-liquid pipe flow with regard to turbulence modification. Chem. Eng. J. 1979, 18, 233–239. [Google Scholar] [CrossRef]
- Hetsroni, G. Particles-turbulence interaction. Int. J. Multiph. Flow 1989, 15, 735–746. [Google Scholar] [CrossRef]
- Gore, R.A.; Crowe, C.T. Modulation of turbulence by dispersed phase. J. Fluids Eng. 1991, 113, 304–307. [Google Scholar] [CrossRef]
- Jianren, F.; Junmei, S.; Youqu, Z.; Kefa, C. The effect of particles on fluid turbulence in a turbulent boundary layer over a cylinder. Acta Mech. Sin. 1997, 13, 36–43. Available online: https://link.springer.com/article/10.1007/BF02487829 (accessed on 7 August 2021). [CrossRef]
- Eaton, J.K.; Paris, A.D.; Burton, T.M. Local distortion of turbulence by dispersed particles. In Proceedings of the 30th Fluid Dynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 394, 97–117. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.575.8674&rep=rep1&type=pdf (accessed on 7 August 2021). [CrossRef]
- Li, D.; Luo, K.; Fan, J. Modulation of turbulence by dispersed solid particles in a spatially developing flat-plate boundary layer. J. Fluid Mech. 2016, 802, 359–394. [Google Scholar] [CrossRef]
- Li, D.; Luo, K.; Wang, Z.; Xiao, W.; Fan, J. Drag enhancement and turbulence attenuation by small solid particles in an unstably stratified turbulent boundary layer. Phys. Fluids 2019, 31, 1–19. [Google Scholar] [CrossRef]
- Sumner, R.J. Concentration Variations and Their Effects on in Flowing Slurries and Emulsions. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 1992. [Google Scholar]
- Xu, J.; Gillies, R.; Small, M.; Shook, C.A. Laminar and turbulent flow of Kaolin slurries. In Proceedings of the Hydrotransport 12, Cranfield, UK, 28–30 September 1993; pp. 595–613. Available online: https://www.src.sk.ca/sites/default/files/resources/pipe%2520flow%2520technology%2520papers%25201991-2007.pdf (accessed on 7 August 2021).
- Fathinia, F.; Parsazadeh, M.; Heshmati, A. Turbulent forced convection flow in a channel over periodic grooves using nanofluids. Int. J. Mech. Mechatron. Eng. 2012, 6, 12–2782. [Google Scholar] [CrossRef]
- Faruk, O.C.; Celik, N. Numerical investigation of the effect of fow and heat transfer of a semi-cylindrical obstacle located in a channel. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2013, 7, 891–896. Available online: https//www.researchgate.net/publication/285116236 (accessed on 7 August 2021).
- Sen, D.; Ghosh, R. A Computational study of very high turbulent flow and heat transfer characteristics in circular duct with hemispherical inline baffles. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2015, 9, 1046–1051. Available online: https://www.researchgate.net/publication/312134104 (accessed on 7 August 2021).
- Zong, Y.; Bai, D.; Zhou, M.; Zhao, L. Numerical studies on heat transfer enhancement by hollow-cross disk for cracking coils. Chem. Eng. Process. Process. Intensif. 2019, 135, 82–92. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Esfahani, J.A. Numerical investigation of heat transfer enhancement inside heat exchanger tubes fitted with perforated hollow cylinders. Int. J. Therm. Sci. 2020, 147, 106153. [Google Scholar] [CrossRef]
- Pandey, L.; Singh, S. Numerical Analysis for Heat Transfer Augmentation in a Circular Tube Heat Exchanger Using a Triangular Perforated Y-Shaped Insert. Fluids 2021, 6, 247. [Google Scholar] [CrossRef]
- Bartosik, A. Numerical Modelling of Fully Developed Pulsating Flow with Heat Transfer. Ph.D. Thesis, Kielce University of Technology, Kielce, Poland, 1989. [Google Scholar]
- Hagiwara, Y. Effects of bubbles, droplets or particles on heat transfer in turbulent channel flows. Flow Turbul. Combust. 2011, 86, 343–367. [Google Scholar] [CrossRef]
- Bayat, H.; Majidi, M.; Bolhasan, M.; Karbalaie Alilou, A.; Mirabdolah, A.; Lavasani, A. Unsteady flow and heat transfer of nanofluid from circular tube in cross-flow. Int. Sch. Sci. Res. Innov. 2015, 9, 2078–2083. [Google Scholar] [CrossRef]
- Hamed, H.; Mohhamed, A.; Khalefa, R.; Habeeb, O. The effect of using compound techniques (passive and active) on the double pipe heat exchanger performance. Egypt. J. Chem. 2021, 64, 2797–2802. [Google Scholar] [CrossRef]
- Harada, E.; Toda, M.; Kuriyama, M.; Konno, H. Heat transfer between wall and solid-water suspension flow in horizontal pipes. J. Chem. Eng. Jpn. 1985, 18, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Harada, E.; Kuriyama, M.; Konno, H. Heat transfer with a solid liquid suspension flowing through a horizontal rectangular duct. Heat Transf. Jpn. Res. 1989, 18, 79–94. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Ku, J.H.; Cho, H.H.; Koo, J.H.; Yoon, S.G.; Lee, J.K. Heat transfer characteristics of liquid-solid suspension flow in a horizontal pipe. KSME Int. J. 2000, 14, 1159–1167. Available online: https://link.springer.com/article/10.1007%2FBF03185070 (accessed on 7 August 2021). [CrossRef]
- Amoura, M.; Alloti, M.; Mouassi, A.; Zeraibi, N. Study of heat transfer of nanofluids in a circular tube. Int. J. Phys. Math. Sci. 2013, 7, 1464–1469. [Google Scholar] [CrossRef]
- Bubbico, R.; Celata, G.P.; D’Annibale, F.; Mazzarotta, B.; Menale, C. Comparison of the Heat Transfer Efficiency of Nanofluids. Chem. Eng. Trans. 2015, 43, 703–708. [Google Scholar] [CrossRef]
- Zakaria, I.A.; Mohamed, W.A.; Mamat, A.M.; Rahman, S. Thermal analysis of heat transfer enhancement and fluid flow for low concentration of Al2O3 water-ethylene glycol mixture nanofluid in a single PEMFC cooling plate. Energy Procedia 2015, 79, 259–264. [Google Scholar] [CrossRef] [Green Version]
- Hamad, F.A.; He, S. Heat transfer from a cylinder in cross-flow of single and multiphase flows. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2017, 11, 370–374. Available online: https://www.researchgate.net/publication/313824654 (accessed on 7 August 2021).
- Jacimovski, D.; Garic-Grulovic, R.; Grbavcic, Z.; Boškovic-Vragolovic, N. Analogy between momentum and heat transfer in liquid-solid fluidized beds. Powder Technol. 2015, 274, 213–216. [Google Scholar] [CrossRef] [Green Version]
- Chavda, N.K.; Patel, G.V.; Bhadauria, M.R.; Makwana, M.N. Effect of nanofluid on friction factor of pipe and pipe fittings: Part ii effect of copper oxide nanofluid. Int. J. Res. Eng. Technol. 2015, 4, 697–700. Available online: https://www.slideshare.net/esatjournals/effect-of-nanofluid-on-friction-factor-of-pipe-and-pipe-fittings-part-ii-effect-of-copper-oxide-nanofluid (accessed on 7 August 2021).
- Rozenblit, R.; Simkhis, M.; Hetsroni, G.; Barnea, D.; Taitel, Y. Heat transfer in horizontal solid-liquid pipe flow. Int. J. Multiph. Flow 2000, 26, 1235–1246. [Google Scholar] [CrossRef] [Green Version]
- Bartosik, A. Simulation of heat transfer to Kaolin slurry which exhibits enhanced damping of turbulence. In Proceedings of the 10th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Orlando, FA, USA, 14–16 July 2014; pp. 2318–2325. Available online: http://hdl.handle.net/2263/44670 (accessed on 7 August 2021).
- Bartosik, A. Simulation of a yield stress influence on Nusselt number in turbulent flow of Kaolin slurry. In Proceedings of the ASME Summer Heat Transfer Conference, Washington, DC, USA, 10–14 July 2016; p. 2. [Google Scholar] [CrossRef]
- Ramisetty, K. Prediction of Concentration Profiles of a Particle-Laden Slurry Flow in Horizontal and Vertical Pipes; Jawaharlal Nehru Technological University Hyderabad: Hyderabad, India, 2010; p. 113. Available online: https://shareok.org/bitstream/handle/11244/10042/Ramisetty_okstate_0664M_11139.pdf?sequence=1 (accessed on 7 August 2021).
- Reynolds, O. On the dynamical theory on incompressible viscous fluids and the determination of the criterion. Philos. Trans. R. Soc. Lond. 1895, 186, 123–164. [Google Scholar] [CrossRef]
- Boussinesque, J. Theorie de l’ecoulement tourbillant. Mem. Acad. Sci. 1877, 23, 46. [Google Scholar]
- Blom, J. An experimental determination of the turbulent Prandtl number in a developing temperature boundary layer. Eindh. Univ. Technol. 1970. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transfer. 1974, 131–138. Available online: https://www.sciencedirect.com/science/article/abs/pii/0094454874901507 (accessed on 7 August 2021).
- Spalding, D.B. Turbulence Models for Heat Transfer; Report HTS/78/2; Department of Mechanical Engineering, Imperial College London: London, UK, 1978. [Google Scholar]
- Spalding, D.B. Turbulence Models—A Lecture Course; Report HTS/82/4; Department of Mechanical Engineering, Imperial College London: London, UK, 1983. [Google Scholar]
- Mathur, S.; He, S. Performance and implementation of the Launder–Sharma low-Reynolds number turbulence model. Comput. Fluids 2013, 79, 134–139. [Google Scholar] [CrossRef]
- Abir, I.A.; Emin, A.M. A comparative study of four low-Reynolds-number k-e turbulence models for periodic fully developed duct flow and heat transfer. Numer. Heat Transf. Part B Fundam. 2016, 69, 234–248. [Google Scholar] [CrossRef]
- Hedlund, A. Evaluation of RANS Turbulence Models for the Simulation of Channel Flow; Teknisk-naturvetenskaplig Fakultet UTH-enheten: Upsala, Sweden, 2014; p. 26. Available online: https://www.diva-portal.org/smash/get/diva2:771689/FULLTEXT01.pdf (accessed on 7 August 2021).
- Davidson, L. An Introduction to Turbulence Models; Chalmers University of Technology: Goteborg, Sweden, 2018. [Google Scholar]
- Lawn, C.J. The determination of the rate of dissipation in turbulent pipe flow. J. Fluid Mech. 1971, 48, 477–505. Available online: http://www.tfd.chalmers.se/~lada/postscript_files/kompendium_turb.pdf (accessed on 7 August 2021). [CrossRef]
- Metzner, A.B.; Reed, J. Flow of non-Newtonian fluids-correlation of the laminar, transition and turbulent flow regions. AIChEJ 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Biswas, P.K.; Gidiwalla, K.M.; Sanyal, S.C.D. A simple technique for measurement of apparent viscosity of slurries: Sand-water system. Mater. Des. 2002, 23, 511–519. [Google Scholar] [CrossRef]
- Bartosik, A. Simulation and Experiments of Axially-Symmetrical Flow of Fine- and Coarse-Dispersive Slurry in Delivery Pipelines; Monograph M-11; Kielce University of Technology: Kielce, Poland, 2009. [Google Scholar]
- Roache, P.J. Computational Fluid Dynamics. Hermosa Publ. Albuq. 1982, 206, 332. [Google Scholar]
- Hermandes-Peres, V.; Abdulkadir, M.; Azzopardi, B.J. Grid generation issues in the CFD modelling of two-phase flow in a pipe. J. Comput. Multiph. Flows 2011, 3, 13–26. [Google Scholar] [CrossRef]
- Bartosik, A. Application of rheological models in prediction of turbulent slurry flow. Flow Turbul. Combust. 2010, 84, 277–293. [Google Scholar] [CrossRef]
- Salamone, J.S.; Newman, M. Water suspensions of solids. Ind. Eng. Chem. 1955, 47, 283–288. [Google Scholar] [CrossRef]
- Ozbelge, T.A.; Somer, T.G. A heat transfer correlation for liquid-solid flows in horizontal pipes. Chem. Eng. J. 1994, 55, 39–44. [Google Scholar] [CrossRef]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 1985, 12, 3–22. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 8th ed.; John Willey & Sons: Hoboken, NJ, USA, 2018; Available online: https://www.wiley.com/en-us/ES81119320425 (accessed on 7 August 2021).
- Sparrow, E.M.; Abraham, J.; Gorman, J. Advances in Heat Transfer; Academic Press: Cambridge, MA, USA; Elsevier Inc.: Amsterdam, The Netherlands, 2017; Volume 49, pp. 1–323. Available online: https://www.elsevier.com/books/advances-in-heat-transfer/sparrow/978-0-12-812411-6 (accessed on 7 August 2021).
- Slatter, P.T. Transitional and Turbulent Flow on Non-Newtonian Slurries in Pipes. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 1994. [Google Scholar]
- Prandtl, L. Bemerkung uber den warmeubergang in rohr. Phys. Z. 1928, 29, 487. [Google Scholar]
- Cebeci, T.; Smith, A.M.O. Analysis of Turbulent Boundary Layers; Academic Press: Cambridge, MA, USA, 1974; Available online: https://www.amazon.com/Analysis-Turbulent-Boundary-Layers-Tuncer/dp/B009DKC2YK (accessed on 7 August 2021).
- Hashizume, K.; Kimura, Y.; Morita, S. Analogy between pressure drop and heat transfer in liquid-solid circulating fluidized beds. Trans. Jpn. Soc. Mech. Eng. 2008, 74, 2014–2019. [Google Scholar] [CrossRef] [Green Version]
- Etheram, H.; Arani, A.A.; Sheikhzadeh, G.A.; Aghaei, A.; Malihi, A.R. The effect of various conductivity and viscosity models considering Brownian motion on nanofluids mixed convection flow and heat transfer. Trans. Phenom. Nano Micro Scales 2016, 4, 78–81. [Google Scholar] [CrossRef]
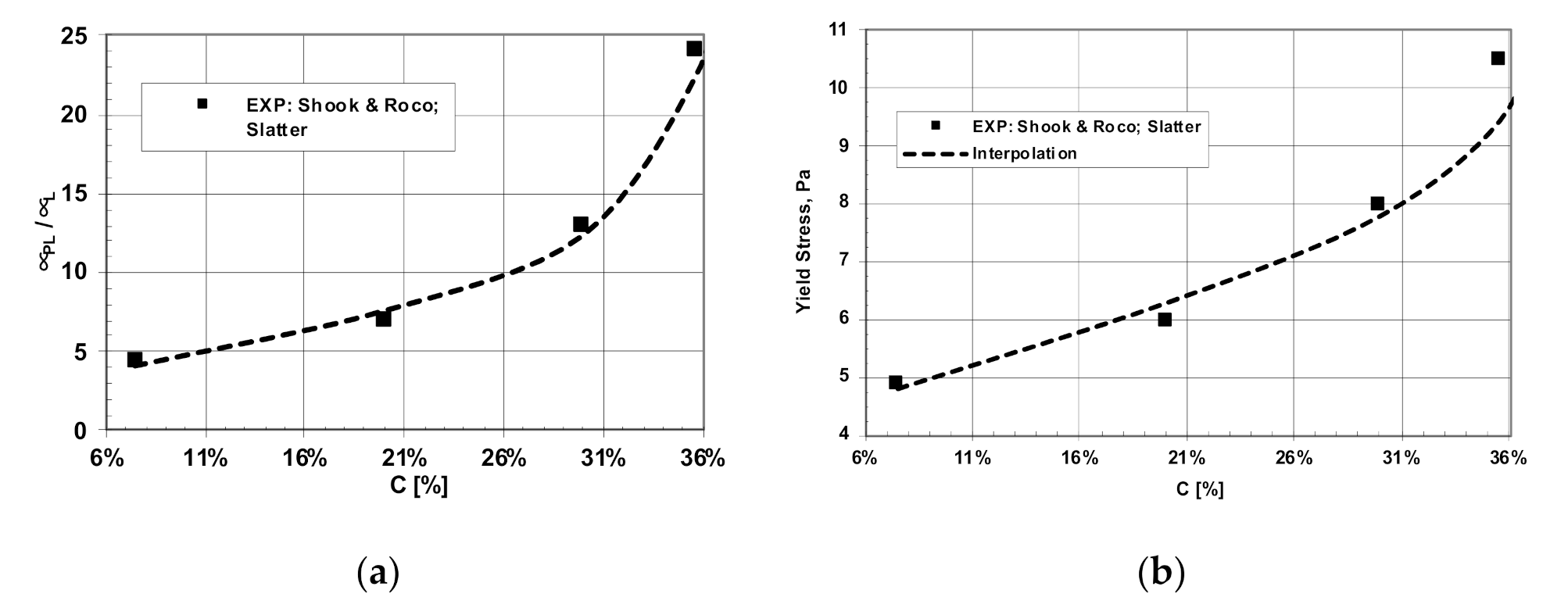
| Solid Volume Concentration | Bingham Model | |
|---|---|---|
| % | τo, Pa | μPL, Pa s |
| 10 | 5.10 | 0.004521 |
| 20 | 6.00 | 0.007032 |
| 30 | 8.00 | 0.013061 |
| Thermal Conduction for the Carrier Liquid | Thermal Conduction for Solid Particles | Specific Heat for the Carrier Liquid | Specific Heat for Solid Particles |
|---|---|---|---|
| W/(m K) | W/(m K) | J/(kg K) | J/(kg K) |
| 0.598 | 1.221 | 4183.00 | 795.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartosik, A. Numerical Modelling of Heat Transfer in Fine Dispersive Slurry Flow. Energies 2021, 14, 4909. https://doi.org/10.3390/en14164909
Bartosik A. Numerical Modelling of Heat Transfer in Fine Dispersive Slurry Flow. Energies. 2021; 14(16):4909. https://doi.org/10.3390/en14164909
Chicago/Turabian StyleBartosik, Artur. 2021. "Numerical Modelling of Heat Transfer in Fine Dispersive Slurry Flow" Energies 14, no. 16: 4909. https://doi.org/10.3390/en14164909






