Opportunities in Jet-Impingement Cooling for Gas-Turbine Engines
Abstract
:1. Introduction
2. Benchmark Studies on Impingement Heat Transfer
3. Key Aspects of Impingement Heat Transfer Related to Gas-Turbine Technologies
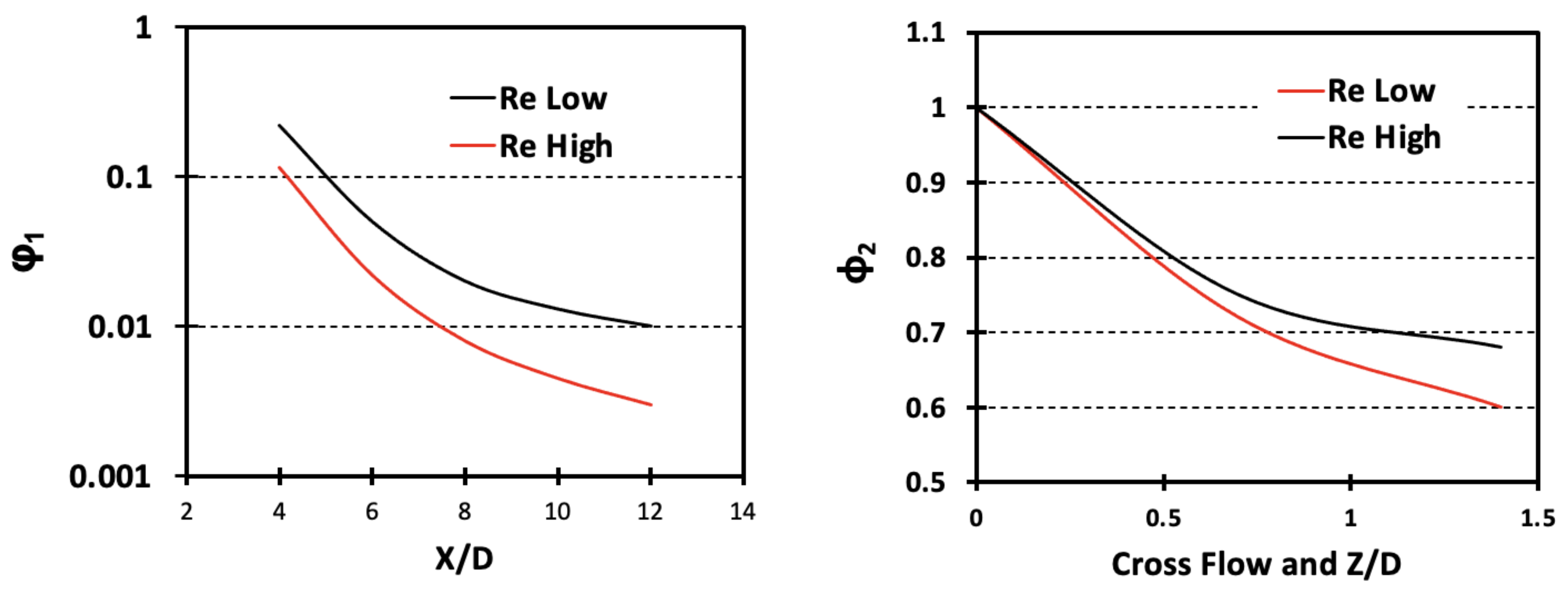
3.1. Jet Entrainment
3.2. Impingement-Effusion Cooling
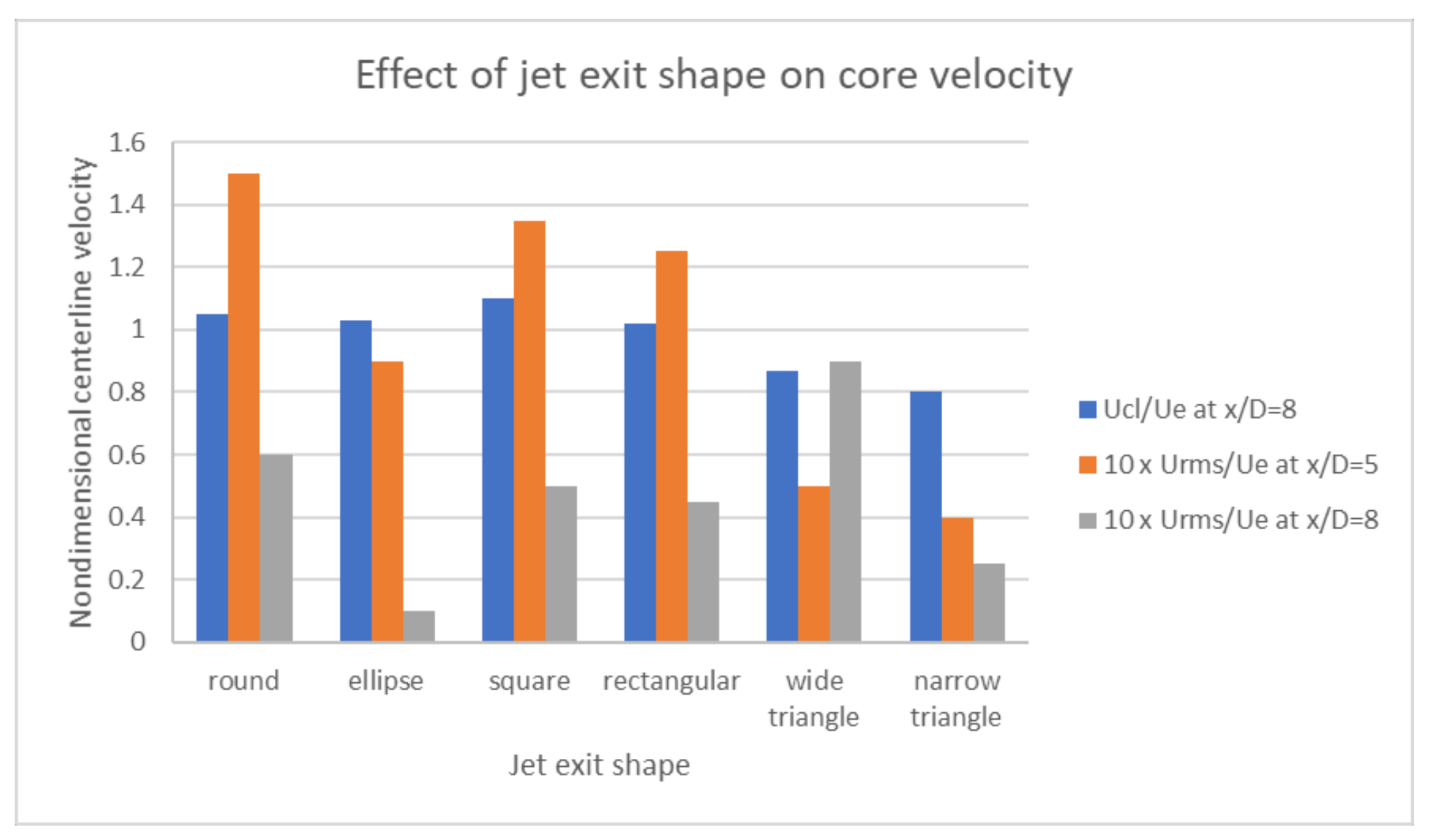
3.3. Jet Orifice
3.3.1. Thermal-Hydraulic Performance of Shaped Jets
3.3.2. Design Equivalency of Shaped Jets
3.4. Backplate Modifications
3.5. Target Surface Modification
3.6. Impingement Channel Modification
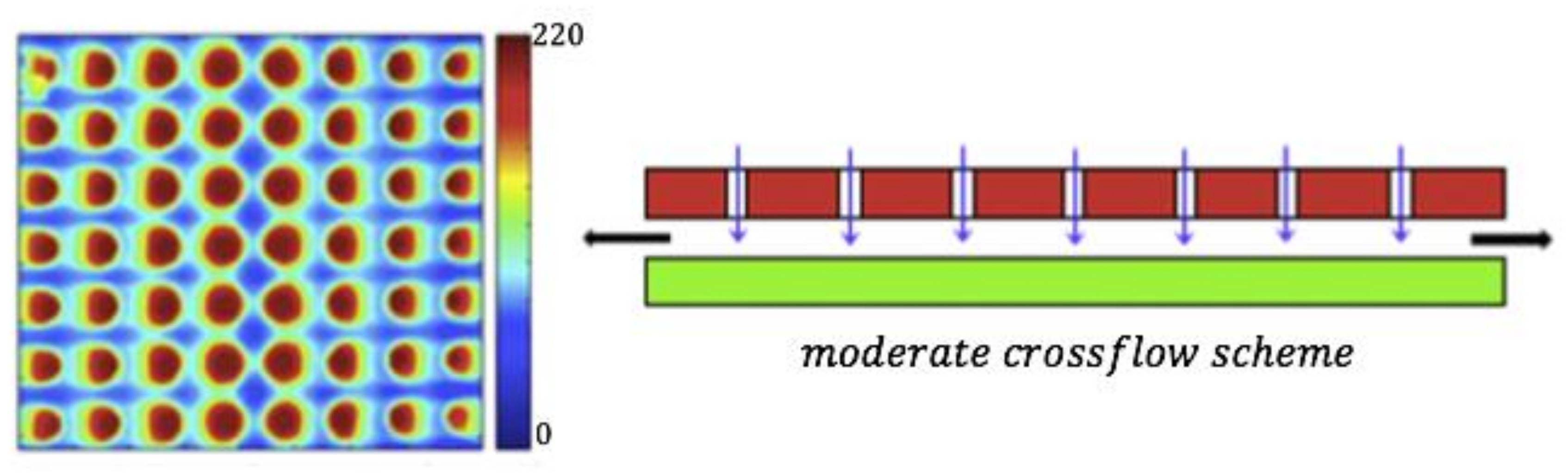
3.7. Crossflow Regulation
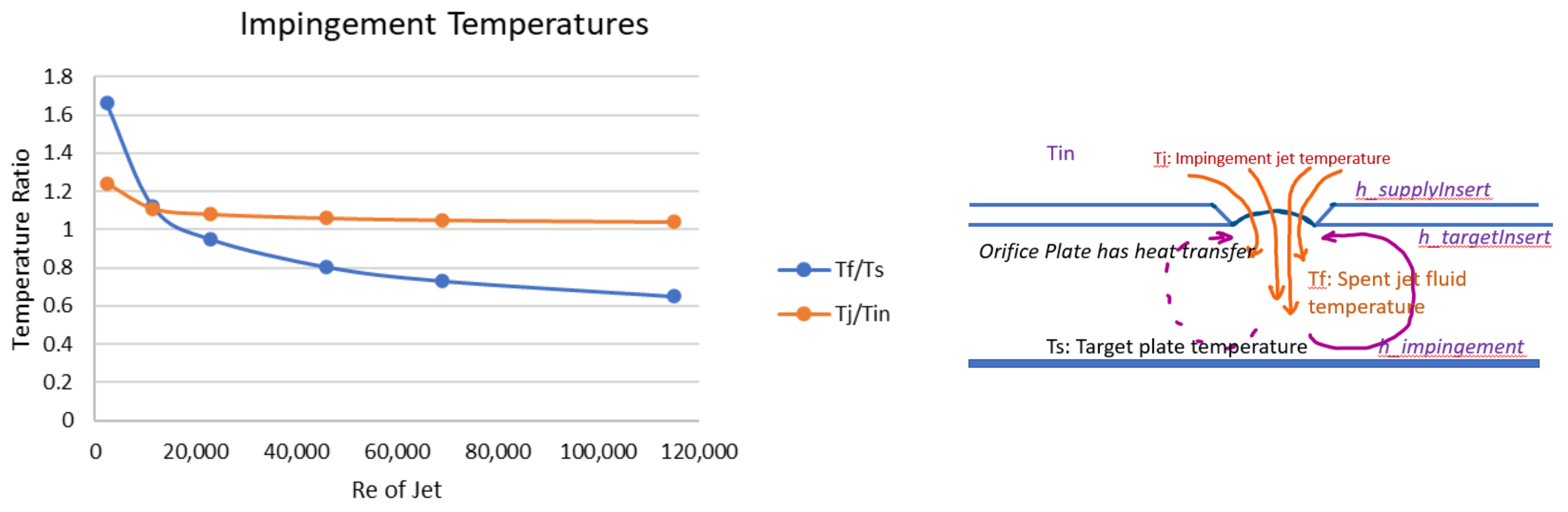
4. Forgotten Recovery Factor in Impingement
5. Detailed Two-Dimensional Thermal Measurements
6. Conclusions
- Separation of crossflow and entrainment effects: Simulate crossflow at room temperature at the entrance of the impingement chamber with forced channel flow; this will have the jet deflection effect but will not have the entrainment of spent jet temperatures. After that, vary the starting crossflow temperature to study the entrainment effects in multiple or single rows of jets. Does it match post-impingement crossflow thermal data? If not, something more than just the flow and temperature needs to be added such as skewness in the flow field and turbulence.
- Evaluate high-performance orifices at a fixed pumping power: Compare data in terms of raw heat transfer coefficient for a given flow rate at a given pressure drop, and not in terms of Nusselt number as nondimensional information masks the true enhancement levels. Prior investigations in this area have not looked at the heat transfer with the concomitant pressure drop. We understand the use of Nu and Re for extrapolating the usable range of experimental data, but to compare the real impact with the same design constraints, raw heat transfer coefficient with a matched pressure drop provides a better understanding.
- Identification of more suitable nondimensional test parameters: Include hole discharge effect along with the hole size. There is perhaps a different nondimensional parameter than the current Reynolds number because Re defined with hole diameter does not include the Cd effect, which effectively reduces the exit diameter of a jet. This new form of jet Reynolds number, when proposed, should be easy enough to be applied in commercial design. Furthermore, the definition of heat transfer coefficient involving a far-field reference temperature should be revisited. The adiabatic wall temperature is perhaps a more suitable option; however, it is not directly measured in transient heat transfer experiments.
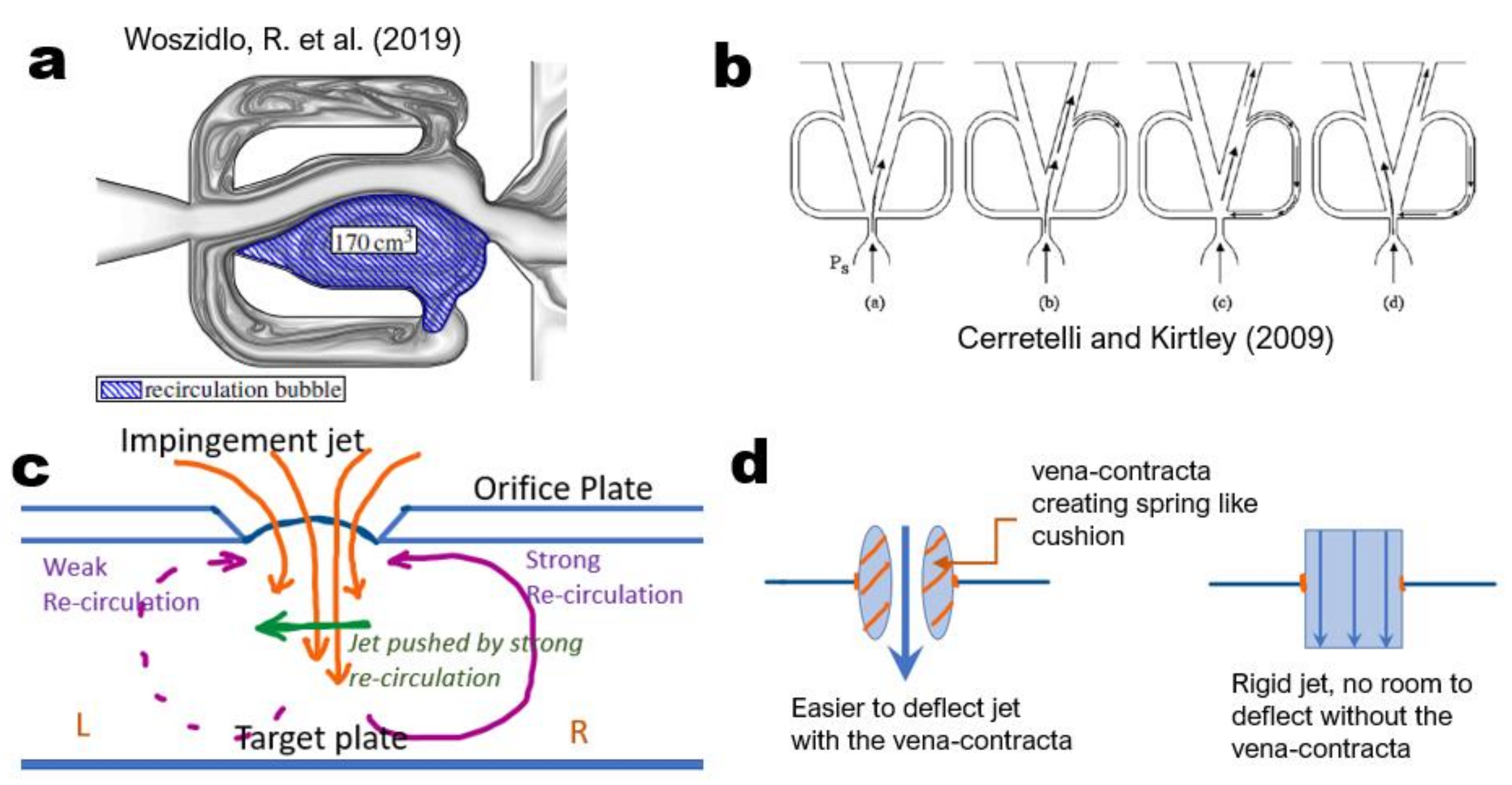
- Fluidic oscillation in low Cd orifice flows with backplate: Add flow oscillations (not axial pulsation) with fluidic devices. The trend in published literature shows that lower Cd is better for impingement heat transfer, but no explanation on the cause has been found yet. A possible explanation of jet oscillation with low Cd orifice is illustrated in this work and perhaps can be verified with detailed experimental unsteady measurements. Fast-changing unsteady heat transfer experiments are difficult to design, which is perhaps why this aspect has not yet been tested. Can the orifice jet heat transfer pattern be reproduced by mechanically oscillating a tube jet? If so, what is the frequency and amplitude of the oscillation?
- Mach number, swirl, and recovery effects on impingement: Use high-velocity compressible flow tests. The high Mach flow with compressibility effects needs to be investigated to simulate real engine conditions as those data are not available in the public literature. Most of the benchmark work done in the 1970s and 1980s was performed in near-atmospheric conditions. Since the experimental facilities and numerical tools have improved significantly, it will be interesting to observe jet impingement with compressibility effects. Impingement tests in low-pressure, low-flow environments cannot simulate recovery factor effects, but real engine operating conditions are extreme. Recovery heating and swirl cooling can play significant roles in engine condition heat transfer performance.
- Local tube jet instead of orifice jet when inlet or exit is close to the impingement chamber: Use tubes instead of orifices where the jet direction is important. The proximity of the channel exit with respect to the last row of jets affects the flow but has not been studied in detail. The proximity of the spent jet that exits near the last row of holes can facilitate additional discharge by suction from the holes near the exit and cause non-uniform jet distribution. It is also noticed that tube jets would have more directionality to penetrate the crossflow than orifice jets. Moreover, the tube length can be controlled to match the pressure losses created by non-uniform flow distribution and perhaps can be optimized. However, the region with lower crossflow should have sharp-edged orifices as they perform better than tube jets in that flow domain.
- Surface microchannels, heat pipes, and effusion cooling: Use surface microchannels with effusion cooling to reduce temperature gradients and cracking. Impingement cooling creates high temperature gradients and can cause cracking in components. To smoothen the thermal gradients, surface microchannels can be adopted along with effusion cooling. Back in 1995 [125], there were discussions on applying heat pipe in turbine structures by a division of DOE to help with the thermal loads, but it has not received a warm welcome from the turbine community. Maybe it is time to revisit that concept as well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, J.-C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology, 2nd ed.; CRC Press: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Bunker, R.S.; Dees, J.E.; Palafox, P. Impingement cooling in gas turbines: Design, applications, and limitations. In Flow Phenomena in Nature; WIT Press: Southampton, UK, 2014; Volume 2, pp. 1–32. [Google Scholar]
- Amano, R.S.; Sunden, B. Impingement Jet Cooling in Gas Turbines; WIT Press: Southampton, UK, 2014. [Google Scholar]
- Dutta, S.; Singh, P. Impingement heat transfer innovations and enhancements: A Discussion on selected geometrical features. In Proceedings of the ASME Conference, Online, 11–17 June 2021. [Google Scholar]
- Han, B.; Goldstein, R.J. Jet-impingement heat transfer in gas turbine systems. Ann. N. Y. Acad. Sci. 2006, 934, 147–161. [Google Scholar] [CrossRef]
- Obot, N.T.; Trabold, T. Impingement heat transfer within arrays of circular jets: Part 1—Effects of minimum, intermediate, and complete crossflow for small and large spacings. J. Heat Transf. 1987, 109, 872–879. [Google Scholar] [CrossRef]
- Shukla, A.; Dewan, A. Flow and thermal characteristics of jet impingement: Comprehensive review. Int. J. Heat Technol. 2017, 35, 153–166. [Google Scholar] [CrossRef] [Green Version]
- Culun, P.; Celik, N.; Pihtili, K. Effects of design parameters on a multi jet impinging heat transfer. Alex. Eng. J. 2018, 57, 4255–4266. [Google Scholar] [CrossRef]
- Baydar, E. Confined impinging air jet at low Reynolds numbers. Exp. Therm. Fluid Sci. 1999, 19, 27–33. [Google Scholar] [CrossRef]
- Zukowski, M. Heat transfer performance of a confined single slot jet of air impinging on a flat surface. Int. J. Heat Mass Transf. 2013, 57, 484–490. [Google Scholar] [CrossRef]
- Florschuetz, L.W.; Metzger, D.E.; Su, C.C. Heat transfer characteristics for jet array impingement with initial crossflow. J. Heat Transf. 1984, 106, 34–41. [Google Scholar] [CrossRef]
- Tong, A.Y. On the impingement heat transfer of an oblique free surface plane jet. Int. J. Heat Mass Transf. 2003, 46, 2077–2085. [Google Scholar] [CrossRef]
- Florschuetz, L.W.; Metzger, D.E.; Takeuchi, D.I.; Berry, R.A. Multiple Jet Impingement Heat Transfer Characteristic—Experimental Investigation of In-Line and Staggered Arrays with Crossflow; Contractor Report #3217; NASA Lewis Research Center: Cleveland, OH, USA, 1980. [Google Scholar]
- Esposito, E.I.; Ekkad, S.V.; Kim, Y.; Dutta, P. Novel jet impingement cooling geometry for combustor liner backside cooling. J. Therm. Sci. Eng. Appl. 2009, 1, 021001. [Google Scholar] [CrossRef]
- Terzis, A.; Ott, P.; Cochet, M.; Von Wolfersdorf, J.; Weigand, B. Effect of varying jet diameter on the heat transfer distributions of narrow impingement channels. J. Turbomach. 2014, 137, 021004. [Google Scholar] [CrossRef]
- Jordan, C.N.; Wright, L.M.; Crites, D.C. Impingement heat transfer on a cylindrical, concave surface with varying jet geometries. ASME J. Heat Transf. 2016, 138. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.-J. The effect of nozzle aspect ratio on stagnation region heat transfer characteristics of elliptic impinging jet. Int. J. Heat Mass Transf. 2000, 43, 555–575. [Google Scholar] [CrossRef]
- Singh, P.; Zhang, M.; Ahmed, S.; Ramakrishnan, K.R.; Ekkad, S. Effect of micro-roughness shapes on jet impingement heat transfer and fin-effectiveness. Int. J. Heat Mass Transf. 2019, 132, 80–95. [Google Scholar] [CrossRef]
- Weigand, B.; Spring, S. Multiple jet impingement—A review. Proc. Int. Symp. Heat Transf. Gas Turbine Syst. 2009, 42, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Cho, H.H.; Kim, B.S. Impingement/effusion cooling methods in gas turbine. Flow Phenom. Nat. 2014, 76, 125–155. [Google Scholar] [CrossRef]
- Yamane, Y.; Yamamoto, M.; Motosuke, M.; Honami, S. Effect of jet shape of square array of multi-impinging jets on heat transfer. In Proceedings of the ASME GT2013-94452, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Kristiawan, M.; Meslem, A.; Nastase, I.; Sobolik, V. Wall shear rates and mass transfer in impinging jets: Comparison of circular convergent and cross-shaped orifice nozzles. Int. J. Heat Mass Transf. 2012, 55, 282–293. [Google Scholar] [CrossRef]
- Violato, D.; Ianiro, A.; Cardone, G.; Scarano, F. Three-dimensional vortex dynamics and convective heat transfer in circular and chevron impinging jets. Int. J. Heat Fluid Flow 2012, 37, 22–36. [Google Scholar] [CrossRef]
- Yang, H.; Kim, T.; Lu, T.; Ichimiya, K. Flow structure, wall pressure and heat transfer characteristics of impinging annular jet with/without steady swirling. Int. J. Heat Mass Transf. 2010, 53, 4092–4100. [Google Scholar] [CrossRef]
- Jeffers, N.M.R.; Punch, J.; Walsh, E.J.; McLean, M. Heat transfer from novel target surface structures to a normally impinging, submerged and confined water jet. J. Therm. Sci. Eng. Appl. 2009, 1, 031001. [Google Scholar] [CrossRef]
- El-Gabry, L.A.; Kaminski, D.A. Experimental investigation of local heat transfer distribution on smooth and roughened surfaces under an array of angled impinging jets. J. Turbomach. 2004, 127, 532–544. [Google Scholar] [CrossRef]
- Moreno, G.; Narumanchi, S.; Venson, T.; Bennion, K. Microstructured surfaces for single-phase jet impingement heat transfer enhancement. J. Therm. Sci. Eng. Appl. 2013, 5, 031004. [Google Scholar] [CrossRef]
- Sambamurthy, V.S.; Madhavan, S.; Singh, P.; Ekkad, S.V. Array jet impingement on high porosity thin metal foams: Effect of foam height, pore-density and spent air crossflow scheme on flow distribution and heat transfer. ASME J. Heat Transf. 2020, 142. [Google Scholar] [CrossRef]
- Madhavan, S.; Ramakrishnan, K.R.; Singh, P.; Ekkad, S.V. Jet impingement heat transfer enhancement by u-shaped crossflow diverters. J. Therm. Sci. Eng. Appl. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Chi, Z.; Liu, H.; Zang, S. Geometrical optimization of nonuniform impingement cooling structure with variable-diameter jet holes. Int. J. Heat Mass Transf. 2017, 108, 549–560. [Google Scholar] [CrossRef]
- Hollworth, B.R.; Wilson, S.I. Entrainment effects on impingement heat transfer: Part I—Measurements of heated jet velocity and temperature distributions and recovery temperatures on target surface. J. Heat Transf. 1984, 106, 797–803. [Google Scholar] [CrossRef]
- Hollworth, B.R.; Gero, L.R. Entrainment effects on impingement heat transfer: Part II—Local heat transfer measurements. J. Heat Transf. 1985, 107, 910–915. [Google Scholar] [CrossRef]
- Baughn, J.W.; Hechanova, A.E.; Yan, X. An experimental study of entrainment effects on the heat transfer from a flat surface to a heated circular impinging Jet. J. Heat Transf. 1991, 113, 1023–1025. [Google Scholar] [CrossRef]
- Immarigeon, A.; Hassan, I. An advanced impingement/film cooling scheme for gas turbines—Numerical study. Int. J. Numer. Methods Heat Fluid Flow 2006, 16, 470–493. [Google Scholar] [CrossRef] [Green Version]
- Mensch, A.; Thole, K.A. Overall effectiveness of a blade endwall with jet impingement and film cooling. J. Eng. Gas Turbines Power 2013, 136, 031901. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Rahnama, S.M. Shape optimization of impingement and film cooling holes on a flat plate using a feedfor-ward ANN and GA. Energy Equip. Sys. 2018, 6, 247–259. [Google Scholar]
- Dutta, S.; Smith, R. Transfer function based optimization of film hole sizes with conjugate heat transfer analysis. In Proceedings of the ASME Turbo-Expo GT2020-14137, Virtual On-Line, 21–25 September 2020. [Google Scholar] [CrossRef]
- Dutta, S.; Smith, R. Nonlinear optimization of turbine conjugate heat transfer with iterative machine learning and training sample replacement. Energies 2020, 13, 4587. [Google Scholar] [CrossRef]
- Smith, R.; Dutta, S. Conjugate thermal optimization with unsupervised machine learning. J. Heat Transf. 2021, 143, 052901. [Google Scholar] [CrossRef]
- Issac, J.; Singh, D.; Kango, S. Experimental and numerical investigation of heat transfer characteristics of jet impingement on a flat plate. Heat Mass Transf. 2020, 56, 531–546. [Google Scholar] [CrossRef]
- Katti, V.V.; Yasaswy, S.N.; Prabhu, S.V. Local heat transfer distribution between smooth flat surface and impinging air jet from a circular nozzle at low Reynolds numbers. Heat Mass Transf. 2011, 47, 237–244. [Google Scholar] [CrossRef]
- Jeffers, N.; Stafford, J.; Conway, C.; Punch, J.; Walsh, E. The influence of the stagnation zone on the fluid dynamics at the nozzle exit of a confined and submerged impinging jet. Exp. Fluids 2016, 57, 1–15. [Google Scholar] [CrossRef]
- Li, W.; Xu, M.; Ren, J.; Jiang, H. Experimental investigation of local and average heat transfer coefficients under an inline impinging jet array, including jets with low impingement distance and inclined angle. J. Heat Transf. 2016, 139, 012201. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Han, J.-C. A transient liquid crystal thermography technique for gas turbine heat transfer measurements. Meas. Sci. Technol. 2000, 11, 957–968. [Google Scholar] [CrossRef]
- Kaçar, E.N.; Erbay, L.B. Numerical Characterization of a Jet Impingement Cooling System Using Coupled Heat Transfer Analysis, ASME Turbo-Expo GT2015-43371. Montreal, QC, Canada, 15–19 June 2015.
- Zuckerman, N.; Lior, N. Jet impingement heat transfer: Physics, correlations, and numerical modeling. Adv. Heat Transf. 2006, 39, 565–631. [Google Scholar] [CrossRef]
- Zu, Y.Q.; Yan, Y.Y.; Maltson, J. Numerical study on stagnation point heat transfer by jet impingement in a confined narrow gap. J. Heat Transf. 2009, 131. [Google Scholar] [CrossRef]
- Williams, R.P.; Dyson, T.E.; Bogard, D.G.; Bradshaw, S.D. Sensitivity of the overall effectiveness to film cooling and internal cooling on a turbine vane suction side. J. Turbomach. 2013, 136, 031006. [Google Scholar] [CrossRef]
- Behbahani, A.I.; Goldstein, R.J. Local heat transfer to staggered arrays of impinging circular air jets. J. Eng. Power 1983, 105, 354–360. [Google Scholar] [CrossRef]
- Florschuetz, L.W.; Truman, C.R.; Metzger, D.E. Streamwise flow and heat transfer distributions for jet array impingement with crossflow. J. Heat Transf. 1981, 103, 337–342. [Google Scholar] [CrossRef]
- Kercher, D.M.; Tabakoff, W. Heat Transfer by a square array of round air jets impinging perpendicular to a flat surface including the effect of spent air. J. Eng. Power 1970, 73–82. [Google Scholar] [CrossRef]
- Team CCJ. Turbine Blade, Vane Cooling—A Primer. 2018. Available online: https://www.ccj-online.com/turbine-blade-vane-cooling-a-primer/ (accessed on 18 September 2021).
- Esposito, E. Jet impingement cooling configurations for gas turbine combustion. Master Thesis, Louisiana State University, Baton Rouge, LA, USA, 2006. [Google Scholar]
- Kratz, J.L.; Chapman, J.W.; Guo, T.-H. A Parametric Study of Actuator Requirements for Active Turbine Tip Clearance Control of a Modern High Bypass Turbofan Engine. In Proceedings of the ASME Turbo Expo, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Liu, H.; Liu, C.; Wu, W. Numerical investigation on the flow structures in a narrow confined channel with staggered jet array arrangement. Chin. J. Aeronaut. 2015, 28, 1616–1628. [Google Scholar] [CrossRef] [Green Version]
- Oxford Thermofluid Institute, Turbine Cooling Group. Available online: https://oti.eng.ox.ac.uk/research-groups/turbine-cooling-group/ (accessed on 18 September 2021).
- Ekkad, S.V.; Huang, Y.; Han, J.-C. Detailed heat transfer distributions in two-pass square channels with rib turbulators and bleed holes. Int. J. Heat Mass Transf. 1998, 41, 3781–3791. [Google Scholar] [CrossRef]
- Wei-Hua, Y.; Jun, C.; Rui, S.; Xu-Sheng, H.; Shuang-Wen, S. Experimental investigation on impingement-effusion film-cooling behaviors in curve section. Acta Astronaut. 2011, 68, 1782–1789. [Google Scholar] [CrossRef]
- Kim, K.M.; Moon, H.; Park, J.S.; Cho, H.H. Optimal design of impinging jets in an impingement/effusion cooling system. Energy 2014, 66, 839–848. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Li, J.; Li, Y. Effects of film cooling hole locations on flow and heat transfer characteristics of impingement/effusion cooling at turbine blade leading edge. Int. J. Heat Mass 2018, 126, 192–205. [Google Scholar] [CrossRef]
- Singh, P.; Ekkad, S.V. Effects of spent air removal scheme on internal-side heat transfer in an impingement-effusion system at low jet-to-target plate spacing. Int. J. Heat Mass Transf. 2017, 108, 998–1010. [Google Scholar] [CrossRef]
- Haneda, Y.; Souma, A.; Kurasawa, H.; Iio, S.; Ikeda, T. Enhancement of impinging jet heat transfer using two parallel confining plates mounted near rectangular nozzle exit. J. Fluids 2014, 2014, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Ravi, B.V.; Ekkad, S. Experimental investigation of heat transfer augmentation by different jet impingement hole shapes under maximum crossflow. In Proceedings of the ASME Turbo Expo, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Etemoglu, A.B.; Isman, M.K.; Can, M. Investigation into the effect of nozzle shape on the nozzle discharge coefficient and heat and mass transfer characteristics of impinging air jets. Heat Mass Transf. 2010, 46, 1395–1410. [Google Scholar] [CrossRef]
- Etemoglu, A.B.; Can, M. Performance studies of energy consumption for single and multiple nozzle systems under impinging air jets. Heat Mass Transf. 2013, 49, 1057–1070. [Google Scholar] [CrossRef]
- Goodro, M.; Ligrani, P.; Fox, M.; Moon, H.-K. Mach Number, Reynolds Number, Jet Spacing Variations: Full Array of Im-pinging jets. J. Thermophys. Heat Transf. 2010, 24, 133–144. [Google Scholar] [CrossRef]
- McInturff, P.; Suzuki, M.; Ligrani, P.; Nakamata, C.; Lee, D.H. Effects of hole shape on impingement jet array heat transfer with small-scale, target surface triangle roughness. Int. J. Heat Mass Transf. 2018, 127, 585–597. [Google Scholar] [CrossRef]
- Hsu, C.M.; Jhan, W.C.; Chang, Y.Y. Flow and heat transfer characteristics of a pulsed jet impinging on a flat plate. Heat Mass Transf. 2020, 56, 143–160. [Google Scholar] [CrossRef]
- Woszidlo, R.; Ostermann, F.; Schmidt, H.-J. Fundamental properties of fluidic oscillators for flow control applications. AIAA J. 2019, 57, 978–992. [Google Scholar] [CrossRef]
- Cerretelli, C.; Kirtley, K. Boundary layer separation control with fluidic oscillators. J. Turbomach. 2009, 131, 041001. [Google Scholar] [CrossRef]
- Ikhlaq, M.; Al-abdeli, Y.M.; Khiadani, M. Nozzle exit conditions and the heat transfer in non-swirling and weakly swirling turbulent impinging jets. Heat Mass Transf. 2020, 56, 269–290. [Google Scholar] [CrossRef]
- Ahmed, Z.U.; Al-abdeli, Y.; Guzzomi, F.G. Impingement pressure characteristics of swirling and non-swirling turbulent jets. Exp. Therm. Fluid Sci. 2015, 68, 722–732. [Google Scholar] [CrossRef]
- Markal, B. The effect of total flowrate on the cooling performance of swirling coaxial impinging jets. Heat Mass Transf. 2019, 55, 3275–3288. [Google Scholar] [CrossRef]
- Markal, B.; Avci, M.; Aydin, O. Conical coaxial impinging air jets: Angle effect on the heat transfer performance. Heat Mass Transf. 2020, 56, 3135–3146. [Google Scholar] [CrossRef]
- Limaye, M.D.; Vedula, R.P.; Prabhu, S.V. Comparison of heat transfer distributions on a flat plate impinged by under-expanded jets from a convergent nozzle and a circular orifice. Heat Mass Transf. 2012, 49, 309–326. [Google Scholar] [CrossRef]
- Muvvala, P.; Balaji, C.; Venkateshan, S.P. Experimental investigation on heat transfer from square jets issuing from perforated nozzles. Heat Mass Transf. 2017, 53, 2363–2375. [Google Scholar] [CrossRef]
- Shakouchi, T.; Kito, M. Heat transfer enhancement of impinging jet by notched—Orifice nozzle. In An Overview of Heat Transfer Phenomena; InTech: London, UK, 2012. [Google Scholar]
- Ozmen, Y.; Baydar, E. Flow structure and heat transfer characteristics of an unconfined impinging air jet at high jet Reynolds numbers. Heat Mass Transf. 2008, 44, 1315–1322. [Google Scholar] [CrossRef]
- Ozmen, Y.; Ipek, G. Investigation of flow structure and heat transfer characteristics in an array of impinging slot jets. Heat Mass Transf. 2016, 52, 773–787. [Google Scholar] [CrossRef]
- Sodjavi, K.; Montagné, B.; Bragança, P.; Meslem, A.; Bode, F.; Kristiawan, M. Impinging cross-shaped submerged jet on a flat plate: A comparison of plane and hemispherical orifice nozzles. Meccanica 2015, 50, 2927–2947. [Google Scholar] [CrossRef] [Green Version]
- Miller, R.; Madnia, C.; Givi, P. Numerical simulation of non-circular jets. Comput. Fluids 1995, 24, 1–25. [Google Scholar] [CrossRef]
- Wei, T.; Oprins, H.; Cherman, V.; Qian, J.; De Wolf, I.; Beyne, E.; Baelmans, M. High-efficiency polymer-based direct multi-jet impingement cooling solution for high-power devices. IEEE Trans. Power Electron. 2018, 34, 6601–6612. [Google Scholar] [CrossRef]
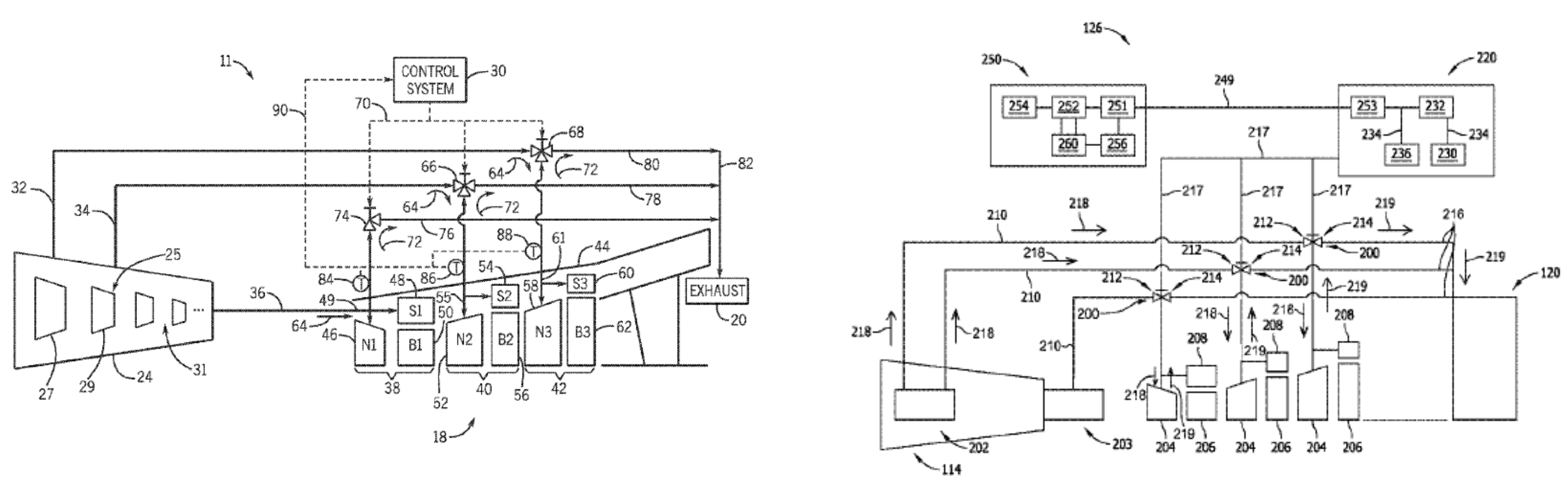
- Maldonado, J.J.; Dutta, S. System and Method for Operating a Gas Turbine Engine. U.S. Patent 9,206,744 B2, 8 December 2015. [Google Scholar]
- Dutta, S. Maldonado, J.J. Systems and Methods for Reconditioning Turbine Engines in Power Generation Systems. U.S. Patent 9,260,968 B2, 16 February 2016. [Google Scholar]
- Lyu, Y.; Zhang, J.; Liu, X.; Shan, Y. Experimental study of single-row chevron-jet impingement heat transfer on concave surfaces with different curvatures. Chin. J. Aeronaut. 2019, 32, 2275–2285. [Google Scholar] [CrossRef]
- Kanamori, A.; Hiwada, M.; Oyakawa, K.; Senaha, I. Effect of orifice shape on flow behavior and impingement heat transfer. Open Transp. Phenom. J. 2011, 3. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.H.; Buchlin, J. Jet impingement heat transfer from lobed nozzles. Int. J. Therm. Sci. 2011, 50, 1199–1206. [Google Scholar] [CrossRef]
- Agricola, L.; Prenter, R.; Lundgreen, R.; Hossain, M.; Ameri, A.; Gregory, J.; Bons, J. Impinging sweeping jet heat transfer. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference; American Institute of Aeronautics and Astronautics, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar]
- Hossain, M.A.; Agricola, L.; Ameri, A.; Gregory, J.W.; Bons, J.P. Effects of curvature on the performance of sweeping jet impingement heat transfer. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Hossain, M.A.; Agricola, L.; Ameri, A.; Gregory, J.W.; Bons, J.P. Sweeping jet impingement heat transfer on a simulated turbine vane leading edge. J. Glob. Power Propuls. Soc. 2018, 2, 5A7OAZ. [Google Scholar] [CrossRef]
- Baydar, E.; Ozmen, Y. An experimental investigation on flow structures of confined and unconfined impinging air jets. Heat Mass Transf. 2006, 42, 338–346. [Google Scholar] [CrossRef]
- Bobusch, B.C.; Woszidlo, R.; Bergada, J.M.; Nayeri, C.N.; Paschereit, C.O. Experimental study of the internal flow structures inside a fluidic oscillator. Exp. Fluids 2013, 54, 1–12. [Google Scholar] [CrossRef]
- Striegl, S.A.; Diller, T.E. An analysis of the effect of entrainment temperature on jet impingement heat transfer. J. Heat Transf. 1984, 106, 804–810. [Google Scholar] [CrossRef]
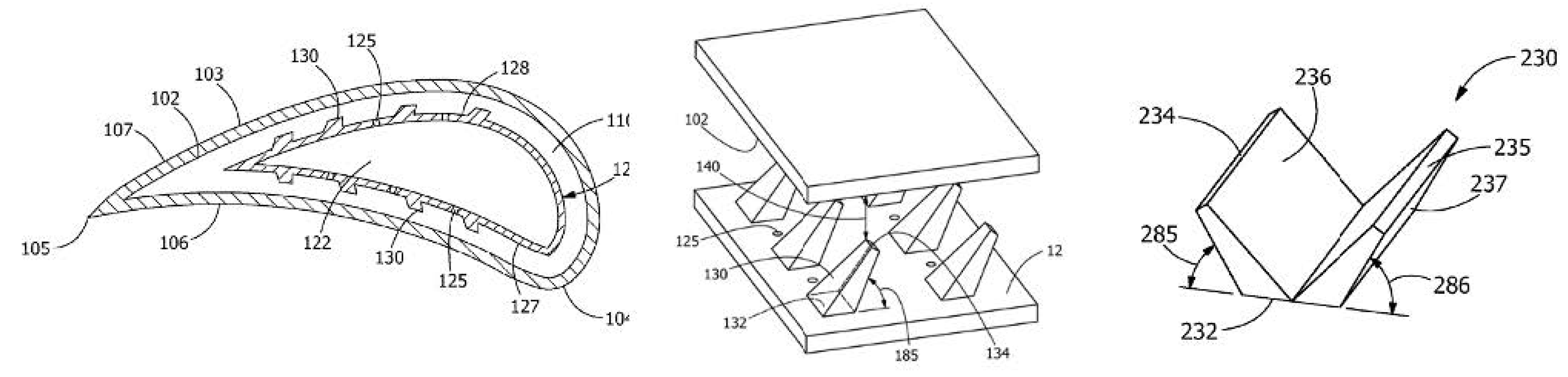
- Dutta, S.; Weber, J.A.; Lacy, B.P. Impingement Insert. U.S. Patent 10,494,948 B2, 3 December 2019. Available online: https://patents.google.com/patent/US10494948B2/en (accessed on 8 March 2020).
- Dutta, S.; Lacy, B.P.; Itzel, G.M.; Snider, Z.J. Impingement Insert for a Gas Turbine Engine. U.S. Patent 20, 180, 149,028 A1, 31 May 2018. Available online: https://patents.google.com/patent/US20180149028A1/en (accessed on 8 March 2020).
- Jambunathan, K.; Lai, E.; Moss, M.; Button, B. A review of heat transfer data for single circular jet impingement. Int. J. Heat Fluid Flow 1992, 13, 106–115. [Google Scholar] [CrossRef]
- Martin, H. Heat and mass transfer between impinging gas jets and solid surfaces. Adv. Heat Transf. 1977, 13, 1–60. [Google Scholar] [CrossRef]
- Bergman, T.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 8th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Takeishi, K.-I.; Krewinkel, R.; Oda, Y.; Ichikawa, Y. Heat transfer enhancement of impingement cooling by adopting circular-ribs or vortex generators in the wall jet region of a round impingement jet. Int. J. Turbomach. Propuls. Power 2020, 5, 17. [Google Scholar] [CrossRef]
- Chiu, R.-S.P.; Hasz, W.C.; Johnson, R.A.; Lee, C.-P.; Abuaf, N. Enhanced Heat Transfer Surface for Cast-in-Bump-Covered Cooling Surfaces and Methods of Enhancing Heat Transfer. U.S. Patent 6,402,464 B1, 1 January 2002. Available online: https://www.osti.gov/servlets/purl/874499 (accessed on 9 October 2021).
- Johnson, R.A.; Schaeffer, J.C.; Lee, C.-P.; Abuaf, N. Method of Salvaging Castings with Defective Cast Cooling Bumps. U.S. Patent 2002/0,150,672 A1, 1 January 2002. [Google Scholar]
- Dailey, G.M.; Son, C.S. Air Impingement Cooling System. U.S. Patent 6,688,110 B2, 10 February 2004. [Google Scholar]
- Singh, P.; Nithyanandam, K.; Zhang, M.; Mahajan, R.L. The effect of metal foam thickness on jet array impingement heat transfer in high-porosity aluminum foams. J. Heat Transf. 2020, 142. [Google Scholar] [CrossRef]
- Singh, P.; Zhang, M.; Mahajan, R.L. Effect of metal foam thickness and pore density on array jet impingement heat transfer. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; Volume 8. [Google Scholar]
- Singh, P.; Zhang, M.; Pandit, J.; Mahajan, R.L. Array jet impingement onto high porosity thin metal foams at zero jet-to-foam spacing. ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar] [CrossRef]
- Madhavan, S.; Singh, P.; Ekkad, S.V. Jet impingement heat transfer enhancement by packing high-porosity thin metal foams between jet exit plane and target surface. J. Therm. Sci. Eng. Appl. 2019, 11, 1–22. [Google Scholar] [CrossRef]
- Andreozzi, A.; Bianco, N.; Lasiello, M.; Naso, V. Numerical Study of Metal Foam Heat Sinks Under Uniform Impinging Flow. J. Phys. Conf. Ser. 2017, 796. [Google Scholar] [CrossRef]
- Singh, P.; Nithyanandam, K.; Mahajan, R.L. An experimental and numerical investigation of forced convection in high porosity aluminum foams subjected to jet array impingement in channel-flow. Int. J. Heat Mass Transf. 2020, 149, 119107. [Google Scholar] [CrossRef]
- Jia, R.; Rokni, M.; Sunden, B. Impingement cooling in a rib-roughened channel with cross-flow. Int. J. Numer. Methods Heat Fluid Flow 2001, 11, 642–662. [Google Scholar] [CrossRef] [Green Version]
- Rao, Y. Jet Impingement heat transfer in narrow channels with different pin fin configurations on target surfaces. J. Heat Transf. 2018, 140. [Google Scholar] [CrossRef]
- Ahmed, S.; Singh, P.; Ekkad, S.V. Three-dimensional transient heat conduction equation solution for accurate determination of heat transfer coefficient. ASME J. Heat Transf. 2020, 142. [Google Scholar] [CrossRef]
- Kanokjaruvijit, K.; Martinez-Botas, R.F. Jet impingement on a dimpled surface with different crossflow schemes. Int. J. Heat Mass Transf. 2005, 48, 161–170. [Google Scholar] [CrossRef]
- Katti, V.V.; Prabhu, S.V. Influence of spanwise pitch on local heat transfer for multiple jets with crossflow. J. Thermophys. Heat Transf. 2008, 22. [Google Scholar] [CrossRef]
- Miao, J.-M.; Wu, C.-Y.; Chen, P.-H. Numerical investigation of confined multiple-jet impingement cooling over a flat plate at different crossflow orientaions. Numer. Heat Transf. Part A Appl. 2009, 55, 1019–1050. [Google Scholar] [CrossRef]
- Ji, Y.; Singh, P.; Ekkad, S.V.; Zang, S. Effect of crossflow regulation by varying jet diameters in streamwise direction on jet impingement heat transfer under maximum crossflow condition. Numer. Heat Transf. Part A Appl. 2017, 72, 579–599. [Google Scholar] [CrossRef]
- Al-Hadhrami, L.M.; Shaahid, S.; Al-Mubarak, A.A. Jet impingement cooling in gas turbines for improving thermal efficiency and power density. In Advances in Gas Turbine Technology; InTech: London, UK, 2011. [Google Scholar]
- Al-Hadhrami, L.M. Study of heat transfer distribution in a channel with inclined target surface cooled by a single array of staggered impinging jets. Heat Transf. Eng. 2010, 31, 234–242. [Google Scholar] [CrossRef]
- Hebert, R.T.; Ekkad, S.V.; Gao, L.; Bunker, R.S. Impingement heat transfer, Part II: Effect of streamwise pressure gradient. J. Thermophys. Heat Transf. 2005, 19, 66–71. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, J.-Z.; Lyu, Y.-W.; Tan, X.-M. Convective heat transfer on a flat target surface impinged by pulsating jet with an additional transmission chamber. Heat Mass Transf. 2020, 56, 183–205. [Google Scholar] [CrossRef]
- Lyu, Y.-W.; Zhang, J.-Z.; Shan, Y.; Tan, X.-M. The Experimental Investigation of Impinging Heat Transfer of Pulsation Jet on the Flat Plate. J. Heat Transf. 2018, 140. [Google Scholar] [CrossRef]
- Goldstein, R.; Behbahani, A.; Heppelmann, K. Streamwise distribution of the recovery factor and the local heat transfer coefficient to an impinging circular air jet. Int. J. Heat Mass Transf. 1986, 29, 1227–1235. [Google Scholar] [CrossRef]
- Dewey, C. A correlation of convective heat transfer and recovery temperature data for cylinders in compressible flow. Int. J. Heat Mass Transf. 1965, 8, 245–252. [Google Scholar] [CrossRef]
- Vortec. Vortex Tubes: Product Overview, (n.d.). Available online: https://www.vortec.com/vortex-tubes-1/overview (accessed on 2 June 2021).
- Goldstein, R.J.; Sobolik, K.A.; Seol, W.S. Effect of entrainment on the heat transfer to a heated circular air jet impinging on a flat surface. J. Heat Transf. 1990, 112, 608–611. [Google Scholar] [CrossRef]
- Zuo, Z.J.; Faghri, A.; Langston, L. Numerical analysis of heat pipe turbine vane cooling. J. Eng. Gas Turbines Power 1998, 120, 735–743. [Google Scholar] [CrossRef]



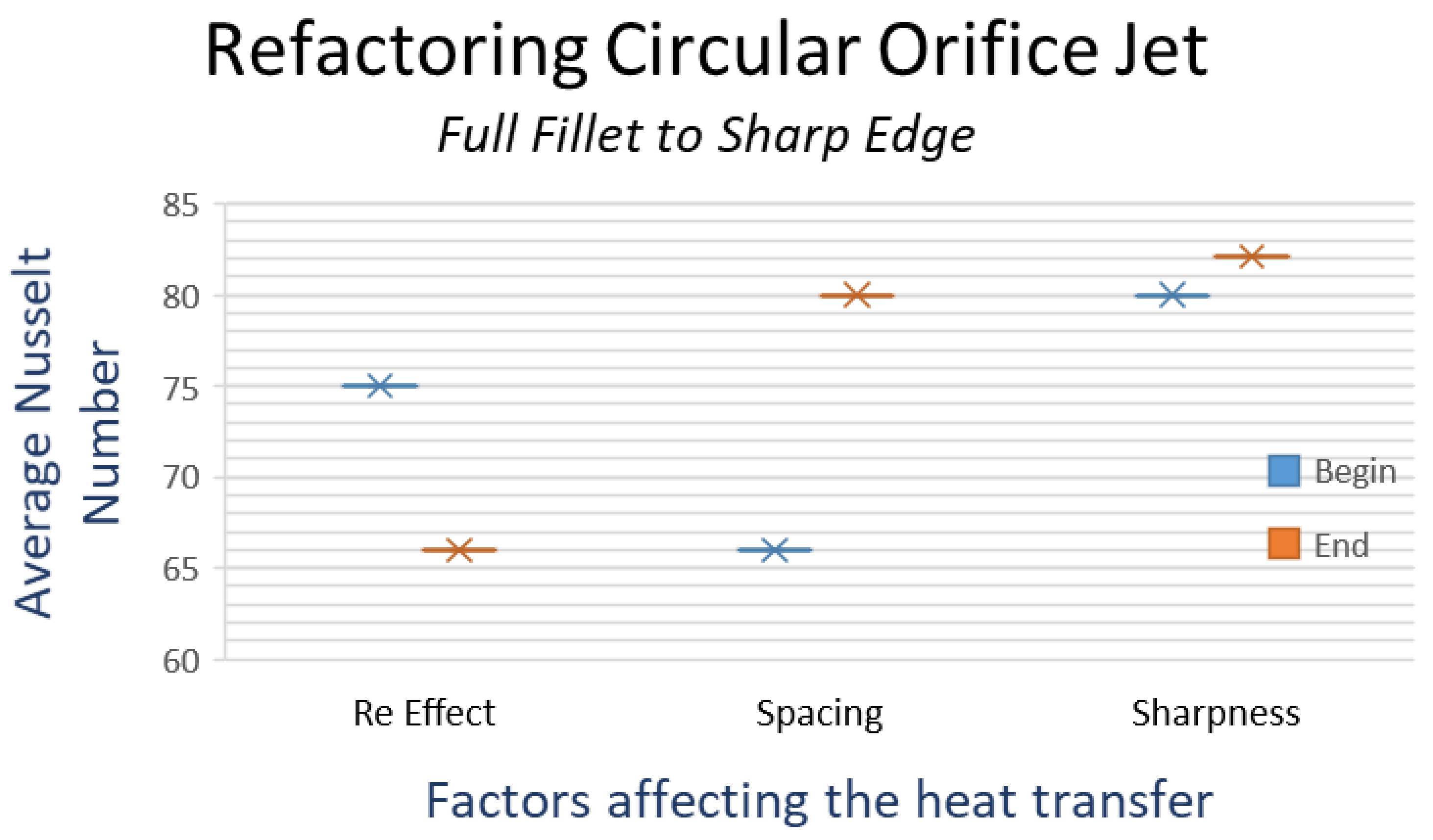
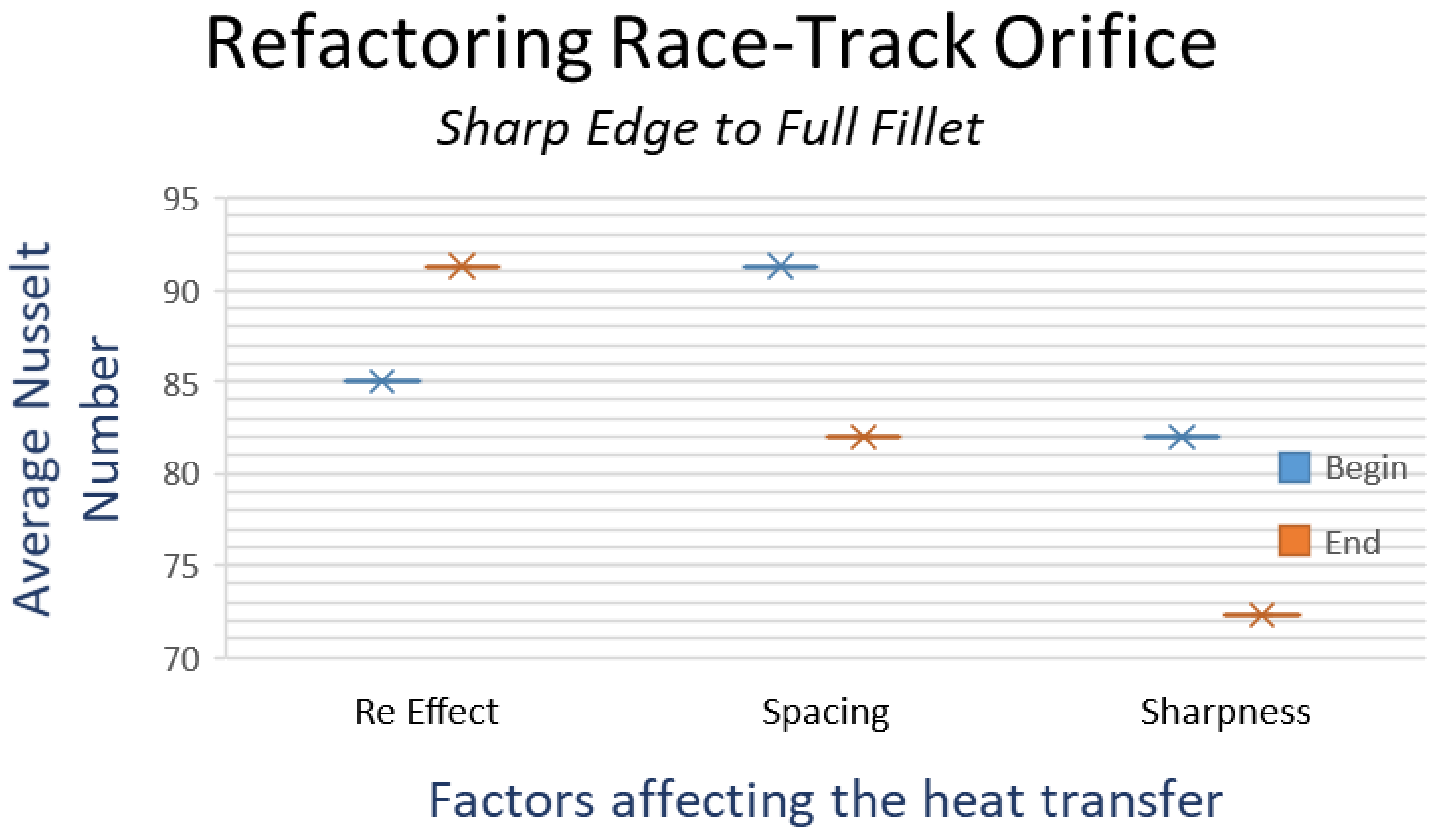

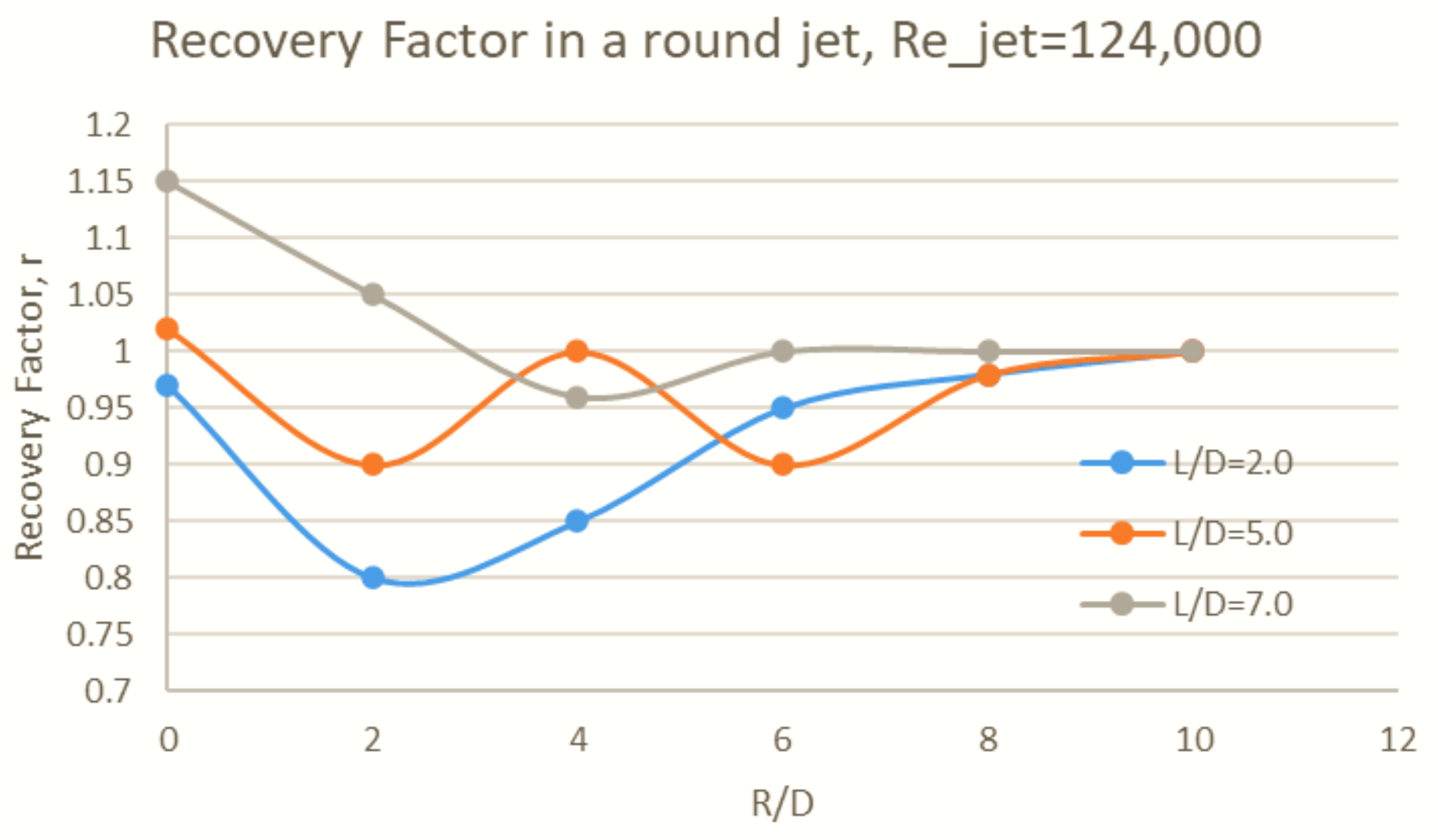
| Factors in Jet Impingement Heat Transfer | Representative Figure |
|---|---|
| Jet entrainment [19] | 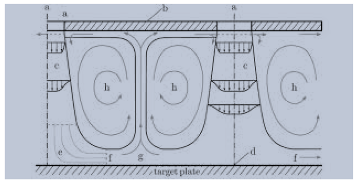 |
| Impingement–Effusion [20] | 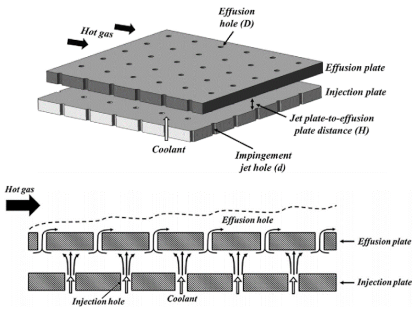 |
| Jet orifice ((a): [21], (b): [22], (c): [23], (d): [24]) | 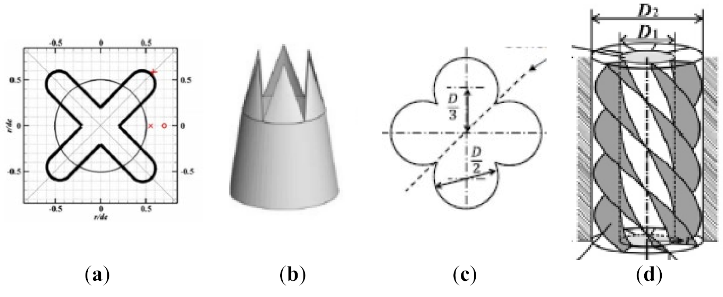 |
| Backplate modifications [25] | 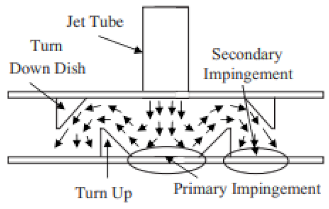 |
| Target surface modifications ((a): [26], (b): [27], (c): [18]) |  |
| Impingement channel modifications ((a): [28], (b): [29], (c): [30]) | 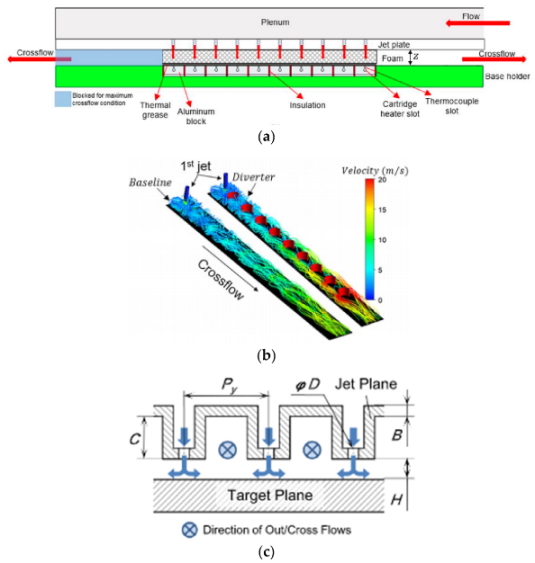 |
| Crossflow regulation [15] |  |
| Cd at Duct 20,000 Re | Cd | Nu Avg. | Re for Nu |
|---|---|---|---|
| Round sq edge | 0.825 | 77 | 27,200 |
| Round part fillet | 0.975 | 79 | 27,200 |
| Round full fillet | 1 | 75 | 27,200 |
| RT sq edge | 0.745 | 85 | 23,000 |
| RT part fillet | 0.825 | 83 | 23,000 |
| RT full fillet | 0.83 | 75 | 23,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, S.; Singh, P. Opportunities in Jet-Impingement Cooling for Gas-Turbine Engines. Energies 2021, 14, 6587. https://doi.org/10.3390/en14206587
Dutta S, Singh P. Opportunities in Jet-Impingement Cooling for Gas-Turbine Engines. Energies. 2021; 14(20):6587. https://doi.org/10.3390/en14206587
Chicago/Turabian StyleDutta, Sandip, and Prashant Singh. 2021. "Opportunities in Jet-Impingement Cooling for Gas-Turbine Engines" Energies 14, no. 20: 6587. https://doi.org/10.3390/en14206587
APA StyleDutta, S., & Singh, P. (2021). Opportunities in Jet-Impingement Cooling for Gas-Turbine Engines. Energies, 14(20), 6587. https://doi.org/10.3390/en14206587