Investigations on Pressure Fluctuations in the S-Shaped Region of a Pump–Turbine
Abstract
:1. Introduction
2. Research Object and Numerical Methods
2.1. Research Object Analysis
2.2. Numerical Simulation Strategy
2.3. Distribution of Monitoring Points
3. Results and Discussions
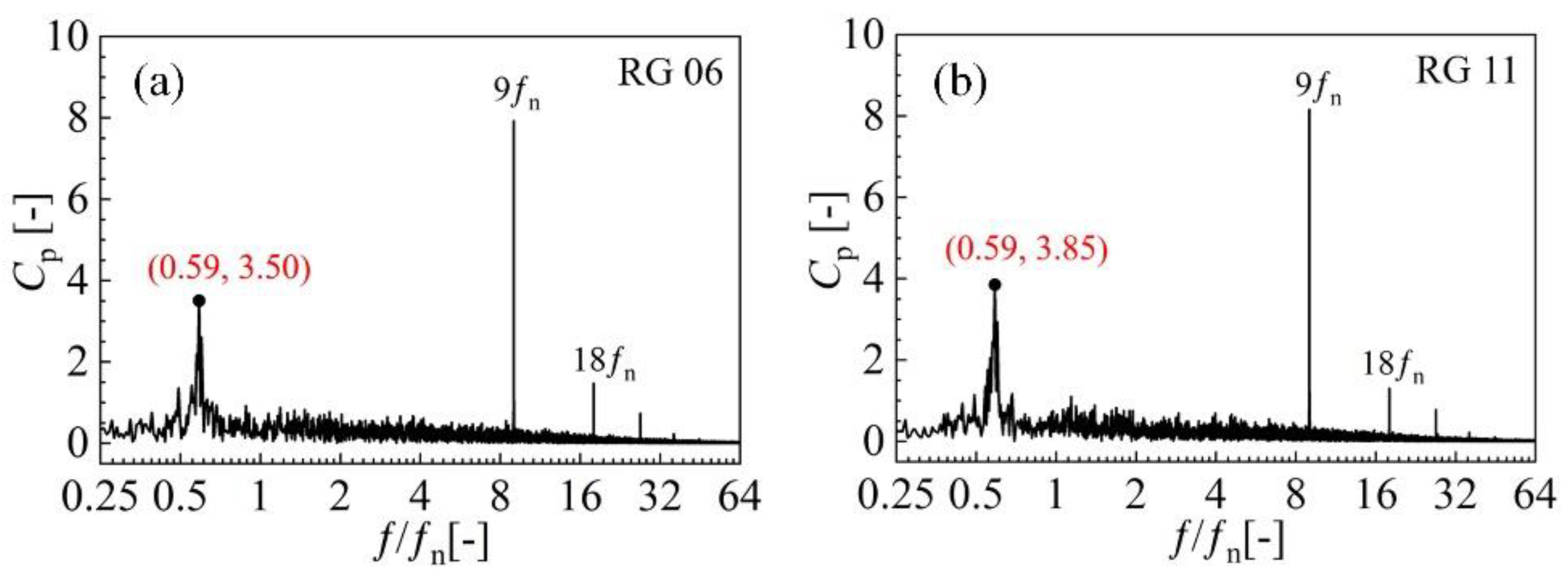
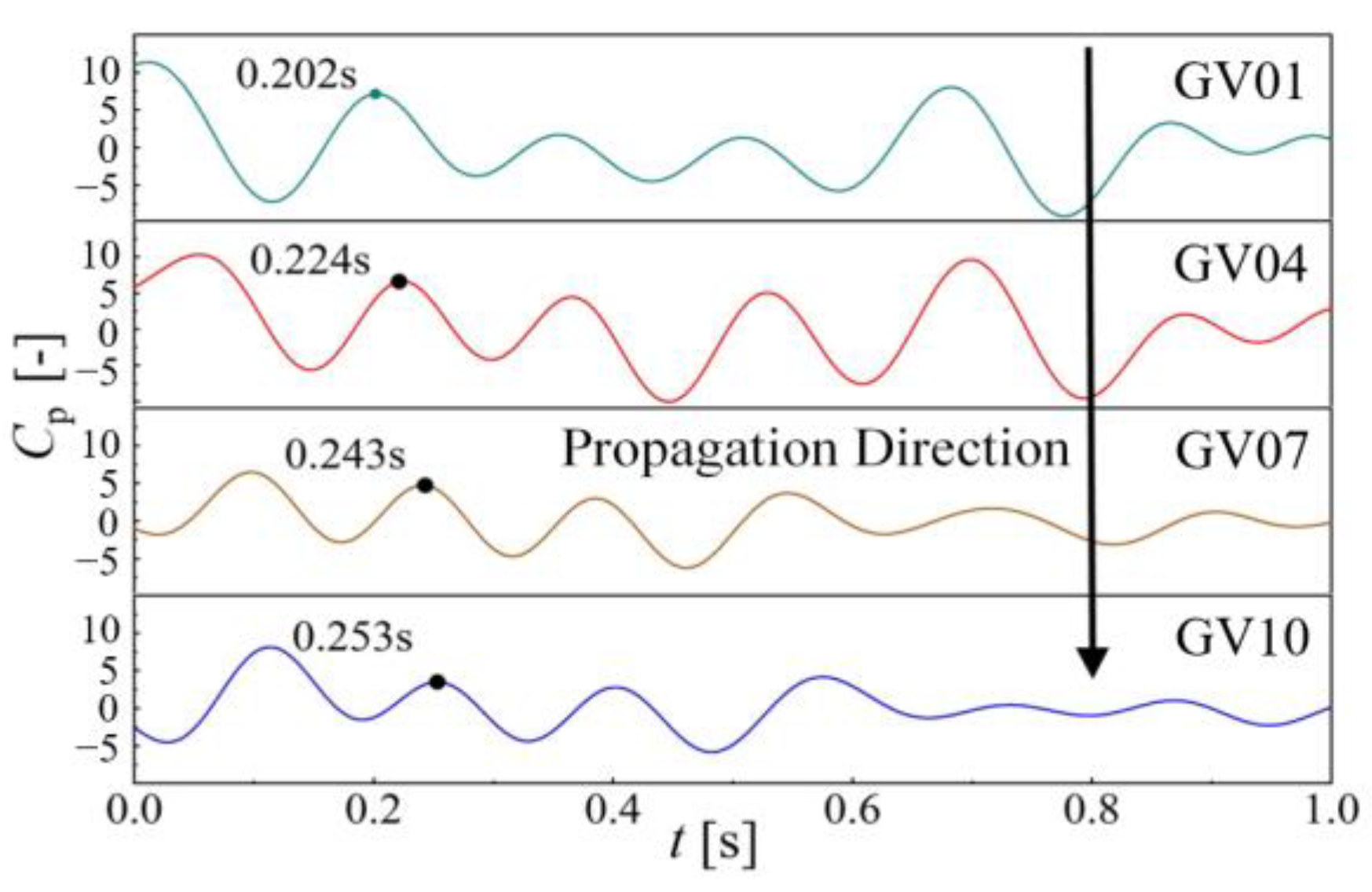
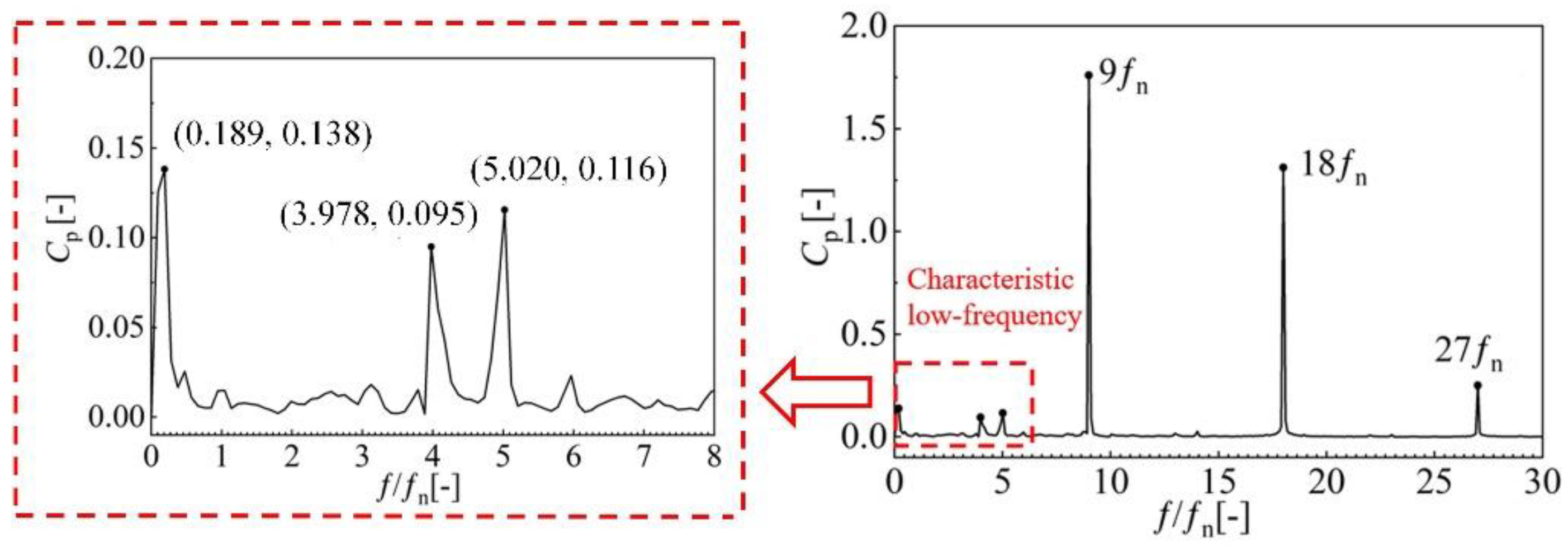
3.1. Pressure Fluctuation Analysis of Turbine Operating Condition
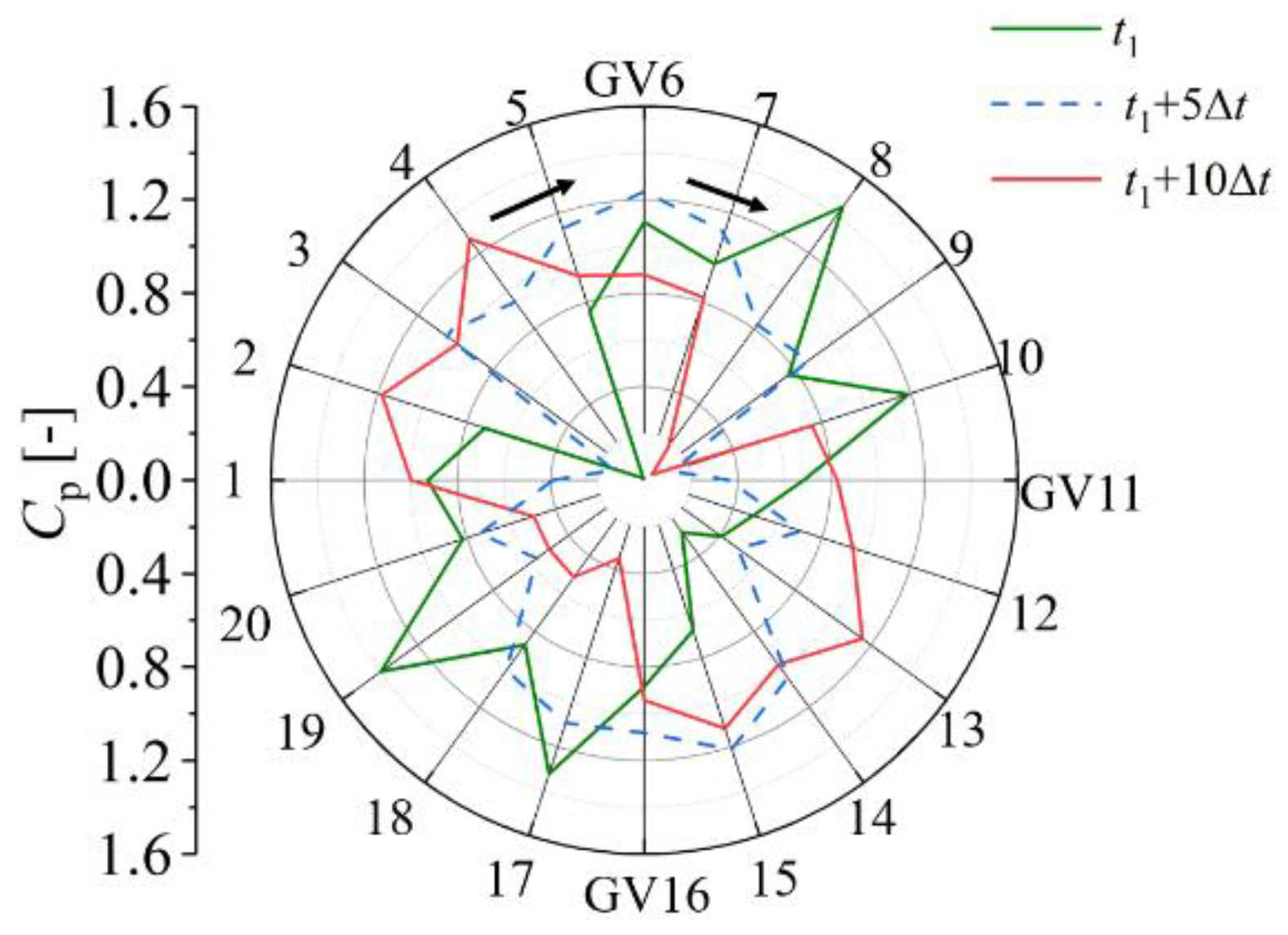
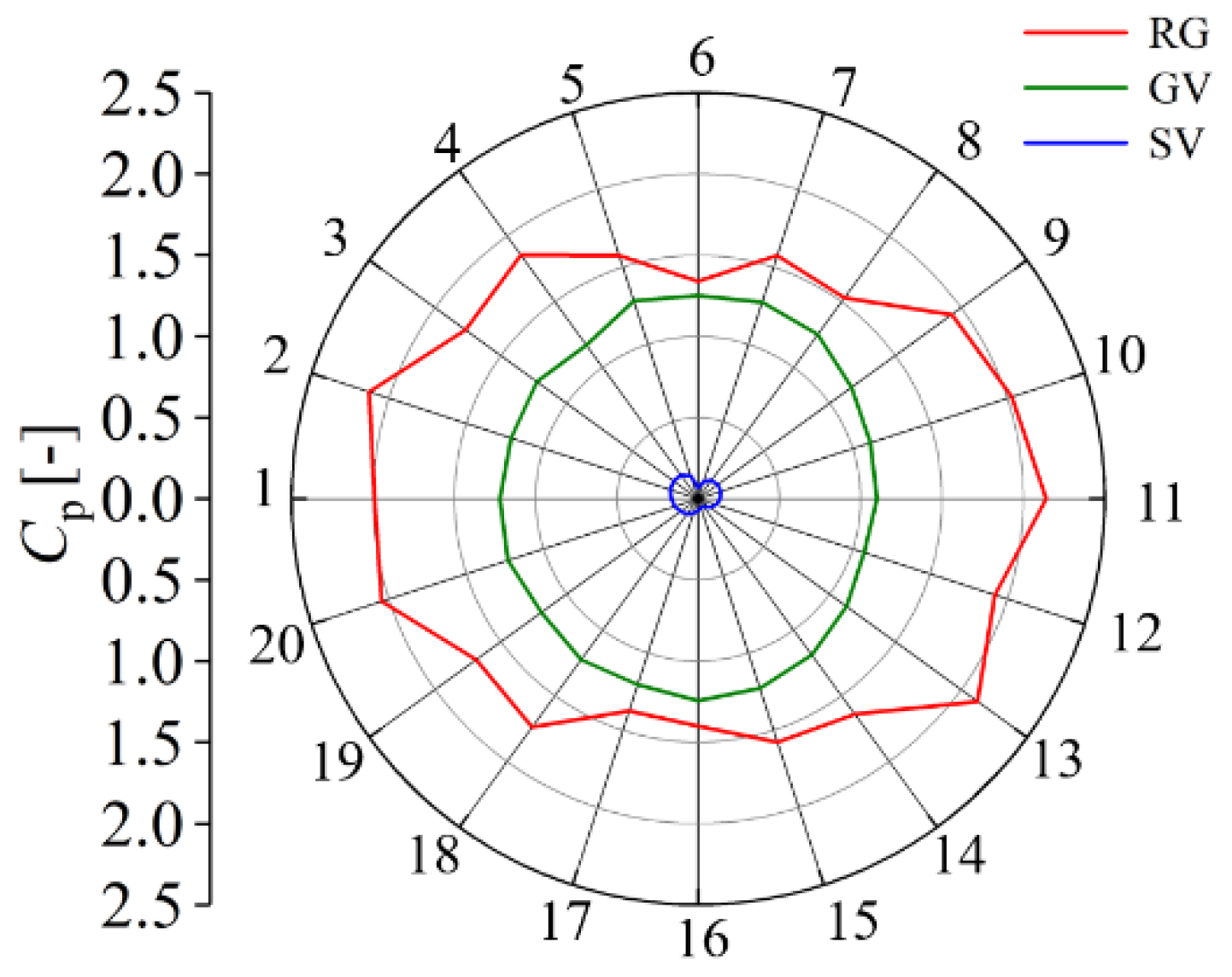
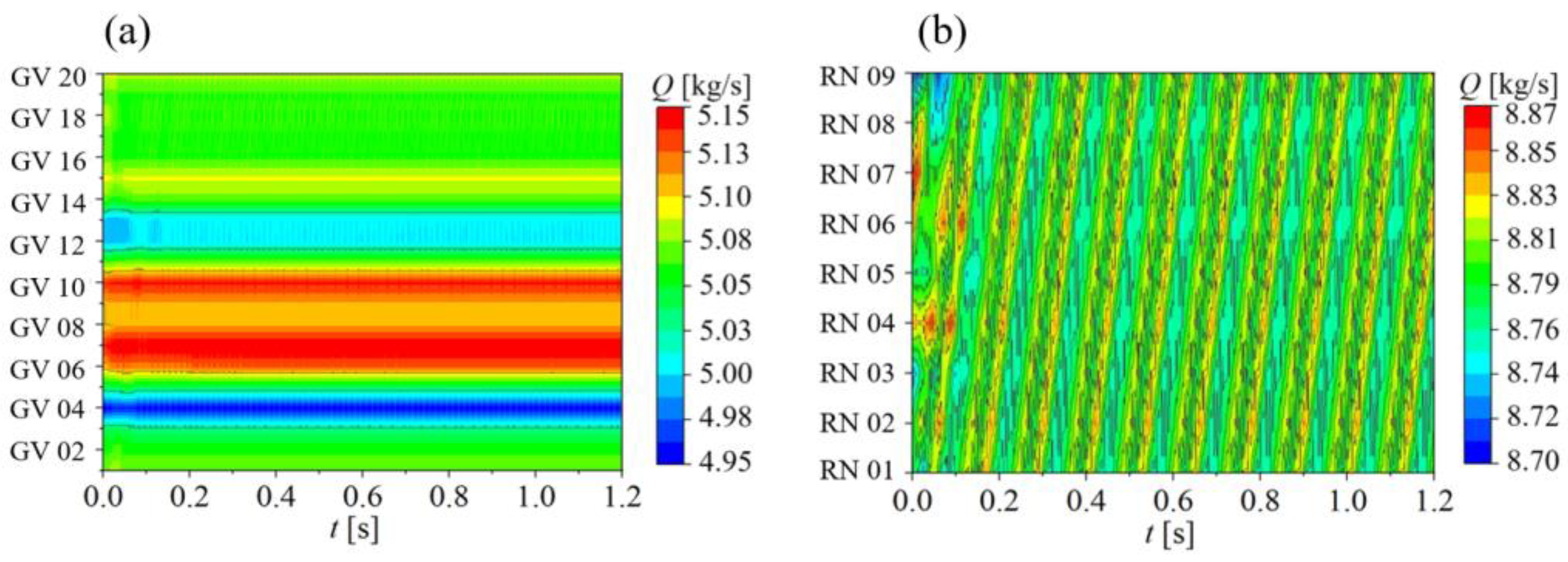
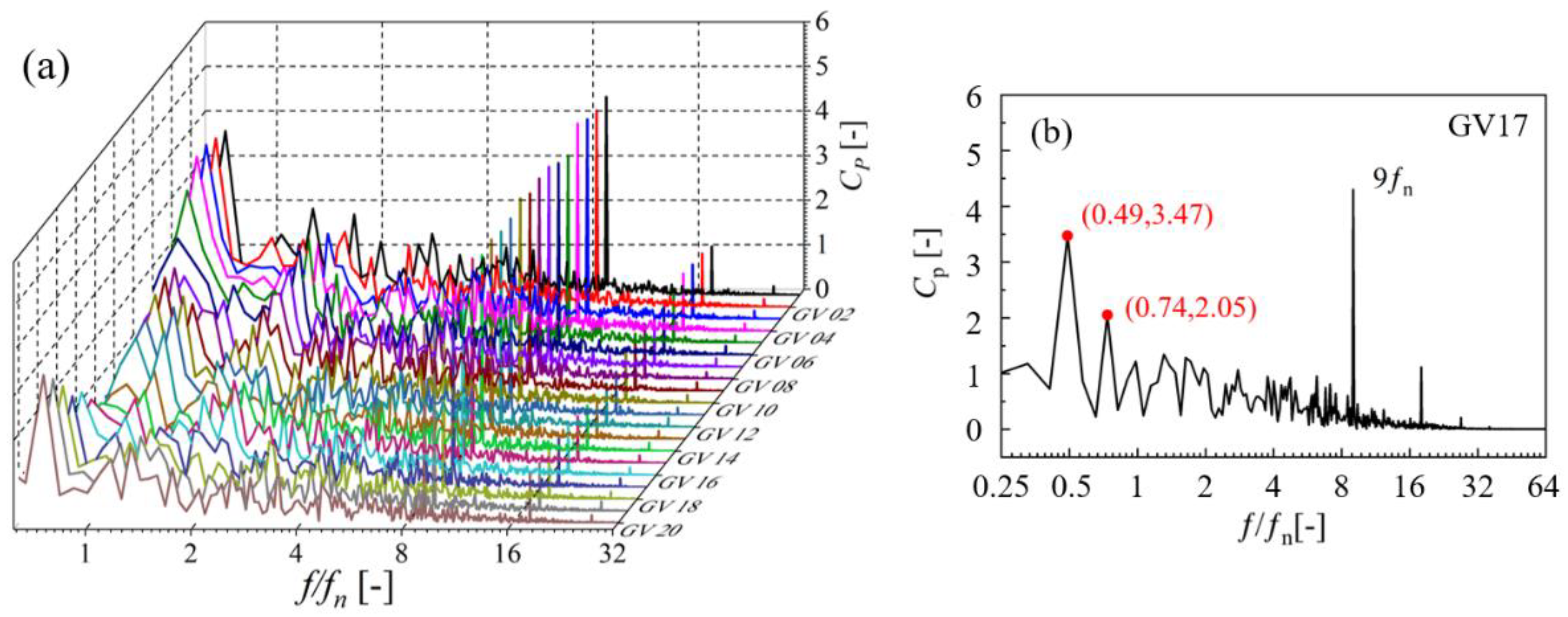
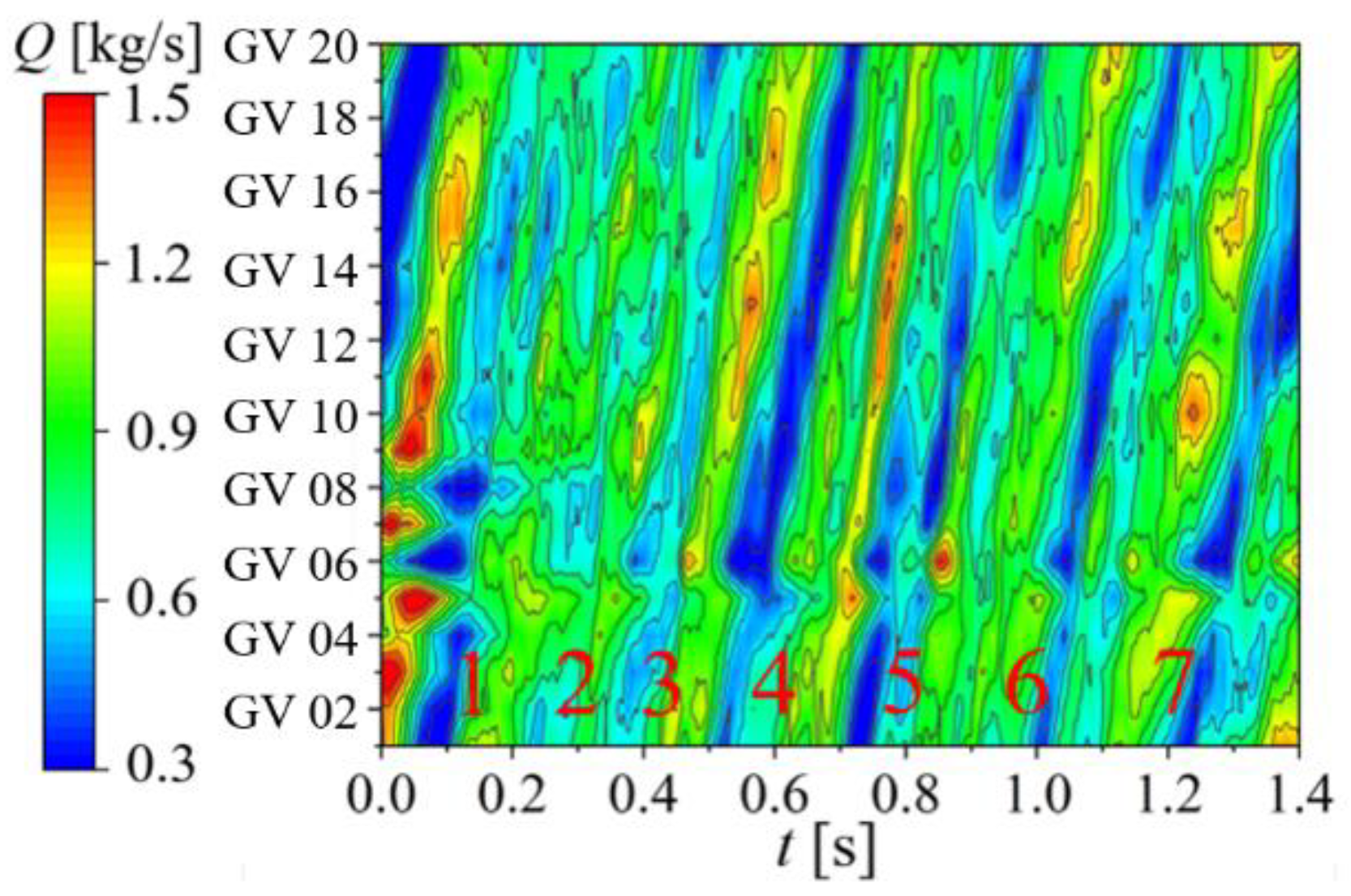
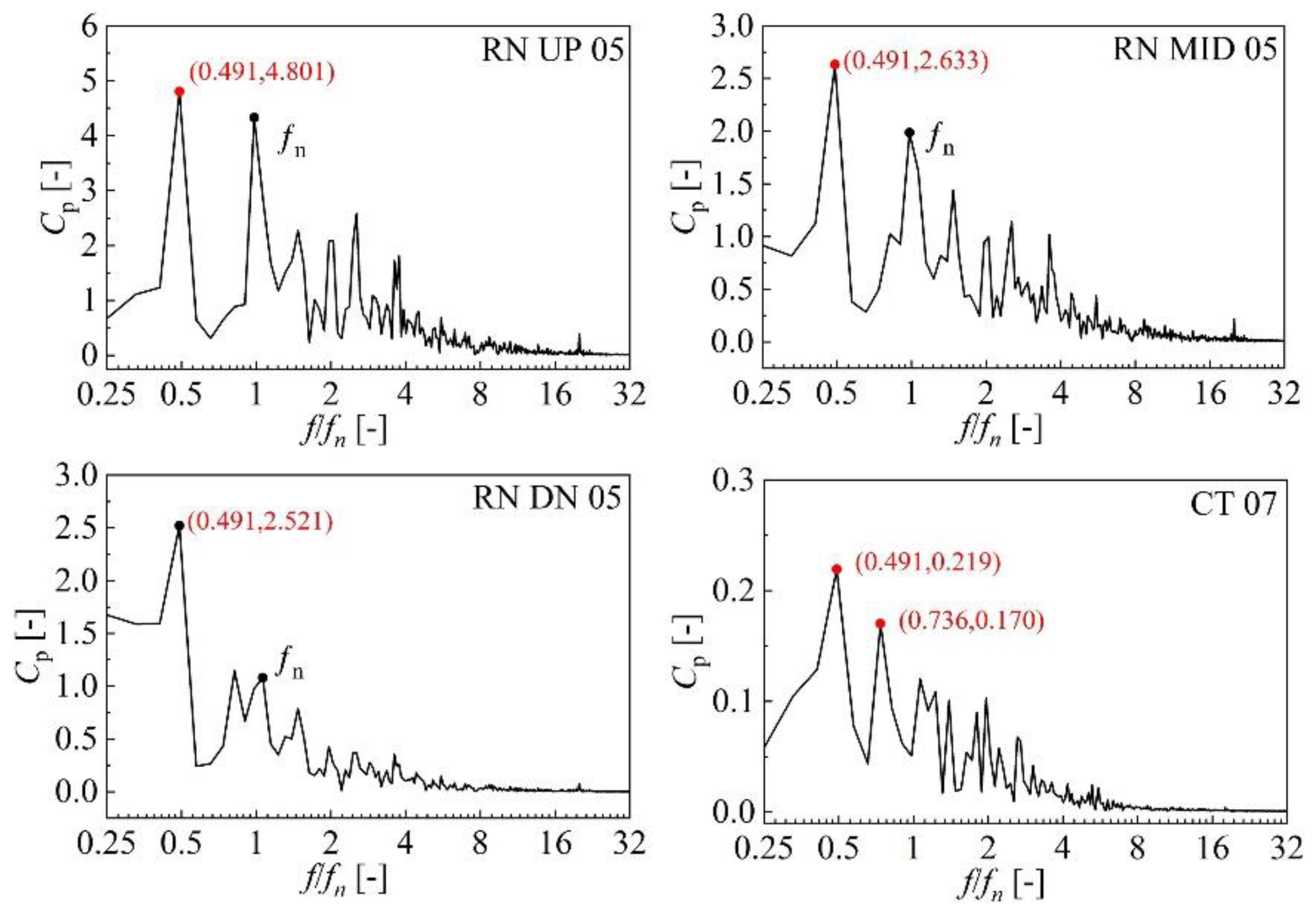
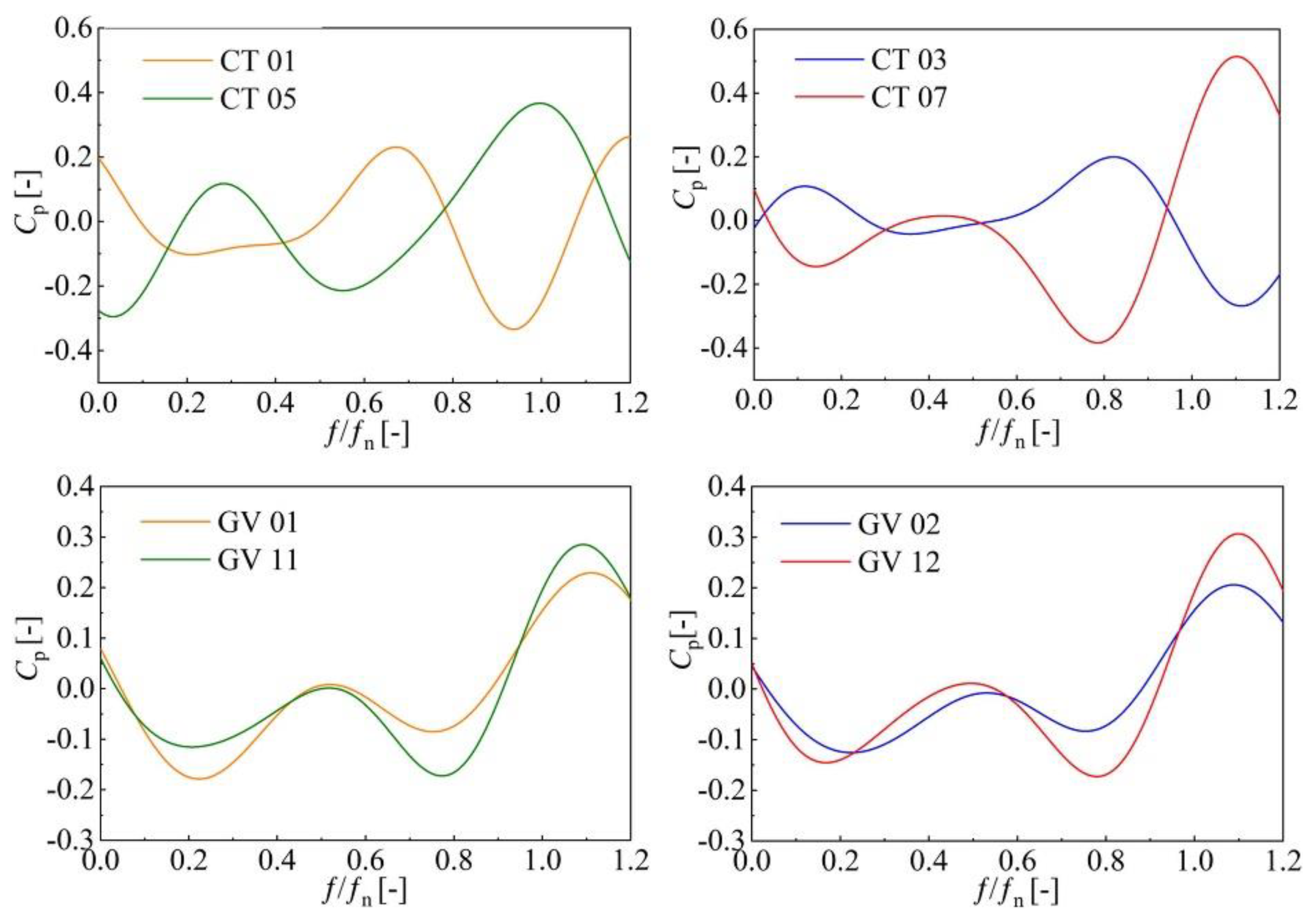
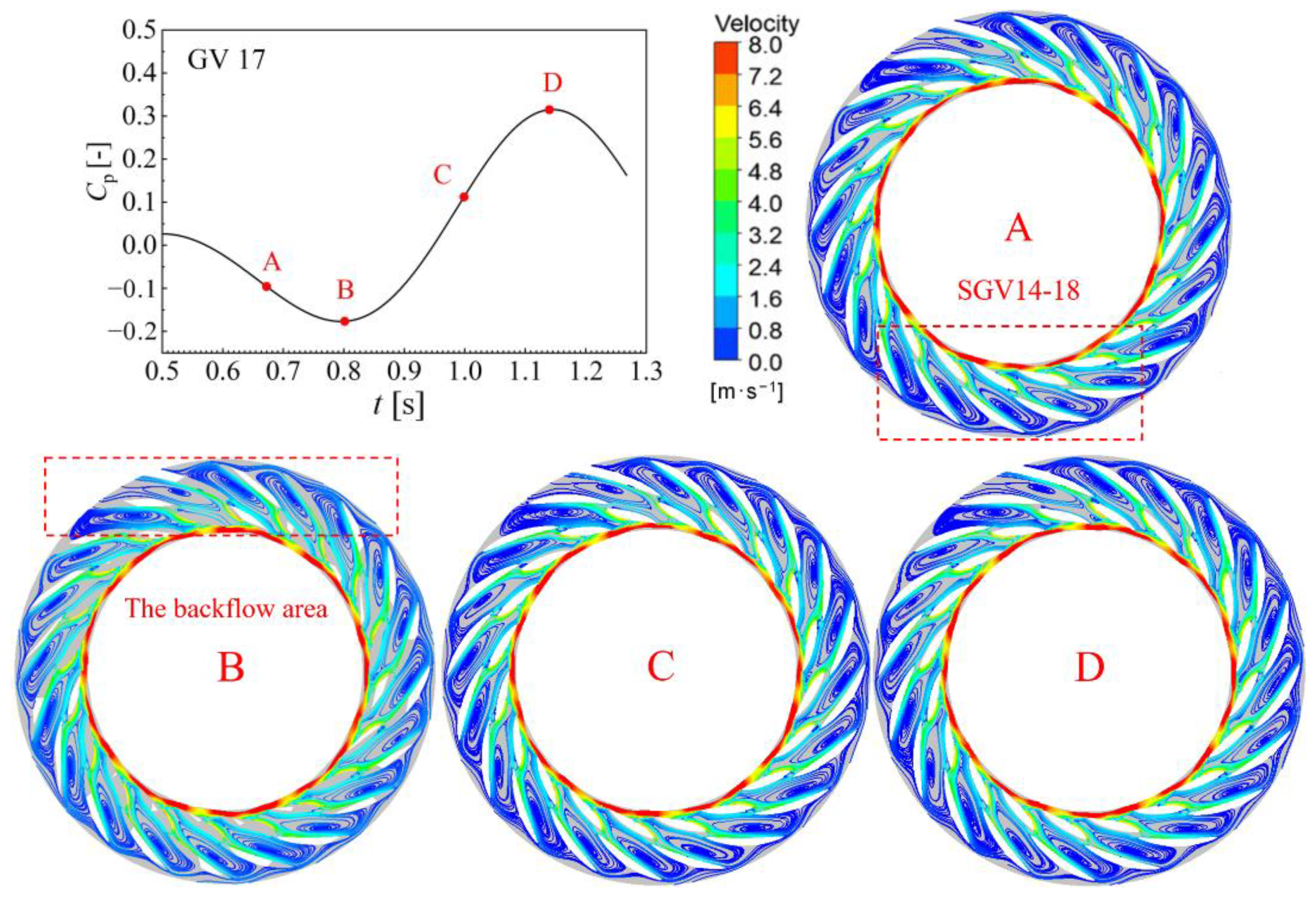
3.2. Pressure Fluctuation Analysis of Braking Operating Condition
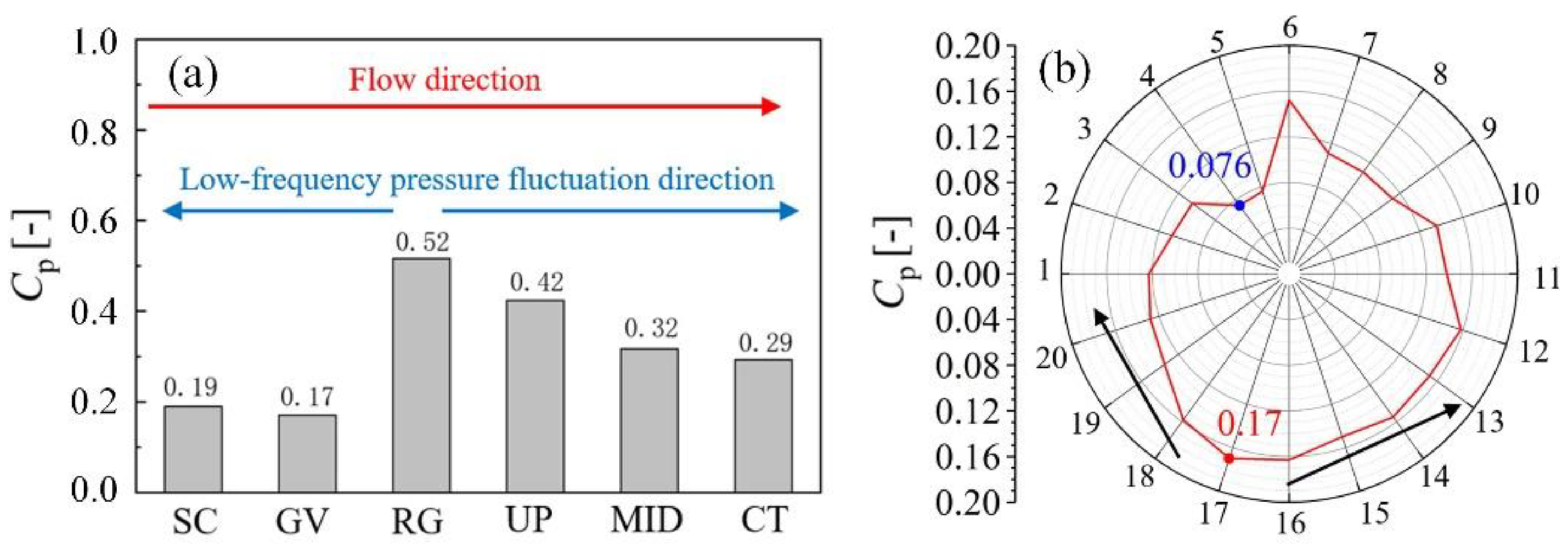
3.3. Pressure Fluctuation Analysis of Reverse Pump Condition
4. Conclusions
- (1)
- It is found that, under the turbine operating condition, pressure fluctuations have obvious periodicity. In terms of frequency, 9 fn is mainly generated by the rotor–stator interaction between guide vanes and runner. There is no backflow area in the flow field, and the fluid velocity changes uniformly. The streamline has high symmetry in the longitudinal and transverse sections.
- (2)
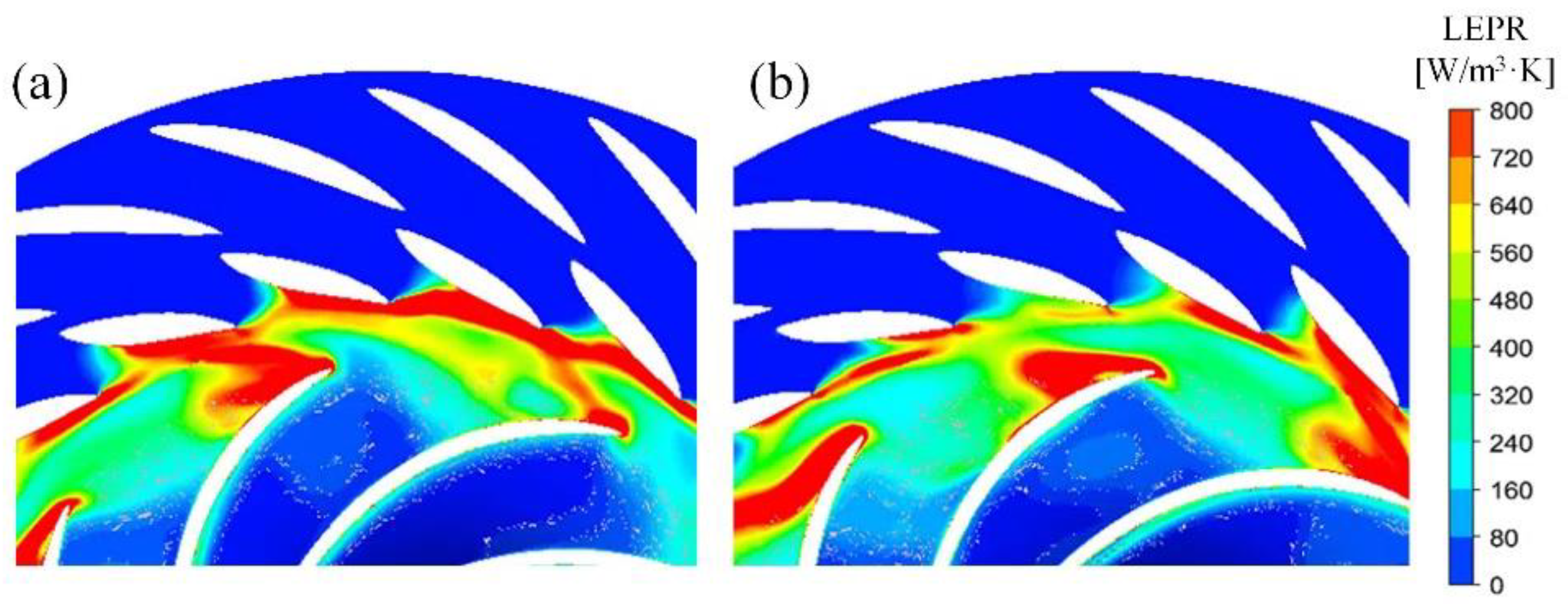
- Under braking operating condition, due to the decrease in discharge and the high speed of the runner, it is difficult for the fluid to reach the runner, and vortexes are formed in the vaneless space to block the guide vanes outlet. It is found that the vortices move circumferentially with the runner rotation. Dominant frequency of guide vanes and vaneless space are still the frequency generated by the rotor–stator interaction. The rotating stall phenomenon occurs periodically in the flow field, forming a 0.49-fn low-frequency pressure fluctuation that propagates to the upstream and downstream of vaneless space, and decreases to the minimum when it spreads to the draft tube. In addition, the local entropy production rate in the vaneless space increases when the large-scale backflow occurs, and causes great hydraulic loss.
- (3)
- By analyzing the reverse pump operating condition, it is found that large vortices occur in the flow channel of stay vanes and guide vanes, which generate a strong blockage. The rotating stall vortex in the vaneless space causes a 0.19-fn low-frequency pressure fluctuation, which propagates along two circumferential directions, and propagates upstream and downstream of the axial flow. The internal flow characteristics of the low discharge reverse pump are relatively stable, and the pressure fluctuations are lower than that of braking operating condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| H | Head [m] |
| n | Rotating speed [r·min−1] |
| Q | Discharge [m3·s−1] |
| T | Torque [N·m] |
| D2 | Runner outlet diameter [m] |
| Z | Runner blade number [-] |
| Zg | Guide vane number [-] |
| Zs | Stay vane number [-] |
| bg | Guide vane height [-] |
| t | Time [s] |
| f | Frequency of pressure fluctuation [Hz] |
| fn | Runner rotation frequency [Hz] |
| ν | Kinematic viscosity [m2/s] |
| μ | Dynamic viscosity [Pa·s] |
| y+ | Dimensionless distance [-] |
| Cp | Dimensionless coefficient of pressure fluctuation, |
| P | Calculation pressure of monitoring points [Pa] |
| Average pressure of monitoring points [Pa] | |
| n11 | Unit speed, [r·m0.5·min−1] |
| Q11 | Unit discharge, [m0.5·s−1] |
| T11 | Unit torque, [N·min2·r−2·m−4] |
| Cal | Simulation value |
| Exp | Experimental value |
References
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Influence of hydrologically based environmental flow methods on flow alteration and energy production in a run-of-river hydropower plant. J. Clean. Prod. 2019, 232, 1028–1042. [Google Scholar] [CrossRef]
- Simão, M.; Ramos, H.M. Hybrid Pumped Hydro Storage Energy Solutions towards Wind and PV Integration: Improvement on Flexibility, Reliability and Energy Costs. Water 2020, 12, 2457. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Venugopal, G.; Ekanayake, J.; Tiong, S. Variable speed pumped hydro storage: A review of converters, controls and energy management strategies. Renew. Sustain. Energy Rev. 2020, 135, 110156. [Google Scholar] [CrossRef]
- Qi, Y.D.; Tang, X.B.; Zhao, J.J.; Sun, P. Present situation and development prospect of pumped storage power station in China. Collect. Work. Pumped Storage Power Stn. Constr. 2019, 5, 11–15. [Google Scholar]
- Tahani, M.; Kandi, A.; Moghimi, M.; Houreh, S.D. Rotational speed variation assessment of centrifugal pump-as-turbine as an energy utilization device under water distribution network condition. Energy 2020, 213, 118502. [Google Scholar] [CrossRef]
- Sallaberger, M.; Gentner, C.; Widmer, C.; Henggeler, U. Stability of Pump Turbine—A Challenge Faced in Design. Northwest Hydropower 2012, S1, 86–90+109. [Google Scholar]
- Li, D.; Fu, X.; Wang, H.; Zhao, R.; Wei, X. Evolution mechanism of a prototype pump-turbine after pump power off. Phys. Fluids 2021, 33, 106109. [Google Scholar] [CrossRef]
- Fu, X.; Zuo, Z.; Chang, H.; Li, D.; Wang, H.; Wei, X. Mechanism of low frequency high amplitude pressure fluctuation in a pump-turbine during the load rejection process. J. Hydraul. Res. 2020, 59, 280–297. [Google Scholar] [CrossRef]
- Cavazzini, G.; Covi, A.; Pavesi, G.; Ardizzon, G. Analysis of the Unstable Behavior of a Pump-Turbine in Turbine Mode: Fluid-Dynamical and Spectral Characterization of the S-shape Characteristic. J. Fluids Eng. 2015, 138, 021105. [Google Scholar] [CrossRef]
- Suh, J.-W.; Kim, S.-J.; Yang, H.-M.; Kim, M.-S.; Joo, W.-G.; Park, J.; Kim, J.-H.; Choi, Y.-S. A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit. Energies 2021, 14, 525. [Google Scholar] [CrossRef]
- Liu, W.; Zheng, J.; Chen, J.; Shi, Q. S-shaped characteristic optimization design of pump turbine in Xianju pumped storage power station. Collect. Work. Pumped Storage Power Stn. Constr. 2013, 5, 148–152. [Google Scholar]
- Casartelli, E.; Del Rio, A.; Mangani, L.; Schmid, A. Capturing S-Shape of Pump-Turbines by CFD Simulations Using an Anisotropic Turbulence Model. In Proceedings of the Fluid Applications and Systems, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Hasmatuchi, V.; Roth, S.; Botero, F.; Avellan, F.; Farhat, M. High-speed flow visualization in a pump-turbine under off-design operating conditions. In Proceedings of the 25th IAHR Symposium on Hydraulic Machinery and Systems, Timişoara, Romania, 20–24 September 2010; Volume 12, p. 012059. [Google Scholar] [CrossRef]
- Sun, H.; Xiao, R.; Liu, W.; Wang, F. Analysis of S Characteristics and Pressure Pulsations in a Pump-Turbine with Misaligned Guide Vanes. J. Fluids Eng. 2016, 129, 12037. [Google Scholar] [CrossRef] [PubMed]
- Rezghi, A.; Riasi, A. Sensitivity analysis of transient flow of two parallel pump-turbines operating at runaway. Renew. Energy 2016, 86, 611–622. [Google Scholar] [CrossRef]
- Olimstad, G.; Nielsen, T.; Børresen, B. Stability Limits of Reversible-Pump Turbines in Turbine Mode of Operation and Measurements of Unstable Characteristics. J. Fluids Eng. 2012, 134, 111202. [Google Scholar] [CrossRef] [Green Version]
- Houdeline, J.B.; Liu, J.; Lavigne, S.; Laurant, Y.; Balara, L. Start-up improvement in turbine mode for high head PSP machine. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2012; Volume 15, p. 042022. [Google Scholar]
- Yamabe, M. Improvement of Hysteresis Characteristics of Francis Pump-Turbines When Operated as Turbine. J. Basic Eng. 1972, 94, 581–585. [Google Scholar] [CrossRef]
- Rodriguez, C.; Egusquiza, E.; Santos, I.F. Frequencies in the Vibration Induced by the Rotor Stator Interaction in a Centrifugal Pump Turbine. J. Fluids Eng. 2007, 129, 1428–1435. [Google Scholar] [CrossRef] [Green Version]
- Jean-Bernard, H.; Liu, J.; Sylvain, L. Starting of high head reversible pump turbine. In Proceedings of the 19th China Symposium on Hydropower Equipment, Tianjin, China, 17 September 2013. [Google Scholar]
- Nielsen, T.K.; Svarstad, M.F. Unstable behaviour of RPT when testing turbine characteristics in the laboratory. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; Volume 22, p. 32038. [Google Scholar]
- Gentner, C.; Sallaberger, M.; Widmer, C.; Braun, O.; Staubli, T. Numerical and experimental analysis of instability phenomena in pump turbines. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2012; Volume 15, p. 032042. [Google Scholar]
- Widmer, C.; Staubli, T.; Ledergerber, N. Unstable Characteristics and Rotating Stall in Turbine Brake Operation of Pump-Turbines. J. Fluids Eng. 2011, 133, 041101. [Google Scholar] [CrossRef]
- Deng, R.; Gao, Z.Y.; Li, Y.L. Research status and recent development of turbulence model. J. Ship Mech. 2019, 23, 360–376. [Google Scholar]
- Olimstad, G.; Nielsen, T.; Børresen, B. Dependency on Runner Geometry for Reversible-Pump Turbine Characteristics in Turbine Mode of Operation. J. Fluids Eng. 2012, 134, 121102. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Dahlhaug, O.G. Numerical Techniques Applied to Hydraulic Turbines: A Perspective Review. Appl. Mech. Rev. 2016, 68, 010802. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Wei, X.; Qin, D. Flow Similarity in the Rotor–Stator Interaction Affected Region in Prototype and Model Francis Pump-Turbines in Generating Mode. J. Fluids Eng. 2016, 138, 061201. [Google Scholar] [CrossRef]
- Li, D.; Song, Y.; Lin, S.; Wang, H.; Qin, Y.; Wei, X. Effect mechanism of cavitation on the hump characteristic of a pump-turbine. Renew. Energy 2020, 167, 369–383. [Google Scholar] [CrossRef]
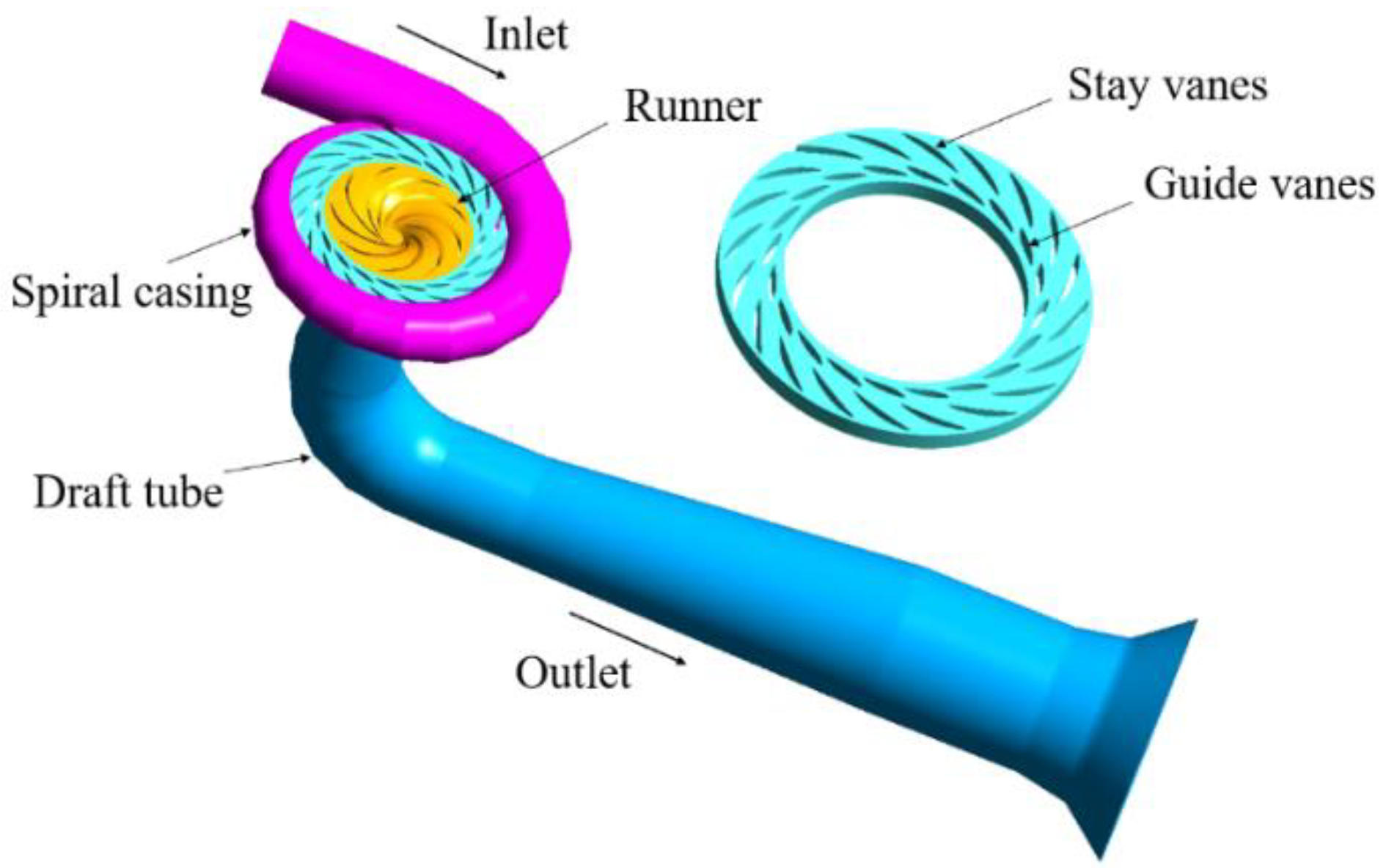

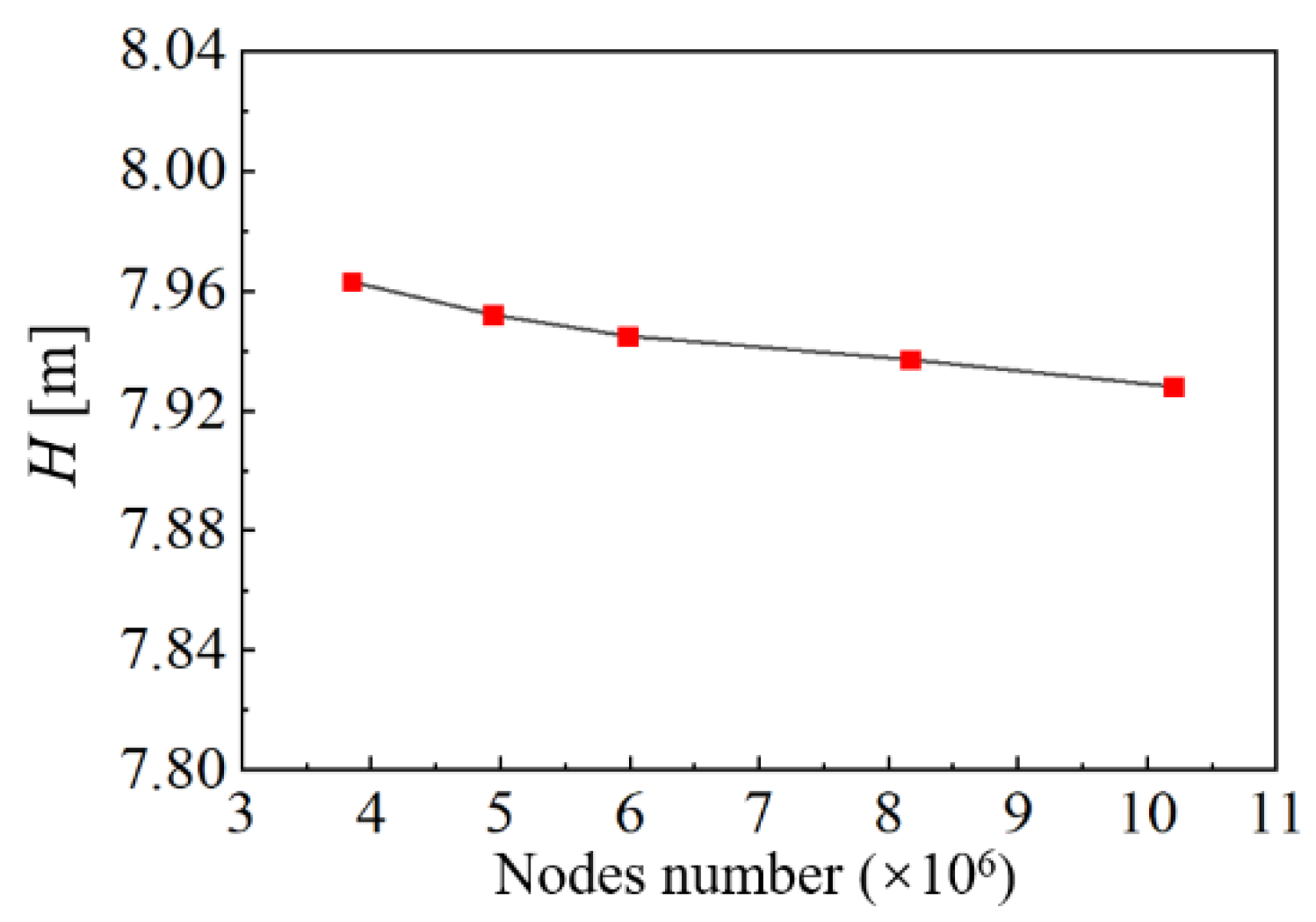

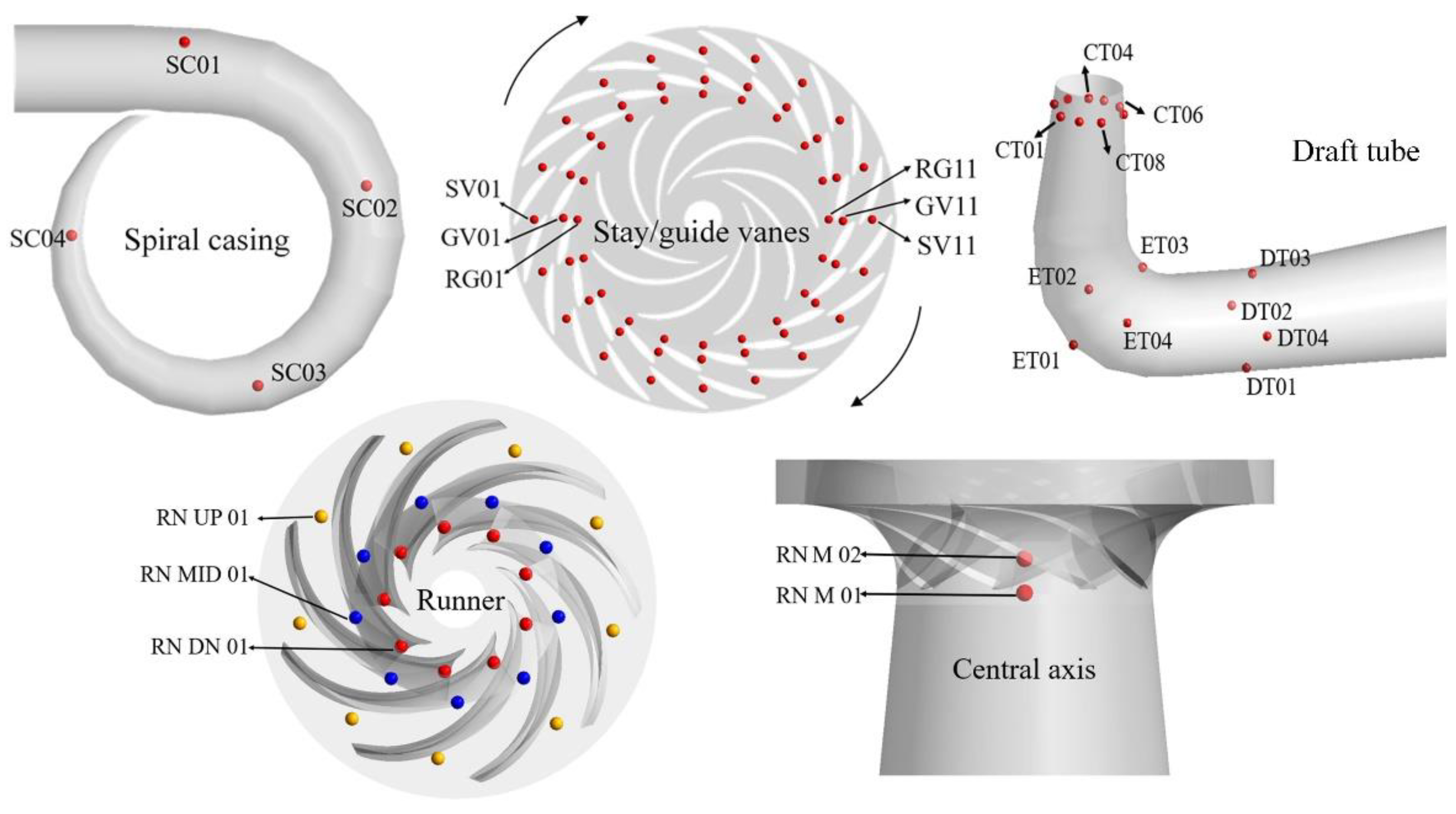







| Operating Condition | Spiral Casing | Stay/Guide Vanes | Runner | Draft Tube |
|---|---|---|---|---|
| Turbine (S03) | 7.5% | 23.6% | 55.3% | 13.2% |
| Runaway (S05) | 0.019% | 15.1% | 79.3% | 5.5% |
| Braking (S06) | 0.47% | 37.6% | 49.4% | 10.5% |
| Reverse pump (S10) | 0.56% | 51.2% | 46.2% | 2.1% |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Runner blade number Z | 9 | Guide vane number Zg | 20 |
| Rotational speed nr (r/min) | 499.850 | Stay vane number Zs | 20 |
| Runner inlet D1m (m) | 0.450 | Guide vane height bg | 0.044 |
| Runner outlet D2m (m) | 0.250 | Guide vane distribution diameter D0 | 0.541 |
| Parts | Mesh I | Mesh II | Mesh III | Mesh IV | Mesh V |
|---|---|---|---|---|---|
| Spiral Casing & Stay/guide Vanes | 1.93 | 2.28 | 2.62 | 4.02 | 5.42 |
| Runner | 1.44 | 1.77 | 2.29 | 2.65 | 3.24 |
| Draft Tube | 0.48 | 0.89 | 1.07 | 1.50 | 1.54 |
| Total | 3.85 | 4.94 | 5.98 | 8.17 | 10.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, J.; Gong, R.; Shang, C.; Li, D.; Wei, X. Investigations on Pressure Fluctuations in the S-Shaped Region of a Pump–Turbine. Energies 2021, 14, 6683. https://doi.org/10.3390/en14206683
Wang H, Wang J, Gong R, Shang C, Li D, Wei X. Investigations on Pressure Fluctuations in the S-Shaped Region of a Pump–Turbine. Energies. 2021; 14(20):6683. https://doi.org/10.3390/en14206683
Chicago/Turabian StyleWang, Hongjie, Jianpeng Wang, Ruzhi Gong, Chaoying Shang, Deyou Li, and Xianzhu Wei. 2021. "Investigations on Pressure Fluctuations in the S-Shaped Region of a Pump–Turbine" Energies 14, no. 20: 6683. https://doi.org/10.3390/en14206683
APA StyleWang, H., Wang, J., Gong, R., Shang, C., Li, D., & Wei, X. (2021). Investigations on Pressure Fluctuations in the S-Shaped Region of a Pump–Turbine. Energies, 14(20), 6683. https://doi.org/10.3390/en14206683







