Three-Dimensional Pore-Scale Simulation of Flow and Thermal Non-Equilibrium for Premixed Gas Combustion in a Random Packed Bed Burner

Abstract

Pore-scale studies of premixed gas combustion in a packed bed is conducted to study the flow and thermal non-equilibrium phenomenon in packed bed. The 3D random packed bed is generated using the EDEM software and solid surface radiation is computed using Discrete Ordinates (DO) model. The simulations are carried out using a commercial software package based on the finite volume method. It is shown that the local variation of species mass fraction, reaction rate et al. in pores near the flame front is significant, the radiation heat flux is transferred layer-by-layer. Cold flow simulation without reaction reveals that flow non-equilibrium is one of the essential characteristics of packing bed and increase in flow velocity leads to intensify non-equilibrium phenomenon. The distributions for content of axial velocity and gas temperature are wave-like shape in the burner and vary with time.

1. Introduction

Random packed bed has been widely used in industrial production, such as solar energy utilization, porous burner/reactor design and electronics cooling, packed bed burner was one of the most important aspects [1]. For premixed gas combustion in pellets packed bed, the complex structures of porous media led to extensive transfer processes in the packed bed.

In the packed bed burner, the geometric and time scales span wide range and this brings up special difficulties to study the reaction and transport processes [2]. The chemical reaction occurs within the pores surrounded by the pellet surfaces, chemical heat is rapidly released there at smaller time scale and subsequently the heat needs to be redistributed in the whole system due to the temperature differences between gas and solid phase and the intra-phase. The physical parameters of porous media are significantly different from those of gas. The heat capacity of solid matrix is about 1000 times of that of gas phase. The thermal conductivity of solid is significantly higher than that of gas, the solid phase plays important role in the heat redistribution process by multi-mode heat transfer methods, including convection heat transfer, heat conduction inside pellets and thermal radiation between pellet surfaces. The thermal conduction of solid skeleton and thermal radiation have been proved to be effective way to recirculate heat from hot products to fresh mixture in the upstream side. In this way, the lean flammability limit can be extended to realize the gas combustion with very low calorific value [3].

Although the porous media structures were complex and it is difficult to study the detailed mechanism of gas flow and heat recirculation in packed bed, extensive investigations on this issue have been conducted by theoretical, experimental and numerical studies [1]. Since the concept of heat recirculation was proposed by Weinberg et al. [4] to burn low-heating-value gas, a series of studies have been conducted based on the volume-average method. Takneo et al. [5,6] suggested a simpler method of producing heat recirculation using a highly conductive solid into the combustion zone. However, the thermal radiation of the porous media was ignored in their theoretical analysis. Their model was extended by the subsequent study, the thermal radiation was considered by assuming that the porous media was optically thickness, thus Rosseland model was used without solving the radiative transfer equation, and the detailed structure of the porous media was ignored. Barra and Ellzey [7] modeled heat recirculation in porous burners using volume-averaged approach, results showed that solid radiation became the dominant method for heat recirculation when the equivalence ratio and fame speed were increased. In this model, the radiative heat flux was treated with volume averaged method and this filtered out the detailed radiation transfer process.

With the rapid development of computer performance and great progress of computational mathematics in the last two decades, pore-scale simulation with simplified or detailed porous structures was gradually becoming powerful tool to simulate transfer processes in the packed bed. This approach is based on the idea of explicitly considering the local structure for 2D/3D porous media and gets insights into the basic transport process at smaller scale. For example, Dixon [8] studied the local transport and chemical reactions in a small ball packed bed. They used numerical method to reconstruct the three-dimensional random packed bed without simplifying the geometry of the burner, the geometric model was consisted of 807 catalytic pellets, results showed inhomogeneous velocity and components profiles in the combustor. However, solid-to-solid radiation was not considered in their computation. Zhdanok et al. [9] studied the filtration combustion in pellet packed bed, it was found that stable combustion can be obtained for CH₄/air with an extremely low equivalence ratio. Shi et al. [10] performed pore-scale simulation of fuel-rich partial combustion with detailed kinetics in three-dimensional arrangement of connected cylinders, considerable heat recirculation by the thermal radiation in the flame zone was predicted by the model.

Numerical simulation of similar applications on porous media and thermal process has been extensively conducted [11,12,13,14,15]. These papers focused on the slot impingement techniques and they analyzed different turbulence models and thermal radiation model showing the strengths and the weakness for each them. In fact, it is clear that turbulence regime are often considered for application similar to the field of filtration combustion. Moreover, it was found that the pressure loss can not be ignored when the flow velocity in porous media is large. Filtration combustion technology has achieved important applications in high-temperature synthesis [16,17,18].

The single global reaction mechanism does not consider all the ways to produce hydrogen and carbon monoxide in super-rich mixtures. The use of detailed chemical mechanisms is a common method to improve the accuracy of the main combustion products prediction. However, the reduced or detailed chemical reaction mechanism includes dozens of components and hundreds of chemical reactions, which brings great challenges to numerical simulation [2]. These mechanisms are commonly used in modeling of filtration based on the volume average method [7,9,19]. Nevertheless, modeling transient combustion in random structure of packed bed is challenging problem due to the huge computational cost [2], the single global reaction mechanism was widely used by the researchers to save computational resource [1], only few studies adopted the more complex reduced scheme or detailed chemical reaction mechanisms [20].

The aim of this work is to present pore-scale study of gas flow and heat recirculation in random packed bed, the bed is generated by EDEM software and CH₄/air combustion is treated with single step irreversible reaction, solid surface radiation is computed using the DO model, the flow, combustion and heat recirculation in packed bed are analyzed. This helps to deeper understand the behaviors of packed bed burner at pore-scale and obtain local information, such as flow, combustion and and heat transfer processes.

2. Physical Model and Dimension

The porous burner [9] is adopted as the physical model. The inner diameter of the burner was 76 mm and it was consisted of 5.6 mm alumina spheres with bed length of 0.5 m. For the purpose of simplification and saving computational resource, the length and diameter of packed bed combustor is reduced to 350 mm and 38 mm, respectively. The geometric model is reconstructed by EDEM software with the predetermined pellet diameter and burner size. All the diameters of the spheres are reduced to 0.99 times of the original sizes to use gap approach meshing the computational zone. The overall porosity of the packed bed is 0.43. The feasibility of the simplified geometric model will be verified below. As dispicted in in Figure 1, the bed length of 353 mm is composed of 2282 pellets. To eliminate the boundary effect, two free zones located in up- and downstream of the burner are included in the computational zone. Finally, the computational zone covers 38 mm × 389 mm in the horizontal and vertical direction.

2.1. Governing Equation

In order to simplify the problem, this article introduces the following assumptions,

(1) The alumina spheres are chemically inert. Specular reflection was assumed at the tube walls.

(2) The CH₄/air combustion is treated with one-step chemical kinetics [21].

(3) The flow of the gas mixture in the packed bed is assumed to be laminar, gas radiation is not considered.

(4) The heat loss to the ambient through burner walls is not considered.

The inlet velocity of the filtration combustion studied in this paper is very small, and its particle Reynolds number is also rather small, so the influence of turbulence on the flow and combustion is not considered. The effect of turbulent on the filtration combustion needs further study. Heat loss may have a significant effect in the filtration combustion. In this study the heat loss to the ambient is not taken into account due to the well insulation of the combustor.

The mathematic model for filtration combustion in random packed bed is as follows [20],

Continuity equation

$$\frac{\partial {\rho }_{\mathrm{g}}}{\partial t}+\nabla \cdot ({\rho }_{g}v)=0$$

(1)

Momentum equation

$$\frac{\partial ({\rho }_{\mathrm{g}}v)}{\partial t}+\nabla \cdot ({\rho }_{\mathrm{g}}vv)=-\nabla \mathrm{p}+\nabla \cdot (\mu \nabla v)$$

(2)

Species conservation equation

$$\frac{\partial ({\rho }_{\mathrm{g}}{Y}_{\mathrm{i}})}{\partial t}+\nabla \cdot ({\rho }_{\mathrm{g}}v{Y}_{\mathrm{i}})-\nabla \cdot ({\rho }_{\mathrm{g}}{D}_{\mathrm{i}}\nabla Y_{\mathrm{i}})-{\omega }_{\mathrm{i}}{W}_{\mathrm{i}}=0$$

(3)

Gas energy equation

$$\frac{\partial ({\rho }_{\mathrm{g}}{c}_{\mathrm{g}}{T}_{\mathrm{g}})}{\partial t}+\nabla \cdot ({\rho }_{\mathrm{g}}{c}_{\mathrm{g}}v{T}_{\mathrm{g}})=\nabla \cdot ({\lambda }_{\mathrm{g}}\nabla T_{\mathrm{g}})+{\displaystyle \sum _{i=1}^n{\dot{\omega }}_{\mathrm{i}}}{h}_{\mathrm{i}}{W}_{\mathrm{i}}$$

(4)

The chemical reaction for CH₄ is expressed as [21],

$${\dot{\omega }}_{{\mathrm{CH}}_4}=A{(Y_{\mathrm{CH}4}/W_{\mathrm{CH}4})}^{0.2}{(Y_{\mathrm{O}2}/W_{\mathrm{O}2})}^{1.3}\exp (-E/R{T}_{\mathrm{g}})$$

(5)

It is noted that a single global reaction mechanism for methane combustion in random structure of packed bed is adopted in this study to capture the physics of the flow field in a simple manner. It is a very challenging problem with reacting flow and huge number of grids. We select this mechanism to save computational resource and the drawback of this mechanism will be discussed in the discussion part.

Solid energy equation

$$\frac{\partial ({\rho }_{\mathrm{s}}{c}_{\mathrm{s}}{T}_{\mathrm{s}})}{\partial t}+\nabla \cdot ({\lambda }_{\mathrm{s}}\nabla T_{\mathrm{s}})=0$$

(6)

2.2. Boundary Conditions

Burner inlet

$$T_{\mathrm{g}}=300\mathrm{K},u_{\mathrm{g}}=u_{\mathrm{g},\mathrm{i}\mathrm{n}},Y_{\mathrm{C}{\mathrm{H}}_4}=Y_{\mathrm{C}{\mathrm{H}}_4}{}_{,\mathrm{i}\mathrm{n}},Y_{{\mathrm{O}}_2}=Y_{{\mathrm{O}}_2}{}_{,\mathrm{i}\mathrm{n}}$$

(7)

Burner outlet

$$\frac{\partial T_{\mathrm{g}}}{\partial \mathrm{z}}=\frac{\partial T_{\mathrm{s}}}{\partial \mathrm{z}}=\frac{\partial Y_{\mathrm{i}}}{\partial \mathrm{z}}=0$$

(8)

The heat loss from solid radiation to the surrounding is calculated by the following formula,

$${\lambda }_s\frac{\partial T_{\mathrm{s}}}{\partial z}=-{\epsilon }_{\mathrm{r}}\sigma (T^4{}_{\mathrm{s},\mathrm{in}/\mathrm{out}}-T_0{}^4)$$

(9)

Burner wall

The non-slip and adiabatic boundary conditions are applied in the burner wall.

Interfacial of solid-fluid surface [20],

$$w=0,T_{\mathrm{g}}=T_{\mathrm{s}},-{\lambda }_{\mathrm{g}}\frac{\partial T_{\mathrm{g}}}{\partial n}=-{\lambda }_{\mathrm{s}}\frac{\partial T_{\mathrm{s}}}{\partial n}+q_{\mathrm{net}}$$

(10)

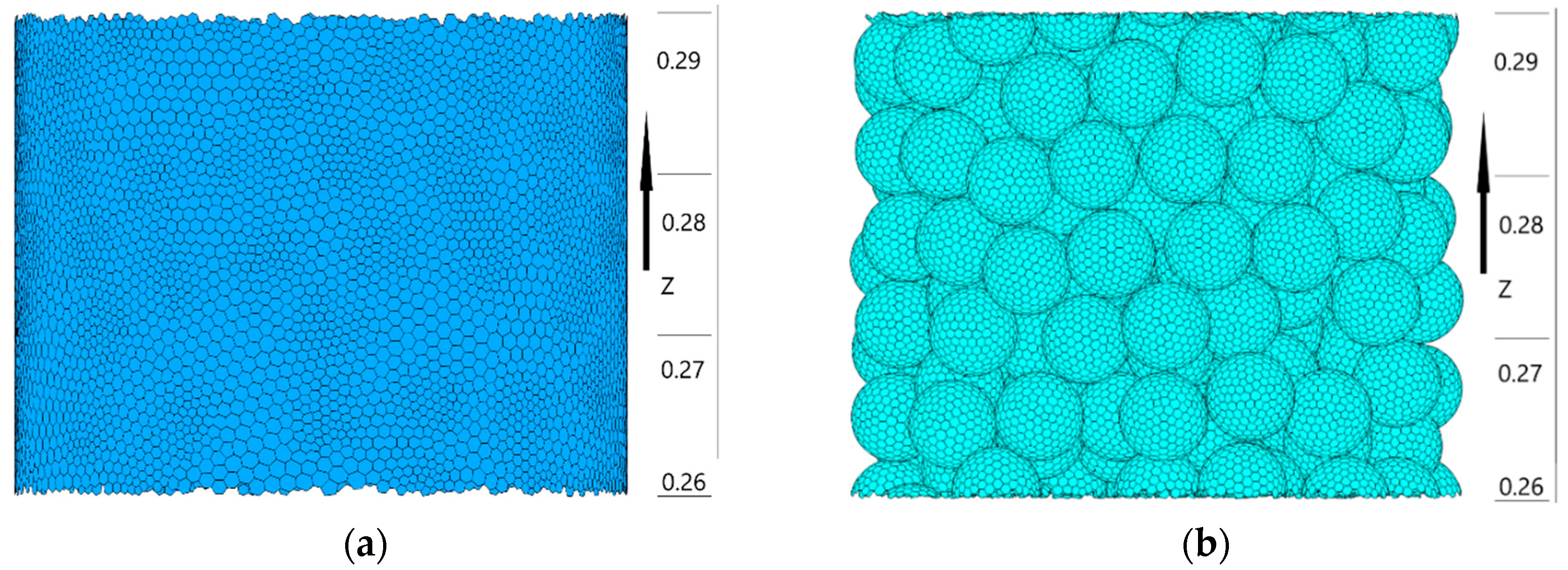
2.3. Mesh, Initial Conditions and Solution Method

The previous study by Yakovlev et al. [20] showed that there are steep temperature gradients and strong convective heat transfer between gas and solid phase in the flame region. Meanwhile, extensive radiation heat exchange occurs between the solid surfaces around the combustion zone. The structure of three-dimensional random sphere packed bed is complex, and the flow area changes constantly when the fluid flows in it, while the two clear zones are simple structures of cylindrical. Taking these factors into consideration, different types and sizes of cells are used in the subzones, hexahedral cell is used in two clear zones, while polyhedral cell is adopted in porous zone, using three prism layers in the fluid sides. Similarly, three boundary layers are used on the burner wall. The independency on mesh number was verified by comparing thermal wave propagation for u_g = 0.43 m/s across the packed bed obtained by using three different grid systems with total 3,100,000 cells, 3,700,000 cells and 4,100,000 cells. Based on three kinds of calculation accuracy, the grid system with 3,700,000 cells was chosen in final computation. For the sake of clarity, only part of the cells with enlarged scale is shown in Figure 2. To simulate the ignition, solid temperatures at t = 0 along the flow direction are specified to be same values as the experiments [9]. The governing equations are solved by the software Fluent 15.0. The coupling of pressure and velocity is solved by SIMPLE algorithm. The second-order upwind method was used to discretize the differential equations.

The time step is specified as 0.1s. The criterion for the convergence of the species equation is that the residual is 1 × 10⁻³, while the criterion for the convergence of other equations is 1 × 10⁻⁶. Gas physical properties are specified as a function of temperature and composition, while solid physical properties come from [19,22]. The main physical parameters of the solid are shown in

Table 1. Properties of Al₂O₃ pellets [19,22].

Nomenclature
${\rho }_{\mathrm{s}}$	3891
cs	33 (293 K), 11.4 (773 K), 7.22 (1273 K), 6.67 (1473 K), 6.34 (1673 K), 6.23 (1773 K)
${\lambda }_{\mathrm{s}}$	755 (293 K), 1165 (773 K), 1255 (1273 K), 1285 (1473 K), 1315 (1673 K), 1330 (1773 K)
${\epsilon }_{\mathrm{r}}$	0.4

. The properties of gas mixture are function of mass fraction of species and gas temperature.

3. Results and Discussion

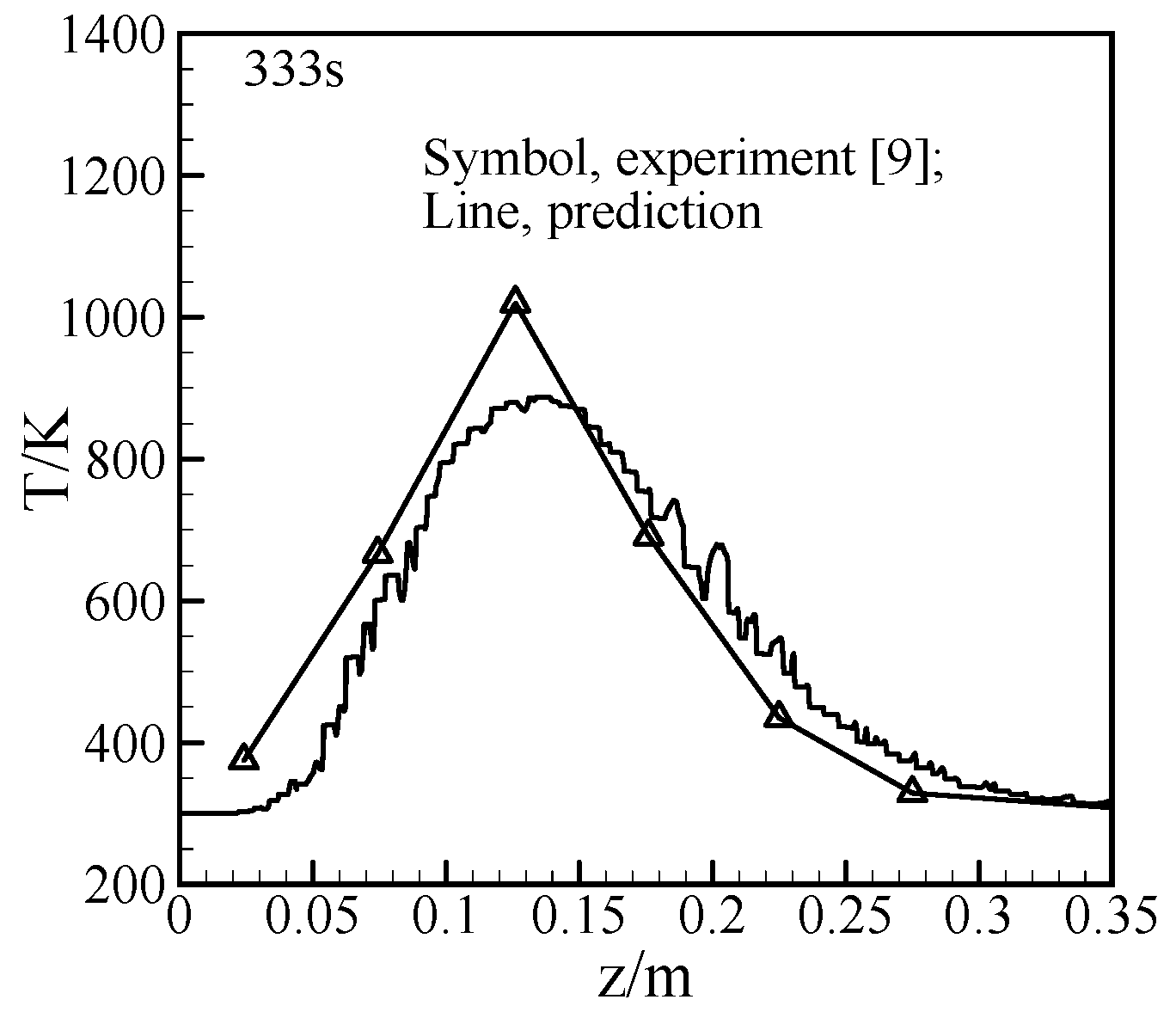
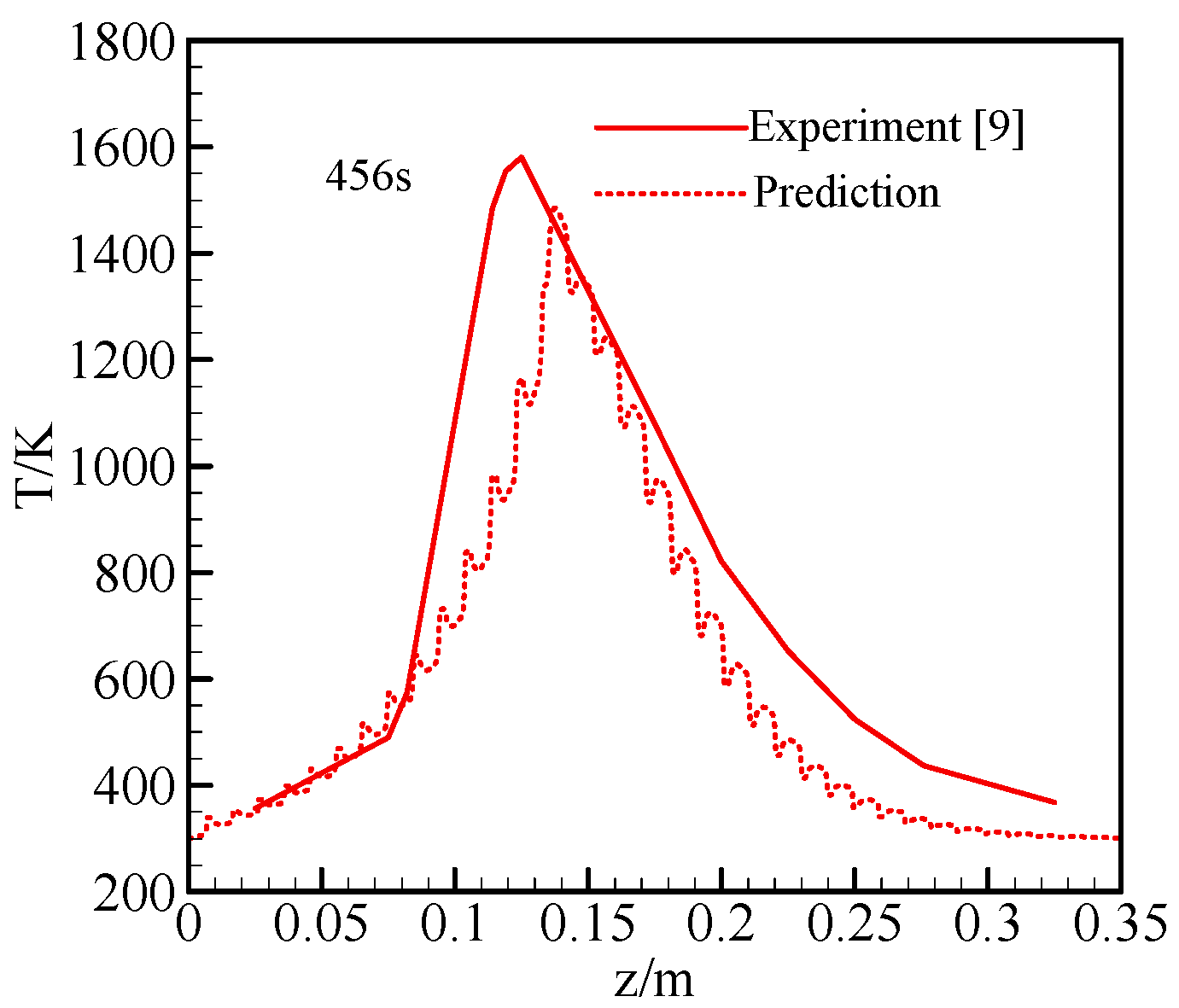
3.1. Model Validation

The properties of the alumina pellets are from the Refs. [19,22]. To verify the solid properties selection and the model, the predicted temperatures along the center line of the combustor are shown in Figure 3, the experimental values are also illustrated for comparison. Thermal wave propagation refers to the temperature propagation in the preheated packed bed when only air passes through the packed bed. We first verify solid properties selection by comparison the predicted thermal wave with experiments for air velocity at t = 333 s. The thermal wave speed ut was expressed as [9],

$$u_{\mathrm{t}}=\frac{\epsilon {\rho }_{\mathrm{g}}{c}_{\mathrm{g}}{u}_{\mathrm{g}}}{(1-\epsilon ){\rho }_{\mathrm{s}}{c}_{\mathrm{s}}}$$

(11)

From Equation (11), one can see that u_t is proportional to the ratio between the gas thermal capacity ${\rho }_{\mathrm{g}}{c}_{\mathrm{g}}$ and solid thermal capacity ${\rho }_{\mathrm{s}}{c}_{\mathrm{s}}$ and reasonable agreement between the predicted results and experimental values is observed in Figure 3. The properties of the gas phase are well-known, this means that the selection of solid phase properties is appropriate. Figure 4 shows the predicted solid temperatures along the center line of the combustor as well as experiment values for u_g = 0.43 m/s at t = 456 s. We find wave-like combustion wave propagation, the deviation between the predictions and experiments is small, this verifies that the present model is appropriate.

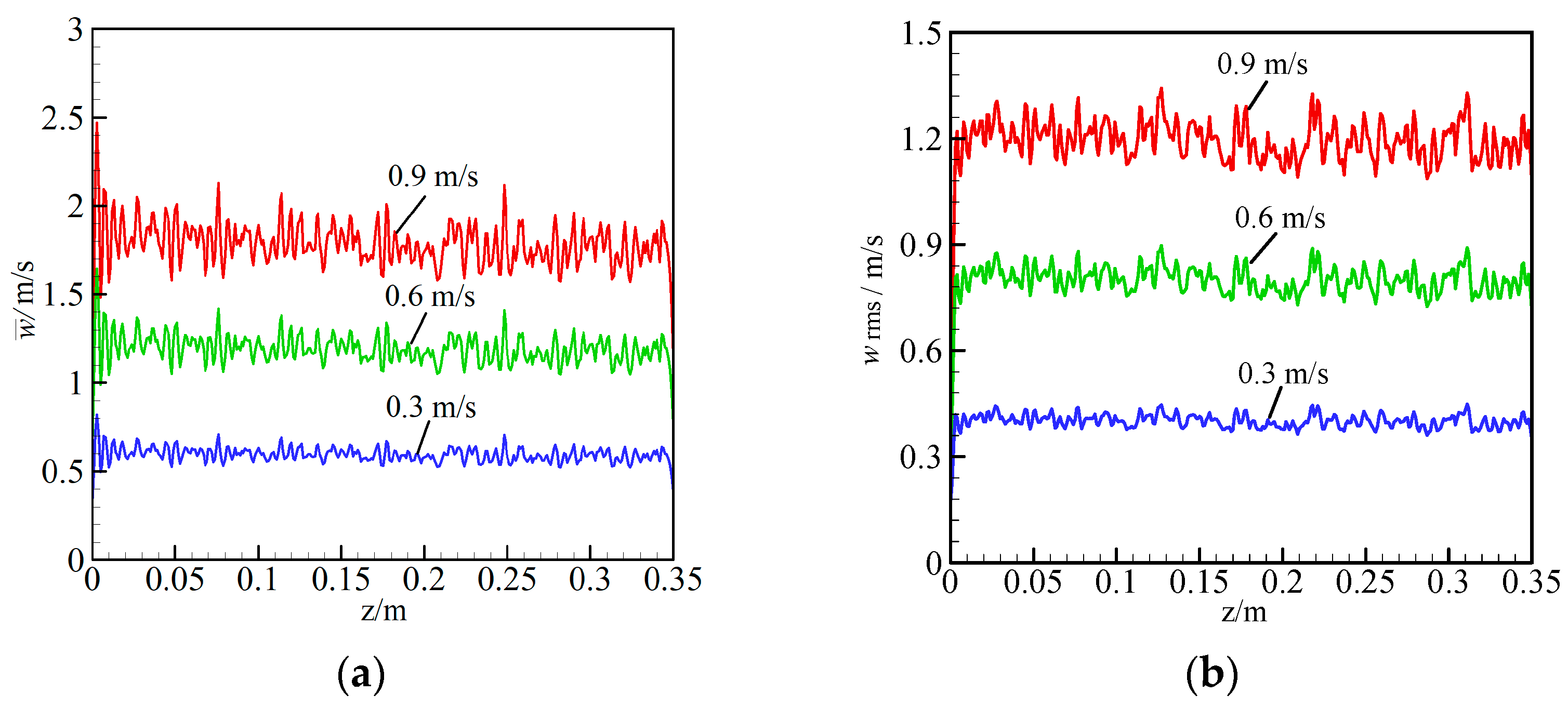
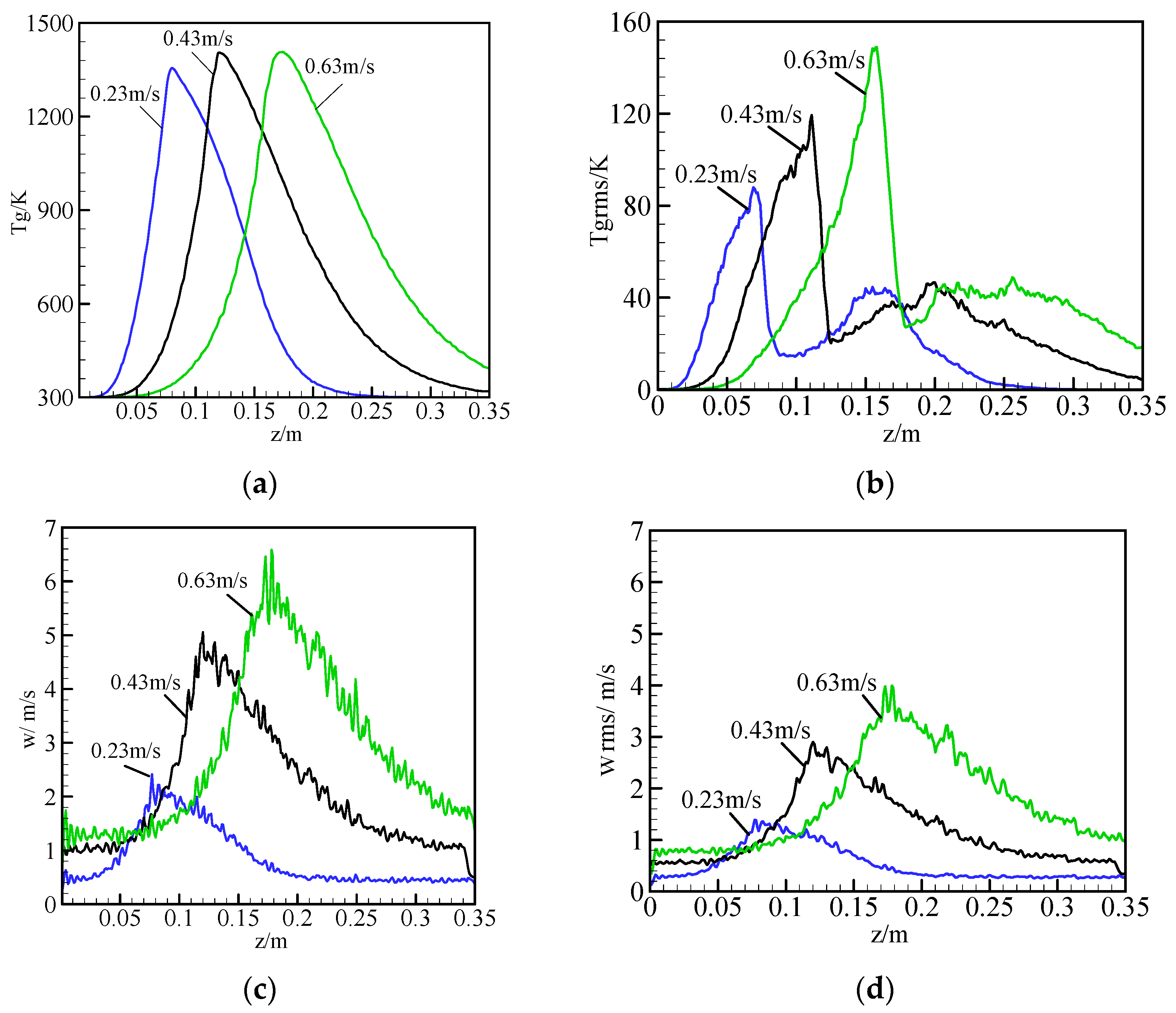
3.2. Variation of Variables in Packed Bed

In Figure 5 the predictions of major parameters in cross section of the burner (y = 0) are shown for u_g = 0.63 m/s at t = 734 s. As shown in Figure 5a,b, the mass fraction of methane decreases sharply from 0.009 to almost zero in a short distance, the methane is almost exhausted due to the lean methane/air mixture. Meanwhile, the mass fraction of CO₂ increases suddenly to its maximum in this short distance. The distribution of reaction rate of methane and reaction heat is inhomogeneous and their shapes are V-shape with their lowest points towards the direction of the fresh mixture as shown in Figure 5c,d. It is noted that the chemistry is treated with a single global reaction and a very narrow flame thickness is predicted by the present model. The prediction by Hsu and Matthews [23] showed that the combustion temperature was over-predicted compared to results by the multi-step reaction mechanism. They pointed out that it was necessary to use multi-step reaction kinetic for accurate prediction of temperature profile, energy release rate. The influence of reaction mechanism on the combustion characteristics such as combustion temperature, flame propagation speed needs further study and this is one of our further work.

After careful observation, we find that the distributions of mass fraction of methane, CO₂, reaction rate of methane and reaction heat in the flame front are very similar and they are all V-shape.

Great change of the axial velocity in the burner is observed in Figure 5e. The distribution of the axial velocity is unform in the clear zone near the burner inlet, and the axial velocity is increased as soon as the mixture enters the zone of porous media due to the decrease of flow area. The mixture velocity is zero at the zones where they are occupied by the solid phase, while the axial velocity is increased. In the pores of the solid framework, then the axial velocity is further increased in the preheating zone owing to the increased gas temperatures by the convection between inter-phase, the maximum mixture velocity is observed near the flame front, this is caused by the heat release in the reaction zone.

From the temperature distributions (Figure 5f), one can see that the flame front locates at about z = 0.29 m. It is observed in Figure 5f that preheating zone covers a wide region in the flow direction and this is the characteristic of porous media combustion compared to the conventional premixed combustion. Heat recirculation occurs by multi-modes heat transfer methods, in the combustion zone chemical reaction releases reaction heat. As a result, flow and thermal non-equilibrium occurs for inter- and intra-phase. The pellets around the flame zone are heated by convection and surface radiation exchanges occurs between solid phases, thus part of the reaction heat is transferred to the flame front by the conduction and radiation of solid phase. As shown in Figure 5f in the upstream of the flame front, solid temperature is higher than the that of gas, then the gas temperature reaches its maximum in the flame front, while gas temperature is greater that that of solid in the downstream of the flame front. It is noted that the equivalence ratio of 0.15 for methane/air cannot support the flame for conventional combustion. However, stable combustion is observed in porous media and this is attributed to heat recirculation through the solid skeleton. We will discuss the heat recirculation in detail in the next section.

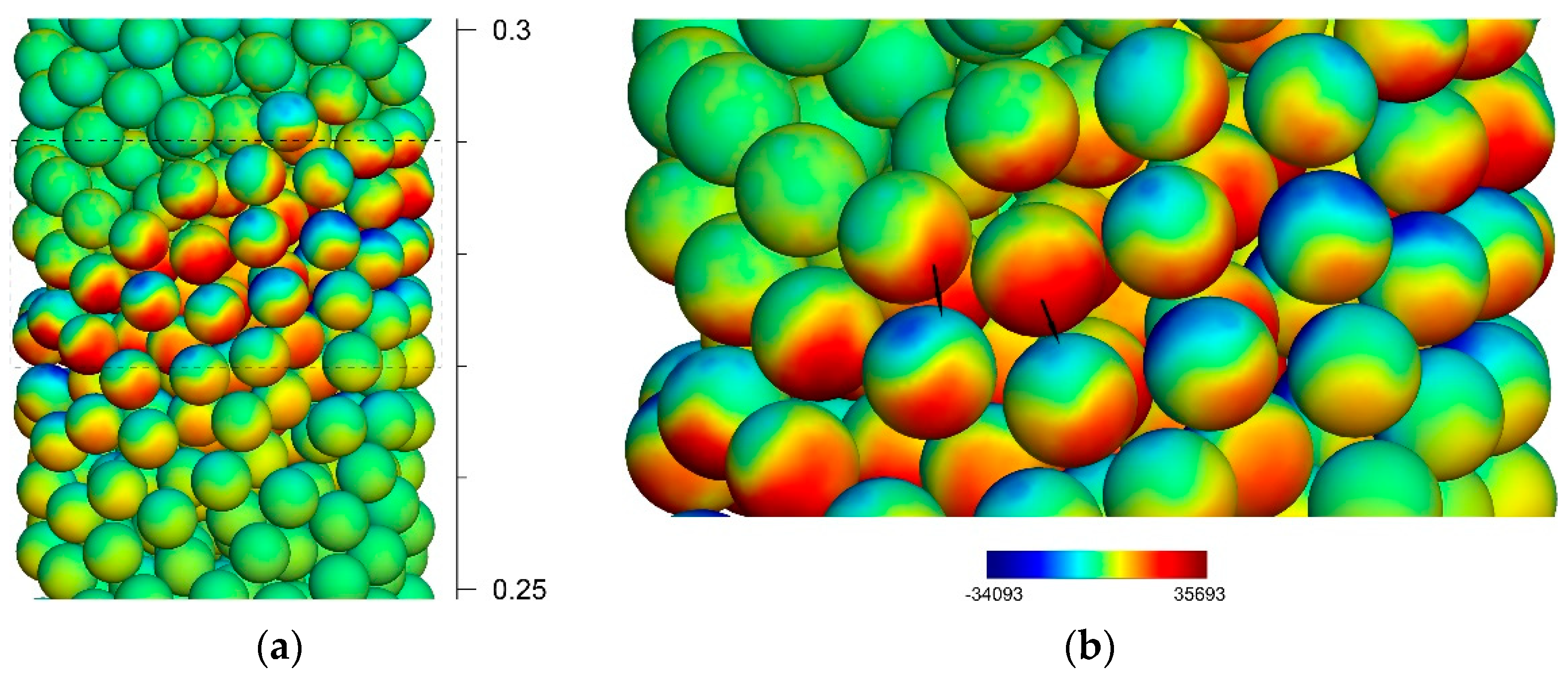
3.3. Heat Recirculation in Pore-Scale

It has been verified by volume-averaged approach that solid conduction and radiation play a significant role in the heat recirculation process in packed bed. For this approach, the thermal radiation is taken into account by Rosseland method, the porous media is considered as optically thickness media and radiation exchange is treated with effective radiation conduction. It was shown by this model that the radiation flux is continuous, its distribution is wave-like and the maximum radiation heat flux is located in the reaction zone. However, for the 3D random packed bed, the pellets are optically opacity and the radiation exchange is blocked by the solid media. In this study, the radiation is computed by solving the radiative transfer equation, thus we can examine the detailed radiation heat flux over the pores.

Figure 6 shows the radiation heat flux around the flame front, it is observed that the maximum radiation heat flux is located around the flame zone as shown in Figure 6a, for the sake of clarity the zone of maximum radiation heat flux is enlarged in Figure 6b. It is shown that this zone covers two or three adjacent pellets along the flow direction and the maximum radiation heat flux is located in the windward side of the pellets, this means that the direction of net radiation heat flux is opposite to the mixture flow direction and that the radiation heat transfer is layer-by-layer due to opaque media. The pore-scale simulation allows observation of radiation heat flux over pores and provides detailed understanding of local phenomena for porous media combustion.

As can be seen from Figure 5d, a large amount of heat is released within pores surrounded by the pellet surfaces, these heat needs to be redistributed in the whole system. Firstly, the temperature of the gas in the combustion region increases, and the temperature of the pellets in the combustion region is increased through convection heat transfer. The heated spheres participate in the heat redistribution through radiative heat transfer and heat conduction. We can clearly see that the direction of the net radiative heat flux is opposite to the direction of gas flow, this is mechanism of heat recirculation by the solid radiation at pore-scale.

3.4. The Non-Equilibrium

We use root mean squares (RMS) of gas mixture velocity of section perpendicular to the flow direction to investigate non-equilibrium content in the burner. The variation of RMS of axial velocity (w_RMS) is computed as [20],

$$\overline{w}=\frac{1}{A}{\displaystyle \sum _{i=1}^{n-1}{w}_{\mathrm{i}}{A}_{\mathrm{i}}}$$

(12)

$$w_{RMS}=\sqrt{\frac{1}{n-1}{\displaystyle \sum _{i=1}^{n-1}{(w-\overline{w})}^2}}$$

(13)

where $\overline{w}$ is average gas velocity, n is total number of cells in the cross-section of burner. The definition of RMS of gas temperature is the same to that of gas mixture velocity.

The content of flow non-equilibrium for cold flow without reaction is first studied. Figure 7 shows the averaged axial velocity ($\overline{w}$) and its root mean square (w_RMS) along the flow direction for three different air velocities. As shown in Figure 7a,b, $\overline{w}$ and w_RMS fluctuate sharply near the inlet of the burner and then the amplitude of the fluctuation becomes relatively moderate along the flow direction for all velocities under investigated. The amplitude of the fluctuation for $\overline{w}$ and w_RMS becomes greater as the mixture is increased. In case of a laminar flow the cross-sectional fluctuations can be explained by the different local porosity, local dead water behind the pellets. This verifies that flow non-equilibrium is one of the essential characteristics of gas flow in porous media and that the content of flow non-equilibrium increases as the flow velocity is increased.

3.5. Effect of Mixture Velocity

Figure 8 presents the influence of mixture velocity on thermal and flow non-equilibrium for u_g = 0.43 m/s and t = 373 s. As illustrated in Figure 8a, the maximum Tg is increased slightly and the flame propagates in the further downstream of the burner with mixture velocity. The maximum value of RMS of Tg is increased and the thickness of the zone of non-equilibrium in the flow direction is widen as the mixture velocity is increased. This indicates that thermal non-equilibrium phenomenon is intensified in the porous burner and the peak content of thermal non-equilibrium is located in the flame front. The influence of mixture velocity on the flow non-equilibrium is similar to that of thermal non-equilibrium. As shown in Figure 8c,d, the distribution of the averaged axial velocity and its RMS are wave-like shape in the burner and their values are constantly fluctuating due to the disturbance by the pellets. On the whole, the distribution curve is same to the distribution of gas phase, this indicates that the gas temperature has the significant influence on the velocity distribution and its RMS value. The axial mixture velocity and its RMS are increasing from burner inlet and reaches their maximums around the flame front, then they are decreased along the flow direction.

4. Conclusions

Three-dimensional pore-scale simulations with reconstructed random pellets for premixed combustion of methane/air mixture in packed bed are performed to investigate the content of non-equilibrium in packed bed. The solid surfaces radiation is taken into account by DO model and the combustion for methane/air combustion is treated with one-step chemical kinetics. The main conclusions are as follows,

(1) Flow non-equilibrium is verified in random packed bed. The increase in gas inlet velocity leads to the increase of the content of flow non-equilibrium in the packed bed. In case of a laminar flow the cross-sectional fluctuations can be explained by the different local porosity, local dead water behind the pellets.

(2) For lean premixed mixture combustion in porous media, the content of flow and thermal non-equilibrium is wave-like shape, the peak value is located in the flame front.

(3) The maximum root mean square of gas temperature is enlarged and the thickness of the zone of non-equilibrium in the flow direction is widen as the mixture velocity is increased.

(4) The radiation heat transfer is layer-by-layer in the flame zone.