Are EDR Devices Undoubtedly Helpful in the Reconstruction of a Road Traffic Accident?
Abstract
:1. Introduction
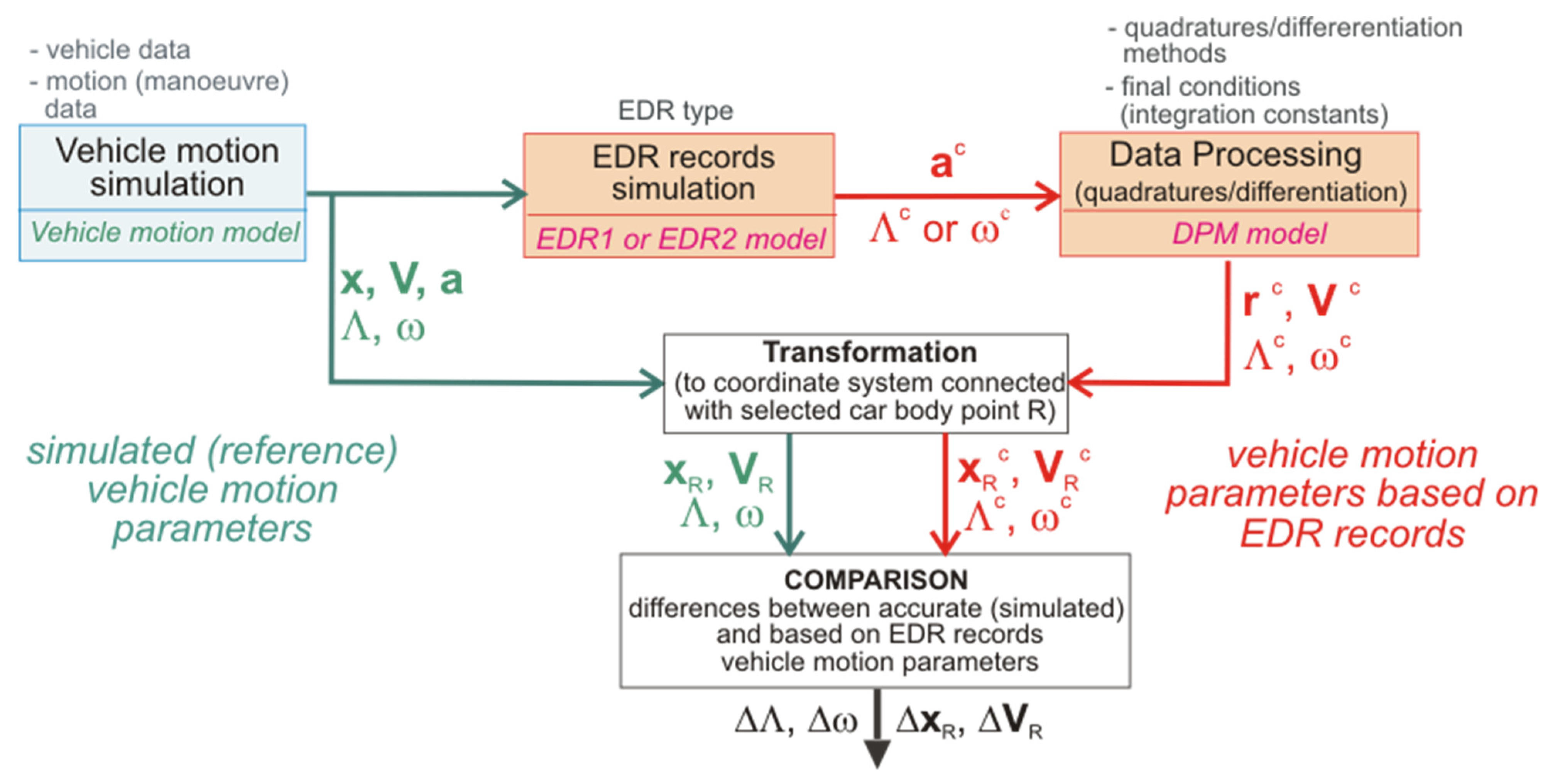
2. Materials and Methods
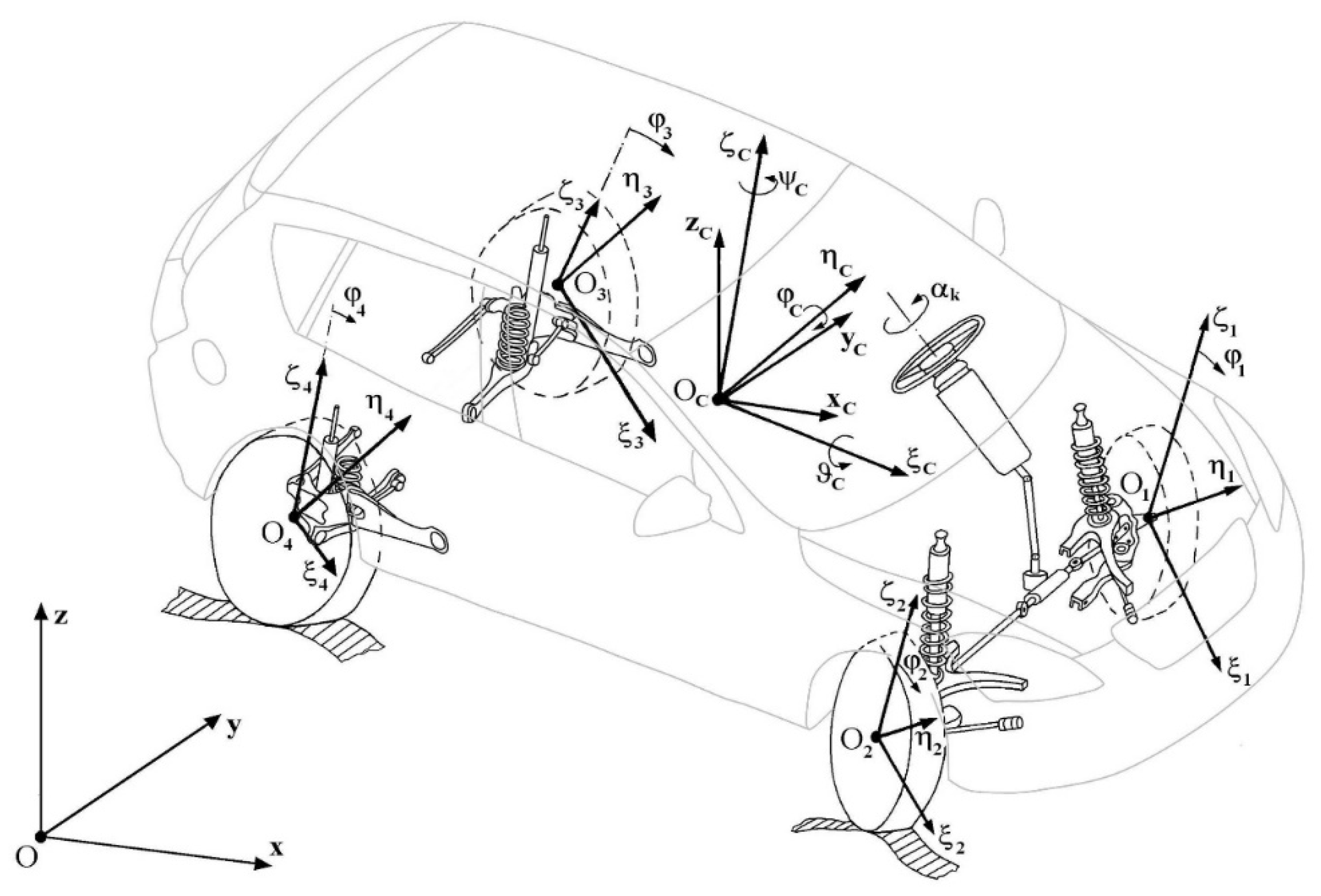
2.1. Vehicle Dynamics Model
- -
- Oxyz—an inertial system, fixed to the road, with the Ox and Oy axes being horizontal and the vertical axis Oz pointing upwards;
- -
- OCxCyCzC—a moving non-inertial system, with its axes being respectively parallel to axes Ox, Oy, and Oz and with its origin situated at the centre of mass of the vehicle body solid Oc;
- -
- moving coordinate systems fixed to the rigid bodies of the model, i.e., body solid (OCξCηCζC) and four road wheels (O1ξ1η1ζ1, O2ξ2η2ζ2, O3ξ3η3ζ3, O4ξ4η4ζ4);
- -
- Auxiliary systems, facilitating the defining of transformation matrices.
- -
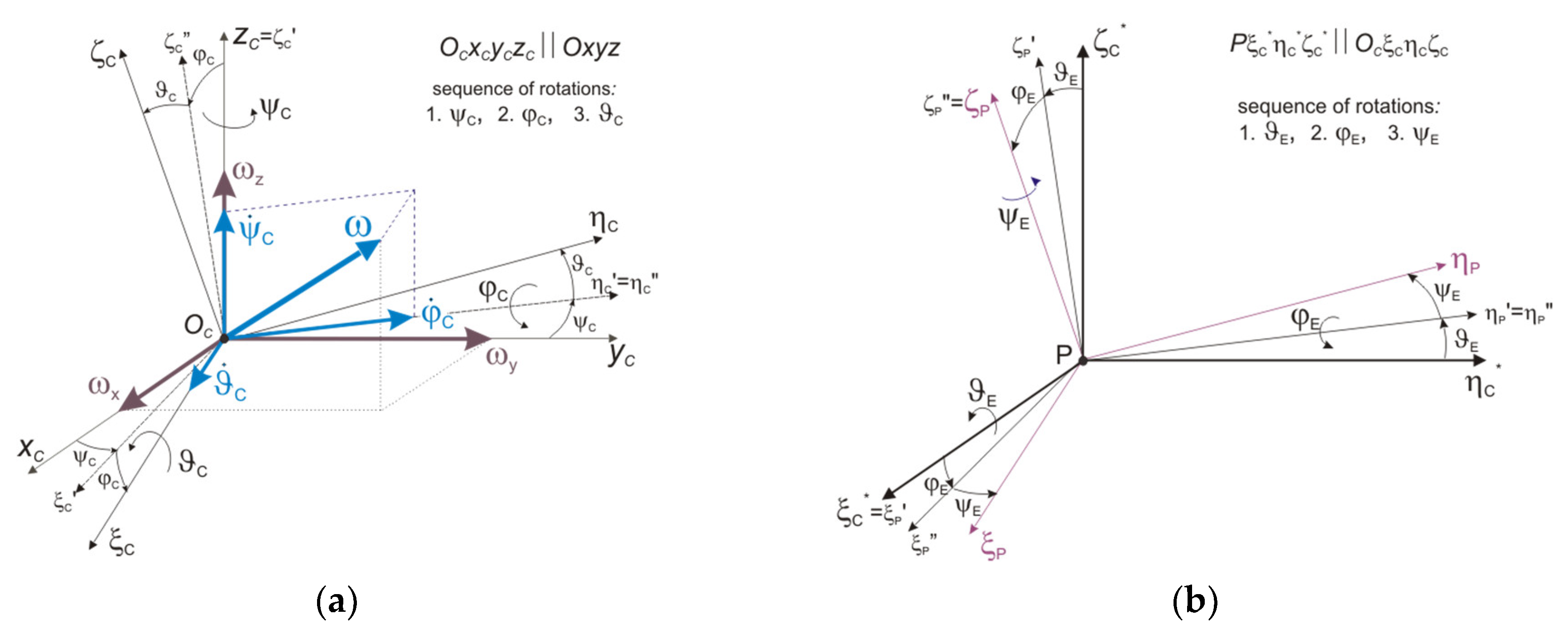
- Yaw angle ψC (rotation about the OCζC axis);
- -
- Pitch angle φC (rotation about the OCηC axis);
- -
- Roll angle ϑC (rotation about the OCξC axis).
- q1 = xOC, q2 = yOC, q3 = zOC—coordinates defining the position of the centre of mass of the vehicle body solid (OC) in the inertial reference system Oxyz;
- q4 = ψC, q5 = φC, q6 = ϑC—coordinates describing the rotation of the vehicle body solid about its centre of mass OC; these are the quasi-Euler (aircraft) angles, i.e., yaw angle, pitch angle, and roll angle, respectively;
- q7 = ζCO1, q8 = ζCO2, q9 = ζCO3, q10 = ζCO4—coordinates describing the motion of points O1, O2, O3, O4 relative to the vehicle body solid in the direction of axis OCζC of the OCξCηCζC coordinate system; to these points, the “unsprung masses” of the suspension system are reduced;
- q11 = ϕ1, q12 = ϕ2, q13 = ϕ3, q14 = ϕ4—angles of rotation of road wheels (front left and right and rear left and right wheel, respectively).
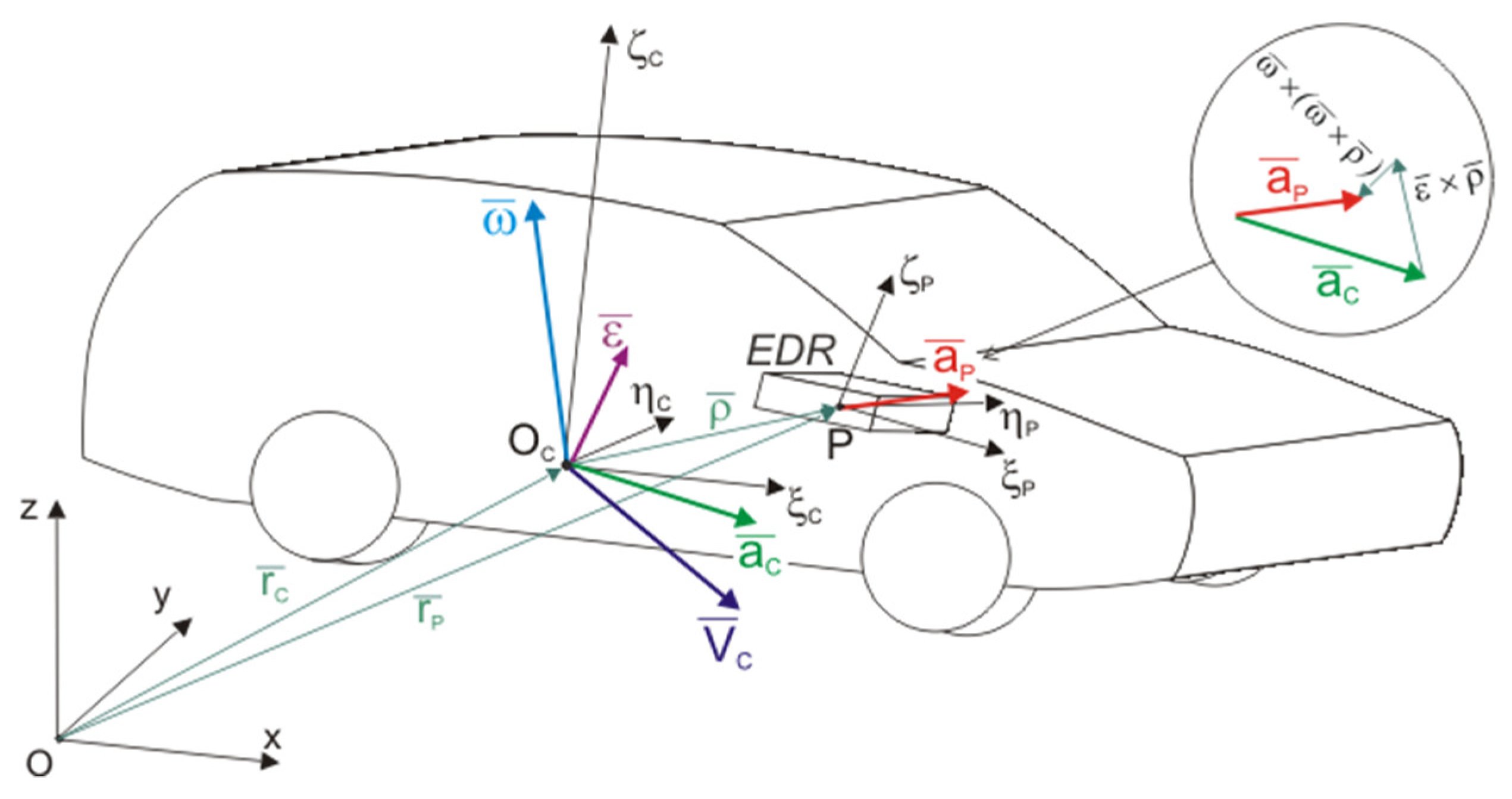
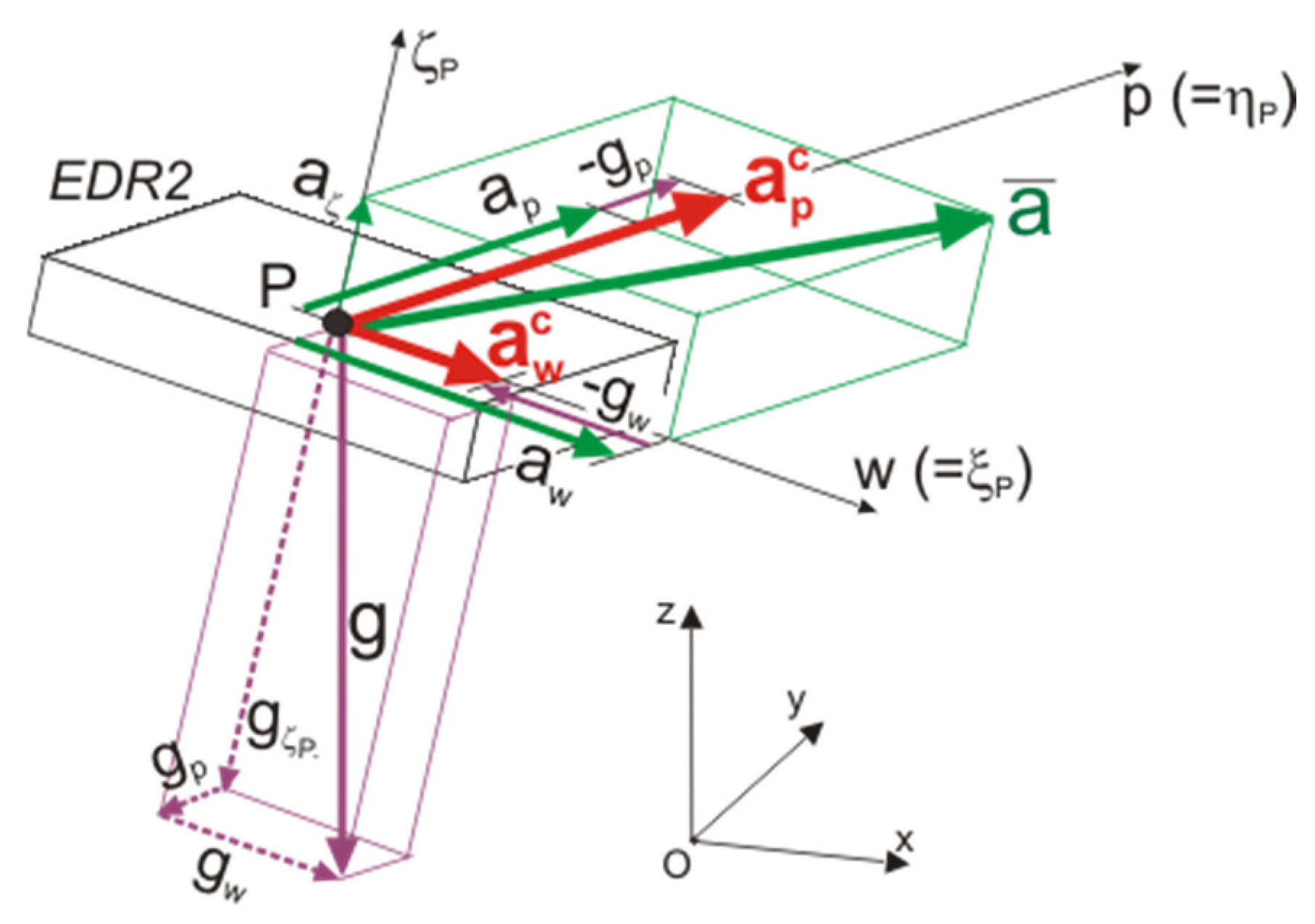
2.2. Model of EDR Records
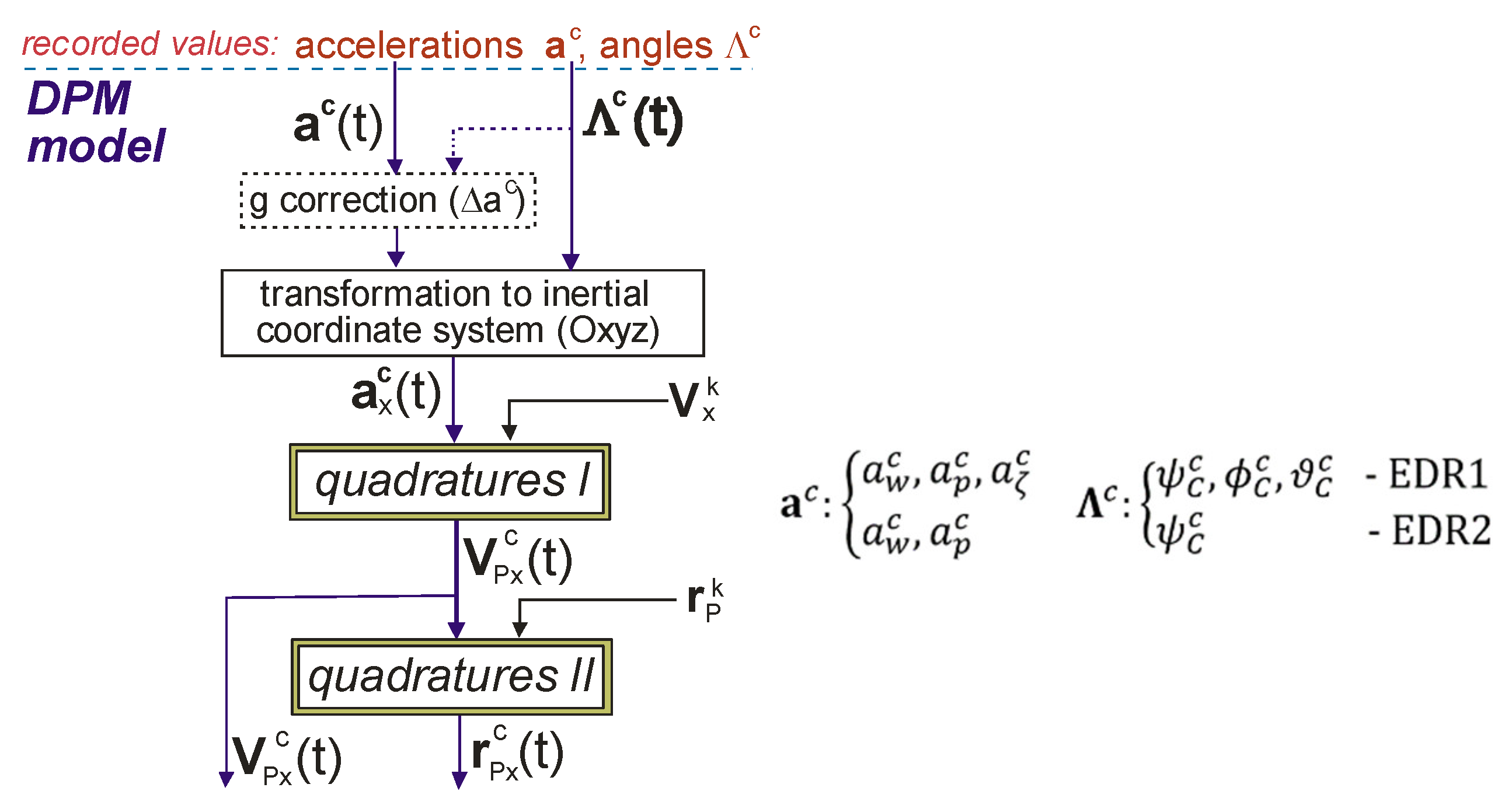
2.3. Reconstruction of Motion (DPM Model)
3. Results
- Straight-line braking;
- Lane-change manoeuvre;
- Entering into a turn;
- Driving in a roundabout (circular motion).
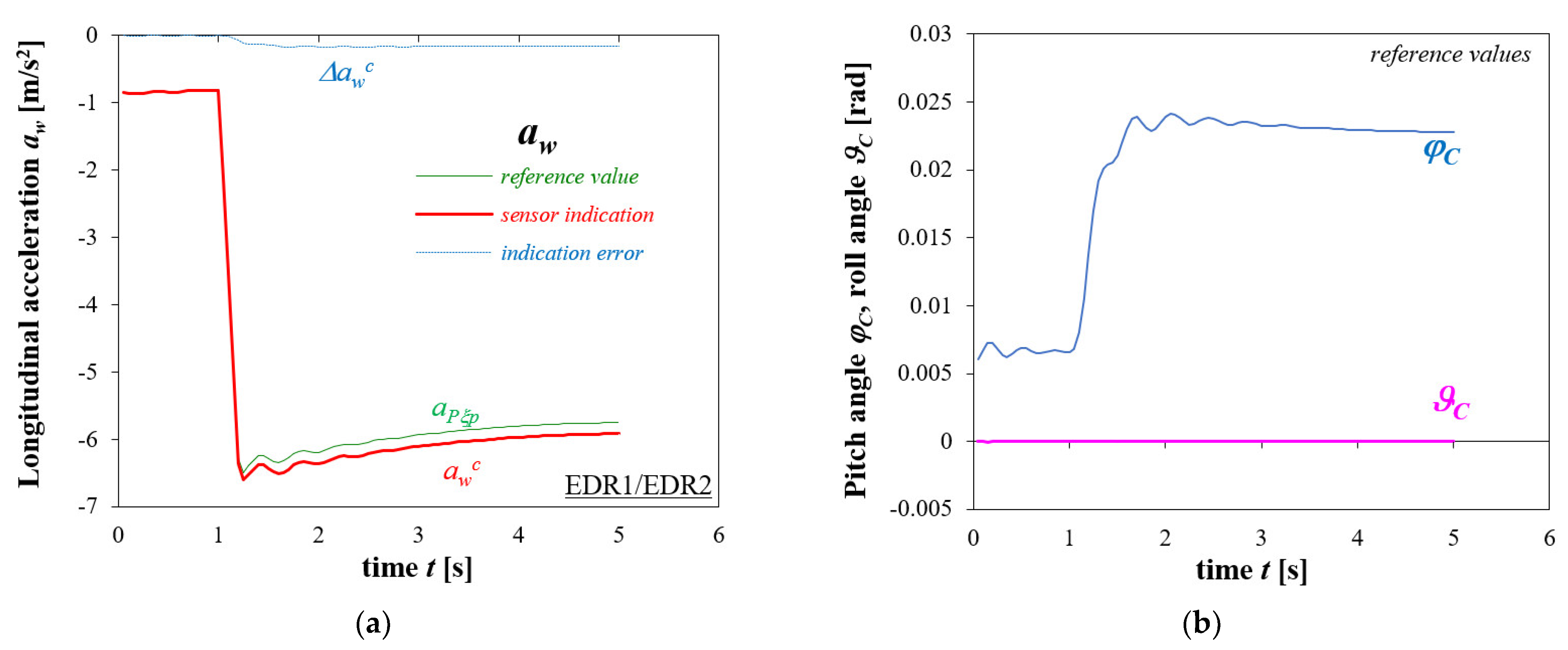
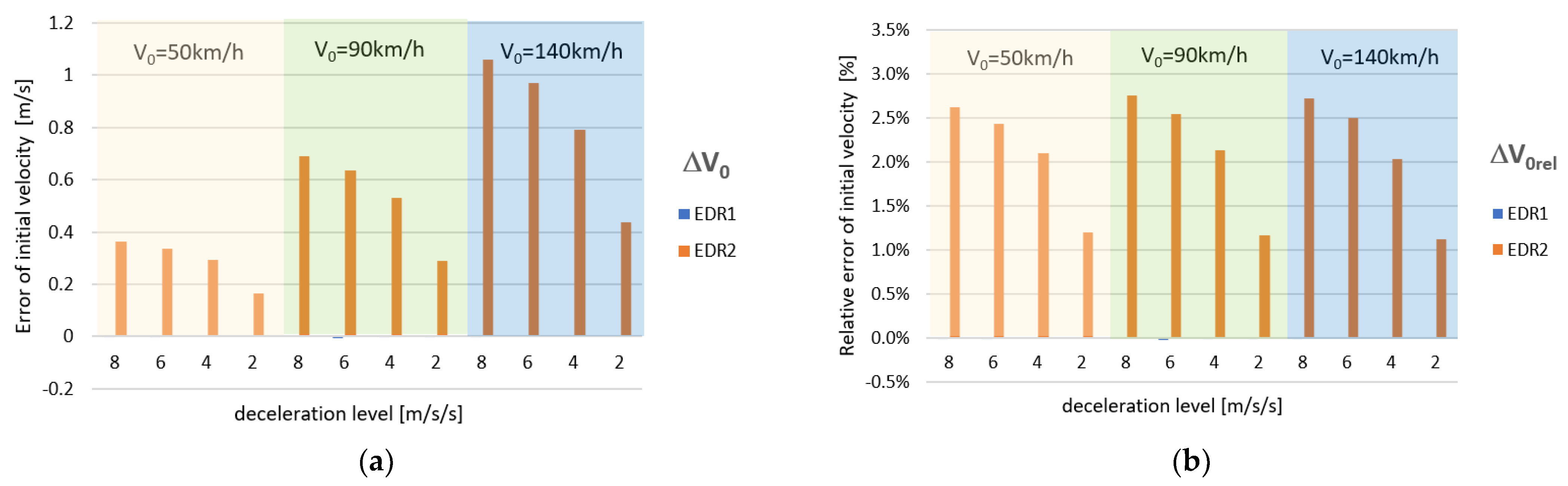
3.1. Straight-Line Braking
3.2. Vehicle Lane-Change Maneuvre
3.3. Entering a Turn
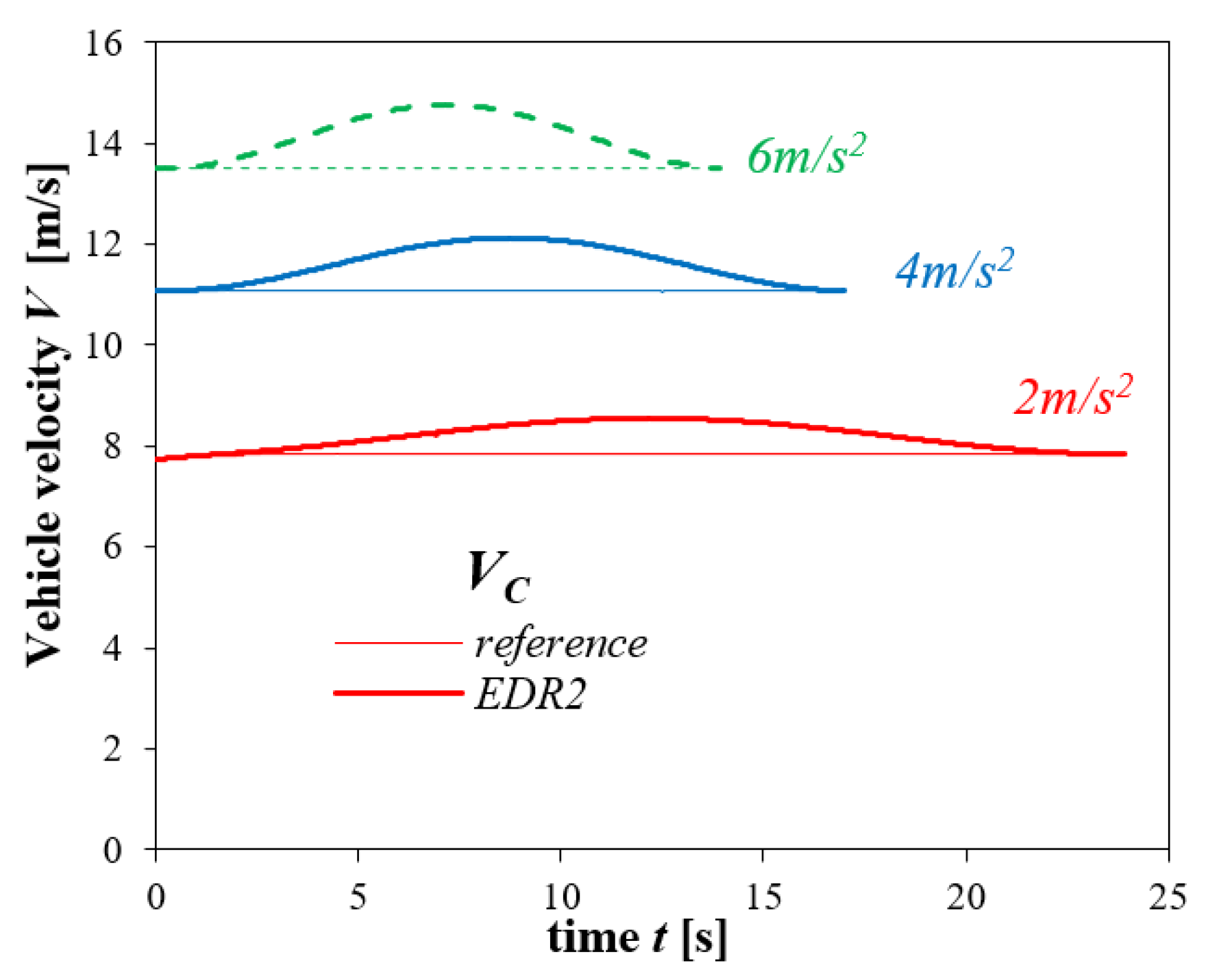
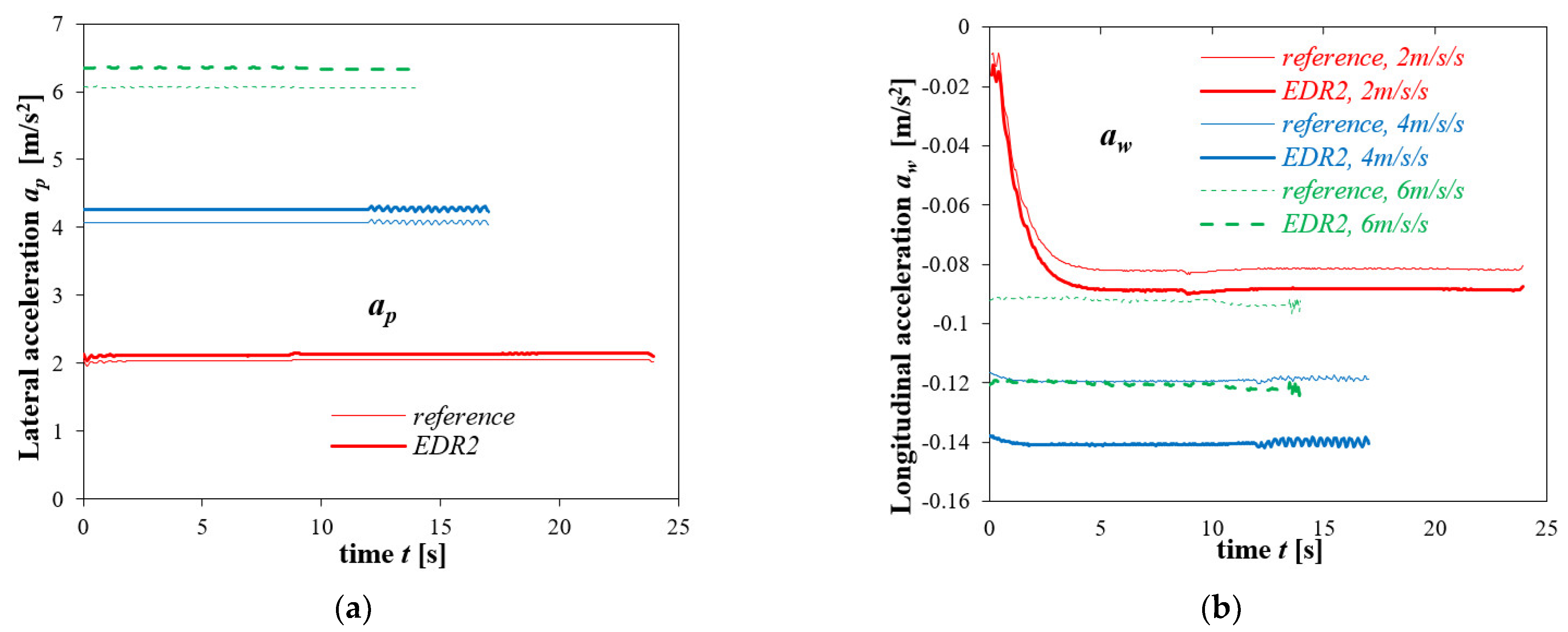
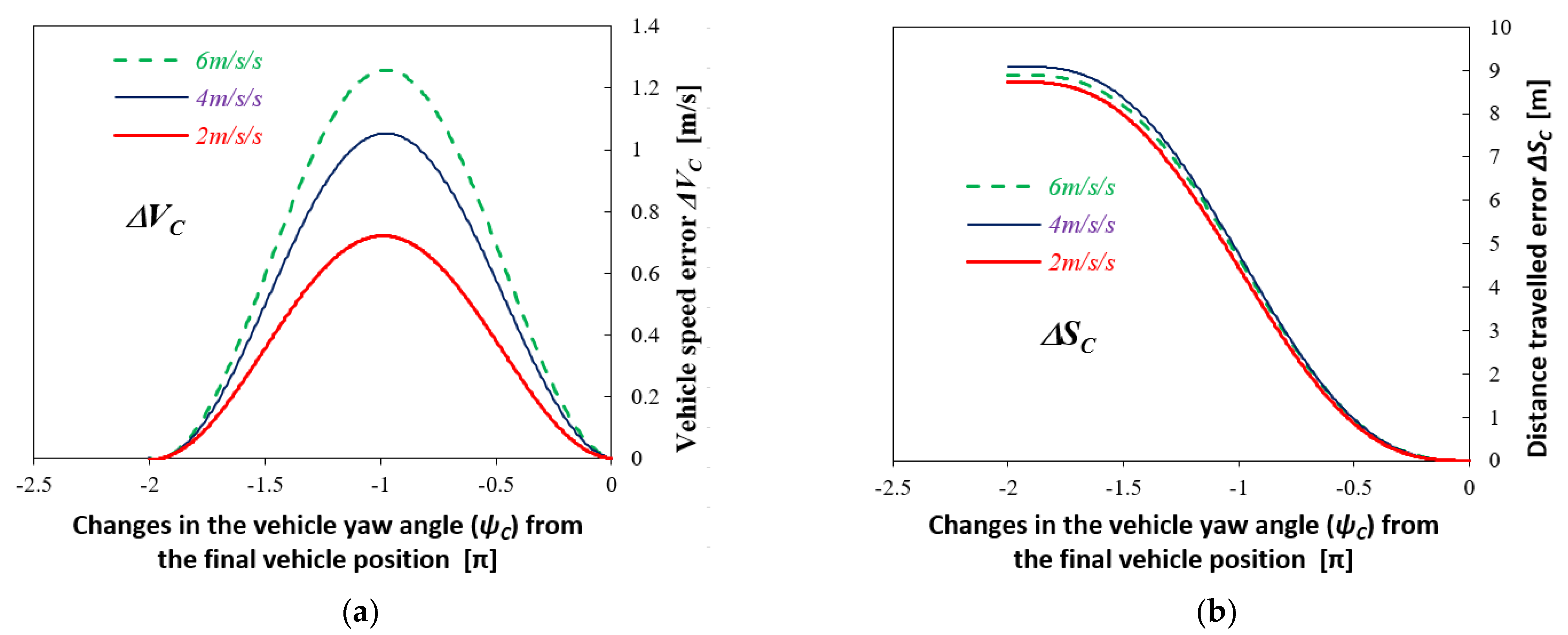
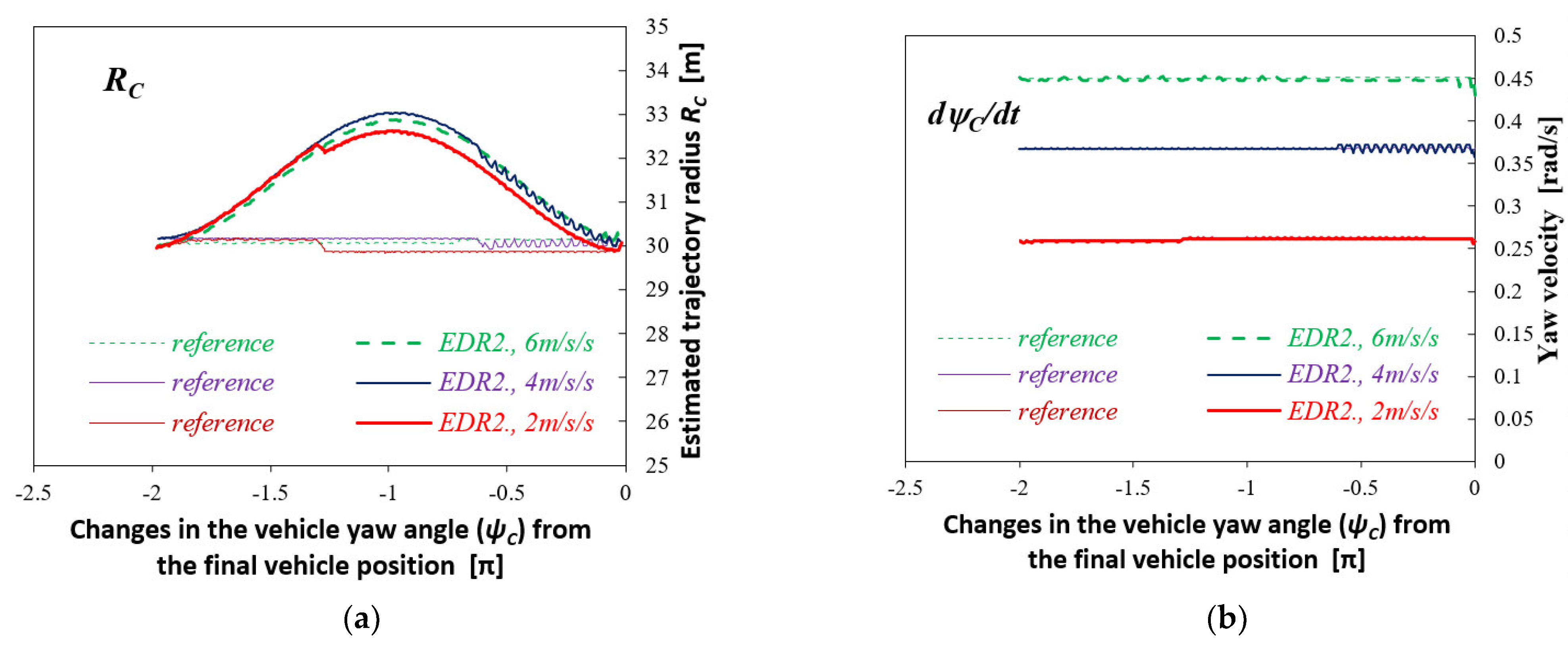
3.4. Driving in a Roundabout (Circular Motion)
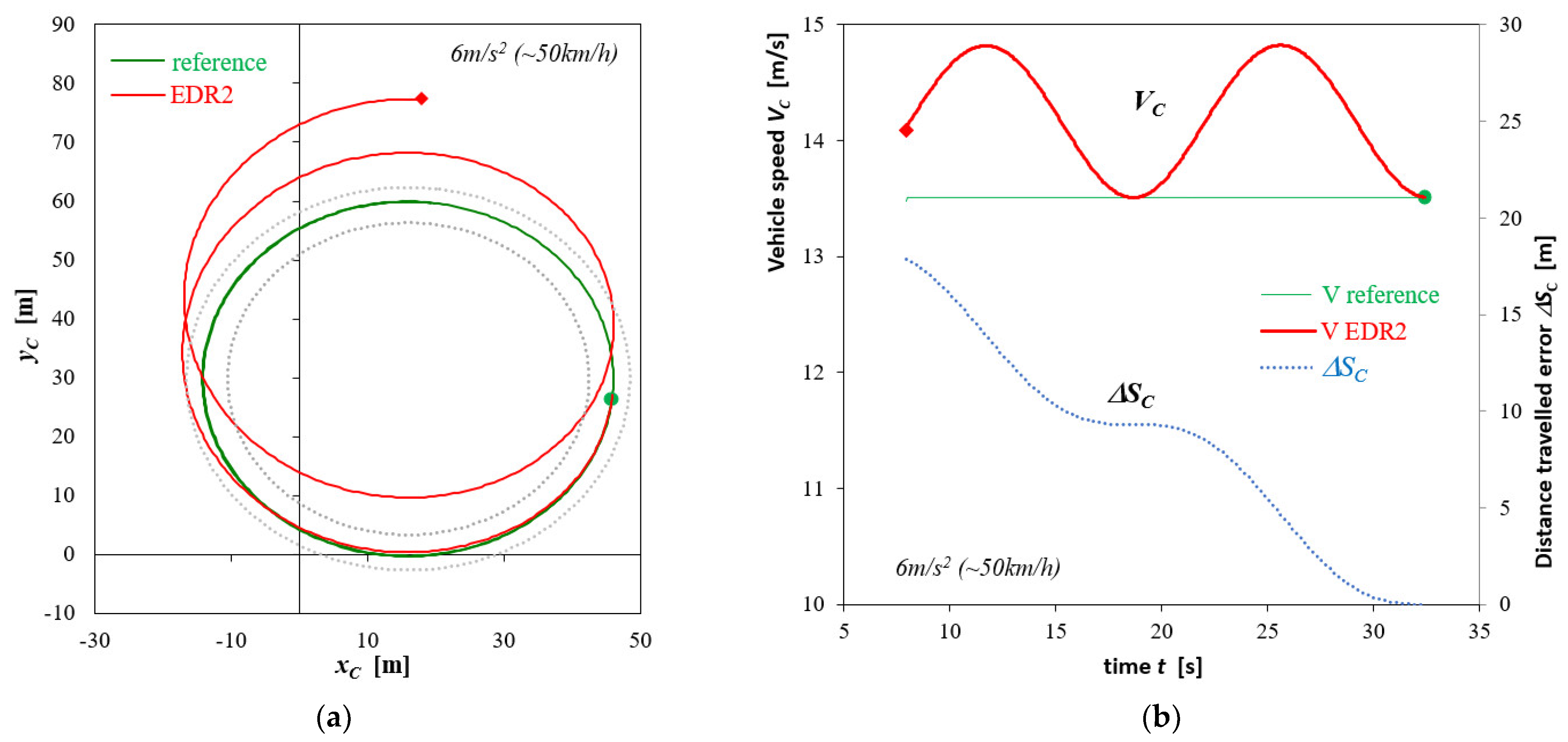
4. Discussion
- -
- In the case of the EDR1-type devices (recording 6 vector components that describe the vehicle motion), the reconstruction results are practically identical with the reference (accurate) data.
- -
- In the case of the EDR2-type devices, the velocities and trajectories may both slightly and significantly differ from the accurate data.
- -
- The qualitative nature of the accident reconstruction errors depends, inter alia, on the vehicle motion type. In the case of straight-line braking, errors arise in determining the initial vehicle velocity and the distance travelled; when curvilinear motion is analysed, deviations from the accurate vehicle trajectory mainly occur.
- -
- In quantitative terms, the errors may be influenced by the intensity of the manoeuvre. In general, the higher intensity is connected with larger reconstruction errors (arising from stronger angular movements of the vehicle body and, in consequence, from bigger errors in the accelerations recorded).
- -
- Another factor that has an impact on the accuracy achieved is the period of time (or the length of the distance travelled) for which the vehicle motion is reconstructed. For short-duration manoeuvres (lasting less than 5 s), good accuracy can be achieved, even if the EDR2 devices are used (with reservations formulated in other conclusions). However, the errors increase with the increasing length of the period for which the motion is reconstructed. Attention should also be paid to the effects reported for the case of circular motion, i.e., a kind of cyclicity of the reconstruction errors.
- -
- A quantitative influence on the accuracy may be exerted by the design and operational features of the vehicle. This concerns the properties that have a considerable impact on the angular movements of the vehicle body solid. The features of particular importance may be suspension system characteristics (e.g., suspension system design, spacing, and stiffness of springs, dry friction, etc.).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U. S. Department of Transportation, National Highway Traffic Safety Administration: Event Data Recorders. 49 CFR Part 563, Docket No. NHTSA-2004-18029. Available online: https://www.nhtsa.gov/fmvss/event-data-recorders-edrs (accessed on 19 August 2021).
- A Proposed Rule by the National Highway Traffic Safety Administration on 12/13/2012, Federal Motor Vehicle Safety Standards; Event Data Recorders. Available online: https://www.federalregister.gov/documents/2012/12/13/2012-30082/federal-motor-vehicle-safety-standards-event-data-recorders (accessed on 19 August 2021).
- A Proposed Rule by the National Highway Traffic Safety Administration on 02/08/2019, Federal Motor Vehicle Safety Standards; Event Data Recorders. Available online: https://www.federalregister.gov/documents/2019/02/08/2019-01651/federal-motor-vehicle-safety-standards-event-data-recorders (accessed on 19 August 2021).
- Regulation (EU) 2019/2144 of the European Parliament and of the Council of 27 November 2019 on Type-Approval Requirements for Motor Vehicles and Their Trailers, and Systems, Components and Separate Technical Units Intended for Such Vehicles, as Regards Their General Safety and the Protection of Vehicle Occupants and Vulnerable Road Users. Available online: https://eur-lex.europa.eu/eli/reg/2019/2144/oj (accessed on 19 August 2021).
- Malinová, K.; Kasanický, G.; Podhorský, J. Usage of Digital Evidence in the Technical Analysis of Traffic Collisions. Transp. Res. Procedia 2021, 55, 1737–1744. [Google Scholar] [CrossRef]
- Iyoda, M.; Trisdale, T.; Sherony, R.; Mikat, D.; Rose, W. Event Data Recorder (EDR) Developed by Toyota Motor Corporation. SAE Int. J. Trans. Saf. 2016, 4, 187–201. [Google Scholar] [CrossRef]
- Smith, G. Reconstructing Vehicle and Occupant Motion from EDR Data in High Yaw Velocity Crashes. In SAE Technical Paper; 2021-01-0892; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Vandiver, W.; Anderson, R.; Ikram, I.; Randles, B.; Furbish, C. Analysis of Crash Data from a 2012 Kia Soul Event Data Recorder. In SAE Technical Paper; 2015-01-1445; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Ruth, R.; Bartlett, W.; Daily, J. Accuracy of Event Data in the 2010 and 2011 Toyota Camry During Steady State and Braking Conditions. SAE Int. J. Passeng. Cars—Electron. Electr. Syst. 2012, 5, 358–372. [Google Scholar] [CrossRef]
- Tsoi, A.; Hinch, J.; Ruth, R.; Gabler, H. Validation of Event Data Recorders in High Severity Full Frontal Crash Tests. SAE Int. J. Trans. Saf. 2013, 1, 76–99. [Google Scholar] [CrossRef]
- Tsoi, A.; Johnson, N.; Gabler, H. Validation of Event Data Recorders in Side-Impact Crash Tests. SAE Int. J. Trans. Saf. 2014, 2, 130–164. [Google Scholar] [CrossRef]
- Carr, L.; Rucoba, R.; Barnes, D.; Kent, S.; Osterhout, A. EDR Pulse Component Vector Analysis. In SAE Technical Paper; 2015-01-1448; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Xing, P.; Lee, F.; Flynn, T.; Wilkinson, C.; Siegmund, G. Comparison of the Accuracy and Sensitivity of Generation 1, 2 and 3 Toyota Event Data Recorders in Low-Speed Collisions. SAE Int. J. Trans. Saf. 2016, 4, 172–186. [Google Scholar] [CrossRef]
- Atarod, M. Reconstruction of Passenger Vehicle Underride: An Analysis of Insurance Institute for Highway Safety Semitrailer Rear Underride Crash Data. In SAE Technical Paper; 2020-01-5091; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Fatzinger, E.; Landerville, J. Using Vehicle EDR Data to Calculate Motorcycle Delta-V in Motorcycle-Vehicle Lateral Front End Impacts. In SAE Technical Paper; 2020-01-0885; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Han, I. Verification and Complement of EDR Speed Data through the Analysis of Real World Vehicle Collision Accidents. Int. J. Automot. Technol. 2019, 20, 897–902. [Google Scholar] [CrossRef]
- Bortles, W.; Biever, W.; Carter, N.; Smith, C. A Compendium of Passenger Vehicle Event Data Recorder Literature and Analysis of Validation Studies. In SAE Technical Paper; 2016-01-1497; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Martinesco, A.; Netto, M.; Neto, A.; Etgens, V. A Note on Accidents Involving Autonomous Vehicles: Interdependence of Event Data Recorder, Human-Vehicle Cooperation and Legal Aspects. IFAC-PapersOnLine 2019, 51, 407–410. [Google Scholar] [CrossRef]
- Riexinger, L.; Sherony, R.; Gabler, H. Methodology for Estimating the Benefits of Lane Departure Warnings using Event Data Recorders. In SAE Technical Paper; 2018-01-0509; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Davis, G. Bayesian Estimation of Drivers’ Gap Selections and Reaction Times in Left-Turning Crashes from Event Data Recorder Pre-Crash Data. In SAE Technical Paper; 2017-01-1411; SAE International: Warrendale, PA, USA, 2017. [Google Scholar] [CrossRef]
- Scanlon, J.; Page, K.; Sherony, R.; Gabler, H. Using Event Data Recorders from Real-World Crashes to Investigate the Earliest Detection Opportunity for an Intersection Advanced Driver Assistance System. In SAE Technical Paper; 2016-01-1457; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Reust, T.; Morgan, J.; Smith, P. Method to Determine Vehicle Speed During ABS Brake Events Using Heavy Vehicle Event Data Recorder Speed. SAE Int. J. Passeng. Cars—Mech. Syst. 2010, 3, 644–652. [Google Scholar] [CrossRef]
- Diacon, A.; Daily, J.; Ruth, R.; Mueller, C. Accuracy and Characteristics of 2012 Honda Event Data Recorders from Real-Time Replay of Controller Area Network (CAN) Traffic. SAE Int. J. Trans. Saf. 2013, 1, 399–419. [Google Scholar] [CrossRef]
- Ruth, R.; Daily, J. Accuracy of Event Data Recorder in 2010 Ford Flex During Steady State and Braking Conditions. SAE Int. J. Passeng. Cars—Mech. Syst. 2011, 4, 677–699. [Google Scholar] [CrossRef]
- Ruth, R.; Brown, T.; Lau, J. Accuracy of EDR During Rotation on Low Friction Surfaces. In SAE Technical Paper; 2010-01-1001; SAE International: Warrendale, PA, USA, 2010. [Google Scholar] [CrossRef]
- Wach, W. Reconstruction of vehicle kinematics by transformations of raw measurement data. In Proceedings of the 2018 XI International Science-Technical Conference Automotive Safety, Casta, Slovakia, 18–20 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Guzek, M.; Lozia, Z. Possible Errors occurring during Accident Reconstruction based on Car "Black Box" Records Guzek Marek, Lozia Zbigniew. In SAE Technical Papers; No 2002-01-0549; SAE International: Warrendale, PA, USA, 2002. [Google Scholar] [CrossRef]
- Guzek, M.; Lozia, Z.; Pieniążek, W. Accident Reconstruction Based on EDR Records—Simulation and Experimental Study. In SAE Technical Papers; No 2007-01-0729; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Guzek, M. Uncertainty in the Analysis of Road Accidents; Warsaw University of Technology: Warszawa, Poland, 2016. (In Polish) [Google Scholar]
- Guzek, M. Vehicle motion reconstruction based on EDR/ADR records—simulation research. IOP Conf. Ser. Mater. Sci. Eng. 2018, 421, 032011. [Google Scholar] [CrossRef]
- Lozia, Z. Vehicle dynamics simulation models of two emergency vehicles. In Technical Transactions “Mechanics”; Cracow University of Technology: Kraków, Poland, 2012; Volume 109, Issue 8/3-M; pp. 19–34. ISSN 0011-4561. (In Polish) [Google Scholar]
- Lozia, Z. Examples of authorial models for the simulation of motor vehicle motion and dynamics. In Proceedings of the Institute of Vehicles; Warsaw University of Technology: Warszawa, Poland, 2015; Volume 104, pp. 9–27. ISSN 1642-347X. [Google Scholar]
- Lozia, Z. Simulation testing of two ways of disturbing the motion of a motor vehicle entering a skid pad as used for tests at Driver Improvement Centres. Arch. Automot. Eng. 2016, 72, 111–125. [Google Scholar]
- Kamiński, E.; Pokorski, J. The car theory. In Dynamics of Suspensions and Drive Systems of Motor Vehicles; WKŁ: Warszawa, Poland, 1983; ISBN 83-206-0348-X. (In Polish) [Google Scholar]
- Dukkipati, R.V.; Pang, J.; Qatu, M.S.; Chen, G.S.; Shuguang, Z. Road Vehicle Dynamics; SAE International: Warrendale, PA, USA, 2008; ISBN 978-0-7680-1643-7. [Google Scholar]
- Lozia, Z. Driving Simulators; WKŁ: Warszawa, Poland, 2008; ISBN 978-83-206-1663-7. (In Polish) [Google Scholar]
- Lozia, Z. The Analysis of the Movement of a Two-Axle Car on the Background of Modelling Its Dynamics; Scientific Papers of Warsaw University of Technology—Transport, Sheet 41; Monograph, Warsaw University of Technology: Warszawa, Poland, 1998; ISSN 1230-9265. (In Polish) [Google Scholar]
- Maryniak, J. The Dynamic Theory of Moving Objects; Scientific Papers of Warsaw University of Technology—Mechanics. Monograph, Warsaw University of Technology: Warszawa, Poland, 1975; ISSN 0137-2335. (In Polish) [Google Scholar]
- Dugoff, H.; Fancher, P.S.; Segel, L. An analysis of tire traction properties and their influence on vehicle dynamic performance. In SAE Technical Paper; 700377; SAE International: Warrendale, PA, USA, 1970. [Google Scholar] [CrossRef]
- Fancher, P.S., Jr.; Bareket, Z. Including roadway and tread factors in semi-empirical model of truck tyres. Veh. Syst. Dyn. 1993, 21, 92–107. [Google Scholar] [CrossRef]
- Schieschke, R. The importance of tire dynamics in vehicle simulation. Presented at the Tire Society 9th Annual Meeting and Conference on Tire Science and Technology, Akron, OH, USA, 20–21 March 1990. [Google Scholar]
- ISO 4138:2012 Passenger Cars—Steady-State Circular driving Behaviour—Open-Loop Test Methods. Standard of International Organization for Standardization. Publication date: 2012-06. Available online: https://www.iso.org/standard/54143.html (accessed on 19 August 2021).
- ISO 7401:2011 Road Vehicles—Lateral Transient Response Test Methods—Open-Loop Test Methods. Standard of International Organization for Standardization. Publication date: 2011-04. Available online: https://www.iso.org/standard/54144.html (accessed on 19 August 2021).
- Regulation No 13 of the Economic Commission for Europe of the United Nations (UN/ECE)—Uniform Provisions Concerning the Approval of Vehicles of Categories M, N and O with Regard to Braking, Annex 4. Available online: https://op.europa.eu/en/publication-detail/-/publication/0a43f880-d612-11e5-a4b5-01aa75ed71a1/ (accessed on 19 August 2021).
- Guzek, M. Methods of Computational Error Determination in an Analysis of Selected Pre-Accident Situations in Road Traffic. Ph.D. Thesis, Warsaw University of Technology, Faculty of Transport, Warsaw, Poland, 2002. (In Polish). [Google Scholar]
- Fortuna, Z.; Macukow, B.; Wąsowski, J. Numerical Methods, 7th ed.; WNT: Warszawa, Poland, 2015; ISBN 9788379262816. (In Polish) [Google Scholar]
- Stoer, J. Introduction to the Numerical Methods; PWN: Warszawa, Poland, 1979; Volume 1. (In Polish) [Google Scholar]
- Recommendation of the Minister of Infrastructure of February 2020. Patterns and standards. WRD-31-3. Guidelines for the Design of Road Intersections. Roundabouts. Available online: https://www.gov.pl/web/infrastruktura/wr-d (accessed on 19 August 2021). (In Polish)


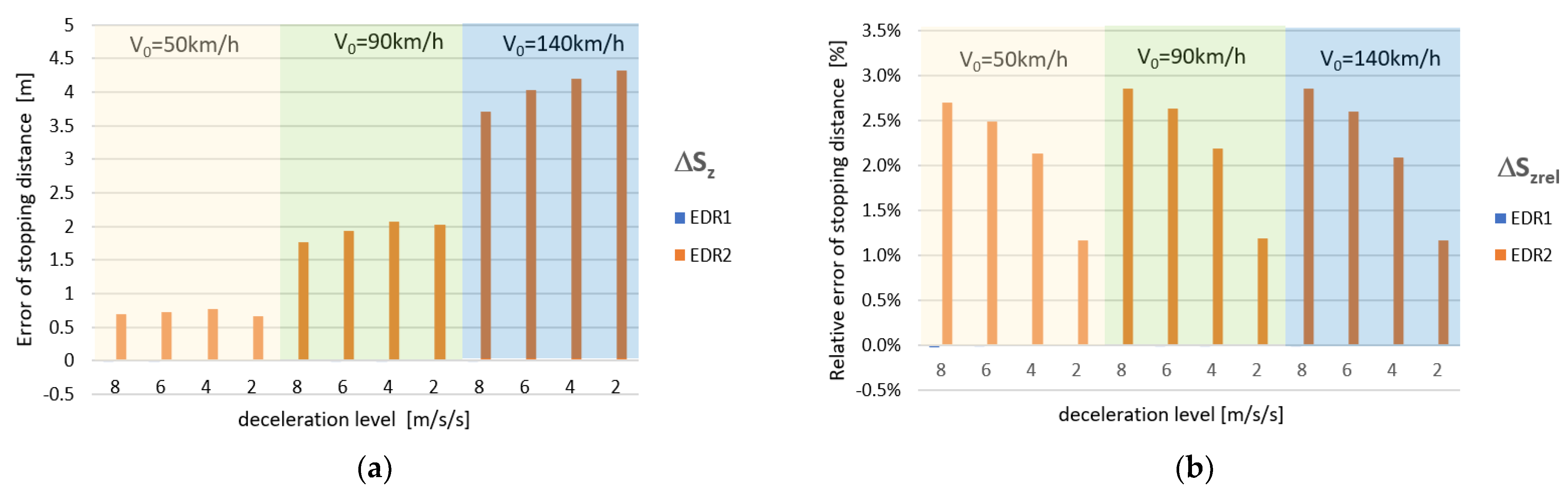
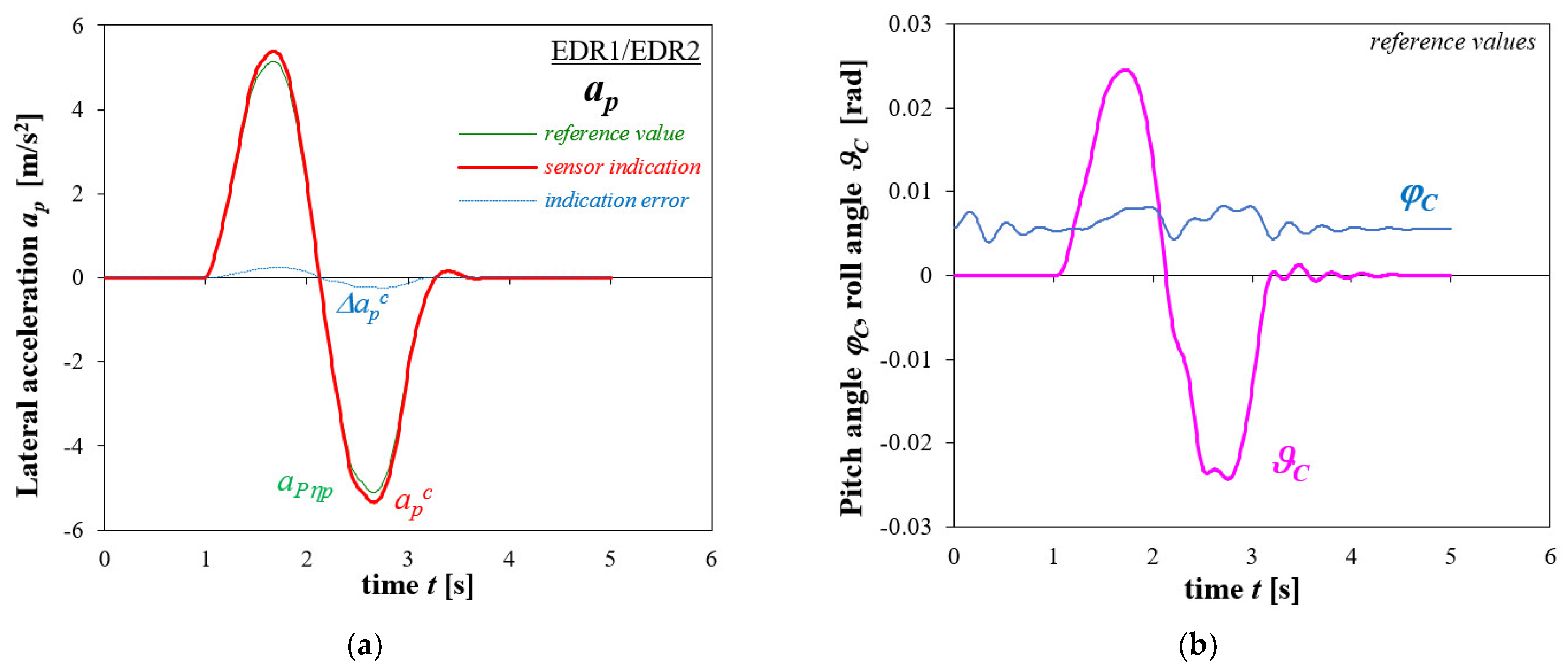
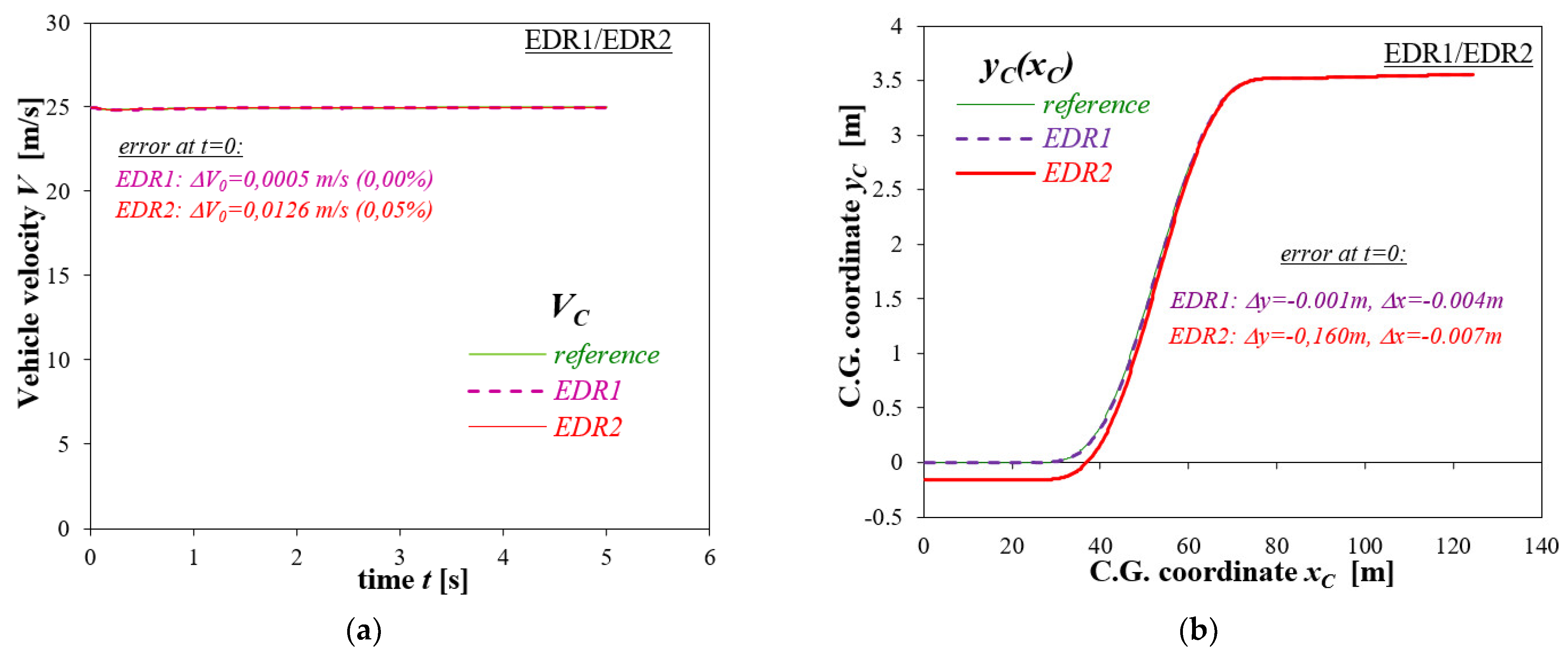
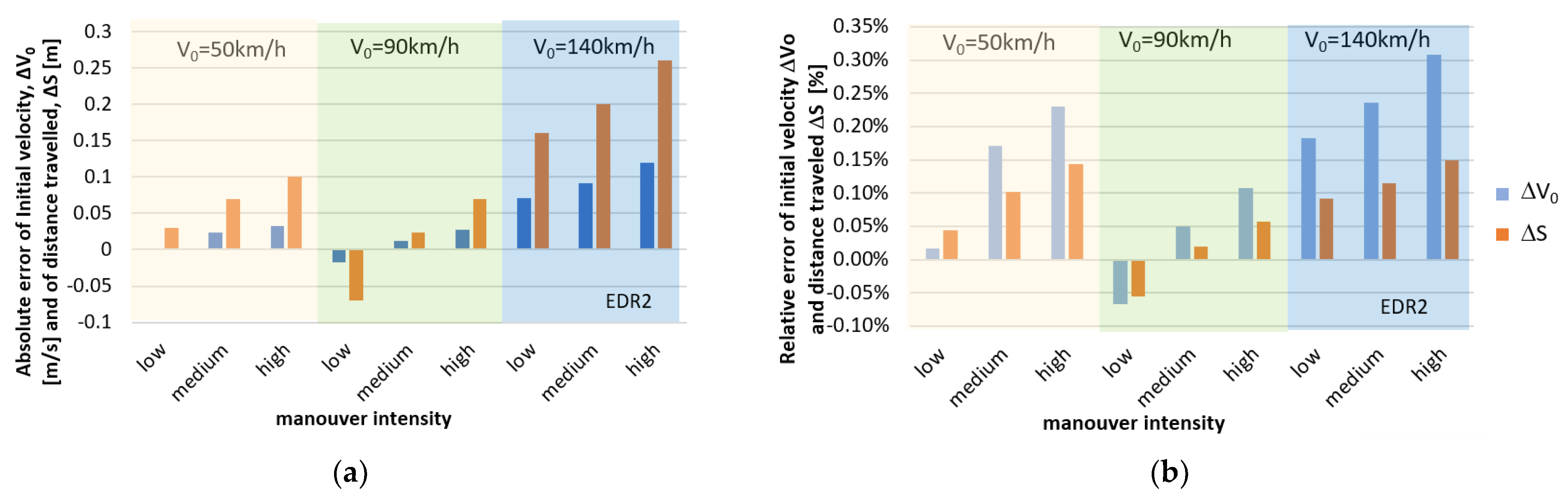
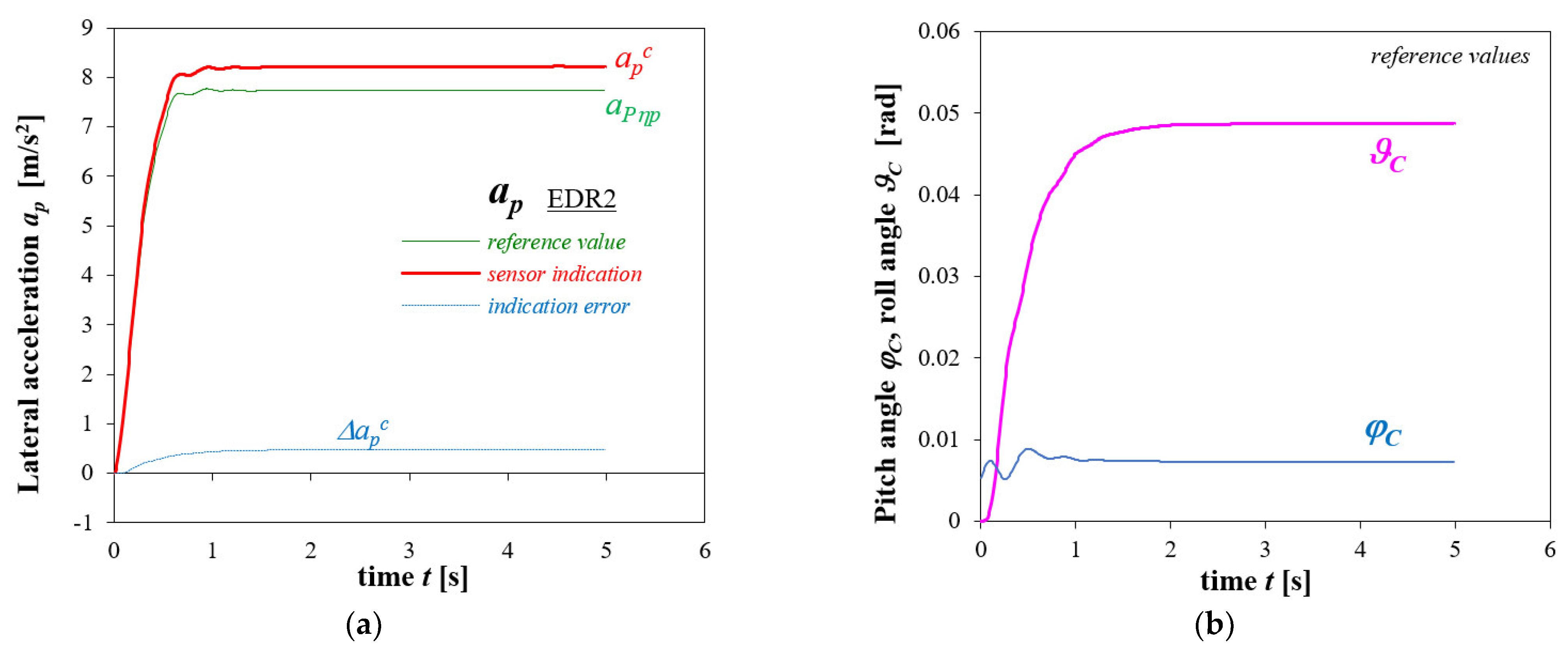


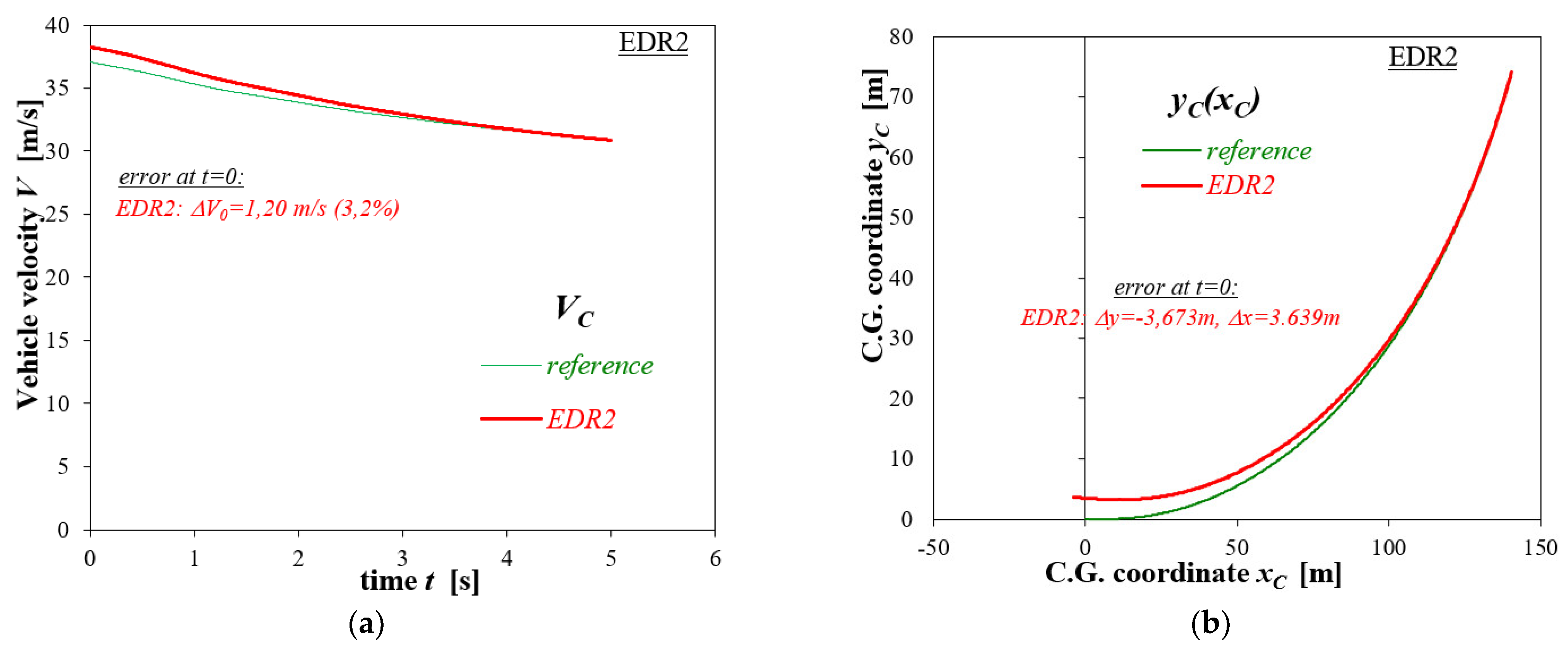

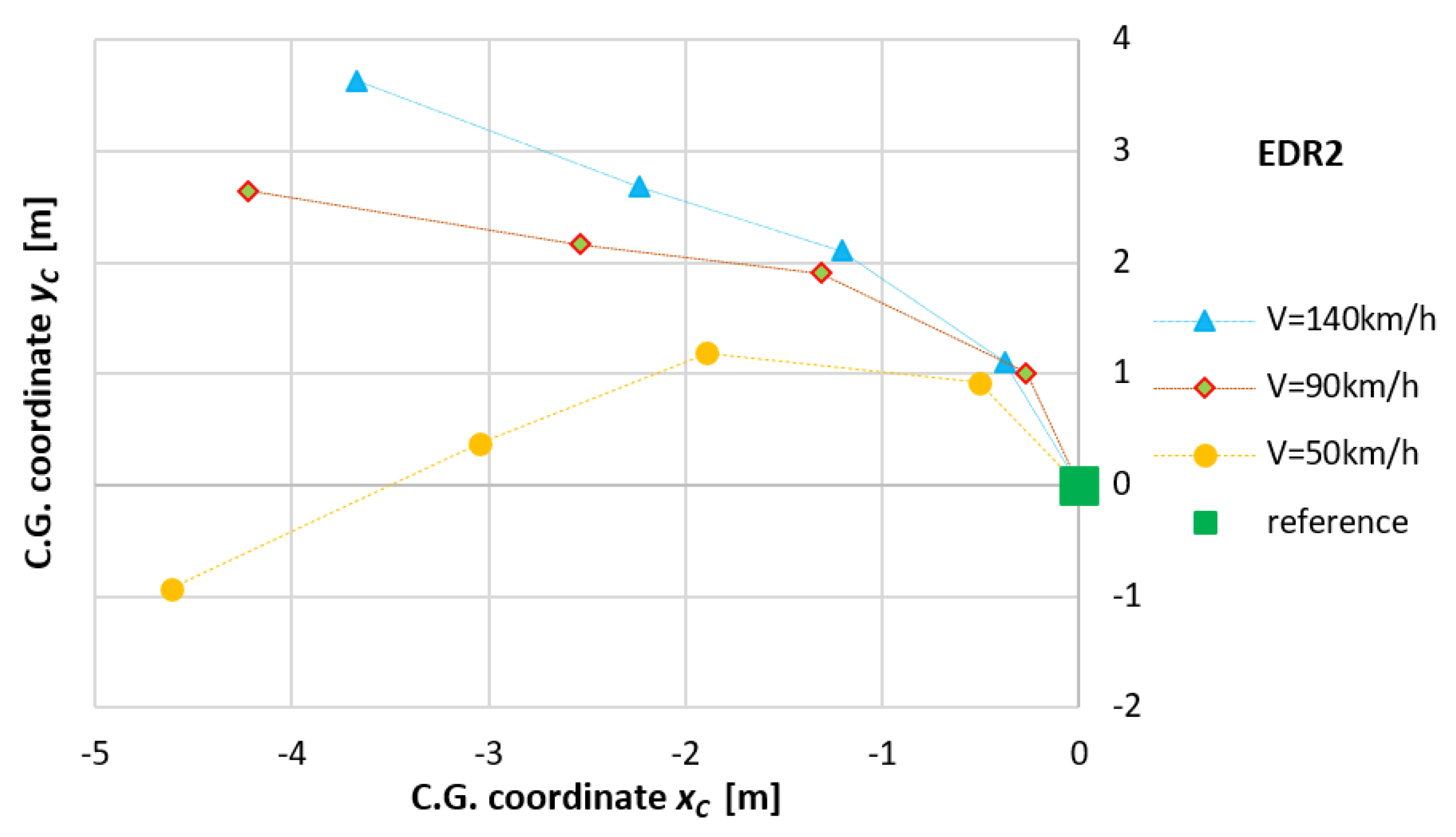
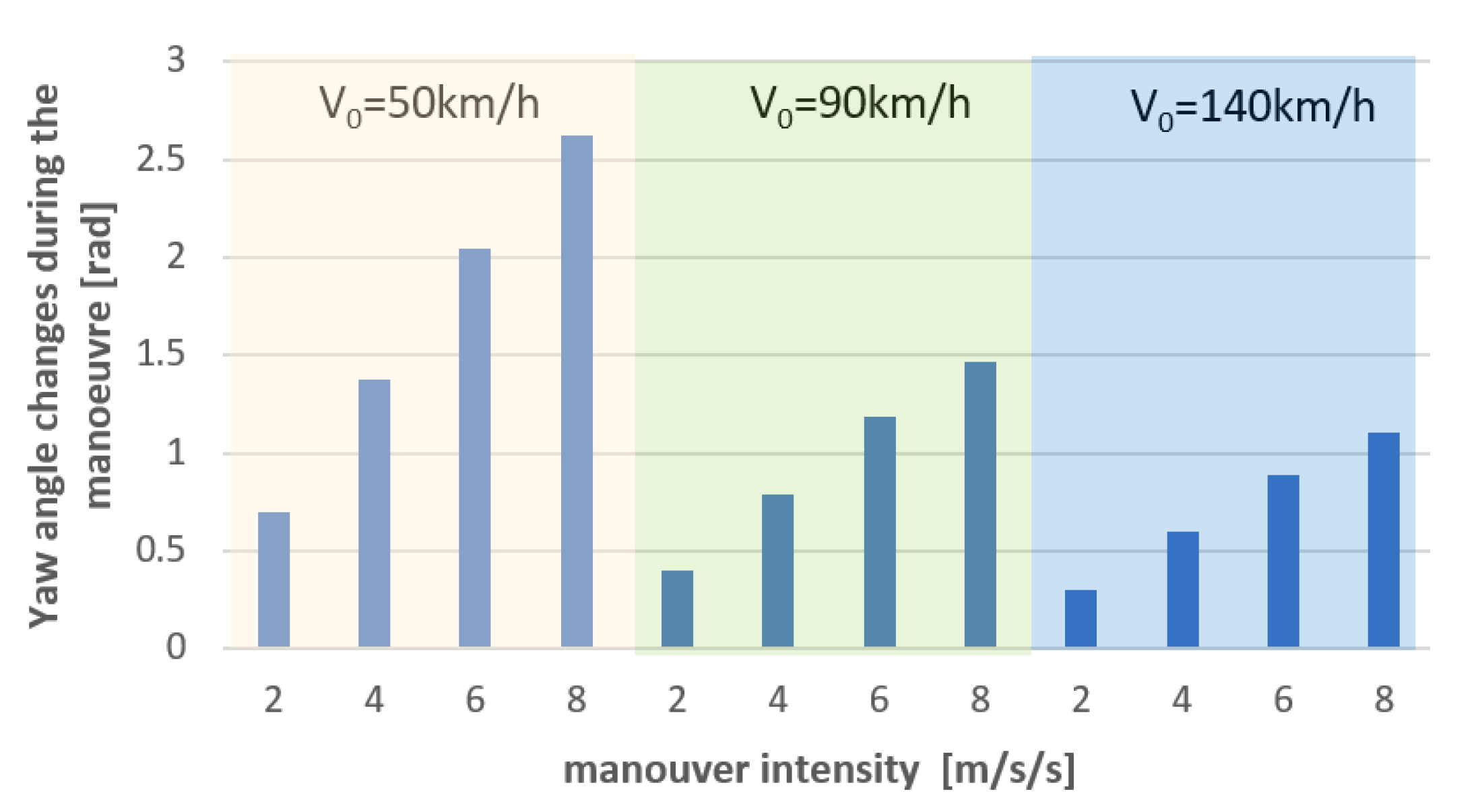

| Initial Velocity V0 [km/h] | Deceleration Level [m/s2] | Initial Velocity V0 [m/s] | Stopping Distance Sz [m] | ||||
|---|---|---|---|---|---|---|---|
| Reference | EDR1 | EDR2 | Reference | EDR1 | EDR2 | ||
| 50 | 8 | 13.871 | 13.869 | 14.235 | 25.691 | 25.686 | 26.384 |
| 6 | 13.869 | 14.208 | 29.325 | 29.32 | 30.053 | ||
| 4 | 13.871 | 14.163 | 36.512 | 36.512 | 37.289 | ||
| 2 | 13.872 | 14.037 | 56.581 | 56.581 | 57.242 | ||
| 90 | 8 | 24.957 | 24.959 | 25.646 | 62.098 | 62.1 | 63.868 |
| 6 | 24.951 | 25.591 | 73.367 | 73.36 | 75.295 | ||
| 4 | 24.955 | 25.489 | 94.944 | 94.942 | 97.016 | ||
| 2 | 24.955 | 25.248 | 171.381 | 171.384 | 173.411 | ||
| 140 | 8 | 38.797 | 38.795 | 39.855 | 129.788 | 129.787 | 133.499 |
| 6 | 38.8 | 39.767 | 155.278 | 155.281 | 159.313 | ||
| 4 | 38.799 | 39.587 | 200.958 | 200.965 | 205.152 | ||
| 2 | 38.803 | 39.234 | 370.088 | 370.113 | 374.406 | ||
| Preset Initial Velocity V0 [km/h] | Intensity (apmax [m/s2]) | Initial Velocity V0 [m/s] | Initial Position Error, EDR2 [m] | Distance Traveled S [m] | |||
|---|---|---|---|---|---|---|---|
| Reference | EDR2 | Δx | Δy | Reference | EDR2 | ||
| 50 | Low (2,4) | 13.884 | 13.886 | −0.0092 | −0.1519 | 69.25 | 69.28 |
| Medium (5,4) | 13.908 | −0.0364 | −0.1694 | 69.3 | 69.37 | ||
| High (8,2) | 13.916 | −0.0468 | −0.2932 | 69.39 | 69.49 | ||
| 90 | Low (2,4) | 24.999 | 24.973 | 0.0883 | −0.1458 | 124.56 | 124.49 |
| Medium (5,0) | 25.004 | −0.0072 | −0.1597 | 124.49 | 124.51 | ||
| High (7,4) | 25.017 | −0.0371 | −0.2323 | 124.24 | 124.31 | ||
| 140 | Low (2,5) | 38.971 | 38.942 | −0.1508 | −0.1554 | 174.96 | 175.12 |
| Medium (5,3) | 38.963 | −0.1884 | −0.1692 | 174.71 | 174.91 | ||
| High (7,1) | 38.991 | −0.2427 | −0.3774 | 173.82 | 174.08 | ||
| Preset Initial Velocity V0 [km/h] | Intensity (ap [m/s2]) | Initial Velocity V0 [m/s] | Initial Position Error, EDR2 [m] | Distance Traveled S [m] | |||
|---|---|---|---|---|---|---|---|
| Reference | EDR2 | Δx | Δy | Reference | EDR2 | ||
| 50 | 2 | 13.935 | 14.097 | −0.5100 | 0.9233 | 69.37 | 69.66 |
| 4 | 14.545 | −1.8910 | 1.1858 | 69.5 | 70.73 | ||
| 6 | 14.944 | −3.0435 | 0.3791 | 69.61 | 71.82 | ||
| 8 | 15.517 | −4.6145 | −0.9273 | 69.49 | 73.26 | ||
| 90 | 2 | 25.009 | 25.091 | −0.2672 | 1.0112 | 124.75 | 124.89 |
| 4 | 25.427 | −1.3101 | 1.9083 | 124.62 | 125.45 | ||
| 6 | 25.824 | −2.5380 | 2.1633 | 124.34 | 125.98 | ||
| 8 | 26.368 | −4.2219 | 2.6445 | 123.88 | 126.56 | ||
| 140 | 2 | 37.068 | 37.210 | −0.3776 | 1.1077 | 169.73 | 170.01 |
| 4 | 37.475 | −1.2059 | 2.1086 | 170.35 | 171.18 | ||
| 6 | 37.804 | −2.2332 | 2.6795 | 170,00 | 171.5 | ||
| 8 | 38.265 | −3.6725 | 3.6388 | 167.12 | 169.52 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzek, M.; Lozia, Z. Are EDR Devices Undoubtedly Helpful in the Reconstruction of a Road Traffic Accident? Energies 2021, 14, 6940. https://doi.org/10.3390/en14216940
Guzek M, Lozia Z. Are EDR Devices Undoubtedly Helpful in the Reconstruction of a Road Traffic Accident? Energies. 2021; 14(21):6940. https://doi.org/10.3390/en14216940
Chicago/Turabian StyleGuzek, Marek, and Zbigniew Lozia. 2021. "Are EDR Devices Undoubtedly Helpful in the Reconstruction of a Road Traffic Accident?" Energies 14, no. 21: 6940. https://doi.org/10.3390/en14216940
APA StyleGuzek, M., & Lozia, Z. (2021). Are EDR Devices Undoubtedly Helpful in the Reconstruction of a Road Traffic Accident? Energies, 14(21), 6940. https://doi.org/10.3390/en14216940







