Design Optimization of Multi-Layer Permanent Magnet Synchronous Machines for Electric Vehicle Applications
Abstract
:1. Introduction
2. Multi-Objective and Multi-Physics Optimization Methodology
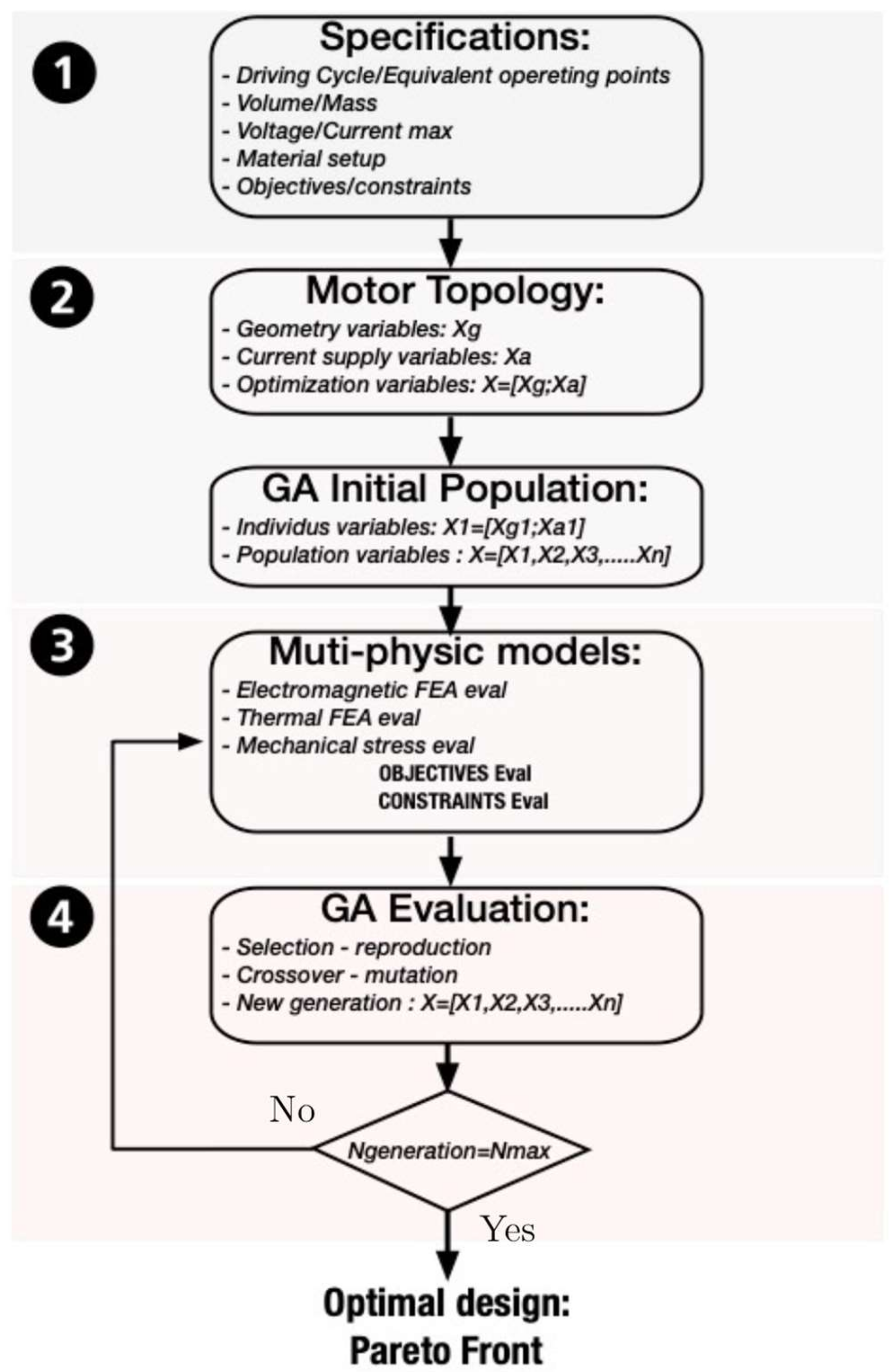
2.1. Optimization Procedure
2.2. Motor Topology
- Geometric variables:
- Supply variables:
2.3. Electromagnetic Models Stepped Rotor Position (abc Model) vs. Fixed Rotor Position (dq Model)
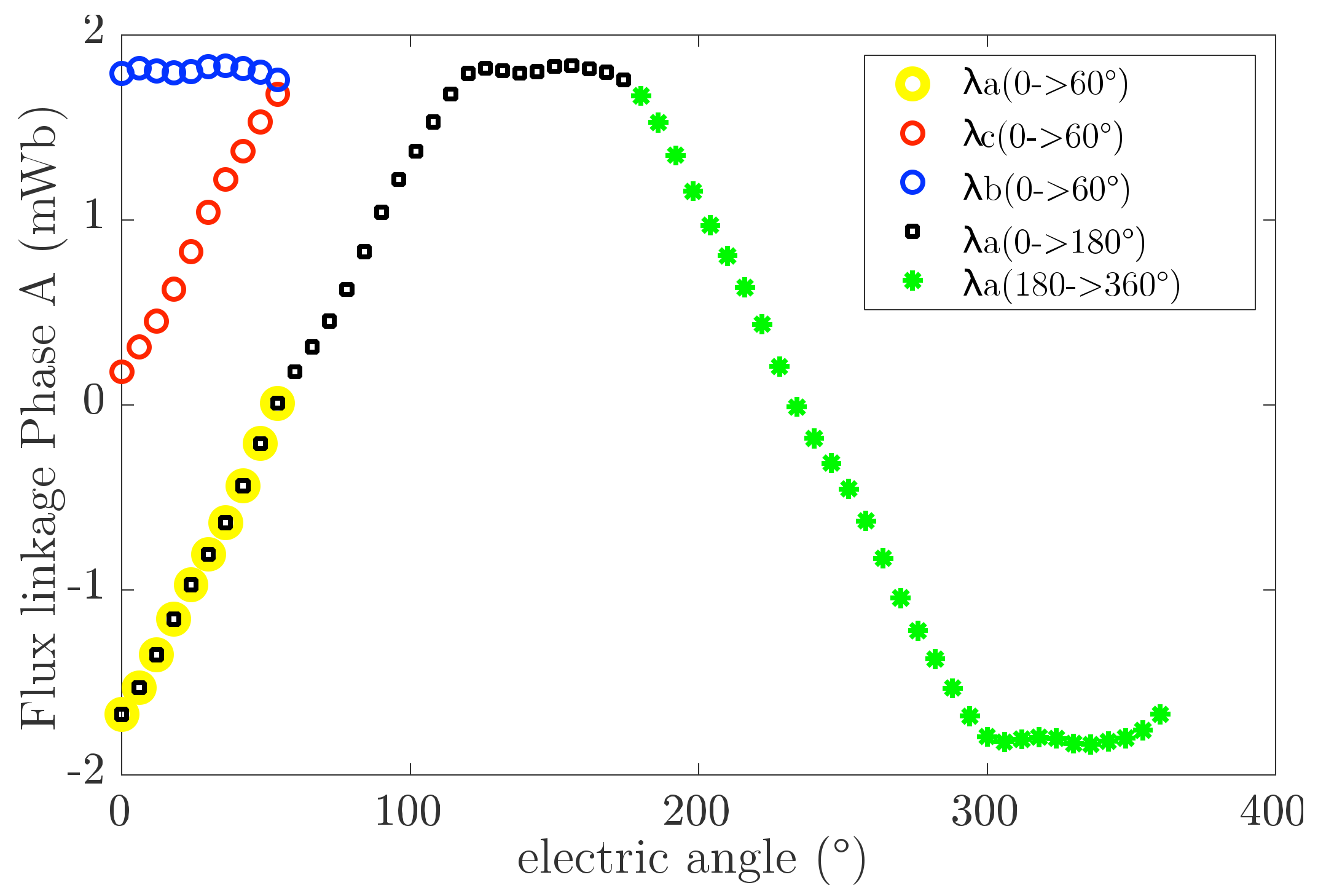
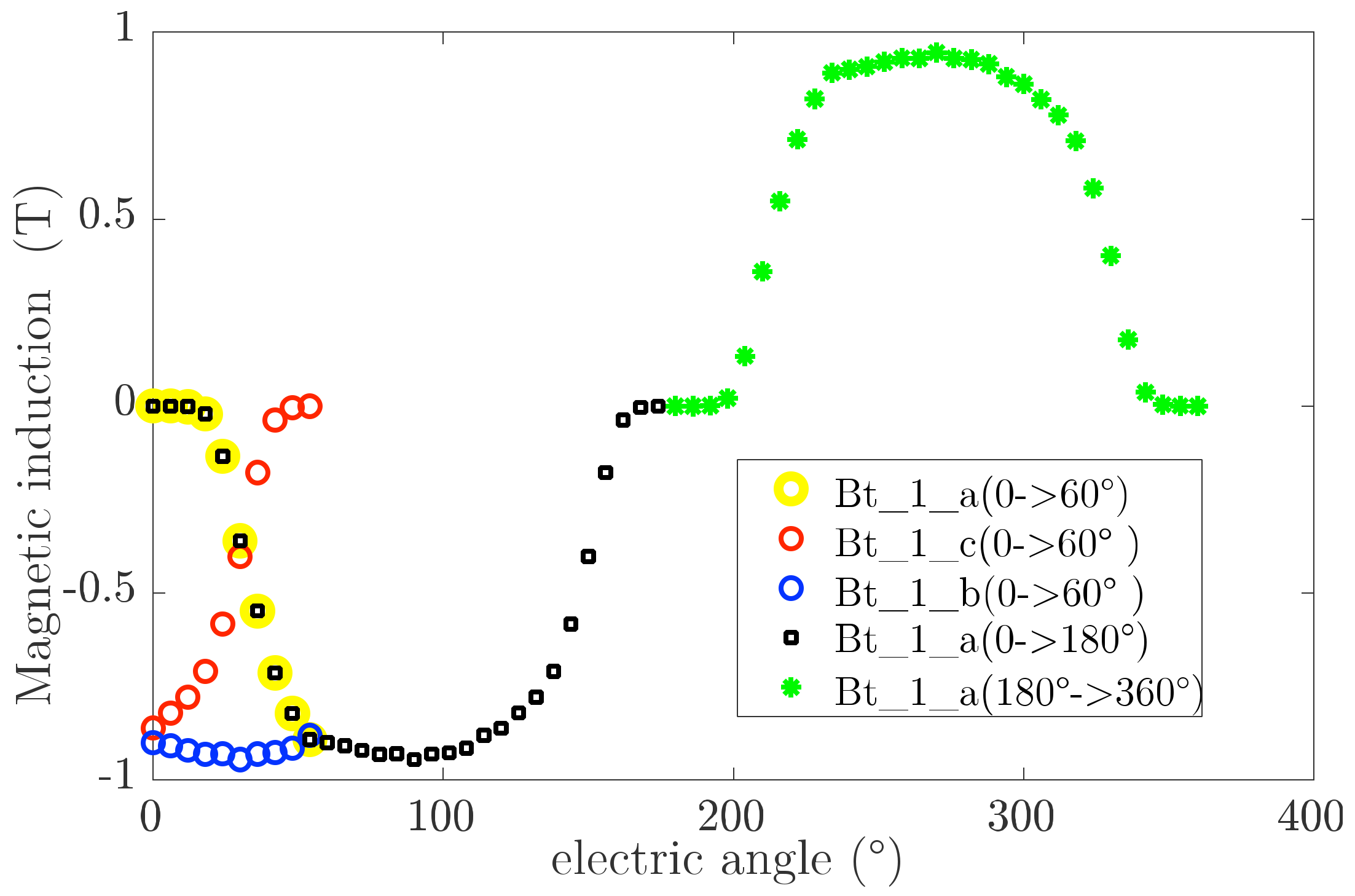
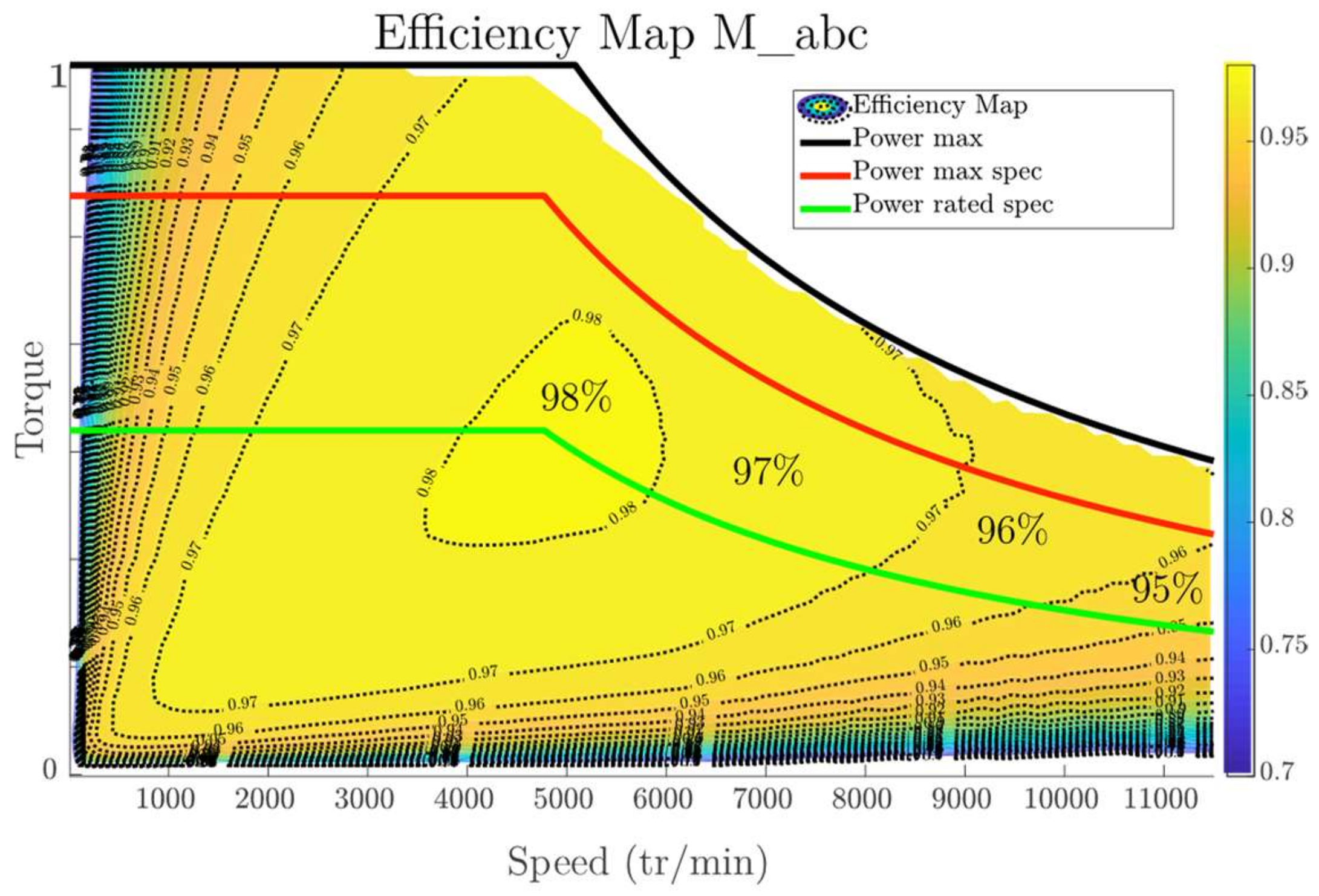
2.3.1. Stepped Rotor Position (abc Model)
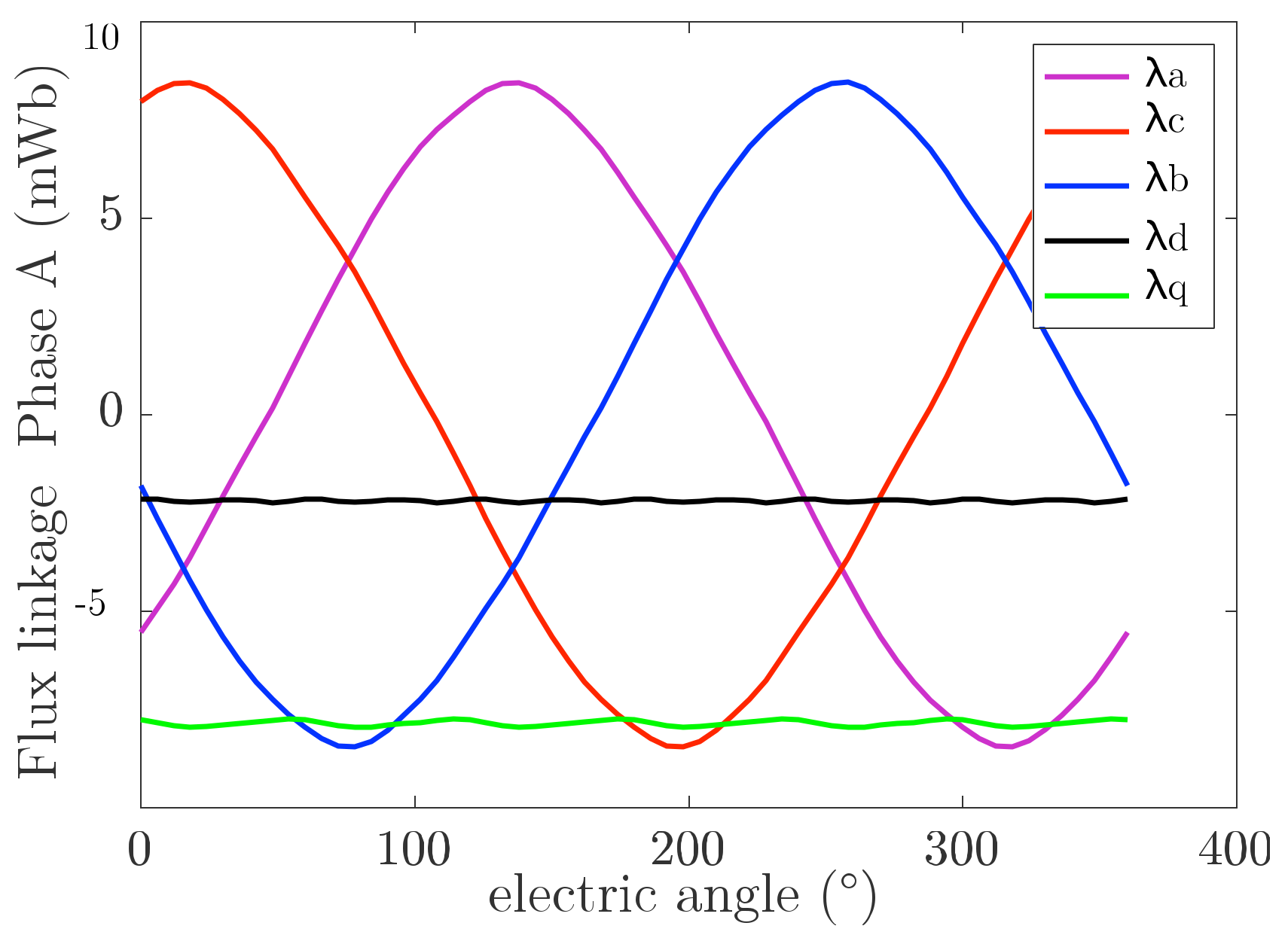
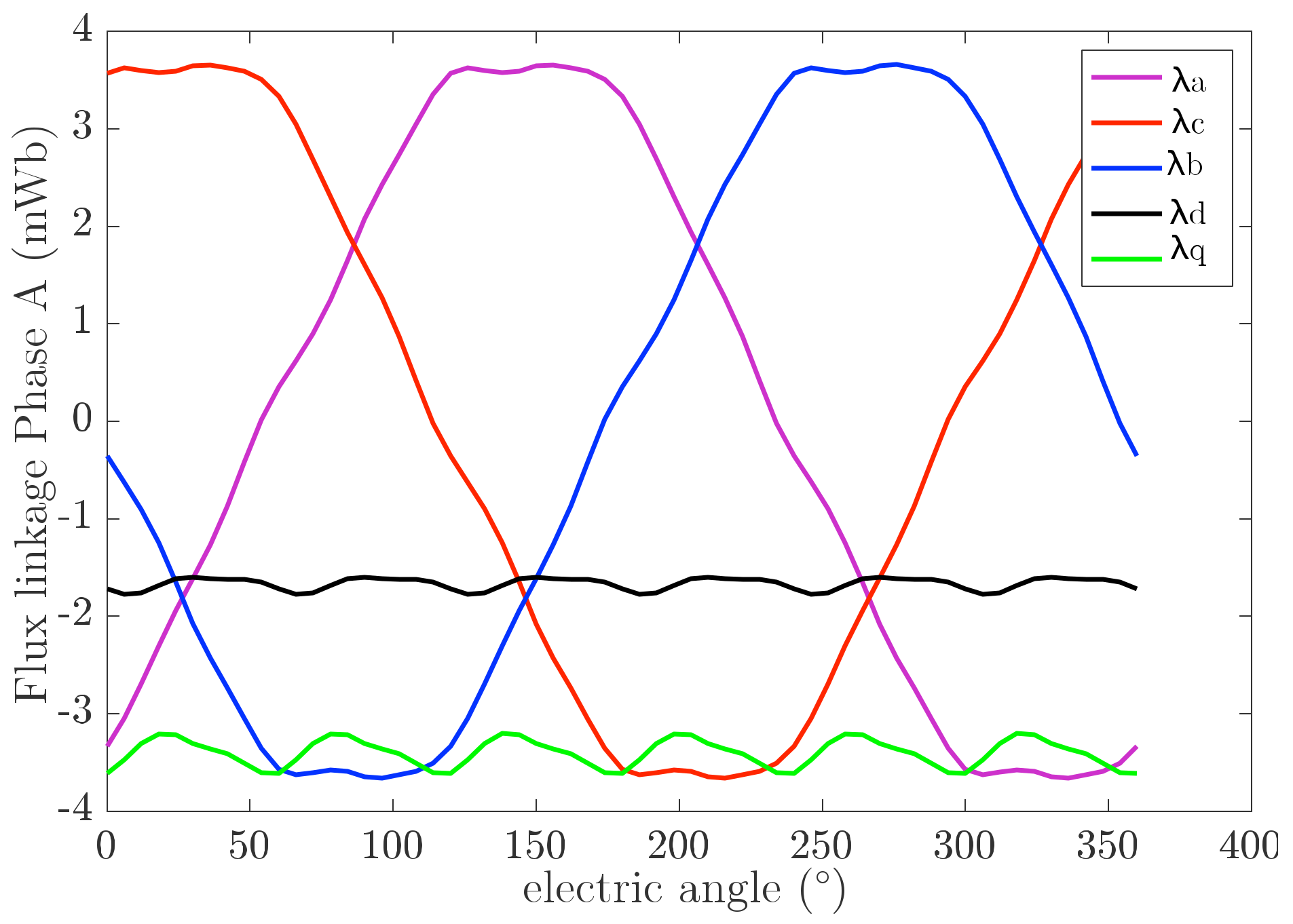
Reconstruction of Flux Linkage
- n is the number of the n-th harmonic
- is the angular position of the rotor in electrical degrees.
- is the phase shift of the n-th harmonic of the flux linkage.
- is the amplitude of the n-th harmonic of the flux linkage.
Reconstruction of Magnetic Induction at the Stator
- is the complex number:
- is the complex operator of rotation of center (0,0) and angle .

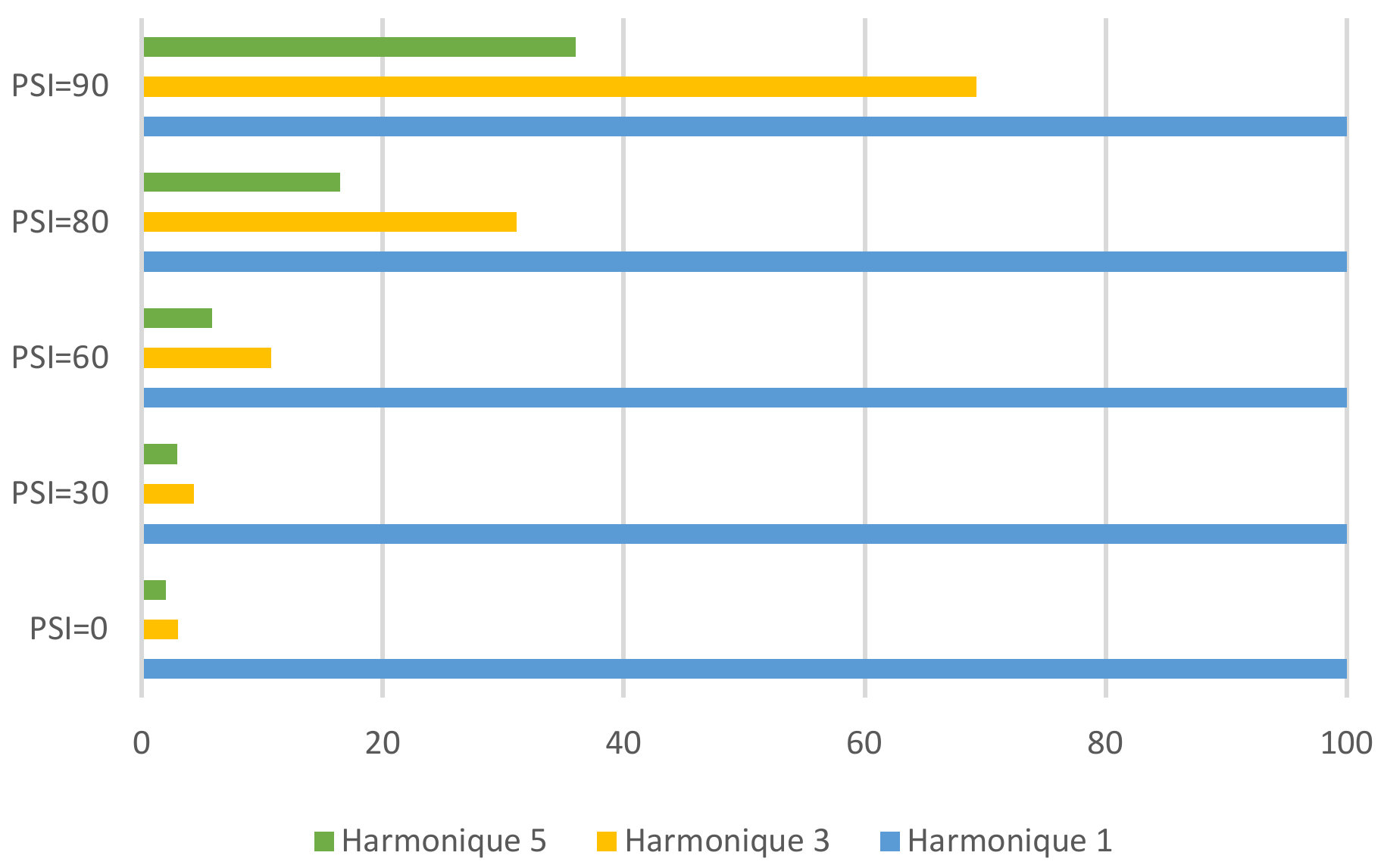
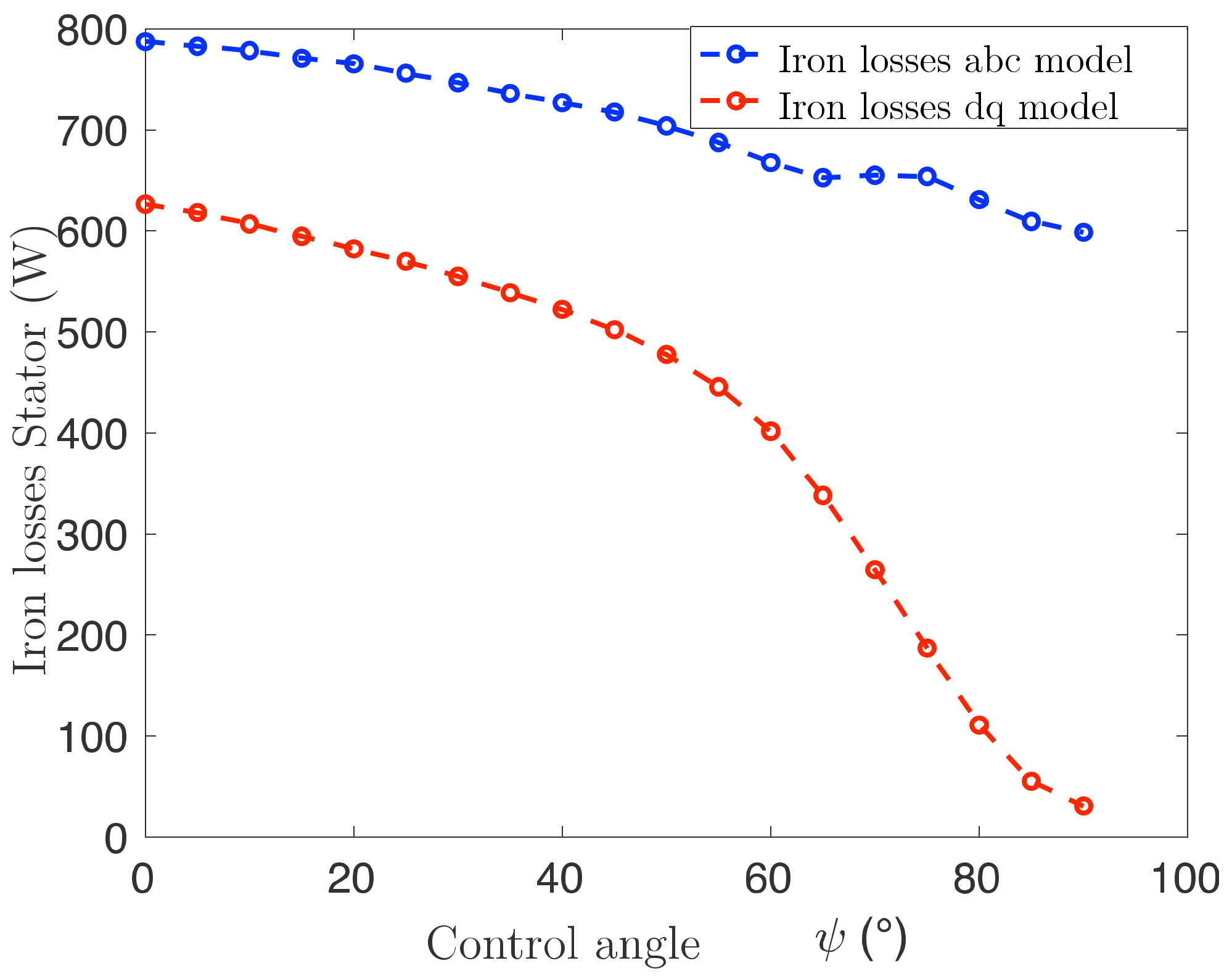
Iron Loss Calculation
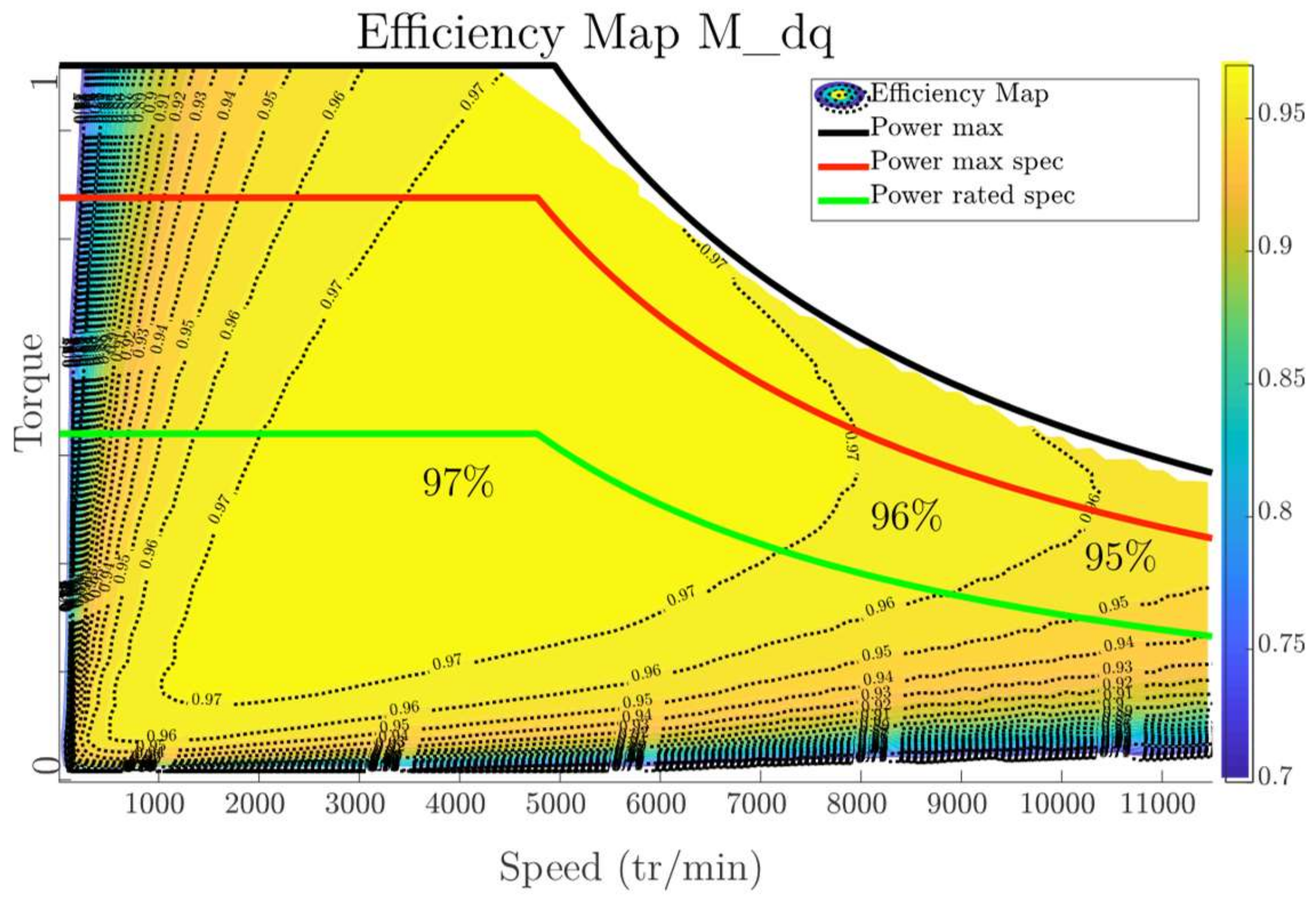
2.3.2. Fixed Rotor Position (DQ Model)
- (a)
- The windings are sinusoidal on the stator periphery. Then, the flux linkages and induce voltage have sinusoidal variation.
- (b)
- The magnetic circuit is linear.
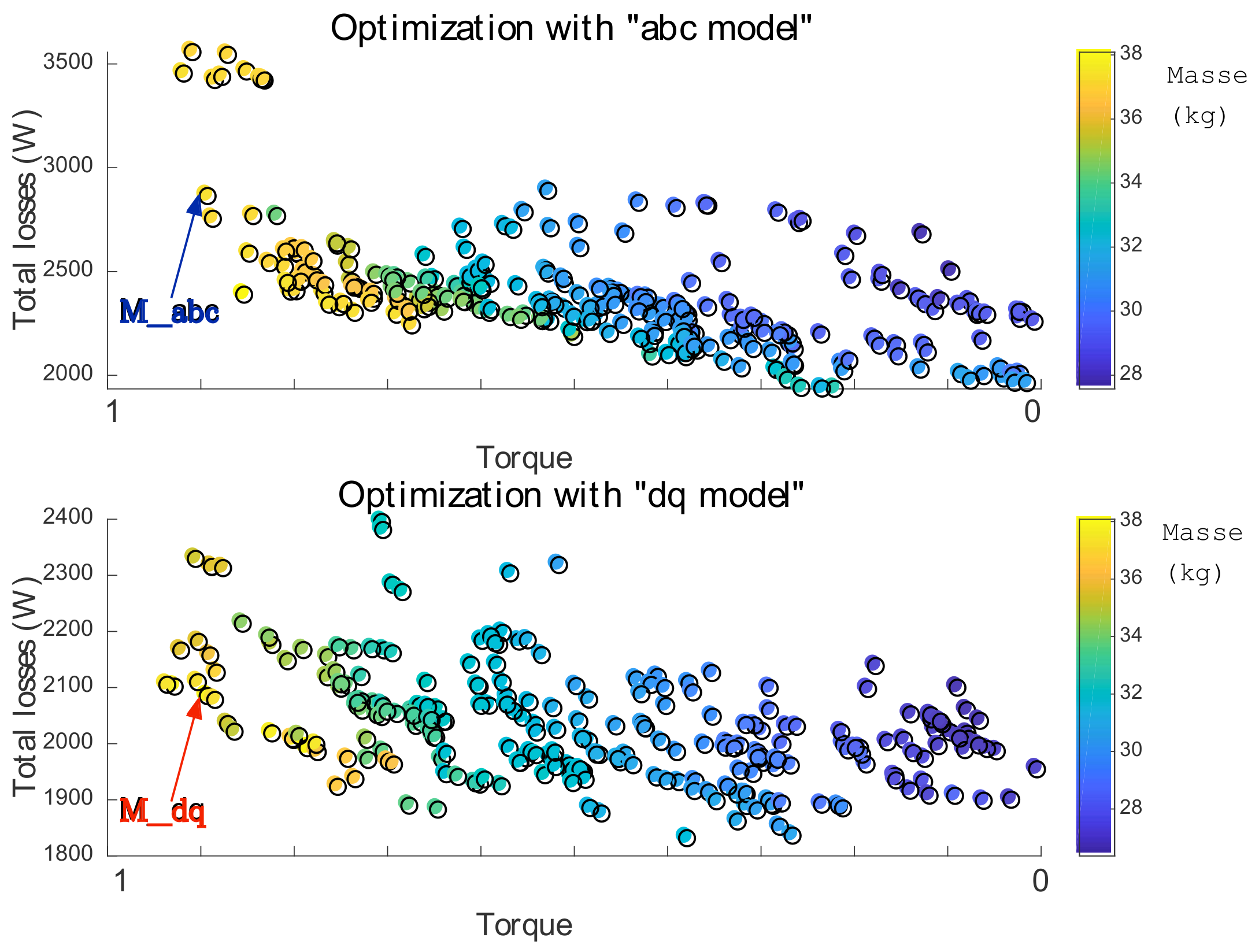
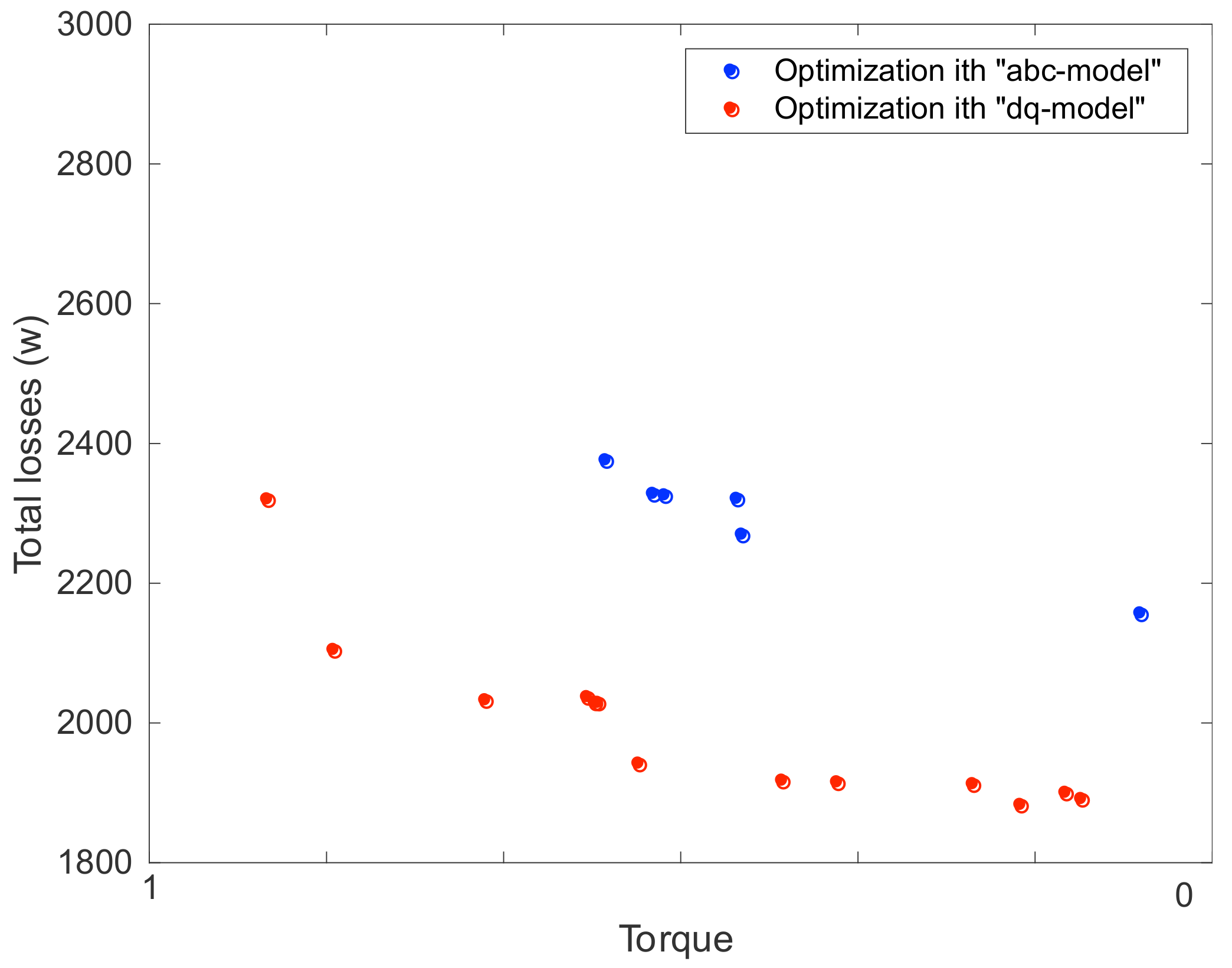
3. Optimization Results
- -
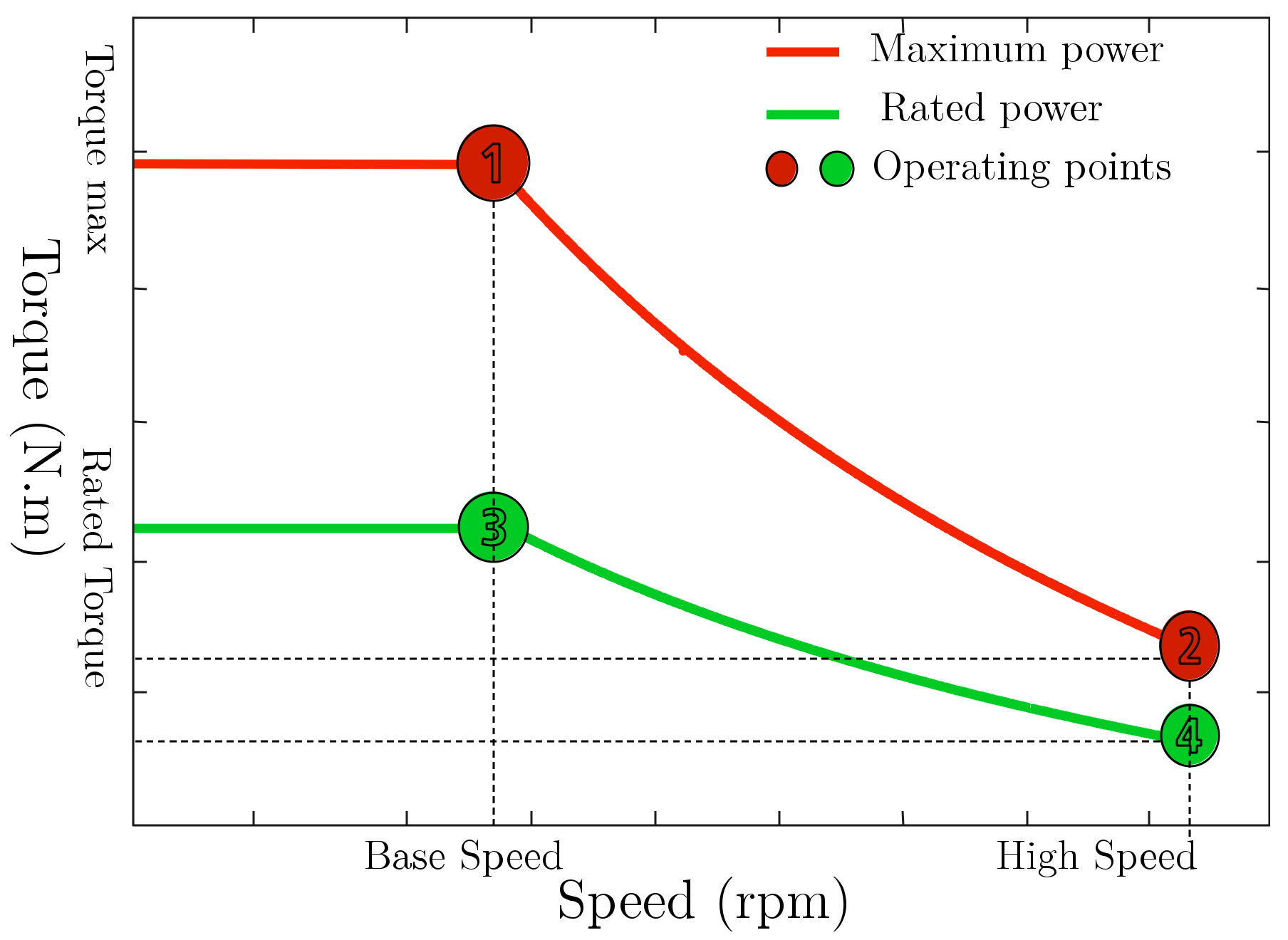
- Maximize the torque at operating point 1
- -
- Minimize the average total loss of operating points 3 and 4 of the rated power: .
- -
- Minimize the total mass of the machine
- : Sinusoidal Pulse With Modulation;
- : Space Vector Pulse With Modulation;
- The maximum Neutral-Phase Voltage;
- The battery voltage.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Castagnaro, E.; Bacco, G.; Bianchi, N. Rotor Iron Losses in High-Speed Synchronous Reluctance Motors. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1310–1316. [Google Scholar] [CrossRef]
- Stipetic, S.; Miebach, W.; Zarko, D. Optimization in design of electric machines: Methodology and workflow. In Proceedings of the 2015 Intl Aegean Conference on Electrical Machines & Power Electronics (ACEMP), Side, Turkey, 2–4 September 2015; pp. 441–448. [Google Scholar] [CrossRef]
- Degano, M.; Di Nardo, M.; Galea, M.; Gerada, C.; Gerada, D. Global design optimization strategy of a synchronous reluctance machine for light electric vehicles. In Proceedings of the IET Conference Proceedings, Edinburgh, UK, 7 March 2016; p. 5. [Google Scholar] [CrossRef]
- Han, W.; van Dang, C.; Kim, J.W.; Kim, Y.J.; Jung, S.Y. Global-Simplex Optimization Algorithm Applied to FEM-Based Optimal Design of Electric Machine. IEEE Trans. Magn. 2017, 53, 2015–2018. [Google Scholar] [CrossRef]
- Sarigiannidis, A.G.; Beniakar, M.E.; Kladas, A.G. Fast Adaptive Evolutionary PM Traction Motor Optimization Based on Electric Vehicle Drive Cycle. IEEE Trans. Veh. Technol. 2017, 66, 5762–5774. [Google Scholar] [CrossRef]
- Li, Q.; Fan, T.; Li, Y.; Guo, J.; Wen, X. Design and Optimization of Permanent Magnet Synchronous Machines for Driving Cycle. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Permanent-magnet optimization in permanent-magnet-assisted synchronous reluctance motor for a wide constant-power speed range. IEEE Trans. Ind. Electron. 2012, 59, 2495–2502. [Google Scholar] [CrossRef]
- Grunditz, E.A.; Thiringer, T. Electric Vehicle Acceleration Performance and Motor Drive Cycle Energy Efficiency Trade-Off. In Proceedings of the 2018 23rd Conference on Electrical Machines, Alexandroupoli, Greece, 3–6 September 2018; pp. 717–723. [Google Scholar]
- Carraro, E.; Morandin, M.; Bianchi, N. Optimization of a traction PMASR motor according to a given driving cycle. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 23–25 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Cardoso, J.F.; Chillet, C.; Gerbaud, L.; Belhaj, L.A. Electrical Machine Design by optimization for E-motor Application: A Drive Cycle Approach. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 2514–2519. [Google Scholar] [CrossRef]
- Li, Q.; Fan, T.; Wen, X.; Li, Y.; Wang, Z.; Guo, J. Design optimization of interior permanent magnet synchronous machines for traction application over a given driving cycle. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1900–1904. [Google Scholar] [CrossRef]
- Günther, S.; Ulbrich, S.; Hofmann, W. Driving cycle-based design optimization of interior permanent magnet synchronous motor drives for electric vehicle application. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014; pp. 25–30. [Google Scholar] [CrossRef]
- Crozier, R.; Mueller, M. A new MATLAB and octave interface to a popular magnetics finite element code. In Proceedings of the 2016 22nd International Conference on Electrical Machines, ICEM 2016, Lausanne, Switzerland, 4–7 September 2016; pp. 1251–1256. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Lei, G.; Zhu, J.; Guo, Y. Multidisciplinary Design Optimization Methods for Electrical Machines and Drive Systems; Springer: Berlin, Germany, 2016. [Google Scholar]
- Murthy, C.A. Genetic Algorithms: Basic principles and applications. In Proceedings of the 2012 2nd National Conference on Computational Intelligence and Signal Processing (CISP), Chongqind, China, 16–18 October 2012; p. 22. [Google Scholar]
- Chehouri, A.; Younes, R.; Khoder, J.; Perron, J.; Ilinca, A. A Selection Process for Genetic Algorithm Using Clustering Analysis. Algorithms 2017, 10, 123. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Cissé, K.M.; Hlioui, S.; Cheng, Y.; Belhadi, M.; Gabsi, M. Optimization of V-shaped Synchronous Motor for Automotive Application. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 906–912. [Google Scholar] [CrossRef]
- Bianchi, N. Electrical Machine Analysis Using Finite Elements; Taylor & Francis Group: Oxford, UK, 2005. [Google Scholar]
- Bianchi, N.; Bolognani, S. Magnetic models of saturated Interior Permanent Magnet motors based on Finite Element Analysis. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference, Thirty-Third IAS Annual Meeting (Cat. No. 98CH36242), St. Louis, MO, USA, 12–15 October 1998; Volume 1, pp. 27–34. [Google Scholar]
- Goss, J.; Mellor, P.H.; Wrobel, R.; Staton, D.A.; Popescu, M. The design of AC permanent magnet motors for electric vehicles: A computationally efficient model of the operational envelope. In Proceedings of the 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK, 27–29 March 2012; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Štumberger, G.; Polajžer, B.; Štumberger, B.; Toman, M.; Dolinar, D. Evaluation of experimental methods for determining the magnetically nonlinear characteristics of electromagnetic devices. IEEE Trans. Magn. 2005, 41, 4030–4032. [Google Scholar] [CrossRef]
- Wang, S.; Degano, M.; Kang, J.; Galassini, A.; Gerada, C. A Novel Newton-Raphson-Based Searching Method for the MTPA Control of Pmasynrm Considering Magnetic and Cross Saturation. In Proceedings of the 2018 23rd International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1360–1366. [Google Scholar]
- Zhou, C.; Huang, X.; Fang, Y.; Wu, L. Comparison of PMSMs with Different Rotor Structures for EV Application. In Proceedings of the 2018 23rd International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 609–614. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]


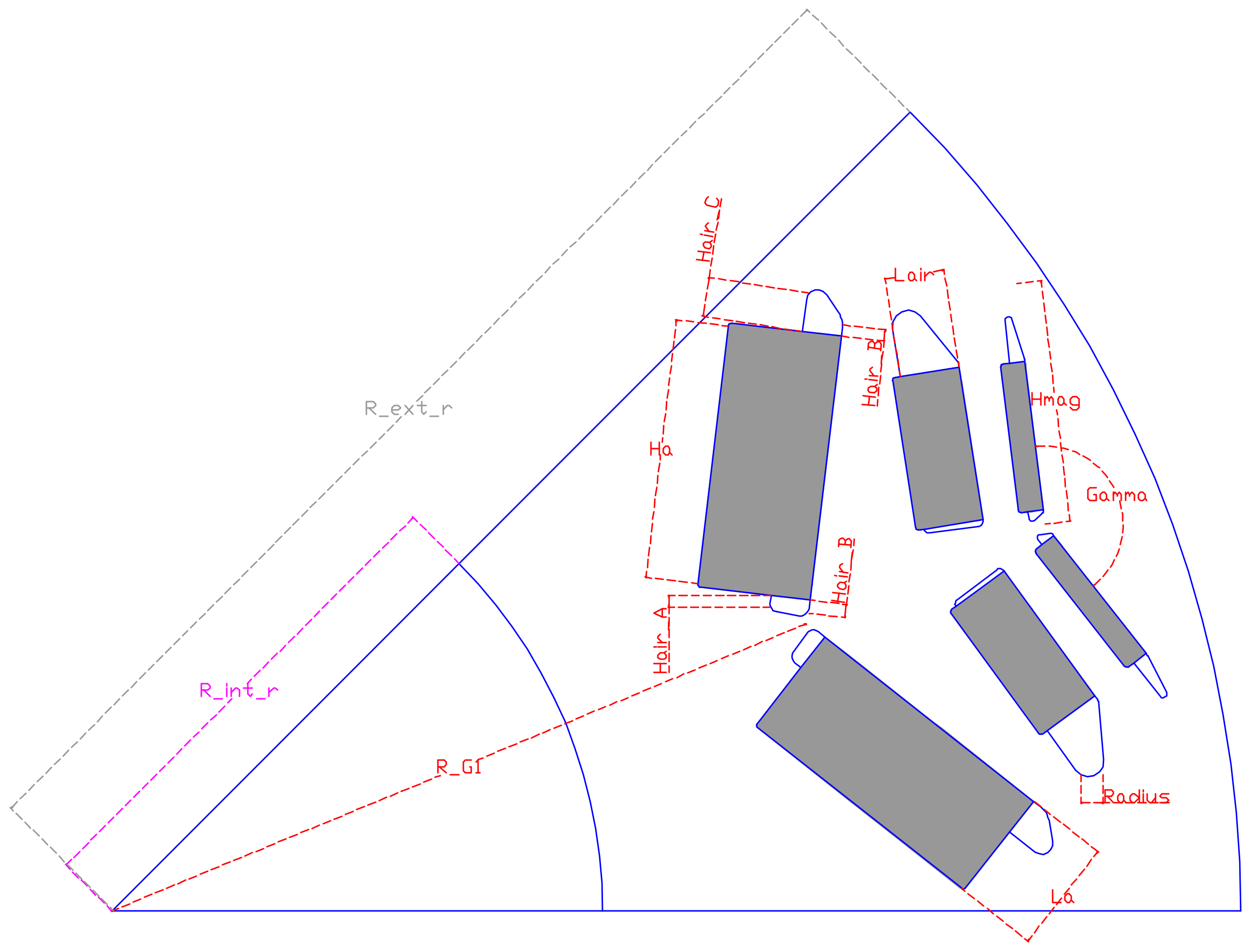
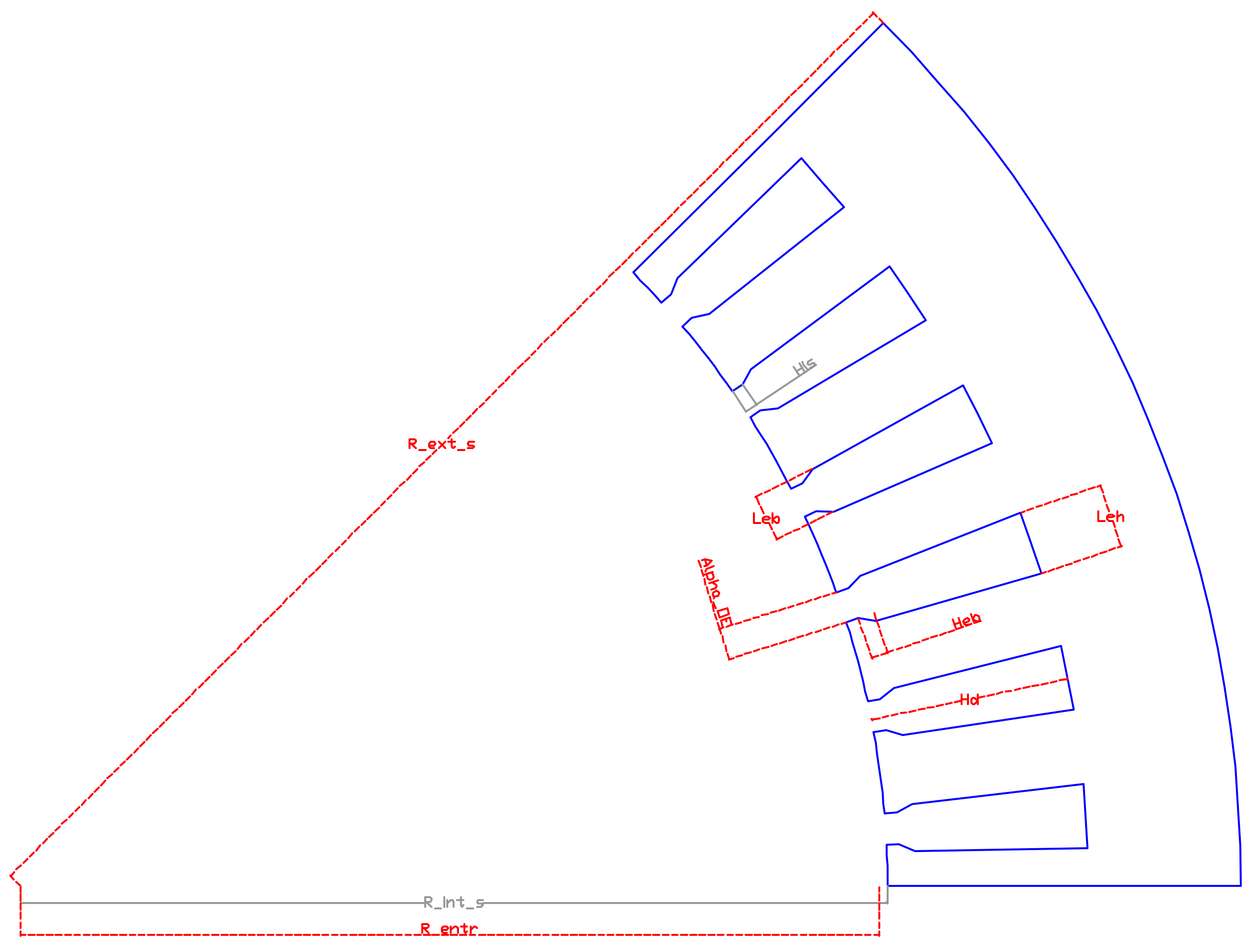



| Rotor | Stator | ||
|---|---|---|---|
| R_int_r | Inner rotor radius | L_active | Active length |
| R_G1 | Layer radial position | R_ext_s | Outer stator radius |
| La | Magnet length | R_entr | Air Gap radius |
| Ha | Magnet width | Alpha_OE | Opening slot |
| Hmag | Layer maximum length | Hd | Slot length |
| Gamma | Layer opening angle | Heb | Isthmus height |
| Lair | Air pocket width | Leb | Bottom slot width |
| Hair_A | Bottom air pocket height A | Leh | Top slot width |
| Hair_B | Bottom air pocket height B | ||
| Hair_C | Top air pocket height C | ||
| Radius | Fillet variable for air pocket |
| Parameters (Unit) | Value | Parameters (Unit) | Value |
|---|---|---|---|
| Min Power to reach (kW) | - | Pole pairs | 4 |
| AigGap (mm) | 0.7 | Steel: M270-35 AMagnet: N38EH | - |
| Rated Power (kW) | 80 | Slots number | 48 |
| Min torque to reach (N.m) | - | DC voltage (V) | 400 |
| Torque point 2 (N.m) | - | Maximum Current (A) | 600 |
| Torque point 3 (N.m) | 0.5·T1 | Maximum outer diameter (mm) | 300 |
| Torque point 4 (N.m) | 0.5·T2 | Maximum active length (mm) | 200 |
| Base speed (rpm) | 4800 | Max speed (rpm) | 11,500 |
| Parameters (Unit) | Mabc | Mdq | Parameters (Unit) | M_abc | M_dq |
| Mass machine (kg) | 37 | 35 | Torque max (N.m) | - | - |
| Mass magnet (kg) | 3.8 | 3.57 | Power max (kW) | - | - |
| Mass copper (kg) | 6.1 | 6.72 | Current max (A) | 596 | 596 |
| Mass iron stator (kg) | 16.6 | 14.6 | Iron losses max (kW) | 3.59 | 4.26 |
| Mass iron rotor (kg) | 10.6 | 10.2 | Cupper losses max (kW) | 3.5 | 3.89 |
| Turn number | 9 | 10 | Total losses max (kW) | 7.10 | 8.05 |
| Active length (mm) | 164 | 162 | Efficiency max | 98% | 97% |
| Outer diameter (mm) | 205 | 203 | Teeth/yoke thickness (mm) | 4.5/12.4 | 3.8/10.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cisse, K.M.; Hlioui, S.; Belhadi, M.; Mermaz Rollet, G.; Gabsi, M.; Cheng, Y. Design Optimization of Multi-Layer Permanent Magnet Synchronous Machines for Electric Vehicle Applications. Energies 2021, 14, 7116. https://doi.org/10.3390/en14217116
Cisse KM, Hlioui S, Belhadi M, Mermaz Rollet G, Gabsi M, Cheng Y. Design Optimization of Multi-Layer Permanent Magnet Synchronous Machines for Electric Vehicle Applications. Energies. 2021; 14(21):7116. https://doi.org/10.3390/en14217116
Chicago/Turabian StyleCisse, Koua Malick, Sami Hlioui, Mhamed Belhadi, Guillaume Mermaz Rollet, Mohamed Gabsi, and Yuan Cheng. 2021. "Design Optimization of Multi-Layer Permanent Magnet Synchronous Machines for Electric Vehicle Applications" Energies 14, no. 21: 7116. https://doi.org/10.3390/en14217116
APA StyleCisse, K. M., Hlioui, S., Belhadi, M., Mermaz Rollet, G., Gabsi, M., & Cheng, Y. (2021). Design Optimization of Multi-Layer Permanent Magnet Synchronous Machines for Electric Vehicle Applications. Energies, 14(21), 7116. https://doi.org/10.3390/en14217116





