Time-Lapse CSEM Monitoring: Correlating the Anomalous Transverse Resistance with SoPhiH Maps
Abstract
:1. Introduction
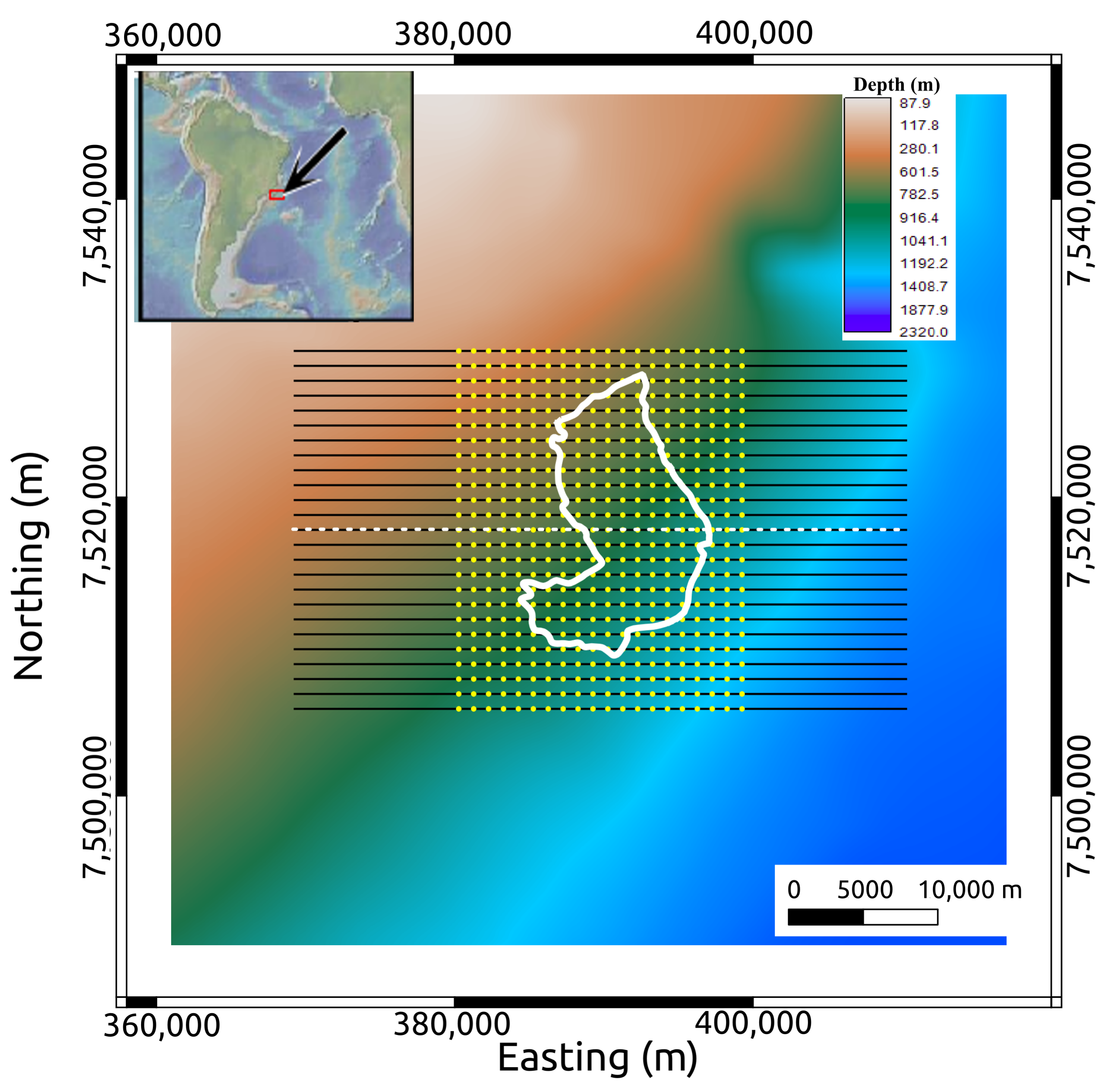
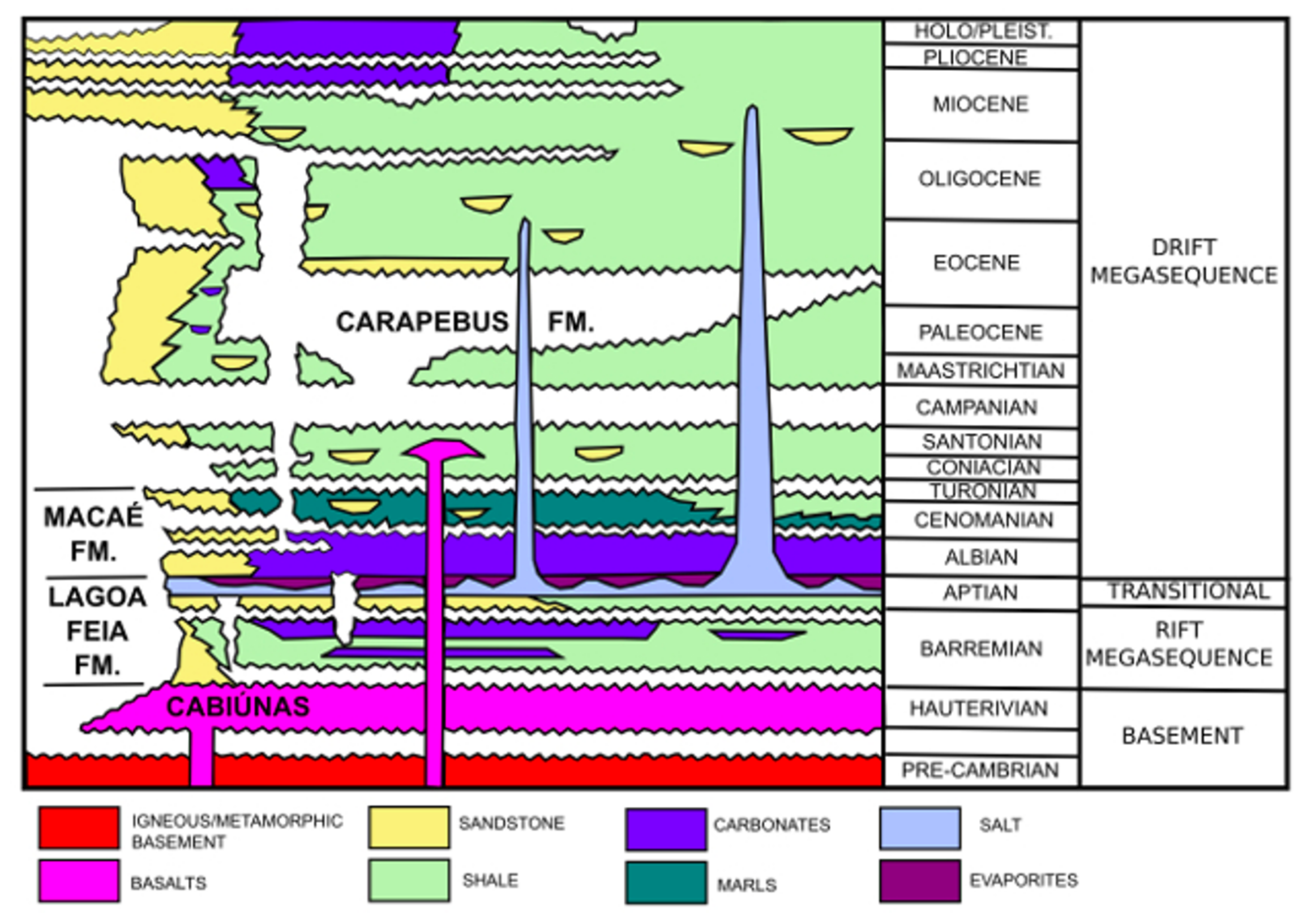
2. Geological Setting of Marlim Field
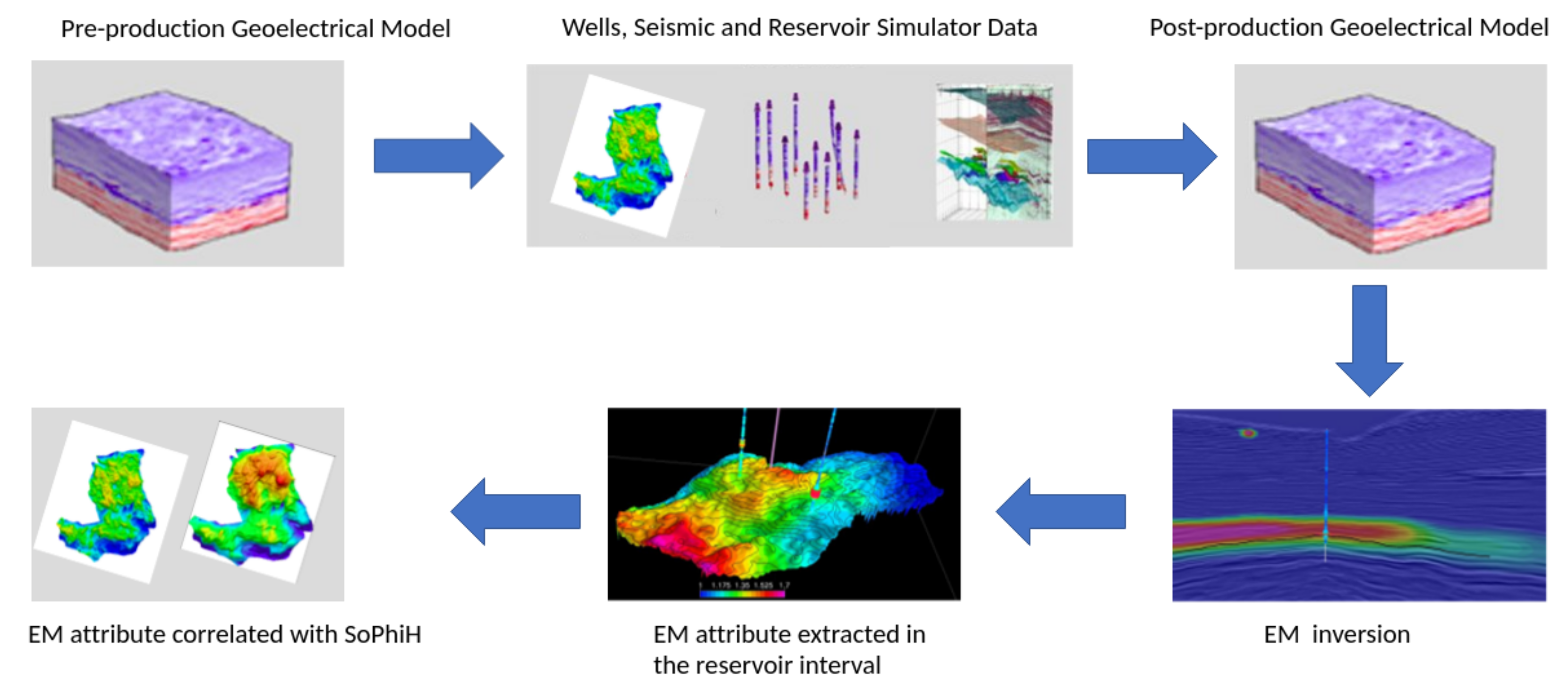
3. Time-Lapse Workflow
3.1. Marlim Time-Lapse Model
- 1.
- Take the harmonic averages that approximate the reservoir’s Rv and Rh resistivity values within the reservoir interval for the resistivity well logs at 36 selected wells. Estimate the water saturation (Sw) using the base year’s flow simulator (1991) and the Rv and Rh for the oil-saturated sand and water-saturated sand.
- 2.
- Estimate and n by linear regression of the logarithms of Rv, Rh, and Sw of the base year (1991) for the selected wells.
- 3.
3.2. CSEM Data
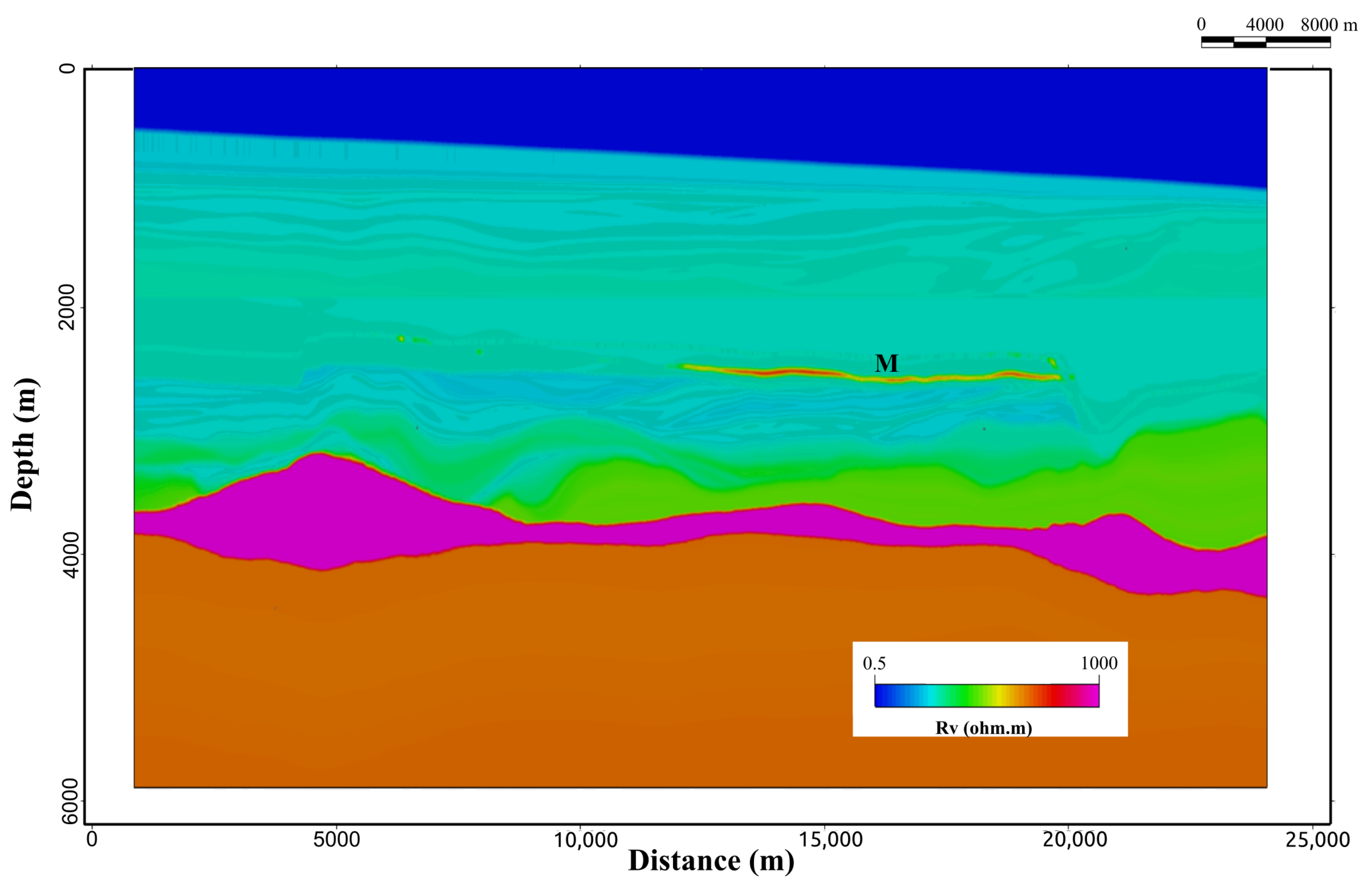
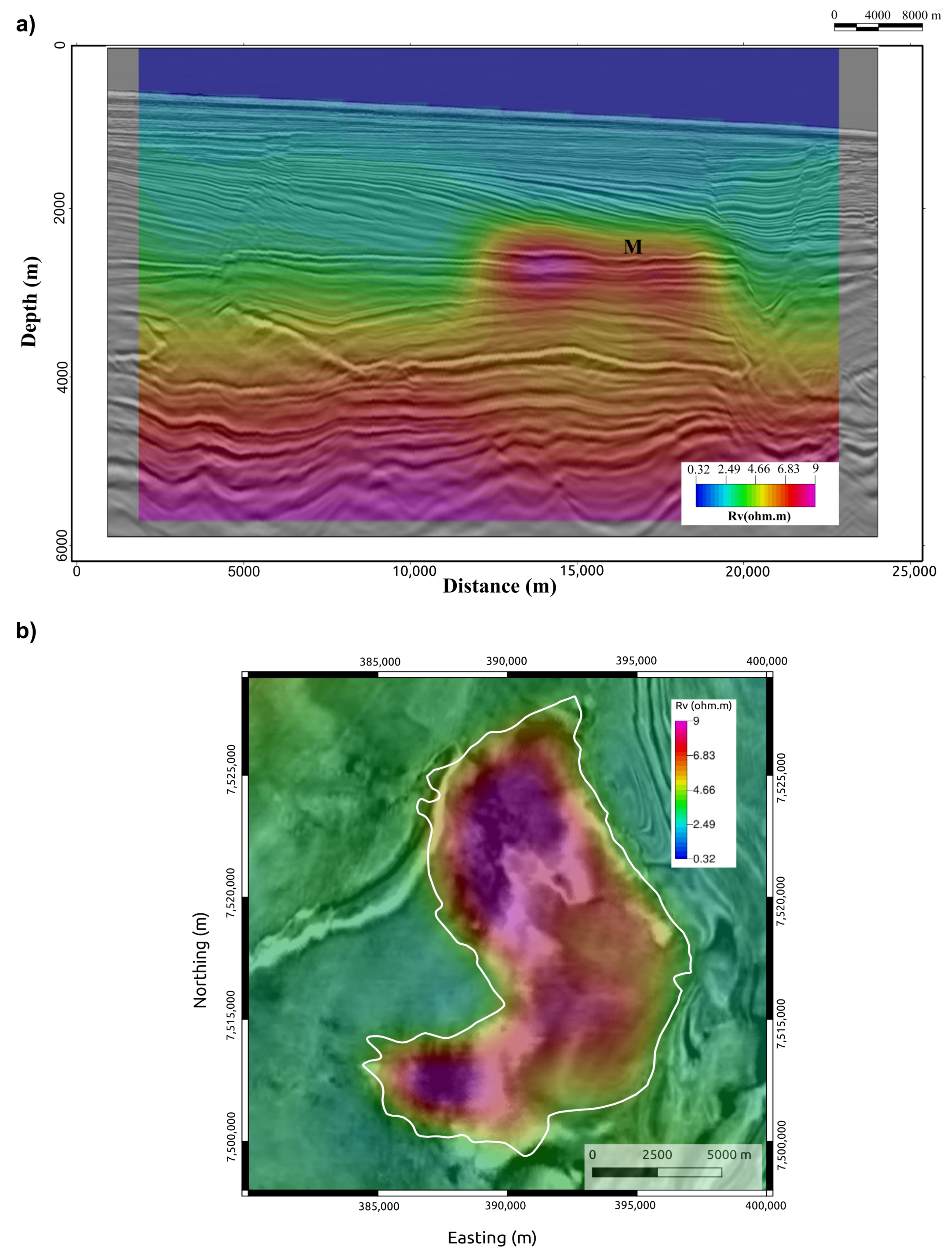
3.3. Inversion of the Time-Lapse Response
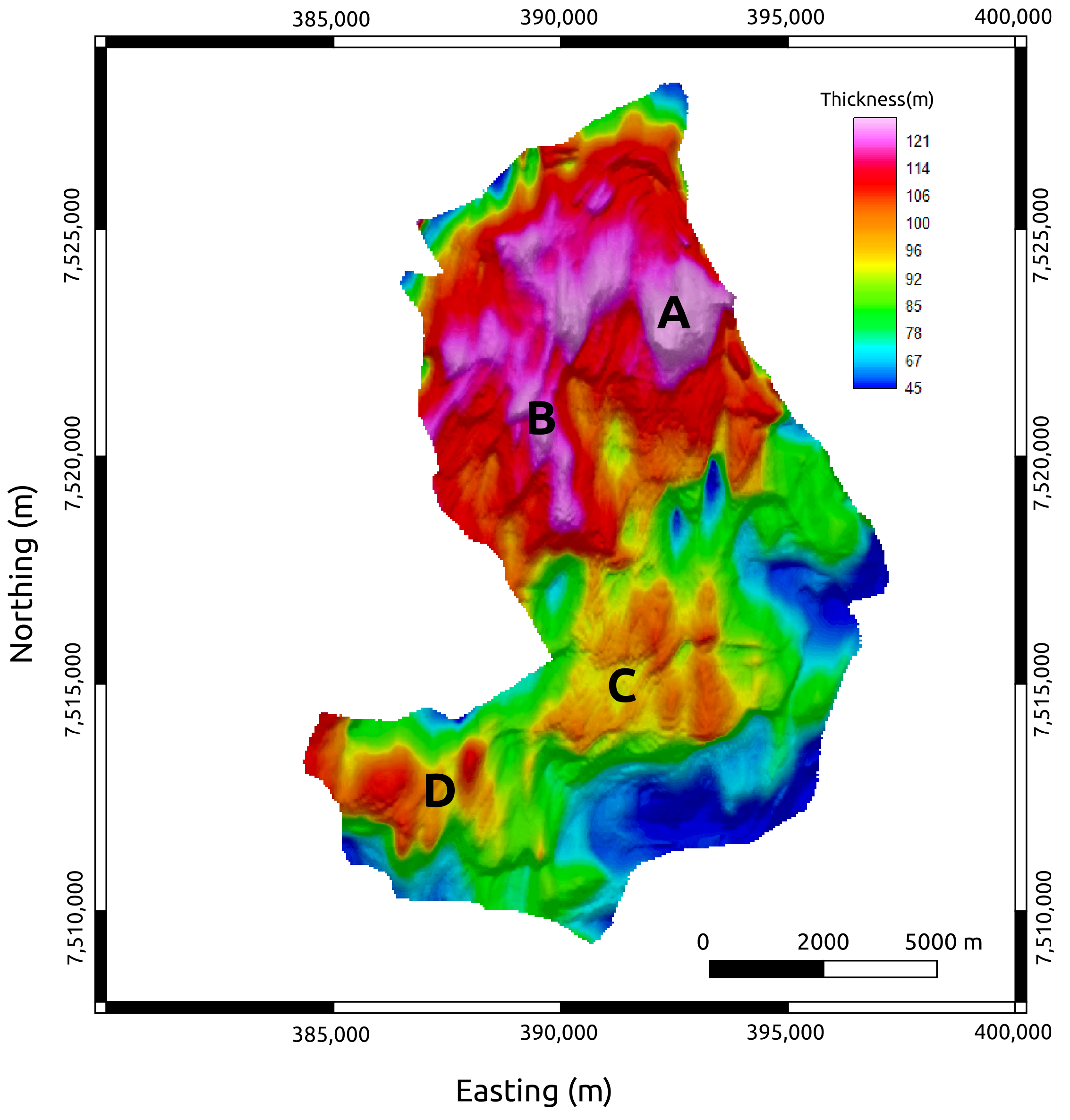
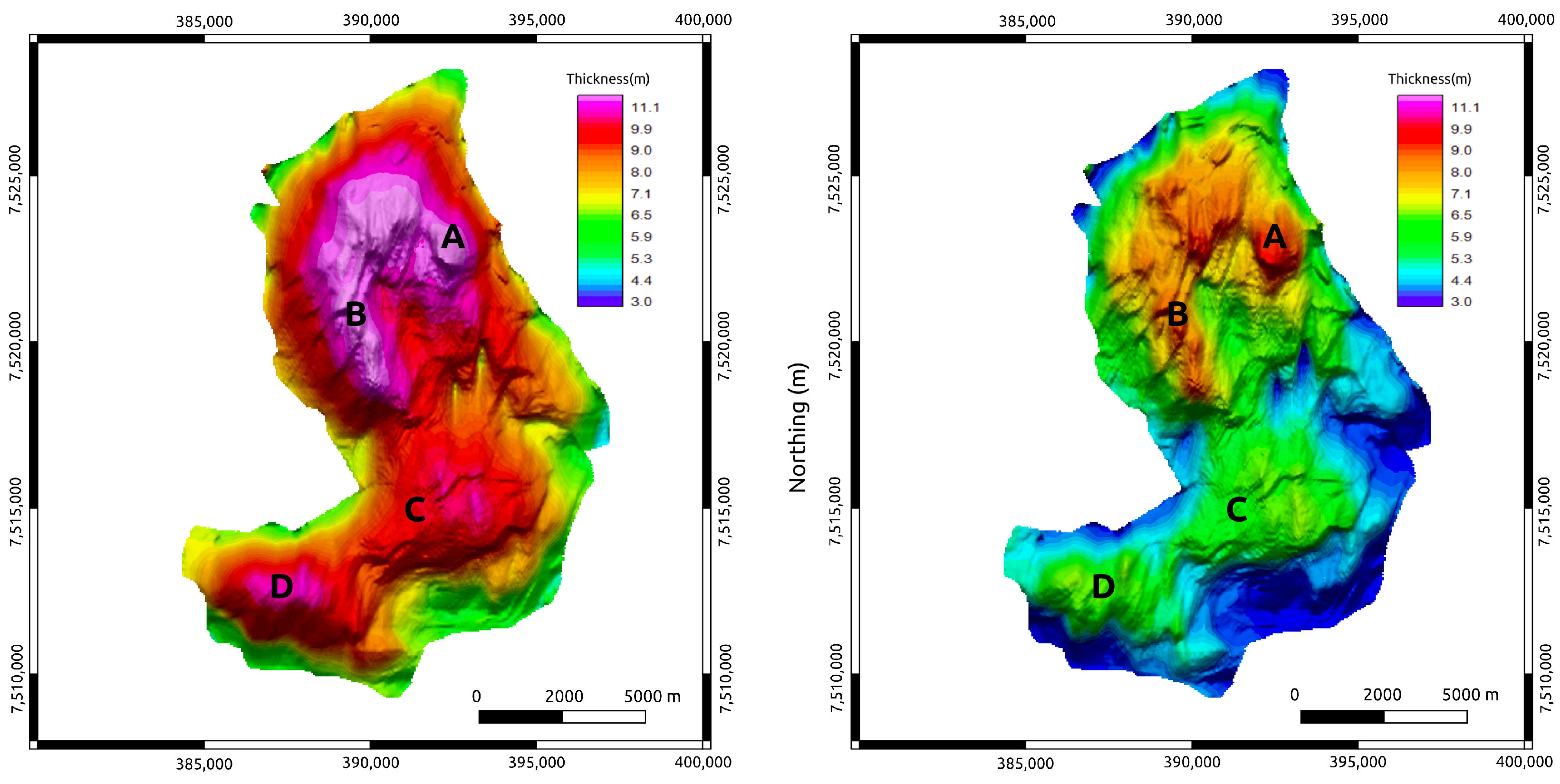
3.4. SoPhiH Maps
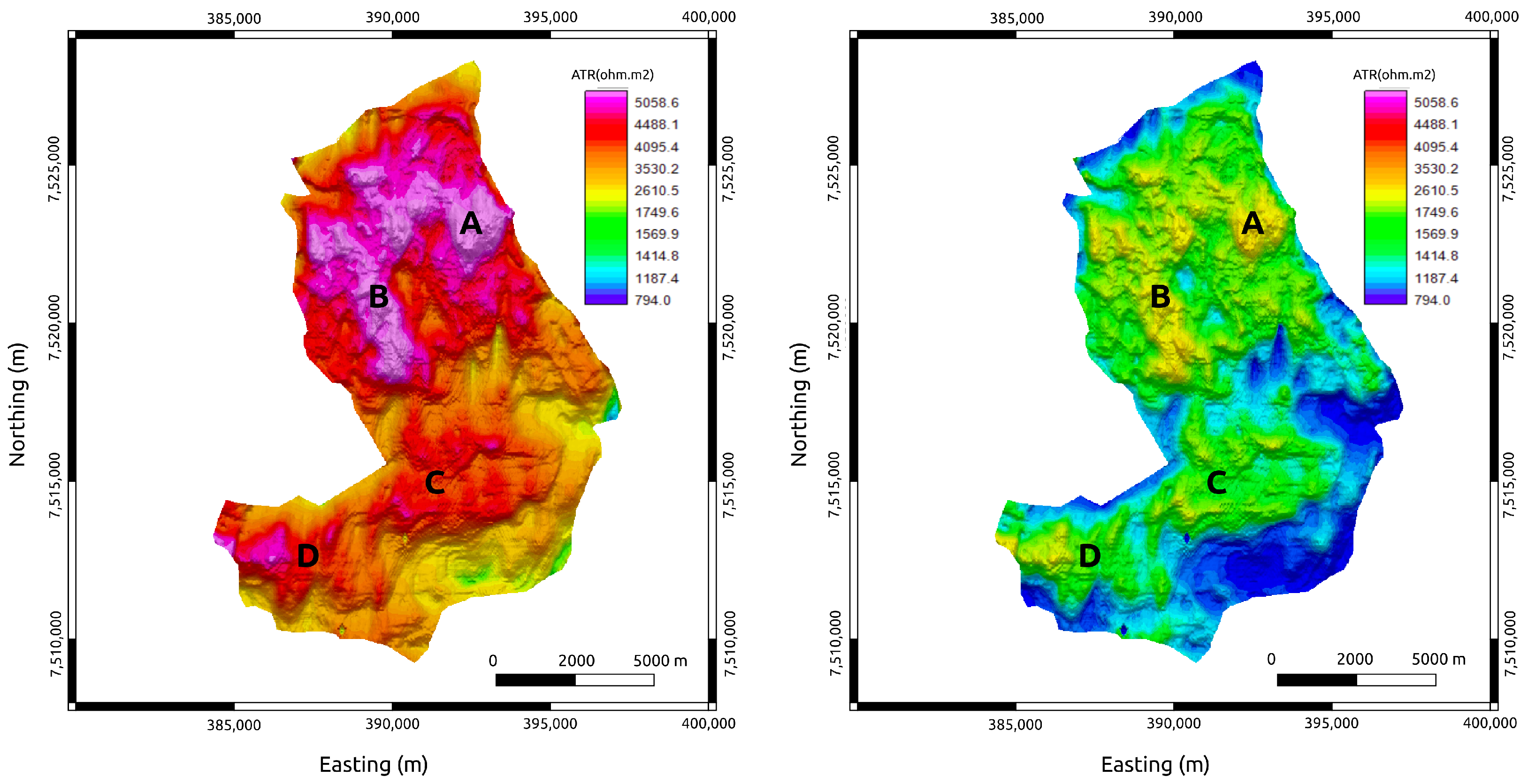
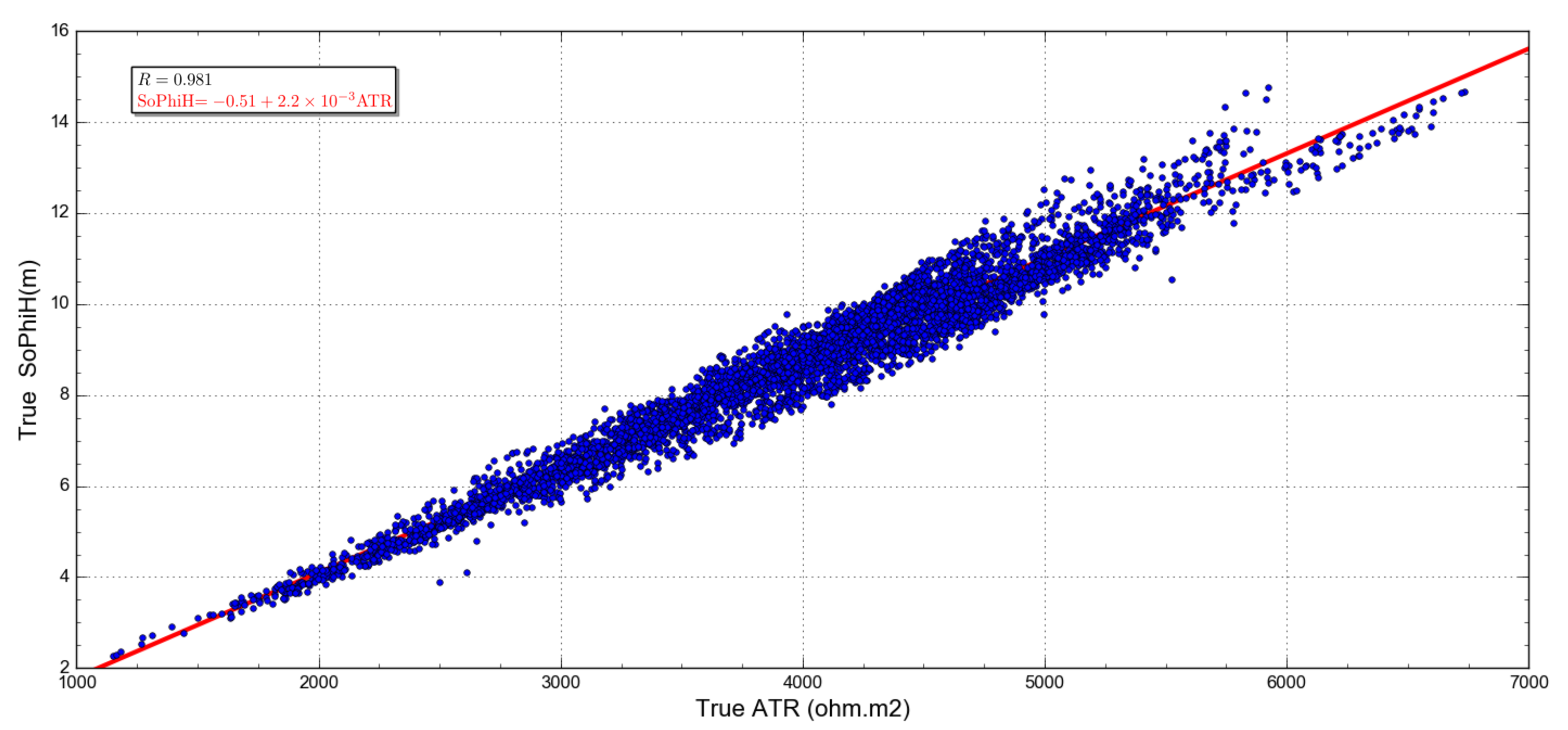
3.5. ATR–SoPhiH Correlation
4. Discussion
SoPhiH Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSEM | Controlled-source electromagnetic |
| BML | Below mud line |
| VTI | Vertical transverse isotropy |
| RAR | Resistivity anisotropy ratio |
| Rv | Vertical resistivity |
| Rh | Horizontal resistivity |
| ATR | Anomalous transverse resistance |
| OWC | Oil–water contact |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
| RMS | Root mean square |
References
- Constable, S.; Srnka, L.J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration. Geophysics 2007, 72, WA3–WA12. [Google Scholar] [CrossRef]
- Landrø, M. Discrimination between pressure and fluid saturation changes from time-lapse seismic data. Geophysics 2001, 66, 836–844. [Google Scholar] [CrossRef]
- MacGregor, L.; Tomlinson, J.; Maver, K.G. CSEM acquisition methods in a multi-physics context. First Break 2019, 37, 67–72. [Google Scholar] [CrossRef]
- Ellingsrud, S.; Eidesmo, T.; Johansen, S.; Sinha, M.C.; MacGregor, L.M.; Constable, S. Remote sensing of hydrocarbon layers by seabed logging (SBL): Results from a cruise offshore Angola. Lead. Edge 2002, 21, 972–982. [Google Scholar] [CrossRef]
- Panzner, M.; Morten, J.P.; Weibull, W.W.; Arntsen, B. Integrated seismic and electromagnetic model building applied to improve subbasalt depth imaging in the Faroe-Shetland Basin. Geophysics 2016, 81, E57–E68. [Google Scholar] [CrossRef]
- Zerilli, A.; Buonora, M.P.; Menezes, P.T.; Labruzzo, T.; Marçal, A.J.; Silva Crepaldi, J.L. Broadband marine controlled-source electromagnetic for subsalt and around salt exploration. Interpretation 2016, 4, T521–T531. [Google Scholar] [CrossRef]
- Buonora, M.P.P.; Correa, J.L.; Martins, L.S.; Menezes, P.T.L.; Pinho, E.J.C.; Silva Crepaldi, J.L.; Ribas, M.P.P.; Ferreira, S.M.; Freitas, R.C. mCSEM data interpretation for hydrocarbon exploration: A fast interpretation workflow for drilling decision. Interpretation 2014, 2, SH1–SH11. [Google Scholar] [CrossRef]
- Lyrio, J.C.S.O.; Menezes, P.T.L.; Correa, J.L.; Viana, A.R. Multiphysics anomaly map: A new data fusion workflow for geophysical interpretation. Interpretation 2020, 8, B35–B43. [Google Scholar] [CrossRef]
- Miotti, F.; Zerilli, A.; Menezes, P.T.L.; Crepaldi, J.L.; Viana, A.R. A new petrophysical joint inversion workflow: Advancing on reservoir’s characterization challenges. Interpretation 2018, 6, SG33–SG39. [Google Scholar] [CrossRef]
- Sambo, C.; Iferobi, C.C.; Babasafari, A.A.; Rezaei, S.; Akanni, O.A. The role of 4d time lapse seismic technology as reservoir monitoring and surveillance tool: A comprehensive review. J. Nat. Gas Sci. Eng. 2020, 80, 103312. [Google Scholar] [CrossRef]
- Black, N.; Zhdanov, M.S. Active geophysical monitoring of hydrocarbon reservoirs using electromagnetic methods. In Active Geophysical Monitoring; Elsevier: Amsterdam, The Netherlands, 2020; pp. 69–95. [Google Scholar]
- Black, N.; Wilson, G.A.; Gribenko, A.V.; Zhdanov, M.S.; Morris, E. 3D inversion of time-lapse CSEM data based on dynamic reservoir simulations of the Harding field, North Sea. In SEG Technical Program Expanded Abstracts 2011; Society of Exploration Geophysicists: Tulsa, OK, USA, 2011; pp. 666–670. [Google Scholar]
- Katterbauer, K.; Hoteit, I.; Sun, S. EMSE: Synergizing EM and seismic data attributes for enhanced forecasts of reservoirs. J. Pet. Sci. Eng. 2014, 122, 396–410. [Google Scholar] [CrossRef]
- Salako, O.; MacBeth, C.; MacGregor, L. Potential applications of time-lapse CSEM to reservoir monitoring. First Break 2015, 33, 35–46. [Google Scholar] [CrossRef]
- Ayani, M.; Grana, D.; Liu, M. Stochastic inversion method of time-lapse controlled source electromagnetic data for CO2 plume monitoring. Int. J. Greenh. Gas Control 2020, 100, 103098. [Google Scholar] [CrossRef]
- Shantsev, D.V.; Nerland, E.A.; Gelius, L.J. Time-lapse CSEM: How important is survey repeatability? Geophys. J. Int. 2020, 223, 2133–2147. [Google Scholar] [CrossRef]
- Ziolkowski, A.; Parr, R.; Wright, D.; Nockles, V.; Limond, C.; Morris, E.; Linfoot, J. Multi-transient electromagnetic repeatability experiment over the North Sea Harding field. Geophys. Prospect. 2010, 58, 1159–1176. [Google Scholar] [CrossRef]
- Zerilli, A.; Labruzzo, T.; Golfre’Andreasi, F.; Menezes, P.D.T.L.; Crepaldi, J.L.S.; Alvim, L.D.M. Realizing 4D CSEM Value on Deep Water Reservoirs—The Jubarte Case Study. In Proceedings of the 80th EAGE Conference and Exhibition 2018, Copenhagen, Denmark, 11–14 June 2018; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2018; Volume 2018, pp. 1–5. [Google Scholar]
- Lucchesi, C.F.; Gontijo, J.E. Deep Water Reservoir Management: The Brazilian Experience. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 1998. [Google Scholar] [CrossRef]
- Lourenço, J.; Menezes, P.T.L.; Barbosa, V.C.F. Connecting onshore-offshore Campos Basin structures: Interpretation of high-resolution airborne magnetic data. Interpretation 2014, 2, SJ35–SJ45. [Google Scholar] [CrossRef]
- Dumas, G.E.S.; Freire, E.B.; Johann, P.R.S.; Silva, L.S.; Vieira, R.A.B.; Bruhn, C.H.L.; Pinto, A.C.C. Reservoir Management of the Campos Basin Brown Fields. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Brinkerhoff, R. Pitfalls in Geological Mapping Within Unconventional Plays. In Proceedings of the AAPG Annual Convention and Exhibition, Calgary, AB, Canada, 21 June 2016. [Google Scholar]
- Carvalho, B.R.; Menezes, P.T.L. Marlim R3D: A realistic model for CSEM simulations-phase I: Model building. Braz. J. Geol. 2017, 47, 633–644. [Google Scholar] [CrossRef] [Green Version]
- Shecaira, F.S.; Daher, J.S.; Gomes, A.C.A.; Capeleiro Pinto, A.C.; Filoco, P.R.; Gomes, J.A.T.; Freitas, L.C.S.; Balthar, S. Injeção de Água no Campo de Marlim—Uma Abordagem Integrada para o Gerenciamento de Reservatórios. In Proceedings of the Rio Oil & Gas Expo and Conference, Rio de Janeiro, Brazil, October 2000; Brazilian Petroleum Institute—IBP: Rio de Janeiro, Brazil, 2000; pp. 1–9. [Google Scholar]
- Bruhn, C.T.; Gomes, J.; Lucchese, C., Jr.; Johann, P. Campos Basin: Reservoir Characterization and Management-Historical Overview and Future Challenges. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2003. [Google Scholar]
- Mohriak, W.U.; Macedo, J.M.; Castellani, R.T. Salt tectonics and structural styles in the deep-water province of the Cabo Frio region, Rio de Janeiro, Brazil. In Salt Tectonics: A Global Perspective: AAPG Memoir 65; Jackson, M.P.A., Roberts, D.G., Snelson, S., Eds.; AAPG: Tulsa, OK, USA, 1996; Chapter 13; pp. 273–304. [Google Scholar]
- Peres, W.E. Shelf-fed turbidite system model and its application to the Oligocene deposits of the Campos Basin, Brazil. AAPG Bull. 1993, 77, 81–101. [Google Scholar]
- Cobbold, P.R.; Meisling, K.E.; Mount, V.S. Reactivation of an obliquely rifted margin, Campos and Santos basins, southeastern Brazil. AAPG Bull. 2001, 85, 1925–1944. [Google Scholar] [CrossRef]
- Guardado, L.R.; Spadini, A.R.; Brandão, J.S.L.; Mello, M.R. Petroleum System of the Campos Basin, Brazil. In Petroleum Systems of South Atlantic Margins: AAPG Memoir 73; Mello, M.R., Katz, B.J., Eds.; AAPG: Tulsa, OK, USA, 2000; Chapter 22; pp. 317–324. [Google Scholar]
- Sansonowski, R.C.; de Oliveira, R.M.; Júnior, N.M.d.S.R.; Bampi, D.; Junior, L.F.C. 4D seismic interpretation in the Marlim Field, Campos Basin, offshore Brazil. In Proceedings of the 10th International Congress of the Brazilian Geophysical Society, Rio de Janeiro, Brazil, 19–23 November 2007; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2007; pp. 1–6. [Google Scholar]
- Johann, P.; Sansonowski, R.; Oliveira, R.; Bampi, D. 4D seismic in a heavy-oil, turbidite reservoir offshore Brazil. Lead. Edge 2009, 28, 718–729. [Google Scholar] [CrossRef]
- Fainstein, R.; Jamieson, G.; Hannan, A.; Biles, N.; Krueger, A.; Shelander, D. Offshore Brazil Santos Basin exploration potential from recently acquired seismic data. In Proceedings of the 7th International Congress of the Brazilian Geophysical Society, Salvador, Brazil, 28–31 October 2001; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2001; pp. 1–6. [Google Scholar]
- Nascimento, T.M.; Menezes, P.T.; Braga, I.L. High-resolution acoustic impedance inversion to characterize turbidites at Marlim Field, Campos Basin, Brazil. Interpretation 2014, 2, T143–T153. [Google Scholar] [CrossRef]
- Correa, J.L.; Menezes, P.T. Marlim R3D: A realistic model for controlled-source electromagnetic simulations—Phase 2: The controlled-source electromagnetic data set. Geophysics 2019, 84, E293–E299. [Google Scholar] [CrossRef]
- Mutti, E.; Cunha, R.S.; Bulhoes, E.; Arienti, L.M.; Viana, A.R. Contourites and turbidites of the Brazilian marginal basins. In Proceedings of the AAPG Annual Convention & Exhibition, Houston, TX, USA, 6–9 April 2014. [Google Scholar]
- Orange, A.; Key, K.; Constable, S. The feasibility of reservoir monitoring using time-lapse marine CSEM. Geophysics 2009, 74, F21–F29. [Google Scholar] [CrossRef]
- Andréis, D.; MacGregor, L. Using CSEM to monitor production from a complex 3D gas reservoir—A synthetic case study. Lead. Edge 2011, 30, 1070–1079. [Google Scholar] [CrossRef]
- Caumon, G.; Mallet, J.L. 3D Stratigraphic models: Representation and stochastic modelling. In Proceedings of the IAMG 2006, International Association for Mathematical Geology XIth International Congress, Liege, Belgium, 3–8 September 2006. [Google Scholar]
- Fanchi, J.R. Chapter 11—Traditional Model Study. In Principles of Applied Reservoir Simulation, 4th ed.; Fanchi, J.R., Ed.; Gulf Professional Publishing: New York, NY, USA, 2018; pp. 195–219. [Google Scholar] [CrossRef]
- Gassmann, F. Elastic waves through a packing of spheres. Geophysics 1951, 16, 673–685. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Glover, P.W.J. A generalized Archie’s law for n phases. Geophysics 2010, 75, E247–E265. [Google Scholar] [CrossRef] [Green Version]
- Maaø, F.A. Fast finite-difference time-domain modeling for marine-subsurface electromagnetic problems. Geophysics 2007, 72, A19–A23. [Google Scholar] [CrossRef]
- Lorenz, L.; Pedersen, H.T.; Buonora, M.P. First results from a Brazilian mCSEM calibration campaign. In Proceedings of the 13th International Congress of the Brazilian Geophysical Society & EXPOGEF, Rio de Janeiro, Brazil, 26–29 August 2013; Society of Exploration Geophysicists and Brazilian Geophysical Society: Rio de Janeiro, Brazil, 2013; pp. 131–136. [Google Scholar]
- Mittet, R.; Morten, J.P. Detection and imaging sensitivity of the marine CSEM method. Geophysics 2012, 77, E411–E425. [Google Scholar] [CrossRef] [Green Version]
- Zach, J.; Bjørke, A.; Støren, T.; Maaø, F. 3D inversion of marine CSEM data using a fast finite-difference time-domain forward code and approximate Hessian-based optimization. In SEG Technical Program Expanded Abstracts 2008; Society of Exploration Geophysicists: Tulsa, OK, USA, 2008; pp. 614–618. [Google Scholar]





| Background Lithology | Rh (ohm.m) | Rv (ohm.m) |
|---|---|---|
| Oligo-Miocene Shales | 1 | 2 |
| Post-Salt Carbonates | 6.5 | 13 |
| Aptian Salt | 1000 | 1000 |
| Pre-Salt Carbonates | 15 | 30 |
| Mesh Parameters | Dimension |
|---|---|
| cell size—X | 100 m |
| cell size—Y | 100 m |
| cell size—Z | 20 m |
| Number of cells—X | 563 |
| Number of cells—Y | 511 |
| Number of cells—Z | 310 |
| Total number of cells | 89,882,950.00 |
| Mesh Parameters | Dimension |
|---|---|
| cell size—X | 200 m |
| cell size—Y | 200 m |
| cell size—Z | 50 m |
| Number of cells—X | 220 |
| Number of cells—Y | 195 |
| Number of cells—Z | 110 |
| Total number of cells | 8,910,000.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menezes, P.T.L.; Correa, J.L.; Alvim, L.M.; Viana, A.R.; Sansonowski, R.C. Time-Lapse CSEM Monitoring: Correlating the Anomalous Transverse Resistance with SoPhiH Maps. Energies 2021, 14, 7159. https://doi.org/10.3390/en14217159
Menezes PTL, Correa JL, Alvim LM, Viana AR, Sansonowski RC. Time-Lapse CSEM Monitoring: Correlating the Anomalous Transverse Resistance with SoPhiH Maps. Energies. 2021; 14(21):7159. https://doi.org/10.3390/en14217159
Chicago/Turabian StyleMenezes, Paulo T. L., Jorlivan L. Correa, Leonardo M. Alvim, Adriano R. Viana, and Rui C. Sansonowski. 2021. "Time-Lapse CSEM Monitoring: Correlating the Anomalous Transverse Resistance with SoPhiH Maps" Energies 14, no. 21: 7159. https://doi.org/10.3390/en14217159
APA StyleMenezes, P. T. L., Correa, J. L., Alvim, L. M., Viana, A. R., & Sansonowski, R. C. (2021). Time-Lapse CSEM Monitoring: Correlating the Anomalous Transverse Resistance with SoPhiH Maps. Energies, 14(21), 7159. https://doi.org/10.3390/en14217159







