CFD Analysis of the Influence of the Front Wing Setup on a Time Attack Sports Car’s Aerodynamics
Abstract
:1. Introduction
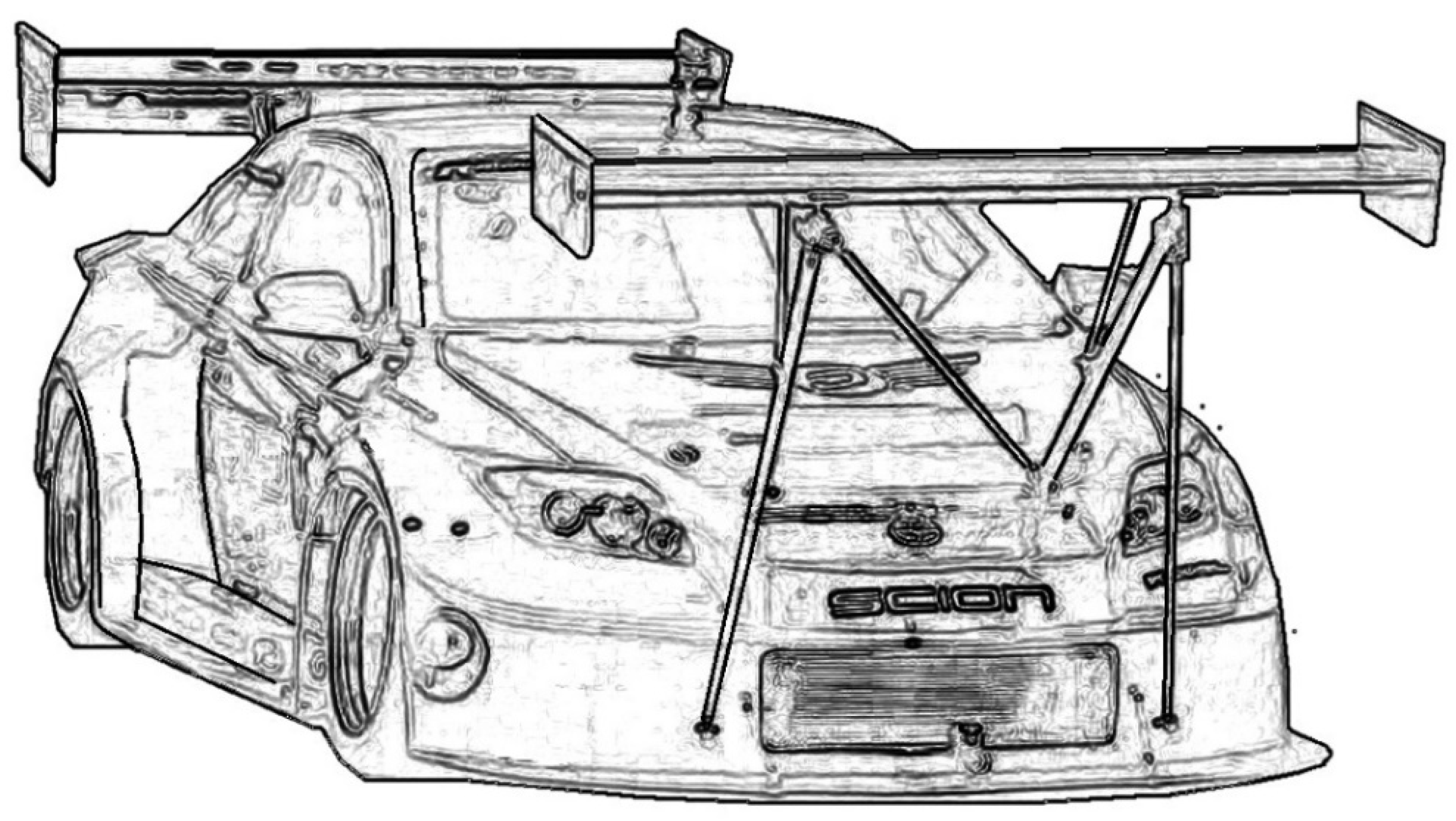
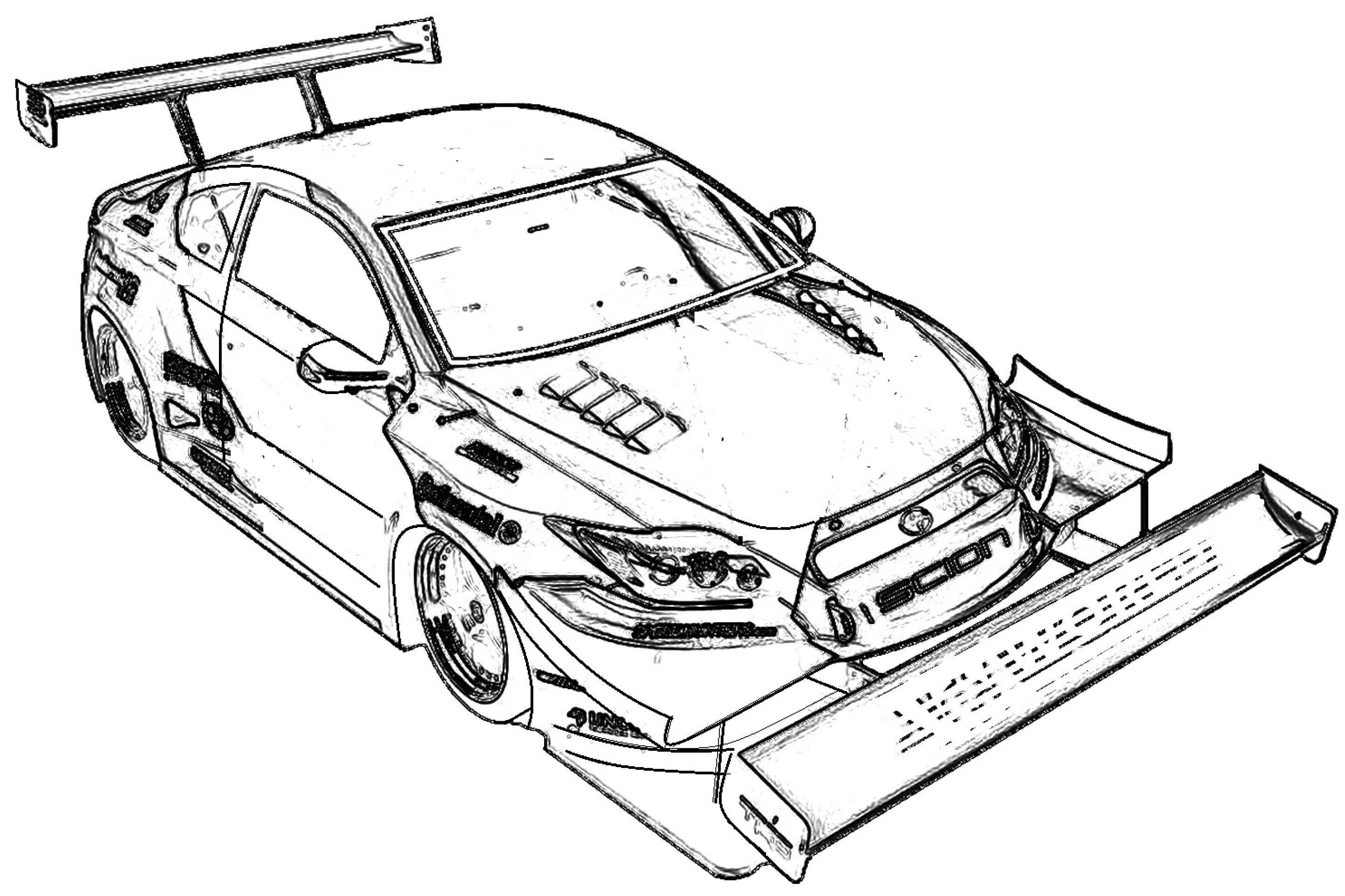
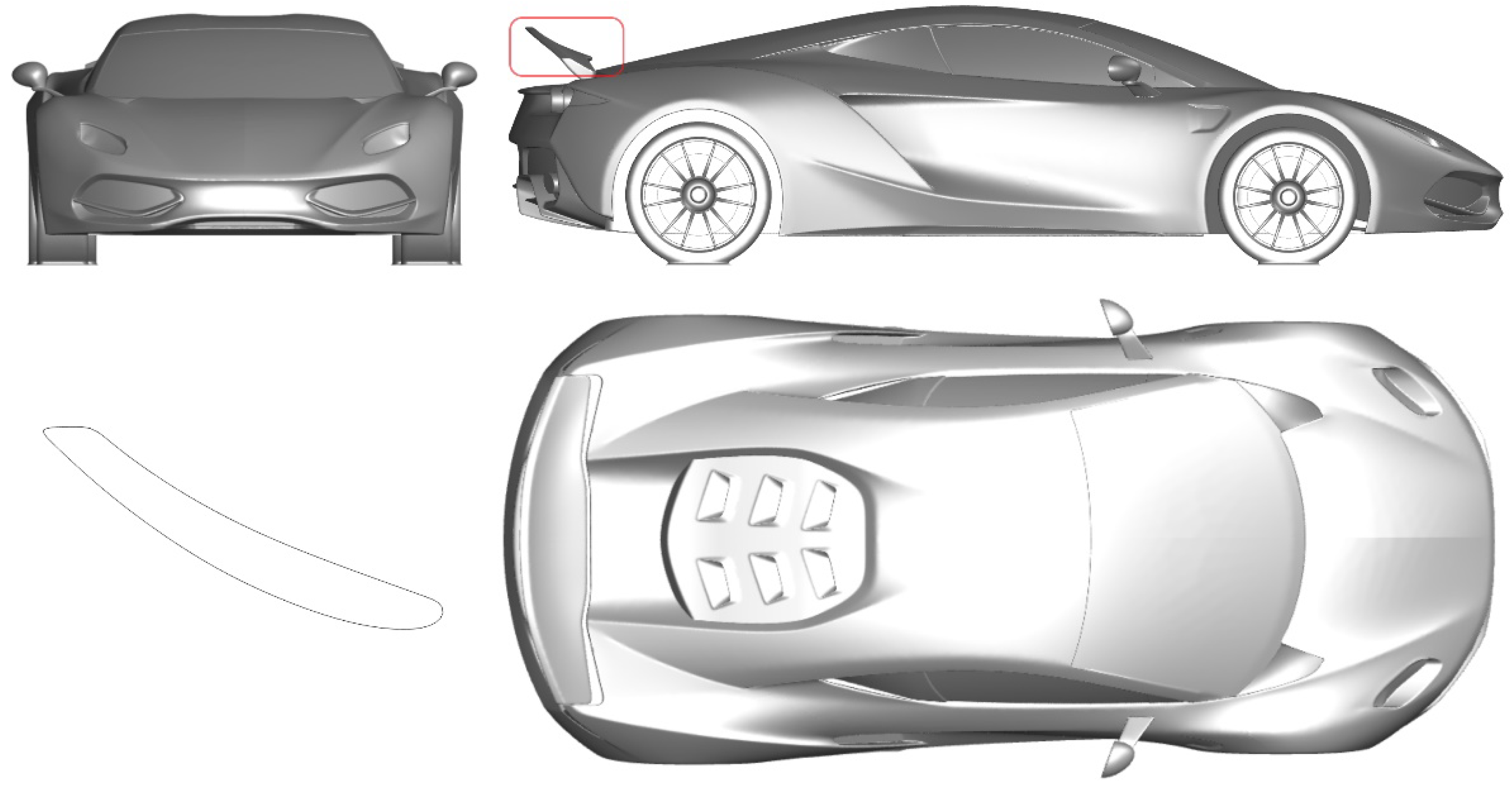
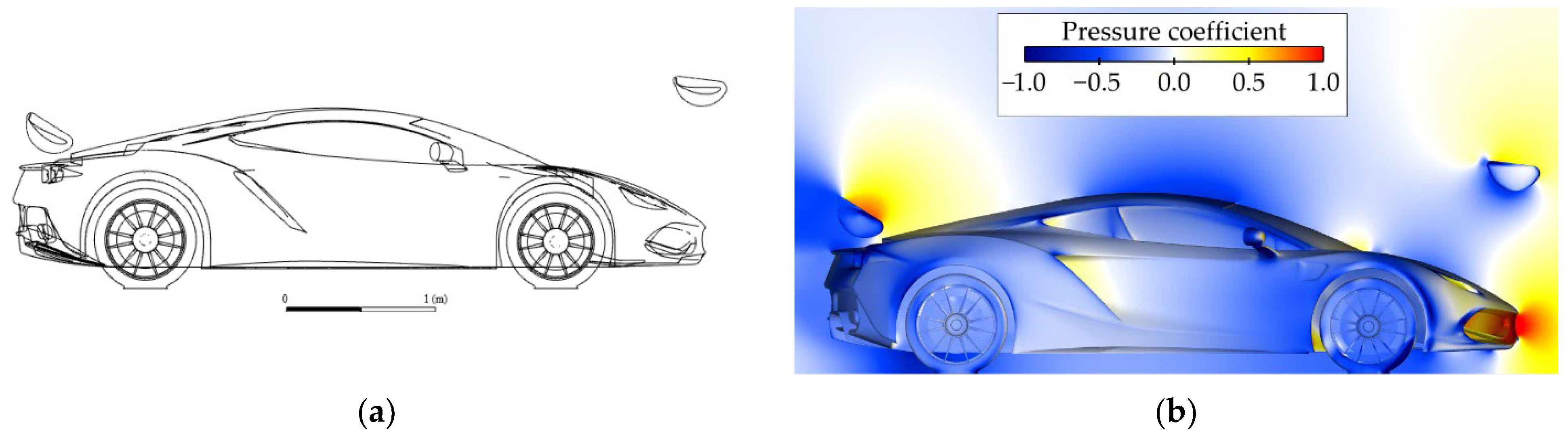
2. Materials and Methods
3. Results and Discussion
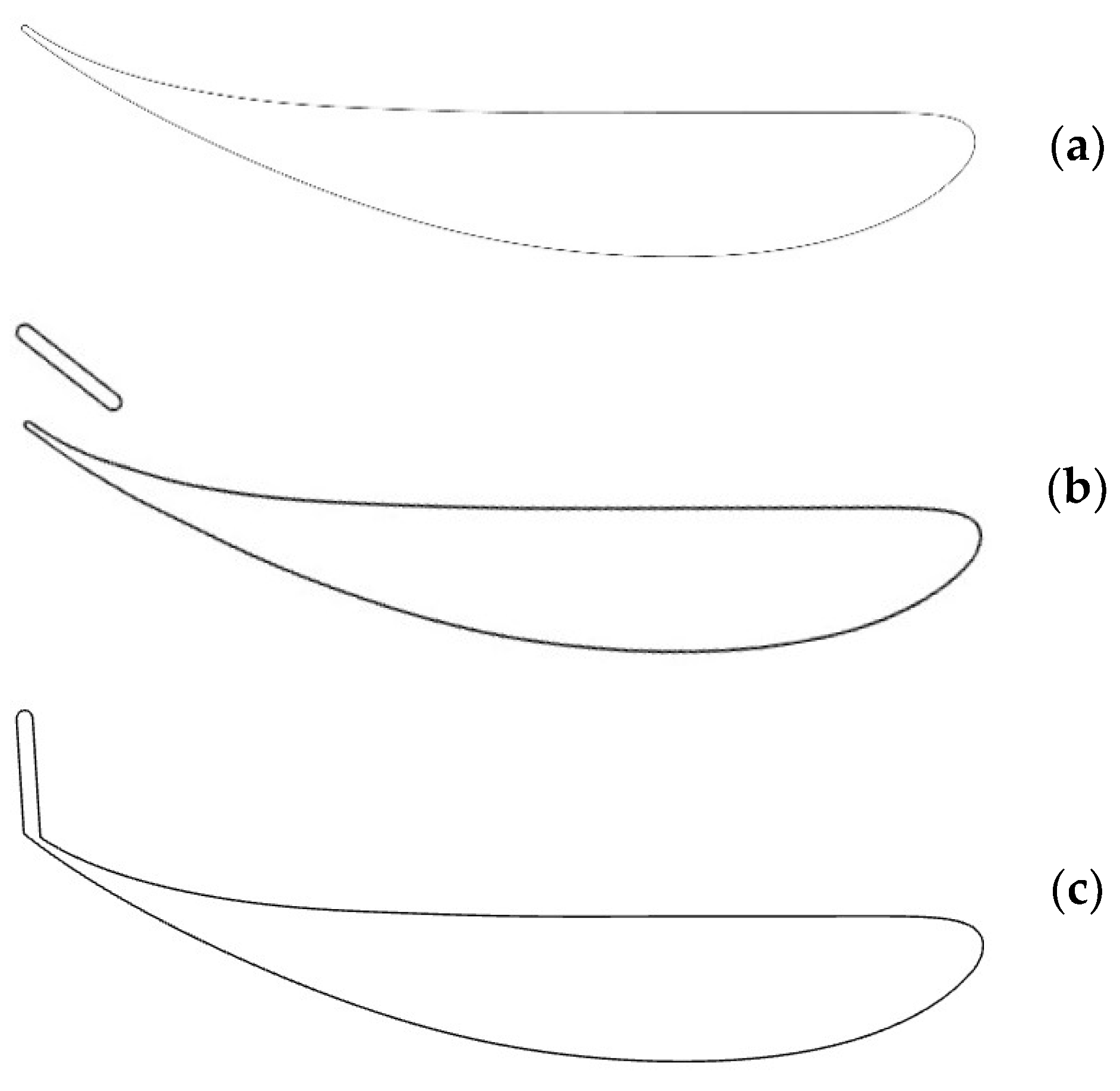
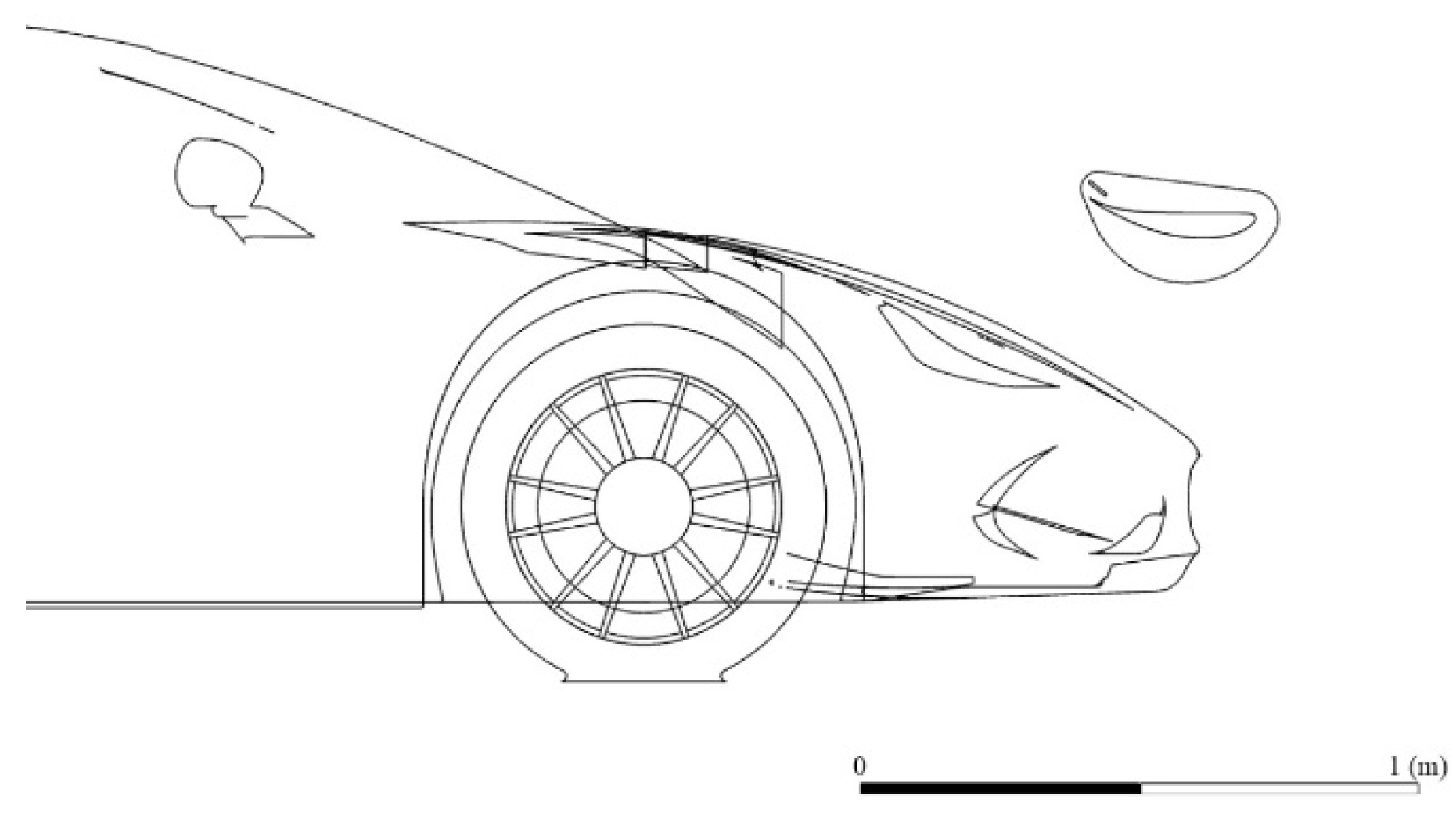
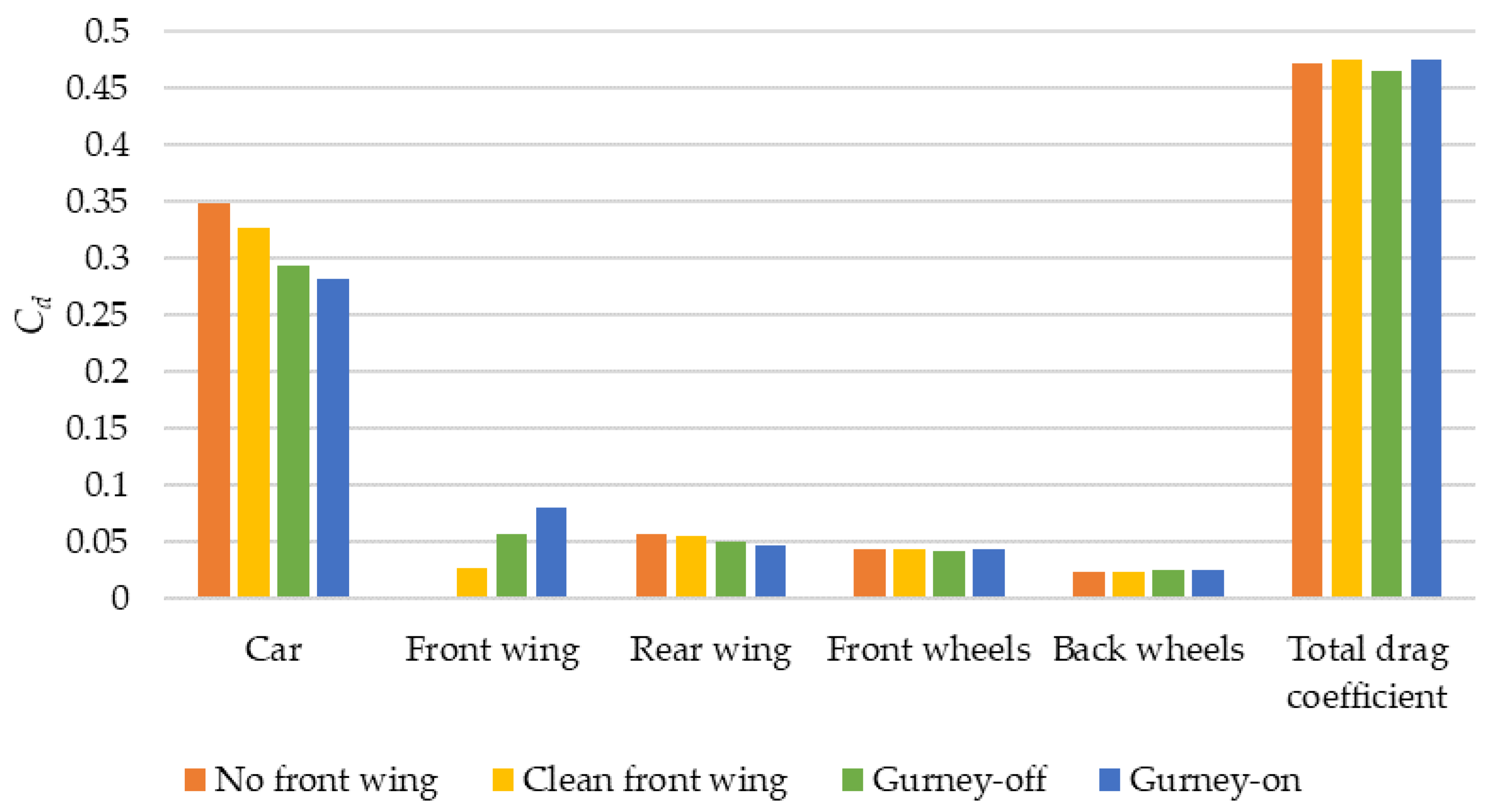
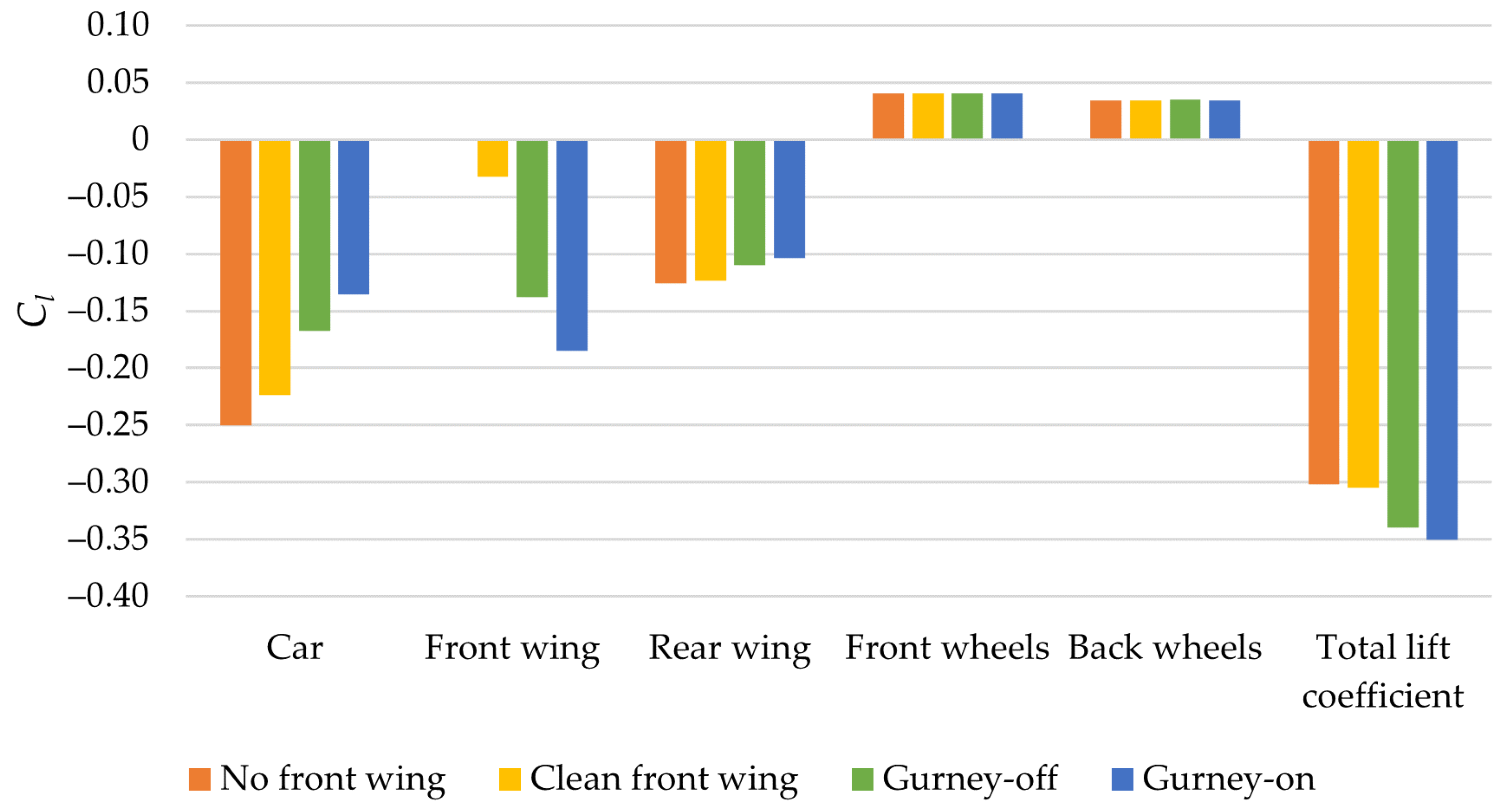
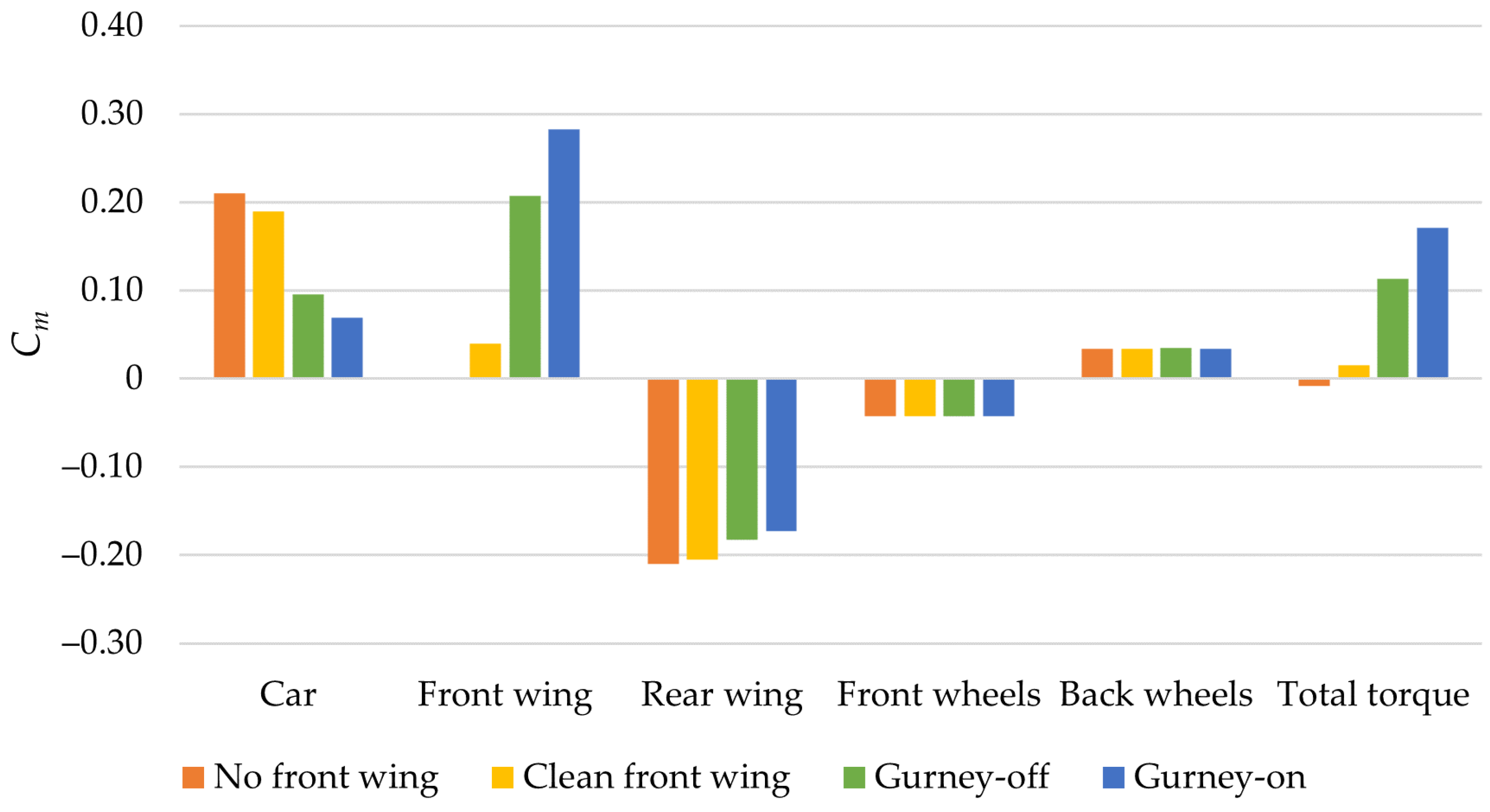
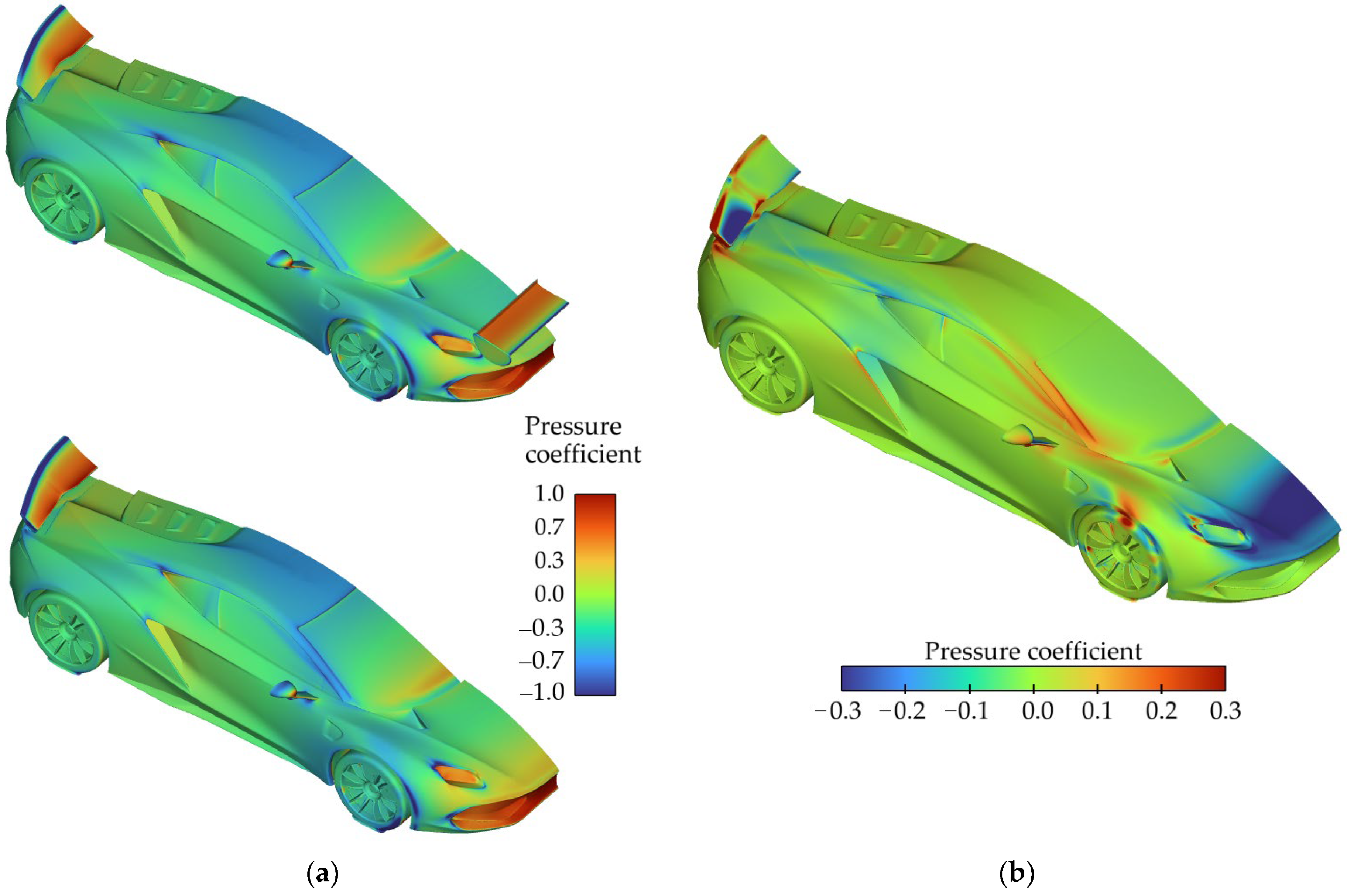
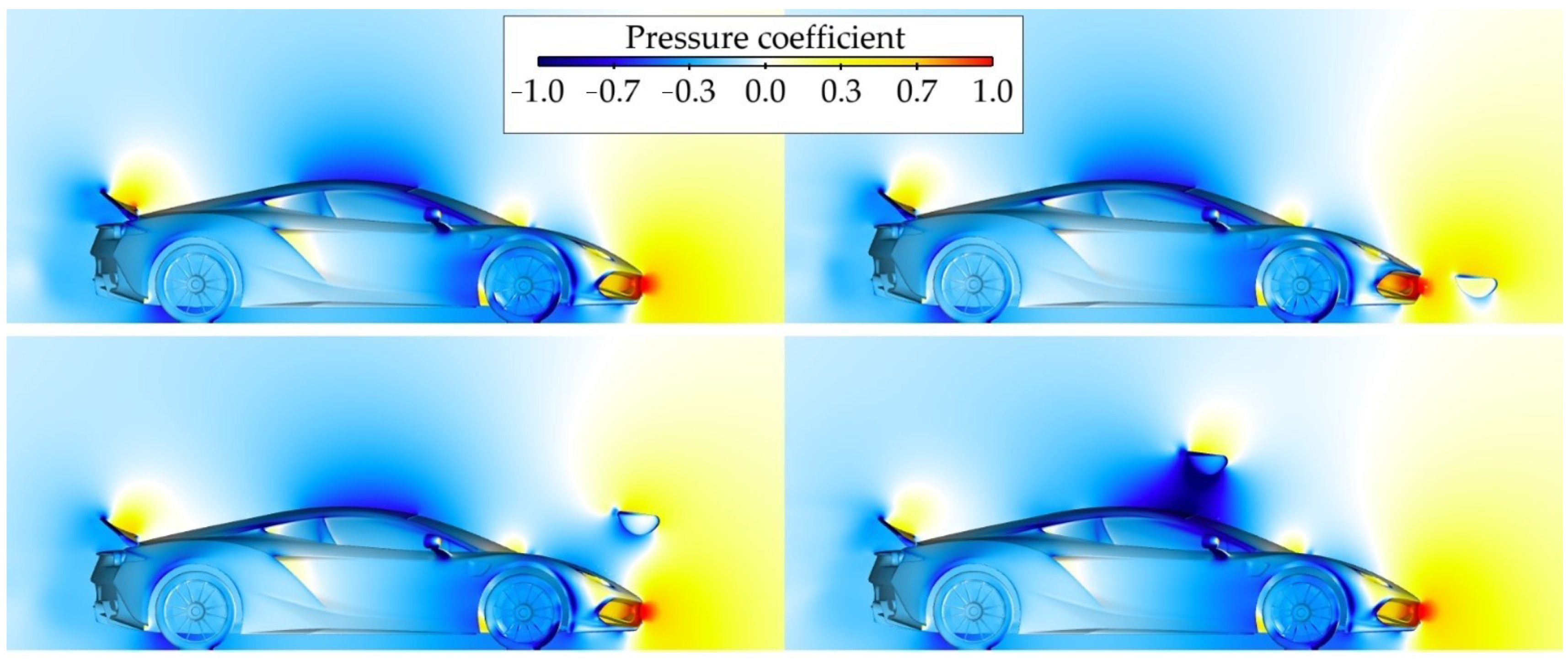
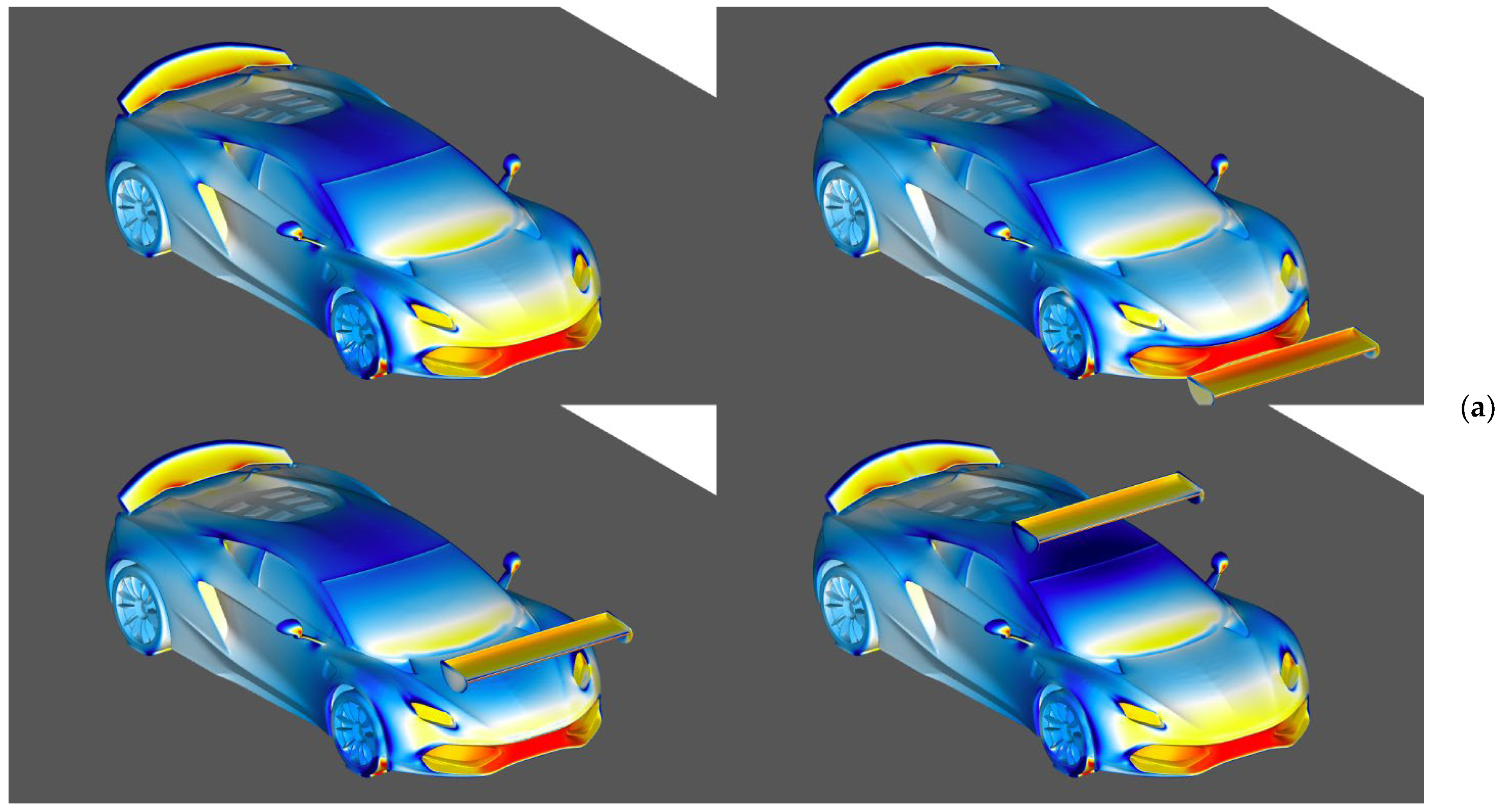
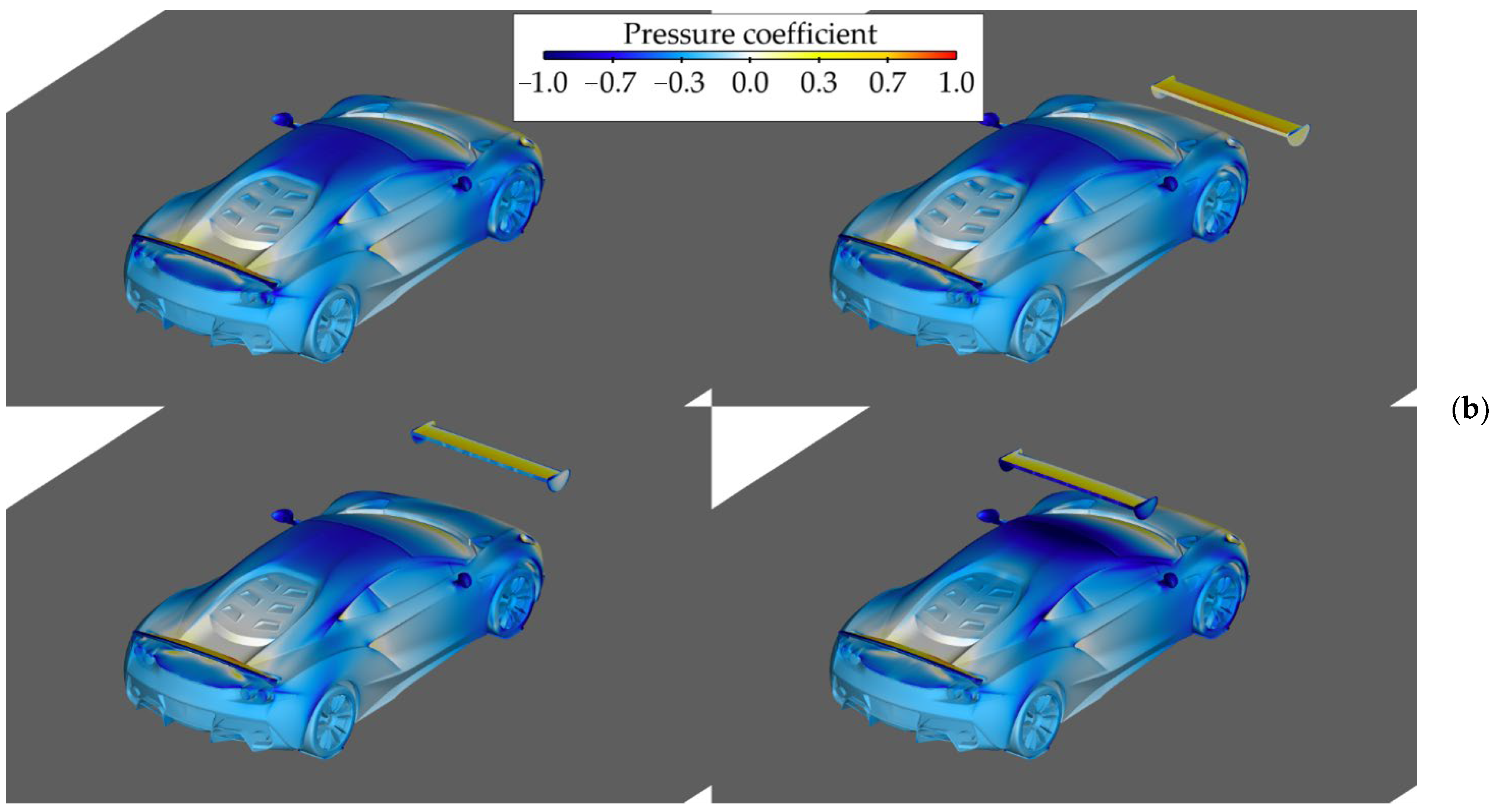
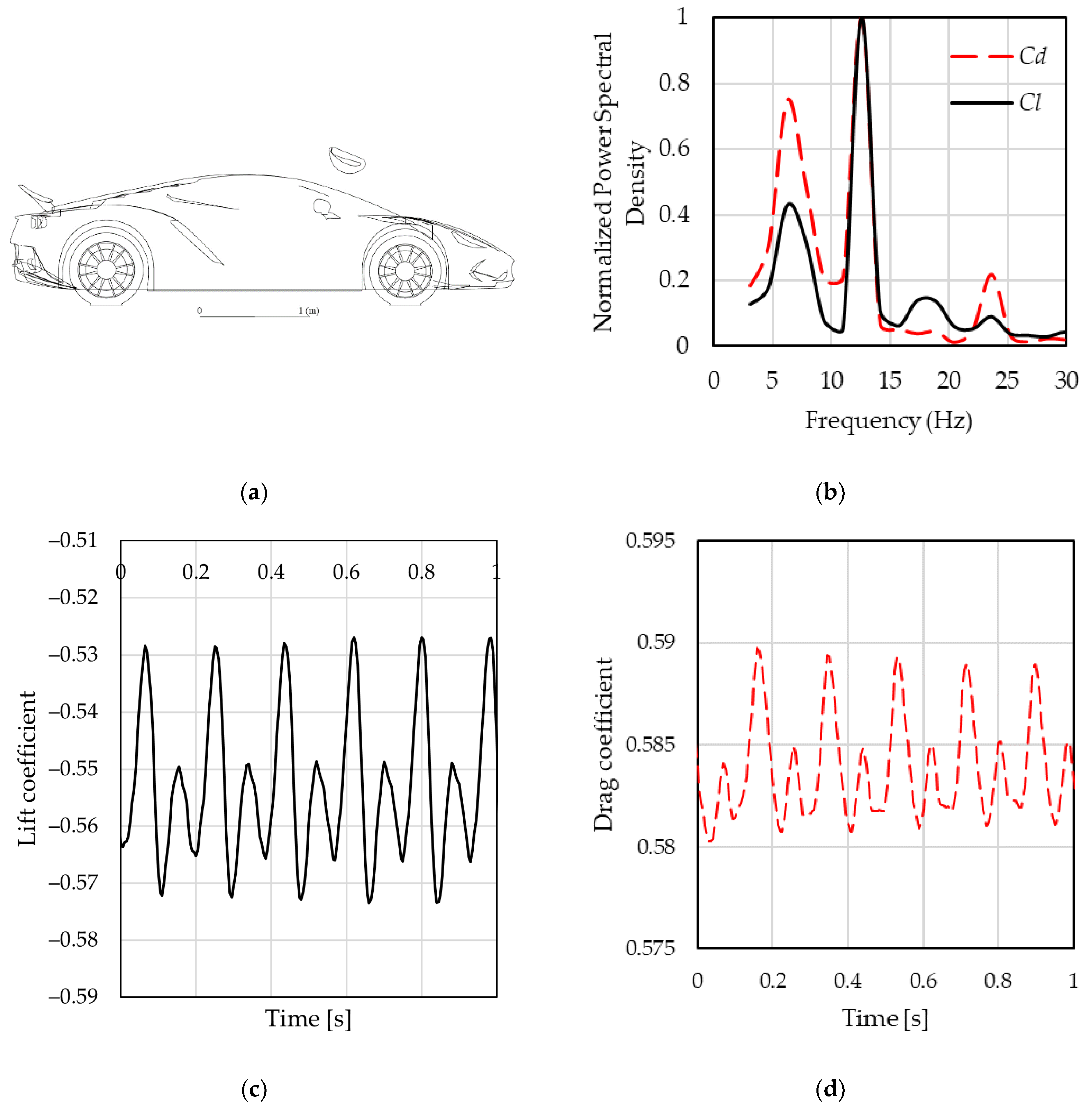
3.1. Front Wing Influence on Forces and Moments
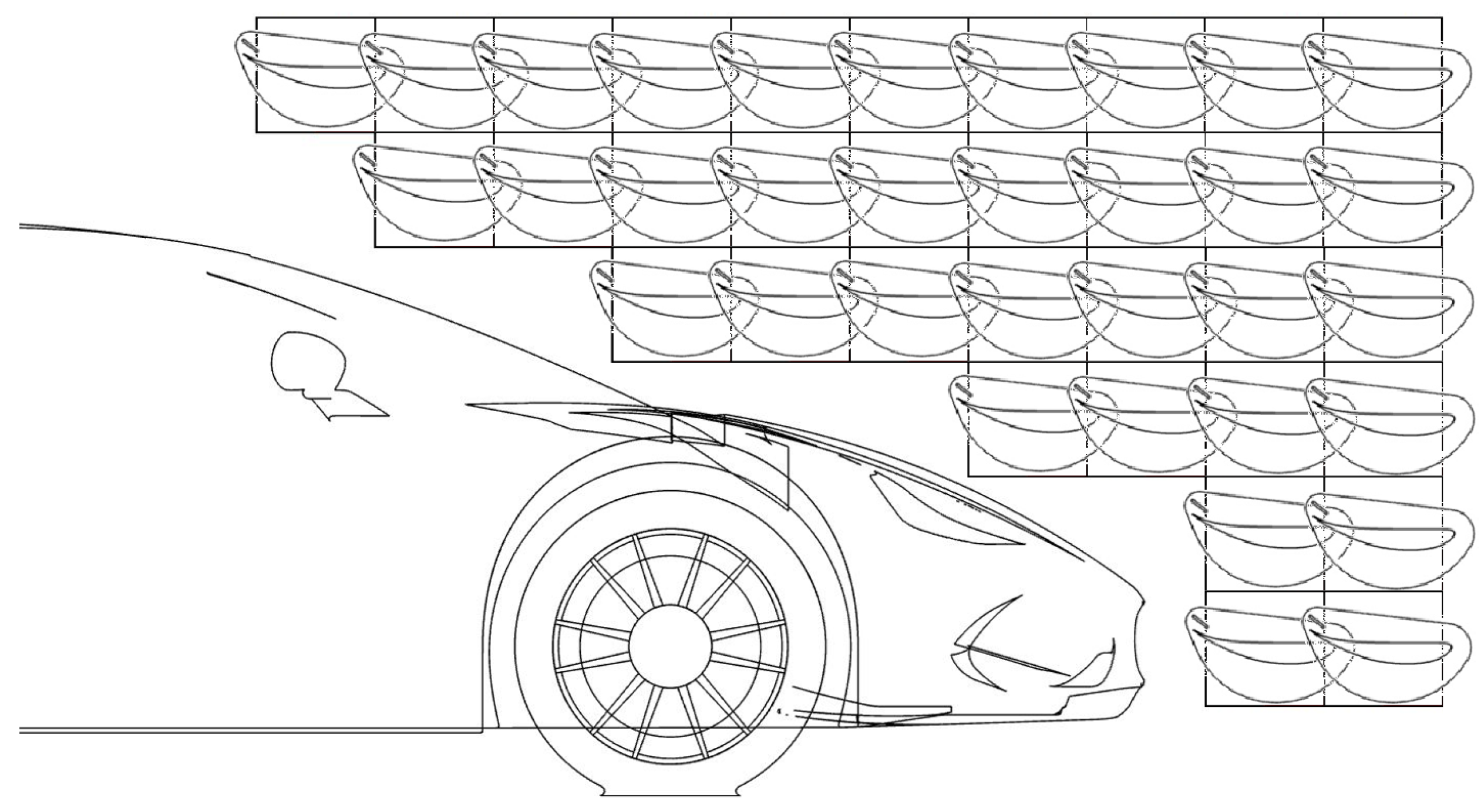
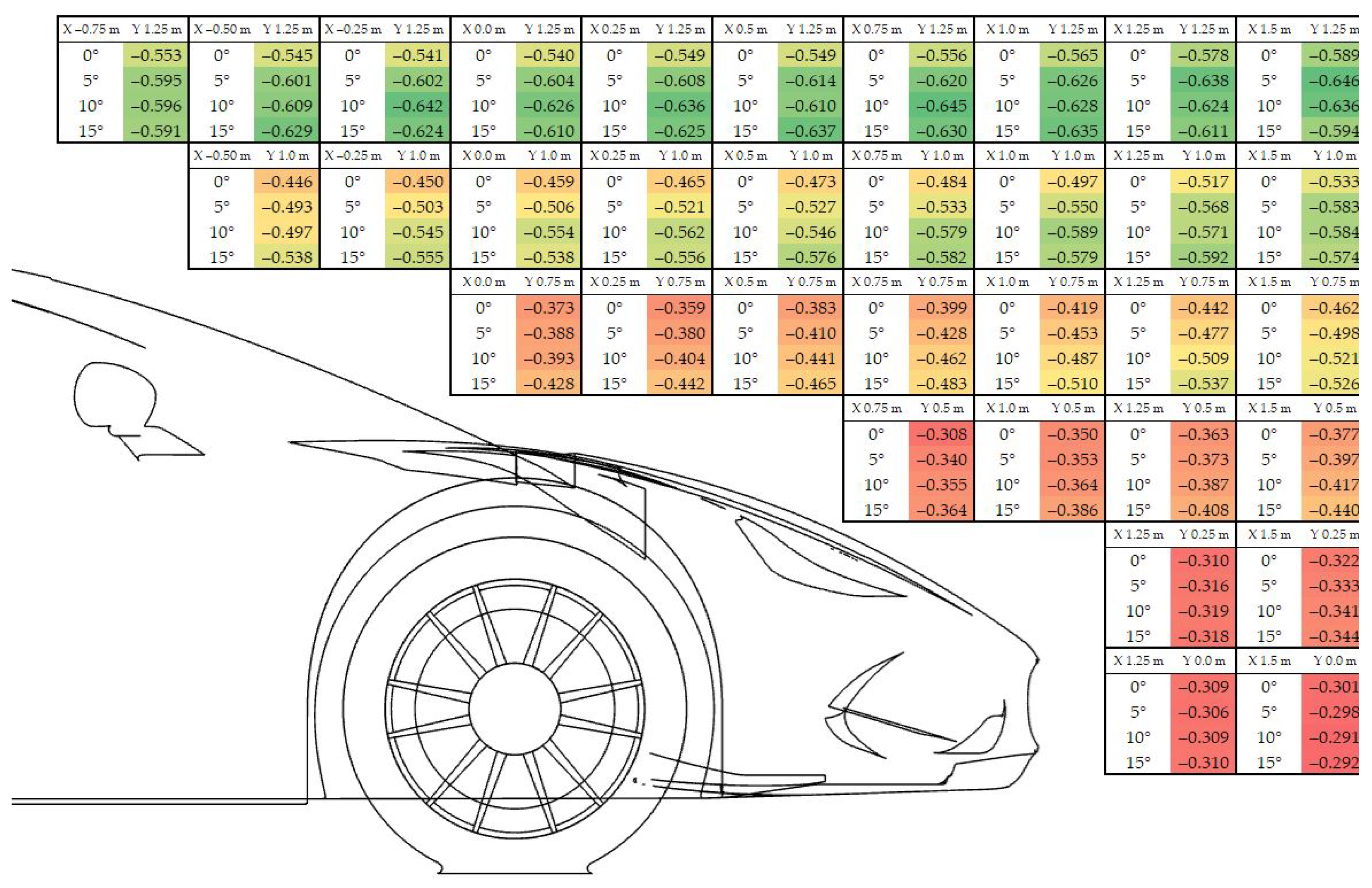
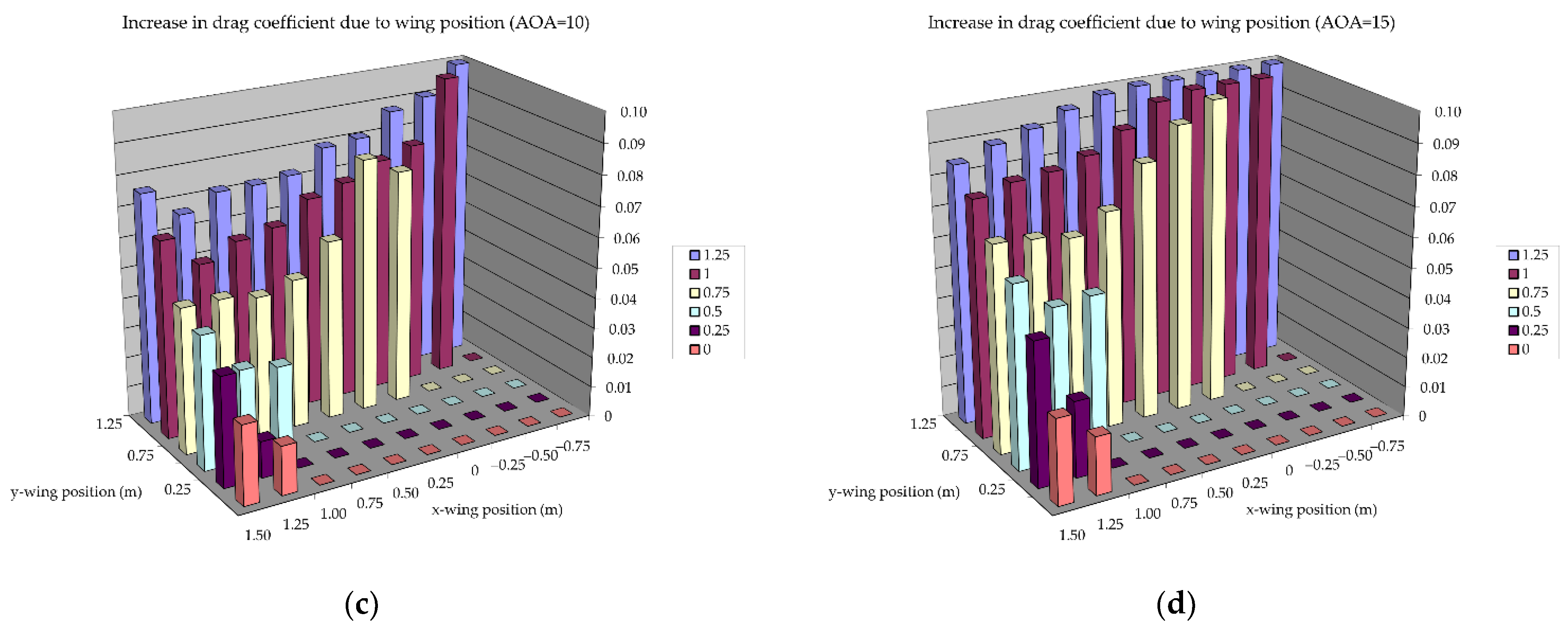
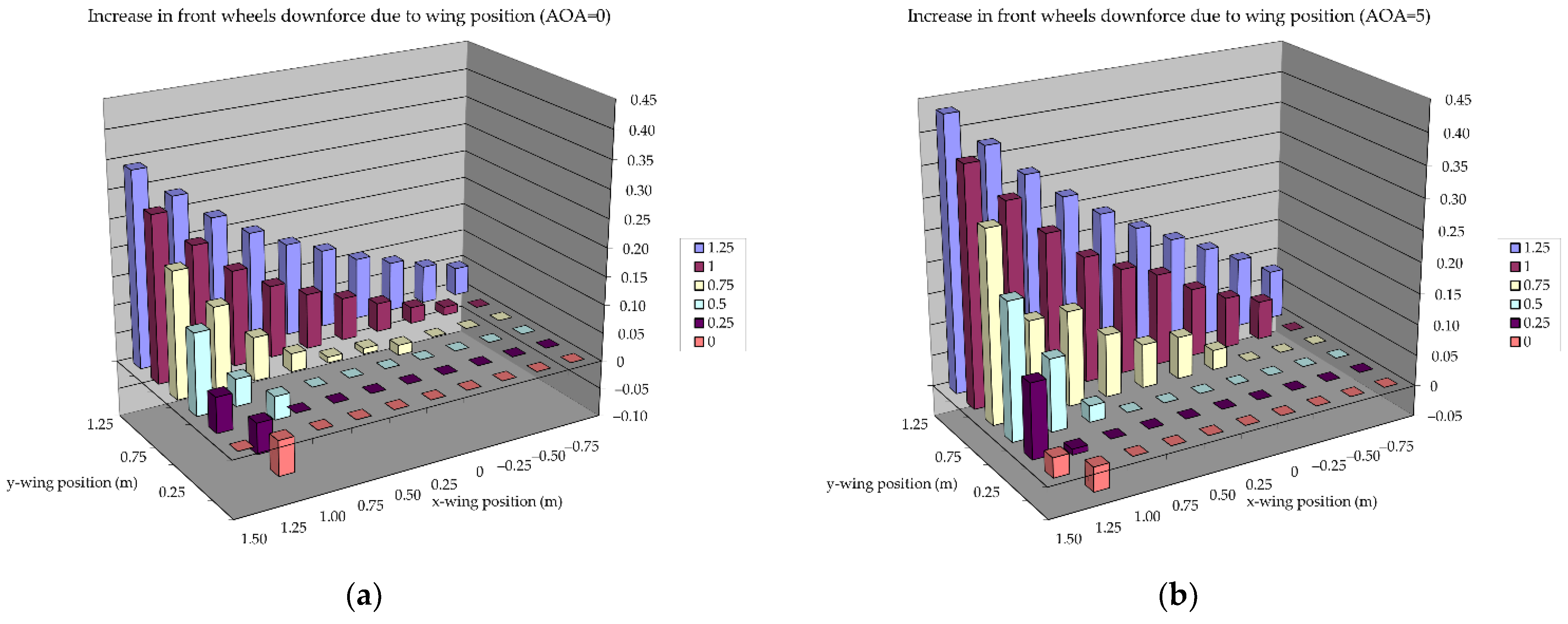
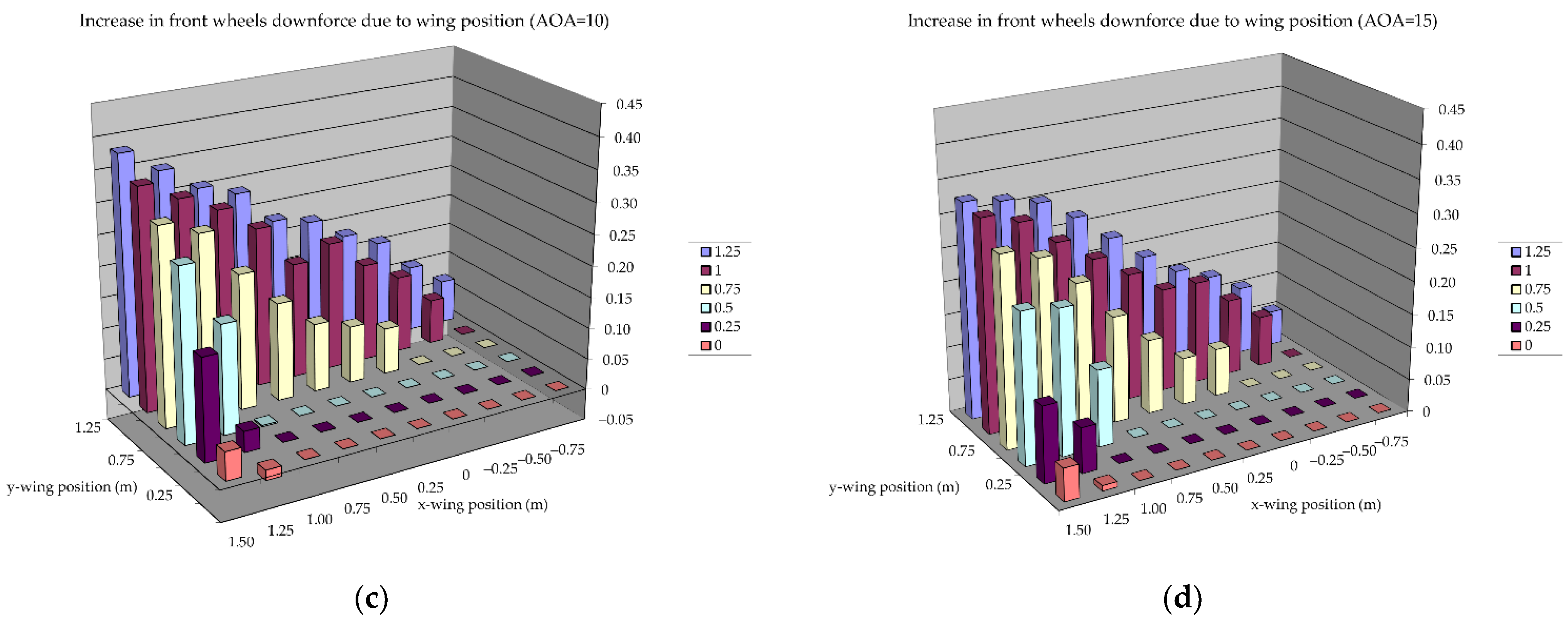
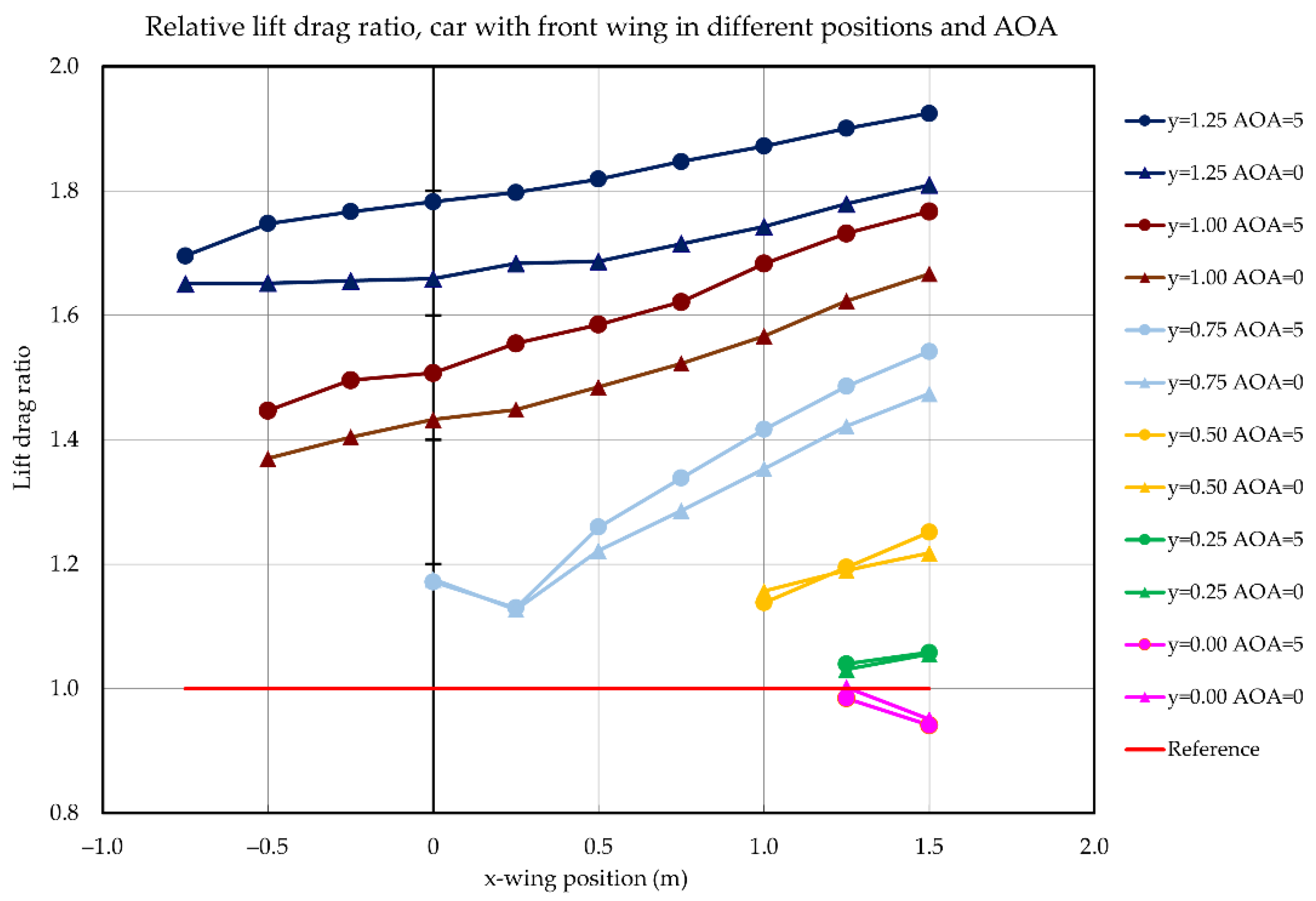
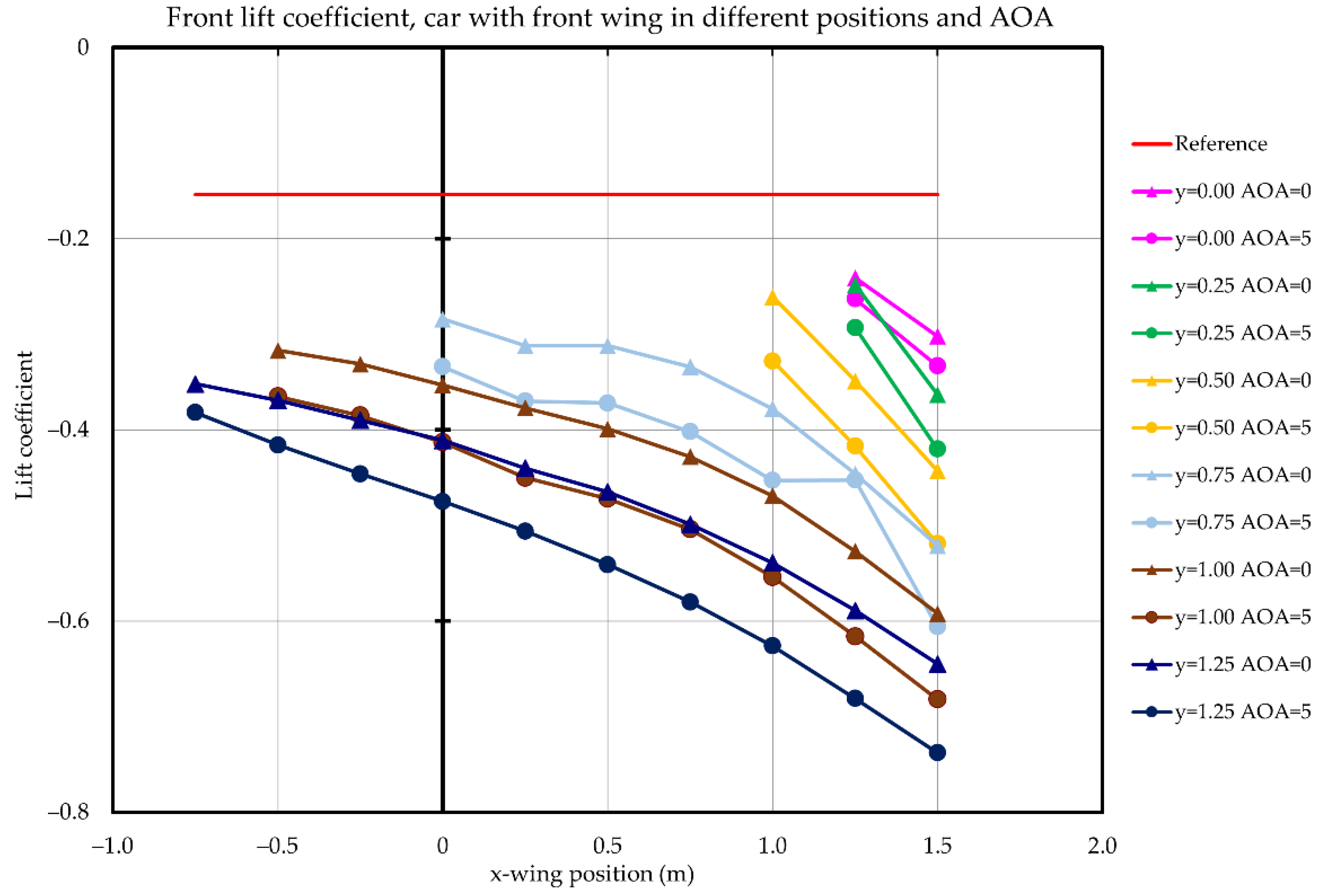
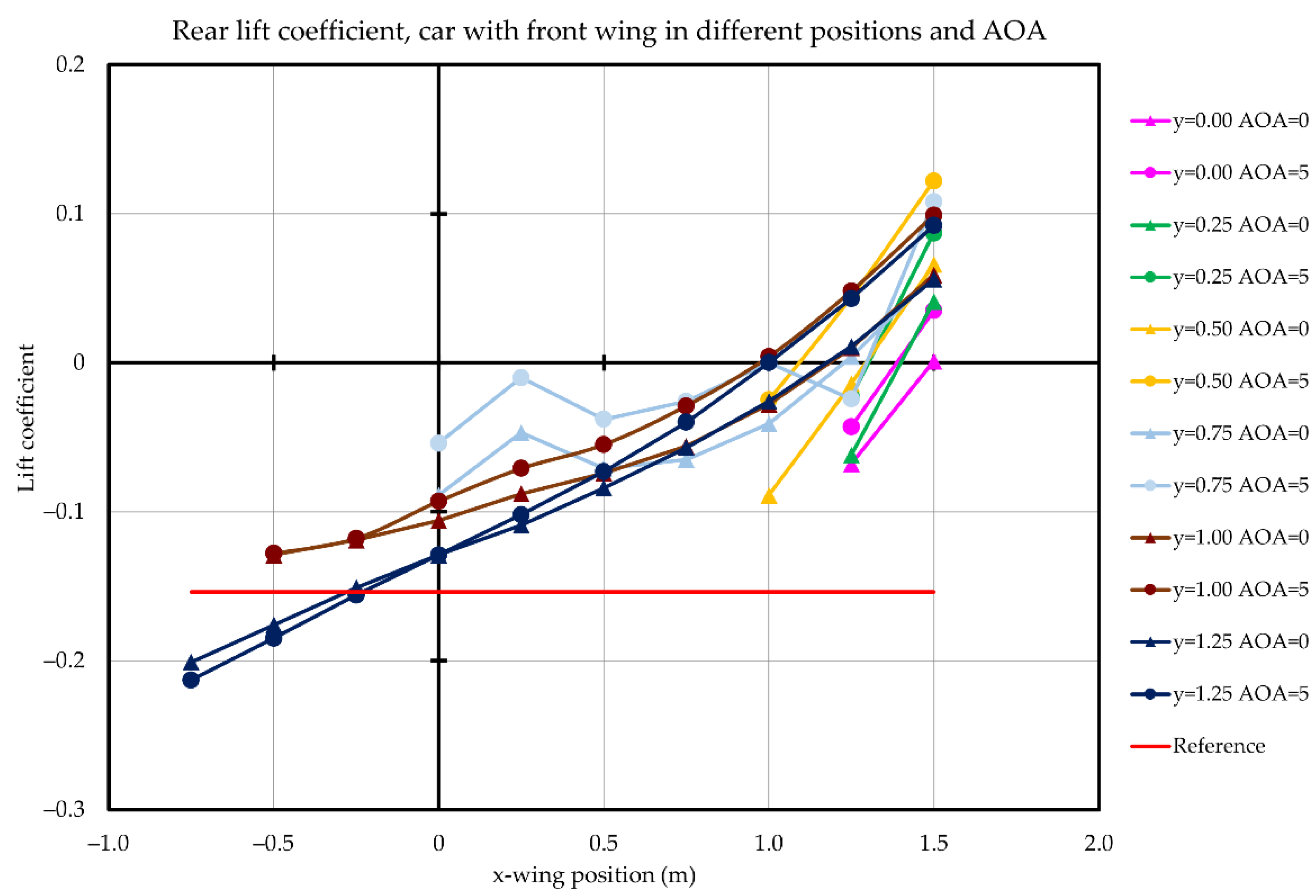
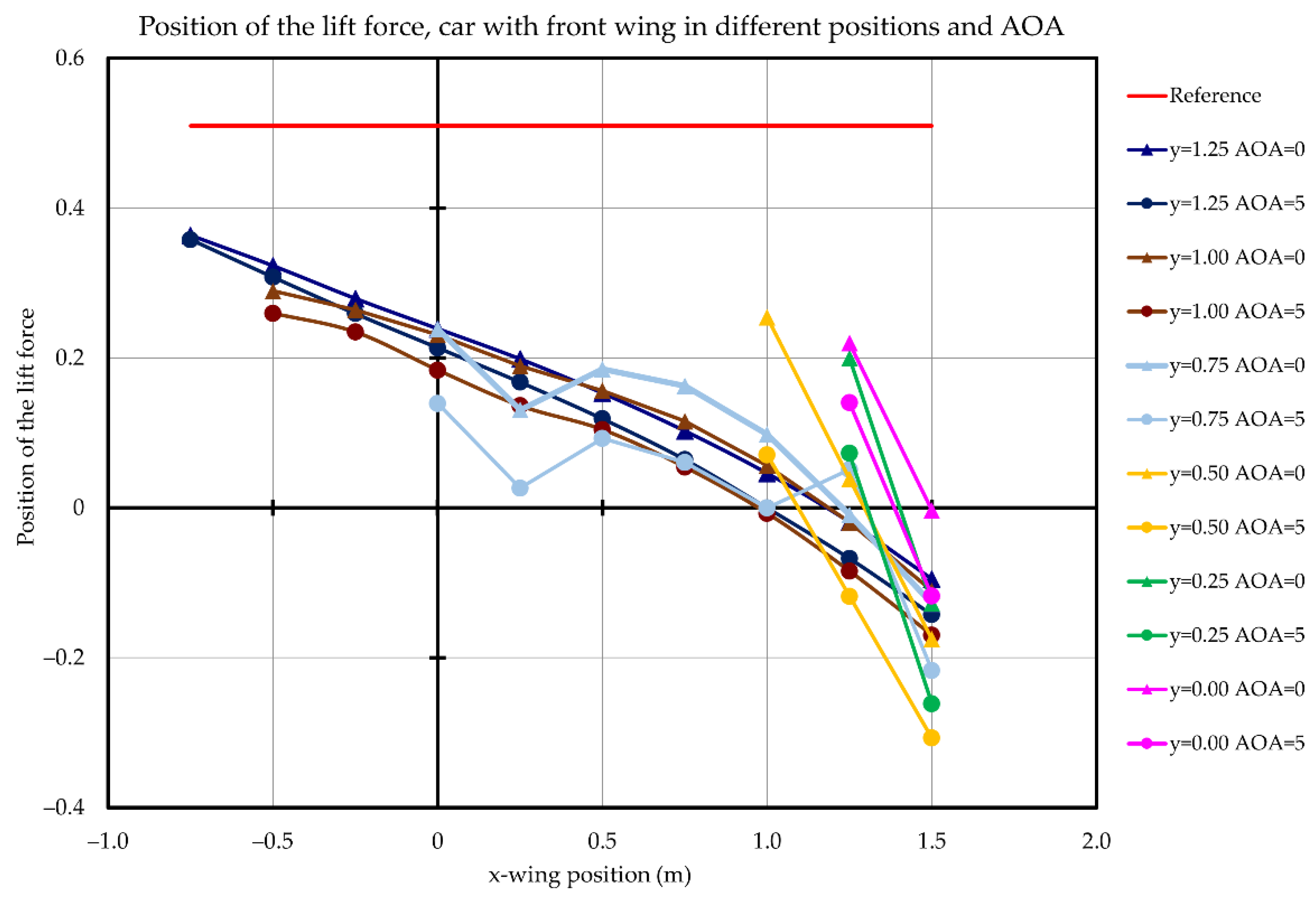
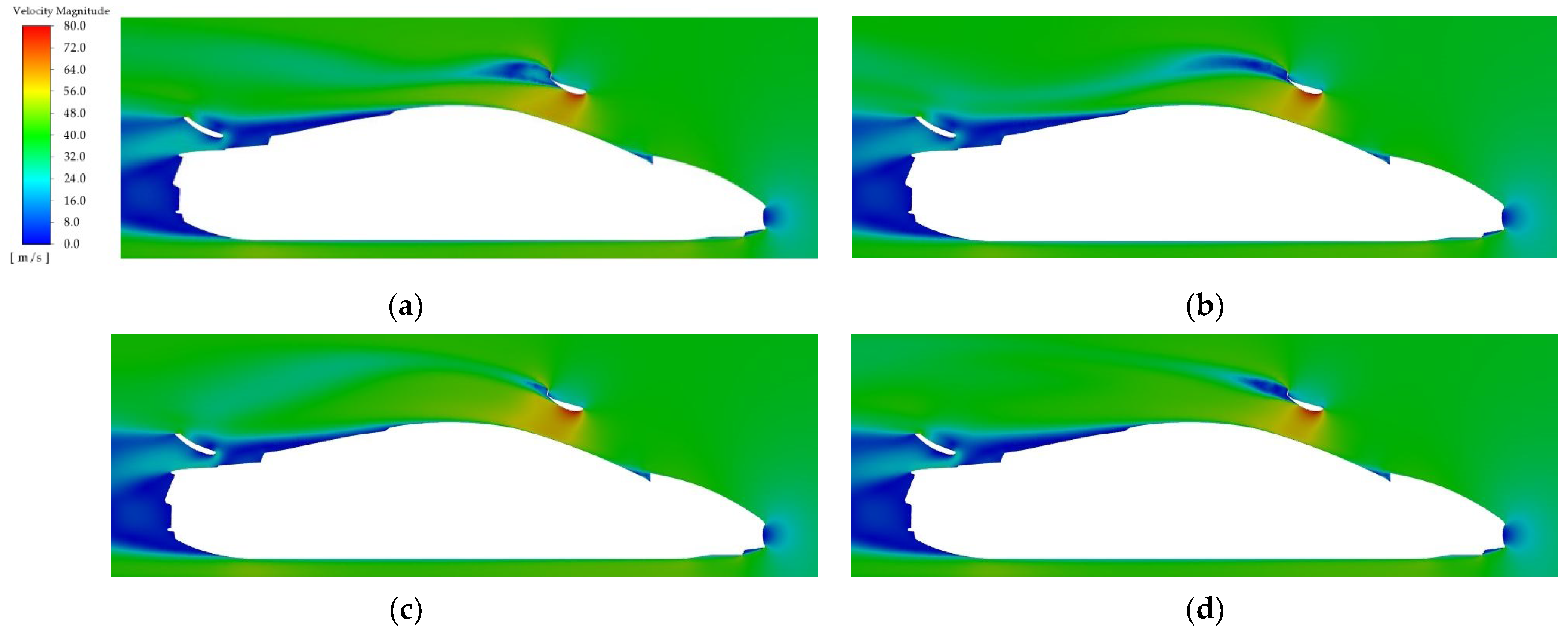
3.2. Parametric Study of Front Wing Setup
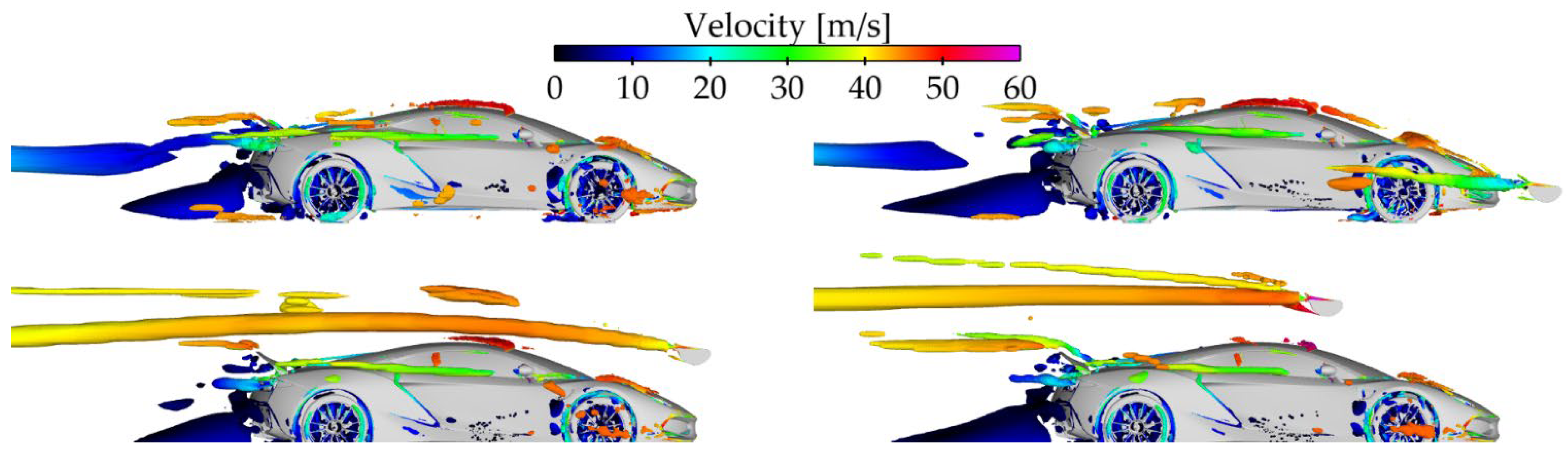
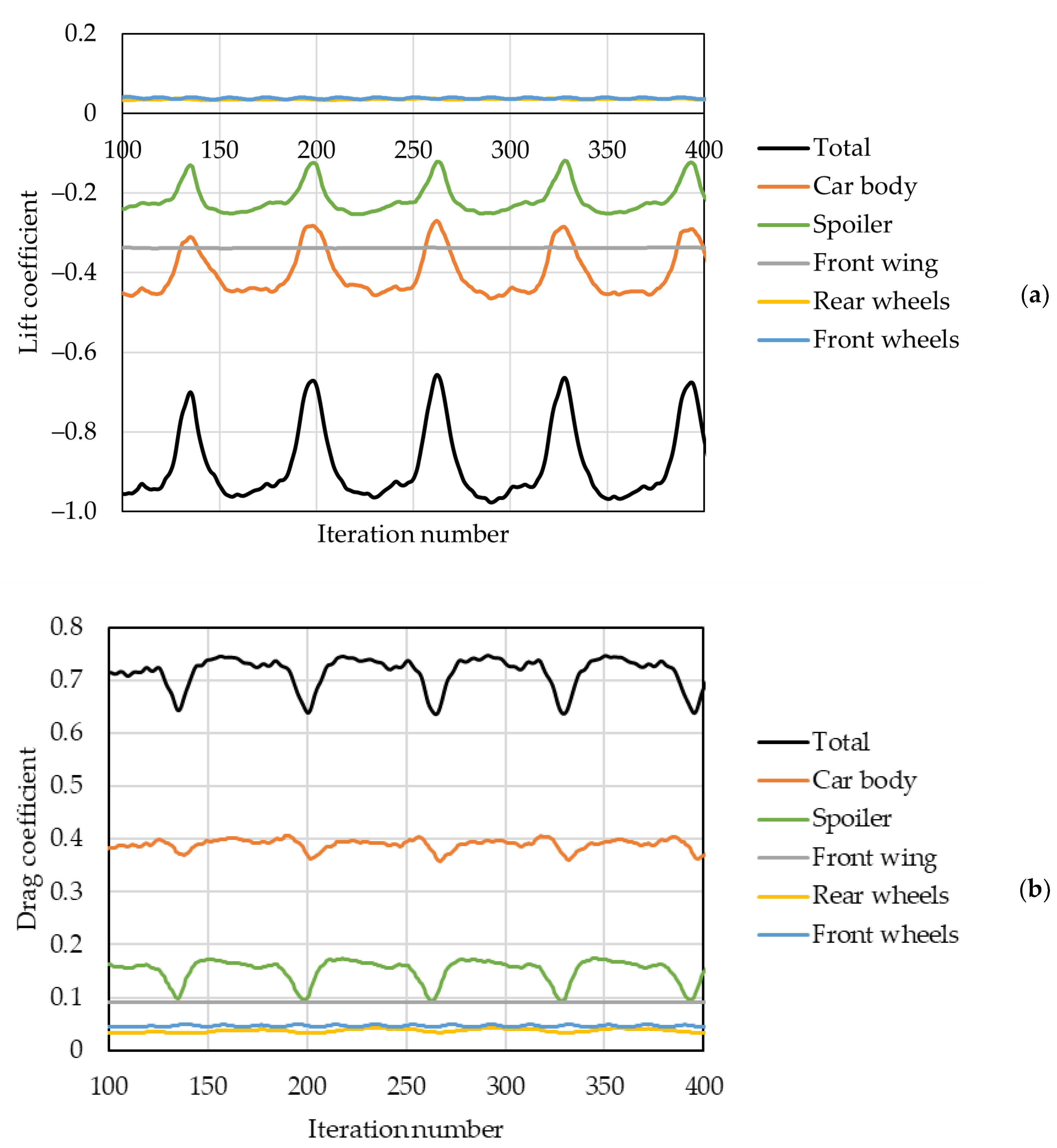
3.3. Transient Analysis of a Selected Front Wing Setup
3.4. An Attempt to Balance the Car with a Larger Spoiler
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- The Basics of Time Attack Aerodynamics—Part 1. Available online: http://timeattackbuilders.com/2016/09/30/the-basics-of-time-attack-aerodynamics-part-1/ (accessed on 10 October 2021).
- Ten Reasons Time Attack Needs Your Attention. Available online: https://www.topgear.com/car-news/motorsport/ten-reasons-time-attack-needs-your-attention (accessed on 10 October 2021).
- Piechna, J.; Rudniak, L.; Piechna, A. CFD analysis of the central engine generic sports car aerodynamics. In Proceedings of the 4th European Automotive Simulation Conference, Munich, Germany, 6–7 July 2009. [Google Scholar]
- Knowles, K.; Donoghue, D.T.; Finnis, M.V. A study of wings in ground effect. In Proceedings of the Royal Aeronautical Society Conference on Vehicle Aerodynamics, Loughborough, UK, 18 July 1994; pp. 22.1–22.13. [Google Scholar]
- Mokhtar, W.A. Numerical Parametric Study of High-Lift Low Reynolds Number Airfoils. In Proceedings of the AIAA 43rd Aerospace Science Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. AIAA Paper No. 2005-1355. [Google Scholar] [CrossRef]
- Mokhtar, W.A. Numerical Study of High-Lift Single Element Airfoils with Ground Effect for Racing Cars; SAE Transactions; SAE International: Warrendale, PA, USA, 2005; Volume 114, pp. 682–688. [Google Scholar]
- Mokhtar, W.A. Aerodynamics of High-lift Wings with Ground Effect for Racecar; SAE Technical Paper No. 2008-01-0656; SAE International: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Mokhtar, W.A.; Lane, J. Racecar front wing aerodynamics. SAE Int. J. Passeng. Cars-Mech. Syst. 2008, 1, 1392–1403. [Google Scholar] [CrossRef]
- Zerihan, J.; Zhang, X. Aerodynamics of a single element wing in ground effect. J. Aircr. 2000, 37, 1058–1064. [Google Scholar] [CrossRef]
- Zhang, X.; Zerihan, J. Aerodynamics of a double-element wing in ground effect. AIAA J. 2003, 41, 1007–1016. [Google Scholar] [CrossRef] [Green Version]
- Zerihan, J.; Zhang, X. Aerodynamics of Gurney flaps on a wing in ground effect. AIAA J. 2001, 39, 772–780. [Google Scholar] [CrossRef]
- Zhang, X.; Zerihan, J. Edge vortices of a double element wing in ground effect. J. Aircr. 2004, 41, 1127–1137. [Google Scholar] [CrossRef]
- Ranzenbach, R.; Barlow, J.; Diaz, R. Multielement airfoil in ground effect—An Experimental and Computational Study. In Proceedings of the AIAA Applied Aerodynamics Conference, 15th, Atlanta, GA, USA, 23–25 June 1997. AIAA No. 1997-2238. [Google Scholar] [CrossRef]
- Angle, G.M.; O’Hara, B.M.; Pertl, F.A.; Smith, J.E. Pitch Stability Analysis of an Airfoil in Ground Effect. J. Aircr. 2009, 46, 756–762. [Google Scholar] [CrossRef]
- Ahmed, M.R.; Takasaki, T.; Kohama, Y. Aerodynamics of a NACA4412 airfoil in ground effect. AIAA J. 2007, 45, 37–47. [Google Scholar] [CrossRef]
- Lee, T.; Majeed, A.; Siddiqui, B.; Tremblay-Dionne, V. Impact of ground proximity on the aerodynamic properties of an unsteady airfoil. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 1814–1830. [Google Scholar] [CrossRef]
- Lee, T.; Tremblay-Dionne, V. Experimental investigation of the aerodynamics and flowfield of a NACA 0015 airfoil over a wavy ground. J. Fluids Eng. 2018, 140, 071202. [Google Scholar] [CrossRef]
- McBeath, S. Competition Car Aerodynamics, 3rd ed.; Veloce Publishing: Dorchester, UK, 2017. [Google Scholar]
- Basso, M.; Cravero, C.; Marsano, D. Aerodynamic Effect of the Gurney Flap on the Front Wing of a F1 Car and Flow Interactions with Car Components. Energies 2021, 14, 2059. [Google Scholar] [CrossRef]
- Roberts, L.S.; Correia, J.; Finnis, M.V.; Knowles, K. Aerodynamic characteristics of a wing-and-flap configuration in ground effect and yaw. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 841–854. [Google Scholar] [CrossRef]
- Katz, J. Aerodynamic model for wing-generated down force on open-wheel-racing-car configurations. SAE Trans. 1986, 1106–1115. [Google Scholar] [CrossRef]
- Katz, J. Aerodynamics of race cars. Annu. Rev. Fluid Mech. 2006, 38, 27–63. [Google Scholar] [CrossRef] [Green Version]
- Martins, D.; Correia, J.; Silva, A. The Influence of Front Wing Pressure Distribution on Wheel Wake Aerodynamics of a F1 Car. Energies 2021, 14, 4421. [Google Scholar] [CrossRef]
- Diasinos, S.; Barber, T.J.; Doig, G. Influence of wing span on the aerodynamics of wings in ground effect. Proc. Inst. Mech. Eng. Part G J Aerosp. Eng. 2013, 227, 564–568. [Google Scholar] [CrossRef]
- Diasinos, S.; Doig, G.; Barber, T.J. On the interaction of a racing car front wing and exposed wheel. Aeronaut. J. 2014, 118, 1385–1407. [Google Scholar] [CrossRef] [Green Version]
- Diasinos, S.; Barber, T.; Doig, G. Numerical analysis of the effect of the change in the ride height on the aerodynamic front wing–wheel interactions of a racing car. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 900–914. [Google Scholar] [CrossRef]
- Ogawa, A.; Mashio, S.; Nakamura, D.; Masumitsu, Y.; Minagawa, M.; Nakai, Y. Aerodynamics Analysis of Formula One Vehicles. Honda R&D Tech. Rev. 2009, 21, 152–162. [Google Scholar]
- Correia, J.; Roberts, L.S.; Finnis, M.V.; Knowles, K. Scale effects on a single-element inverted wing in ground effect. Aeronaut J. 2014, 118, 797–809. [Google Scholar] [CrossRef]
- Katz, J.; Largman, R. Experimental Study of the Aerodynamic Interaction between an Enclosed-Wheel Racing-Car and its Rear Wing. ASME J. Fluids Eng. 1989, 111, 154–159. [Google Scholar] [CrossRef]
- Gogal, D.; Sakurai, H. The Effects of End Plates on Downforce in Yaw, Motorsports Engineering Conference and Exhibition, Dearborn, Michigan; SAE 2006-01-3647; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Kurec, K.; Remer, M.; Piechna, J. The influence of different aerodynamic setups on enhancing a sports car’s braking. Int. J. Mech. Sci. 2019, 164, 105140. [Google Scholar] [CrossRef]
- Broniszewski, J.; Piechna, J. A fully coupled analysis of unsteady aerodynamics impact on vehicle dynamics during braking. Eng. Appl. Comput. Fluid Mech. 2019, 13, 623–641. [Google Scholar] [CrossRef]
- Steger, J.L.; Dougherty, F.C.; Benek, J.A. A chimera grid scheme. Multiple overset body-conforming mesh system for finite difference adaptation to complex aircraft configurations. Advances in grid generation. In Proceedings of the Applied Mechanics, Bioengineering, and Fluids Engineering Conference, Houston, TX, USA, 20–22 June 1983; American Society of 137 Mechanical Engineers: Houston, TX, USA, 1983; pp. 59–69. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids. Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]



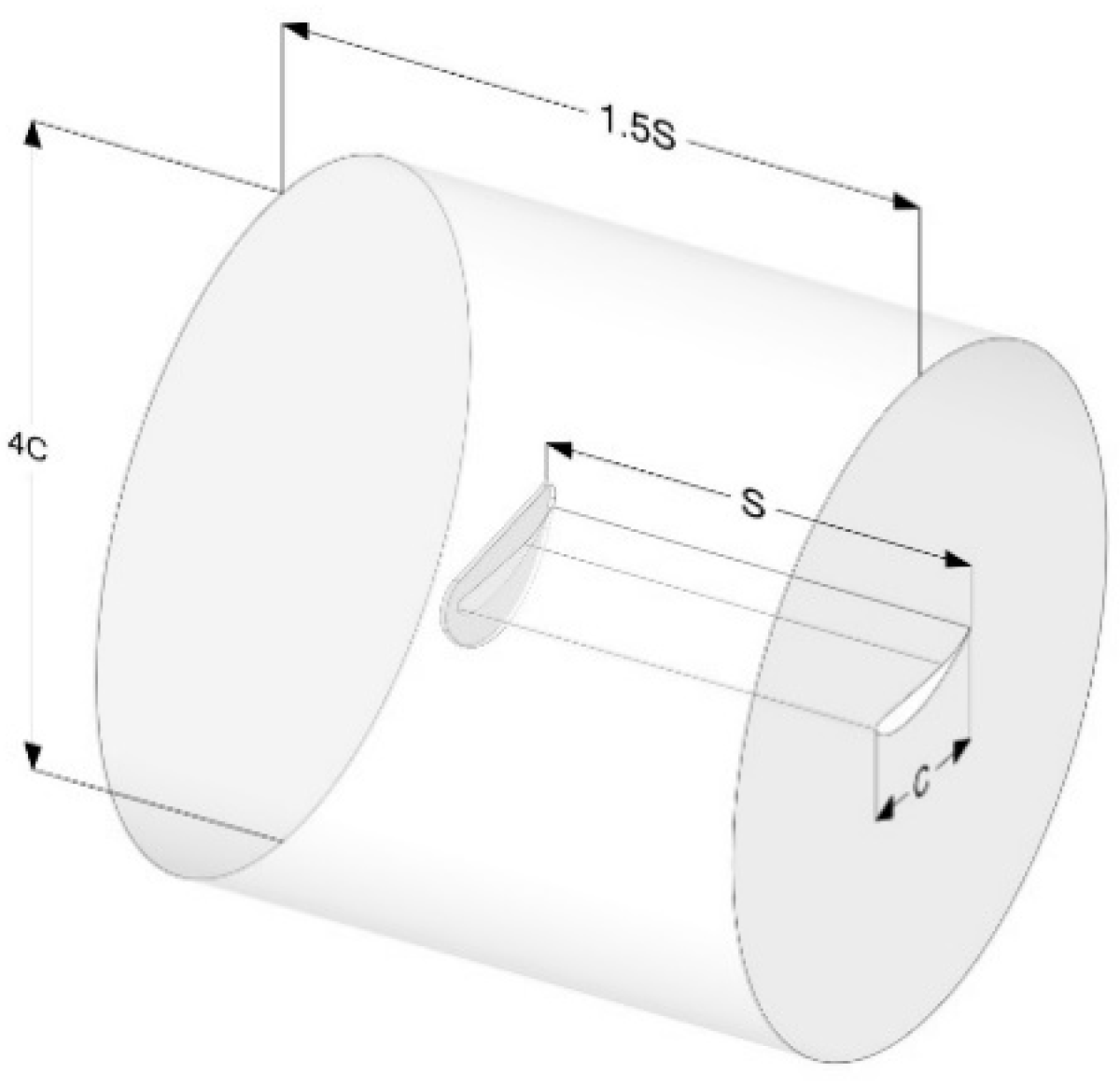
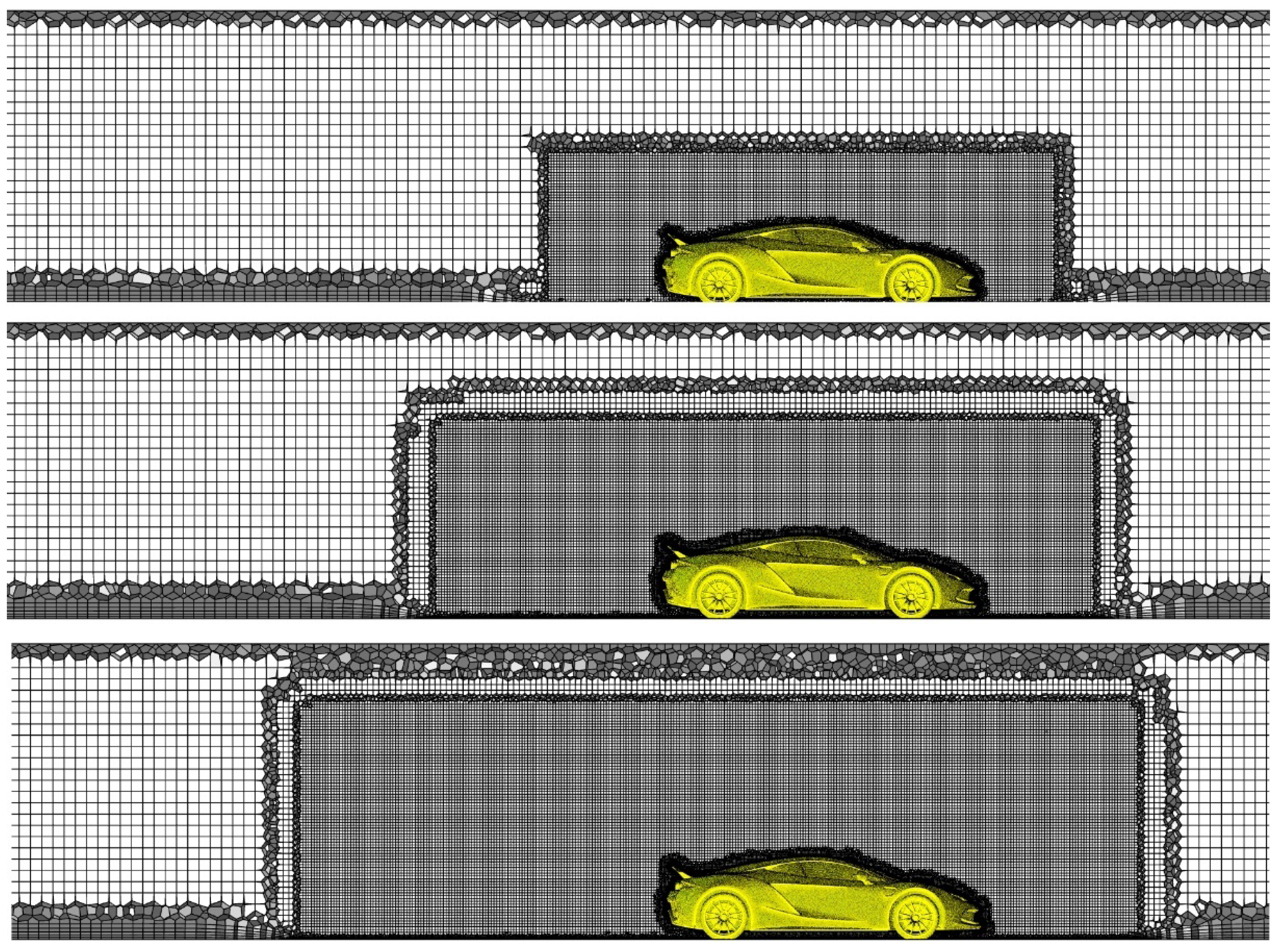










| BOI Size | Side | Top | Front | Back |
|---|---|---|---|---|
| 1 | 1W | 1H | 0.2L | 0.4L |
| 2 | 1.25W | 1.5H | 0.3L | 0.7L |
| 3 | 1.5W | 2H | 0.4L | 1.1L |
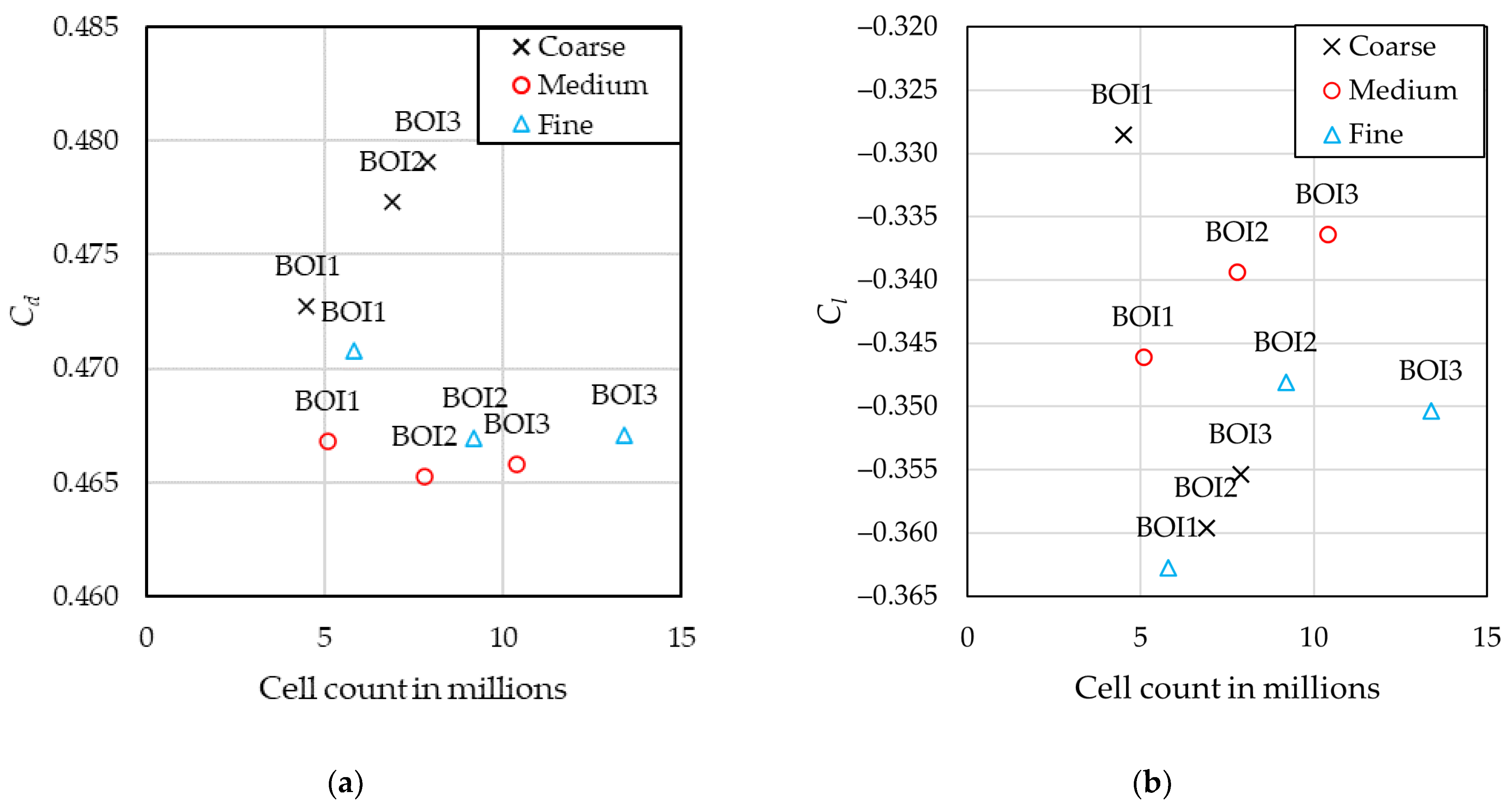
| BOI Size | Coarse Mesh | Medium Mesh | Fine Mesh | Fine-Grid Grid Convergence Index |
|---|---|---|---|---|
| Characteristic cell size h in m | 0.04 | 0.031 | 0.024 | - |
| Drag coefficient Cd | 0.477 | 0.465 | 0.467 | 0.1% |
| Lift coefficient Cl | −0.36 | −0.339 | −0.348 | 2.4% |
| Front Wing Type | Cd | Cl | Clr | Clf | Cm |
|---|---|---|---|---|---|
| No front wing | 0.475 | −0.302 | −0.154 | −0.146 | −0.01 |
| Clean | 0.475 | −0.315 | −0.147 | −0.163 | 0.02 |
| Gurney off | 0.473 | −0.344 | −0.113 | −0.227 | 0.11 |
| Gurney on | 0.476 | −0.352 | −0.089 | −0.261 | 0.17 |
| Analysis Type | Cd | Cl | Clr | Clf | Cm |
|---|---|---|---|---|---|
| Steady-state | 0.592 | −0.538 | −0.158 | −0.380 | 0.111 |
| Transient | 0.584 | −0.553 | −0.162 | −0.391 | 0.115 |
| Relative difference in % | −1.4 | 2.7 | 2.5 | 2.8 | 3.5 |
| Spoiler | Cd | Cl | Clr | Clf | Cm |
|---|---|---|---|---|---|
| Small | 0.504 | −0.458 | −0.106 | −0.353 | 0.124 |
| Large | 0.725 | −0.928 | −0.453 | −0.475 | 0.011 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szudarek, M.; Piechna, J. CFD Analysis of the Influence of the Front Wing Setup on a Time Attack Sports Car’s Aerodynamics. Energies 2021, 14, 7907. https://doi.org/10.3390/en14237907
Szudarek M, Piechna J. CFD Analysis of the Influence of the Front Wing Setup on a Time Attack Sports Car’s Aerodynamics. Energies. 2021; 14(23):7907. https://doi.org/10.3390/en14237907
Chicago/Turabian StyleSzudarek, Maciej, and Janusz Piechna. 2021. "CFD Analysis of the Influence of the Front Wing Setup on a Time Attack Sports Car’s Aerodynamics" Energies 14, no. 23: 7907. https://doi.org/10.3390/en14237907
APA StyleSzudarek, M., & Piechna, J. (2021). CFD Analysis of the Influence of the Front Wing Setup on a Time Attack Sports Car’s Aerodynamics. Energies, 14(23), 7907. https://doi.org/10.3390/en14237907







