Design Centering of Compact Microwave Components Using Response Features and Trust Regions
Abstract
1. Introduction
2. Microwave Design Centering by Response Features and Trust Regions
2.1. Formulation of Design Centering Problem
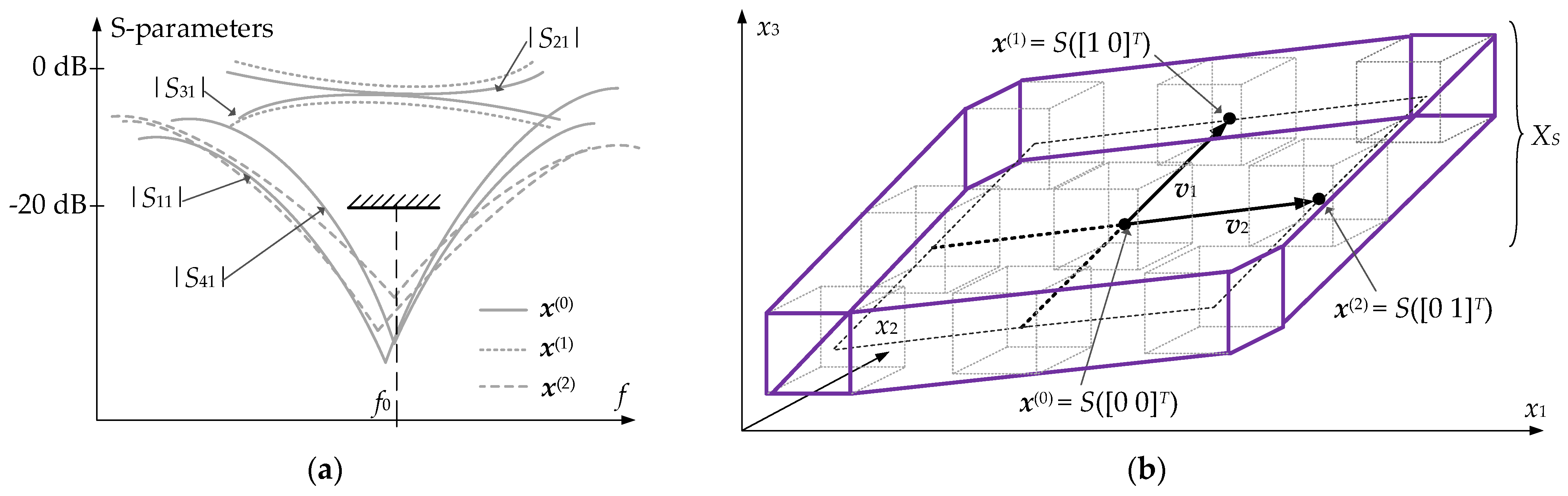
2.2. Design Specifications Verification Using Response Features
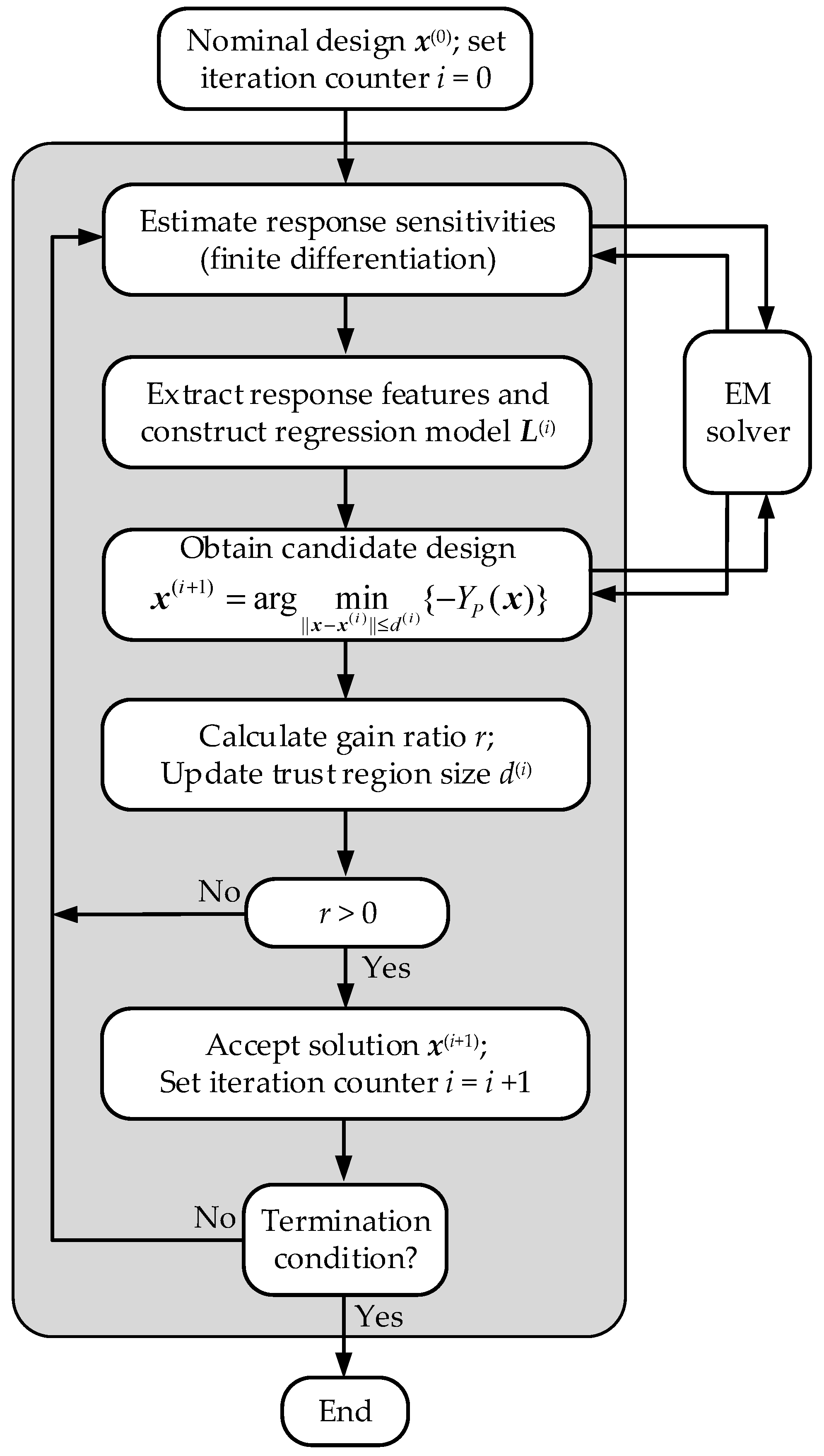
2.3. Design Centering by Means of Feature-Based Surrogates and Trust Regions
2.4. Complete Algorithm
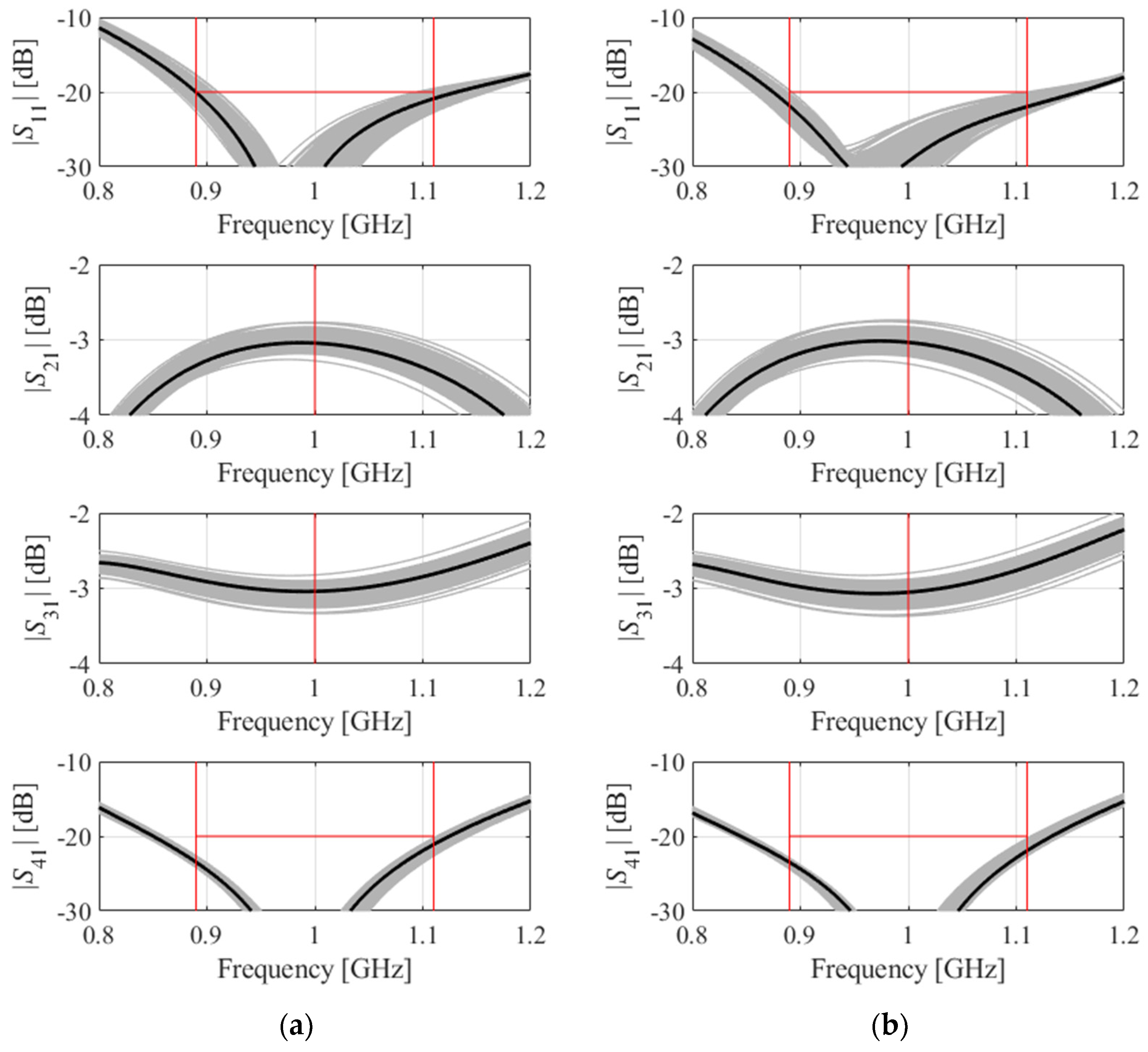
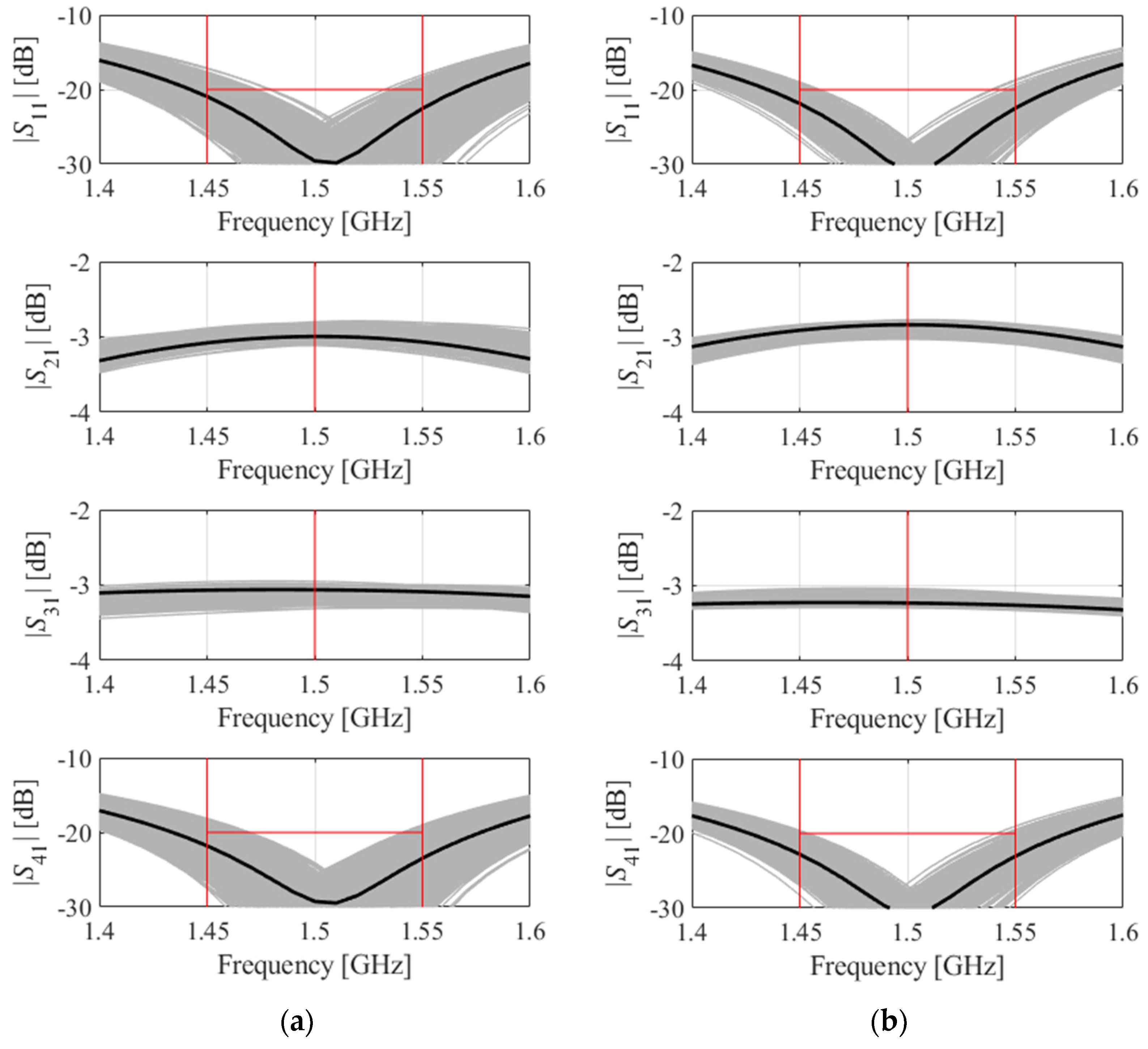
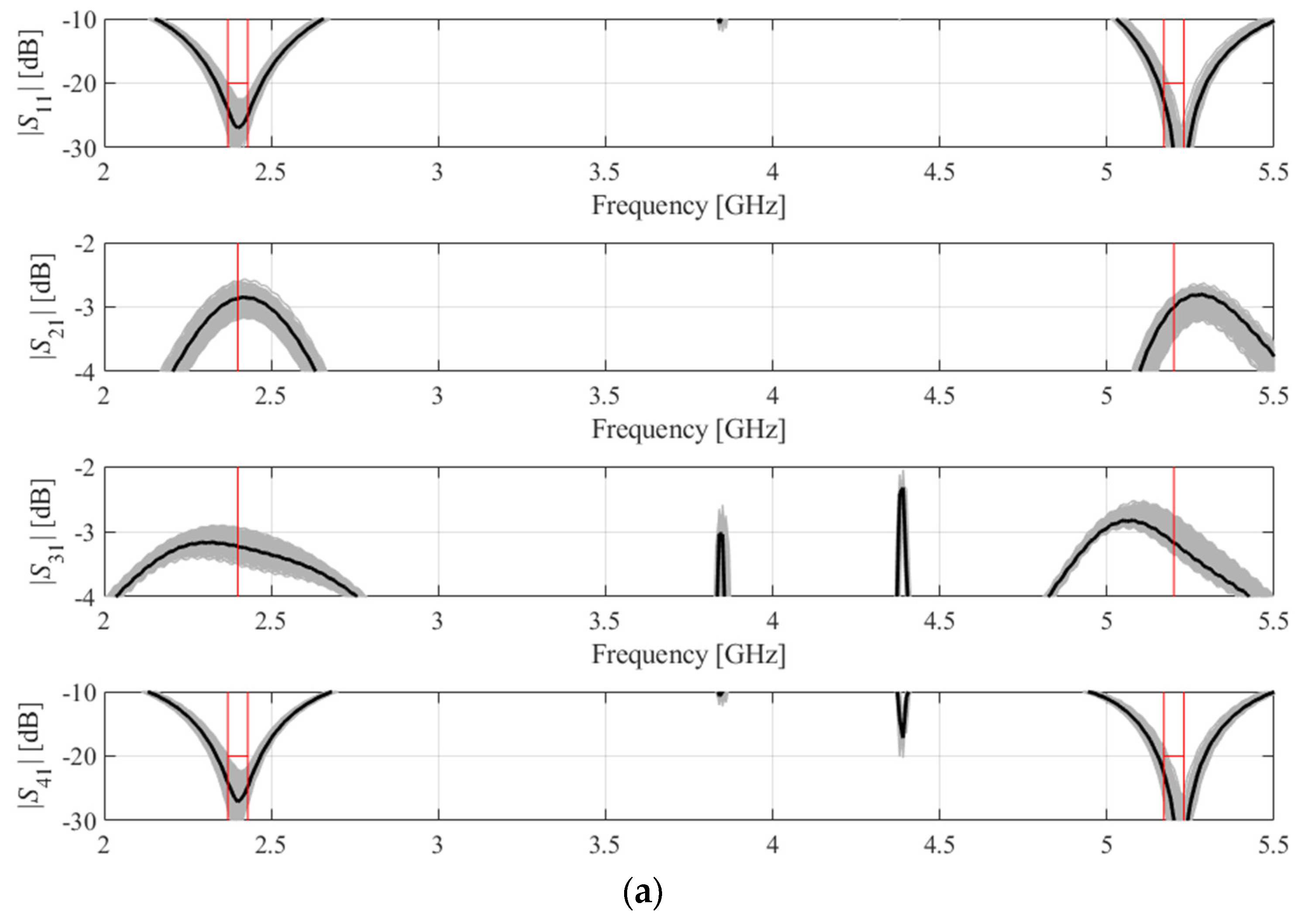
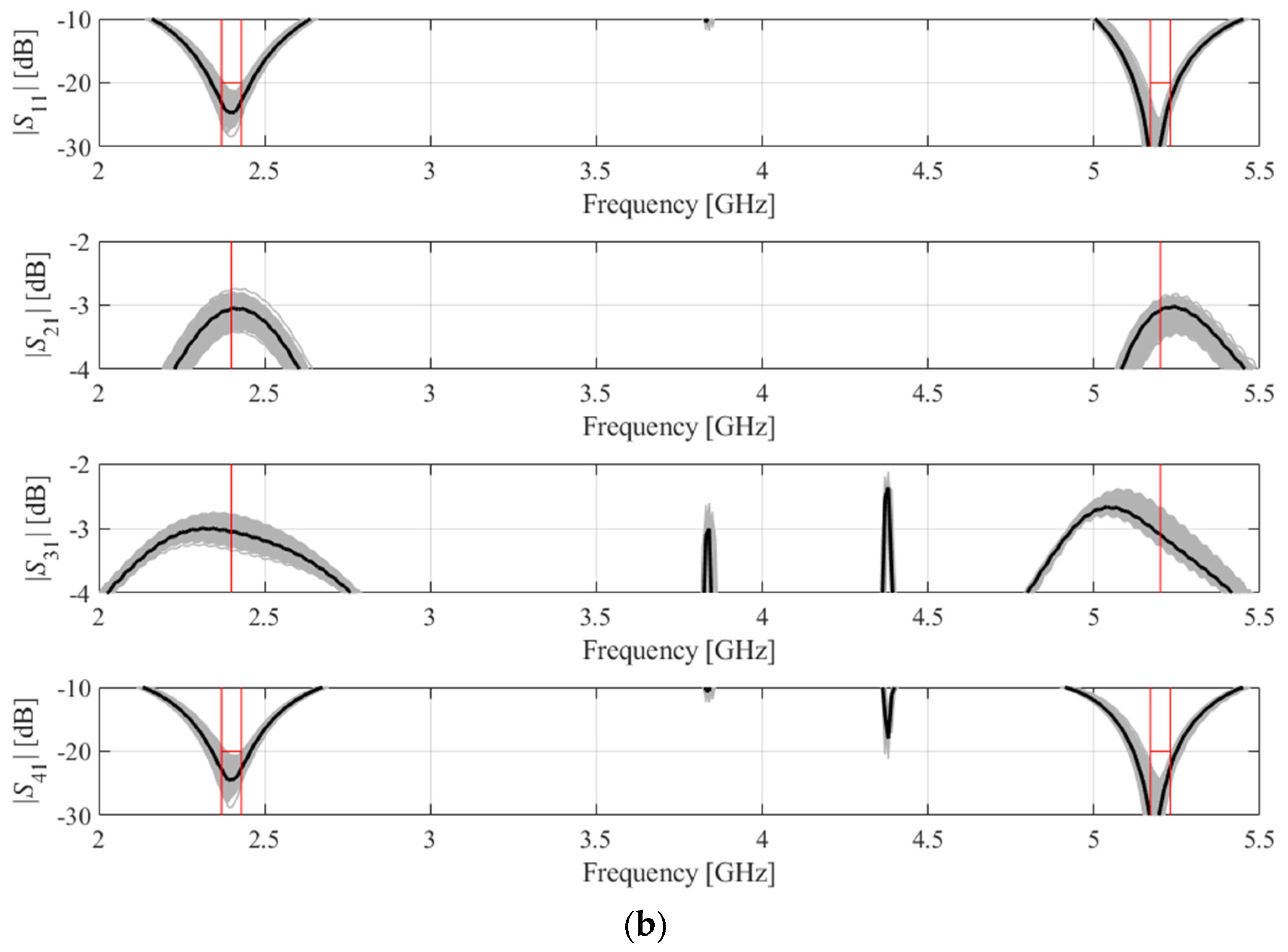
3. Numerical Verification
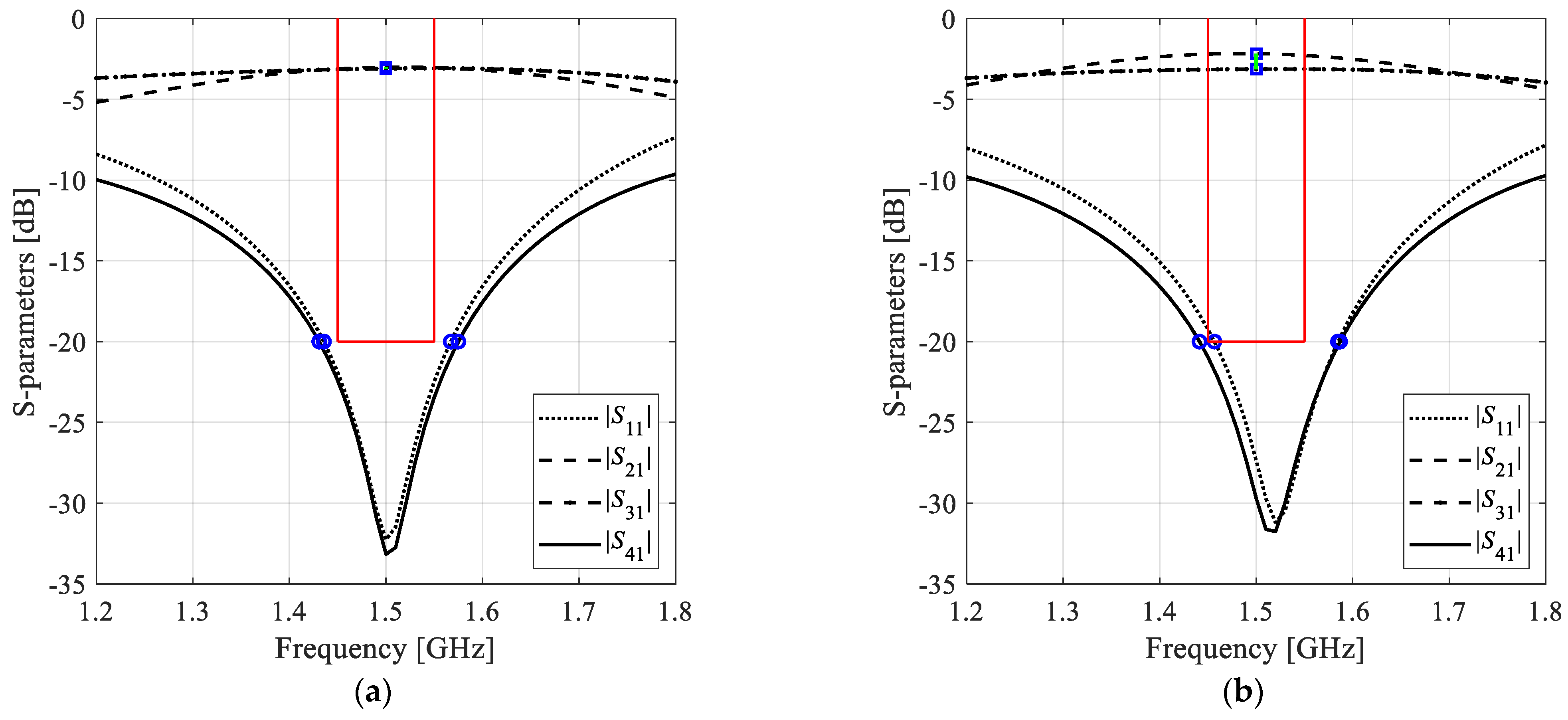
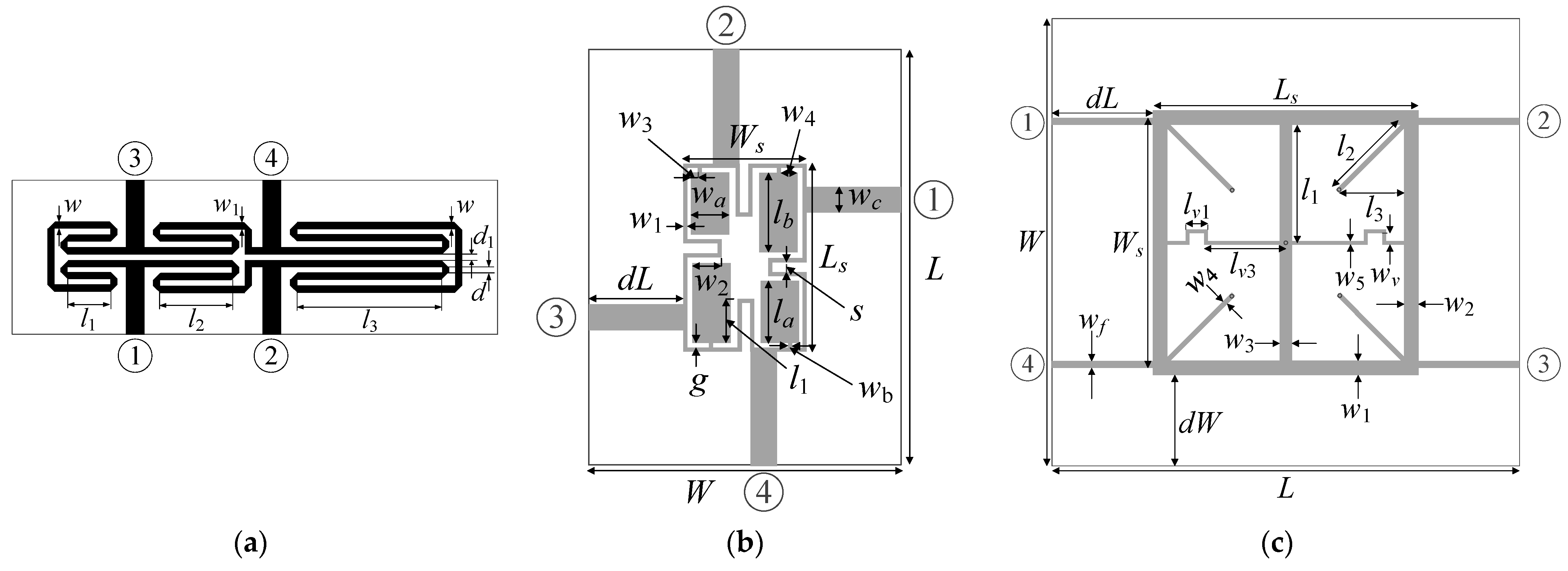
3.1. Case Studies
3.2. Reference Algorithms
3.3. Results and Discussion
- Circuit I: x* = [4.65 11.22 21.73 0.73 0.94 0.86]T;
- Circuit II: x* = [0.64 5.50 9.27 12.49 1.27 2.06 1.05 0.32 2.85 0.24]T;
- Circuit III: x* = [25.16 0.80 0.77 1.89 1.25 0.42 0.75 0.30 0.30]T.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Teberio, F.; Soto, P.; Arregui, I.; Lopetegi, T.; Cogollos, S.; Arnedo, I.; Martin-Iglesias, P.; Boria, V.E.; Laso, M.A.G. Waveguide band-pass filter with reduced sensitivity to fabrication tolerances for Q-band payloads. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honolulu, HI, USA, 4–9 June 2017; pp. 1464–1467. [Google Scholar]
- Martinez-Mendoza, M.; Ernst, C.; Lorente, J.A.; Alvarez-Melcon, A.; Seyfert, F. On the relation between stored energy and fabrication tolerances in microwave filters. IEEE Trans. Microw. Theory Technol. 2012, 60, 2131–2141. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, Y.; Wang, C.; Wen, Z.; Wu, Y.; Xu, R. A large-signal statistical model and yield estimation of GaN HEMTs based on response surface methodology. IEEE Microw. Wirel. Comp. Lett. 2016, 26, 690–692. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, F.; Na, W.; Yan, S.; Zhang, Q. Parallel space-mapping based yield-driven EM optimization incorporating trust region algorithm and polynomial chaos expansion. IEEE Access 2019, 7, 143673–143683. [Google Scholar] [CrossRef]
- Kapse, I.; Prasad, A.K.; Roy, S. Analyzing impact of epistemic uncertainty in high-speed circuit simulation using fuzzy variables and global polynomial chaos surrogates. In Proceedings of the 2017 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization for RF, Microwave, and Terahertz Applications (NEMO), Seville, Spain, 17–19 May 2017; pp. 320–322. [Google Scholar]
- Zeng, Z.; Kang, R.; Wen, M.; Zio, E. A model-based reliability metric considering aleatory and epistemic uncertainty. IEEE Access 2017, 5, 15505–15515. [Google Scholar] [CrossRef]
- Rayas-Sanchez, J.E.; Koziel, S.; Bandler, J.W. Advanced RF and microwave design optimization: A journey and a vision of future trends. IEEE J. Microw. 2021, 1, 481–493. [Google Scholar] [CrossRef]
- Rayas-Sanchez, J.E.; Gutierrez-Ayala, V. EM-based Monte Carlo analysis and yield prediction of microwave circuits using linear-input neural-output space mapping. IEEE Trans. Microw. Theory Technol. 2006, 54, 4528–4537. [Google Scholar] [CrossRef]
- Firmansyah, T.; Alaydrus, M.; Wahyu, Y.; Rahardjo, E.T.; Wibisono, G. A highly independent multiband bandpass filter using a multi-coupled line stub-SIR with folding structure. IEEE Access 2020, 8, 83009–83026. [Google Scholar] [CrossRef]
- Chen, S.; Guo, M.; Xu, K.; Zhao, P.; Dong, L.; Wang, G. A frequency synthesizer based microwave permittivity sensor using CMRC structure. IEEE Access 2018, 6, 8556–8563. [Google Scholar] [CrossRef]
- Sengupta, M.; Saxena, S.; Daldoss, L.; Kramer, G.; Minehane, S.; Cheng, J. Application-specific worst case corners using response surfaces and statistical models. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2005, 24, 1372–1380. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, F.; Zhang, Q.-J. Rapid yield estimation of microwave passive components using model-order reduction based neuro-transfer function models. IEEE Microw. Wirel. Comp. Lett. 2021, 31, 333–336. [Google Scholar] [CrossRef]
- Matoglu, E.; Pham, N.; De Araujo, D.; Cases, M.; Swaminathan, M. Statistical signal integrity analysis and diagnosis methodology for high-speed systems. IEEE Trans. Adv. Packag. 2004, 27, 611–629. [Google Scholar] [CrossRef]
- Prasad, A.K.; Roy, S. Reduced dimensional Chebyshev-polynomial chaos approach for fast mixed epistemic-aleatory uncertainty quantification of transmission line networks. IEEE Trans. Comp. Packag. Manuf. Technol. 2019, 9, 1119–1132. [Google Scholar] [CrossRef]
- Du, J.; Roblin, C. Statistical modeling of disturbed antennas based on the polynomial chaos expansion. IEEE Ant. Wirel. Prop. Lett. 2017, 16, 1843–1847. [Google Scholar] [CrossRef]
- Kersaudy, P.; Mostarshedi, S.; Sudret, B.; Picon, O.; Wiart, J. Stochastic analysis of scattered field by building facades using polynomial chaos. IEEE Trans. Ant. Propag. 2014, 62, 6382–6393. [Google Scholar] [CrossRef]
- Koziel, S.; Mahouti, P.; Calik, N.; Belen, M.A.; Szczepanski, S. Improved modeling of miniaturized microwave structures using performance-driven fully-connected regression surrogate. IEEE Access 2021, 9, 71470–71481. [Google Scholar] [CrossRef]
- Ochoa, J.S.; Cangellaris, A.C. Random-space dimensionality reduction for expedient yield estimation of passive microwave structures. IEEE Trans. Microw. Theory Technol. 2013, 61, 4313–4321. [Google Scholar] [CrossRef]
- Leifsson, L.; Du, X.; Koziel, S. Efficient yield estimation of multi-band patch antennas by polynomial chaos-based kriging. Int. J. Numer. Modeling 2020, 33, e2722. [Google Scholar] [CrossRef]
- Spina, D.; Ferranti, F.; Antonini, G.; Dhaene, T.; Knockaert, L. Efficient variability analysis of electromagnetic systems via polynomial chaos and model order reduction. IEEE Trans. Comp. Packag. Manuf. Technol. 2014, 4, 1038–1051. [Google Scholar] [CrossRef][Green Version]
- Kennedy, M.C.; O’Hagan, A. Predicting the output from complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
- Abdel-Malek, H.L.; Hassan, A.S.O.; Soliman, E.A.; Dakroury, S.A. The ellipsoidal technique for design centering of microwave circuits exploiting space-mapping interpolating surrogates. IEEE Trans. Microw. Theory Technol. 2006, 54, 3731–3738. [Google Scholar] [CrossRef]
- Biernacki, R.; Chen, S.; Estep, G.; Rousset, J.; Sifri, J. Statistical analysis and yield optimization in practical RF and microwave systems. In Proceedings of the IEEE MTT-S International Microwave Symposium digest. IEEE MTT-S International Microwave Symposium, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. Available online: https://ieeexplore.ieee.org/document/6259360 (accessed on 17 November 2021).
- Scotti, G.; Tommasino, P.; Trifiletti, A. MMIC yield optimization by design centering and off-chip controllers. IET Proc.-Circuits Devices Syst. 2005, 152, 54–60. [Google Scholar] [CrossRef]
- Ma, B.; Lei, G.; Liu, C.; Zhu, J.; Guo, Y. Robust tolerance design optimization of a PM claw pole motor with soft magnetic composite cores. IEEE Trans. Magn. 2018, 54, 8102404. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Y.; Zio, E. Random fuzzy extension of the universal generating function approach for the reliability assessment of multi-state systems under aleatory and epistemic uncertainties. IEEE Trans. Reliab. 2014, 63, 13–25. [Google Scholar] [CrossRef]
- Easum, J.A.; Nagar, J.; Werner, P.L.; Werner, D.H. Efficient multiobjective antenna optimization with tolerance analysis through the use of surrogate models. IEEE Trans. Ant. Propag. 2018, 66, 6706–6715. [Google Scholar] [CrossRef]
- Rossi, M.; Dierck, A.; Rogier, H.; Vande Ginste, D. A stochastic framework for the variability analysis of textile antennas. IEEE Trans. Ant. Prop. 2014, 62, 6510–6514. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Feng, F.; Zhang, W.; Ma, J.; Zhang, Q.J. Polynomial chaos-based approach to yield-driven EM optimization. IEEE Trans. Microw. Theory Technol. 2018, 66, 3186–3199. [Google Scholar] [CrossRef]
- Du, J.; Roblin, C. Stochastic surrogate models of deformable antennas based on vector spherical harmonics and polynomial chaos expansions: Application to textile antennas. IEEE Trans. Ant. Propag. 2018, 66, 3610–3622. [Google Scholar] [CrossRef]
- Tomy, G.J.K.; Vinoy, K.J. A fast polynomial chaos expansion for uncertainty quantification in stochastic electromagnetic problems. IEEE Ant. Wirel. Propag. Lett. 2019, 18, 2120–2124. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, F.; Jin, J.; Zhang, Q.-J. Efficient yield estimation of microwave structures using mesh deformation-incorporated space mapping surrogates. IEEE Microw. Wirel. Comp. Lett. 2020, 30, 937–940. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A. Sequential approximate optimization for statistical analysis and yield optimization of circularly polarized antennas. IET Microw. Ant. Prop. 2018, 12, 2060–2064. [Google Scholar] [CrossRef]
- Koziel, S. Fast simulation-driven antenna design using response-feature surrogates. Int. J. RF Microw. CAE 2015, 25, 394–402. [Google Scholar] [CrossRef]
- Koziel, S.; Bandler, J.W. Rapid yield estimation and optimization of microwave structures exploiting feature-based statistical analysis. IEEE Trans. Microw. Theory Technol. 2015, 63, 107–114. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S. Numerically efficient algorithm for compact microwave device optimization with flexible sensitivity updating scheme. Int. J. RF Microw. CAE 2019, 29, e21714. [Google Scholar] [CrossRef]
- Kim, D.; Kim, M.; Kim, W. Wafer edge yield prediction using a combined long short-term memory and feed- forward neural network model for semiconductor manufacturing. IEEE Access 2020, 8, 215125–215132. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. Trust Region Methods; MPS-SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Koziel, S.; Pietrenko-Dabrowska, A. Reduced-cost surrogate modeling of compact microwave components by two-level kriging interpolation. Eng. Opt. 2019, 52, 960–972. [Google Scholar] [CrossRef]
- Tseng, C.; Chang, C. A rigorous design methodology for compact planar branch-line and rat-race couplers with asymmetrical T-structures. IEEE Trans. Microw. Theory Technol. 2012, 60, 2085–2092. [Google Scholar] [CrossRef]
- Xia, L.; Li, J.; Twumasi, B.A.; Liu, P.; Gao, S. Planar dual-band branch-line coupler with large frequency ratio. IEEE Access 2020, 8, 33188–33195. [Google Scholar] [CrossRef]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidynathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Performance-Driven Surrogate Modeling of High-Frequency Structures; Springer: New York, NY, USA, 2020. [Google Scholar]
- Pietrenko-Dabrowska, A. Rapid tolerance-aware design of miniaturized microwave passives by means of confined-domain surrogates. Int. J. Numer. Modeling 2021, 33, e2779. [Google Scholar]
| Case Study 1 | |||
|---|---|---|---|
| Circuit I | Circuit II | Circuit III | |
| Substrate | RO4003 (εr = 3.38, h = 0.76 mm) | AD300 (εr = 2.97, h = 0.76 mm) | RO4003 (εr = 3.5, h = 0.51 mm) |
| Design parameters | x = [l1 l2 l3 d w w1]T | x = [g l1r la lb w1 w2r w3r w4r wa wb]T | x = [Ls Ws l3r w1 w2 w3 w4 w5 wv]T |
| Other parameters | d1 = d + |w − w1|, d = 1.0, w0 = 1.7, and l0 = 15 | L = 2dL + Ls, Ls = 4w1 + 4g + s + la + lb, W = 2dL + Ws, Ws = 4w1 + 4g + s + 2wa, l1 = lbl1r, w2 = waw2r, w3 = w3rwa, and w4 = w4rwa | dL = dW = 10 mm, L = 2dL + Ls, W = 2dW + 2w1 + (Ws − 2wf), l1 = Ws/2, l2 = l321/2, l3 = l3r((Ls − w3)/2 − w4/21/2), lv1 = l3/3, lv3 = Ls/2 − w3/2 − l3 + lv1; wf = 1.15 mm |
| Operating bands | 0.89 GHz–1.11 GHz | 1.45 GHz–1.55 GHz | 2.36 GHz–2.44 GHz 5.16 GHz–5.24 GHz |
| Maximum power split error | 0.4 dB at 1 GHz | 0.5 dB at 1.5 GHz | 0.5 dB at 2.4 GHz 0.5 dB at 5.2 GHz |
| Nominal design | x(0) = [4.50 11.08 21.81 0.65 0.94 0.86]T | x(0) = [0.63 5.90 9.34 12.45 1.29 2.02 0.99 0.32 2.81 0.22]T | x(0) = [25.05 0.85 0.76 1.90 1.23 0.36 0.71 0.30 0.30]T |
| Optimization Algorithm | Initial Yield | Optimized Yield | CPU Cost 1 | ||
|---|---|---|---|---|---|
| Estimated by Surrogate Model | EM-Based | Estimated by Surrogate Model | EM-Based | ||
| Reference algorithm 1 | 50% | 42% | 100% | 97% | 400 |
| Reference algorithm 2 | 45% | 42% | 97% | 97% | 200 2 |
| Reference algorithm 3 | 44% | 42% | 98% | 98% | 82 |
| This work (Section 2) | 45% | 42% | 99% | 98% | 25 |
| Optimization Algorithm | Initial Yield | Optimized Yield | CPU Cost 1 | ||
|---|---|---|---|---|---|
| Estimated by Surrogate Model | EM-Based | Estimated by Surrogate Model | EM-Based | ||
| Reference algorithm 1 | 82% | 77% | 93% | 88% | 800 |
| Reference algorithm 2 | 76% | 77% | 94% | 93% | 320 2 |
| Reference algorithm 3 | 79% | 77% | 92% | 93% | 112 |
| This work (Section 2) | 79% | 77% | 90% | 92% | 37 |
| Optimization Algorithm | Initial Yield | Optimized Yield | CPU Cost 1 | ||
|---|---|---|---|---|---|
| Estimated by Surrogate Model | EM-Based | Estimated by Surrogate Model | EM-Based | ||
| Reference algorithm 1 | 80% | 71% | 99% | 93% | 800 |
| Reference algorithm 2 | 88% | 71% | 96% | 91% | 500 1 |
| Reference algorithm 3 | 74% | 71% | 94% | 92% | 123 |
| This work (Section 2) | 71% | 71% | 93% | 89% | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrenko-Dabrowska, A.; Koziel, S. Design Centering of Compact Microwave Components Using Response Features and Trust Regions. Energies 2021, 14, 8550. https://doi.org/10.3390/en14248550
Pietrenko-Dabrowska A, Koziel S. Design Centering of Compact Microwave Components Using Response Features and Trust Regions. Energies. 2021; 14(24):8550. https://doi.org/10.3390/en14248550
Chicago/Turabian StylePietrenko-Dabrowska, Anna, and Slawomir Koziel. 2021. "Design Centering of Compact Microwave Components Using Response Features and Trust Regions" Energies 14, no. 24: 8550. https://doi.org/10.3390/en14248550
APA StylePietrenko-Dabrowska, A., & Koziel, S. (2021). Design Centering of Compact Microwave Components Using Response Features and Trust Regions. Energies, 14(24), 8550. https://doi.org/10.3390/en14248550







