Integration of Electric Vehicles and Energy Storage System in Home Energy Management System with Home to Grid Capability
Abstract
:1. Introduction
- Includes RT appliances, ST appliances, PV, EV, and ESS simultaneously to minimize the operating cost.
- Fully utilizes the PV power by shiftable appliances, EV, and ESS while the surplus power is fed back to the grid for economic benefits.
- The charging and discharging schemes have been presented, including the constraints of ESS and EV. The scheme utilizes the RTP, maximum demand limit, and availability of EV to rationally manage the energy flow between home and utility. The EV and ESS are charged during low RTP periods and provide power to peak energy periods. The discharging power is utilized by domestic appliances while the surplus power is sold back to the grid.
- A multi-objective problem is formulated, which minimizes the operating cost, PAR, and user’s discomfort simultaneously in the HEMS paradigm.
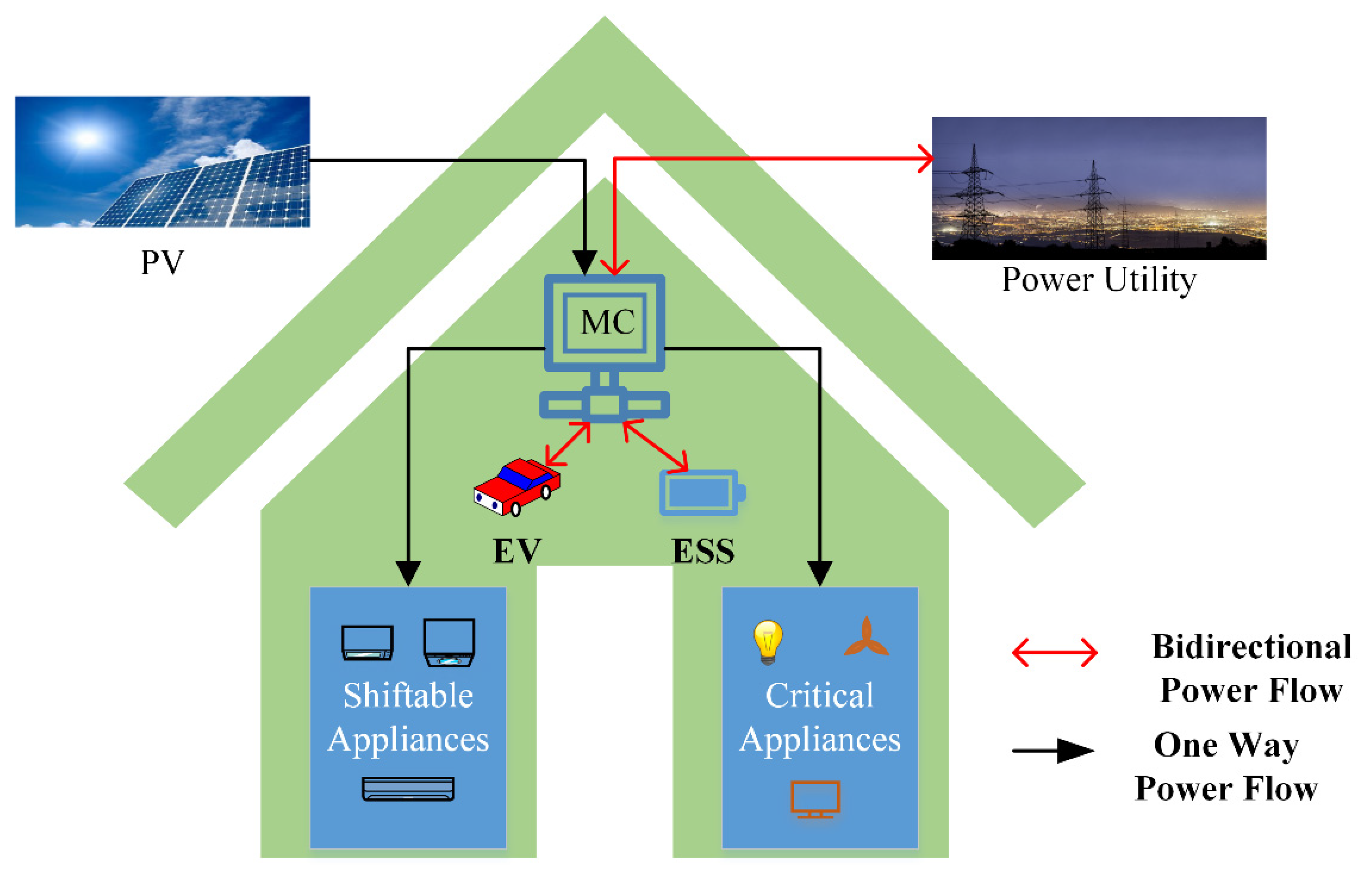
2. System Description
3. Problem Formulation
3.1. Appliances Modeling
- (a)
- RT appliances: RT appliances are those that must be turned on in real time, such as the lighting system, television, and refrigerator. RT appliances should be ON when needed; otherwise, they are OFF. Let the set of RT appliances be ; where denotes the RT appliance. There are M number of RT appliances in HEMS. The RT appliance should be ON or OFF according to the HEMS scheme.
- (b)
- ST appliances: ST appliances are ones that can operate at any time of day, such as a washing machine, dishwasher, and vacuum cleaner. Let the set of shiftable appliances be ; where Y denotes the number of ST, and denotes the shiftable appliance. The starting time of each ST have shown in vector ; where denotes the starting time of appliance. Let binary variable define the status of shiftable appliance as follows:where is the status of shiftable appliances in time slot and is the number of time slots required to complete the operation of appliance. If the appliance is ON, the value of is 1; otherwise, it is zero. The operation of each appliance started at and finished at without interruption.
- (c)
- RES: PV has been utilized as RES in this proposed work as shown in Figure 1. The output power of PV has been calculated according to the following Equation (9):where SI is solar horizontal irradiation, A is the total area of the solar panel, and is the solar conversion efficiency of the installed PV system. The power generated by PV in time t with time interval is calculated as follows:
- (d)
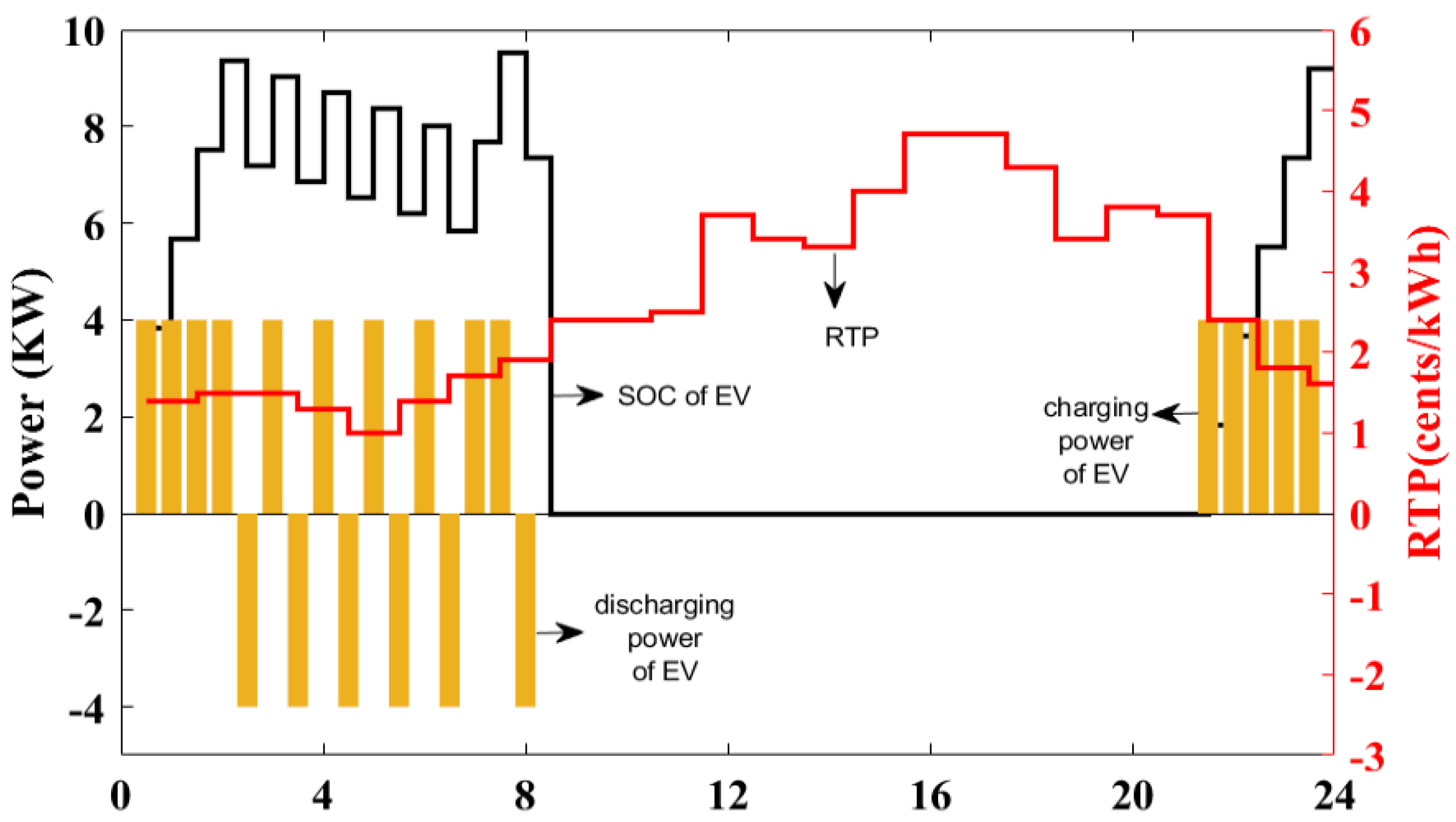
- ESS: The intrusion of ESS in-home significantly increases the capability of HEMS. HEMS controls the charging and discharging of ESS according to the available surplus energy. The power and energy of ESS are modeled as follows:where is the power supplied/consumed by ESS, is the charging power of ESS, is the discharging power of ESS and shows the status of ESS ( means charging, means discharging).The total energy consumed/delivered in a day by ESS, , is given by:
- (e)
- EV: The use of EV is increasing very sharply. The installation and maintenance cost of EV is lower than ESS. Therefore, EV is the best choice for energy storage and power transfer in home premises. Similar to ESS, the power and energy have been calculated using the following equation:where is the power supplied/consumed by EV, is the charging power of EV, is the discharging power of EV, and shows the status of EV ( means charging, means discharging).The total energy consumed/delivered in a day by ESS is given by:
- (f)
- Load demand: The HEMS schedules the home appliances along with ESS, EV, and RES and controls the energy exchange between the home and the main grid (MG). The total energy consumed in the home in a day is calculated in Equation (31).
3.2. Objective Function Modeling
- (a)
- Total energy cost minimization: Our objective is to minimize the cost of energy, which is calculated as follows:
- (b)
- PAR: In HEMS, the appliances are scheduled to minimize the overall cost of energy. This may lead to peak demands in low-cost time slots. Higher peak demand leads to the failure of MG. To reduce the peak demand, PAR should be minimum. It is defined as the ratio of peak demand to an average of all demands in a day. PAR is calculated as follows:Our objective is to minimize the PAR
- (c)
- DI: The domestic appliances have their desirable operating time interval. Optimal scheduling of appliance changes its desirable operating time interval to optimal OPI. Any change in desirable OPI causes discomfort to the users. A DI has been introduced to determine the difference between desirable and optimal OPI. The DI is defined as:where is the desirable OPI of appliances. Our objective is to minimize the user’s discomfort, which is defined below:
- (d)
- MOF: We have now considered the above mentioned objective functions as a single objective function obtained using the weighted sum method and the optimized simultaneously. The MOF is defined as follows:where denote the weights of respective objectives.
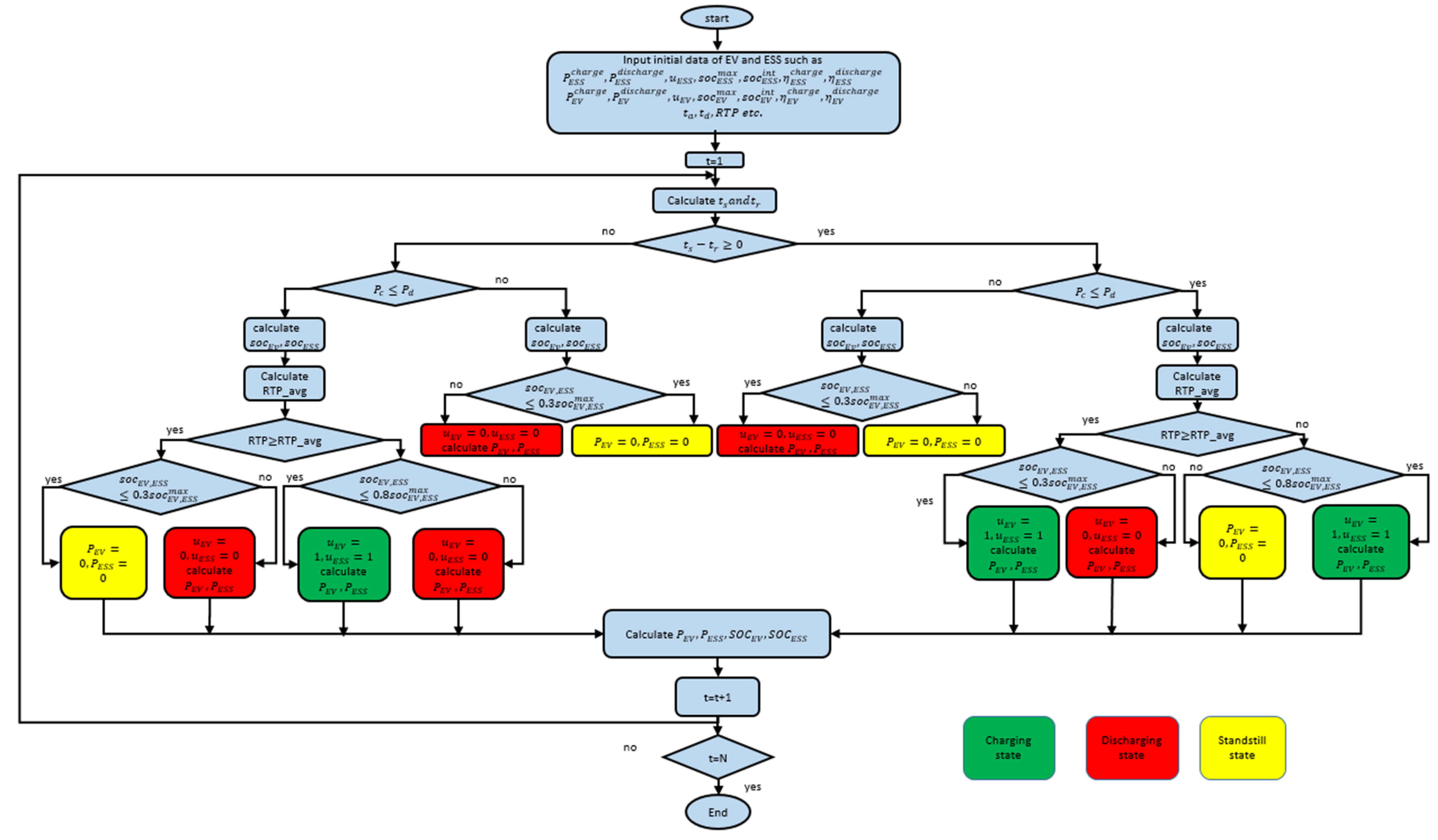
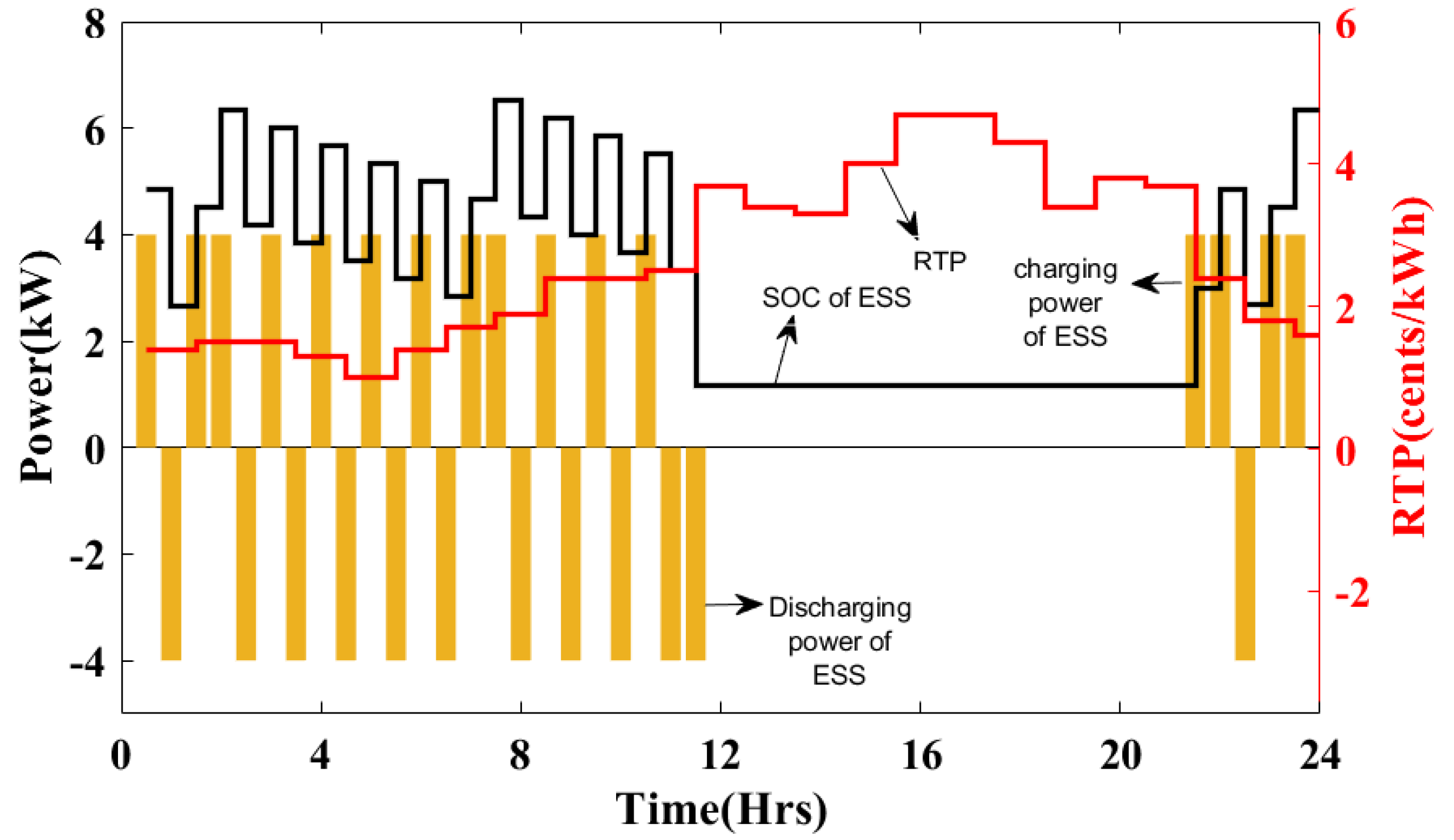
4. Charging and Discharging Schemes
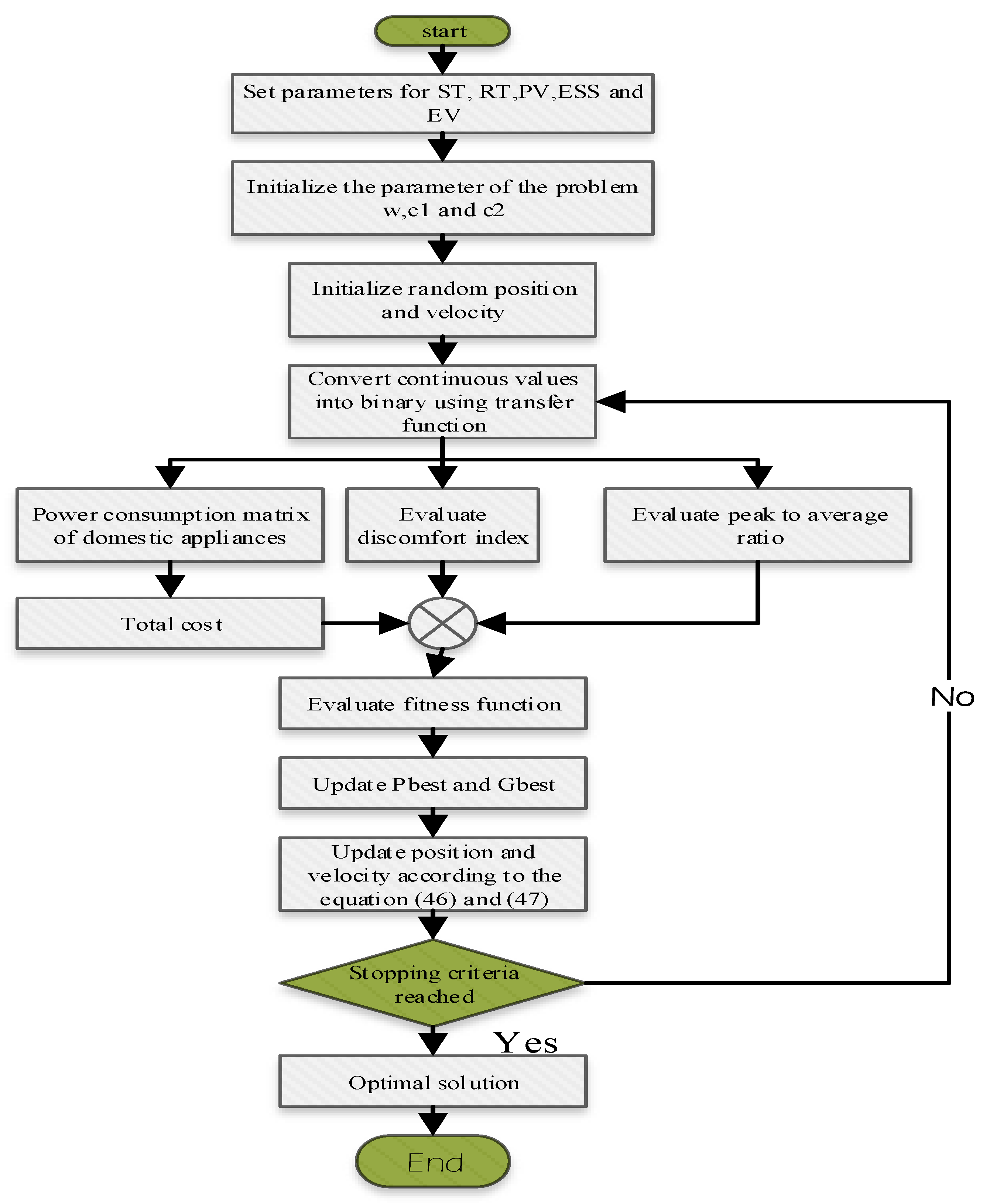
5. Optimization Module
- All particles have initialized with random values.
- For all particles, velocities are defined using Equation (46).
- Calculate probabilities for changing the elements of position vector using Equation (48).
- Update the elements of position vectors with Equation (49)
- Calculate the objective function “O”.
- Repeat until satisfying the end condition.
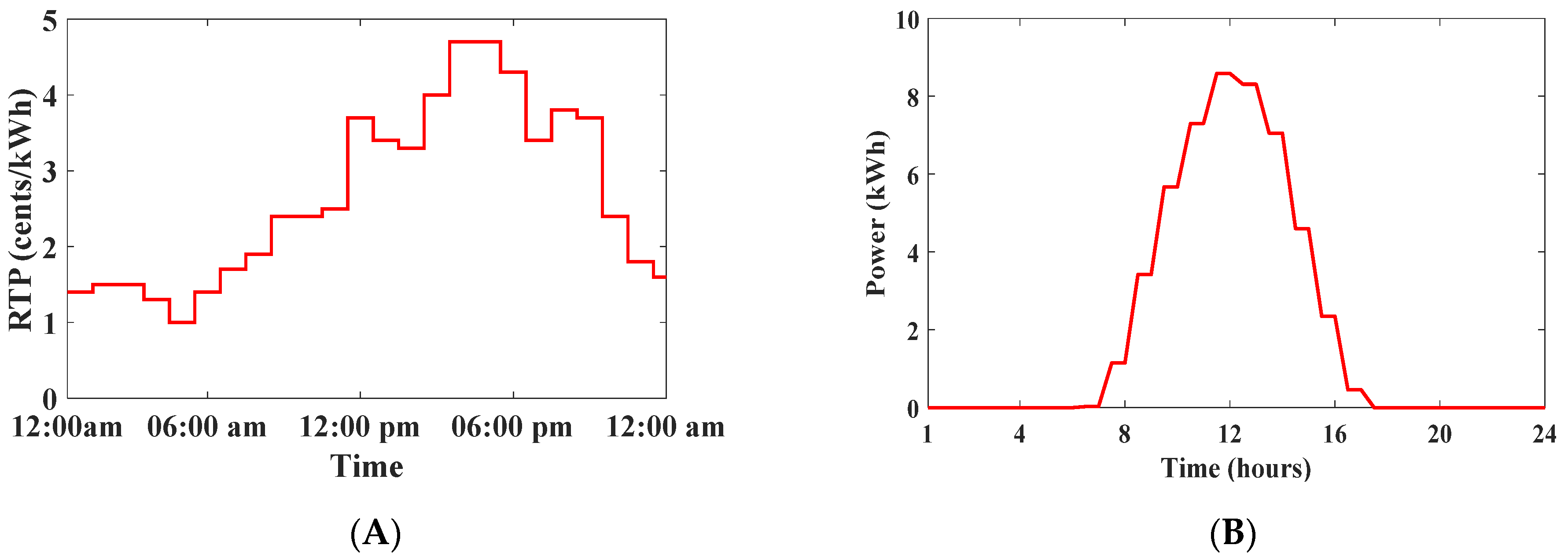
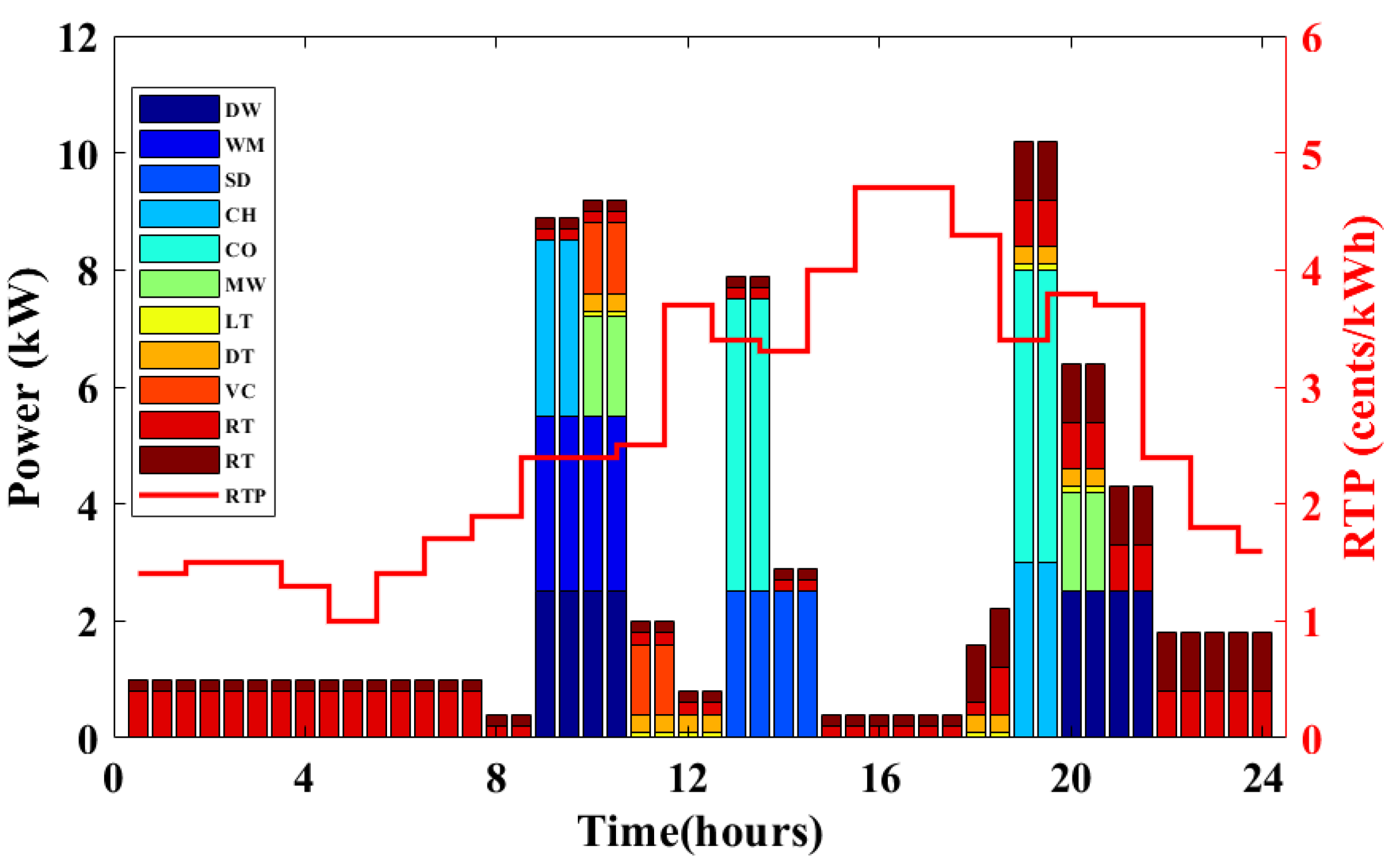
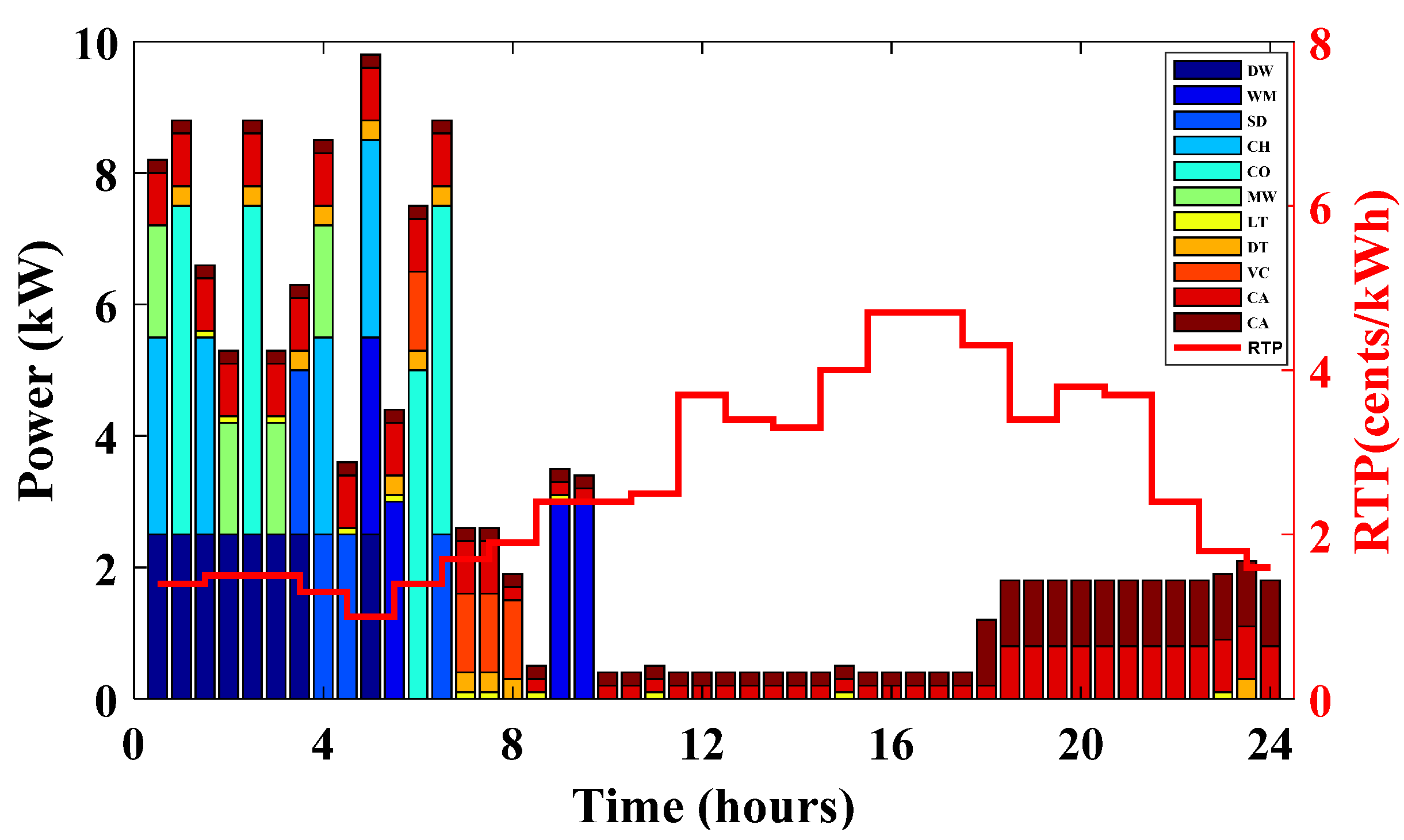
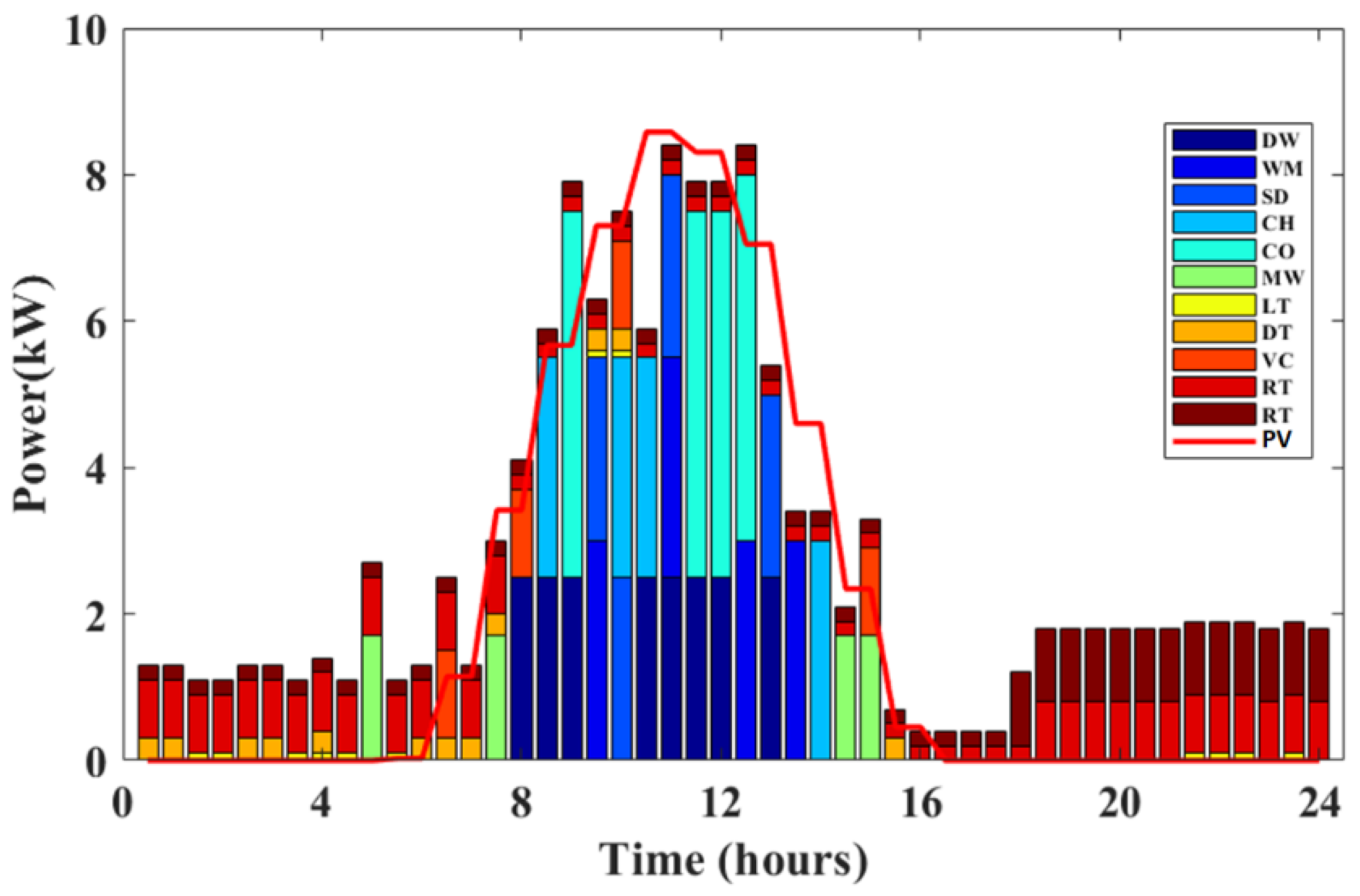
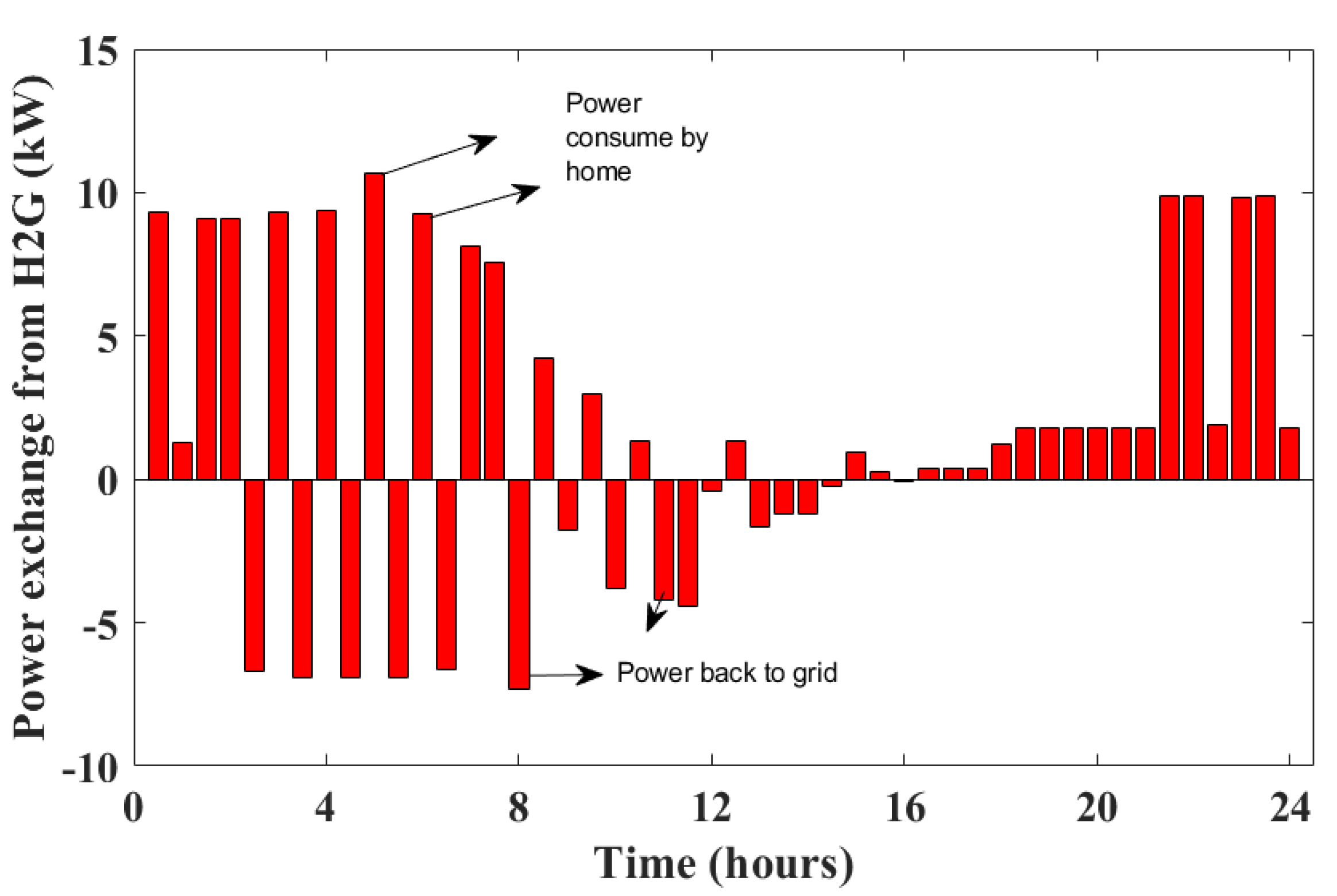
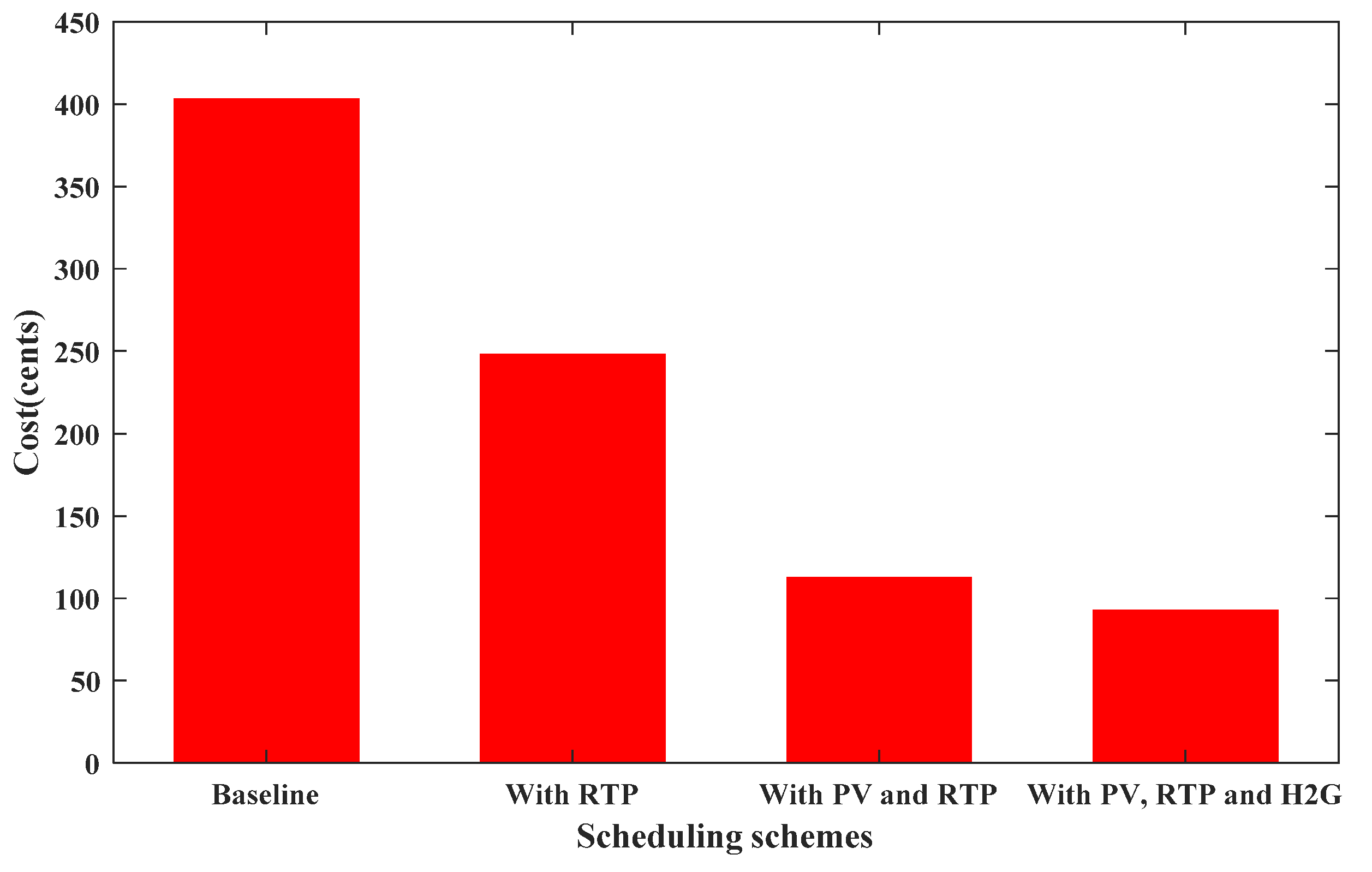
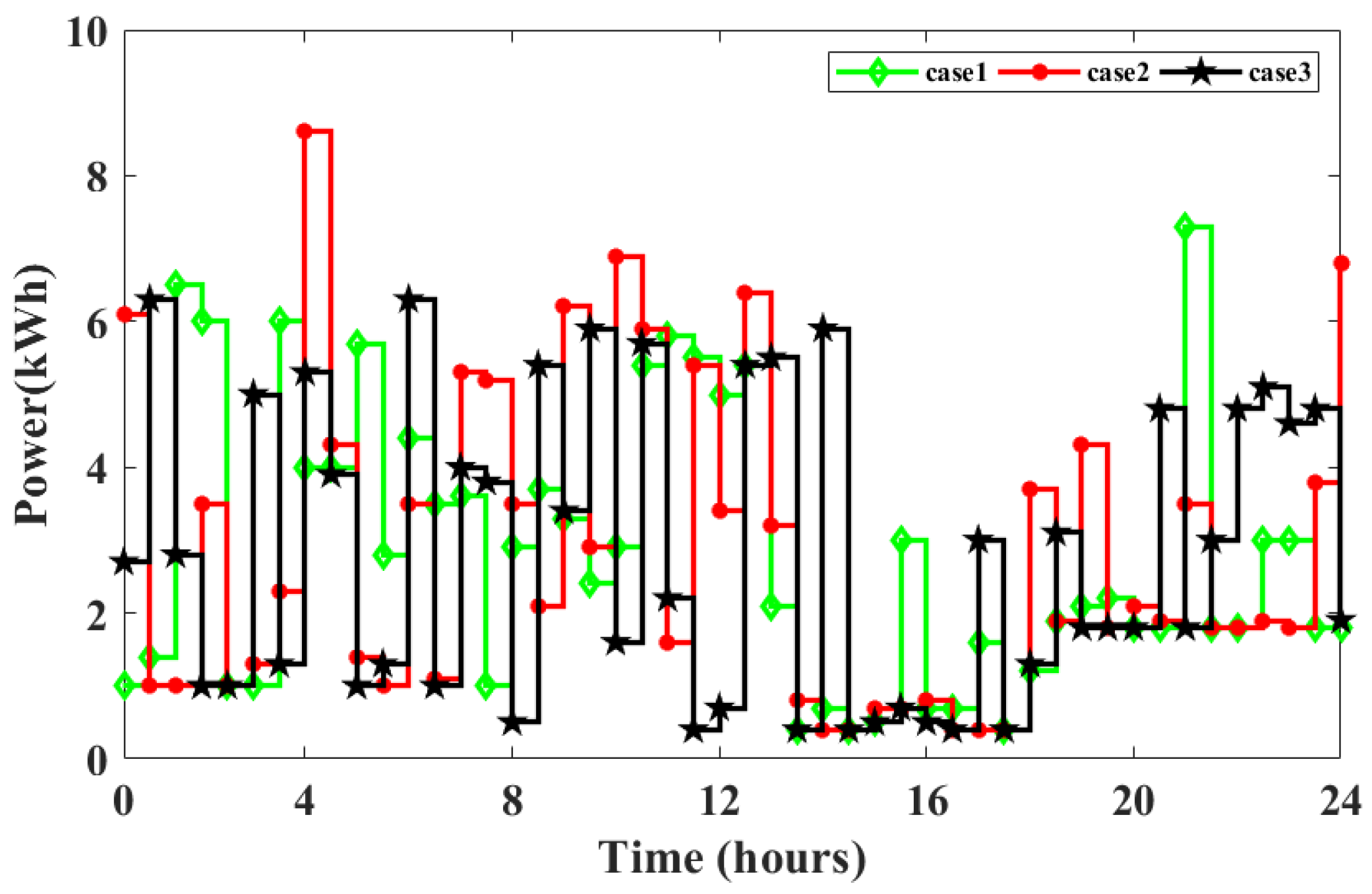
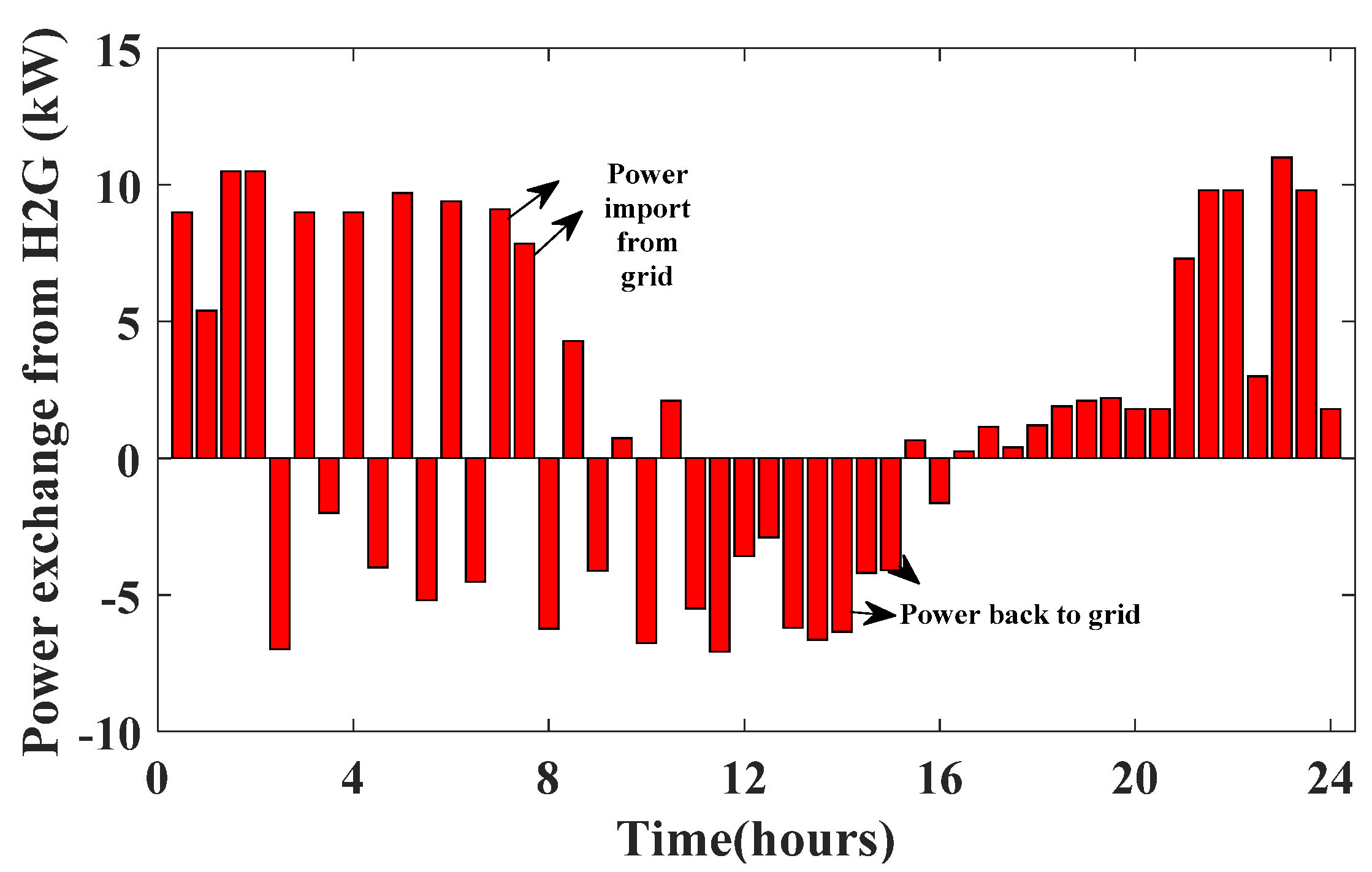
6. Result and Discussion
6.1. Case 1: Single Objective Optimization
6.2. Case 2: Multi-Objective Optimazation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
| Nomenclature | |
| HEMS | Home Energy Management System |
| HPEMC | Heuristic-Based Programmable Energy Management Controller |
| RES | Renewable Energy Resources |
| WT | Wind Turbines |
| DG | Distributed Generation |
| HP | Heat Pump |
| PV | Photovoltaic |
| ESS | Energy Storage System |
| EV | Electric Vehicle |
| SM | Smart Meter |
| MC | Main Controller |
| MG | Main Grid |
| PSO | Particle Swarm Optimization |
| BPSO | Binary Particle Swarm Optimization |
| ELPSO | Enhance Leader Particle Swarm Optimization |
| MILP | Mixed-Integer Linear Programming |
| GA | Genetic Algorithm |
| MINLP | Mixed-Integer Nonlinear Programming |
| GWO | Grey Wolf Optimizer |
| DP | Dynamic Programming |
| RBA | Rule-Based Algorithm |
| HGPO | Hybrid Genetic Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| WDO | Wind-Driven Optimization |
| BOA | Butterfly Optimization Algorithm |
| V2H | Vehicle To Home |
| V2G | Vehicle To Grid |
| H2G | Home To Grid |
| G2H | Grid To Home |
| DSM | Demand Side Management |
| DR | Demand Response |
| RTP | Real Time Pricing |
| TOU | Time of Use |
| PAR | Peak to Average Ratio |
| DI | Discomfort Index |
| EMC | Energy Management Controller |
| IBR | Inclination Block Rate |
| BFA | Bacterial Foraging Algorithm |
| DFA | Dragonfly Algorithm |
| AHP | Analytical Hierarchy Process |
| LP | Linear Programming |
| MEH | Multiple Energy Hubs |
| MHS | Modified Harmony Search |
| DEMS | District Energy Management System |
| MIQP | Mixed-Integer Quadratic Programming |
| GSA | Gravitational Search Algorithm |
| CSO | Cuckoo Search Optimization |
| RT | Real-Time Appliance |
| ST | Shiftable Appliance |
| MOF | Multi-Objective Function |
| Abbreviations | |
| Status of real-time appliance in time slot. | |
| The power consumption of RT appliances in slot | |
| The energy consumption of RT appliances in slot | |
| Time interval | |
| The total energy consumed in a day by RT appliance | |
| The starting time of appliance | |
| The status of shiftable appliances in time slot | |
| Lower bound starting time for shiftable appliance | |
| Upper bound starting time for shiftable appliance | |
| The number of time slots are required to complete the operation of each ST appliance | |
| The power consumption of ST appliances in slot | |
| The energy consumption of ST appliances in slot | |
| The total energy consumed in a day by ST appliance | |
| The output power of PV | |
| Solar horizontal irradiation | |
| Solar conversion efficiency of the installed PV system | |
| The energy generated by PV in time interval | |
| The PV energy utilized by the appliance load | |
| The PV energy used for EV charging | |
| The PV energy used for ESS charging | |
| The total energy consumption of home in a day | |
| The surplus energy transferred back to the MG | |
| The energy transfer variable status from G2H or H2G | |
| The power supplied/consumed by ESS | |
| The charging power of ESS | |
| The discharging power of ESS | |
| The status of ESS | |
| The total energy consumed/delivered in a day by ESS | |
| State of charge of EV | |
| Charging efficiency of ESS | |
| Discharging efficiency of ESS | |
| Intial state of charge of ESS | |
| Maximum charging power of ESS | |
| Maximum discharging power of ESS | |
| The power supplied/consumed by EV | |
| The charging power of EV | |
| The discharging power of EV | |
| The status of EV | |
| The total energy consumed/delivered in a day by EV | |
| State of charge of EV | |
| Charging efficiency of EV | |
| Discharging efficiency of EV | |
| Intial state of charge of EV | |
| Maximum charging power of EV | |
| Maximum discharging power of EV | |
References
- Nguyen, H.T.; Nguyen, D.T.; Le, L.B. Energy management for households with solar assisted thermal load considering renewable energy and price uncertainty. IEEE Trans. Smart Grid 2015, 6, 301–314. [Google Scholar] [CrossRef]
- Rottondi, C.; Barbato, A.; Chen, L.; Verticale, G. Enabling privacy in a distributed game-theoretical scheduling system for domestic appliances. IEEE Trans. Smart Grid 2017, 8, 1220–1230. [Google Scholar] [CrossRef]
- Molla, T.; Khan, B.; Moges, B.; Alhelou, H.H.; Zamani, R.; Siano, P. Integrated energy optimization of smart home appliances with cost-effective energy management system. CSEE J. Power Energy Syst. 2019, 5, 249–258. [Google Scholar] [CrossRef]
- Celik, B.; Roche, R.; Bouquain, D.; Miraoui, A. Decentralized neighborhood energy management with coordinated smart home energy sharing. IEEE Trans. Smart Grid 2018, 9, 6387–6397. [Google Scholar] [CrossRef] [Green Version]
- Rezaee Jordehi, A. Enhanced leader particle swarm optimisation (ELPSO): A new algorithm for optimal scheduling of home appliances in demand response programs. Artif. Intell. Rev. 2020, 53, 2043–2073. [Google Scholar] [CrossRef]
- Althaher, S.; Member, S.; Mancarella, P.; Member, S. Management System Under Dynamic Pricing. IEEE Trans. Smart Grid 2015, 6, 1874–1883. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, W.C.; Shin, Y.; Song, K. Bin An optimal power scheduling method for demand response in home energy management system. IEEE Trans. Smart Grid 2013, 4, 1391–1400. [Google Scholar] [CrossRef]
- Dinh, H.T.; Yun, J.; Kim, D.M.; Lee, K.H.; Kim, D. A Home Energy Management System with Renewable Energy and Energy Storage Utilizing Main Grid and Electricity Selling. IEEE Access 2020, 8, 49436–49450. [Google Scholar] [CrossRef]
- Abdelaal, G.; Gilany, M.I.; Elshahed, M.; Sharaf, H.M.; El’Gharably, A. Integration of Electric Vehicles in Home Energy Management Considering Urgent Charging and Battery Degradation. IEEE Access 2021, 9, 47713–47730. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Ifrim, G. Flattening the electricity consumption peak and reducing the electricity payment for residential consumers in the context of smart grid by means of shifting optimization algorithm. Comput. Ind. Eng. 2018, 122, 125–139. [Google Scholar] [CrossRef]
- Dinh, H.T.; Kim, D. An Optimal Energy-Saving Home Energy Management Supporting User Comfort and Electricity Selling with Different Prices. IEEE Access 2021, 9, 9235–9249. [Google Scholar] [CrossRef]
- Sarker, E.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Stojcevski, A. Optimal management of home loads with renewable energy integration and demand response strategy. Energy 2020, 210, 118602. [Google Scholar] [CrossRef]
- Kaluthanthrige, R.; Rajapakse, A.D. Demand response integrated day-ahead energy management strategy for remote off-grid hybrid renewable energy systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106731. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Preda, Ș.; Tor, O.B. A Smart Adaptive Switching Module Architecture Using Fuzzy Logic for an Efficient Integration of Renewable Energy Sources. A Case Study of a RES System Located in Hulubești, Romania. Sustainability 2020, 12, 6084. [Google Scholar] [CrossRef]
- Sangswang, A.; Konghirun, M. Optimal Strategies in Home Energy Management System Integrating Solar Power, Energy Storage, and Vehicle-to-Grid for Grid Support and Energy Efficiency. IEEE Trans. Ind. Appl. 2020, 56, 5716–5728. [Google Scholar] [CrossRef]
- Imran, A.; Hafeez, G.; Khan, I.; Member, S.; Qazi, A.B.; Khalid, A.; Thoben, K. Heuristic-Based Programable Controller for Efficient Energy Management Under Renewable Energy Sources and Energy Storage System in Smart Grid. IEEE Access 2020, 8, 139587–139608. [Google Scholar] [CrossRef]
- Ben Slama, S. Design and implementation of home energy management system using vehicle to home (H2V) approach. J. Clean. Prod. 2021, 312, 127792. [Google Scholar] [CrossRef]
- Alilou, M.; Tousi, B.; Shayeghi, H. Home energy management in a residential smart micro grid under stochastic penetration of solar panels and electric vehicles. Sol. Energy 2020, 212, 6–18. [Google Scholar] [CrossRef]
- Aznavi, S.; Fajri, P.; Asrari, A.; Harirchi, F. Realistic and Intelligent Management of Connected Storage Devices in Future Smart Homes Considering Energy Price Tag. IEEE Trans. Ind. Appl. 2020, 56, 1679–1689. [Google Scholar] [CrossRef]
- Yousefi, M.; Hajizadeh, A.; Soltani, M.N.; Hredzak, B. Predictive Home Energy Management System with Photovoltaic Array, Heat Pump, and Plug-In Electric Vehicle. IEEE Trans. Ind. Inform. 2021, 17, 430–440. [Google Scholar] [CrossRef]
- ur Rehman, U.; Yaqoob, K.; Adil Khan, M. Optimal power management framework for smart homes using electric vehicles and energy storage. Int. J. Electr. Power Energy Syst. 2022, 134, 107358. [Google Scholar] [CrossRef]
- van der Kam, M.; van Sark, W. Smart charging of electric vehicles with photovoltaic power and vehicle-to-grid technology in a microgrid; a case study. Appl. Energy 2015, 152, 20–30. [Google Scholar] [CrossRef] [Green Version]
- Poursmaeil, B.; Hosseinpour Najmi, P.; Najafi Ravadanegh, S. Interconnected-energy hubs robust energy management and scheduling in the presence of electric vehicles considering uncertainties. J. Clean. Prod. 2021, 316, 128167. [Google Scholar] [CrossRef]
- Rabiee, A.; Sadeghi, M.; Aghaeic, J.; Heidari, A. Optimal operation of microgrids through simultaneous scheduling of electrical vehicles and responsive loads considering wind and PV units uncertainties. Renew. Sustain. Energy Rev. 2016, 57, 721–739. [Google Scholar] [CrossRef]
- Zeynali, S.; Rostami, N.; Ahmadian, A.; Elkamel, A. Stochastic energy management of an electricity retailer with a novel plug-in electric vehicle-based demand response program and energy storage system: A linearized battery degradation cost model. Sustain. Cities Soc. 2021, 74, 103154. [Google Scholar] [CrossRef]
- AL-Dhaifallah, M.; Ali, Z.M.; Alanazi, M.; Dadfar, S.; Fazaeli, M.H. An efficient short-term energy management system for a microgrid with renewable power generation and electric vehicles. Neural Comput. Appl. 2021, 33, 16095–16111. [Google Scholar] [CrossRef]
- Torres-Moreno, J.; Gimenez-Fernandez, A.; Perez-Garcia, M.; Rodriguez, F. Energy Management Strategy for Micro-Grids with PV-Battery Systems and Electric Vehicles. Energies 2018, 11, 522. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Guan, X.; Wu, J.; Li, P.; Zan, P.; Xu, H. Integrated Energy Exchange Scheduling for Multimicrogrid System with Electric Vehicles. IEEE Trans. Smart Grid 2016, 7, 1762–1774. [Google Scholar] [CrossRef] [Green Version]
- Fanti, M.P.; Mangini, A.M.; Roccotelli, M.; Ukovich, W. District Microgrid Management Integrated with Renewable Energy Sources, Energy Storage Systems and Electric Vehicles *. * This work is supported by the project Smart Cities and Communities and Social Innovation Pilot 2014–2016-ASMARA. IFAC-PapersOnLine 2017, 50, 10015–10020. [Google Scholar] [CrossRef]
- Raya-Armenta, J.M.; Bazmohammadi, N.; Avina-Cervantes, J.G.; Sáez, D.; Vasquez, J.C.; Guerrero, J.M. Energy management system optimization in islanded microgrids: An overview and future trends. Renew. Sustain. Energy Rev. 2021, 149, 111327. [Google Scholar] [CrossRef]
- Lee, J.Y.; Choi, S.G. Linear programming based hourly peak load shaving method at home area. In Proceedings of the 16th International Conference on Advanced Communication Technology; Global IT Research Institute (GIRI), Pyeongchang, Korea, 16–19 February 2014; pp. 310–313. [Google Scholar]
- Emami Javanmard, M.; Ghaderi, S.F.; Sangari, M.S. Integrating energy and water optimization in buildings using multi-objective mixed-integer linear programming. Sustain. Cities Soc. 2020, 62, 102409. [Google Scholar] [CrossRef]
- Ogunjuyigbe, A.S.O.; Ayodele, T.R.; Oladimeji, O.E. Management of loads in residential buildings installed with PV system under intermittent solar irradiation using mixed integer linear programming. Energy Build. 2016, 130, 253–271. [Google Scholar] [CrossRef]
- Wittmann, F.M.; Lopez, J.C.; Rider, M.J. Nonintrusive Load Monitoring Algorithm Using Mixed-Integer Linear Programming. IEEE Trans. Consum. Electron. 2018, 64, 180–187. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, W.; Hou, B. A hybrid algorithm for mixed integer nonlinear programming in residential energy management. J. Clean. Prod. 2019, 226, 940–948. [Google Scholar] [CrossRef]
- Killian, M.; Zauner, M.; Kozek, M. Comprehensive smart home energy management system using mixed-integer quadratic-programming. Appl. Energy 2018, 222, 662–672. [Google Scholar] [CrossRef]
- Jeddi, B.; Mishra, Y.; Ledwich, G. Dynamic programming based home energy management unit incorporating PVs and batteries. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Mokhtara, C.; Negrou, B.; Settou, N.; Bouferrouk, A.; Yao, Y. Design optimization of grid-connected PV-Hydrogen for energy prosumers considering sector-coupling paradigm: Case study of a university building in Algeria. Int. J. Hydrog. Energy 2021, 46, 37564–37582. [Google Scholar] [CrossRef]
- Azaza, M.; Wallin, F. Multi objective particle swarm optimization of hybrid micro-grid system: A case study in Sweden. Energy 2017, 123, 108–118. [Google Scholar] [CrossRef]
- Mokhtara, C.; Negrou, B.; Settou, N.; Settou, B.; Samy, M.M. Design optimization of off-grid Hybrid Renewable Energy Systems considering the effects of building energy performance and climate change: Case study of Algeria. Energy 2021, 219, 119605. [Google Scholar] [CrossRef]
- Javaid, N.; Ullah, I.; Akbar, M.; Iqbal, Z.; Khan, F.A.; Alrajeh, N.; Alabed, M.S. An Intelligent Load Management System with Renewable Energy Integration for Smart Homes. IEEE Access 2017, 5, 13587–13600. [Google Scholar] [CrossRef]
- Kong, X.; Sun, B.; Kong, D.; Li, B. Home energy management optimization method considering potential risk cost. Sustain. Cities Soc. 2020, 62, 102378. [Google Scholar] [CrossRef]
- Zupančič, J.; Filipič, B.; Gams, M. Genetic-programming-based multi-objective optimization of strategies for home energy-management systems. Energy 2020, 203, 117769. [Google Scholar] [CrossRef]
- Jordehi, A.R. Optimal scheduling of home appliances in home energy management systems using grey Wolf optimisation (Gwo) algorithm. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ayub, S.; Ayob, S.M.; Tan, C.W.; Ayub, L.; Bukar, A.L. Optimal residence energy management with time and device-based preferences using an enhanced binary grey wolf optimization algorithm. Sustain. Energy Technol. Assess. 2020, 41, 100798. [Google Scholar] [CrossRef]
- Kazemi, S.-F.; Motamedi, S.-A.; Sharifian, S. A home energy management system using Gray Wolf Optimizer in smart grids. In Proceedings of the 2017 2nd Conference on Swarm Intelligence and Evolutionary Computation (CSIEC), Kerman, Iran, 7–9 March 2017; pp. 159–164. [Google Scholar]
- Li, N.; Su, Z.; Jerbi, H.; Abbassi, R.; Latifi, M.; Furukawa, N. Energy management and optimized operation of renewable sources and electric vehicles based on microgrid using hybrid gravitational search and pattern search algorithm. Sustain. Cities Soc. 2021, 75, 103279. [Google Scholar] [CrossRef]
- Wang, X.; Mao, X.; Khodaei, H. A multi-objective home energy management system based on internet of things and optimization algorithms. J. Build. Eng. 2021, 33, 101603. [Google Scholar] [CrossRef]
- Shaban, A.; Maher, H.; Elbayoumi, M.; Abdelhady, S. A cuckoo load scheduling optimization approach for smart energy management. Energy Rep. 2021, 7, 4705–4721. [Google Scholar] [CrossRef]
- Zuhaib, M.; Khan, H.A.; Rihan, M. Performance Analysis of a Utility-Scale Grid Integrated Solar Farm Considering Physical and Environmental Factors. J. Inst. Eng. Ser. B 2020, 102, 363–375. [Google Scholar] [CrossRef]
| Paper | Optimization Algorithm | Scheduling Home Appliances | Problem Objectives | Integration | Charging and Discharging Scheme of EV/ESS | H2G Capability | V2G/V2H Capability | Selling Capability | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min Cost | Min DI | Min PAR | RES | ESS | EV | |||||||
| [5] | ELPSO | ✓ | ✓ | ✓ | ||||||||
| [6] | MILP | ✓ | ✓ | ✓ | ||||||||
| [7] | GA | ✓ | ✓ | ✓ | ||||||||
| [8] | BPSO | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [9] | RBA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [10] | RBA | ✓ | ✓ | ✓ | ||||||||
| [11] | MINLP | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| [12] | MILP | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [13] | PSO | ✓ | ✓ | ✓ | ✓ | |||||||
| [14] | Fuzzy logic | ✓ | ✓ | ✓ | ✓ | |||||||
| [15] | DP and RBA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [16] | HGPO, ACO, GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [17] | MILP | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [18] | DFA & AHP | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [19] | RBA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [21] | MILP & RBA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| [22] | LP | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| [23] | simplex | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| [24] | MH & RBA | ✓ | ✓ | ✓ | ✓ | |||||||
| [25] | MILP | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [27] | Two stage RBA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [29] | LP | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| Out proposed work | BPSO | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Appliances | Rated Power (kwh) | Time Duration for Appliances ON (h) | Baseline Operating Time Span | |
|---|---|---|---|---|
| Schedulable appliance | Dishwasher (DW) | 2.5 | 4 | 09:00–11:00 & 20:00–22:00 |
| Washing machine (WM) | 3 | 2 | 09:00–11:00 | |
| Spine dryer (SD) | 2.5 | 2 | 13:00–15:00 | |
| Cooker hub (CH) | 3 | 2 | 09:00–10:00 & 19:00–20:00 | |
| Cooker oven (CO) | 5 | 2 | 13:00–14:00 & 20:00–21:00 | |
| Microwave (MW) | 1.7 | 2 | 10:00–11:00 & 20:00–21:00 | |
| Laptop (LT) | 0.1 | 6 | 10:00–13:00 & 18:00–21:00 | |
| Desktop (DT) | 0.3 | 6 | 10:00–13:00 & 18:00–21:00 | |
| Vaccum cleaner (VC) | 1.2 | 2 | 10:00–12:00 | |
| Real-Time appliance (RT) | Fan | 0.2 | 14 | 06:00pm–8:00 am |
| Light | 0.1 | 8 | 06:00 p.m.–12:00 a.m. & 06:00 a.m.–8:00 a.m. | |
| Television | 0.2 | 4 | 08:00 p.m.–12:00 a.m. | |
| Refrigerator | 1 | 24 | 00:00 a.m.–12:00 a.m. | |
| ESS Parameter | EV Parameter | ||
|---|---|---|---|
| (kWh) | 6 | (kWh) | 10 |
| (kWh) | 3 | (kWh) | 2 |
| (kW) | 4 | (kW) | 4 |
| (kW) | −4 | (kW) | −4 |
| 0.92 | 0.92 | ||
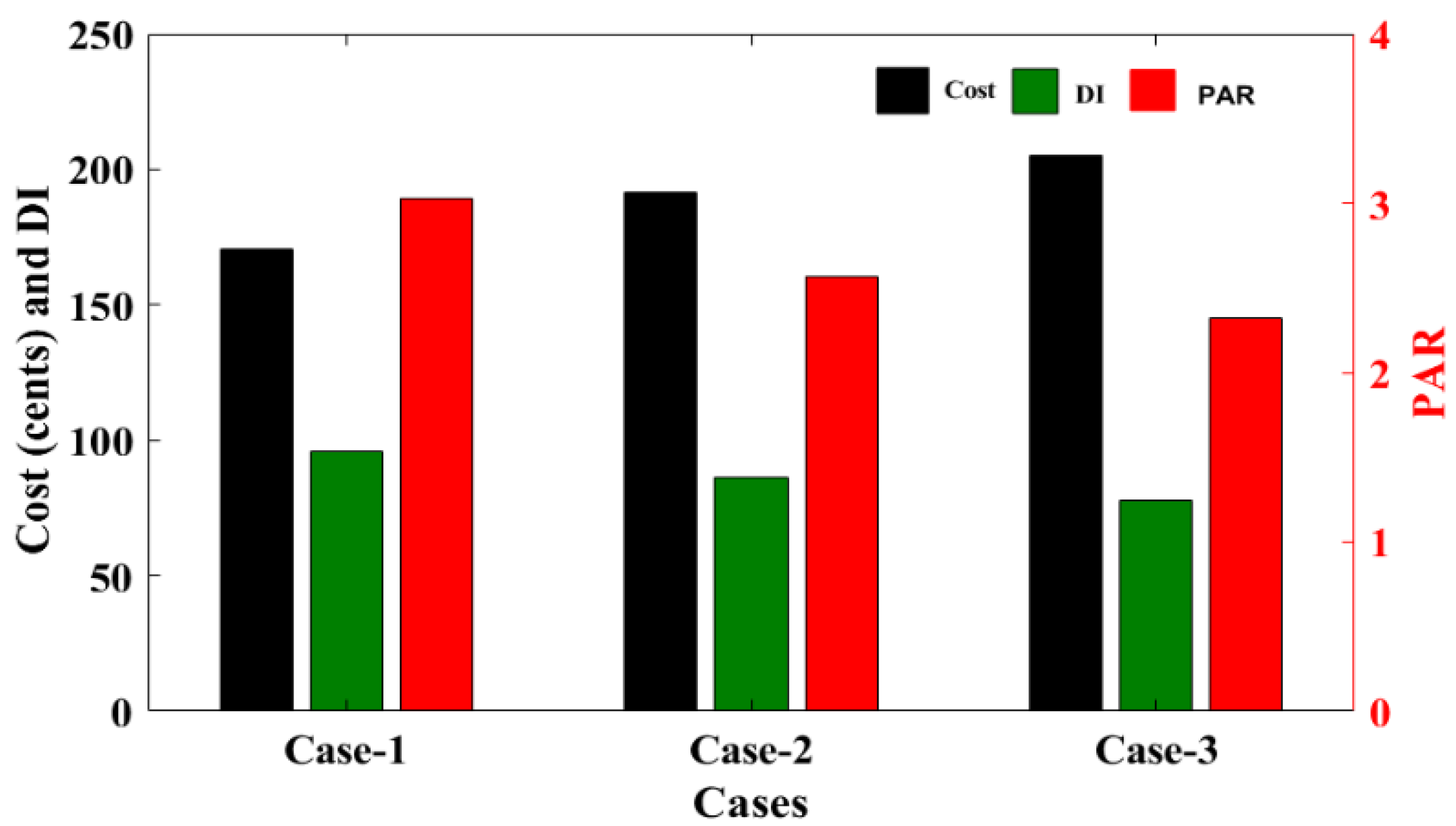
| Cases | W1 | W2 | W3 | Cost (Cents) | PAR | DI |
|---|---|---|---|---|---|---|
| Case-1 | 1 | 0 | 0 | 170.41 | 3.0308 | 96 |
| Case-2 | 1 | 20 | 5 | 191.46 | 2.5727 | 80 |
| Case-3 | 1 | 40 | 20 | 205.14 | 2.3260 | 68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad, A.; Zuhaib, M.; Ashraf, I.; Alsultan, M.; Ahmad, S.; Sarwar, A.; Abdollahian, M. Integration of Electric Vehicles and Energy Storage System in Home Energy Management System with Home to Grid Capability. Energies 2021, 14, 8557. https://doi.org/10.3390/en14248557
Mohammad A, Zuhaib M, Ashraf I, Alsultan M, Ahmad S, Sarwar A, Abdollahian M. Integration of Electric Vehicles and Energy Storage System in Home Energy Management System with Home to Grid Capability. Energies. 2021; 14(24):8557. https://doi.org/10.3390/en14248557
Chicago/Turabian StyleMohammad, Arshad, Mohd Zuhaib, Imtiaz Ashraf, Marwan Alsultan, Shafiq Ahmad, Adil Sarwar, and Mali Abdollahian. 2021. "Integration of Electric Vehicles and Energy Storage System in Home Energy Management System with Home to Grid Capability" Energies 14, no. 24: 8557. https://doi.org/10.3390/en14248557
APA StyleMohammad, A., Zuhaib, M., Ashraf, I., Alsultan, M., Ahmad, S., Sarwar, A., & Abdollahian, M. (2021). Integration of Electric Vehicles and Energy Storage System in Home Energy Management System with Home to Grid Capability. Energies, 14(24), 8557. https://doi.org/10.3390/en14248557








