ELM-QR-Based Nonparametric Probabilistic Prediction Method for Wind Power
Abstract
1. Introduction
2. Quantile Regression Algorithm Based on Extreme Learning Machine
2.1. Extreme Learning Machine
2.2. Quantile Regression Based on Extreme Learning Machine
3. Probabilistic Prediction Model of Wind Power
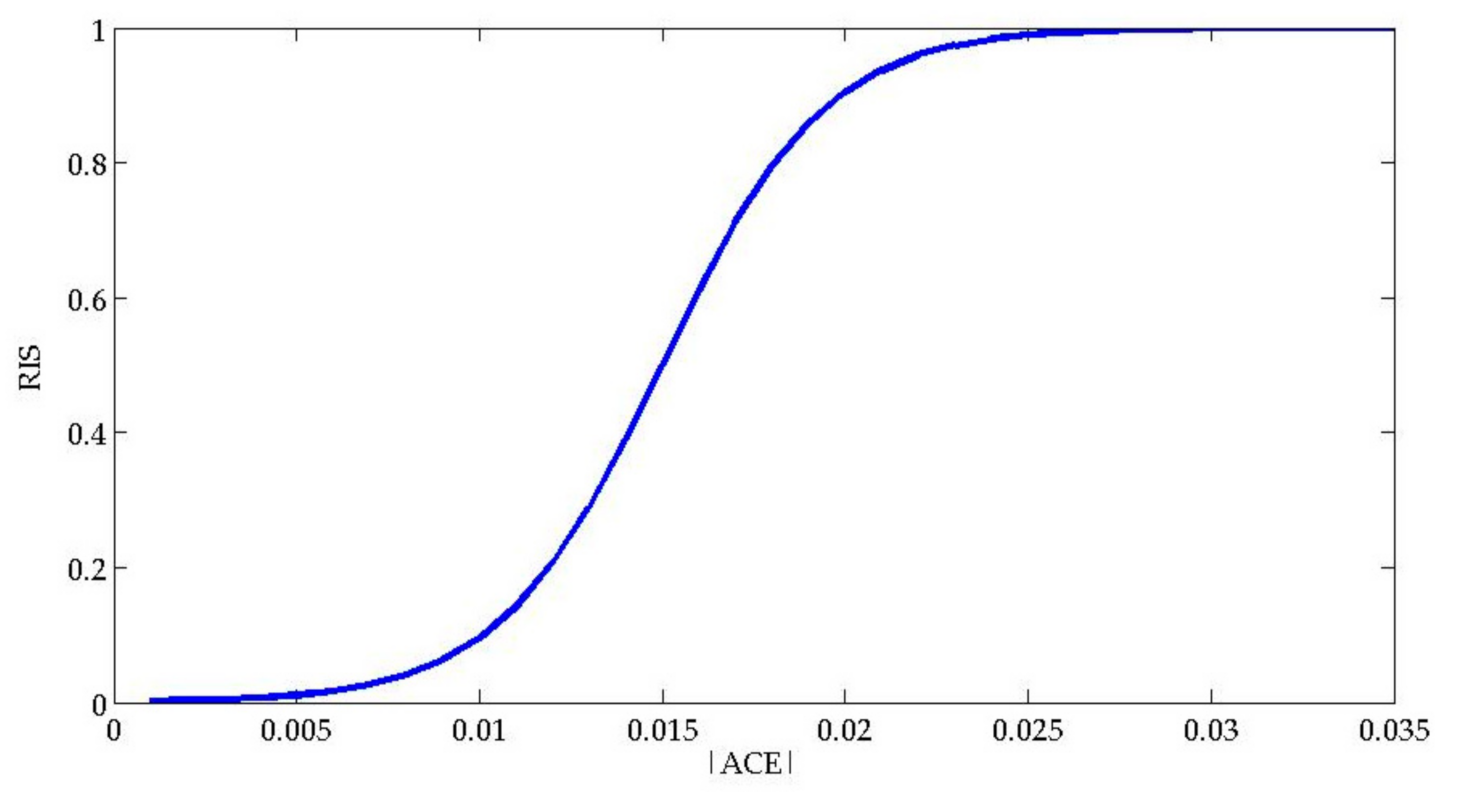
3.1. New Comprehensive Index
3.1.1. Reliability
3.1.2. Sharpness
3.1.3. New Comprehensive Index
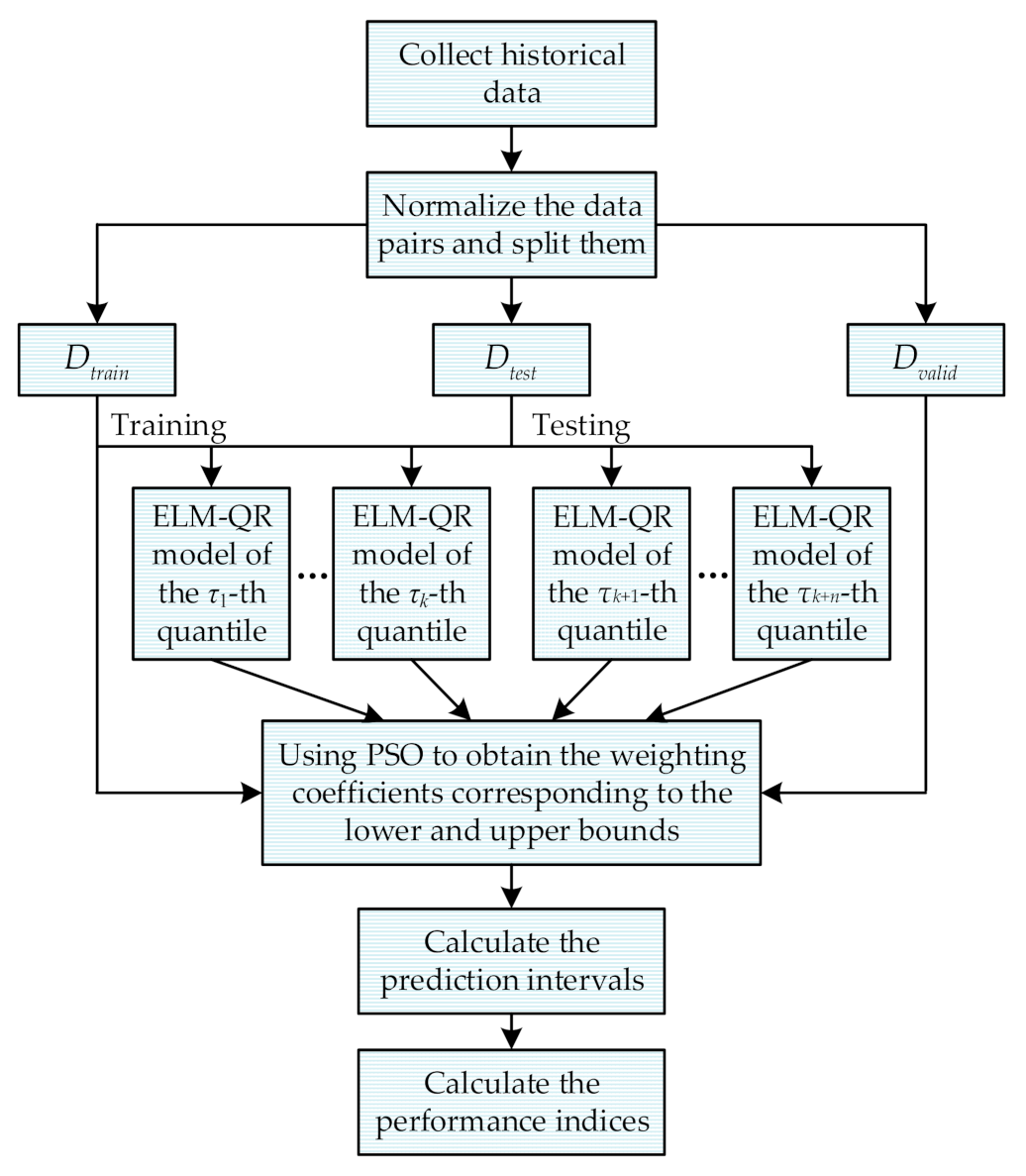
3.2. Probabilistic Prediction Model Based on ELM-QR
3.2.1. Structure of the Probabilistic Prediction Model
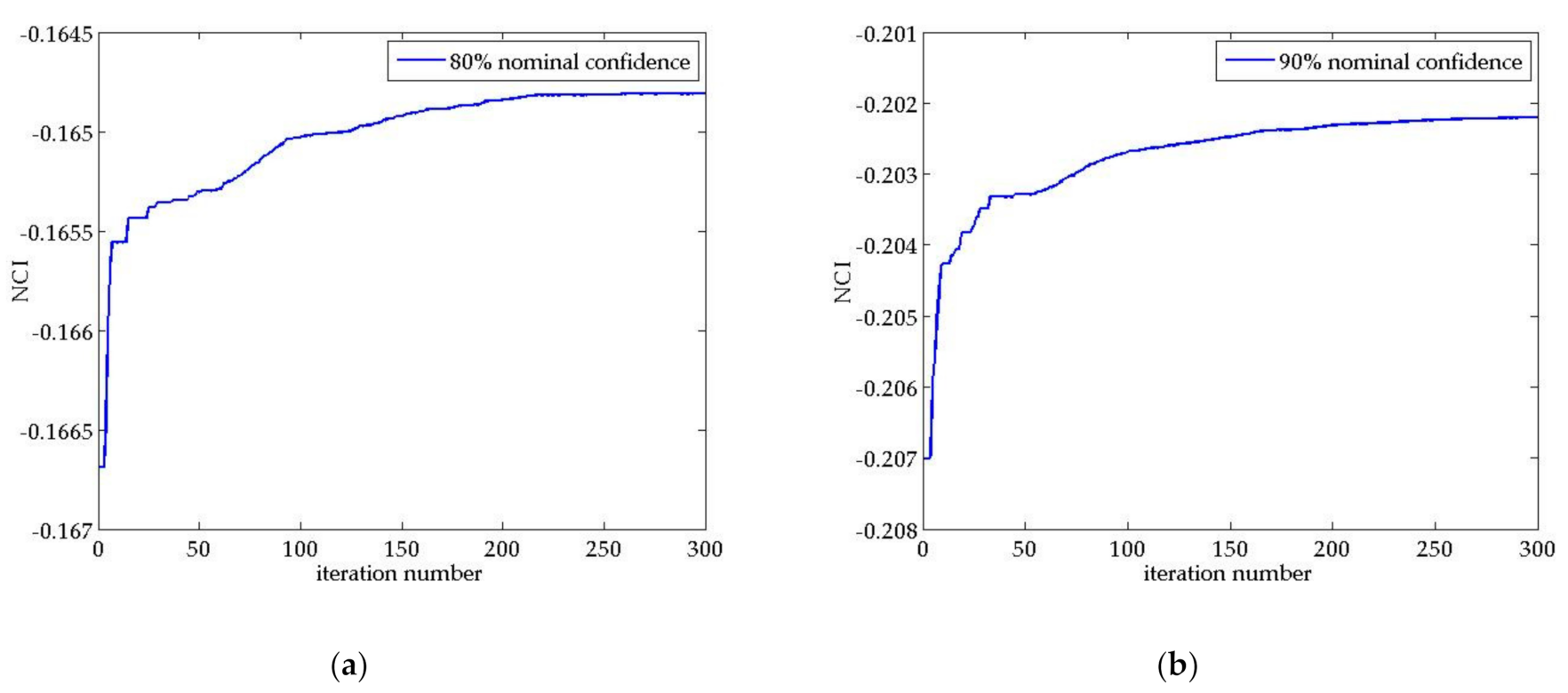
3.2.2. Solution of the Probabilistic Prediction Model
- (a)
- For each particle in the population, calculate the corresponding PI and NCI over Dtrain and Dvalid, NCI is used as the fitness.
- (b)
- Compare the fitness of particle’s current position with its historical best position (pbest), and update the historical best position with the current position if the fitness of current position is higher.
- (c)
- Compare the fitness of particle’s current position with the fitness of global best position (gbest). If the fitness of the current position is higher, the global best position is updated with the current position.
- (d)
- Update particle position and rate according to pbest and gbest.
- (e)
- Increment the iteration counter.
4. Case Study
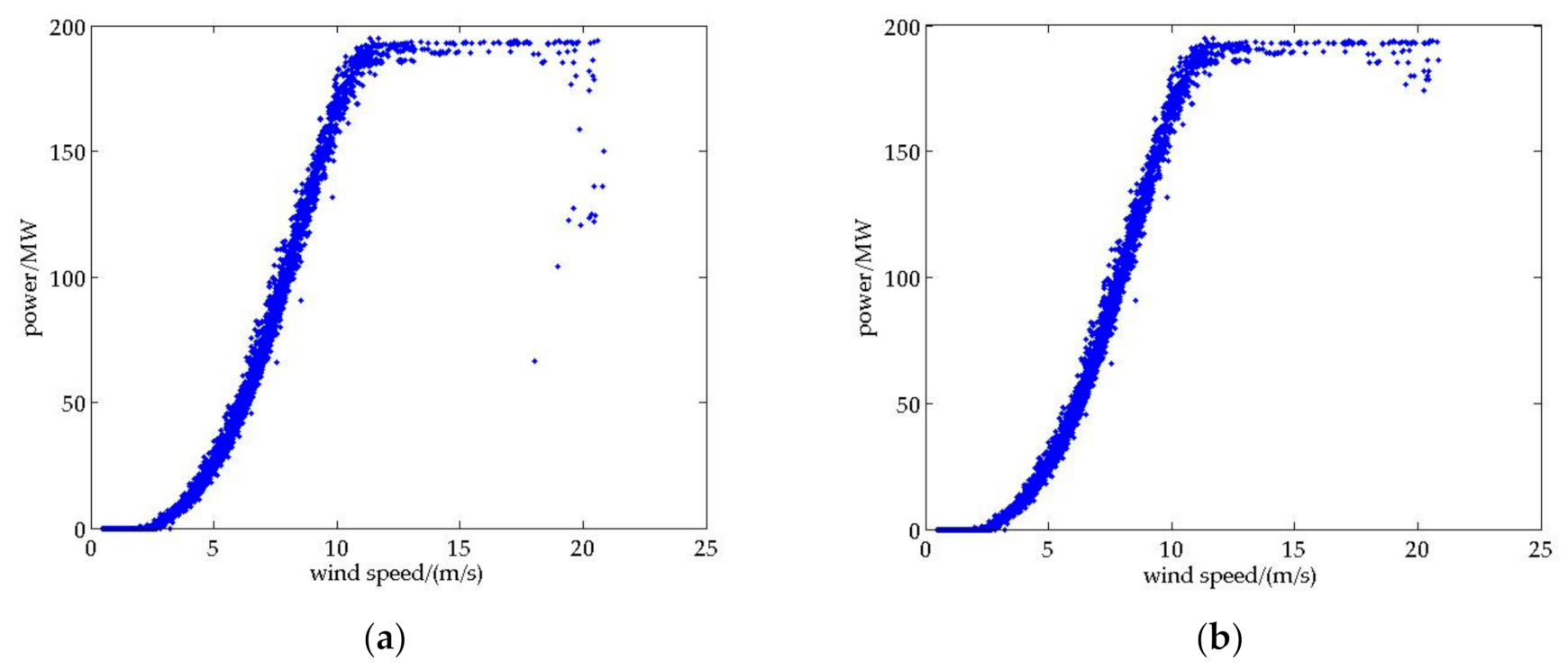
4.1. Simulation Data and Parameter Setting
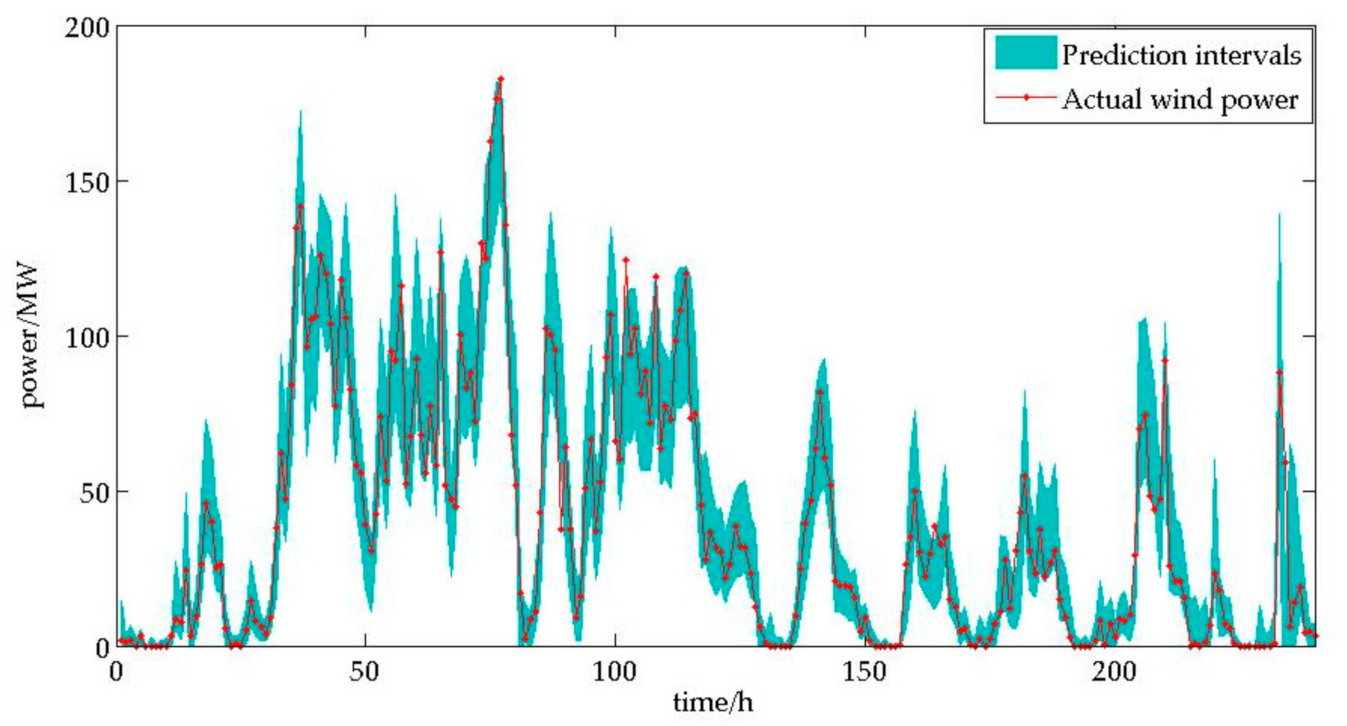
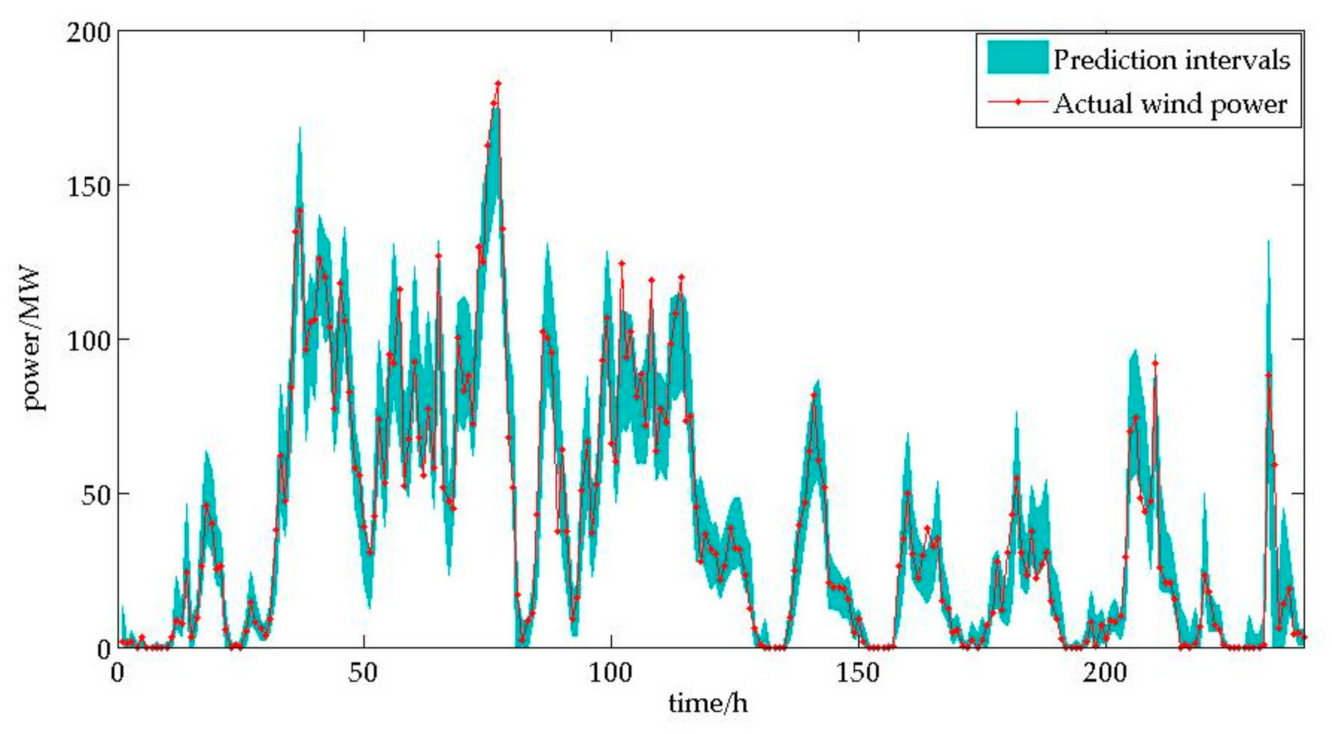
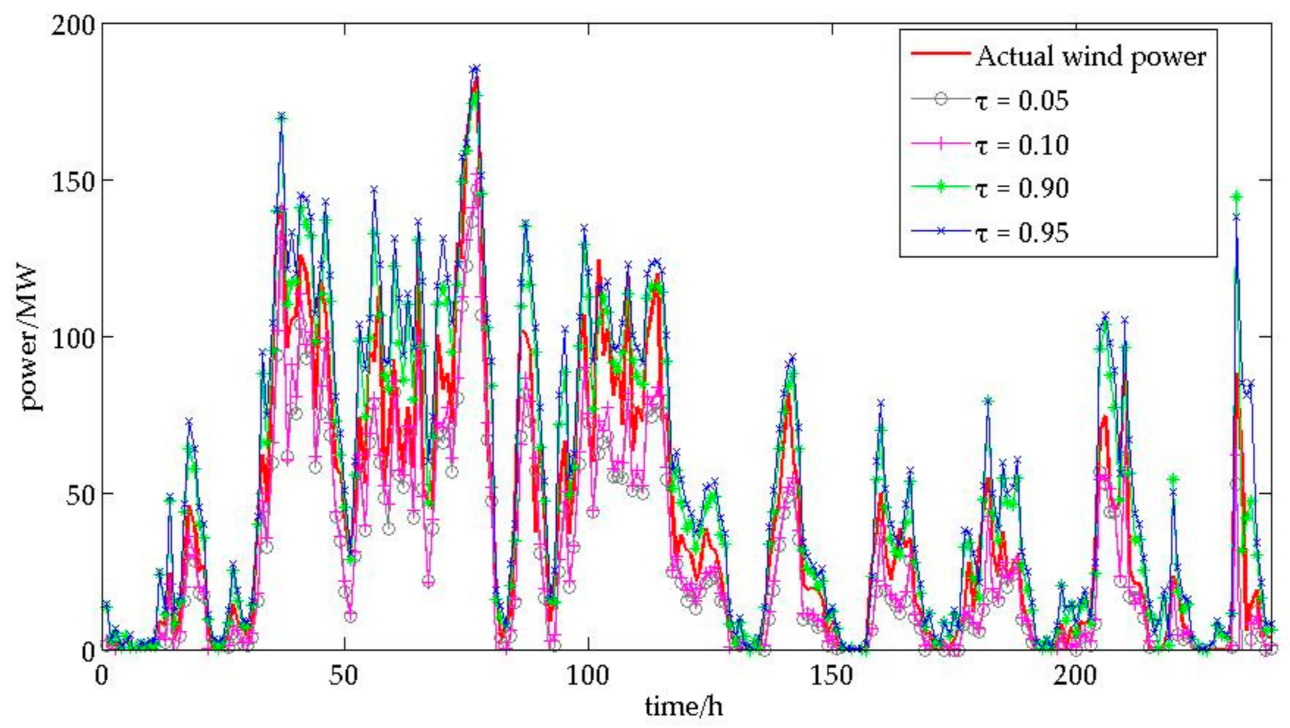
4.2. Prediction Results
4.3. Comparative Analysis
5. Conclusions
- (1)
- Make full use of the fast learning and strong generalization ability of ELM to obtain the quantile regression models effectively.
- (2)
- A novel comprehensive performance evaluation index is proposed, which can adjust the assessment keypoints adaptively according to different situations, so as to balance reliability and sharpness more reasonably.
- (3)
- A new model structure is proposed. Based on NCI, the weighting coefficients are obtained through PSO, which fully integrates the advantages of multiple algorithms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.Z.; Liu, H.; Xu, Y.H.; Jiang, W. A Hybrid Framework for Short Term Multi-Step Wind Speed Forecasting Based on Variational Model Decomposition and Convolutional Neural Network. Energies 2018, 11, 2292. [Google Scholar] [CrossRef]
- Bokde, N.; Feijoo, A.; Villanueva, D.; Kulat, K. A Novel and Alternative Approach for Direct and Indirect Wind-Power Prediction Methods. Energies 2018, 11, 2923. [Google Scholar] [CrossRef]
- Yildiz, C.; Acikgoz, H.; Korkmaz, D.; Budak, U. An improved residual-based convolutional neural network for very short-term wind power forecasting. Energy Convers. Manag. 2021, 228. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Tian, X.; Fang, S.; Cheng, Y.; Chang, Y.; Liu, H. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short-term memory neural network. Energy 2021, 214. [Google Scholar] [CrossRef]
- Kisvari, A.; Lin, Z.; Liu, X. Wind power forecasting—A data-driven method along with gated recurrent neural network. Renew. Energy 2021, 163, 1895–1909. [Google Scholar] [CrossRef]
- Lange, M. On the uncertainty of wind power predictions—Analysis of the forecast accuracy and statistical distribution of errors. J. Sol. Energy Eng. Trans. ASME 2005, 127, 177–184. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Dominguez-Navarro, J.A.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Bruninx, K.; Delarue, E. A Statistical Description of the Error on Wind Power Forecasts for Probabilistic Reserve Sizing. IEEE Trans. Sustain. Energy 2014, 5, 995–1002. [Google Scholar] [CrossRef]
- Liu, F.; Pan, Y.; Liu, H.; Ding, Q.; Li, Q.; Wang, Z. Piecewise Exponential Distribution Model of Wind Power Forecasting Error. Autom. Electr. Power Syst. 2013, 37, 14–19. [Google Scholar]
- Guan, J.; Lin, J.; Guan, J.; Mokaramian, E. A novel probabilistic short-term wind energy forecasting model based on an improved kernel density estimation. Int. J. Hydrog. Energy 2020, 45, 23791–23808. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic Forecasting of Wind Power Generation Using Extreme Learning Machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Sun, M.; Feng, C.; Zhang, J. Multi-distribution ensemble probabilistic wind power forecasting. Renew. Energy 2020, 148, 135–149. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Wang, J.H.; Song, Y.H.; Dong, Z.Y. Direct Quantile Regression for Nonparametric Probabilistic Forecasting of Wind Power Generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Hu, J.M.; Tang, J.W.; Lin, Y.Y. A novel wind power probabilistic forecasting approach based on joint quantile regression and multi-objective optimization. Renew. Energy 2020, 149, 141–164. [Google Scholar] [CrossRef]
- Cai, L.; Gu, J.; Ma, J.H.; Jin, Z.J. Probabilistic Wind Power Forecasting Approach via Instance-Based Transfer Learning Embedded Gradient Boosting Decision Trees. Energies 2019, 12, 159. [Google Scholar] [CrossRef]
- He, Y.; Li, H.; Wang, S.; Yao, X. Uncertainty analysis of wind power probability density forecasting based on cubic spline interpolation and support vector quantile regression. Neurocomputing 2020. [Google Scholar] [CrossRef]
- He, F.; Zhou, J.; Mo, L.; Feng, K.; Liu, G.; He, Z. Day-ahead short-term load probability density forecasting method with a decomposition-based quantile regression forest. Appl. Energy 2020, 262. [Google Scholar] [CrossRef]
- Yang, X.; Fu, G.; Zhang, Y.; Kang, N.; Gao, F. A Naive Bayesian Wind Power Interval Prediction Approach Based on Rough Set Attribute Reduction and Weight Optimization. Energies 2017, 10, 1903. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Optimal Prediction Intervals of Wind Power Generation. IEEE Trans. Power Syst. 2014, 29, 1166–1174. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Lohia, K.; Panigrahi, B.K. A multiobjective framework for wind speed prediction interval forecasts. Renew. Energy 2016, 87, 903–910. [Google Scholar] [CrossRef]
- Hu, M.Y.; Hu, Z.J.; Yue, J.P.; Zhang, M.L.; Hu, M.Y. A Novel Multi-Objective Optimal Approach for Wind Power Interval Prediction. Energies 2017, 10, 419. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Khosravi, A.; Panigrahi, B.K. Prediction Interval Estimation of Electricity Prices Using PSO-Tuned Support Vector Machines. IEEE Trans. Ind. Inform. 2015, 11, 322–331. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y. Electrical Energy Demand Forecasting Model Development and Evaluation with Maximum Overlap Discrete Wavelet Transform-Online Sequential Extreme Learning Machines Algorithms. Energies 2020, 13, 2307. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Alrbai, M.; Qawasmeh, B.R. Extreme Learning Machines for Solar Photovoltaic Power Predictions. Energies 2018, 11, 2725. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Bai, Y. Short-term wind speed prediction using an extreme learning machine model with error correction. Energy Convers. Manag. 2018, 162, 239–250. [Google Scholar] [CrossRef]
- Luo, J.; Wong, C.-M.; Vong, C.-M. Multinomial Bayesian extreme learning machine for sparse and accurate classification model. Neurocomputing 2021, 423, 24–33. [Google Scholar] [CrossRef]
- Peng, X.; Zheng, W.; Zhang, D.; Liu, Y.; Lu, D.; Lin, L. A novel probabilistic wind speed forecasting based on combination of the adaptive ensemble of on-line sequential ORELM (Outlier Robust Extreme Learning Machine) and TVMCF (time-varying mixture copula function). Energy Convers. Manag. 2017, 138, 587–602. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Jin, F.; Wu, Z. A self-adaptive kernel extreme learning machine for short-term wind speed forecasting. Appl. Soft Comput. 2021, 99. [Google Scholar] [CrossRef]
- Yang, H.-F.; Chen, Y.-P.P. Representation learning with extreme learning machines and empirical mode decomposition for wind speed forecasting methods. Artif. Intell. 2019, 277. [Google Scholar] [CrossRef]
- Zheng, W.; Peng, X.; Lu, D.; Zhang, D.; Liu, Y.; Lin, Z.; Lin, L. Composite quantile regression extreme learning machine with feature selection for short-term wind speed forecasting: A new approach. Energy Convers. Manag. 2017, 151, 737–752. [Google Scholar] [CrossRef]
- Ul Haque, A.; Nehrir, M.H.; Mandal, P. A Hybrid Intelligent Model for Deterministic and Quantile Regression Approach for Probabilistic Wind Power Forecasting. IEEE Trans. Power Syst. 2014, 29, 1663–1672. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.M.; Ding, X.J.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]

| PINC | PICP | ACE | Score | NCI |
|---|---|---|---|---|
| 90% | 89.17% | −0.83% | −3.73% | −0.234 |
| 80% | 79.69% | −0.31% | −5.96% | −0.154 |
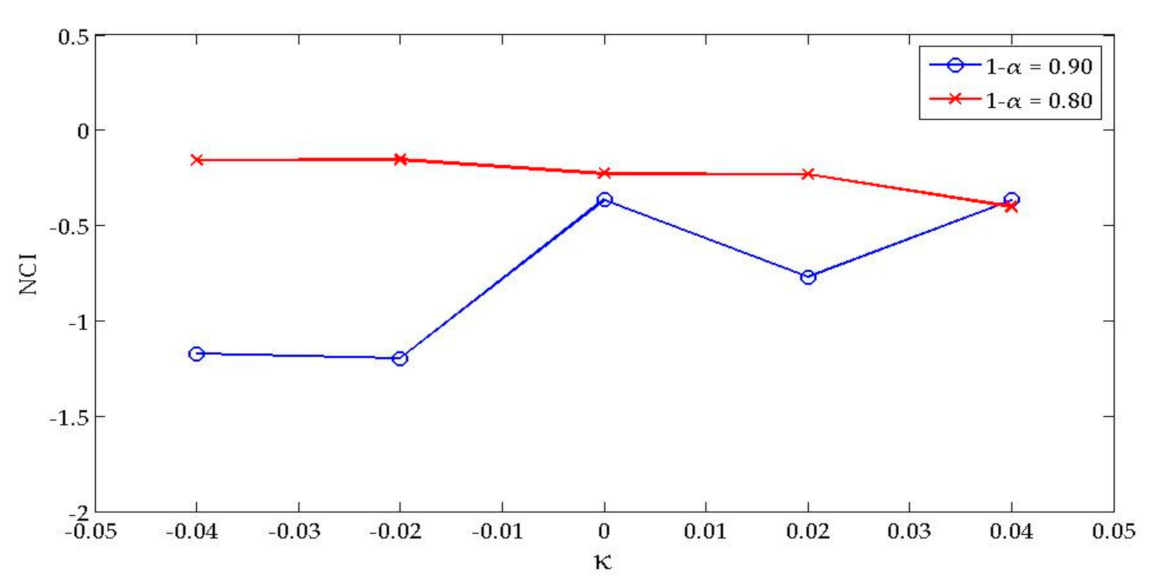
| PINC | κ | PICP | ACE | Score | NCI |
|---|---|---|---|---|---|
| 90% | −0.04 | 87.71% | −2.29% | −4.01% | −1.173 |
| −0.02 | 86.98% | −3.02% | −3.97% | −1.197 | |
| 0 | 88.85% | −1.15% | −3.92% | −0.365 | |
| 0.02 | 88.44% | −1.56% | −3.98% | −0.769 | |
| 0.04 | 88.85% | −1.15% | −3.92% | −0.365 | |
| 80% | −0.04 | 80.10% | 0.10% | −6.20% | −0.157 |
| −0.02 | 80.10% | 0.10% | −6.08% | −0.155 | |
| 0 | 79.06% | −0.94% | −6.14% | −0.227 | |
| 0.02 | 79.06% | −0.94% | −6.27% | −0.230 | |
| 0.04 | 78.75% | −1.25% | −6.25% | −0.401 |
| PINC | Methods | PICP | ACE | Score | NCI |
|---|---|---|---|---|---|
| 90% | BELM | 88.02% | −1.98% | −4.74% | −1.133 |
| KDE | 91.52% | 1.52% | −4.76% | −0.807 | |
| 80% | BELM | 79.79% | −0.21% | −7.33% | −0.186 |
| KDE | 78.96% | −1.04% | −7.28% | −0.295 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Yang, Y.; Zeng, L.; Li, Y. ELM-QR-Based Nonparametric Probabilistic Prediction Method for Wind Power. Energies 2021, 14, 701. https://doi.org/10.3390/en14030701
Niu H, Yang Y, Zeng L, Li Y. ELM-QR-Based Nonparametric Probabilistic Prediction Method for Wind Power. Energies. 2021; 14(3):701. https://doi.org/10.3390/en14030701
Chicago/Turabian StyleNiu, Honghai, Yu Yang, Lingchao Zeng, and Yiguo Li. 2021. "ELM-QR-Based Nonparametric Probabilistic Prediction Method for Wind Power" Energies 14, no. 3: 701. https://doi.org/10.3390/en14030701
APA StyleNiu, H., Yang, Y., Zeng, L., & Li, Y. (2021). ELM-QR-Based Nonparametric Probabilistic Prediction Method for Wind Power. Energies, 14(3), 701. https://doi.org/10.3390/en14030701







