Application of Decision Trees for Optimal Allocation of Harmonic Filters in Medium-Voltage Networks
Abstract
:1. Introduction
- optimal phasor measurement unit (PMU) placement for voltage security assessment [18,19], including power system islanding identification [20] and line outage detection [21,22,23]—fast and direct measurement results by PMUs combined with decision trees gives more time for corrective or preventive actions;
- optimal planning of storage in power systems integrated with wind power generation [35];
2. Optimization Problem Definitions and Solution Algorithms
2.1. Goal Functions
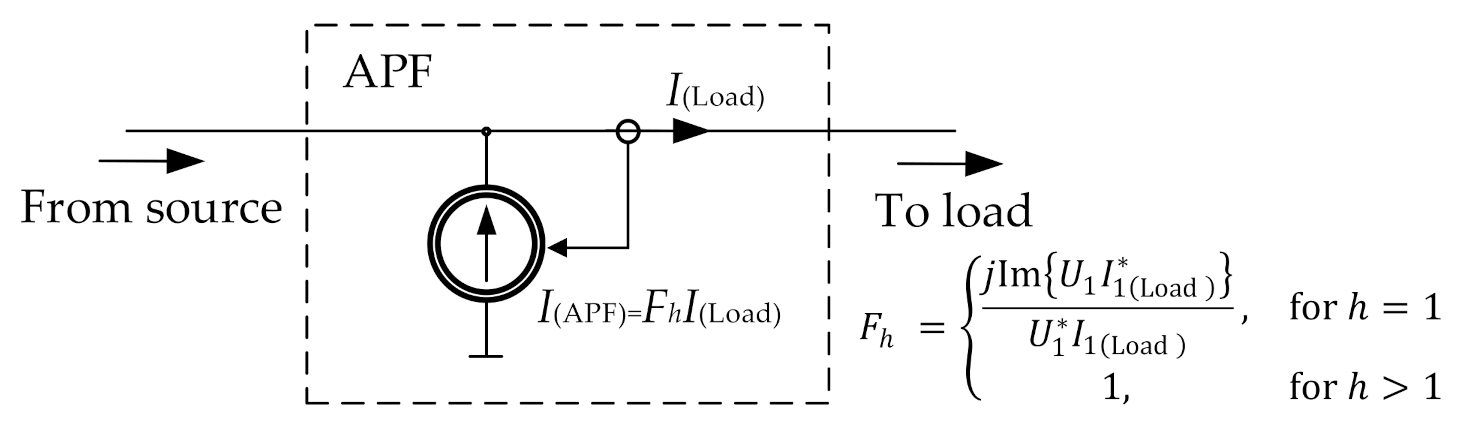
- —state of the APF in i-th node (1—APF placed, 0—no APF),
- for all APF list , where —denotation of i-th APF.
2.1.1. Power Losses Criterion
- —number of power system elements in which power losses occur (transformers, lines, coils, etc.), .
- —power losses of m-th element.
- —independent variable of the goal function that is subjected to minimization.
2.1.2. Cost Criterion
- —function assigning the cost to i-th APF depending on its RMS current value,
- —APF number, ,
- —RMS current of i-th APF, calculated as:
- —RMS current of h-th harmonic of i-th APF,
- —harmonic number, .
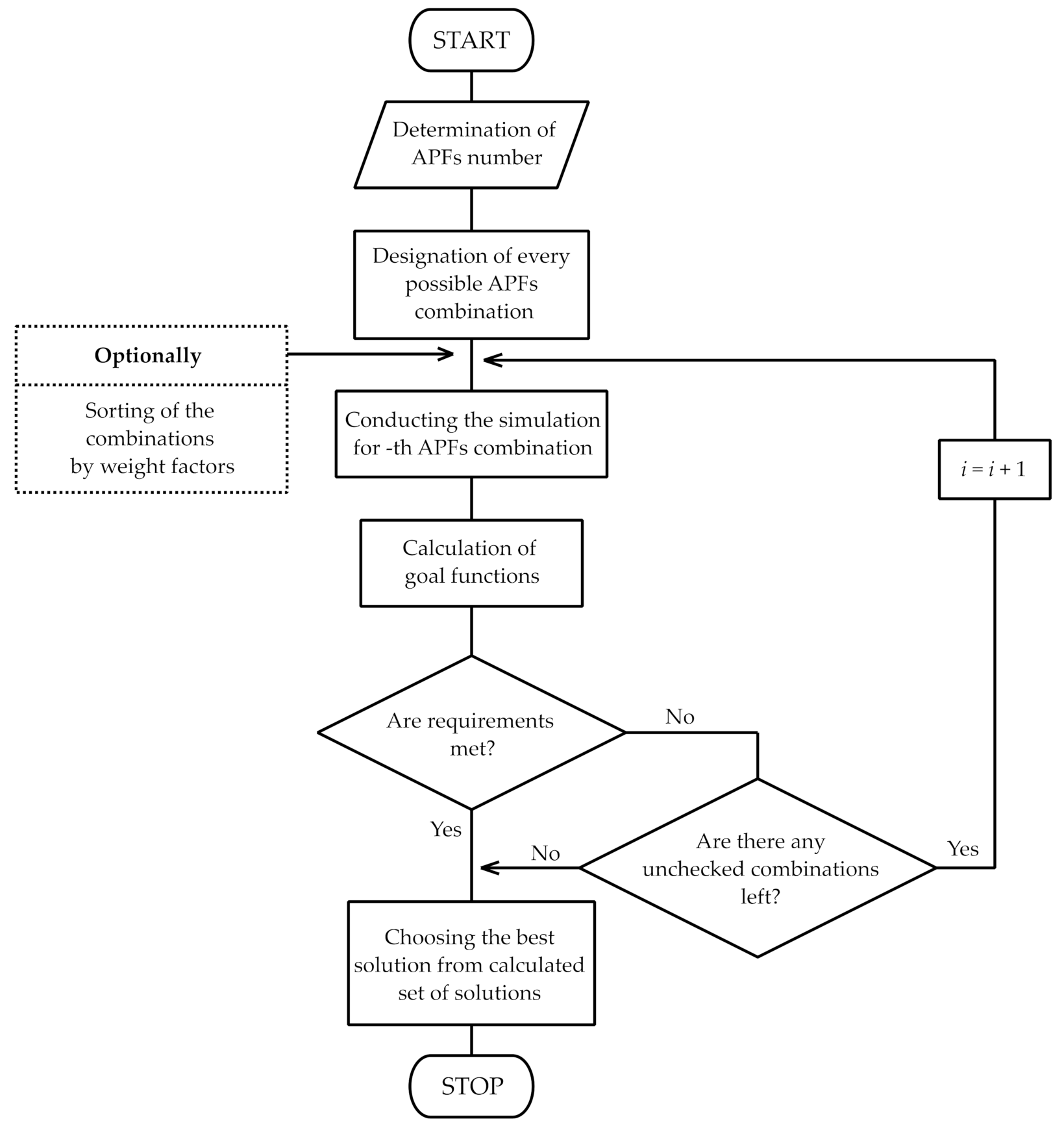
2.2. Brute Force Algorithm
2.3. Optimization with Decision Trees
- —difference between goal function values for the current state and a state after moving the APF to the next node,
- —difference between goal function values for the current state and a state after moving the APF to the previous node,
- —difference between goal function values for the current state and a state after adding a new APF, modified by the correctional coefficient, Wcorr,
- —zero value connected with staying in the current state.
3. Optimization Results
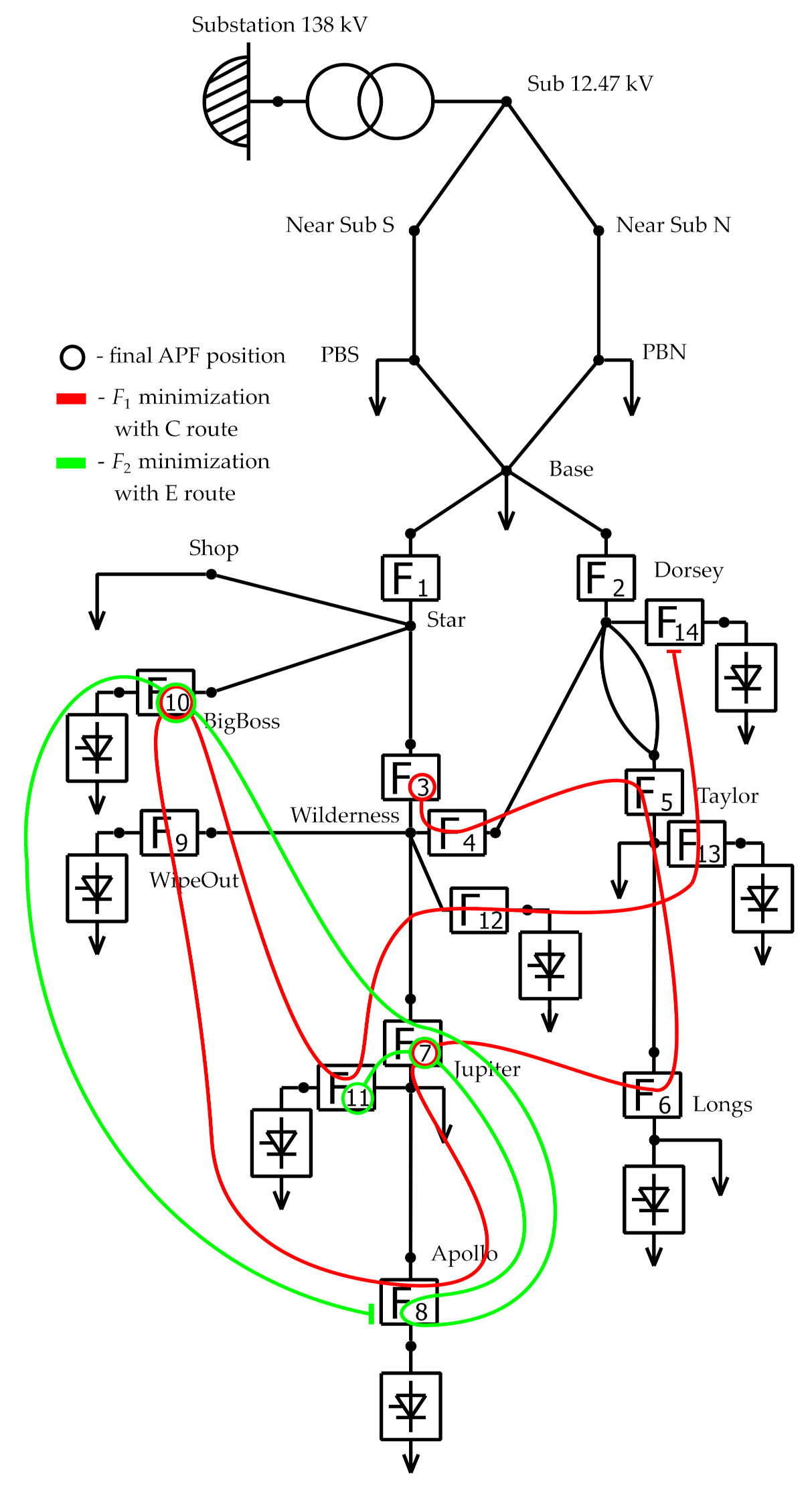
3.1. Test System
3.2. Brute Force Results
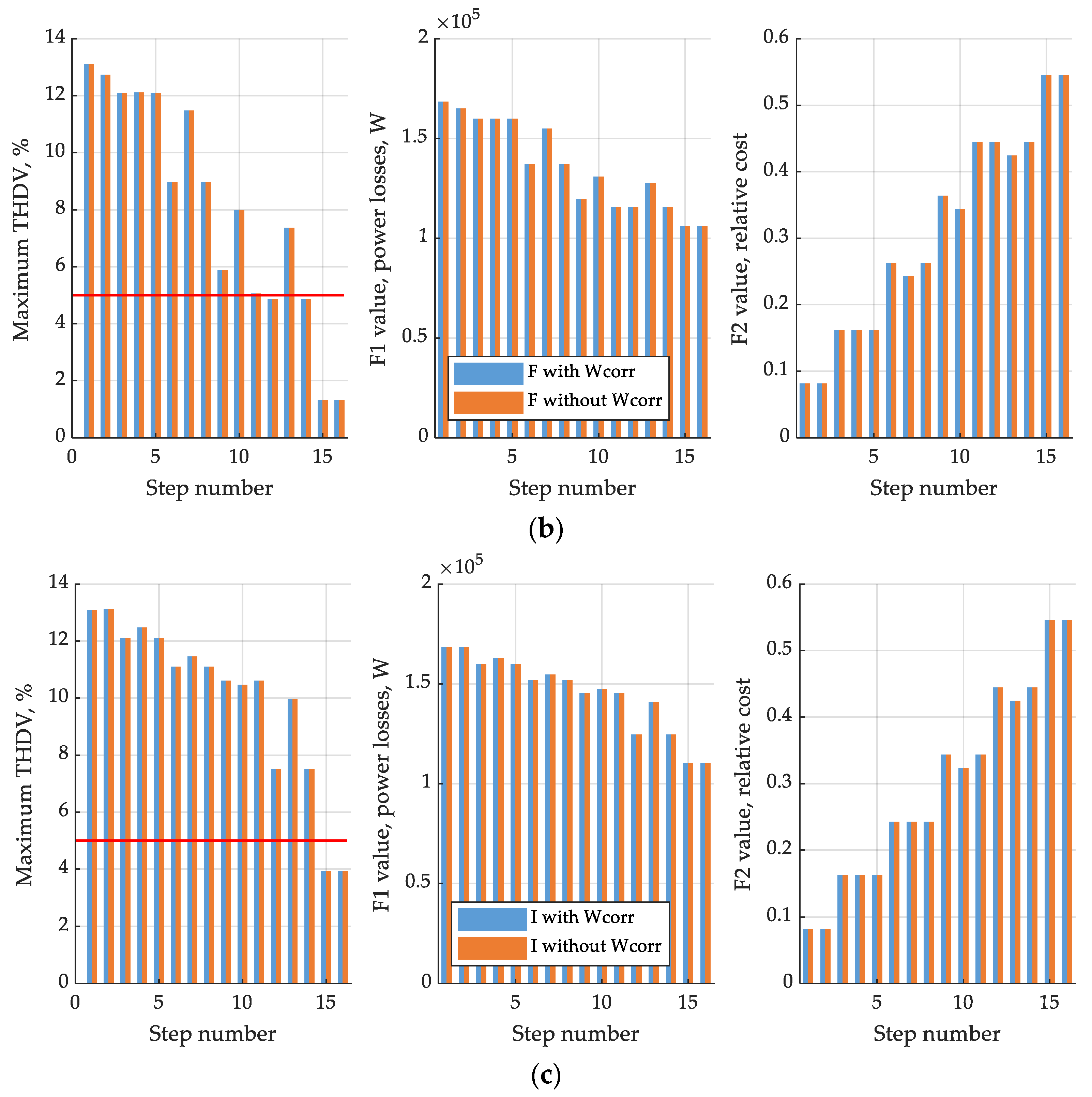
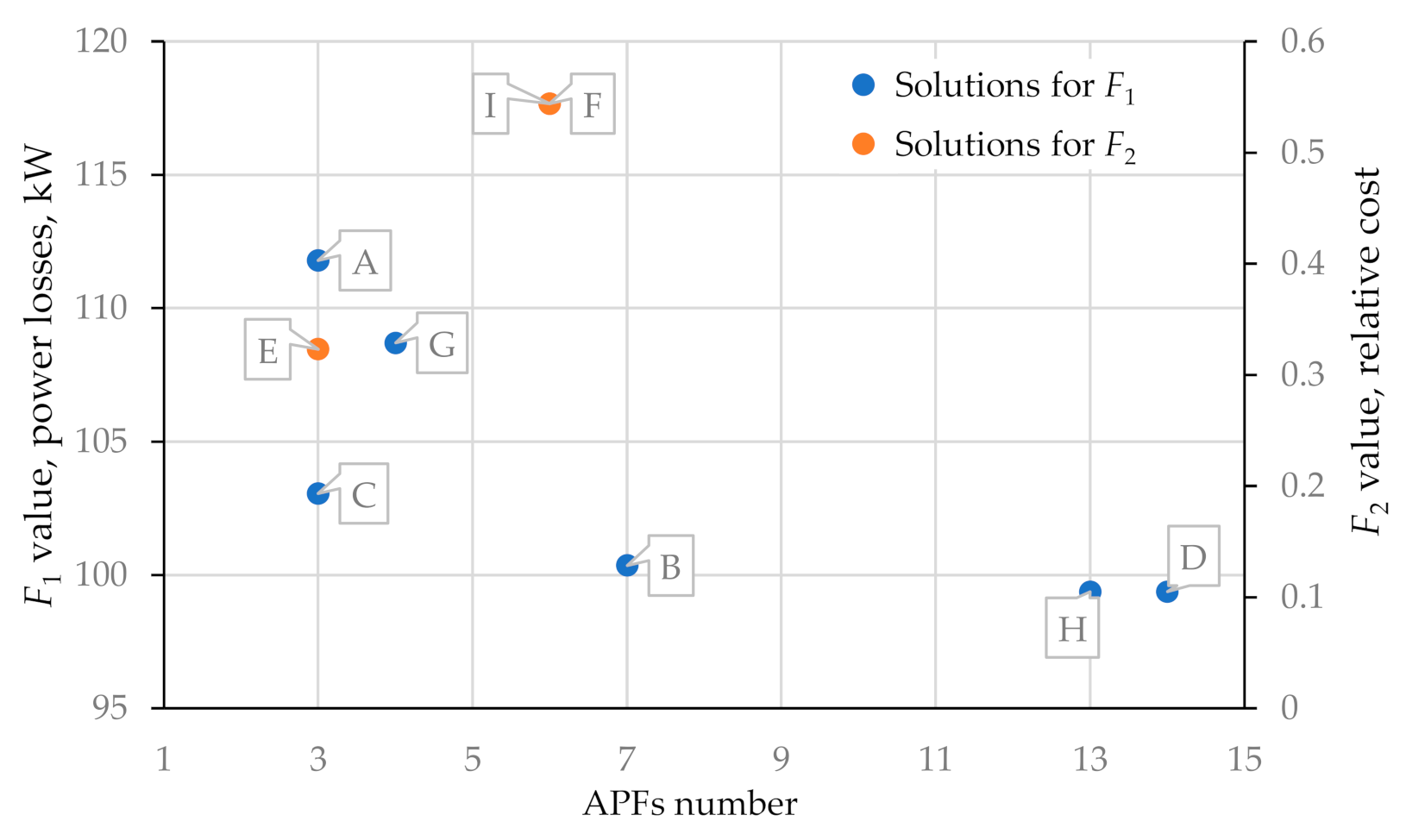
3.3. Decision Tree Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ziari, I.; Jalilian, A. Optimal placement of an active filter in a power system. In Proceedings of the 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 1150–1154. [Google Scholar]
- Guo, M.; Jin, Q.; Yao, Z. Implementation of Adaptive Step-Size Algorithm in Distribution Network for Optimal Location and Sizing of SAPFs. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–16 July 2020; pp. 1562–1566. [Google Scholar]
- Alhaddad, F.M.; El-Hawary, M. Optimal Filter Placement and Sizing Using Ant Colony Optimization in Electrical Distribution System. In Proceedings of the 2014 IEEE Electrical Power and Energy Conference, Calgary, AB, Canada, 12–14 November 2014; pp. 128–133. [Google Scholar]
- Shivaie, M.; Salemnia, A.; Ameli, M.T. A multi-objective approach to optimal placement and sizing of multiple active power filters using a music-inspired algorithm. Appl. Soft Comput. 2014, 22, 189–204. [Google Scholar] [CrossRef]
- Rosyadi, A.; Penangsang, O.; Soeprijanto, A. Optimal filter placement and sizing in radial distribution system using whale optimization algorithm. In Proceedings of the 2017 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 28–29 August 2017; pp. 87–92. [Google Scholar] [CrossRef]
- Lakum, A.; Mahajan, V. Optimal placement and sizing of multiple active power filters for radial distribution system using grey wolf optimizer. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 562–567. [Google Scholar]
- Sindhu, M.R.; Jisma, M.; Maya, P.; Krishnapriya, P.; Vivek, M.M. Optimal Placement and Sizing of Harmonic and Reactive Compensators in Interconnected Systems. In Proceedings of the 15th IEEE India Council International Conference, Coimbatore, India, 16–18 December 2018; pp. 1–6. [Google Scholar]
- Belchior, F.N.; De Lima, L.R.; Ribeiro, P.F.; Castro, J.F.C. A novel approach towards passive filter placement. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Maciążek, M.; Grabowski, D.; Pasko, M. Genetic and combinatorial algorithms for optimal sizing and placement of active power filters. Int. J. Appl. Math. Comput. Sci. 2015, 25, 269–279. [Google Scholar] [CrossRef] [Green Version]
- El-Arwash, H.M.; Azmy, A.M.; Rashad, E.M. A GA-based initialization of PSO for optimal APFS allocation in water desali-nation plant. In Proceedings of the Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19 December 2017; pp. 1378–1384. [Google Scholar]
- Milovanović, M.; Radosavljević, J.; Klimenta, D.; Perović, B. GA-based approach for optimal placement and sizing of passive power filters to reduce harmonics in distorted radial distribution systems. Electr. Eng. 2019, 101, 787–803. [Google Scholar] [CrossRef]
- Moghbel, M.; Masoum, M.A.S.; Fereidouni, A.; Deilami, S. Optimal Sizing, Siting and Operation of Custom Power Devices with STATCOM and APLC Functions for Real-Time Reactive Power and Network Voltage Quality Control of Smart Grid. IEEE Trans. Smart Grid 2018, 9, 5564–5575. [Google Scholar] [CrossRef]
- Moghbel, M.; Deilami, S.; Masoum, M.A. Optimal Siting and Sizing of Multiple Active Power Line Conditioners to Minimize Network THD Considering Harmonic Couplings. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, Australia, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Tian, S.; Jia, Q.; Xue, S.; Yu, H.; Qu, Z.; Gu, T. Collaborative optimization allocation of VDAPFs and SVGs for simultaneous mitigation of voltage harmonic and deviation in distribution networks. Int. J. Electr. Power Energy Syst. 2020, 120, 106034. [Google Scholar] [CrossRef]
- Subramani, C.; Jimoh, A.-G.A.; Dash, S.S.; Harishkiran, S. PSO Application to Optimal Placement of UPFC for Loss Minimization in Power System. In Advances in Intelligent Systems and Computing, Proceedings of the Sproceedings of the 2nd International Conference on IntelPubligent Computshing and Applications, Amsterdam, The Netherlands, 22 February 2017; Springer: Singapore, Singapore, 2017; pp. 223–230. [Google Scholar]
- Chakeri, V.; Hagh, M.T. Optimal allocation of the distributed active filters based on total loss reduction. Int. J. Smart Electr. Eng. 2017, 6, 171–175. [Google Scholar]
- Li, D.; Wu, Z.; Zhao, B.; Zhang, X.; Zhang, L. An Adaptive Active Power Optimal Allocation Strategy for Power Loss Minimization in Islanded Microgrids. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 292–297. [Google Scholar]
- Lopez, J.A.; Lu, C.-N. A comparison of placement methods for collecting PMU data used in angular stability detection. In Proceedings of the 2017 19th International Conference on Intelligent System Application to Power Systems (ISAP), San Antonio, TX, USA, 17–20 September 2017; pp. 1–6. [Google Scholar]
- Alhalaseh, R.; Tokel, H.A.; Chakraborty, S.; Alirezaei, G.; Mathar, R. Feature-Selection based PMU Placement for Detection of Faults in Power Grids. In Proceedings of the 2018 28th International Telecommunication Networks and Applications Conference (ITNAC), Sydney, NSW, Australia, 21–23 November 2018; pp. 1–6. [Google Scholar]
- Samudrala, A.N.; Amini, M.H.; Kar, S.; Blum, R.S. Optimal Sensor Placement for Topology Identification in Smart Power Grids. In Proceedings of the 2019 53rd Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 20–22 March 2019; pp. 1–6. [Google Scholar]
- Sevlian, R.A.; Zhao, Y.; Rajagopal, R.; Goldsmith, A.; Poor, H.V. Outage Detection Using Load and Line Flow Measurements in Power Distribution Systems. IEEE Trans. Power Syst. 2018, 33, 2053–2069. [Google Scholar] [CrossRef]
- Alhalaseh, R.; Tokel, H.A.; Chakraborty, S.; Alirezaei, G.; Mathar, R. PMU Placement with Power Grid Partitioning for Line Outage Detection. In Proceedings of the 2019 4th International Conference on Smart and Sustainable Technologies (SpliTech), Split, Croatia, 18–21 June 2019; pp. 1–6. [Google Scholar]
- Samudrala, A.N.; Amini, M.H.; Kar, S.; Blum, R.S. Sensor Placement for Outage Identifiability in Power Distribution Net-works. IEEE Trans. Smart Grid 2020, 11, 1996–2013. [Google Scholar] [CrossRef] [Green Version]
- Sharma, G.; Mahela, O.P.; Kumar, M.; Kumar, N. Detection and Classification of Transmission Line Faults Using Stockwell Transform and Rule Based Decision Tree. In Proceedings of the 2018 International Conference on Smart Electric Drives and Power System (ICSEDPS), Nagpur, India, 12–13 June 2018; pp. 1–5. [Google Scholar]
- Godse, R.; Bhat, S. Mathematical Morphology-Based Feature-Extraction Technique for Detection and Classification of Faults on Power Transmission Line. IEEE Access 2020, 8, 38459–38471. [Google Scholar] [CrossRef]
- Gong, C.-S.A.; Su, C.-H.S.; Tseng, K.-H. Implementation of Machine Learning for Fault Classification on Vehicle Power Transmission System. IEEE Sens. J. 2020, 20, 15163–15176. [Google Scholar] [CrossRef]
- Ribeiro, E.G.; Dias, G.L.; Barbosa, B.H.G.; Ferreira, D.D. Real-time system for automatic classification of power quality dis-turbances. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 908–913. [Google Scholar]
- Shams, N.; Wall, P.; Terzija, V. Active Power Imbalance Detection, Size and Location Estimation Using Limited PMU Meas-urements. IEEE Trans. Power Syst. 2019, 34, 1362–1372. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, P.; Zhang, D. Decision Tree for Online Voltage Stability Margin Assessment Using C4.5 and Relief-F Algorithms. Energies 2020, 13, 3824. [Google Scholar] [CrossRef]
- Jindal, A.; Dua, A.; Kaur, K.; Singh, M.; Kumar, N.; Mishra, S. Decision Tree and SVM-Based Data Analytics for Theft Detection in Smart Grid. IEEE Trans. Ind. Inform. 2016, 12, 1005–1016. [Google Scholar] [CrossRef]
- Guerrero, J.I.; Monedero, I.; Biscarri, F.; Biscarri, J.; Millan, R.; Leon, C. Non-Technical Losses Reduction by Improving the Inspections Accuracy in a Power Utility. IEEE Trans. Power Syst. 2017, 33, 1209–1218. [Google Scholar] [CrossRef]
- Swetapadma, A.; Yadav, A. A Novel Decision Tree Regression-Based Fault Distance Estimation Scheme for Transmission Lines. IEEE Trans. Power Deliv. 2017, 32, 234–245. [Google Scholar] [CrossRef]
- Pessoa, A.L.D.S.; Oleskovicz, M.; Martins, P.E.T. A multi-stage methodology for fault location in radial distribution systems. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- Araújo, M.A.; Flauzino, R.A.; Moraes, L.A.; Borges, F.A.S.; Spatti, D.H. Decision Trees Applied to Fault Locations in Distri-bution Systems with Smart Meters. In Proceedings of the IEEE International Conference on Environment and Electrical Engi-neering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Xiong, P.; Singh, C. Optimal Planning of Storage in Power Systems Integrated with Wind Power Generation. IEEE Trans. Sustain. Energy 2016, 7, 232–240. [Google Scholar] [CrossRef]
- Lee, C.-T.; Horng, S.-C. Abnormality Detection of Cast-Resin Transformers Using the Fuzzy Logic Clustering Decision Tree. Energies 2020, 13, 2546. [Google Scholar] [CrossRef]
- Sai, T.; Kumar, P.S.; Reddy, K. Towards intelligent decision making in power plant operation. In Proceedings of the 2014 Annual IEEE India Conference (INDICON), Puni, India, 11–13 December 2014; pp. 1–6. [Google Scholar]
- Mosavi, A.; Salimi, M.; Ardabili, S.F.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the Art of Machine Learning Models in Energy Systems, a Systematic Review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef] [Green Version]
- Leonidaki, E.; Georgiadis, D.; Hatziargyriou, N. Decision Trees for Determination of Optimal Location and Rate of Series Compensation to Increase Power System Loading Margin. IEEE Trans. Power Syst. 2006, 21, 1303–1310. [Google Scholar] [CrossRef]
- Couronné, R.; Probst, P.; Boulesteix, A.-L. Random forest versus logistic regression: A large-scale benchmark experiment. BMC Bioinform. 2018, 19, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Tian, W.; Lei, C.; Tian, M. Dynamic Prediction of Building HVAC Energy Consumption by Ensemble Learning Approach. In Proceedings of the 2018 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, Nevada, USA, 13–15 December 2018; pp. 254–257. [Google Scholar]
- Grady, W.M. Understanding Power System Harmonics. Available online: http://web.ecs.baylor.edu/faculty/grady/ (accessed on 18 January 2021).
- Buła, D.; Lewandowski, M. Steady state simulation of a distributed power supplying system using a simple hybrid time-frequency model. Appl. Math. Comput. 2018, 319, 195–202. [Google Scholar] [CrossRef]
- Buła, D.; Grabowski, D.; Lewandowski, M.; Maciążek, M.; Piwowar, A. Software Solution for Modeling, Sizing, and Allocation of Active Power Filters in Distribution Networks. Energies 2020, 14, 133. [Google Scholar] [CrossRef]
- Buła, D.; Lewandowski, M. Comparison of frequency domain and time domain model of a distributed power supplying system with active power filters (APFs). Appl. Math. Comput. 2015, 267, 771–779. [Google Scholar] [CrossRef]


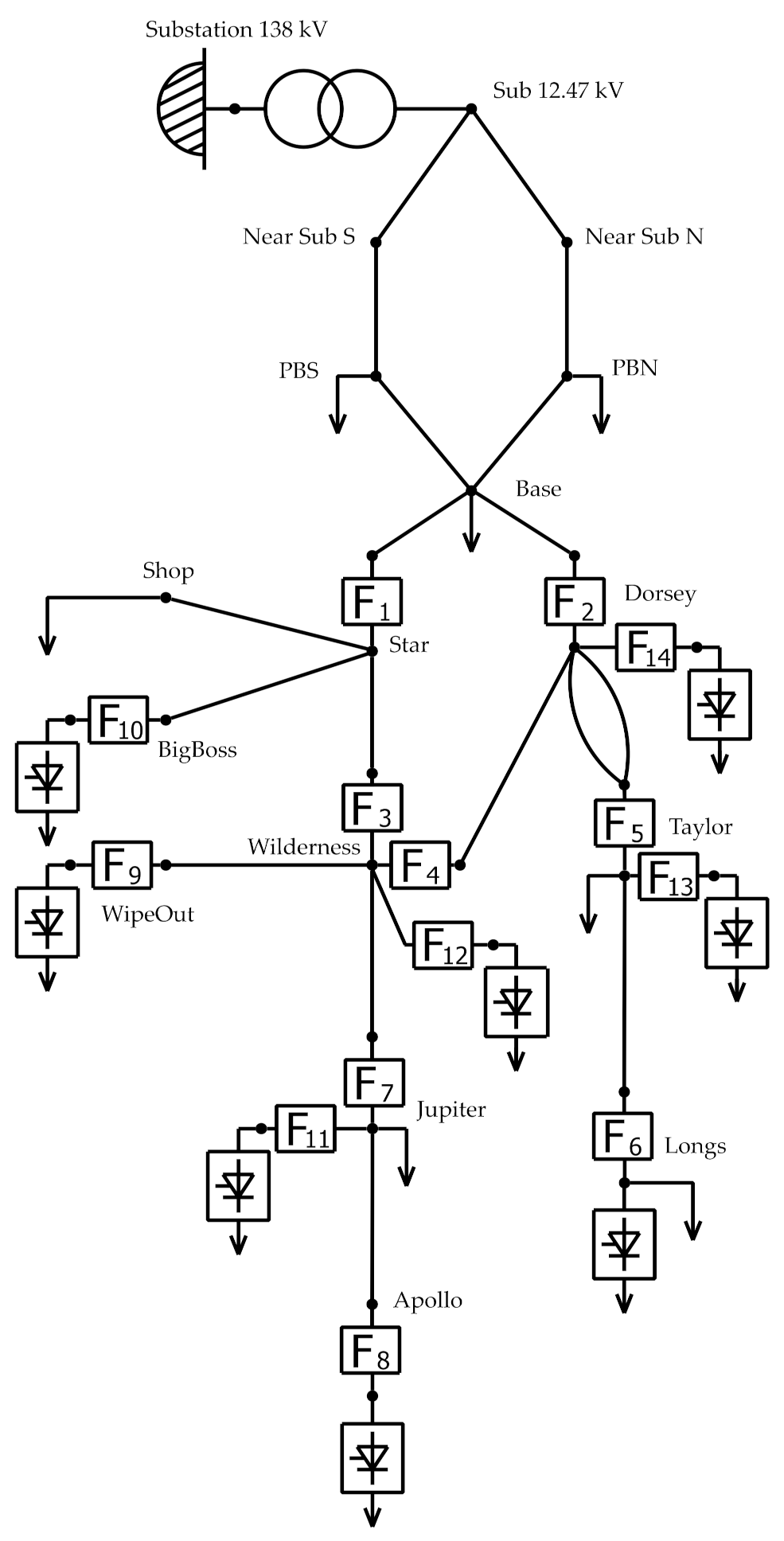
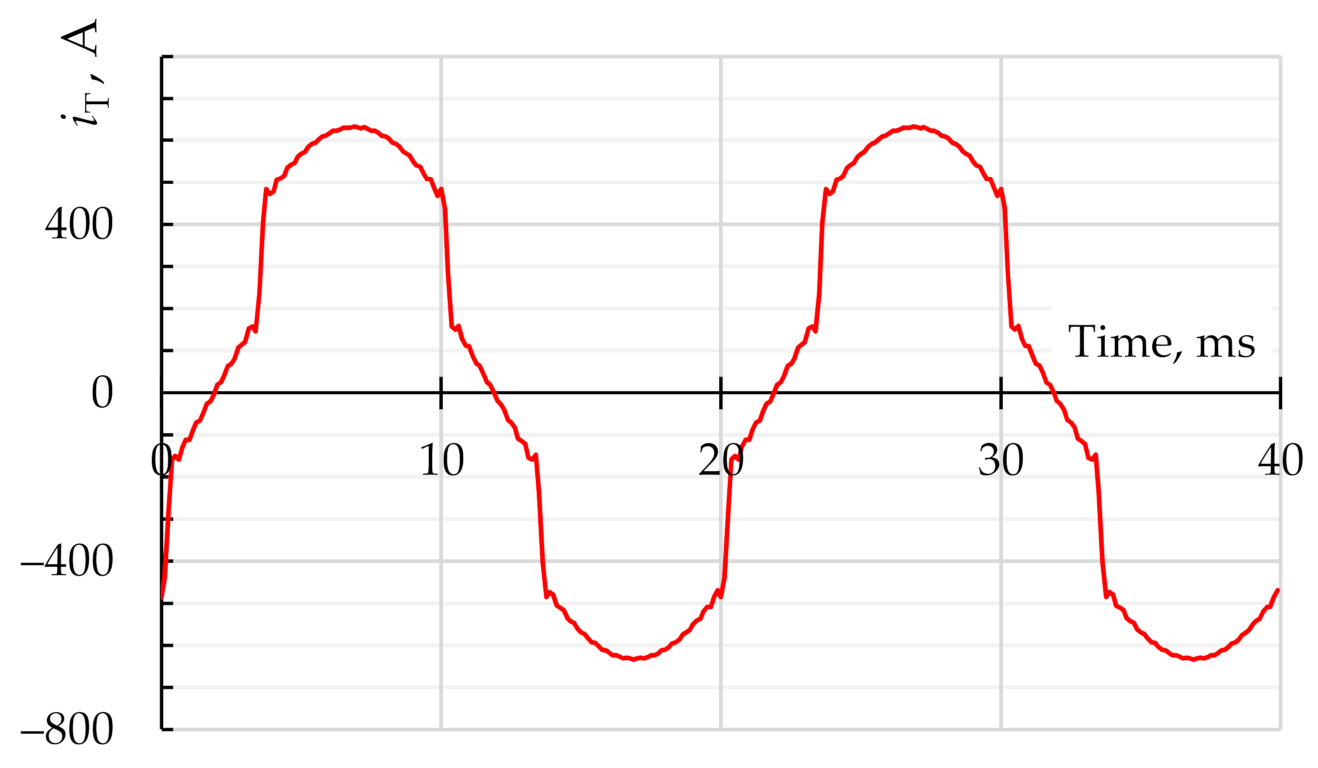
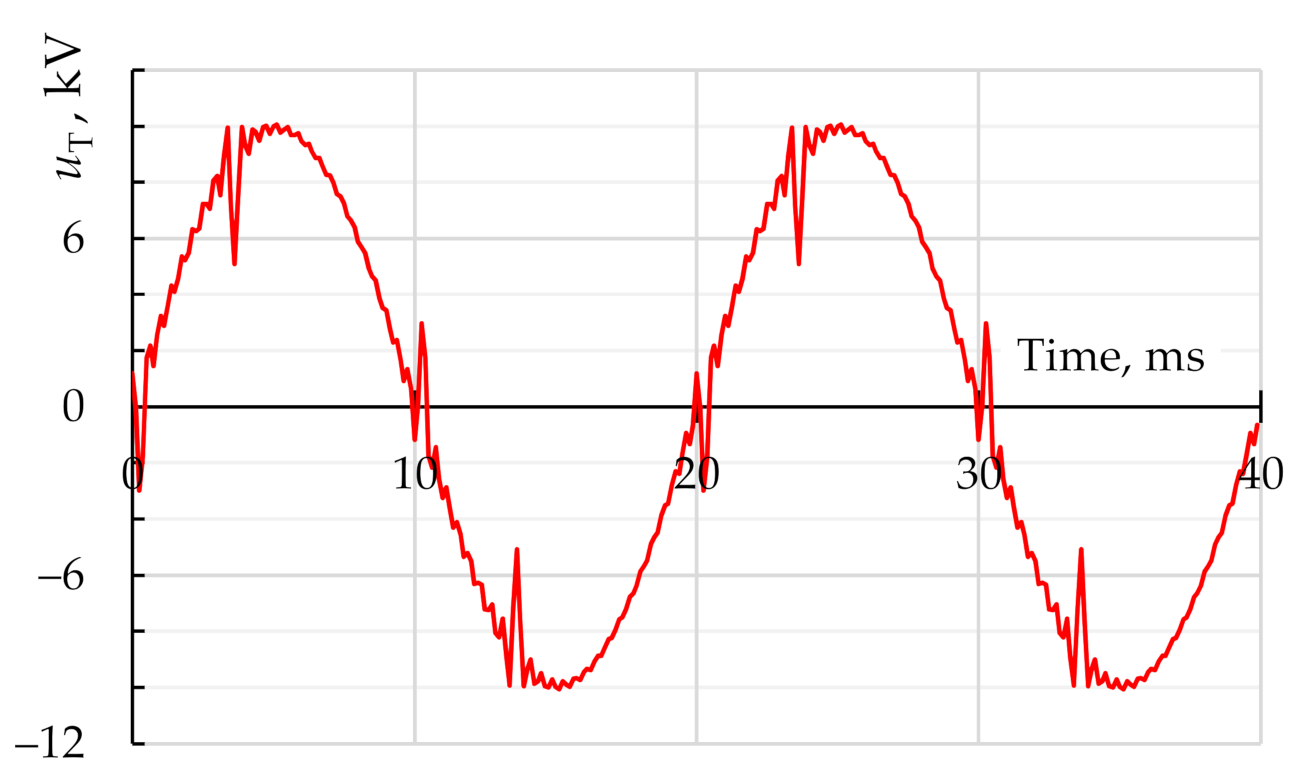

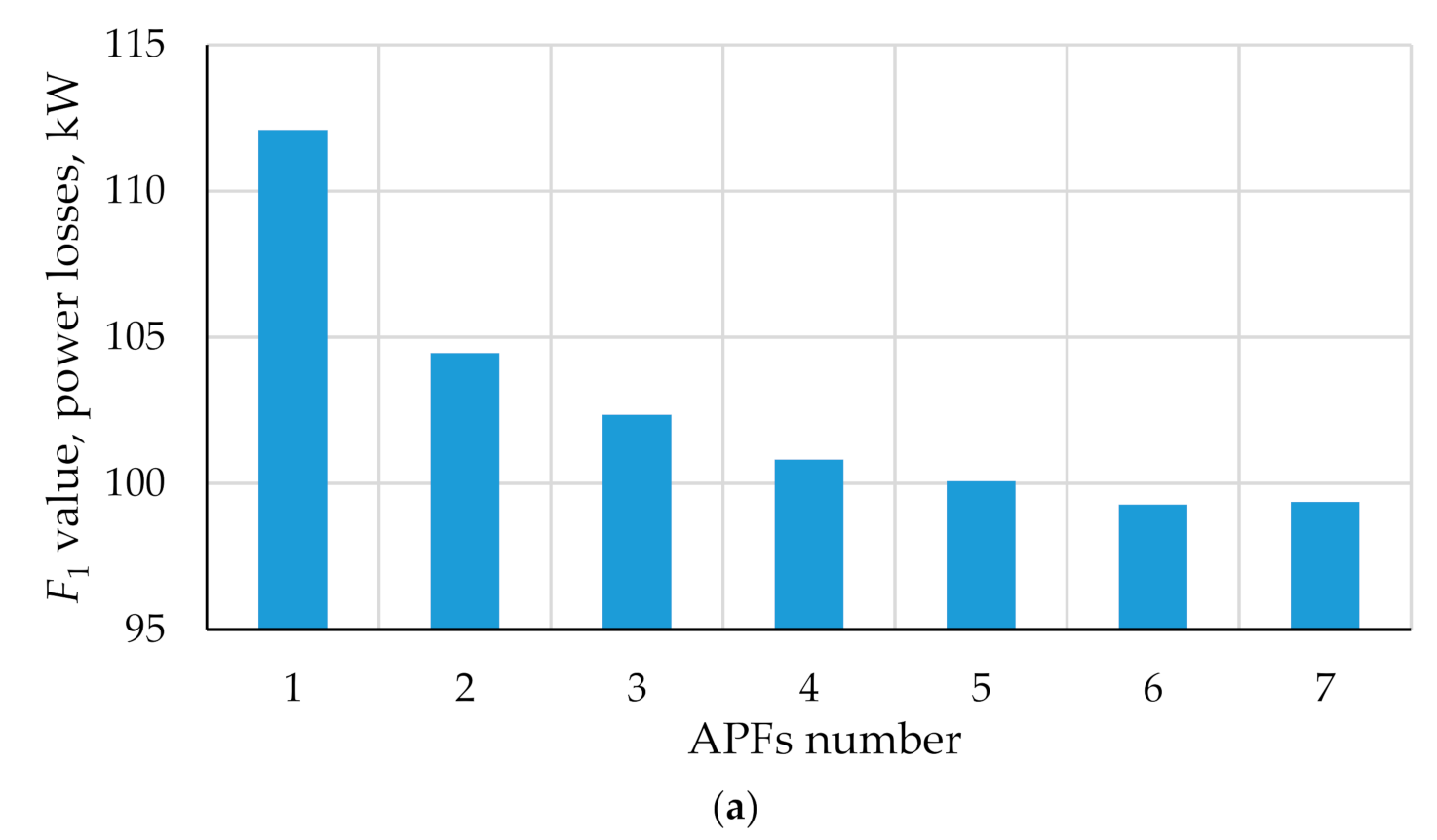

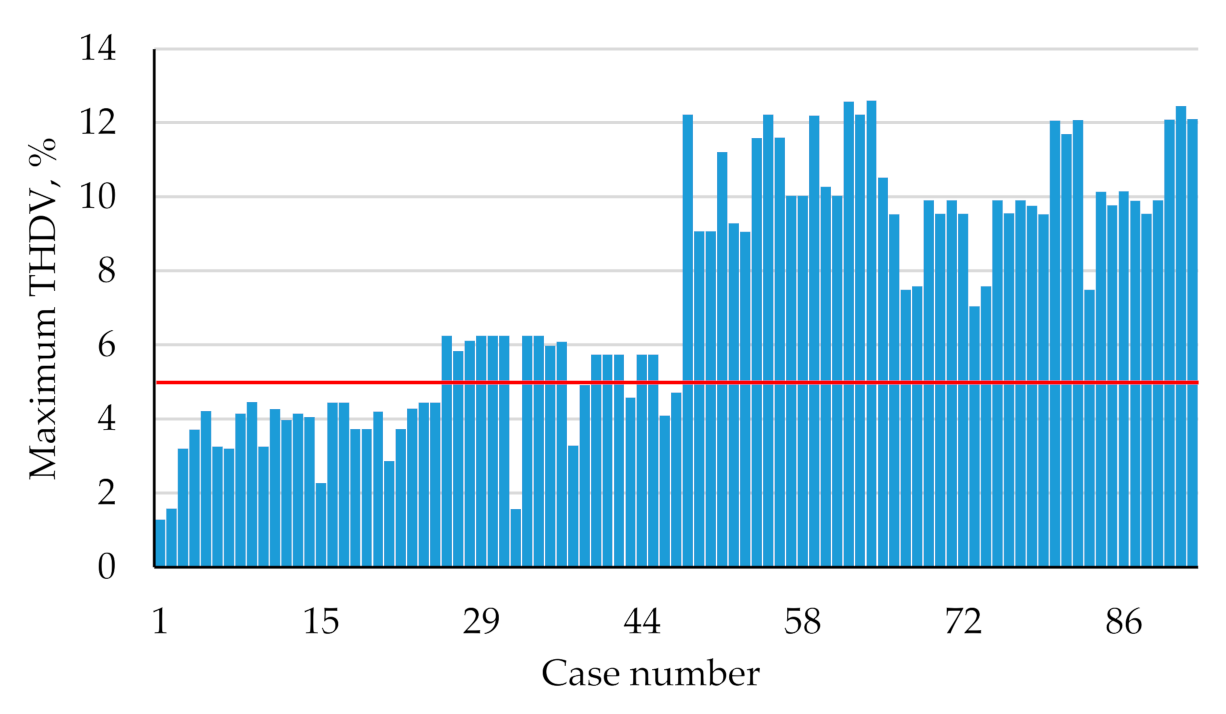
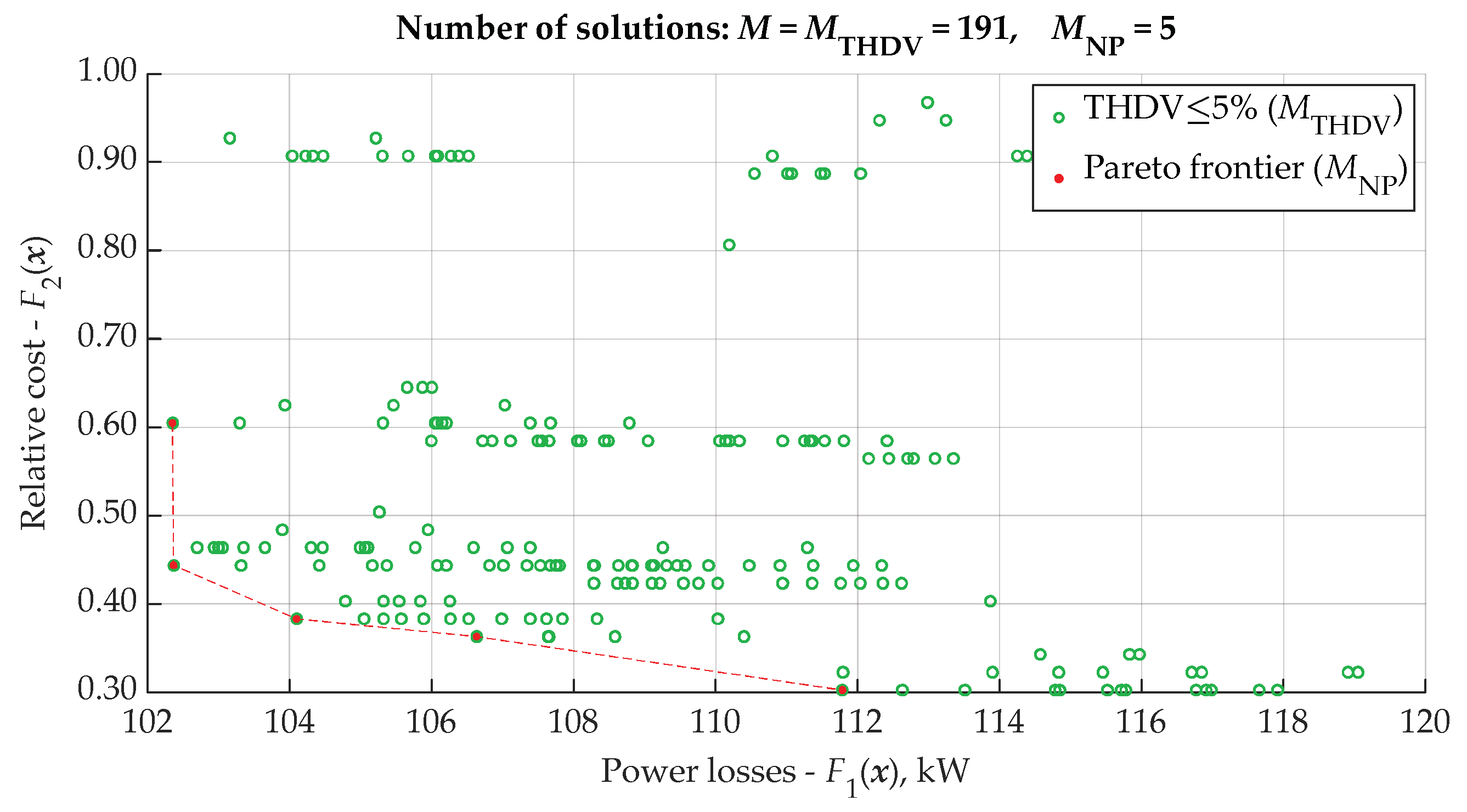
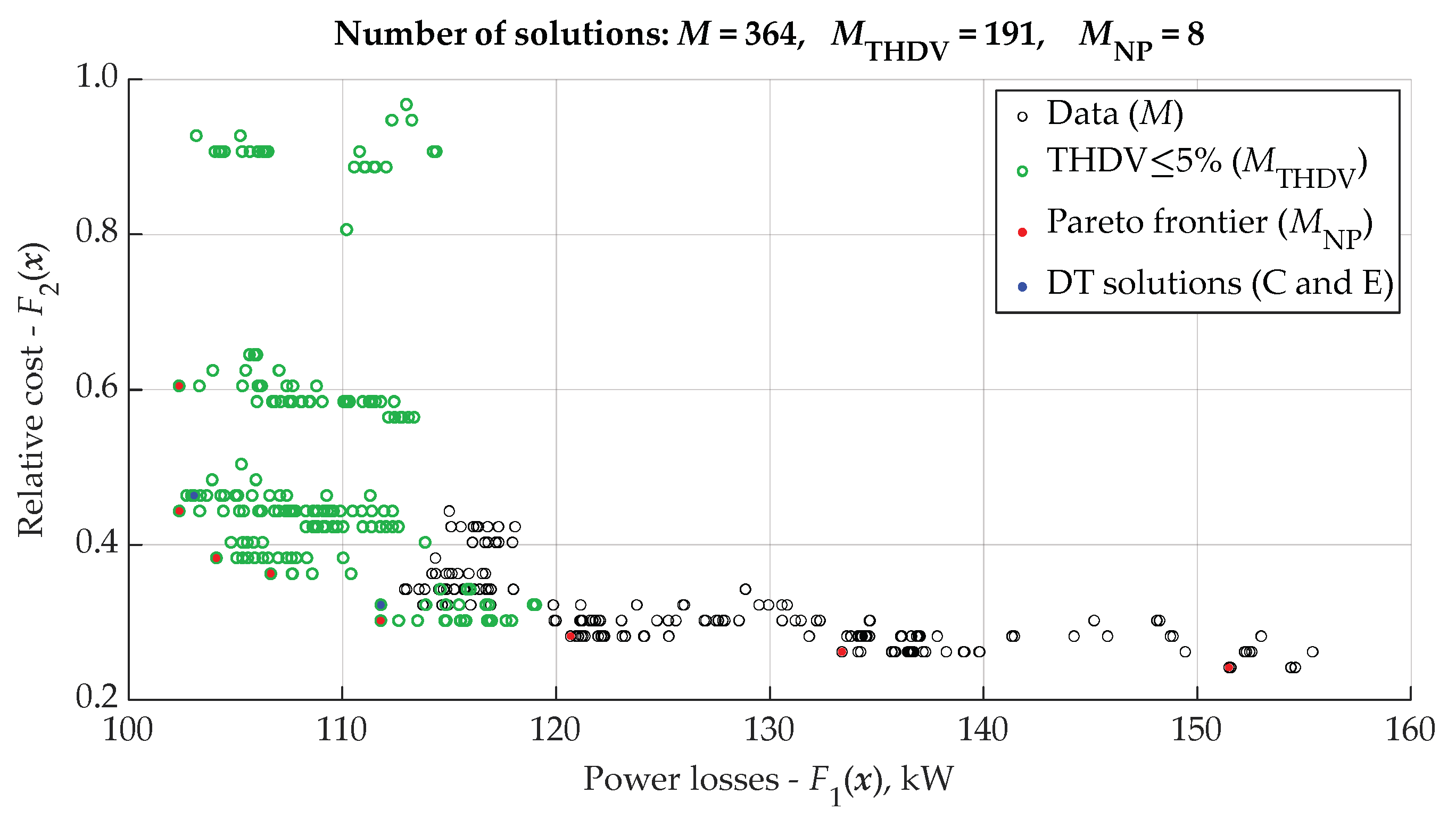
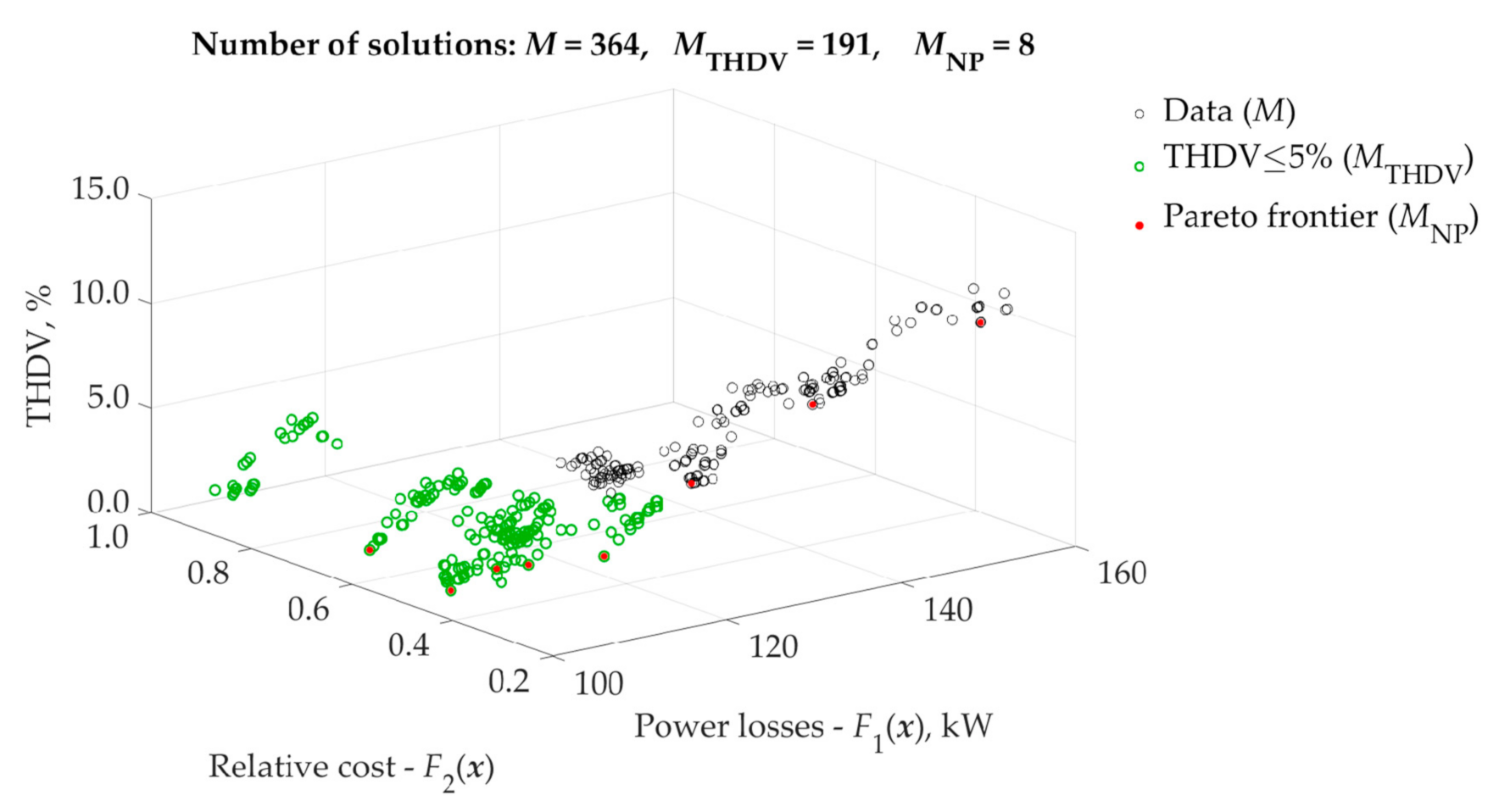
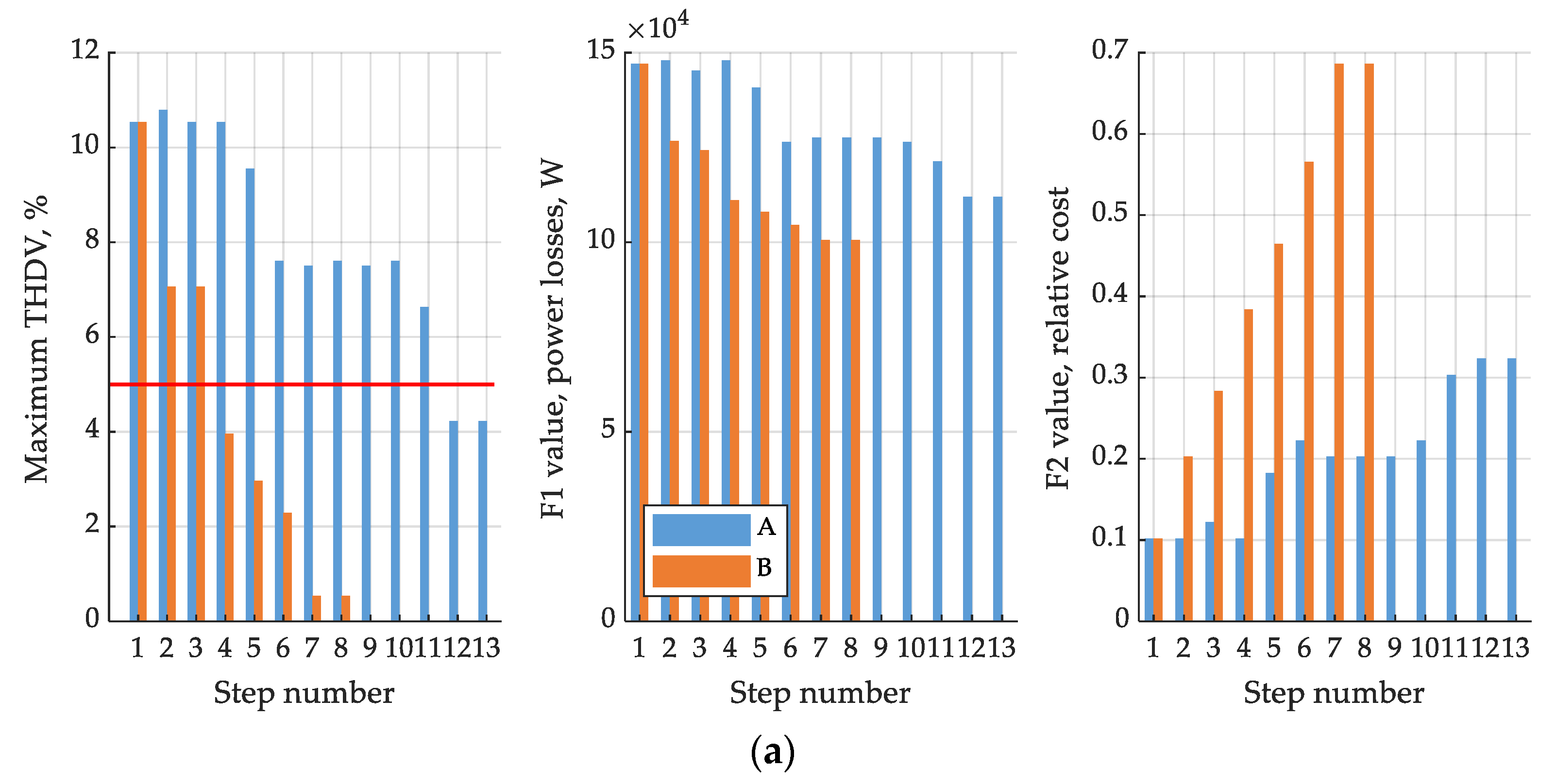
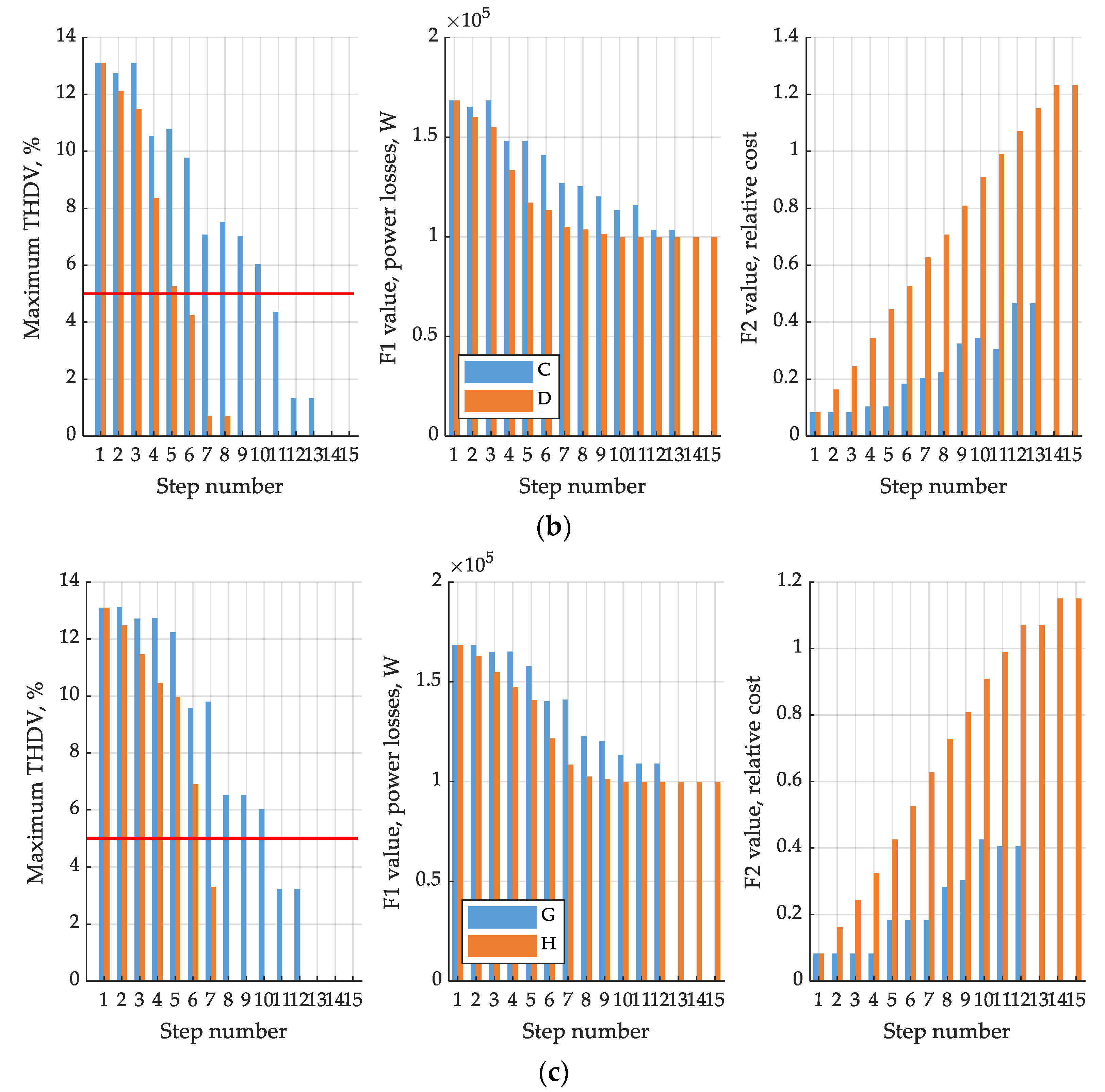

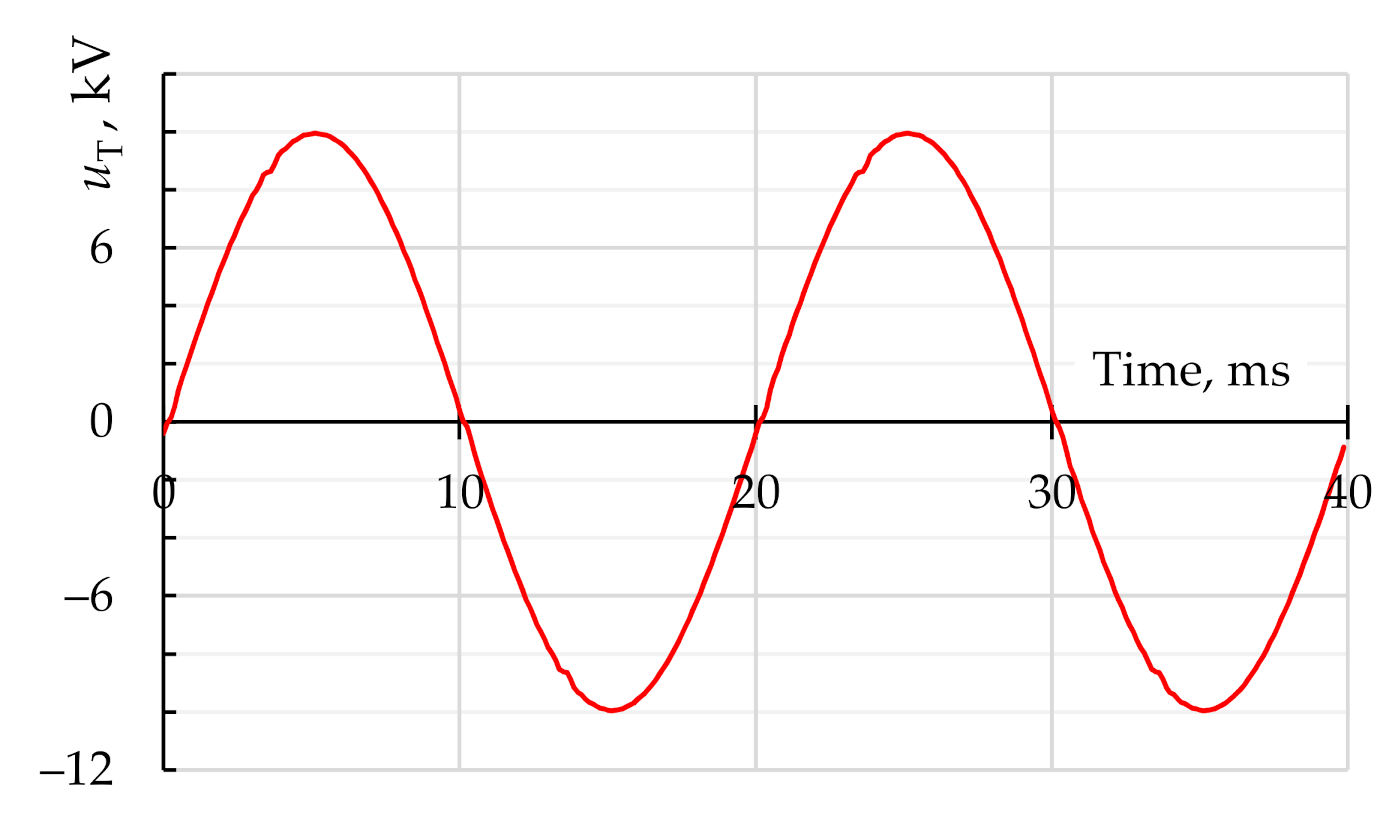
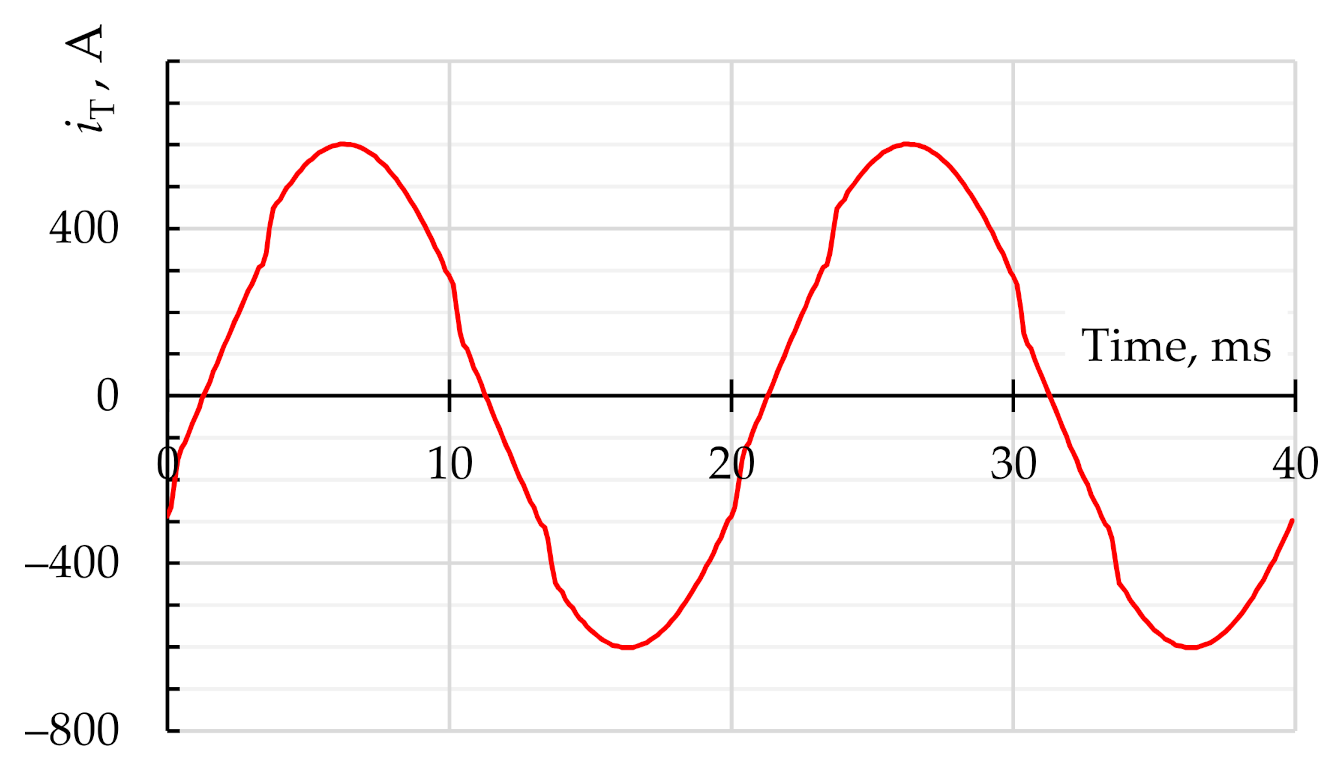
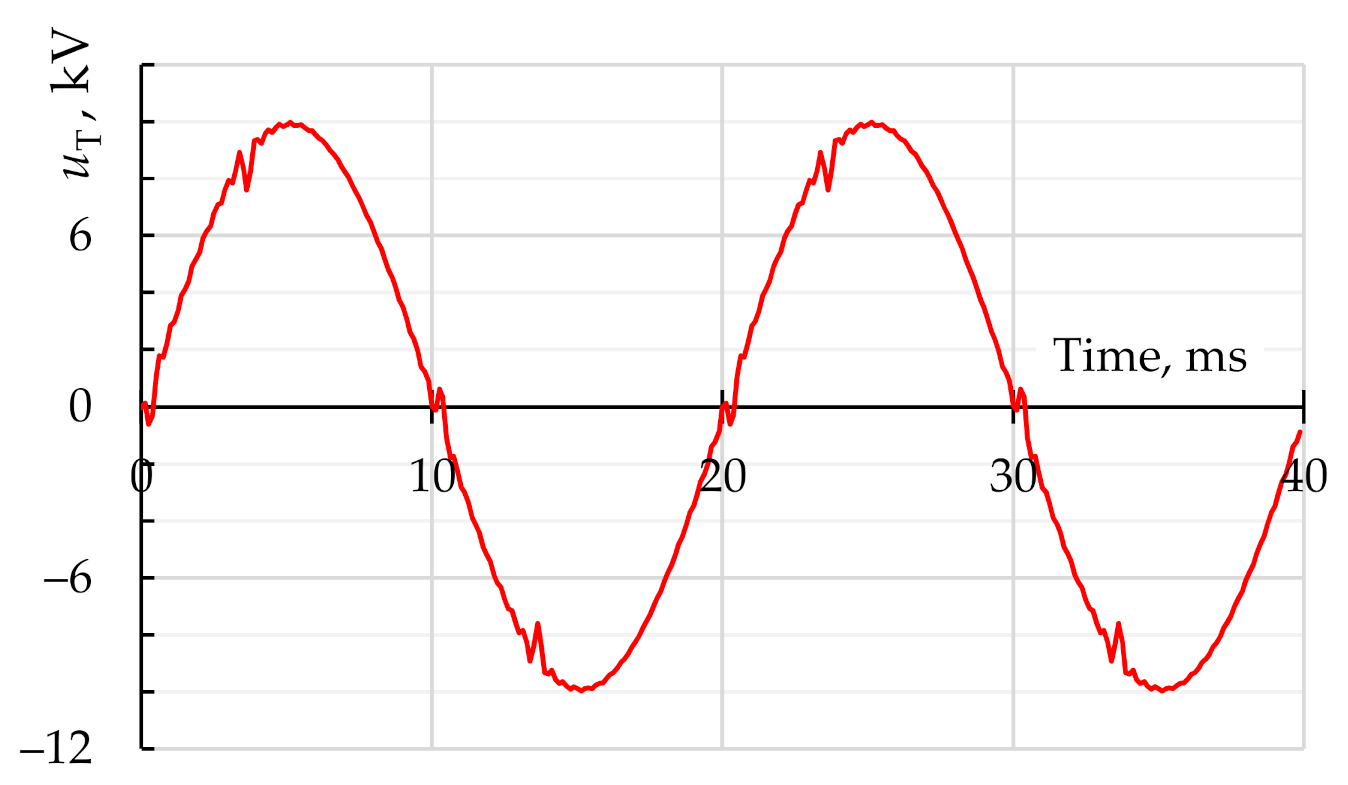
| Node Name | Node Number | THDV, % | Line | THDI, % |
|---|---|---|---|---|
| Sub 12.47 kV | 1 | 11.3 | 20-1 | 11.0 |
| Near Sub S | 2 | 11.4 | 1-2 | 11.0 |
| Near Sub N | 3 | 11.4 | 1-3 | 11.0 |
| PBS | 4 | 11.7 | 2-4 | 10.9 |
| PBN | 5 | 11.7 | 3-5 | 10.9 |
| Base | 6 | 11.9 | 4-6 | 12.2 |
| Star | 7 | 12.4 | 5-6 | 12.2 |
| Wilderness | 8 | 12.5 | 6-7 | 22.3 |
| Dorsey | 9 | 12.4 | 6-9 | 19.3 |
| Taylor | 10 | 12.4 | 7-16 | 3.4 |
| Longs | 11 | 12.5 | 7-15 | 30.7 |
| Apollo | 12 | 13.1 | 7-8 | 16.7 |
| Jupiter | 13 | 12.8 | 8-9 | 40.2 |
| WipeOut | 14 | 12.7 | 8-14 | 32.8 |
| BigBoss | 15 | 13.0 | 8-13 | 23.0 |
| Shop | 16 | 12.4 | 13-12 | 29.7 |
| Sub 138 kV | 20 | 3.3 | 9-10 | 6.9 |
| 10-11 | 6.1 |
| APF Numbers | Number of APFs | ||||||
|---|---|---|---|---|---|---|---|
| For a Minimum of F1 | |||||||
| 1 | 2 | ||||||
| 2 | 3 | 10 | |||||
| 3 | 2 | 8 | 10 | ||||
| 4 | 3 | 5 | 8 | 10 | |||
| 5 | 2 | 6 | 8 | 10 | 11 | ||
| 6 | 2 | 3 | 4 | 8 | 10 | 13 | |
| 7 | 1 | 2 | 4 | 6 | 8 | 10 | 11 |
| For a Minimum of F2 | |||||||
| 1 | 1 | ||||||
| 2 | 4 | 10 | |||||
| 3 | 4 | 10 | 13 | ||||
| 4 | 4 | 8 | 10 | 12 | |||
| 5 | 4 | 8 | 9 | 10 | 14 | ||
| 6 | 2 | 3 | 4 | 8 | 10 | 13 | |
| 7 | 4 | 7 | 8 | 9 | 10 | 12 | 13 |
| Index | Minimized Function | Route Sorted by | Wcorr | F1, kW | F2 | Calculation Time, s | APF Number | Number of Installed APFs |
|---|---|---|---|---|---|---|---|---|
| A | F1 | THDV | Yes | 111.8 | 0.32 | 1.4 | 3 | 10, 7, 11 |
| B | F1 | THDV | No | 100.4 | 0.69 | 1.3 | 7 | 8, 10, 7, 11, 9, 6, 3 |
| C | F1 | Number of APF | Yes | 103.0 | 0.46 | 1.4 | 3 | 10, 7, 3 |
| D | F1 | Number of APF | No | 99.4 | 1.23 | 4.3 | 14 | 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 |
| E | F2 | THDV | Both | 111.8 | 0.32 | 0.7 | 3 | 10, 7, 11 |
| F | F2 | Number of APF | Both | 105.6 | 0.54 | 2.1 | 6 | 13, 12, 11, 10, 9, 8 |
| G | F1 | Current | Yes | 108.7 | 0.40 | 1.3 | 4 | 13, 10, 11, 7 |
| H | F1 | Current | No | 99.4 | 1.15 | 3.9 | 13 | 12, 14, 9, 13, 6, 8, 10, 11, 7, 5, 4, 1, 2 |
| I | F2 | Current | Both | 110.1 | 0.54 | 2.2 | 6 | 14, 9, 13, 6, 8, 10 |
| F1 Minimization with C Route | F2 Minimization with E Route | |||
|---|---|---|---|---|
| Step | Number of APF | Decision | Number of APF | Decision |
| 1 | 14 | Next | 8 | Next |
| 2 | 13 | Next | 10 | Place APF |
| 3 | 12 | Next | 7 | Previous |
| 4 | 11 | Next | 8 | Next |
| 5 | 10 | Place APF | 7 | Place APF |
| 6 | 9 | Next | 11 | Place APF |
| 7 | 8 | Next | Terminate algorithm | |
| 8 | 7 | Place APF | ||
| 9 | 6 | Next | ||
| 10 | 5 | Next | ||
| 11 | 4 | Next | ||
| 12 | 3 | Place APF | ||
| 13 | Terminate algorithm | |||
| Node | THDV, % C Route | THDV, % E Route | Line | THDI, % C Route | THDI, % E Route |
|---|---|---|---|---|---|
| 1 | 0.6 | 3.3 | 20-1 | 0.7 | 11.0 |
| 2 | 0.6 | 3.3 | 1-2 | 0.7 | 11.0 |
| 3 | 0.6 | 3.3 | 1-3 | 0.7 | 11.0 |
| 4 | 0.6 | 3.4 | 2-4 | 0.7 | 10.9 |
| 5 | 0.6 | 3.4 | 3-5 | 0.7 | 10.9 |
| 6 | 0.6 | 3.5 | 4-6 | 0.8 | 12.2 |
| 7 | 0.6 | 3.7 | 5-6 | 0.8 | 12.2 |
| 8 | 0.6 | 3.8 | 6-7 | 0.0 | 22.3 |
| 9 | 0.7 | 3.8 | 6-9 | 2.3 | 19.3 |
| 10 | 0.7 | 3.8 | 7-16 | 0.6 | 3.4 |
| 11 | 0.9 | 4.0 | 7-15 | 0.0 | 30.7 |
| 12 | 1.4 | 4.2 | 7-8 | 0.0 | 16.7 |
| 13 | 0.9 | 3.8 | 8-9 | 12.6 | 40.2 |
| 14 | 0.8 | 4.0 | 8-14 | 32.8 | 32.8 |
| 15 | 0.6 | 3.7 | 8-13 | 13.9 | 23.0 |
| 16 | 0.6 | 3.7 | 13-12 | 29.7 | 29.7 |
| 20 | 0.1 | 0.8 | 9-10 | 6.9 | 6.9 |
| 10-11 | 6.1 | 6.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimas, M.; Grabowski, D.; Buła, D. Application of Decision Trees for Optimal Allocation of Harmonic Filters in Medium-Voltage Networks. Energies 2021, 14, 1173. https://doi.org/10.3390/en14041173
Klimas M, Grabowski D, Buła D. Application of Decision Trees for Optimal Allocation of Harmonic Filters in Medium-Voltage Networks. Energies. 2021; 14(4):1173. https://doi.org/10.3390/en14041173
Chicago/Turabian StyleKlimas, Maciej, Dariusz Grabowski, and Dawid Buła. 2021. "Application of Decision Trees for Optimal Allocation of Harmonic Filters in Medium-Voltage Networks" Energies 14, no. 4: 1173. https://doi.org/10.3390/en14041173
APA StyleKlimas, M., Grabowski, D., & Buła, D. (2021). Application of Decision Trees for Optimal Allocation of Harmonic Filters in Medium-Voltage Networks. Energies, 14(4), 1173. https://doi.org/10.3390/en14041173








