A Heuristic Algorithm for Combined Heat and Power System Operation Management

Abstract

This paper presents a computationally efficient novel heuristic approach for solving the combined heat and power economic dispatch (CHP-ED) problem in residential buildings considering component interconnections. The proposed solution is meant as a substitute for the cutting-edge approaches, such as model predictive control, where the problem is a mixed-integer nonlinear program (MINLP), known to be computationally-intensive, and therefore requiring specialized hardware and sophisticated solvers, not suited for residential use. The proposed heuristic algorithm targets simple embedded hardware with limited computation and memory and, taking as inputs the hourly thermal and electrical demand estimated from daily load profiles, computes a dispatch of the energy vectors including the CHP. The main idea of the heuristic is to have a procedure that initially decomposes the three energy vectors’ requests: electrical, thermal, and hot water. Then, the latter are later combined and dispatched considering interconnection and operational constraints. The proposed algorithm is illustrated using series of simulations on a residential pilot with a nano-cogenerator unit and shows around 25–30% energy savings when compared with a meta-heuristic genetic algorithm approach.

1. Introduction

Buildings equipped with multi-energy systems are an increasing trend due to the high energy efficiencies that could be achieved. In particular, the combined heat and power (CHP) systems that generate both electrical and thermal energy exploiting their inherent operating cycle [1,2] are vital components. There have been concerted efforts from building owners to replace single energy generators with higher efficiency CHP units. In comparison with traditional electrical and heat-only units, the CHP units can save 10–40% of the costs of generation, which means an equal amount of heat and electricity production with less fuel [3]. While this transition has increased CHP deployments across buildings (residential, commercial, and institutional), there are concerns regarding their return on investments. In addition, coordinating CHP units with roof-top solar, energy storage devices, and other components is important for building energy management. The CHP economic dispatch (CHP-ED) that aims to minimize fuel cost/consumption respecting constraints (operating and physical) is seen as a promising solution to guarantee fast return on investments [4]. However, multi energy systems (MES) scheduling, due to nonlinearity and non-convexity, is a quite challenging optimization problem [5]. Solving CHP-ED problem requires specialized hardware and sophisticated algorithm/solvers with large computation resources, long solution time, and sensitivity to initial conditions, thereby making their adoption in buildings difficult. In general, the need for a scalable and simple scheduling approach for solving CHP-ED problems is widely recognized in industry (see, [6,7,8,9] and references therein) especially for the building level units. This investigation aims to propose one of such approaches for deploying CHP-ED problems on simple embedded hardware with minimum memory and computing power.

Contributions

The main contributions of the paper are:

• A fast heuristic algorithm for single CHP plant to address residential CHP-ED problems. The main idea here is to decompose the problem into three parts: electrical, domestic hot water, and heat demands. Then, a suitable heuristic is designed to combine them:
• A linear single CHP algorithm incorporating thermal and electrical demands and a holistic model for capturing the interactions among energy vectors in a building.
• Illustrating the proposed heuristics on a nano-cogenerator and multi-energy systems in a building.

The paper is organized as follows: in Section 2, relevant papers from the literature will be revised; Section 3 presents the mathematical model of the CHP system and an evaluation criterion; Section 4 proposes a benchmarking optimization problem for the proposed heuristic method; finally, in Section 6, the results of some numerical experiments are showed.

2. Literature Review

The achievement of a stable economic growth where the possible increase of energy consumption and greenhouse gas emissions can be handled in a sustainable perspective is one of the main aspects the principal policy-makers are focused on today. In particular, the sustainable economic growth should be pursued with policies appealing also for emerging economies so as to maximize their impact worldwide. For instance, Larissa et al. [10] show that the aim of achieving a low carbon economy or a green economy is inherent with the concept of sustainable development. It also calls for preventing the depletion of natural resources, which should benefit future generations. The authors also believe that the adjusted net savings constitute one of the means to attain this aim. They highlight that the policy makers should promote new policies in accordance with the other elements of adjusted net savings, for the purpose of increasing the gross domestic product, consolidating a strong level of sustainable economic growth and reducing ${\mathrm{CO}}_2$ emissions and greenhouse gas effects. Ioan et al. in [11] argue that the sustainable economic growth is a desirable goal for every economy, as it helps to implement the Paris Agreement on global warming [12]. Sustainable economy includes certain core principles such as the consumption of renewable and non-renewable resources without depriving society of future benefits, sustainable human development, sustainable investment, and innovation. Specifically, sustainable development means achieving development without environmental degradation. In this context, sustainable growth suggests a transformation of the brown economy into a green or low-carbon economy.

The energy sector is the main contributor to global warming with 42% share of green house gas emissions [13]. To reduce the environmental impact of the energy sector, it is necessary to target not only the energy supply but also the energy end-use. Policies have been globally implemented to encourage the decarbonization of energy supply by incentivizing the switch to less polluting fuels (e.g., from coal to gas) and the deployment of wind and solar renewable power plants [14]. Concerning the decarbonization of the energy end-use, instead, policies and incentives have been widely studied and already implemented in the industrial/commercial sector, while the residential sector is often not considered despite its potentially significant role in emissions reduction [15]. One option to reduce the carbon emissions associated with the electric demand of a residential facility is through on-site Variable Renewable Energy (VRE) generation. Renewable sources such as solar and wind could be exploited on-site to generate fuel-free electricity, reducing the annual energy costs and the ${\mathrm{CO}}_2$ emissions [16]. However, electricity demand accounts only for around 30% of the total EU industrial energy consumption [17], while the remaining 70% consists of thermal energy demand at various temperatures. Heat is a relatively carbon intensive end-use since it mostly relies on fossil fuels: e.g., in 2000, the majority of the final consumption of heat in Europe was from oil (59%) and gas (24%). By 2018, the share of heat produced from gas increased to 40% and the share of heat from oil decreased to 42%, but, despite this switch, ${\mathrm{CO}}_2$ emissions related to the heating sector increased by 6.4% [18].

Among the many, one possible solution for reducing the environmental impact of both electricity and heat demand is Combined Heat and Power (CHP). CHP is an efficient and cleaner way to generate electrical power and heat energy from a single fuel source. In order to utilize CHP units more efficiently, the economic dispatch problem is applied to determine the optimal combination of the power and heat sources’ outputs to satisfy heat and power demand of a system, simultaneously, accounting for and operational constraints.

The CHP-ED approach presented in this research work complies fully with the sustainable energy development strategies that typically involve three major technological changes: energy savings, efficiency improvements in the energy production, and maximization of the integration of renewable energy sources via fossil fuels’ usage reduction.

Existing approaches for solving CHP-ED problems could be broadly discerned into: (i) mathematical programming based techniques, (ii) heuristics, (iii) meta-heuristics, and (iv) hybrid techniques.

Mathematical programming and, in particular, linear programming (LP) models have been the traditional tool to model CHP-ED problems thanks to their ability to capture complex switching behaviors [19,20]. In addition, the mixed integer linear programming (MILP) technique has been used in [21] for scheduling CHP units in residential buildings. Steen et al. [20] apply the MILP technique to assess the viability of integrating the distributed energy resources with a thermal energy storage (TES) system. Wouters et al. [22] used MILP to identify the optimal design of the existing grid infrastructures through integration of renewable energy units and microgrids. In [23,24], residential application based energy management systems (EMSs) are presented. Ford et al. [25] show that home energy market products may help users to save energy through load shifting with the trade off of potential benefits comfort, convenience, and security. However, other mathematical programming approaches such as Benders decomposition [26], Lagrangian relaxation [27], branch-and-bound algorithms [28,29], and mixed-integer nonlinear programming [30] have also been studied for CHP-ED problems. The main objective in these works is to minimize the operational costs for meeting energy demand over the entire planning horizon [31]. However, their implementation is cumbersome.

This could be overcome by heuristic and meta-heuristic methods. In the past, such methods have shown promise as well for CHP-ED problem [32].

Rafique et al. [23] employs a genetic algorithm (GA) for a smart home energy management to obtain electrical and gas resources optimal scheduling. Instead, Allegrini et al. [33] developed a model based software tools that addresses district-level energy systems. Ahmadi et al. in [6] presented a multi-objective optimization technique which was solved using a GA-based fuzzy decision algorithm. Alomoush et al. [34] presented an improved stochastic fractal search algorithm to solve the CHP-ED optimization problem by satisfying different inequality and equality constraints and interdependent limits. The algorithm handled the constraints by penalizing infeasible solutions during the iterative process, where the constrained CHP-ED problem is transformed into an unconstrained one. Nazari et al. [35] presented a “whale optimization algorithm” (WOA) for solving the CHP-ED problem; WOA is a new meta-heuristic approach for solving optimization problems, inspired by the social behavior of humpback whales. The authors proved WOA efficiency, feasibility, and capability of obtaining better solutions with respect to other meta-heuristics optimization techniques in terms of operational cost and its implementation ability at larger scales. Maleki et al. [36] propose a GA-based improved penalty function formulation to solve the CHP-ED problem. However, their applicability to EMS is arguable due to their solution times, and parameter initialization effects on the solution.

Hybrid algorithms combine meta-heuristics and mathematical approaches to solve the CHP-ED problem, but their complexity is still high. The heuristic based solvers provide advantages over existing approaches [37] in that they can treat the complex behaviors and reduce computational costs. Notwithstanding this, building the right heuristic is challenging, especially in the presence of operational and physical constraints. To the best of our knowledge, a heuristic approach which could be implemented on simple hardware has not been fully explored for the multi-vector scheduling problems for building applications.

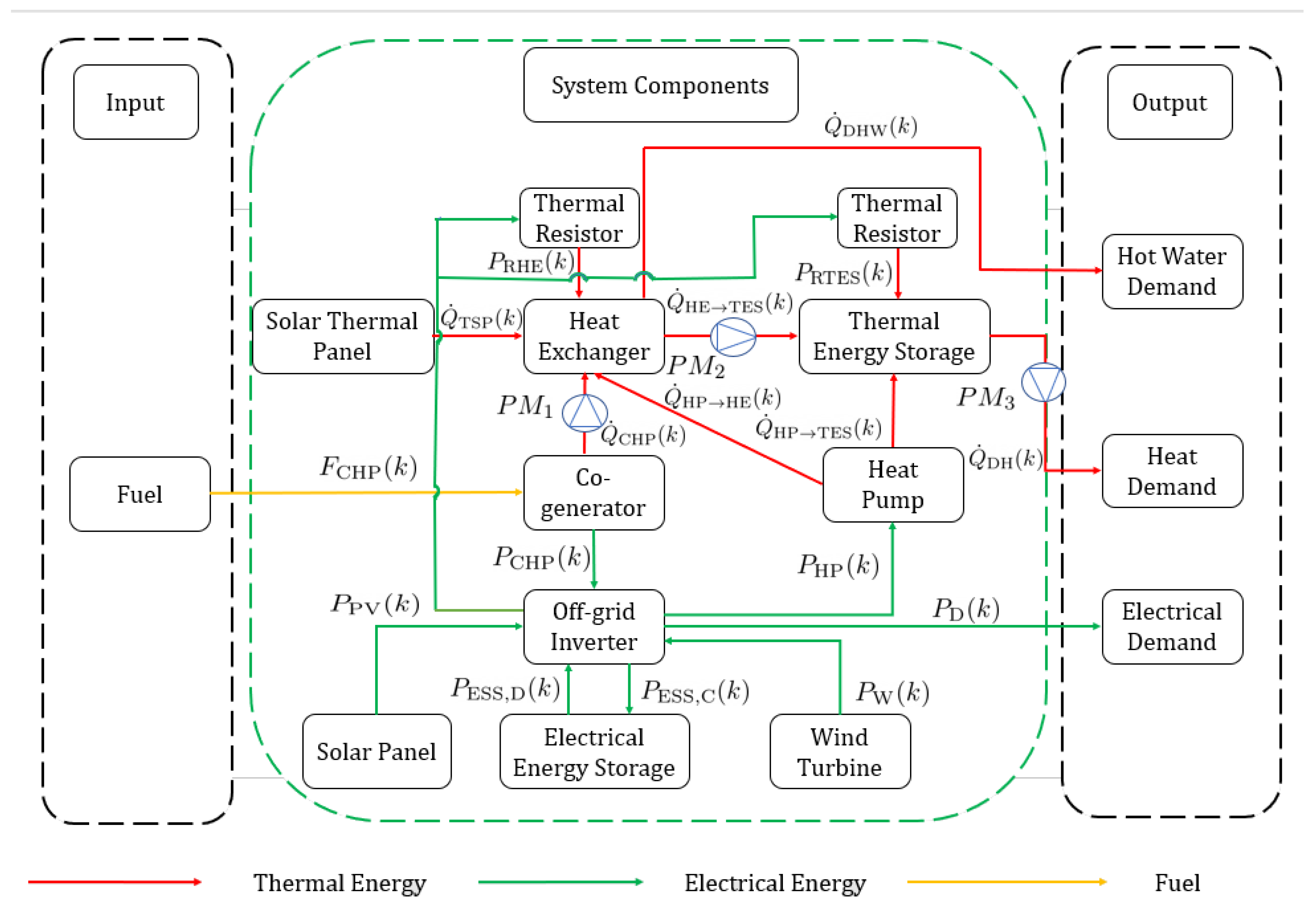
3. System Description and Modeling

Figure 1 depicts the considered CHP system architecture along with the relevant energy flows of all the energy vectors involved. The system consists of a nano co-generation unit (CHP) which provides both electrical and thermal energy. The other thermal units consist of a thermal solar panel (TSP), a heat exchanger (HE), a thermal energy storage (TES) and a heat pump (HP). The electrical system comprises photo-voltaic panels (PVs), wind turbines (WTs), electrical storage systems (ESSs). Furthermore, the water pumps ${\mathrm{PM}}_1$, ${\mathrm{PM}}_2$, and ${\mathrm{PM}}_3$ are reported as they either enable or disable the corresponding flow toward the downstream system and will be operated according to the heuristic strategy here developed. This section describes the model of the system used in this study. The total power required by the system is equal to the sum of the demands for electric, heating, and hot water powers. The description of the parameters, the electric powers, and the thermal power requests used in the proposed formulation are described in

Table 1. System model parameters.

Parameters	Description
$\Delta t$	Sampling time [ $\mathrm{h}$]
${\delta }_{\mathrm{CHP}}$	ON-OFF state of the nano co-generation unit (CHP)
${\delta }_{\mathrm{HP}}$	ON-OFF state of the heat pump (HP)
$P_{\mathrm{CHP}}$	CHP Output Electrical power
${\dot{Q}}_{\mathrm{CHP}}$	CHP Output thermal power [ $\mathrm{k}$$\mathrm{W}$]
${\sigma }_{\mathrm{CHP}}$	Operational state of the CHP
$P_{\mathrm{CHP}}^{max}$	Rated power output of CHP [ $\mathrm{k}$$\mathrm{W}$]
${\delta }_{{\mathrm{PM}}_1}\left(k\right)$	ON-OFF state of the Water Pump 1
${\delta }_{{\mathrm{PM}}_2}\left(k\right)$	ON-OFF state of the Water Pump 2
${\delta }_{{\mathrm{PM}}_3}\left(k\right)$	ON-OFF state of the Water Pump 3
$P_{{\mathrm{PM}}_1}\left(k\right)$	Water Pump 1 rated electrical consumption [ $\mathrm{k}$$\mathrm{W}$]
$P_{{\mathrm{PM}}_2}\left(k\right)$	Water Pump 2 rated electrical consumption [ $\mathrm{k}$$\mathrm{W}$]
$P_{{\mathrm{PM}}_3}\left(k\right)$	Water Pump 3 rated electrical consumption [ $\mathrm{k}$$\mathrm{W}$]
${\mathrm{SOC}}_{\mathrm{ESS}}$	Electrical storage system (ESS) State of charge [ $\mathrm{k}$$\mathrm{W}$$\mathrm{h}$]
${\mathrm{SOC}}_{\mathrm{ESS}}^{min}$	Minimum value of ${\mathrm{SOC}}_{\mathrm{ESS}}$
${\mathrm{SOC}}_{\mathrm{ESS}}^{max}$	Minimum value of ${\mathrm{SOC}}_{\mathrm{ESS}}$
${\eta }_{\mathrm{C}}$	Charging efficiency of ESS
${\eta }_{\mathrm{D}}$	Discharging efficiency of ESS
$P_{\mathrm{ESS},\mathrm{Ch}}$	ESS rated charging power [ $\mathrm{k}$$\mathrm{W}$]
$P_{\mathrm{ESS},\mathrm{D}}$	ESS rated discharging power [ $\mathrm{k}$$\mathrm{W}$]
${\mathrm{SOC}}_{\mathrm{HE}}$	State of charge of the heat exchanger [ $\mathrm{k}$$\mathrm{W}$$\mathrm{h}$]
${\dot{Q}}_{\mathrm{HP}\to \mathrm{HE}}$	Heat pump to heat exchanger thermal power shunting [ $\mathrm{k}$$\mathrm{W}$]
$P_{\mathrm{RHE}}$	Electrical power of the thermal energy storage resistor [ $\mathrm{k}$$\mathrm{W}$]
${\sigma }_{\mathrm{RHE}}$	Resistor heat-power ratio
${\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}$	Thermal power flow from heat exchanger-thermal energy storage [ $\mathrm{k}$$\mathrm{W}$]
${\mathrm{SOC}}_{\mathrm{TES}}$	State of charge of thermal energy system [ $\mathrm{k}$$\mathrm{W}$$\mathrm{h}$]
${\dot{Q}}_{\mathrm{HP}\to \mathrm{TES}}$	Heat pump to thermal energy storage thermal power flow [ $\mathrm{k}$$\mathrm{W}$]
${\delta }_{\mathrm{RTES}}$	ON-OFF state of the thermal energy storage resistor
${\delta }_{\mathrm{RHE}}$	ON-OFF state of the heat exchanger resistor
${\sigma }_{\mathrm{RTES}}$	Heat-power ratio of the resistor associated with thermal energy storage
$P_{\mathrm{RTES}}$	Electrical power of the thermal energy storage resistor [ $\mathrm{k}$$\mathrm{W}$]
$c_{\mathrm{F}}$	Fuel cost [ $€\mathrm{L}$${}^{-1}$]
$V_{\mathrm{HE}}$	Heat exchanger tank volume [ $\mathrm{L}$]
$T_{\mathrm{HE}}$	Heat exchanger temperature [ $\mathrm{K}$]
$T_{\mathrm{HE}}^{\mathrm{set}}$	Set point temperature of the heat exchanger [ $\mathrm{K}$]
$V_{\mathrm{TES}}$	Tank volume of the thermal energy storage [ $\mathrm{L}$]
$T_{\mathrm{TES}}$	Thermal energy storage temperature [ $\mathrm{K}$]
$T_{\mathrm{TES}}^{\mathrm{set}}$	Set point temperature of the thermal energy storage [ $\mathrm{K}$]
${\dot{Q}}_{\mathrm{HP}}^{min}$	Heat pump minimum thermal flow [ $\mathrm{k}$$\mathrm{W}$]
${\dot{Q}}_{\mathrm{HP}}^{max}$	Heat pump maximum thermal flow [ $\mathrm{k}$$\mathrm{W}$]
$T_{\mathrm{HP}}$	Heat pump temperature [ $\mathrm{K}$]
$T_{\mathrm{amb}}$	Ambient temperature [ $\mathrm{K}$]

,

Table 2. Electric powers.

Power Forecasts	Description
$P_{\mathrm{PV}}$	Solar power production [ $\mathrm{k}$$\mathrm{W}$]
$P_{\mathrm{W}}$	Wind power production [ $\mathrm{k}$$\mathrm{W}$]
$P_{\mathrm{D}}$	Electric demand [ $\mathrm{k}$$\mathrm{W}$]

and

Table 3. Thermal powers.

Forecasts	Description
${\dot{Q}}_{\mathrm{TSP}}$	Thermal solar panel production [ $\mathrm{k}$$\mathrm{W}$]
${\dot{Q}}_{\mathrm{DH}}$	Heat demand [ $\mathrm{k}$$\mathrm{W}$]
${\dot{Q}}_{\mathrm{DHW}}$	Hot water demand [ $\mathrm{k}$$\mathrm{W}$]

.

3.1. Nano Co-Generation Unit

We let the ON-OFF state of the CHP at the time instant k be identified by the binary operating signal ${\delta }_{\mathrm{CHP}}$. Thus,

$${\delta }_{\mathrm{CHP}}\left(k\right)=1\Rightarrow P_{\mathrm{CHP}}^{min}\le P_{\mathrm{CHP}}\left(k\right)\le P_{\mathrm{CHP}}^{max},$$

(1)

where $P_{\mathrm{CHP}}^{max}$ and $P_{\mathrm{CHP}}^{min}$ are the maximum and minimum rated output powers of the CHP. When the CHP is in the ON state, the produced heat that is recovered through a water jacket from the exhaust output is

$${\dot{Q}}_{\mathrm{CHP}}\left(k\right)={\sigma }_{\mathrm{CHP}}{\delta }_{\mathrm{CHP}}\left(k\right)P_{\mathrm{CHP}}\left(k\right),$$

(2)

where $0<{\sigma }_{\mathrm{CHP}}<1$ is the heat-to-power conversion ratio of the CHP. The water flow inside the water jacket is controlled by a water pump (${\mathrm{PM}}_1$), whose operation regulates the water flow from the CHP to the HE. Thus,

$${\delta }_{\mathrm{CHP}}\left(k\right)=1\Leftarrow {\delta }_{{\mathrm{PM}}_1}\left(k\right)=1,{\delta }_{\mathrm{CHP}}\left(k\right),{\delta }_{{\mathrm{PM}}_1}\left(k\right)\in \{0,1\},\forall k,$$

(3)

where ${\delta }_{\mathrm{CHP}}\left(k\right)$ is the logical variable used to model the state of the CHP, while ${\delta }_{{\mathrm{PM}}_1}\left(k\right)$ is the ${\mathrm{PM}}_1$ logical state variable. In other words, in order to use the available energy efficiently, ${\mathrm{PM}}_1$ can be ON only if CHP is ON.

3.2. Electrical Storage System

The ESS is modeled by considering its state of charge ${\mathrm{SOC}}_{\mathrm{ESS}}\left(k\right)$ at each instant k. The dynamical model is

$${\mathrm{SOC}}_{\mathrm{ESS}}(k+1)={\mathrm{SOC}}_{\mathrm{ESS}}\left(k\right)+\left({\eta }_{\mathrm{C}}{P}_{\mathrm{ESS},\mathrm{C}}\left(k\right)-\frac{1}{{\eta }_{\mathrm{D}}}{P}_{\mathrm{ESS},\mathrm{D}}\left(k\right)\right)\Delta t,$$

(4)

where $P_{\mathrm{ESS},\mathrm{C}}\left(k\right)$ is the charging power, $P_{\mathrm{ESS},\mathrm{D}}\left(k\right)$ is the discharging power, ${\eta }_{\mathrm{C}}$, ${\eta }_{\mathrm{D}}\in$ (0,1) are the charging and discharging efficiencies of the system, respectively. It has to be noted that the charging and discharging powers, and the storage capacity are bounded. The upper and lower limit can be depicted using the followingsimple constraints:

$$\begin{array}{cc}\hfill P_{\mathrm{ESS},\mathrm{C}}^{min}& \le P_{\mathrm{ESS},\mathrm{C}}\left(k\right)\le P_{\mathrm{ESS},\mathrm{C}}^{max},\hfill \\ \hfill P_{\mathrm{ESS},\mathrm{D}}^{min}& \le P_{\mathrm{ESS},\mathrm{D}}\left(k\right)\le P_{\mathrm{ESS},\mathrm{D}}^{max},\hfill \\ \hfill {\mathrm{SOC}}_{\mathrm{ESS}}^{min}& \le {\mathrm{SOC}}_{\mathrm{ESS}}\left(k\right)\le {\mathrm{SOC}}_{\mathrm{ESS}}^{max},\hfill \end{array}$$

(5)

where the ${\mathrm{SOC}}_{\mathrm{ESS}}^{min}$, and the ${\mathrm{SOC}}_{\mathrm{ESS}}^{max}$ are the minimum and the maximum ${\mathrm{SOC}}_{\mathrm{ESS}}$ within the range of 10% and 90%, respectively.

3.3. Heat Exchanger

In this study, the HE is storage, capable of supplying domestic hot water, and the water mixer is installed inside it. For the description of the $\mathrm{SOC}$ dynamics, we use a single-mass model [38], i.e.,

$$\begin{array}{ccc}\hfill \frac{{\mathrm{SOC}}_{\mathrm{HE}}(k+1)-{\mathrm{SOC}}_{\mathrm{HE}}\left(k\right)}{\Delta t}=& {\dot{Q}}_{\mathrm{CHP}}\left(k\right)+{\dot{Q}}_{\mathrm{TSP}}\left(k\right)+{\dot{Q}}_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)+{\delta }_{\mathrm{RHE}}\left(k\right){\sigma }_{\mathrm{RHE}}{P}_{\mathrm{RHE}}-{\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}\left(k\right)\hfill & \\ \hfill & -{\dot{Q}}_{\mathrm{DHW}}\left(k\right)-{\dot{Q}}_{\mathrm{HE},\mathrm{LOSS}}\left(k\right),\hfill \end{array}$$

(6)

where ${\mathrm{SOC}}_{\mathrm{HE}}\left(k\right)$ is state of the charge of the HE (kWh), ${\dot{Q}}_{\mathrm{DHW}}$ is hot water demand (kW), ${\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}$ is the thermal power from the HE to the TES (kW), ${\dot{Q}}_{\mathrm{CHP}}$ is the thermal power output of the CHP (kW) at time instant k, ${\dot{Q}}_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)$ is the transfer of the thermal power from the HP to the HE, $P_{\mathrm{RHE}}$ is the rated electrical power (kW) consumption by the resistor (RHE) if it is operating, i.e., ${\delta }_{\mathrm{RHE}}\left(k\right)=1$, $0<{\sigma }_{\mathrm{RHE}}<1$ is the power-to-heat conversion factor of the RHE and ${\dot{Q}}_{\mathrm{HE},\mathrm{LOSS}}\left(k\right)$ is the loss term and depends upon the temperature difference between the HE and the ambient, and also on the heat loss coefficient and the surface area of the HE. The relation between ${\mathrm{SOC}}_{\mathrm{HE}}\left(k\right)$ and the temperature of the heat exchanger $T_{\mathrm{HE}}$ is given by

$${\mathrm{SOC}}_{\mathrm{HE}}\left(k\right)=V_{\mathrm{HE}}{\rho }_{\mathrm{w}}{C}_{\mathrm{w}}(T_{\mathrm{HE}}\left(k\right)-T_{\mathrm{HE}}^{\mathrm{set}}),$$

(7)

where $V_{\mathrm{HE}}$ is the volume of the HE and $T_{\mathrm{HE}}^{\mathrm{set}}$ is the minimum set-point temperature. In addition, to maintain the minimum set-point temperature, the following constraint is imposed:

$${\mathrm{SOC}}_{\mathrm{HE}}\left(k\right)\ge 0.$$

(8)

3.4. Thermal Storage System

Similar to the HE, the TES SOC is modeled as

$$\begin{array}{cc}\hfill \frac{{\mathrm{SOC}}_{\mathrm{TES}}(k+1)-{\mathrm{SOC}}_{\mathrm{TES}}\left(k\right)}{\Delta t}=& {\dot{Q}}_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)+{\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}\left(k\right)+{\delta }_{\mathrm{RTES}}\left(k\right){\sigma }_{\mathrm{RTES}}{P}_{\mathrm{RTES}}-{\dot{Q}}_{\mathrm{DH}}\left(k\right)\hfill \\ \hfill & -{\dot{Q}}_{\mathrm{TES},\mathrm{LOSS}}\left(k\right),\hfill \end{array}$$

(9)

where ${\mathrm{SOC}}_{\mathrm{TES}}\left(k\right)$ is the state of charge of the TS (kWh), ${\dot{Q}}_{\mathrm{DH}}$ is the heat demand (kW), ${\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}$ is the thermal power from the HE to the TES (kW), ${\dot{Q}}_{\mathrm{HP}}$ is the thermal power output of the HP (kW), and ${\dot{Q}}_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)$ is the transfer of the thermal power from the HP to the TES, $P_{\mathrm{RTES}}$ is the rated electrical power (kW) consumption by the resistor (RTES) if it is operating, i.e., ${\delta }_{\mathrm{RTES}}\left(k\right)=1$, $0<{\sigma }_{\mathrm{RTES}}<1$ is the power-to-heat ratio of the RTES and ${\dot{Q}}_{\mathrm{TES},\mathrm{LOSS}}\left(k\right)$ is the loss and depends upon the temperature difference of the TES and the ambient, and also on the heat loss coefficient and the surface area of TES. Similar to the HE, the ${\mathrm{SOC}}_{\mathrm{TES}}\left(k\right)$ and $T_{\mathrm{TES}}$ relation is given by

$${\mathrm{SOC}}_{\mathrm{TES}}\left(k\right)=V_{\mathrm{TES}}{\rho }_{\mathrm{w}}{C}_{\mathrm{w}}(T_{\mathrm{TES}}\left(k\right)-T_{\mathrm{TES}}^{\mathrm{set}}),$$

(10)

where $V_{\mathrm{TES}}$ is the volume of the TES and $T_{\mathrm{TES}}^{\mathrm{set}}$ is the minimum set-point temperature. In addition, for the TES, the following constraint is imposed to maintain the minimum set-point temperature,

$${\mathrm{SOC}}_{\mathrm{TES}}\left(k\right)\ge 0.$$

(11)

3.5. Heat Pump

The HP is operated by electricity and, considering its coefficient of performance (COP) and operating state ${\delta }_{\mathrm{HP}}\left(k\right)$,is modeled as

$$\begin{array}{cc}\hfill {\dot{Q}}_{\mathrm{HP}}\left(k\right)& ={\mathrm{COP}}_{\mathrm{HP}}\times P_{\mathrm{HP}}\left(k\right),\hfill \\ \hfill {\delta }_{\mathrm{HP}}\left(k\right){\dot{Q}}_{\mathrm{HP}}^{min}\le {\dot{Q}}_{\mathrm{HP}}\left(k\right)& \le {\delta }_{\mathrm{HP}}\left(k\right){\dot{Q}}_{\mathrm{HP}}^{max},{\delta }_{\mathrm{HP}}\left(k\right)\in \{0,1\}.\hfill \end{array}$$

(12)

In general, the ${\mathrm{COP}}_{\mathrm{HP}}$ can vary according to the operating point of the HP as

$${\mathrm{COP}}_{\mathrm{HP}}=\mathsf{\Psi }\left[{\dot{Q}}_{\mathrm{HP}}\left(k\right)\right],$$

(13)

where the nonlinear function $\mathsf{\Psi }\left[·\right]$ can be obtained by analyzing the $P_{\mathrm{HP}}\mathrm{v}\mathrm{s}.{\dot{Q}}_{\mathrm{HP}}$ curve. However, we assume the COP value to be constant in the operating range considered.

3.6. Heat Pump Shunting between Heat Exchanger and Thermal Energy Storage

Both the HE and the TES can store thermal energy from the HP by proper shunting. The shunting operations are modeled by means of two binary signals denoted as ${\delta }_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)$, ${\delta }_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)$ and the auxiliarybinary variable ${\delta }_{\mathrm{shunt}}\left(k\right)$ as

$$\begin{array}{c}\hfill {\delta }_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)=1\Rightarrow {\dot{Q}}_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)={\dot{Q}}_{\mathrm{HP}}\left(k\right),\\ \hfill {\delta }_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)=1\Rightarrow {\dot{Q}}_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)={\dot{Q}}_{\mathrm{HP}}\left(k\right).\end{array}$$

(14)

The following integer linear constraint denotes that only a single operation mode of the shunting is allowed at each time k:

$${\delta }_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)+{\delta }_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)={\delta }_{\mathrm{shunt}}\left(k\right).$$

(15)

3.7. Power Balance

For benchmarking purposes, a GA optimization problem is also set up and presented later. The essence of the optimization model is to meet the thermal and electrical demands with renewable generation, using the CHP as a last option and, in case this happens, effectively exploiting the combined generation of heat and electrical power. In order to achieve a realistic optimal control policy, the following power balance equations must be satisfied ateach time-step k:

$$\begin{array}{cc}\hfill P_{\mathrm{D}}\left(k\right)& \le P_{\mathrm{PV}}\left(k\right)+P_{\mathrm{W}}\left(k\right)+P_{\mathrm{CHP}}\left(k\right)-P_{\mathrm{ESS},\mathrm{Ch}}\left(k\right)+P_{\mathrm{ESS},\mathrm{Dis}}\left(k\right)-P_{\mathrm{HP}}\left(k\right)-P_{{\mathrm{PM}}_1}{\delta }_{{\mathrm{PM}}_1}\left(k\right)\hfill \\ & -P_{{\mathrm{PM}}_2}{\delta }_{{\mathrm{PM}}_2}\left(k\right)-P_{{\mathrm{PM}}_3}{\delta }_{{\mathrm{PM}}_3}\left(k\right)-P_{\mathrm{RTES}}{\delta }_{\mathrm{RTES}}\left(k\right)-P_{\mathrm{RHE}}{\delta }_{\mathrm{RHE}}\left(k\right),\hfill \\ \hfill {\dot{Q}}_{\mathrm{DH}}\left(k\right)& \le {\dot{Q}}_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)+{\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}\left(k\right)+{\delta }_{\mathrm{TES}}\left(k\right){\sigma }_{\mathrm{RTES}}{P}_{\mathrm{RTES}}+\frac{{\mathrm{SOC}}_{\mathrm{TES}}\left(k\right)}{\Delta t},\hfill \\ \hfill {\dot{Q}}_{\mathrm{DHW}}\left(k\right)& \le {\dot{Q}}_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)+{\delta }_{\mathrm{RHE}}\left(k\right){\sigma }_{\mathrm{RHE}}{P}_{\mathrm{RHE}}+{\dot{Q}}_{\mathrm{CHP}}\left(k\right)+{\dot{Q}}_{\mathrm{TSP}}\left(k\right)-{\dot{Q}}_{\mathrm{HE}\to \mathrm{TES}}\left(k\right)+\frac{{\mathrm{SOC}}_{\mathrm{HE}}\left(k\right)}{\Delta t},\hfill \end{array}$$

(16)

where $P_{{\mathrm{PM}}_1},P_{{\mathrm{PM}}_2},P_{{\mathrm{PM}}_3}$ are the power consumptions of ${\mathrm{PM}}_1$, ${\mathrm{PM}}_2$ and ${\mathrm{PM}}_3$, respectively.

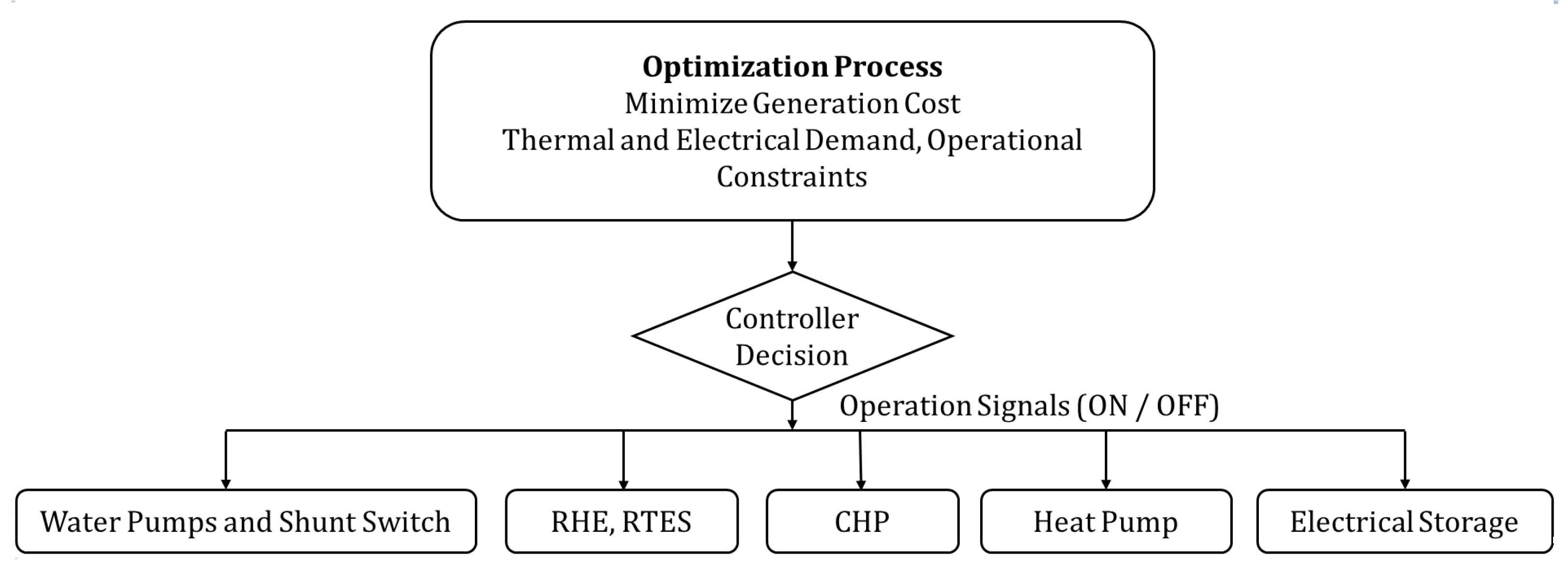
4. Proposed Heuristics Formulation

The objective of the proposed heuristic energy dispatch strategy is to provide ON/OFF commands to the CHP system under investigation. The flow chart in Figure 2 describes the controller decision process.

The CHP system has to be operated the least possible without sacrificing the comfort in terms of electric, heat, and hot water. The overall problem is to decide how to effectively meet the electric and thermal demands of the commercial building by answering the following questions:

• When should each equipment be switched on or off, and how much should it produce?
• When should the electric and thermal storage be charged or discharged?

The CHP operation schedule is calculated with the proposed heuristic-based algorithm for heat, hot water, and electric demand and presented in the next subsections. It is worth mentioning that the heuristics developed for heat and hot water demand satisfactions consider the electrical energy consumption of the equipments i.e., the heat pump and the water pumps.

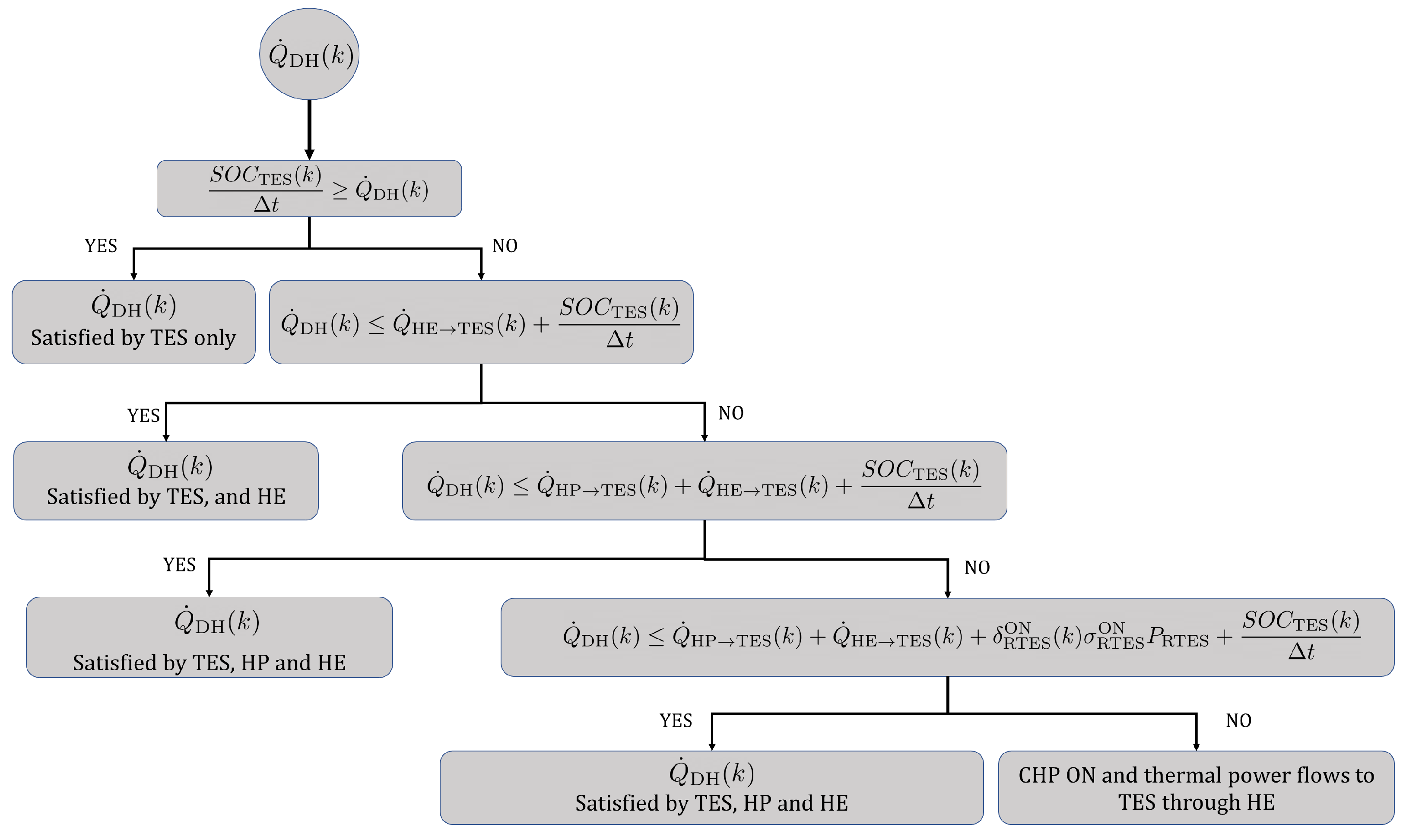
4.1. Heuristic Algorithm Module for Heat Demand Satisfaction

The heuristic algorithm is detailed in Figure 3 and described as follows:

Step 1

The heat demand ${\dot{Q}}_{\mathrm{DH}}\left(k\right)$ is first compared with the thermal energy stored in TES, by checking ${\mathrm{SOC}}_{\mathrm{TES}}$.

Step 2

In case ${\dot{Q}}_{\mathrm{DH}}\left(k\right)$ is not achievable with the available ${\mathrm{SOC}}_{\mathrm{TES}}$ only, the algorithm is designed to set ${\mathrm{PM}}_2$ to ON state, connecting HE with the TES so that both thermal storage are used.

Step 3

If ${\dot{Q}}_{\mathrm{DH}}\left(k\right)$ can not be satisfied even with HE and TES, the heat pump will be set to its ON state to cover the mismatch between the ${\dot{Q}}_{\mathrm{DH}}\left(k\right)$ and the available thermal energy in the storage.

Step 4

If the ${\dot{Q}}_{\mathrm{DH}}\left(k\right)$ is not achieved with the available thermal power from heat pump, and thermal storage, the controller set the thermal resistor to ON state (${\delta }_{\mathrm{RTES}}=1$).

Step 5

As a last resort, if ${\dot{Q}}_{\mathrm{DH}}\left(k\right)$ at a certain time is so large it can not be satisfied with the storage, the generation units, the thermal resistor, and the heat pump, the CHP will be set to ON state to meet the requested heat demand.

4.2. Heuristic Algorithm Module for Hot Water Demand Satisfaction

The heuristic algorithm for hot water demand satisfaction is detailed in Figure 4 and described as follows:

Step 1

The hot water demand ${\dot{Q}}_{\mathrm{DHW}}\left(k\right)$ is first compared with the thermal solar panel generation ${\dot{Q}}_{\mathrm{TSP}}\left(k\right)$, and the thermal energy stored in HE, by checking ${\mathrm{SOC}}_{\mathrm{HE}}$.

Step 2

If ${\dot{Q}}_{\mathrm{DHW}}\left(k\right)$ is not achievable with the available ${\mathrm{SOC}}_{\mathrm{HE}}$, and ${\dot{Q}}_{\mathrm{TSP}}\left(k\right)$, the heat pump is set to ON state so that the additional thermal power is shunted towards HE to meet the required ${\dot{Q}}_{\mathrm{DHW}}\left(k\right)$.

Step 3

If ${\dot{Q}}_{\mathrm{DHW}}\left(k\right)$ is not achieved with the available thermal power from heat pump and thermal storage, the controller sets the thermal resistor to ON state (${\delta }_{\mathrm{RHE}}=1$).

Step 4

In case ${\dot{Q}}_{\mathrm{DHW}}\left(k\right)$ is achievable through the available energy from generation, storage, heat pump, and thermal resistor, the fuel cost of the CHP would be saved. Contrarily, CHP will be ON to fulfill the demand as a last resort.

4.3. Heuristic Algorithm Module for Electric Demand Satisfaction

The heuristic algorithm for the electric demand satisfaction is showed in Figure 5. The objective is to minimize the usage of the CHP while satisfying all the system constraints and maximizing utilization of the power coming from the renewable sources. Since the nature of the renewable sources is intermittent, a backup battery is used for storing energy surpluses. The heuristic algorithm for electric demand satisfaction is described as follows:

Step 1

At each time k, the available $P_{\mathrm{RES}}\left(k\right)$ is first checked in order to meet electric demand $P_D\left(k\right)$, as well as the power needed to charge ${\mathrm{SOC}}_{\mathrm{ESS}}$ to its maximum level.

Step 2

In the second step, $P_{\mathrm{RES}}\left(k\right)$ is compared with the electric demand $P_D\left(k\right)$ only. If $P_D\left(k\right)$ cannot be satisfied with it, the batteries act as a backup source in order to satisfy the power balance equation.

Step 3

In case $P_D\left(k\right)$ cannot be met with the renewable sources as well as with the battery ${\mathrm{SOC}}_{\mathrm{ESS}}$, then the CHP is switched ON in order to meet that electric demands.

5. A GA-Solved Optimization Problem for Benchmarking

We compared the proposed heuristic approach with the performance of the popular meta-heuristic GA minimizing the power produced by the CHP, and hence its operation cost. The vector $\mathbf{u}\left(k\right)$ aggregates all the decision variables at time instant k, and is defined as

$$\begin{array}{cc}\hfill \mathbf{u}\left(k\right)=& \left[\begin{array}{ccccccc}{\delta }_{\mathrm{CHP}}\left(k\right)& {\delta }_{\mathrm{HP}}\left(k\right)& {\delta }_{\mathrm{RHE}}\left(k\right)& {\delta }_{\mathrm{RTES}}\left(k\right)& {\delta }_{{\mathrm{PM}}_1}\left(k\right)& {\delta }_{{\mathrm{PM}}_2}\left(k\right)& {\delta }_{{\mathrm{PM}}_3}\left(k\right)\end{array}\right.\hfill \\ \hfill & \begin{array}{c}{\left.\begin{array}{cc}{\delta }_{\mathrm{HP}\to \mathrm{TES}}\left(k\right)& {\delta }_{\mathrm{HP}\to \mathrm{HE}}\left(k\right)\end{array}\right]}^{\top }.\hfill \end{array}\hfill \end{array}$$

(17)

Mathematically, the minimization problem computed at each time instant k is defined as

$$\begin{array}{ccc}\hfill \underset{\mathbf{u}\left(k\right)}{min}& P_{\mathrm{CHP}}\left(k\right),\hfill & \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill \\ \hfill & \mathrm{Constraints}\left(4\right)–\left(11\right),\left(14\right)–\left(16\right),\hfill \\ \hfill & \mathbf{u}\left(k\right)\in {\{0,1\}}^9,\hfill \end{array}$$

(18)

where $P_{\mathrm{CHP}}\left(k\right)$ represents the co-generator output power; assuming a constant price of the fuel and a constant efficiency of the CHP, such minimization is equivalent to minimizing the cost of CHP fuel.

GA is an evolution-based population direct search method which mimics the natural crossover and selection process [39,40,41,42] of a biological population to solve optimization problems.

Similar to other meta-heuristic optimization process, GA starts searching the solution space with a set of candidate solutions or seeds, otherwise known as population vectors. In our problem, we implement real-coded GA (RCGA), which improves the computational efficiency [41,42]. There exist different types of crossover and mutation strategies to generate off-spring vectors for subsequent generations and for preserving diversity within the candidate solutions. However, the practice shows that the choice of a certain type of techniques is largely based on experiments and dependent upon the problem specifications. In particular, the adaptive selection of a particular crossover or mutation from their ensemble is adopted to enhance the performance of RCGA. The selection of an off-spring from a particular cross-over or mutation is dependent upon the objective function value as well as the degree of constraint violation. For a detailed description and understanding of the working mechanism and principles of RCGA, the reader can refer to [41]. The algorithm takes into account the following steps:

Step 1

Read the electric and thermal power requests, maximum number of iterations, and population size.

Step 2

Generate an initial population $P_0$. The chromosomes length is equal to the number of decision variables in Equation (17).

Step 3

Check the constraints that correspond to the individuals in $P_0$. Infeasible solutions are then removed from the solution space through the assignment of a large penalty cost.

Step 4

Evaluate the “fitness function” for individuals in $P_0$ using the objective function in Equation (18). The population is then indexed by the iteration number i (i.e., population = $P_i$).

Step 5

Generate a new pool of candidate solution $P_{i+1}$ through the application of the operators selection, crossover, and mutation to $P_i$ [42].

Step 6

Check the constraints formulation for all the individuals mentioned in $P_{i+1}$.

Step 7

Evaluate the objective function for all the individuals listed in $P_{i+1}$. The less constraint-violating solutions from $P_i$ and $P_{i+1}$ will be retained.

Step 8

If the solution with the best objective value remains unchanged for a significant number of iterations, the algorithm goes to report the results at step 9, if not, it goes to step 5.

Step 9

Report the results.

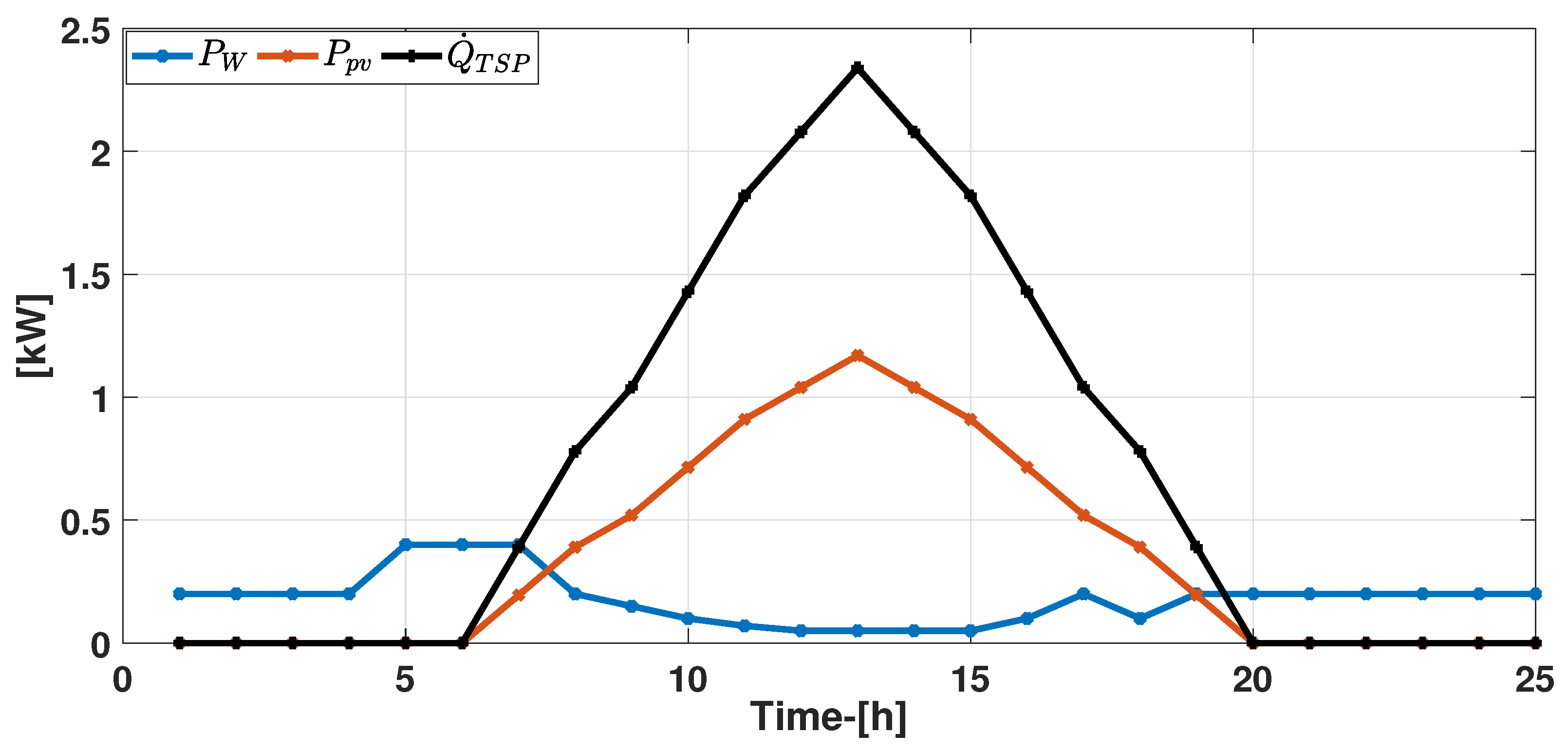
6. Simulations and Numerical Results

6.1. Simulation Setup

The parameters taken in this study for the controller setup are as follows: The fuel cost considered is assumed to be a constant, $1.54$ [€/$\mathrm{L}$]. Meanwhile, we take solar and wind power generations data with 1 h time resolution from literature. To generate power and heat, the default heat-power ratio of the CHP system under investigation is assumed to be 1:1. In this study, the proposed heuristic approach is implemented and compared with the standard GA meta-heuristic algorithm using MATLAB R2020a on a laptop with anIntel Core (TM) i7-7700 HQ 2.8 GHz processor and 16 GB of memory.

6.2. Test Runs

In order to prove the efficiency of the proposed heuristics, a series of test runs have been performed for a 24 h period. Specifically, extensive simulation scenarios have been conducted to compare the results obtained with the proposed heuristics against a genetic algorithm solver. Related histogram is reported showing the effectiveness of the proposed approach in energy cost saving. Before reporting such a cumulative comparison, two selected comparison scenarios among the ones considered are reported in details, to highlight the behaviors of the two different algorithms. It can be clearly seen from the simulations that both the thermal and the electric demands have always been satisfied either directly with the thermal panel, PVs, wind generator, with the stored electrical and thermal energy, or as a last resort with the CHP unit.

6.3. Example 1

Figure 6 depicts the electric and thermal generations data from the renewable sources (WTs, PVs, TSP) considered in this numerical example.

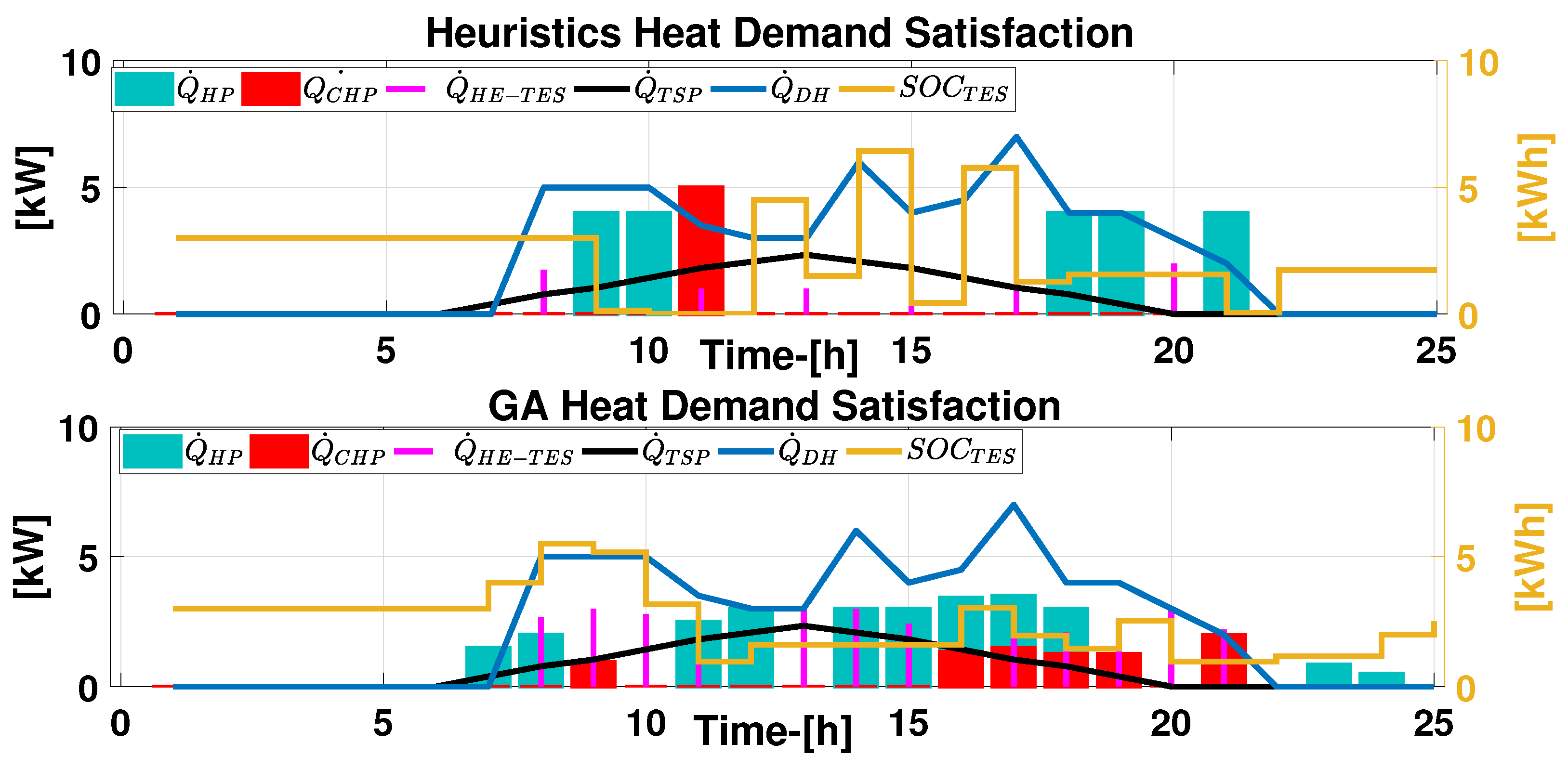
6.3.1. Heat Demand Satisfaction

In order to prove the efficacy of the implemented controller, the operational ON/OFF signals of the CHP system under investigation are shown for a case with frequent mismatch between available system thermal energy and the heat demand over the 24 h simulation. Figure 7 shows that the heat load through the proposed heuristic algorithm is met mostly with the thermal energy stored in the thermal energy storage tank, followed by the energy from the heat exchanger storage by switching on ${\mathrm{PM}}_2$ or from the heat pump depending on the battery state of charge. In order to meet the demand, the Figure 7 top panel shows that the CHP unit is switched ON at hour 11 only, i.e., in one hour over 24 h simulations. Contrarily, the frequent switching of the CHP unit for heat load satisfaction through GA can be seen in Figure 7. It can be observed that the daily cost obtained by the proposed heuristic algorithm is 3.42 €, which is less than the one obtained with the GA 5.28 €. The heuristics performance is also more appealing than the performance of the GA algorithm, in terms of execution time, as it will be showed later in Section 6.5.

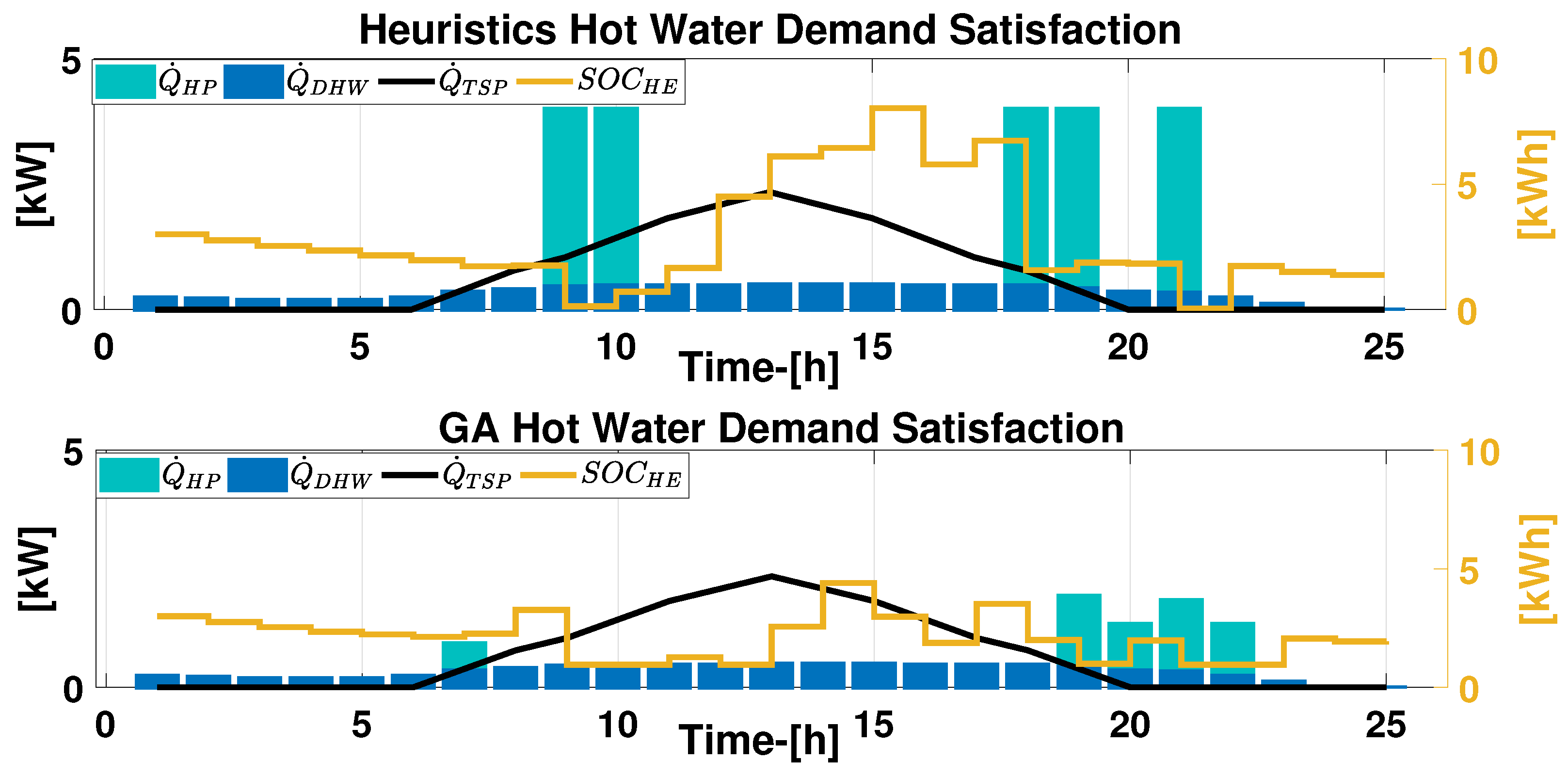
6.3.2. Hot Water Demand Satisfaction

Figure 8 shows the proposed heuristics and the GA for a hot water demand satisfaction simulation of the residential facility. It can be observed that the hot water demand is present for all 24 h of the day, while the available thermal power from solar thermal panel, as given in Figure 6, is only available between the hours 7–19. In that case, for the first 6 h, the hot water demand is met with the heat exchanger storage, as shown in Figure 8. It can be observed that the thermal energy level in the heat exchanger is at the minimum level between hours 9–10, 18–19, and 21 in the proposed heuristics simulations, while, for the GA, it is at the minimum between the hours 7, and 19–22. Therefore, the controller depending on the battery state of charge $\left({\mathrm{SOC}}_{\mathrm{ESS}}\right)$ switches the HP to ON for delivering mismatched thermal power. In conclusion, Figure 8 shows that, for all 24 h, the available thermal energy from the renewable resources, HE storage, and from HP is always greater than the requested demand. Thus, no CHP operations are seen towards hot water demand satisfaction.

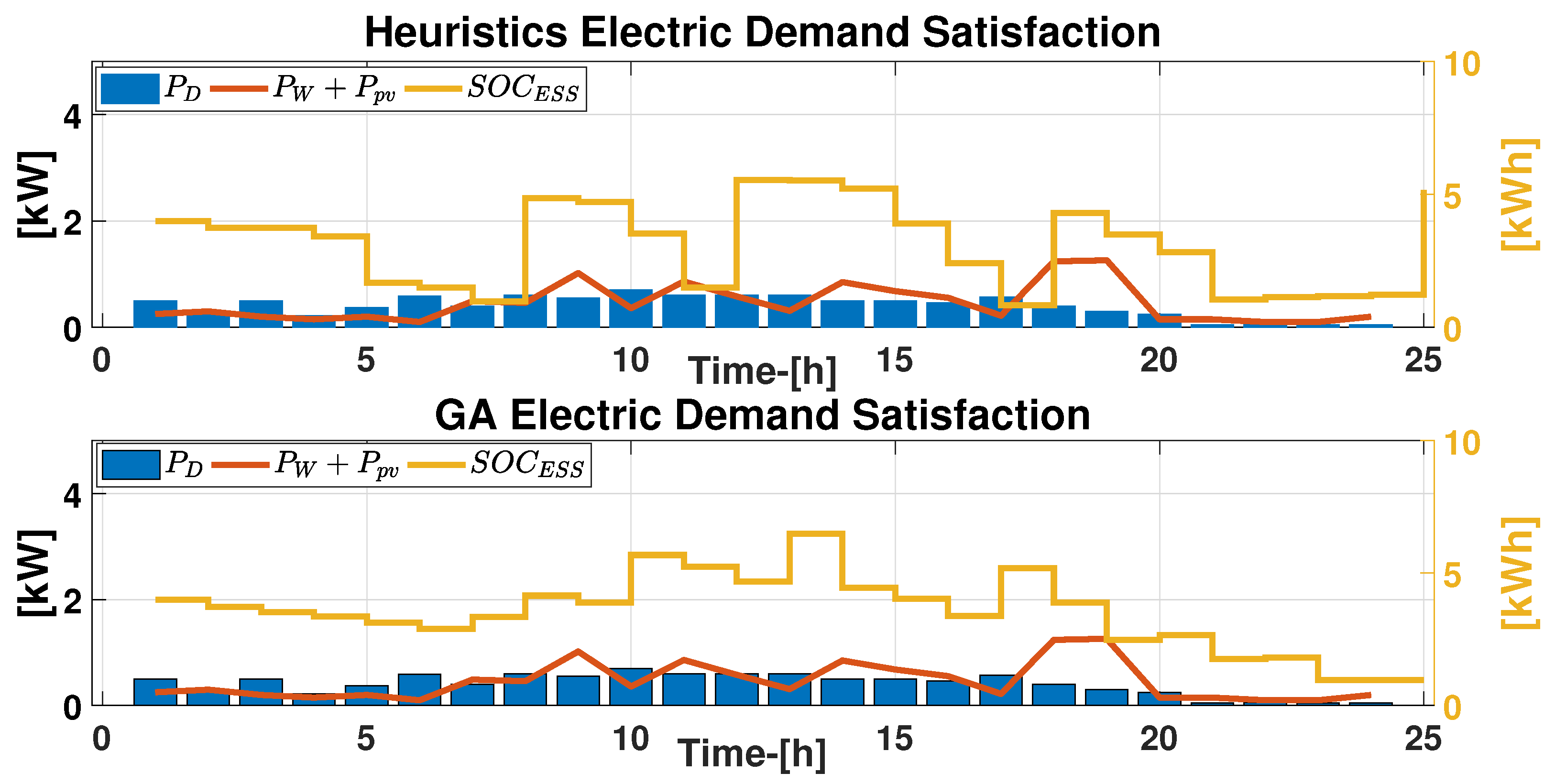
6.3.3. Electric Demand Satisfaction

To examine the effectiveness of the proposed heuristic algorithm for the electrical power demand satisfaction case, a 24 h electrical energy demand scenario has been considered. In Figure 9, it is possible to notice that, during the hours when solar or wind production is higher than the electric and thermal demands, both the heuristics and the GA controllers switch the batteries to charging state subject to the current level of ${\mathrm{SOC}}_{\mathrm{ESS}}$ (Figure 9). As per the goal of the system, the priority is given to the power demand satisfaction with the renewable energy sources or with the batteries or a combination of both. In case the power demand is still higher than the electrical energy available in the system, then the controller switches the CHP unit to ON in order to balance the power equation.

Figure 9 shows the ${\mathrm{SOC}}_{\mathrm{ESS}}$. The batteries supply power to the electrical demand when there is low or nearly zero renewable energy resources. Furthermore, as HP is operated by electricity, the batteries also supply power to the heat pump that contributes to heat and hot water demand satisfaction as shown in Figure 7, and Figure 8, respectively. The controller switches the batteries to discharging mode during the hours with frequent mismatch between solar or wind generation and electric load demand. We stress that the electric demand for both the heuristics and the GA is met only with the system available electric energy.

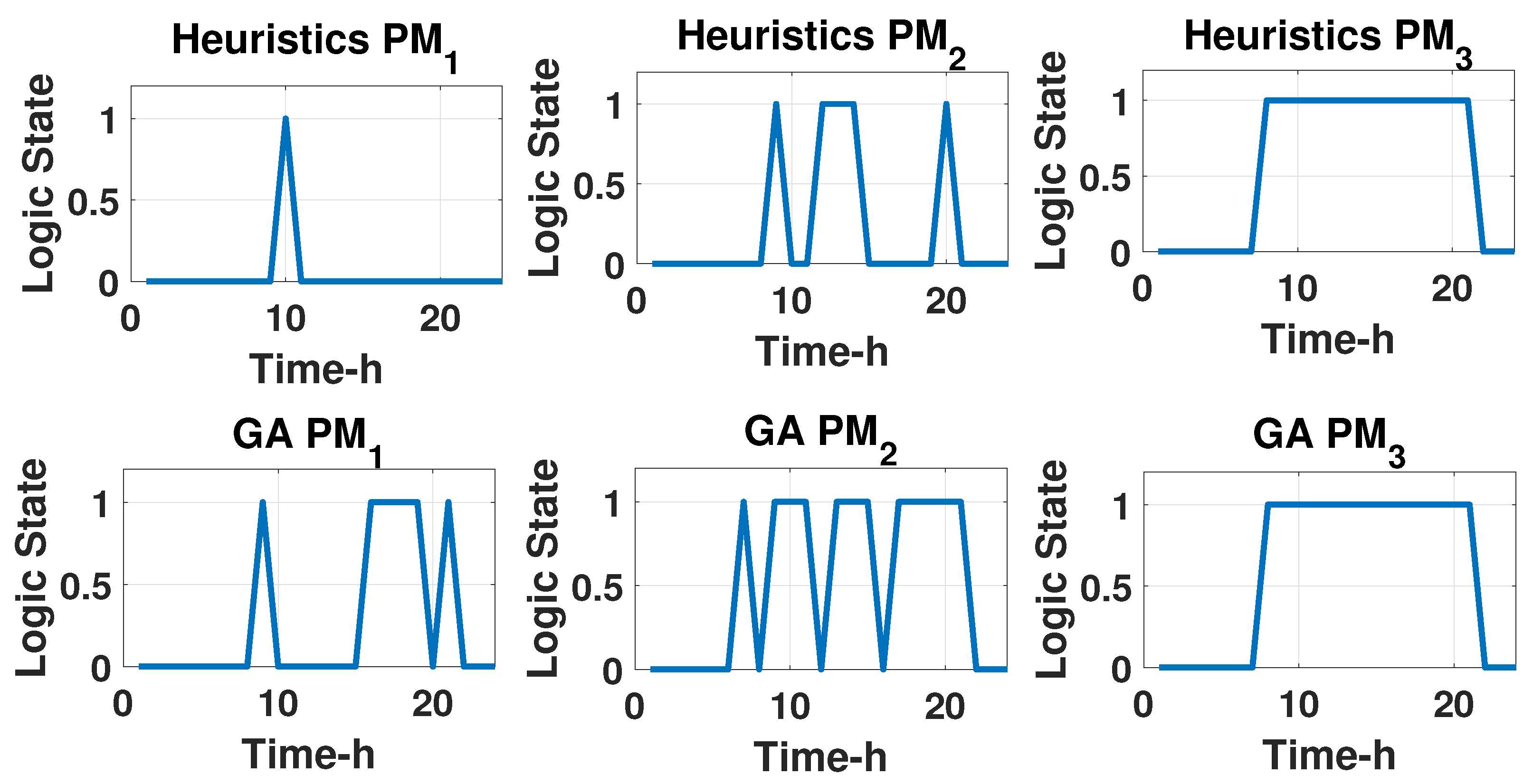
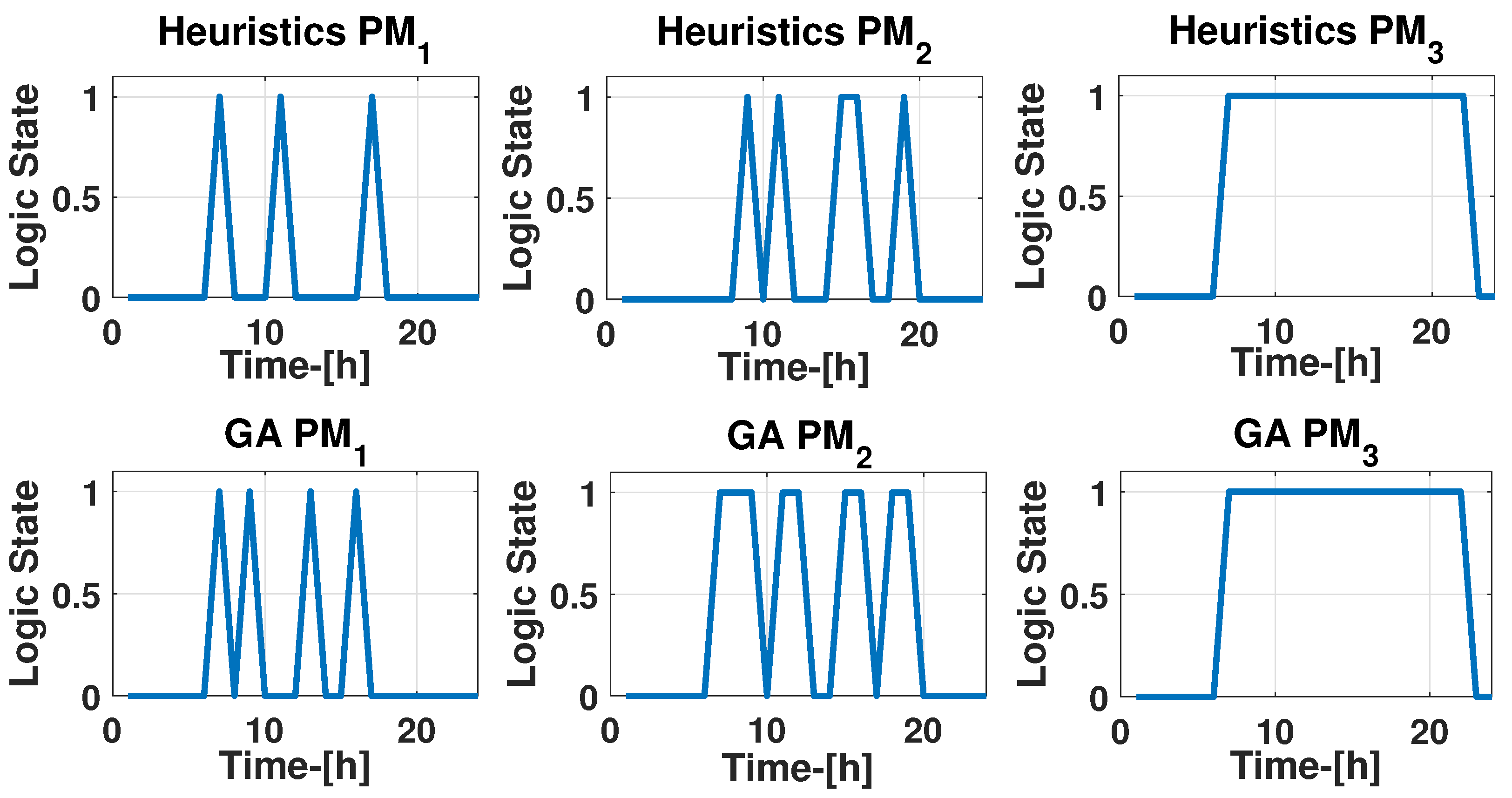
6.3.4. Water Pumps

Figure 10 shows the water pumps ${\mathrm{PM}}_1$, ${\mathrm{PM}}_2$, and ${\mathrm{PM}}_3$ switching states given by the heuristics and the GA algorithms. As shown in Figure 1, all three water pumps control the flow of hot water throughout the network. The water pump ${\mathrm{PM}}_1$ is placed between the exhaust of CHP and HE. The water pump ${\mathrm{PM}}_2$ is placed between HE and TES and is responsible for supplying hot water from HE to TES in case TES has storage scarcity. Similarly, the water pump ${\mathrm{PM}}_3$ operates only when there is a heat demand signal.

6.4. Example 2

In order to show the effectiveness of the proposed heuristics, a stressing plant scenario with limited availability of the renewable powers has been considered. In this scenario, the controller due to low renewable generations mostly relies on the energy available in the storage, or on the CHP unit that has to be switched ON in order to fulfill electric and thermal demands. The electric and thermal generation data from the renewable sources (WTs, PVs, TSP) considered are shown in Figure 11.

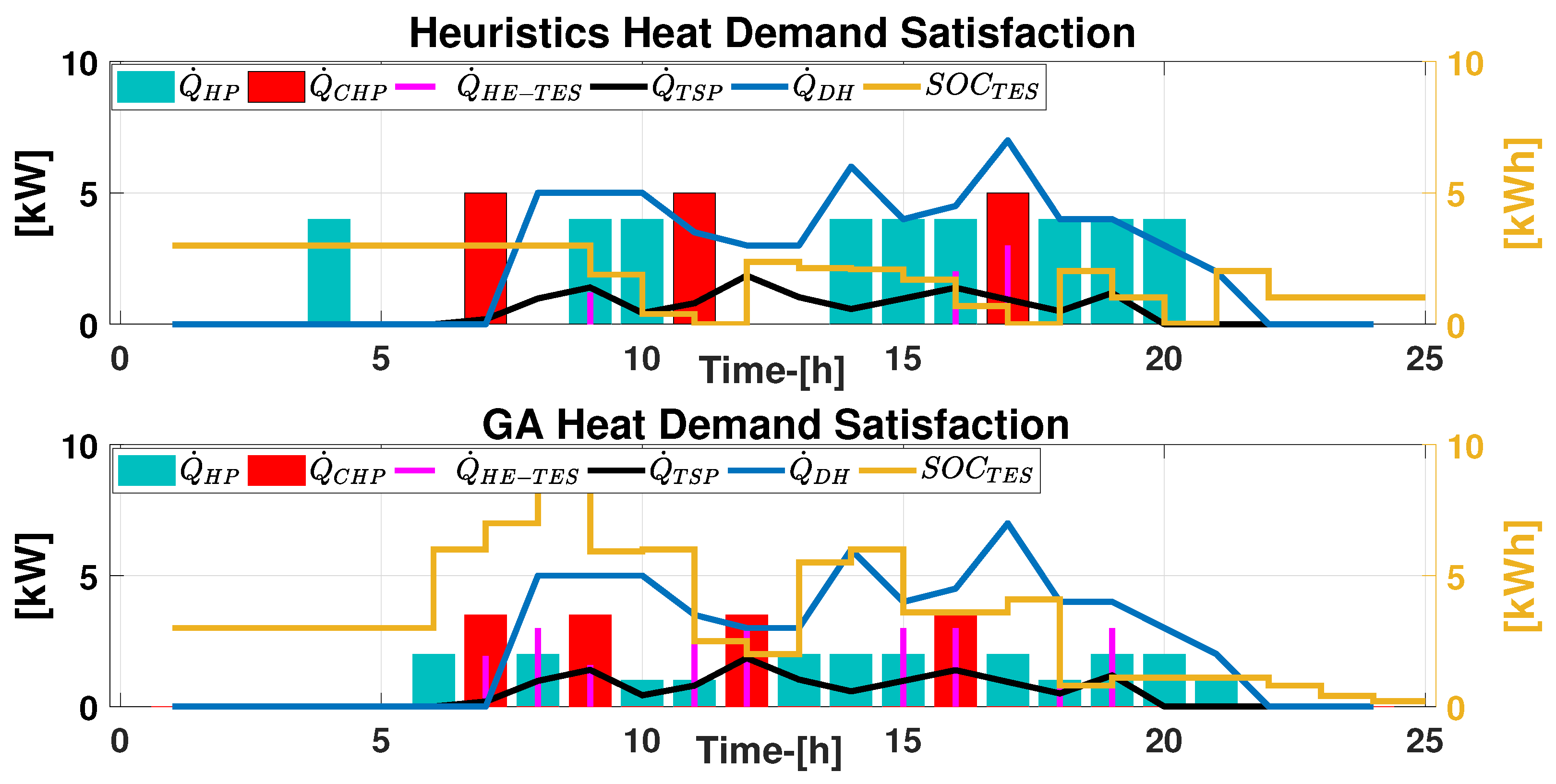
6.4.1. Heat Demand Satisfaction

For the stressing plant scenario, the analysis has been conducted through simulations for a day with less renewable availability. As explained above, the purpose is to supply both the electric and thermal loads appropriately via exploiting the renewable production, the electric and thermal storage capacity, and the CHP unit.

Figure 12 shows that both the heuristics and the GA supply the heat load correctly. Initially, the heuristic algorithm switches the HP ON because of the hot water demand (detailed later in the next section). In the following hours, if the system available thermal energy for heat demand satisfaction is below the heat load, the shortfall is made up by switching ON the CHP unit, as can be seen during the hours 7, 11 and 17. On the other hand, the GA turns ON the CHP unit during the hours 6, 9–13, and 15 for heat load satisfaction, as can be seen in the panel below of Figure 12. It is observable that the cost obtained by the proposed heuristic algorithm for a day with limited renewable sources is 10.16 €, which is a slightly higher than the one obtained for the same day with the GA 9.80 €. However, the performance of the heuristics in terms of execution time is more appealing than that of the GA, as will be showed later in Section 6.5.

6.4.2. Hot Water Demand Satisfaction

The residential hot water demand satisfaction through the heuristics and the GA is reported in Figure 13. The hot water demand spans all 24 h of the day, while the renewable sources are very limited. In order to supply the hot water load, during the first 3 h, both the control strategies exploited the heat exchanger storage ${\mathrm{SOC}}_{\mathrm{HE}}$. Any mismatch between the available system thermal energy and the hot water demand has been supplied by switching ON the ($\mathrm{HP}$) depending on the battery state-of-charge ${\mathrm{SOC}}_{\mathrm{ESS}}$. It is also possible to notice that the heuristics algorithm relies on the HP less than the GA, thus resulting in more utilization of the renewable sources and the thermal storage. In this way, the heuristic algorithm saves the battery ${\mathrm{SOC}}_{\mathrm{ESS}}$ for the future electric load, and at the same time avoids the conversion of the $\mathrm{HP}$ from electric to thermal, when possible. Figure 13 shows that the heuristics supplied the hot water demand by exploiting more the ${\mathrm{SOC}}_{\mathrm{HE}}$, and relied less on the $\mathrm{HP}$ operations. On the other hand, the GA frequently switched ON the $\mathrm{HP}$ in order to balance the mismatch between the ${\dot{\mathrm{Q}}}_{\mathrm{TSP}}$ and the hot water demand. The frequent HP switching in GA resulting in more ${\dot{\mathrm{Q}}}_{\mathrm{HE}-\mathrm{TES}}$ supply than the heuristics for the heat demand satisfaction. In conclusion, with the proper coordination of both the storage (${\mathrm{SOC}}_{\mathrm{HE}}$ and the ${\mathrm{SOC}}_{\mathrm{HE}}$), and with the use of HP, both the heuristics and the GA supplied hot water demand correctly.

6.4.3. Electric Demand Satisfaction

Figure 14 shows the electric demand satisfaction for both control strategies. In the scenario at hand, the renewable data and the reference power demand are such that both exceeding and missing power are considered, with a power flow towards or from the storage. In order to show the effectiveness of the implemented heuristics, the unit commitment has been shown for a case with frequent imbalances between the reference demand and the limited available renewable power over the 24 h simulation. In Figure 14, it is possible to notice that the renewable power available from the wind and the photo voltaic are mostly less than the requested load. Therefore, in order to supply the electric load, both the heuristics and the GA controllers switch the batteries to discharging state subject to certain constrains on the battery bank ${\mathrm{SOC}}_{\mathrm{ESS}}$, and no CHP unit working is observed.

6.4.4. Water Pumps

Similar to the previous example, Figure 15 shows the heuristics and the GA water pumps ${\mathrm{PM}}_1$, ${\mathrm{PM}}_2$, and ${\mathrm{PM}}_3$ switching states. In comparison to Figure 10, the frequent switching of water pump ${\mathrm{PM}}_1$ can be observed, as the absence of the renewable sources led the controllers to frequently operate the CHP unit in order to fulfill both the electric and the thermal demands.

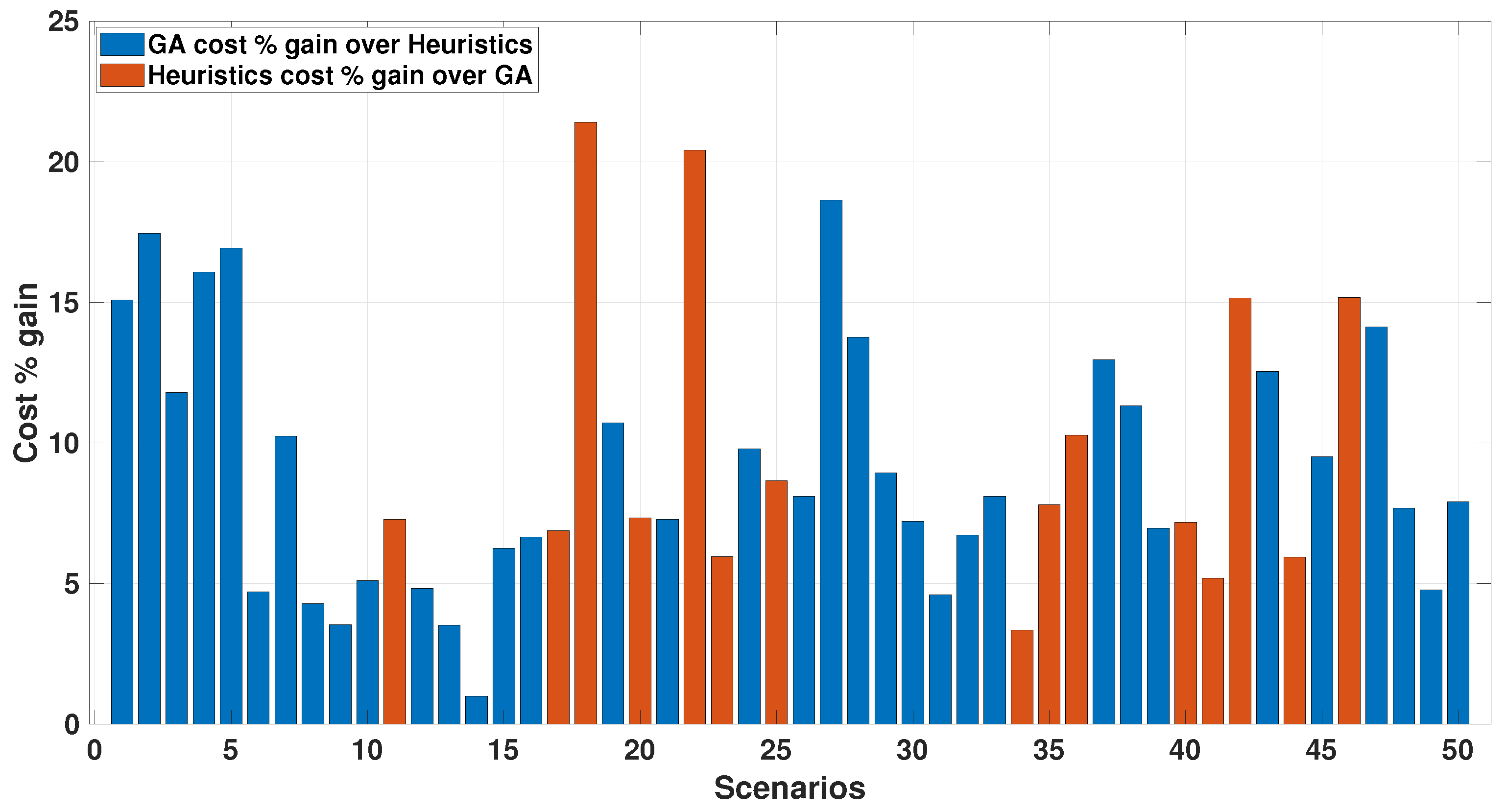
6.5. Algorithms Comparison

This subsection summarizes the performance of the proposed heuristic algorithm and those of the GA. Fifty test runs of the system under study have been conducted over a 24 h simulation period. As representative examples, two of them have been reported in the previous sections. The obtained results are summarized in

Table 4. Heuristics and GA test runs comparison. The CHP unit, the $\mathrm{HP}$, and the thermal storage operating ranges considered in the test runs are $5\left[\mathrm{k}\mathrm{W}\right]$, $4\left[\mathrm{k}\mathrm{W}\right]$, and $10\left[\mathrm{k}\mathrm{W}\mathrm{h}\right]$, respectively. The average cost and the CPU time of the heuristics over 50 test runs are 6.48 €, and 0.45 s, respectively, while the average cost and the CPU time for the GA are 5.97 €, and 127.15 s, respectively.

Table Frame No. 1
Algorithm	Values	Case 01	Case 02	Case 03	Case 04	Case 05	Case 06	Case 07
Heuristics	Cost Value €	3.38	3.78	5.42	3.42	4.78	7.22	3.22
	CPU Time (s)	0.42	0.40	0.50	0.41	0.43	0.44	0.39
GA	Cost Value €	2.87	3.12	4.78	2.87	3.98	6.87	2.89
	CPU Time (s)	123.12	120.72	120.1	123.15	123.75	122.45	121.05
Table Frame No. 2
Algorithm	Values	Case 08	Case 09	Case 10	Case 11	Case 12	Case 13	Case 14
Heuristics	Cost Value €	6.98	10.16	9.27	8.09	8.27	9.90	6.94
	CPU Time (s)	0.41	0.40	0.49	0.42	0.42	0.41	0.41
GA	Cost Value €	6.68	9.80	8.79	8.68	7.87	9.55	6.47
	CPU Time (s)	127.13	120.72	122.10	121.05	124.70	123.75	123.75
Table Frame No. 3
Algorithm	Values	Case 15	Case 16	Case 17	Case 18	Case 19	Case 20	Case 21
Heuristics	Cost Value €	7.16	6.16	6.97	3.13	4.85	4.77	5.48
	CPU Time (s)	0.42	0.41	0.50	0.41	0.44	0.41	0.38
GA	Cost Value €	7.18	5.75	7.45	3.80	4.33	5.12	5.08
	CPU Time (s)	124.02	120.27	119.51	122.65	120.75	121.95	123.75
Table Frame No. 4
Algorithm	Values	Case 22	Case 23	Case 24	Case 25	Case 26	Case 27	Case 28
Heuristics	Cost Value €	3.38	6.378	5.41	6.23	5.42	3.97	4.43
	CPU Time (s)	0.38	0.49	0.50	0.44	0.43	0.40	0.41
GA	Cost Value €	4.07	6.75	4.88	6.77	4.98	3.23	3.82
	CPU Time (s)	112.12	121.52	119.01	129.55	118.47	125.95	121.05
Table Frame No. 5
Algorithm	Values	Case 29	Case 30	Case 31	Case 32	Case 33	Case 34	Case 35
Heuristics	Cost Value €	4.01	9.43	7.16	5.27	5.42	4.78	4.87
	CPU Time (s)	0.37	0.44	0.45	0.49	0.39	0.44	0.44
GA	Cost Value €	4.18	8.75	6.83	5.83	4.98	4.93	5.25
	CPU Time (s)	130.12	121.92	116.10	114.50	121.05	123.45	126.32
Table Frame No. 6
Algorithm	Values	Case 36	Case 37	Case 38	Case 39	Case 40	Case 41	Case 42
Heuristics	Cost Value €	3.11	4.47	4.77	5.43	5.22	6.15	3.97
	CPU Time (s)	0.41	0.40	0.40	0.49	0.53	0.40	0.42
GA	Cost Value €	3.43	4.07	4.23	5.05	4.87	6.47	3.43
	CPU Time (s)	121.21	120.27	125.10	121.57	123.50	119.73	120.67
Table Frame No. 7
Algorithm	Values	Case 43	Case 44	Case 45	Case 46	Case 47	Case 48	Case 49
Heuristics	Cost Value €	6.77	8.39	6.77	5.93	8.08	7.54	5.43
	CPU Time (s)	0.46	0.46	0.50	0.49	0.42	0.49	0.42
GA	Cost Value €	5.92	8.89	6.15	6.83	6.93	6.96	5.17
	CPU Time (s)	113.42	118.20	119.56	123.59	121.67	120.50	121.95

. In all the considered scenarios, both the heuristic and the meta-heuristic GA meet the electric and thermal demands of the residential facility. The heuristics and the GA cost per scenario is reported in Figure 16. Furthermore, the cost percentage gain of both approaches with respect to each other has also been reported in Figure 17. From Table 4, it is observable that the proposed heuristics in comparison with the optimally designed GA, competed reasonably well in terms of fuel costs minimization, despite the fact it uses a very simplified system model compared to the GA. Furthermore, the simulation time of the proposed algorithm in all fifty scenarios is almost 300 times faster than the execution time taken by the GA. Hence, the proposed heuristic algorithm is deployable both on standard and low-performance hardware, contrary to a standard meta-heuristics strategy which cannot run on low-performance hardware.

7. Conclusions

This paper proposes a fast heuristic approach for solving the CHP-ED problem considering that the presence of multiple energy vectors through a novel was the computational efficient model of the system. The proposed heuristics were compared with Genetic Algorithm (GA), a meta-heuristic approach. The results show that the heuristic approach implies higher costs with respect to the GA; however, with the major benefit of being computationally simpler and faster so as to be run also on low-cost, low-performance platforms. Implementing the heuristics on an embedded hardware and studying implementation aspects are future paths for this investigation as well as the handling of renewable generation and load forecasts, to some extent, and the optimal tuning of the thresholds for improved performances.