Multi-Electrode Architecture Modeling and Optimization for Homogeneous Electroporation of Large Volumes of Tissue
Abstract
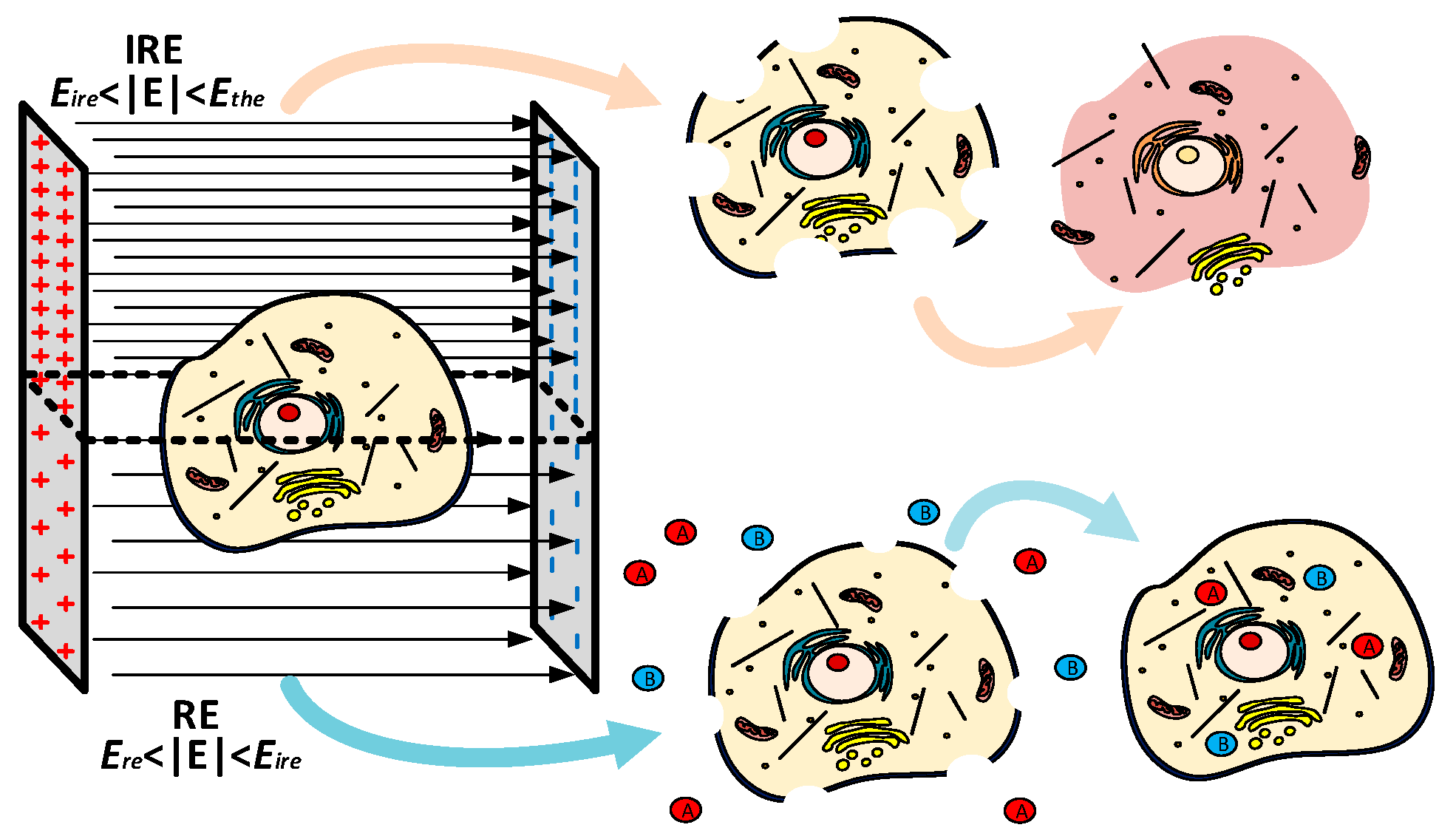
:1. Introduction
- −
- −
- −
- Electroporation is compatible with many of the current treatments, such as radiotherapy and chemotherapy, being an effective adjuvant mechanism [6].
2. Materials and Methods
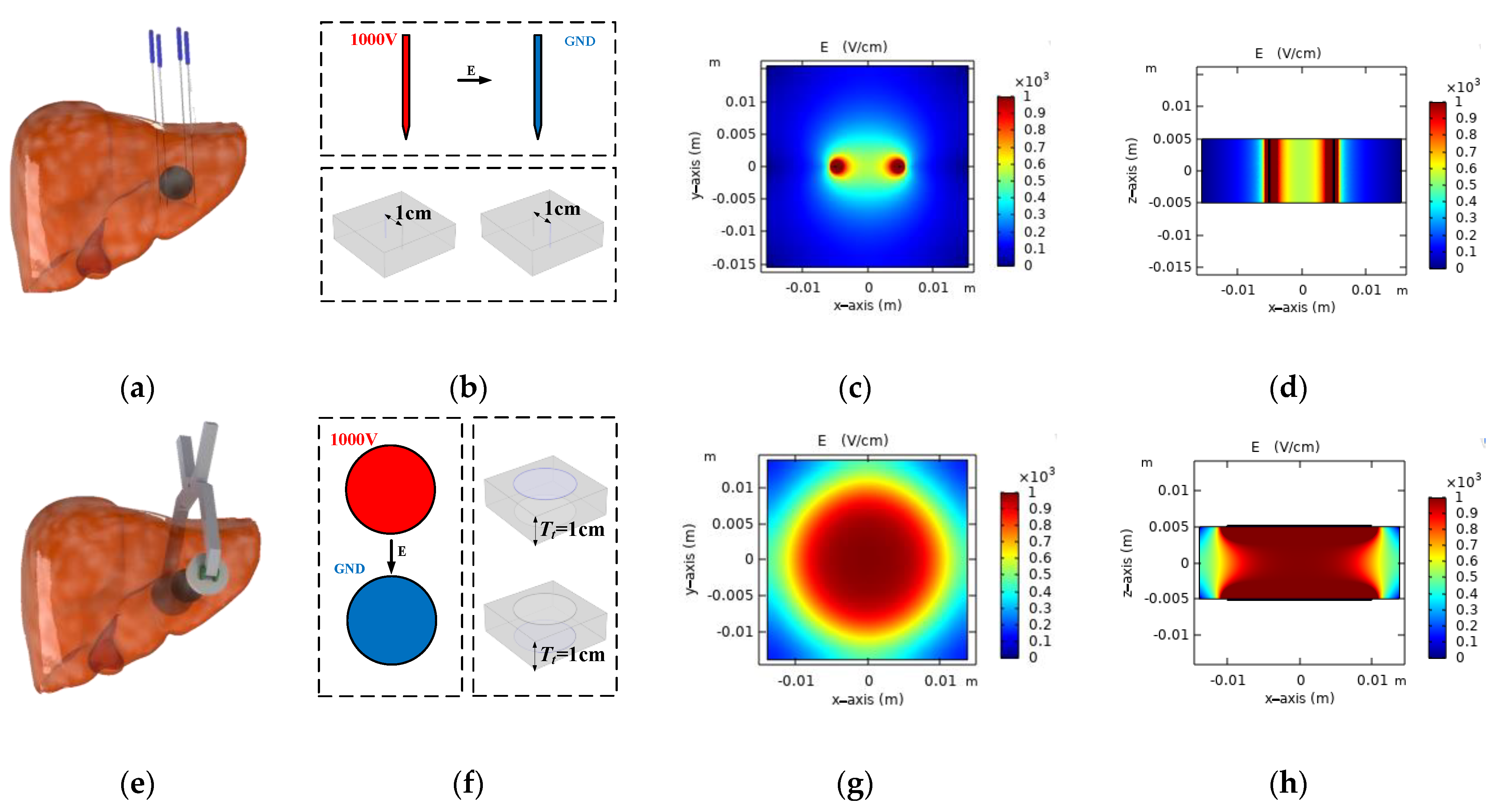
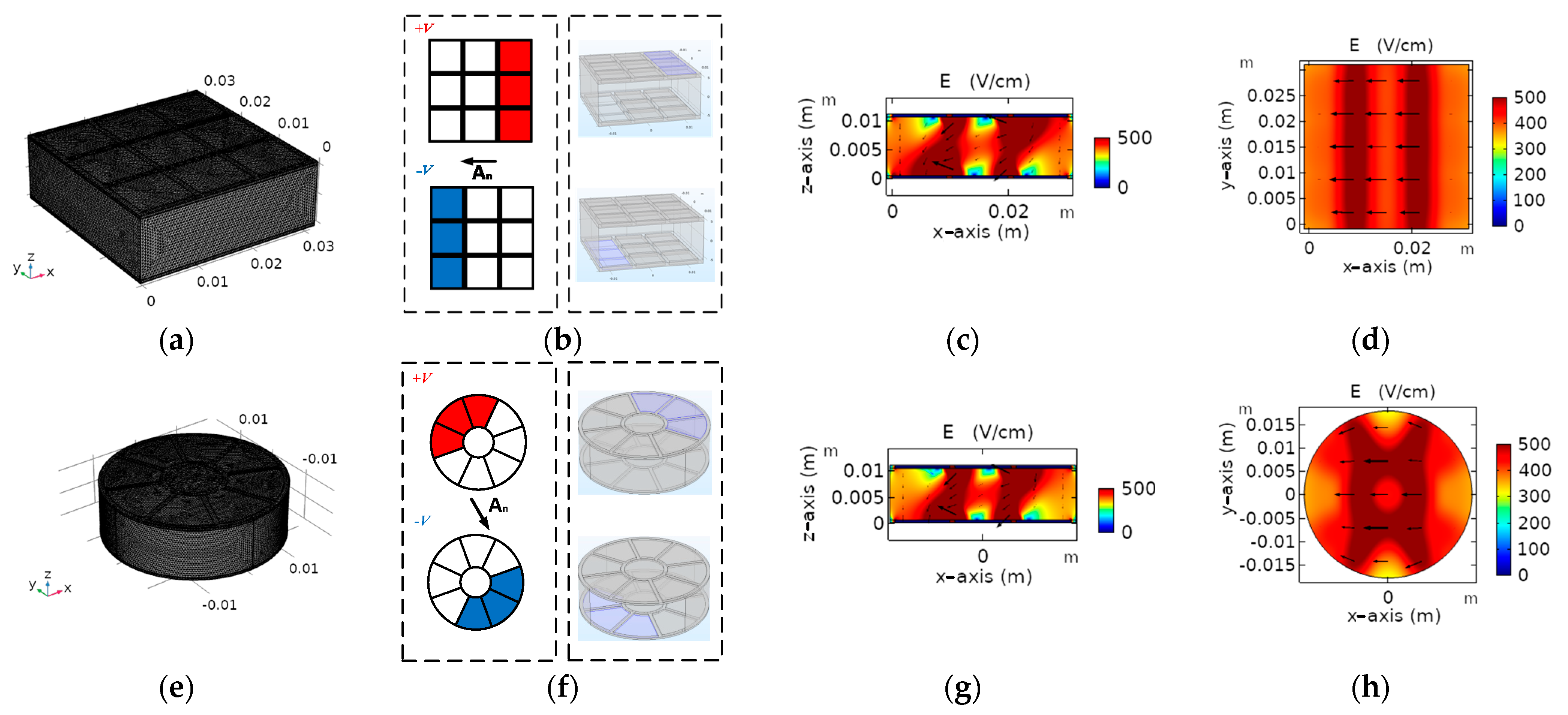
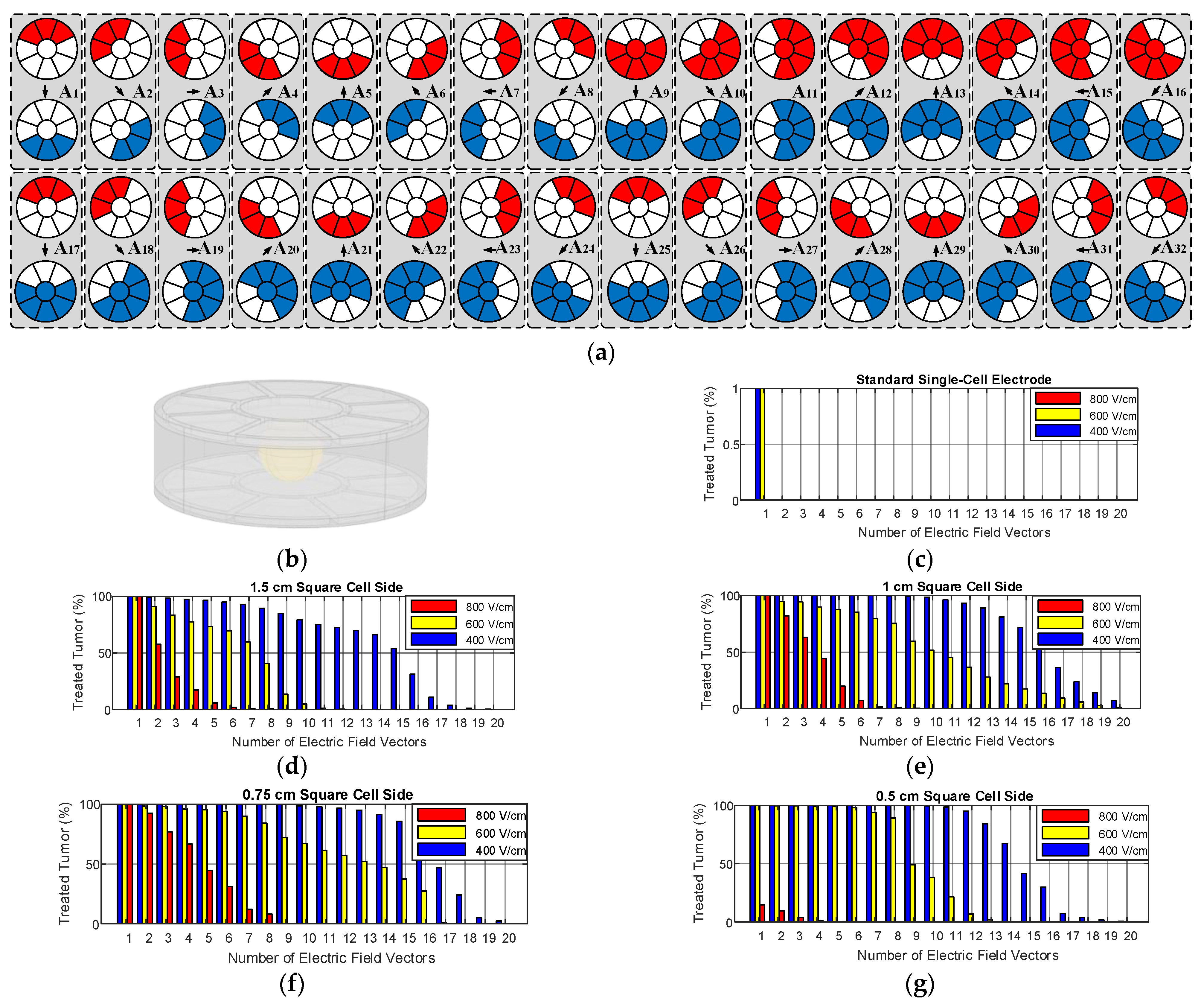
2.1. Proposed Multi-Electrode Architecture
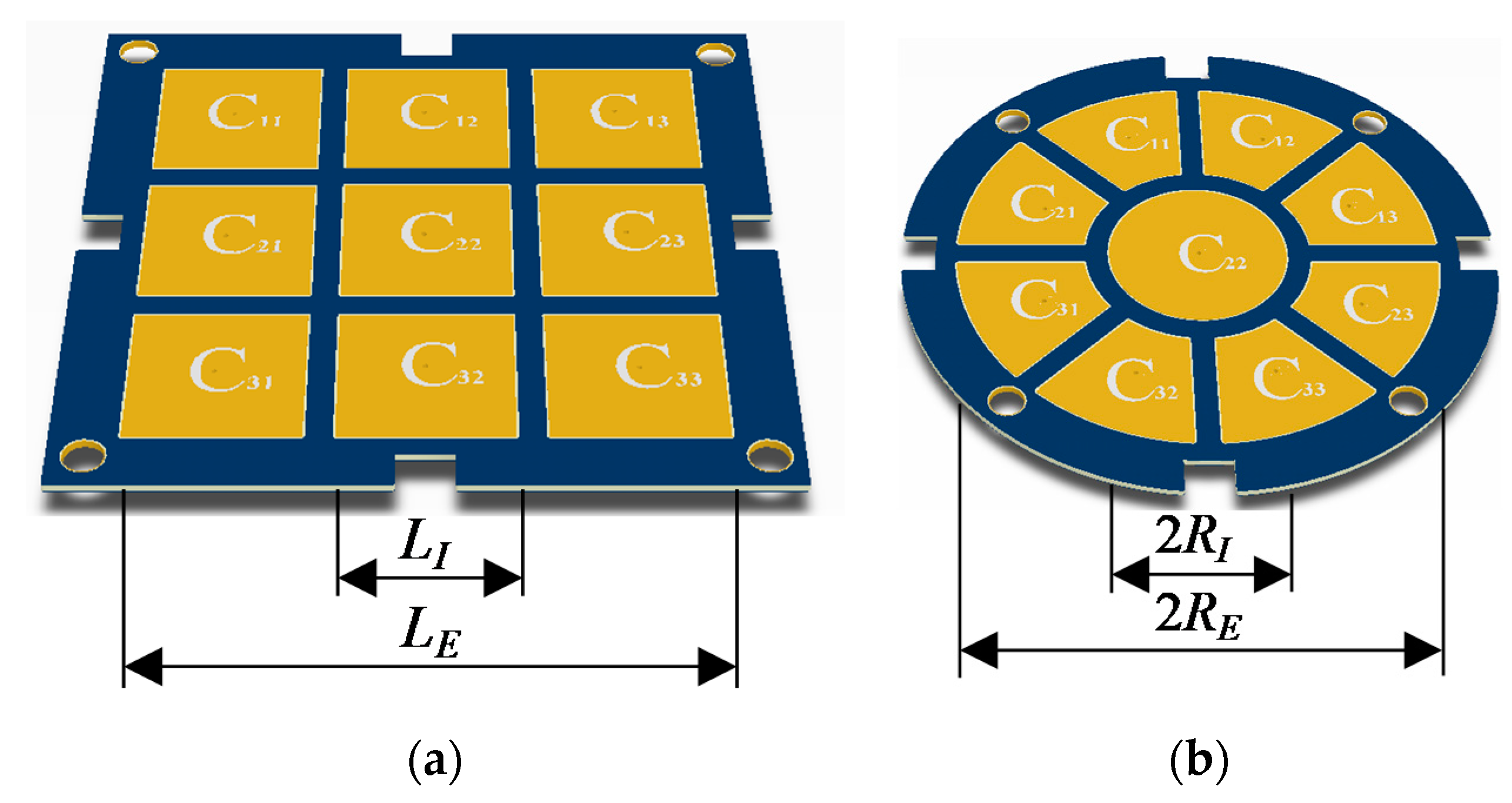
2.1.1. Proposed Multi-Electrode Geometries
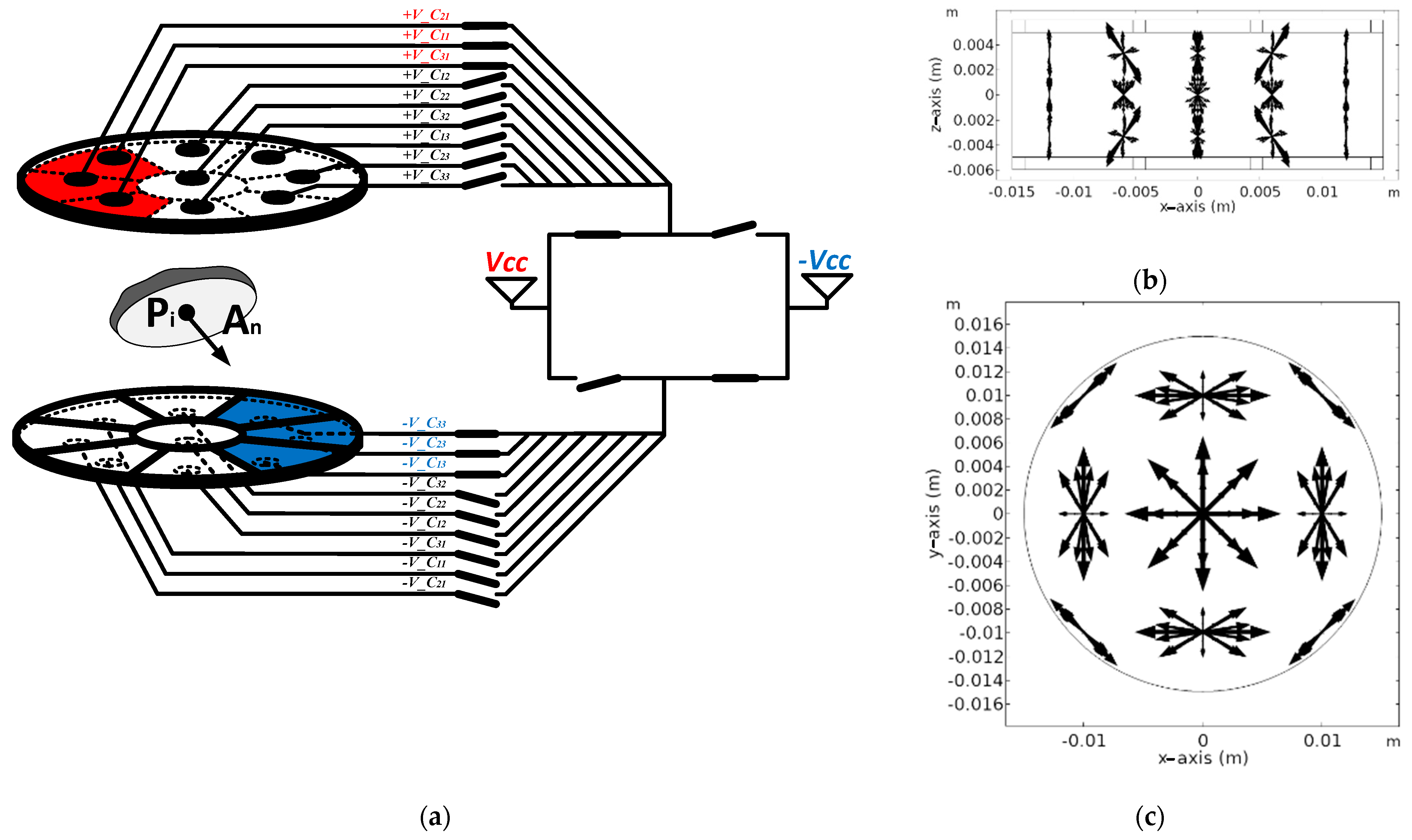
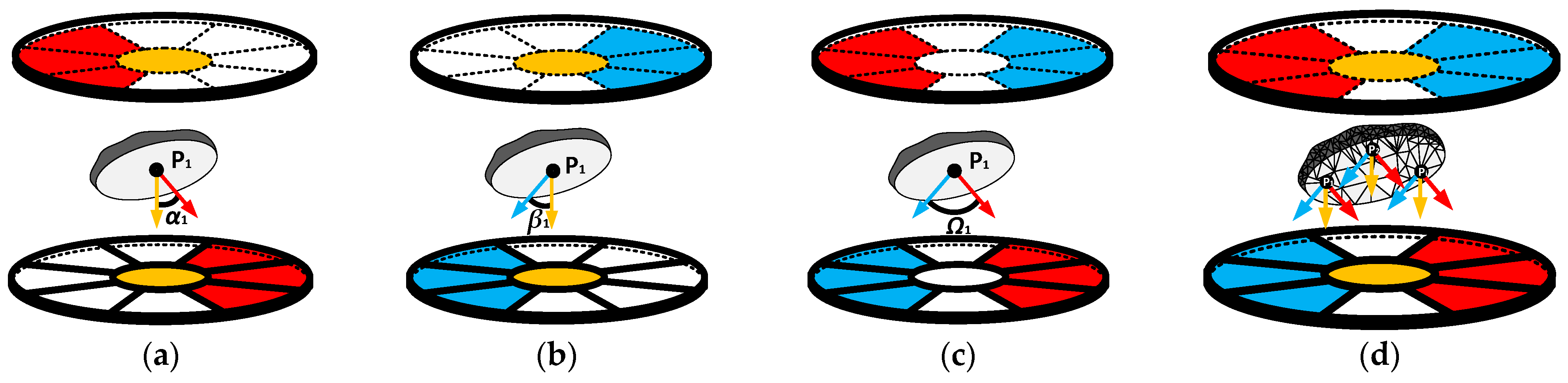
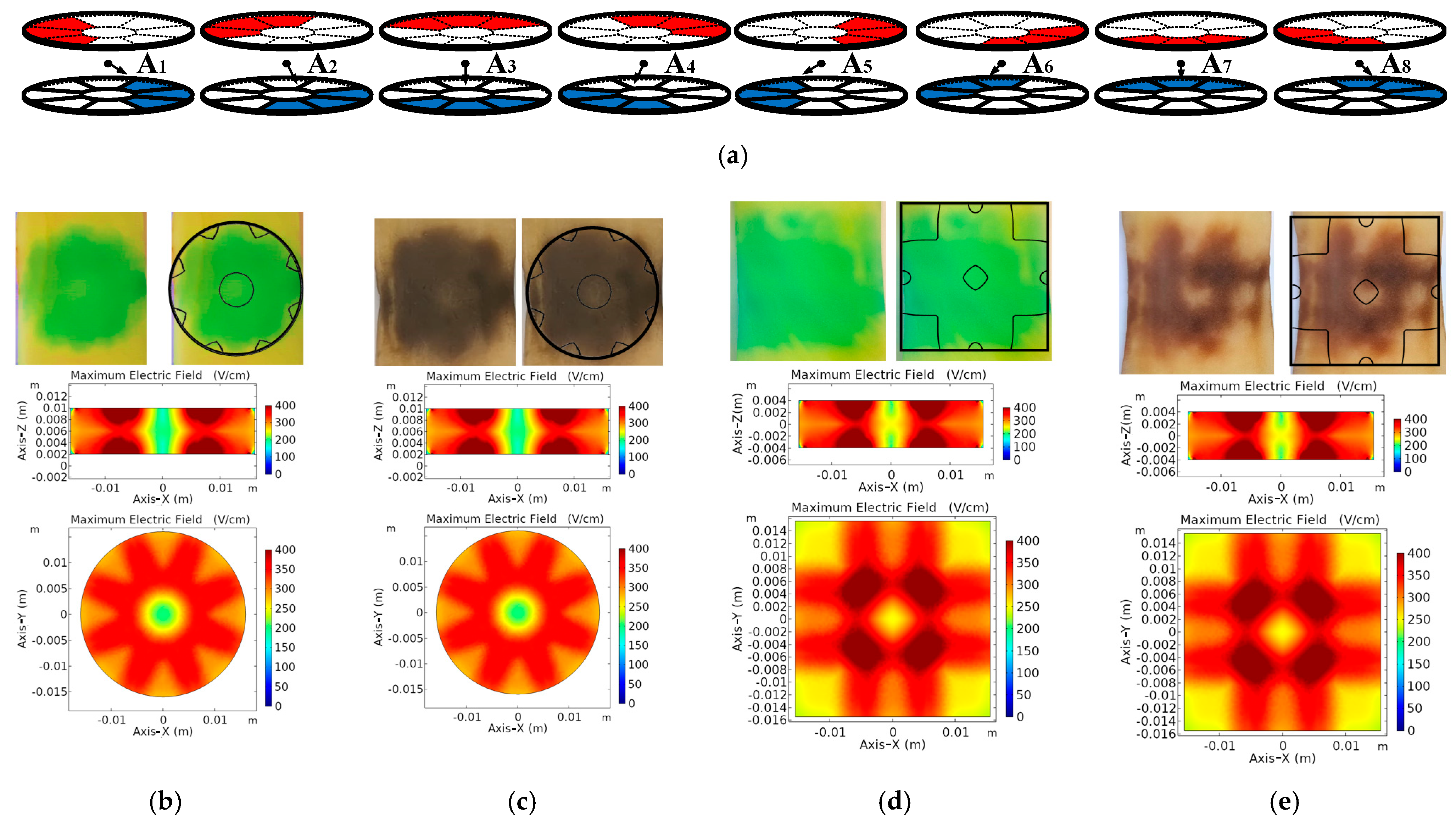
2.1.2. Operation of Proposed Multi-Electrode
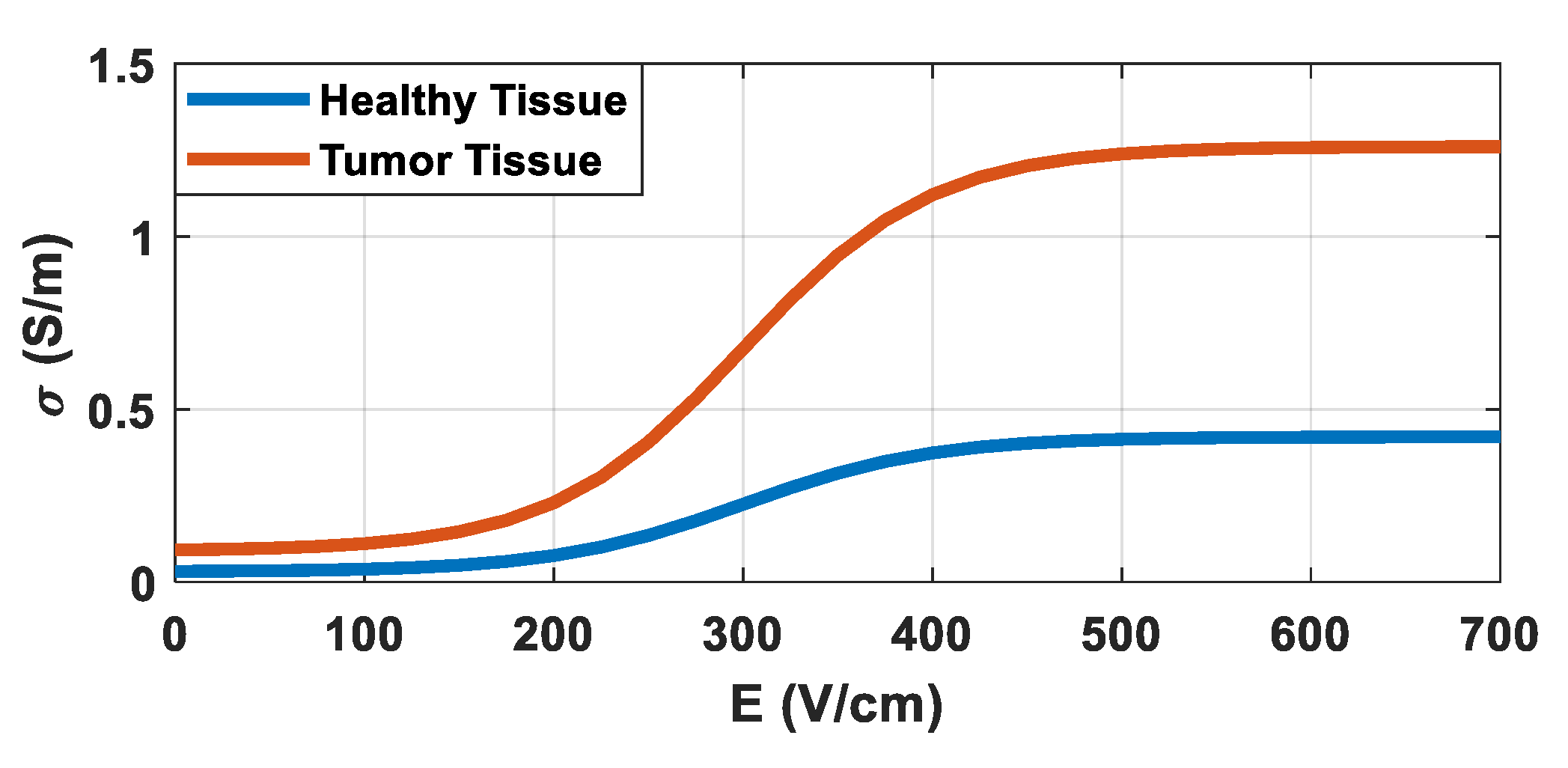
2.2. MPPE Modeling and Evaluation
2.2.1. MPPE Model
2.2.2. Evaluation of Independent Electric Field Vectors
3. Experimental and Simulation Results and Discussion
- High voltage generator. This test-bench subset consists of high voltage monitoring/acquiring: an 8-bit LeCroy oscilloscope Wavesurfer 3024, three differential high-voltage probes LeCroy HVD3206, and one Pearson current monitor model 110.
- Electroporation ad hoc multioutput generator, which has been designed to be able to power eighteen outputs and to provide online impedance measurements [27]. The proposed generator is based on a multiple-output structure featuring IGBT (1700-V 100-A 3-phase IGBT power module FS100R17N3E4) an MOSFET (40-V NVMTS0D4N04CTXG MOSFETs) devices [31]. This implementation allows high-performance omnidirectional electroporation treatments.
- Experimentation area, where the potato specimens are carved and placed.
3.1. Electric Field Distribution
3.2. Size and Geometry Optimization
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Junquera, M.C.; Castiella, T.; Gracia-Llanes, J.; López-Alonso, B.; Hernáez, A.; García-Hernández, L.; Güemes, A.; Mejía, E.; Iruzubieta, P.; Naval, A.; et al. Electron microscope evaluation of irreversible electroporation on the liver in a porcine model. Histol. Histopathol. 2017, 32, 125. [Google Scholar]
- Weaver, J.C. Electroporation of cells and tissues. IEEE Trans. Plasma Sci. 2000, 28, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Alonso, B.; Hernaez, A.; Sarnago, H.; Naval, A.; Guemes, A.; Junquera, C.; Burdio, J.M.; Castiella, T.; Monleon, E.; Gracia-Llanes, J.; et al. Histopathological and Ultrastructural Changes after Electroporation in Pig Liver Using Parallel-Plate Electrodes and High-Performance Generator. Sci. Rep. 2019, 9, 12. [Google Scholar] [CrossRef] [PubMed]
- Monleón, E.; Castiella, T.; Mejía, E.; Gracia-Llanes, J.; Iruzubieta, P.; Junquera, M.C.; Hernáez, A.; Güemes, A.; López-Alonso, B.; Sarnago, H.; et al. Remodelling of liver tissue after irreversible electroporation in porcine. Histol. Histopathol. 2019, 34, 132. [Google Scholar]
- Iruzubieta, P.; Gracia-Llanes, J.; Meleón, E.; Mejía, E.; Castiella, T.; Hernáez, A.; Güemes, A.; López-Alonso, B.; Sarnago, H.; Lucía, O.; et al. Ultrastructural study of pig liver regeneration following ablation with irreversible electroporation. Histol. Histopathol. 2019, 34, 131. [Google Scholar]
- Geboers, B.; Scheffer, H.J.; Graybill, P.M.; Ruarus, A.H.; Nieuwenhuizen, S.; Puijk, R.S.; Tol, P.M.; Davalos, R.V.; Rubinsky, B.; Gruijl, T.D.; et al. High-Voltage Electrical Pulses in Oncology: Irreversible Electroporation, Electrochemotherapy, Gene Electrotransfer, Electrofusion, and Electroimmunotherapy. Radiology 2020, 295, 254–272. [Google Scholar] [CrossRef]
- Yarmush, M.L.; Golberg, A.; Sersa, G.; Kotnik, T.; Miklavcic, D. Electroporation-Based Technologies for Medicine: Principles, Applications, and Challenges. In Annual Review of Biomedical Engineering; Annual Reviews; Yarmush, M.L., Ed.; Palo Alto: Santa Clara, CA, USA, 2014; Volume 16, pp. 295–320. [Google Scholar]
- O’Brien, T.; Passeri, M.; Lorenzo, M.; Sulzer, J.; Lyman, W.; Swet, J.; Vrochides, D.; Baker, E.; Iannitti, D.; Davalos, R.; et al. Experimental High-Frequency Irreversible Electroporation Using a Single-Needle Delivery Approach for Nonthermal Pancreatic Ablation In Vivo. J. Vasc. Interv. Radiol. 2019, 30, 854–862.e7. [Google Scholar] [CrossRef]
- Zhang, Y.; Lyu, C.; Liu, Y.; Lv, Y.; Chang, T.T.; Rubinsky, B. Molecular and histological study on the effects of non-thermal irreversible electroporation on the liver. Biochem. Biophys. Res. Commun. 2018, 500, 665–670. [Google Scholar] [CrossRef] [PubMed]
- Mathy, R.M.; Tinoush, P.; da Florencia, R.D.; Braun, A.; Ghamarnejad, O.; Radeleff, B.; Kauczor, H.-U.; Chang, D.-H. Impact of needle positioning on ablation success of irreversible electroporation: A unicentric retrospective analysis. Sci. Rep. 2020, 10, 21902. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Zhao, D.; Li, J.; Du, L.; Wei, Z.; Liang, Z.; Li, Z. In A minimally invasive in vivo electroporation method utilizing flexile electrode and microneedle roller. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung City, Taiwan, 18–22 June 2017; pp. 1684–1687. [Google Scholar]
- Neal, R.E., 2nd; Singh, R.; Hatcher, H.C.; Kock, N.D.; Torti, S.V.; Davalos, R.V. Treatment of breast cancer through the application of irreversible electroporation using a novel minimally invasive single needle electrode. Breast Cancer Res. Treat. 2010, 123, 295–301. [Google Scholar] [CrossRef] [Green Version]
- Berkenbrock, J.A.; Machado, R.G.; Suzuki, D.O.H. Electrochemotherapy Effectiveness Loss due to Electric Field Indentation between Needle Electrodes: A Numerical Study. J. Healthc. Eng. 2018, 2018, 6024635. [Google Scholar] [CrossRef]
- Davalos, R.V.; Garcia, P.A.; Edd, J.F. Thermal Aspects of Irreversible Electroporation. In Irreversible Electroporation; Rubinsky, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 123–154. [Google Scholar]
- Biasiolo, L.; Bariani, P.; Marchi, N.; Dughiero, F.; Sieni, E.; Campana, L. An Electrode for the Treatment of Large Surfaces in ECT. In Proceedings of the IECON 2018 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 3319–3323. [Google Scholar]
- Hansen, H.; Bourke, M.; Stigaard, T.; Clover, A.; Buckley, M.; O’Riordain, M.; Winter, D.; Johannesen, H.; Hansen, R.; Heebøll, H.; et al. Electrochemotherapy for colorectal cancer using endoscopic electroporation: A phase 1 clinical study. Endosc. Int. Open 2020, 8, E124–E132. [Google Scholar]
- Rombouts, S.J.E.; van Dijck, W.P.M.; Nijkamp, M.W.; Derksen, T.C.; Brosens, L.A.A.; Hoogwater, F.J.H.; van Leeuwen, M.S.; Borel Rinkes, I.H.M.; van Hillegersberg, R.; Wittkampf, F.H.; et al. Clinical and pathological outcomes after irreversible electroporation of the pancreas using two parallel plate electrodes: A porcine model. Hpb Off. J. Int. Hepato Pancreato Biliary Assoc. 2017, 19, 1058–1065. [Google Scholar] [CrossRef] [Green Version]
- Panella, C.; Castellvi, Q.; Moll, X.; Quesada, R.; Villanueva, A.; Iglesias, M.; Naranjo, D.; Sanchez-Velazquez, P.; Andaluz, A.; Grande, L.; et al. Focused transhepatic electroporation mediated by hypersaline infusion through the portal vein in rat model. Preliminary results on differential conductivity. Radiol. Oncol. 2017, 51, 415–421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Denzi, A.; Strigari, L.; Di Filippo, F.; Botti, C.; Di Filippo, S.; Perracchio, L.; Ronchetti, M.; Cadossi, R.; Liberti, M. Modeling the positioning of single needle electrodes for the treatment of breast cancer in a clinical case. Biomed. Eng. Online 2015, 14, S1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cvetkoska, A.; Pirc, E.; Rebersek, M.; Magjarevic, R.; Miklavcic, D. Towards standardization of electroporation devices and protocols. IEEE Instrum. Meas. Mag. 2020, 23, 74–81. [Google Scholar] [CrossRef]
- Bernardis, A.; Bullo, M.; Campana, L.G.; Barba, P.D.; Dughiero, F.; Forzan, M.; Mognaschi, M.E.; Sgarbossa, P.; Sieni, E. Electric field computation and measurements in the electroporation of inhomogeneous samples %. J. Open Phys. 2017, 15, 790–796. [Google Scholar] [CrossRef]
- Pavliha, D.; Kos, B.; Marcan, M.; Zupanic, A.; Sersa, G.; Miklavcic, D. Planning of Electroporation-Based Treatments Using Web-Based Treatment-Planning Software. J. Membr. Biol. 2013, 246, 833–842. [Google Scholar] [CrossRef] [Green Version]
- Campana, L.G.; Bullo, M.; Di Barba, P.; Dughiero, F.; Forzan, M.; Mognaschi, M.E.; Sgarbossa, P.; Tosi, A.L.; Bernardis, A.; Sieni, E. Effect of Tissue Inhomogeneity in Soft Tissue Sarcomas: From Real Cases to Numerical and Experimental Models. Technol. Cancer Res. Treat. 2018, 17, 1533033818789693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castiello, M.; Dughiero, F.; Scandola, F.; Sieni, E.; Campana, L.; Rossi, C.; Mattei, M.; Pellati, A.; Ongaro, A. A New Grid Electrode for Electrochemotherapy Treatment of Large Skin Tumors. Dielectr. Electr. Insul. IEEE Trans. 2014, 21, 1424–1432. [Google Scholar] [CrossRef]
- Ongaro, A.; Campana, L.; Mattei, M.; Dughiero, F.; Forzan, M.; Pellati, A.; Rossi, C.; Sieni, E. Evaluation of the Electroporation Efficiency of a Grid Electrode for Electrochemotherapy: From Numerical Model to In Vitro Tests. Technol. Cancer Res. Treat. 2015, 15, 296–307. [Google Scholar] [CrossRef]
- López-Alonso, B.; Sarnago, H.; Burdío, J.M.; Lucía, Ó. In Multi-Electrode Architecture Analysis and Modeling for Cancer Treatment using Electroporation. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 718–723. [Google Scholar]
- López-Alonso, B.; Sarnago, H.; Lucía, O.; Briz, P.; Burdío, J.M. Real-Time Impedance Monitoring During Electroporation Processes in Vegetal Tissue Using a High-Performance Generator. Sensors 2020, 20, 3158. [Google Scholar] [CrossRef] [PubMed]
- López-Alonso, B.; Sarnago, H.; Burdío, J.M.; Lucía, O. Electro-thermal modeling of irreversible electroporation and validation method of electric field distribution. Int. J. Appl. Electromagn. Mech. 2020, 63, 41–50. [Google Scholar] [CrossRef]
- Corovic, S.; Lackovic, I.; Sustaric, P.; Sustar, T.; Rodic, T.; Miklavcic, D. Modeling of electric field distribution in tissues during electroporation. Biomed. Eng. Online 2013, 12, 16. [Google Scholar] [CrossRef] [Green Version]
- Breton, M.; Buret, F.; Krähenbühl, L.; Leguèbe, M.; Mir, L.; Perrussel, R.; Poignard, C.; Scorretti, R.; Voyer, D. Non-Linear Steady-State Electrical Current Modeling for the Electropermeabilization of Biological Tissue. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [Green Version]
- López-Alonso, B.; Sarnago, H.; Lucía, O.; Burdío, J.M. In Multiple-Output Generator for Omnidirectional Electroporation and Real-Time Process Monitoring. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC21), Phenix, AZ, USA, 9–12 June 2021. [Google Scholar]
- Castellví, Q.; Banús, J.; Ivorra, A. 3D Assessment of Irreversible Electroporation Treatments in Vegetal Models. In 1st World Congress on Electroporation and Pulsed Electric Fields in Biology, Medicine and Food & Environmental Technologies; Jarm, T., Kramar, P., Eds.; Springer: Singapore, 2016; pp. 294–297. [Google Scholar]
- Valic, B.; Golzio, M.; Pavlin, M.; Schatz, A.; Faurie, C.; Gabriel, B.; Teissié, J.; Rols, M.P.; Miklavcic, D. Effect of electric field induced transmembrane potential on spheroidal cells: Theory and experiment. Eur. Biophys. J. 2003, 32, 519–528. [Google Scholar] [CrossRef]
- Reberšek, M.; Faurie, C.; Kandušer, M.; Čorović, S.; Teissié, J.; Rols, M.-P.; Miklavčič, D. Electroporator with automatic change of electric field direction improves gene electrotransfer in-vitro. Biomed. Eng. Online 2007, 6, 25. [Google Scholar] [CrossRef] [Green Version]
- Čorović, S.; Županič, A.; Kranjc, S.; Al Sakere, B.; Leroy-Willig, A.; Mir, L.M.; Miklavčič, D. The influence of skeletal muscle anisotropy on electroporation: In vivo study and numerical modeling. Med. Biol. Eng. Comput. 2010, 48, 637–648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leticia Vera-Tizatl, A.; Elizabeth Vera-Tizatl, C.; Vera-Hernandez, A.; Leija-Salas, L.; Rodriguez, S.; Miklavcic, D.; Kos, B. Computational Feasibility Analysis of Electrochemotherapy with Novel Needle-Electrode Arrays for the Treatment of Invasive Breast Ductal Carcinoma. Technol. Cancer Res. Treat. 2018, 17, 1533033818794939. [Google Scholar] [CrossRef]
- Brock, R.M.; Beitel-White, N.; Davalos, R.V.; Allen, I.C. Starting a Fire Without Flame: The Induction of Cell Death and Inflammation in Electroporation-Based Tumor Ablation Strategies. Front. Oncol. 2020, 10, 1235. [Google Scholar] [CrossRef]



| Symbol | Parameter | Value (Unit) |
|---|---|---|
| σi | Insulating Electrical Conductivity | 0.0001 (S/m) |
| σs | Steel Electrical Conductivity | 300000 (S/m) |
| σf_h | Final Healthy Electrical Conductivity | 0.4 (S/m) |
| σ0_h | Initial Healthy Electrical Conductivity | 0.03 (S/m) |
| Kv_h | Healthy Slope Constant | 0.01 |
| Eth_h | Healthy Electric Field Threshold | 300 (V/cm) |
| σf_t | Final Tumor Electrical Conductivity | 1.2 (S/m) |
| σ0_t | Initial Tumor Electrical Conductivity | 0.09 (S/m) |
| Kv_t | Tumor Slope Constant | 0.01 |
| Eth_t | Tumor Electric Field Threshold | 300 (V/cm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Alonso, B.; Sarnago, H.; Burdío, J.M.; Briz, P.; Lucía, O. Multi-Electrode Architecture Modeling and Optimization for Homogeneous Electroporation of Large Volumes of Tissue. Energies 2021, 14, 1892. https://doi.org/10.3390/en14071892
López-Alonso B, Sarnago H, Burdío JM, Briz P, Lucía O. Multi-Electrode Architecture Modeling and Optimization for Homogeneous Electroporation of Large Volumes of Tissue. Energies. 2021; 14(7):1892. https://doi.org/10.3390/en14071892
Chicago/Turabian StyleLópez-Alonso, Borja, Héctor Sarnago, José M. Burdío, Pablo Briz, and Oscar Lucía. 2021. "Multi-Electrode Architecture Modeling and Optimization for Homogeneous Electroporation of Large Volumes of Tissue" Energies 14, no. 7: 1892. https://doi.org/10.3390/en14071892
APA StyleLópez-Alonso, B., Sarnago, H., Burdío, J. M., Briz, P., & Lucía, O. (2021). Multi-Electrode Architecture Modeling and Optimization for Homogeneous Electroporation of Large Volumes of Tissue. Energies, 14(7), 1892. https://doi.org/10.3390/en14071892








