Optimizing Power and Heat Sector Coupling for the Implementation of Carbon-Free Communities
Abstract
:1. Introduction
- A thermal storage planning model is proposed to cover the annual DH demand of a community solely by P2H conversion using wind power, thus leading to a fully carbon-free DH system.
- Chronological clustering is applied to accurately capture the midterm dynamics of wind power and track the energy level of storage and thermal comfort level of each end-user, while keeping the proposed planning model computationally tractable.
- The P2H conversion is performed using a novel 2-km deep well heat pump (DWHP) system. The thermal analysis of DWHP is conducted separately in Finnish conditions over a 25-year study period. Moreover, the DWHP is used for both heat extraction and heat injection.
- Space heating load, thermal comfort and the associated DR are modeled using a two-capacity building thermal model.
- The effect of interannual weather variability on storage size is studied by simulating the optimization model with different weather inputs.
2. System Description
2.1. Two-Capacity Building Model
2.2. Deep Well (Borehole) Heat Pump System
2.3. Time Series Aggregation
- The algorithm initializes as every single entry of the time series as its own cluster. Fix the initial number of clusters r to the total number of time steps, i.e., 8760, in our case.
- Compute the centroid of each cluster K according to Equation (1)
- Evaluate the dissimilarity index between each pair of contiguous clusters K and L according to Ward’s criterion, as in Equation (2). denotes the number of hours in cluster K.
- Based on the dissimilarity matrix, combine the two closest adjacent clusters to form a new cluster (K’, L’); (K’, L’)Є argmin D(K, L), where L belongs to the set of clusters adjacent to the cluster K.
- Update r with r − 1.
- If r = R’, proceed to step VII; otherwise go to step II.
- Replace the clusters formed in Xk with their cluster centroids. The duration of each time step (cluster) in the representative time series is equal to the number of hours forming that cluster.
- The times series is rescaled to obtain the absolute values.
3. Optimization Model
4. Case Study
4.1. Simulation Parameters
4.2. Simulation Results
5. Conclusions
- The simulation results proved that considering a small thermal storage in tandem with the DWHP prototype can cover the DH demand of a community. On average, the required optimal size of the thermal storage in the BAU case is just 29.172 MWh, i.e., 2.58% of the DH demand.
- DR can play a complementary role to economically satisfy the DH demand without oversizing the wind generation, which would otherwise result in an increased power spillage. Activating DR reduces the storage size, on average, to 13.99 MWh, i.e., 1.24% of the DH demand.
- The precision of the results was evaluated by increasing the number of representative time periods. The storage size increased slightly when the time series representation increased from 1252 clusters to 2920 clusters. However, the simulation time rose rapidly.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Sets | |
| t, T | index and set of time steps |
| n, N | index and set of households |
| i, I | index and set of breakpoints for SOS2 variables during heat injection |
| j, J | index and set of breakpoints for SOS2 variables during heat extraction |
| Parameters | |
| A1, A2, A3 | Regression coefficients for heat extracted by the DWHP |
| B1, B2, B3 | Regression coefficients for the heat extracted by the deep bore hole alone |
| C1, C2, C3 | Regression coefficients for the heat injected into the deep bore hole alone |
| Thermal capacitance of indoor air (Wh/°C/m2) | |
| Thermal capacitance of building fabric (Wh/°C/m2) | |
| Di, Ej | Breakpoints for SOS2 variables |
| Heat conductance between indoor air and building fabric (W/°C/m2) | |
| Heat conductance between external air and indoor air (W/°C/m2) | |
| Heat conductance between external air and building fabric (W/°C/m2) | |
| Heat conductance between heating air and indoor air (W/°C/m2) | |
| Heat conductance between indoor air and ground (W/°C/m2) | |
| M | a big number |
| Wind power generation in time step t (W) | |
| Maximum charging power of the thermal storage (W) | |
| Minimum and maximum input power of the DWHP during heat extraction, respectively (W) | |
| Minimum and maximum input power of the DWHP during heat injection, respectively (W) | |
| Rated power of the heating unit of house n (W) | |
| Maximum discharging heat power of the thermal storage (W) | |
| Minimum allowed state of charge of the thermal storage (Wh) | |
| Tg | Ground node temperature (°C) |
| Tx | Temperature of heating air (°C) |
| Indoor set-point temperature of household n (°C) | |
| Wind curtailment level | |
| Δ | Width of the temperature dead band (°C) |
| Annual space heating demand of household n (Wh) | |
| Duration of time step t (hours) | |
| Charging and discharging efficiency of the thermal storage | |
| Thermal storage loss coefficient | |
| Solar and internal heat gains in house n in time step t, respectively (W) | |
| Variables | |
| Charging power of the thermal storage (W) | |
| Input power of the DWHP during heat extraction in time step t (W) | |
| Input power of the DWHP during heat injection in time step t (W) | |
| Wind power curtailed in time step t (W) | |
| Discharging power of the thermal storage (W) | |
| Heating power required in house n in time step t (W) | |
| Heat extracted by the DWHP in time step t (W) | |
| Heat extracted and injected to the deep bore hole in time step t, respectively (W) | |
| Maximum capacity and instantaneous capacity of the thermal storage in time t, respectively (Wh) | |
| Indoor ambient temperature of house n in time step t (°C) | |
| Building mass temperature of house n in time step t (°C) | |
| Binary variables for the heat extraction and heat injection, respectively | |
| Binary variable for the heating power of household n in time step t | |
| SOS2 variables for calculating the square of continuous variables | |
| Storage losses of the thermal storage in time step t (Wh) | |
References
- Arabzadeh, V.; Pilpola, S.; Lund, P.D. Coupling Variable Renewable Electricity Production to the Heating Sector through Curtailment and Power-to-heat Strategies for Accelerated Emission Reduction. Future Cities Environ. 2019, 5. [Google Scholar] [CrossRef] [Green Version]
- Statistics Finland. 2019. Available online: https://www.stat.fi/til/asen/2019/asen_2019_2020-11-19_tie_001_en.html (accessed on 12 January 2021).
- Arabzadeh, V.; Mikkola, J.; Jasiūnas, J.; Lund, P.D. Deep decarbonization of urban energy systems through renewable energy and sector-coupling flexibility strategies. J. Environ. Manag. 2020, 260, 110090. [Google Scholar] [CrossRef] [PubMed]
- Helin, K.; Syri, S.; Zakeri, B. Improving district heat sustainability and competitiveness with heat pumps in the future Nordic energy system. Energy Procedia 2018, 149, 455–464. [Google Scholar] [CrossRef]
- Lund, P.D.; Skytte, K.; Bolwig, S.; Bolkesjö, T.F.; Bergaentzlé, C.; Gunkel, P.A.; Kirkerud, J.G.; Klitkou, A.; Koduvere, H.; Gravelsins, A.; et al. Pathway Analysis of a Zero-Emission Transition in the Nordic-Baltic Region. Energies 2019, 12, 3337. [Google Scholar] [CrossRef] [Green Version]
- Mikkola, J.; Lund, P.D. Modeling flexibility and optimal use of existing power plants with large-scale variable renewable power schemes. Energy 2016, 112, 364–375. [Google Scholar] [CrossRef]
- Salpakari, J.; Mikkola, J.; Lund, P.D. Improved flexibility with large-scale variable renewable power in cities through optimal demand side management and power-to-heat conversion. Energy Convers. Manag. 2016, 126, 649–661. [Google Scholar] [CrossRef] [Green Version]
- Pilpola, S.; Arabzadeh, V.; Mikkola, J.; Lund, P. Analyzing National and Local Pathways to Carbon-Neutrality from Technology, Emissions, and Resilience Perspectives—Case of Finland. Energies 2019, 12, 949. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.; Ekström, J.; Lehtonen, M. Sizing Hydrogen Energy Storage in Consideration of Demand Response in Highly Renewable Generation Power Systems. Energies 2018, 11, 1113. [Google Scholar] [CrossRef] [Green Version]
- Bashir, A.A.; Pourakbari-Kasmaei, M.; Contreras, J.; Lehtonen, M. A novel energy scheduling framework for reliable and economic operation of islanded and grid-connected microgrids. Electr. Power Syst. Res. 2019, 171, 85–96. [Google Scholar] [CrossRef]
- Bashir, A.; Pourakbari Kasmaei, M.; Safdarian, A.; Lehtonen, M. Matching of Local Load with On-Site PV Production in a Grid-Connected Residential Building. Energies 2018, 11, 2409. [Google Scholar] [CrossRef] [Green Version]
- Bashir, A.A.; Lund, A.; Pourakbari-Kasmaei, M.; Lehtonen, M. Minimizing Wind Power Curtailment and Carbon Emissions by Power to Heat Sector Coupling—A Stackelberg Game Approach. IEEE Access 2020, 8, 211892–211911. [Google Scholar] [CrossRef]
- Helistö, N.; Kiviluoma, J.; Holttinen, H.; Lara, J.D.; Hodge, B.-M. Including operational aspects in the planning of power systems with large amounts of variable generation: A review of modeling approaches. Wiley Interdiscip. Rev. Energy Environ. 2019, 8, e341. [Google Scholar] [CrossRef]
- Frew, B.A.; Jacobson, M.Z. Temporal and spatial tradeoffs in power system modeling with assumptions about storage: An application of the POWER model. Energy 2016, 117, 198–213. [Google Scholar] [CrossRef] [Green Version]
- Asensio, M.; Meneses de Quevedo, P.; Munoz-Delgado, G.; Contreras, J. Joint Distribution Network and Renewable Energy Expansion Planning Considering Demand Response and Energy Storage—Part I: Stochastic Programming Model. IEEE Trans. Smart Grid 2018, 9, 655–666. [Google Scholar] [CrossRef]
- Dvorkin, Y.; Fernandez-Blanco, R.; Kirschen, D.S.; Pandzic, H.; Watson, J.-P.; Silva-Monroy, C.A. Ensuring Profitability of Energy Storage. IEEE Trans. Power Syst. 2017, 32, 611–623. [Google Scholar] [CrossRef]
- De Sisternes, F.J.; Jenkins, J.D.; Botterud, A. The value of energy storage in decarbonizing the electricity sector. Appl. Energy 2016, 175, 368–379. [Google Scholar] [CrossRef] [Green Version]
- Tejada-Arango, D.A.; Domeshek, M.; Wogrin, S.; Centeno, E. Enhanced Representative Days and System States Modeling for Energy Storage Investment Analysis. IEEE Trans. Power Syst. 2018, 33, 6534–6544. [Google Scholar] [CrossRef] [Green Version]
- Brijs, T.; van Stiphout, A.; Siddiqui, S.; Belmans, R. Evaluating the role of electricity storage by considering short-term operation in long-term planning. Sustain. Energy Grids Netw. 2017, 10, 104–117. [Google Scholar] [CrossRef] [Green Version]
- Pineda, S.; Morales, J.M. Chronological Time-Period Clustering for Optimal Capacity Expansion Planning With Storage. IEEE Trans. Power Syst. 2018, 33, 7162–7170. [Google Scholar] [CrossRef]
- Raventós, O.; Bartels, J. Evaluation of Temporal Complexity Reduction Techniques Applied to Storage Expansion Planning in Power System Models. Energies 2020, 13, 988. [Google Scholar] [CrossRef] [Green Version]
- European Commission: Climate and Energy Framework. Available online: https://ec.europa.eu/clima/policies/strategies/2030_en (accessed on 1 December 2020).
- Bashir, A.A.; Lehtonen, M. Day-Ahead Rolling Window Optimization of Islanded Microgrid with Uncertainty. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–6. [Google Scholar]
- Alimohammadisagvand, B.; Alam, S.; Ali, M.; Degefa, M.; Jokisalo, J.; Sirén, K. Influence of energy demand response actions on thermal comfort and energy cost in electrically heated residential houses. Indoor Built Environ. 2017, 26, 298–316. [Google Scholar] [CrossRef]
- Decree (1009/2017) of the Ministry of the Environment on Indoor Climate and Ventilation in the New Building, 2017; Ministry of Housing, Energy and the Environment: Helsinki, Finland, 2017.
- Helsingin Geoenergiapotentiaali; Kaupunkiympäristön julkaisuja 2019:25. Helsinki, 2019. Available online: https://www.hel.fi/static/liitteet/kaupunkiymparisto/julkaisut/julkaisut/julkaisu-25-19.pdf (accessed on 10 October 2020).
- Wang, Z.; Wang, F.; Liu, J.; Ma, Z.; Han, E.; Song, M. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Convers. Manag. 2017, 153, 603–615. [Google Scholar] [CrossRef]
- Holmberg, H.; Acuña, J.; Næss, E.; Sønju, O.K. Thermal evaluation of coaxial deep borehole heat exchangers. Renew. Energy 2016, 97, 65–76. [Google Scholar] [CrossRef]
- Lund, A.; Karvinen, T.; Lehtonen, M. Analysis of deep-heat energy wells for heat pump systems. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Hague, The Netherlands, 26–28 October 2020; pp. 574–578. [Google Scholar]
- Lund, A. Analysis of Deep-Heat Energy Wells for Heat Pump Systems; Aalto University: Espoo, Finland, 2019. [Google Scholar]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Pourakbari Kasmaei, M.; Asensio, M.; Lehtonen, M.; Contreras, J. Trilateral Planning Model for Integrated Community Energy Systems and PV-based Prosumers-A Bilevel Stochastic Programming Approach. IEEE Trans. Power Syst. 2019, 35, 346–361. [Google Scholar] [CrossRef] [Green Version]
- Alahäivälä, A.; Corbishley, J.; Ekström, J.; Jokisalo, J.; Lehtonen, M. A control framework for the utilization of heating load flexibility in a day-ahead market. Electr. Power Syst. Res. 2017, 145, 44–54. [Google Scholar] [CrossRef]
- Ekström, J.; Koivisto, M.; Mellin, I.; Millar, J.; Saarijärvi, E.; Haarla, L. Assessment of large scale wind power generation with new generation locations without measurement data. Renew. Energy 2015, 83, 362–374. [Google Scholar] [CrossRef]
- Finnish Meteorological Institute, Finland. Available online: http://en.ilmatieteenlaitos.fi/ (accessed on 10 October 2020).
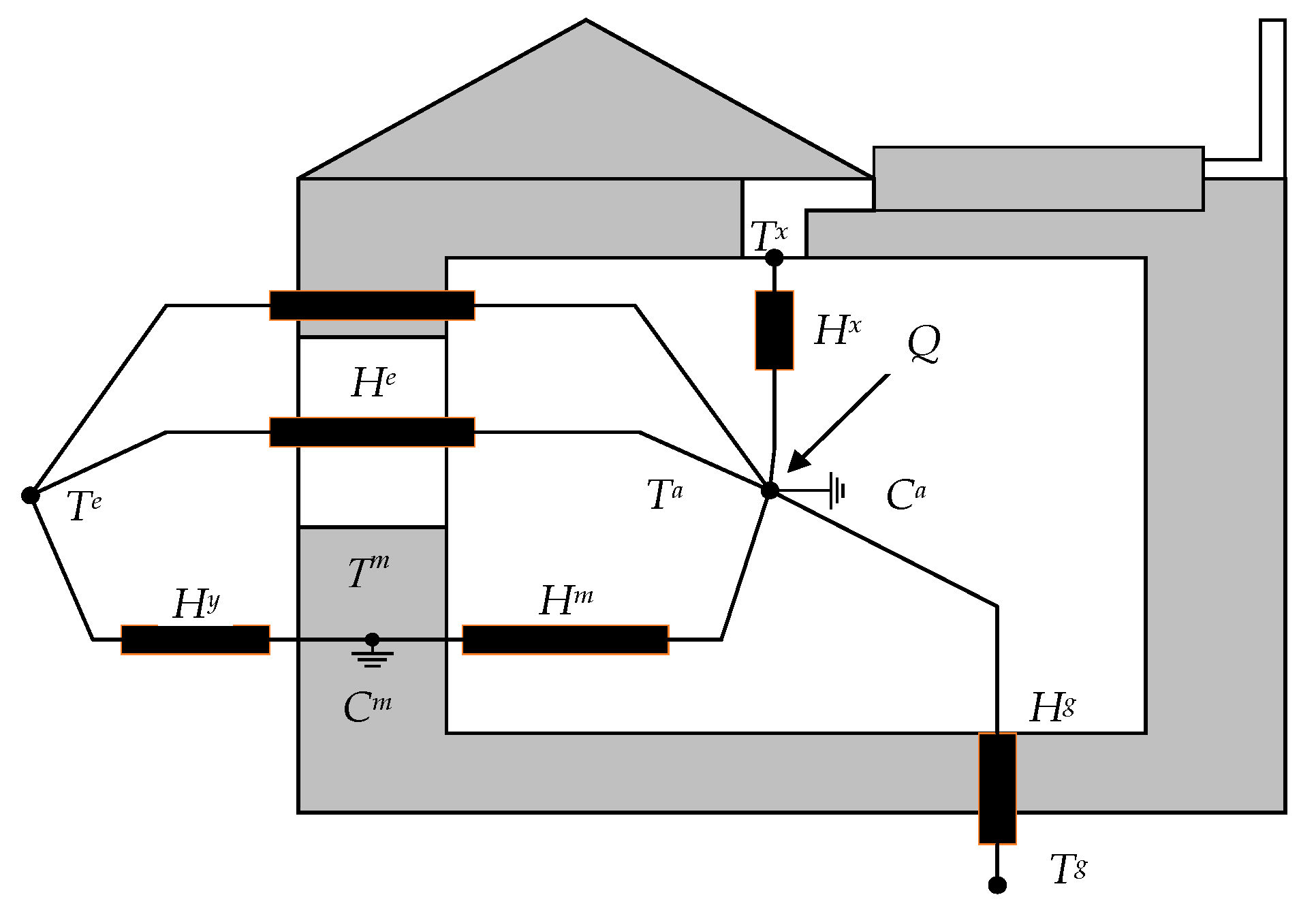



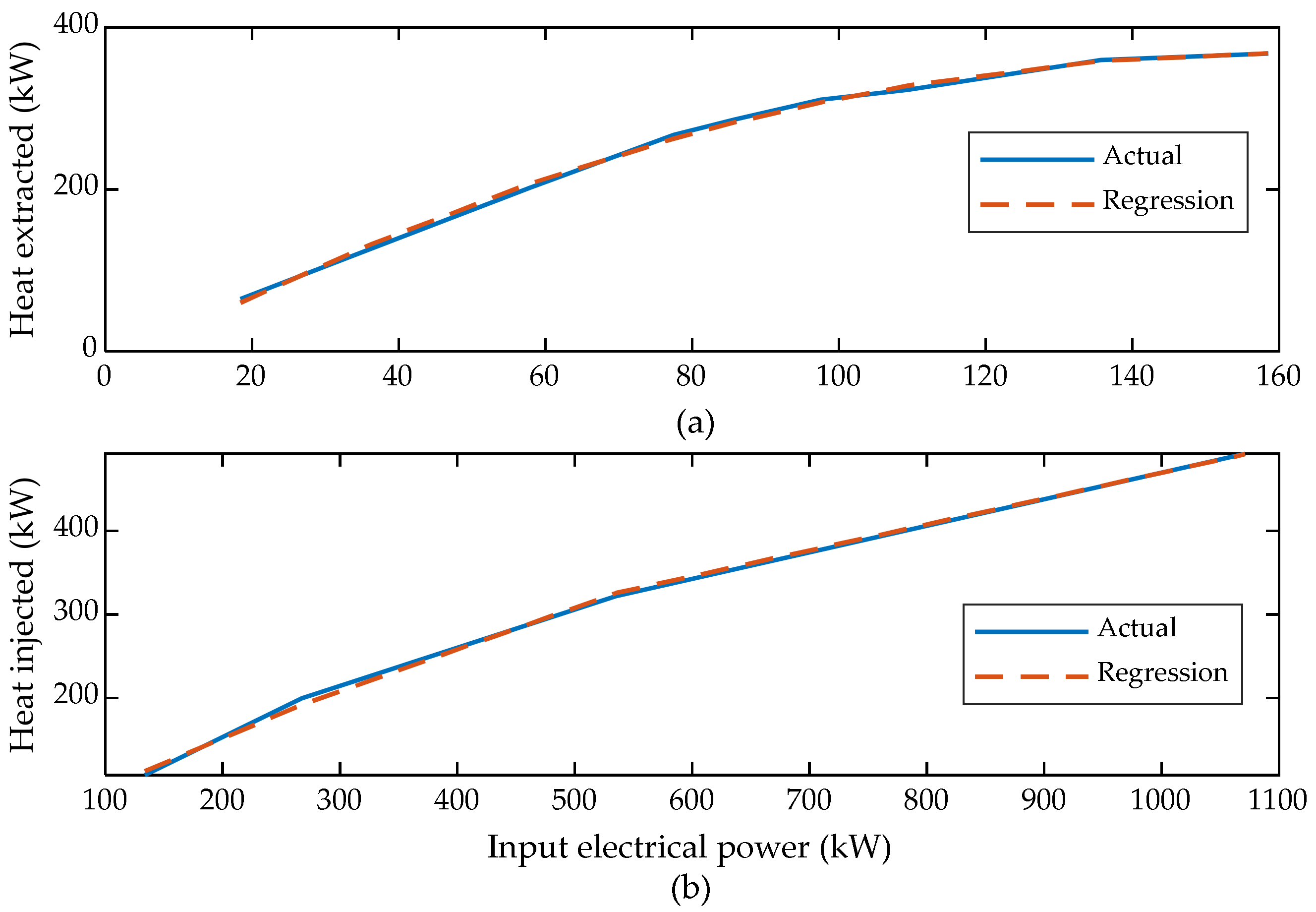
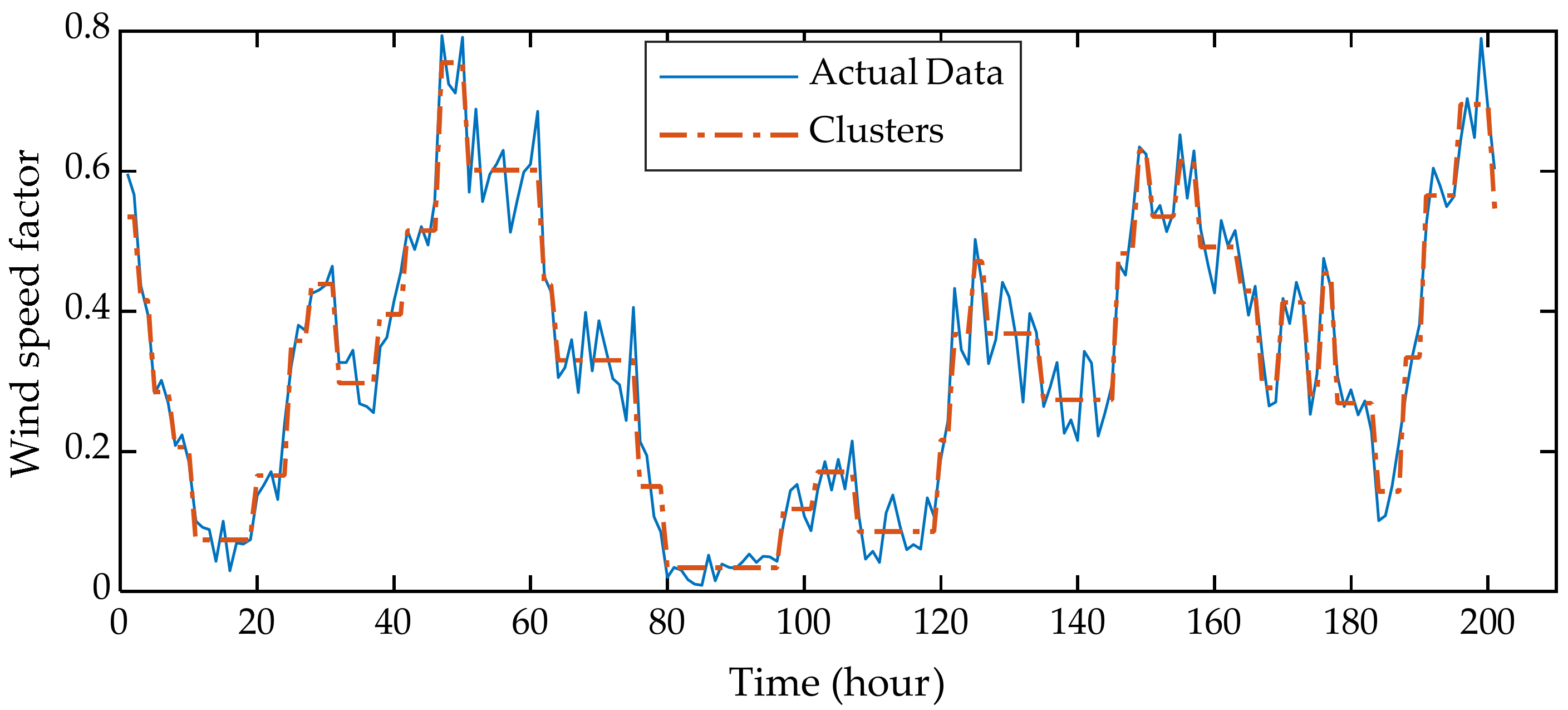
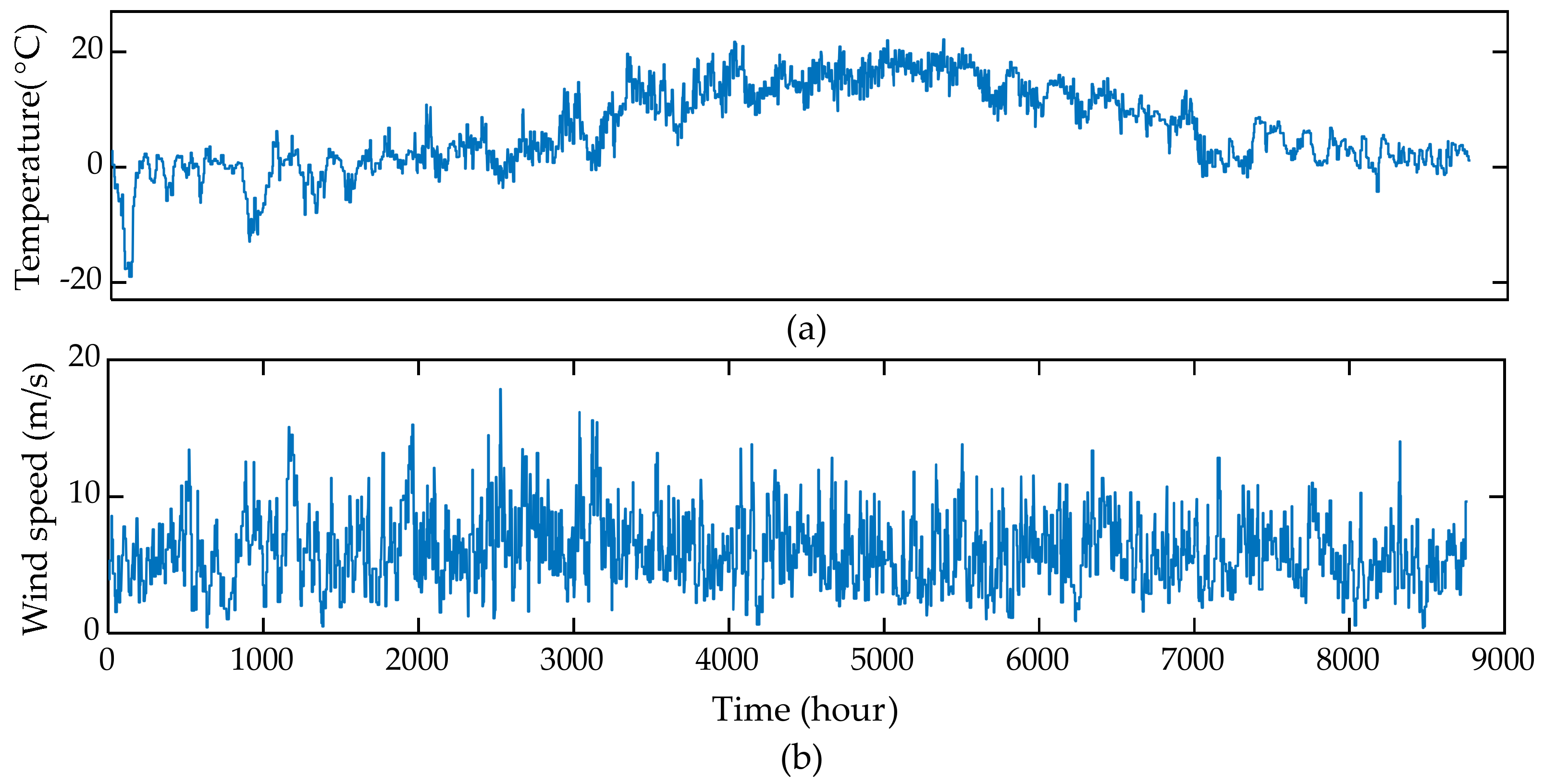

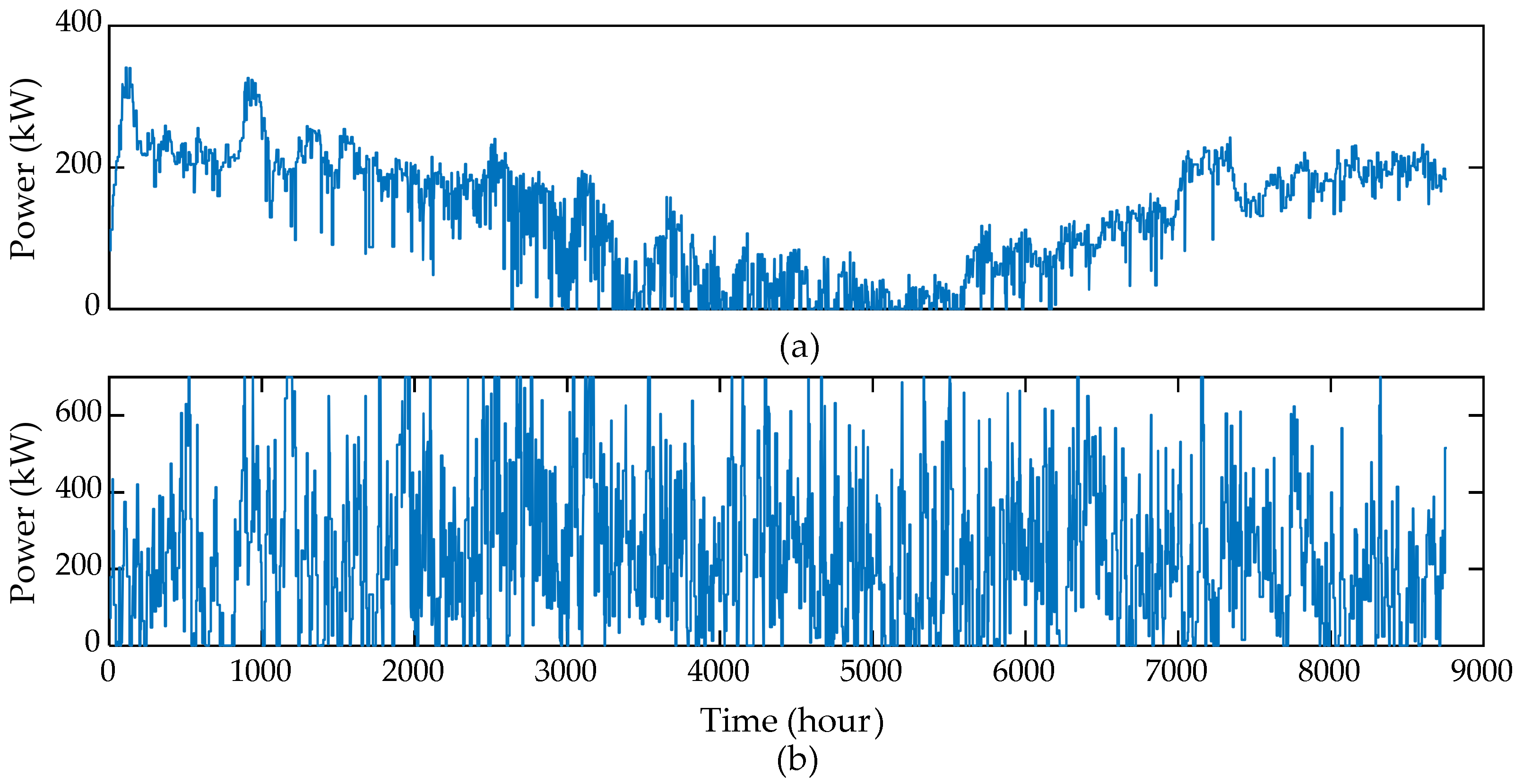
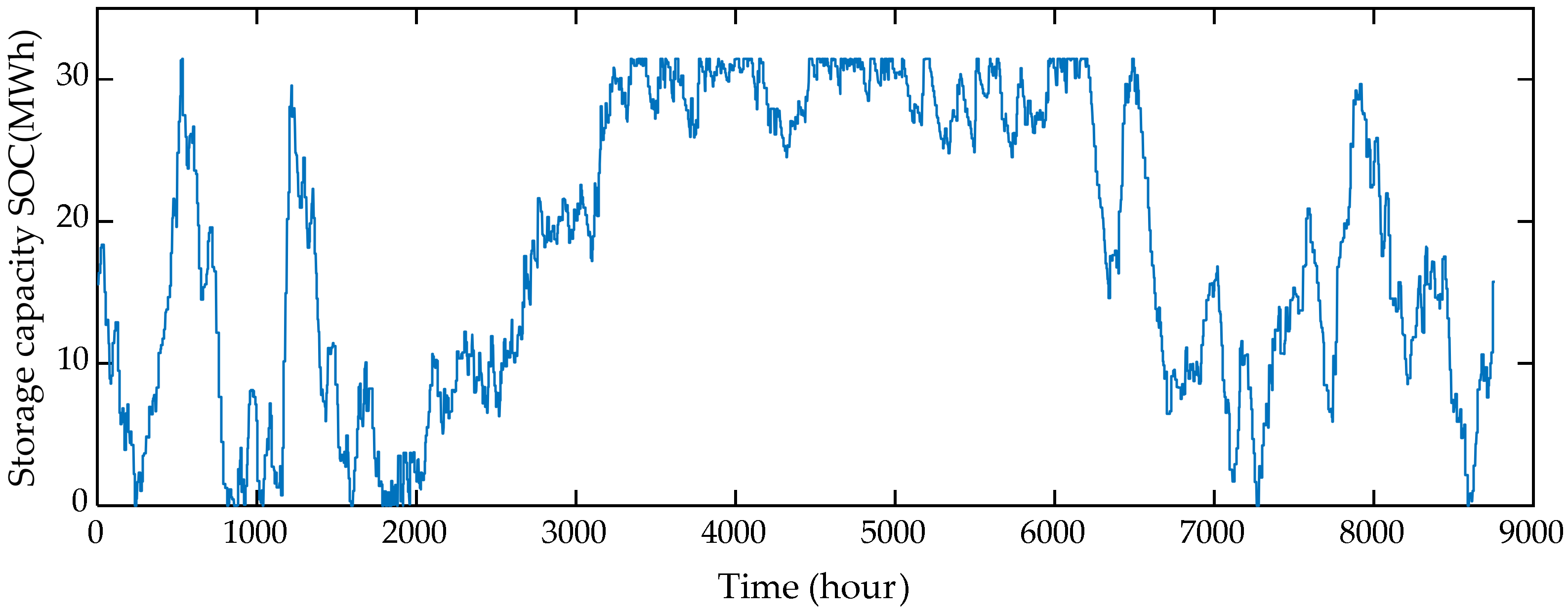
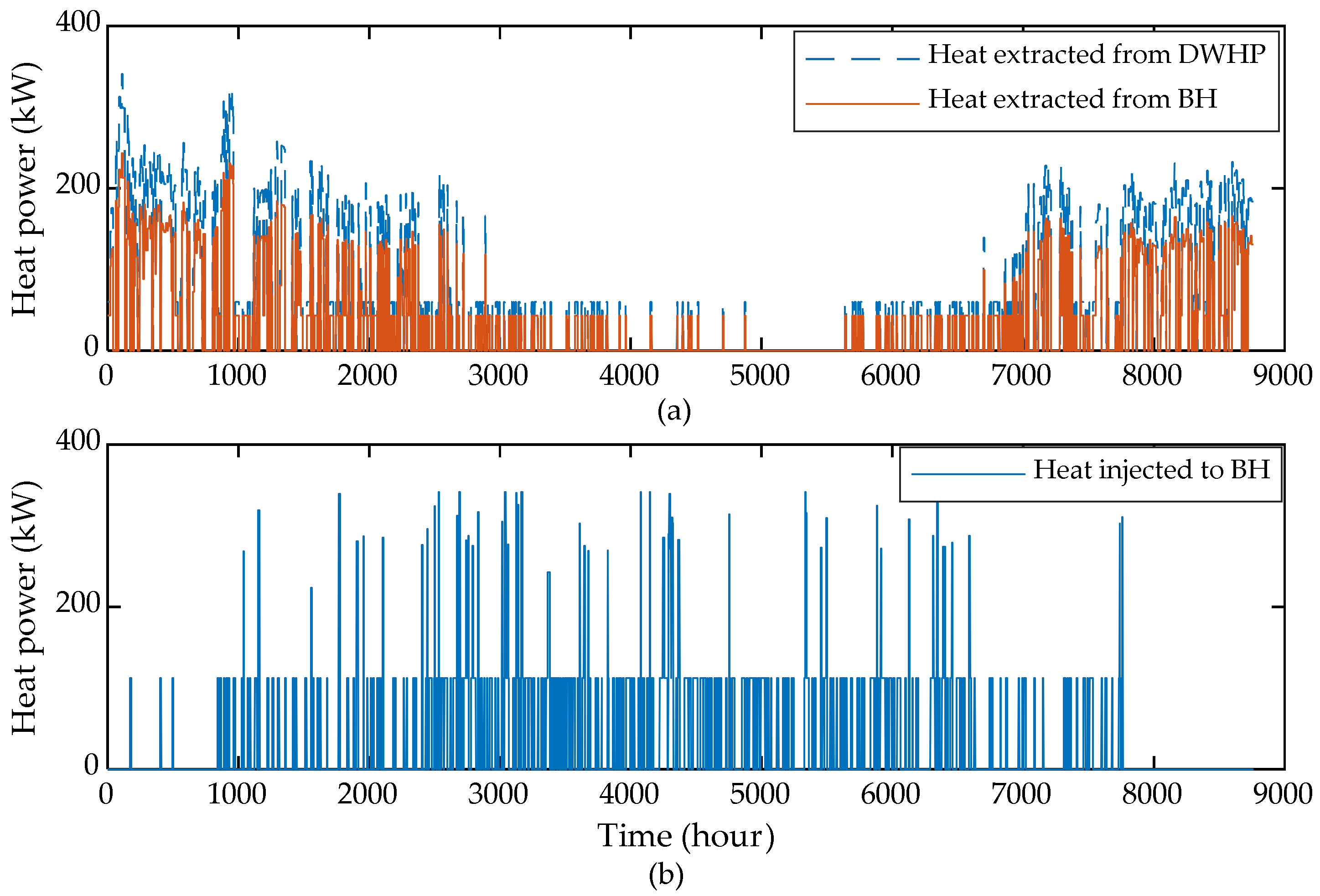
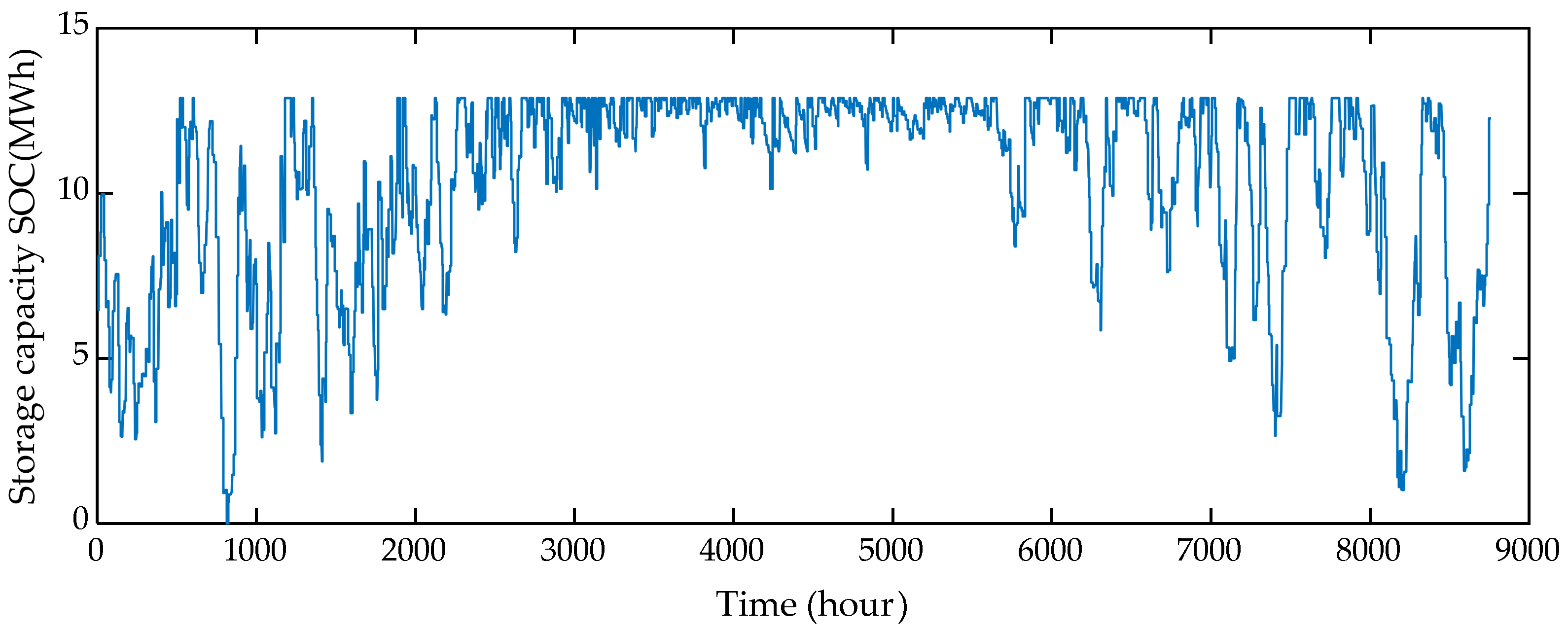
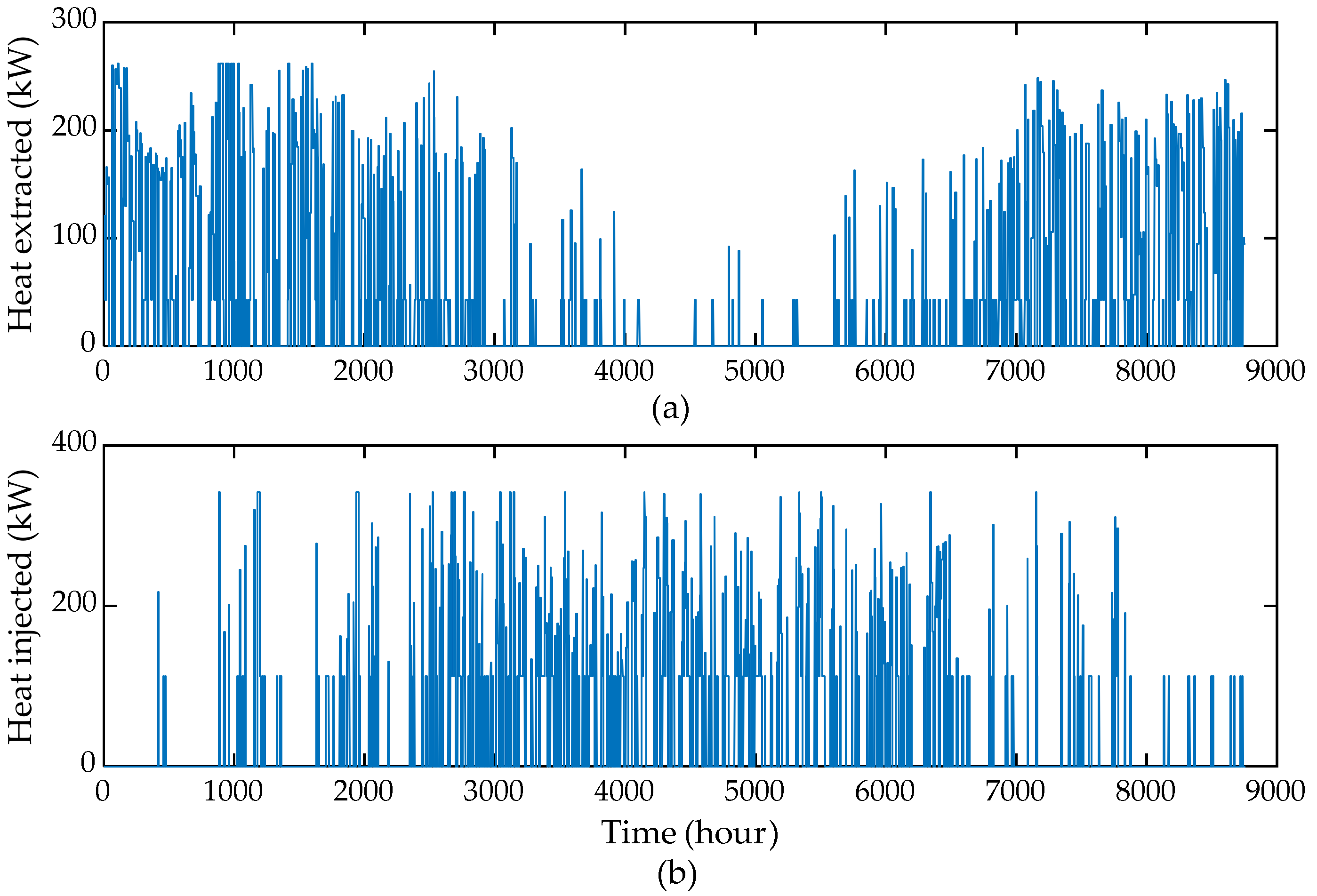
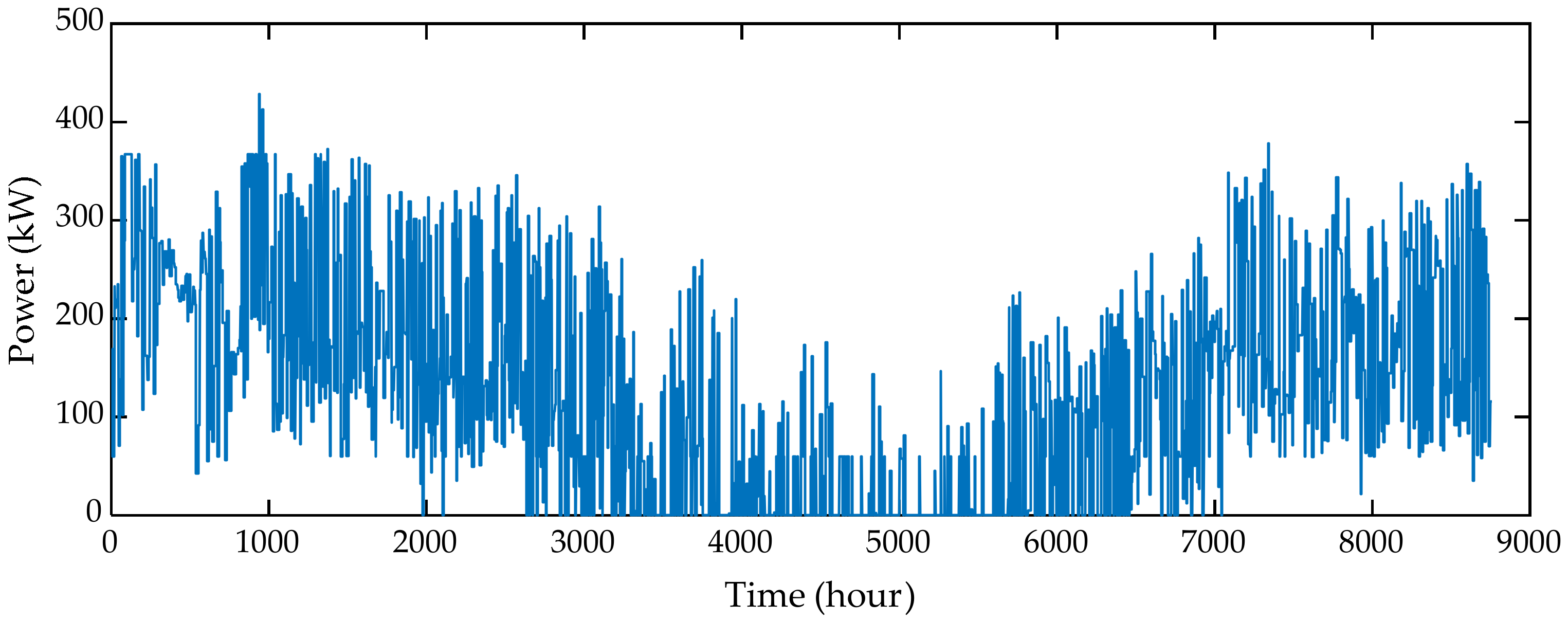


| Parameter | Unit | Value |
|---|---|---|
| He, Hm, Hg, Hx, Hy | W/°C/m2 | 0.29, 5.16, 0.05, 0.48, 0.33 |
| Cm, Ca | Wh/°C/m2 | 31.14, 3.616 |
| Tx, Tg | °C | 18, 10 |
| Case | Mean (MWh) | Standard Deviation (MWh) | Lower 95% Confidence Bound (MWh) | Upper 95% Confidence Bound (MWh) |
|---|---|---|---|---|
| BAU | 29.172 | 7.66 | 25.72 | 32.61 |
| DR | 13.99 | 5.37 | 11.58 | 16.40 |
| No. of Representative Time Periods | Time Series Representation (×8760) | Storage Size (MWh) | Simulation Time |
|---|---|---|---|
| 1252 | 1/7 | 12.87 | 6 min 46 s |
| 1460 | 1/6 | 12.53 | 14 min 38 s |
| 1752 | 1/5 | 12.81 | 32 min 39 s |
| 2190 | 1/4 | 13.27 | 1 h 49 s |
| 2920 | 1/3 | 13.32 | 2 h 16 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, A.A.; Lund, A.; Pourakbari-Kasmaei, M.; Lehtonen, M. Optimizing Power and Heat Sector Coupling for the Implementation of Carbon-Free Communities. Energies 2021, 14, 1911. https://doi.org/10.3390/en14071911
Bashir AA, Lund A, Pourakbari-Kasmaei M, Lehtonen M. Optimizing Power and Heat Sector Coupling for the Implementation of Carbon-Free Communities. Energies. 2021; 14(7):1911. https://doi.org/10.3390/en14071911
Chicago/Turabian StyleBashir, Arslan Ahmad, Andreas Lund, Mahdi Pourakbari-Kasmaei, and Matti Lehtonen. 2021. "Optimizing Power and Heat Sector Coupling for the Implementation of Carbon-Free Communities" Energies 14, no. 7: 1911. https://doi.org/10.3390/en14071911
APA StyleBashir, A. A., Lund, A., Pourakbari-Kasmaei, M., & Lehtonen, M. (2021). Optimizing Power and Heat Sector Coupling for the Implementation of Carbon-Free Communities. Energies, 14(7), 1911. https://doi.org/10.3390/en14071911








