A Comparison of Integrated Filtering and Prediction Methods for Smart Grids
Abstract
:1. Introduction
2. Materials and Methods
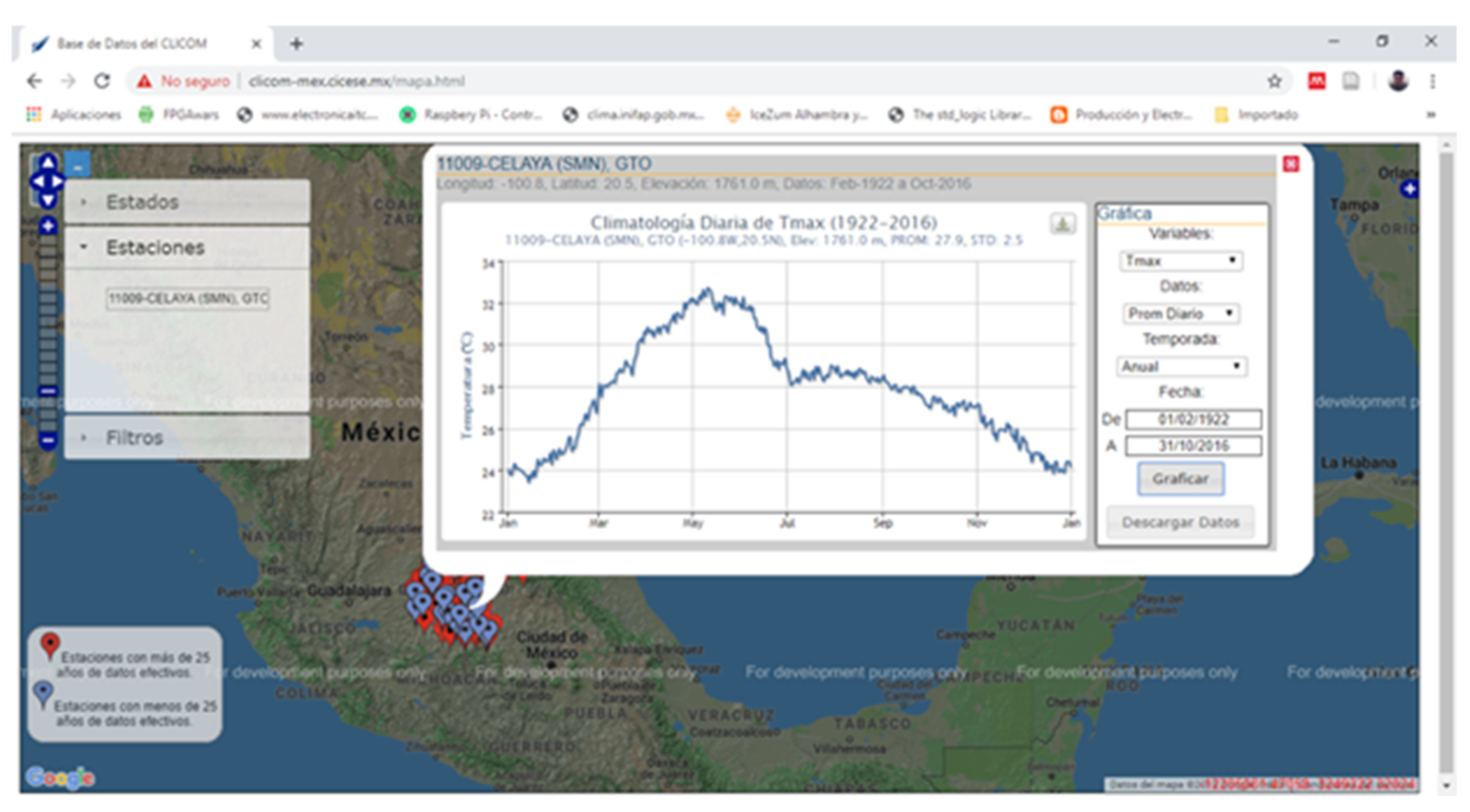
2.1. Data Processing
2.2. Linear Regression Models
2.3. Support Vector Machine (SVM) Model
- Linear Kernel, offers the possibility of solving problems with the approximation to a linear function.
- Kernel Polynomial, offers the possibility to solve problems with a polynomial kernel with different degrees and coefficients .
- Radial kernel, offers the possibility to solve problems with a Gaussian kernel with different values of .
- Sigmoidal kernel, offers the possibility to solve problems with a sigmoidal kernel with different and values.In the above expressions, represents the value of the line and the projection on the hyperplane, while , and are parameters of the equations. represents the scalar product of and , and represents the Euclidian norm of .
2.4. Neural Network Models
2.5. Data Scaling/Filtering
2.6. Selection Criteria
3. Results
3.1. Prediction of Maximum Temperature by Regression
3.2. Maximum Temperature Prediction by Support Vector Machines
3.3. Maximum Temperature Prediction by Neural Networks
3.4. Cross Validation
3.5. Prediction of Energy Conditions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Craparo, E.; Karatas, M.; Singham, D.I. A robust optimization approach to hybrid microgrid operation using ensemble weather forecasts. Appl. Energy 2017, 201, 135–147. [Google Scholar] [CrossRef]
- Mattig, I.E. Predicción de la Potencia Para la Operación de Parques Eólicos; Universidad de Chile: Santiago, Chile, 2010. [Google Scholar]
- Agüera-Pérez, A.; Palomares-Salas, J.C.; de la Rosa, J.J.G.; Florencias-Oliveros, O. Weather forecasts for microgrid energy management: Review, discussion and recommendations. Appl. Energy 2018, 228, 265–278. [Google Scholar] [CrossRef]
- Cecati, C.; Mokryani, G.; Piccolo, A.; Siano, P. An overview on the smart grid concept. In Proceedings of the IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 3322–3327. [Google Scholar]
- Kadlec, M.; Bühnová, B.; Tomšík, J.; Herman, J.; Družbíková, K. Weather forecast based scheduling for demand response optimization in smart grids. In Proceedings of the 2017 Smart Cities Symposium Prague, SCSP 2017-IEEE Proceedings, Prague, Czech Republic, 25–26 May 2017; pp. 1–6. [Google Scholar]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2016, 1, 38–46. [Google Scholar] [CrossRef]
- Sarwat, A.I.; Amini, M.; Domijan, A.; Damnjanovic, A.; Kaleem, F. Weather-based interruption prediction in the smart grid utilizing chronological data. J. Mod. Power Syst. Clean Energy 2016, 4, 308–315. [Google Scholar] [CrossRef] [Green Version]
- Bansal, A.; Rompikuntla, K.; Gopinadhan, J.; Kaur, A.; Kazi, Z.A. Energy Consumption Forecasting for Smart Meters. In Proceedings of the International Conference on Business and Information, BAI 2015, Cotai, Macao, 3–4 July 2014; pp. 1–20. [Google Scholar]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Cook, D.J.; Chinarro, D.; Gómez, J. A study of the relationship between weather variables and electric power demand inside a smart grid/smart world framework. Sensors 2012, 12, 11571–11591. [Google Scholar] [CrossRef] [Green Version]
- Calanca, P.; Bolius, D.; Weigel, A.P.; Liniger, M.A. Application of long-range weather forecasts to agricultural decision problems in Europe. J. Agric. Sci. 2011, 149, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Kavitha, R.; Anuvelavan, M.S. Weather MasterMobile Application of Cyclone Disaster Refinement Forecast System in Location Based on GIS Using Geo Algorithm. Int. J. Sci. Eng. Res. 2015, 6, 88–93. [Google Scholar]
- Hasan, N.; Nath, N.C.; Rasel, R.I. A support vector regression model for forecasting rainfall. In Proceedings of the 2nd International Conference on Electrical Information and Communication Technologies, EICT 2015, Khulna, Bangladesh, 10–12 December 2015; pp. 554–559. [Google Scholar]
- Ngeleja, R.C.; Luboobi, L.S.; Nkansah-Gyekye, Y. The Effect of Seasonal Weather Variation on the Dynamics of the Plague Disease. Int. J. Math. Math. Sci. 2017, 2017, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Bouza, C.N.; Garcia, J.; Santiago, A.; Rueda, M. Modelos Matemáticos Para el Estudio de Medio Ambiente, Salud y Desarrollo Humano (TOMO 3), 1st ed.; UGR: Granada, Spain, 2017. [Google Scholar]
- Les, U.D.E.; Balears, I.; Doctoral, T. Redes Neuronales Artificiales Aplicadas al Análisis de Datos; Universitat de les Illes Balears: Illes Balears, Spain, 2002. [Google Scholar]
- Sobhani, M.; Campbell, A.; Sangamwar, S.; Li, C.; Hong, T. Combining Weather Stations for Electric Load Forecasting. Energies 2019, 12, 1510. [Google Scholar] [CrossRef] [Green Version]
- Vincenti, S.S.; Zuleta, D.; Moscoso, V.; Jácome, P.; Palacios, E. Análisis Estadístico de Datos Metereológicos Mensuales y Diarios Para la Determinación de Variabilidad Climática y Cambio Climático en el Distrito Metropolitano de Quito. La Granja 2012, 16, 23–47. [Google Scholar] [CrossRef]
- Jacobson, T.; James, J.; Schwertman, N.C. An example of using linear regression of seasonal weather patterns to enhance undergraduate learning. J. Stat. Educ. 2009, 17, 2009. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Singhal, G. Weather Prediction Using Normal Equation Method and Linear regression Techniques. Int. J. Comput. Sci. Inf. Technol. 2016, 7, 1490–1493. [Google Scholar]
- Mori, H.; Kanaoka, D. Application of support vector regression to temperature forecasting for short-term load forecasting. In Proceedings of the IEEE International Conference on Neural Networks-Conference Proceedings, Orlando, FL, USA, 12–17 August 2007; pp. 1085–1090. [Google Scholar]
- Radhika, Y.; Shashi, M. Atmospheric Temperature Prediction using Support Vector Machines. Int. J. Comput. Theory Eng. 2009, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Narvekar, M.; Fargose, P. Daily Weather Forecasting using Artificial Neural Network. Int. J. Comput. Appl. 2015, 121, 9–13. [Google Scholar] [CrossRef]
- Ali, J.; Kashyap, P.S.; Kumar, P. Temperature forecasting using artificial neural networks. J. Hill Agric. 2013, 4, 110–112. [Google Scholar]
- Paisan, Y.P.; Moret, J.P. La Repetibilidad Y Reproducibilidad En El Aseguramiento De La Calidad De Los Procesos De Medición. Tecnol. Química 2010, 2, 117–121. [Google Scholar]
- De Almeida, C.T.; Galvão, L.S.; Aragão, L.E.d.C.e.; Ometto, J.P.H.B.; Jacon, A.D.; de Souza Pereira, F.R.; Sato, L.Y.; Lopes, A.P.; de Alencastro Graça, P.M.L.; de Jesus Silva, C.V.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Jahromi, K.G.; Gharavian, D.; Mahdiani, H. A novel method for day-ahead solar power prediction based on hidden Markov model and cosine similarity. Soft Comput. 2019. [Google Scholar] [CrossRef]
- Raffán, L.C.P.; Romero, A.; Martinez, M. Solar energy production forecasting through artificial neuronal networks, considering the Föhn, north and south winds in San Juan, Argentina. J. Eng. 2019, 2019, 4824–4829. [Google Scholar] [CrossRef]
- Valappil, V.K.; Temimi, M.; Weston, M.; Fonseca, R.; Nelli, N.R.; Thota, M.; Kumar, K.N. Assessing Bias Correction Methods in Support of Operational Weather Forecast in Arid Environment. Asia Pac. J. Atmos. Sci. 2019, 56, 333–347. [Google Scholar] [CrossRef]
- CICESE. Datos Climáticos Diarios Del CLICOM Del SMN a Través de su Plataforma Web Del CICESE. 2018. Available online: http://clicom-mex.cicese.mx/ (accessed on 19 May 2019).
- Mathur, S. A Simple Weather Forecasting Model Using Mathematical Regression. Indian Res. J. Ext. Educ. 2012, I, 161–168. [Google Scholar]
- Foley, J.D.; Fischler, M.A.; Bolles, R.C. Graphics and Image Processing Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 1–15. [Google Scholar]
- Yaniv, Z. Random Sample Consensus (RANSAC) Algorithm, A Generic Implementation. Insight J. 2010, I, 1–14. [Google Scholar]
- Djurović, I. QML-RANSAC: PPS and FM signals estimation in heavy noise environments. Signal Process. 2017, 130, 142–151. [Google Scholar] [CrossRef]
- Choi, S.; Kim, T.; Yu, W. Performance Evaluation of RANSAC Family. DBLP 2009. [Google Scholar] [CrossRef] [Green Version]
- Scikit-Learn.org. r2 Score. Available online: https://scikit-learn.org/stable/modules/model_evaluation.html#r2-score (accessed on 27 March 2021).
- Scikit-Learn.org. Mean Squared Error. Available online: https://scikit-learn.org/stable/modules/model_evaluation.html#mean-squared-error (accessed on 27 March 2021).
- UCI Machine Learning Repository: Individual Household Electric Power Consumption Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/individual+household+electric+power+consumption# (accessed on 10 November 2020).





| Evaporation | Heat | Maximum Temperature | |
|---|---|---|---|
| Count | 17,043 | 33,366 | 33,374 |
| Value | Evaporation (mm) | Heat (°D [29]) | Maximum Temperature (°C) |
|---|---|---|---|
| mean | 5.6782 | 9.771292 | 27.917457 |
| std | 2.02045 | 3.066121 | 4.172621 |
| min | 0.03 | 0 | 5.5 |
| 25% | 4.2 | 7.5 | 25.5 |
| 50% | 5.6 | 10 | 28 |
| 75% | 7 | 12.17 | 30.6 |
| max | 17 | 17.64 | 41.5 |
| Variable | Month | Day | Year | Evaporation (mm) | Heat (°D [29]) | Precipitation (mm) | Max Temp (°C) |
|---|---|---|---|---|---|---|---|
| Month | 1 | 0.01052 | −0.006825 | −0.047733 | 0.033247 | 0.071304 | −0.027083 |
| Day | 0.01052 | 1 | −6.00 × 10−0.6 | 0.002199 | 0.006425 | 0.000221 | 0.005417 |
| Year | −0.006825 | −6.00 × 10−0.6 | 1 | 0.743474 | 0.012017 | 0.00366 | 0.050503 |
| Evaporation | −0.047733 | 0.002199 | 0.743474 | 1 | 0.193724 | 0.010533 | 0.209749 |
| Heat | 0.033247 | 0.006425 | 0.012017 | 0.193724 | 1 | 0.121701 | 0.868202 |
| Precipitation | 0.071304 | 0.000221 | 0.00366 | 0.010533 | 0.121701 | 1 | 0.032883 |
| Max Temp | −0.027083 | 0.005417 | 0.050503 | 0.209749 | 0.868202 | 0.032883 | 1 |
| Model | Coefficient of Determination | Mean Square Error (MSE) |
|---|---|---|
| Persistence (from 2015 to 2016) | −0.4672 | 13.8483 |
| Meteorology (average from 2010 to 2016, compared to 2016). | −18.5945 | 1.6548 |
| Value | Evaporation | Heat | Max Temp |
|---|---|---|---|
| count | 25,916 | 25,916 | 25,916 |
| mean | 3.069529 | 10.000068 | 28.282077 |
| std | 3.228479 | 2.842567 | 3.508896 |
| min | 0 | 0 | 12 |
| 25% | 0 | 7.78 | 26 |
| 50% | 2.9 | 10.25 | 28.3 |
| 75% | 5.9 | 12.25 | 30.8 |
| max | 17 | 17.29 | 39.3 |
| Filtering/Scaling | Parametrization | MSE | |||
|---|---|---|---|---|---|
| Training | Testing | Training | Testing | ||
| Fit_intercept | 0.7638 | 0.4644 | 10.3486 | 5.7705 | |
| Maximum and Minimum | Fit_intercept | 0.7445 | 0.2606 | 11.20 | 7.9659 |
| L2 Norm | Fit_intercept | 0.8097 | 0.6765 | 8.3371 | 3.4853 |
| Poly = 2 | Fit_intercept (Grade = 2) | 0.9075 | 0.6564 | 4.0508 | 3.7021 |
| Poly = 7 | Fit_intercept (Grade = 7) | 0.9443 | 0.8187 | 2.4370 | 1.9526 |
| Standard scale | Fit_intercept | 0.7638 | 0.4644 | 10.3486 | 5.7705 |
| RANSAC | Fit_intercept | 0.8518 | 0.7878 | 1.8269 | 1.6438 |
| RANSAC & Maximum and Minimum | Fit_intercept | 0.8518 | 0.4921 | 1.8269 | 3.9343 |
| RANSAC & L2 Norm | Fit_intercept | 0.9277 | 0.8843 | 0.8916 | 0.8960 |
| RANSAC & Poly = 7 | Fit_intercept | 0.8883 | 0.8039 | 1.3767 | 1.5190 |
| RANSAC & standard scale | Fit_intercept | 0.8518 | 0.7878 | 1.8269 | 1.6438 |
| Filtering/Scaling | Parametrization | MSE | |||
|---|---|---|---|---|---|
| Training | Testing | Training | Testing | ||
| Kernel = linear, C = 1, gamma = 0.1 | −3.5084 | −34.1601 | 197.5425 | 378.8428 | |
| Kernel = poly, C = 1, degree = 1 | 0.7323 | 0.2150 | 11.7257 | 8.4573 | |
| Kernel = rbf, C = 1, gamma = 0.1 | 0.8874 | 0.3772 | 4.9328 | 6.7100 | |
| Kernel = sigmoid, C = 1, gamma = 0.1 | −0.0229 | 0.2712 | 44.8203 | 13.6970 | |
| Kernel = rbf, C = 1000, gamma = 0.01 | 0.9643 | 0.6319 | 1.5638 | 3.9656 | |
| Maximum and Minimum | Kernel = poly, C = 1, degree = 1 | 0.7055 | 0.6088 | 12.9033 | 4.2149 |
| Maximum and Minimum | Kernel = rbf, C = 1, gamma = 0.1 | 0.8055 | 0.6315 | 4.9328 | 3.9704 |
| L2 Norm | Kernel = poly, C = 1, degree = 1 | −0.0195 | −0.2638 | 44.6710 | 13.6179 |
| L2 Norm | Kernel = rbf, C = 1, gamma = 0.1 | −0.0188 | −0.2624 | 44.6412 | 13.6022 |
| Standard scale | Kernel = rbf, C = 1000, gamma = 0.1 | 0.9476 | 0.8483 | 2.2919 | 1.6344 |
| RANSAC | Kernel = poly, C = 1, degree = 1 | 0.8166 | 0.6809 | 2.2619 | 2.4719 |
| RANSAC | Kernel = rbf, C = 1, gamma = 0.1 | 0.8930 | 0.4424 | 1.3194 | 4.3198 |
| RANSAC | Kernel = rbf, C = 1000, gamma = 0.01 | 0.9258 | 0.6164 | 0.9144 | 2.9720 |
| RANSAC & Maximum and Minimum | Kernel = rbf, C = 1, gamma = 0.1 | 0.8664 | −0.1981 | 1.6478 | 4.6336 |
| RANSAC & L2 Norm | Kernel = rbf, C = 1, gamma = 0.1 | 0.0051 | −0.2725 | 12.2721 | 9.8592 |
| RANSAC & standard scale | Kernel = rbf, C = 1000, gamma = 0.1 | 0.9024 | 0.7026 | 1.2038 | 1.1508 |
| Filtering/Scaling | Parametrization | MSE | |||
|---|---|---|---|---|---|
| Training | Testing | Training | Testing | ||
| Activation = ‘identity’ random_state = 4 | 0.7635 | 0.4784 | 10.3621 | 5.6195 | |
| Activation = ‘logistic’ random_state = 4 | −0.0002 | −0.6276 | 43.8286 | 17.5373 | |
| Activation n = ‘tanh’ random_state = 4 | −2.1122 | −0.6670 | 43.8173 | 17.9626 | |
| Activation = ‘ReLU’ random_state = 50 | 0.9049 | 0.6454 | 4.1657 | 3.8201 | |
| Maximum and Minimum | Activation = ‘identity’ random_state = 4 | 0.7637 | 0.1098 | 10.3526 | 9.5912 |
| L2 Norm | Activation = ‘identity’ random_state = 4 | 0.7633 | 0.5179 | 10.3712 | 5.1936 |
| Maximum and Minimum | Activation = ‘ReLU’ random_state = 50 | 0.9402 | −0.6558 | 2.6180 | 17.6260 |
| L2 Norm | Activation = ‘ReLU’ random_state = 50 | 0.7649 | 0.5331 | 10.2998 | 5.0298 |
| Standard scale | Activation = ‘ReLU’ Random_satate = 320 | 0.9486 | 0.8528 | 2.2511 | 1.5852 |
| RANSAC | Activation = ‘identity’ random_state = 4 | 0.8397 | 0.7106 | 1.9770 | 2.2417 |
| RANSAC | Activation = ‘ReLU’ random_state = 50 | 0.8270 | 0.7721 | 2.1336 | 1.7654 |
| RANSAC & Maximum and Minimum | Activation = ‘identity’ random_state = 4 | 0.8515 | 0.4815 | 1.8317 | 4.0166 |
| RANSAC & Maximum and Minimum | Activation = ‘ReLU’ random_state = 50 | 0.8874 | −1.8747 | 1.3889 | 22.2727 |
| RANSAC & L2 Norm | Activation = ‘identity’ random_state = 4 | 0.8520 | 0.7854 | 1.8252 | 1.6624 |
| RANSAC & L2 Norm | Activation = ‘ReLU’ random_state = 50 | 0.8525 | 0.7853 | 1.8189 | 1.6627 |
| RANSAC & standard scale | Activation = ‘tanh’ Random_state = 4225 | 0.8955 | 0.8627 | 1.2886 | 1.0633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escobar-Avalos, E.; Rodríguez-Licea, M.A.; Rostro-González, H.; Soriano-Sánchez, A.G.; Pérez-Pinal, F.J. A Comparison of Integrated Filtering and Prediction Methods for Smart Grids. Energies 2021, 14, 1980. https://doi.org/10.3390/en14071980
Escobar-Avalos E, Rodríguez-Licea MA, Rostro-González H, Soriano-Sánchez AG, Pérez-Pinal FJ. A Comparison of Integrated Filtering and Prediction Methods for Smart Grids. Energies. 2021; 14(7):1980. https://doi.org/10.3390/en14071980
Chicago/Turabian StyleEscobar-Avalos, Emmanuel, Martín A. Rodríguez-Licea, Horacio Rostro-González, Allan G. Soriano-Sánchez, and Francisco J. Pérez-Pinal. 2021. "A Comparison of Integrated Filtering and Prediction Methods for Smart Grids" Energies 14, no. 7: 1980. https://doi.org/10.3390/en14071980
APA StyleEscobar-Avalos, E., Rodríguez-Licea, M. A., Rostro-González, H., Soriano-Sánchez, A. G., & Pérez-Pinal, F. J. (2021). A Comparison of Integrated Filtering and Prediction Methods for Smart Grids. Energies, 14(7), 1980. https://doi.org/10.3390/en14071980










