Perforation Optimization of Intensive-Stage Fracturing in a Horizontal Well Using a Coupled 3D-DDM Fracture Model
Abstract
:1. Introduction
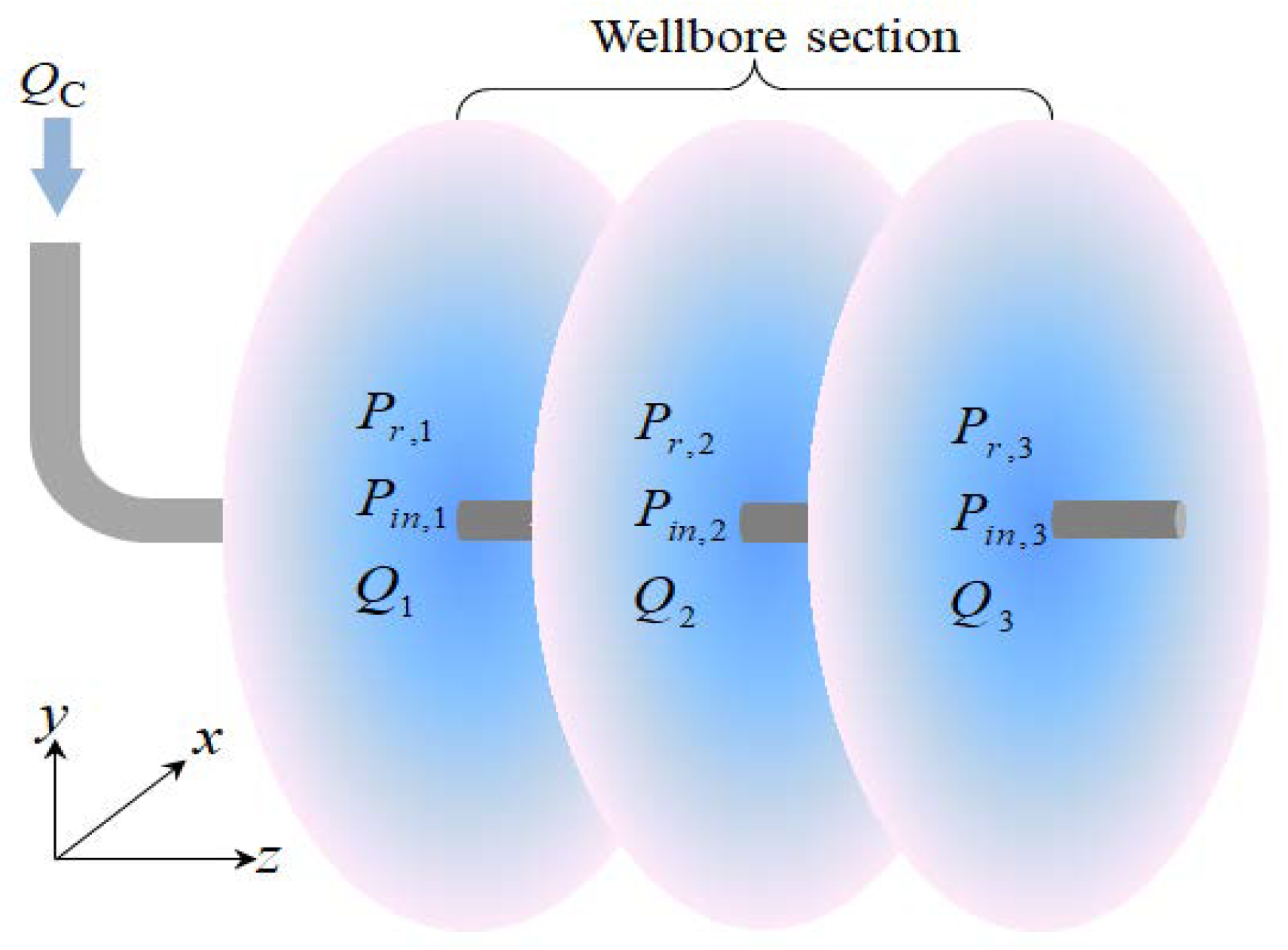
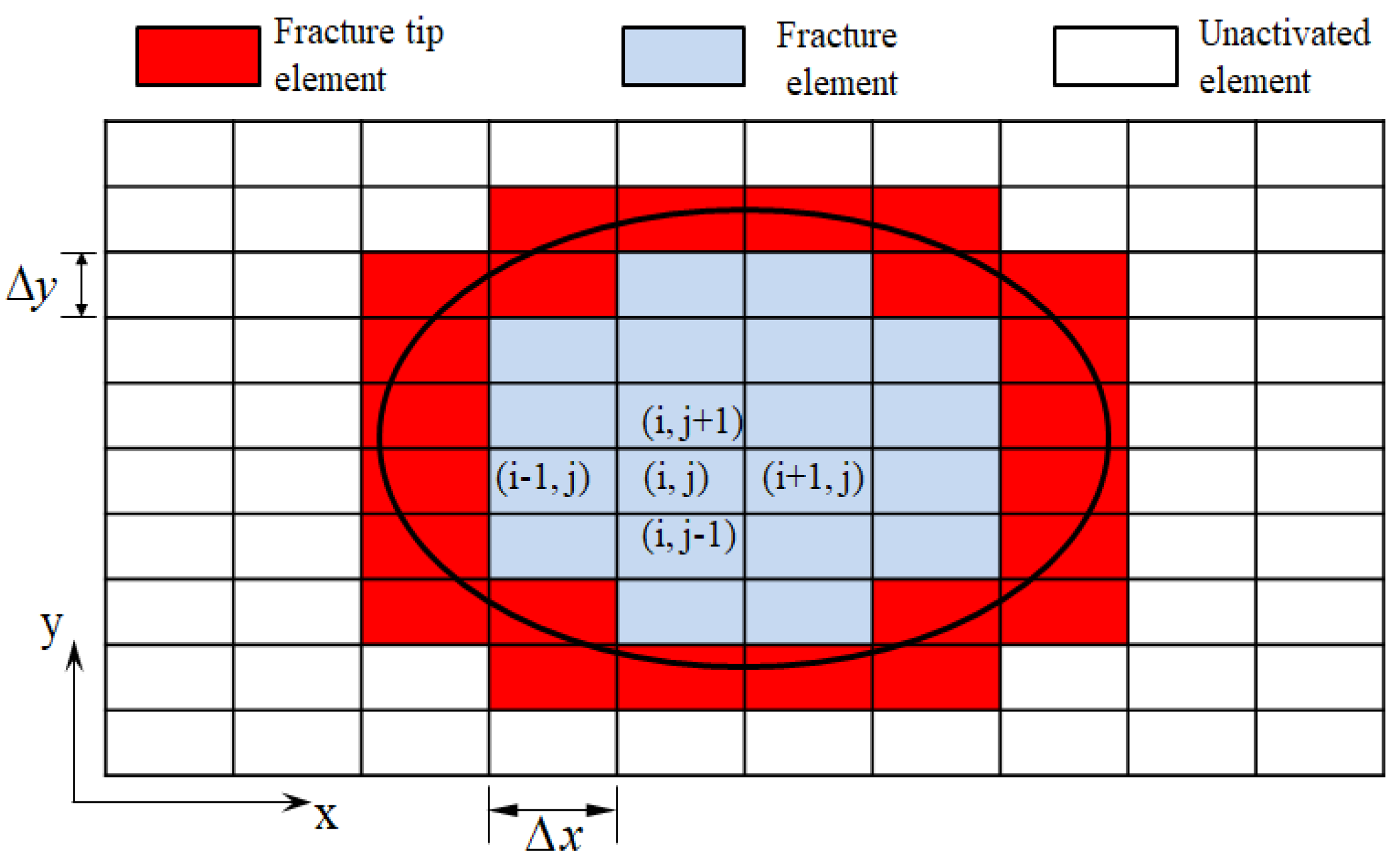
2. Three-Dimensional Fracture Model of Intensive-Stage Fracturing
2.1. Basic Hypothesis
2.2. Fracture Deformation
2.3. Flow of Fracturing Fluid
2.4. Fracture Propagation Condition
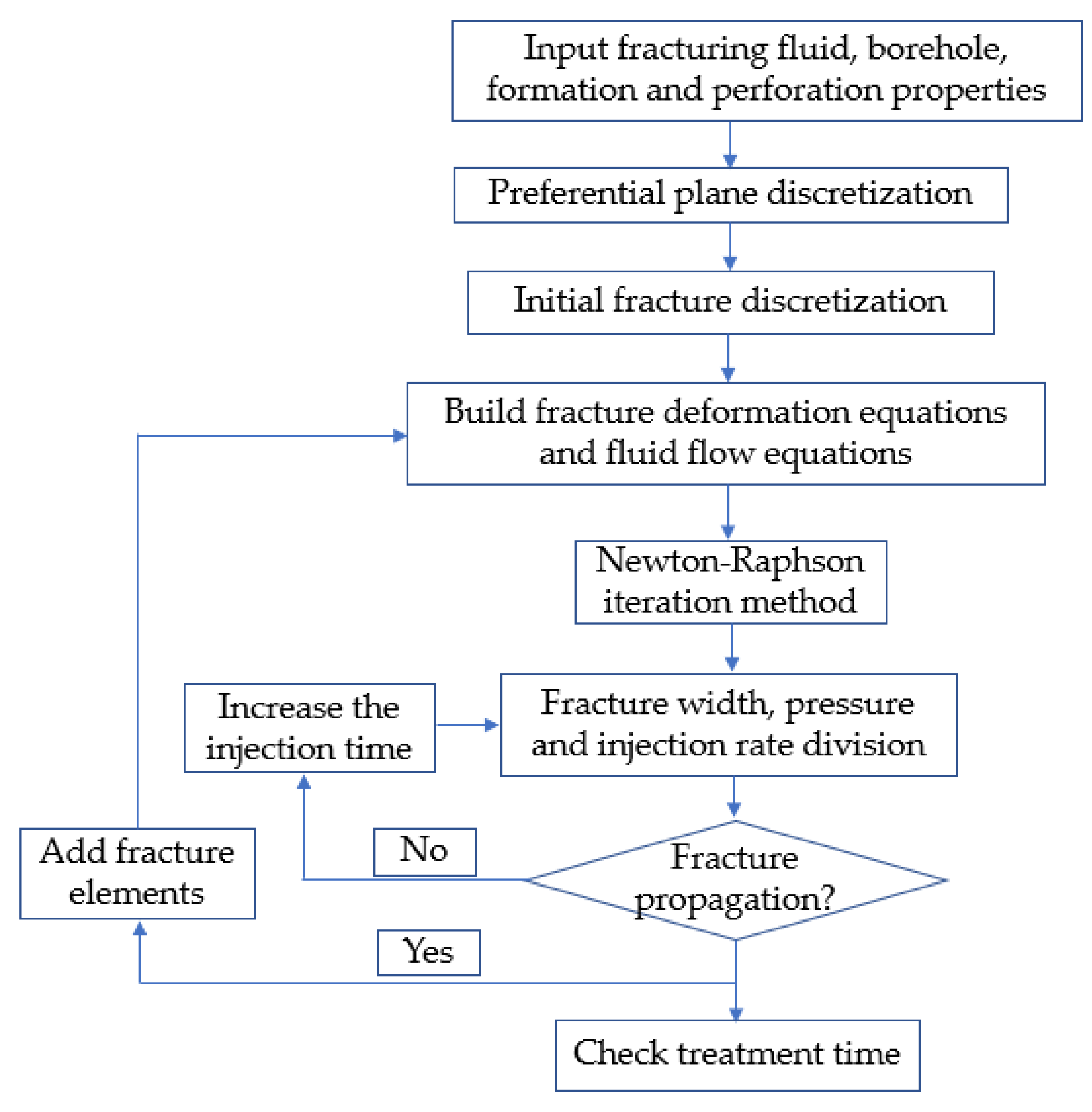
2.5. Fluid–Solid Coupling Method
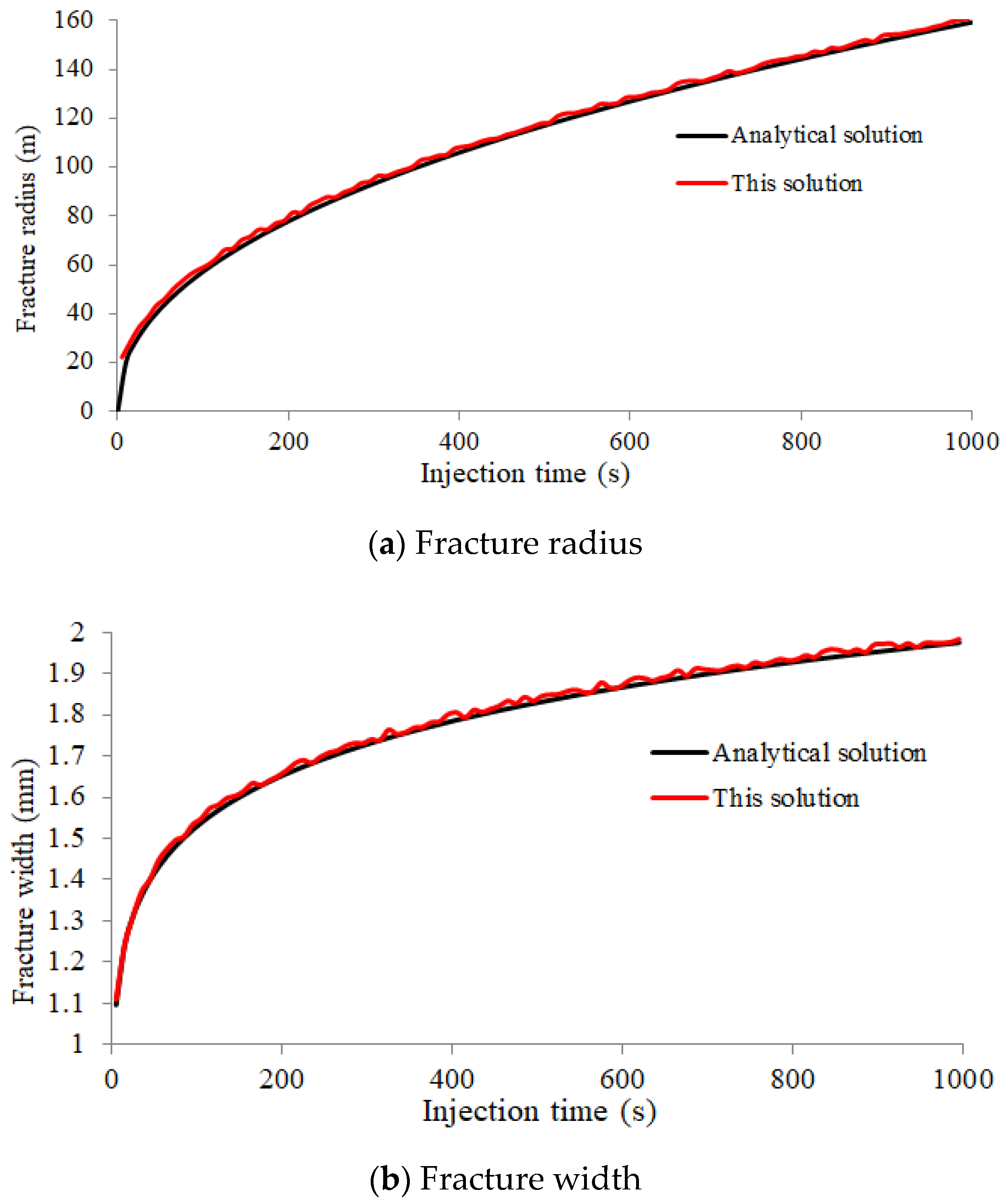
2.6. Benchmarking
3. Fracture Geometry and Stress Field Analysis
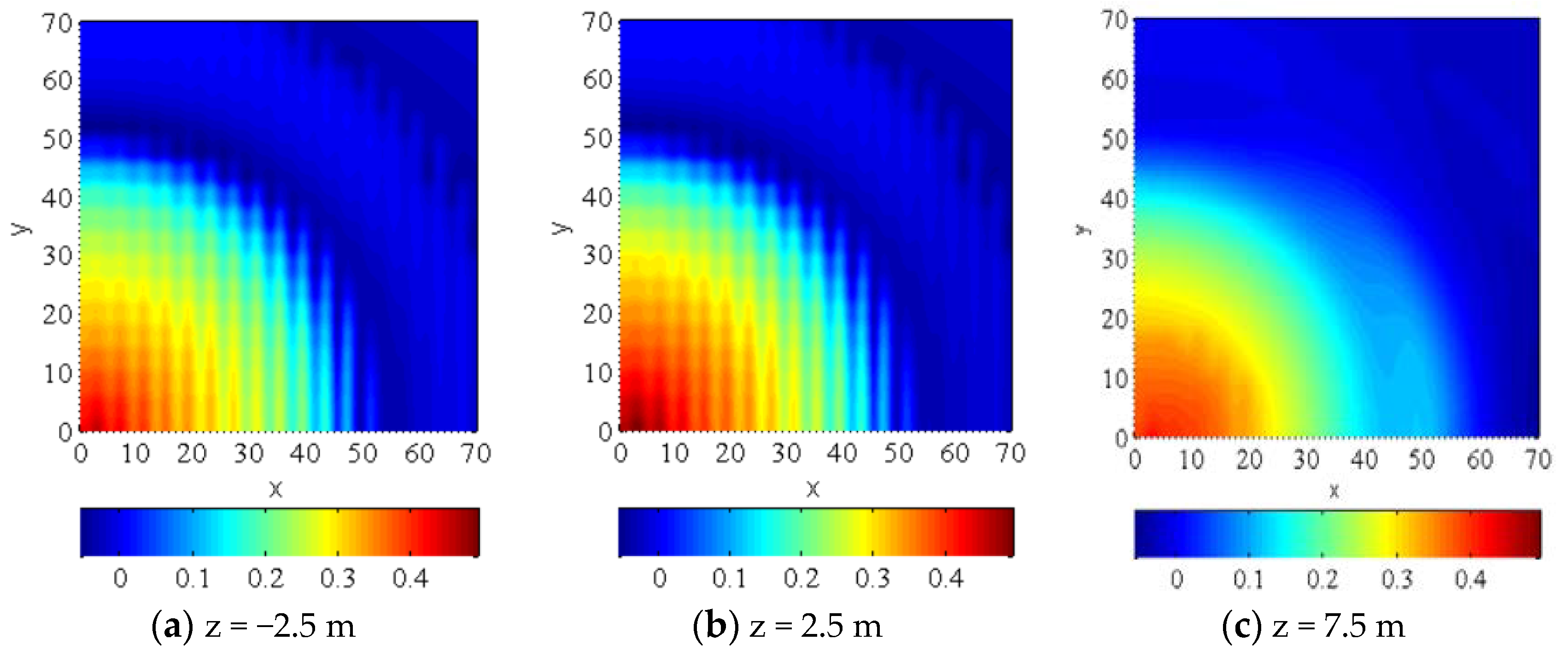
3.1. Fracture Geometry
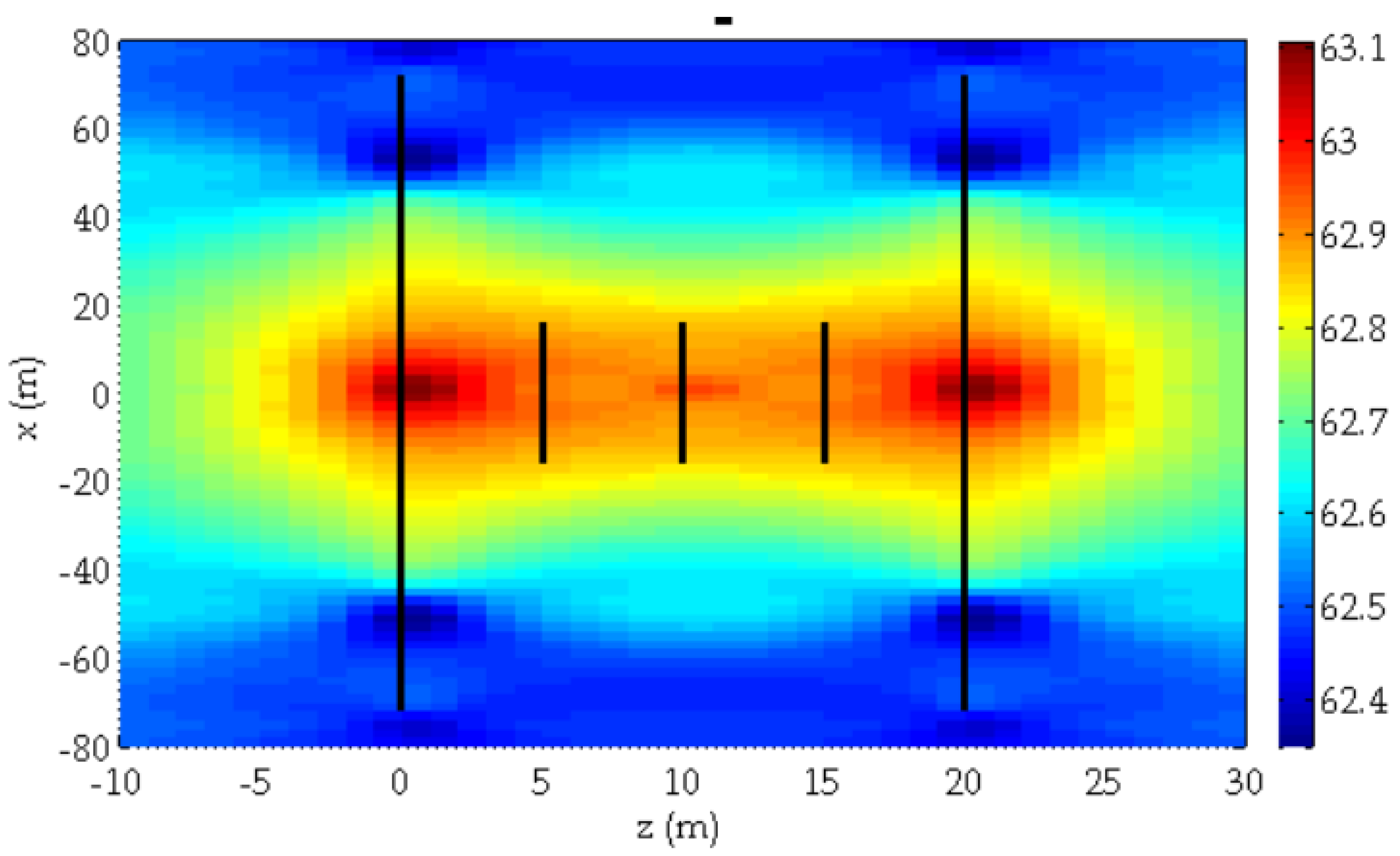
3.2. Stress Field
4. Perforation Parameter Optimization
4.1. Perforation Number Optimization
4.2. Perforation Cluster Number Optimization
4.3. Perforation Hole Diameter Optimization
5. Conclusions
- (1)
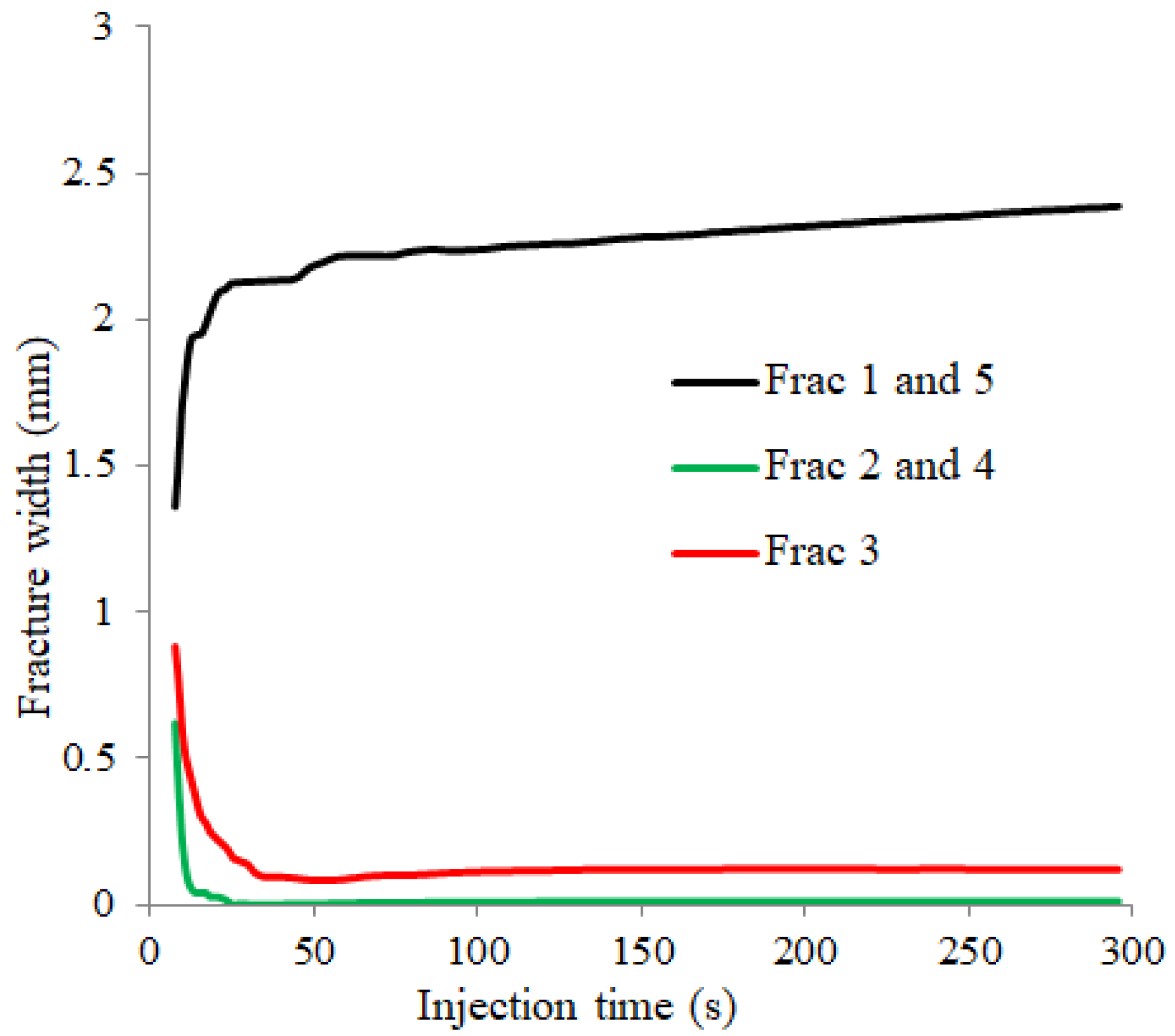
- Under the uniform perforation parameters, the exterior fractures become the main fractures with the largest widths, while the interior fractures are strongly restrained and have the smallest widths. The fracture geometry equilibrium is very low under the uniform perforation parameters. Due to the symmetry, the exterior fractures’ widths have the same variation versus the injection time. With increasing injection time, the fracture width increases drastically in the beginning and then gradually increases.
- (2)
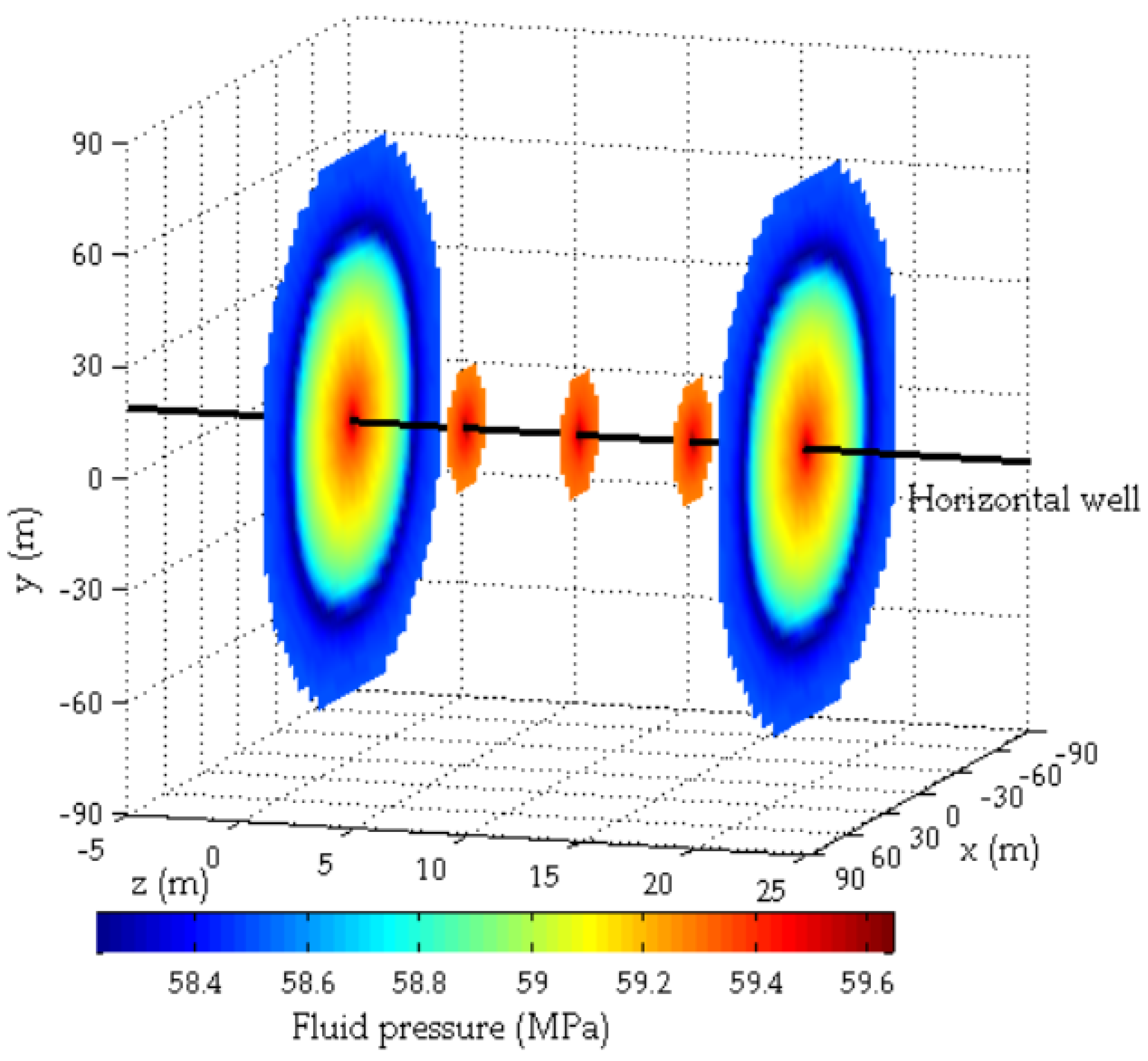
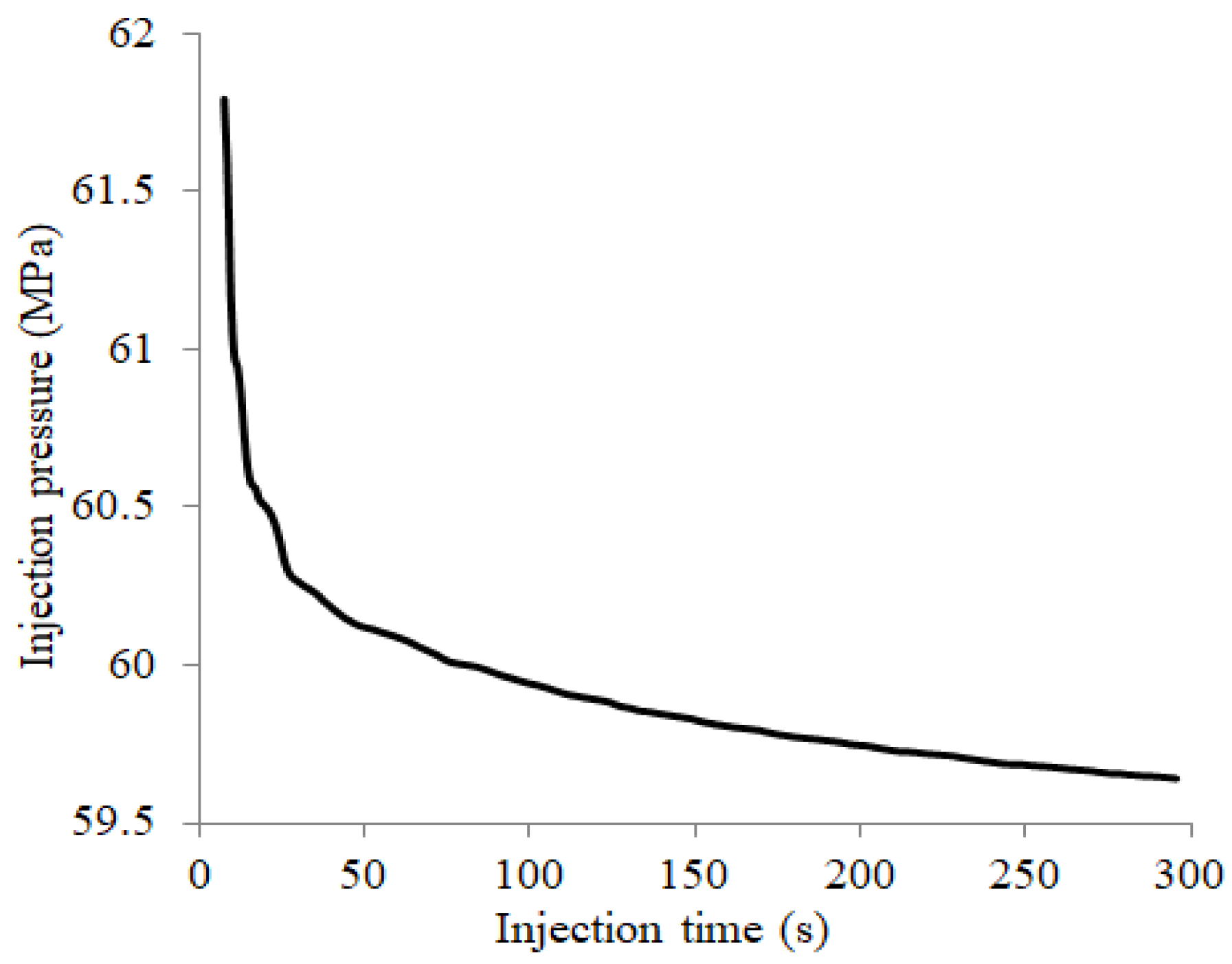
- The inlet’s fluid pressure is the highest, while the fluid pressure at the fracture tip is the lowest. The injection pressure declines rapidly in the beginning and then gradually declines later. The final injection pressure tends to the original minimum horizontal stress.
- (3)
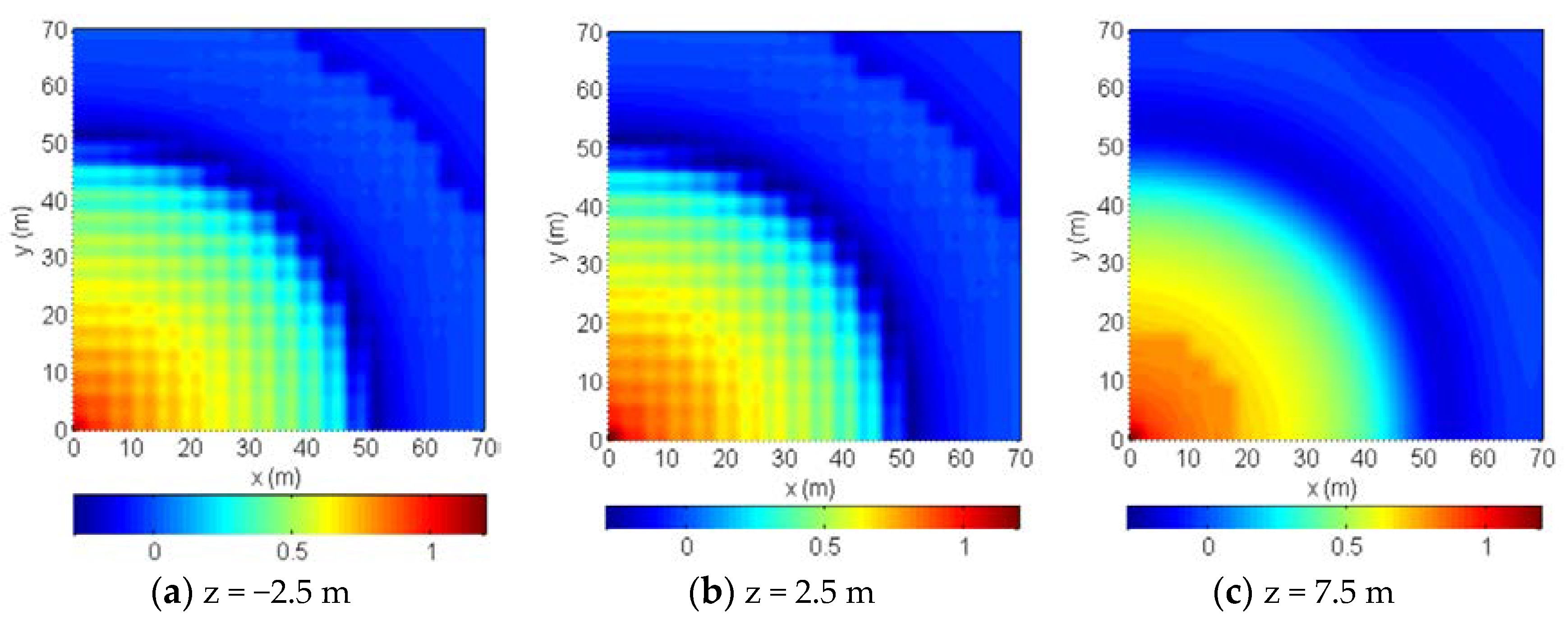
- The Szz in the middle area is much greater than the original minimum horizontal stress, indicating strong compression along the z-axis. In the area far from the horizontal well, Szz is less than the original minimum horizontal stress, indicating tension along the z-axis induced by the opening fracture. Due to the stress interaction, the interior fractures suffer strong compressive stress, and their propagations are strongly restrained.
- (4)
- The horizontal stress contrast in the middle area declines after the hydraulic fracturing process. The horizontal stress contrast in the far-field increases after the hydraulic fracturing process. The area close to the wellbore is more likely to include a complex fracture network after the intensive-stage fracturing process.
- (5)
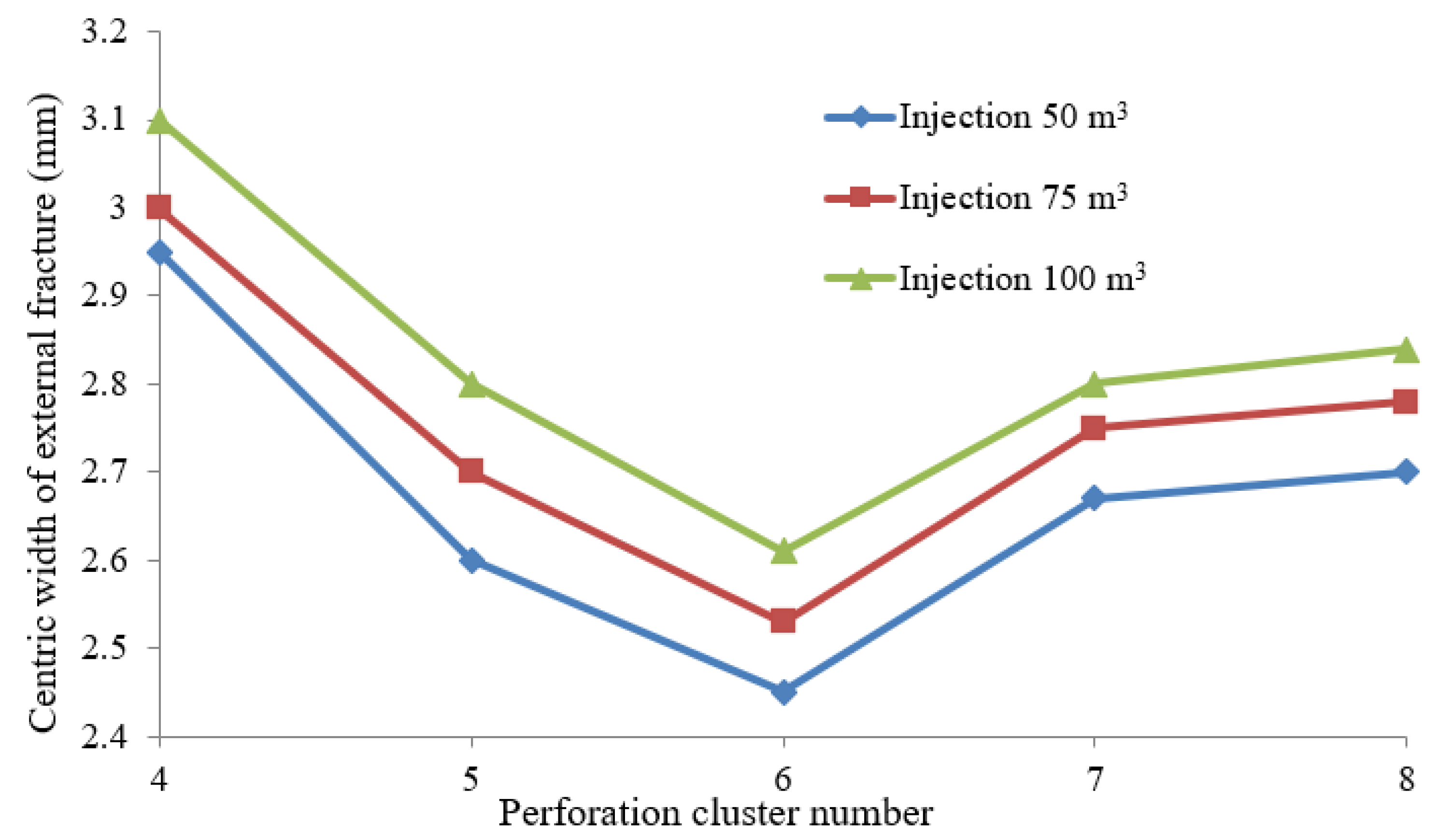
- Only increasing the perforation cluster number in each stage cannot improve the fracture geometry equilibrium in the intensive-stage fracturing. In this study, site 5-cluster perforation is the best choice for improving the stimulation efficiency. To improve the fracture geometry equilibrium, it is suggested to design more perforation numbers in each perforation cluster and ensure that both the perforation number and diameter in the interior perforation cluster are greater than those of the exterior ones.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2006, 44, 39–757. [Google Scholar] [CrossRef]
- Castonguay, S.T.; Mear, M.E.; Dean, R.H.; Schmidt, J.H. Predictions of the growth of multiple interacting hydraulic fractures in three dimensions. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013. [Google Scholar]
- Chan, H.C.M.; Li, V.; Einstein, H.H. A hybridized displacement discontinuity and indirect boundary element method to model fracture propagation. Int. J. Fract. 1990, 45, 263–282. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, S.; Xu, Y.; Ma, X.; Zou, Y. A numerical method for simulating planar 3D multi-fracture propagation in multi-stage fracturing of horizontal well. Pet. Explor. Dev. 2020, 47, 163–174. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Zhao, J.; Xu, W.; Fu, D. Numerical investigation for simultaneous growth of hydraulic fractures in multiple horizontal wells. J. Nat. Gas Sci. Eng. 2018, 51, 44–52. [Google Scholar] [CrossRef]
- Cheng, C.; Bunger, A.P.; Peirce, A.P. Optimal Perforation Location and Limited entry design for Promoting Simultaneous Growth of Multiple Hydraulic Fractures. SPE J. 2016, 21, 145–159. [Google Scholar]
- Cheng, W.; Jiang, G.; Jin, Y. Numerical simulation on fracture path and nonlinear closure for simultaneous and sequential fracturing in a horizontal Well. Comput. Geotech. 2017, 88, 242–255. [Google Scholar] [CrossRef]
- Cheng, W.; Jiang, G.; Tian, H.; Zhu, Q. Numerical investigations of the fracture geometry and fluid distribution of multistage consecutive and alternative fracturing in a horizontal well. Comput. Geotech. 2017, 92, 41–56. [Google Scholar] [CrossRef]
- Cheng, W.; Jiang, G.; Xie, J.; Wei, Z.; Zhou, Z.; Li, X. A simulation study comparing the Texas two-step and the multistage consecutive fracturing method. Pet. Sci. 2019, 16, 1121–1133. [Google Scholar] [CrossRef] [Green Version]
- Dontsov, E.V.; Suarez-Rivera, R. Propagation of multiple hydraulic fractures in different regimes. Int. J. Rock Mech. Min. Sci. 2020, 128, 104270. [Google Scholar] [CrossRef]
- Dontsov, E.V.; Peirce, A.P. A multiscale implicit level set algorithm (ILSA) to model hydraulic fracture propagation incorporating combined viscous, toughness, and leak-off asymptotics. Comput. Methods Appl. Mech. Eng. 2017, 313, 53–84. [Google Scholar] [CrossRef]
- Gunaydin, D.; Peirce, A.P.; Bunger, A. Laboratory experiments contrasting growth of uniformly and nonuniformly-spaced hydraulic fractures. J. Geophys. Res. Solid Earth 2021, 126. [Google Scholar] [CrossRef]
- He, J.; Zhang, Z.; Li, X. Numerical analysis on the formation of fracture network during the hydraulic fracturing of shale with pre-existing fractures. Energies 2017, 10, 736. [Google Scholar] [CrossRef] [Green Version]
- Long, G.; Xu, G. The effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J.; Liu, W.; Feng, Y.; Cao, W.; Wang, P.; Hou, Y. Numerical simulation of limited-entry multi-cluster fracturing in horizontal well. J. Pet. Sci. Eng. 2017, 152, 443–455. [Google Scholar] [CrossRef]
- Kumar, D.; Ghassemi, A. A three-dimensional analysis of simultaneous and sequential fracturing of horizontal wells. J. Pet. Sci. Eng. 2016, 146, 1006–1025. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Lian, H.; Rabczuk, T.; Bordas, S. Modelling hydraulic fractures in porous media using flow cohesive interface elements. Eng. Geol. 2017, 225, 68–82. [Google Scholar] [CrossRef]
- Olson, J.E.; Pollard, D.D. Inferring paleostresses from natural fracture patterns: A new method. Geology 1989, 17, 345–348. [Google Scholar] [CrossRef]
- Peirce, A.P.; Bunger, A. Interference fracturing: Nonuniform distributions of perforation clusters that promote simultaneous growth of multiple hydraulic fractures. SPE J. 2015, 20, 384–395. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Cai, Y.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Methods Eng. 2016, 108, 1451–1476. [Google Scholar]
- Ren, H.; Zhuang, X.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Methods Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef] [Green Version]
- Sesetty, V.; Ghassemi, A. A numerical study of sequential and simultaneous hydraulic fracturing in single and multi-lateral horizontal wells. J. Pet. Sci. Eng. 2015, 132, 65–76. [Google Scholar] [CrossRef]
- Shen, B.; Shi, J. A numerical scheme of coupling of fluid flow with three-dimensional. Eng. Anal. Bound. Elem. 2019, 106, 243–251. [Google Scholar] [CrossRef]
- Shou, K.J.; Siebrits, E.; Crouch, S.L. A higher order displacement discontinuity method for three-dimensional elastostatic problems. Int. J. Roch Mech. Min. Sci. 1997, 34, 317–322. [Google Scholar] [CrossRef]
- Tang, H.; Winterfeld, P.H.; Wu, Y.; Huang, Z.; Di, Y.; Pan, Z.; Zhang, J. Integrated simulation of multi-stage hydraulic fracturing in unconventional reservoirs. J. Nat. Gas Sci. Eng. 2018, 51, 44–52. [Google Scholar] [CrossRef]
- Tang, H.; Wang, S.; Zhang, R.; Li, S.; Zhang, L.; Wu, Y. Analysis of stress interference among multiple hydraulic fractures using a fully three-dimensional displacement discontinuity method. J. Pet. Sci. Eng. 2019, 179, 378–393. [Google Scholar] [CrossRef]
- Wang, W.; Dahi Taleghani, A. Simulating multizone fracturing in vertical wells. J. Energy Resour. Technol. 2014, 136, 124–136. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Simultaneous multifracture treatments: Fully coupled fluid flow and fracture mechanics for horizontal wells. SPE J. 2015, 20, 334–346. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. A simplified three-dimensional displacement discontinuity method for multiple fracture simulations. Int. J. Fract. 2015, 193, 191–204. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E.; Balhoff, M.; Yu, W. Numerical Analysis for Promoting Uniform Development of Simultaneous Multiple-Fracture Propagation in Horizontal Wells. SPE Prod. Oper. 2016, 32, 155–167. [Google Scholar]
- Wu, R.; Bunger, A.P.; Jeffrey, R.G.; Siebrits, E. A comparison of numerical and experimental results of hydraulic fracture growth into a zone of lower confining stress. In Proceedings of the 42nd U.S. Rock Mechanics Symposium, San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Vahab, M.; Khalili, N. X-FEM modeling of multizone hydraulic fracturing treatments within saturated porous media. Rock Mech. Rock Eng. 2018, 51, 3219–3239. [Google Scholar] [CrossRef]
- Xu, G. Interaction of multiple non-planar hydraulic fractures in horizontal wells. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar]
- Yew, C.H.; Weng, X. Mechanics of Hydraulic Fracturing [M]; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Zeng, Q.; Liu, W.; Yao, J. Numerical modeling of multiple fractures propagation in anisotropic formation. J. Nat. Gas Sci. Eng. 2018, 53, 337–346. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E. Modeling hydraulic fracture propagation and proppant transport in a two-layer formation with stress drop. Eng. Fract. Mech. 2018, 199, 705–720. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Yuan, W.; He, J.; Li, G.; Wu, Y. Numerical analysis on the optimization of hydraulic fracture networks. Energies 2015, 8, 12061–12079. [Google Scholar] [CrossRef]
- Zheng, Y.; Fan, Y.; Yong, R.; Zhou, X. A new fracturing technology of intensive stage+high-intensity proppant injection for shale gas reservoir. Nat. Gas Ind. 2020, 7, 292–297. [Google Scholar] [CrossRef]
- Zeller, S.S.; Pollard, D.D. Boundary conditions for rock fracture analysis using the boundary element method. J. Geophys. Res. 1992, 97, 1991–1997. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S.; Sheng, M.; Li, G. On the hydraulic fracturing in naturally-layered porous media using the phase field method. Eng. Geol. 2020, 266, 105306. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. An extended finite element solution for hydraulic fracturing with thermo-hydro-elastic–plastic coupling. Comput. Methods Appl. Mech. Eng. 2020, 364, 112967. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Tang, M.; Du, X.; Xu, C.; Tang, J.; Damjanac, B. Numerical investigation on hydraulic fracturing of extrenme limited entry perforating in plug-and-perforation completion of shale oil reservoir in Changqing oilfield, China. Rock Mech. Rock Eng. 2021, 02, 1–18. [Google Scholar]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modulus | 21 GPa | Fracturing fluid viscosity | 0.6 mPa·s |
| Poisson’s ratio | 0.2 | Injection rate | 5 m3/min |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modulus | 21 GPa | Fracture toughness | 1 MPa·m0.5 |
| Poisson’s ratio | 0.3 | Leakoff coefficient | 1.5 × 10−7 m/s0.5 |
| Fracturing fluid viscosity | 20 mPa·s | Perforation cluster spacing | 5 m |
| Injection rate | 5 m3/min | Perforation cluster number | 5 |
| Minimum horizontal stress | 58.5 MPa | Perforation number of each cluster | 15 |
| Maximum horizontal stress | 62.5 MPa | Diameter of perforation hole | 16 mm |
| Vertical stress | 85 MPa | - | - |
| No. | Perforation Number of 3 Clusters | Centric Width of Fracture (mm) | Fracture Surface Area (m2) |
|---|---|---|---|
| 1 | 10, 10, 10 | 2.3, 0.4, 2.3 | 8950, 1211, 8950 |
| 2 | 15, 15, 15 | 2.4, 0.3, 2.4 | 10,925, 1125, 10,925 |
| 3 | 20, 20, 20 | 2.45, 0.3, 2.45 | 11,525, 1125, 11,525 |
| 4 | 10, 15, 10 | 2.4, 0.3, 2.4 | 8325, 1325, 8325 |
| 5 | 10, 20, 10 | 2.42, 0.25, 2.42 | 8205, 1450, 8205 |
| 6 | 15, 10, 15 | 2.35, 0.23, 2.35 | 9488, 1104, 9488 |
| 7 | 15, 20, 15 | 2.35, 0.25, 2.35 | 9985, 1255, 9985 |
| 8 | 20, 10, 20 | 2.35, 0.23, 2.35 | 9488, 1104, 9488 |
| 9 | 20, 15, 20 | 2.35, 0.22, 2.35 | 9988, 1114, 9988 |
| Perforation Cluster Number | Injection Volume (m3) | Centric Width of Fracture (mm) | Fracture Surface Area (m2) |
|---|---|---|---|
| 4 | 50 | 2.95, 0.18, 0.18, 2.95 | 13,200, 1104, 1104, 13,200 |
| 75 | 3.0, 0.2, 0.2, 3.0 | 21,328, 1104, 1104, 21,328 | |
| 100 | 3.1, 0.2, 0.2, 3.1 | 34,128, 1104, 1104, 34,128 | |
| 5 | 50 | 2.6, 0.06, 0.1, 0.06, 2.6 | 29,968, 1104, 1104, 1104, 29,968 |
| 75 | 2.7, 0.05, 0.1, 0.05, 2.7 | 43,472, 1104, 1104, 1104, 43,472 | |
| 100 | 2.8, 0.05, 0.1, 0.05, 2.8 | 54,416, 1104, 1104, 1104, 54,416 | |
| 6 | 50 | 2.45, 0.08, 0.45, 0.45, 0.08, 2.45 | 27,024, 1552, 1232, 1232, 1552, 27,024 |
| 75 | 2.53, 0.08, 0.43, 0.43, 0.08, 2.53 | 40,656, 1552, 1232, 1232, 1552, 40,656 | |
| 100 | 2.61, 0.08, 0.43, 0.43, 0.08, 2.61 | 53,625, 1552, 1232, 1232, 1552, 53,625 | |
| 7 | 50 | 2.67, 0.05, 0.1, 0.1, 0.1, 0.05, 2.67 | 25,040, 1104, 1104, 1104, 1104, 1104, 25,040 |
| 75 | 2.75, 0.05, 0.1, 0.1, 0.1, 0.05, 2.75 | 37,480, 1104, 1104, 1104, 1104, 1104, 37,480 | |
| 100 | 2.8, 0.05, 0.1, 0.1, 0.1, 0.05, 2.8 | 49,480, 1104, 1104, 1104, 1104, 1104, 49,480 | |
| 8 | 50 | 2.7, 0.05, 0.1, 0.1, 0.1, 0.1, 0.05, 2.7 | 24,464, 1104, 1104, 1104, 1104, 1104, 1104, 24,464 |
| 75 | 2.78, 0.04, 0.1, 0.1, 0.1, 0.1, 0.04, 2.78 | 35,344, 1104, 1104, 1104, 1104, 1104, 1104, 35,344 | |
| 100 | 2.84, 0.04, 0.1, 0.1, 0.1, 0.1, 0.04, 2.84 | 41,296, 1104, 1104, 1104, 1104, 1104, 1104, 41,296 |
| No. | Perforation Diameter (mm) | Centric Width of Fracture (mm) | Fracture Surface Area (m2) |
|---|---|---|---|
| 1 | 12, 12, 12 | 3.2, 0.3, 3.2 | 30,100, 1125, 30,100 |
| 2 | 14, 14, 14 | 2.7, 0.4, 2.7 | 32,696, 1552, 32,696 |
| 3 | 16, 16, 16 | 2.5, 0.8, 2.5 | 37,400, 1552, 37,400 |
| 4 | 12, 14, 12 | 2.9, 0.45, 2.9 | 37,400, 1525, 37,400 |
| 5 | 12, 16, 12 | 2.8, 0.95, 2.8 | 39,000, 1525, 39,000 |
| 6 | 14, 12, 14 | 3.2, 0.3, 3.2 | 31,700, 1025, 31,700 |
| 7 | 14, 16, 14 | 2.6, 0.85, 2.6 | 37,400, 1552, 37,400 |
| 8 | 16, 12, 16 | 3.2, 0.25, 3.2 | 32,600, 985, 32,600 |
| 9 | 16, 14, 16 | 2.9, 0.4, 2.9 | 35,100, 1155, 35,100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Lu, C.; Xiao, B. Perforation Optimization of Intensive-Stage Fracturing in a Horizontal Well Using a Coupled 3D-DDM Fracture Model. Energies 2021, 14, 2393. https://doi.org/10.3390/en14092393
Cheng W, Lu C, Xiao B. Perforation Optimization of Intensive-Stage Fracturing in a Horizontal Well Using a Coupled 3D-DDM Fracture Model. Energies. 2021; 14(9):2393. https://doi.org/10.3390/en14092393
Chicago/Turabian StyleCheng, Wan, Chunhua Lu, and Bo Xiao. 2021. "Perforation Optimization of Intensive-Stage Fracturing in a Horizontal Well Using a Coupled 3D-DDM Fracture Model" Energies 14, no. 9: 2393. https://doi.org/10.3390/en14092393
APA StyleCheng, W., Lu, C., & Xiao, B. (2021). Perforation Optimization of Intensive-Stage Fracturing in a Horizontal Well Using a Coupled 3D-DDM Fracture Model. Energies, 14(9), 2393. https://doi.org/10.3390/en14092393






