Analysis of the Magnetohydrodynamic Behavior of the Fully Developed Flow of Conducting Fluid

Abstract

Important industrial applications are based on magnetohydrodynamics (MHD), which concerns the flow of electrically conducting fluids immersed in external magnetic fields. Using the Finite Volume Method, we performed a 3D numerical study of the MHD flow of a conducting fluid in a circular duct. The flow considered was laminar and fully developed. Along the initial section of the duct, there were magnets placed around the duct producing magnetic fields in the radial direction. Two arrangements of magnetic field orientation were considered: fields pointing toward and away from the duct’s center alternately, and all fields pointing toward the duct’s center. For each arrangement of magnets, various intensities of magnetic fields were considered to evaluate two effects: the influence of the magnetic field on the flow velocity, and the influence of the flow velocity on magnetic field induction. It was found that for the second arrangement of magnets and Hartmann numbers larger than 10, the flow velocity was reduced by as much as 35%, and the axial magnetic induction was as high as the field intensity applied by each magnet. Those effects were negligible for the first arrangement and low fields because of the distribution of field lines inside the duct for these situations.

1. Introduction

Magnetohydrodynamics (MHD) is the study of interactions due to the relative movement between magnetic fields and electrically conducting fluids [1]. The seminal works of Hartmann [2] and Alfvén [3] initiated this field of study, laying out the fundamental principle of MHD: “If a conductive fluid moves immersed in a magnetic field, the induced currents tend to inhibit flow velocity, which in turn changes the magnetic field”.

Over the years, this fundamental principle of MHD was discovered to yield several phenomena of practical interest. This motivated the application of magnetohydrodynamic analysis to engineering as of the 1960s, and it has been gaining increasing attention in the literature [1,4,5,6] due to environmental and energy concerns.

There are many traditional industrial applications of MHD, such as electromagnetic pumping, metallurgy, nuclear fusion reactors and power generation [1,7]. Other applications are in aluminum reduction cells and electromagnetic launchers. The reason for the wide use of MHD is that it provides a non-invasive way of controlling the flow of conducting fluids [1].

In metallurgy, magnetohydrodynamics is routinely used to heat, pump, stir, damp and levitate liquid metals [8]. The work [9] analyzed the magnetohydrodynamic instabilities in aluminum reduction cells. MHD instabilities refer to the interfacial gravity waves developing at the electrolyte–aluminum interface. A mathematical model was developed that described the MHD physics involved, including the distribution of magnetic field and current density. The model was solved numerically to analyze the influences of factors such as current intensity and distance between the anode and cathode on instability. Results showed that the factors with the greatest influence on instability are current intensity and current perturbations in the anode and cathode. One useful principle of MHD is damping, whereby the velocity of conducting fluids immersed in magnetic fields is reduced. In the steel continuous-casting process, for example, electromagnetic braking is widely used to control the flow of molten steel into the casting molds in a double-roll pattern [10]. Reference [10] presents a numerical study of the transient MHD turbulent flow in continuous-casting molds. The influences of several boundary conditions on the flow and on electromagnetic fields, such as wall conductivity, were studied. For insulating walls, the authors observed that the flow is more unstable and subjected to low-frequency oscillation, whereas for conducting walls the flow is more stable due to the larger induced currents, which gives rise to Lorentz forces.

In nuclear fusion, magnetic fields are employed to confine the very-high temperature plasma away from the reactor walls. A promising use case of nuclear fusion is to produce electricity from the heat of fusion reactions. A recent article [11] brought important contributions to the MHD modelling of reversed-field pinch (RFP) plasmas. RFP is a technology used in nuclear fusion reactors that employs toroidal pinch with a unique magnetic field configuration to confine hot plasmas. In the RFP configuration, a global self-organization process occurs for high currents that imposes a helical format to the plasma, which is beneficial to confinement. Among the contributions of the paper, it was shown that the occurrence of new helical states, as predicted by the nonlinear MHD model, can be confirmed by measurements in a RFP reactor. Reference [12] covers liquid metal fusion blanket, which is a promising technology for nuclear fusion reactors due in part to efficient thermoelectric conversion. In those reactors, the motion of liquid metal under strong magnetic fields causes serious MHD effects, such as the buoyancy due to non-uniform volumetric heat deposited by fusion neutrons. Those effects can significantly change flow field; thus, they need to be investigated. In the paper, they studied the MHD buoyant flow of a dual functional lead lithium (DFLL) blanket under typical magnetic fields and non-uniform volumetric nuclear heating. They also evaluated the MHD buoyant effect on the thermal distribution in the DFLL blanket. Based on the findings, suggestions were given to optimize the blanket design.

Other means of MHD power generation include propelling ionized gases through magnetic fields. Reference [13] is related to two-phase liquid metal MHD (LMMHD) power generation systems, in which a low-boiling gas and high-temperature liquid metal (heated by a source like solar energy, geothermal etc) are mixed, and the resulting fluid flows through a transverse magnetic field, where electricity is generated. They performed a numerical analysis study to determine the influences of related variables in the mixing process and the two-phase flow characteristics, which significantly affect the generation efficiency. A major challenge hindering the wide use of LMMHD and other types of thermal generators is the low power conversion efficiency. Analyses of exergy [14] and the optimization of operating conditions, using, for example, genetic algorithms as in [15], are essential to the design of thermal machines of improved efficiency. In [16], a new configuration of disk MHD generator was proposed, in which the apparatus is segmented into several parts. The proposed generator was modeled in numerical simulations, and the results showed that the novel design weakened tangential currents, which reduced Lorentz forces and in turn improved plasma uniformity and ionization stability. The results were higher energy conversion efficiency and power output.

The use of magnetic fields has also been proposed as an anti-scaling technology. It attracts interest, as it would be a cheaper and more environmentally friendly alternative than the traditional chemical treatment. Reference [17] reviews past uses of magnetic fields in water treatment systems for fouling prevention, and discusses the possible physical mechanisms involved. Although there are many documented cases of successful uses of magnetic devices for fouling prevention, the physical mechanisms involved are not yet fully understood, which brings skepticism to the technique [17]. Despite this issue, a Brazilian oil company has been investigating the use of magnetic devices to prevent or delay fouling in oil pipes [18]. The potential of this technology was demonstrated by a laboratory experiment which showed that the use of magnetic fields reduces the precipitation of the chemical substance commonly found in oil pipe incrustations. The work also reported experimental tests carried out by the oil company in which prototype magnetic devices were installed around pipes in an oil extraction facility [18]. Manual inspections revealed a significant reduction of fouling in the pipes, leading to operational cost savings and less maintenance interventions.

The aforementioned works cover several MHD applications based on different underlying physical principles. The principle of interest in this paper is magnetic braking, whereby the relative movement between the fluid and applied magnetic field generates induces currents, which reduce flow velocity by means of Lorentz forces. Of the works mentioned, the control of liquid metal movement [10] and most likely the anti-scaling technology [17,18] are also based on this principle. In the MHD analyses of many works, the magnetic field is assumed to be uniform, which is an idealization. One of the novelties of this paper is that it considers a realistic distribution of the magnetic field, obtained with magnets.

The classic MHD formulation describes physical phenomena accurately for a wide range of physical conditions. However, for very high temperature and low fluid density—in which microscopic and macroscopic dynamics are weakly linked—such a formulation has poor accuracy. When an electrically conducting fluid flows in the presence of electromagnetic fields, the relative movement induces electric currents, which in turn generate secondary fields that affect the primary field. This two-way coupling must be taken into account for realistic formulations. In the framework of continuous mechanics, by neglecting the effect of rarefied gases, the classic formulation of MHD was established by integrating Maxwell’s equations of electromagnetics with Navier–Stokes equations of fluids [19].

Multiphysics problems involving electromagnetics are complex and usually solved by means of numerical methods. Electromagnetic phenomena are most commonly solved with the Finite Element Method (FEM) [20,21]. In Computational Fluid Dynamics (CFD), on the other hand, the Finite Volume Method (FVM) is the favorable solution [22,23,24] due to its conservative properties [25].

In this context, this paper presents a 3D numerical analysis of the magnetohydrodynamics behavior of the laminar flow of a conducting fluid in a circular duct. We verify the influence of the magnetic field on the flow velocity due to induced currents, along with the changes in magnetic field induced by flow velocity. For the first time, the analysis considers different configurations of magnetic field in the duct walls.

2. Multiphysics Magnetohydrodynamic Equations

Before presenting the results and contributions of this work, in this section the main equations governing the multiphysics phenomena of interest are reviewed.

2.1. Maxwell’s Equations

Maxwell’s equations govern electromagnetic phenomena, and are given by [26,27]

$$\nabla \times \overrightarrow{B}=\mu \overrightarrow{J}$$

(1)

$$\nabla \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$$

(2)

$$\nabla ·\overrightarrow{B}=0$$

(3)

$$\nabla ·\overrightarrow{D}={\rho }_c,$$

(4)

where $\overrightarrow{B}$ is the magnetic flux density, $\overrightarrow{D}$ the electric flux density, $\overrightarrow{J}$ the current density, $\overrightarrow{E}$ the electric field, $\mu$ the magnetic permeability and ${\rho }_c$ the electric charge density. Equation (1) shows Ampère’s law, (2) is Faraday’s law, (3) is Gauss’ law for magnetic fields and (4) is the Gauss’ law for electric fields.

Ohm’s law is also necessary for this analysis:

$$\overrightarrow{J}=\sigma \left(\overrightarrow{E}+\overrightarrow{u}\times \overrightarrow{B}\right),$$

(5)

where $\sigma$ is the electrical conductivity and $\overrightarrow{u}$ is the velocity vector.

2.2. Magnetohydrodynamics Equations

The governing equations for an electrically conducting, incompressible Newtonian fluid are obtained by coupling Maxwell’s equations for electromagnetism with Navier–Stokes equations for fluid dynamics [26]:

$$\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}·\nabla \overrightarrow{u}=-\frac{1}{\rho }\nabla p+\frac{\eta }{\rho }{\nabla }^2\overrightarrow{u}+\frac{1}{\rho }\left(\overrightarrow{J}\times \overrightarrow{B}\right),$$

(6)

where p is pressure, $\rho$ is the density of the fluid and $\eta$ is the dynamic viscosity of the fluid.

For incompressible fluids, the continuity law applies [26]:

$$\nabla ·\overrightarrow{u}=0.$$

(7)

The above equations can be written in their nondimensional forms as

$$\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}·\nabla \overrightarrow{u}=-\nabla p+\frac{1}{\mathrm{Re}}{\nabla }^2\overrightarrow{u}+\mathrm{Al}\left[\left(\nabla \times \overrightarrow{B}\right)\times \overrightarrow{B}\right]$$

(8)

and

$$\frac{\partial \overrightarrow{B}}{\partial t}=\nabla \times \left(\overrightarrow{u}\times \overrightarrow{B}\right)+\frac{1}{{\mathrm{Re}}_{\mathrm{m}}}{\nabla }^2\overrightarrow{B},$$

(9)

where $\mathrm{Re}=\rho UL/\eta$, ${\mathrm{Re}}_{\mathrm{m}}=\mu \sigma UL$ and $\mathrm{Al}=B_0^2/\left(\mu \rho U^2\right)$ denote the Reynolds, magnetic Reynolds and Alfvén numbers, respectively. U, L and $B_0$ denote, respectively, the characteristic velocity, characteristic length and intensity of magnetic flux density. For circular pipes, usually L is the pipe diameter and U is the average of flow velocity over the cross-section.

The Reynolds number is the ratio of induced to applied components of magnetic field. The Alfvén number is the relation of applied magnetic energy to kinetic energy. Formula (8) is the Navier–Stokes equations with the addition of the Lorentz force component. Equation (9) is the Maxwell equation coupled in a nonlinear fashion with (8).

The Hartmann number (Ha) and Stuart number (N) are calculated, respectively, as ${\mathrm{Ha}}^2={\mathrm{ReRe}}_{\mathrm{m}}\mathrm{Al}$ and $N={\mathrm{Re}}_{\mathrm{m}}\mathrm{Al}$.

The Hartmann parameter is the ratio of electromagnetic and viscous forces on the fluid, as given by (10). It measures how far the fluid behavior is from its standard hydrodynamic behavior.

$$\mathrm{Ha}={\left(\frac{\mathrm{Electromagnetic}\mathrm{forces}}{\mathrm{Viscous}\mathrm{forces}}\right)}^{1/2}=B_{0}L\sqrt{\frac{\sigma }{\rho \nu }},$$

(10)

where $\nu =\eta /\rho$ is the kinematic viscosity of the fluid.

The Stuart number quantifies the relative intensity between the electromagnetic and inertial forces. It is related to Ha and Re by means of [28]

$$N=\frac{\mathrm{Electromagnetic}\mathrm{forces}}{\mathrm{Inertial}\mathrm{forces}}=\frac{{\mathrm{Ha}}^2}{\mathrm{Re}}=\frac{B_0^{2}L\sigma }{\rho U}=\frac{L}{U\tau }.$$

(11)

The term $\tau =\rho /\left(\sigma B_0^2\right)$ is named magnetic damping time and quantifies the characteristic time during which the flow’s kinetic energy is dissipated by the magnetic field. If $N\ll 1$, $\tau$ is large and the electromagnetic drag has little influence on the flow. Otherwise, Lorentz forces dominate the flow, which is then regarded as inertia-less.

The electromagnetic drag caused by Lorentz forces depends on the paths of induced currents in the fluid. The average resistivity along the current’s path influences the magnetohydrodynamic pressure drop, and the path geometry may result in local areas of reduced Lorentz forces. Flow characteristics are influenced by the wall conductance ratio (c), which is a relation between the duct wall’s and fluid’s conductivities calculated as [28]

$$c=\frac{{\sigma }_w}{\sigma }\frac{t}{L}.$$

(12)

Very low values of wall conductance ratio ($c\to 0$) correspond to walls of poor conductivity, whereas $c>1$ refers to walls of non-negligible conductivity. Even slight differences of c can result in significantly different flow characteristics. There are three special cases of MHD flow in rectangular ducts as a function of c: Shercliff [29], Ufland [28] and Hunt [30] flows. In the Shercliff flow, all duct walls are perfect insulators ($c=0$), whereas for the Ufland case the walls are perfect conductors ($c=\infty$). In the Hunt flow, the walls parallel to the applied magnetic field are perfectly insulating, and the walls perpendicular to the magnetic field have non-zero finite conductivity.

2.3. Analytical Equations for Fully Developed MHD Flow in Circular Pipes

The MHD flow of conducting fluids in circular pipes has attracted much attention by researchers due to its industrial applications. Works such as [31,32] have derived analytical equations for the scenario of a conducting fluid flowing in a circular pipe of insulated walls, immersed in a uniform transverse magnetic field. Those equations are briefly shown here, as they will be used in Section 4.4 for analytical verification of the numerical simulations of this paper.

Equations are given in cylindrical coordinates $(r,\theta )$, with the origin at the center of the duct’s cross-section. r is the radial distance to the duct axis and $\theta$ is the angle relative to the direction of applied magnetic field.

Let the pipe be oriented in the x direction and a be the pipe radius. The analytical equations of flow velocity $u_x$[32] and induced magnetic field $H_x$ [31] in the axial direction are given by

$$\begin{array}{cc}\hfill \frac{u_x(r,\theta )}{U}=-\frac{K}{\mathrm{Ha}}[& cosh(\alpha rcos\theta )\sum _{n=0}^{\infty }{ϵ}_n\frac{I_{2n}^{{}^{\prime }}\left(\alpha \right)}{I_{2n}\left(\alpha \right)}{I}_{2n}\left(\alpha r\right)cos\left(2n\theta \right)\hfill \\ \hfill & -sinh(\alpha rcos\theta )\sum _{n=0}^{\infty }2\frac{I_{2n+1}^{{}^{\prime }}\left(\alpha \right)}{I_{2n+1}\left(\alpha \right)}{I}_{2n+1}\left(\alpha r\right)cos\left((2n+1)\theta \right)]\hfill \end{array}$$

(13)

and

$$\frac{H_x(r,\theta )}{U\sqrt{\sigma \eta }}=-\frac{K}{2\mathrm{Ha}}\left[\sum _{n=-\infty }^{\infty }\left(e^{-\alpha rcos\theta }-{(-1)}^n{e}^{\alpha rcos\theta }\right)\frac{I_n^{{}^{\prime }}\left(\alpha \right)}{I_n\left(\alpha \right)}{I}_n\left(\alpha r\right)e^{in\theta }-2rcos\left(\theta \right)\right],$$

(14)

where $\alpha =\mathrm{Ha}/2$; $K=\frac{a^2}{U\eta }\frac{\partial p}{\partial x}$; ${ϵ}_n$ equals 1 for $n=0$ or 2 for $n>0$; $i=\sqrt{-1}$; $I_n$ is the modified Bessel function of the first kind of order n and $I_n^{{}^{\prime }}\left(x\right)=\frac{1}{2}\left(I_{n-1}\left(x\right)+I_{n+1}\left(x\right)\right)$. In those equations, Ha is the Hartmann number calculated considering the duct radius as the characteristic length ($L=a$).

3. Finite Volume Method for Magnetohydrodynamic Problems

Computational Fluid Dynamics (CFD) is a widely used computer aided engineering tool. It is composed of a well-established set of numerical techniques, such as Finite Element Analysis, which has been used in the design of solid mechanics and vibration engineering problems since the mid-1980s. The Finite Volume Method is another important technique in the CFD field [33], and one of its main applications is the numerical calculation of the Navier–Stokes equation. The Navier–Stokes equation accurately models several fluid phenomena, ranging from turbulent or laminar single-phase incompressible flows to compressible multiphase flows.

Numerical methods solve complicated equations by means of approximations. Certain constraints must be met in order for those approximations to converge to the exact solution in a stable manner [28]. For a 2D problem, the Courant–Friedrichs–Lewy condition ($\mathcal{C}$) must be obeyed

$$\mathcal{C}\le 0.5.$$

(15)

Other conditions must be satisfied due to the coupling between fluid velocity and magnetic field. One in particular is the following relation between the magnetic damping time $\tau$ and the time step $\Delta t$ [1], given by

$$\Delta t<\tau .$$

(16)

The von Neumann stability analysis for a one-dimensional simulation gives rise to the $\mathcal{L}$ parameter, equal to

$$\mathcal{L}=\frac{\sigma B_0^2\Delta t}{\rho }.$$

(17)

For a stable numerical scheme, the relation $\mathcal{L}\le 2$ must be satisfied (with the exception of $\mathcal{L}=1$). The highest accuracy was observed for $\mathcal{L}\to 2$ and $\mathcal{L}\to 0$, and in 3D simulations the value $\mathcal{L}<0.2$ is recommended for performance reasons [34]. For higher values of Hartmann number, the condition on $\mathcal{L}$ is the most strict. Furthermore, for a monotone scheme, the following condition must be met:

$$\mathcal{C}+2\mathcal{L}+\frac{\nu \Delta t}{{(\Delta x)}^2}\le 1,$$

(18)

where $\Delta x$ is the spatial step.

4. Magnetohydrodynamic Model in a Duct

4.1. OpenFOAM Numerical Software for Solving MHD Problems

The problems analyzed in this paper were numerically modeled with the Finite Volume Method, by means of the MHD standard solver (named “mhdFoam”) of OpenFOAM software [35]. OpenFOAM is well-established in academia and industry for solving real-world problems in continuum mechanics, particularly those related to CFD.

The used solver mhdFoam is based on the magnetic induction formulation and was first proposed in [36]. It is applicable for solving MHD problems of laminar flows and incompressible fluids, considering the bi-directional coupling between the magnetic field and velocity fields [28].

After discretizing the analysis domain in polyhedral cells with a proper mesh, mhdFoam approximates the MHD equations of Section 2.2 into a system of algebraic equations, which are solved with a finite-volume cell-centered approach iteratively in time. The coupling between pressure and velocity is achieved with a PISO-like algorithm [28,36].

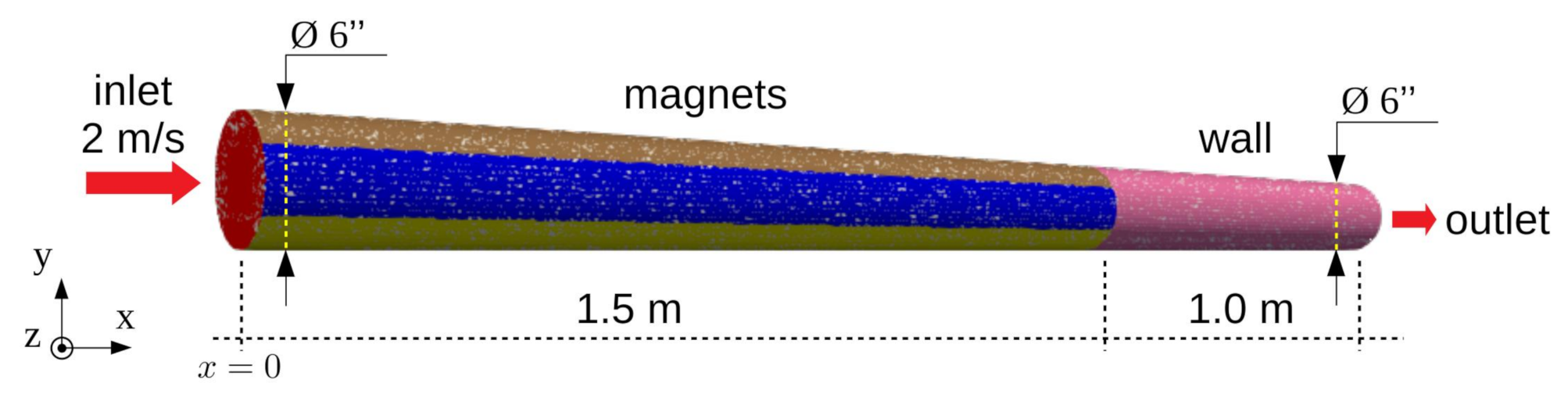
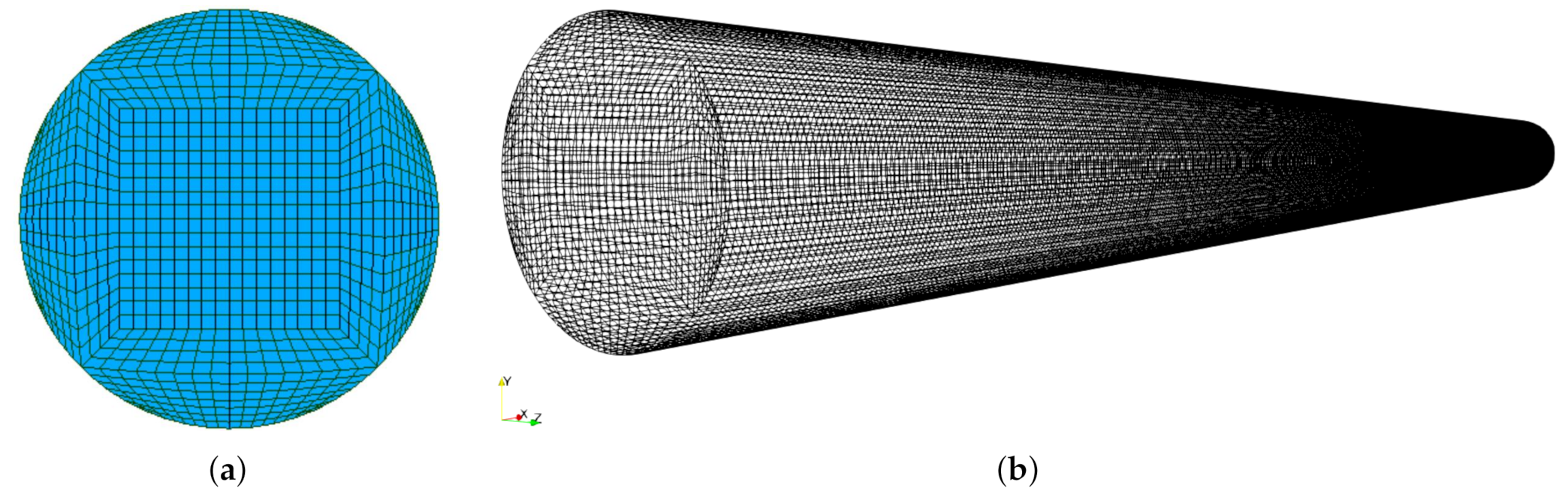
4.2. Geometry Model

The modeled 3D geometry is shown in Figure 1. The duct was 2.5 m-long cylinder, with a 6-inch diameter. The first 1.5 m-long section of the duct was under the influence of magnetic fields generated by magnets placed around the duct; there were no magnets in the final 1.0 m-long section. The fluid flow was fully developed, with a velocity of 2 m/s at the duct’s inlet, as shown in Figure 1. The duct walls were perfectly insulated.

Six magnets were placed in a circular manner around the duct, as shown in the cross-section view of Figure 2. Each magnet was 1.5 m-long in the x axis, starting from the inlet. Their magnetic fields were orientated radially relative to the duct, pointing either outward from or inward to the center of the duct cross-section. A combination of directions of the magnetic fields produced by magnets is called a magnetic configuration. In this analysis, two magnetic configurations were considered. The first was of attractive nature (Figure 2a), where the magnetic field of each magnet had the same direction of the field of the diametrically opposed magnet, and had opposite direction to its neighboring magnets. The second configuration was repulsive (Figure 2b), in which all magnetic fields pointed towards the center of the duct’s cross-section.

4.3. Parameters of MHD Simulations

In the 3D computational simulations using OpenFOAM, a 10%-hydrochloric acid solution (10% HCl) was considered, for which $\rho =1\times {10}^3$ kg/m³, the magnetic permeability was $0.999991{\mu }_0$ kg.m/s². A² (${\mu }_0$ is the magnetic permeability of free space), $\sigma =70.9$ S/m and the kinematic viscosity was $\nu =3.81\times {10}^{-4}$ m²/s. Flow was of laminar nature and the fluid was incompressible, with $\mathrm{Re}=800$ and ${\mathrm{Re}}_{\mathrm{m}}=2.7156\times {10}^{-5}$. Four scenarios were analyzed, in which the magnets around the duct generate magnetic induction of intensities 0.5, 1.2, 5 and 10 T, for which the Hartmann numbers were, respectively, ${\mathrm{Ha}}_1=1.0395$, ${\mathrm{Ha}}_2=2.4947$, ${\mathrm{Ha}}_3=10.3948$ and ${\mathrm{Ha}}_4=20.7896$. Such values were chosen to facilitate experimental validation in future works. Moreover, all simulations were performed with time step $\Delta t={10}^{-4}$ s.

Simulations were performed using the aforementioned parameters for the attractive and repulsive configurations of the magnets (Figure 2); the case without external magnetic influence (no magnets) was also considered for comparison purposes. Profiles of several quantities (e.g., velocity profile) were analyzed along the duct at the x positions 0.5 m (initial portion of the duct with the presence of magnets), 1.0 m (magnets are present), 1.5 m (transition zone) and 2.0 m (no magnets). Those position values were measured from the duct’s inlet along the x axis (Figure 1).

In all simulations, the region of analysis was spatially discretized with the mesh shown in Figure 3. The mesh was structured and composed of 480 thousand hexaedrical cells. Cells of different sizes were used (non-uniform mesh). In the central region of the cross-section, cells were arranged approximately as a rectangular grid, but toward the duct walls, cells were of smaller size and their shape conformed to the rounded border (Figure 3a). A more refined discretization near the border was essential for accurate results, due to the higher velocity gradients caused by the higher shear stress imposed by the duct walls [28]. The smallest spatial step used in the mesh was $5\times {10}^{-4}$ m.

Regarding boundary conditions, the no-slip condition ($\overrightarrow{u}=0$) was used at the duct walls, with fixed flow velocity of 2 m/s at the inlet and zero pressure at the outlet. The magnetic induction produced by magnets was modeled as a uniform field on the entire surface of the magnets’ poles.

Despite the highly robust numerical software used, the methodology has its limitations. First, it is difficult to experimentally reproduce the simulations, because of the large dimensions of magnets (1.5 m-long) and the strong magnetic fields (as high as 10 T) involved. Another limitation is that simulations did not model the distortion that the induced currents in the fluid impose on the external magnetic field. However, that is not an issue because this effect is negligible for ${\mathrm{Re}}_{\mathrm{m}}\ll 1$ [34], which is the case in this paper.

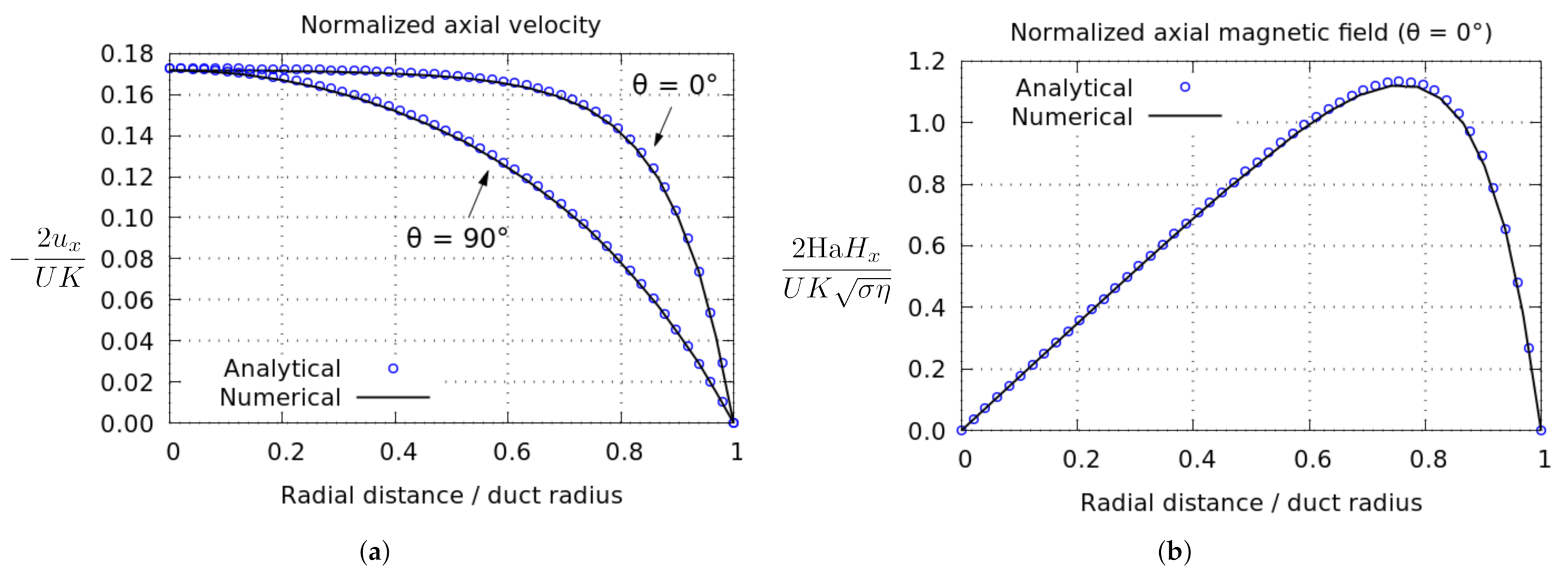
4.4. Verification of Results

In this section, the numerical setup (geometry, mesh, software, time step and most boundary conditions) described in Section 4.2 and Section 4.3 is verified through a slightly different scenario, by comparing the numerical results to the analytical solutions. The case analyzed in this verification was briefly reviewed in Section 2.3; it is the same as the one of Section 4.2 and Section 4.3, except that instead of magnets around the duct, the applied magnetic field was uniform throughout the region analyzed.

The simulated case has analytical solutions for the axial component of flow velocity and induced magnetic field, displayed in Equations (13) and (14), respectively. A simulation was performed and the mentioned variables were compared to the analytical solution in Figure 4. In the figure, results are evaluated in the cross-section at the middle of the duct’s length ($x=1.25$ m), along the directions parallel ($\theta =0^{\circ }$) and perpendicular ($\theta ={90}^{\circ }$) to the orientation of applied magnetic field.

Excellent agreement can be observed between numerical and analytical solutions. Accurate numerical results obtained in a case similar to the one considered in this paper verify the numerical scheme proposed in Section 4.2 and Section 4.3.

After verification, the proposed numerical scheme is was used to model the geometry described in Section 4.2, for the repulsive and attractive configurations of magnetic field.

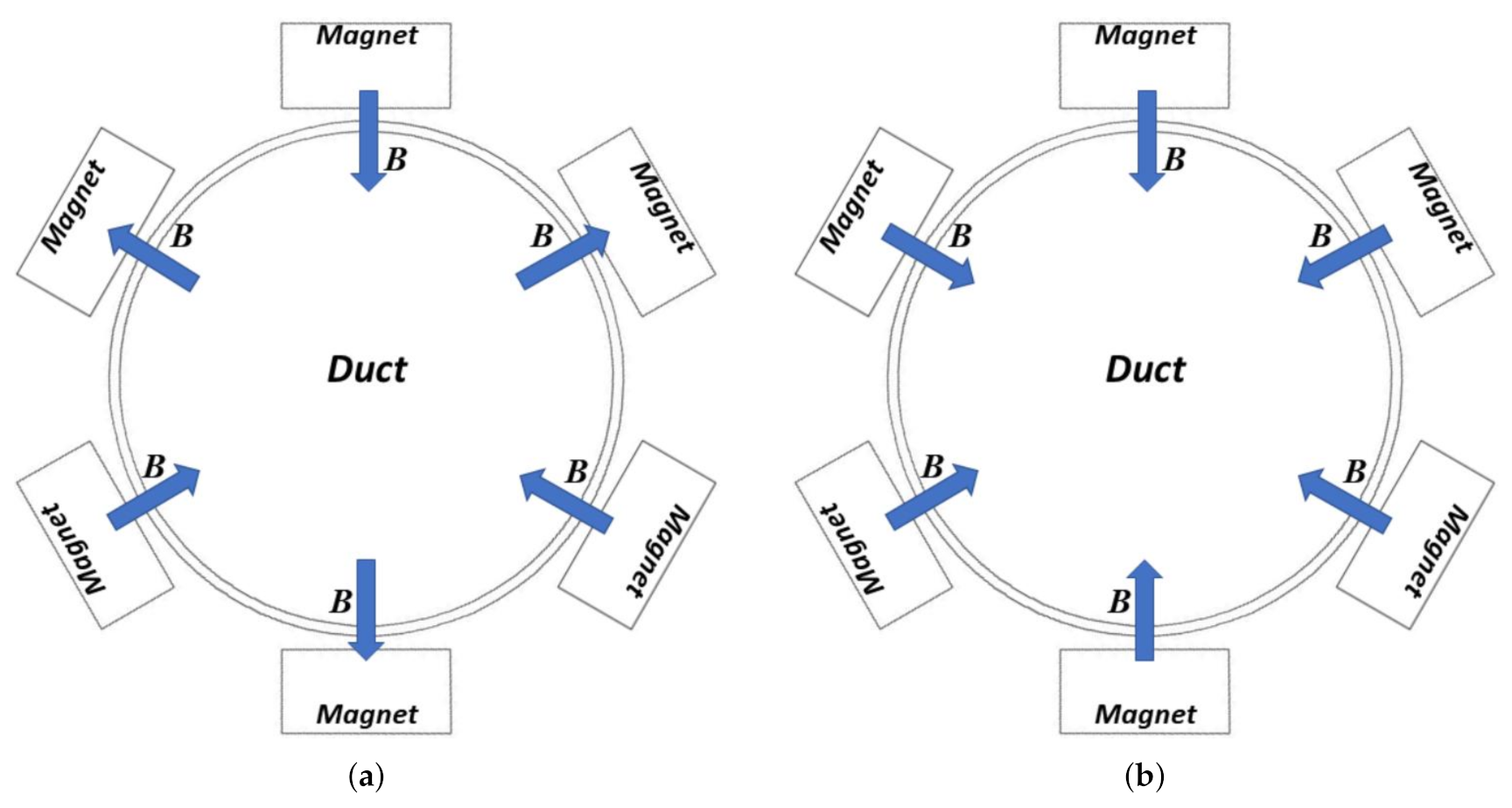
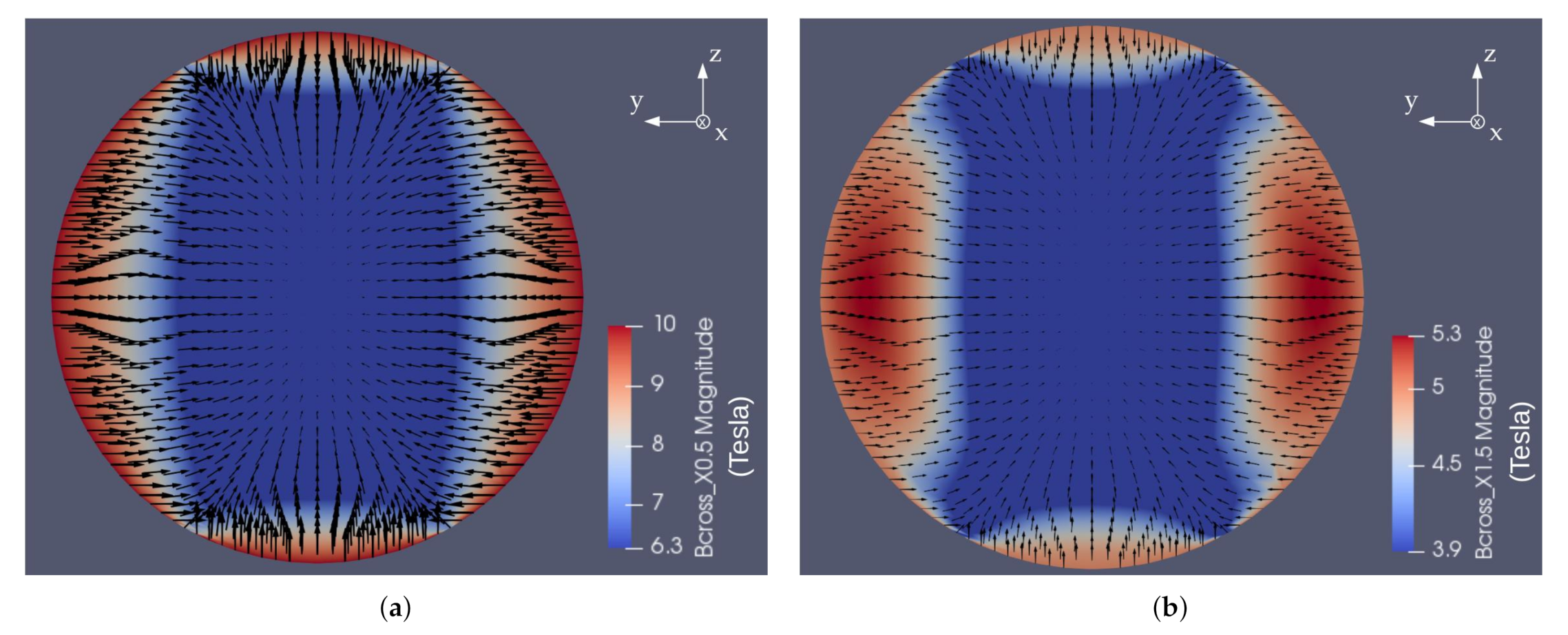
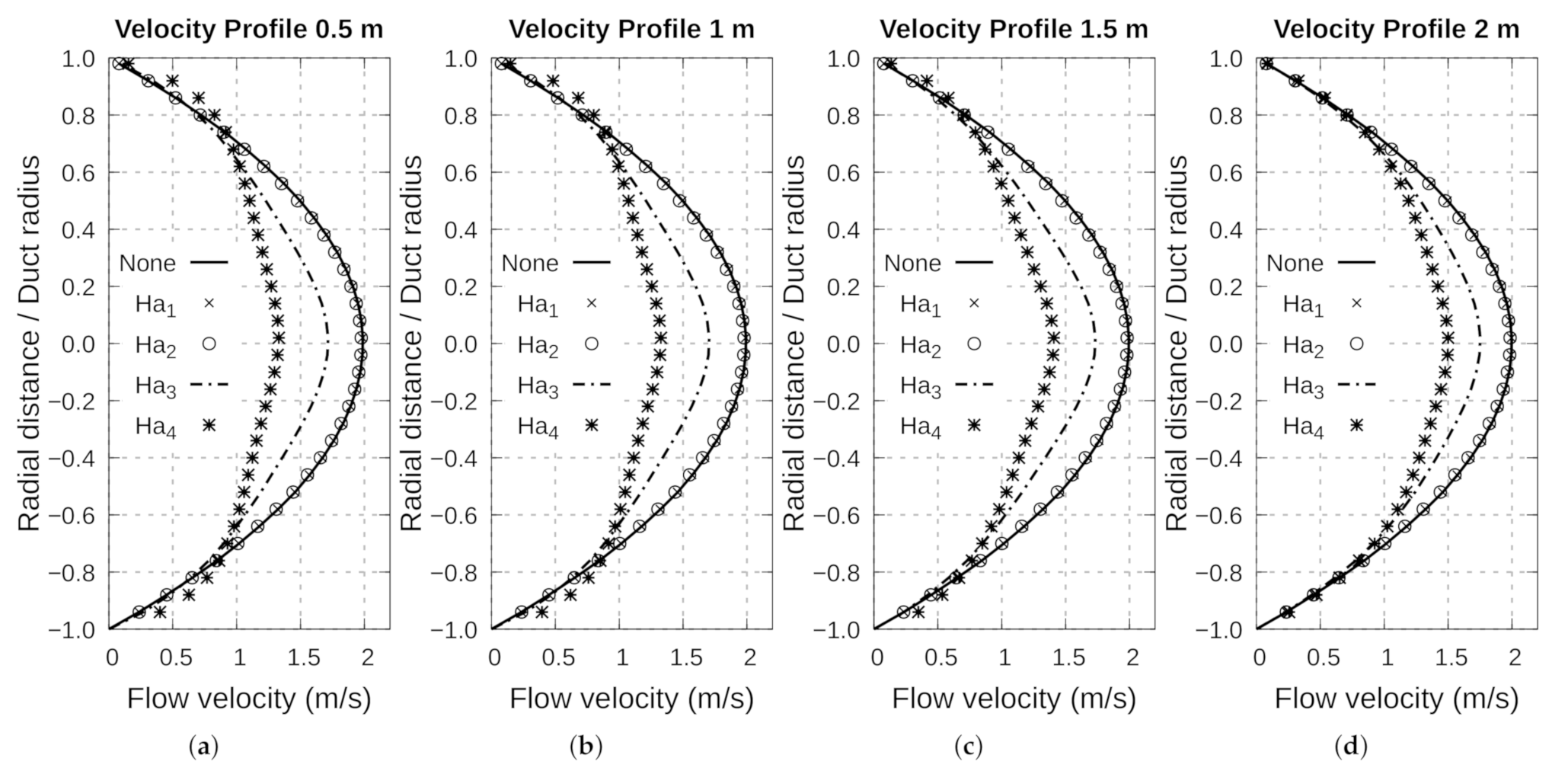
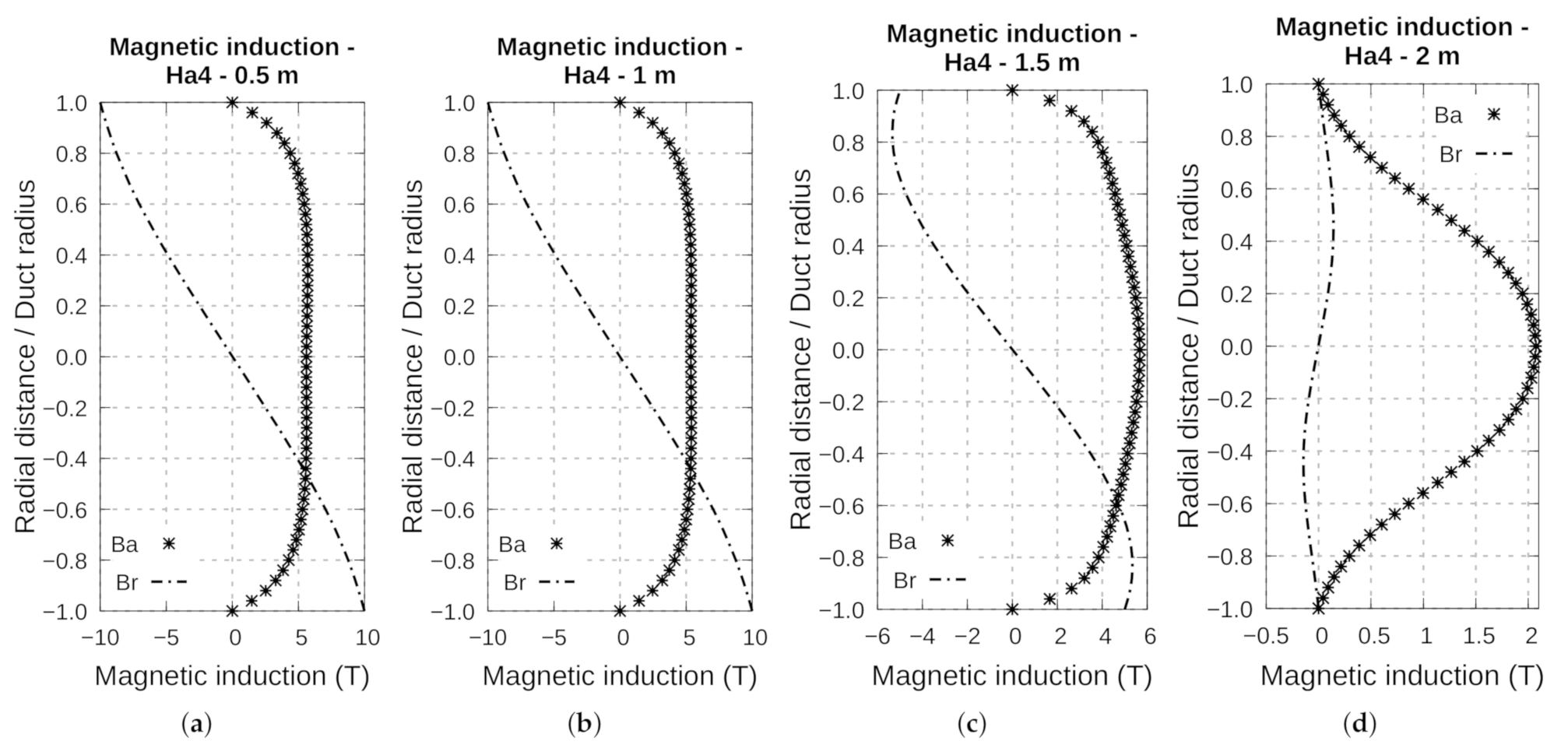
4.5. Analysis of Fluid Behavior in the Repulsive Configuration

In this section, we analyze the fluid behavior under magnetic fields generated by magnets in the repulsive configuration (Figure 2b). The distributions of magnetic induction in the transverse and longitudinal planes are shown in Figure 5 and Figure 6 respectively. In these figures and in all others displaying a distribution of magnetic induction, colors code the field intensity and vector orientation at each point of the domain.

Figure 7 shows the velocity profiles at different x positions along the duct length. For the repulsive configuration, it was observed that the presence of magnetic fields tends to reduce fluid velocity for the Hartmann numbers Ha₃ and Ha₄, whereas for Ha₁ and Ha₂ this effect was negligible. Therefore, the reduction of fluid velocity was significant for Hartmann numbers larger than about 10, and this effect was more intense the larger the Hartmann number.

This effect of “braking” is due to the interaction between the flow velocity and applied magnetic field [37]. In MHD channel flows, the movement of conducting fluid in a magnetic field induces a current density $\overrightarrow{J}$ perpendicular to the flow velocity and to the magnetic lines according to (5). The components of current perpendicular to the magnetic field lines induce the Lorentz force $\overrightarrow{f_L}=\overrightarrow{J}\times \overrightarrow{B}$. In the central region of the channel (core), Lorentz forces are oriented in the direction opposite to that of the flow. At first there is a net force opposite to the flow, which reduces velocity until an equilibrium between pressure gradient and $\overrightarrow{f_L}$ is reached. Points in the core with higher initial velocity experience stronger deceleration than other points with lower velocities. The result is a flattening of the normally parabolic velocity profile, as seen in Figure 7.

The more significant velocity reduction for Ha₃ and Ha₄ observed in Figure 7 occurred because higher magnetic fields generate stronger Lorentz forces.

The principle of magnetohydrodynamic braking finds many practical applications. It is widely used in metallurgy, where a static magnetic field is employed to suppress undesirable motion of liquid metals. An example is the suppression of motion of molten steel within the mold during the continuous casting of large steel slabs [1,10]. Magnetic fields can also be used to dampen turbulent flows back to the laminar state, a process called relaminarization.

The effect of reduction of velocity flow was present in the entire length of the simulated duct, in its portions with and without magnets. Although the transverse magnetic field was negligible in the final portion of the duct (Figure 6), velocity was reduced in this region due to inertia. The braking effects imposed by magnets in the initial portion of the duct were still felt at $x>1.5$ m. However, a careful observation of Figure 7c,d revealed that, at position 2 m, velocities were slightly higher than those at $x=1.5$ m. This happens because, once the perturbation imposed by magnets ceases, the flow starts to gradually recover speed until reaching its original fully developed state (parabolic velocity profile) [38].

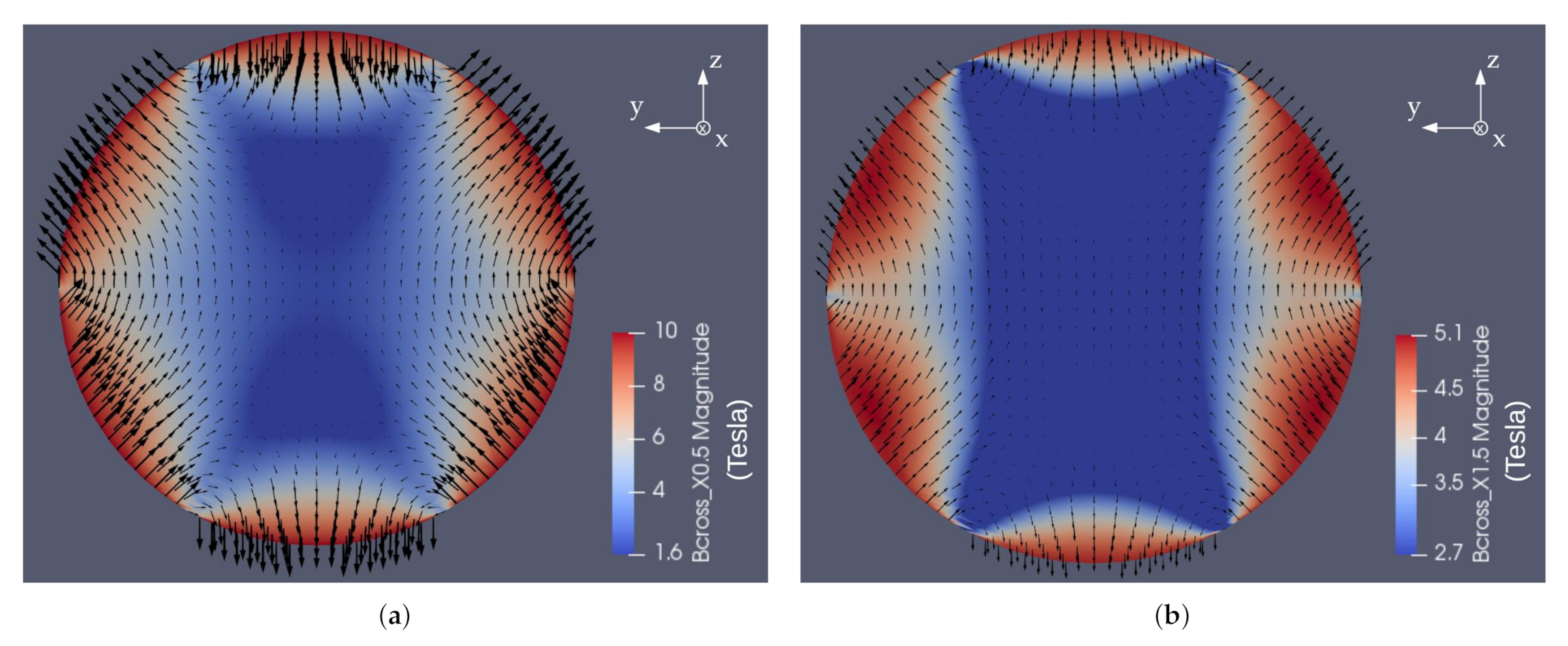
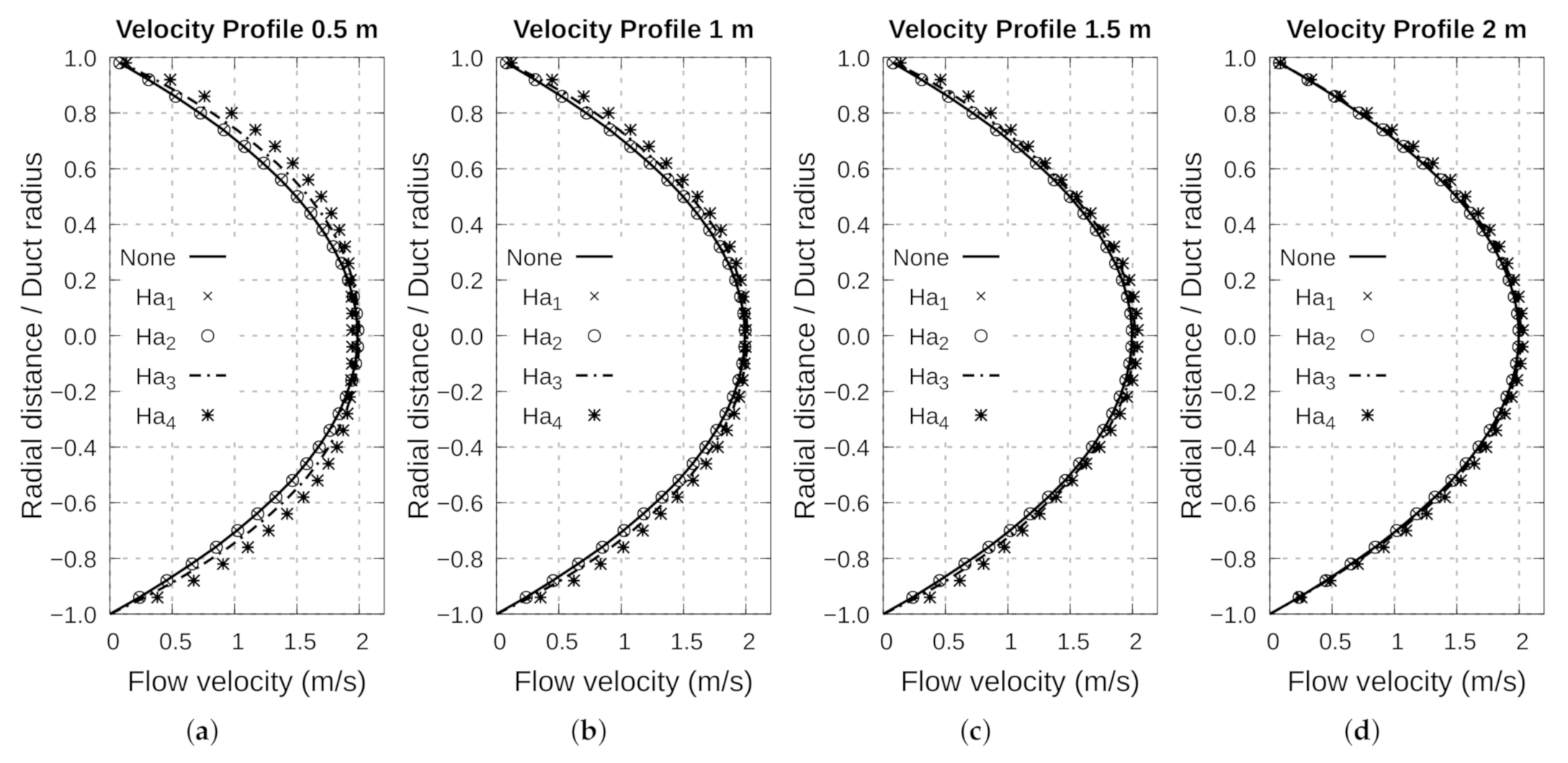
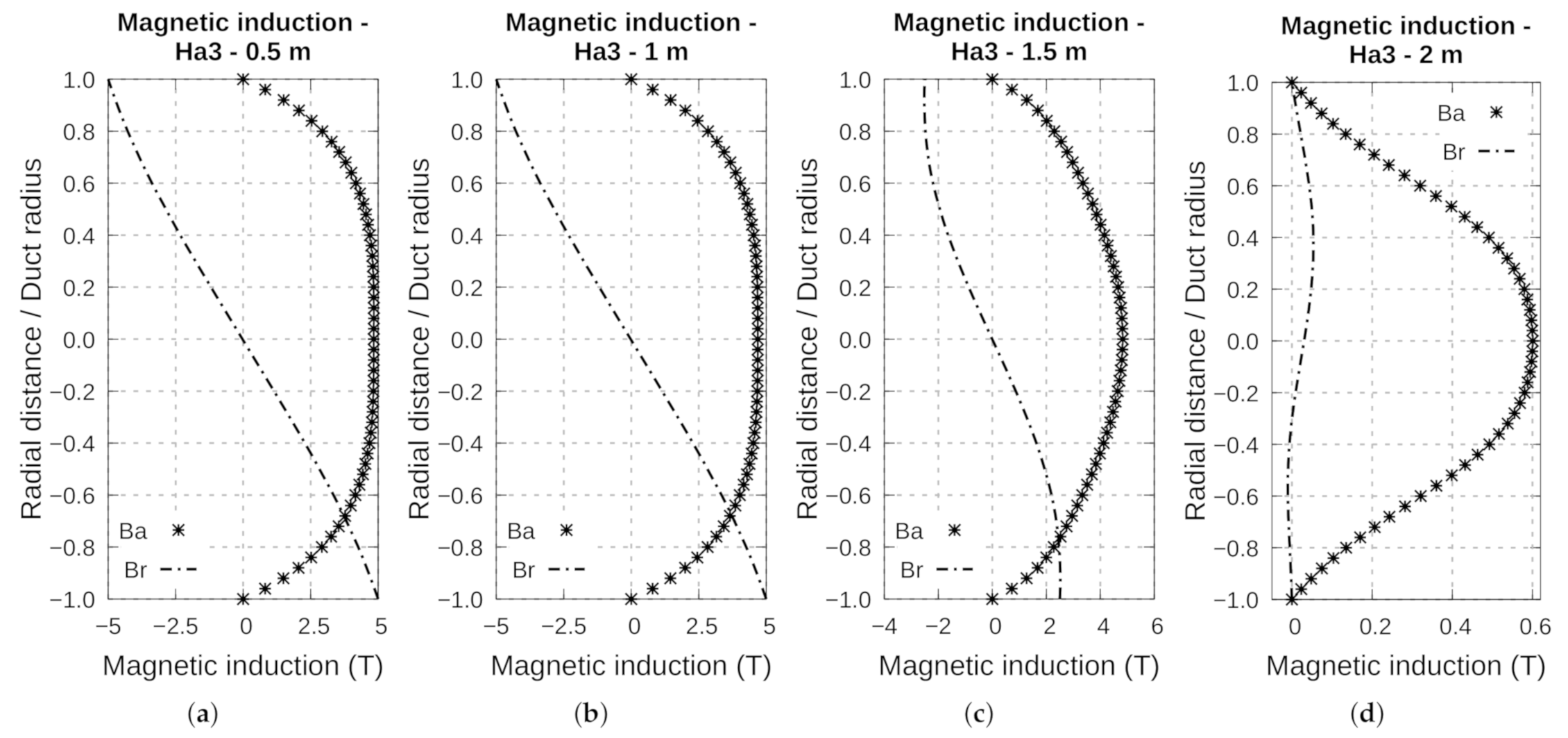
4.6. Analysis of Fluid Behavior in the Attractive Configuration

The same analysis of Section 4.5 is shown here for the attractive configuration of magnetic fields (Figure 2a). The distribution of magnetic induction is shown in Figure 8 and Figure 9.

The influence of magnetic field on fluid behavior is shown in the velocity profiles of Figure 10. This figure shows that the velocity profiles are approximately the same along x axis, at points with varying intensities of magnetic fields (due to different distances from the magnets). Therefore, for the attractive configuration, the intensity of magnetic fields exerts little influence on a fully developed flow. This is caused by the distribution of the magnetic field lines inside the duct. In Figure 8 and Figure 9, one observes that a significant portion of the inward magnetic field leaves the duct without spreading to the core region. Of the field lines that reach the core, they are arranged such that they cancel out each other in the central region of the duct. As a result, low currents are induced in the fluid, generating low Lorentz forces and negligible braking effects.

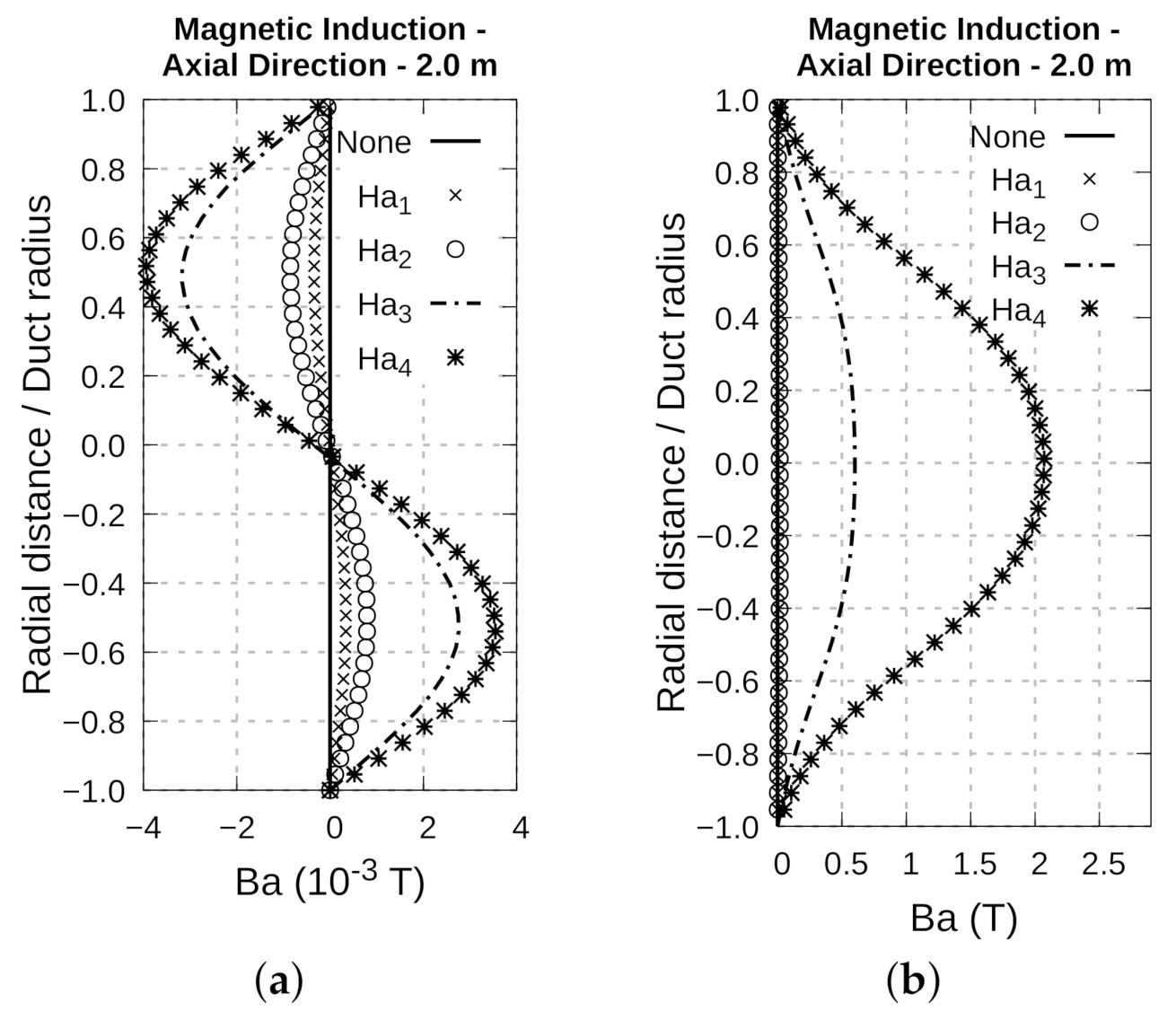
4.7. Comparative Analysis of Electromagnetic Behavior

For both magnetic configurations (Figure 2), we analyzed the effect of fluid velocity on the induction of a magnetic field.

Figure 11 illustrates the intensity of the axial component of magnetic induction ($B_a$) at the position 2.0 m from the duct inlet (portion of the duct without magnets). In the attractive configuration (Figure 11a), the axial component of magnetic flux density is negligible (less than 4 mTesla), even for Ha₃ and Ha₄. For the repulsive configuration (Figure 11b), $B_a$ peaks at about 2 Tesla.

From the comparative analysis of Figure 11, it is clear that the magnetic induction in the axial direction is negligible for Ha₁ and Ha₂, in both attractive and repulsive configurations.

At this point, we analyze the magnetic induction in the repulsive configuration for Hartmann numbers Ha₃ and Ha₄, conditions in which the magnetic induction effect is significant.

In Figure 12, the axial ($B_a$) and radial ($B_r$) components of magnetic induction are illustrated at different positions along the duct. One notices that the values of magnetic induction along the axial direction at the duct center are approximately equal to the radial component of magnetic induction at the duct portion where magnets are present (Figure 12a,b) and the transition zone (Figure 12c). In the region without magnets (Figure 12d), magnetic induction in the axial direction is about 0.6 Teslas at the duct center.

In Figure 13, analysis analogous to that of Figure 12 is shown for Hartmann number Ha₄. It can be observed that the axial magnetic induction $B_a$ presents a more rectangular profile compared to the Ha₃ case in the regions with magnets (Figure 13a,b), but the peak value of induction is approximately the same for the Ha₃ and Ha₄ cases. The magnetic induction curves for Ha₃ and Ha₄ are similar to each other at the transition zone (Figure 13c). In the region where magnets are absent (Figure 13d), the axial magnetic induction is approximately 2 Teslas at the duct center.

5. Final Remarks

In this case study, the Finite Volume Method was used to model the magnetohydrodynamic behavior of the laminar and fully developed flow of an electrically conducting fluid. The fluid flowed in a duct of which one portion was surrounded by magnets producing magnetic field in the radial direction. Two arrangements regarding the directions of magnetic fields produced by the magnets were considered: an attractive configuration (Figure 2a) and a repulsive configuration (Figure 2b). For both configurations, two effects were analyzed: (i) the influence of magnetic field intensity on flow velocity; and (ii) the influence of flow velocity on magnetic induction.

Results showed that these two effects are of little importance in the attractive configuration. For the repulsive configuration, on the other hand, these effects are significant only above a certain value of Hartmann number.

For a fully developed flow, it was observed that for a Hartmann number above 10, the magnetic fields tend to reduce flow velocity, and this effect is more intense the higher the Hartmann number. This principle may be used to stabilize fluid velocity.

It was also verified that flow velocity induces magnetic fields in the axial direction. This induction is noticeable for Hartmann number starting from 10, and increases with higher Hartmann numbers. The induction effect was maintained in the duct region where there was no imposed radial magnetic field; that is, the induced magnetic field propagated to the region without magnets.

The studied magnetohydrodynamic effects can be used in a wide array of useful industrial applications. The reduction of flow velocity by the external magnetic field, for example, can be used for reverting turbulent flows to the laminar stage (relaminarization). MHD is also a promising piece of technology for the prevention of fouling in pipes, although the physical mechanisms involved in this phenomenon are not yet fully understood.

In future works, the authors intend to validate these analyses experimentally. We plan to assess to which extent the magnetic fields inhibit the flow of conducting fluids, and to determine how far the induced magnetic fields propagate in ducts without the presence of magnets.