Path Selection for the Inspection Robot by m-Generalized q-Neutrosophic PROMETHEE Approach

Abstract

Path planning can be considered the most vital task of the autonomous robot. In this task, selecting an optimal route from the starting to the target position becomes an important problem that must be addressed when multiple competing optimization priorities are considered. Thus, a novel route assessment strategy based on a multi-criteria decision-making approach is proposed. The m-generalized q-neutrosophic PROMETHEE (PROMETHEE-mGqNS) method is applied to aggregate the competing route assessment requirements and choose an optimal route. A case study is investigated to explain the proposed strategy for path planning in a typical environment and indicates the method stability when incomplete input data characteristics are present.

1. Introduction

Since the promotion stage, the impressive progress of mobile robots can be perceived throughout industry. All real-life areas of human activity, such as space observation, agriculture, military, medicine, rescuing, mining and entertainment, are affected by the growing application of mobile robots [1,2].

During the last decade, the existing real-life applications changed from automated guided vehicles to autonomous mobile robots. Conventional mobile robots usually follow fixed paths and can choose to move to the predefined positions in the operational space. On the other hand, autonomous mobile robots use a guiding system expanded by prevalent sensors and powerful hardware and software systems to navigate the operational space without any a priori information.

Motion planning can be considered of utmost importance in the vision-based guidance systems. Many different proposals to accomplish this task have been introduced [3] and are distinguished into two categories: traditional and reactive techniques. The following condition characterizes the classical approaches: the path can be constructed, or the path does not exist.

The first considered approach is the cell decomposition technique. The essence of this technique is to divide the navigation space into non-overlapping grids and apply the connectivity graphs to pass through one cell to another to accomplish the goal position [4,5,6].

The second approach of the traditional path planning strategies is the roadmap approach. By this strategy, the path is constructed by a set of curves that depend on the applied navigation space model. The navigation space is usually modelled applying the Voronoi diagram or the visibility graph [7,8].

The third section of the traditional path planning strategies is the artificial potential field method. By this approach, the navigational space is modelled as the potential field, which creates the imaginary forces. These forces direct the robot toward the final destination point while avoiding the obstacle space [9,10].

During the last decade, active research has developed reactive algorithms for the path planning of mobile robots. Different techniques such as genetic algorithms, fuzzy logic, neural networks, swarm-based optimization, multi-objective optimization-based methods and other diverse algorithms have been dedicated to solving pathfinding problems [11,12,13,14,15,16,17,18,19,20].

Most of the proposals mentioned above take into account only the navigation space characteristics and do not consider the other aspects that are of utmost importance for the maintenance of the mobile robots or other organizational management aspects. These aspects can be utilized in the path planning problem applying multi-criteria decision making (MCDM). MCDM can be considered as a framework that enables possibilities to make decisions when several competing objectives (criteria) are taken into account [21]. Navigation aspects for harsh environment exploration by the autonomous mobile robot have been studied in [22]. The research presented in this paper addressed the safety and re-usability aspects of the autonomous mobile agent, taking into account the economic sustainability aspects. For this purpose, a new extension of the well-known MCDM method, WASPAS-SVNS, was applied to deal with the vague and uncertain initial information, which was modelled by neutrosophic sets.

Another aspect that can be considered of utmost importance is the possibility to model incomplete and uncertain information that arises in modern, real-life applications of pathfinding problems of autonomous mobile robots. The most attractive approach to solving this problem is to apply various fuzzy sets to construct the mathematical model [23,24,25,26].

The fuzzy set theory, which was proposed by Zadeh [27], takes into account the initial information uncertainty and vagueness when modelling real-life applications. According to this theory, each entity in the real problem model is described by a single, relatively graded membership and non-membership function. Atanassov [28] proposed the extension to a fuzzy set theory by introducing intuitionistic fuzzy sets (IFN) to incorporate the degree of hesitation into the decision-making processes. Since the intuitionistic fuzzy set theory requires keeping the sum of the membership and non-membership degrees in the closed interval of [0, 1], it also raises some limitations for the application into real-life decision problems [29].

To overcome these limitations, Yager [30] proposed Pythagorean fuzzy sets, where the membership degree ζ and non-membership degree ϑ follow the condition ζ² + ϑ² ≤ 1. This feature accommodates additional uncertainties of the initial information. Nowadays, decision making faces a growing complexity in real-life applications that indulge both generality and flexibility of the operations used. Smarandache [31] proposed a concept that a neutrosophic set is a generalization of multiple fuzzy sets, including the intuitionistic fuzzy sets. These generalized concepts of the neutrosophic sets are successfully utilized by developing the new MULTIMOORA, PROMETHEE and WASPAS extensions under m-generalized q-neutrosophic sets [32,33,34].

The present paper is organized as follows. The proposed path planning strategy model, the algebraic operations of m-generalized q-neutrosophic sets and the applied WASPAS-mGqNS method are discussed in Section 2. Section 3 represents the computational example of the path planning process. Finally, the discussion and conclusions are presented in Section 3 and Section 4.

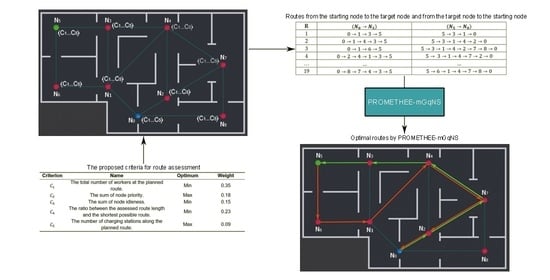
2. Path Selection for the Autonomous Inspection Robot

In this research, a path planning problem with multiple optimization priorities for an autonomous inspection robot is considered. The proposed path planning strategy considers spatial data of the environment and social aspects since this strategy covers robot functions such as monitoring, people avoidance and battery charging. The operational environment is modelled by a graph in which each node characterizes the point of interest in the space that the robot can monitor. Unlike path planning problems for patrolling tasks [35], in the proposed strategy a robot must visit a target node by choosing a route that enables it to balance multiple competing requirements (e.g., selecting the shortest route while also avoiding areas that were visited recently). After reaching the target and completing a given inspection task, the robot must return to the starting position.

The proposed path planning strategy is implemented applying the MCDM framework. This strategy implements two main issues that must be addressed: What route assessment strategy should be implemented when comparing multiple paths, and what method should be applied when aggregating multiple competing optimization requirements? In this research, a novel MCDM-based strategy is proposed in which every possible route from the start node $N_a$ to the target node $N_b$ is calculated. The optimal path is selected by aggregating a set of optimization priorities and applying the multi-criteria decision-making method, modelled under the m-generalized q-neutrosophic environment, namely PROMETHEE-mGqNS.

2.1. Route Assessment Strategy

The proposed path planning approach for monitoring and inspection tasks is based on the offline node assessment strategy. As all nodes that characterize the environment are known in advance, and backtracking behavior between the nodes is forbidden. Every possible route from the robot starting position $N_a$ to the target position $N_b$ can be computed, and the optimal one can be selected according to the list of optimization priorities. In this research, several possible criteria could be considered to assess routes when considering monitoring and inspection tasks within indoor environments, when human personnel work in the same environment as the autonomous robot. The proposed criteria set is presented in

Table 1. The proposed route assessment strategy.

Criterion	Name	Optimum	Weight
$C_1$	The total number of workers at the planned route.	Min	0.35
$C_2$	The sum of node priority.	Max	0.18
$C_3$	The sum of node idleness.	Min	0.15
$C_4$	The ratio between the assessed route length and the shortest possible route.	Min	0.23
$C_5$	The number of charging stations along the planned route.	Max	0.09

. It is also worth noting that the proposed criteria set is finite and can be further extended within the scope of the given problem.

As the considered task involves monitoring the nodes along the planned route, it is reasonable that the robot should avoid selecting crowded routes and disturbing human personnel working in the area. Thus, the total number of workers at the planned route is a minimized criterion applied to direct the robot to currently empty and, essentially, unmonitored areas.

Considering the given monitoring task, one can identify multiple areas in the environment that could be prioritized above others [36]. In inspection and monitoring tasks, these areas could be, for example, areas with dangerous substances or important machinery. Thus, the sum of node priority is a proposed maximized criterion which enables the robot to choose the route that would lead it to areas prioritized by the robot operator (in this research, the node priority value $N_p$ is proposed to be set in the closed interval [0, 1]).

As in the considered task, the robot must return to its starting position after reaching the designated target node; the route idleness (expressed as the sum of node idleness) is also evaluated. To obtain the value of this criterion, the robot considers the last time the node was visited and minimizes the total. This strategy is expected to enable the robot to return to the starting position by choosing the nodes that were not visited or visited at the early stages of navigation while moving to the target area.

Reducing the robot travelling cost (the travelled distance) is a common optimization requirement when considering autonomous navigation [37]. Thus, the ratio between the route length and the shortest possible route length is considered to enable the robot to preserve energy while balancing this requirement with the other optimization priorities.

Finally, it could be considered that there are multiple robot charging stations in the environment in addition to the one at the robot starting position, as it would allow the robot to charge the battery when required and temporarily dock at other areas in the environment. Therefore, the number of robot-charging stations along the planned route can be included in the considered criteria set.

2.2. PROMETHEE-MGQNS method

To aggregate the competing requirements of the route assessment task, the PROMETHEE method, modelled under the m-generalized q-neutrosophic set, namely PROMETHEE-mGqNS, is applied. The method is selected to enable the robot operator to switch between the fuzzy sets that govern the robot decision-making process. In addition, the applied method shows stability and effectiveness when considering incomplete or varying input data [38], which could be useful in situations where some initial input data characteristics are uncertain.

2.2.1. The Preliminaries of the m-Generalized q-Neutrosophic Set

In this research, the decision of which route the robot should follow is made by applying a PROMETHEE MCDM method, modeled under the m-generalized q-neutrosophic set (mGqNS) environment. In general, the mGqNS can be defined as $=\left\{d, \xi \left(d\right),\vartheta \left(d\right),\eta \left(d\right):d \in U\right\}$, where $m$ and $q$ values are applied to define different variations of fuzzy sets [34], $\xi ,\vartheta ,\eta :U\to \left[0,r\right]$ and $0\le r\le 1$. The $\xi ,\vartheta , \eta$. are the m-generalized q-neutrosophic truth, indeterminacy and falsity functions that follow the conditions of:

$$0\le \xi \left(d\right),\vartheta \left(d\right),\eta \left(d\right)\le 1;$$

(1)

$$0\le {\left(\xi \left(d\right)\right)}^q+{\left(\vartheta \left(d\right)\right)}^q+{\left( \eta \left(d\right)\right)}^q\le \frac{3}{m};$$

(2)

$$q\ge 1 \& m=1 or 3.$$

(3)

The triplet $\tau =\left\{\xi ,\vartheta ,\eta \right\}$ is called m-generalized q-neutrosophic number mGqNN. If ${\tau }_1=\left\{\xi ,\vartheta ,\eta \right\}$ and ${\tau }_2=\left\{\xi ,\vartheta ,\eta \right\}$ are two mGqNNs, and $\mathsf{\lambda }>0$ is a real number, the algebraic operations between these mGqNNs are calculated as follows:

$${\tau }_1\oplus {\tau }_2=\langle {(1-\left(1-{\xi }_1^q\right)\left(1-{\xi }_2^q\right))}^{\frac{1}{q}},{\vartheta }_1{\vartheta }_2,{\eta }_1{\eta }_2\rangle$$

(4)

$${\tau }_1\otimes {\tau }_2={\xi }_1{\xi }_2,{(1-\left(1-{\vartheta }_1^q\right)\left(1-{\vartheta }_2^q\right))}^{\frac{1}{q}},{(1-\left(1-{\eta }_1^q\right)\left(1-{\eta }_2^q\right))}^{\frac{1}{q}}$$

(5)

$$\lambda \cdot {\tau }_1=\langle {(1-{(1-{\xi }_1^q)}^{\lambda })}^{\frac{1}{q}},{\vartheta }_1^{\lambda },{\eta }_1^{\lambda }\rangle$$

(6)

$$\lambda \odot {\tau }_1=\langle {\xi }_1^{\lambda },{(1-{(1-{\vartheta }_1^q)}^{\lambda })}^{\frac{1}{q}},{(1-{(1-{\eta }_1^q)}^{\lambda })}^{\frac{1}{q}}\rangle$$

(7)

$${\tau }_1\ominus {\tau }_2=\left({\left(\frac{{\xi }_1^q-{\xi }_2^q}{1-{\xi }_2^q}\right)}^{\frac{1}{q}},\frac{{\vartheta }_1}{{\vartheta }_2},\frac{{\eta }_1}{{\eta }_2}\right),where({\xi }_1>{\xi }_2;{\xi }_2\langle 1;{\vartheta }_2\rangle {\vartheta }_1;{\eta }_2>{\eta }_1)$$

(8)

$${\tau }_1\oslash {\tau }_2=\left(\frac{{\xi }_1}{{\xi }_2},{\left(\frac{{\vartheta }_1^q-{\vartheta }_2^q}{1-{\vartheta }_2^q}\right)}^{\frac{1}{q}},{\left(\frac{{\eta }_1^q-{\eta }_2^q}{1-{\eta }_2^q}\right)}^{\frac{1}{q}}\right),where({\xi }_1>{\xi }_2;{\vartheta }_1>{\vartheta }_2;{\vartheta }_2\langle 1;{\eta }_1\rangle {\eta }_2;{\eta }_2<1)$$

(9)

The ranking of the two mGqNNs ${\tau }_1$ and ${\tau }_2$ is performed by the following rules:

$$If S\left({\tau }_1\right)>S\left({\tau }_2\right), then {\tau }_1>{\tau }_2$$

(10)

$$If S\left({\tau }_1\right)=S\left({\tau }_2\right), then {\tau }_1={\tau }_2$$

(11)

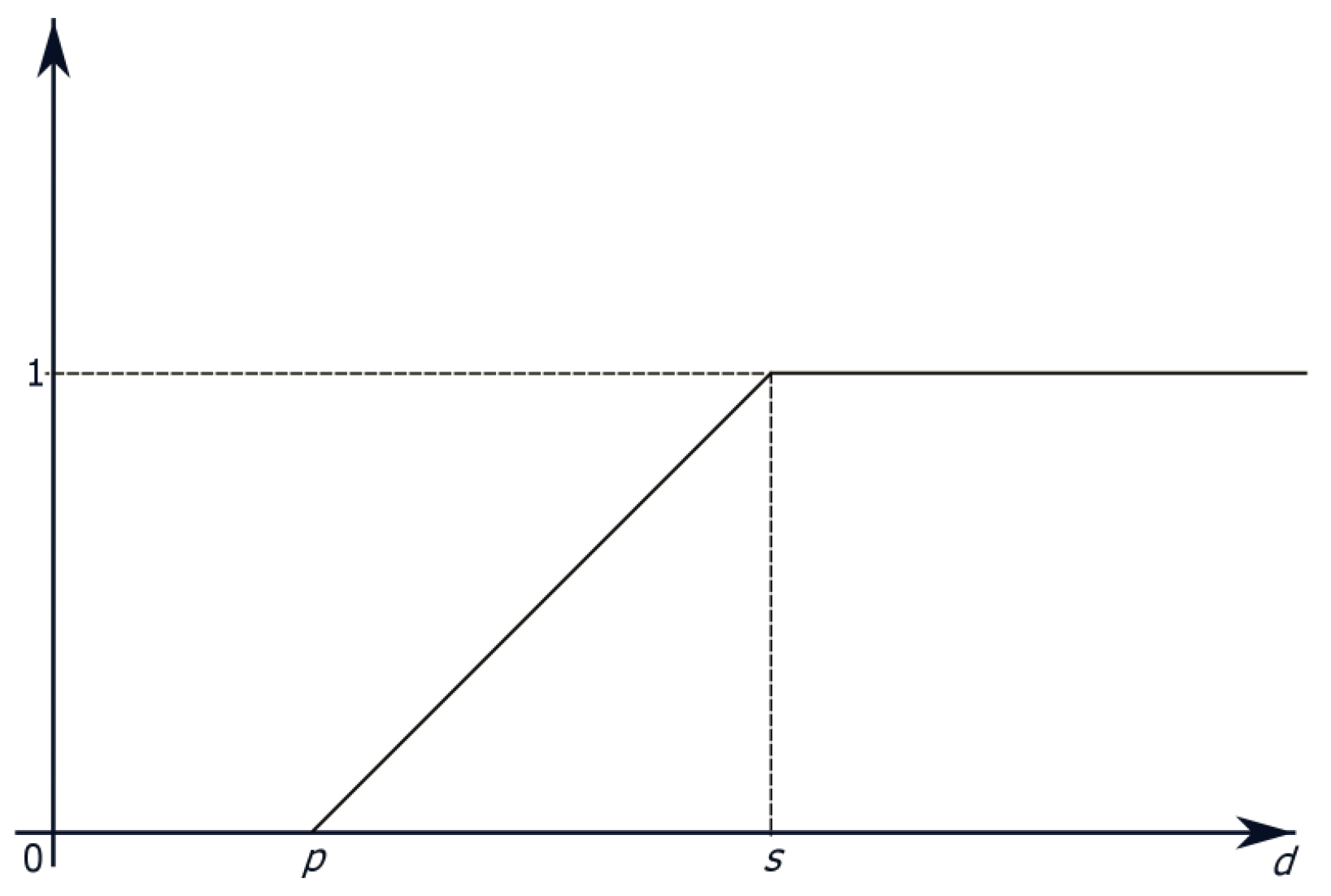
2.2.2. The m-Generalized q-Neutrosophic PROMETHEE

The core of the applied PROMETHEE-mGqNS multi-criteria decision-making method is constructed from the following eight steps:

• The decision matrix $D$ is constructed from the $d_{ij}$ elements, where each element $i=1,2,\dots ,n; j=1,2,\dots ,m$ represents the $i^{th}$ criterion value, relative to the $j^{th}$ alternative.

2.

The decision matrix $D$ is then normalized by applying vector normalization approach. The result of this step is a normalized decision matrix $\overline{D}$, with the elements ${\overline{d}}_{ij}$ calculated as follows:

$${\overline{d}}_{ij}=\frac{d_{ij}}{\sqrt{{{\displaystyle \sum }}_{i=1}^m{d}_{ij}^2}}$$

(12)

3.

Next, the neutrosophic conversion of the decision matrix is conducted by applying the standard modification rates [39]. After this step, the elements of the decision matrix are modeled as the m-generalized q-neutrosophic form of ${\tilde{\tau }}_{ij}=\left\{{\tilde{\xi }}_{ij},{\tilde{\vartheta }}_{ij},{\tilde{\eta }}_{ij}\right\}$. Here, $\check{\xi },\check{\vartheta },\tilde{\eta }:U\to \left[0,1\right]$ correspond to the truth, indeterminacy and falsity membership functions, which follow the condition of $0\le {\xi }_{ij}+{\vartheta }_{ij}+{\eta }_{ij}\le 3$.

4.

Alternatives (in this case—candidate routes $N$) are ranked by comparing between all pairs of $N_j$ and $N_p$, and the aggregated preference index is calculated by:

$$\pi \left(N_j,N_p\right)={\displaystyle \sum }_{i=1}^m{w}_i{p}_t\left({\phi }_i\left(N_j,N_p\right)\right)$$

(13)

Here $w_i$ is the weight of the $i^{th}$ criterion. The difference ${\phi }_i$ between the two mGqNNs ${\tilde{\tau }}_{ij}$ and ${\tilde{\tau }}_{ip}$ is calculated as ${\phi }_i\left(N_j,N_p\right)={\tilde{\tau }}_{ij}\ominus {\tilde{\tau }}_{ip}$. The construction $p_t\left(\phi \right)=p_t({\phi }_i\left(N_j,N_p\right))$ represents the $p^{th}$ preference function set by the decision-maker for the $i^{th}$ criterion. In this study, the V-shaped preference functions presented in Figure 1 are applied.

5.

Then, the calculation of the positive $F_j^{+}$ and the negative $F_j^{-}$ outranking flows is conducted by the following equations:

$$F_j^{+}={\displaystyle \sum }_{p=1}^n\pi \left(N_j, N_p\right), j=1,2,\dots ,m$$

(14)

$$F_j^{-}={\displaystyle \sum }_{p=1}^n\pi \left(N_p, N_j\right), j=1,2,\dots ,m$$

(15)

6.

The net flow value $F_j$ is measured to determine the final rank of an alternative:

$$F_j=F_j^{+}-F_j^{-}$$

(16)

The negative net flow values are measured by applying the neutrosophic algebra as follows:

$$F_j^c=F_j^{-}-F_j^{+}$$

(17)

7.

The deneutrosophication of the net flow value $F_j$ is completed by calculating the score value $S\left(F_j\right)$ for each route by applying the following equation:

$$S\left(F_j\right)=\frac{3+3{\xi }^q-2{\vartheta }^q-{\eta }^q}{6}$$

(18)

8.

The final interpretation of the PROMETHEE-mGqNS results is conducted. The ranking of the alternatives with the positive score value $+S\left(F_j\right)$ is taken as is, while the best alternatives for the negative score values $-S\left(F_j\right)$ have the smallest score value.

3. Case Study: Results and Discussion

The proposed route assessment strategy is tested in a hypothetical indoor environment, presented in Figure 2. Here, a total of nine nodes are applied to define the monitored space. Each node represents an area of interest the robot can visit. The priority of each area (defined by $C_2$ criterion) and the current area crowding (defined by $C_1$ criterion) are set in advance by the robot operator. It is also assumed that the target node, in which the robot must complete some specific tasks (e.g., inspect the possible defects in structures [40]), exists, and after the tasks are finished, the robot must return to the starting node. In the considered example, the robot starting position is node $N_0$ (represented by a blue marker in Figure 2), and the target is node $N_5$ (represented by a green marker in Figure 2).

Next, the computational example of the route assessment problem is presented. First, every possible route from the start node (in this example $N_0$) to the target node (in this example $N_5$) is computed. Then, the same is done from the target node to the start node, as presented in

Table 2. The computed routes from the starting node $N_0$ to the target node $N_5$ and from the target node $N_5$ to the starting node $N_0$.

R	$\mathbf{\left(}{\mathit{N}}_{\mathbf{0}}\mathbf{\to }{\mathit{N}}_{\mathbf{5}}\mathbf{\right)}$	$\mathbf{(}{\mathit{N}}_{\mathbf{5}}\mathbf{\to }{\mathit{N}}_{\mathbf{0}}\mathbf{)}$
1	$0\to 1\to 3\to 5$	$5\to 3\to 1\to 0$
2	$0\to 1\to 4\to 3\to 5$	$5\to 3\to 1\to 4\to 2\to 0$
3	$0\to 1\to 6\to 5$	$5\to 3\to 1\to 4\to 2\to 7\to 8\to 0$
4	$0\to 2\to 4\to 1\to 3\to 5$	$5\to 3\to 1\to 4\to 7\to 2\to 0$
5	$0\to 2\to 4\to 1\to 6\to 5$	$5\to 3\to 1\to 4\to 7\to 8\to 0$
6	$0\to 2\to 4\to 3\to 1\to 6\to 5$	$5\to 3\to 4\to 1\to 0$
7	$0\to 2\to 4\to 3\to 5$	$5\to 3\to 4\to 2\to 0$
8	$0\to 2\to 7\to 4\to 1\to 3\to 5$	$5\to 3\to 4\to 2\to 7\to 8\to 0$
9	$0\to 2\to 7\to 4\to 1\to 6\to 5$	$5\to 3\to 4\to 7\to 2\to 0$
10	$0\to 2\to 7\to 4\to 3\to 1\to 6\to 5$	$5\to 3\to 4\to 7\to 8\to 0$
11	$0\to 2\to 7\to 4\to 3\to 5$	$5\to 6\to 1\to 0$
12	$0\to 8\to 7\to 4\to 3\to 5$	$5\to 6\to 1\to 3\to 4\to 2\to 0$
13	$0\to 8\to 7\to 2\to 4\to 1\to 3\to 5$	$5\to 6\to 1\to 3\to 4\to 2\to 7\to 8\to 0$
14	$0\to 8\to 7\to 2\to 4\to 1\to 6\to 5$	$5\to 6\to 1\to 3\to 4\to 7\to 2\to 0$
15	$0\to 8\to 7\to 2\to 4\to 3\to 5$	$5\to 6\to 1\to 3\to 4\to 7\to 8\to 0$
16	$0\to 8\to 7\to 4\to 1\to 3\to 5$	$5\to 6\to 1\to 4\to 2\to 0$
17	$0\to 8\to 7\to 4\to 1\to 6\to 5$	$5\to 6\to 1\to 4\to 2\to 7\to 8\to 0$
18	$0\to 8\to 7\to 4\to 3\to 1\to 6\to 5$	$5\to 6\to 1\to 4\to 7\to 2\to 0$
19	$0\to 8\to 7\to 4\to 3\to 5$	$5\to 6\to 1\to 4\to 7\to 8\to 0$

:

Then, the criteria values are calculated for each route. The criteria values considered in this example are presented in

Table 3. The criteria values for the $N_0\to N_5$ routes.

R	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$	${\mathit{C}}_{\mathbf{5}}$
$R_1\left(N_0\to N_5\right)$	2	1.5	0	1	0
$R_2\left(N_0\to N_5\right)$	2	1.6	0	1.539	0
$R_3\left(N_0\to N_5\right)$	1	0.8	0	1	1
$R_4\left(N_0\to N_5\right)$	2	2.1	0	1.998	1
$R_5\left(N_0\to N_5\right)$	1	1.4	0	1.954	1
$R_6\left(N_0\to N_5\right)$	2	2.1	0	2.179	1
$R_7\left(N_0\to N_5\right)$	1	1.5	0	1.408	0
$R_8\left(N_0\to N_5\right)$	3	2.7	0	2.361	1
$R_9\left(N_0\to N_5\right)$	2	2	0	2.359	2
$R_{10}\left(N_0\to N_5\right)$	3	2.7	0	2.584	2
$R_{11}\left(N_0\to N_5\right)$	2	2.1	0	1.813	1
$R_{12}\left(N_0\to N_5\right)$	5	2.7	0	3.048	1
$R_{13}\left(N_0\to N_5\right)$	4	2	0	3.045	2
$R_{14}\left(N_0\to N_5\right)$	5	2.7	0	3.271	2
$R_{15}\left(N_0\to N_5\right)$	4	2.1	0	2.499	1
$R_{16}\left(N_0\to N_5\right)$	5	2.2	0	2.602	1
$R_{17}\left(N_0\to N_5\right)$	4	1.5	0	2.6	2
$R_{18}\left(N_0\to N_5\right)$	5	2.2	0	2.825	2
$R_{19}\left(N_0\to N_5\right)$	4	1.6	0	2.054	1

for the $N_0\to N_5$ routes and

Table 4. The criteria values for the $N_5\to N_0$ routes.

R	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$	${\mathit{C}}_{\mathbf{5}}$
$R_1\left(N_5\to N_0\right)$	2	1.3	60	1	0
$R_2\left(N_5\to N_0\right)$	2	1.9	120	1.998	0
$R_3\left(N_5\to N_0\right)$	5	2.5	150	3.048	1
$R_4\left(N_5\to N_0\right)$	3	2.5	150	2.361	1
$R_5\left(N_5\to N_0\right)$	5	2	130	2.602	1
$R_6\left(N_5\to N_0\right)$	2	1.4	100	1.539	0
$R_7\left(N_5\to N_0\right)$	1	1.3	120	1.408	0
$R_8\left(N_5\to N_0\right)$	4	1.9	150	2.499	1
$R_9\left(N_5\to N_0\right)$	2	1.9	150	1.813	1
$R_{10}\left(N_5\to N_0\right)$	4	1.4	130	2.054	1
$R_{11}\left(N_5\to N_0\right)$	1	0.6	10	1	1
$R_{12}\left(N_5\to N_0\right)$	2	1.9	120	2.179	1
$R_{13}\left(N_5\to N_0\right)$	5	2.5	150	3.271	2
$R_{14}\left(N_5\to N_0\right)$	3	2.5	150	2.584	2
$R_{15}\left(N_5\to N_0\right)$	5	2	130	2.825	2
$R_{16}\left(N_5\to N_0\right)$	1	1.2	70	1.954	1
$R_{17}\left(N_5\to N_0\right)$	4	1.8	100	3.045	2
$R_{18}\left(N_5\to N_0\right)$	2	1.8	100	2.359	2
$R_{19}\left(N_5\to N_0\right)$	4	1.3	80	2.6	2

for the $N_5\to N_0$ routes.

In this example, the node priority vector is set as

$N_p=\left\{ 0.0, 0.6, 0.5, 0.7, 0.1, 0.2, 0.0, 0.6, 0.0 \right\}$, the node crowding (number of personnel currently working in the area) vector is set as $N_c=\left\{ 0, 1, 0, 1, 0, 0, 0, 1, 2\right\}$, and $N_6$ and $N_7$ nodes are set to contain additional robot charging stations.

It is also worth noting that the $C_3$ criterion (the sum of node idleness) is set to be zero for all routes while computing $N_0\to N_5$. Therefore, this input parameter is not considered when assessing the utility of a candidate route to the target node. However, when the $N_5\to N_0$ routes are computed, the node idleness values are set according to the estimated node visitation time. In this example, to represent node visitation time, a linear increase in parameter value is considered to simplify the estimates.

Finally, the node priority value is not added to the value of the $C_2$ criterion (the sum of node priority) if the considered node is equivalent to the robot starting position. For example, if the robot is located at $N_5$, the priority value of 0.2 is not considered when the $N_5\to N_0$ routes are computed.

By applying the PROMETHEE-mGqNS method, the score value of each route is measured, and the optimal route (considering the proposed route assessment strategy, defined in Table 1) is selected. The obtained score values are presented in

Table 5. Score values and ranks for the $N_0\to N_5$ and $N_5\to N_0$ routes obtained by applying PROMETHEE-MGQNS.

$\mathit{S}\mathbf{\left(}{\mathit{N}}_{\mathbf{0}}\mathbf{\to }{\mathit{N}}_{\mathbf{5}}\mathbf{\right)}$	Rank	$\mathit{S}\mathbf{(}{\mathit{N}}_{\mathbf{5}}\mathbf{\to }{\mathit{N}}_{\mathbf{0}}\mathbf{)}$	Rank
0.00146	10	0.0021	6
0.0018	7	0.005	3
0.0006	11	−0.0003	15
0.00147	9	0.0002	10
0.002	6	−0.0197	19
0.0318	3	0.0018	7
0.0015	8	0.0009	8
0.045	2	−0.0152	18
0.0069	4	0.0003	9
0.0063	5	−0.0019	16
0.061	1	0.0024	5
−0.00002	13	0.0223	2
−0.0042	17	−0.00002	13
−0	12	0.0001	11
−0.0086	18	−0.0023	17
−0.0201	19	0.0031	4
−0.0022	14	−0.0001	14
−0.0023	15	0.0524	1
−0.0035	16	−0	12

.

Considering the PROMETHEE-mGqNS provided results, the optimal route for moving to the target node $N_5$ is $R_{11}\left(N_0\to N_5\right) : 0\to 2\to 7\to 4\to 3\to 5$. After completing its tasks in the area, the robot should return to the starting node $N_0$ by the route $R_{18}\left(N_5\to N_0\right): 5\to 6\to 1\to 4\to 7\to 2\to 0$. The selected routes are presented in Figure 3.

From the obtained example results, it can be observed that the proposed strategy increases the overall robot traveling distance. However, this is done to address the requirement of visiting multiple prioritized nodes and avoiding crowded areas. Consider that the node $N_8$ was not visited in this example due to it having no priority set by the robot operator and having two members of personnel working in the area. In addition, the node has no additional charging station. Thus, after combining all optimization priorities, the routes that include this node return the lowest score values and are effectively disregarded as viable routes.

Bearing in mind the results obtained in the example route assessment, it could be argued that the proposed area monitoring strategy enables the robot operator to balance competing requirements efficiently. The proposed strategy can also be adapted in different situations. Consider, for example, the following scenarios related to the environment graph presented in the example:

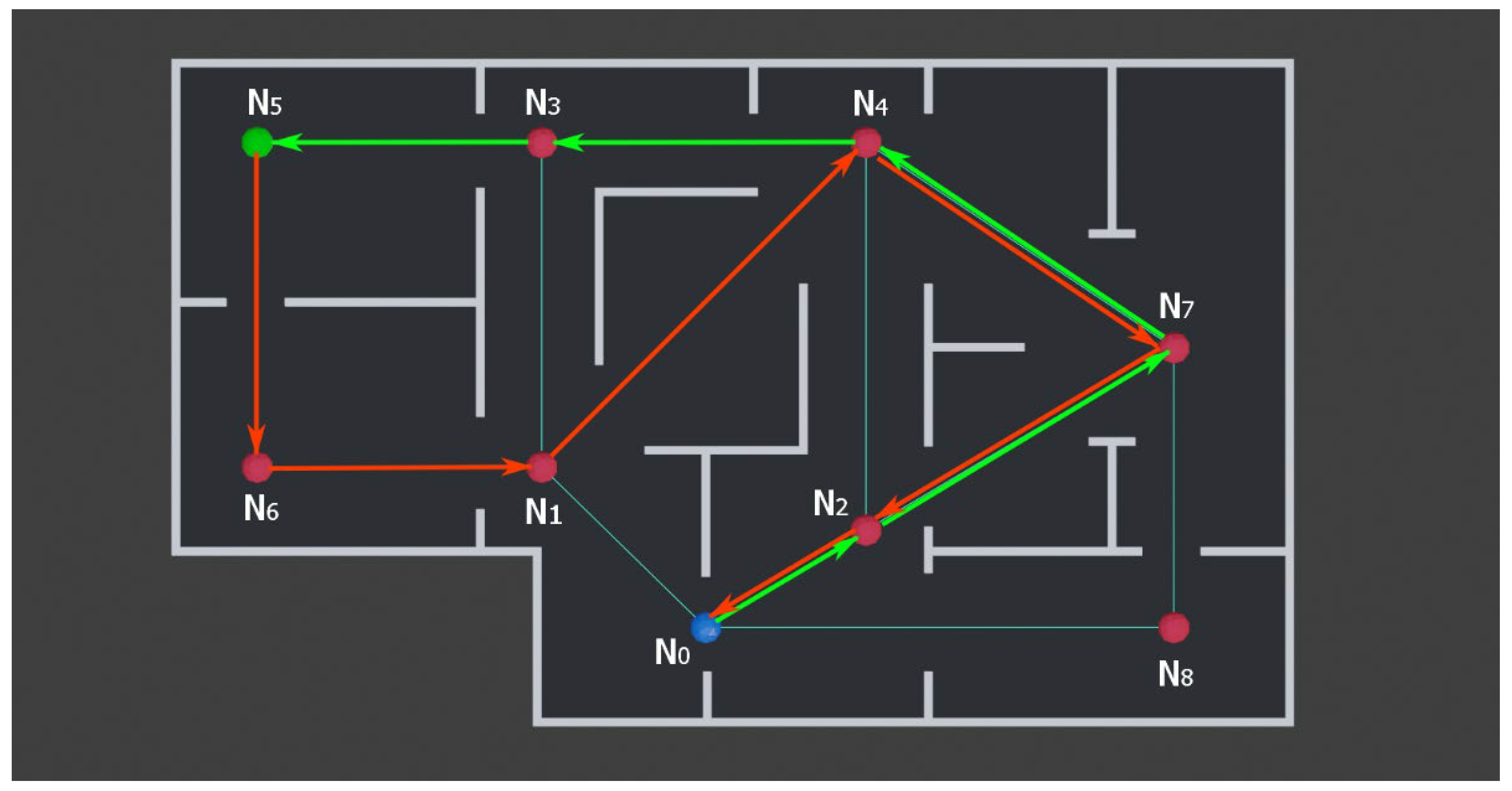
• Scenario 1: setting the node priority vector to $N_p=\left\{0.0,0.9,0.5,0.7,0.1,0.2,0.0,0.0,0.0\right\}$ and the node crowding vector $N_c=\left\{ 0,3,0,2,0,0,0,0,0\right\}$ computes the route $R_9\left(N_0\to N_5\right) : 0\to 2\to 7\to 4\to 1\to 6\to 5$ to the target node, and $R_9\left(N_5\to N_0\right) : 5\to 3\to 4\to 7\to 2\to 0$ route to the robot starting position. In this scenario, it can be observed that all of the prioritized nodes are visited by the monitoring robot. Additionally, node $N_3$ is avoided while moving to the target, and node $N_1$ is avoided while moving back to the starting position. Thus, it can be reasoned that the proposed strategy can balance the route optimization requirements of avoiding multiple crowded nodes, while also increasing the number of monitored areas along the way, showcasing the stability of the proposed strategy.
• Scenario 2: setting the node priority $N_p$ and the crowding vector $N_c$ values to zero computes the same path to the target node and back to the robot control station $R_3\left(N_0\to N_5\right) : 0\to 1\to 6\to 5$ and $R_{11}\left(N_5\to N_0\right) : 5\to 6\to 1\to 0$. In this scenario, the node priority and node crowding criteria values are not considered when selecting the optimal route. Therefore, the decision-making strategy optimizes the three remaining criteria: the sum of node idleness, the ratio between the computed route and the shortest route, and the number of charging stations along the planned route. As the shortest routes between the $N_0$ and $N_5$ are $0\to 1\to 3\to 5$ and $0\to 1\to 6\to 5$, and the sum of idleness is also zero, the route with an additional robot charging station is prioritized.

The obtained results highlight how the proposed monitoring strategy influences the route selection process and how it can be effectively applied in situations where only partial information is present.

Although the route planning problem could be considered comparable, different route assessment strategies and different MCDM methods are applied [41]. In other words, the considered criteria set is applied to this specific problem model. Therefore, a fair comparison cannot be made.

4. Conclusions

The application of autonomous robots is increasingly growing in many real-world areas, including monitoring and inspection tasks. In this research, a novel route assessment and selection strategy was proposed for the autonomous inspection robot, which implements the m-generalized q-neutrosophic PROMETHEE MCDM method, namely PROMETHEE-mGqNS.

The proposed route assessment strategy provides stable and predictable results, enabling the inspection robot to balance the competing route assessment requirements and choose an optimal route between the starting and target areas. The considered examples also show that the PROMETHEE-mGqNS method can be effectively applied in decision-making tasks where incomplete input data are present, allowing the decision-maker (in the context of this research—inspection robot) to compute optimal routes by addressing only the partial information. It is also worth noting that the main limitations of the proposed route assessment strategy stem from the amount of a priori information that is available before each route planning task. For example, to include the proposed criteria of current area crowding into consideration, an autonomous human tracking system should be implemented in the considered workplace.