Arc Voltage Distortion as a Source of Higher Harmonics Generated by Electric Arc Furnaces

Abstract

Due to high unit capacities, electric arc furnaces are among the receivers that significantly affect the power system from which they are supplied. Arc furnaces generate a number of disturbances to the power grid, including fast-changing voltage fluctuations causing the phenomenon of flickering light, asymmetry, and deformation of the voltage curve. The main issues discussed in the article are problems related to the distortion of current and voltage waveforms, resulting from the operation of electric arc furnaces. An analysis of the indices characterizing the voltage distortion recorded in the supply network of the arc furnaces is presented. The changes in the range of current and voltage waveform deformation in individual smelting phases in the arc furnace are also presented. Furthermore, the changes in the degree of deformation of the current and voltage waveforms in the individual smelting phases in an arc furnace are presented. A multi-voltage electric arc model used in computer simulations is proposed.

1. Introduction

Arc furnaces are among the receivers whose load changes in both dynamic and stochastic ways. These changes are caused by the technological process carried out in the furnace, which uses an electric arc to melt the charge. The mathematical description of an electric arc is very complex, as it includes electromagnetic and gasodynamic phenomena, as well as chemical reactions. The knowledge of the arc model is necessary to determine the optimal operating point of the arc device, i.e., ensuring the maximization of the arc power during scrap melting [1,2]. The stabilization of the operating point is achieved through the use of electrode shift control systems, which use algorithms dependent on the adopted arc model [3,4].

The nature and value of the arc device current are influenced by many factors. They can be divided into several groups. The first includes factors related to the parameters of the supply line. These are mainly the supply voltage level, resistance, and reactance of the supply network, which determine the amount of short-circuit power at the connection point of the arc furnaces. The second group depends on the parameters of the arc furnace: the furnace power in relation to the short-circuit power of the network, the construction of the high-current circuit, and the measures used to limit the impact of the furnace on the power system. Another group consists of factors related to the method of smelting, including the chemical composition of the medium in which the arc takes place, its pressure and temperature, the distance between the electrodes, their material, scrap quality, and the amount of injected oxygen [5,6].

The complexity and variability of the physicochemical processes occurring at various phases of the technological process, in the arc itself, as well as in the environment of the electrodes, and the conditions of supplying the arc from the power system make the analysis of the operation of a circuit with an electric arc a complicated task. The result has been the publication of a great variety of arch models. One of the first models of the arc was proposed by Cassie, in which he assumed that the arc has a cylindrical column with a uniform temperature and current density [7,8]. Mayer proposed an improved model in which he assumed that the arc had a constant diameter with varying temperature and conductivity. He considered that the power losses were due to heat conduction at low currents. This means that the conductance is strongly dependent on the temperature and independent of the arc cross-sectional area [9]. The models proposed by Cassie and Mayr were analyzed, among others, in [10,11,12].

The literature on the subject presents many different arc models, including nonlinear resistance models [13,14], models using current–voltage characteristics [15,16,17,18,19], models represented by voltage sources [20,21], models based on the relationship between arc length and voltage [22,23], and models using neural networks and fuzzy logic [24,25,26,27]. In many publications, the influence of arc furnaces on voltage distortion in the supply network was presented on the basis of modeling with the use of simulation programs [28,29,30].

The present article is a continuation of the issues concerning the impact of electric arc furnaces on the power system, described by the author in [31,32,33,34]. In [32,33], voltage fluctuations generated by arc furnaces were characterized in detail. The results of measurements of indicators characterizing energy quality (including light flicker coefficients) were presented. The results of model tests were proposed in which the electric arc of the electric arc furnace was replaced with a voltage whose value depends on the arc length. The phenomenon of current and voltage asymmetry in the lines supplying arc furnaces was presented in [34].

The aim of the research presented in the article was to evaluate the influence of electric arc furnaces on the deformation of the voltage supplying the arc devices.

The presented results are an extension of the information presented in [31]. An analysis of changes in the indices characterizing distorted voltage waveforms (THD, U_h) recorded in the lines supplying the arc furnaces was performed.

The measurements were carried out for various supply conditions of the steelworks (at different short-circuit powers of the supply networks) and for arc furnaces with different power of furnace transformers.

In the model tests, the electric arc model of the electric arc furnace developed by the author was used. The presented model studies were aimed at estimating how the deformation of the electric arc voltage affects the power system from which the arc furnaces are supplied. The main objective of the model tests was to determine the influence of the supply conditions (short-circuit power of supply lines) in metallurgical plants (steel mills). The influence of the arc voltage deformation on the melting power (active power consumed by the arc furnace) was also determined.

The article does not deal with the issues related to limiting the distortion of currents and voltages generated by arc furnaces.

2. Deformation of Voltages and Currents Arising during Steel Smelting in an Electric Arc Furnace

The source of higher harmonics in the supply networks of arc furnaces is the nonlinear nature of the arc. The arc voltage changes its shape during the smelting from close to rectangular in the initial stage of smelting the scrap, and from triangular to sinusoidal in the final stage of smelting.

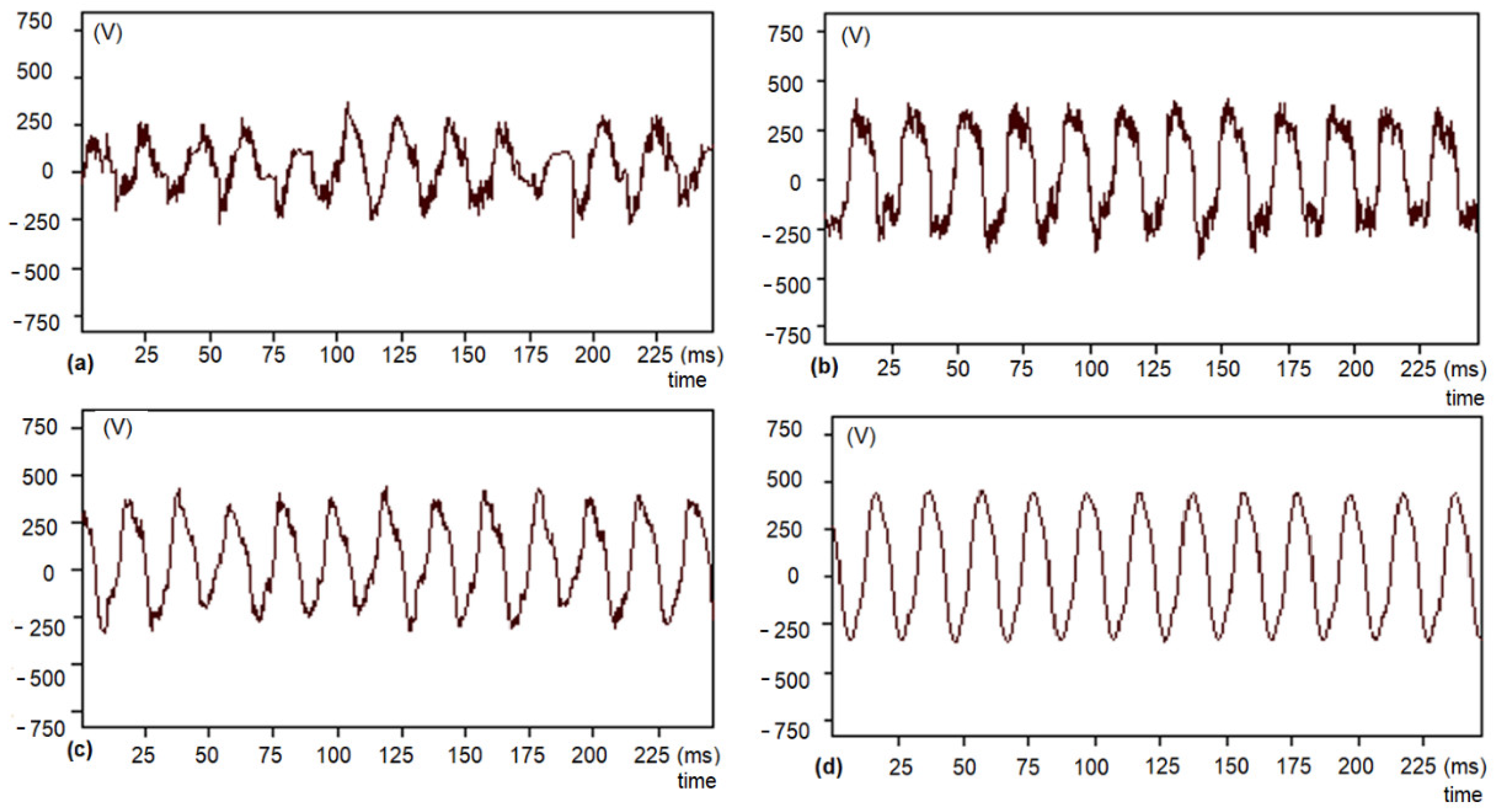
Arc furnaces generate the greatest disturbances in the initial phase of scrap melting. This is caused by dynamic changes in the electric arc voltage. The arc furnace operates from the short-circuit of the electrodes with the charge to the idle state (electric arc break). After ignition of the electric arc between the charge and the electrodes, the arc voltage curve changes very dynamically (Figure 1a).

The electric arc of the electric arc furnace changes its length, which causes a change in the voltage value between the charge and the electrodes. As the scrap melts, the arc voltage at this stage is closer to the square wave (Figure 1b), which can be used to extract the arc voltage frequency. In the next step of smelting the scrap, the arc voltage is triangular in shape (Figure 1c). In the final stage of smelting the scrap, the arc voltage is sinusoidal (Figure 1d). The electric arc is covered with foamed slag, which causes thermal stabilization of the furnace operation [31].

Changes in the arc voltage waveform distort the arc furnace current waveform. The result of current distortion in the mains supplying the arc devices is a distorted voltage drop. As a result, the supply voltage of the steelworks has a deformed course.

Figure 2 presents the changes in the value of the harmonic distortion of the THD_I current and the THD_U voltage, recorded during one smelting in the arc furnace. There is a significant correlation between the THD_I and THD_U waveforms. The correlation coefficient is r_THDI-U = 0.71.

Analytical determination of the indices characterizing the deformation of voltages and currents in the circuits of arc furnaces is very difficult due to the fact that the values of these indices are random variables. Additionally, the shape of the current (similar to the arc voltage—Figure 1) changes with the time of smelting. The harmonic content of the voltage in the electric arc furnace supply network increases with the increase in the furnace power and decreases with the increase in the short-circuit power of the network.

The main cause of the arc furnace current distortion is the arc voltage distortion between the electrodes and the charge. The distorted current is the cause of the distorted voltage drop on the impedance of the arc supply line. As a result, the supply voltage of the steel plant does not have a perfect sinusoidal wave.

Figure 3 shows the current waveform recorded in the initial stage of smelting in the arc furnace supply network with the power of a 20 MVA furnace transformer. In this phase, there are changes in which the frequency of the current cannot be clearly determined because it is not periodic.

In the next part of the smelting, powerless periods occur sporadically. The current, however, shows dynamic changes in value, which in turn causes voltage fluctuations in the supply network (Figure 4).

In the last stage of the smelting, with the melt and the smelting with foamed slag, it is possible to speak of a furnace current whose shape is similar to a sinusoidal course (Figure 5).

In order to assess the voltage distortion in the networks supplying arc devices, measurements were made, and then an analysis of changes in the indices characterizing distorted waveforms (THD, U_h) was carried out. Figure 6 shows the changes in the THD_U harmonic distortion coefficient recorded in the steelwork supply network (110 kV) and in the arc furnace supply line (30 kV).

For the presented power supply system of the steelworks (rated voltage of the supply line U_N = 110 kV), the ratio of the short-circuit power of the network to the power of the arc furnace is S_cc/S_trc = 134. It was estimated that the influence of the electric arc furnace on voltage distortion at the level of 110 kV is small. Changes of the THD_U_110 kV coefficient are typical for the waveforms corresponding to the daily changes of the power system load. In the case of the furnace transformer supply line (rated line voltage U_N = 30 kV), the influence of the arc furnace on voltage distortion is much greater. There is a visible increase in THD_U_30 kV during the operation of the arc furnace. For the analyzed line, the ratio of the short-circuit power of the network to the power of the electric arc furnace is S_cc/S_trc = 20.

During the individual stages of steel smelting in the electric arc furnace, the values of the parameters characterizing the energy quality change. The reason for this is the dynamically changing current of the arc furnace. The indices determining the deformation of the supply voltage, i.e., THD_U and U_h, also change during the smelting. Figure 7 shows the changes in the total harmonic distortion of the THD voltage recorded during one smelting.

After starting steel smelting in the electric arc furnace, when the arc voltage is the most deformed (the shape of the voltage curve is close to a square wave), the greatest deformation of the furnace current also occurs. This results in the greatest distortion of the voltage supplied to the arc furnaces (Figure 7, point a). Then, there are odd harmonics (U₍₃₎ = 1.238%, U₍₅₎ = 1.913%, U₍₇₎ = 0.428%, and U₍₉₎ = 0.151%) and even harmonics (U₍₂₎ = 0.372%, U₍₄₎ = 0.252%, U₍₆₎ = 0.267%, U₍₈₎ = 0.191%, and U₍₁₀₎ = 0.151%), as shown in Figure 8a When the scrap is melted, the voltage distortion and the content of individual harmonics are reduced, e.g., U₍₂₎ = 0.111%, U₍₄₎ = 0.116%, U₍₆₎ = 0.03%, U₍₈₎ = 0.015%, U₍₁₀₎ = 0.035% and odd U₍₃₎ = 0.186%, U₍₅₎ = 0.982%, U₍₇₎ = 0.554%, and U₍₉₎ = 0.015% (Figure 8b). Figure 8c shows the spectrum of voltage harmonics recorded with the arc furnace off, where U₍₅₎ = 0.644% of the fundamental harmonic, while U₍₃₎ = 0.367% and U₍₇₎ = 0.267%.

The changing spectrum of harmonics, in terms of both the value of individual components and their order (odd and even harmonics appearing—Figure 9 and Figure 10), may cause disturbances in the operation of the furnace system equipment.

Capacitor batteries used to compensate for the reactive power of the arc furnace are particularly at risk. A voltage surge may occur at the capacitor terminals due to resonance conditions. Figure 11 shows a damaged capacitor battery used to compensate for reactive power of the arc furnace. The cause of the capacitor failure was resonance phenomena causing an increase in the voltage supplying the capacitor bank. The next section of the article presents model studies presenting the influence of power supply conditions for arc furnaces (short-circuit power of the network) on transient phenomena resulting from switching on the capacitor bank.

3. Multi-Voltage Model of the Arc Device

Voltage distortion in arc supply networks depends both on disturbances caused by arc furnaces and on the influence of other nonlinear loads supplied from the power system. This is confirmed in Figure 6, showing changes in the THD_U coefficient recorded over a week in the power line supplying arc furnaces (at the voltage level of 110 kV or 30 kV). The value of the THD_U factor also depends on the short-circuit power of the network from which the steel plant is supplied and changes with the phases of smelting in the arc furnace. Additionally, during smelting, the spectrum of harmonics of the current and arc voltage changes. These factors make modeling of voltage distortions caused by arc devices extremely difficult. Due to the very high rated powers of furnace transformers and the dynamically changing load, arc furnaces are complex research facilities. Therefore, a certain compromise should be taken into account between the degree of complexity of the model and the accuracy (approximation) in reproducing the real conditions and its practical use.

Due to the fact that, in individual phases, there is a very large correlation between the changes in the total distortion factor voltage harmonics, by analyzing the voltage distortion caused by arc furnaces, the article considers the phase with the greatest deformation (the highest THD_U value), which results from a very large correlation between changes in the THD_U value in individual phases, e.g., for the steelworks supply line (Figure 12), i.e., r_THD12 = 0.995, r_THD23 = 0.995, and r_THD31 = 0.995.

Analyzing the THD_U changes recorded in the individual phases of the steel supply line (Figure 13), during one melt (at 5 s measurement intervals), a significant correlation was also found, i.e., r_THD12 = 0.905, r_THD23 = 0.880, and r_THD31 = 0.897.

Taking into account the significant correlation of THD changes in individual phases of the supply line to the arc furnaces, a single-phase equivalent diagram of the arc device with a multi-voltage electric arc model is proposed in Figure 14 [31].

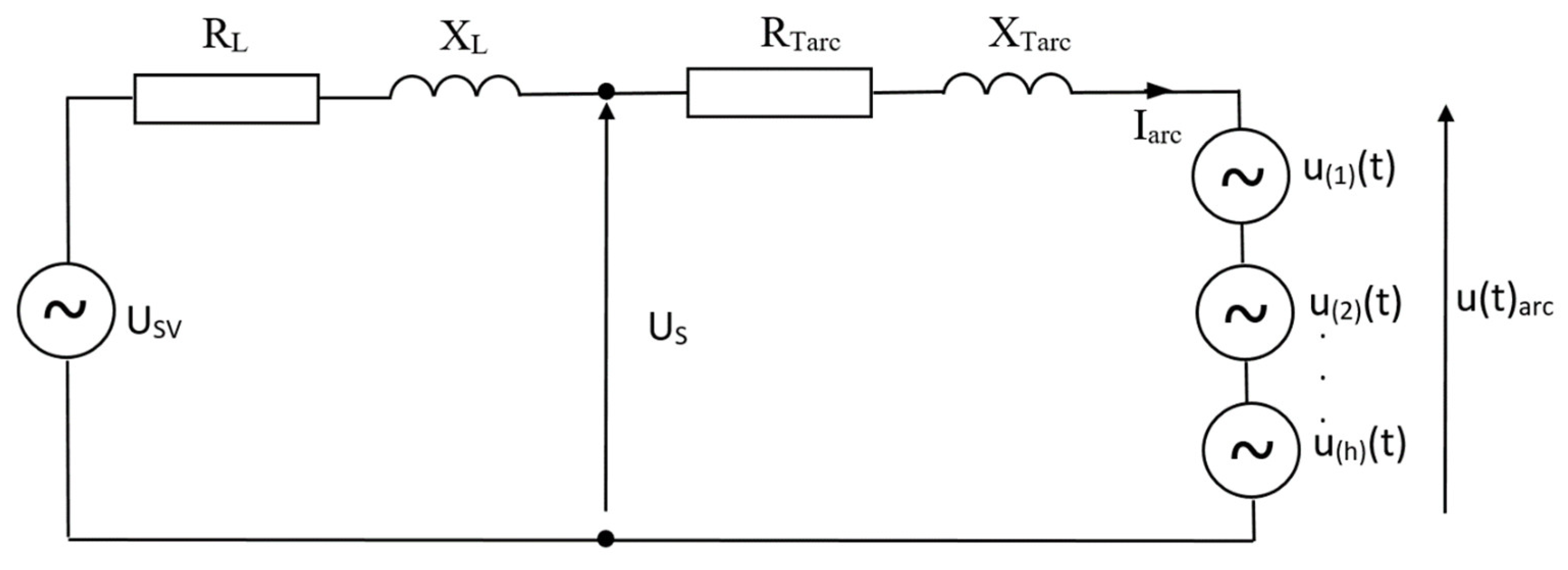
The following designations are adopted in Figure 14: U_SV—rated voltage, U_S—steelwork supply voltage, R_L, X_L—power line resistance and reactance, R_Tarc, X_Larc—resistance and reactance high-current path with the furnace transformer, I_arc—arc furnace current, U₍₁₎(t), U₍₂₎(t), …, U_(h)(t)—voltage harmonics, and U(t)_arc—arc voltage.

The article proposes a model based on harmonic voltage (harmonic voltage source model—HVSM). In this model, the arc furnace is represented as a series connection of the resistance R_T and the reactance X_T representing the high-current path and the arc voltage U_arc(t) (Figure 15).

The arc voltage is calculated as the difference between the measured voltage U_S(t),

$$U_S(t)={\displaystyle \sum _{h=1}^n{U}_h}\sin (h\omega \mathrm{t}+{\phi }_h),$$

(1)

and that determined on the basis of the measured current, i_arc(t), with the voltage U_S(t) on the impedance of the high-current circuit.

$$U_S(t)=R_T{i}_{arc}(t)+L_T\frac{d{i}_{arc}(t)}{d(t)}.$$

(2)

Hence,

$$U_{arc}(t)=U_S(t)-U_{SV}(t).$$

(3)

The presented two models based on the measurements of real voltages and currents in networks supplying arc devices can be classified as dynamic models of the arc device.

Parallel to the measurements of indicators characterizing the quality of electric energy (e.g., THD_U, U_h) in the lines supplying the arc furnaces, the voltage of the electric arc was recorded. The recorded waveforms of the electric arc voltage were the basis for the development of a multi-voltage model of the arc device. The proposed model takes into account changes in the arc voltage shape during the smelting process. This model consists of series connected voltage sources of successive harmonics representing the changing arc voltage. The change in both the value and the shape of the arc voltage is taken into account. Figure 16a shows an example of the recorded arc voltage. The spectrum of the true arc voltage is determined using FFT. Knowing the spectrum of voltage harmonics, the arc device was modeled using the proposed model (Figure 16b) [31].

Taking into account the change in the arc voltage shape and the change in the content of higher harmonics of this voltage, the operation of the arc device in the phase after melting the scrap in the arc furnace was modeled (Figure 17).

The power supply conditions of the steelworks have a decisive influence on the deformation of the voltage supplying arc furnaces. These conditions are determined by the ratio of the short-circuit power of the network supplying the arc devices to the power of the arc furnace at the short-circuit of the electrodes with the charge—S_cc/S_ts. Assuming the actual supply conditions of the steel mill, two different ratios of the short-circuit power of the network to the power of the furnace at the short-circuit of the electrodes with the charge were assumed: S_cc/S_ts = 134—Figure 18a and S_cc/S_ts = 20—Figure 18b.

The article proposes a single-phase equivalent diagram of the arc device. A certain simplification of the presented electric arc furnace based on the multi-voltage model of the electric arc is the two-voltage model of the arc device—Figure 19.

Figure 20 shows the spectrum of voltage harmonics for an ideal square wave. In the case of a square wave, the harmonic distortion factor THD_Urec is about 0.483, assuming the amplitude of the first harmonic as 1.

The harmonic distortion factor THD for a rectangular arc voltage can also be determined from Equation (4).

$$TH{D}_{Urec}=\frac{\sqrt{{\displaystyle \sum _{\upsilon =2}^{\infty }{U}_{rec\upsilon }^2}}}{U_{rec1}}=\sqrt{\frac{U_{rec0}^2-U_{rec1}^2}{U_{rec1}^2}}=\sqrt{\frac{U_{rec0}^2}{U_{rec1}^2}-1}=\sqrt{\frac{{\pi }^2}{8}-1}=0.4834$$

(4)

Figure 21 shows the changes in the value of the arc voltage distortion coefficient THD_Uarc as a function of parameter b. For the parameter b = 0, the arc voltage waveform is rectangular (THD_Uarc = 0.483); when b = 1, the arc voltage shape is sinusoidal (THD_Usin = 0).

The THD_Uarc factor for a given arc voltage waveform distortion is described by Equation (5).

$$TH{D}_{Uarc}=(1-b)\sqrt{\frac{{\pi }^2}{8}-1}.$$

(5)

In the PSpice program, model tests were carried out with the use of a three-voltage model of the electric arc furnace. The purpose of the model tests was, among others, to estimate the distortion of the supply voltage depending on the degree of deformation of the arc voltage and the supply conditions of the arc furnaces. Figure 21 shows the spectrum of harmonics and the waveform of the voltage supplied to the steel mill U_S. A rectangular shape of the arc voltage U_arc was assumed, and the ratio of the short-circuit power of the S_cc network to the short-circuit power of the electrodes with the S_trc charge was S_cc/S_trc = 134—Figure 22.

Figure 23 shows the spectrum of harmonics and the voltage waveform of the U_S steelwork supply, at the rectangular arc voltage U_arc, for the ratio of the short-circuit power of the S_cc network to the short-circuit power of the electrodes with the charge S_trc equal to S_cc/S_trc = 20. This corresponds to the actual supply conditions for the metallurgical plant and the steel plant from which the arc furnaces are powered.

Arc furnaces are characterized by a high consumption of inductive reactive power. This is due to the high inductance of the high-current circuit supplying the arc. Therefore, it becomes necessary to use reactive power compensation, mainly with the use of capacitors. When the arc furnace is turned on (the arc burns without interruption, and the arc voltage has a rectangular waveform U_arc(t)), the voltage drops on the impedance of the supply network, which causes a decrease in the value and voltage distortion on the rails of the U_S(t) steel plant (Figure 24).

Using the proposed model of the electric arc, the influence of the connected capacitor bank on the improvement of the power supply conditions was analyzed.

Figure 25 shows the course of the supply voltage U_S(t) at the moment of switching on the capacitor bank. A sharp increase in the U_S voltage is visible. The arc voltage waveform U_arc(t) has a rectangular shape [31].

Depending on the supply conditions of arc furnaces (supply line parameters: resistance R_L and reactance X_L), there may be transients of different duration. The waveforms for the supply voltage U_SV(t), the voltage steelworks U_S(t), and the current i(t) during the capacitors’ connection are shown in Figure 26. The supply line is characterized by a low short-circuit power in relation to the power of arc furnaces.

In the case of worse supply conditions for the arc furnace (lower short-circuit power), the furnace has a greater influence on the value and deformation of the voltage supplying the steel plant. Sudden voltage increases due to transients occurring during the capacitor bank switching on can be limited by the use of suppressors.

4. Influence of the Arc Voltage Distortion on the Melting Power of the Electric Arc Furnace

On the basis of the proposed model of the arc device, an analysis was made of the influence of the electric arc voltage deformation on the scrap melting power (maximum electric arc power). The adoption of the single-phase circuit of the arc device was based on, inter alia, on analyzing the results of measurements of indicators recorded in the networks supplying arc devices and symmetry of the high-current track structure with elements of the furnace installation, conducting the steel smelting process under operational symmetry, i.e., with the same currents and arc voltages in each phase. Figure 27 shows the single-phase equivalent power supply diagram of the arc device. The impedance of the supply line to the smelter was omitted (as opposed to the diagram shown in Figure 14 and Figure 19). The voltage Us is in this case the supply voltage of the steelworks.

This circuit includes the arc supply system, consisting of an equivalent, ideal voltage source, with the phase voltage U_S(t),

$$U_S(t)=U_S\mathit{sin}(\omega t+\psi ),$$

(6)

and equivalent resistance R_T and inductance L_T or, for fundamental harmonic, reactance X_T = ωL_T.

The electric arc of the electric arc furnace is replaced by a system of ideal voltage sources connected in series, one with a sinusoidal waveform U_sin(t) and the other with a square waveform U_rec(t),

$$U_{arc}(t)=U_{\mathit{sin}}(t)+U_{rec}(t)=U_{\mathit{sin}}\sin \omega t+U_{rec}sign(i)=b{U}_{arc1}\sin \omega t+\frac{(1-b)\pi }{4}{U}_{arc1}sign(i),$$

(7)

where U_arc1 is the amplitude of the fundamental harmonic of the arc voltage.

The waveform i(t), in the circuit given in Figure 27, is determined by the following differential equation:

$$U_S(t)=R_{T}i(t)+L_T\frac{di}{dt}+U_{\mathit{sin}}(t)+U_{rec}(t).$$

(8)

The instantaneous value of the current in the circuit (in steady state) resulting from this equation is the sum of three waveforms,

$$i(t)=i_1(t)+i_{\mathit{sin}}(t)+i_{rec}(t).$$

(9)

The value of i₁(t) is forced by the voltage of the supply source Formula (10) and is equal to

$$i_1(t)=\frac{U_S}{Z_T}\sin (\omega t+\psi -\phi ),$$

(10)

where

$$Z_T=\sqrt{R_T^2+{(\omega L_T)}^2},$$

(11)

$$\phi =arctg(\omega L_T/R_T).$$

(12)

The i_sin(t) waveform is forced by the sinusoidal component of the arc voltage U_sin(t), i.e., the first of the expressions in

$$i_{\mathit{sin}}(t)=\frac{U_{\mathit{sin}}}{Z_T}\sin (\omega t-\phi ),$$

(13)

and the wave of i_rec(t), forced by the rectangular component of the arc voltage U_rec(t), i.e., the second of the expressions in

$$i_{rec}(t)=A-(A+\frac{2U_{rec}}{3R})(1-\exp (-\omega t/\tau )),$$

(14)

where the auxiliary quantities are

$$\tau =\frac{L_T}{\omega R_T},$$

(15)

$$A=\frac{2U_{rec}}{3R}B,$$

(16)

$$B=C(4-4C+C^2)/(1+{(1-C)}^3),$$

(17)

$$C=1-\exp (-\frac{\pi }{6}/\tau ).$$

(18)

The instantaneous value of the arc power is given by the formula

$$p_{arc}(t)=u_{arc}(t)i=(U_{\mathit{sin}}(t)+U_{rec}(t))(i_1(t)+i_{\mathit{sin}}(t)+i_{rec}(t)).$$

(19)

The calculations for an exemplary arc device are presented below. The calculations were performed in relative units, taking the following as the basic quantities:

Supply phase amplitude,

$$U_S=1p.u.(100\%);$$

(20)

arc device rated current,

$$I_N=1p.u.(100\%).$$

(21)

The reactance of the supply circuit was determined assuming that the theoretical short-circuit current of the electrodes with the charge is twice as high as the rated one.

$$I_{tsc}=U_S/X_T=2p.u.(200\%).$$

(22)

The assumed reactance value is

$$X_T=U_S/I_{tsc}=0.5p.u.(50\%).$$

(23)

The circuit resistance was assumed to be five times lower than the reactance, i.e.,

$$R_T=X_T/5=0.1p.u.(10\%).$$

(24)

Similar assumptions were made when analyzing the voltage fluctuations generated by the arc furnaces presented in [31,32]. The operating characteristics of the power released in the arcs as a function of the current consumed by the arc device were determined (Figure 28).

This power is expressed as a percentage of the maximum value occurring at the sinusoidal current (assumption b = 1, i.e., U_rec = 0).

Maximum power occurs at the following current:

$$I_M=I_N\sqrt{2}\sqrt{1-\cos \phi }.$$

(25)

The value of the maximum arc power decreases with the increase in the nonlinearity of the arc, i.e., with the decrease in the parameter b value from unity U_rec = 0 to zero|U_sin = 0. The relative reduction of the maximum arc power as a function of parameter b is shown in Figure 29.

The arc power value decreases gradually from the value p = 100% for b = 1 to p = 97.8% for b = 0.75, through p = 96.1% for b = 0.5, p = 94.3% for b = 0.25, and p = 92.5% for b = 0.

5. Summary

In the case of complex research objects such as arc devices, a certain compromise should be taken into account between the degree of model complexity and the accuracy (approximation) in reproducing the real conditions and its practical use.

The presented measurements show that the voltage distortion in the networks supplying the arc devices is influenced by both the arc furnaces and other nonlinear loads supplied from the same part of the power system. This is evidenced by the waveforms of the total coefficient of distortion of the THD voltage, the changes of which recorded during the week of measurements are typical for daily changes in the power system load. The THD value also depends on the short-circuit power of the network from which the steel plant is supplied. Additionally, during smelting, the spectrum of harmonics of the current and arc voltage changes. All these factors make modeling of voltage distortions caused by arc devices extremely difficult.

The multi-voltage model of the arc furnace presented in the article is a compromise between the accuracy of the determined deformation of the supply voltage and its practical application. In this model, the electric arc voltage waveforms registered in industrial conditions are used.

On the basis of the analysis of the results of the measurements of arc voltage and furnace current recorded herein, several conclusions can be drawn. The changing shape of the arc voltage and its length cause distortion of the furnace current and changes in its value, which are the reason for the generation of higher harmonics and voltage fluctuations by arc furnaces. The waveforms of the arc voltage and furnace current, especially in the initial stage of smelting, are not symmetrical with respect to the time axis and are also not periodic. During the smelting process in the arc furnace, the shape and value of the arc voltage change, starting from an almost rectangular waveform, through a triangular curve, ending with a waveform close to a sinusoidal one. The time when the arc furnace causes the greatest disturbances in the power system (the beginning of smelting), to a large extent, depends on the quality of the scrap, which affects the speed of the formation of the melt wells under the electrodes. Loading subsequent baskets with scrap causes a renewed increase in disturbances generated by arc furnaces. The greatest disturbances occur when loading the first basket (commencement of smelting).

The conclusion from the conducted theoretical considerations and model calculations is that the maximum power generated in the arcs occurs at a very similar value of the arc current (with an accuracy of less than 0.5%), and the value of this maximum decreases with an increase in the nonlinearity of the arc (a decrease in the value of parameter b).