Design of Intelligent Solar PV Power Generation Forecasting Mechanism Combined with Weather Information under Lack of Real-Time Power Generation Data
Abstract
:1. Introduction
2. Literature Review
3. Long Short-Term Memory Neural Network
4. Solar Photovoltaic Power Generation Forecasting Strategy
4.1. Data Correlation Analysis
4.2. Data Standardization and Anti-Standardization
4.3. Deep Neural Network
4.4. Forecasting Strategy
- Step 1: Obtain historical solar PV power generation data from the database.
- Step 2: Data preprocessing via the data standardization in (8).
- Step 3: Set the maximum iteration of the training process and the cutoff threshold of the training error.
- Step 4: Initialize the learning rates, the weights and the biases of the LSTM in Section 3.
- Step 5: Input standardized solar PV power generation data into the LSTM.
- Step 6: Obtain the forecasting power generation via the data anti-standardization in (9) from the LSTM output.
- Step 7: Calculate the training error between the actual power generation and the forecasting one, and then use training errors to adjust the parameters in the LSTM.
- Step 8: Repeat steps 5–7 and check whether the maximum iteration of the training process or the cutoff threshold of the training error is achieved.
- Step 9: Finish the training process if the terminated condition is satisfied.
- Step 1: Obtain historical solar PV power generation, irradiance and temperature data from the database.
- Step 2: Data preprocessing via the data standardization in (8).
- Step 3: Set the maximum iteration of the training process and the cutoff threshold of the training error.
- Step 4: Initialize the learning rates, the weights and the biases of the DNN in (10)–(12).
- Step 5: Input standardized irradiance and temperature into the DNN.
- Step 6: Obtain the forecasting power generation via the data anti-standardization in (9) from the DNN output.
- Step 7: Calculate the training error between the actual power generation and the forecasting one, and then use training errors to adjust the parameters in the DNN.
- Step 8: Repeat steps 5–7 and check whether the maximum iteration of the training process or the cutoff threshold of the training error is achieved.
- Step 9: Finish the training process if the terminated condition is satisfied.
- Step 1: Obtain data from the database.
- Step 2: Judge whether the data are real-time solar PV power generation information or not.
- Step 3: If they are not real-time data, one should obtain the weather information, including irradiance and temperature, from nearby solar PV power generation fields or weather stations, and implement the trained DNN data fitting via steps 5 and 6.
- Step 4: If they are real-time data, it goes to step 7.
- Step 5: Input standardized irradiance and temperature into the trained DNN.
- Step 6: Obtain the data-fitting solar PV power generation via the data anti-standardization in (9) from the trained DNN output.
- Step 7: Input standardized actual or data-fitting power generation data into the trained LSTM.
- Step 8: Obtain the forecasting power generation via the data anti-standardization in (9) from the trained LSTM output.
- Step 9: Calculate the forecasting error between the actual power generation and the forecasting one, and then use forecasting errors to adjust the parameters in the trained LSTM for on-line learning.
- Step 10: Repeat the above steps until the on-line forecasting programing is finished.
4.5. Performance Evaluation Index
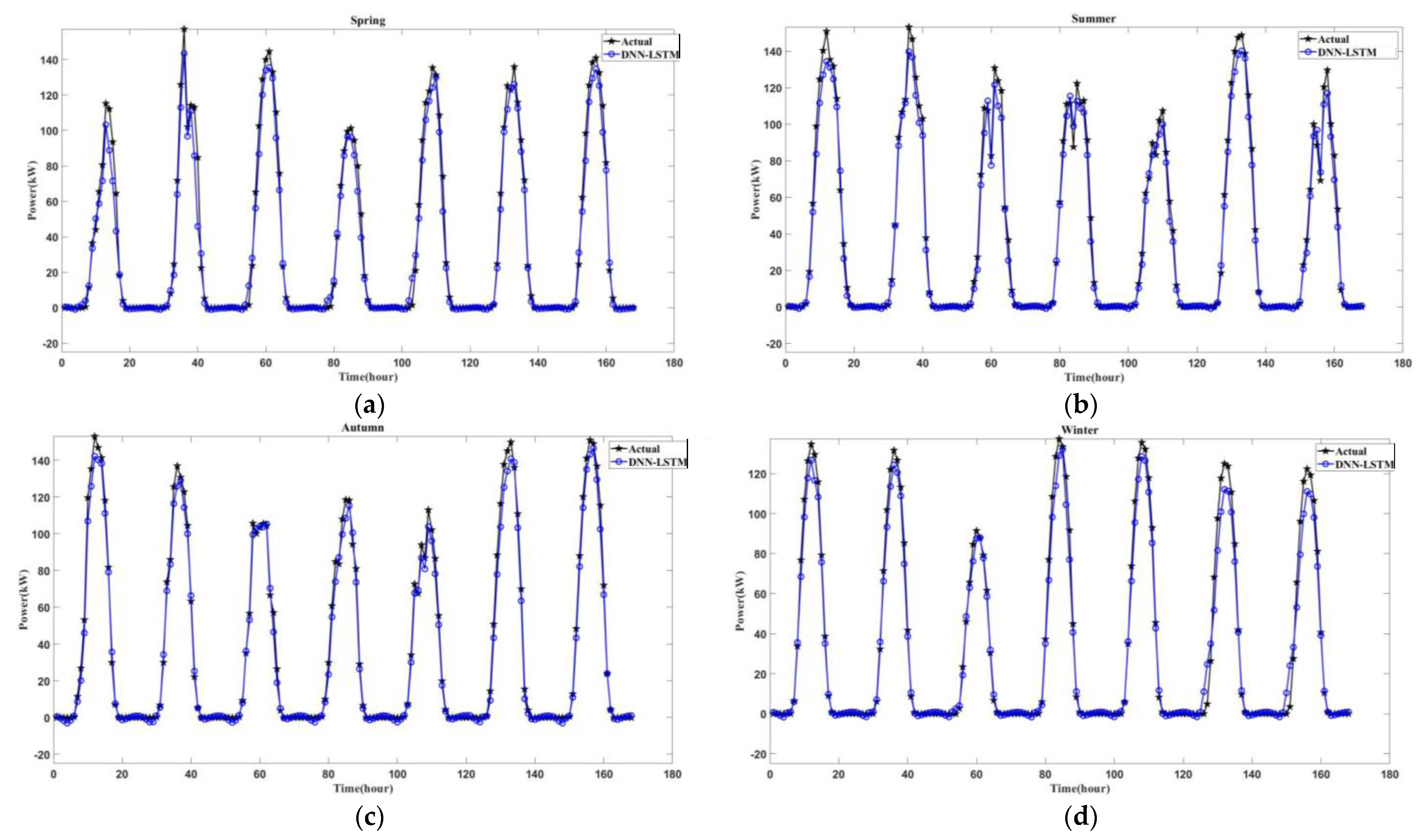
5. Experimental Results
5.1. Solar PV Power Generation Forecasting
5.1.1. Solar Power Plant A
5.1.2. Solar Power Plant B
5.1.3. Solar Power Plant C
5.1.4. Solar Power Plant D
5.1.5. Solar Power Plant E
5.1.6. Solar Power Plant F
5.2. Discussion
5.3. Data Fitting Performance with Irradiance and Temperature
5.4. Model Universal Applicability Verification
5.5. On-Line Learning Ability Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IEA. Global Energy Review 2020. The Impacts of the COVID-19 Crisis on Global Energy Demand and CO2 Emission. International Energy Agency. 2020. Available online: https://www.iea.org/reports/global-energy-review-2020 (accessed on 1 May 2022).
- Cirés, E.; Marcos, J.; de la Parra, I.; García, M.; Marroyo, L. The potential of forecasting in reducing the LCOE in PV plants under ramp-rate restrictions. Energy 2019, 188, 116053. [Google Scholar]
- IEA. Renewable Energy Market Update-May 2022. International Energy Agency. 2022. Available online: https://www.iea.org/reports/renewable-energy-market-update-may-2022 (accessed on 1 May 2022).
- Golubchik, L.; Khuller, S.; Mukherjee, K.; Yao, Y. To send or not to send: Reducing the cost of data transmission. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2472–2478. [Google Scholar]
- Porter, K.; Fink, S.; Buckley, M.; Rogers, J.; Hodge, B.M. Review of Variable Generation Integration Charges; Technical Report NREL/TP-5500-57583; National Renewable Energy Laboratory: Golden, CO, USA, 2013.
- Lew, D.; Piwko, N.; Miller, D.; Jordan, G.; Clark, K.; Freeman, L. NREL: How do High Levels of Wind and Solar Impact the Grid? The Western Wind and Solar Integration Study; Technical Report NREL/TP-5500-50057; National Renewable Energy Laboratory: Golden, CO, USA, 2010.
- Shaker, H.; Manfre, D.; Zareipour, H. Forecasting the aggregated output of a large fleet of small behind-the-meter solar photovoltaic sites. Renew. Energy 2020, 147, 1861–1869. [Google Scholar]
- Ketterer, J.C. The impact of wind power generation on the electricity price in Germany. Energy Econ. 2014, 44, 270–280. [Google Scholar]
- Vos, K.D. Negative wholesale electricity prices in the German, French and Belgian day-ahead, intra-day and real-time markets. Electr. J. 2015, 28, 36–50. [Google Scholar] [CrossRef]
- Elliott, E. Green Power Curtailment in China. Renewable: Option and Review. 2019. Available online: https://physicsworld.com/a/green-power-curtailment-in-china/ (accessed on 1 May 2022).
- Tang, N.; Zhang, Y.; Niu, Y.; Du, X. Solar energy curtailment in China: Status quo, reasons and solutions. Renew. Sustain. Energy Rev. 2018, 97, 509–528. [Google Scholar] [CrossRef]
- Li, C.; Shi, H.; Cao, Y.; Wang, J.; Kuang, Y.; Tan, Y.; Wei, J. Comprehensive review of renewable energy curtailment and avoidance: A specific example in China. Renew. Sustain. Energy Rev. 2015, 41, 1067–1079. [Google Scholar]
- Chou, K.L. Constructing a power system with high renewable energy ratios in Taiwan: The key issues of long-term developmental pathways and energy storage strategies to fulfill net-zero emissions. Sustain. Ind. Dev. Newsl. 2021, 22, 7–8. [Google Scholar]
- Yang, D.; Dong, Z. Operational photovoltaics power forecasting using seasonal time series ensemble. Sol. Energy 2018, 166, 529–541. [Google Scholar] [CrossRef]
- Wang, G.; Su, Y.; Shu, L. One-day-ahead daily power forecasting of photovoltaic systems based on partial functional linear regression models. Renew. Energy 2016, 96, 469–478. [Google Scholar] [CrossRef] [Green Version]
- Kang, M.; Sohn, J.; Park, J.; Lee, S.; Yoon, Y. Development of algorithm for day ahead PV generation forecasting using data mining method. In Proceedings of the IEEE 54th International Midwest Symposium on Circuits and Systems (MWSCAS), Seoul, Korea, 7–10 August 2011; pp. 1–4. [Google Scholar]
- Kashyap, Y.; Bansal, A.; Sao, A.K. Solar radiation forecasting with multiple parameters neural networks. Renew. Sustain. Energy Rev. 2015, 49, 825–835. [Google Scholar]
- Kushwaha, V.; Pindoriya, N.M. Very short-term solar PV generation forecast using SARIMA model: A case study. In Proceedings of the 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 430–435. [Google Scholar]
- Pierro, M.; Bucci, F.; Felice, M.D.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Multi-model ensemble for day ahead prediction of photovoltaic power generation. Sol. Energy 2016, 134, 132–146. [Google Scholar]
- Yang, C.; Thatte, A.A.; Xie, L. Multitime-scale data-driven spatio-temporal forecast of photovoltaic generation. IEEE Trans. Sustain. Energy 2015, 6, 104–112. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Wen, H.; Jiang, L.; Xiao, W. Forecasting-based power ramp-rate control strategies for utility-scale PV systems. IEEE Trans. Ind. Electron. 2019, 66, 1862–1871. [Google Scholar] [CrossRef]
- Massidda, L.; Marrocu, M. Use of multilinear adaptive regression splines and numerical weather prediction to forecast the power output of a PV plant in Borkum, Germany. Sol. Energy 2017, 146, 141–149. [Google Scholar] [CrossRef]
- Reikard, G.; Haupt, S.E.; Jensen, T. Forecasting ground-level irradiance over short horizons: Time series, meteorological, and time-varying parameter models. Renew. Energy 2017, 112, 474–485. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Lughi, V. Short-term forecasting of power production in a large-scale photovoltaic plant. Sol. Energy 2014, 105, 401–413. [Google Scholar] [CrossRef]
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef] [Green Version]
- Durrani, S.P.; Balluff, S.; Wurzer, L.; Krauter, S. Photovoltaic yield prediction using an irradiance forecast model based on multiple neural networks. J. Mod. Power Syst. Clean Energy 2018, 6, 255–267. [Google Scholar] [CrossRef]
- Alfadda, A.; Rahman, S.; Pipattanasomporn, M. Solar irradiance forecast using aerosols measurements: A data driven approach. Sol. Energy 2018, 170, 924–939. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Convolutional neural network for short-term solar panel output prediction. In Proceedings of the IEEE 7th World Conference Photovoltaic Energy Conversion (WCPEC) (Joint Conf. 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2357–2361. [Google Scholar]
- Yu, Y.; Cao, J.; Wan, X.; Zeng, F.; Xin, J.; Ji, Q. Comparison of short-term solar irradiance forecasting methods when weather conditions are complicated. J. Renew. Sustain. Energy 2018, 10, 053501. [Google Scholar] [CrossRef]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting electricity consumption for commercial and residential buildings using deep recurrent neural networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Tang, P.J.; Wang, H.L.; Xu, K.S. Multi-objective layer-wise optimization and multi-level probability fusion for image description generation using LSTM. Acta Autom. Sin. 2018, 40, 1237–1249. [Google Scholar]
- Yang, L.; Zheng, Y.; Cai, X.; Dai, H.; Mu, D.; Guo, L.; Dai, T. A LSTM based model for personalized context-aware citation recommendation. IEEE Access 2018, 6, 59618–59627. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Yu, Y.; Cao, J.; Zhu, J. An LSTM short-term solar irradiance forecasting under complicated weather conditions. IEEE Access 2019, 7, 145651–145666. [Google Scholar] [CrossRef]
- Yang, T.; Li, B.; Xun, Q. LSTM-attention-embedding model-based day-ahead prediction of photovoltaic power output using Bayesian optimization. IEEE Access 2019, 7, 171471–171484. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-term photovoltaic power forecasting using an LSTM neural network and synthetic weather forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, C.; Srivastava, A.K.; Jin, C.; Sharma, R.K. Data-driven day-ahead PV estimation using autoencoder-LSTM and persistence model. IEEE Trans. Ind. Appl. 2020, 56, 7185–7192. [Google Scholar] [CrossRef]
- Liu, C.H.; Gu, J.C.; Yang, M.T. A simplified LSTM neural network for one day-ahead solar power forecasting. IEEE Access 2021, 9, 17174–17195. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Pareek, V.; Chaudhury, S. Deep learning-based gas identification and quantification with auto-tuning of hyper-parameters. Soft Comput. 2021, 25, 14155–14170. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Mirjalili, S.; Piras, G.; Garcia, D.A. Quaternion convolutional long short-term memory neural model with an adaptive decomposition method for wind speed forecasting: North aegean islands case studies. Energy Convers. Manag. 2022, 259, 115590. [Google Scholar] [CrossRef]
- Xie, Y.Y.; Li, C.S.; Tang, G.; Liu, F.J. A novel deep interval prediction model with adaptive interval construction strategy and automatic hyperparameter tuning for wind speed forecasting. Energy 2021, 216, 119179. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar irradiance forecasting using deep neural networks. Procedia Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 9, 533–536. [Google Scholar] [CrossRef]
- Ostertagová, E. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
















| References | Research Background or Merits | Limitations |
|---|---|---|
| [14,19] | Numerical weather prediction is a method of forecasting that the physical laws of atmospheric behavior are expressed through mathematical equations. | It relies heavily on the accuracy of weather forecasting. |
| [15] | Partial functional linear regression can process or predict nonlinear data. | There are many characteristic parameters, which are more troublesome to select training parameters. |
| [16] | The method using K-means has a good performance and a fast calculation speed. | This algorithm is sensitive to the initial status of clustering, and its performance relies heavily on the accuracy of weather center information. |
| [17,25] | ANN has high accuracy and can process noisy data effectively. | This prediction method requires a huge network framework with many coefficients to be adjusted and spends more training time. |
| [18] | SARIMA solves the limitation of ARIMA on seasonality and clarifies the seasonal elements in the simulation data. | The processing effect of nonlinear data may be deteriorated. |
| [20] | The prediction effect of spatio-temporal-ARX model is better than persistence model. | For different weather conditions, e.g., non-sunny weather, its prediction effect may be degenerate. |
| [21] | A method of DSTR with GBSFS to achieve the objective of solar PV power generation prediction. | This method is unsuitable for data with strong noise. |
| [22] | Multi-linear adaptive regression splines method can process or predict nonlinear data. | This method needs more input data to improve accuracy, and the input data need to be time-efficient. |
| [23] | It uses ARIMA with DICast and NWP to predict solar PV power generation. | Unstable data and inaccurate weather forecasting will lead to a decrease in the forecasting accuracy. |
| [24] | It proposes an AFFNN to judge weather conditions through NWP, and then uses different AFFNNs to predict power generation. | This method, which uses three distinct ANN models to be applied to three typical types of day (sunny, partly cloudy and overcast), is more complicated than only one unified model. |
| [26] | The irradiance prediction model via the multi-layer feedforward neural network is used for power generation prediction, which is divided into illuminance, temperature, and energy prediction models. | There are lots of input parameters during the training process, and three models to be trained are time-consuming. |
| [27] | It uses the MLP model to predict solar PV power generation in the desert, which can effectively predict power generation on sunny days. | Except for sunny day, the effect of the model may be deteriorated for non-sunny days |
| [28] | It uses CNN to predict power generation via sky images and historical power generation data. | The training process of CNN is always time-consuming. |
| [29] | RNN is used to predict solar PV power generation. | The problem of gradient explosion in RNN should be further avoided. |
| References | Forecasting Method | Input Feature Factors | Weather Data | Model Complexity | Requirement of Real-Time Power Generation Data |
|---|---|---|---|---|---|
| [33] | LSTM and attention mechanism | Less (P,T) | No | Simple | Yes |
| [34] | LSTM with weather conditions | More (P, IR, ST, D PT, T, PW, RH, SZA, WS, WD) | Yes | High | Yes |
| [35] | LSTM-attention-embedding | More (P, TI, IR, T, RH, WD) | Yes | High | Yes |
| [36] | LSTM and synthetic weather forecast | More (P, IR, T, WS, RH, ST) | Yes | Medium | Yes |
| [37] | Auto-encoder LSTM and persistence model | More (P, T, RH, WS, IR, TI) | Yes | Medium | Yes |
| [38] | Simplified LSTM | More (P, IR, ST, WS) | Yes | Simple | Yes |
| Related Factor/R(x,y) Value | Irradiance | Temperature |
|---|---|---|
| Solar PV power generation | 0.9432 | 0.8561 |
| Plant | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| A | From 12 February 2020 to 18 February 2020 | From 30 May 2020 to 5 June 2020 | From 10 January 2019 to 7 October 2019 | From 3 January 2020 to 9 January 2020 |
| B | From 17 February 2020 to 23 February 2020 | From 5 May 2020 to 11 May 2020 | From 19 September 2019 to 25 September 2019 | From 5 November 2019 to 11 November 2019 |
| C | From 22 February 2020 to 28 February 2020 | From 31 May 2020 to 6 June 2021 | From 1 October 2019 to 7 October 2019 | From 23 November 2019 to 29 November 2019 |
| D | From 31 January 2020 to 6 February 2020 | From 12 May 2020 to 18 May 2021 | From 19 September 2019 to 25 September 2019 | From 5 November 2019 to 11 November 2019 |
| E | From 15 April 2020 to 21 April 2020 | From 1 May 2020 to 7 May 2020 | From 10 October 2019 to 16 October 2019 | From 12 November 2019 to 18 November 2019 |
| F | From 19 February 2020 to 25 February 2020 | From 16 June 2020 to 22 June 2020 | From 14 September 2019 to 20 September 2019 | From 11 November 2019 to 17 November 2019 |
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Season | |||||||
| nMAE (%) | Spring | 2.80 | 6.90 | 1.76 | 1.94 | 0.93 | |
| Summer | 5.30 | 12.77 | 6.83 | 3.92 | 2.59 | ||
| Autumn | 3.66 | 9.53 | 2.43 | 2.91 | 1.94 | ||
| Winter | 2.98 | 7.10 | 1.69 | 1.57 | 1.07 | ||
| Average | 3.69 | 9.08 | 3.18 | 2.59 | 1.63 | ||
| nRMSE (%) | Spring | 4.82 | 10.50 | 2.10 | 3.55 | 1.42 | |
| Summer | 9.30 | 18.57 | 10.79 | 8.73 | 4.82 | ||
| Autumn | 6.52 | 14.39 | 4.37 | 7.38 | 3.02 | ||
| Winter | 5.40 | 10.87 | 2.23 | 2.84 | 1.55 | ||
| Average | 6.50 | 13.58 | 4.87 | 5.62 | 2.70 | ||
| Accuracy (%) | Spring | 97.20 | 93.10 | 98.24 | 98.06 | 99.07 | |
| Summer | 94.70 | 87.23 | 93.17 | 96.08 | 97.41 | ||
| Autumn | 96.34 | 90.47 | 97.57 | 97.09 | 98.06 | ||
| Winter | 97.02 | 92.90 | 98.31 | 98.43 | 98.93 | ||
| Average | 96.31 | 90.92 | 96.82 | 97.41 | 98.37 | ||
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Season | |||||||
| nMAE (%) | Spring | 3.55 | 13.62 | 3.09 | 7.88 | 2.08 | |
| Summer | 5.15 | 13.84 | 2.10 | 8.10 | 1.84 | ||
| Autumn | 4.52 | 13.51 | 2.73 | 7.36 | 1.56 | ||
| Winter | 3.18 | 12.50 | 2.64 | 6.80 | 1.87 | ||
| Average | 4.10 | 13.37 | 2.64 | 7.53 | 1.84 | ||
| nRMSE (%) | Spring | 5.88 | 20.65 | 4.10 | 20.13 | 3.63 | |
| Summer | 8.93 | 19.43 | 3.33 | 18.15 | 2.82 | ||
| Autumn | 7.67 | 19.20 | 3.57 | 17.07 | 2.28 | ||
| Winter | 5.10 | 18.30 | 3.70 | 19.50 | 3.02 | ||
| Average | 6.90 | 19.40 | 3.68 | 18.71 | 2.94 | ||
| Accuracy (%) | Spring | 96.45 | 86.38 | 96.91 | 92.12 | 97.92 | |
| Summer | 94.85 | 86.16 | 97.90 | 91.90 | 98.16 | ||
| Autumn | 95.48 | 86.49 | 97.27 | 92.64 | 98.44 | ||
| Winter | 96.82 | 87.50 | 97.36 | 93.20 | 98.13 | ||
| Average | 95.90 | 86.63 | 97.36 | 92.47 | 98.16 | ||
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Season | |||||||
| nMAE (%) | Spring | 3.64 | 12.18 | 5.95 | 5.54 | 2.30 | |
| Summer | 5.77 | 13.30 | 7.11 | 5.41 | 3.56 | ||
| Autumn | 3.35 | 11.47 | 6.33 | 4.66 | 2.64 | ||
| Winter | 2.77 | 10.79 | 4.37 | 3.50 | 2.07 | ||
| Average | 3.88 | 11.94 | 5.94 | 4.78 | 2.64 | ||
| nRMSE (%) | Spring | 6.30 | 18.90 | 11.01 | 10.00 | 3.82 | |
| Summer | 9.66 | 19.83 | 11.63 | 9.73 | 6.04 | ||
| Autumn | 5.81 | 16.54 | 11.11 | 8.16 | 4.40 | ||
| Winter | 4.76 | 15.83 | 7.61 | 6.34 | 3.33 | ||
| Average | 6.63 | 17.78 | 10.36 | 8.56 | 4.40 | ||
| Accuracy (%) | Spring | 96.36 | 87.82 | 94.05 | 94.46 | 97.71 | |
| Summer | 94.23 | 86.70 | 92.89 | 94.59 | 96.44 | ||
| Autumn | 96.66 | 88.53 | 93.67 | 95.34 | 97.36 | ||
| Winter | 97.23 | 89.21 | 95.63 | 96.50 | 97.93 | ||
| Average | 96.12 | 88.06 | 94.06 | 95.22 | 97.36 | ||
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Season | |||||||
| nMAE (%) | Spring | 2.56 | 12.28 | 7.50 | 3.09 | 1.62 | |
| Summer | 3.62 | 10.90 | 2.77 | 3.26 | 1.76 | ||
| Autumn | 4.27 | 13.07 | 6.18 | 5.91 | 2.78 | ||
| Winter | 2.83 | 10.37 | 4.76 | 3.08 | 2.10 | ||
| Average | 3.32 | 11.66 | 5.30 | 3.83 | 2.06 | ||
| nRMSE (%) | Spring | 4.09 | 19.00 | 11.62 | 5.48 | 2.54 | |
| Summer | 5.99 | 16.17 | 4.43 | 5.49 | 3.05 | ||
| Autumn | 6.68 | 19.11 | 10.11 | 11.49 | 4.69 | ||
| Winter | 4.78 | 15.16 | 7.55 | 5.31 | 3.53 | ||
| Average | 5.38 | 17.36 | 8.43 | 6.94 | 3.46 | ||
| Accuracy (%) | Spring | 97.44 | 87.72 | 92.50 | 96.91 | 98.38 | |
| Summer | 96.38 | 89.10 | 97.23 | 96.74 | 98.24 | ||
| Autumn | 95.73 | 86.93 | 93.82 | 94.09 | 97.22 | ||
| Winter | 97.17 | 89.63 | 95.24 | 96.92 | 97.90 | ||
| Average | 96.68 | 88.34 | 94.70 | 96.17 | 97.94 | ||
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Season | |||||||
| nMAE (%) | Spring | 6.86 | 13.13 | 7.16 | 9.35 | 4.44 | |
| Summer | 3.99 | 13.01 | 6.34 | 8.99 | 3.14 | ||
| Autumn | 3.39 | 9.59 | 3.29 | 3.67 | 2.16 | ||
| Winter | 2.27 | 8.29 | 2.52 | 2.42 | 1.74 | ||
| Average | 4.13 | 11.00 | 4.83 | 6.11 | 2.87 | ||
| nRMSE (%) | Spring | 12.84 | 20.08 | 11.71 | 19.25 | 8.21 | |
| Summer | 7.51 | 19.61 | 10.85 | 18.47 | 5.50 | ||
| Autumn | 6.52 | 14.96 | 6.18 | 8.71 | 3.64 | ||
| Winter | 3.83 | 12.67 | 3.93 | 4.60 | 3.04 | ||
| Average | 7.68 | 16.83 | 8.17 | 12.76 | 5.10 | ||
| Accuracy (%) | Spring | 93.14 | 86.87 | 92.84 | 90.65 | 95.56 | |
| Summer | 96.01 | 86.99 | 93.66 | 91.01 | 96.86 | ||
| Autumn | 96.61 | 90.41 | 96.71 | 96.33 | 97.84 | ||
| Winter | 97.73 | 91.71 | 97.48 | 97.58 | 98.26 | ||
| Average | 95.87 | 89.00 | 95.17 | 93.89 | 97.13 | ||
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Season | |||||||
| nMAE (%) | Spring | 2.04 | 7.93 | 1.79 | 3.00 | 1.37 | |
| Summer | 4.62 | 11.07 | 4.26 | 4.17 | 2.74 | ||
| Autumn | 2.84 | 7.84 | 1.89 | 3.15 | 1.37 | ||
| Winter | 1.75 | 7.13 | 1.59 | 2.53 | 1.37 | ||
| Average | 2.81 | 8.49 | 2.38 | 3.21 | 1.71 | ||
| nRMSE (%) | Spring | 3.59 | 12.10 | 2.49 | 6.35 | 2.26 | |
| Summer | 8.24 | 15.69 | 6.76 | 7.06 | 5.67 | ||
| Autumn | 5.07 | 11.64 | 3.12 | 6.49 | 2.35 | ||
| Winter | 3.15 | 10.34 | 2.71 | 4.90 | 2.10 | ||
| Average | 5.01 | 12.44 | 3.77 | 6.20 | 3.10 | ||
| Accuracy (%) | Spring | 97.96 | 92.08 | 98.21 | 97.00 | 98.63 | |
| Summer | 95.38 | 88.93 | 95.74 | 95.83 | 97.27 | ||
| Autumn | 97.16 | 92.16 | 98.11 | 96.85 | 98.63 | ||
| Winter | 98.25 | 92.88 | 98.41 | 97.47 | 98.63 | ||
| Average | 97.19 | 91.51 | 97.62 | 96.79 | 98.29 | ||
| Index | Model | LSTM in [39] | DNN in [43] | SVM in [44] | BPNN in [45] | Proposed DNN-LSTM | |
|---|---|---|---|---|---|---|---|
| Plants | |||||||
| nMAE (%) | Plant A | 3.69 | 9.08 | 3.18 | 2.59 | 1.07 | |
| Plant B | 4.10 | 13.37 | 2.64 | 7.53 | 1.84 | ||
| Plant C | 3.88 | 11.94 | 5.94 | 4.78 | 2.64 | ||
| Plant D | 3.32 | 11.66 | 5.30 | 3.83 | 2.06 | ||
| Plant E | 4.13 | 11.00 | 4.83 | 6.11 | 2.87 | ||
| Plant F | 2.81 | 8.49 | 2.38 | 3.21 | 1.71 | ||
| Average | 3.66 | 10.92 | 4.05 | 4.68 | 2.03 | ||
| nRMSE (%) | Plant A | 6.50 | 13.58 | 4.87 | 5.62 | 2.70 | |
| Plant B | 6.90 | 19.40 | 3.68 | 18.71 | 2.94 | ||
| Plant C | 6.63 | 17.78 | 10.36 | 8.56 | 4.40 | ||
| Plant D | 5.38 | 17.36 | 8.43 | 6.94 | 3.46 | ||
| Plant E | 7.68 | 16.83 | 8.17 | 12.76 | 5.10 | ||
| Plant F | 5.01 | 12.44 | 3.77 | 6.20 | 3.10 | ||
| Average | 6.35 | 16.23 | 6.55 | 9.80 | 3.62 | ||
| Accuracy (%) | Plant A | 96.31 | 90.92 | 96.82 | 97.41 | 98.37 | |
| Plant B | 95.90 | 86.63 | 97.36 | 92.47 | 98.16 | ||
| Plant C | 96.12 | 88.06 | 94.06 | 95.22 | 97.36 | ||
| Plant D | 96.68 | 88.34 | 94.70 | 96.17 | 97.94 | ||
| Plant E | 95.87 | 89.00 | 95.17 | 93.89 | 97.13 | ||
| Plant F | 97.19 | 91.51 | 97.62 | 96.79 | 98.29 | ||
| Average | 96.35 | 89.08 | 95.96 | 95.33 | 97.88 | ||
| Index | Model | LR | ARIMA | Improvement Rate (LR vs. DNN-LSTM) | Improvement Rate (ARIMA vs. DNN-LSTM) | |
|---|---|---|---|---|---|---|
| Plants | ||||||
| nMAE (%) | Plant A | 13.30 | 6.52 | 50.98% | 91.95% | |
| Plant B | 20.65 | 8.68 | 57.97% | 91.09% | ||
| Plant C | 17.99 | 8.26 | 54.06% | 83.33% | ||
| Plant D | 17.91 | 9.24 | 48.41% | 88.49% | ||
| Plant E | 15.48 | 8.10 | 47.67% | 81.46% | ||
| Plant F | 12.77 | 6.14 | 51.92% | 86.61% | ||
| Average | 16.35 | 7.82 | 52.17% | 87.58% | ||
| nRMSE (%) | Plant A | 16.40 | 8.68 | 47.07% | 85.54% | |
| Plant B | 24.43 | 11.23 | 54.03% | 87.97% | ||
| Plant C | 21.33 | 10.63 | 50.16% | 79.37% | ||
| Plant D | 21.12 | 11.97 | 43.32% | 83.62% | ||
| Plant E | 19.69 | 10.38 | 47.28% | 74.09% | ||
| Plant F | 15.14 | 7.84 | 48.22% | 79.52% | ||
| Average | 19.69 | 10.12 | 48.60% | 81.62% | ||
| Accuracy (%) | Plant A | 86.70 | 93.48 | 13.46% | 5.23% | |
| Plant B | 79.35 | 91.32 | 23.71% | 7.49% | ||
| Plant C | 82.01 | 91.74 | 18.72% | 6.13% | ||
| Plant D | 82.09 | 90.76 | 19.31% | 7.91% | ||
| Plant E | 84.52 | 91.90 | 14.92% | 5.69% | ||
| Plant F | 87.23 | 93.86 | 12.68% | 4.50% | ||
| Average | 83.65 | 92.18 | 17.01% | 6.18% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wai, R.-J.; Lai, P.-X. Design of Intelligent Solar PV Power Generation Forecasting Mechanism Combined with Weather Information under Lack of Real-Time Power Generation Data. Energies 2022, 15, 3838. https://doi.org/10.3390/en15103838
Wai R-J, Lai P-X. Design of Intelligent Solar PV Power Generation Forecasting Mechanism Combined with Weather Information under Lack of Real-Time Power Generation Data. Energies. 2022; 15(10):3838. https://doi.org/10.3390/en15103838
Chicago/Turabian StyleWai, Rong-Jong, and Pin-Xian Lai. 2022. "Design of Intelligent Solar PV Power Generation Forecasting Mechanism Combined with Weather Information under Lack of Real-Time Power Generation Data" Energies 15, no. 10: 3838. https://doi.org/10.3390/en15103838
APA StyleWai, R.-J., & Lai, P.-X. (2022). Design of Intelligent Solar PV Power Generation Forecasting Mechanism Combined with Weather Information under Lack of Real-Time Power Generation Data. Energies, 15(10), 3838. https://doi.org/10.3390/en15103838







