Vibration Suppression of Hub Motor-Air Suspension Vehicle

Abstract

Aiming at the negative vibration effect caused by the increased unsprung mass of the hub motor-air suspension (HM-AS) vehicle and the unbalanced magnetic force (UMF) of the hub motor, a linear quadratic regulator (LQR) air suspension control strategy based on a genetic algorithm is proposed. Considering the coupling effect of road surface excitation and UMF, the model of the HM-AS vehicle is established. Then, according to optimal control theory and the genetic algorithm, the LQR controller is designed to suppress the vibration of the HM-AS vehicle, and the weight matrix of the LQR controller is optimized through the genetic algorithm. The simulation results show that the proposed LQR control strategy effectively improves the ride comfort and motor safety of the HM-AS vehicle.

1. Introduction

At present, the problems of environmental pollution and energy shortage are widely concerning around the world, which makes the automobile industry pay more attention to the development of electric vehicles. HM-AS vehicles have the advantages of saving energy, flexible control, and efficient transmission, and are considered to be the ideal design for future electric vehicles. The HM-AS system is a complex electromechanical coupling system composed of a wheel, hub motor, and air suspension. Integrating the hub motor into the wheel will have a significant impact on vehicle dynamics [1,2,3]. The eccentricity of the hub motor generated by the vehicle on uneven roads will cause the motor to generate UMF, which is transmitted to the wheels and car body, resulting in the deterioration of the car’s ride comfort.

In order to suppress the vibration of the air suspension, many scholars have conducted valuable research. Lou et al. [4] built an integrated controller of the semi-active suspension system and the ABS system, based on sliding mode control theory. Simulation results showed that the controller can prevent wheel locking, shorten braking distance and braking time, and improve vehicle comfort. Zhang et al. [5] designed an optimal state feedback vibration control law, which significantly improved the vibration reduction performance of the vehicle. Zhou et al. [6] proposed an active suspension LQG control strategy to improve handling stability and ride comfort. Sathishkumar et al. [7] compared the control effect of fuzzy controllers and PID controllers, based on the semi-active air suspension system. Yin et al. [8] proposed the concept of active energy regenerative suspension. The simulation results showed that active energy regeneration suspension has good ride comfort and energy regeneration potential. Ibrahim et al. [9] described fuzzy and H∞ control strategies for the automobile active suspension system. Zhang et al. [10] designed a sliding mode controller using a constant velocity approximation law. The simulation results showed that the chattering suppression of the neural sliding mode control is more stable. Fan et al. [11] proposed an adaptive neuro-fuzzy inference system for vibration control of vehicle active suspension systems. Bao et al. [12] studied the active fault-tolerant control strategy of suspension in the case of sensor failure and actuator failure, respectively, and improved the performance of the active fault-tolerant system, thereby improving the handling stability of the vehicle. Gokul et al. [13] applied the particle swarm optimization algorithm to the LQR controlled air suspension to determine the optimal control weight matrix. Rui [14] designed a nonlinear adaptive sliding mode controller for the semi-active air suspension system. Shalabi et al. [15] proposed a fuzzy inference system based on Z number to control the automobile air spring suspension system, which improved the performance of the air suspension. Wen et al. [16] used the sliding mode control strategy of the radial basis function neural network adaptive approximation to control the electromagnetic suspension system, which has stability and convergence for the control of complex nonlinear electromagnetic suspension systems. Zhang et al. [17] proposed an active suspension control method based on a multi-agent prediction algorithm to improve the ride comfort of the vehicle suspension. Ahmed et al. [18] compared an uncontrolled suspension system, a suspension system based on a neural network controller, and an active suspension system based on a linear quadratic regulator. Ma et al. [19] proposed a method for matching the stiffness and damping of a semi-active air suspension system to ensure the best ride comfort when the vehicle is driving on different levels of roads at different speeds. Li et al. [20] designed a model predictive controller and a constrained optimal controller to improve driving comfort and safety of the vehicle in response to the negative vertical vibration of the hub direct drive and the air suspension system. Shalabi et al. [21] proposed an adaptive neuro-fuzzy inference system control, which significantly reduced the sprung mass acceleration and improved the vehicle ride comfort. Yu et al. [22] used a genetic algorithm to determine the optimal solution of the objective function of the LQR controller, which improved the ride comfort of the vehicle. Jin et al. [23] proposed a robust constrained H∞ control strategy to improve the vehicle ride comfort and road holding ability. Jeong et al. [24] introduced a preview control of the automotive active suspension systems to improve ride comfort through vehicle-to-vehicle (V2V) communication. The above scholars suppressed the negative vibration of the air suspension by optimizing and controlling the suspension. However, there are few studies considering the vertical performance of the hub motor and air suspension coupling system, and most studies use a quarter vehicle model as the research object.

Therefore, it is necessary to propose a damping control method to suppress the vertical vibration of the HM-AS vehicle. The primary contributions of this study are as follows: (1) building an eleven-degree-of-freedom HM-AS vehicle model; (2) designing an LQR controller to suppress the vibration of the HM-AS vehicle.

This article is arranged as follows. In Section 2, according to dynamics and electromagnetics, an eleven-degree-of-freedom HM-AS vehicle mathematical model is built. In Section 3, the vehicle road test is conducted to prove the accuracy of the HM-AS vehicle model. In Section 4, an LQR air suspension control strategy is designed and the optimal control weight matrix of the LQR controller is determined through a genetic algorithm. In Section 5, the effectiveness of the control strategy is proved by running simulations.

2. HM-AS Vehicle Model

2.1. Motor Model

A permanent magnet brushless direct current (PM BLDC) motor has the advantages of high transmission efficiency, compact structure, and low noise. In this research, an outer rotor PM BLDC motor is used as the hub motor.

The current equation of the outer rotor PM BLDC is [25]:

$$\left[\begin{array}{c}{u}_{\mathrm{a}}\\ u_{\mathrm{b}}\\ u_{\mathrm{c}}\end{array}\right]=\left[\begin{array}{ccc}R& 0& 0\\ 0& R& 0\\ 0& 0& R\end{array}\right]\left[\begin{array}{c}{i}_{\mathrm{a}}\\ i_{\mathrm{b}}\\ i_{\mathrm{c}}\end{array}\right]+\frac{d}{dt}\left[\begin{array}{ccc}L-M& 0& 0\\ 0& L-M& 0\\ 0& 0& L-M\end{array}\right]\left[\begin{array}{c}{i}_{\mathrm{a}}\\ i_{\mathrm{b}}\\ i_{\mathrm{c}}\end{array}\right]+\left[\begin{array}{c}{e}_{\mathrm{a}}\\ e_{\mathrm{b}}\\ e_{\mathrm{c}}\end{array}\right]$$

(1)

where $u_{\mathrm{a}}$, $u_{\mathrm{b}}$, $u_{\mathrm{c}}$ are phase voltages of three-phase windings; $R$ is the equivalent resistance of stator windings; $L$ is the self-inductance of stator windings; $M$ is the mutual inductance of stator windings; $i_{\mathrm{a}}$, $i_{\mathrm{b}}$, $i_{\mathrm{c}}$ are phase currents of three-phase windings; and $e_{\mathrm{a}}$, $e_{\mathrm{b}}$, $e_{\mathrm{c}}$ are back electromotive forces of three-phase windings.

The electromagnetic torque equation of motor is [25]:

$$T_{\mathrm{e}}=\frac{1}{{\omega }_{\mathrm{m}}}\left(e_{\mathrm{a}}{i}_{\mathrm{a}}+e_{\mathrm{b}}{i}_{\mathrm{b}}+e_{\mathrm{c}}{i}_{\mathrm{c}}\right)$$

(2)

where $T_{\mathrm{e}}$ is the electromagnetic torque of motor, and ${\omega }_{\mathrm{m}}$ is the angular velocity of rotor.

The mechanical motion equation of motor is [25]:

$$J_{\mathrm{m}}\frac{d{\omega }_{\mathrm{m}}}{dt}+B{\omega }_{\mathrm{m}}=T_{\mathrm{e}}-T_{\mathrm{L}}$$

(3)

where $J_{\mathrm{m}}$ is the moment of inertia of motor, $T_{\mathrm{L}}$ is the load torque of motor, and $B$ is the friction coefficient.

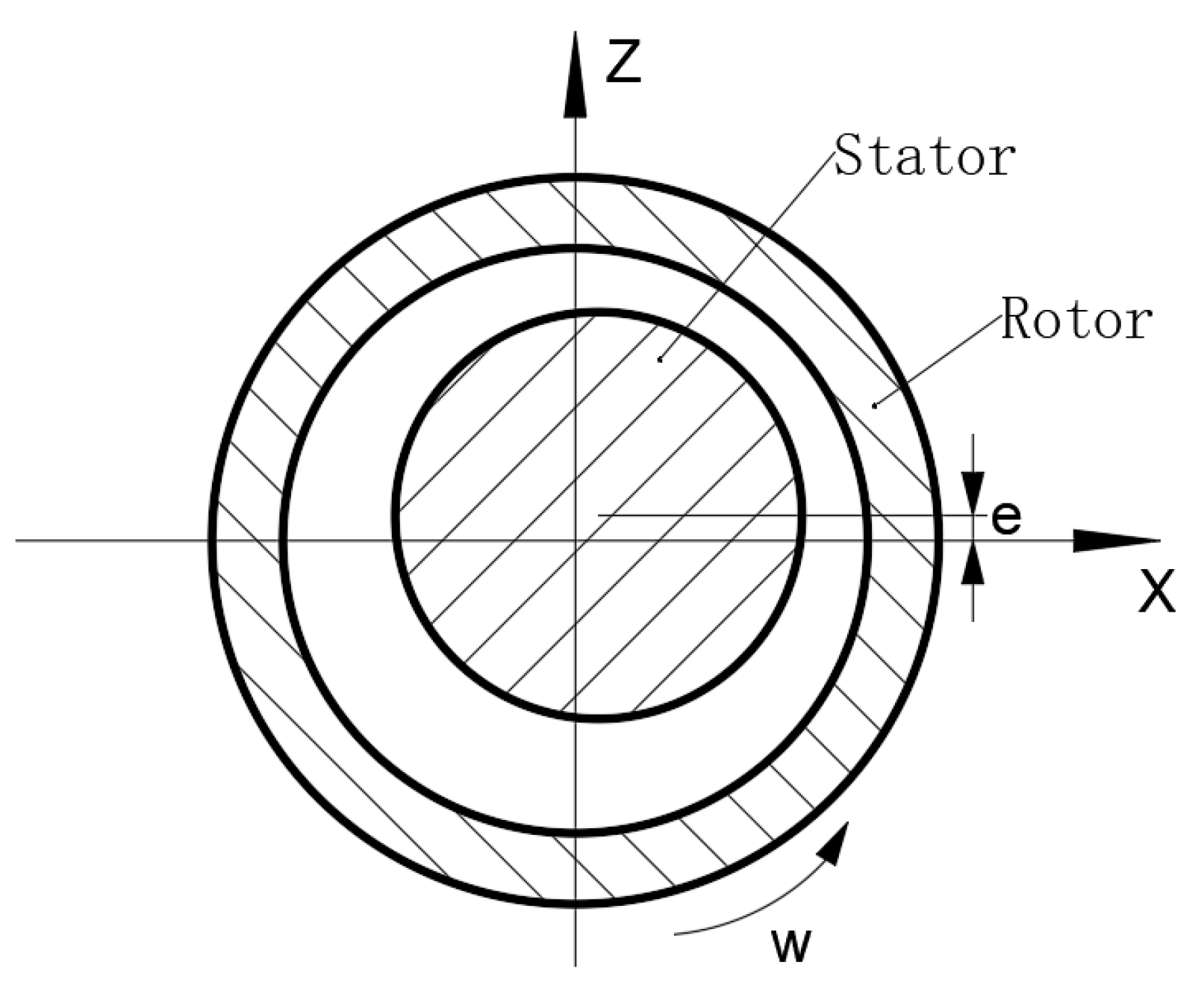
2.2. UMF Calculation Model

Due to the complex installation condition and mechanical environment of the hub motor, and due to the motor bearing a vertical load during operation, an eccentric distance is generated between the stator and rotor of the motor, resulting in an UMF. The eccentricity between the stator and rotor of the PM BLDC motor is shown in Figure 1.

In the eccentric state of the hub motor, the air gap radial magnetic field $B_{\mathrm{er}}$ and the air gap tangential magnetic field $B_{\mathrm{et}}$ are [26]:

$$B_{\mathrm{er}}(r,\hspace{0.17em}\alpha ,\hspace{0.17em}t)=[B_{\mathrm{mr}}(r,\hspace{0.17em}\alpha ,\hspace{0.17em}t)+B_{\alpha \mathrm{r}}(r,\hspace{0.17em}\alpha ,\hspace{0.17em}t)]{\epsilon }_{\delta }$$

(4)

$$B_{\mathrm{et}}(r,\hspace{0.17em}\alpha ,\hspace{0.17em}t)=[B_{\mathrm{mt}}(r,\hspace{0.17em}\alpha ,\hspace{0.17em}t)+B_{\alpha \mathrm{t}}(r,\hspace{0.17em}\alpha ,\hspace{0.17em}t)]{\epsilon }_{\delta }$$

(5)

where $r$ is the air gap radius; $\alpha$ is the stator angle; $t$ is the time; $B_{\mathrm{mr}}$ is the radial magnetic field of permanent magnet; $B_{\mathsf{\alpha }\mathrm{r}}$ is the radial magnetic field of armature reaction; $B_{\mathrm{mt}}$ is the tangential magnetic field of permanent magnet; and $B_{\mathsf{\alpha }\mathrm{t}}$ is the tangential magnetic field of armature reaction.

The vertical UMF $F_{\mathrm{ez}}$ and the longitudinal UMF $F_{\mathrm{ex}}$ of the hub motor are [26]:

$$F_{\mathrm{ez}}=\frac{Lr}{2{\mu }_0}{{\displaystyle \int }}_0^{2\pi }\{[B_{\mathrm{er}}{\left(r,\alpha ,t\right)}^2-B_{\mathrm{et}}{\left(r,\alpha ,t\right)}^2\left]\sin \alpha +2\right[B_{\mathrm{er}}\left(r,\alpha ,t\right)·B_{\mathrm{et}}\left(r,\alpha ,t\right)]\cos \alpha \}d\alpha$$

(6)

$$F_{\mathrm{ex}}=\frac{Lr}{2{\mu }_0}{{\displaystyle \int }}_0^{2\pi }\{[B_{\mathrm{er}}{\left(r,\alpha ,t\right)}^2-B_{\mathrm{et}}{\left(r,\alpha ,t\right)}^2\left]\cos \alpha -2\right[B_{\mathrm{er}}\left(r,\alpha ,t\right)·B_{\mathrm{et}}\left(r,\alpha ,t\right)]\sin \alpha \}d\alpha$$

(7)

where $L$ is the axial length of the motor, and ${\mu }_0$ is the vacuum permeability.

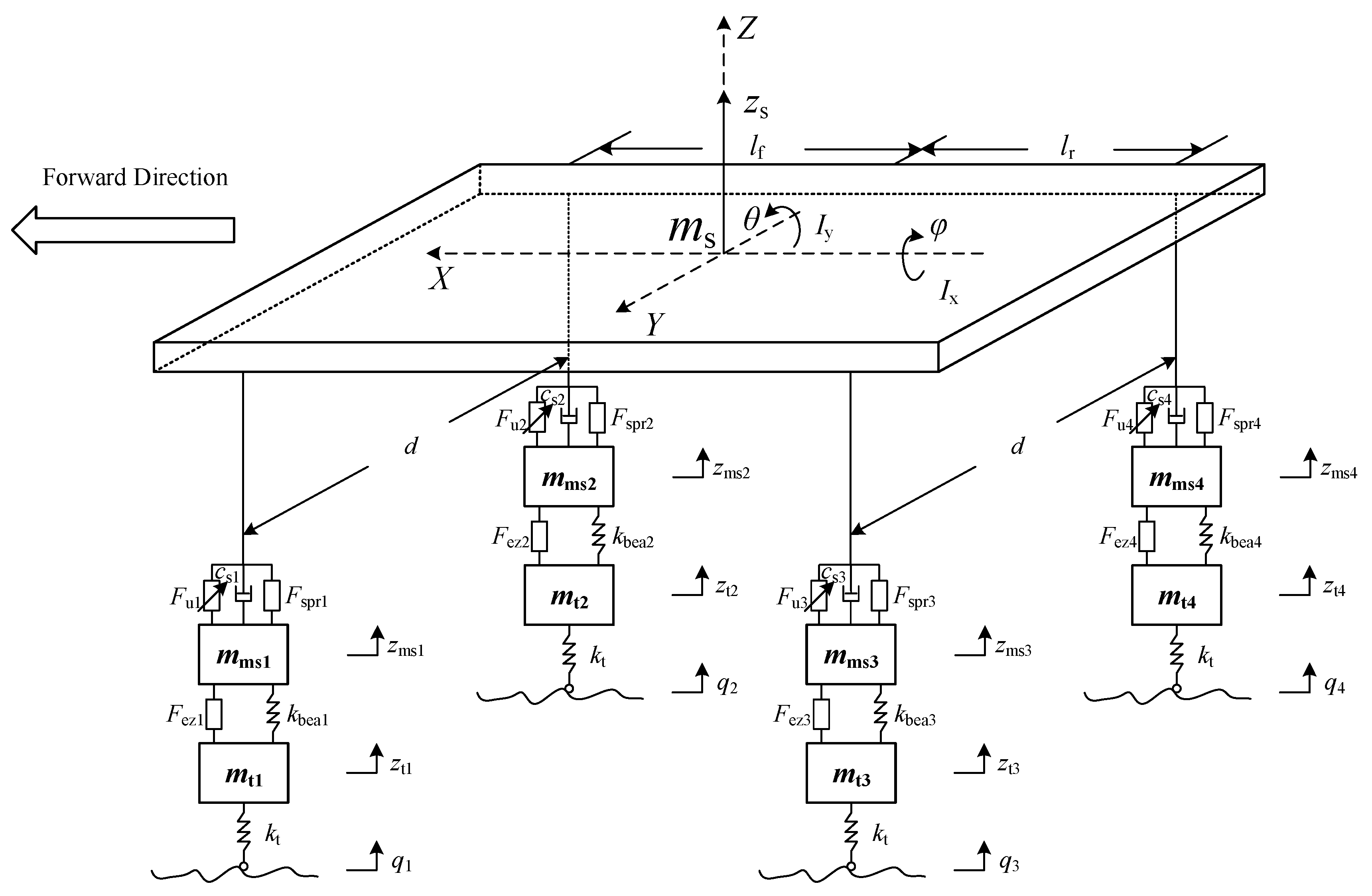
2.3. Vehicle Vertical Vibration Model

The eleven-degrees-of-freedom vehicle model is shown in Figure 2.

According to vehicle dynamics, the vehicle model can be expressed as:

$$\{\begin{array}{c}{m}_{\mathrm{s}}{\ddot{z}}_{\mathrm{s}}=-\left(F_{\mathrm{s}1}+F_{\mathrm{s}2}+F_{\mathrm{s}3}+F_{\mathrm{s}4}\right)\\ I_{\mathrm{x}}\ddot{\phi }=\left[\left(F_{\mathrm{s}2}-F_{\mathrm{s}1}\right)+\left(F_{\mathrm{s}4}-F_{\mathrm{s}3}\right)\right]\frac{d}{2}\\ I_{\mathrm{y}}\ddot{\theta }=\left(F_{\mathrm{s}1}+F_{\mathrm{s}2}\right)l_{\mathrm{f}}-\left(F_{\mathrm{s}3}+F_{\mathrm{s}4}\right)l_{\mathrm{r}}\\ m_{\mathrm{msi}}{\ddot{z}}_{\mathrm{msi}}=F_{\mathrm{si}}-F_{\mathrm{ezi}}-F_{\mathrm{beazi}}\\ m_{\mathrm{ti}}{\ddot{z}}_{\mathrm{ti}}=F_{\mathrm{ezi}}+F_{\mathrm{beazi}}-F_{\mathrm{di}}\end{array}$$

(8)

to be specific,

$$\{\begin{array}{c}{F}_{\mathrm{si}}=F_{\mathrm{spri}}+c_{\mathrm{si}}{\dot{f}}_{\mathrm{di}}-F_{\mathrm{ui}}\\ F_{\mathrm{di}}=k_{\mathrm{ti}}(z_{\mathrm{ti}}-q_{\mathrm{i}})\\ F_{\mathrm{spri}}=\frac{(k·P_{\mathrm{i}}·A_{\mathrm{e}}^2·f_{\mathrm{di}})}{V_{0\mathrm{i}}}\\ f_{\mathrm{di}}=z_{\mathrm{si}}-z_{\mathrm{msi}}\\ P_1=P_2=\frac{m_{\mathrm{s}}·g·l_{\mathrm{r}}}{2(l_{\mathrm{f}}+l_{\mathrm{r}})A_{\mathrm{e}}}+P_{\mathrm{a}}\\ P_3=P_4=\frac{m_{\mathrm{s}}·g·l_{\mathrm{f}}}{2(l_{\mathrm{f}}+l_{\mathrm{r}})A_{\mathrm{e}}}+P_{\mathrm{a}}\\ F_{\mathrm{beazi}}=k_{\mathrm{beai}}(z_{\mathrm{msi}}-z_{\mathrm{ti}})\end{array}$$

(9)

where i = 1, 2, 3, 4, represent the front-left suspension, front-right suspension, rear-left suspension, and rear-right suspension, respectively; $m_{\mathrm{s}}$ is the sprung mass; $m_{\mathrm{msi}}$ is the mass of the stator core; $m_{\mathrm{ti}}$ is the mass of the rotor core and wheel; $l_{\mathrm{f}}$ is the distance from the center of the front wheel to the center of the vehicle’s mass; $l_{\mathrm{r}}$ is the distance from the center of the rear wheel to the center of the vehicle’s mass; $d$ is the distance between the two wheels; $\phi$ is the roll angle of the sprung mass; $\theta$ is the pitch angle of the sprung mass; $I_{\mathrm{x}}$ is the moment of inertia of the sprung mass around the X axis; $I_{\mathrm{y}}$ is the moment of inertia of the sprung mass around the Y axis; $z_{\mathrm{s}}$ is the vertical displacement of the sprung mass; $z_{\mathrm{si}}$ is the vertical displacement of the contact point of the suspension to the sprung mass; $z_{\mathrm{msi}}$ is the vertical displacement of the stator core; $z_{\mathrm{ti}}$ is the vertical displacement of the rotor core and wheel; $q_{\mathrm{i}}$ is the road excitation; $f_{\mathrm{di}}$ is the stroke of the suspension; $c_{\mathrm{si}}$ is the damping of the suspension; $F_{\mathrm{si}}$ is the force of the suspension; $F_{\mathrm{di}}$ is the dynamic load of the tire; $F_{\mathrm{ui}}$ is the damping control force of the suspension; $F_{\mathrm{spri}}$ is the air spring force of the suspension; $F_{\mathrm{ezi}}$ is the vertical UMF of the motor; $F_{\mathrm{beazi}}$ is the vertical bearing force of the motor; $k_{\mathrm{ti}}$ is the residual stiffness of the tire; $k_{\mathrm{beai}}$ is the bearing stiffness of the motor; $P_{\mathrm{i}}$ is the initial air pressure of the air spring; $k$ is the adiabatic index; $A_{\mathrm{e}}$ is the initial cross-sectional area of the air spring; $V_{0\mathrm{i}}$ is the initial volume of the air spring; $P_{\mathrm{a}}$ is the atmospheric pressure; and $g$ is the acceleration of gravity. According to the test vehicle, the parameters of the HM-AS vehicle model are shown in

Table 1. Parameters of the HM-AS vehicle model.

Parameter	Value	Parameter	Value
$m_{\mathrm{s}} \left(\mathrm{kg}\right)$	710	$m_{\mathrm{msi}} \left(\mathrm{kg}\right)$	30.4
$m_{\mathrm{ti}} \left(\mathrm{kg}\right)$	34.4	$d \left(\mathrm{m}\right)$	1.55
$l_{\mathrm{f}} \left(\mathrm{m}\right)$	0.795	$l_{\mathrm{r}} \left(\mathrm{m}\right)$	0.975
$I_{\mathrm{x}} \left(\mathrm{kg}·{\mathrm{m}}^2\right)$	340	$I_{\mathrm{y}} \left(\mathrm{kg}·{\mathrm{m}}^2\right)$	910
$k_{\mathrm{ti}} \left(\mathrm{N}/\mathrm{m}\right)$	260,000	$k_{\mathrm{beai}} \left(\mathrm{N}/\mathrm{m}\right)$	5,000,000
$c_{\mathrm{si}} \left(\mathrm{N}·\mathrm{s}/\mathrm{m}\right)$	1767	$k$	1.4
$A_{\mathrm{e}} \left({\mathrm{m}}^2\right)$	0.007	$V_{0\mathrm{i}} \left({\mathrm{m}}^3\right)$	0.0024
$P_{\mathrm{a}} \left(\mathrm{Pa}\right)$	100,000	$g \left(\mathrm{m}/{\mathrm{s}}^2\right)$	9.8

.

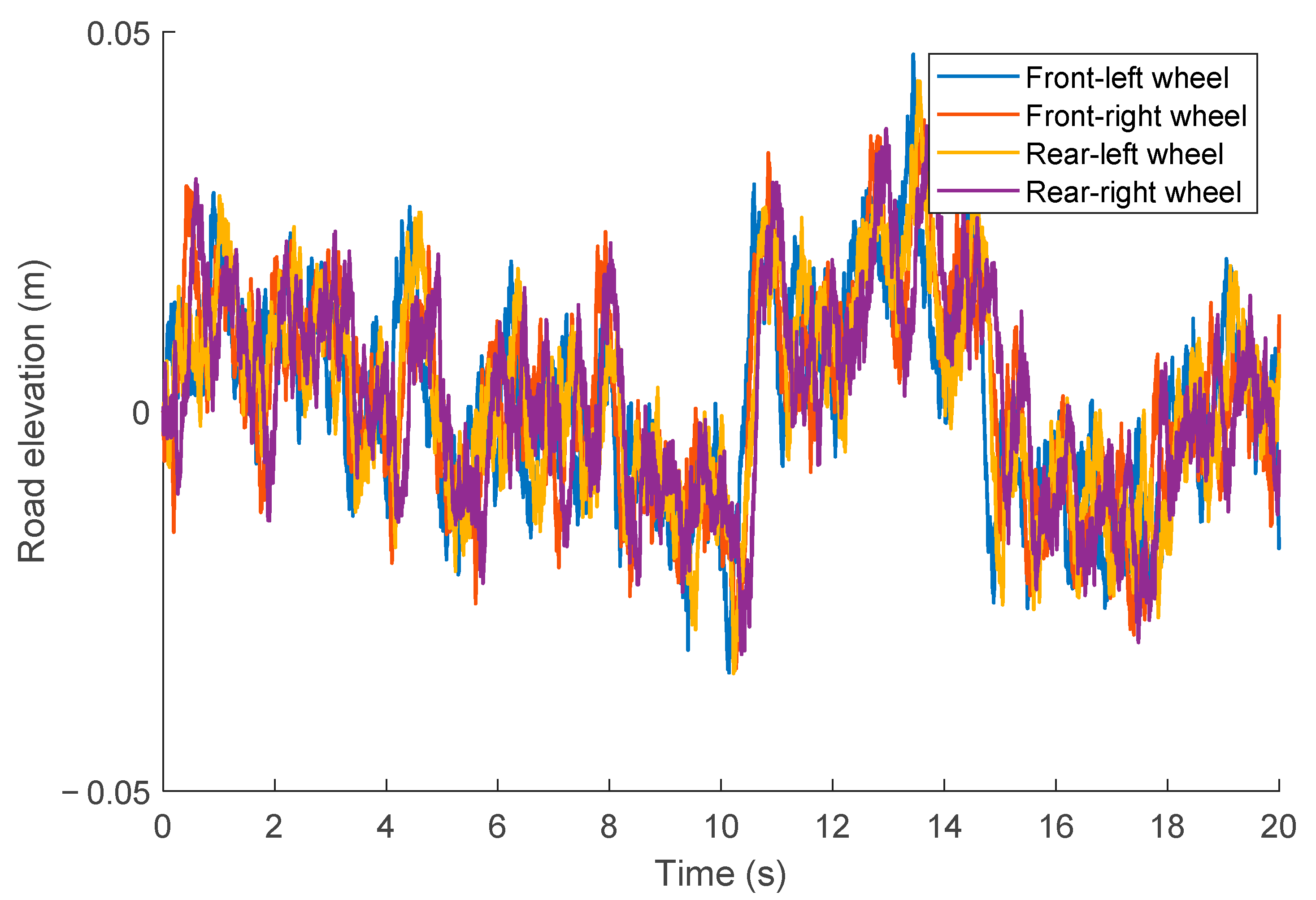
2.4. Random Road Excitation Model

The left and right road surfaces are coherent, and the road surface traveled by the rear axle wheels has a lag when compared with the surface traveled by the front axle wheels. Therefore, to build a four-wheel random road excitation model, it is necessary to consider both the front axle road excitation and the rear axle road excitation.

2.4.1. Road Excitations of the Left and Right Wheels of the Front Axle

The road excitation obeys a normal distribution with zero mean, and its statistical characteristics are described by a power spectrum. The frequency spectral density of road roughness is [27]:

$$G_{\mathrm{q}}\left(n\right)=G_{\mathrm{q}}\left(n_0\right){\left(\frac{n}{n_0}\right)}^{-W}$$

(10)

where $n$ is the spatial frequency; $n_0$ is the reference spatial frequency; $G_{\mathrm{q}}\left(n_0\right)$ is the power spectral density at reference spatial frequency; and $W$ is the frequency index.

The speed power spectral density of road space frequency domain is [27]:

$$G_{\mathrm{v}}\left(n\right)=4{\pi }^2{n}_0{}^2{G}_{\mathrm{q}}\left(n_0\right)v$$

(11)

where $v$ is the vehicle speed.

The road elevation is a kind of colored noise with limited bandwidth, so the time domain signal of the road elevation can be generated by filtering white noise. The filter is [28]:

$$H\left(s\right)=\frac{2\pi \sqrt{G_{\mathrm{q}}\left(n_0\right)v}}{s+2\pi f_0}$$

(12)

where $f_0$ is the cutoff frequency.

The road time domain signal is [29]:

$$\dot{q}\left(t\right)=-2\pi f_{0}q\left(t\right)+2\pi \sqrt{G_{\mathrm{q}}\left(n_0\right)v}w\left(t\right)$$

(13)

where $w\left(t\right)$ is the white noise.

During the driving process of the vehicle, the road excitation of the left and right wheels is different from time to time, and they are not independent of each other, so the coherence function $\gamma$ is used to describe the road excitation of the left and right wheels [30]:

$$\gamma \left(n,T_{\mathrm{w}}\right)={\left[1+{\left(\frac{n{T}_{\mathrm{w}}^a}{n_0}\right)}^W\right]}^{-p}$$

(14)

where $T_{\mathrm{w}}$ is the distance between two coaxial wheels, $p$ is the reference factor, and $a$ is the constant exponent of $T_{\mathrm{w}}$.

For given white noise road excitations $q_{\mathrm{l}}\left(t\right)$ and $q_{\mathrm{r}}\left(t\right)$, the transfer function $G\left(s\right)$ of $q_{\mathrm{r}}\left(t\right)$ to $q_{\mathrm{l}}\left(t\right)$ is:

$$G\left(s\right)=\frac{Q_{\mathrm{r}}\left(s\right)}{Q_{\mathrm{l}}\left(s\right)}=\frac{a_0+a_{1}s+a_2{s}^2\dots }{b_0+b_{1}s+b_2{s}^2\dots }$$

(15)

where $Q_{\mathrm{l}}\left(\mathrm{s}\right)$ and $Q_{\mathrm{r}}\left(\mathrm{s}\right)$ are Laplace transforms of $q_{\mathrm{l}}\left(t\right)$ and $q_{\mathrm{r}}\left(t\right)$, respectively.

Combining the Formulas (14) and (15), we get:

$$\left|G\left(s\right)\right|=\left|\gamma \left(n,T_{\mathrm{w}}\right)\right|$$

(16)

The road excitations of the left and right wheels of the front axle are:

$$q_1\left(t\right)=q_{\mathrm{l}}\left(t\right)$$

(17)

$$q_2\left(t\right)={ℒ}^{-1}\left\{G\left(s\right)ℒ\left[q_1\left(t\right)\right]+\left[1-G\left(s\right)\right]ℒ\left[q_{\mathrm{r}}\left(t\right)\right]\right\}$$

(18)

2.4.2. Road Excitations of the Left and Right Wheels of the Rear Axle

Assuming that the vehicle runs in a straight line, and that the road on which the rear wheels of the vehicle travel is roughly the same as the road on which the front wheels travel, there is a lag between the road excitation of the rear wheels and the road excitation of the front wheels. The road excitations of the left and right wheels of the rear axle are:

$$q_3\left(t\right)=q_1\left(t-\tau \right)$$

(19)

$$q_4\left(t\right)=q_2\left(t-\tau \right)$$

(20)

where $\tau$ is the lag time, which is the quotient of the vehicle wheelbase and the vehicle speed. $t\ge \tau$.

Considering that the lag is difficult to linearize, it is described by using a transfer function in the complex domain. The road excitations of the left and right wheels of the rear axle are:

$$q_3\left(t\right)={ℒ}^{-1}\left\{G_3\left(s\right)ℒ\left[q_1\left(t\right)\right]\right\}$$

(21)

$$q_4\left(t\right)={ℒ}^{-1}\left\{G_4\left(s\right)ℒ\left[q_2\left(t\right)\right]\right\}$$

(22)

where $G_3\left(s\right)$ and $G_4\left(s\right)$ are the transfer function of $q_3\left(t\right)$ to $q_4\left(t\right)$, and the transfer function of $q_4\left(t\right)$ to $q_3\left(t\right)$, respectively.

2.5. Bump Road Excitation Model

The longitudinal section profile of the bump belt is represented by a cosine function. The bump road excitations of the four wheels are:

$$\{\begin{array}{l}{q}_1(t)=q_2(t)=\{\begin{array}{cc}\frac{H_{\mathrm{b}}}{2}\{1-\cos [\frac{2\pi v}{L_{\mathrm{b}}}(t-t_0)]\}& \hspace{1em}\hspace{1em}{t}_0\le t\le t_0+\frac{L_{\mathrm{b}}}{v}\\ 0& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}else\end{array}\hfill \\ q_3(t)=q_4(t)=\{\begin{array}{cc}\frac{H_{\mathrm{b}}}{2}\{1-\cos [\frac{2\pi v}{L_{\mathrm{b}}}(t-t_0-\tau )]\}& t_0+\tau \le t\le t_0+\tau +\frac{L_{\mathrm{b}}}{v}\\ 0& else\end{array}\hfill \end{array}$$

(23)

where $H_{\mathrm{b}}$ is the height of the bump belt, $L_{\mathrm{b}}$ is the width of the bump belt, and $t_0$ is the point at which the front wheels begin to contact the speed bump.

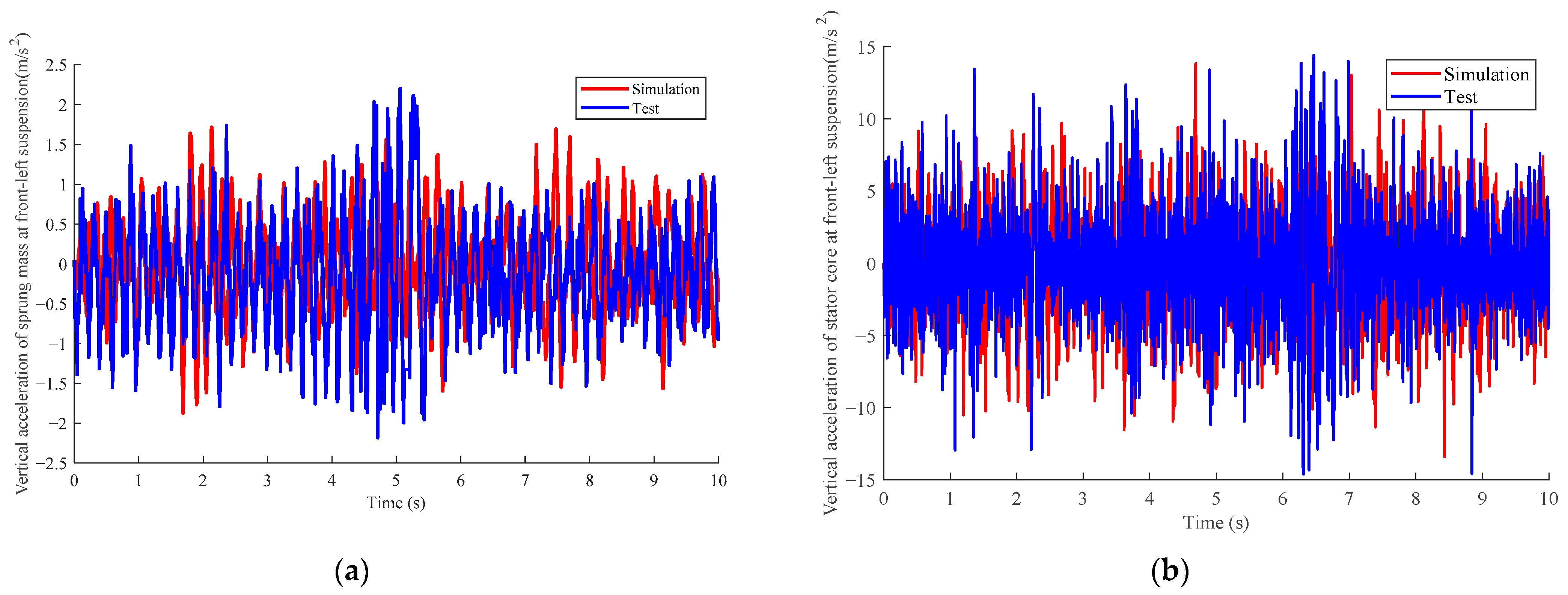
3. Model Validation

3.1. Test Vehicle Refitting and Sensor Arrangement

The vehicle road test is carried out to prove the correctness of the HM-AS vehicle model. The test vehicle is electric and has been modified for research purposes. The current vehicle features four hub motors and four air suspensions. The HM-AS test vehicle is shown in Figure 3. The air suspension is shown in Figure 4.

The sampling frequency of the sensor is up to 3 KHz, and the maximum range is up to 50 times the acceleration of gravity, which can meet the requirements of this experiment.

The signals collected by the sensor are the acceleration of sprung mass and the acceleration of unsprung mass at the front-left wheel and rear-left wheel. The sensor to collect the acceleration of sprung mass is installed on the upper end of the air suspension. The sensor to collect the acceleration of unsprung mass is installed on the lower end of the air suspension.

3.2. Vehicle Road Test

The random road was used in this test. The road selected is shown in the Figure 5. The road is asphalt pavement, which is flat and dry without protrusion.

The height of the vehicle driver and passenger is about 1.7 m and the weight is about 65 kg. The driver should start the vehicle and maintain the test speed about 50 m before crossing the test road. The data were recorded at the beginning of the test road and finished 10 s later.

The data used for comparison are ${\ddot{z}}_{\mathrm{s}1}$ and ${\ddot{z}}_{\mathrm{ms}1}$. Figure 6 shows the comparison of the simulation and test at a speed of 30 km/h, and the root-mean-square values of the simulation and test are shown in

Table 2. The root-mean-square values of the simulation and test.

Evaluation Index	Simulation	Test	Relative Error
${\ddot{z}}_{\mathrm{s}1} \left(\mathrm{m}/{\mathrm{s}}^2\right)$	$0.6098$	$0.6866$	$11.19\%$
${\ddot{z}}_{\mathrm{ms}1} \left(\mathrm{m}/{\mathrm{s}}^2\right)$	$3.6335$	$3.3067$	$9.88\%$

.

It can be seen from the comparison that the trend and amplitude of the simulation and test are basically the same, and the different values are about 10%. Therefore, the established dynamic model of the HM-AS vehicle can accurately reflect the real dynamic characteristics of hub-driven vehicles.

4. Optimal Control of the HM-AS Vehicle

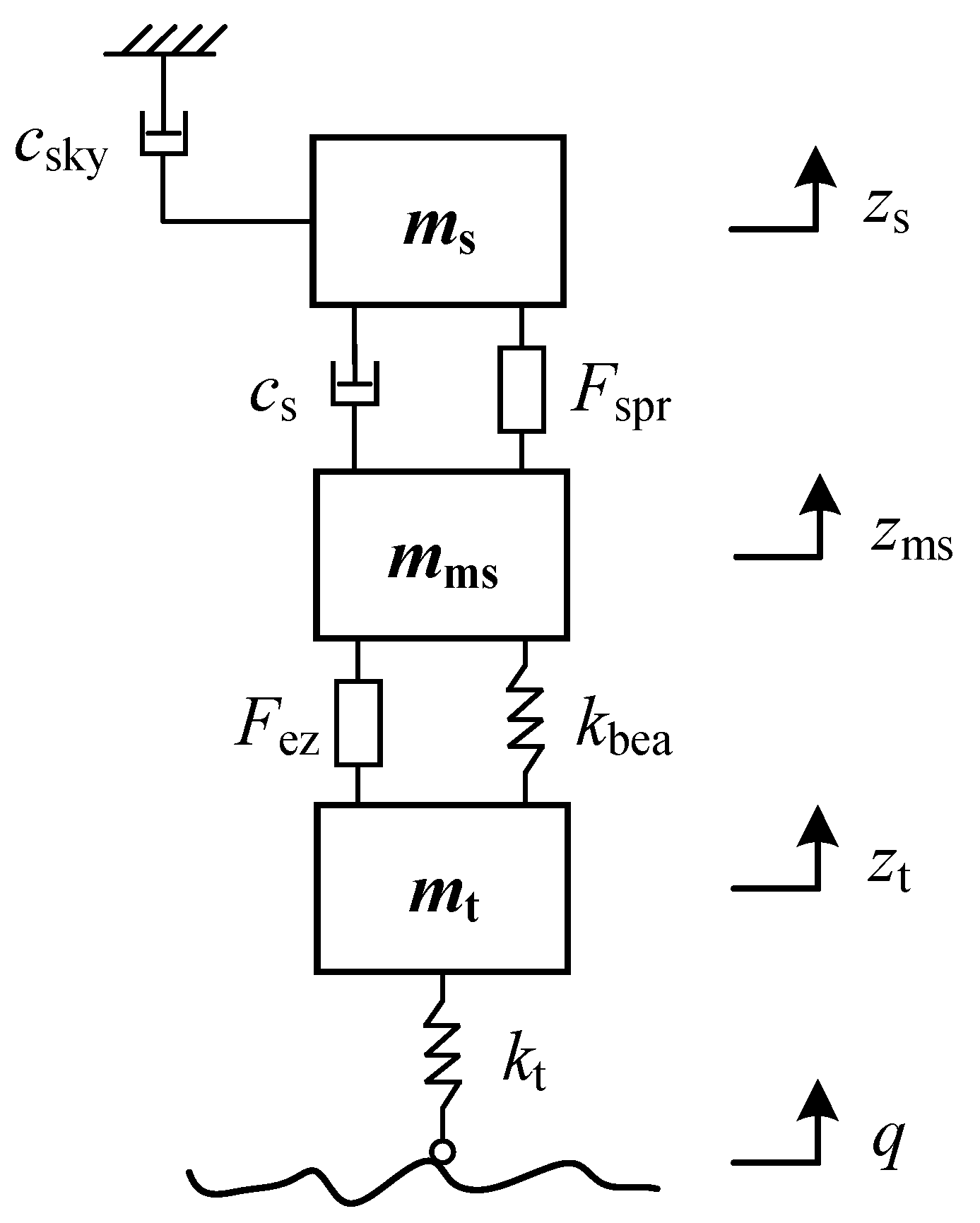
4.1. LQR Controller Design

The state quantity of the HM-AS vehicle model is:

$$x={\left[z_{\mathrm{s}} \phi \theta z_{\mathrm{t}1} z_{\mathrm{t}2} z_{\mathrm{t}3} z_{\mathrm{t}4} z_{\mathrm{ms}1} z_{\mathrm{ms}2} z_{\mathrm{ms}3} z_{\mathrm{ms}4} {\dot{z}}_{\mathrm{s}} \dot{\phi } \dot{\theta } {\dot{z}}_{\mathrm{t}1} {\dot{z}}_{\mathrm{t}2} {\dot{z}}_{\mathrm{t}3} {\dot{z}}_{\mathrm{t}4} {\dot{z}}_{\mathrm{ms}1} {\dot{z}}_{\mathrm{ms}2} {\dot{z}}_{\mathrm{ms}3} {\dot{z}}_{\mathrm{ms}4}\right]}^T$$

(24)

The control input of the HM-AS vehicle model is:

$$u={\left[F_{\mathrm{u}1} F_{\mathrm{u}2} F_{\mathrm{u}3} F_{\mathrm{u}4}\right]}^T$$

(25)

The disturbance input of the HM-AS vehicle model is:

$$\omega ={\left[q_1 q_2 q_3 q_4 F_{\mathrm{ez}1} F_{\mathrm{ez}2} F_{\mathrm{ez}3} F_{\mathrm{ez}4}\right]}^T$$

(26)

The output of the HM-AS vehicle model is:

$$y={\left[{\ddot{z}}_{\mathrm{s}} e_1 e_2 e_3 e_4 F_{\mathrm{d}1} F_{\mathrm{d}2} F_{\mathrm{d}3} F_{\mathrm{d}4} \ddot{\phi } \ddot{\theta }\right]}^T$$

(27)

to be specific,

$$e_{\mathrm{i}}=z_{\mathrm{msi}}-z_{\mathrm{ti}}$$

(28)

${\ddot{z}}_{\mathrm{s}}$, $e_{\mathrm{i}}$, $F_{\mathrm{di}}$, $\ddot{\phi }$, $\ddot{\theta }$ are selected to be evaluation indices. Among them, ${\ddot{z}}_{\mathrm{s}}, \ddot{\phi }, \ddot{\theta }$ show ride comfort, $e_{\mathrm{i}}$ shows motor safety, and $F_{\mathrm{di}}$ shows handling stability. The smaller these evaluation indices, the better the performance of the HM-AS vehicle. In this research, the vehicle moves in a straight line at a constant speed, and therefore the ride comfort is the more important assessment criteria, especially ${\ddot{z}}_{\mathrm{s}}$. Considering the HM-AS vehicle is equipped with four hub motors, motor safety is necessary to be improved. Under the driving condition of constant speed, handling stability has a smaller weight.

The state space equation of the HM-AS vehicle model is:

$$\{\begin{array}{c}\dot{x}=Ax+B_{\mathrm{u}}u+B_{\mathsf{\omega }}\omega \\ y=Cx+D_{\mathrm{u}}u+D_{\mathsf{\omega }}\omega \end{array}$$

(29)

where $A$ is the state matrix; $B_{\mathrm{u}}$ and $B_{\mathsf{\omega }}$ are the input matrices; $C$ is the output matrix; and $D_{\mathrm{u}}$ and $D_{\mathsf{\omega }}$ are the feedforward matrices.

$$\{\begin{array}{c}A=\frac{\partial \dot{x}}{\partial x} B_{\mathrm{u}}=\frac{\partial \dot{x}}{\partial u} B_{\mathsf{\omega }}=\frac{\partial \dot{x}}{\partial \omega } \\ C=\frac{\partial \dot{y}}{\partial x} D_{\mathrm{u}}=\frac{\partial \dot{y}}{\partial u} D_{\mathsf{\omega }}=\frac{\partial \dot{y}}{\partial \omega }\end{array}$$

(30)

The performance index function of the LQR controller is:

$$J={{\displaystyle \int }}_0^{\infty }[y^{T}Qy+u^{T}Ru]dt={{\displaystyle \int }}_0^{\infty }{\left[\begin{array}{c}x\\ u\end{array}\right]}^T\left[\begin{array}{c}{Q}_{\mathrm{c}}\\ N_{\mathrm{c}}^T\end{array}\begin{array}{c}{N}_{\mathrm{c}}\\ R_{\mathrm{c}}\end{array}\right]\left[\begin{array}{c}x\\ u\end{array}\right]dt$$

(31)

to be specific,

$$\{\begin{array}{c}Q=diag[p_1\hspace{0.17em}{p}_2\hspace{0.17em}{p}_3\hspace{0.17em}{p}_4\hspace{0.17em}{p}_5\hspace{0.17em}{p}_6\hspace{0.17em}{p}_7\hspace{0.17em}{p}_8\hspace{0.17em}{p}_9\hspace{0.17em}{p}_{10}\hspace{0.17em}{p}_{11}]\\ R=diag[s_1\hspace{0.17em}{s}_2\hspace{0.17em}{s}_3\hspace{0.17em}{s}_4]\\ Q_{\mathrm{c}}=C^{T}QC\\ R_{\mathrm{c}}=D_{\mathrm{u}}^{T}Q{D}_{\mathrm{u}}+R\\ N_{\mathrm{c}}=C^{T}Q{D}_{\mathrm{u}}\end{array}$$

(32)

where $Q$ is the state quantity weight matrix; $p_1~p_{11}$ are the state quantity weight coefficients, corresponding to 11 evaluation indices, respectively; $R$ is the control quantity weight matrix; $s_1~s_4$ are the control quantity weight coefficients, corresponding to four suspension damping control forces, respectively; and $Q_{\mathrm{c}}$, $R_{\mathrm{c}}$, $N_{\mathrm{c}}$ are the weighting matrices of the cross product terms.

Calling the LQR toolbox of MATLAB, the optimal feedback gain matrix $K$ and the control input $u$ of the system can be calculated.

$$\{\begin{array}{c}K=lqr\left(A,B_{\mathrm{u}},Q_{\mathrm{c}},R_{\mathrm{c}},N_{\mathrm{c}}\right)\\ u=-Kx\end{array}$$

(33)

4.2. Weight Distribution of the LQR Controller Based on Genetic Algorithm

Genetic algorithm (GA) is a computational model that simulates Darwin’s theory of evolution and Mendel’s theory of genetics. It obtains the optimal solution of a problem to be solved by continuously copying, crossing, and mutating with a group of chromosomes according to the principle of survival of the fittest. Different from other optimization algorithms, the genetic algorithm needs to convert the initial population from decimal to binary encoding, that is, to form a chromosome population. Then, according to the designed fitness function and crossover mutation probability, individuals in the chromosome population are passed on to the next generation through replication, crossover, and mutation. In the process of continuous repetition, the new generation of the chromosome population will meet the requirements of the fitness function more than the previous generation; the optimal solution in the last generation population is then decoded, which is the approximate optimal solution of problem to be solved.

The root-mean-square values of the evaluation indices of the HM-AS vehicle are selected to form the optimization objective function of the genetic algorithm, and the weight matrices $Q$ and $R$ of the LQR controller are selected as optimization variables. Due to the different dimensions of the optimization objectives, it is necessary to normalize each component of the objective function when constructing the fitness function. The sum of the ratios of the root-mean-square values of each evaluation index, both under LQR control and without control, is used as the fitness function:

$$\begin{array}{ll}H=\frac{RMS({\ddot{z}}_{\mathrm{s}})}{RMS{({\ddot{z}}_{\mathrm{s}})}_{\mathrm{u}}}\hfill & +\frac{RMS(e_1)}{RMS{(e_1)}_{\mathrm{u}}}+\frac{RMS(e_2)}{RMS{(e_2)}_{\mathrm{u}}}+\frac{RMS(e_3)}{RMS{(e_3)}_{\mathrm{u}}}+\frac{RMS(e_4)}{RMS{(e_4)}_{\mathrm{u}}}+\frac{RMS(F_{\mathrm{d}1})}{RMS{(F_{\mathrm{d}1})}_{\mathrm{u}}}+\frac{RMS(F_{\mathrm{d}2})}{RMS{(F_{\mathrm{d}2})}_{\mathrm{u}}}+\frac{RMS(F_{\mathrm{d}3})}{RMS{(F_{\mathrm{d}3})}_{\mathrm{u}}}\hfill \\ \hfill & +\frac{RMS(F_{\mathrm{d}4})}{RMS{(F_{\mathrm{d}4})}_{\mathrm{u}}}+\frac{RMS(\ddot{\phi })}{RMS{(\ddot{\phi })}_{\mathrm{u}}}+\frac{RMS(\ddot{\theta })}{RMS{(\ddot{\theta })}_{\mathrm{u}}}\hfill \end{array}$$

(34)

where $H$ is the fitness function value, and the subscript “$\mathrm{u}$” represents the root mean square value of each evaluation index that is not controlled under the same working condition.

The constraints of the genetic algorithm are:

$$\{\begin{array}{c}{p}_{1~11}\in \left[1,1\times {10}^{15}\right]\\ s_{1~4}\in \left[1,1\times {10}^{15}\right]\\ RMS\left({\ddot{z}}_{\mathrm{s}}\right)\le 1.2RMS{\left({\ddot{z}}_{\mathrm{s}}\right)}_{\mathrm{u}}\\ RMS\left(e_{\mathrm{i}}\right)\le 1.2RMS{\left(e_{\mathrm{i}}\right)}_{\mathrm{u}}\\ RMS\left(F_{\mathrm{di}}\right)\le 1.2RMS{\left(F_{\mathrm{di}}\right)}_{\mathrm{u}}\\ RMS\left(\ddot{\phi }\right)\le 1.2RMS{\left(\ddot{\phi }\right)}_{\mathrm{u}}\\ RMS\left(\ddot{\theta }\right)\le 1.2RMS{\left(\ddot{\theta }\right)}_{\mathrm{u}}\end{array}$$

(35)

Substitute the weight matrix, which is randomly generated by the genetic algorithm, into the model, and then calculate the value of the objective function according to Formula (34), that is, the fitness function required by the genetic algorithm. If each parameter output by the model operation satisfies the constraint of Formula (35), the fitness function is the output; otherwise, the fitness function value under this assignment is given a large positive number by the penalty function, so as to ensure the evolution of the population in the direction that satisfies the constraint.

Set the population size of the genetic algorithm to 100 and the number of iterations to 200.

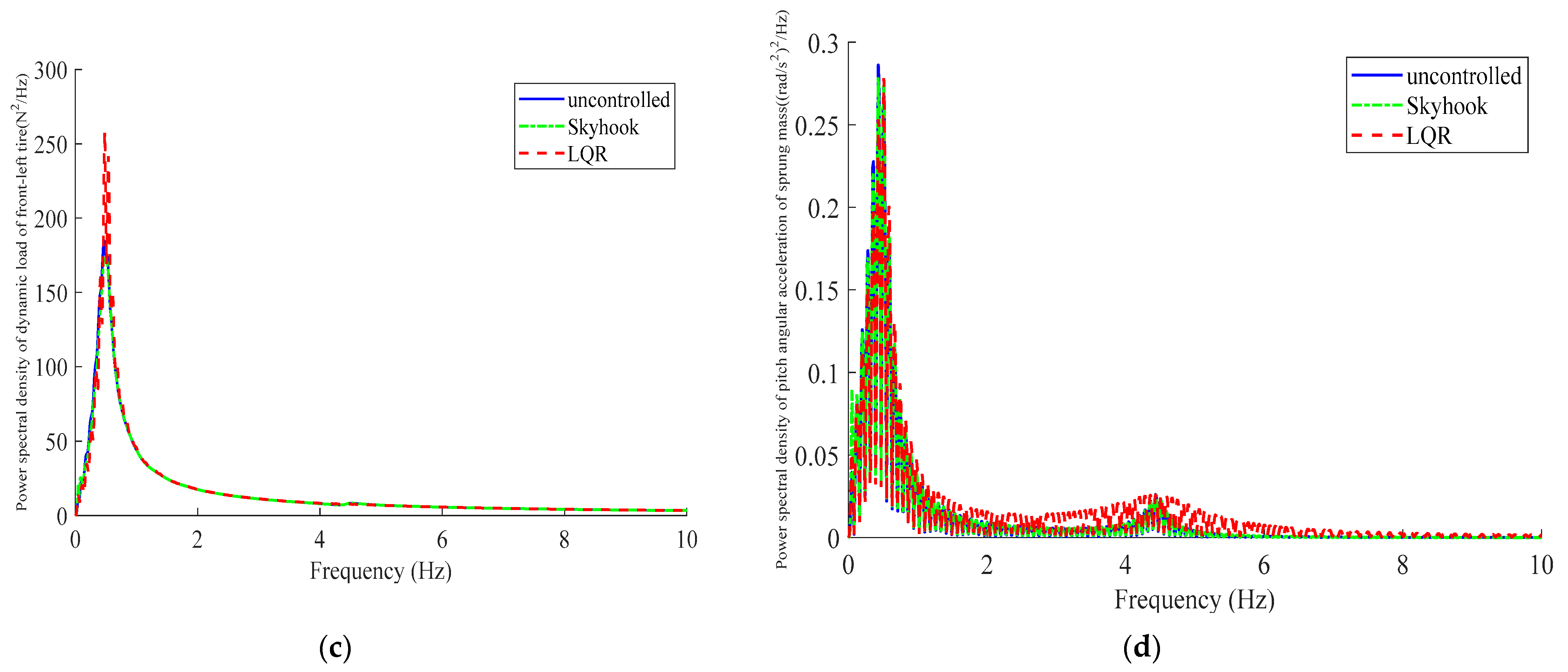
5. Simulation Results

The simulation model is established in MATLAB/Simulink. The simulation is carried out under two driving conditions, namely a random road and a bump road.

Skyhook damping control strategy is a classic vehicle suspension control method. Due to its simple structure and low cost, it is widely used in the study of suspension control and has been applied in some commercial models. The Skyhook control method assumes that the damper is mounted between the sprung mass and the virtual inertial space. The suspension is controlled by the feedback of the vertical vibration velocity of the sprung mass. The ideal Skyhook damping force is:

$$F_{\mathrm{skyi}}=-c_{\mathrm{skyi}}{\dot{z}}_{\mathrm{si}}$$

(36)

where $c_{\mathrm{skyi}}$ is the Skyhook damping coefficient.

The Skyhook suspension control model is shown in Figure 7.

In order to show the superiority of the LQR controller, the Skyhook control is used as a comparison.

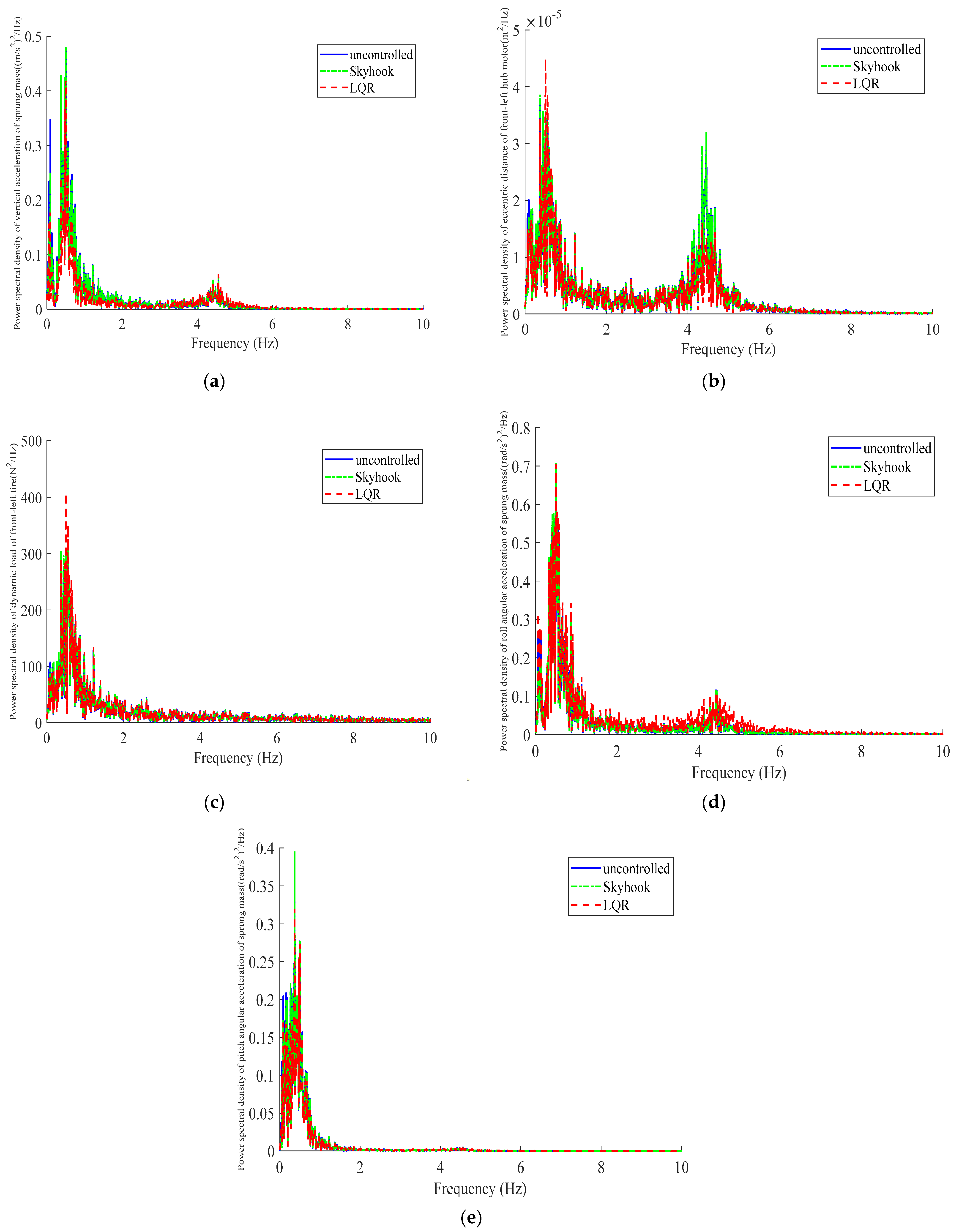
5.1. Simulation on Random Road

The input of the simulation model is the C-level random road excitation with the vehicle speed of 72 km/h, and the simulation time is 20 s. The road excitation amplitudes corresponding to the front-left, front-right, rear-left and rear-right wheels are shown in Figure 8.

The root-mean-square values of the evaluation indices and improvement rates are shown in

Table 3. The root-mean-square values of the evaluation indices and improvement rates.

Evaluation Index	Uncontrolled (RMS)	Skyhook (RMS)	LQR without GA (RMS)	LQR (RMS)
${\ddot{z}}_{\mathrm{s}} \left(\mathrm{m}/{\mathrm{s}}^2\right)$	$1.0755$	$1.0363\left(\uparrow 3.65\%\right)$	$0.9652\left(\uparrow 10.26\%\right)$	$0.8533\left(\uparrow 20.66\%\right)$
$e_1 \left(\mathrm{m}\right)$	$1.4282\times {10}^{-4}$	$1.4453\times {10}^{-4}\left(\downarrow 1.19\%\right)$	$1.3800\times {10}^{-4}\left(\uparrow 3.38\%\right)$	$1.2598\times {10}^{-4}\left(\uparrow 11.79\%\right)$
$e_2 \left(\mathrm{m}\right)$	$1.3803\times {10}^{-4}$	$1.3937\times {10}^{-4}\left(\downarrow 0.97\%\right)$	$1.3309\times {10}^{-4}\left(\uparrow 3.58\%\right)$	$1.2165\times {10}^{-4}\left(\uparrow 11.87\%\right)$
$e_3 \left(\mathrm{m}\right)$	$1.3965\times {10}^{-4}$	$1.4302\times {10}^{-4}\left(\downarrow 2.42\%\right)$	$1.3737\times {10}^{-4}\left(\uparrow 1.63\%\right)$	$1.2780\times {10}^{-4}\left(\uparrow 8.49\%\right)$
$e_4 \left(\mathrm{m}\right)$	$1.3544\times {10}^{-4}$	$1.3805\times {10}^{-4}\left(\downarrow 1.92\%\right)$	$1.3328\times {10}^{-4}\left(\uparrow 1.60\%\right)$	$1.2520\times {10}^{-4}\left(\uparrow 7.56\%\right)$
$F_{\mathrm{d}1} \left(\mathrm{N}\right)$	$974.9738$	$1002.3197\left(\downarrow 2.80\%\right)$	$981.7208\left(\downarrow 0.69\%\right)$	$1009.0915\left(\downarrow 3.50\%\right)$
$F_{\mathrm{d}2} \left(\mathrm{N}\right)$	$958.6238$	$982.3319\left(\downarrow 2.47\%\right)$	$963.5110\left(\downarrow 0.51\%\right)$	$991.6134\left(\downarrow 3.44\%\right)$
$F_{\mathrm{d}3} \left(\mathrm{N}\right)$	$927.0863$	$946.1489\left(\downarrow 2.06\%\right)$	$951.9213\left(\downarrow 2.68\%\right)$	$987.6471\left(\downarrow 6.53\%\right)$
$F_{\mathrm{d}4} \left(\mathrm{N}\right)$	$917.3267$	$931.1189\left(\downarrow 1.50\%\right)$	$945.5256\left(\downarrow 3.07\%\right)$	$992.1608\left(\downarrow 8.16\%\right)$
$\ddot{\phi } \left(\mathrm{rad}/{\mathrm{s}}^2\right)$	$1.7435$	$1.7178\left(\uparrow 1.48\%\right)$	$1.7838\left(\downarrow 2.31\%\right)$	$1.8358\left(\downarrow 5.39\%\right)$
$\ddot{\theta } \left(\mathrm{rad}/{\mathrm{s}}^2\right)$	$0.7555$	$0.7508\left(\uparrow 0.62\%\right)$	$0.7022\left(\uparrow 7.05\%\right)$	$0.6544\left(\uparrow 13.39\%\right)$

“$\uparrow$” means improving, “$\downarrow$” means deteriorating.

. The comparison in time domain is shown in Figure 9. The comparison in frequency domain is shown in Figure 10.

It can be seen from Table 3 and Figure 9 that the designed LQR controller can effectively improve ${\ddot{z}}_{\mathrm{s}}$, $e_{\mathrm{i}}$ and $\ddot{\theta }$, which means ride comfort and motor safety are optimized. However, when using the LQR controller, $F_{\mathrm{di}}$ and $\ddot{\phi }$ deteriorate slightly.

The human body is sensitive to vibration frequencies between 4 and 8 Hz. As is shown in Figure 10, the power spectral density of ${\ddot{z}}_{\mathrm{s}}$ has been improved a lot by the LQR controller and shows superiority between 4 and 8 Hz. With LQR control, the power spectral density of $F_{\mathrm{di}}$ and the power spectral density of $\ddot{\phi }$ worsen slightly, whereas the power spectral density of $e_{\mathrm{i}}$ and the power spectral density of $\ddot{\theta }$ become better than those with the Skyhook control.

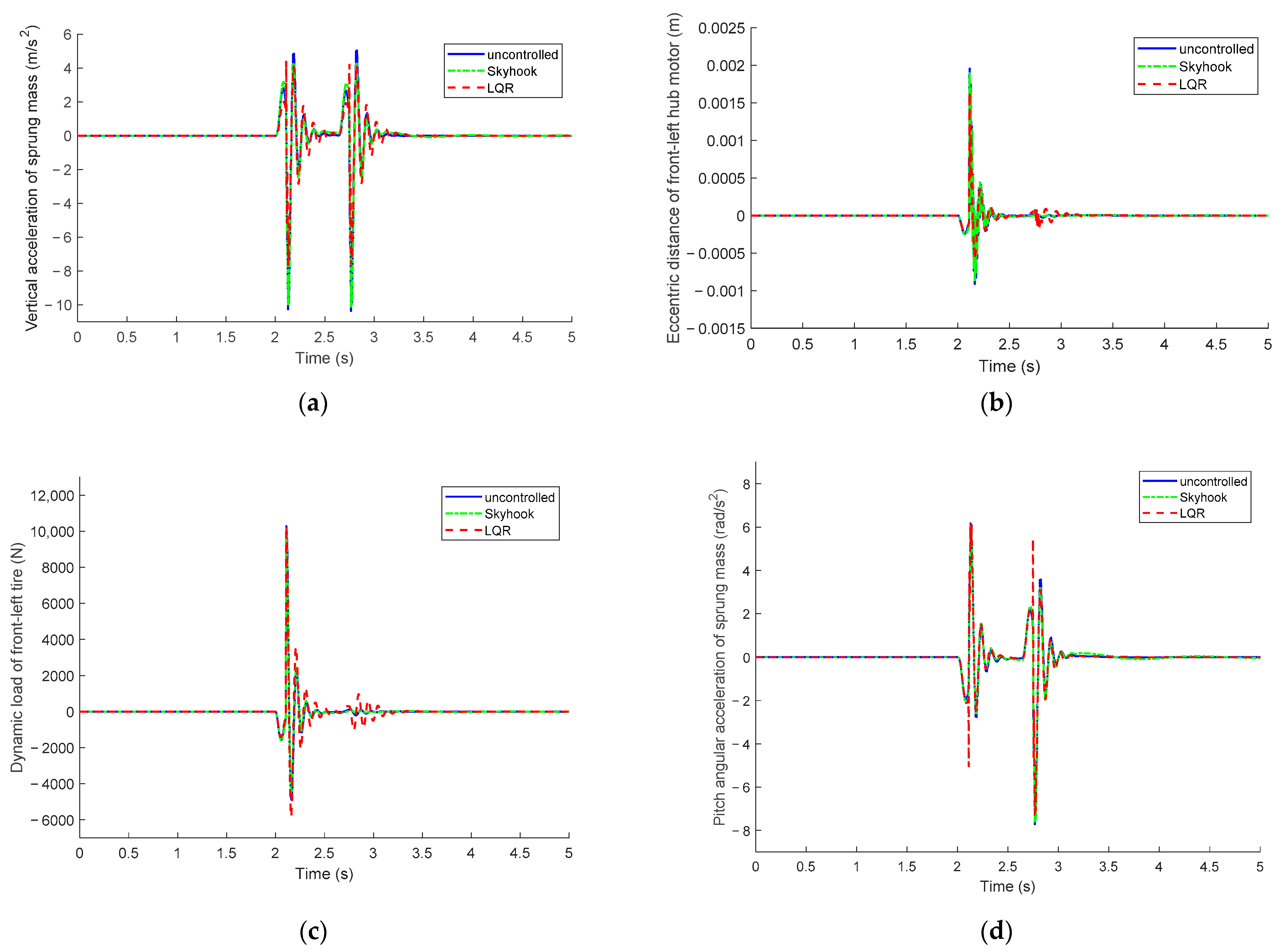
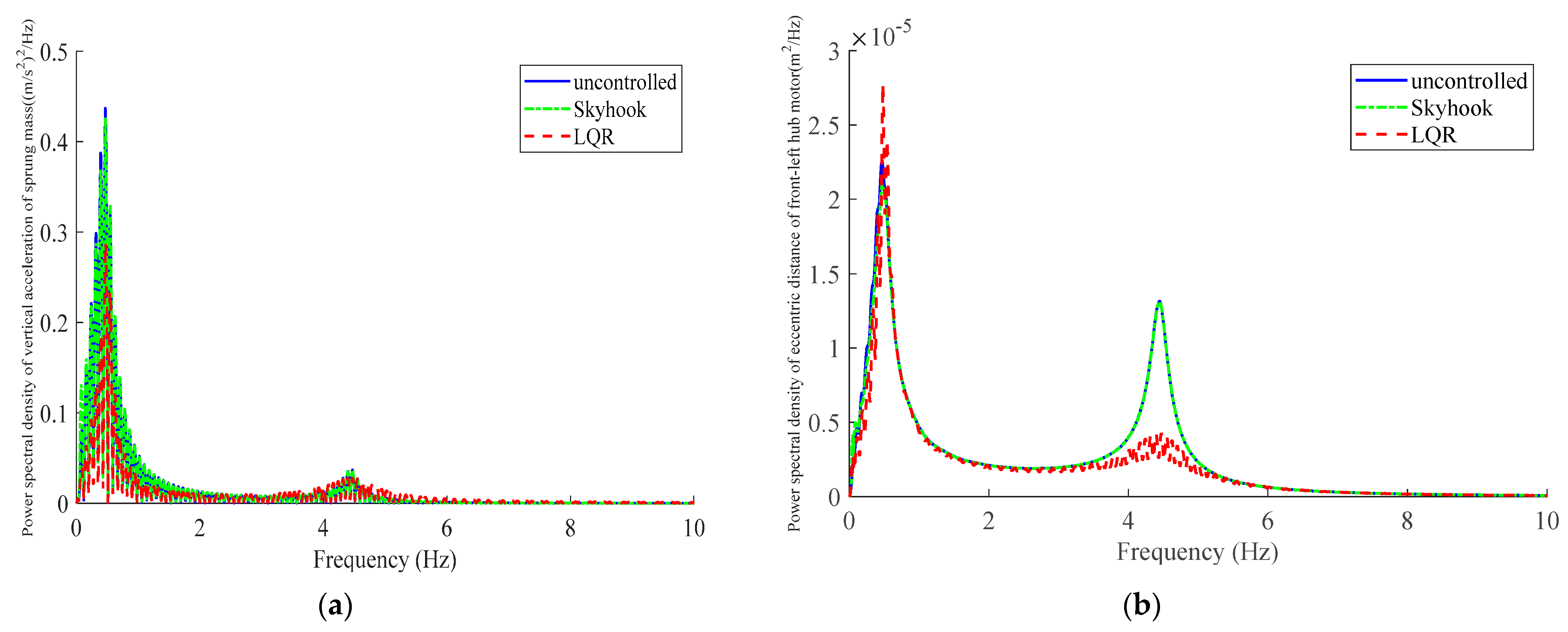
5.2. Simulation on Bump Road

In the simulation, the HM-AS vehicle moves in a straight line at 10 km/h and hits the speed bump at 2 s. The simulation time is 5 s. The road excitation amplitudes corresponding to the front-left, front-right, rear-left and rear-right wheels are shown in Figure 11. Under this driving condition, the roll angular acceleration of sprung mass is 0. The root-mean-square values of the evaluation indices and improvement rates are shown in

Table 4. The root-mean-square values of the evaluation indices and improvement rates.

Evaluation Index	Uncontrolled (RMS)	Skyhook (RMS)	LQR without GA (RMS)	LQR (RMS)
${\ddot{z}}_{\mathrm{s}} \left(\mathrm{m}/{\mathrm{s}}^2\right)$	$1.1826$	$1.1789\left(\uparrow 0.32\%\right)$	$1.1237\left(\uparrow 4.98\%\right)$	$0.9266\left(\uparrow 21.65\%\right)$
$e_1 \left(\mathrm{m}\right)$	$1.0380\times {10}^{-4}$	$1.0108\times {10}^{-4}\left(\uparrow 2.62\%\right)$	$9.5080\times {10}^{-5}\left(\uparrow 8.40\%\right)$	$8.7936\times {10}^{-5}\left(\uparrow 15.28\%\right)$
$e_2 \left(\mathrm{m}\right)$	$1.0380\times {10}^{-4}$	$1.0108\times {10}^{-4}\left(\uparrow 2.62\%\right)$	$9.5080\times {10}^{-5}\left(\uparrow 8.40\%\right)$	$8.7936\times {10}^{-5}\left(\uparrow 15.28\%\right)$
$e_3 \left(\mathrm{m}\right)$	$1.0523\times {10}^{-4}$	$1.0204\times {10}^{-4}\left(\uparrow 3.03\%\right)$	$9.7054\times {10}^{-5}\left(\uparrow 7.77\%\right)$	$8.8847\times {10}^{-5}\left(\uparrow 15.57\%\right)$
$e_4 \left(\mathrm{m}\right)$	$1.0523\times {10}^{-4}$	$1.0204\times {10}^{-4}\left(\uparrow 3.03\%\right)$	$9.7054\times {10}^{-5}\left(\uparrow 7.77\%\right)$	$8.8847\times {10}^{-5}\left(\uparrow 15.57\%\right)$
$F_{\mathrm{d}1} \left(\mathrm{N}\right)$	$726.9732$	$750.7347\left(\downarrow 2.92\%\right)$	$743.9668\left(\downarrow 2.34\%\right)$	$786.1485\left(\downarrow 8.14\%\right)$
$F_{\mathrm{d}2} \left(\mathrm{N}\right)$	$726.9732$	$750.7347\left(\downarrow 2.92\%\right)$	$743.9668\left(\downarrow 2.34\%\right)$	$786.1485\left(\downarrow 8.14\%\right)$
$F_{\mathrm{d}3} \left(\mathrm{N}\right)$	$738.1623$	$712.5902\left(\uparrow 3.46\%\right)$	$765.4318\left(\downarrow 3.69\%\right)$	$794.3556\left(\downarrow 7.61\%\right)$
$F_{\mathrm{d}4} \left(\mathrm{N}\right)$	$738.1623$	$712.5902\left(\uparrow 3.46\%\right)$	$765.4318\left(\downarrow 3.69\%\right)$	$794.3556\left(\downarrow 7.61\%\right)$
$\ddot{\phi } \left(\mathrm{rad}/{\mathrm{s}}^2\right)$	$0$	$0$	$0$	$0$
$\ddot{\theta } \left(\mathrm{rad}/{\mathrm{s}}^2\right)$	$0.8111$	$0.8091\left(\uparrow 0.24\%\right)$	$0.7443\left(\uparrow 8.24\%\right)$	$0.8048\left(\uparrow 0.77\%\right)$

“$\uparrow$” means improving, “$\downarrow$” means deteriorating.

. The comparison in time domain is shown in Figure 12. The comparison in frequency domain is shown in Figure 13.

As is shown in Table 4 and Figure 12, the values of ${\ddot{z}}_{\mathrm{s}}$, $e_{\mathrm{i}}$ are significantly decreased by the LQR controller, which makes the HM-AS vehicle more comfortable. At the same time, the RMS of $F_{\mathrm{di}}$ increases slightly, and the RMS of $\ddot{\theta }$ is almost unchanged.

In Figure 13, the power spectral density of ${\ddot{z}}_{\mathrm{s}}$ of the LQR control is lower than that of the Skyhook control by between 4 and 8 Hz. With LQR control, the power spectral density of $F_{\mathrm{di}}$ and the power spectral density of $\ddot{\theta }$ worsen slightly, and the power spectral density of $e_{\mathrm{i}}$ shows good results.

6. Conclusions

(1)

Based on electromagnetics and vehicle dynamics, the vertical vibration model of the HM-AS vehicle is established. The vehicle road test is carried out, and the simulation results are compared with the test results, which proves that the dynamic model is correct.

(2)

Vertical acceleration of sprung mass, eccentric distance of each hub motor, dynamic load of each tire, roll angular acceleration of sprung mass, and pitch angular acceleration of sprung mass are proposed as evaluation indices, which can show changes in vehicle’s ride comfort, motor safety, and handling stability.

(3)

An LQR controller is designed for the HM-AS vehicle, and the optimal control weight matrix is determined by genetic algorithm. Simulation analysis is carried out and compared with the Skyhook control strategy under random road excitation and bump road excitation. The simulation results are analyzed in the time domain and the frequency domain. As simulation results show, compared with the Skyhook controller, the LQR controller can effectively improve ride comfort and motor safety; however, handling stability deteriorates slightly.