Magnetic Field Analysis of an Inner-Mounted Permanent Magnet Synchronous Motor for New Energy Vehicles
Abstract
:1. Introduction
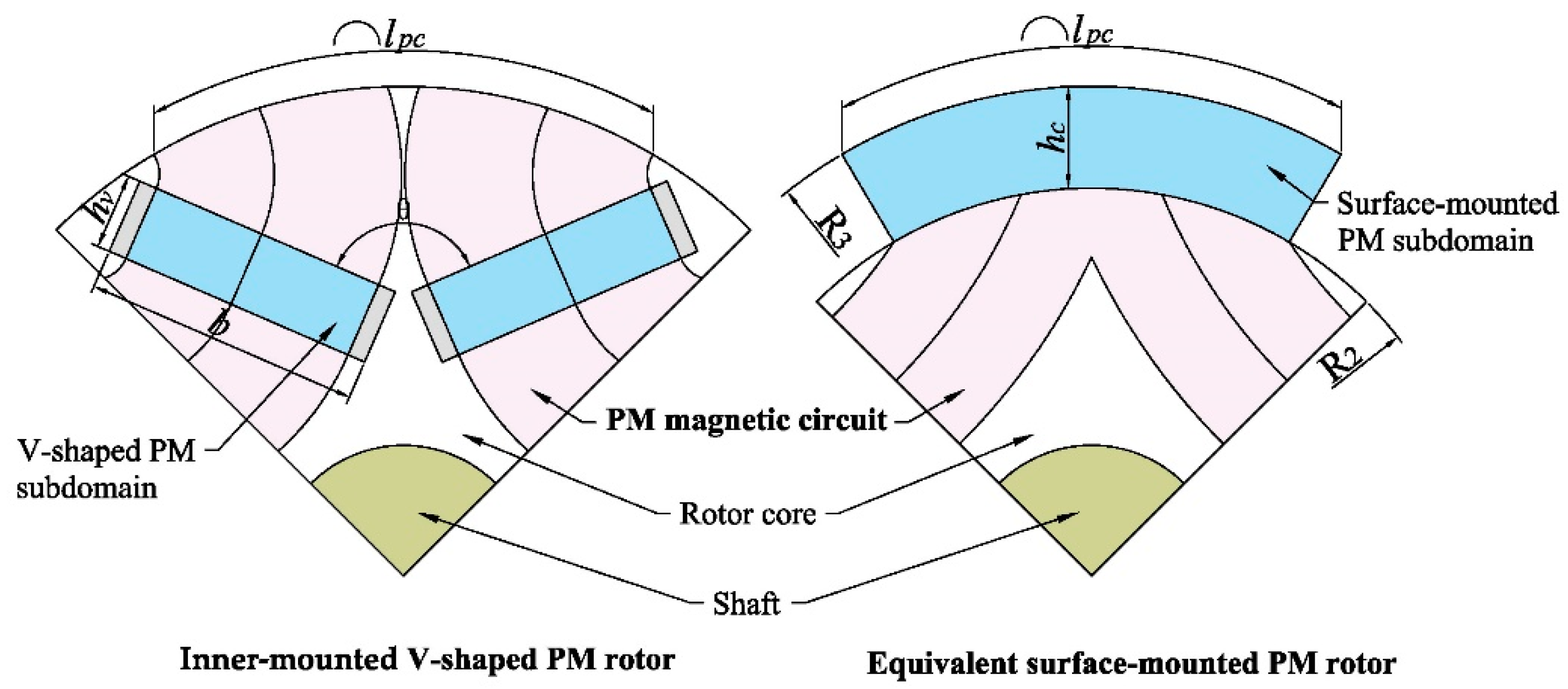
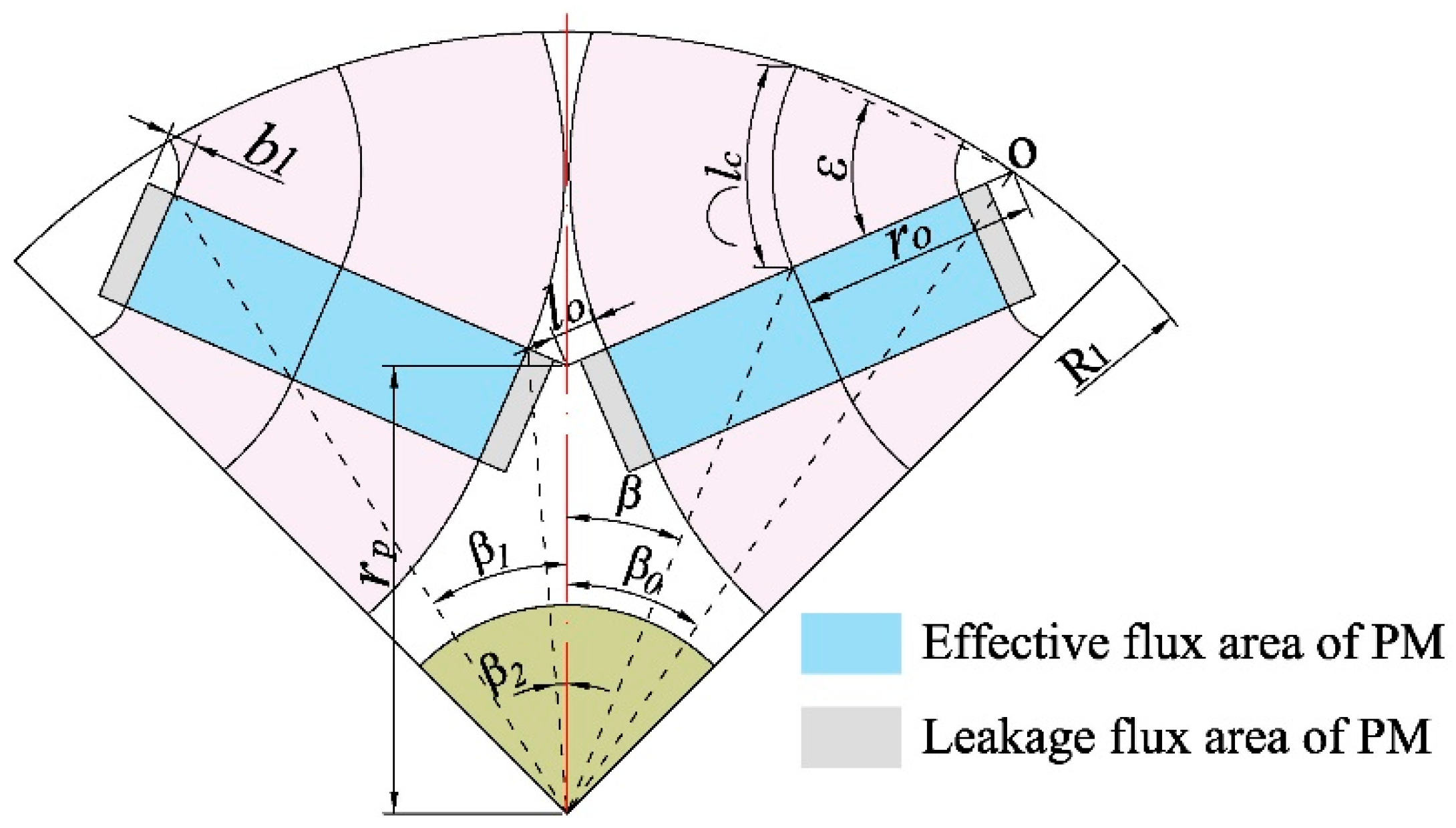
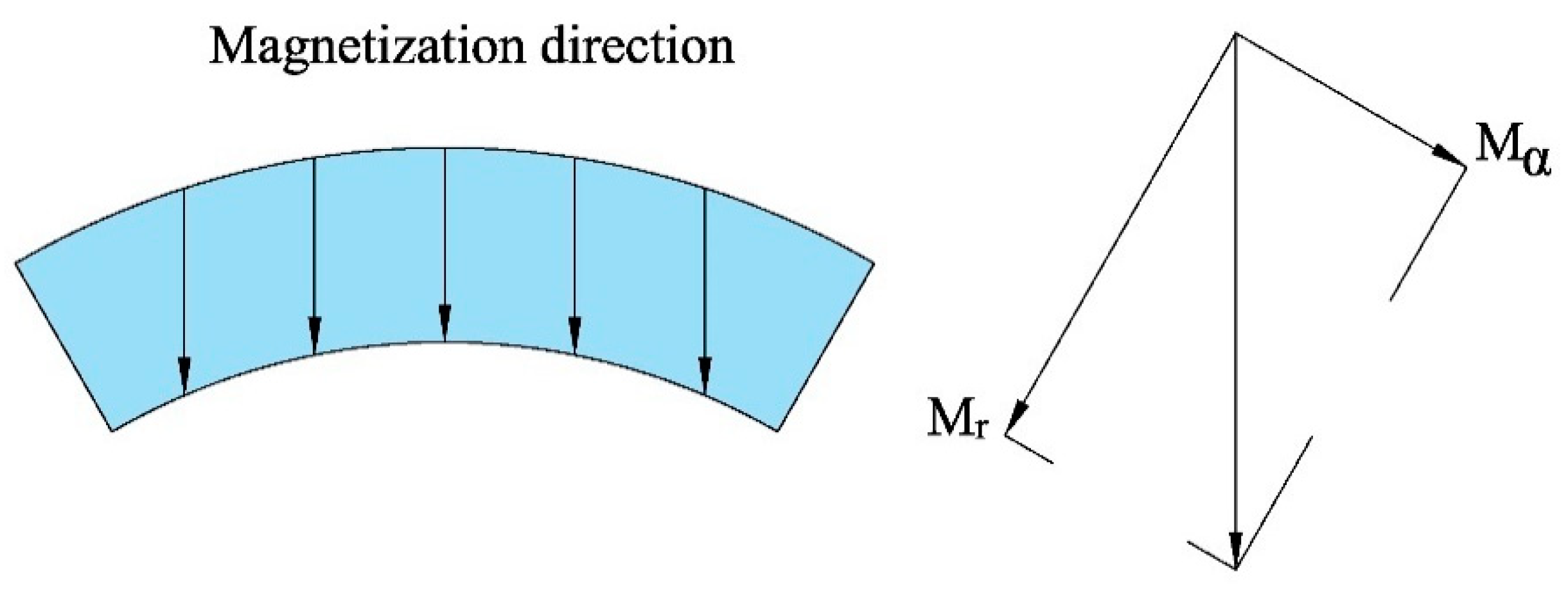
2. Analysis Model of the Magnetic Field of IPMSM
- Ignore eddy current loss and hysteresis loss;
- The magnetic permeability of the stator and rotor cores is infinite, and the influence of the magnetic resistance is ignored;
- Ignore the end effect and the difference of axial magnetic field distribution; it is assumed that the axial magnetic field distribution is uniform;
- The magnetic flux distribution in the 2-D plane is linear and the magnetic field distribution is uniform;
- The boundaries of each subdomain are in the radial or tangential direction;
- The current density in the coil in the stator slot is evenly distributed, and there is only one component in the z-axis direction;
- The permeability of armature winding is constant;
- The demagnetization curve of PM material is linear;
- Ignore the effect of temperature rise on the magnetic field.
2.1. General Solution of Each Subdomain
2.2. Calculation of Undetermined Coefficients of Each Subdomain
2.3. Analytical Model of the Magnetic Field in Each Subdomain
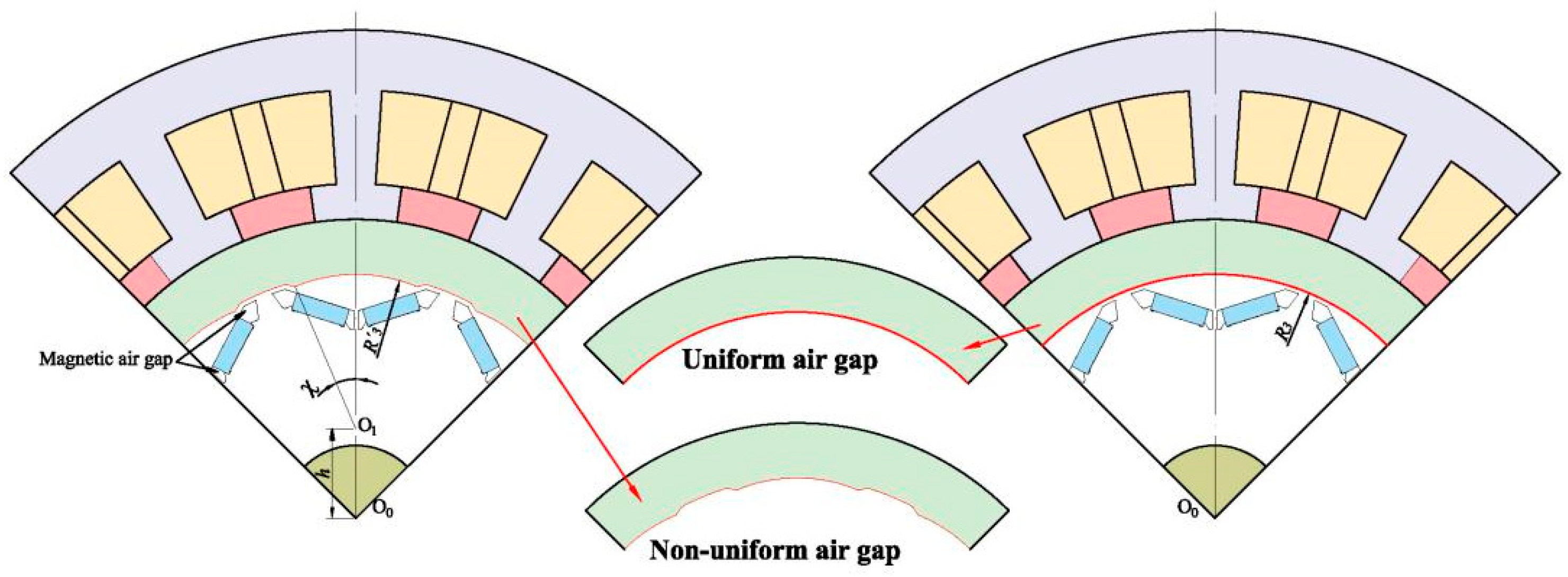
3. Verification and Analysis of the Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Equivalent rotor magnetomotive force of PM subdomain | |
| Arc length of fan-shaped PM subdomain | |
| Outer radius of the equivalent rotor | |
| Residual magnetic induction intensity of PM material | |
| Thickness of fan-shaped PM subdomain | |
| Permeability of PM material | |
| Included angle between the center of the magnetic pole and the connecting line between any point in the effective PM subdomain and the rotor circle’s center | |
| Intersection of the inner extension line of the rectangular PM and the outer circle of the rotor as the center of the circle | |
| Included angle between the outer end of the effective calculated length of rectangular PM and the center line of the rotor magnetic pole | |
| Included angle between the inner end of the effective calculated length of rectangular PM and the center line of rotor magnetic pole | |
| Inclination angle of the inner side of two V-shaped rectangular PMs | |
| The distance from the intersection point of the inner side of V-shaped PM to its inner end of effective calculated length | |
| The distance from the intersection point of the inner side of V-shaped PM to the center of rotor circle | |
| Length of rectangular PM | |
| The distance of the PM length occupied by the leakage flux at one end of the rectangular PM | |
| Radius corresponding to the magnetic circuit inside the rectangular PM | |
| Angle corresponding to the magnetic circuit inside the rectangular PM | |
| Included angle between the center of the rotor magnetic pole and the connecting line from the center to the center of the rotor circle | |
| Outer diameter of the rotor | |
| Distance from the top of the V-shaped PM to the center of the rotor | |
| Inner magnetic circuit length of rectangular PM at any angle within the effective calculation angle | |
| Rotor magnetomotive force of V-shaped PM subdomain | |
| Magnetic flux density of rotor core | |
| Length in the magnetization direction of rectangular PM | |
| Permeability of rotor core | |
| Vector magnetic potential in z-axis direction of stator slot subdomain | |
| Vector magnetic potential in z-axis direction of stator slot notch subdomain | |
| Vector magnetic potential in z-axis direction of air-gap subdomain | |
| Vector magnetic potential in z-axis direction of PM subdomain | |
| Radius from a point in the subdomain to the center of the stator circle | |
| Circumferential angle | |
| Permeability of vacuum | |
| Current density | |
| Magnetization’s radial components under one pair of magnetic poles | |
| Magnetization’s tangential components under one pair of magnetic poles | |
| Radius of the bottom circle of the stator slot | |
| Radius of the top circle of the stator slot | |
| Radius of the top circle of the stator slot notch | |
| Inner diameter of equivalent rotor outer | |
| i-th circumference | |
| Stator slot width | |
| Stator slot notch width | |
| n | Spatial harmonic logarithm in the stator slot subdomain |
| Current density of left winding in slot | |
| Current density of right winding in slot | |
| Harmonic coefficients of the stator slot subdomain | |
| Harmonic coefficients of the stator slot subdomain | |
| n-th back EMF | |
| Harmonic coefficients of the stator slot subdomain | |
| Harmonic coefficients of the stator slot subdomain | |
| Harmonic coefficients of the stator slot subdomain | |
| Harmonic coefficients of the stator slot subdomain | |
| m | Spatial harmonic logarithm in the stator slot notch subdomain |
| Harmonic coefficients of the air-gap subdomain | |
| Harmonic coefficients of the air-gap subdomain | |
| Harmonic coefficients of the air-gap subdomain | |
| Harmonic coefficients of the air-gap subdomain | |
| k | Spatial harmonic logarithm in the air-gap subdomain |
| l | Spatial harmonic logarithm in the PM subdomain |
| Polar arc coefficient | |
| p | Number of motor pole pairs |
| Left circumferential angle of PM field | |
| Right circumferential angle of PM field | |
| Harmonic coefficients of the PM subdomain | |
| Harmonic coefficients of the PM subdomain | |
| Harmonic coefficients of the PM subdomain | |
| Harmonic coefficients of the PM subdomain | |
| Tangential magnetic field intensity vectors of stator slot notch subdomain | |
| Tangential magnetic field intensity vectors of stator slot subdomain | |
| Tangential magnetic field intensity vectors of air-gap subdomain | |
| Tangential magnetic field intensity vectors of PM subdomain | |
| Vector magnetic potential of subdomain | |
| Radial components of the magnetic flux density | |
| Tangential components of the magnetic flux density | |
| Radial components of the magnetic flux density in the stator slot notch subdomain | |
| Tangential components of the magnetic flux density in the stator slot notch subdomain | |
| Radial components of the magnetic flux density in the stator slot subdomain | |
| Tangential components of the magnetic flux density in the stator slot subdomain | |
| Radial components of the magnetic flux density in the air-gap subdomain | |
| Tangential components of the magnetic flux density in the air-gap subdomain | |
| Radius of the eccentric circle | |
| Rotor eccentricity | |
| Included angle between the radius of any eccentric circle and the center of the circle | |
| Variation of eccentric rotor radius | |
| Radial components of the magnetic flux density in the PM subdomain | |
| Tangential components of the magnetic flux density in the PM subdomain | |
| Magnetic linkage of the left coils | |
| Magnetic linkage of the right coils | |
| Axial length of the core | |
| Turns of armature winding | |
| Armature winding surface area | |
| Total magnetic linkage in one stator slot | |
| Magnetic linkage of phase A | |
| Magnetic linkage of phase B | |
| Magnetic linkage of phase C | |
| Number of parallel branches | |
| Calculation constant of magnetic linkage | |
| Magnetic linkage in slot 1 | |
| Magnetic linkage in slot 2 | |
| Magnetic linkage in slot 2 | |
| Magnetic linkage in slot 2 | |
| Number of stator slots | |
| Back EMF of phase A | |
| Cogging torque of the motor | |
| Angle between the centerline of a specified PM and the centerline of a specified stator tooth |
References
- Ullah, K.; Guzinski, J.; Mirza, A.F. Critical Review on Robust Speed Control Techniques for Permanent Magnet Synchronous Motor (PMSM) Speed Regulation. Energies 2022, 15, 1235. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C.; Dai, B.; Li, Z. Dynamic Simulation of Permanent Magnet Synchronous Motor (PMSM) Electric Vehicle Based on Simulink. Energies 2022, 15, 1134. [Google Scholar] [CrossRef]
- Tanaka, C.N.; Chabu, I.E. Flux Reversal Free Splittable Stator Core Doubly Salient Permanent Magnet Motor. IEEE Lat. Am. Trans. 2020, 18, 1329–1336. [Google Scholar] [CrossRef]
- Zhou, R.; Li, G.; Wang, Q.; He, J. Torque Calculation of Permanent-Magnet Spherical Motor Based on Permanent-Magnet Surface Current and Lorentz Force. IEEE Trans. Magn. 2020, 56, 1–9. [Google Scholar] [CrossRef]
- Iwama, K.; Noguchi, T. Operation Characteristics of Adjustable Field IPMSM Utilizing Magnetic Saturation. Energies 2022, 15, 52. [Google Scholar] [CrossRef]
- Liu, M.; Zou, J.; Xu, Y.; Lan, H.; Yu, G. Vibration Enhancement or Weakening Effect Caused by Permanent Magnet Synchronous Motor Radial and Tangential Force Formed by Tooth Harmonics. Energies 2022, 15, 744. [Google Scholar] [CrossRef]
- Zhang, X.; Du, Q.; Xu, J.; Zhao, Y.; Ma, S. Development and Analysis of the Magnetic Circuit on Double-Radial Permanent Magnet and Salient-Pole Electromagnetic Hybrid Excitation Generator for Vehicles. Chin. J. Mech. Eng. 2019, 32, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Song, I.-S.; Jo, B.-W.; Kim, K.-C. Analysis of an IPMSM Hybrid Magnetic Equivalent Circuit. Energies 2021, 14, 5011. [Google Scholar] [CrossRef]
- Zhao, W.; Yang, Z.; Liu, Y.; Wan, X.g. Analysis of a Novel Surface-Mounted Permanent Magnet Motor with Hybrid Magnets for Low Cost and Low Torque Pulsation. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Tan, Q.; Wang, M.; Li, L. Analysis of a New Flux Switching Permanent Magnet Linear Motor. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, X.; Tong, L.; Ma, Q.; Xu, M.; Zhang, Y.; Wang, L. Performance Optimization Analysis of Hybrid Excitation Generator with the Electromagnetic Rotor and Embedded Permanent Magnet Rotor for Vehicle. IEEE Access 2021, 9, 163640–163653. [Google Scholar] [CrossRef]
- Jeong, W.-S.; Lee, Y.-S.; Lee, J.-H.; Lee, C.-H.; Won, C.-Y. Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives. Energies 2022, 15, 266. [Google Scholar] [CrossRef]
- Hayslett, S.; Strangas, E. Analytical Design of Sculpted Rotor Interior Permanent Magnet Machines. Energies 2021, 14, 5109. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, X.; Si, T.; Tong, L.; Ma, Q.; Xu, M. Analysis of the Rotor Magnetomotive Force of Built-In Radial Permanent Magnet Generator for Vehicle. Int. J. Rotating Mach. 2021, 2021, 5319615. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, X.; Yin, H.; Geng, H.; Zhang, Y.; Shi, L. Analysis of Magnetic Field and Electromagnetic Performance of a New Hybrid Excitation Synchronous Motor with dual-V type Magnets. Energies 2020, 13, 1501. [Google Scholar] [CrossRef] [Green Version]
- Geng, H.; Zhang, X.; Zhang, Y.; Hu, W.; Lei, Y.; Xu, X.; Wang, A.; Wang, S.; Shi, L. Development of Brushless Claw Pole Electrical Excitation and Combined Permanent Magnet Hybrid Excitation Generator for Vehicles. Energies 2020, 13, 4723. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Z.; Yang, J.; Tuo, J.; Zhang, Y. Analytical Calculation and Analysis of Magnetic Field in Surface-mounted Permanent Magnet Motor. Automot. Eng. 2018, 40, 850–857. (In Chinese) [Google Scholar]
- Guo, S.; Zhou, L. Analytical Solution of Magnetic Field in Surface-Inset Permanent Magnet Machines. Proc. CSEE 2015, 35, 710–718. (In Chinese) [Google Scholar]
- Oner, Y.; Zhu, Z.Q.; Wu, L.; Xiao, G.; Chen, J. Analytical on-load subdomain field model of permanent-magnet vernier machines. IEEE Trans. Ind. Electron. 2016, 63, 4105–4117. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D.; Bolte, E.; Ackermann, B. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. I. Open-circuit field. IEEE Trans. Magn. 2002, 29, 143–151. [Google Scholar] [CrossRef]
- Chen, X.; Hu, J.; Chen, K.; Peng, Z. Modeling of electromagnetic torque considering saturation and magnetic field harmonics in permanent magnet synchronous motor for HEV. Simul. Model. Pract. Theory 2016, 66, 212–225. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. A Two-Dimensional Analytical Calculation of Magnetic Field and lectromagnetic Torque for Surface-Inset Permanent-Magnet Motors. IEEE Trans. Magn. 2012, 48, 2080–2091. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance. IEEE Trans. Magn. 2006, 42, 1828–1837. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical solution for cogging torque in surface permanent-magnet motors using conformal mapping. IEEE Trans. Magn. 2006, 44, 52–65. [Google Scholar] [CrossRef]
- Dubas, F.; Espanet, C. Analytical solution of the magnetic field in permanent-magnet motors taking into account slotting effect: No-load vector potential and flux density calculation. IEEE Trans. Magn. 2009, 45, 2097–2109. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, B.; Ding, Y.; Lu, G. Semi-analytical approach for armature reaction field of surface mounted permanent magnet brushless motors. Trans. China Electrotech. Soc. 2009, 24, 47–51. (In Chinese) [Google Scholar]
- Kim, U.; Lieu, D.K. Magnetic field calculation in permanent magnet motors with rotor eccentricity: Without slotting effect considered. IEEE Trans. Magn. 1998, 34, 2243. [Google Scholar] [CrossRef]
- Gysen, B.; Meessen, K.J.; Paulides, J.; Lomonova, E.A. General formulation of the electromagnetic field distribution in machines and devices using fourier analysis. IEEE Trans. Magn. 2009, 46, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Lubin, T.; Mezani, S.; Rezzoug, A. 2-D Exact Analytical model for surface-mounted permanent-magnet motors with semi-closed slots. IEEE Trans. Magn. 2011, 47, 479–492. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Huang, X.; Zhou, B.; Yu, H.; Huang, Q. Design principle of a 16-pole 18-slot two-sectional modular permanent magnet linear synchronous motor with optimisation of its end tooth. IET Electr. Power Appl. 2020, 14, 441–447. [Google Scholar] [CrossRef]
- Wei, X.; Kai, Y.; Pan, Z.; Xie, H.; Zhang, Y. Design of a novel axial-radial flux permanent magnet motor. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Berlin, Germany, 2–5 September 2014; pp. 80–84. [Google Scholar] [CrossRef]
- Wu, H.; Huang, K.; Lv, W.; Mo, X.; Huang, S. DC-link voltage control strategy of Z-source inverter for high-speed permanent magnet motor. IET Electr. Power Appl. 2020, 14, 911–920. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Wu, L.J.; Xia, Z.P. An accurate sub-domain model for magnetic field computation in slotted surface-mounted permanent-magnet machines. IEEE Trans. Magn. 2009, 46, 1100–1115. [Google Scholar] [CrossRef]


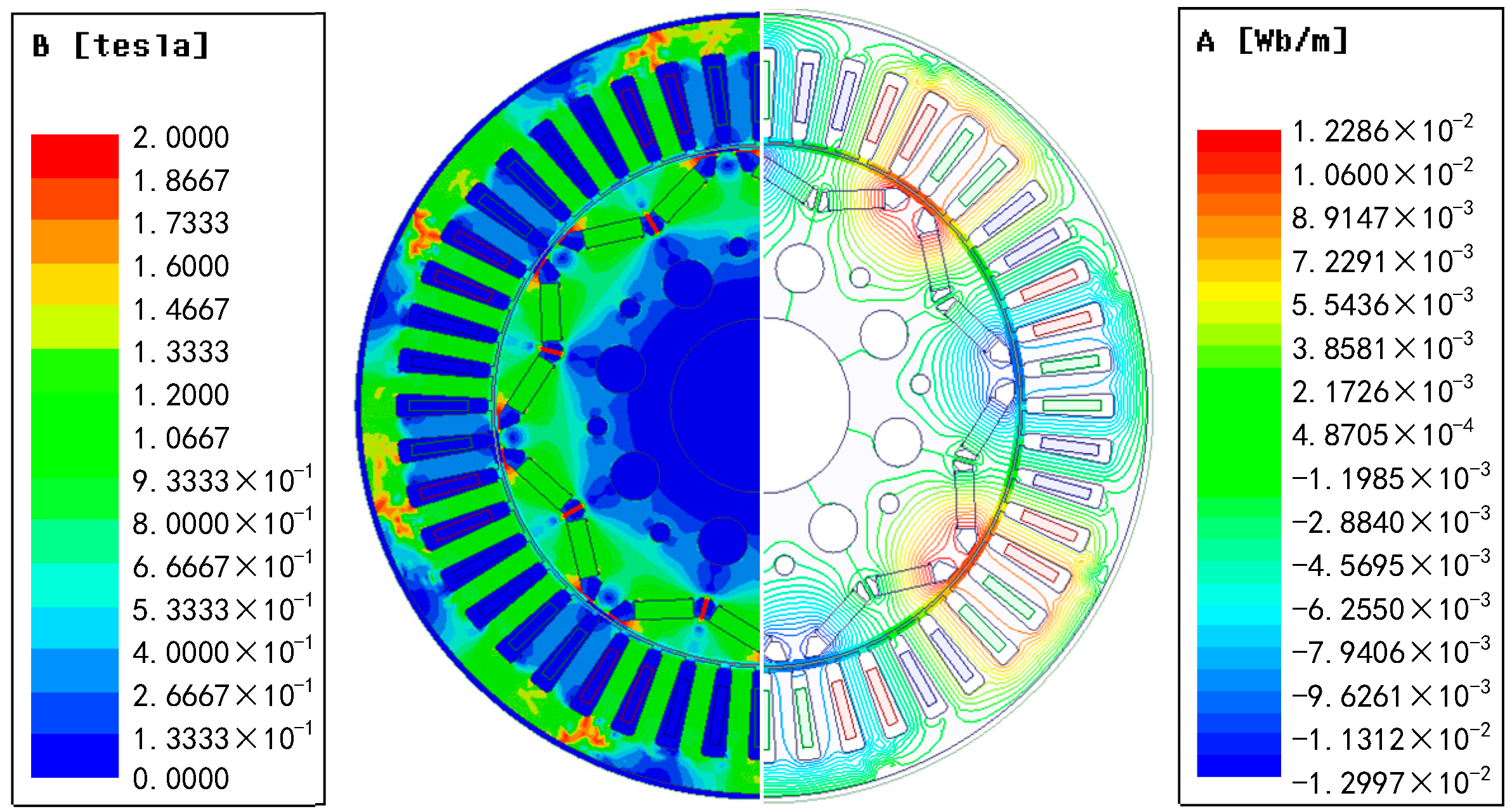

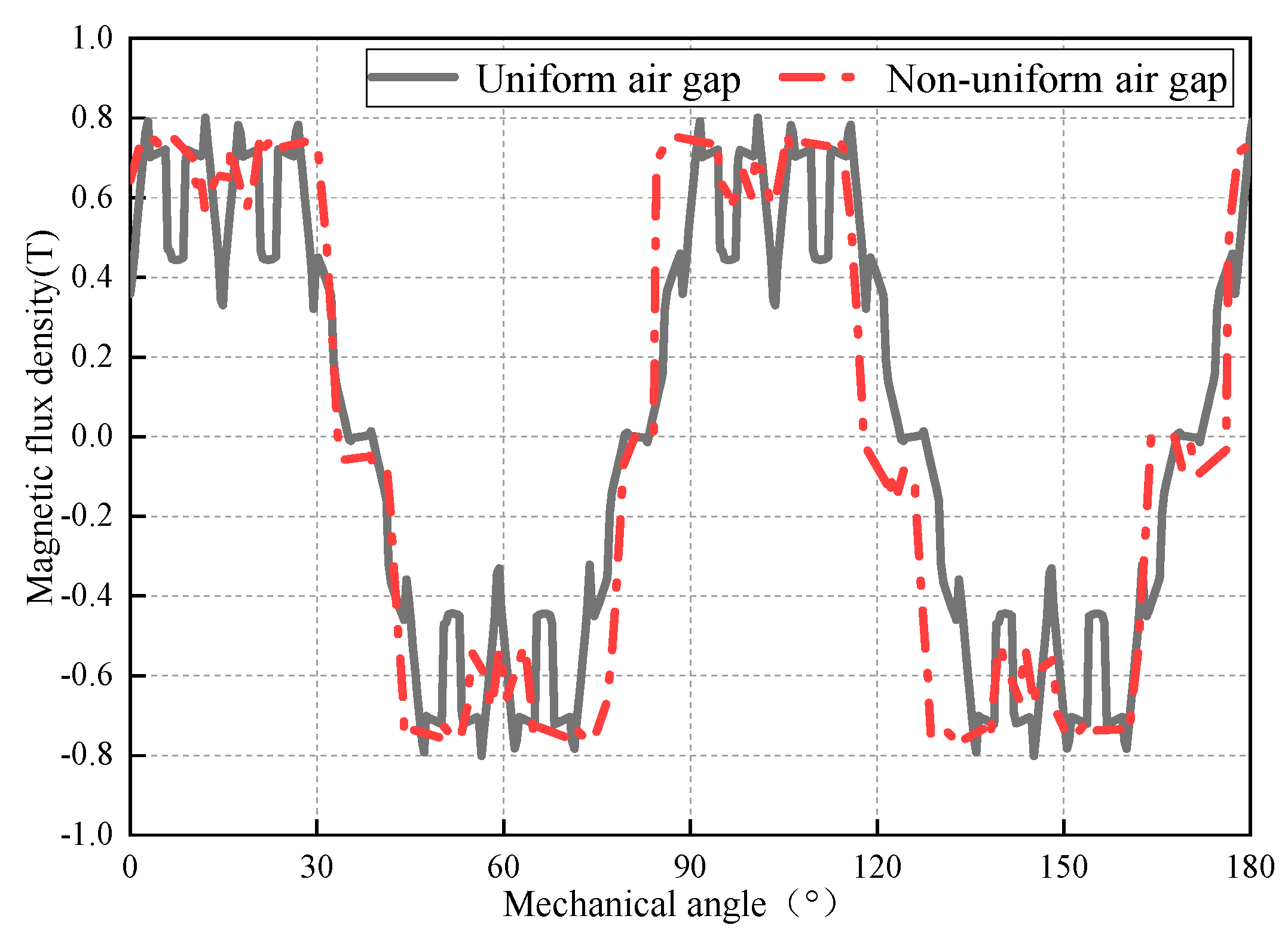
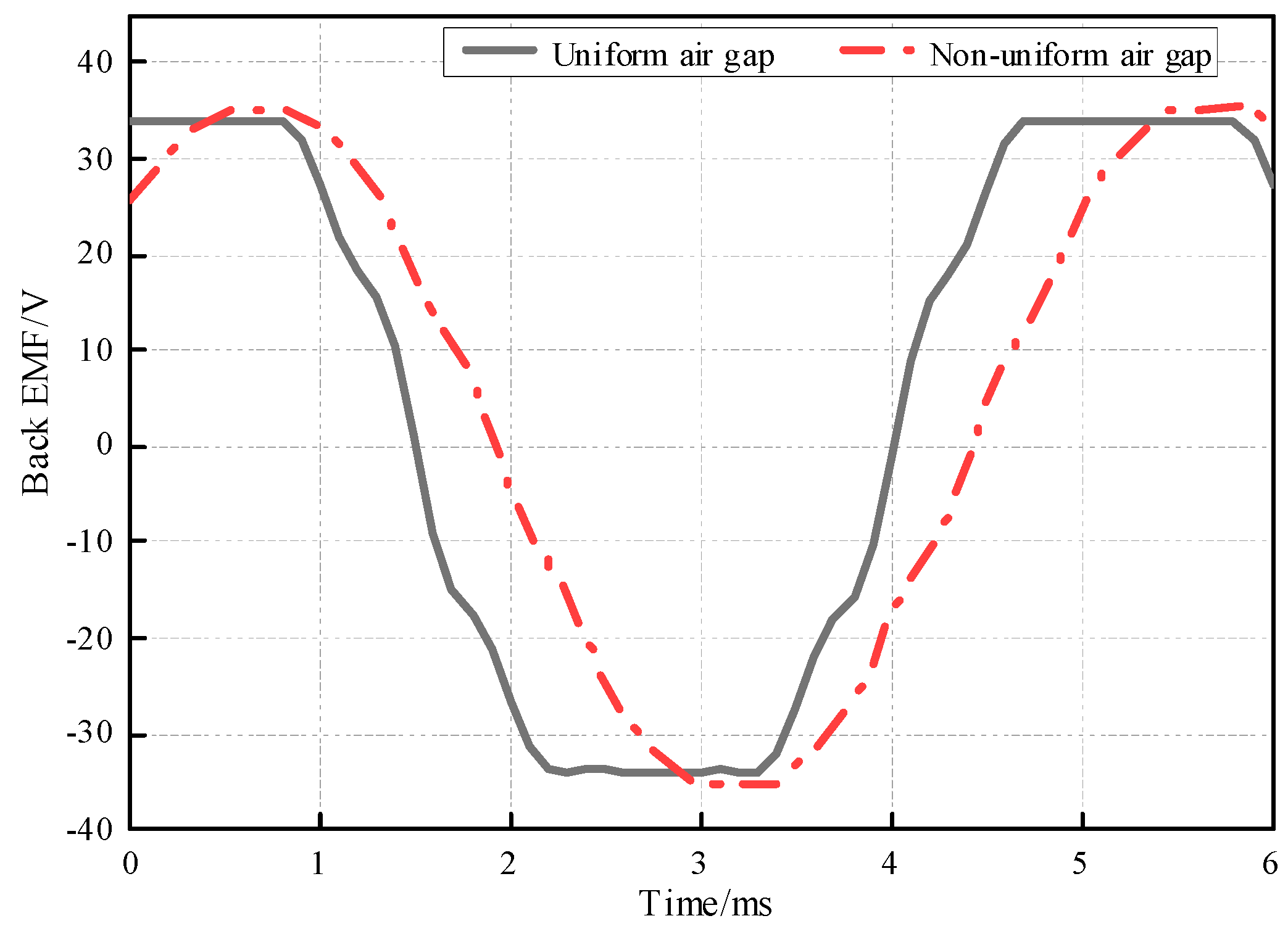
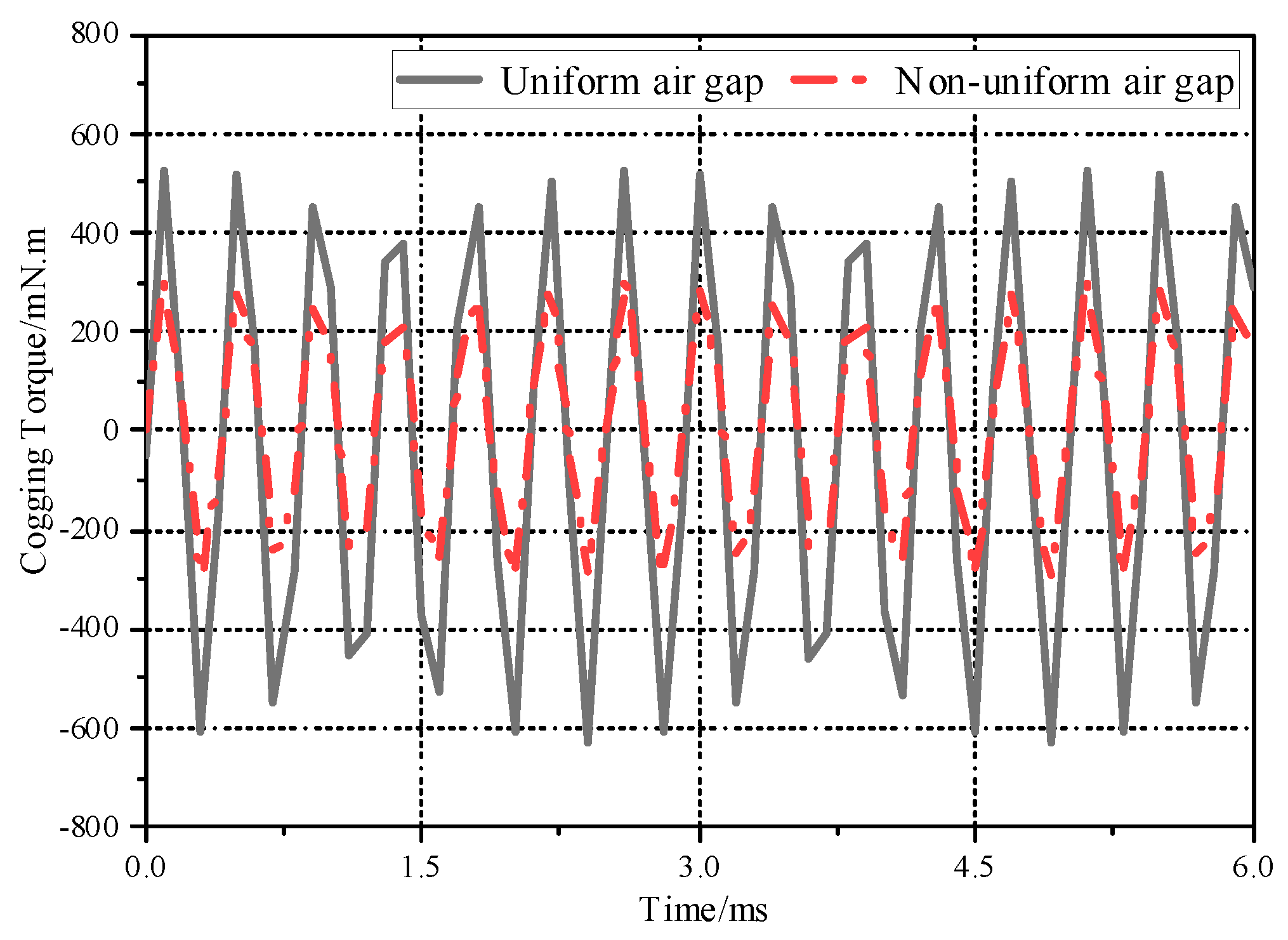
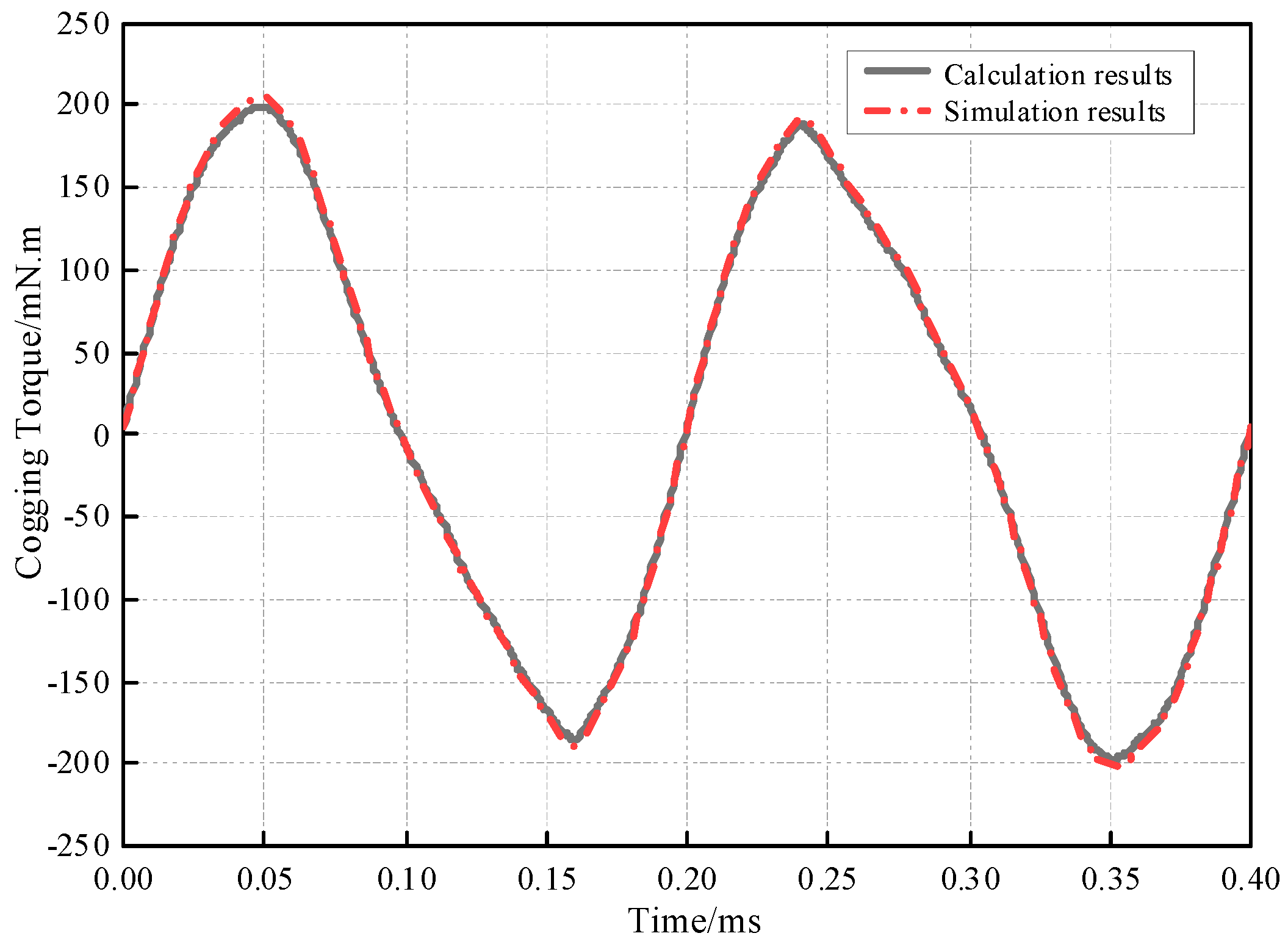



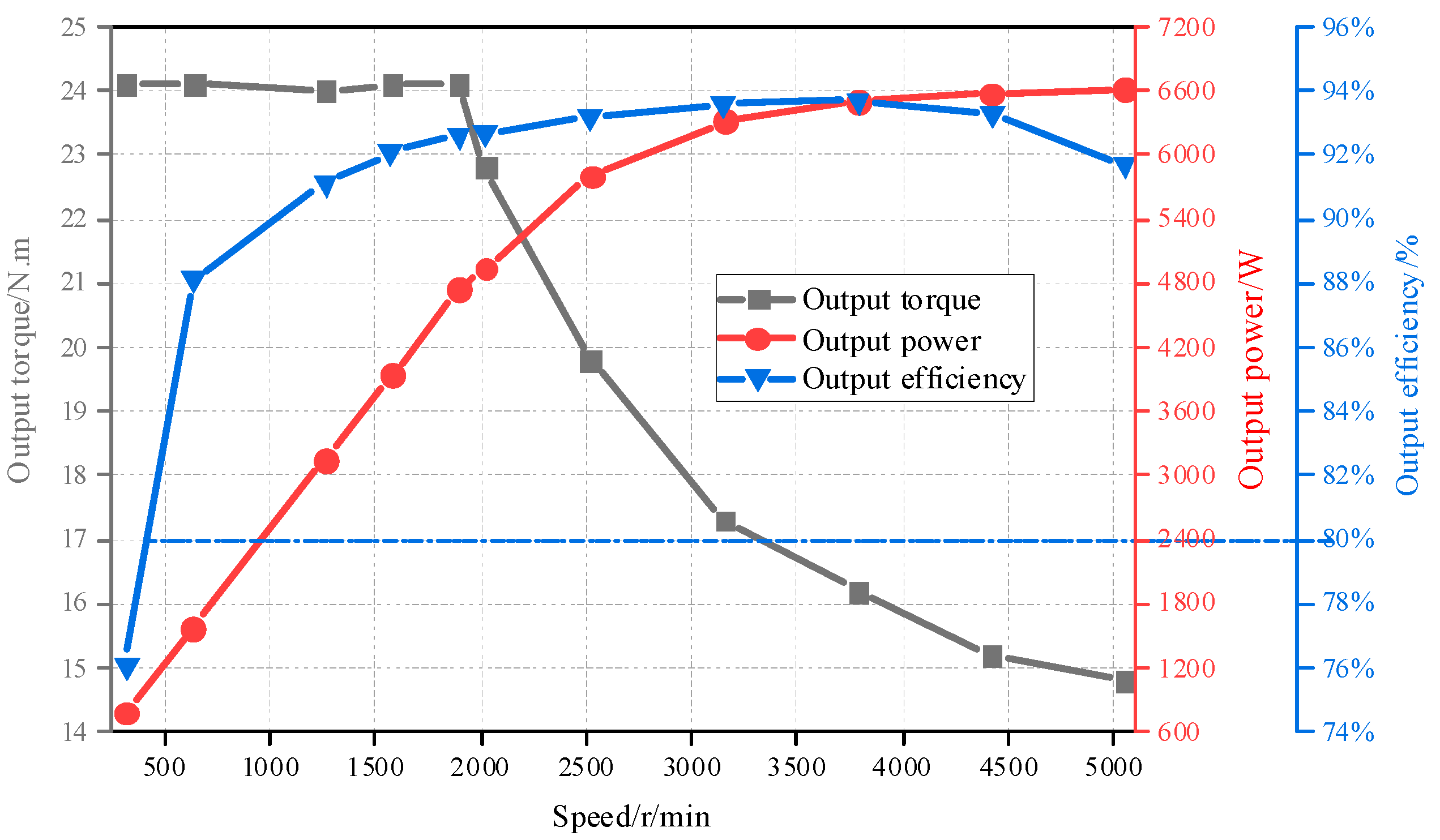
| Parameter | Value |
|---|---|
| Rated Power | 6 kW |
| Rated Speed | 3000 r/min |
| Rated Torque | 19.5 N∙m |
| Rated Voltage | 72 V |
| Number of Phases | 3 |
| Numbers of Slots/Poles | 48/8 |
| Air-Gap Length | 0.6 mm |
| Stator Outer Radius | 84.3 mm |
| Axial Length | 55 mm |
| Slot Depth | 18.2 mm |
| Rotor Outer Radius | 53.4 mm |
| Number of Turns Per Phase | 12 turns |
| Methods | Peak Value | Peak Error | Maximum Deviation | Root Mean Square of Relative Error | Correlation Coefficient |
|---|---|---|---|---|---|
| Simulation Results | 35.99 V | 2.343% | 2.345% | 0.023 | 0.999999 |
| Test Results | 33.621 V | 4.393% | 6.887% | 0.108 | 0.999736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, H.; Zhang, X.; Yan, S.; Zhang, Y.; Wang, L.; Han, Y.; Wang, W. Magnetic Field Analysis of an Inner-Mounted Permanent Magnet Synchronous Motor for New Energy Vehicles. Energies 2022, 15, 4074. https://doi.org/10.3390/en15114074
Geng H, Zhang X, Yan S, Zhang Y, Wang L, Han Y, Wang W. Magnetic Field Analysis of an Inner-Mounted Permanent Magnet Synchronous Motor for New Energy Vehicles. Energies. 2022; 15(11):4074. https://doi.org/10.3390/en15114074
Chicago/Turabian StyleGeng, Huihui, Xueyi Zhang, Shilong Yan, Yufeng Zhang, Lei Wang, Yutong Han, and Wei Wang. 2022. "Magnetic Field Analysis of an Inner-Mounted Permanent Magnet Synchronous Motor for New Energy Vehicles" Energies 15, no. 11: 4074. https://doi.org/10.3390/en15114074
APA StyleGeng, H., Zhang, X., Yan, S., Zhang, Y., Wang, L., Han, Y., & Wang, W. (2022). Magnetic Field Analysis of an Inner-Mounted Permanent Magnet Synchronous Motor for New Energy Vehicles. Energies, 15(11), 4074. https://doi.org/10.3390/en15114074






