An Accurate Evaluation of Switching Impulse Voltages for High-Voltage Tests

Abstract

For assessment of the insulation performance of high-voltage (HV) equipment installed in extra-high-voltage (EHV) systems, switching impulse voltage tests are performed in an HV testing laboratory. The waveform parameters of the switching impulse voltages are defined by peak voltage (U_p), time to crest (T_p), and time to half (T₂) according to IEC 60060-1. In this paper, a new, simplified, and accurate approach used for determination of the waveform parameters of the switching impulse voltages is presented. The formula used in the evaluation of T_p was derived from analytically simulated two-exponential waveforms, where T_p and T₂ are in the ranges of 20 μs to 300 μs and 1000 μs to 4000 μs, respectively. The accuracy of the proposed approach was validated by the waveforms collected from the test waveform data generator (TDG) provided by IEC 61083-2, simulations, and experiments. It is found that the accuracy of the proposed approach is relatively higher than the expressions provided by IEC 60060-1 and previously developed. The proposed method is an alternative and useful approach for evaluating the waveform parameters of the standard switching impulse voltage.

1. Introduction

The main causes of insulation failures in high-voltage equipment are overvoltages due to lightning and switching operations in high-voltage (HV) energy transmission and distribution systems. Therefore, the international standards [1,2,3,4,5] suggest performing impulse voltage tests on HV equipment to confirm its insulation performance. The standard lightning and switching impulse voltages can be generated by a simple resistor and capacitor circuit [6]. Switching overvoltages are caused by switching operations of circuit breakers and disconnecting switches in HV power systems, and the insulation performance of HV equipment under switching overvoltages has still not been completely studied [7,8,9]. Switching overvoltages produce high electrical field stresses with quite a long time period (several milliseconds) on the insulation of the HV equipment and can possibly cause insulation failures. Thus, according to IEC standards [4], the insulation performance of HV equipment operating at a system voltage of not less than 300 kV must be confirmed using a switching impulse voltage test.

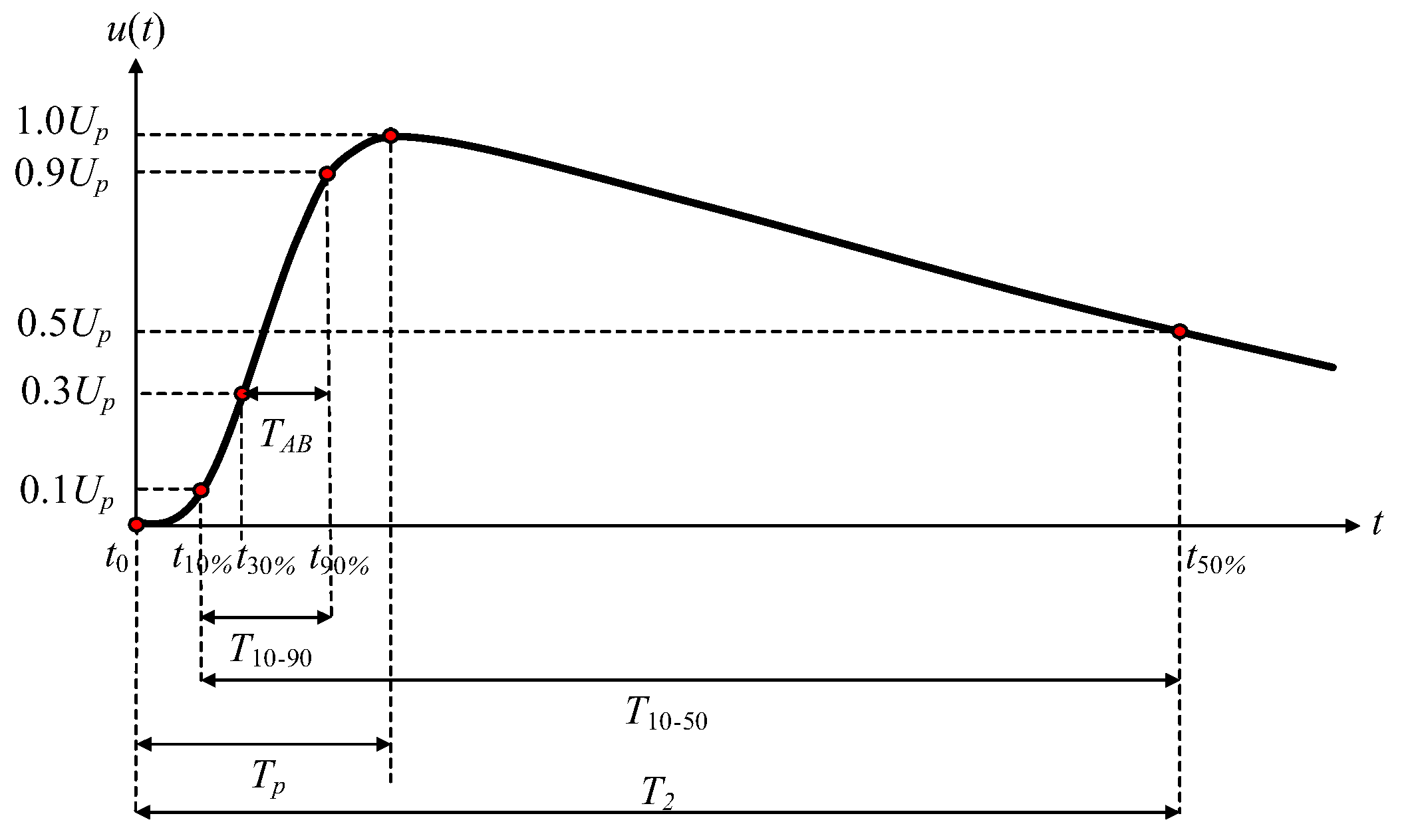
In impulse voltage tests, the software used for the evaluation of the impulse waveform parameters must be assessed for accuracy using the waveform generated by the test data generator (TDG) program attached to IEC 61083-2 [10]. The evaluation of the lightning and switching impulse voltage waveform parameters has been widely studied [11,12,13,14,15,16,17]. In the switching impulse voltage tests, the waveform parameters must be adjusted as per the standard requirements [1,2,3,4,5]. As illustrated in Figure 1, the time to crest (T_p), the time to half (T₂), and the peak voltage (U_p) shall be 250 μs ± 20%, 2500 μs ± 60%, and the specified value depending on the system voltage with a tolerance of ±3%, respectively. T₂ is defined as the duration time from the actual origin time (t₀) to the time (t_50%) at 50% of the peak voltage at the tail part of the waveform. T₂ can be determined by proper search and interpolation algorithms. U_p can be determined by searching for the maximum value for the positive waveform or the minimum value for the negative waveform after the offset voltage is removed from the considered waveform. However, there are some difficulties in determining t₀ and T_p due to noise superimposing on the recorded waveform. In addition, T_p cannot be determined precisely due to noise and a long duration time around the peak voltage. According to the standard [1], T_p can be calculated by Equation (1), where K and T_AB are defined as Equations (2) and (3).

$$T_p=K{T}_{AB}$$

(1)

$$K=2.42-3.08\times {10}^{-3}{T}_{AB}+1.51\times {10}^{-4}{T}_2$$

(2)

$$T_{AB}=t_{90\%}-t_{30\%}$$

(3)

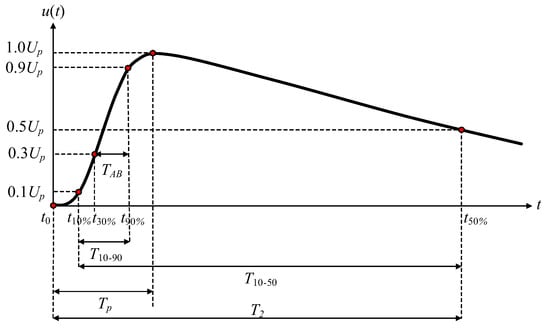
Figure 1. Switching impulse voltage waveform and the waveform parameters.

For determination of T_p, however, it was reported that T_p determined by Equation (1) is accurate in only some cases where the times to crest and the times to half are close to 250 μs and 2500 μs, respectively. There is some research which presents approaches for the determination of the accurate time to crest [16]. The analytical formulas for estimating the waveform parameters T_p, T₂, and U_p were proposed in [16]. T_p is also determined from T_AB and the estimated starting point of the considered waveform. The formulas can estimate the waveforms derived from simulated two-exponential waveforms precisely, but deviations in the parameters are increased in the cases of experimental waveforms. In [17], two-exponential fitting based on a non-linear regression on the waveform data around the crest value was employed to estimate the waveform parameters accurately. Since this method requires software for estimation of the parameters, it is not useful for test engineers for determination of the waveform parameters when compared with the standard and previously developed formulas.

In this paper, a practical approach for the determination of the waveform parameters of the switching impulse voltage was developed. A simple, but relatively accurate approach for the determination of t₀ is proposed. Furthermore, the accurate formula used in the evaluation of T_p was derived from the analytically simulated two-exponential waveforms, where T_p and T₂ are in the ranges of 20 μs to 300 μs and 1000 μs to 4000 μs, respectively. The waveforms collected from the standard [10], simulations and experiments were utilized for verification of the proposed approach. The proposed approach provides relatively high accuracy when compared with those calculated by the standard [1] and the previously developed formula [16]. This paper is organized as follows. Section 1 introduces the problem of evaluation of the waveform parameters of the switching impulse voltages in HV tests and performs the literature review. Section 2 describes an approach for the analytical generation of switching impulse voltages on the basis of the two-exponential function employed for the development of the new expressions. The development of a new and accurate expression for the determination of the waveform parameters is also presented. The proposed expressions and their verification are presented in Section 3. At the end of this paper, the conclusions are addressed.

2. Development of the Approach for Evaluation of the Switching Impulse Voltage Parameters

The new accurate approach for evaluation of the switching impulse voltage parameters is developed from the waveform parameters of the impulse voltage waveforms in the form of a two-exponential function, as given in Equation (4). It is quite straightforward to determine T_p and T₂ from the known τ₁ and τ₂. From Equation (4), T_p can be calculated analytically by Equation (5), but there is no analytical expression of T₂; it can be calculated by Equation (6) using a numerical approach. A simple Newton–Raphson algorithm [18] is an effective method used in this paper.

$$u(t)=U_0\left(e^{-t/{\tau }_2}-e^{-t/{\tau }_1}\right)$$

(4)

$$T_p=\frac{\ln \left({\tau }_2/{\tau }_1\right)}{1/{\tau }_1-1/{\tau }_2}$$

(5)

$$0.5U_0=U_0\left(e^{-T_2/{\tau }_2}-e^{-T_2/{\tau }_1}\right)$$

(6)

However, accurate τ₁ and τ₂ computed from T_p and T₂ are required for the development of the proposed approach. In this section, the effective approach for determination of τ₁ and τ₂ from T_p and T₂ will be presented in Section 2.1, and the analytical formula for the required waveform parameters will be presented in Section 2.2.

2.1. Analytical Generation of Switching Impulse Waveforms

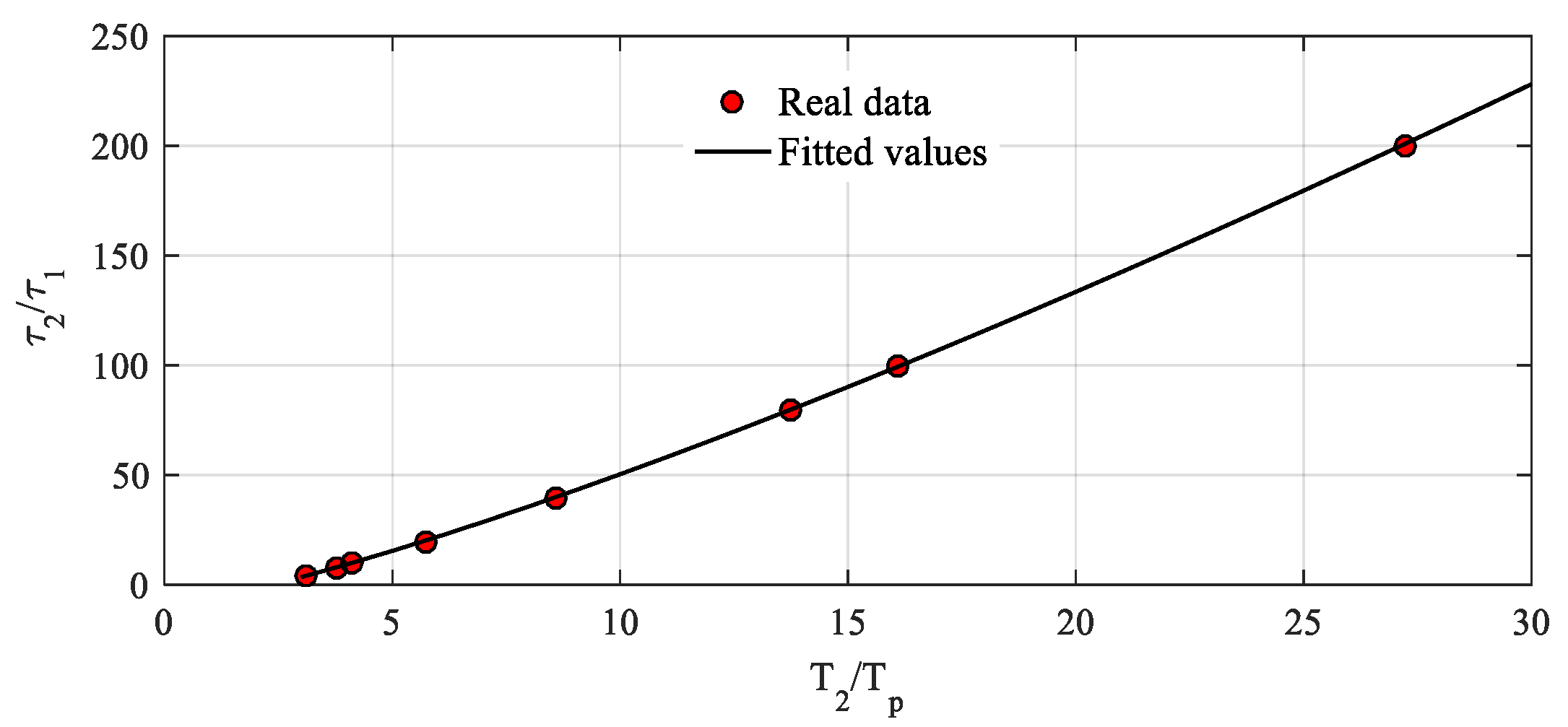
For generation of the accurate waveform in the form of a two-exponential function described by T₂ and T_p, it is necessary to know the accurate time constants of τ₁ and τ₂. In this paper, a time normalization technique was utilized to reduce the number of variables, and the secant method [18] was employed to determine the solution or the required time parameters. It is noticed that the ratio of T₂ to T_p (T₂/T_p) has a monotonic relation with the ratio of τ₂ to τ₁ (τ₂/τ₁), as expressed in Figure 2, of which the range covers T_p of 20 μs to 300 μs and T₂ of 1000 μs to 4000 μs. Therefore, the relation of T₂/T_p and τ₂/τ₁ can be represented as functions in Equations (7) and (8).

$$T_2/T_p=f({\tau }_2/{\tau }_1)$$

(7)

$${\tau }_2/{\tau }_1=f^{-1}(T_2/T_p)=g(T_2/T_p)$$

(8)

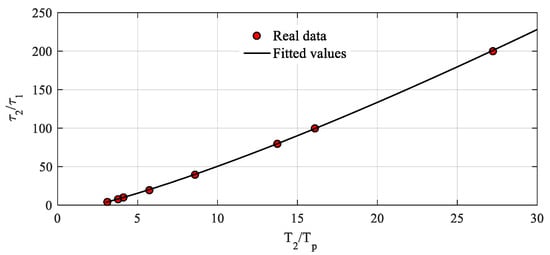
Figure 2. τ₂/τ₁ as the function of T₂/T_p and the fitting curve.

In this paper, the normalized base was selected to be τ₁, and all normalized time parameters (τ_1n, τ_2n, T_2n, and T_pn) are given by Equation (9).

$$\begin{array}{l}{\tau }_{1n}={\tau }_1/{\tau }_1=1\\ {\tau }_{2n}={\tau }_2/{\tau }_1\\ T_{2n}=T_2/{\tau }_1\\ T_{pn}=T_p/{\tau }_1\end{array}$$

(9)

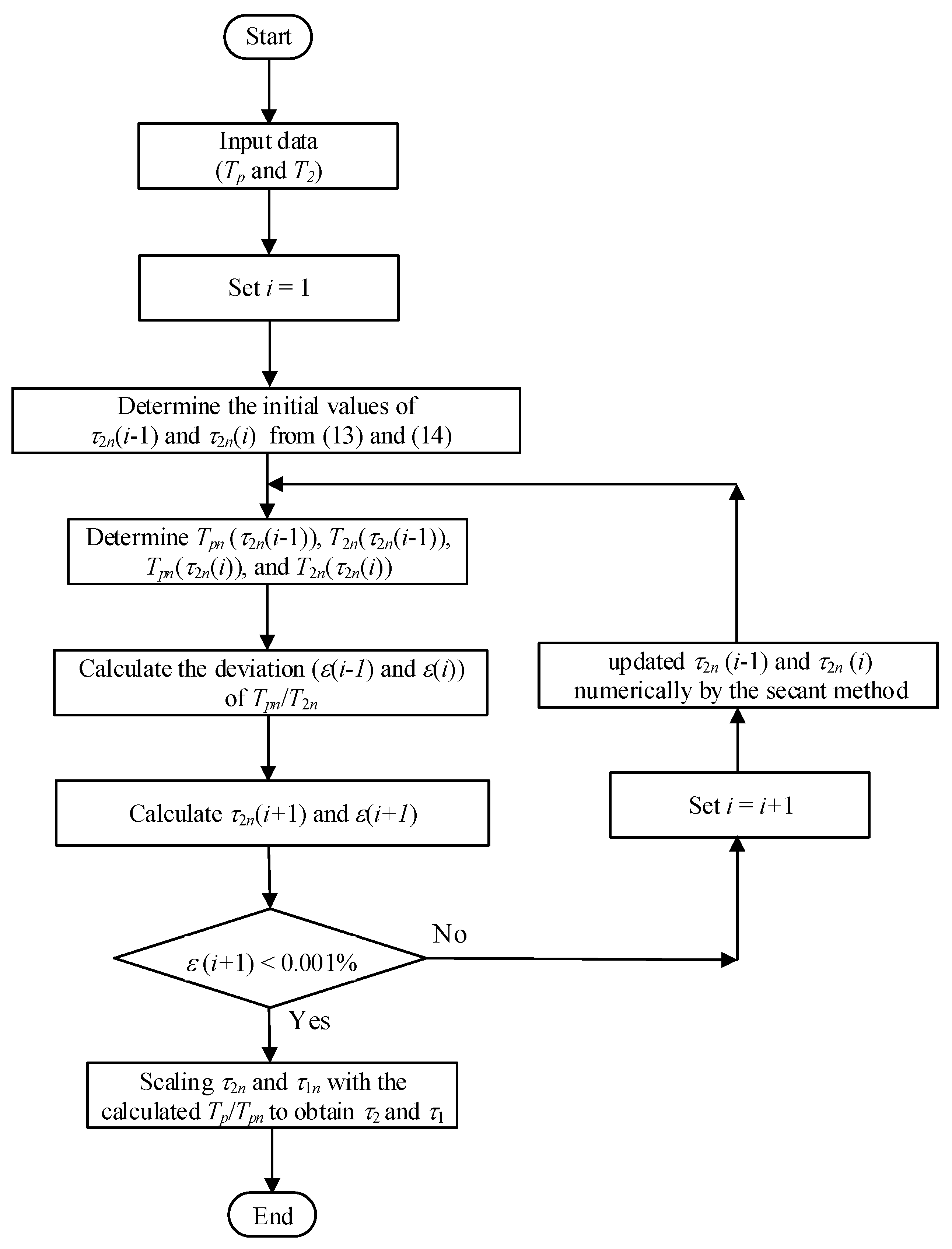
The procedure for determination of τ₁ and τ₂ from the input variable of T₂ and T_p is presented in the flowchart shown in Figure 3.

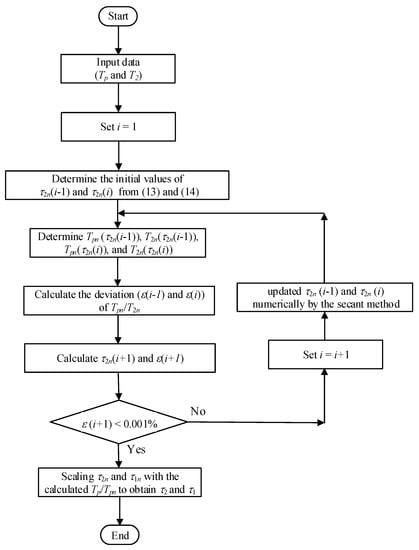
Figure 3. Algorithm used for generation of the impulse switching waveform with the specified T₂ and T_p.

From Equation (10), the secant method is employed to find the solutions of τ_2n from T_pn/T_2n, which equals T_p/T₂. The goal of the secant method is to determine τ_2n where the deviation (ε) of T_pn/T_2n is minimized, and the deviation goal was set to be 0.001%. Equation (11) can be utilized to calculate the deviation ε(i) of the solution of the ith iteration, where T_2n(τ_2n(i)) is the normalized parameter calculated by the Newton–Raphson algorithm [18] at τ_2n(i), and T_pn(τ_2n(i)) is calculated by the analytical formula expressed by Equation (5). From the calculated ε(i), (τ_2n(i + 1)) is calculated by Equation (12). τ_2n is calculated repetitively until the deviation goal is reached.

$$T_2/T_p=T_{2n}/T_{pn}=f({\tau }_2/{\tau }_1)=f({\tau }_{2n})$$

(10)

$$\epsilon (i)=\frac{\frac{T_{2n}({\tau }_{2n}(i))}{T_{pn}({\tau }_{2n}(i))}-\frac{T_2}{T_p}}{\frac{T_2}{T_p}}$$

(11)

$${\tau }_{2n}(i+1)={\tau }_{2n}(i)-\frac{\epsilon (i)\left({\tau }_{2n}(i)-{\tau }_{2n}(i-1)\right)}{\epsilon (i)-\epsilon (i-1)}$$

(12)

The secant method requires the initial values of τ_2n(0) and τ_2n(1). From the relation of T₂/T_p and τ₂/τ₁ in Figure 3, the initial values are set as given by Equations (13) and (14).

$${\tau }_{2n}(0)=8\left(T_2/T_p\right)-24$$

(13)

$${\tau }_{2n}(1)=1.01{\tau }_{2n}(0)$$

(14)

With the initial values in Equations (13) and (14), only two or three iterations are required to reach the deviation goal. Finally, τ₁ and τ₂ can be determined from Equation (9) with the known T_p and T_pn, which can be calculated by Equation (5). Using the proposed method for the determination of τ₁ and τ₂ from the specified T₂ and T_p, the switching impulse voltage waveforms with T_p from 10 μs to 300 μs and T₂ from 1000 μs to 4000 μs can be precisely generated analytically.

From the calculated τ₂/τ₁ determined by T₂/T_p using the proposed method, a numerical curve fitting based on a Levenberg–Marquardt algorithm [19] was employed and the formula of the fitting curve given in Equation (15) was obtained. It is noted that the formula can be used for the initial values in the secant method. In fact, the formula is quite accurate and the maximum deviation of the value from the formula and the actual value is less than 0.5%. However, if more accurate results are required, it is recommended to utilize the proposed method, as it is used in the paper with a deviation of less than 0.001%.

$${\tau }_{2n}(0)=3.389{\left(\frac{T_2}{T_p}\right)}^{1.25}-9.89$$

(15)

2.2. The New Approach for Evaluation of the Switching Impulse Voltage Parameters

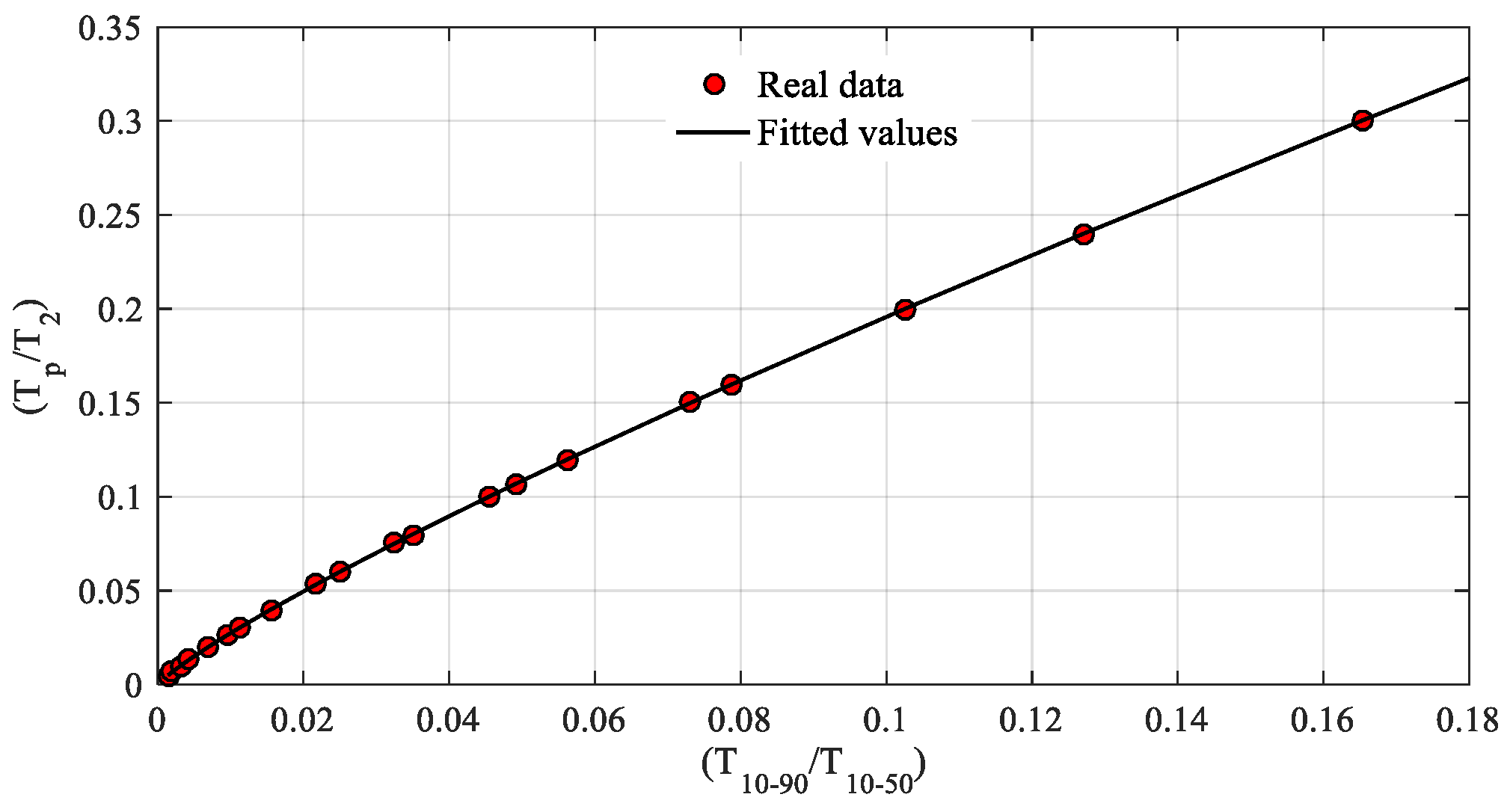
In the proposed method, analytical switching impulse voltage waveforms generated by the approach presented in Section 2.1 were utilized for development of the formula used for time to crest estimation. The time parameters, i.e., t_10%, t_90%, and t_50% shown in Figure 1, are calculated by the Newton–Raphson method due to no analytical solution, and T_p and T₂ are considered in the ranges of 20 μs to 300 μs and 1000 μs to 4000 μs, respectively, which cover the waveform parameters used in the practical tests. t₀ is zero. It is found that T_p/T₂ has a monotonic relation with T_10–50/T_10–90, as shown in Figure 4, and parameters used for calculation of such proportions can be calculated by Equations (16)–(18).

$$T_2=t_{50\%}-t_0$$

(16)

$$T_{10-90}=t_{90\%}-t_{10\%}$$

(17)

$$T_{10-50}=t_{50\%}-t_{10\%}$$

(18)

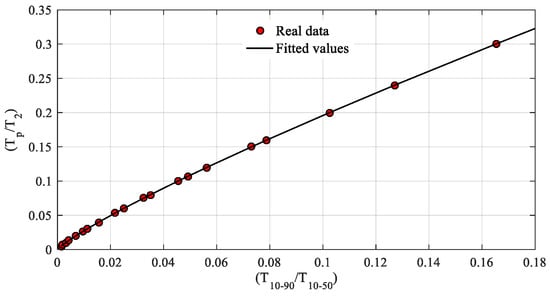
Figure 4. Real data and fitted values of T_p/T₂ versus T_10–50/T_10–90.

From the data of T_p/T₂ and T_10–50/T_10–90, the fitting curve can be determined by a non-linear regression based on a Levenberg–Marquardt algorithm [19]. The expression of the fitted curve is given as Equation (19). From Equation (19) and the required T₂, T_p can be calculated by Equation (20). U_p can also be determined by searching for the crest voltage of the considered waveform. It is noted that the approach for the crest voltage determination is the same as those of the standard and previously developed methods [1,16].

$$\frac{T_p}{T_2}=h\left(\frac{T_{10-90}}{T_{10-50}}\right)=1.389{\left(\frac{T_{10-90}}{T_{10-50}}\right)}^{0.8506}-2.537\times {10}^{-4}$$

(19)

$$T_p=h\left(\frac{T_{10-90}}{T_{10-50}}\right)T_2$$

(20)

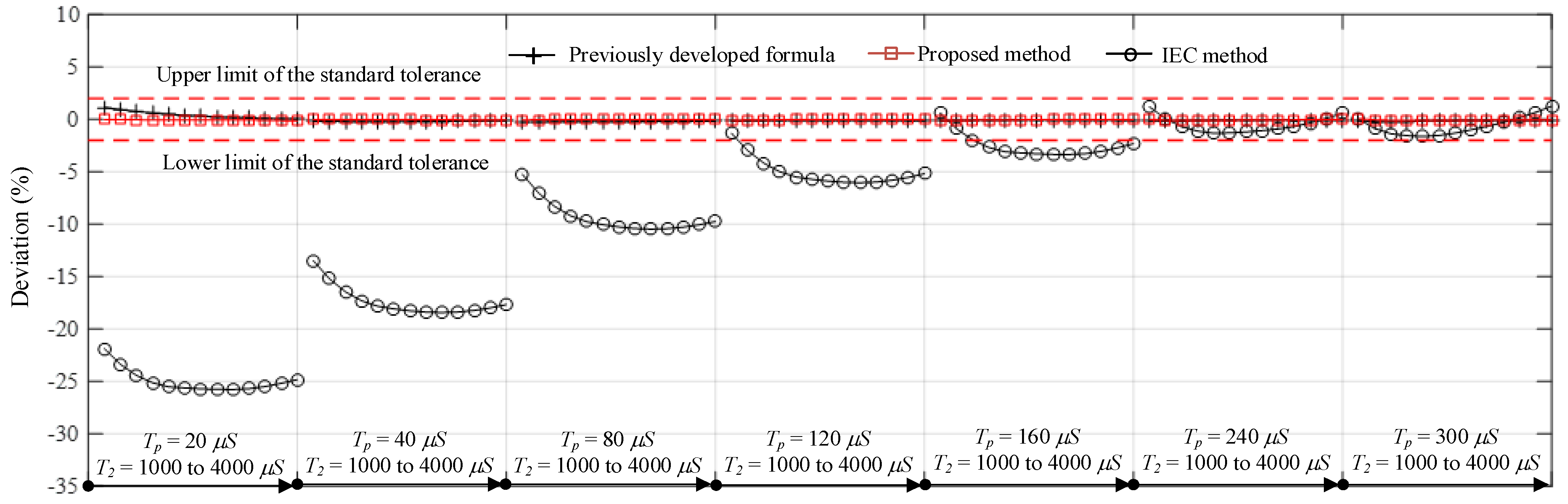
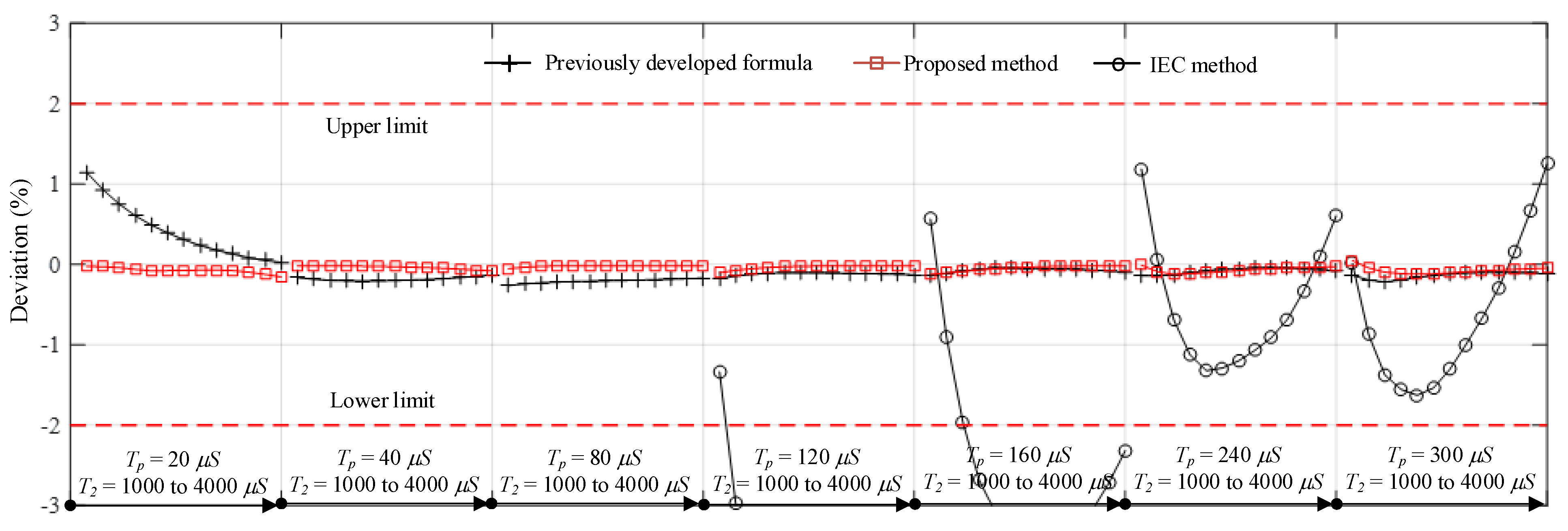
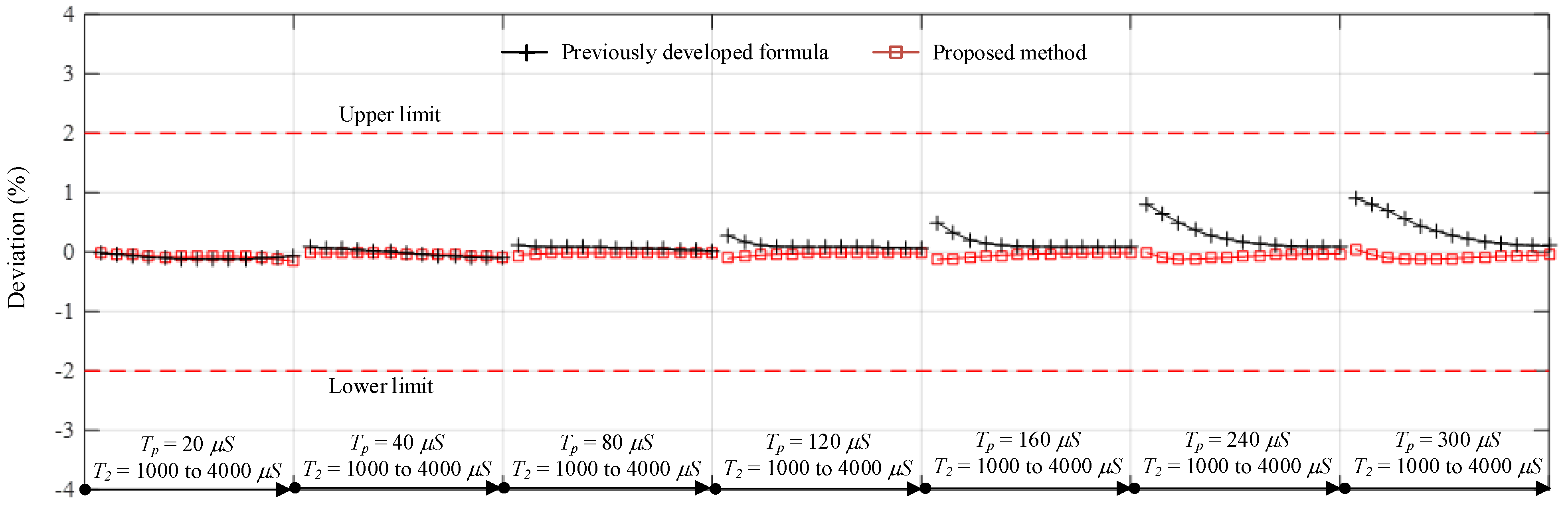
Comparisons of the times to crest computed by the proposed, standard, and previously developed formulas [1,16] are presented in Figure 5 and Figure 6. It is noticed that the proposed formula provides the best accuracy with a maximum deviation of 0.156%, whereas the standard and previously developed formulas [1,16] provide maximum deviations of 25.778% and 1.147%, respectively. From the results of all test cases, the previously developed and proposed formula can provide T_p within the acceptable limits defined by the standard [10]. The standard formula is accurate in cases of the waveform with time to crest close to the standard time to peak (250 μs). The shorter the T_p is, the higher the deviation is. Additionally, as shown in Figure 7 the proposed approach for the T₂ determination also provides promising accuracy when it is compared with the previously developed formula [1]. The maximum deviations of the proposed and previously developed formulas are 0.165% and 0.98%, respectively.

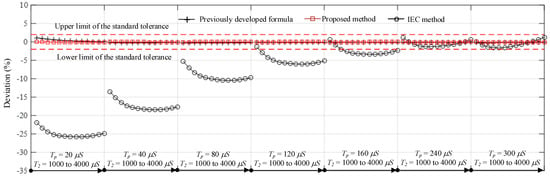
Figure 5. Comparisons of the computed times to crest by the proposed, standard, and previously developed formulas [1,16] and the standard tolerance [10].

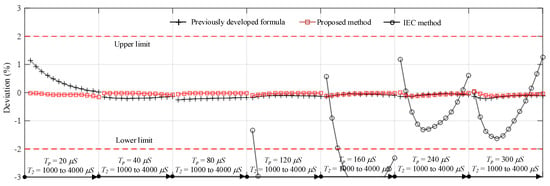
Figure 6. Zoom-in results of Figure 5.

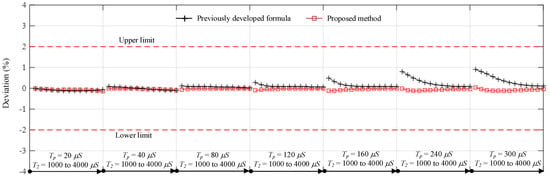
Figure 7. Comparisons of the computed T₂ by the proposed and previously developed formulas [16] and the standard tolerance [10].

3. Verification of the Proposed Method

By using the presented approach for determination of the waveform parameters, the offset voltage is removed and the time parameters are determined. t₀ can be estimated by searching for the time at which the voltage is less than 0.1% of the peak voltage, and the approach for searching starts from the peak voltage in reversed order. The other time parameters, i.e., t_10%, t_90%, and t_50% shown in Figure 1, are calculated by the Newton–Raphson method due to no analytical solutions. Then, using such time parameters, T_10–50/T_10–90 is calculated by Equations (17) and (18) and substituted in Equation (19) to obtain T_p/T₂. Eventually, T₂ is calculated by Equation (16), T_p is determined from T_p/T₂ with the known T₂, and U_p is determined by the crest value of the considered waveform.

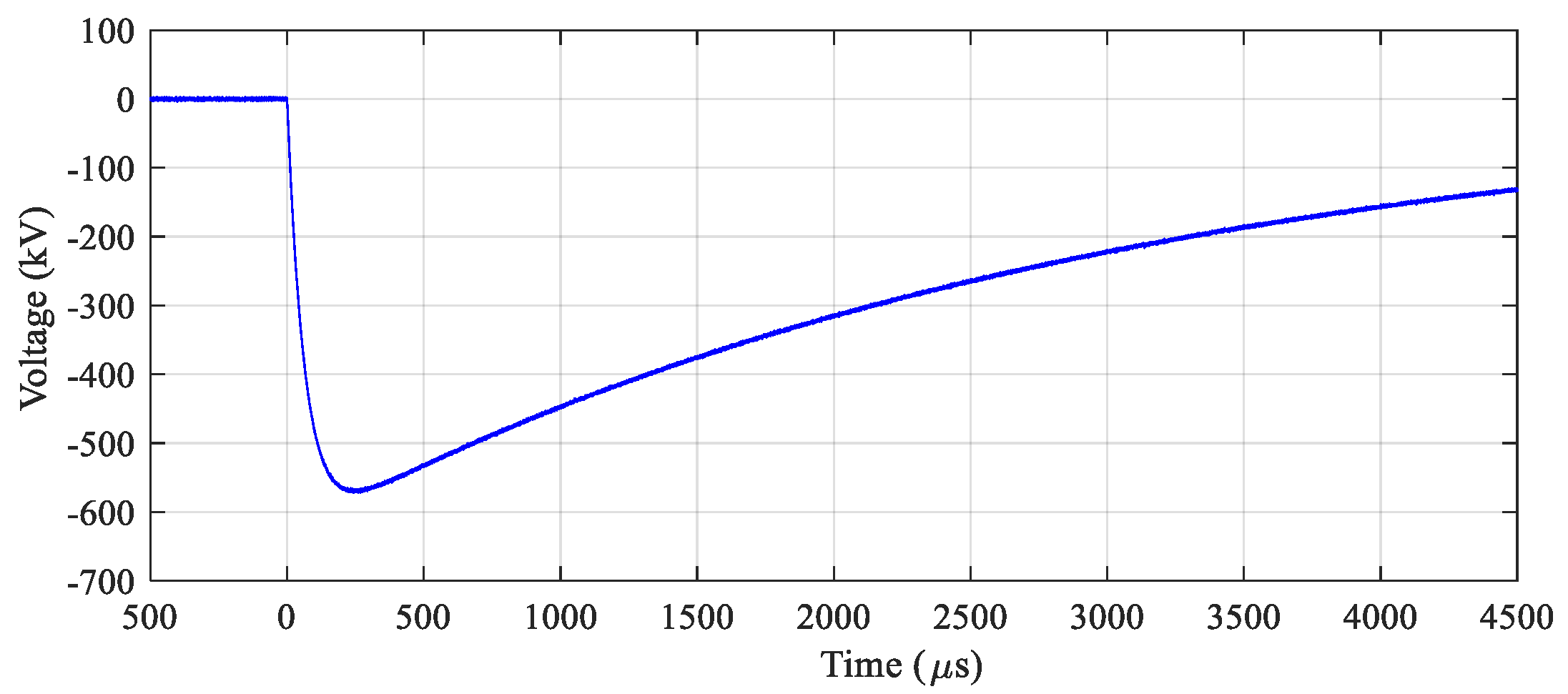
The proposed method is verified by the waveform parameter evaluation of waveforms composed of four groups collected from (1) analytically simulated two-exponential waveforms used in the method development; (2) IEC 61083-2 [10], composed of SI-A1 to SI-A3 (simulation waveforms) and SI-M1 and SI-M2 (waveforms measured in experiments); (3) simulations with and without additional noise signal (SI-X1 and SI-X2), and (4) experiments (SI-X3 and SI-X4). The example experimental waveform is presented in Figure 8. Additionally, the accuracy of the proposed method is compared with those of the standard and previously developed methods [1,16] as expressed in Table 1 and Table 2. It is to be mentioned that the reference values in the cases of SI-X3 and SI-X4 have been collected from commercial software [20]. The approved measuring system, composed of a 1500 kV voltage divider, a measuring cable, and a 12-bit digital recorder, was utilized to measure the switching impulse voltage in the experiments.

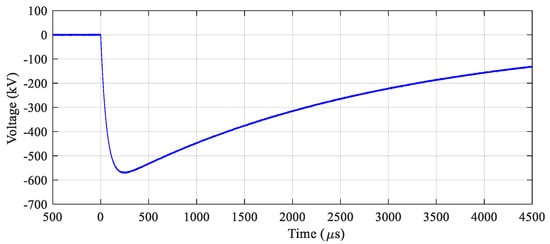
Figure 8. Switching impulse voltage waveform in the Case SI-X3.

Table 1. Reference and calculated values, acceptable limits, and deviations of T_p.

Case	Reference Values (Acceptable Limits)	Value from the Standard Formula (Deviations)	Value from the Formula in [16] (Deviations)	Value from Proposed Method (Deviations)
SI-A1	250.7 μs (±2%)	248.703 μs (−0.797%)	251.630 μs (+0.371%)	251.621 μs (+0.367%)
SI-A2	19.89 μs (±2%)	15.300 μs (−23.076%)	20.232 μs (+1.720%)	20.051 μs (+0.809%)
SI-A3	43.08 μs (±2%)	35.999 μs (−16.437%)	43.214 μs (+0.310%)	43.252 μs (+0.398%)
SI-M1	186.6 μs (±5%)	177.619 μs (−4.81%)	170.227 μs (−8.775%)	189.085 μs (+1.332%)
SI-M2	218.0 μs (±5%)	221.943 μs (+1.809%)	225.264 μs (+3.332%)	220.781 μs (+1.276%)
SI-X1	250.00 μs (±2%)	246.908 μs (−1.237%)	249.862 μs (−0.056%)	249.842 μs (−0.063%)
SI-X2	250.00 μs (±5%)	251.779 μs (+0.711%)	254.712 μs (+1.885%)	253.626 μs (+1.450%)
SI-X3	247.35 μs (±5%)	250.087 μs (+1.105%)	253.221 μs (+2.372%)	252.291 μs (+1.996%)
SI-X4	269.44 μs (±5%)	273.007 μs (+1.324%)	276.028 μs (+2.445%)	271.913 μs (+1.289%)

Table 2. Reference and calculated values, acceptable limits, and deviations of T₂ and U_p.

Case	Reference Values (Acceptable Limits)		Value from Proposed Method (Deviations)
	T2	Up	T2	Up
SI-A1	2512.00 μs (±2%)	950.28 kV (±0.1%)	2511.50 μs (−0.0199%)	950.23 kV (−0.005%)
SI-A2	1321.00 μs (±2%)	987.67 V (±0.1%)	1320.75 μs (−0.0189%)	987.67 V (+0.001%)
SI-A3	3987.00 μs (±2%)	99.219 kV (±0.1%)	3987.05 μs (+0.0013%)	99.219 kV (0.0000%)
SI-M1	655.00 μs (±2%)	−590.70 V (±0.5%)	655.335 μs (+0.0512%)	−590.70 V (+0.0799%)
SI-M2	2407.00 μs (±2%)	3.680 kV (±0.5%)	2396.20 μs (−0.4487%)	3.680 kV (−0.0027%)
SI-X1	2500.00 μs (±2%)	521.582 kV (±0.1%)	2499.90 μs (−0.0039%)	521.582 kV (0.0000%)
SI-X2	2500.00 μs (±2%)	521.988 kV (±0.5%)	2465.06 μs (−1.3978%)	521.988 kV (+0.4754%)
SI-X3	2293.37 μs (±2%)	−569.982 kV (±0.5%)	2256.80 μs (−1.5948%)	−569.982 kV (+0.4023%)
SI-X4	3775.51 μs (±2%)	453.788 kV (±0.5%)	3784.21 μs (−0.9843%)	449.321 kV (+0.2304%)

From the test results of the evaluation of the waveform parameters, it is clear that the accuracy of the proposed method is relatively higher than that of the standard and previously developed methods. All waveform parameters determined by the proposed method are within the standard tolerances [1,10]. The deviations of T_p in the cases of the waveforms, simulated by two-exponential function, provided by the standard, additional simulation with and without noise signal, and collected from the experiments are within 0.156%, 1.34%, 1.45%, and 2.00%, respectively. The deviations of T₂ of the waveforms from simulation and measured experimentally are within 0.06% and 1.60%, respectively. In cases of the waveforms from simulation and measured experimentally, the deviations of U_p are within 0.005% and 0.48%, respectively.