Abstract
An autonomous microgrid is often formed by incorporating distributed generators into the distribution system. However, distributed generators have less inertia compared to traditional synchronous generators, and can cause the system frequency to become unstable. Additionally, as more clusters are integrated into the distribution microgrid, frequency instability increases. To resolve frequency instability in the microgrid cluster, this study proposes a supercapacitor control approach. The microgrid consists of several clusters which integrate wind power generators, solar PV, STP, fuel cells, aqua electrolyzers, and diesel generators. Initially, a small signal model is developed to facilitate the control design. A fractional-order supercapacitor controller is augmented with the developed small-signal model to stabilize the frequency of the microgrid. Furthermore, the controller parameters are optimized to guarantee robust controller performance. The proposed fractional-order supercapacitor controller provides more degrees of freedom compared to the conventional controller. Time-domain simulations were carried out considering several real-time scenarios to test the performance of the proposed controller. We observed that the presented approach is capable of stabilizing the system frequency in all cases. Furthermore, the proposed approach outperforms existing approaches in stabilizing the frequency of the microgrid cluster.
1. Introduction
Nowadays, more renewable energy sources (RESs) are integrated with the power distribution system with reduced inertia. A paradigm shift in conventional power systems is being observed due to the need to integrate several distributed generators and energy storage devices, such as solar photovoltaic (PV), solar thermal power (STP), wind systems, fuel cells, and battery power. For instance, wind power generation systems have very limited inertia compared to conventional synchronous generators, while solar PV systems have no inertia [1]. Thus, distribution networks face difficulties in supporting power system frequency during faults in case of large-scale integration of RESs such as distributed generators (DGs) [2]. Another challenge is that the RESs have intermittency in power generation, further exasperating frequency control [3].
Distribution networks are experiencing a paradigm shift due to the integration of RESs to form microgrids. The concept of microgrids has evolved to facilitate the integration of fuel cells, aqua electrolyzers, diesel generators, concentrated solar power, and energy storage devices such as batteries and supercapacitors [4]. In microgrids, several components are integrated with interfaced power electronic converters. This reduces system inertia, and frequency control becomes difficult. Several approaches have been proposed in the literature to reduce the frequency excursion, including the auxiliary load frequency (LFC) control methodology, the inertia emulation technique, the deloading technique, the droop strategy, and energy storage-based techniques [5,6,7]. The frequency stability improvement of an islanded microgrid incorporating RESs and electric vehicles (EVs) is proposed in [8], with linear matrix inequlity (LMI) techniques considering both communication latency and delay effect. In [9], a fuzzy tilt-integral-derivative controller is introduced to reduce the frequency deviation for microgrids incorporating several energy storage devices. However, the proposed controller shows a slow response due to the complex fuzzy tuning approach. Frequency control via charging station operators [10] and the droop control approach [11,12] have been proposed for microgrids. Nonetheless, poor transient performance, ignoring load dynamics, lack of black startup capability, poor distribution network performance, inability to provide accurate power-sharing with output impedance uncertainties, unsuitability for nonlinear loads, and inability to impose a fixed system frequency are all disadvantages of the droop control method that limit its applicability for modern power systems [13,14]. Reference [15] provides a thorough analysis of various load frequency control (LFC) structures in different power system configurations. An overview of a renewable energy-based power system is provided with a need for the development of LFC. In single-area, multi-area, and multi-stage power system topologies, various LFC controllers were enumerated. An H-infinity LFC control strategy for DG-integrated systems was developed considering intermittent demand side resources [16]. This approach improved the critical stability and robust performance of the system. Due to the lack of a stiff AC grid source, an islanded microgrid frequently faces particular difficulties with regard to voltage, current, frequency regulation, power flow control, and power-sharing. A virtual impedance-based droop system was developed in [17] to demonstrate power-sharing in a isolating low voltage AC microgrid made up of three parallel inverters. However, droop control strategy continues to face bus voltage deviations. Thus, the concept of adaptive droop control approach has been evolved to mitigate the problems of the conventional droop approach in microgrids [18].
The working principle of a synchronous generator could be imitated by employing the virtual synchronous generator (VSG) concept [19,20]. However, VSG approaches use simple frequency regulation without considering non-error frequency regulation capability. Therefore, the frequency control of the microgrid is beyond the offset limit during complex operating conditions, including large microgrid load interruptions [21]. VSG-based centralized control approaches have been presented in [22,23,24] to provide the power setting value of individual DGs. Although these approaches help to reduce frequency deviation and achieve appropriate power-sharing, they depend heavily on communication links, which reduces the overall reliability of microgrid frequency control. A robust control approach for secondary frequency control is presented [25]. Again, this approach is a centralized one which has less reliability due to dependency on communication links. In order to improve reliability and protect the microgrid frequency control against single-point failure, decentralized and distributed approaches have been introduced [26,27,28]. However, these approaches may not provide simultaneous frequency control and power-sharing. In a nutshell, most of the control techniques without any auxiliary device have limitations in terms of frequency control. Therefore, many auxiliary devices are installed and controlled in a microgrid for frequency control.
Microgrids use many auxiliary devices for frequency control, such as superconducting magnetic energy storage (SMES), batteries, flywheel energy storage, and variable frequency drivers. In [29], SMES is proposed as a viable option for a low-inertia microgrid. A virtual inertia control loop was implemented using the conventional derivative approach. However, the design of feedback and gains in proportion were not discussed in this work. Moreover, it is a costly solution to keep the SMES temperature below the critical value to achieve zero loss in normal conditions. Doubly fed induction generator (DFIG)-based low-inertia wind systems can benefit from another energy storage option, the battery, as presented in [30]. Due to DFIG system disturbances and battery voltage dropouts, an active power exchange was scheduled to reduce the frequency deviation. A flywheel energy storage approach is presented in [31] with a low sampling resolution controller, which can provide frequency support for renewable energy integrated microgrid. However, the proposed technique requires communication links among all sources and loads, reducing its reliability. Due to the low power density, most of the energy storage has limited applications in frequency control of the microgrids. On the other hand, the supercapacitor has a very high active power density, and can ramp up and or ramp down output power promptly to minimize frequency excursion.
It is worth mentioning that most of the proposed approaches utilize a conventional proportional-integral-derivative (PID) controller, which has fewer degrees of freedom. On the other hand, a fractional-order controller can provide more degrees of freedom due to the option to choose any order with fractional numbers [32,33]. By incorporating additional real parameters, fractional-order controllers outperform conventional PI controllers in terms of system performance [34]. However, parameter tuning for a factional order controller is difficult compared to a conventional controller. The artificial bee colony (ABC) [35] technique has been presented to tune fractional-order controller parameters, which is complex in objective function evaluation and slow to convergence. From this critical discussion, it can be concluded that there is a research gap in the frequency control of microgrid clusters with fractional order supercapacitor approaches. To bridge this research gap, this study develops efficient supercapacitor control techniques for microgrid clusters. The advantages of the proposed controller include more degrees of freedom, quick power balance, improvements in overshoot, undershoot, and setting time, less frequency deviation, and robustness against uncertainties. A complete mathematical model for the microgrid clusters is developed to facilitate parameter tuning with an optimization approach. Several case studies are considered, including small and large load disturbances, repeated load changes, and uncertain renewable energy generation. The proposed controller is compared with conventional approaches, demonstrating better performance with the proposed approach.
Following is a breakdown of the manuscript. System dynamics, including RES, energy storage systems (ESS), fuel cells, and aqua electrolysers are detailed in Section 2. Small-signal modeling is presented in Section 3. Section 4 discusses the fractional-order supercapacitor controller design technique. Section 5 focuses on simulation results. Finally, the findings of this study are summarized in Section 6.
2. Conceptual Microgrid Cluster with Renewable Energy
A microgrid can be described as a link between a variety of distributed energy resources and a variety of distributed loads. While each microgrid has its own unique set of distributed energy resources, the majority of the power integrated in the microgrid system is generated by solar power, wind power, diesel generators, fuel cells, and energy storage systems (ESS). A conceptual diagram of a microgrid cluster is shown in Figure 1.
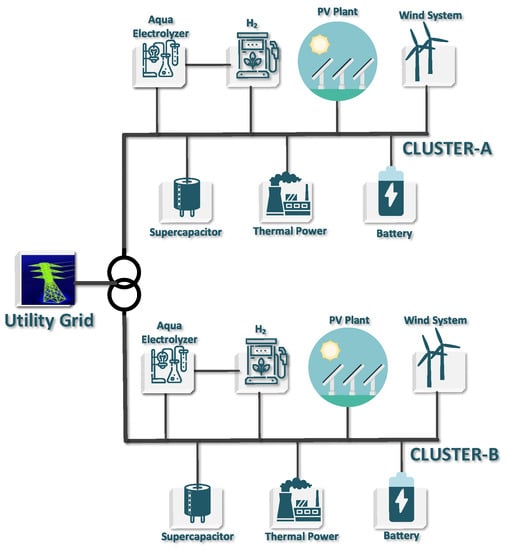
Figure 1.
Conceptual diagram of microgrid cluster.
The conceptual AC microgrid has two clusters, each having solar PV systems, wind systems, energy storage devices, aqua electrolysers, fuel cells, concentrated solar power, etc. The main objective of this study is to improve the frequency stability of the microgrid during any disturbances. Thus, a simplified model with two clusters is considered. However, the proposed strategy of frequency stabilization can work for any number of clusters. There is a control and monitoring center that keeps track of the measured frequencies and tie-line signals. Due to low inertia, the system is expected to support inertia via the control center, which communicates with energy storage devices in both clusters. Decentralized control, primary control, and droop control can be used in the absence of a communication link. Two major renewable energy sources, namely, wind and solar PV, are heavily integrated in both the clusters to emulate a low-inertia system. The output power of a wind turbine primarily depends upon four variables [36,37], which are provided in Equation (1) below.
Here, → air density, A→ swept area of the blade, → power coefficient, and → wind velocity. The swept area of the blade can be calculated using the diameters of the blade. The power coefficient, , depends on two variables, the tip ratio and pitch angle , expressed as Equation (2):
Here, the wind speed is , which depends on the four parameters shown in Equation (3) [38]:
where → the velocity of primary wind, → the component of gust wind, → the component of ramp wind, and → the component of noise wind.
Solar photovoltaic cells directly convert solar radiation into usable power. This is one of the primary power generation methods without any rotating parts; hence, no mechanical loss can occur. However, the efficiency of conversion of solar radiation through PV panels is low, around 20 to 30%. The power output of PV depends on four variables:
- Direct solar irradiance conversion efficiency
- Total area of the panels
- Irradiation of the sun
- Weather temperature
A fuel cell converts chemical energy into electrical energy. It uses hydrogen as chemical fuel, and electricity and water are produced as the byproduct of the reaction. Fuel cells are considered a promising future option because of their very low impact on the environment, highly efficient electric power conversion, and the high energy density of hydrogen.
3. Small Signal Modeling of Microgrid Clusters
3.1. Aqua Electrolysers
An aqua Electrolyser uses power from wind turbines and solar PV for electrolysis, producing hydrogen gas. This produced hydrogen is collected in a storage tank. The transfer function of an aqua electrolyser is
where and are the gain and time constant of the aqua electrolyser, respectively.
3.2. Diesel Engines
A diesel engine uses fossil fuel to produce mechanical energy that rotates a synchronous machine to generate electricity. The electrical and mechanical power output and fuel consumption rate of the engine depends on the specific model. The first-order simplest transfer function can be expressed as
where and are the gain and time constant of the diesel power generator, respectively.
3.3. Batteries
Among possible energy storage devices, batteries are most widely used for minimizing fluctuation in the microgrid. One important feature of a battery is that it has high energy density. In other words, a battery can absorb/supply power for a long time. Thus, battery systems are heavily integrated with the microgrid to balance active power. In general, a bidirectional converter is used with battery storage systems. Complex modeling and state-of-charge (SoC) estimation for batteries are available in the literature [4]. However, this study considers the simplest first-order model for the battery transfer function provided below. It is worth mentioning that batteries cannot ramp the power output up or down promptly, and are thus not a suitable option to support system frequency due to their practical limitations. Thus, in this study, a novel fractional-order supercapacitor approach is presented, which is described in the next section.
where and are the gain and time constant of the battery, respectively.
3.4. Fuel Cells
Energy from hydrogen or any other fuel can be converted directly into electricity using fuel cells (FCs). An anode, cathode, and electrolyte membrane make up a fuel cell. Hydrogen is used at the anode and oxygen at the cathode to power a typical fuel cell’s reaction. Electrons and protons are separated from each other by a catalyst at the anode location. Porous membranes allow protons to pass through, while electrons are forced through a circuit, generating an electrical current. Water molecules are formed at the cathode by combining protons, electrons, and oxygen. Fuel cells are extremely reliable and silent, because there are no moving parts. For frequency analysis in the microgrid, the transfer function of an FC is provided below.
where and are the gain and time constant of the fuel cell, respectively.
3.5. Wind Power
AC microgrids facilitate the integration of wind power generators, because it is distributed in nature. Increased renewable energy, less reliance on diesel generator backup power, and longer battery life are just a few of the many advantages of adding small wind turbines to microgrids. A first-order lag is used to model the wind power generation system microgrid as below:
where and are the gain and time constant of the wind turbine, respectively.
3.6. Solar PV
A solar photovoltaic system consists of several solar cells that are connected in series and parallel to create the desired voltage and current. Solar PV cells have nonlinear current–voltage properties. Solar insolation and ambient temperature both influence the power output of a solar panel.
where represents the packing factor, which has values between 0.9 to 0.95, A is the solar panel area in , is the solar energy insolation in kW/m, is the ambient temperature in degrees Celsius, and is the percentage efficiency of the solar panel. In general, maximum power point tracking (MPPT) algorithms are employed in PV systems to harness maximum power during adverse atmospheric conditions, including partial shading [39]. The small-signal model transfer function for a solar PV system can be derived by neglecting several non-linearities, as below [40]:
3.7. Solar Thermal Power Plant
Power plants that generate electricity by raising a fluid’s temperature using solar radiation are known as solar thermal power plants. The heat from this fluid is then transferred to water, resulting in the formation of steam that has been heated to an extremely high temperature. Turbines in the power plant begin to rotate, and this motion is then converted into electrical energy by a generator. Instead of burning fossil fuels to generate electricity, this method heats steam instead of using sunlight to eliminate the need for that step in the production process. The sun’s rays are focused on a single point by solar collectors, which are used in these systems to achieve the necessary high temperatures. The following small-signal model is used for solar thermal power plants:
where , , , and are the solar gain, solar time constant, thermal gain, and thermal time constant, respectively.
3.8. Integrated Small-Signal Modeling
This subsection describes the process of developing integrated small-signal modeling of the microgrid clusters. Connecting various energy sources into a hybrid system is essential in distributed generation for power security. The small-signal model of several energy sources and components have been presented in the previous subsections. Those models are systematically connected together to form a complete model of the microgrid clusters. Although clusters are generally very close to each other, it is important to connect them through the tie-line. A control area is assumed for each cluster. Tie-line bias is a microgrid system control characteristic that determines how much a particular area of an interconnected system should respond to system frequency variations. Tying the clusters together can serve as a backup power supply in the event of a power outage as well. An area’s frequency can deviate if there is an imbalance between generated power and load demand.
The representation of the tie-line for connecting the two clusters is shown in Figure 2. The tie-line power deviation can be expressed in terms of the frequency deviation:
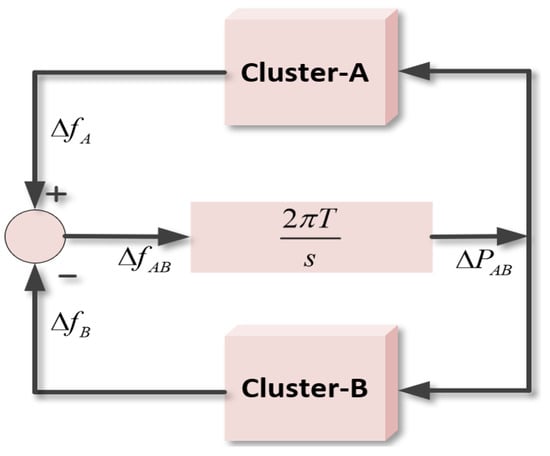
Figure 2.
Tie-line modeling for microgrid clusters.
Here, is the tie-line power deviation, is the cluster A frequency deviation, and is the cluster B frequency deviation. Simplifying and using Laplace transformation, the transfer function for the tie-line is derived as below:
Finally, from the presented small-signal equations, the integrated small-signal model of the microgrid clusters is developed as shown in Figure 3. The next section provides details of the fractional-order supercapacitor controller.
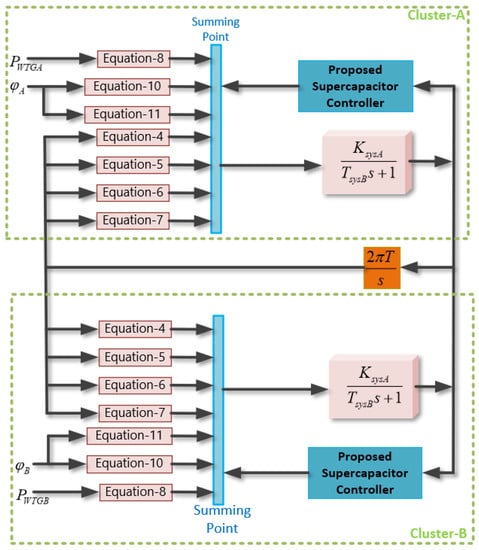
Figure 3.
Control diagram for microgrid clusters.
4. Fractional Order Supercapacitor Controller
4.1. Supercapacitor
A supercapacitor energy storage system is examined in this research for microgrid frequency stabilization. A series-parallel combination of supercapacitor modules can be used to achieve the desired current and voltage. For supercapacitor modeling, an impedance can be connected in series with a state of charge (SoC)-dependent voltage source.
Different fabrication technologies, including lithium-ion, lead–acid, hybrid capacitor, double-layer capacitor, and more, can influence the parameters of supercapacitors [41,42]. From the generalized model of the supercapacitor, the following equation can be derived:
where , , , and Z are the output voltage, internal voltage, supercapacitor current, and impedance, respectively. Several complex models to calculate the SoC of supercapacitors are available in the literature [43,44]; however, the simplest is provided by the following equation:
where and are the supercapacitor’s nominal capacity defined by the manufacturer and the initial state of charge, respectively. The complexity of the supercapacitor model increases with the increase in the amount of loss to be considered in the model. For small-signal modeling excluding the higher-order non-linearities, we use the following transfer function:
where and are the gain and time constant of the supercapacitor, respectively.
4.2. Controller Design
A fractional-order supercapacitor approach is presented in this work to improve the frequency stability of microgrid clusters. Fractional-order calculus is a branch of mathematics that deals with non-integer order integrals and derivatives [33,34]. Fractional-order controllers are utilized in many engineering applications because they are more efficient than conventional integer-order controllers.
A fractional-order controller can be represented in the time domain as follows:
where represents the error signal, represents the proportional gain, represents the integral gain, and represents any real number greater than zero. The fractional-order controller can be represented in the frequency domain by taking the Laplace transformation as below:
The fractional-order calculus must be approximated to integer-order in order to apply the theory of integer-order controllers to fractional-order controllers. For the fractional order calculus operator, a continuous rational transfer function model is constructed for fractional-order calculus operator using the modified Oustaloup approximation [45] in the fitted frequency range of to :
where , ; can be represented as follows:
Using this approximation method, the fractional-order controller can be represented on the axis. However, it is difficult to obtain the optimal value for the fractional-order controller due to non-linearities. In this research, an optimization method is adopted to tune the parameters of the controller for both clusters of the microgrids. Additionally, the approximation method mentioned in this subsection could be easily implemented in real-time with the FOMCON toolbox [45,46].
4.3. Controller Parameter Tuning Approach
Metaheuristic optimization techniques in power systems require an appropriate cost function. As a rule, the goal of a cost function is to optimize a set of variables. Several metaheuristic approaches have been proposed in the literature, including particle swarm optimization (PSO), differential evolution (DE), and harmony search (HS). PSO is a metaheuristic optimization method that was initially motivated by the social behavior of flocking birds, whereas DE is motivated by Charles Darwin’s notion of natural evolution [47]. This study uses the whale optimization algorithm (WOA) to optimize the fractional order controller parameters. The WOA offers outstanding optimization performances compared to other algorithms, as described below [48,49]:
- The adaptive exploration and exploitation mechanism of WOA guarantees the global solution
- Unlike traditional methods such as PSO, DE, and HS, WOA is not sensitive to the initial solution(s), which may have a significant impact on their convergence and performance
- It is easily applicable due to its gradient-free nature
- It is easy to implement and flexible, making it ideal for a wide range of problem types and environments
- Less time is required compared to many algorithms
- It is easy to use and provides accurate results
Because the main objective of this work is to improve the frequency stability of the microgrid clusters, the frequency deviations in several clusters were used to define the cost function:
where the subscript is the maximum value and the minimum value of the design variables. Fractional order controller applications in power systems are the primary factors that guide the selection of the minimum/maximum limits of the variables. represents the frequency deviation in cluster A, and represents the frequency deviation in cluster B. is the fractional proportional gain in cluster A, is the fractional integral gain in cluster A, and is the fractional order for cluster A. Similarly, is the fractional proportional gain in cluster B, is the fractional integral gain in cluster B, and is the fractional order for cluster B. The WOA code was written in MATLAB script (.m files) and linked to the MATLAB Simulink (.slx files) environment for optimization. Coding of WOA involved several steps, which are described below.
Using a metaheuristic algorithm, WOA mimics the unique hunting strategy of the humpback whale. These whales use bubble-net hunting to catch prey such as krill and small fish in their hunt for food. In order to catch prey, a hunter has to first encircle their prey, then use the bubble-net feeding method, and finally search for new prey.
4.3.1. Prey Encirclement
When the humpback whale finds its prey, it circles around them and advances toward the most effective search agent. This behavior can be expressed mathematically during the course of iteration as follows:
where k represents the current iteration, represents the vector for the current position, and represents best solution vector up to the current iteration. The coefficient vectors are updated as follows:
where r is a random vector within the range 0 to 1, is a number that starts from 2 and then linearly decreases to 0 in the last iteration, and is updated as where is the maximum number of iterations.
4.3.2. Bubble-Net Feeding
The bubble-net feeding step starts by pushing bubbles and moving towards the prey in a spiral-shaped path. Humpback whale and prey positions mimic a helix-shaped motion, which can be described as follows:
where j represents a random number between −1 to 1 and b defines the spiral motion of the whale.
The spiral motions and shrinking behavior of bubble attacks are differentiated with the probability 0.5, as below:
4.3.3. Searching for Prey
The search space is expanded by in order to increase the variety of possible solutions and arrive at a global solution. Humpback whales are therefore forced to move away from an unknown whale position during the prey search phase. The following is a typical prey search equation:
where is the new random position vector of the whale selected from the current position vectors.
The above-mentioned three steps were implemented in optimizing controller parameters, as shown in Figure 4.
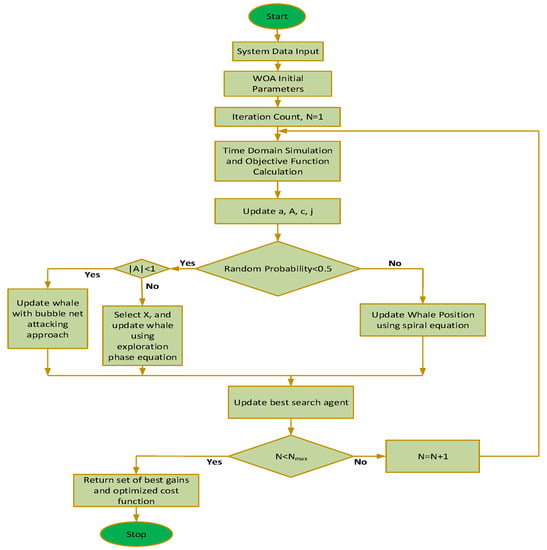
Figure 4.
WOA flowchart for controller parameter optimization.
Several measurements were optimized with WOA, and are visualized along with the implementation of a fractional-order supercapacitor using the FOMCON tool in Figure 5.
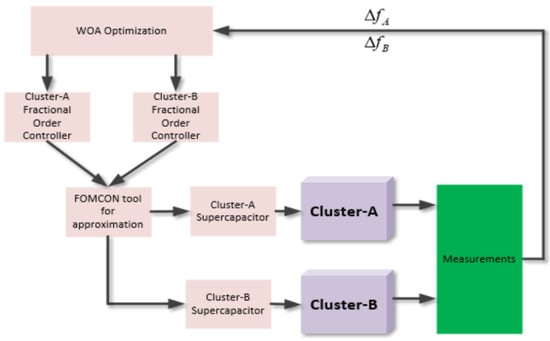
Figure 5.
Fractional-order supercapacitor implementation process.
4.3.4. Sensitivity and Stability Analysis of the Controller
Sensitivity analysis shows how resistant the controller is to disturbances and uncertainty. By comparing the integral absolute error and integral square error to the plant uncertainty, the performance of the fractional-order controller can be evaluated. In general, a sensitivity function is developed in the s-plane. Feedback design is directly tied to sensitivity analysis. Amplification and attenuation occur when the sensitivity function of the system is less than one and greater than one , respectively [50,51]. Attenuation or amplification would not occur if the sensitivity function were set to one . This study analyzes the sensitivity of the controller parameters’ variation with the WOA-based heuristic approach. However, this work could be further extended by analysing the sensitivity of the controller transfer function provided in Equation (18) while considering feedback design.
The stability of the fractional order controller, on the other hand, can be determined by setting a global stability region in the , -space in Equation (18). In stability analysis, the integral order () is set to any real number greater than zero. A complete mathematical model for the fractional-order controller with the concept of fractional-order calculus can be developed such that the stability range of parameters can be obtained, guaranteeing prespecified gain and phase margin requirements [52]. This study, however, utilizes heuristic optimization methods to determine the range of the stable controller parameters.
5. Results and Discussion
The proposed load-frequency control for microgrid clusters was validated with a simulation study. A microgrid cluster dynamic model was developed and several case studies were simulated to observe the frequency of the microgrid clusters. The model supercapacitor with optimized fractional-order controller was tested against different disturbances in the microgrids. Each cluster in the microgrid consisted of solar PV, solar thermal, wind generator, diesel engine generator, fuel cell, aqua electrolyser, battery storage, and aggregated load. The whale optimization code was developed and linked with the microgrid dynamic model to optimize the fractional-order PI parameters of the supercapacitor controller. The optimized controller parameters and the system parameters are listed in Table 1. Detailed simulation parameters can be found in [40,53]. After optimization was carried out, the dynamic system model i=was rebuilt and dynamic time-domain simulations were carried out to test the effectiveness of the optimized controllers.

Table 1.
Parameters for the microgrid clusters and controllers.
Several disturbances, ranging from light load changes to heavy load changes, were executed for three cases: without a supercapacitor, with a conventional controller, and with the optimized supercapacitor controller. The robustness of the proposed controller was tested with system parameter variations. The proposed controller was found to guarantee robust performance against parameter uncertainties.
5.1. Cluster A Small Load Disturbances
Initially, the superiority of the proposed approach in frequency stabilization was tested with load disturbances applied in cluster A. In this case, a step load disturbance of 0.01 p.u. was executed in cluster A at 25 s during the time-domain simulation. The microgrid cluster without any support from the additional controller becomes unstable due to the 0.01 p.u. disturbance in cluster A, as shown in Figure 6. Although the conventional integrator controller improves the dynamic performance of the system by stabilizing the frequency response, it experiences huge frequency excursion. On the other hand, the proposed supercapacitor control approach reduces the frequency excursion greatly, to only 0.025 Hz. More importantly, it shows stable operation during the time domain simulation study.
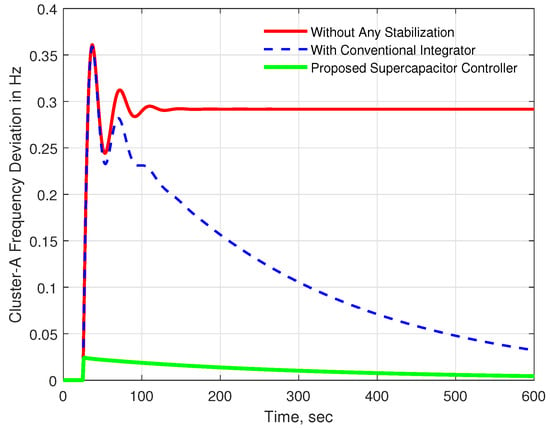
Figure 6.
Frequency response for cluster A with 0.01 p.u. disturbance in cluster A.
A similar improved frequency response was achieved for cluster B, as shown in Figure 7.
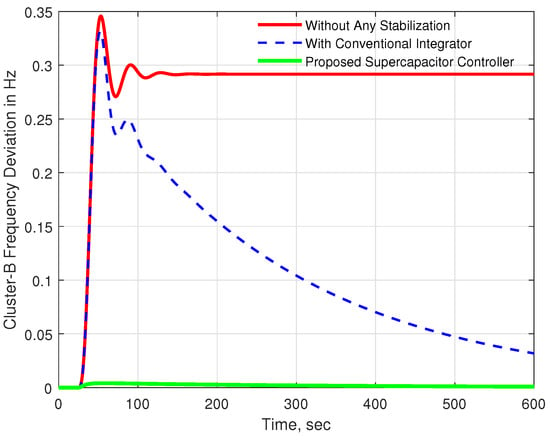
Figure 7.
Frequency response for cluster B with 0.01 p.u. disturbance in cluster A.
5.2. Cluster A Large Load Disturbances
After executing a small load disturbance, a large load disturbance was executed in cluster A to test the capability of the proposed supercapacitor approach in stabilizing the frequency of the microgrid cluster. It was noted that both the case without any stabilization and the case with a conventional integrator showed very high frequency deviation for a load disturbance of 0.15 p.u. The frequency deviation was around 5.5 Hz (Figure 8) in both cases, which is beyond the acceptable limit. In this situation, system frequency does not return to a nominal value without any stabilization. The conventional integrator approach showed a declining frequency deviation during the time-domain simulation. On the other hand, the proposed approach experienced a frequency deviation of only 0.4 Hz, which declined faster compared to the other two approaches.
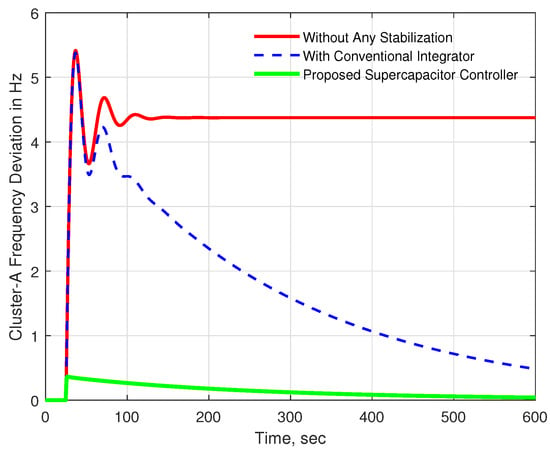
Figure 8.
Frequency response for cluster A with 0.15 p.u. disturbance in cluster A.
The frequency response of cluster B was significantly improved with the proposed supercapacitor method compared to the other approaches as well (Figure 9).
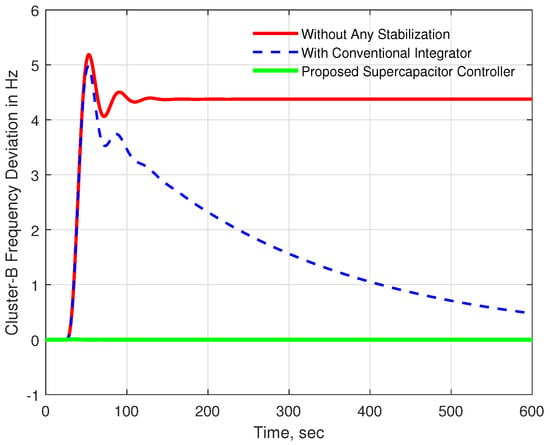
Figure 9.
Frequency response for cluster B with 0.15 p.u. disturbance in cluster A.
An overall comparison for the disturbances applied in Cluster A is depicted in Figure 10.
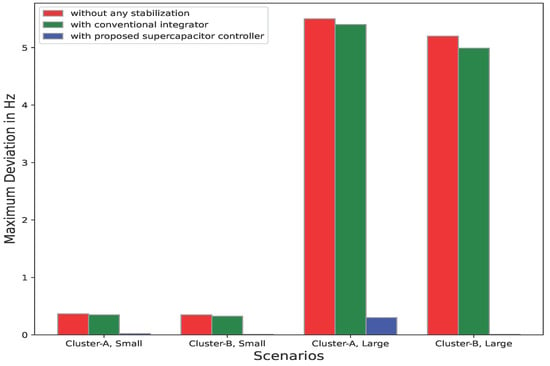
Figure 10.
Frequency response for all disturbance scenarios applied in cluster A.
5.3. Cluster B Small Load Disturbances
Small load disturbances in Cluster B were used to test the superiority of the suggested approach in frequency stabilization. During the time-domain simulation, a step load disturbance of 0.01 p.u. was tested in cluster B at 25 s. In this circumstance the microgrid cluster became unstable without any additional controller support, as demonstrated in Figure 11. While the traditional integrator controller increased the system’s dynamic performance by stabilizing the frequency response, it had a large frequency excursion. The proposed supercapacitor control technique, on the other hand, considerably minimized the frequency excursion. More importantly, it demonstrated very stable operation during the time domain simulation investigation.
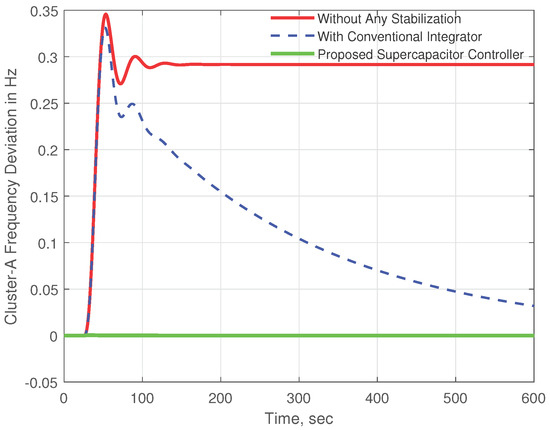
Figure 11.
Frequency response for cluster A with 0.01 p.u. disturbance in cluster B.
Likewise, the frequency response in cluster B improved with a small disturbance of 0.01 p.u., as depicted in Figure 12.
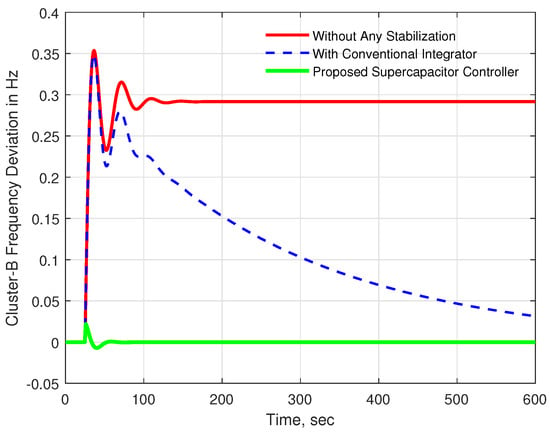
Figure 12.
Frequency response for cluster B 0.01 p.u. disturbance in cluster B.
5.4. Comparison with Existing Approaches
The superiority of the proposed fractional order supercapacitor was compared with recent approaches published in the technical literature. In recent years, superconducting energy storage systems have been applied in power networks to support virtual inertia. For example, superconducting magnetic energy storage (SMES) devices have been applied in low-inertia systems to stabilize system frequency during disturbances [54,55]. A virtual inertia support system with SMES as presented in [55] was compared with the fractional-order supercapacitor approach developed here. The supercapacitor approach was found to be more effective in damming frequency oscillation in the microgrid clusters. As shown in Figure 13a, for a small disturbance (0.01 p.u. load change) in cluster A, the fractional order supercapacitor shows better performance compared to the SMES approach. Similarly, for a large load disturbance of 0.15 p.u. in cluster A, the frequency oscillation is well damped with the proposed approach as compared to the existing approach (Figure 13b).
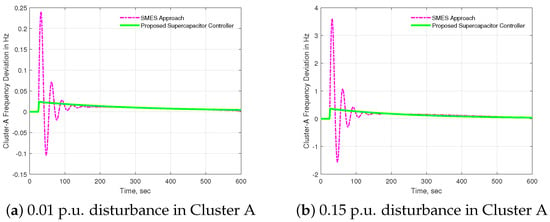
Figure 13.
Comparison of frequency deviation in cluster-A.
5.5. Cluster B Large Disturbance
For a load disturbance of 0.15 p.u. applied in cluster B, both the case without any stabilization and the case with a classical integrator showed extremely high frequency variation. The frequency deviation in both situations was roughly 5.25 Hz (Figure 14), which is well above the permitted range. Without any stabilization, the system frequency does not revert to its nominal value. During the time-domain simulation, however, the frequency deviation of the typical integrator approach decreases. The proposed approach, on the other hand, has almost zero frequency variation. Figure 15 shows the frequency deviation improvements in cluster B for large disturbances.
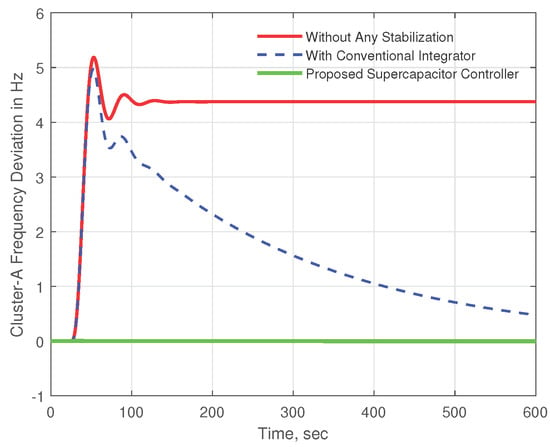
Figure 14.
Frequency response for cluster A 0.15 p.u. disturbance in cluster B.
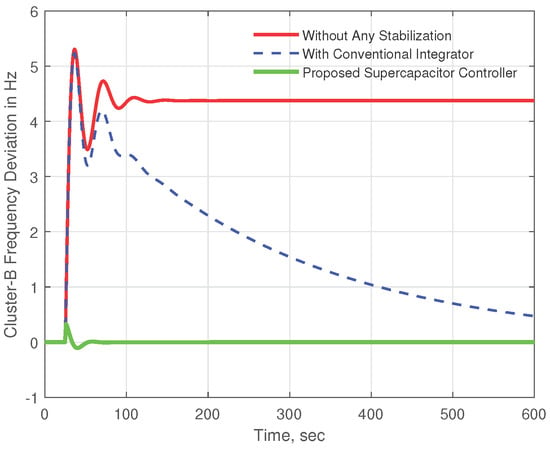
Figure 15.
Frequency response for cluster B 0.15 p.u. disturbance in cluster B.
A comparison of disturbances applied in Cluster B is depicted in Figure 16 for all scenarios.
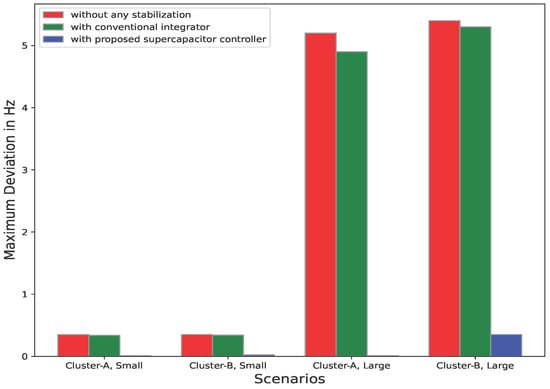
Figure 16.
Frequency response for all disturbance scenarios applied in cluster B.
5.6. Repeated Load Disturbances
Repeated load change scenarios were used to verify the effectiveness of the proposed supercapacitor control technique for the microgrid cluster. The repeated load change scenarios are plotted in Figure 17a. The load changes are 0.05 p.u., 0.15 p.u., 0.01 p.u., 0.2 p.u., and 0.075 p.u. at 100 s, 200 s, 300 s, 400 s, and 500 s, respectively. As shown, the microgrid cluster frequency response is very poor within the entire simulation period without any stabilization method. The conventional integrator approach slightly improves the frequency excursion. However, both approaches fail to return the frequency deviation to zero before the next disturbance. The proposed approach, on the other hand, is capable of reducing the frequency excursion in both clusters as well as stabilizing the system. Moreover, the proposed method performs substantially better in terms of overshoot, undershoot, and settling time in this scenario, as depicted in Figure 17b,c.
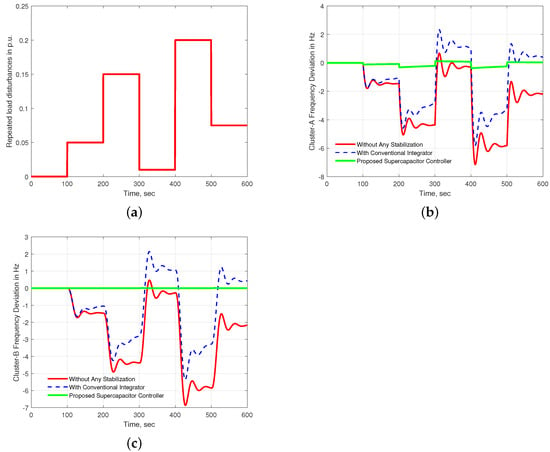
Figure 17.
(a) Repeated load change in cluster B; (b) frequency variation in cluster A; (c) frequency variation in cluster B.
5.7. Renewable Energy Variation Disturbances
In general, renewable energy sources integrated as a form of distributed generator are highly variable in nature due to the natural variations of sunlight and wind speed. In order to emulate the actual scenario, varying renewable energy was simulated in cluster B; the results are shown in Figure 18a. As can be seen, the injection of fluctuating power in cluster B causes frequency variation over the entire simulation time. In addition, the microgrid cluster is unstable in terms of frequency deviation both without any stabilization and with conventional integrator approaches. However, the system is stable and frequency variation is negligible for both cluster A and cluster B when the proposed supercapacitor control approach is used, as shown in Figure 18b,c.
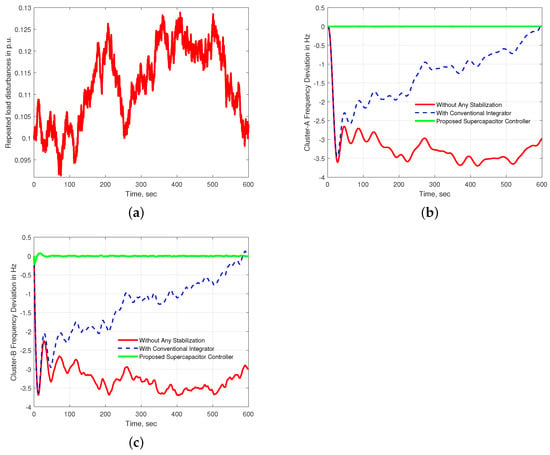
Figure 18.
(a) Renewable energy fluctuation; (b) frequency oscillation in cluster A; (c) frequency oscillation in cluster B.
6. Conclusions
An efficient fractional-order supercapacitor controller is presented in this work to stabilize the frequency of a microgrid cluster consisting of STP, solar PV, wind, diesel generator, aqua electrolyzer, and fuel cell power sources. A small-signal model of the microgrid clusters was developed along with the fractional-order supercapacitor controller. The parameters of the controller were tuned using the whale optimization approach. With the developed supercapacitor controller, the system response was analyzed with different scenarios, including small disturbance, large disturbance, repeated disturbance, and varying renewable energy generation. Time-domain simulations were carried out in MATLAB Simulink to observe the frequency excursion of several clusters. The proposed supercapacitor controller guarantees microgrid frequency stability for all disturbances. The frequency excursion is kept well below the acceptable limits with the proposed controller compared to existing methods such as integrator and fractional-order SMES controls. Our comparative results analysis shows that the proposed method is more stable in controlling system frequency during disturbances. Furthermore, the simulation results support green efforts to increase sustainability by demonstrating the potential benefits of fractional-order supercapacitor controllers in high-level renewable energy integration. In the future, more detailed modeling of the microgrid clusters will be considered with fractional-order PID controllers for frequency stability improvement.
Author Contributions
Conceptualization, M.S.A.; Methodology, M.S.A.; Formal analysis, M.S.A., A.A.A. and F.S.A.-I.; Writing—original draft preparation, M.S.A. and M.A.I.; Writing—review and editing, A.A.A., F.S.A.-I., M.A.H., M.A.I., M.S. and A.U.; Supervision, A.A.A. and M.A.H. Funding acquisition, A.A.A. and M.A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Md Shafiul Alam and Fahad Saleh Al-Ismail would like to acknowledge the support provided by King Fahd University of Petroleum and Minerals (KFUPM) through directly funded project No. INRE2209.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alam, M.S.; Al-Ismail, F.S.; Salem, A.; Abido, M.A. High-Level Penetration of Renewable Energy Sources Into Grid Utility: Challenges and Solutions. IEEE Access 2020, 8, 190277–190299. [Google Scholar] [CrossRef]
- Khaki, B.; Kiliç, H.; Yilmaz, M.; Shafie-Khah, M.; Lotfi, M.; Catalão, J.P. Active Fault Tolerant Control of Grid-Connected DER: Diagnosis and Reconfiguration. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 4127–4132. [Google Scholar]
- Ali, A.O.; Elmarghany, M.R.; Abdelsalam, M.M.; Sabry, M.N.; Hamed, A.M. Closed-loop home energy management system with renewable energy sources in a smart grid: A comprehensive review. J. Energy Storage 2022, 50, 104609. [Google Scholar] [CrossRef]
- Alam, M.S.; Al-Ismail, F.S.; Abido, M.A. Power management and state of charge restoration of direct current microgrid with improved voltage-shifting controller. J. Energy Storage 2021, 44, 103253. [Google Scholar] [CrossRef]
- Saxena, P.; Singh, N.; Pandey, A.K. Enhancing the dynamic performance of microgrid using derivative controlled solar and energy storage based virtual inertia system. J. Energy Storage 2020, 31, 101613. [Google Scholar] [CrossRef]
- Ma, H.; Chowdhury, B. Working towards frequency regulation with wind plants: Combined control approaches. IET Renew. Power Gener. 2010, 4, 308–316. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load frequency control: Self Adaptive Modified Bat Algorithm. Int. J. Electr. Power Energy Syst. 2015, 71, 254–261. [Google Scholar] [CrossRef]
- Kiliç, H.; Khaki, B.; Gumuş, B.; Yilmaz, M.; Asker, M.E. Stability Analysis of Islanded Microgrid with EVs. In Proceedings of the 2018 Smart Grid Conference (SGC), Sanandaj, Iran, 28–29 November 2018; pp. 1–5. [Google Scholar]
- Rai, A.; Das, D.K. The development of a fuzzy tilt integral derivative controller based on the sailfish optimizer to solve load frequency control in a microgrid, incorporating energy storage systems. J. Energy Storage 2022, 48, 103887. [Google Scholar] [CrossRef]
- Iqbal, S.; Xin, A.; Jan, M.U.; ur Rehman, H.; Masood, A.; Rizvi, S.A.A.; Salman, S. Aggregated electric vehicle-to-grid for primary frequency control in a microgrid—A review. In Proceedings of the 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–7 November 2018; pp. 563–568. [Google Scholar]
- Iqbal, S.; Xin, A.; Jan, M.U.; Salman, S.; Zaki, A.U.M.; Rehman, H.U.; Shinwari, M.F.; Abdelbaky, M.A. V2G strategy for primary frequency control of an industrial microgrid considering the charging station operator. Electronics 2020, 9, 549. [Google Scholar] [CrossRef] [Green Version]
- Jan, M.U.; Xin, A.; Abdelbaky, M.A.; Rehman, H.U.; Iqbal, S. Adaptive and fuzzy PI controllers design for frequency regulation of isolated microgrid integrated with electric vehicles. IEEE Access 2020, 8, 87621–87632. [Google Scholar] [CrossRef]
- Kim, J.; Guerrero, J.M.; Rodriguez, P.; Teodorescu, R.; Nam, K. Mode adaptive droop control with virtual output impedances for an inverter-based flexible AC microgrid. IEEE Trans. Power Electron. 2010, 26, 689–701. [Google Scholar] [CrossRef]
- Delghavi, M.B.; Yazdani, A. An adaptive feedforward compensation for stability enhancement in droop-controlled inverter-based microgrids. IEEE trans. Power Deliv. 2011, 26, 1764–1773. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Iqbal, M.; Shahzad, S.; Muqeet, H.A.; Shahzad, M.; Hussain, M.M. Load Frequency Control (LFC) Strategies in Renewable Energy-Based Hybrid Power Systems: A Review. Energies 2022, 15, 3488. [Google Scholar] [CrossRef]
- Ming, G.; Geng, J.; Liu, J.; Chen, Y.; Yuan, K.; Zhang, K. Load Frequency Robust Control Considering Intermittent Characteristics of Demand-Side Resources. Energies 2022, 15, 4370. [Google Scholar] [CrossRef]
- Buraimoh, E.; Aluko, A.O.; Oni, O.E.; Davidson, I.E. Decentralized Virtual Impedance-Conventional Droop Control for Power Sharing for Inverter-Based Distributed Energy Resources of a Microgrid. Energies 2022, 15, 4439. [Google Scholar] [CrossRef]
- Wang, S.; Lu, L.; Han, X.; Ouyang, M.; Feng, X. Virtual-battery based droop control and energy storage system size optimization of a DC microgrid for electric vehicle fast charging station. Appl. Energy 2020, 259, 114146. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Nguyen, P.L.; Ma, Z.; Sheng, W. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2013, 29, 617–630. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.C. Small-signal modeling and parameters design for virtual synchronous generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Fathi, A.; Shafiee, Q.; Bevrani, H. Robust frequency control of microgrids using an extended virtual synchronous generator. IEEE Trans. Power Syst. 2018, 33, 6289–6297. [Google Scholar] [CrossRef]
- Tan, K.T.; Peng, X.; So, P.L.; Chu, Y.C.; Chen, M.Z. Centralized control for parallel operation of distributed generation inverters in microgrids. IEEE Trans. Smart Grid 2012, 3, 1977–1987. [Google Scholar] [CrossRef] [Green Version]
- Mehrizi-Sani, A.; Iravani, R. Potential-function based control of a microgrid in islanded and grid-connected modes. IEEE Trans. Power Syst. 2010, 25, 1883–1891. [Google Scholar] [CrossRef]
- Qian, T.; Liu, Y.; Zhang, W.; Tang, W.; Shahidehpour, M. Event-triggered updating method in centralized and distributed secondary controls for islanded microgrid restoration. IEEE Trans. Smart Grid 2019, 11, 1387–1395. [Google Scholar] [CrossRef]
- Bevrani, H.; Feizi, M.R.; Ataee, S. Robust frequency control in an islanded microgrid: H-infinity and mu-synthesis approaches. IEEE Trans. Smart Grid 2015, 7, 706–717. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed secondary control for islanded microgrids—A novel approach. IEEE Trans. Power Electron. 2013, 29, 1018–1031. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, Q.; Stefanović, Č.; Dragičević, T.; Popovski, P.; Vasquez, J.C.; Guerrero, J.M. Robust networked control scheme for distributed secondary control of islanded microgrids. IEEE Trans. Ind. Electron. 2013, 61, 5363–5374. [Google Scholar] [CrossRef] [Green Version]
- Khayat, Y.; Heydari, R.; Naderi, M.; Dragicevic, T.; Shafiee, Q.; Fathi, M.; Bevrani, H.; Blaabjerg, F. Decentralized frequency control of AC microgrids: An estimation-based consensus approach. IEEE J. Emerg. Select. Top. Power Electron. 2020, 9, 5183–5191. [Google Scholar] [CrossRef]
- Kerdphol, T.; Watanabe, M.; Mitani, Y.; Phunpeng, V. Applying Virtual Inertia Control Topology to SMES System for Frequency Stability Improvement of Low-Inertia Microgrids Driven by High Renewables. Energies 2019, 12, 3902. [Google Scholar] [CrossRef] [Green Version]
- Gomez, L.A.; Grilo, A.P.; Salles, M.B.C.; Sguarezi Filho, A.J. Combined Control of DFIG-Based Wind Turbine and Battery Energy Storage System for Frequency Response in Microgrids. Energies 2020, 13, 894. [Google Scholar] [CrossRef] [Green Version]
- Kikusato, H.; Ustun, T.S.; Suzuki, M.; Sugahara, S.; Hashimoto, J.; Otani, K.; Ikeda, N.; Komuro, I.; Yokoi, H.; Takahashi, K. Flywheel energy storage system based microgrid controller design and PHIL testing. Energy Rep. 2022, 8, 470–475. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control. 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Li, H.; Luo, Y.; Chen, Y. A fractional order proportional and derivative (FOPD) motion controller: Tuning rule and experiments. IEEE Trans. Control Syst. Technol. 2009, 18, 516–520. [Google Scholar] [CrossRef]
- Komathi, C.; Umamaheswari, M. Design of Gray Wolf Optimizer Algorithm-Based Fractional Order PI Controller for Power Factor Correction in SMPS Applications. IEEE Trans. Power Electron. 2019, 35, 2100–2118. [Google Scholar] [CrossRef]
- Kesarkar, A.A.; Selvaganesan, N. Tuning of optimal fractional-order PID controller using an artificial bee colony algorithm. Syst. Sci. Control Eng. 2015, 3, 99–105. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.S.; Abido, M.A.Y.; Hussein, A.E.D.; El-Amin, I. Fault Ride through Capability Augmentation of a DFIG-Based Wind Integrated VSC-HVDC System with Non-Superconducting Fault Current Limiter. Sustainability 2019, 11, 1232. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.S.; Abido, M.A.Y.; El-Amin, I. Fault current limiters in power systems: A Comprehensive Review. Energies 2018, 11, 1025. [Google Scholar] [CrossRef] [Green Version]
- Anderson, P.; Bose, A. Stability simulation of wind turbine systems. IEEE Trans. Power Appar. Syst. 1983, 102, 3791–3795. [Google Scholar] [CrossRef]
- Celikel, R.; Yilmaz, M.; Gundogdu, A. A voltage scanning-based MPPT method for PV power systems under complex partial shading conditions. Renew. Energy 2022, 184, 361–373. [Google Scholar] [CrossRef]
- Ray, P.; Mohanty, S.; Kishor, N. Small-signal analysis of autonomous hybrid distributed generation systems in presence of ultracapacitor and tie-line operation. J. Electr. Eng. 2010, 61, 205. [Google Scholar] [CrossRef] [Green Version]
- Barsali, S.; Ceraolo, M. Dynamical models of lead-acid batteries: Implementation issues. IEEE Trans. Energy Convers. 2002, 17, 16–23. [Google Scholar] [CrossRef]
- Garakani, M.A.; Bellani, S.; Pellegrini, V.; Oropesa-Nuñez, R.; Castillo, A.E.D.R.; Abouali, S.; Najafi, L.; Martín-García, B.; Ansaldo, A.; Bondavalli, P.; et al. Scalable spray-coated graphene-based electrodes for high-power electrochemical double-layer capacitors operating over a wide range of temperature. Energy Storage Mater. 2020, 34, 1–11. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2017, 6, 1832–1843. [Google Scholar] [CrossRef]
- Leontaritis, I.; Billings, S.A. Input-output parametric models for non-linear systems part I: Deterministic non-linear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Tepljakov, A.; Vunder, V.; Petlenkov, E.; Nakshatharan, S.S.; Punning, A.; Kaparin, V.; Belikov, J.; Aabloo, A. Fractional-order modeling and control of ionic polymer-metal composite actuator. Smart Mater. Struct. 2019, 28, 084008. [Google Scholar] [CrossRef]
- Mirjalili, S.; Dong, J.S.; Lewis, A. Nature-Inspired Optimizers; Springer: Cham, Switzerland, 2020; pp. 69–85. [Google Scholar]
- Alam, M.; Alotaibi, M.A.; Alam, M.A.; Hossain, M.; Shafiullah, M.; Al-Ismail, F.S.; Rashid, M.; Ur, M.; Abido, M.A. High-Level Renewable Energy Integrated System Frequency Control with SMES-Based Optimized Fractional Order Controller. Electronics 2021, 10, 511. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yadav, M.; Patel, H.K.G. Sensitivity analysis of IMC-PID controller with smith predictor using different filters. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 11–13 December 2020; pp. 1–6. [Google Scholar]
- Srinivasan, V.; Sukavanam, N. Sensitivity analysis of nonlinear fractional order control systems with state delay. Int. J. Comput. Math. 2016, 93, 160–178. [Google Scholar] [CrossRef]
- Hamamci, S.E. An algorithm for stabilization of fractional-order time delay systems using fractional-order PID controllers. IEEE Trans. Autom. Control 2007, 52, 1964–1969. [Google Scholar] [CrossRef]
- Fathy, A.; Yousri, D.; Rezk, H.; Thanikanti, S.B.; Hasanien, H.M. A Robust Fractional-Order PID Controller Based Load Frequency Control Using Modified Hunger Games Search Optimizer. Energies 2022, 15, 361. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Nour, M.; Petlenkov, E. A new virtual synchronous generator design based on the SMES system for frequency stability of low-inertia power grids. Energies 2020, 13, 5641. [Google Scholar] [CrossRef]
- Alam, M.S.; Al-Ismail, F.S.; Abido, M.A. PV/wind-integrated low-inertia system frequency control: PSO-optimized fractional-order PI-based SMES approach. Sustainability 2021, 13, 7622. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).