Development and Performance Verification of Frequency Control Algorithm and Hardware Controller Using Real-Time Cyber Physical System Simulator
Abstract
:1. Introduction
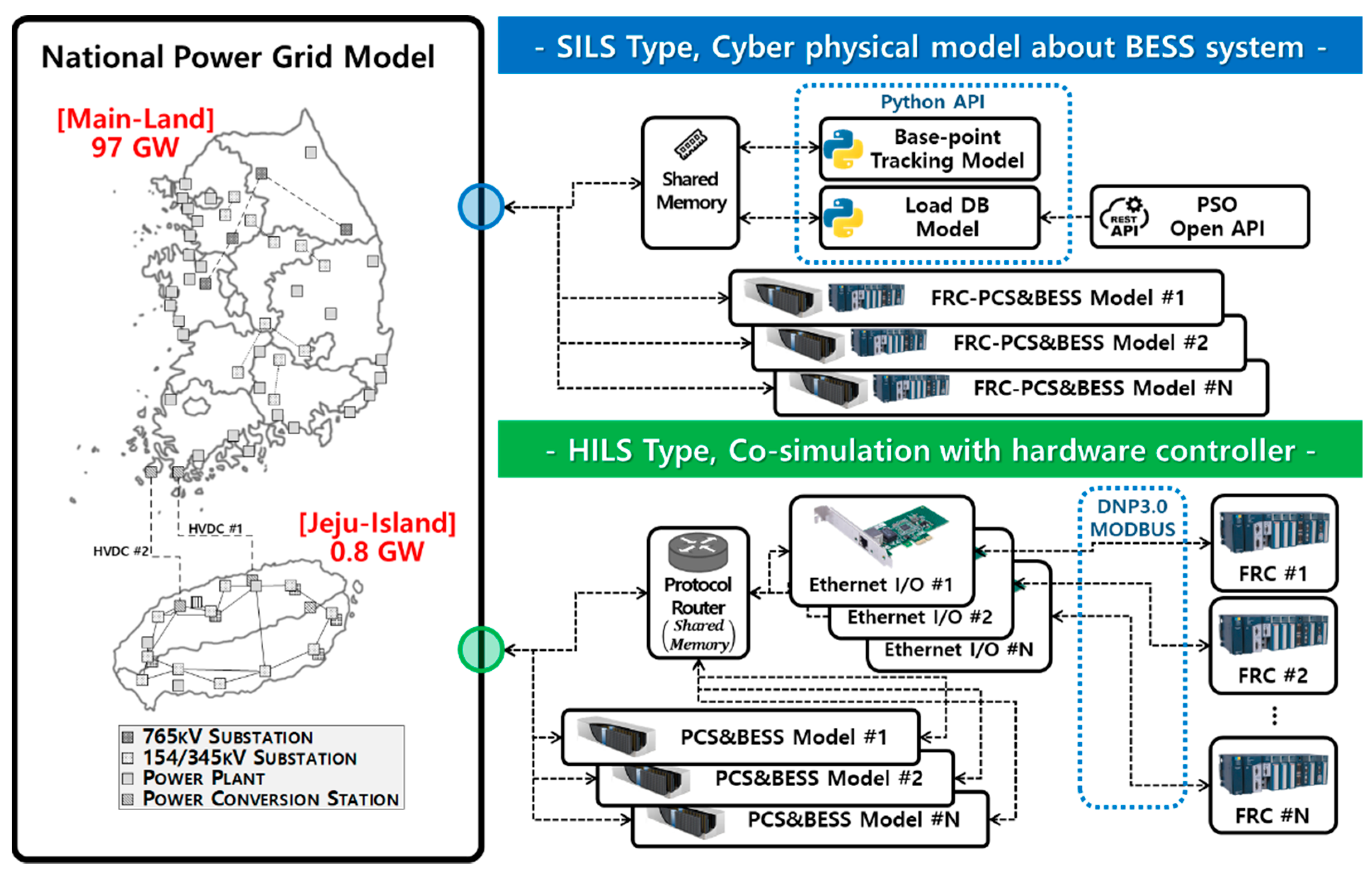
2. Development of Co-Simulation “A1GridSim”
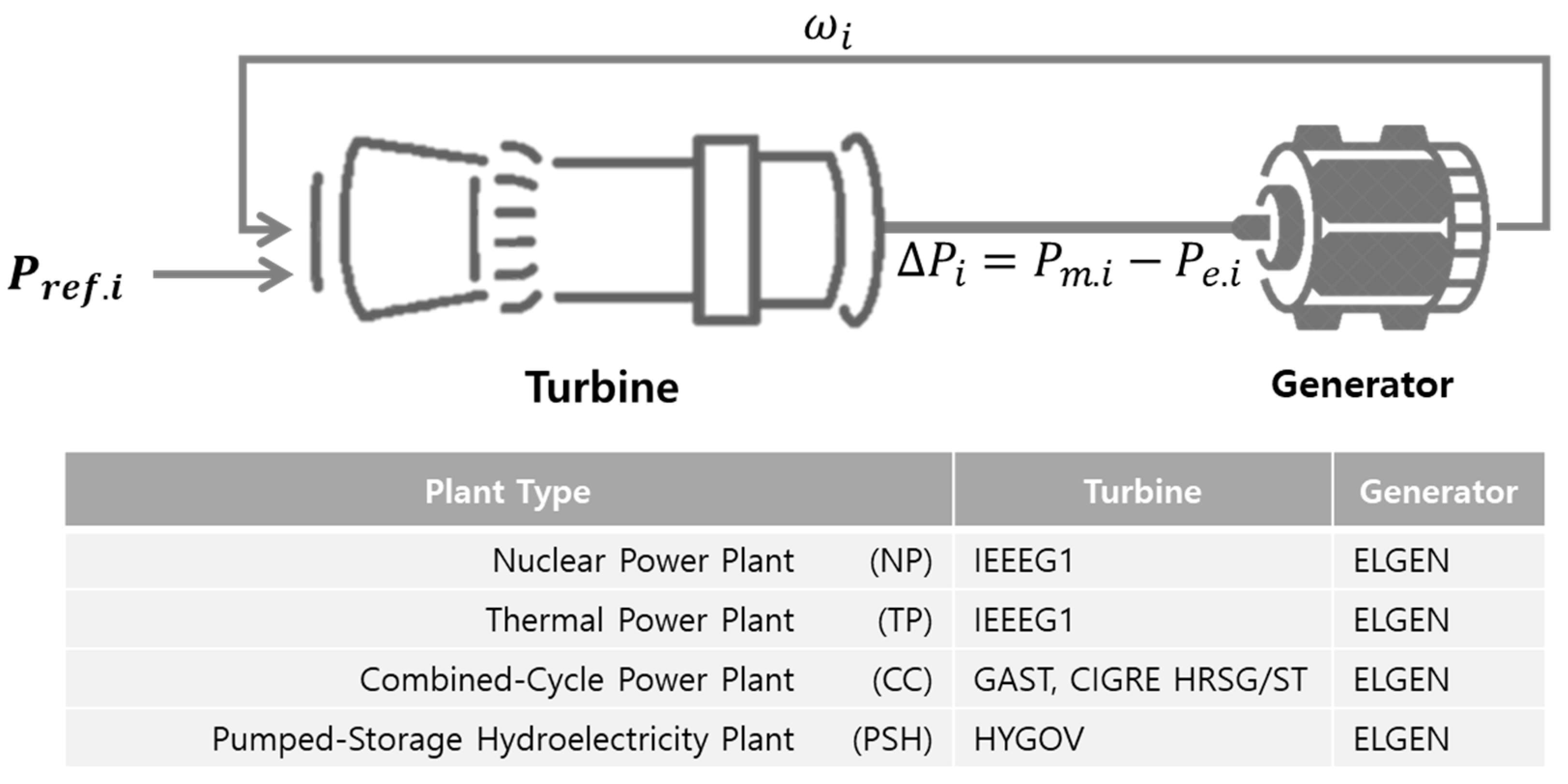
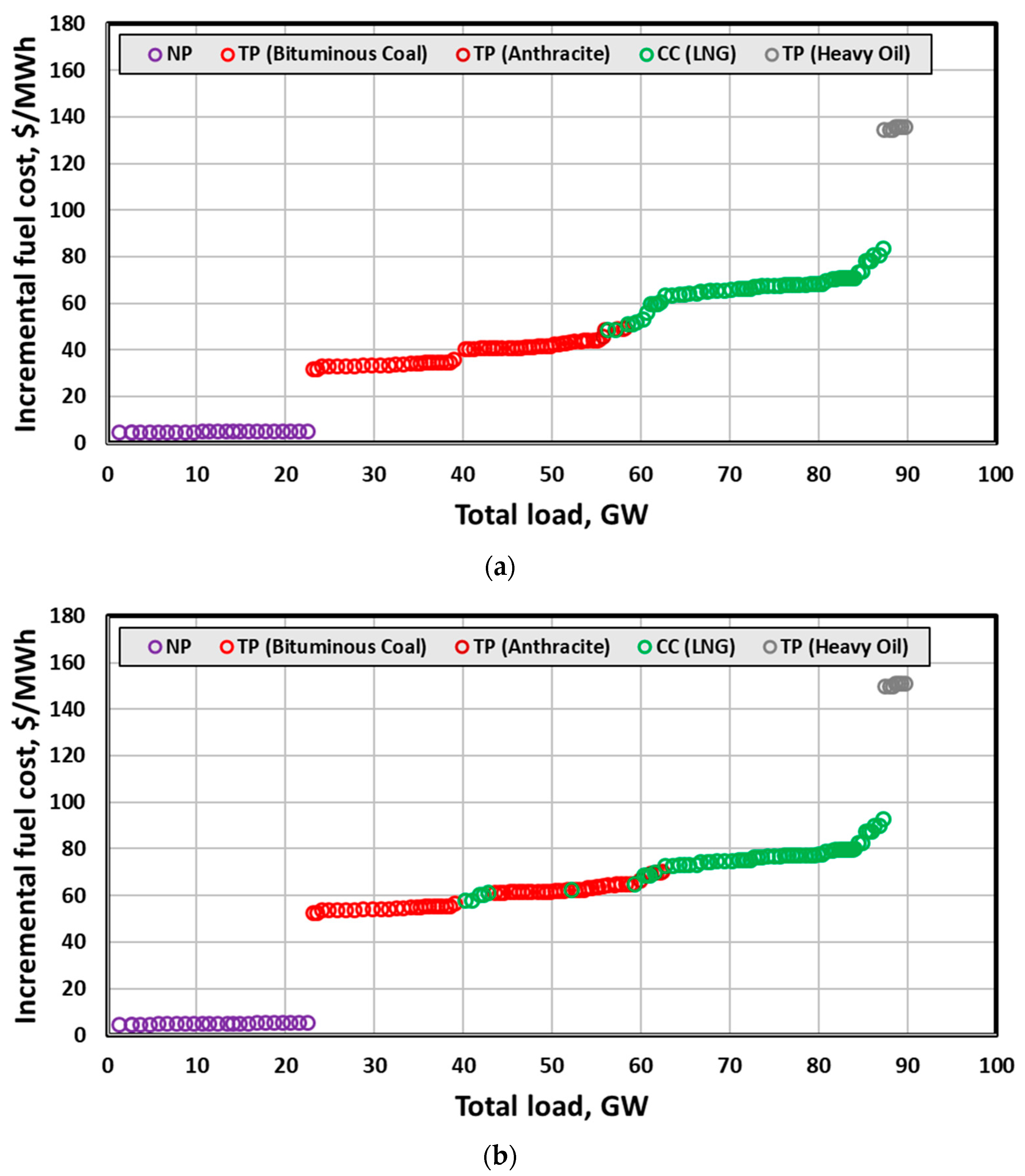
2.1. Centralised Power Plant (CPP) Model
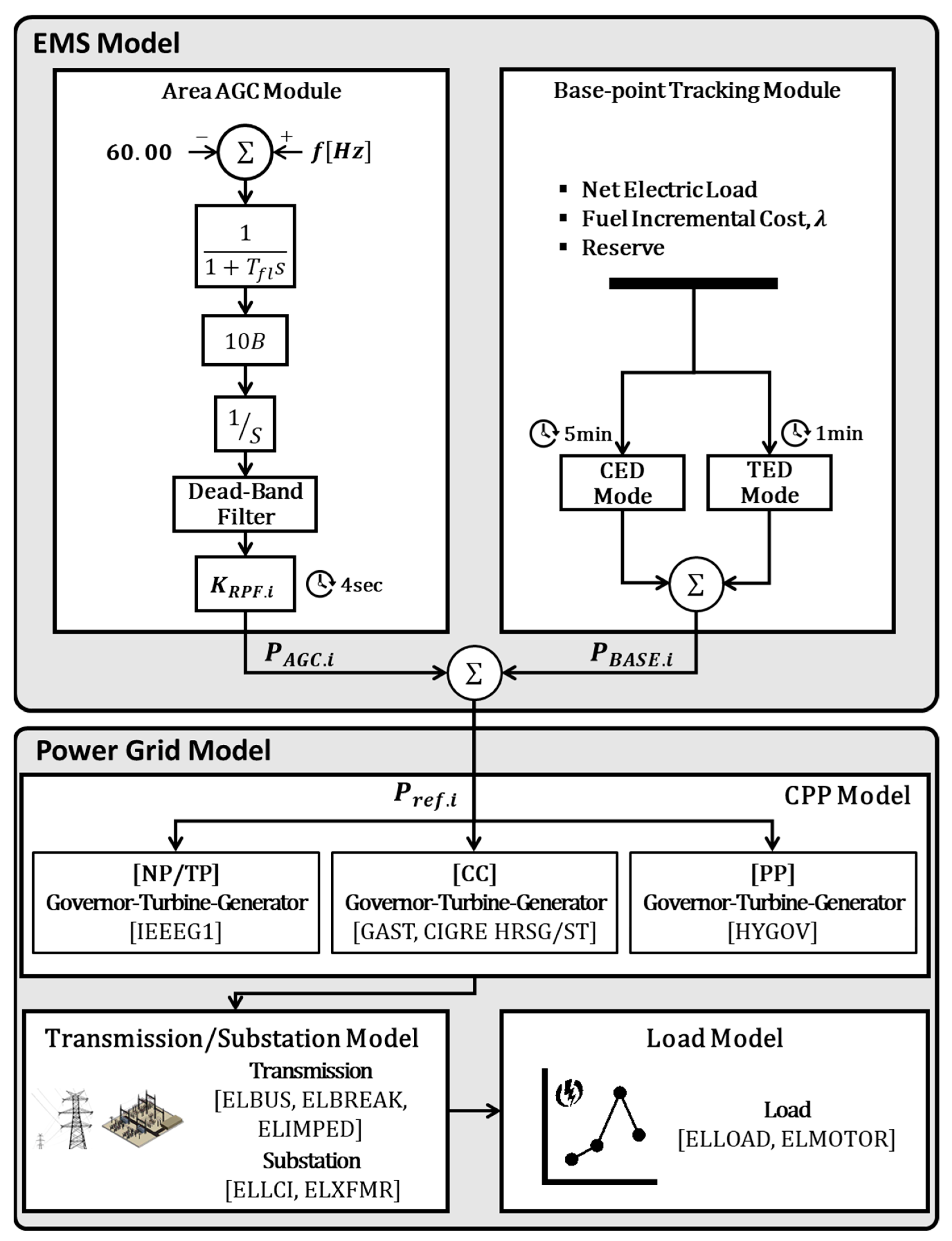
2.2. Energy Management System (EMS) Model
- 1.
- Control Economic/Environmental Dispatch
- Import cvxpy as cp
- Import numpy as np
- def Control_ED(n,, , , , , ):
- = cp.variable(shape=n, nonneg=True)
- = cp.variable(shape=n, nonneg=True)
- = cp.parameter(shape=n)
- = cp.parameter(shape=n)
- = cp.parameter(shape=n)
- = cp.parameter(shape=n)
- = cp.parameter(shape=n)
- .value = np.array()
- .value = np.array()
- .value = np.array()
- .value = np.array()
- .value = np.array()
- Constraints = list()
- Constraints.append()
- Constraints.append()
- Constraints.append)
- Constraints.append()
- Object = cp.Minimize(max())
- Prob = cp.Problem(Object, Constraints)
- Prob.solve()
- Return.value,.value
- 2.
- Tracking Economic/Environmental Dispatch
- def Traking_ED(, , ):
- If :
- :
- Return .value
2.3. Dynamic Frequency Model
2.4. BESS System Model
3. Software in the Loop Simulation for BESS System
3.1. Verification of Dynamic Frequency Model
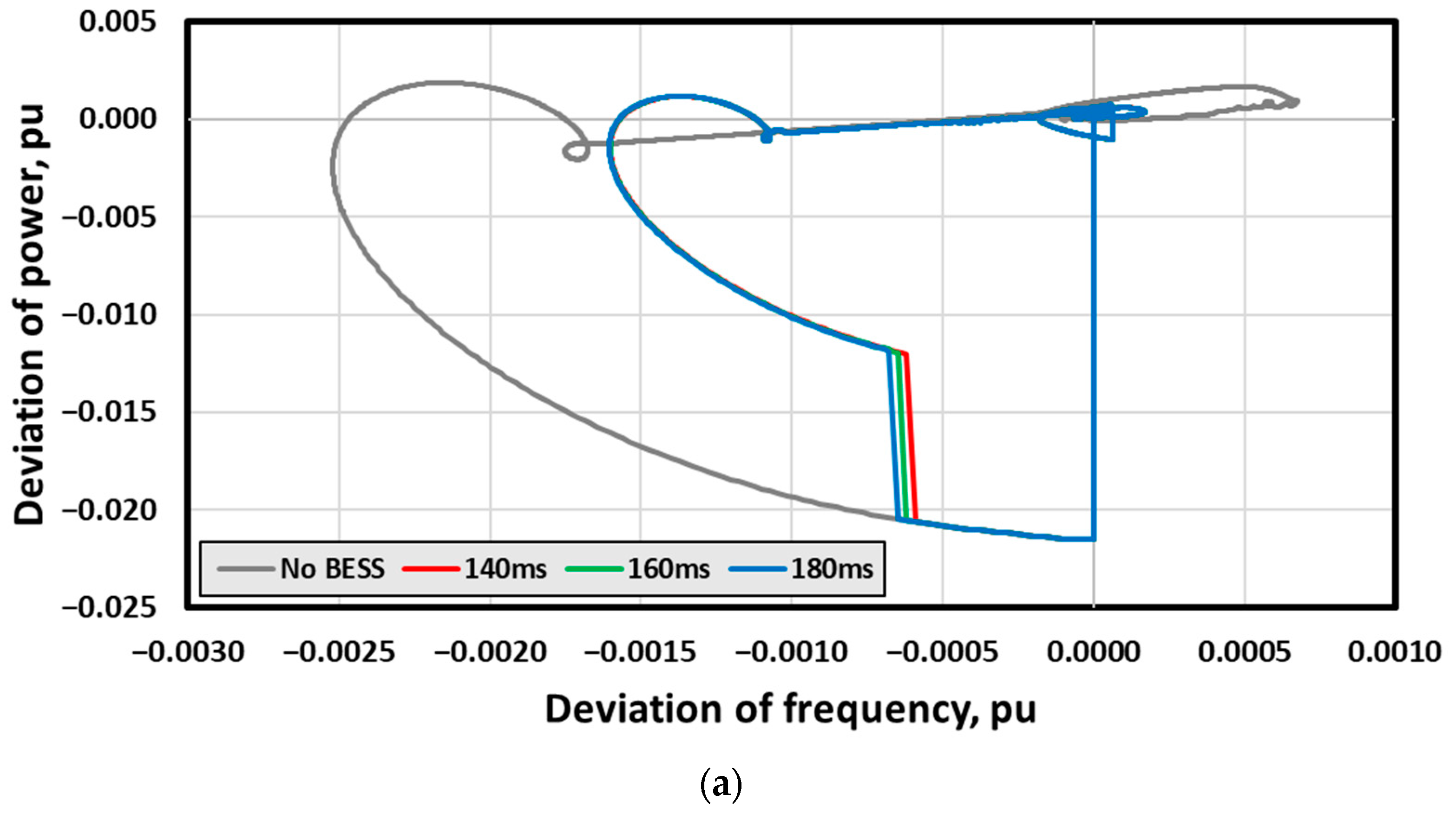
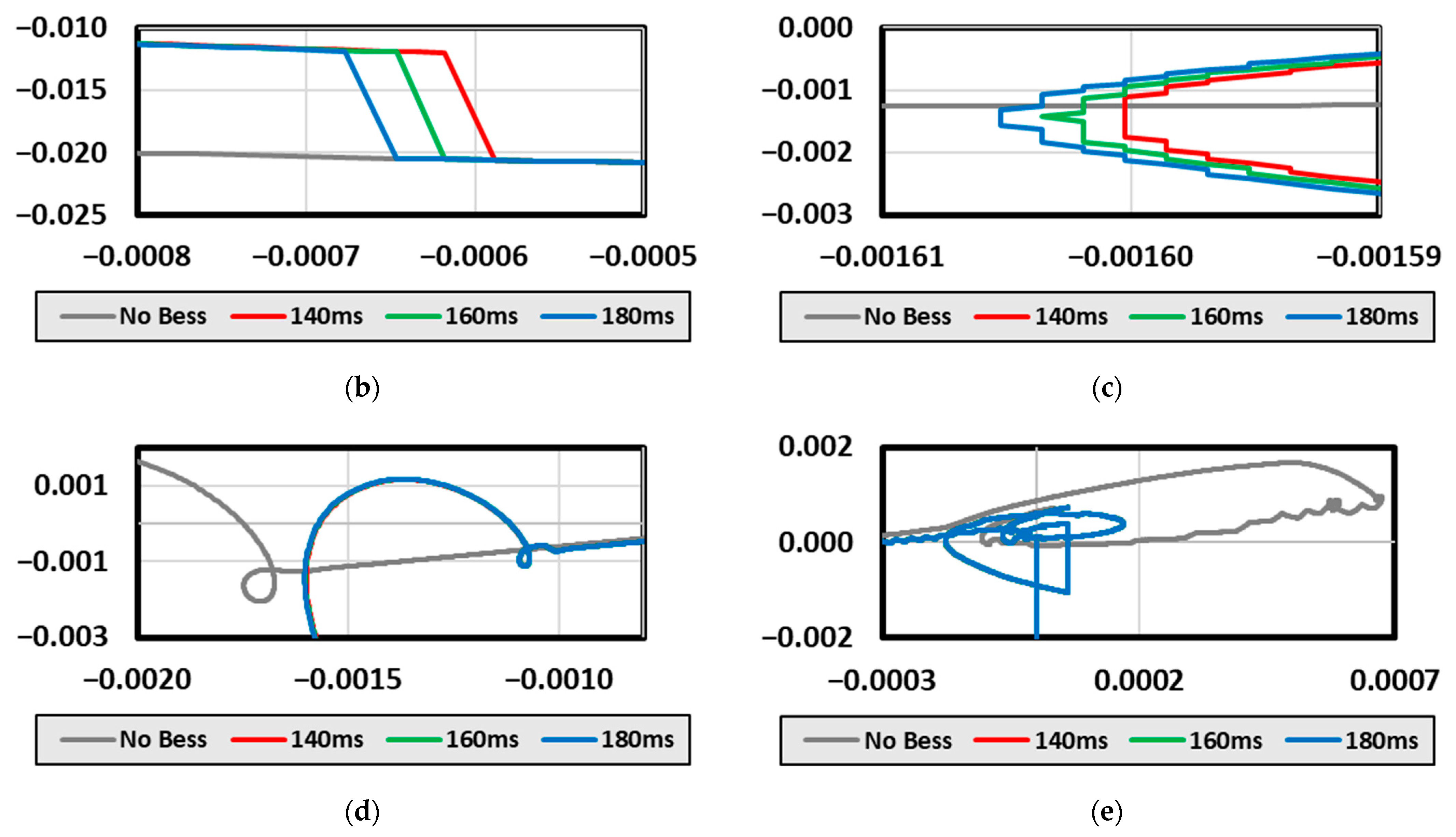
3.2. Performance Verification of the BESS System for PFC
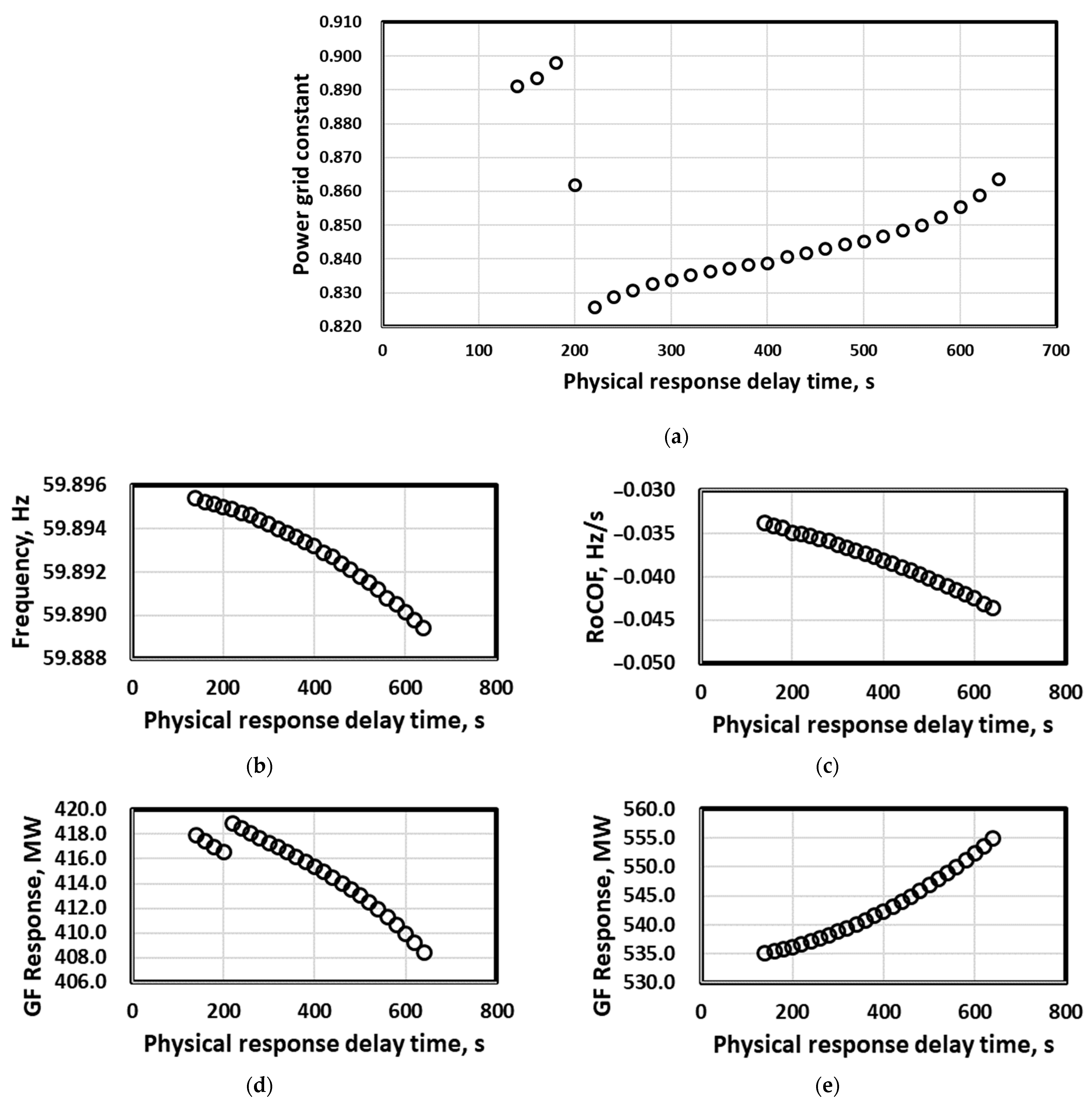
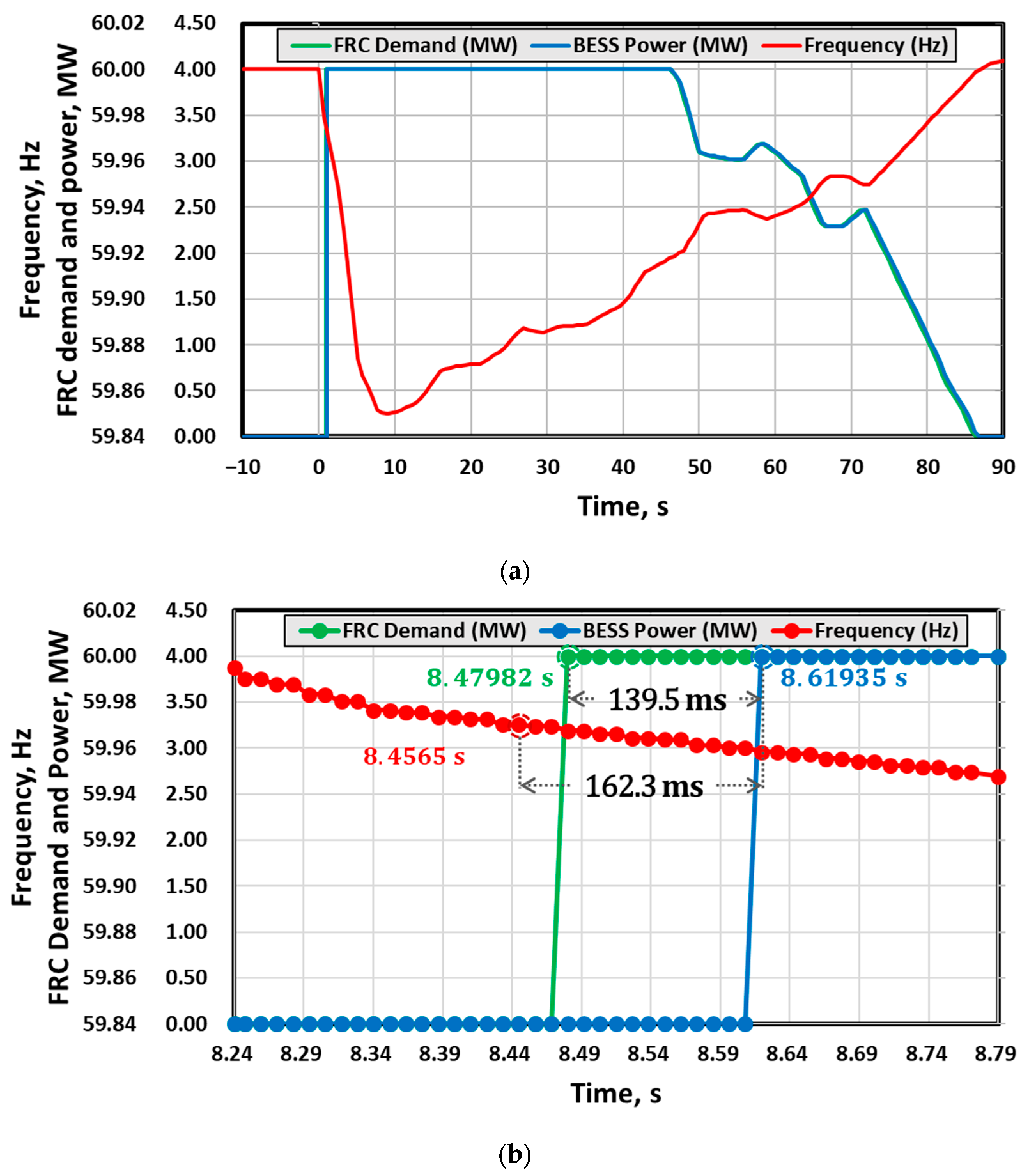
3.3. Analysis of Impact on Physical Response Delay Time between FRC and PCS
4. Hardware in the Loop Simulation for BESS System
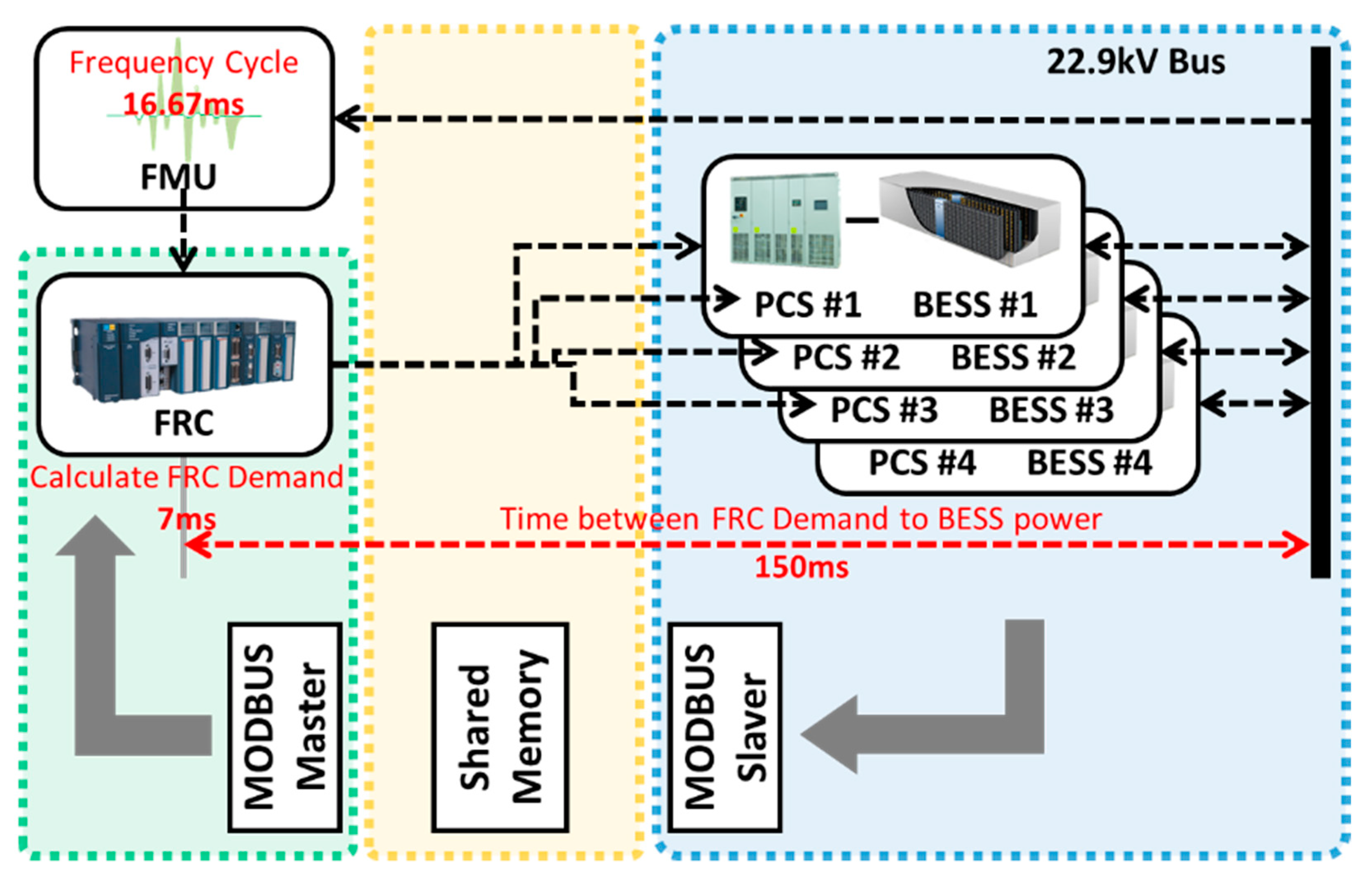
4.1. Configuration of the HILS System for Response Performance Evaluation
4.2. Result of BESS’s Response Performance Evaluation by HILS
5. Summary Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| Power demand of generator about primary frequency control | MW | |
| Rated power of generator | MW | |
| Rated rotating speed of generator | rad/s | |
| Rotating speed of generator | rad/s | |
| Droop coefficient of generator | %/100 | |
| Inertia constant of generator | s | |
| Rated capacity of generator | MVA | |
| Mechanical power of generator | MW | |
| Electrical power of generator | MW | |
| Total AGC demand in power system | MW | |
| Area control error | MW | |
| Control gain of AGC | MW/Hz | |
| Deviation of frequency | Hz | |
| AGC demand of generator | MW | |
| Ramp rate of generator | %/100 | |
| Base point of generator by tertiary frequency control | MW | |
| Heat rate equation of generator | MBtu/MWh | |
| Fuel cost equation of generator by EcoLD mode | $/h | |
| Fuel cost equation of generator by EnvLD mode | $/h | |
| Cost of fuel used by generator | $ | |
| CO2 trading price | $ | |
| CO2 emission coefficient | %/100 | |
| Incremental fuel cost equation of generator | $ /MWh | |
| Maximum power of generator | MW | |
| Minimum power of generator | MW | |
| Start up state of generator | - | |
| Power of generator | MW | |
| Power demand of generator by CED | MW | |
| Power demand of generator by TED | MW | |
| Rated frequency of power system | Hz | |
| Frequency of power system | Hz | |
| Load constant of power system | MW/0.1Hz | |
| Power consumption | MW | |
| Change of frequency | Hz | |
| Change of electric power | MW | |
| Proportional gain of power system | Hz/MW | |
| Frequency time constant | s | |
| Time for reaching the nadir frequency at frequency transient state | s | |
| Initial frequency before frequency transient state | Hz | |
| Nadir frequency at frequency transient state | Hz | |
| Frequency deviation between initial frequency and nadir frequency | Hz | |
| Average rate of change of frequency | Hz/s | |
| Rate of change of frequency at BESS response point | Hz/s | |
| Maximum governor free response | MW | |
| Time to recover from transient state | s | |
| Deviation of electric power in transient state | pu | |
| Deviation of electric frequency in transient state | pu | |
| Total generation power in power system at time t | MW | |
| Total generation power in power system at initial time | MW | |
| Total load in power system at time t | MW | |
| Total load in power system at initial time | MW | |
| Frequency at time t | Hz | |
| Frequency at initial time | Hz | |
| Power grid constant | pu |
References
- Tremblay, O.; Dessaint, L.-A. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lyden, S.; de la Barra, B.L.; Haque, M.E. Optimization of Tremblay’s battery model parameters for plug-in hybrid electric vehicle applications. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Surya, S.; Channegowda, J.; Datar, S.D.; Jha, A.S.; Victor, A. Accurate battery modeling based on pulse charging using MATLAB/Simulink. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–3. [Google Scholar]
- Xia, Q.; Yang, D.; Wang, Z.; Ren, Y.; Sun, B.; Feng, Q.; Qian, C. Multiphysical modeling for life analysis of lithium-ion battery pack in electric vehicles. Renew. Sustain. Energy Rev. 2020, 131, 109993. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, W.; Wang, Z.; An, F.; Li, H.; Jiang, J. Simplified battery pack modeling considering inconsistency and evolution of current distribution. IEEE Trans. Intell. Transp. Syst. 2020, 22, 630–639. [Google Scholar] [CrossRef]
- Dubarry, M.; Baure, G.; Pastor-Fernández, C.; Yu, T.F.; Widanage, W.D.; Marco, J. Battery energy storage system modeling: A combined comprehensive approach. J. Energy Storage 2019, 21, 172–185. [Google Scholar] [CrossRef]
- Tan, R.H.; Tinakaran, G.K. Development of battery energy storage system model in MATLAB/Simulink. Int. J. Smart Grid Clean Energy 2020, 9, 180–188. [Google Scholar] [CrossRef]
- Rancilio, G.; Lucas, A.; Kotsakis, E.; Fulli, G.; Merlo, M.; Delfanti, M.; Masera, M. Modeling a large-scale battery energy storage system for power grid application analysis. Energies 2019, 12, 3312. [Google Scholar] [CrossRef] [Green Version]
- Jo, H.; Choi, J.; Agyeman, K.A.; Han, S. Development of frequency control performance evaluation criteria of BESS for ancillary service: A case study of frequency regulation by KEPCO. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies–Asia (ISGT–Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–5. [Google Scholar]
- Sanduleac, M.; Toma, L.; Eremia, M.; Boicea, V.A.; Sidea, D.; Mandis, A. Primary frequency control in a power system with battery energy storage systems. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar]
- Stein, K.; Tun, M.; Matsuura, M.; Rocheleau, R. Characterization of a fast battery energy storage system for primary frequency response. Energies 2018, 11, 3358. [Google Scholar] [CrossRef] [Green Version]
- Bang, H.; Aryani, D.R.; Song, H. Application of battery energy storage systems for relief of generation curtailment in terms of transient stability. Energies 2021, 14, 3898. [Google Scholar] [CrossRef]
- Meng, Y.; Li, X.; Liu, X.; Cui, X.; Xu, P.; Li, S. A Control Strategy for Battery Energy Storage Systems Participating in Primary Frequency Control Considering the Disturbance Type. IEEE Access 2021, 9, 102004–102018. [Google Scholar] [CrossRef]
- Izadkhast, S.; Cossent, R.; Frías, P.; García-González, P.; Rodríguez-Calvo, A. Performance Evaluation of a BESS Unit for Black Start and Seamless Islanding Operation. Energies 2022, 15, 1736. [Google Scholar] [CrossRef]
- Abayateye, J.; Corigliano, S.; Merlo, M.; Zimmerle, D. BESS Primary Frequency Control Strategies for the West Africa Power Pool. Energies 2022, 15, 990. [Google Scholar] [CrossRef]
- Schiapparelli, G.P.; Massucco, S.; Namor, E.; Sossan, F.; Cherkaoui, R.; Paolone, M. Quantification of primary frequency control provision from battery energy storage systems connected to active distribution networks. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Zhu, D.; Zhang, Y.-J.A. Optimal coordinated control of multiple battery energy storage systems for primary frequency regulation. IEEE Trans. Power Syst. 2018, 34, 555–565. [Google Scholar] [CrossRef]
- Toma, L.; Sanduleac, M.; Baltac, S.A.; Arrigo, F.; Mazza, A.; Bompard, E.; Musa, A.; Monti, A. On the virtual inertia provision by BESS in low inertia power systems. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Choi, W.Y.; Kook, K.S.; Yu, G.R. Control strategy of BESS for providing both virtual inertia and primary frequency response in the Korean Power System. Energies 2019, 12, 4060. [Google Scholar] [CrossRef] [Green Version]
- Pinthurat, W.; Hredzak, B. Decentralized Frequency Control of Battery Energy Storage Systems Distributed in Isolated Microgrid. Energies 2020, 13, 3026. [Google Scholar] [CrossRef]
- Obaid, Z.A.; Cipcigan, L.; Muhssin, M.T.; Sami, S.S. Control of a population of battery energy storage systems for frequency response. Int. J. Electr. Power Energy Syst. 2020, 115, 105463. [Google Scholar] [CrossRef]
- Amin, M.R.; Negnevitsky, M.; Franklin, E.; Alam, K.S.; Naderi, S.B. Application of battery energy storage systems for primary frequency control in power systems with high renewable energy penetration. Energies 2021, 14, 1379. [Google Scholar] [CrossRef]
- Manbachi, M.; Sadu, A.; Farhangi, H.; Monti, A.; Palizban, A.; Ponci, F.; Arzanpour, S. Real-time co-simulation platform for smart grid volt-VAR optimization using IEC 61850. IEEE Trans. Ind. Inform. 2016, 12, 1392–1402. [Google Scholar] [CrossRef]
- Mana, P.T.; Schneider, K.P.; Du, W.; Mukherjee, M.; Hardy, T.; Tuffner, F.K. Study of microgrid resilience through co-simulation of power system dynamics and communication systems. IEEE Trans. Ind. Inform. 2020, 17, 1905–1915. [Google Scholar]
- Adewole, A.C.; Tzoneva, R. Co-simulation platform for integrated real-time power system emulation and wide area communication. IET Gener. Transm. Distrib. 2017, 11, 3019–3029. [Google Scholar] [CrossRef]
- Garau, M.; Ghiani, E.; Celli, G.; Pilo, F.; Corti, S. Co-simulation of smart distribution network fault management and reconfiguration with lte communication. Energies 2018, 11, 1332. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, A.; Masutomi, K.; Ono, I.; Ishii, H.; Onoda, T. Cps-sim: Co-simulation for cyber-physical systems with accurate time synchronization. IFAC Pap. 2018, 51, 70–75. [Google Scholar] [CrossRef]
- Cao, Y.; Shi, X.; Li, Y.; Tan, Y.; Shahidehpour, M.; Shi, S. A simplified co-simulation model for investigating impacts of cyber-contingency on power system operations. IEEE Trans. Smart Grid 2017, 9, 4893–4905. [Google Scholar] [CrossRef]
- Jin, T.-H.; Chung, M.; Shin, K.-Y.; Park, H.; Lim, G.-P. Real-time dynamic simulation of Korean power grid for frequency regulation control by MW battery energy storage system. J. Sustain. Dev. Energy Water Environ. Syst. 2016, 4, 392–407. [Google Scholar] [CrossRef] [Green Version]
- ProTRAX, Energy Solutions. Available online: https://energy.traxintl.com/protrax (accessed on 27 June 2022).
- Turbine-Governor Models: Standard Dynamic Turbine-Govorner System in NEPLAN Power System Analysis Tool; NEPLAN AG: Küsnacht, Switzerland, 2015.
- Araújo, P. Dynamic Simulations in Realistic-Size Networks. Master’s Thesis, Universidade Técnica De Lisboa, Lisboa, Portugal, 2010. [Google Scholar]
- PSS/E 34 Model Library; Siemens, PTI: New York, NY, USA, 2015.
- ProTRAX Analyst’s Instruction Manual; Version 7.2; TRAX International: Virginia, VA, USA, 2014.
- Korea Power Exchanger, Electric Power Statistics Information System: Generator Detail Contents. Available online: http://epsis.kpx.or.kr/epsisnew/selectEkfaFclDtlChart.do?menuId=020600 (accessed on 10 June 2021).
- Kundur, P. Power system stability. In Power System Stability and Control; Grigsby, L.L., Ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kothari, D.P.; Nagrath, I. Modern Power System Analysis; Tata McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
- Lim, G.-P.; Han, H.-G.; Chang, B.-H.; Yang, S.-K.; Yoon, Y.-B. Demonstration to operate and control frequency regulation of power system by 4MW energy storage system. Trans. Korean Inst. Electr. Eng. P 2014, 63, 169–177. [Google Scholar] [CrossRef] [Green Version]
- Han, J.B.; Kook, K.S.; Chang, B. A study on the criteria for setting the dynamic control mode of battery energy storage system in power systems. Trans. Korean Inst. Electr. Eng. 2013, 62, 444–450. [Google Scholar] [CrossRef] [Green Version]
- Yun, J.Y.; Yu, G.; Kook, K.S.; Rho, D.H.; Chang, B.H. SOC-based control strategy of battery energy storage system for power system frequency regulation. Trans. Korean Inst. Electr. Eng. 2014, 63, 622–628. [Google Scholar] [CrossRef] [Green Version]
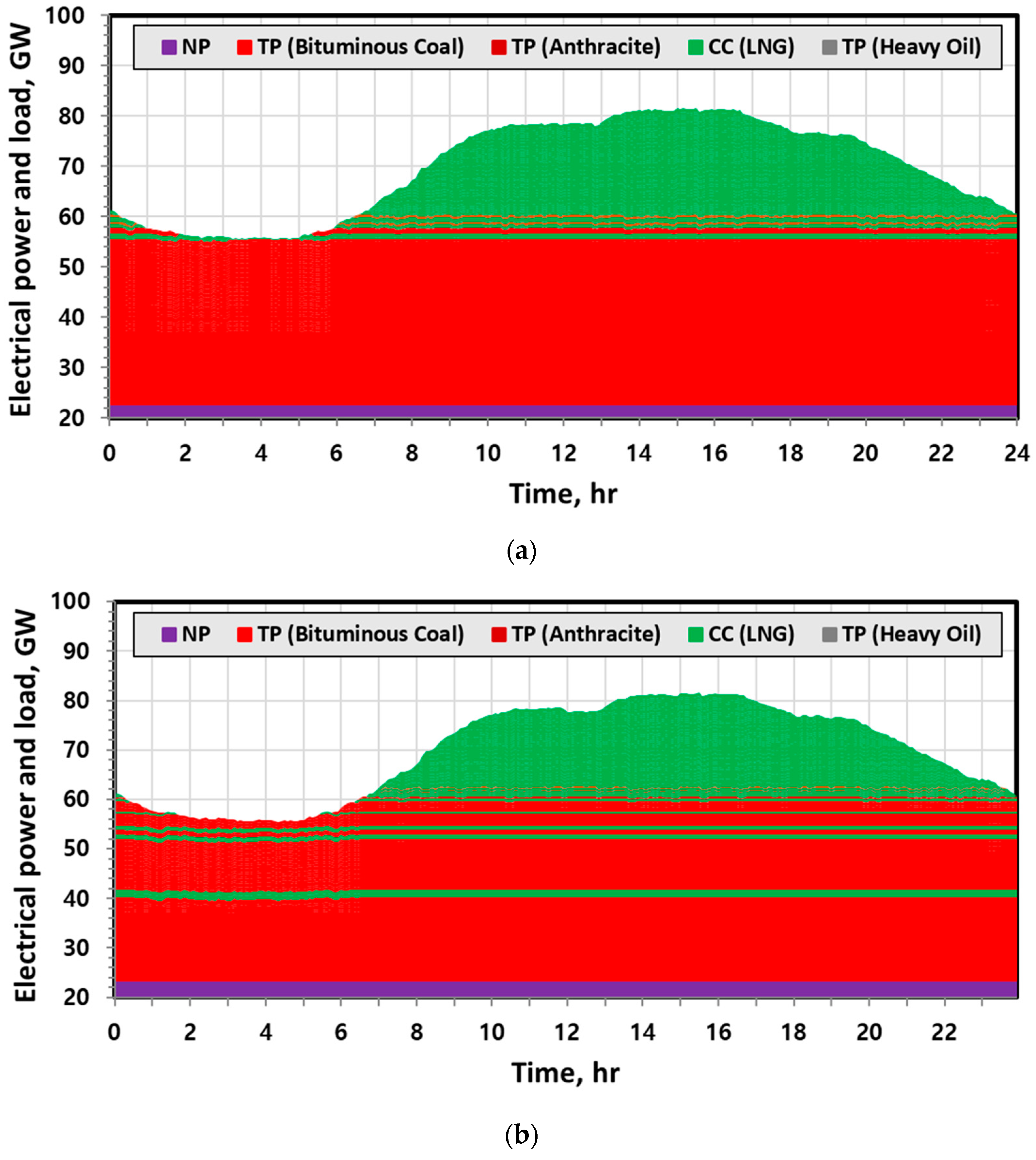
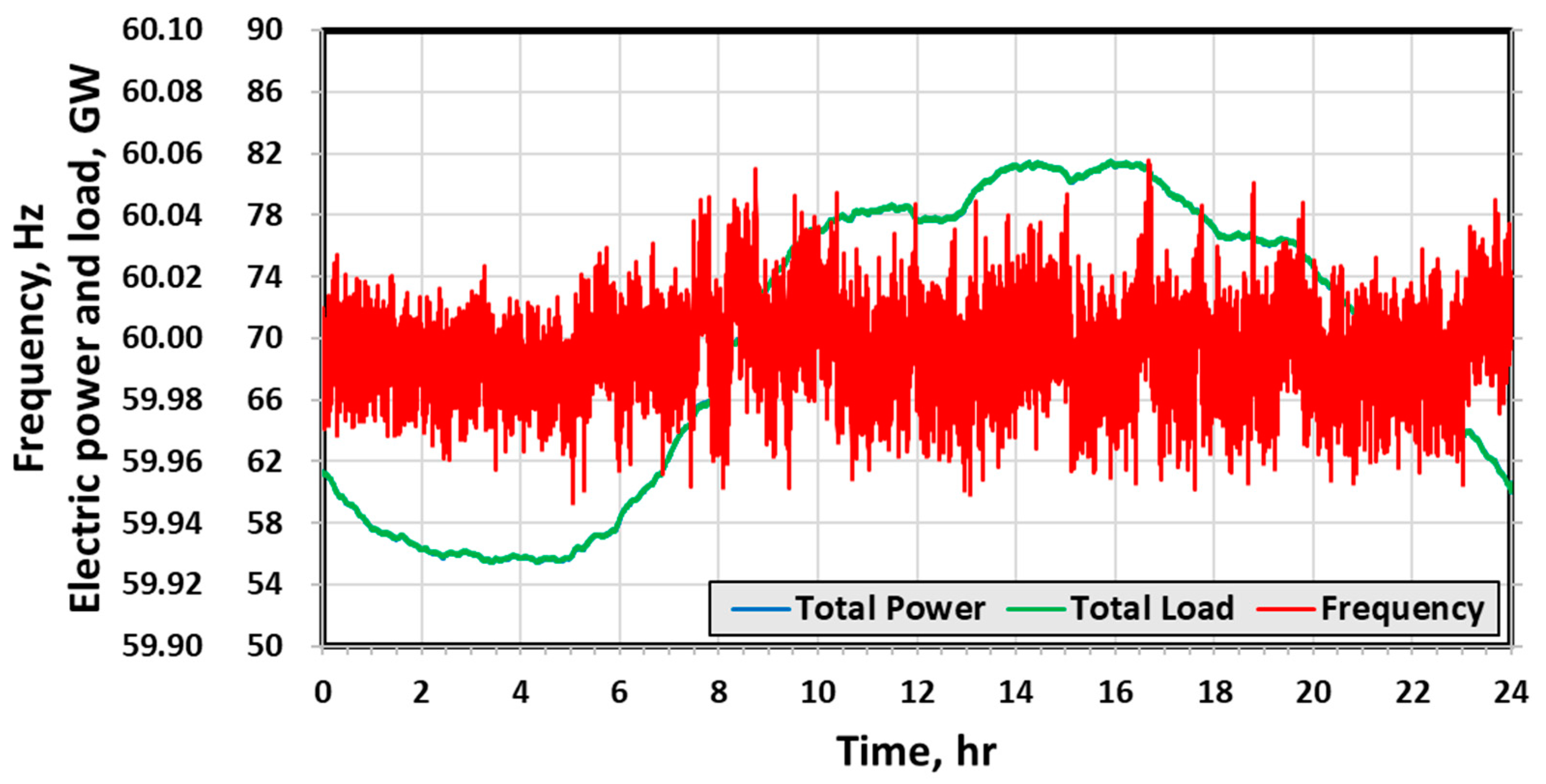

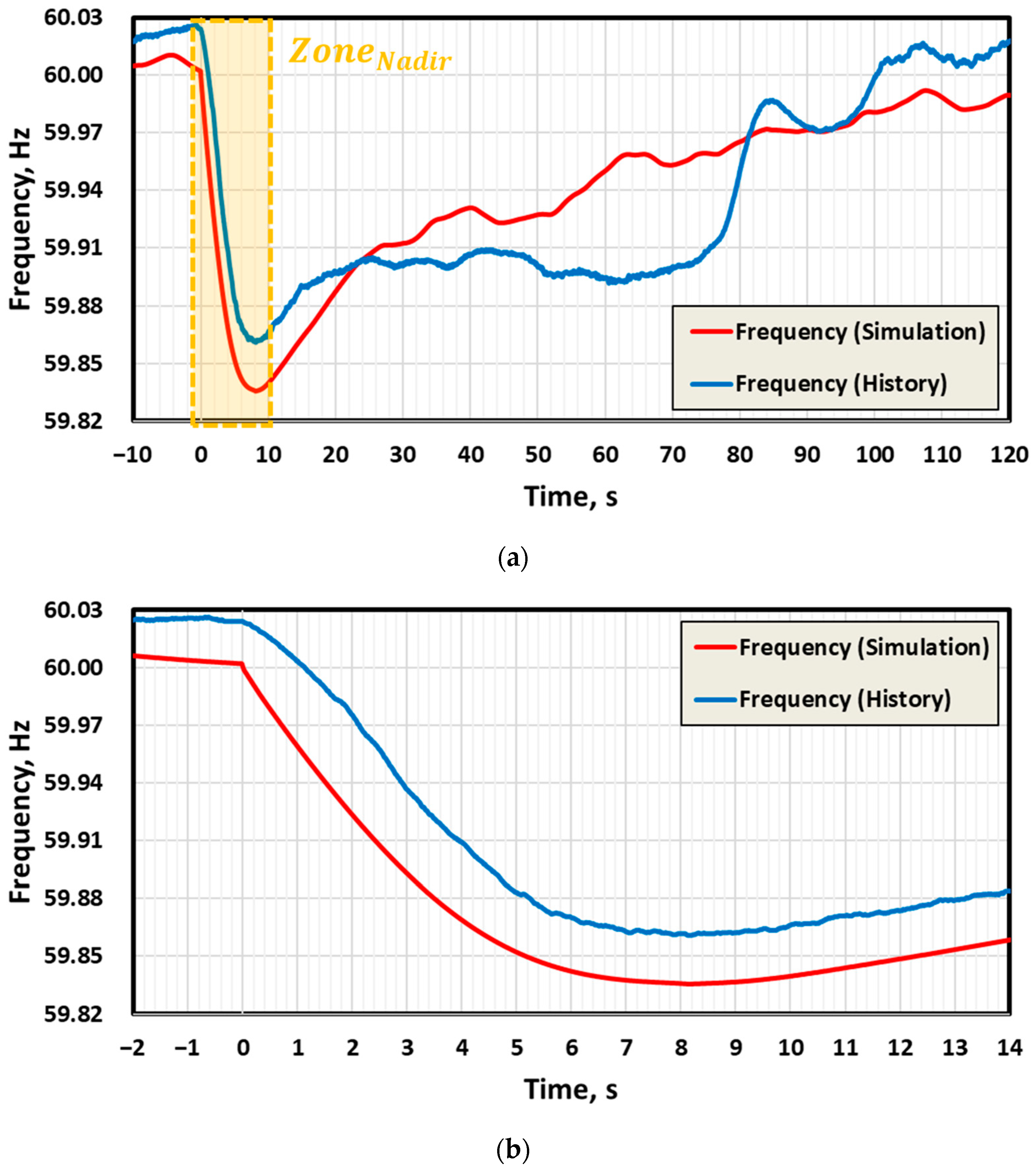

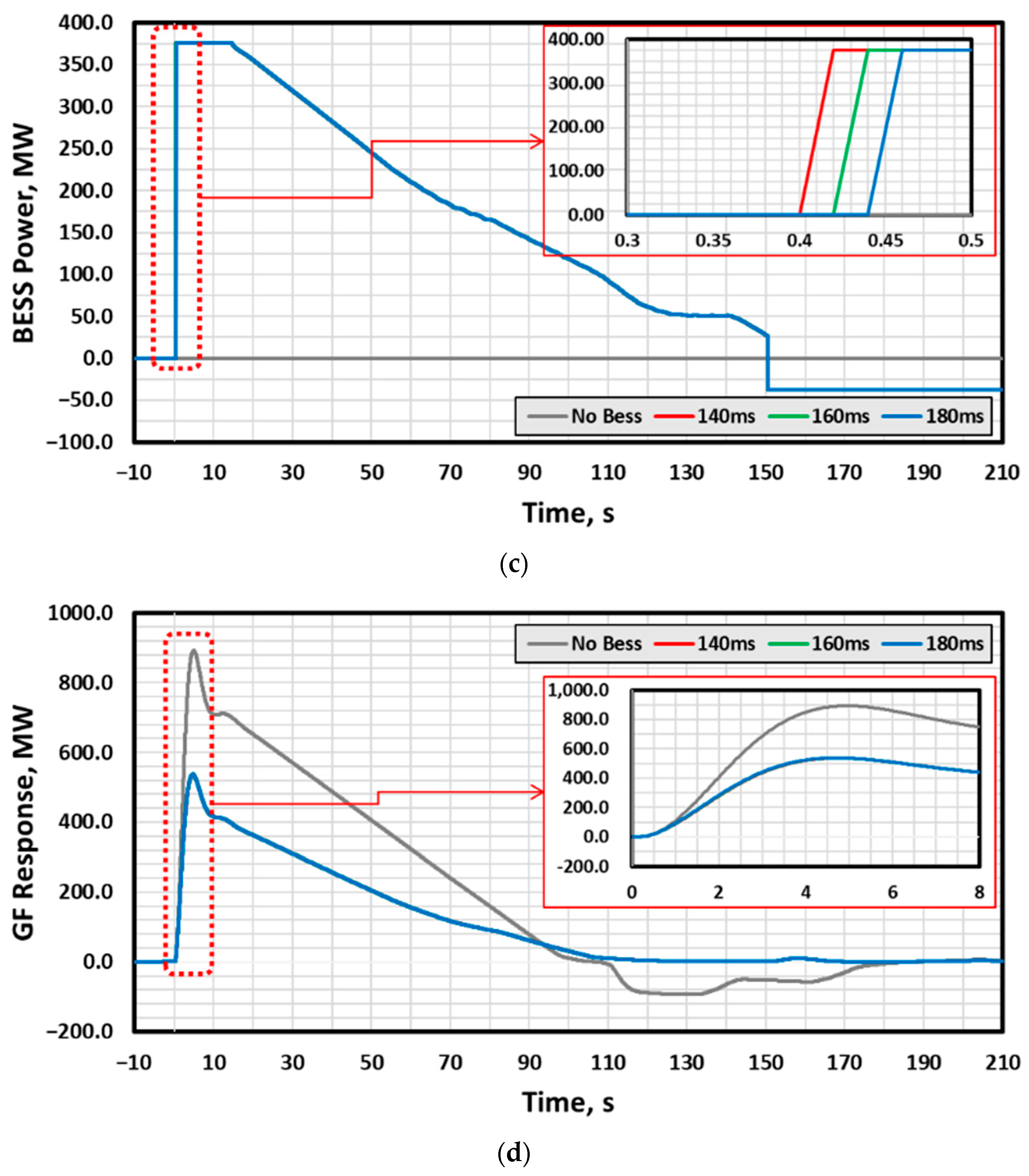
| NP | TP | TP | CC | PSH | |
|---|---|---|---|---|---|
| Fuel Type | Nuclear | Coal | Heavy Oil | LNG | Water |
| Rated capacity (GW) | 23.25 | 35.74 | 2.95 | 32.48 | 3.7 |
| Number (EA) | 24 | 65 | 13 | 63 | 12 |
| Efficiency (%) | 33.0~39.0 | 33.0~42.0 | 32.0~33.0 | 42.0~54.0 | 76.0~82.0 |
| Inertia Constant (s) | 6.0~9.0 | 4.0~7.0 | 4.0~5.0 | 3.0~6.0 | 2.0~4.0 |
| Turbine speed (RPM) | 1800 | 3600 | 3600 | 3600 | 300~600 |
| Droop (%) | - | 5~9 | 4~6 | 6~8 | 3~4 |
| Dead band (Hz) | - | ±0.0~±0.038 | ±0.01~±0.03 | ±0~±0.06 | ±0.02~±0.033 |
| Ramp rate (%MW/min) | - | 0.7~3.1 | 1.1~2.3 | 2.6~16.0 | 22.0~32.0 |
| Heat rate (MBtu/MWh) | 9200~10,700 | 8000~10,900 | 11,000~11,200 | 6400~8500 | - |
| NP | TP Bituminous | TP Anthracite | CC LNG | TP Heavy Oil | |
|---|---|---|---|---|---|
| Fuel Cost ($/MWh) | 4.96 | 44.17 | 53.35 | 72.46 | 141.11 |
| Emission Factor | - | 0.8867 | 0.8867 | 0.3889 | 0.6588 |
| No BESS (Case1) | 140 ms (Case2) | 160 ms (Case3) | 180 ms (Case4) | |
|---|---|---|---|---|
| 59.9914 | 59.9914 | 59.9914 | 59.9914 | |
| 3.04 | 2.84 | 2.82 | 2.80 | |
| 59.8401 | 59.8954 | 59.8952 | 59.8951 | |
| 0.1599 | 0.1046 | 0.1048 | 0.1049 | |
| 0.05259 | 0.0368 | 0.0372 | 0.0375 | |
| - | −0.0510 | −0.0505 | −0.0500 | |
| 893.86 | 535.02 | 538.72 | 539.11 | |
| 105.1 | 150.2 | 150.2 | 150.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, T.-H.; Shin, K.-Y.; Chung, M.; Lim, G.-P. Development and Performance Verification of Frequency Control Algorithm and Hardware Controller Using Real-Time Cyber Physical System Simulator. Energies 2022, 15, 5722. https://doi.org/10.3390/en15155722
Jin T-H, Shin K-Y, Chung M, Lim G-P. Development and Performance Verification of Frequency Control Algorithm and Hardware Controller Using Real-Time Cyber Physical System Simulator. Energies. 2022; 15(15):5722. https://doi.org/10.3390/en15155722
Chicago/Turabian StyleJin, Tae-Hwan, Ki-Yeol Shin, Mo Chung, and Geon-Pyo Lim. 2022. "Development and Performance Verification of Frequency Control Algorithm and Hardware Controller Using Real-Time Cyber Physical System Simulator" Energies 15, no. 15: 5722. https://doi.org/10.3390/en15155722
APA StyleJin, T.-H., Shin, K.-Y., Chung, M., & Lim, G.-P. (2022). Development and Performance Verification of Frequency Control Algorithm and Hardware Controller Using Real-Time Cyber Physical System Simulator. Energies, 15(15), 5722. https://doi.org/10.3390/en15155722







