Speed Control of Switched Reluctance Motor Based on Regulation Region of Switching Angle

Abstract

This paper studies the speed control strategy of a switched reluctance motor based on angle-position control (APC). The switched reluctance motor has three control parameters: turn-on angle, turn-off angle and voltage PWM duty cycle. This paper studies the function of the three parameters and designs the control algorithms of the parameters, respectively, which can reduce the coupling degree, simplify the control process, and realize the optimal control of the switched reluctance motor. By studying the nonlinear characteristics of the switched reluctance motor, the optimal current waveform in the effective working range of the inductor is obtained, and then a control strategy of the turn-on angle is designed to realize the ideal winding current waveform. According to the torque characteristics of the motor, taking the coincidence of the freewheeling zero point and the position angle at the end of the maximum inductance interval as the control target, a control strategy for the turn-off angle that makes full use of the effective inductance working interval is proposed, which improves the efficiency of the system. For the nonlinear and time-variant switched reluctance motor running process, a data-driven model-free adaptive control algorithm is introduced, and a switched reluctance motor speed control algorithm based on voltage PWM duty cycle is designed. The main contribution of this paper is to propose a control strategy that is generally applicable to switched reluctance motors, which does not depend on the precise mathematical model of the motor. The control algorithms are designed separately for the three control parameters according to the characteristics of the motor, which reduces the degree of coupling among them. A switched reluctance motor drive system based on angle-position control is designed. This strategy is especially suitable for driving the load with sudden large torque pulsation.

1. Introduction

The switched reluctance motor has a simple strong structure and low cost and has been widely used in recent years with the development of power electronics technology [1]. The switched reluctance motor has the characteristics of saturation, nonlinearity, time-varying, etc. It is difficult to obtain an accurate mathematical model [2], and the control effect of the model-based control theory is not ideal [3]. Many scholars have devoted themselves to research on the control strategy of switched reluctance motor [4,5], in order to obtain the ideal control effect. In practical applications, the switched reluctance motor usually works in the speed regulation mode, so it is necessary to design an appropriate control strategy to track the target speed.

At present, the speed control methods of switched reluctance motors generally include direct torque control and indirect control. The direct torque control method generally fixes the turn-on angle and the turn-off angle is unchanged. According to the difference between the actual speed and the target speed, the reference torque is generated, and the actual torque is estimated according to the rotor position and the feedback current value, and then controls the switch of the power device according to the comparison value of the reference torque and the estimated torque [6]. The more commonly used torque estimation methods include look-up table method [7], support vector machine [8], neural network [9] and so on. The accuracy of the torque estimation model has a great influence on the effect of direct torque control [10]. The switched reluctance motor has nonlinear and time-varying characteristics, and its torque model changes with the speed and motor current [11]; it is not easy to achieve accurate modeling, so the effect of direct torque control is not good. Indirect control is generally a double closed-loop control method, including an inner loop and an outer loop; the outer loop is a speed loop, and the inner loop is a current loop. The speed loop generates a given signal of the current loop according to the error signal of the rotational speed, and the current loop realizes the closed-loop tracking control of the current according to the error between the given current signal and the feedback current signal. The function of the speed loop is to generate a reference current according to the difference between the actual speed and the target speed. The commonly used speed loop control algorithms include fuzzy control [12], PID control, iterative learning control [13], and synovial film control [14]. The current loop controls the switch of the power device to make the actual current value close to the reference current value [15]. Current loop includes current waveform control mode and switching angle control mode. The current waveform control method controls the current of the motor to track the reference current at any time in the entire commutation cycle [16], which is suitable for the method of changing the reference current. However, for different speeds, different loads and different motors, the reference current is different, and the torque–current modeling is difficult, so it is difficult to design a control algorithm with universal applicability. The current loop of the switching angle control method only controls the current between the opening angle and the closing angle [17], and the difficulty is still the construction of a current–torque model that conforms to the nonlinear characteristics of the motor. In fact, due to the saturation, nonlinearity, and time-varying characteristics of switched reluctance motor, it is difficult to establish an accurate current torque model in the full speed range and power range, so the control strategy of switched reluctance motor based on torque and current have certain limitations.

The switched reluctance motor has a doubly salient structure, and the torque ripple and noise are larger, especially at low speed. A large part of the above-mentioned current or torque-based speed regulation is to overcome its torque ripple and noise [18]. In fact, many applications require the motor to operate at medium or high speed, and the noise and vibration requirements of the motor are not high, such as textile, petroleum, mining machinery, etc. On the other hand, multi-pole motor structure or reducer can be used to reduce the impact of torque ripple, and a relatively simple angle-position control (APC) mode can be adopted to realize the speed regulation control of switched reluctance motor through the voltage PWM duty cycle [19]. The switch reluctance motor speed control strategy based on the angle-position method has three parameters: turn-on angle, turn-off angle, and voltage PWM duty cycle. Studies have shown that the turn-on and turn-off angles have a great influence on the efficiency and torque of the motor [20,21], and the voltage PWM duty cycle is the main parameter for speed control. Therefore, it is necessary to optimize the control strategy of the three parameters to achieve the goal of speed tracking from the perspective of improving efficiency [22]. However, there is a coupling relationship among the three parameters of turn-on angle, turn-off angle, and voltage PWM duty cycle, which greatly increases the difficulty of speed control optimization. At present, in many studies on the optimal control of a switched reluctance motor, the coupling problem of control parameters has not been well solved. Therefore, starting from the main control functions of the three parameters, this paper designs the corresponding control strategies, respectively, which greatly reduces the coupling degree among them, and realizes the speed tracking control by using the model free adaptive control algorithm.

According to the linear inductance model of the switched reluctance motor, the phase winding current outputs the driving torque in the inductance rising interval [23], and outputs the negative torque in the inductance falling interval [24]. The winding current starts to decrease gradually after the turn-off angle, when the current decreases to 0, the corresponding rotor position angle is called the freewheeling zero point. If the freewheeling zero point continues to the inductance drop range, the current will generate negative torque and reduce the system efficiency. On the contrary, when the freewheeling current drops to 0 prematurely, the inductance rise interval is not fully utilized, which will also reduce the efficiency of the motor. A reasonable turn-off angle control strategy must be designed, so that the freewheeling zero point is located near the end of the maximum inductance, so as to maximize the performance of the motor and improve the efficiency of the motor.

The nonlinear inductance model of the switched reluctance motor [7] shows that in the rising range of inductance, the saturation degree of the magnetic field increases with the increase in the inductance, resulting in a decrease in the slope of the inductance curve; even if the winding current is increased, the output torque of the motor increase is not big. The ideal current waveform is that the current is larger at the beginning of the inductance rising interval, which can generate larger torque; after that, as the inductance increases, the current gradually decreases, and the saturation of the magnetic field will decrease accordingly, which will increase the torque output capability per unit current. The voltage equation of the linear inductance model of the switched reluctance motor shows that in order to make the winding current drop in the inductance rising interval, the moving potential must be made larger than the external voltage [25], that is, a lower voltage PWM duty cycle is used. Since the duty ratio of the voltage PWM is relatively small, the turn-on angle must be reduced so that the winding current has sufficient rise time before entering the inductance rising interval, so as to ensure that it has a large enough current to generate a large torque when it enters the inductance rising interval. For a fixed external voltage, when the turn-on angle is less than a certain value θ_K, the current can meet the requirements of the ideal waveform. Therefore, adjusting the turn-on angle within a feasible turn-on angle range [θ₁, θ_K] can realize the current slope in the effective range of the inductor is negative optimal current waveform.

Three parameters—the turn-on angle, turn-off angle, and voltage PWM duty cycle—have a coupling relationship in the process of speed control. According to the different control functions of the three parameters, combined with the ideal current waveform, the control strategies are designed separately, which can greatly reduce the degree of coupling among them. The main function of the turn-on angle and turn-off angle is to control the current waveform of the winding to realize the optimal control of the current. The voltage PWM duty cycle can adjust the average voltage applied to the motor to achieve a wide range of speed tracking control. Since the switched reluctance motor is nonlinear and time-varying, its model changes constantly with the working conditions. It is necessary to use an algorithm with self-adaptive ability to realize the speed tracking control according to the real-time operating data of the motor. Model-free adaptive control (MFAC) theory and method is a typical data-driven control method [26]. MFAC uses a new dynamic linearization method and a concept called pseudo partial derivative (PPD) for discrete-time nonlinear systems, establishes an equivalent dynamic linearization data model at each dynamic working point of the closed-loop system, and then designs a controller based on this equivalent virtual data model and carries out the theoretical analysis of the control system, so as to realize the adaptive control of the nonlinear system. At present, the MFAC method has been applied in driverless [27], unmanned surface vehicles [28], urban transportation network [29], power system damping control [30], motor drive control [31,32], and other fields. Both theoretical analysis and practical application show that MFAC has simple calculation and strong robustness. The most important thing is that it does not need any system model information and only needs the input and output data of the system to control, which has strong applicability. In this paper, the control algorithm is designed for the three parameters, respectively, to reduce the coupling among them, and then the data-driven model free adaptive control algorithm is introduced into the speed control of a switched reluctance motor to achieve a good speed control effect.

In the speed control method based on current chopping, the control period of the current loop is much smaller than that of the speed loop. In some sudden large torque pulsation conditions, the torque generated by the motor current is much smaller than the load torque, and the motor speed drops rapidly. For the APC speed control method based on the voltage PWM duty cycle, the output of the speed loop is the voltage PWM duty cycle, which is unchanged in a commutation period. When a sudden large torque pulsation occurs, the speed of the motor decreases rapidly, and the rotating electromotive force also decreases, so the average voltage is greater than the rotating electromotive force, the winding current of the motor increases rapidly, and the output torque also increases rapidly, that is, the output current increases following the sudden increase in the load, which can suppress the torque ripple. Therefore, the algorithm proposed in this paper has obvious advantages in controlling sudden large torque loads.

In summary, the main contributions of this paper are as follows:

(1)

A control strategy that does not depend on the exact model of switched reluctance motor is designed, which provides a feasible algorithm for switched reluctance motor control.

(2)

According to the characteristics of the switched reluctance motor, the turn-off angle control algorithm based on the optimal freewheeling zero point, the turn-on angle control algorithm based on the optimized current waveform, and the voltage PWM speed regulation control algorithm based on the model-free adaptive control are designed. The control strategies of three key parameters are designed, respectively, which greatly reduces the degree of coupling among them and simplifies the control algorithm.

(3)

The control strategy proposed in this paper can realize the speed tracking control of switched reluctance motor, especially suitable for driving loads with sudden large torque ripple.

2. Linear Model Analysis of Switched Reluctance Motor

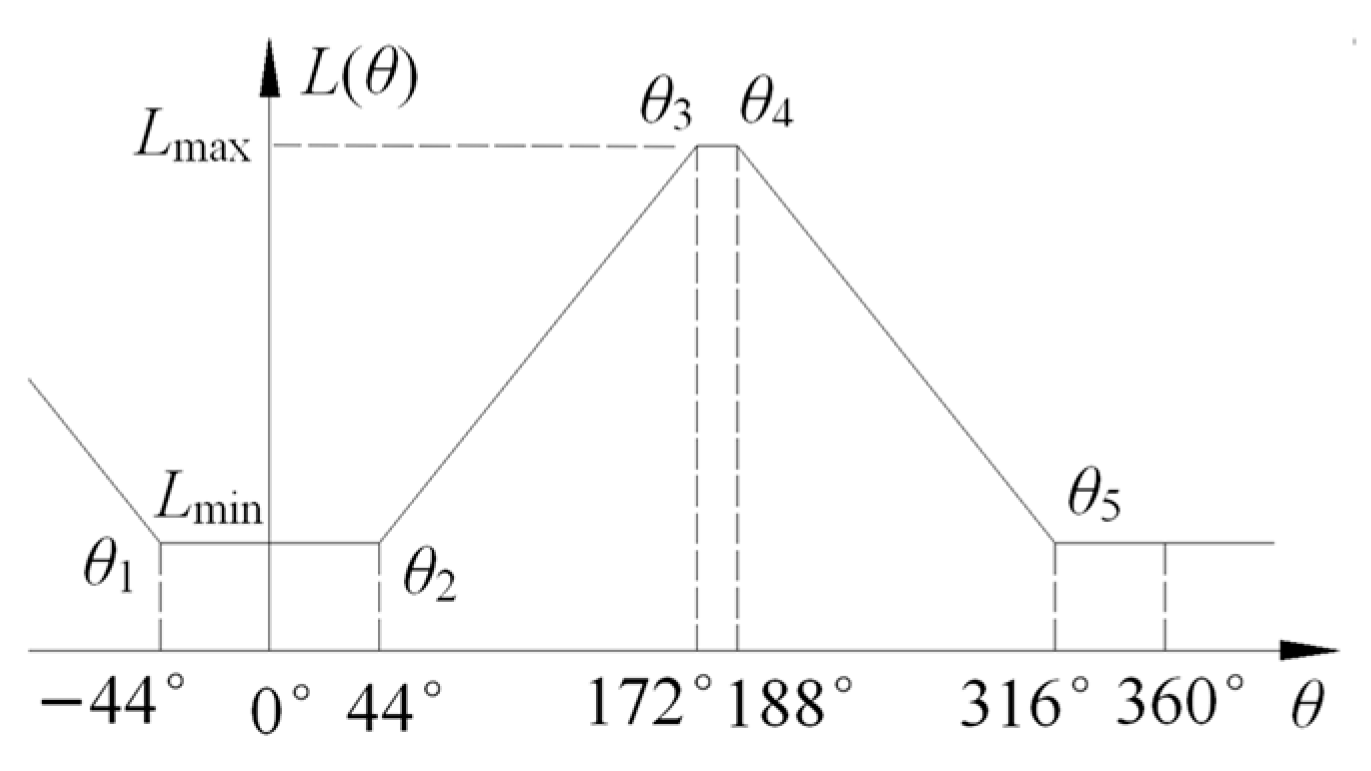
2.1. Linear Inductance Model of One Phase Winding

As shown in Figure 1, the upper part is the linear inductance curve of one-phase winding of stator, the lower part is the current curve of one-phase winding under APC control mode, the horizontal axis is the position angle of rotor θ, and the longitudinal axis is inductance L(θ) and current i(θ). L_max is the maximum inductance value of one-phase winding, L_min is the minimum inductance value of one-phase winding, θ_on is the turn-on angle, θ_off is the turn-off angle, i_θ2, i_θoff, i_θ3, i_θ4 and i_θ0 at the round black spot, respectively, represent the current when the rotor position angle θ is θ₂, θ_off, θ₃, θ₄ and θ₀. According to the shape of the linear inductance curve, the rotor position is divided into different working sections: the minimum inductance section [θ₁, θ₂], inductance rising range [θ₂, θ₃], maximum inductance section [θ₃, θ₄], inductance drop range [θ₄, θ₅]. Curve 1 in the current curve is the current in section [θ_on, θ₂] after the turn-on angle, curve 2 is the current when the rotor position angle θ is in the [θ₂, θ_off] range, curve 3 is the current when rotor position angle θ is in section [θ_off, θ₃], curve 4 is the current when the rotor position angle θ is in section [θ₃, θ₄], curve 5 is the current when rotor position angle θ is in section [θ₄, θ₀], and θ₀ is the rotor position angle when the current drops to zero.

The linear inductance equation of the stator phase winding of switched reluctance motor is:

$$L\left(\theta \right)=\{\begin{array}{l}{L}_{\min }\\ K\left(\theta -{\theta }_2\right)+L_{\min }\\ L_{\max }\\ L_{\max }-K\left(\theta -{\theta }_4\right)\end{array}\begin{array}{cc}& \begin{array}{l}{\theta }_1\le \theta <{\theta }_2\\ {\theta }_2\le \theta <{\theta }_3\\ {\theta }_3\le \theta <{\theta }_4\\ {\theta }_4\le \theta <{\theta }_5\end{array}\end{array}$$

(1)

where K = (L_max − L_min)/(θ₃ − θ₂), indicating the slope of inductance change.

The torque equation of switched reluctance motor based on linear inductance model is:

$$T=\{\begin{array}{l}0\\ K{i}^2\left(\theta \right)/2\\ 0\\ -K{i}^2\left(\theta \right)/2\end{array}\begin{array}{cc}& \begin{array}{c}{\theta }_1\le \theta <{\theta }_2\\ {\theta }_2\le \theta <{\theta }_3\\ {\theta }_3\le \theta <{\theta }_4\\ {\theta }_4\le \theta <{\theta }_5\end{array}\end{array}$$

(2)

Equation (2) shows that the current in the two inductance sections [θ₂, θ₃] and [θ₄, θ₅] can generate torque, the current in interval [θ₂, θ₃] can produce output driving torque, [θ₂, θ₃] is called the effective working interval. The current has no torque output in the minimum inductance section [θ₁, θ₂] and the maximum inductance section [θ₃, θ₄].

The linear inductance L(θ) of stator winding is a function of rotor position angle θ, and the voltage equation of the switched reluctance motor is:

$$\pm U_s=i\left(t\right)·R+L\left(\theta \right)\frac{di\left(\theta \right)}{d\theta }{\omega }_r+i\left(\theta \right)\frac{dL\left(\theta \right)}{d\theta }{\omega }_r$$

(3)

where U_s is the power voltage and “±” is the voltage direction of the winding. Assuming that one direction at both ends of the winding is “+”, the other direction is “−”, and ω_r is the rotor speed. In Equation (3), the first term on the right is the resistance voltage drop of phase winding, which is represented by u_r; the second item is the back potential caused by the change in current in the winding, which is called transformer potential and is represented by E_i; and the third item is the back potential generated by the winding inductance changing with the rotor position, which is called the rotating potential, and is represented by E_ω.

2.2. APC Control Analysis Based on Linear Inductance Model

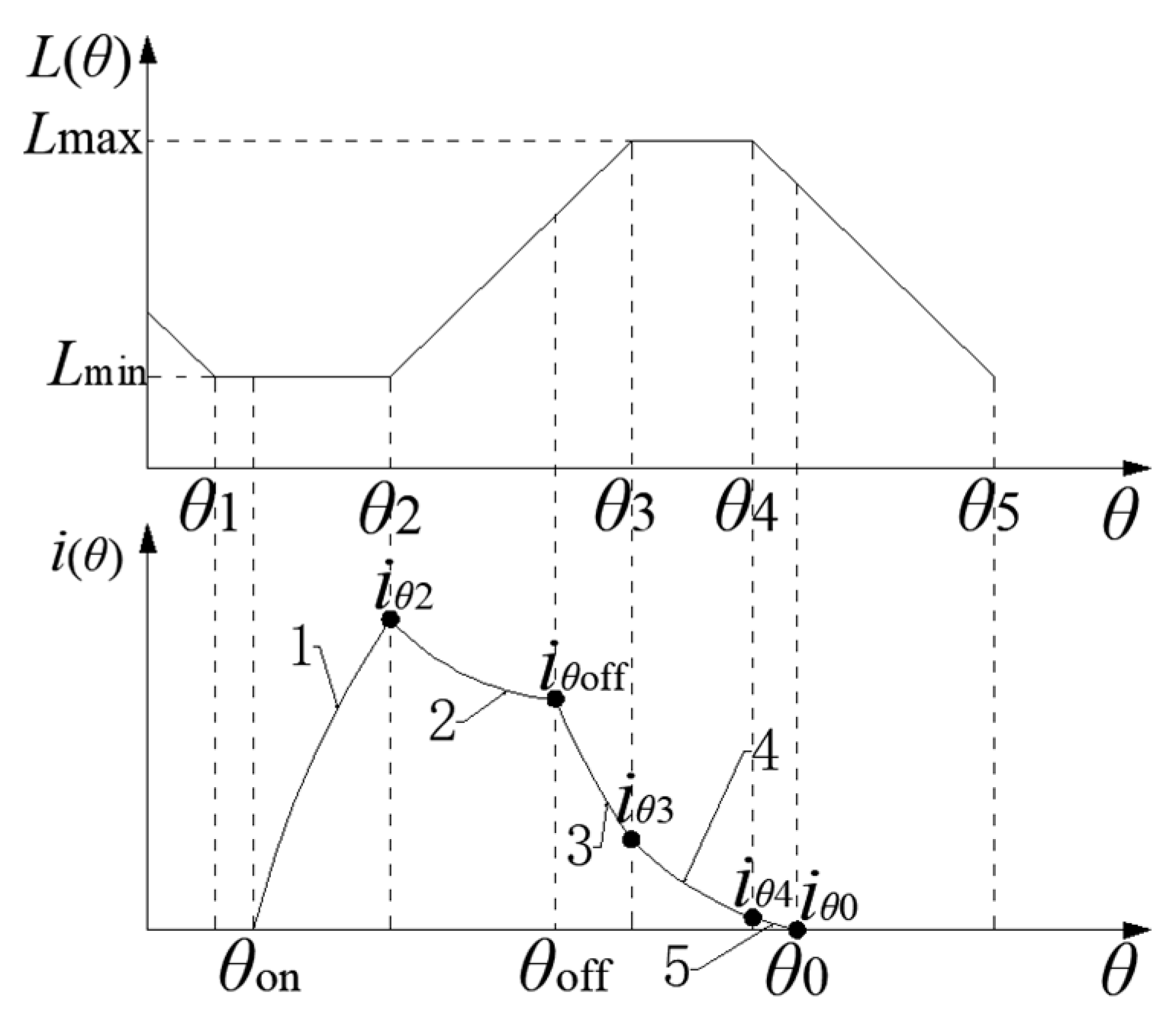
2.2.1. Current Analysis of Section [θ₁, θ₂]

As shown in Figure 1, when the rotor position angle θ is in section [θ₁, θ₂], the winding inductance L(θ) is the minimum value L_min. The switch tube of the main circuit is turned on at the position angle θ_on, the phase winding is powered on, and the current i(θ) is generated. The initial value is 0, ignoring the winding resistance voltage drop; the third operating potential in Equation (3) is 0; and the expression of current i(θ) is:

$$i\left(\theta \right)=\frac{U_S\left(\theta -{\theta }_{\mathrm{on}}\right)}{L_{\min }{\omega }_r}$$

(4)

The change rate of current is:

$$\frac{\mathrm{d}i\left(\theta \right)}{\mathrm{d}t}=\frac{U_S}{L_{\min }}=const>0$$

(5)

Equations (4) and (5) shows that the current of phase winding rises rapidly in the minimum inductance range. The smaller the θ_on, the longer the current rise time, the greater the winding current i_θ2 when the rotor reaches position θ₂, and the greater the torque generated by the motor in the effective inductance range [θ₂, θ₃].

2.2.2. Current Analysis of Section [θ₂, θ_off]

[θ₂, θ_off] is located in the front section of section [θ₂, θ₃], and the winding current can generate torque in this section. Bring θ₂ into Equation (4), which can obtain the initial current value i(θ₂) in section [θ₂, θ_off], ignore the winding resistance, and use Equations (1) and (3) to obtain the function of winding current varying with θ in this rotor position range:

$$i\left(\theta \right)=\frac{U_S\left(\theta -{\theta }_{\mathrm{on}}\right)}{{\omega }_r[L_{\min }+K\left(\theta -{\theta }_2\right)]}$$

(6)

The change rate of current is:

$$\frac{\mathrm{d}i\left(\theta \right)}{\mathrm{d}t}=\frac{U_S\left[L_{\min }+K\left({\theta }_{on}-{\theta }_2\right)\right]}{{[L_{\min }+K\left(\theta -{\theta }_2\right)]}^2}$$

(7)

Equation (7) shows that the turn-on angle θ_on determines the sign of current change rate. The winding current curves with different turn-on angles are shown in Figure 2. Curves 1, 2, and 3 represent the current changes when the turn-on angles are θ_on1, θ_on2 and θ_on3, respectively. The turn-off angle of the three curves is the same, and the winding currents at turn-off angle are, respectively, i_θoff1, i_θoff2 and i_θoff3. θ₀₁, θ₀₂ andθ₀₃ are the rotor position angles when the winding current drops to 0. The sign of the winding current change rate needs to be discussed in three cases.

(1)

θ_on < θ₂ − L_min/K

θ_on is relatively small, the current change rate is less than 0, the current gradually decreases in the rising range of inductance, and its initial value i(θ₂) is relatively large. The sum of transformer potential E_i and rotating potential E_r is greater than the supply voltage U_s, resulting in the decrease in current i(θ), as shown in curve 1 in Figure 2.

(2)

θ_on = θ₂ − L_min/K

The current change rate is equal to 0, the current remains unchanged in the inductance rising region, and the sum of transformer potential E_i and rotating potential E_r is equal to power supply voltage U_s, as shown in curve 2 in Figure 2.

(3)

θ_on > θ₂ − L_min/K

The change rate of current is greater than 0, the current increases in the rising region of inductance. θ_on is relatively large, the initial value of current i(θ₂) is relatively small, the sum of transformer potential E_i and rotating potential E_r is less than power supply voltage U_s, and current i(θ) rises, as shown in curve 3 in Figure 2.

To generate the same average torque, the starting current of curve 1 is large, and the turn-off angle is small. According to Equation (2), the motor will produce large torque ripple. The starting current of curve 3 is small, so the turn-off angle must be increased. Considering the saturation nonlinearity of the motor, the saturation degree of the motor increases and the efficiency decreases during the gradual increase in the current, and the freewheeling current of curve 3 is likely to continue to the area where the inductance decreases, resulting in negative torque, further reducing the efficiency of the motor. For curve 2, the winding current remains unchanged in the inductance rising range, and the motor outputs a constant torque, which is ideal.

2.2.3. Current Analysis Current Analysis of Section [θ_off, θ₃]

This section is at the rear of inductance rising section [θ₂, θ₃], the power tube of the controller is closed, and the winding current flows into the power through the freewheeling diode. In Equation (3), the symbol in front of U_s is “−”, the direction of transformer potential E_i is the same as that of current, the direction of rotating potential E_r is the same as that of (−U_s), and the current drops rapidly, as shown in curve 3 in Figure 1. Bring θ_off into Equation (7) to obtain the initial current, ignore the winding resistance voltage drop, and the analytical expression of freewheeling current i(θ) is:

$$i\left(\theta \right)=\frac{U_S\left(2{\theta }_{\mathrm{off}}-{\theta }_{\mathrm{on}}-\theta \right)}{{\omega }_r[L_{\min }+K\left(\theta -{\theta }_2\right)]}$$

(8)

It is known from Equation (2) that the freewheeling current can still generate driving torque in this section, so the turn-off angle θ_off should be increased as much as possible to increase the effective driving torque.

2.2.4. Current Analysis of Section [θ₃, θ₄]

The inductance in this section is the maximum value L_max, the symbol in front of U_s in Equation (3) is “−”, the rotating potential E_r becomes 0, the direction of transformer potential E_i is the same as the current direction, and the phase current decreases slowly. Bring θ₃ to Equation (8) to obtain the initial current, ignore the winding resistance voltage drop, and the analytical expression of freewheeling current i(θ) is:

$$i\left(\theta \right)=\frac{U_S\left(2{\theta }_{\mathrm{off}}-{\theta }_{\mathrm{on}}-\theta \right)}{{\omega }_r{L}_{\max }}$$

(9)

The change rate of current is:

$$\frac{\mathrm{d}i\left(\theta \right)}{\mathrm{d}t}=-\frac{U_S}{L_{\max }}=const<0$$

(10)

The current in this section gradually decreases, but due to the large inductance value, the rate of current decline slows down, as shown in curve 4 in Figure 1. According to Equation (2), the freewheeling current in this stage does not output torque but feeds back to the power.

2.2.5. Efficiency Analysis of Motors in APC Mode

In the APC control mode of fixed voltage, the smaller θ_on is, the longer the energization time of the phase winding is, and the larger the current i_θ2 in Figure 2 is. On the contrary, the larger the θ_on is, the shorter the energization time of the phase winding is, and the smaller the current i_θ2 is.

Figure 3 shows the winding current waveform when the turn-off angle θ_off is the same and the turn-on angle θ_on is different, in which θ_on1, θ_on2, and θ_on3 are three different turn-on angles, θ_off is the turn-off angle, and θ_m is the rotor position angle where the current of curve 3 reaches I_lim, L is the inductance curve, L_max is the maximum inductance, and L_min is the minimum inductance. Assume that the target current of the winding at θ₂ is I_lim, the curves 1 to 3 are the current waveforms of the winding in the minimum inductance interval at different turn-on angles, and the curves 4 and 5 are the current waveforms of the winding in the interval [θ₂, θ_off], respectively.

Assuming that the winding current needs to reach I_lim at θ₂, the turn-on angle θ_on1 of curve 3 in Figure 3 is small, the current rises rapidly, reaches I_lim at θ_m(θ_m < θ₂), and then remains at I_lim until θ₂ position. According to Equation (2), the inductor current has no torque output in the interval [θ_on1, θ₂], and the current in the interval [θ_m, θ₂] only produces copper loss in the winding, which reduces the efficiency of the motor. The current of curve 2 in Figure 3 just reaches I_lim at θ₂, there is no excess loss, and the efficiency is high. Curve 4 and curve 5 in Figure 3 are the current waveforms when the inductor enters the effective interval [θ₂, θ₃]. The turn-on angle θ_on3 of curve 1 is larger, the current rise time is shorter, and the winding current at θ₂ is smaller. After entering the inductance rising interval, the current continues to rise, as shown in curve 5 in Figure 3. When entering the effective range of the inductance [θ₂, θ₃], the current is small and the output torque is also small. With the gradual saturation of the inductance, although the current increases, the increase in the output torque is not large, resulting in lower efficiency of the motor. The effect of curve 4 in Figure 3 is better. In the non-saturation stage of the effective range of the inductor, the current is larger and the output torque is larger. With the increase in the inductance, the current gradually decreases, which will reduce the saturation degree of the inductor and increase the torque output capacity per unit current and improve the efficiency of the motor.

To sum up, from the perspective of improving the motor efficiency, the turn-on angle θ_on and the voltage PWM duty cycle D_PWM should be adjusted comprehensively so that the winding current just reaches the maximum value I_lim at θ₂ and the current gradually decreases in the rising range of the inductance, as shown in curve 2 and curve 4 in Figure 3. This is precisely the current waveform that can be achieved with APC control.

2.2.6. Analysis of Optimal Turn-Off Angle

Under the same working conditions, the larger the phase current i_θoff at the θ_off position, the longer the current freewheeling time, as shown in Figure 2, i_θoff1 < i_θoff2 < i_θoff3, and the corresponding rotor position where the freewheeling current drops to zero θ₀₁ < θ₀₂ < θ₀₃. If the turn-off angle θ_off is large, the freewheeling current will cross θ₄ and enter interval [θ₄, θ₅], as shown in the freewheeling zero point θ₀₃ shown in Figure 2. From Equation (2), the freewheeling current will generate negative torque, reducing the efficiency of the motor, and is also prone to torque ripple. On the contrary, if the turn-off angle θ_off is small, the freewheeling current drops to 0 earlier than θ₄, which shortens the power supply time of the power supply to the windings in the effective working range [θ₂, θ₃]; the freewheeling zero point θ₀₁ is shown in Figure 2. If the same average torque is to be generated, the duty cycle of the voltage PWM must be increased to increase the winding current, which will increase the torque ripple of the motor and reduce the performance of the motor. The turn-off angle θ_off2 of the current curve 2 in Figure 2 is ideal, and the position angle θ₀₂ at which the freewheeling current drops to 0 coincides with θ₄, which not only makes full use of the effective working range of the inductance that can output torque but also does not produce negative torque.

3. Switched Reluctance Motor Control Considering Nonlinearity

When a switched reluctance motor operates with load, it has strong nonlinearity and saturation. It is difficult to obtain a good control effect only by the linear inductance model. It is necessary to analyze the influence of saturation and nonlinearity on the motor model and design the corresponding control strategy.

3.1. Simulation Analysis of Nonlinear Inductance Model

Figure 4 shows the inductance curve of one-phase winding of switched reluctance motor obtained by finite-element simulation analysis. The horizontal axis is the rotor position angle and the vertical axis is the winding inductance. With the gradual increase in excitation current of phase winding, the nonlinear inductance curve has the following characteristics:

(1)

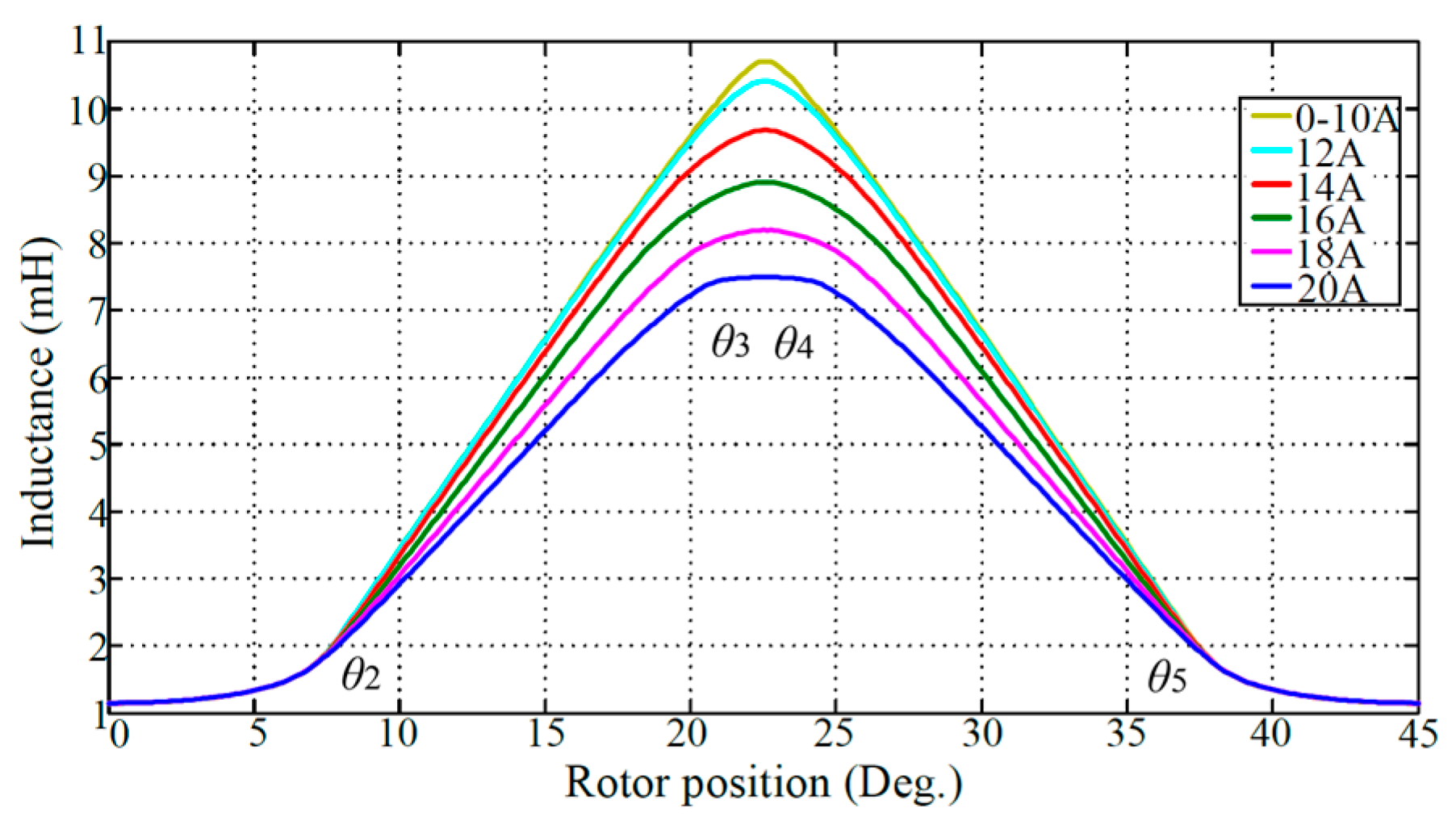
The position angle θ₂, θ₃, θ₄, θ₅ is given according to the structural dimensions of the motor, and there is no clear dividing line for the inductance curve during the actual operation of the motor.

(2)

With the increase in winding current, the rising slope of inductance in the effective working range gradually decreases. Although the winding current increases, the output torque does not increase in proportion to the square of the current.

(3)

Generally, the maximum inductance range of switched reluctance motor is designed to be small, and the inductance in this region is an approximately flat top wave when the motor is running. With the increase in rotor position angle θ, the inductance gradually increases in section [θ₂, θ₃], with the increase in load current, the saturation degree of the inductance becomes more and more serious, resulting in a gradual decline in the inductance, showing nonlinear characteristics. From the point of view of a switched reluctance motor design, this saturation characteristic is necessary, which is conducive to the performance of the switched reluctance motor, which determines that the switched reluctance motor has the characteristics of saturation and nonlinearity. With the increase in load current, the saturation degree of the maximum inductance section becomes more serious, and the inductance value decreases gradually, which is equivalent to increasing the width of the maximum inductance section.

(4)

After the switch tube of phase winding is turned off, the winding current gradually decreases, and the winding inductance will gradually withdraw from saturation, so the current in the inductance range [θ_off, θ₃] can also output large torque.

3.2. Switching Angle Control Considering Nonlinear Characteristics

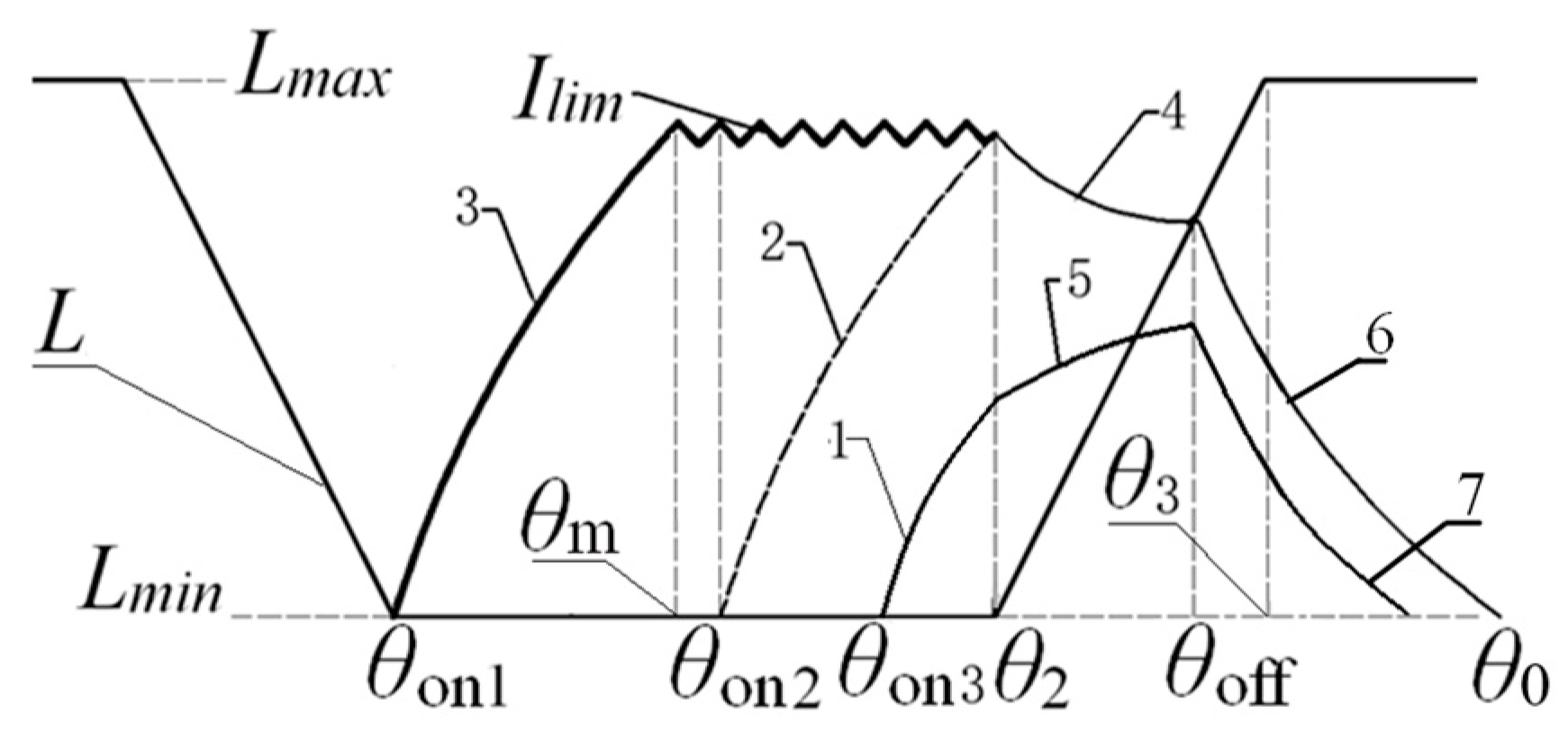
3.2.1. Optimal Winding Current Waveform

Considering the saturation of the winding inductance, the current waveform curve 1 in Figure 2 is ideal. When the rotor is at θ₂, the value of the winding current i_θ2 is large, and the inductance is not saturated at the initial stage of interval [θ₂, θ₃], so it can output a large torque. With the increase in rotor position angle θ, the inductance tends to saturation, and increasing the current is not conducive to the increase in torque. Therefore, the winding current should be appropriately reduced, which is conducive to reducing the saturation degree of inductance, reducing the iron loss of the motor and improving efficiency.

According to Equation (3), to reduce the current in the interval [θ₂, θ₃], it is necessary to make the motion potential E_r greater than the external voltage U_s. As the winding current drops, the transformer potential E_i is negative, releasing energy to maintain the winding current. From Equations (6) and (7), to obtain the current waveform of curve 1 in Figure 2 and to gradually reduce the current in the effective range [θ₂, θ₃] of the inductance, the opening angle must satisfy the inequality θ_on < θ₂ − L_min/K.

Therefore, to realize the current waveform shown in curve 1 in Figure 2, the duty cycle of the voltage PWM should be reduced as much as possible, and the average voltage U_s of the winding should be reduced. This requires reducing the turn-on angle θ_on and increasing the energization time in the [θ_on, θ₂] interval, so that the current i_θ2 obtains a larger value at θ₂. Since U_s is small, the winding current gradually decreases in the [θ₂, θ_off] interval, thus obtaining an ideal current waveform.

3.2.2. Optimal Control of Turn-On Angle θ_on

It can be seen from the above analysis that due to the nonlinear characteristics of the switched reluctance motor, the ideal current curve of the motor is shown in curve 1 in Figure 2 during APC speed control. Set θ_K = (θ₂ − L_min/K), in the interval [θ₂, θ_off], the slope of the winding current should be less than zero, and the value range of the turn-on angle θ_on should be [θ₂, θ_K]. For different load currents, the saturation degree of the winding inductance is different, and θ_K varies with the winding current.

Therefore, the optimal control strategy of the turn-on angle θ_on needs to determine the value of θ_K and the control method of θ_on. When the motor is running stably, if the turn-on angle θ_on is reduced, the charging time of the winding in the interval [θ_on, θ₂] will become longer, the current i_θ2 at θ₂ position will become larger, and the motor speed will increase accordingly. In order to maintain the stable operation of the motor, it is necessary to reduce the duty cycle of the voltage PWM, that is, to reduce the voltage U_S in Equation (3), so that the amplitude of the rotating electromotive force E_r exceeds U_S, and finally, the winding current in the interval [θ₂, θ_off] is decreased. This shows that when the turn-on angle θ_on is adjusted in the bounded interval [θ₂, θ_K], the slope of the winding current in the interval [θ₂, θ_off] can also change monotonically in a bounded interval. Therefore, the PI adjustment algorithm with self-adaptive ability can realize the slope control of the winding current in the interval [θ₂, θ_off], and its stability can be guaranteed.

Suppose the current at θ₂ is i_θ2, the current at θ_off is i_θoff, and Δ_i is the difference between them, namely:

$${\Delta }_{\mathrm{i}}\left(k+1\right)=i_{\theta 2}\left(k\right)-i_{\theta \mathrm{off}}\left(k\right)$$

(11)

Design the PI control rule with limiting function as shown in Equation (12):

$${{\theta }^{\prime }}_{\mathrm{on}}\left(k+1\right)=\{\begin{array}{l}{\theta }_1\\ K_{\mathrm{pon}}·\left[{\Delta }_{\mathrm{i}}\left(k\right)-\sigma \right]+{\displaystyle \sum _{j=0}^k{K}_{\mathrm{Ion}}·}\left[{\Delta }_{\mathrm{i}}\left(k\right)-\sigma \right]\\ {\theta }_{\mathrm{K}}\end{array}\begin{array}{cc}& \begin{array}{l}{\theta }_{\mathrm{on}}\left(k+1\right)\le {\theta }_1\\ {\theta }_1<{\theta }_{\mathrm{on}}\left(k+1\right)<{\theta }_2\\ {\theta }_{\mathrm{on}}\left(k+1\right)\ge {\theta }_2\end{array}\end{array}$$

(12)

where θ′_on(k + 1) is the turn-on angle, K_pon is the proportional coefficient, K_Ion is the integral coefficient. σ is the preset current difference. The purpose of setting σ is to ensure that i_θ2 is greater than i_θoff, so that the slope of the current in the [θ₂, θ_off] interval is negative, so the value of σ can be set to a smaller value, such as 1~2 A. Taking the slope of the winding current in the interval [θ₂, θ_off] to be a negative value close to 0 as the target, the maximum turn-on angle θ′_on that makes the current slope negative can be calculated by using Equation (12), taking θ′_on as θ_K, the value range [θ₁, θ_K] of the turn-on angle can be obtained. Since the inductance of the switched reluctance motor is nonlinear, the value of θ_K varies, and its calculation method is shown in Equation (13). When (Δi − σ) < 0, use Equation (12) to calculate θ_K until (Δ_i − σ) ≥ 0, and then keep θ_K unchanged. Thus, the value range [θ₁, θ_K] of the turn-on angle is determined.

$${\theta }_{\mathrm{K}}=\{\begin{array}{l}{\theta }_{\mathrm{K}}\\ {{\theta }^{\prime }}_{\mathrm{on}}\left(k+1\right)\end{array}\begin{array}{cc}& \begin{array}{l}{\Delta }_{\mathrm{i}}\left(k\right)-\sigma \ge 0\\ {\Delta }_{\mathrm{i}}\left(k\right)-\sigma \le 0\end{array}\end{array}$$

(13)

When the duty cycle of the voltage PWM is kept at a certain fixed value, the turn-on angle θ_on can adjust the motor speed within a certain range, so a PI speed control algorithm based on the turn-on angle is designed, as shown in Equation (14).

$${\theta }_{\mathrm{on}}\left(k+1\right)=\{\begin{array}{l}{\theta }_1\\ K_{\mathrm{sp}}·\left[{\omega }_{\mathrm{f}}\left(k\right)-{\omega }^{*}\left(k\right)\right]+{\displaystyle \sum _{j=0}^k{K}_{\mathrm{si}}·}\left[{\omega }_{\mathrm{f}}\left(k\right)-{\omega }^{*}\left(k\right)\right]\\ {\theta }_{\mathrm{K}}\end{array}\begin{array}{cc}& \begin{array}{l}{\theta }_{\mathrm{on}}\left(k+1\right)\le {\theta }_1\\ {\theta }_1<{\theta }_{\mathrm{on}}\left(k+1\right)<{\theta }_{\mathrm{K}}\\ {\theta }_{\mathrm{on}}\left(k+1\right)\ge {\theta }_{\mathrm{K}}\end{array}\end{array}$$

(14)

where ω_f is the feedback motor speed, ω* is the set motor speed, K_sp is the proportional coefficient, and K_si is the integral coefficient. The value of θ_on is limited to the interval [θ₁, θ_K] by the clipping function. Equation (14) is a discrete PI control algorithm, and its control period is the commutation period T_s of the switched reluctance motor, which can be used as the inner loop of speed control to adjust the speed of the motor within a certain range. The speed control based on the voltage PWM duty cycle can adjust the motor speed in a wide range, which is the outer loop of the speed control, and its control period can be set to more than ten times the commutation period T_s. In the voltage PWM control period, the speed is adjusted by the turn-on angle. When the target speed increases or the load torque increases, the motor speed must be adjusted by increasing the voltage PWM duty cycle if θ_on decreases to θ₁. On the contrary, when the target rotational speed decreases or the load torque decreases and if θ_on increases to θ_K, it is also necessary to adjust the rotational speed of the motor by reducing the voltage PWM duty cycle.

3.2.3. Optimal Control of Turn-Off Angle

The ideal turn-off angle θ_off makes the freewheeling current of the winding drop to 0 just at θ₄, that is, the freewheeling zero point θ₀ coincides with θ₄. The freewheeling process after θ_off is relatively complex, and it is not easy to establish an accurate freewheeling model. The control algorithm must be established according to the position characteristics of θ_off and the freewheeling zero point θ₀. Experiments show that under the same rotation speed, when the off current i_θoff is the same, the larger the θ_off, the larger the θ₀, that is to say, as the θ_off increases, the θ₀ also increases monotonically. The range of the controlled variable θ₀ and the control variable θ_off is small, and the position PI algorithm with adaptive ability can be used to design the control strategy of the turn-off angle. As shown in Figure 5, the control system continuously detects the freewheeling current of the winding after θ_off, obtains the freewheeling zero point θ₀, takes θ₄ as the target value of the freewheeling zero point, and designs the position PI algorithm, as shown in Equation (15).

$${\theta }_{\mathrm{off}}\left(k+1\right)=\{\begin{array}{l}\left({\theta }_2+{\theta }_3\right)/2\\ K_{\mathrm{cp}}·\left[{\theta }_4-{\theta }_0\left(k\right)\right]+{\displaystyle \sum _{j=0}^k{K}_{\mathrm{ci}}·}\left[{\theta }_4-{\theta }_0\left(k\right)\right]\\ {\theta }_3\end{array}\begin{array}{cc}& \begin{array}{l}{\theta }_{\mathrm{off}}\left(k\right)\le \left({\theta }_2+{\theta }_3\right)/2\\ \left({\theta }_2+{\theta }_3\right)/2<{\theta }_{\mathrm{off}}\left(k\right)<{\theta }_3\\ {\theta }_{\mathrm{off}}\left(k\right)\ge {\theta }_3\end{array}\end{array}$$

(15)

Among them, K_cp is the proportional coefficient, K_ci is the integral coefficient. (θ₂ + θ₃)/2 is the midpoint position of the inductance rising interval, Formula (15) is the limiting function, which limits the output turn-off angle within a reasonable range, and the control period is the same as the turn-on angle, which are the commutation periods of the windings.

3.3. Switching Angle Control Considering Nonlinear Characteristics

The switched reluctance motor has three control parameters: turn-on angle θ_on, turn-off angle θ_off and voltage PWM duty cycle D_PWM. It can be seen from the above analysis that the turn-on angle and turn-off angle are used to control the current waveform of the winding and improve the operating efficiency of the motor. To achieve a wide range of motor speed regulation, it is necessary to adjust the voltage PWM duty cycle. In this way, the coupling degree of the three parameters can be reduced, and the multi-variable control of the switched reluctance motor can be changed into a single-variable speed control based on the voltage PWM duty cycle. Since the switched reluctance motor has strong nonlinearity and is not easy to model accurately, a model-free adaptive control algorithm that does not depend on the system model is used to realize the speed control. In this method, the control system is designed by a data-driven method only according to the data during the operation of the system.

3.3.1. Compact Linearized Nonparametric Models for Nonlinear Systems

The switched reluctance motor speed control system based on the voltage PWM duty cycle can be regarded as a general discrete-time nonlinear system with single input and single output, and its expression is as follows:

$$y(k+1)=f(y(k),y(k-1),\dots ,y(k-n_y),u(k),u(k-1),\dots ,u(k-n_u))$$

(16)

where y(k) ∈R, is the controlled variable, representing the speed of the controlled motor; u(k)∈R, is the control variable, representing the voltage PWM duty cycle; n_y and n_u represent the unknown output and input quantities order; and f(…) is an unknown discrete time-varying nonlinear function. For expression (16), the following three assumptions are proposed [33]:

Assumption 1.

In the system (16), for the bounded desired output signal y*(k + 1), there is a bounded control input signal u*(k), so the formula y (k + 1) = y*(k + 1) is established under the driving of u*(k).

Assumption 2.

The partial derivatives of f(…) with respect to the (n_y + 2)th variable are continuous.

Assumption 3.

System (16) satisfies the Lipschitz condition, that is, for any k₁ ≠ k₂ and u(k₁) ≠ u(k₂):

$$\left|y(k_1+1)-y(k_2+1)\right|\le b\left|u(k_1)-u(k_2)\right|$$

(17)

where y(k_i + 1) = f(y(k_i), …, y(k_i − n_y), u(k_i), …, u(k_i − n_u)), i = 1, 2; b > 0 is a constant. From an energy point of view, a bounded change in input energy produces a bounded change in output energy within the system. For practical systems, Assumption 3 is true.

Lemma 1

([33]). For the nonlinear system (16), if the assumptions 1–3 are satisfied, there must be a time-varying parameter called pseudo partial derivative (PPD) when |Δu(k)| ≠ 0, so that the system (16) can be transformed into the following compact format dynamic linearization (CPDL) mathematical model:

$$\Delta y(k+1)={\varphi }_c(k)\Delta u(k)$$

(18)

where Δy(k + 1) = y(k + 1) − y(k) is the change in output at two adjacent moments; Δu(k) = u(k) − u(k − 1) is the change in the input quantity at two adjacent moments; in Equation (18), ϕ_c(k) is bounded at any time k. For the proof of Lemma 1, please refer to Section V-A of [33], which is ignored here.

The switched reluctance motor speed control system based on the voltage PWM duty cycle satisfies the following conditions:

(1)

The switched reluctance motor is a continuous motion system, and its dynamic system satisfies certain smoothness conditions.

(2)

When the bounded D_PWM is input, the speed ω_f of the motor does not exceed the allowable range, that is, when the generalized Lipschitz condition is satisfied, the bounded change in the system input will inevitably cause bounded change in the system.

Therefore, the switched reluctance motor speed control system based on the voltage PWM duty cycle can be described by the CPDL mathematical model shown in Equation (18). The control input u(k) is the voltage PWM duty cycle D_PWM of the switched reluctance motor at time k. The system output y(k) is the feedback speed ω_f(k) of the switched reluctance motor at time k. The control target y(k + 1) is the given rotational speed ω*(k) of the system.

3.3.2. Model-Free Adaptive Control Law Design

Consider the following control input criterion function [26,34]:

$$J(u(k))={\left|y^{\ast }\left(k+1\right)-y\left(k+1\right)\right|}^2+\lambda {\left|u\left(k\right)-u\left(k-1\right)\right|}^2$$

(19)

where y*(k + 1) is the signal expected by the system, λ > 0 is the weighting coefficient, and the main function is to limit the change rate of the control quantity.

Substituting Equation (18) into Equation (19), the control algorithm can be obtained as follows:

$$u(k)=u(k-1)+\frac{\rho {\varphi }_c(k)}{\lambda +|{\varphi }_c(k){|}^2}(y^{\ast }(k+1)-y(k))$$

(20)

where ρ is the step size factor, and ρ∈(0,1], λ is the penalty factor that controls the change in the input. The smaller λ is, the faster the system responds, but it may cause overshoot and even instability. The larger λ is, the slower the response of the system is, but the more stable the system output is, the smaller the overshoot is.

3.3.3. Estimation Algorithms of Pseudo Partial Derivatives

From the perspective of eliminating steady-state deviation and ensuring system stability, consider the following quadratic index function:

$$J({\widehat{\varphi }}_c(k))={\left[y\left(k\right)-y\left(k-1\right)-{\widehat{\varphi }}_c(k)\cdot \Delta u\left(k-1\right)\right]}^2+\mu {\left[{\widehat{\varphi }}_c\left(k\right)-{\widehat{\varphi }}_{\mathrm{c}}\left(k-1\right)\right]}^2$$

(21)

where y(k) is the actual output of the system, ${\widehat{\varphi }}_{\mathrm{c}}(k)$ is the estimated value of ϕ_c(k), and μ > 0 is the weight parameter.

Solving for $\frac{\partial J\left({\widehat{\varphi }}_{\mathrm{c}}(k)\right)}{\partial {\widehat{\varphi }}_{\mathrm{c}}(k)}=0$, the estimation algorithm to obtain the pseudo partial derivative is:

$${\stackrel{\wedge }{\varphi }}_c(k)=\stackrel{\wedge }{{\varphi }_c}(k-1)+\frac{\eta \Delta u(k-1)}{\mu +{\left|\Delta u(k-1)\right|}^2}\times \left[\Delta y(k)-\stackrel{\wedge }{{\varphi }_c}(k-1)\Delta u(k-1)\right]$$

(22)

$$\mathrm{If}{\stackrel{\wedge }{\varphi }}_c(k)\le \epsilon \mathrm{or}\left|\Delta u\left(k-1\right)\le \epsilon \right|,\mathrm{then}:{\stackrel{\wedge }{\varphi }}_c(k)={\stackrel{\wedge }{\varphi }}_c(1)$$

(23)

where ${\stackrel{\wedge }{\varphi }}_{\mathrm{c}}(1)$ is the initial value of ${\stackrel{\wedge }{\varphi }}_{\mathrm{c}}(k)$, and $\epsilon$ is a sufficiently small positive number.

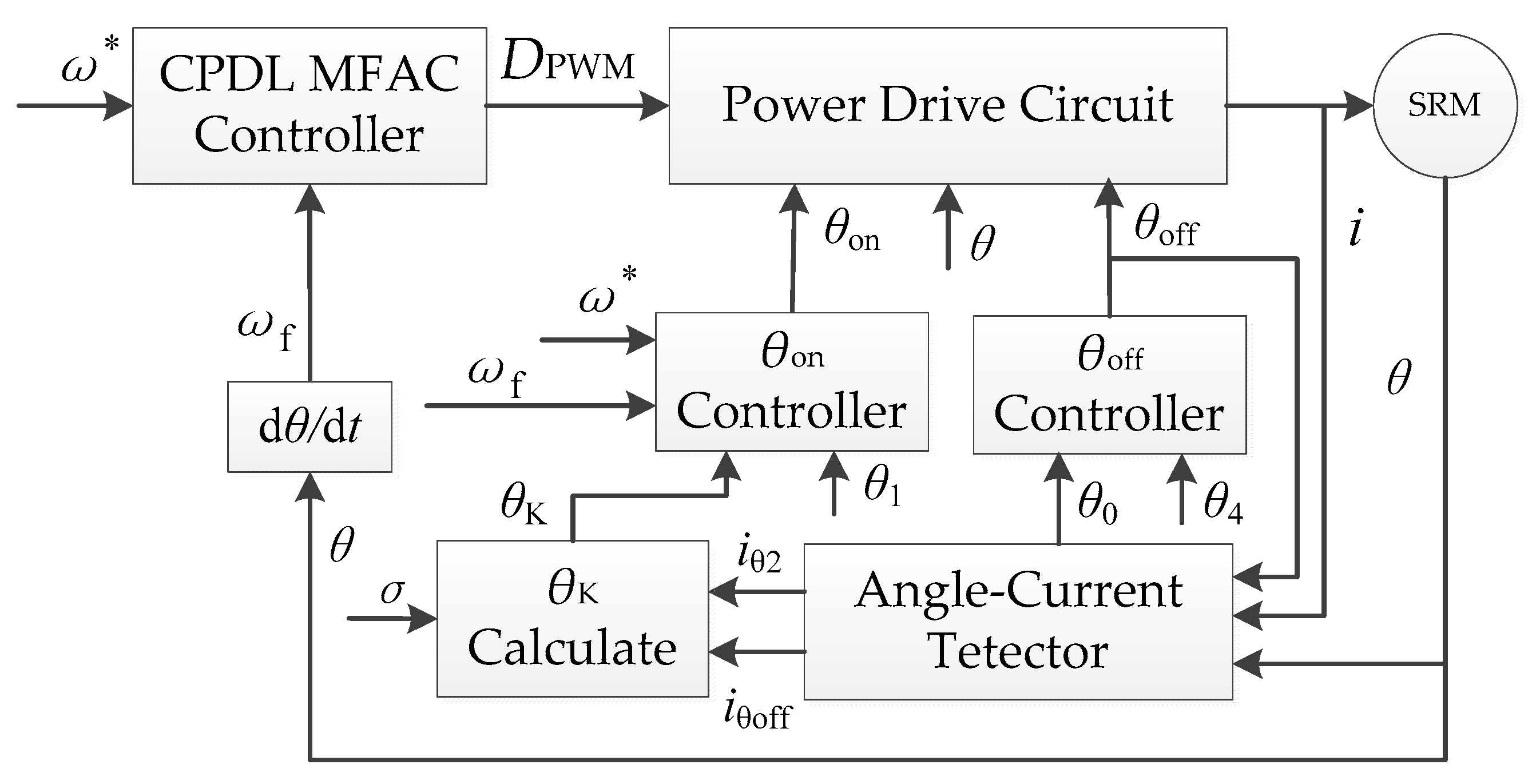
4. Control System Design

According to the above control algorithm, a closed-loop speed control system of switched reluctance motor is designed. The structure is shown in Figure 5, including power drive circuit, angle-current detector, CPDL MFAC controller, θ_K calculation module, θ_on controller and θ_off controller.

The angle-current detector detects the rotor position angle θ and the current of the phase in real time, obtains the currents i_θ2 and i_θoff, and obtains the rotor position angle θ₀ at the freewheeling zero point. The input of the CPDL MFAC controller is the target speed ω* and the feedback speed ω_f, and the output voltage PWM duty cycle D_PWM is calculated according to Equations (20) and (21). The input of the θ_on controller is the target speed ω* and the feedback speed ω_f, and the turn-on angle θ_on is calculated according to Equation (14). The input of the θ_K calculation module is i_θon, i_θoff and the preset current difference σ, and θ_K is calculated according to Equation (13). The input of the θ_off controller is θ₀ and θ₄, and the turn-off angle θ_off is calculated according to Equation (15). The power drive circuit controls the operation of the switched reluctance motor according to D_PWM, θ_on and θ_off.

The CPDL MFAC controller is the outer loop of speed control. The motor speed can be adjusted in a wide range by adjusting the voltage PWM duty cycle, and the θ_on controller can only adjust the speed in a certain range. The control cycle of the CPDL MFAC controller is ten times or even dozens of times that of the θ_on controller. During the control cycle of the CPDL MFAC controller, the motor speed is adjusted by the θ_on controller. When the load or target speed increases too much, the output of the θ_on controller reaches θ₁, and lost the speed control ability, then the system adjusts the motor speed by the CPDL MFAC controller, so that the θ_on controller exits saturation and restores the speed control ability. On the contrary, if the load or the target speed is greatly reduced, the output of the θ_on controller reaches θ_K, and the control ability of the speed is lost. The system also adjusts the speed of the motor through the CPDL MFAC controller, so that the θ_on controller exits saturation and resumes speed control capability.

In the speed control based on current chopping, there are two feedback control loops: the speed loop and the current loop. The control cycle of the current loop is the commutation cycle of the motor. Generally, the control period of the speed loop is much larger than that of the current loop. In the case of sudden large torque ripple, the torque output by the current of the motor is much smaller than the load torque, so that the speed of the motor drops rapidly, and the speed loop response is slow, and eventually there will be large speed fluctuations or even shutdown. Based on the APC control of PWM chopper, the output of the speed loop is the duty cycle of the voltage PWM, and the voltage PWM duty cycle is constant during a commutation period. When a sudden large torque pulsation occurs, the speed of the motor decreases rapidly, and the rotating electromotive force decreases, so that the average voltage of the motor is much larger than the rotating electromotive force. Due to the characteristics of the motor (voltage equation), the current of the winding increases rapidly, and the output torque also increases, which will suppress the sudden load torque pulsation in time.

5. Experimental Test

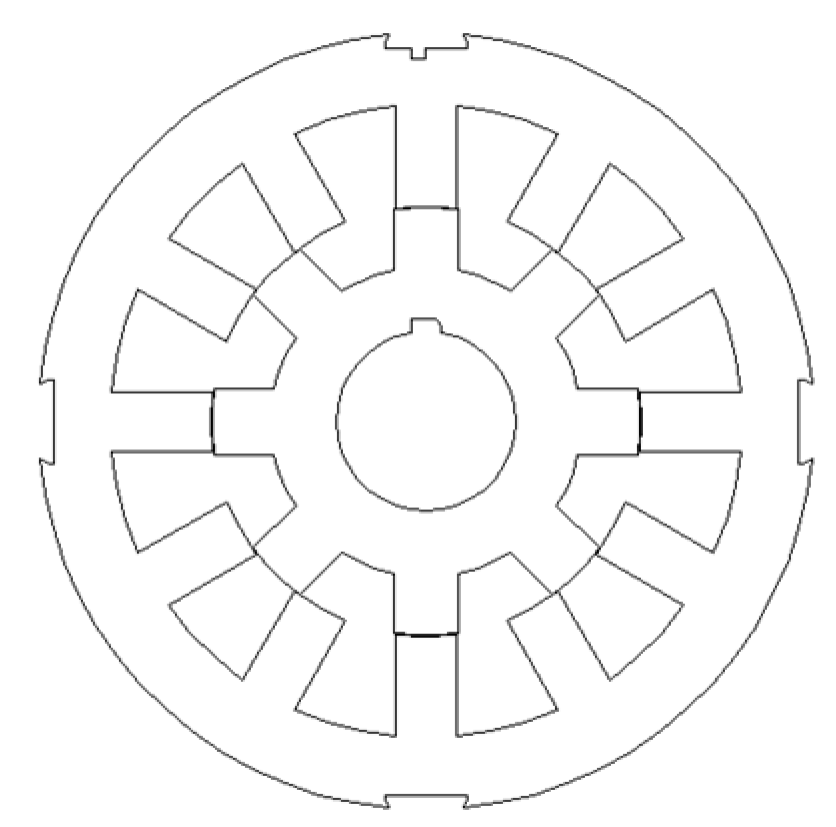
5.1. Experimental Prototype

In order to verify the feasibility of the proposed SRM speed control system based on the switching angle range, the power test is carried out for the 12/8 pole SRM with rated power of 3 KW, rated voltage of 60 V and rated speed of 3000 r/min. The experimental prototype is shown in Figure 6, in which Figure 6a is the field picture of the power test of the motor and control system; Figure 6b shows the measured SRM, and Figure 6c shows the designed SRM controller.

Figure 7 shows the stator and rotor cogging structure of the tested three-phase 12/8 pole SRM. The number of stator teeth is 12 and the number of rotor teeth is 8. Along the circumference of the air gap, the mechanical angle occupied by the stator teeth is 16°, the mechanical angle occupied by the stator slot is 14°, the mechanical angle occupied by the rotor teeth is 18°, and the mechanical angle occupied by the rotor slot is 27°.

Figure 8 shows the linear inductance curve of the one-phase winding of the motor. The horizontal axis is the electrical angle of the rotor relative to stator, and the vertical axis is the inductance value of the one-phase winding. The minimum inductance interval [θ₁, θ₂] is [−44°, 44°] and the electrical angle crossed is 88°, the inductance rise interval [θ₂, θ₃] is [44°, 172°] and the electrical angle crossed is 128°, the falling interval [θ₄, θ₅] is [188°, 316°] and the crossing electrical angle is also 128°, and the maximum inductance interval [θ₃, θ₄] is [172°, 188°] and the electrical angle crossed is 16°.

5.2. Speed Regulation Performance Experiment

The designed control algorithm is implemented on the control platform. Several key rotor position angles of the inductance model are given in Figure 8. θ₁, θ₂, θ₃ and θ₄ are −44°, 44°, 172° and 188°, respectively. It is given according to the structural size of the designed motor. The experiment verifies the proposed control strategy from the aspects of the turn-off angle, turn-on angle and speed control.

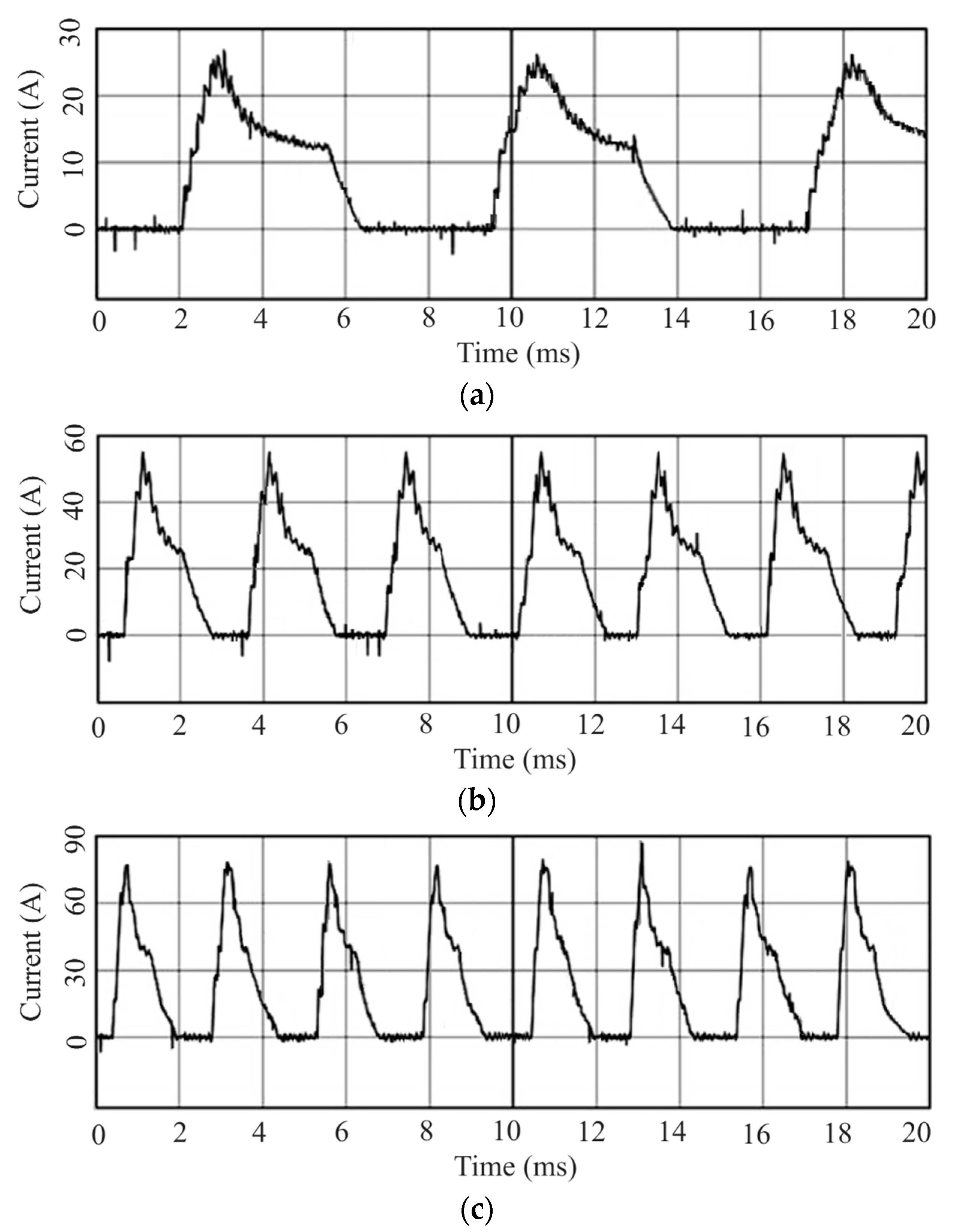
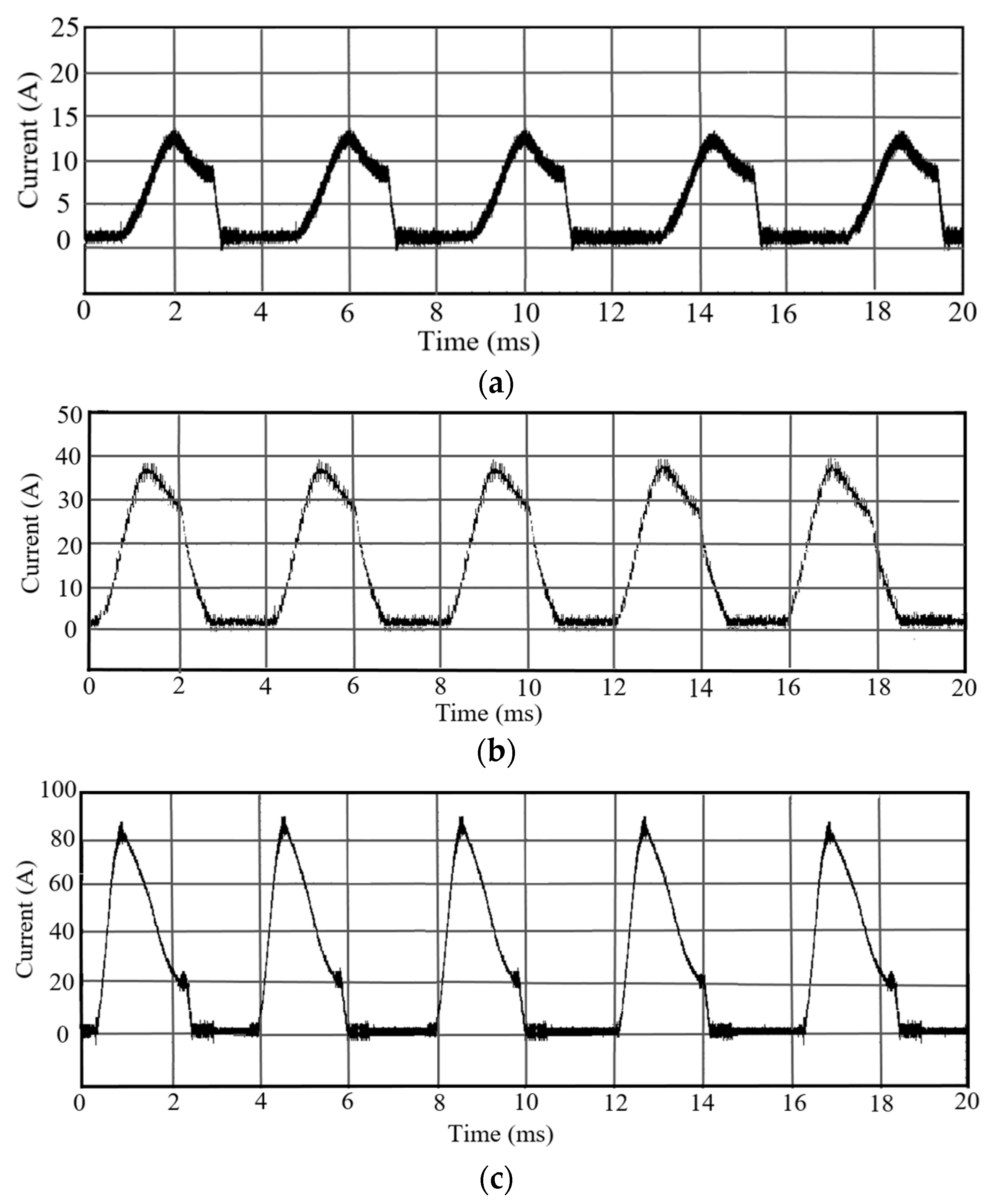
5.2.1. Control Test of Turn-Off Angle

The fixed turn-on angle θ_on is −10°, for different turn-off angles θ_off; the PI control algorithm is adopted, and speed tracking control is realized by adjusting voltage PWM duty cycle D_PWM. Set the turn-off angle θ_off1 as 108° and θ_off2 as 129°. Turn-off angle θ_off3 is calculated according to Equation (13), and θ₀ is set to θ₄, which is 188°.

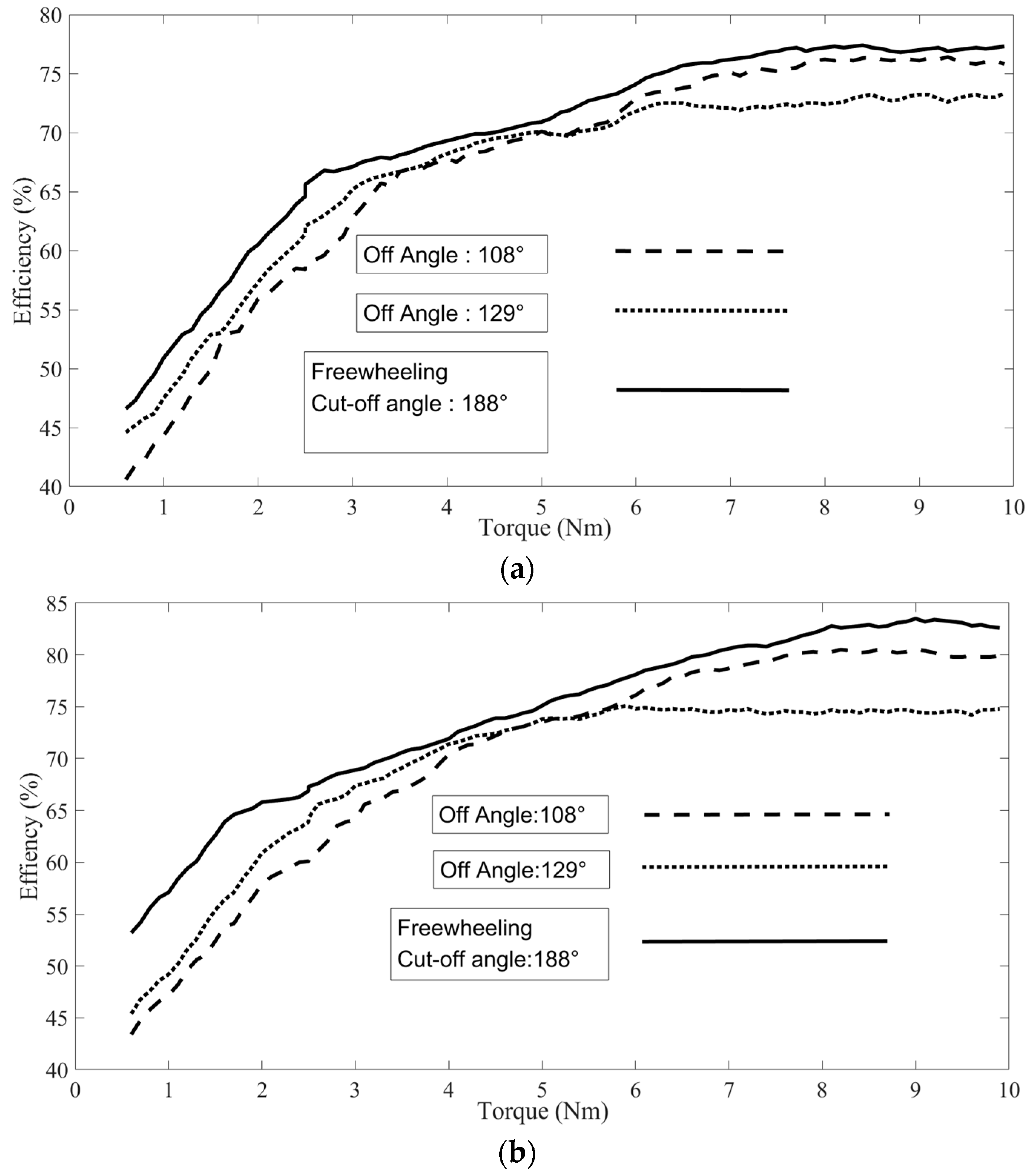
(1)

Efficiency comparison of different rotating speeds and shut-off angles

Control the motor speed at 1000 r/min, 2000 r/min and 3000 r/min, respectively, through the controller, gradually increase the resistance torque of the dynamometer to 8 N·m, and test the efficiency of the system at different speeds according to the set turn-off angle. Figure 9a shows the system efficiency when the turn-off angle is 108°, and Figure 9b shows the system efficiency when the turn-off angle is 129°. It can be seen that although the turn-off angle is different, the efficiency of the system increases with the increase in speed; on the other hand, for different motor speeds, the efficiency of the system increases with the increase in output power, which is in line with the general law of motor speed regulation with load, and also shows that the control strategy of turn-off angle is feasible.

(2)

Comparative test of different cut-off angles at the same speed

Figure 10 shows the efficiency test comparison curve with the speed of 2000 r/min and 3000 r/min, respectively, the off angle of 108°, 129° and the fixed freewheeling angle of 188°. It can be seen that at different speeds, the efficiency of the fixed freewheeling angle of 188° is the highest, which explains the effectiveness of the shut-off angle control based on the optimal freewheeling angle proposed in the text.

Under a light load, the efficiency of 108° turn-off angle is lower and the system efficiency of 129° turn-off angle is higher, while under a heavy load, the efficiency of 108° turn-off angle is higher, and the efficiency of 129° turn-off angle is higher system is less efficient. The reason is that under low load conditions, when the turn-off angle is 108°, the phase current of the motor is turned off earlier, and the rising area of the winding inductance is not fully utilized, so the efficiency is low. With the increase in load, the current also gradually increases. After the phase winding switch is turned off, the freewheeling time of the current gradually increases. The 108° turn-off angle allows the winding to have enough time for freewheeling, and the freewheeling current decreases to 0 near 188°, which does not produce negative torque and has high efficiency. For a larger phase winding current, when the turn-off angle is 129°, the freewheeling time is longer and the winding current has not fallen to 0 at 188°, so negative torque is generated and efficiency is reduced.

5.2.2. Control Test of Turn-On Angle

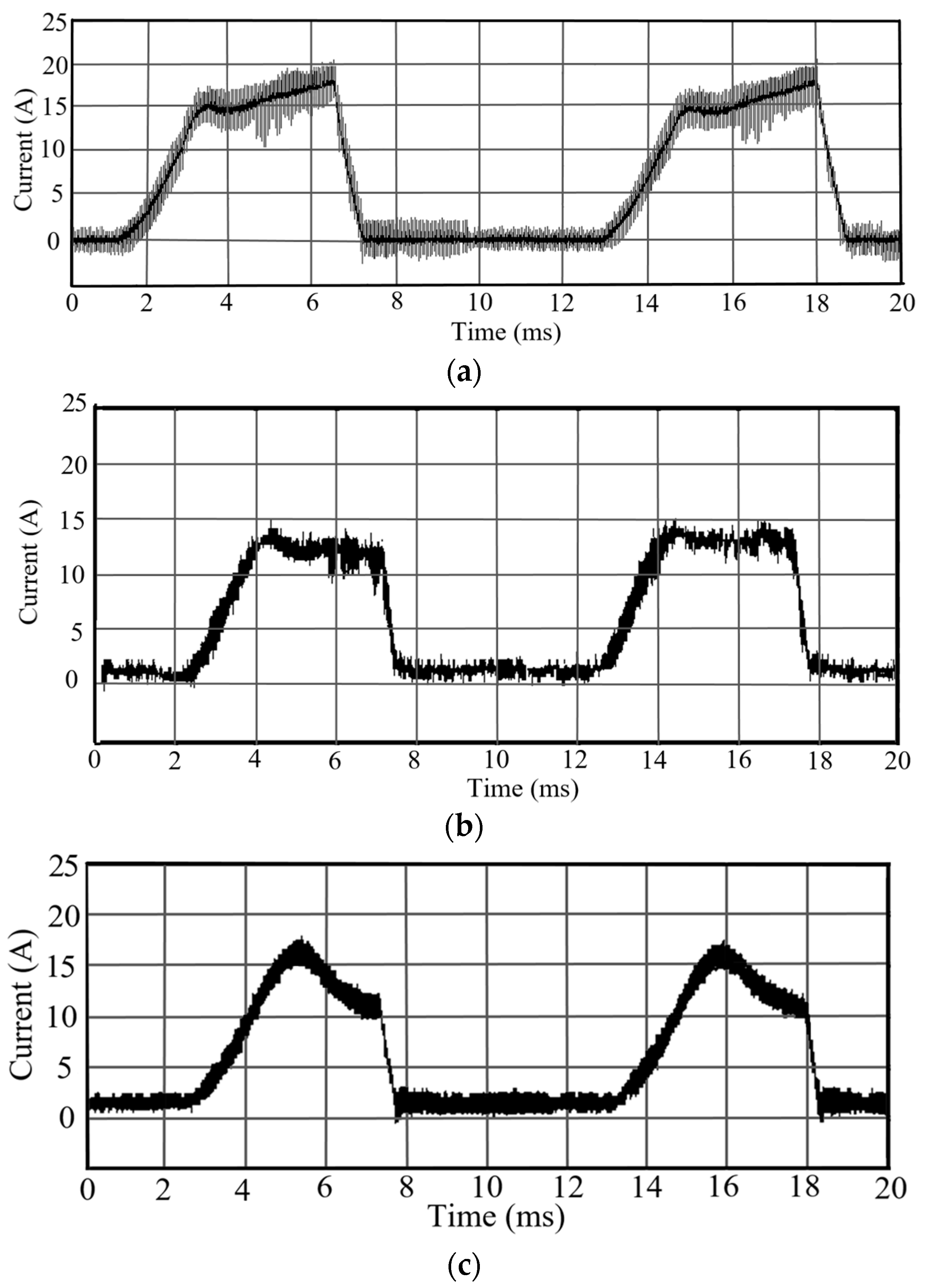
(1)

Current waveform test with fixed turn-on angle

Figure 11 shows the current waveforms when the motor speed is 800 r/min, the load torque is 6 N∙m, and the turn-on angles are 20°, 0°, and −20°, respectively. Figure 11a has a larger turn-on angle, the slope of the current in [θ₂, θ_off] is positive, and the average current value in the interval is about 16 A. Figure 11b shows the current waveform with the turn-on angle of 0, the slope of the current in [θ₂, θ_off] interval is approximately 0, and the average value of the current in this interval is about 12.5 A. Figure 11c shows the current waveform with the turn-on angle of −22°. The turn-on angle is small, the slope of the current in [θ₂, θ_off] interval is less than 0, and the average value of the current in this interval is about 13 A. Figure 11 shows that the magnitude of the turn-on angle determines the slope of the current in the interval [θ₂, θ_off]. As the turn-on angle decreases, the current slope changes from positive to negative. Giving the same load torque, if the turn-on angle is larger, the current is larger. The average current value with 0 and 20° turn-on angle is not much different. Therefore, it is beneficial that the slope of the current in the [θ₂, θ_off] interval is less than 0.

(2)

Tests with the same load torque and different rotational speeds

Figure 12 shows the current waveform at different speeds, and the turn-off angle θ_off is set to 115°; the turn-on angle θ_off controls according to the algorithm given in Equations (12)–(14). The σ of Equation (12) is set to 50% of the current peak, the load torque of the dynamometer is set to 8 Nm, and the traditional PI algorithm is used for speed control. Figure 12a shows the current waveform at the speed of 1000 r/min, Figure 12b shows the current waveform at the speed of 2000 r/min, and Figure 12c shows the current waveform at the speed of 3000 r/min.

In Figure 12, the current waveform under three different speed conditions meets the ideal current waveform, which shows that the ideal current waveform can be achieved through the control algorithm of the opening angle, and the opening angle control strategy proposed in this paper is effective.

(3)

Current waveforms with the same rotational speed and different load torques

Figure 13 shows the current waveforms when the rotational speed is 1500 r/min and the load torque is 4 N∙m, 8 N∙m, and 12 N∙m, respectively. The turn-on angle θ_on is controlled according to Equations (12)–(14), the turn-off angle is controlled according to Equation (15), and σ in Equation (12) is set to 2 A, and the model-free adaptive control algorithm is used for speed control. Figure 13a is the current waveform with the load torque of 4 N∙m. Figure 13b is the current waveform with the load torque of 8 N∙m. Figure 13c is the current waveform with the load torque of 12 N∙m. In Figure 13, the slope angle of the current waveform in the [θ₂, θ_off] interval increases with the increase in the load, indicating that the turn-on angle control strategy proposed in this paper is effective.

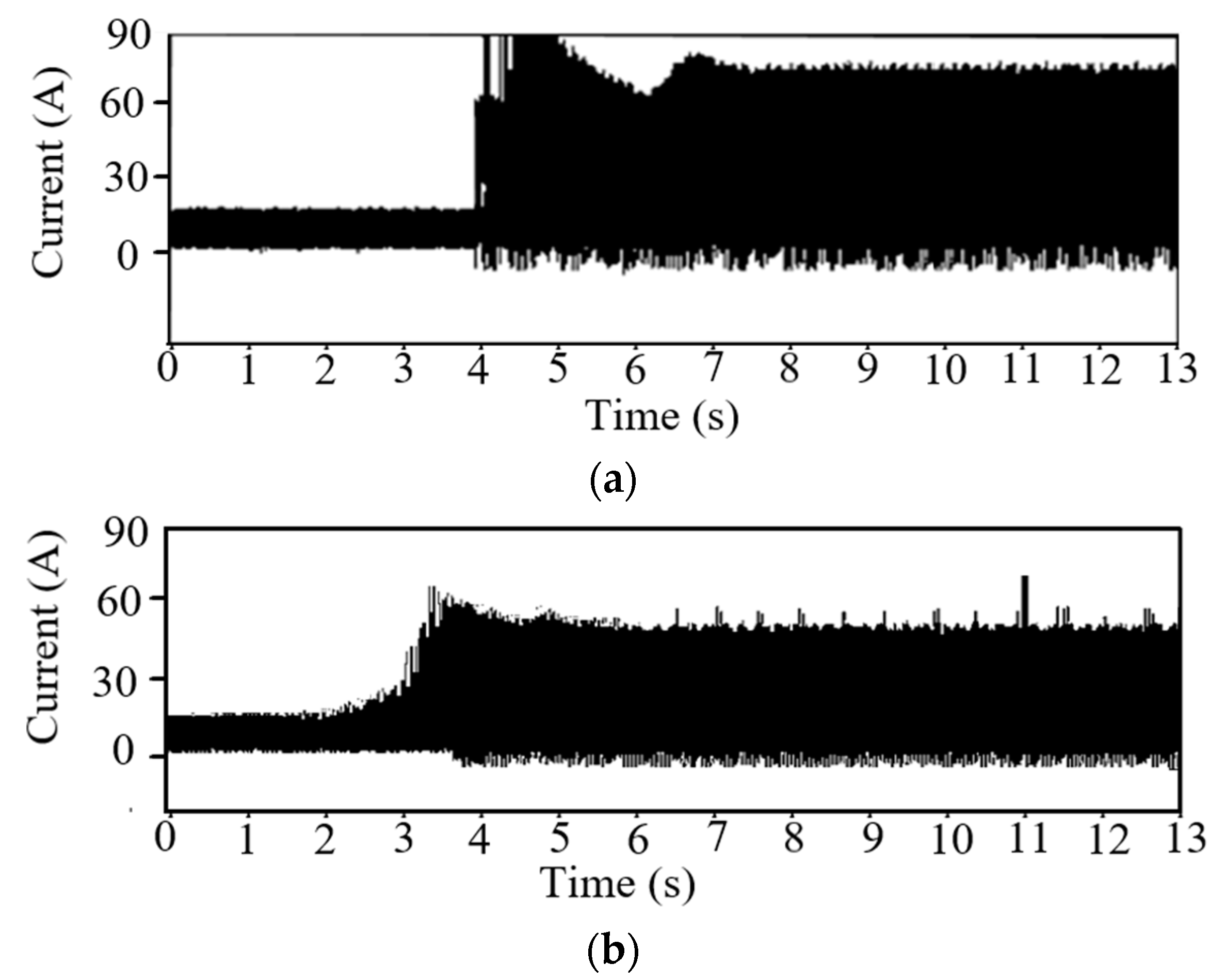
5.2.3. Speed Control Test

(1)

Constant torque load test

Set the dynamometer to apply a torque of 8 Nm, set σ as 2 A. The motor control strategy shown in Figure 5 is realized, and the tracking performance of the control algorithm is tested. The parameters of the model free adaptive control algorithm are set as: ${\widehat{\varphi }}_{\mathrm{c}}(1)=0.5$, ε = 0.005, μ = 1, η = 1, ρ = 0.5, λ = 1.0. The tracking curve of speed is shown in Figure 14. First, make the motor run at a speed of 1000 r/min, then set the target speed to 3000 r/min, and the motor can complete the tracking of step speed regulation. Then, set the target speed to 2000 r/min, and the motor can also complete the speed regulation control of speed tracking.

(2)

Sudden Torque Test

The target speed is set to 1200 r/min, and the switch reluctance motor control strategy proposed in Figure 5 is adopted. The load torque is set as 4 N∙m at first, and then 12 N∙m is suddenly added. Figure 15 shows the current waveform during speed tracking. Figure 15a shows the current waveform of APC speed control based on switching angle. A load torque of 12 N∙m is suddenly applied at about 4 s, and the current increases rapidly. Figure 15b shows the current waveform of the speed control method based on current chopping. The load torque of 12 N∙m is suddenly applied at about 2 s, and the current increases after nearly 500 ms later. This shows that the APC speed control based on the switching angle proposed in this paper can quickly suppress the change in the load torque and has advantages under the load with sudden large pulsation.

Figure 16 is a graph of the speed change corresponding to the two control methods in Figure 15. The upper part of Figure 16 is the speed change curve of the APC speed regulation control method, and the lower part is the speed change curve of the current chopping control speed regulation method. It can be seen that the APC speed control method above has a smaller speed reduction (200 r/min) and a shorter speed recovery time (1 s), while the current chopping speed control method below has a larger speed drop (400 r/min), and the speed longer recovery time (2 s). It also shows that the control strategy proposed in this paper has advantages for a sudden large-pulse load.

5.3. Test Conclusion

For the switched reluctance motor, the turn-off angle efficiency comparison test, the turn-on angle current waveform test, the speed tracking test, and the speed tracking comparison test under sudden heavy load conditions are carried out. The test results show that the speed control strategy of the switched reluctance motor based on the switching angle interval proposed in this paper is feasible.

6. Conclusions

In this paper, through the analysis of the linear inductance model of the switched reluctance motor, combined with the nonlinear inductance model obtained by electromagnetic simulation, a control strategy that does not depend on the accurate motor model is designed. In terms of the switch reluctance motor control strategy, the turn-off angle control algorithm based on the optimal freewheeling zero point, the turn-on angle control algorithm based on the optimized current waveform and the voltage PWM speed control algorithm for switched reluctance motor based on model-free adaptive control are designed, respectively. Through the separate design of the control strategies for the three key parameters, the degree of coupling among them is greatly reduced, the control algorithm is simplified and easy to implement. Analysis and experiments show that the control strategy proposed in this paper can realize the speed tracking control of the switched reluctance motor, especially suitable for the load with sudden large torque ripple.