Probabilistic Description of the State of Charge of Batteries Used for Primary Frequency Regulation
Abstract
:1. Introduction
2. Primary Frequency Regulation Employing Battery Energy Storage Systems
2.1. The Problem of Frequency Regulation
2.2. Use of the Battery Energy Storage System for Frequency Regulations
- -
- controlling the charging/discharging power according to the up- and down-regulation,
- -
- recovering the SOC according to a reference value (typically set at 0.5 p.u.), when frequency falls within the dead-band, and
- -
- keeping the SOC within a range which avoids battery degradation (e.g., p.u.).
3. Stochastic Characterization of Power System Frequency
3.1. Logistic Autoregressive Mode
3.2. Ornstein–Uhlenbeck
4. Stochastic Characterization of SoC
4.1. Stochastic Characterization of the Regulation Power in Absence of the Dead-Band
4.2. Stochastic Characterization of the Regulation Power in Presence of the Dead-Band
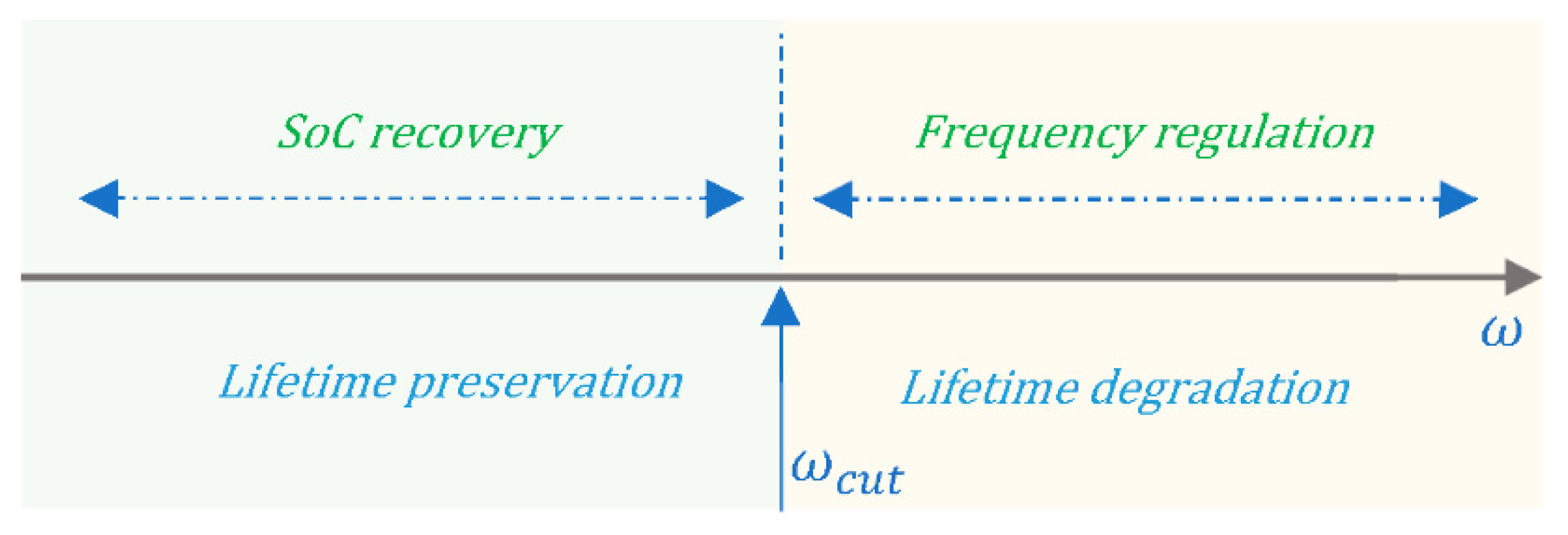
4.3. Stochastic Characterization of the State of Charge
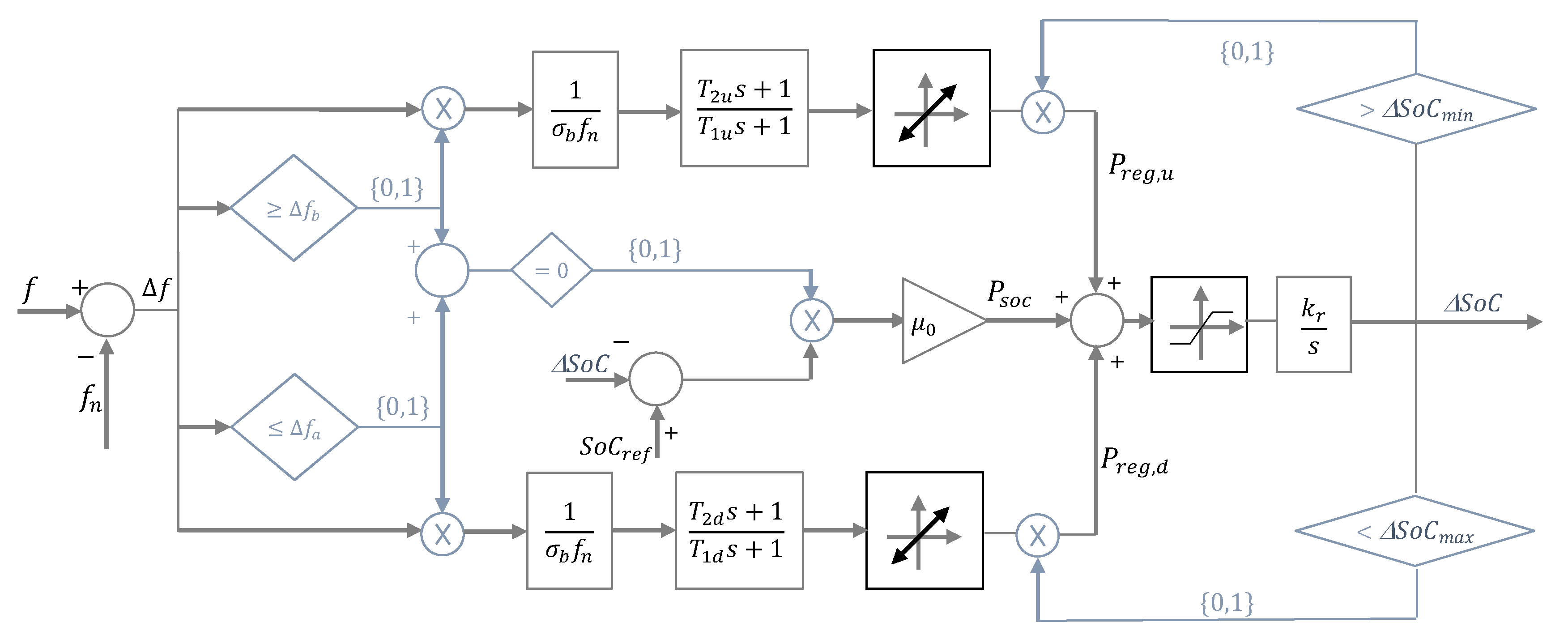
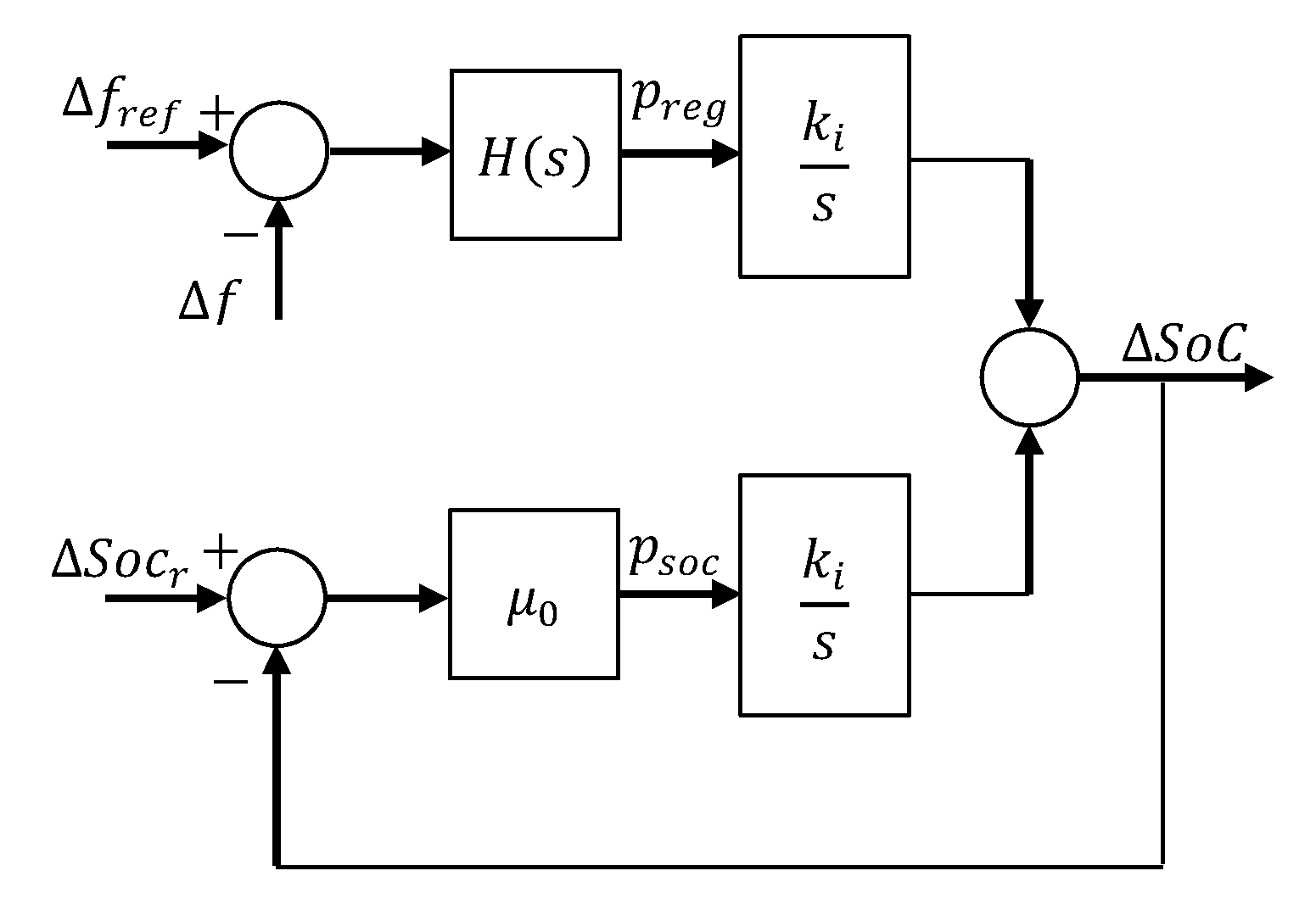
4.4. BESS Control Scheme
- which relates the output, i.e., , to the disturbance, i.e., .
- which relates the output, i.e, , to the input, i.e., .
5. Numerical Applications
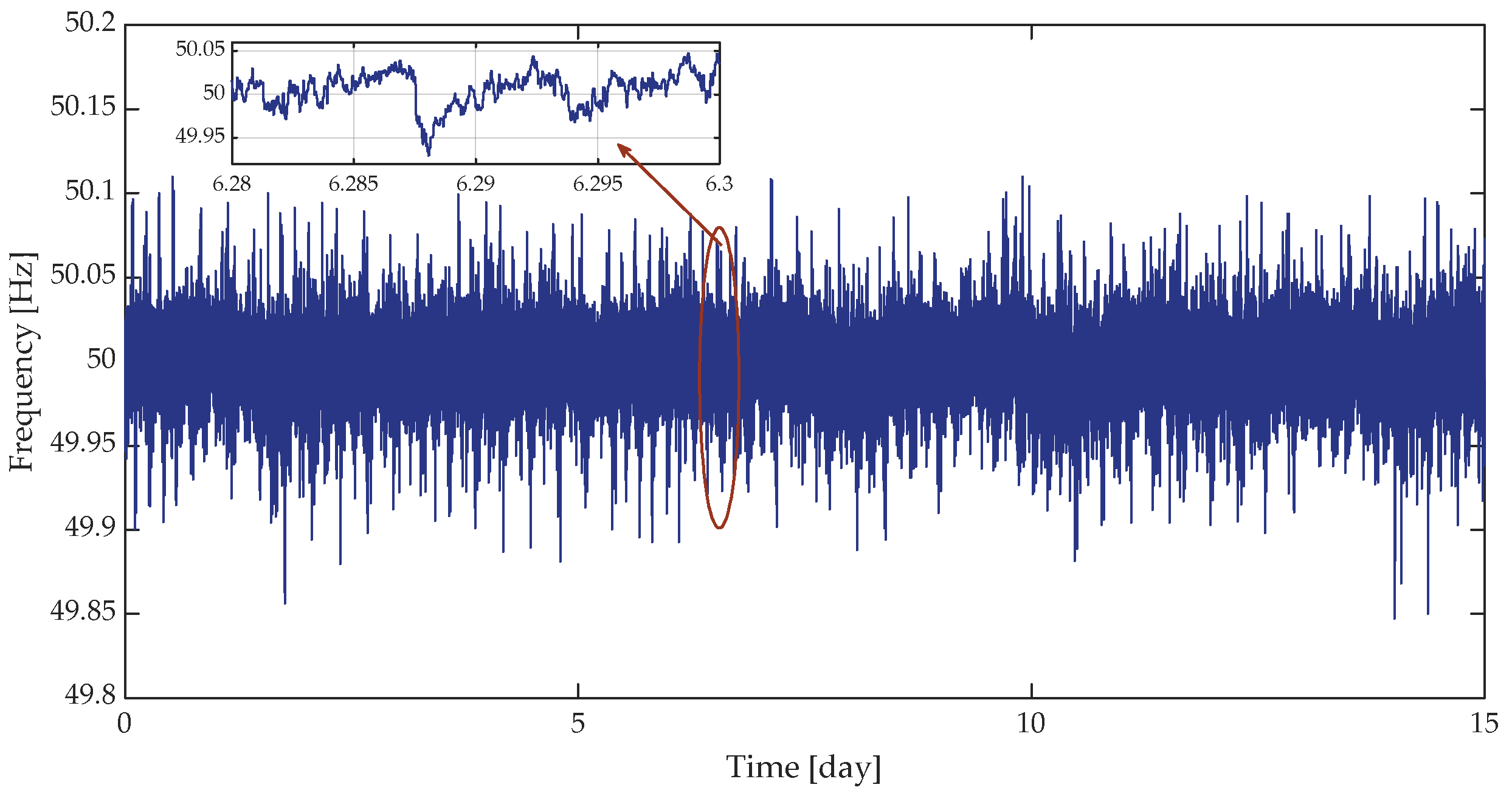
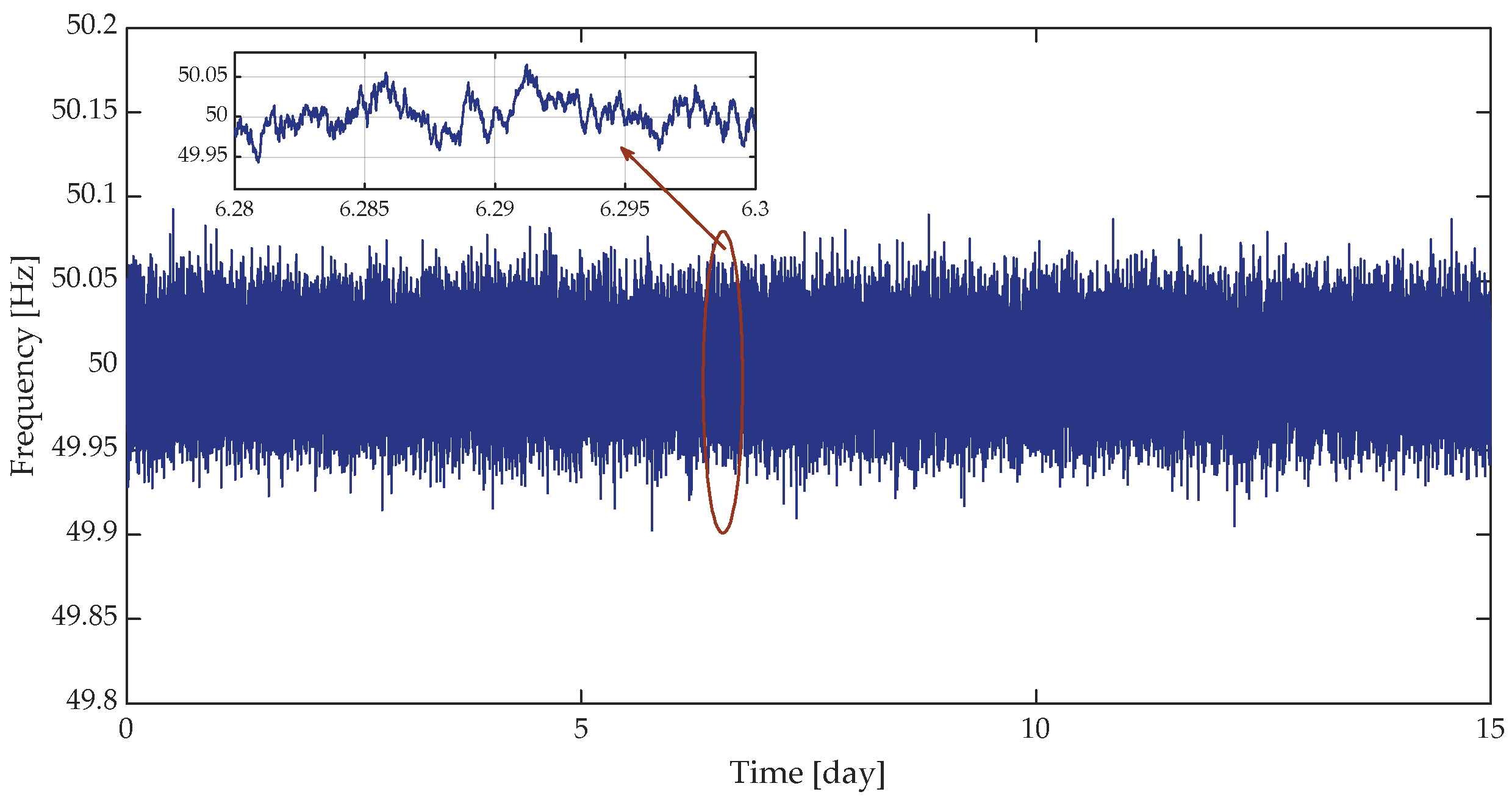
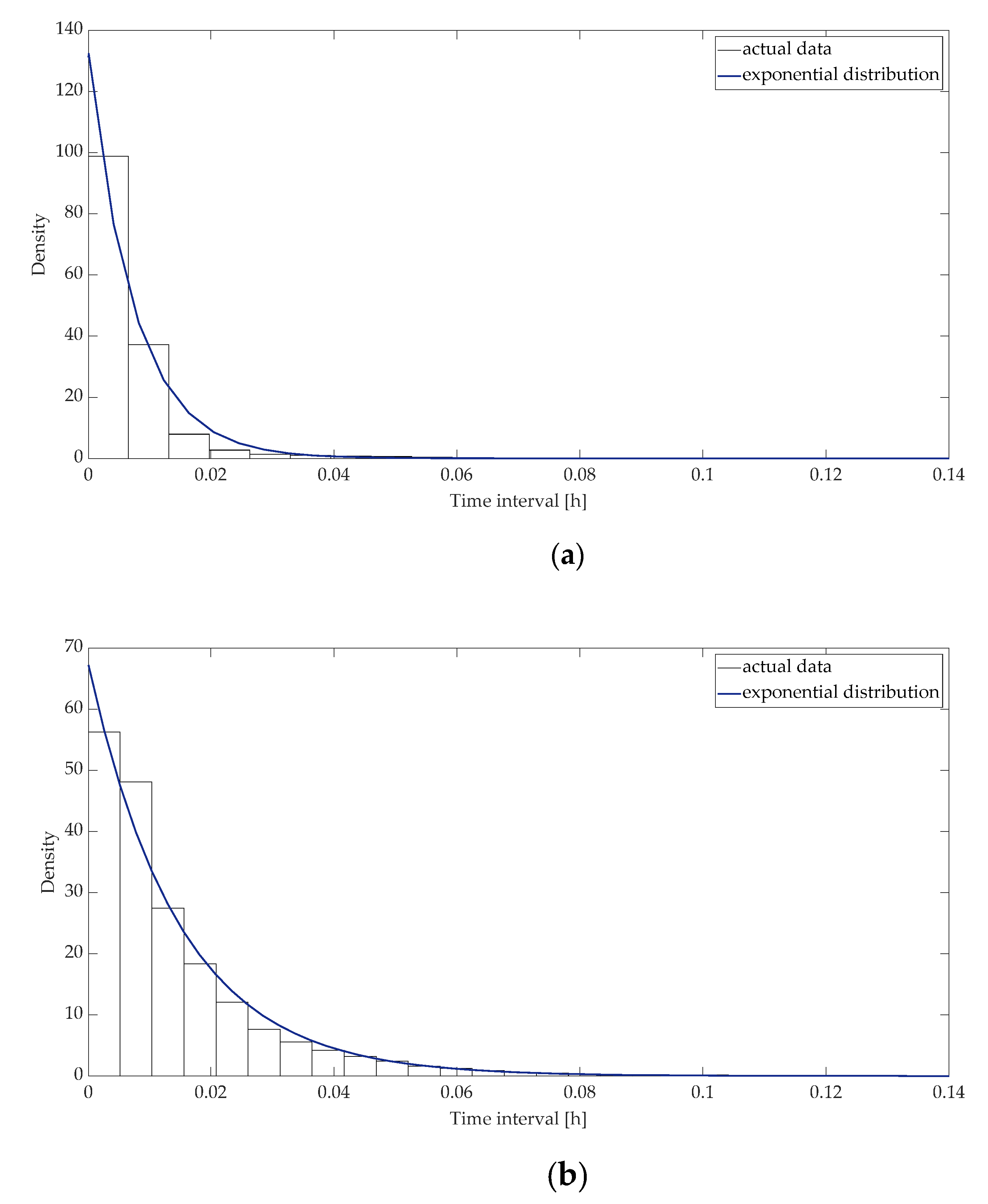
5.1. Analysis of Frequency Data
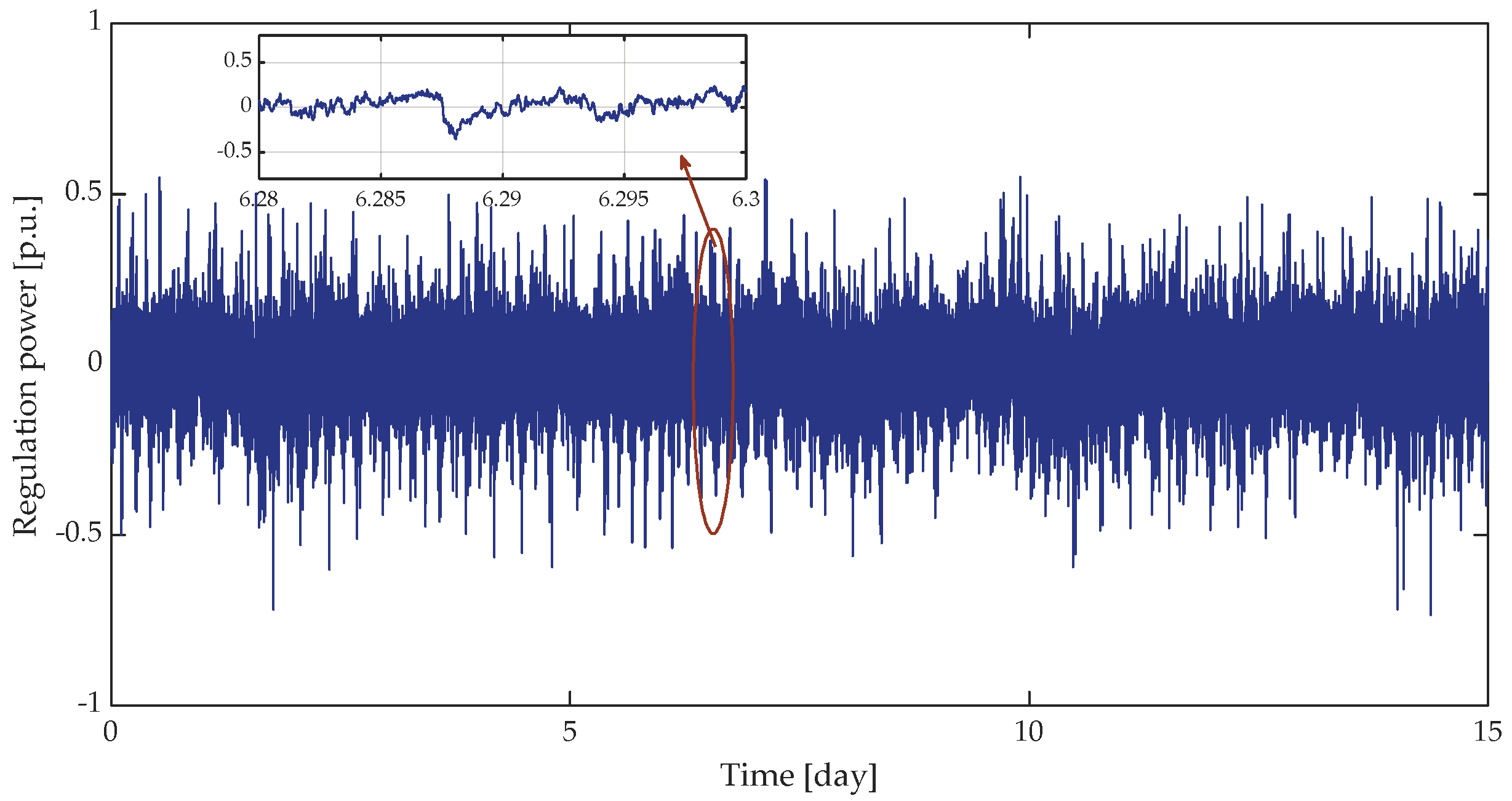
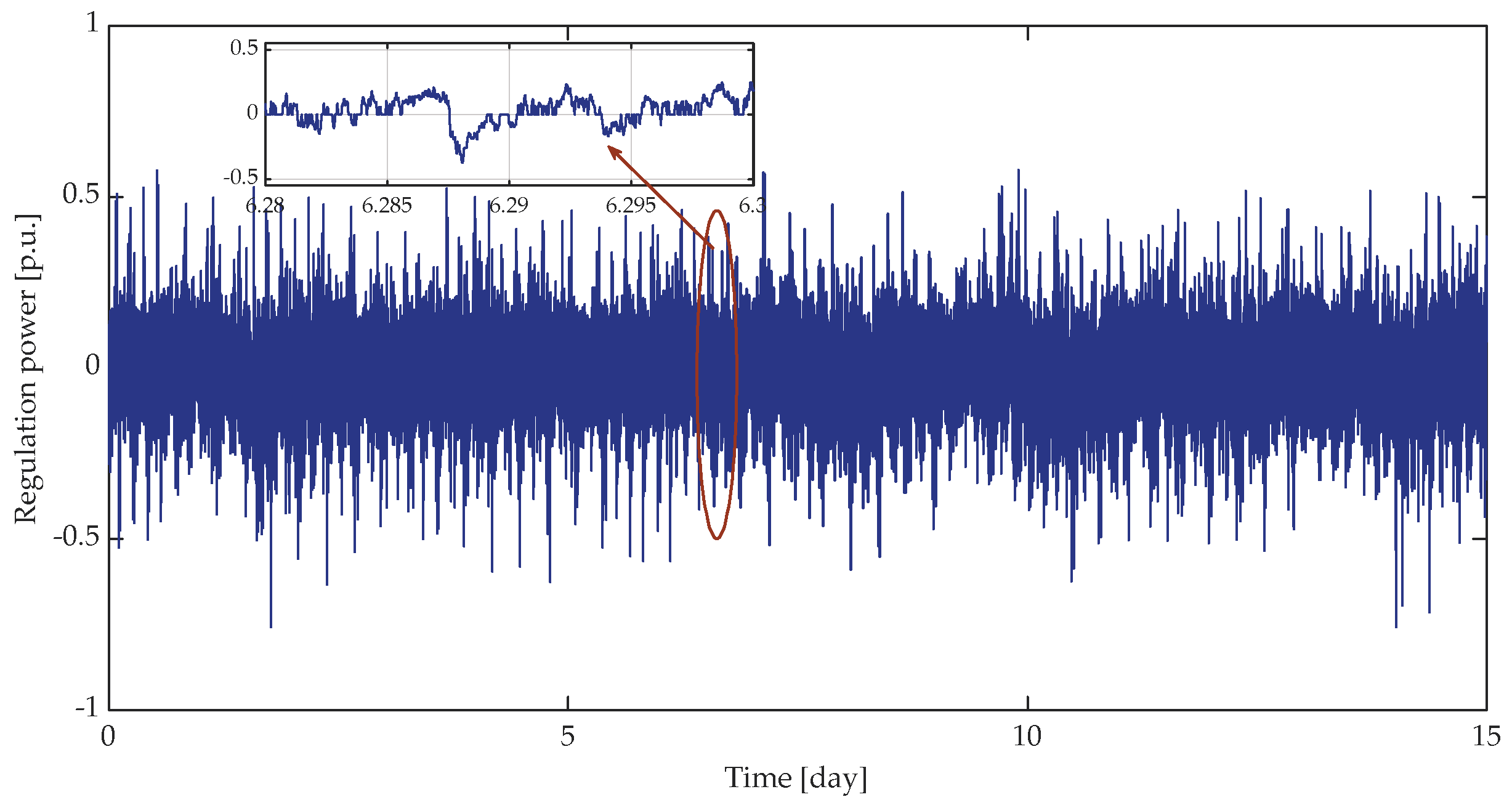
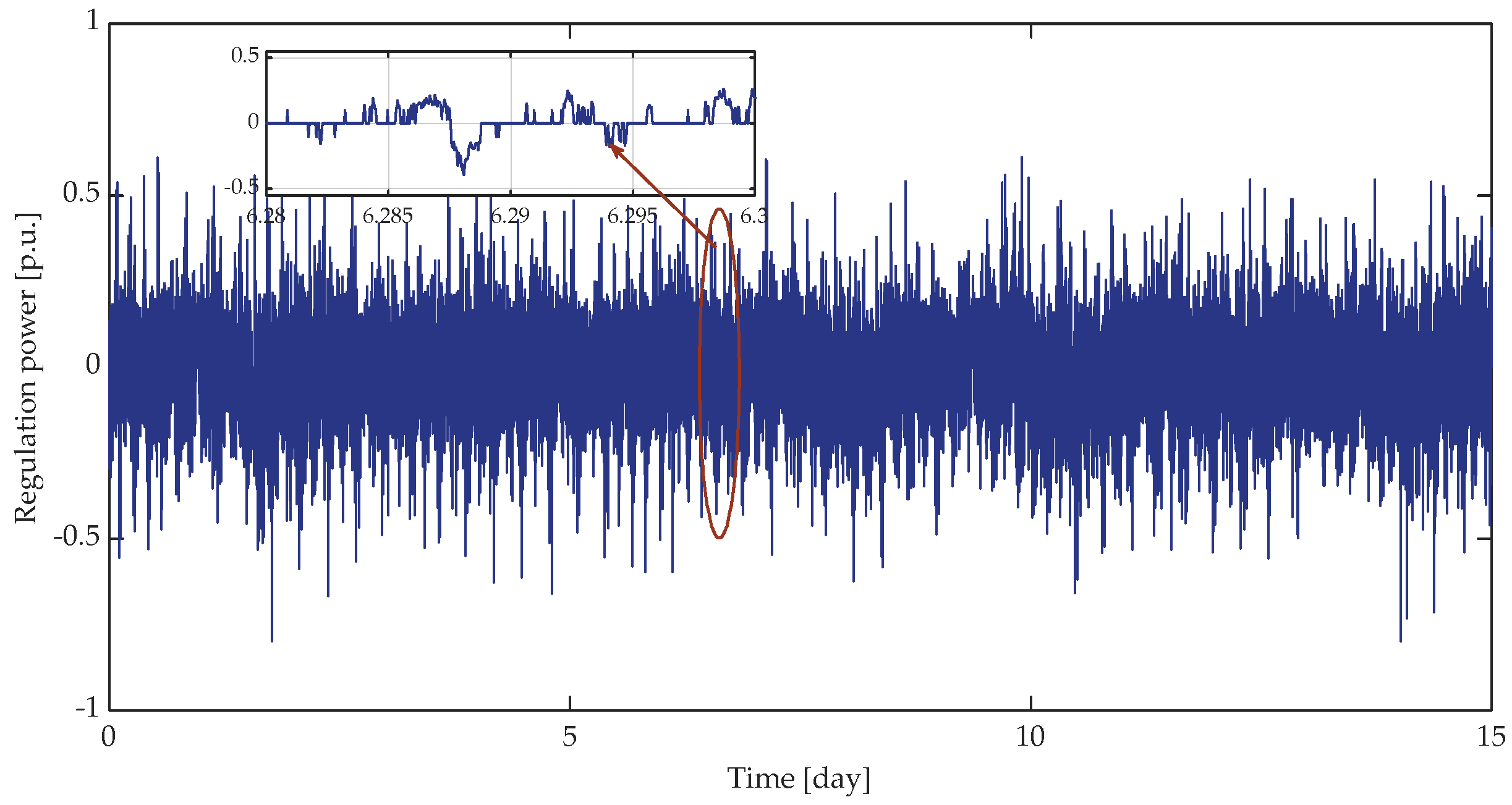
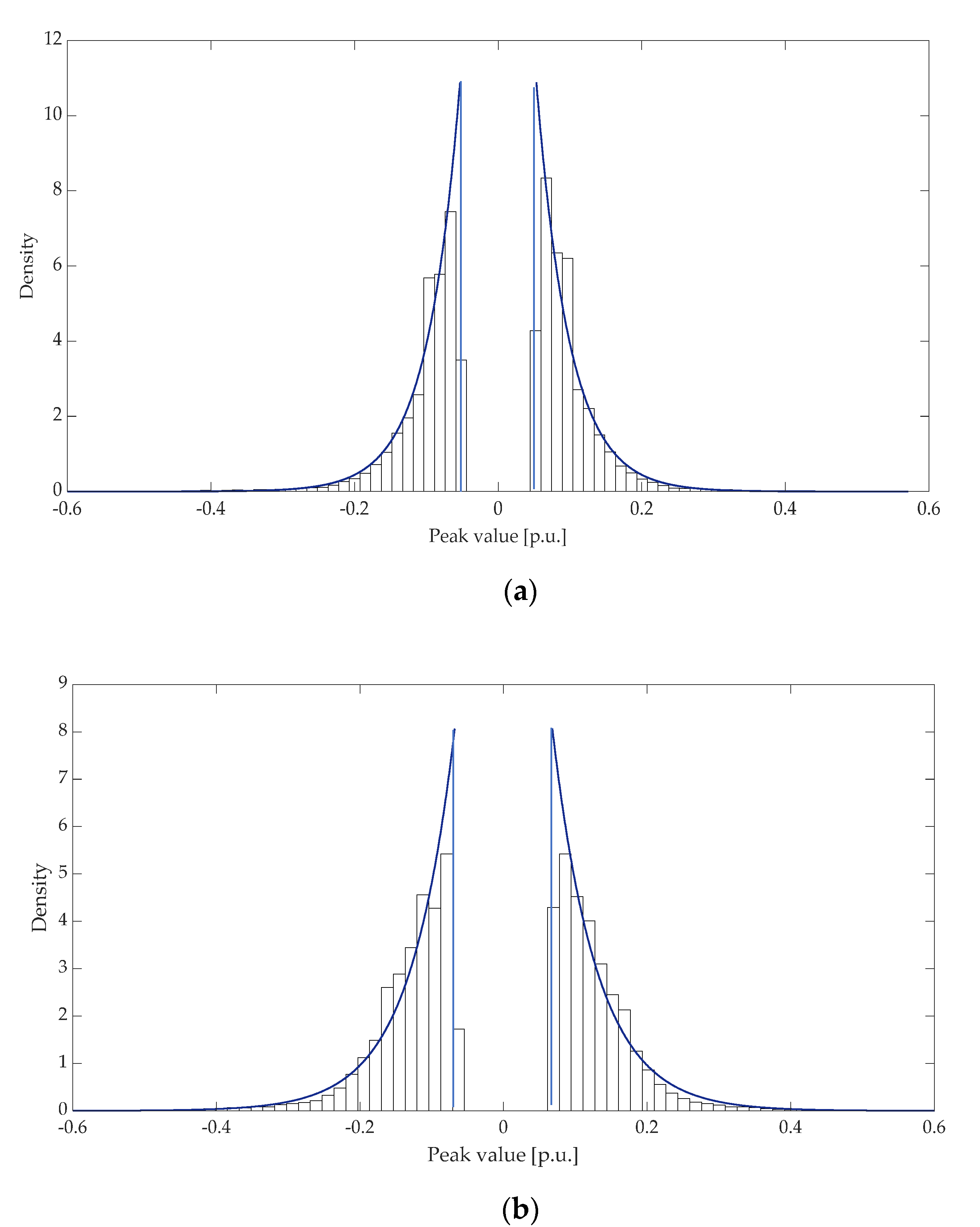
5.2. Analysis of Regulation Power
- Case 1: the dead-band is not considered;
- Case 2: the dead-band is ;
- Case 3: the dead-band is .
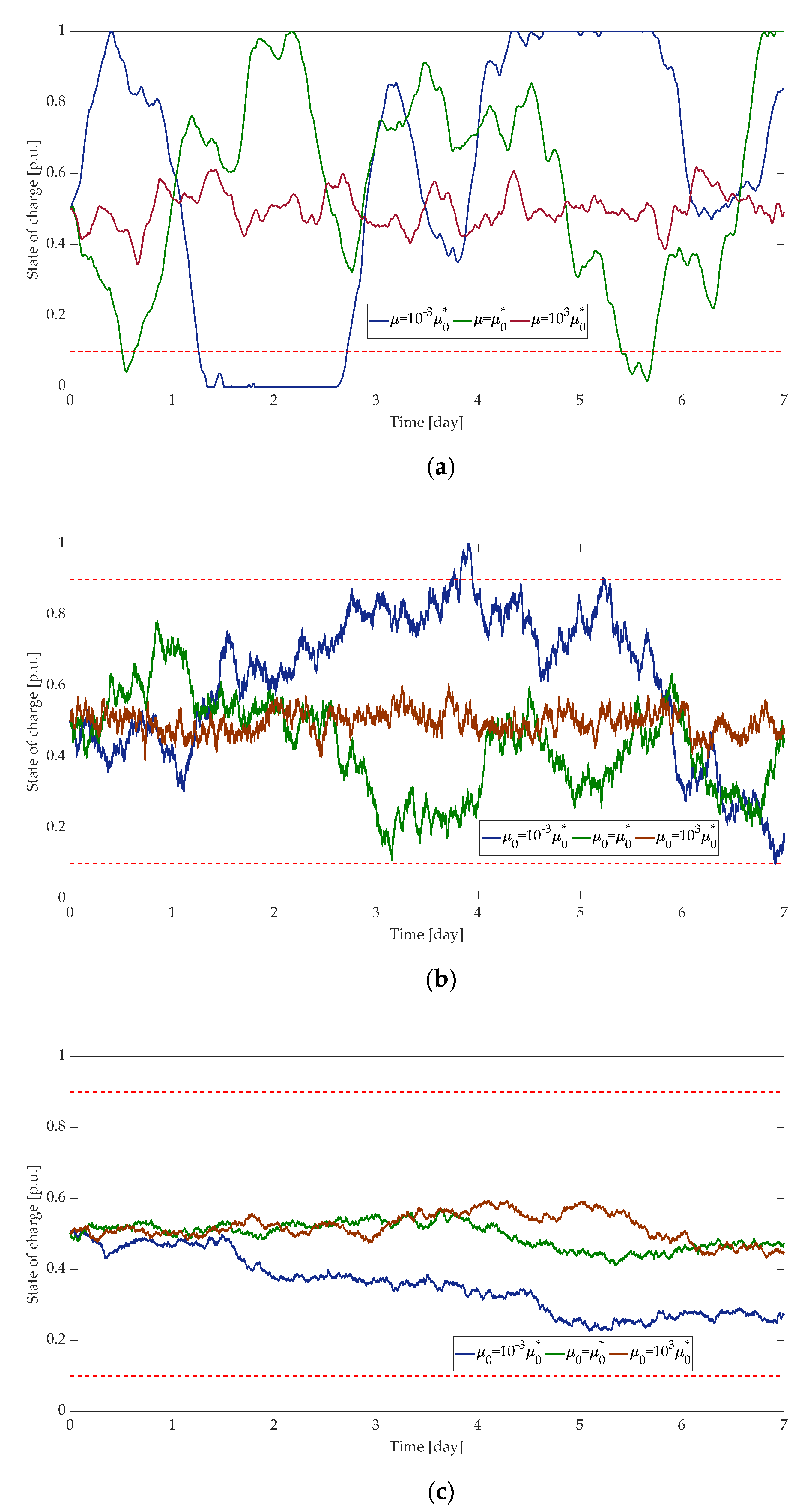
5.3. Analysis of State of Charge
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Brivio, C.; Mandelli, S.; Merlo, M. Battery energy storage system for primary control reserve and energy arbitrage. Sustain. Energy Grids Netw. 2016, 6, 152–165. [Google Scholar] [CrossRef]
- Guerra, K.; Haro, P.; Gutiérrez, R.E.; Gómez-Barea, A. Facing the high share of variable renewable energy in the power system: Flexibility and stability requirements. Appl. Energy 2022, 310, 118561. [Google Scholar] [CrossRef]
- Carlini, E.M.; Del Pizzo, F.; Giannuzzi, G.M.; Lauria, D.; Mottola, F.; Pisani, C. Online analysis and prediction of the inertia in power systems with renewable power generation based on a minimum variance harmonic finite impulse response filter. Int. J. Electr. Power Energy Syst. 2021, 131, 107042. [Google Scholar] [CrossRef]
- IRENA. Battery Storage for Renewables: Market Status and Technology Outlook. 2015. Available online: https://www.irena.org/publications/2015/Jan/Battery-Storage-for-Renewables-Market-Status-and-Technology-Outlook (accessed on 4 July 2022).
- Thien, T.; Axelsen, H.; Merten, M.; Axelsen, H.; Merten, M.; Zurmùhlen, S.; Münderlein, J.; Leuthold, M.; Sauer, D.U. Planning of grid-scale battery energy storage systems: Lessons learned from a 5 MW hybrid battery storage project in Germany. In Proceedings of the Battcon International Stationary Battery Conference, Orlando, FL, USA, 12–14 May 2015. [Google Scholar]
- Fu, H.; Tong, X.; Pan, Z.; Liu, F.; Wang, F.; Zhang, W. Research on BESS Participating in Power System Primary Frequency Regulation Control Strategy Considering State-of-Charge Recovery. In Proceedings of the 5th International Conference on Energy, Electrical and Power Engineering, Chongqing, China, 22–24 April 2022. [Google Scholar]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a Battery Energy Storage System for Primary Frequency Control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Stroe, D.; Knap, V.; Swierczynski, M.; Stroe, A.; Teodorescu, R. Operation of a Grid-Connected Lithium-Ion Battery Energy Storage System for Primary Frequency Regulation: A Battery Lifetime Perspective. IEEE Trans. Ind. Appl. 2017, 53, 430–438. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A.V. An optimal operation of wind energy storage system for frequency control based on model predictive control. Renew. Energy 2012, 48, 127–132. [Google Scholar] [CrossRef]
- Andrenacci, N.; Chiodo, E.; Lauria, D.; Mottola, F. Life Cycle Estimation of Battery Energy Storage Systems for Primary Frequency Regulation. Energies 2018, 11, 3320. [Google Scholar] [CrossRef]
- Wu, F.; Sioshansi, R. A stochastic operational model for controlling electric vehicle charging to provide frequency regulation. Transp. Res. Part D Transp. Environ. 2019, 67, 475–490. [Google Scholar] [CrossRef]
- Scarabaggio, P.; Carli, R.; Cavone, G.; Dotoli, M. Smart Control Strategies for Primary Frequency Regulation through Electric Vehicles: A Battery Degradation Perspective. Energies 2020, 13, 4586. [Google Scholar] [CrossRef]
- Meng, G.; Lu, Y.; Liu, H.; Ye, Y.; Sun, Y.; Tan, W. Adaptive Droop Coefficient and SOC Equalization-Based Primary Frequency Modulation Control Strategy of Energy Storage. Electronics 2021, 10, 2645. [Google Scholar] [CrossRef]
- Tan, Z.; Li, X.; He, L.; Li, Y.; Huang, J. Primary frequency control with BESS considering adaptive SoC recovery. Int. J. Electr. Power Energy Syst. 2020, 117, 105588. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbič, G.; Kim, H.; Hur, K. On Droop Control of Energy-Constrained Battery Energy Storage Systems for Grid Frequency Regulation. IEEE Access 2019, 7, 166353–166364. [Google Scholar] [CrossRef]
- Dang, J.; Seuss, J.; Suneja, L.; Harley, R.G. SOC feedback control for wind and ESS hybrid power system frequency regulation. In Proceedings of the IEEE Power Electronics and Machines in Wind Applications Conference, Denver, CO, USA, 16–18 July 2012. [Google Scholar]
- Marconato, R. Electric Power Systems Vol. 2: Steady-State Behaviour Controls, Short Circuits and Protection Systems, 2nd ed.; CEI: Milan, Italy, 2004. [Google Scholar]
- Vorobev, P.; Greenwood, D.M.; Bell, J.H.; Bialek, J.W.; Taylor, P.C.; Turitsyn, K. Deadbands, Droop, and Inertia Impact on Power System Frequency Distribution. IEEE Trans. Power Syst. 2019, 34, 3098–3108. [Google Scholar] [CrossRef]
- Quint, R.; Ramasubramanian, D. Impacts of droop and deadband on generator performance and frequency control. In Proceedings of the IEEE Power and Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Knap, V.; Chaudhary, S.K.; Stroe, D.I.; Swierczynski, M.; Craciun, B.I.; Teodorescu, R. Sizing of an Energy Storage System for Grid Inertial Response and Primary Frequency Reserve. IEEE Trans. Power Syst. 2016, 31, 3447–3456. [Google Scholar] [CrossRef]
- del Giudice, D.; Brambilla, A.; Grillo, S.; Bizzarri, F. Effects of inertia, load damping and dead-bands on frequency histograms and frequency control of power systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106842. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kallas, M.; Honeine, P.; Richard, C.; Francis, C.; Amoud, H. Prediction of time series using Yule-Walker equations with kernels. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012. [Google Scholar]
- Hassanzadeh, M.; Evrenosoğlu, C.Y.; Mili, L. A Short-term nodal voltage phasor forecasting method using temporal and spatial correlation. IEEE Trans. Power Syst. 2016, 31, 3881–3890. [Google Scholar] [CrossRef]
- Wong, W.K.; Bian, G. Estimating parameters in autoregressive models with asymmetric innovations. Stat. Probab. Lett. 2005, 71, 61–70. [Google Scholar] [CrossRef]
- Holý, V.; Tomanová, P. Estimation of Ornstein-Uhlenbeck Process Using Ultra-High-Frequency Data with Application to Intraday Pairs Trading Strategy. arXiv 2019, arXiv:1811.09312v2. [Google Scholar]
- Smith, P.L. From Poisson shot noise to the integrated Ornstein–Uhlenbeck process: Neurally principled models of information accumulation in decision-making and response time. J. Math. Psychol. 2010, 54, 266–283. [Google Scholar] [CrossRef]
- RTE. Network Frequency. Available online: https://www.services-rte.com/en/view-data-published-by-rte.html (accessed on 4 July 2022).






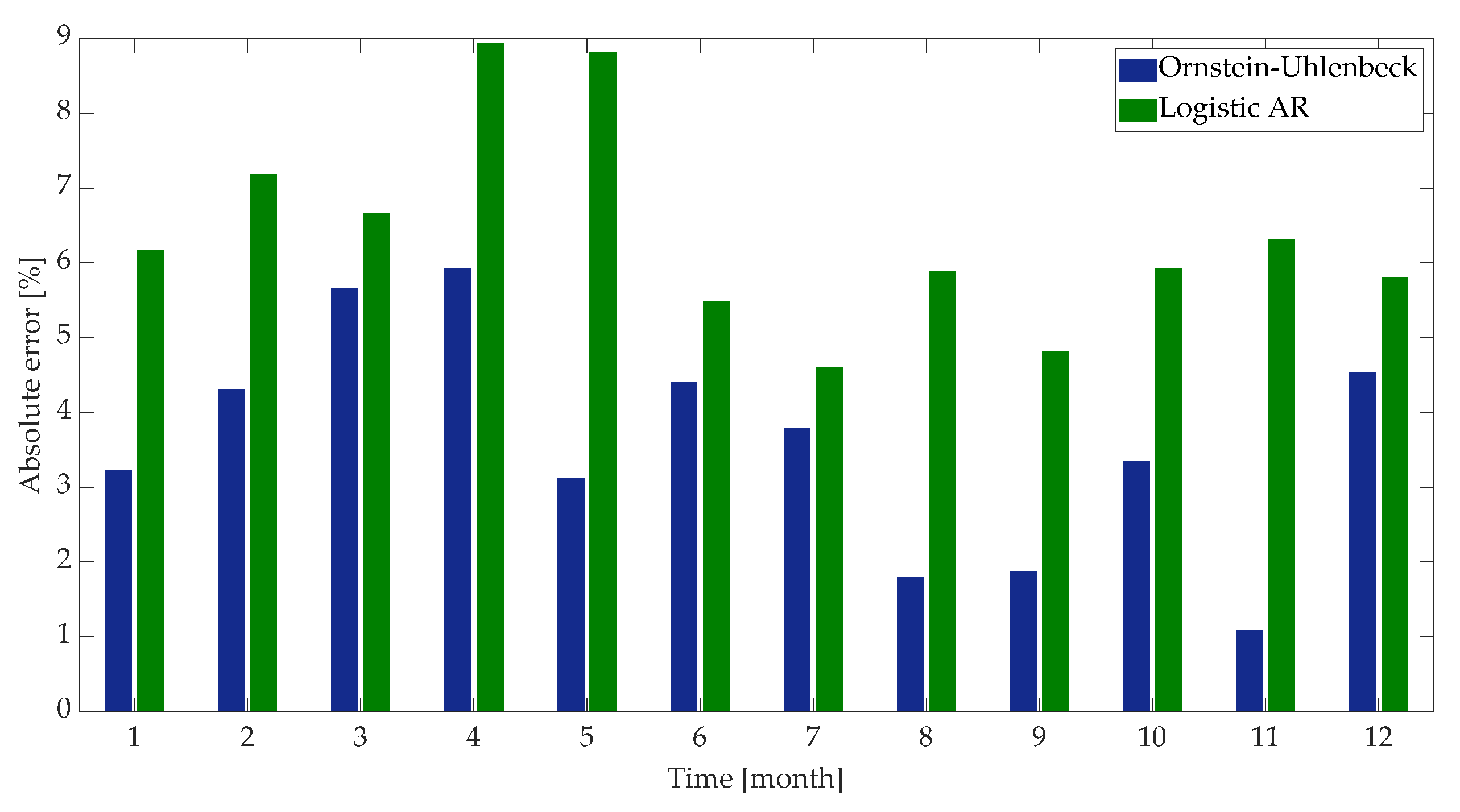
| Error | Mean [%] | Variance [%] | |
|---|---|---|---|
| Process | |||
| Monthly | |||
| Logistic Autoregressive | 7.2 × 10−4 | 6.2 | |
| Ornstein–Uhlenbeck | 3.5 × 10−4 | 3.0 | |
| Weekly | |||
| Logistic Autoregressive | 2.0 × 10−3 | 8.8 | |
| Ornstein–Uhlenbeck | 6.8 × 10−4 | 3.3 | |
| Daily | |||
| Logistic Autoregressive | 6.7 × 10−3 | 7.9 | |
| Ornstein–Uhlenbeck | 1.8 × 10−3 | 5.3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiodo, E.; Lauria, D.; Mottola, F.; Proto, D.; Villacci, D.; Giannuzzi, G.M.; Pisani, C. Probabilistic Description of the State of Charge of Batteries Used for Primary Frequency Regulation. Energies 2022, 15, 6508. https://doi.org/10.3390/en15186508
Chiodo E, Lauria D, Mottola F, Proto D, Villacci D, Giannuzzi GM, Pisani C. Probabilistic Description of the State of Charge of Batteries Used for Primary Frequency Regulation. Energies. 2022; 15(18):6508. https://doi.org/10.3390/en15186508
Chicago/Turabian StyleChiodo, Elio, Davide Lauria, Fabio Mottola, Daniela Proto, Domenico Villacci, Giorgio Maria Giannuzzi, and Cosimo Pisani. 2022. "Probabilistic Description of the State of Charge of Batteries Used for Primary Frequency Regulation" Energies 15, no. 18: 6508. https://doi.org/10.3390/en15186508











