Upgrading Conventional Power System for Accommodating Electric Vehicle through Demand Side Management and V2G Concepts
Abstract
:1. Introduction
- An accurate estimation of the loads due to an EV is introduced using a novel stochastic strategy.
- Optimal sizing for EV charging stations containing hybrid RES, the green hydrogen storage system (GHSS), and battery energy storage systems (BESS) is introduced to support the proposed EV charging station and the whole power system.
- A novel and effective DR strategy, using FLC, adds support to the EV charging station and the power system as well.
- A novel day ahead forecasting strategy adds more support to the power system during any unexpected operating conditions.
- Optimal operation of the whole power system, using several EV chargers, is proposed by using a novel model for the whole system.
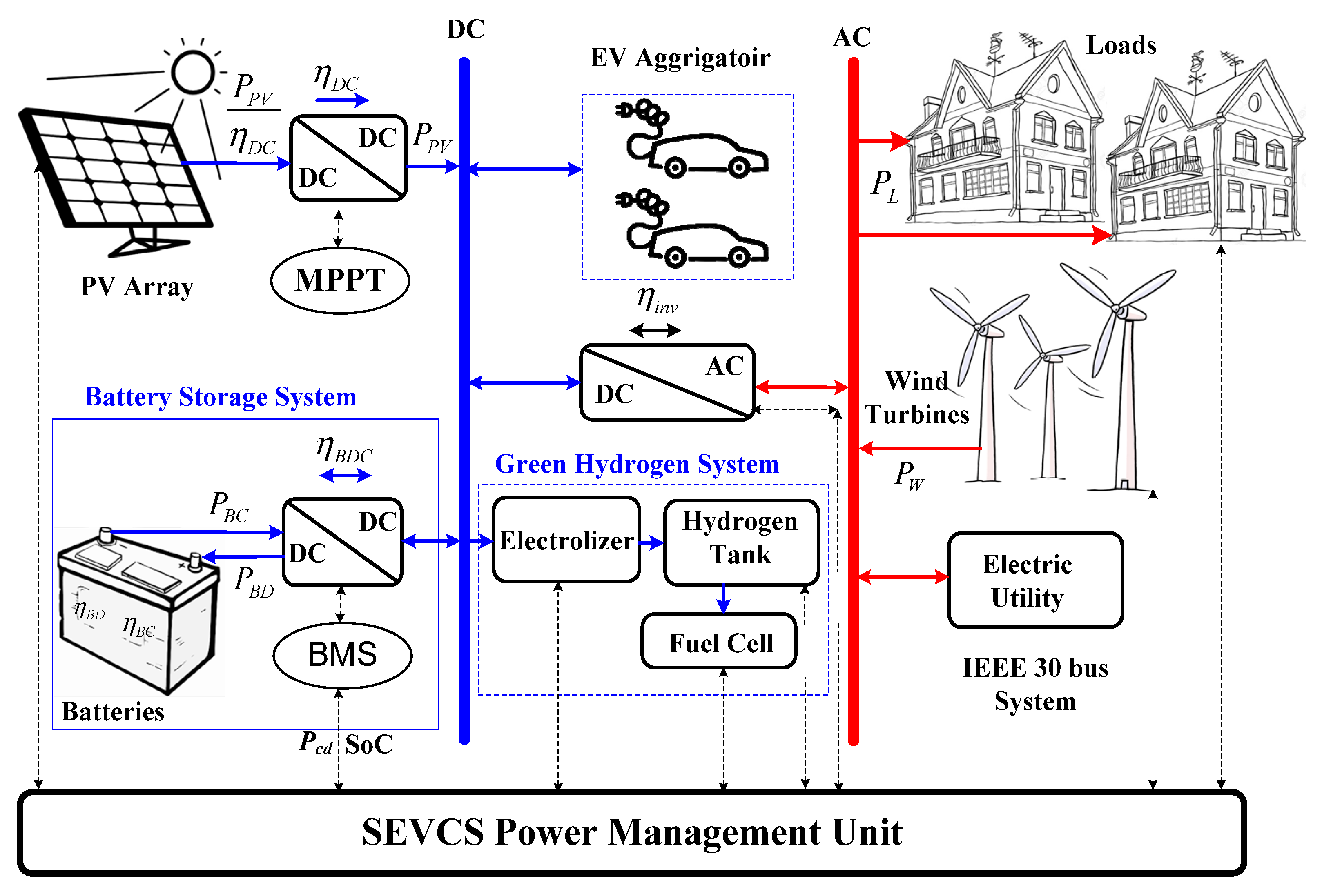
2. Smart EV Charging Station (SEVCS) Modeling
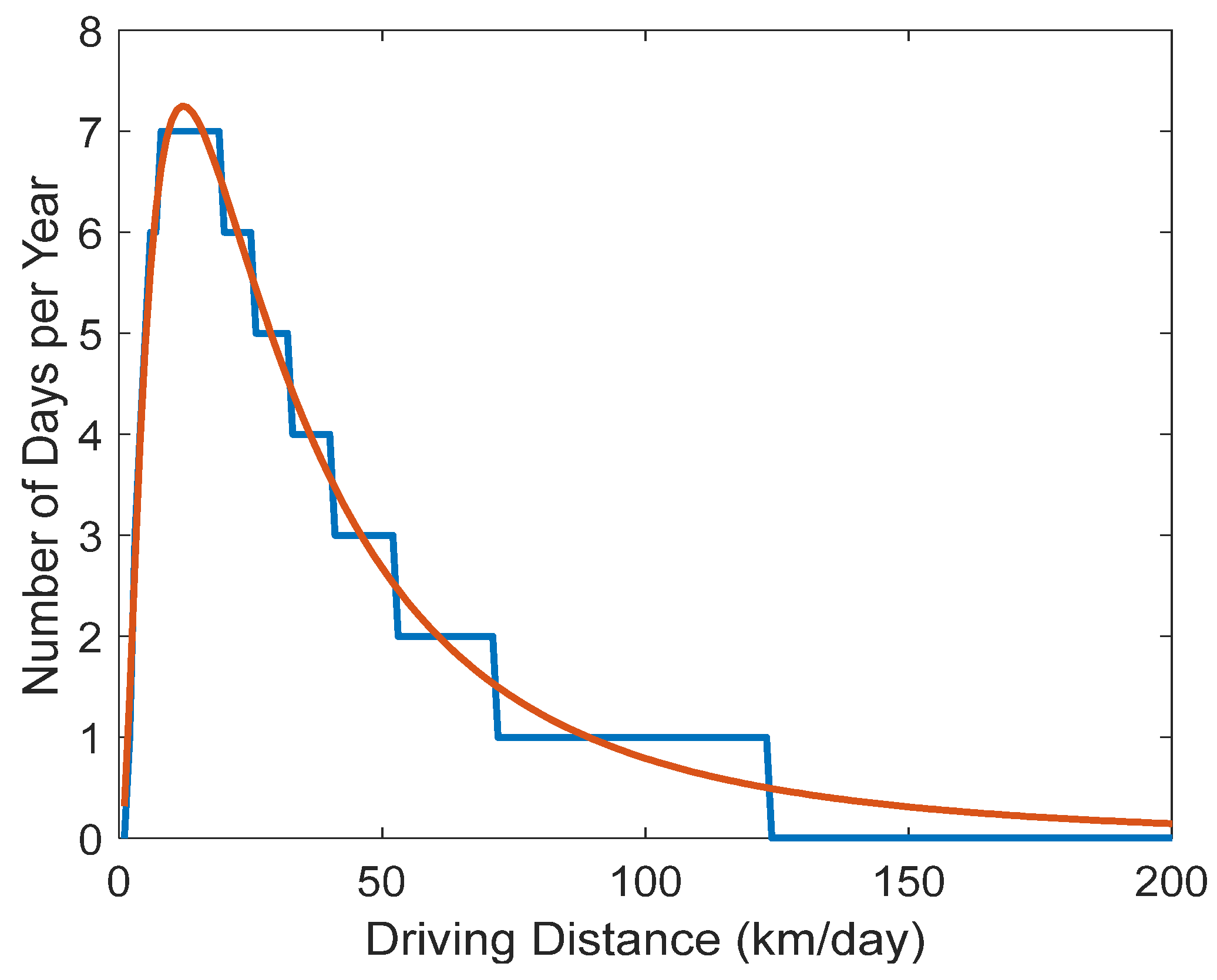
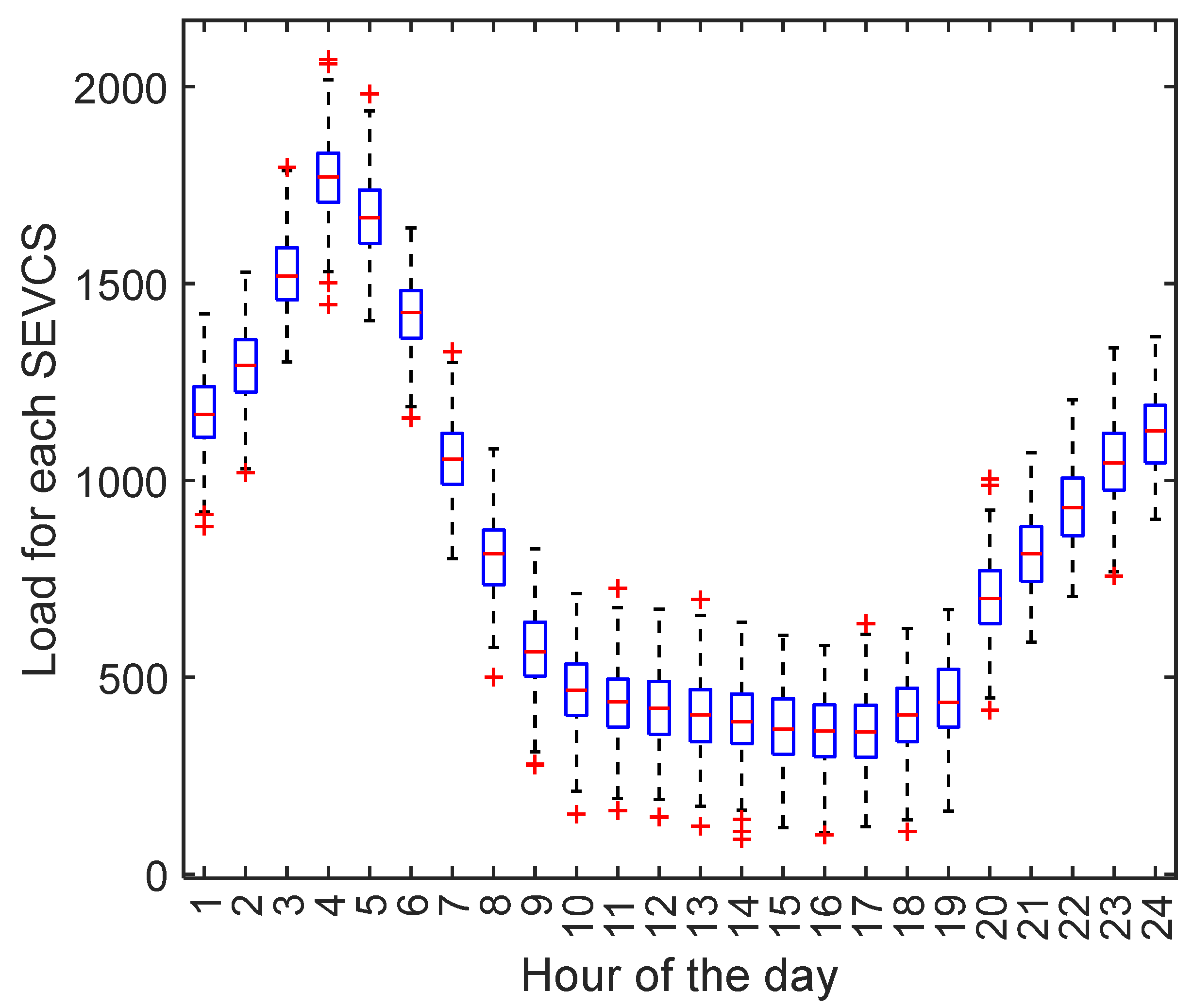
2.1. EV Load Estimation
2.2. Wind Energy System Modeling
2.3. Photovoltaic Energy System Modeling
2.4. Battery Energy Storage Model
2.5. Green Hydrogen Storage System (GHSS) Modeling
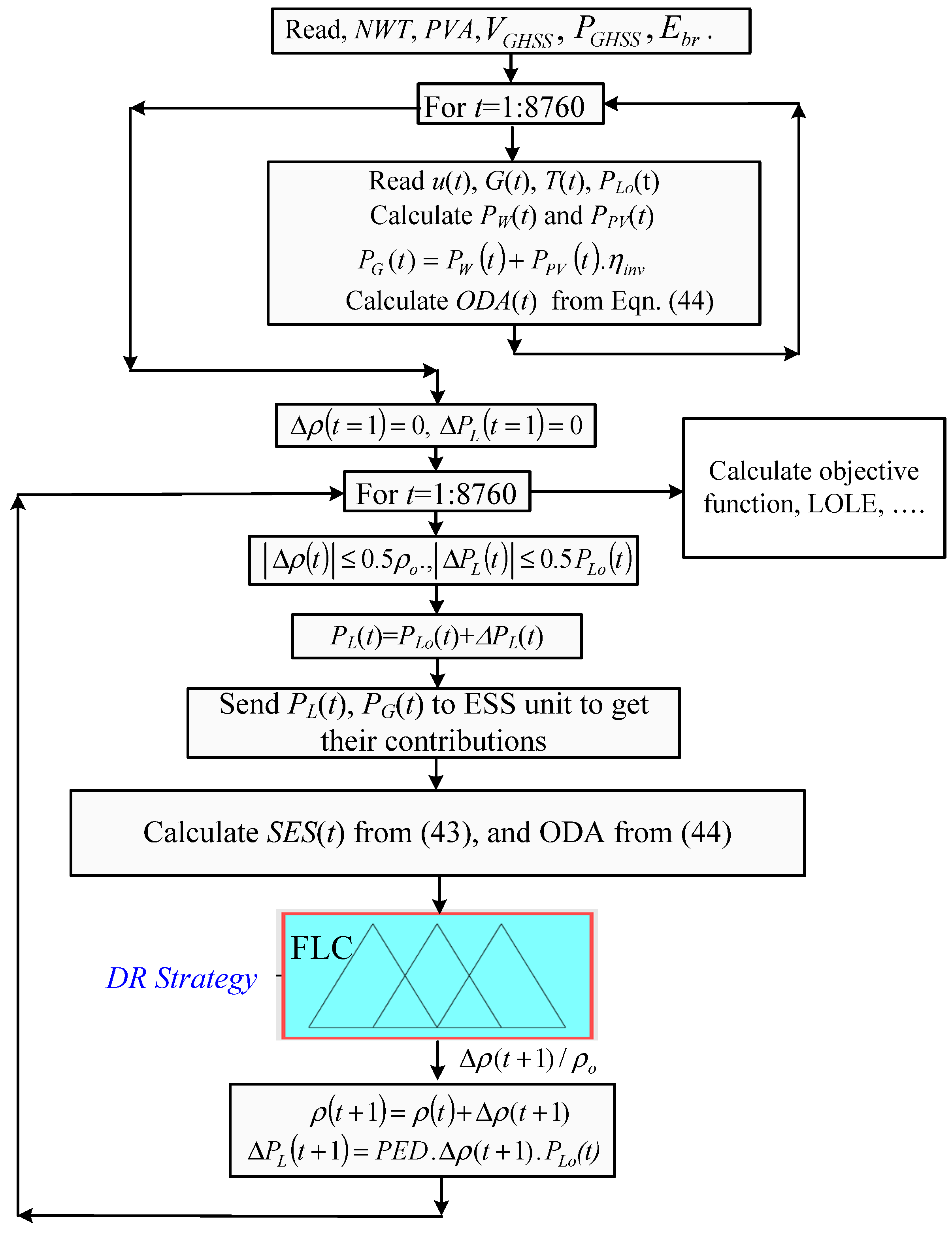
2.6. Power Dispatch Strategy
- ➣
- Check the constraints shown in Equation (21), if not valid, then and update the using Equation (28).
- ➣
- Check the constraints shown in Equation (22), if not valid, then, , and update the charging power of the SEVCS using Equation (29).
- ➣
- Check the constraints shown in Equation (21), if not valid, then , ( is the rated discharge power from the SEVCS battery) and update the using Equation (31).
- ➣
- Check the constraints shown in Equation (22), i not valid, then and update the charging power of the SEVCS using Equation (32).
2.7. Modeling of the Demand Response Strategy
2.8. Levelized Cost of Energy (LCE) Estimation
2.9. Particle Swarm Optimization Algorithm
- t: Iteration number
- i: Particle number
- : Inertia weight in a range of [0.5, 1].
- c1 & c2: Self-confidence and swarm confidence constants, respectively.
- a1 & a2: Random numbers in the range [0, 1].
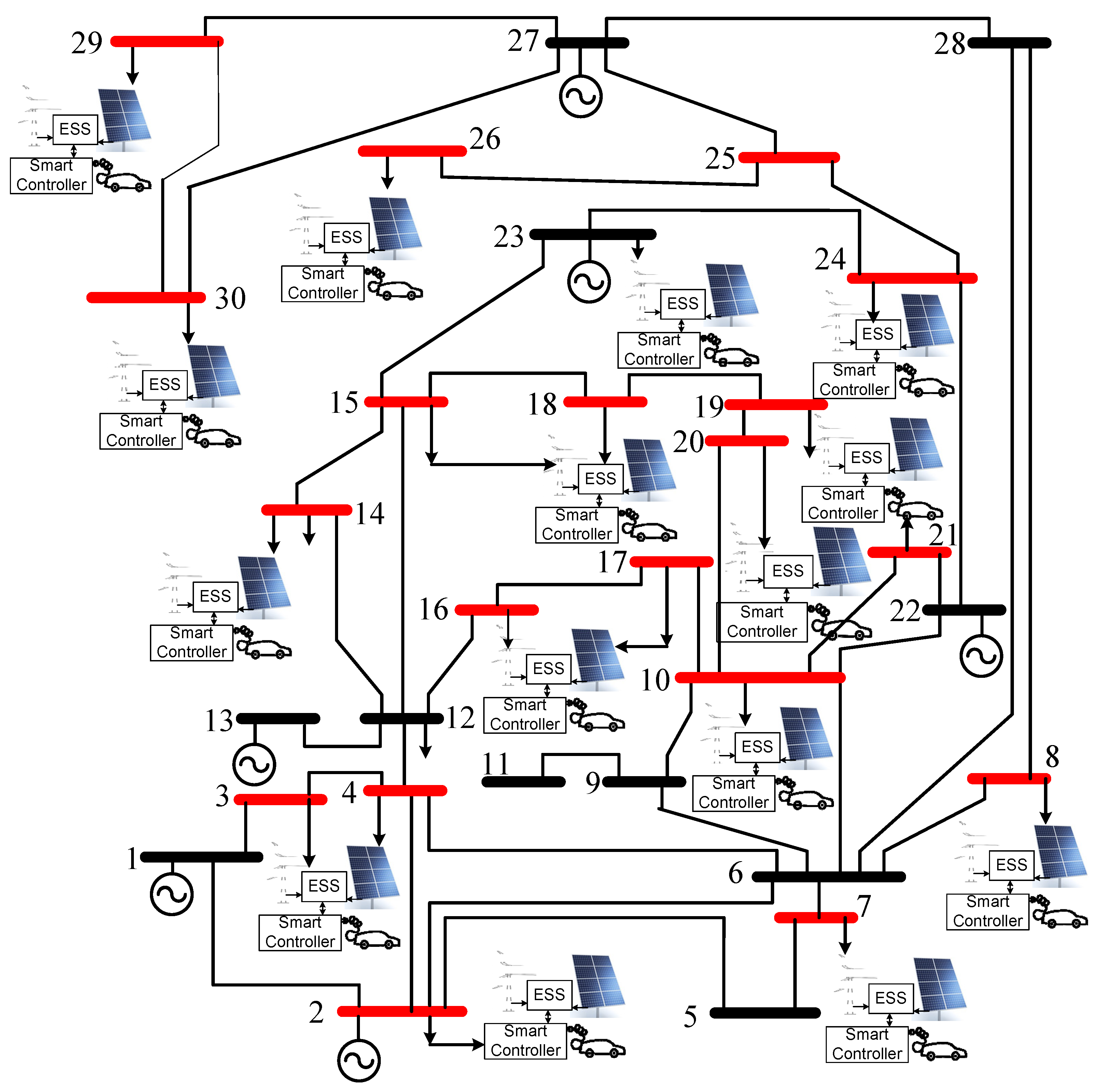
3. IEEE 30 Bus System Modeling
3.1. Analysis of Optimal Power Flow
- ≤ ≤
- ≤ ≤
- ≤ ≤
- ≤ ≤
3.2. Multi-Objective OPF Algorithm
- fi is a single objective function.
- x represents the set of decision variables.
- n is the number of SO functions.
3.3. Voltage Weakening Index
4. Simulation Result
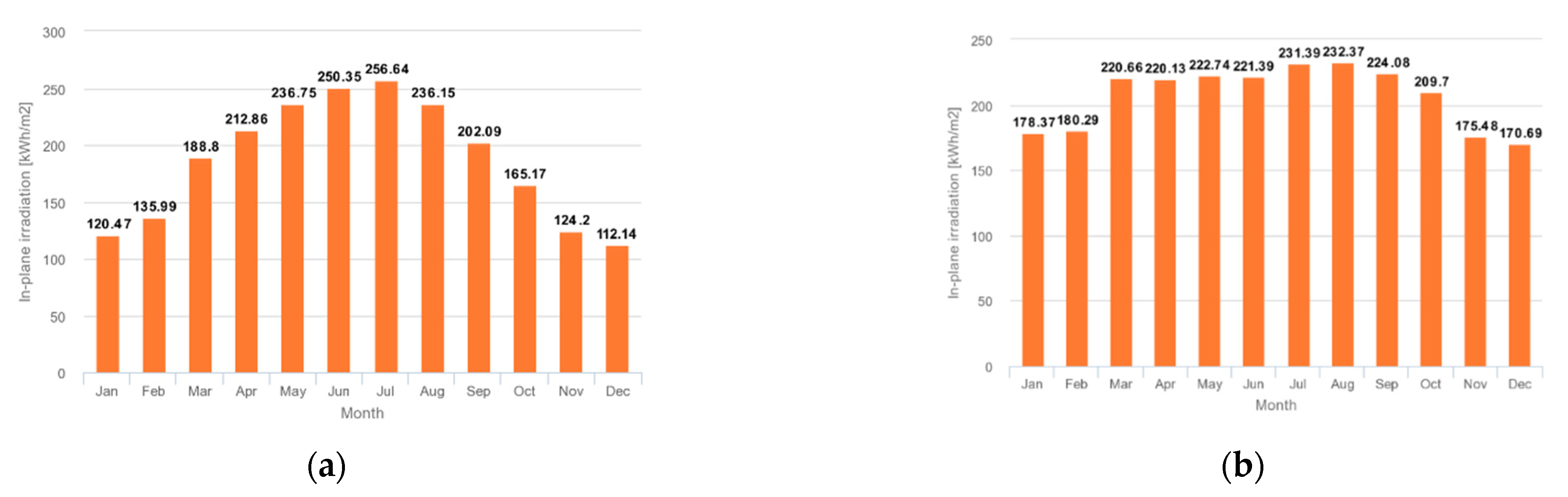
4.1. Input Data
4.2. Optimal SEVCS Sizing
4.3. Optimal Operation of the IEEE 30 bus System with EV
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Complete Form | Abbreviation | Complete Form |
| BESS | Battery energy storage systems | ODA | One-day ahead |
| BEV | Specific power consumption | PED | Price elasticity of demand |
| CRF | Capital recovery factor | PV | Photovoltaic |
| DG | Distributed generator | PVA | Area of the PV array |
| DoD | Depth of discharge | RDN | Radial distribution network |
| DR | Demand response | RES | Renewable energy sources |
| DSM | Demand side management | SES | Situation of the energy storage |
| ESS | Energy storage system | SEVCS | Smart EV charging station |
| EV | Electric vehicle | SoC | State of charge |
| FLC | Fuzzy logic controller | SoH | State of health |
| GHSS | Green hydrogen storage system | ToU | Time of use tariff |
| LCE | Levelized Cost of Energy | V2G | Vehicle to grid |
| LIB | Lithium-ion batteries | WT | Wind Turbine |
| NPC | Net present cost | MO | Multi-objective |
Symbols
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| PW | Output power of wind energy system | YE | Yearly generated energy |
| PPV | Output power from PV energy system | r | Interest rate |
| ηBC | Battery charging efficiency | T | Project lifetime |
| ηBD | Battery discharging efficiency | pbesti | Particle best values |
| ηBDC | Battery charger efficiency | gbest | Position of this global best |
| ηinv | Inverter efficiency | xi | Current particle position |
| σEV | Average daily distance of EV | vi | Particle velocity |
| μEV | Variance of the daily distance of EV | t | Iteration number |
| Tr | Return time of EV | i | Particle number |
| Td | Departure time of EV | Inertia weight | |
| BEV | Power consumption per day | c1 | Self-confidence constant |
| LEV | Daily distance of EV | c2 | Swarm confidence constant |
| Specific power consumption (kWh/km) | a1 & a2 | Random numbers in the range [0, 1] | |
| , ha | Height of the anemometers | Vi & Vj | Buses voltages of busbars i and j, respectively. |
| hwt | Hub height of the wind turbine, | & | Angles of ith, and jth busbars, respectively |
| u | Hourly wind speed | Yij | Admittance between buses i and j |
| UC | Cut-in wind speed of the WT | Admittance angle of | |
| UR | Rated wind speed of the WT | NB | Number of buses |
| UF | Cut-off wind speed of the WT | ND | Number of load buses |
| K | Shape Weibull parameter of the site and WT | NG | Number of generator buses |
| PR | Rated power of the WT | PGi | Generation power at busbar i |
| Ht | Solar irradiance | PDi | Load power at busbar i |
| Efficiencies of the PV array | PLL | Total transmission losses | |
| Efficiencies of the DC-DC converter | Pmin | Minimum active power constraints for each generator | |
| ηcr | Rated efficiency | Pmax | Maximum active power constraints for each generator |
| Tcr | Module rated temperature | Qmin | Minimum and maximum reactive power constraints for each generator |
| Tc | Cell temperature | Qmax | Maximum reactive power constraints for each generator. |
| βt | Temperature coefficient | Vmin | Minima voltage magnitude constraints for each bus |
| Ta(t) | Ambient temperature | Vmax | Maxima voltage magnitude constraints for each bus |
| αb and βb | Constants depending on the type of battery and the charging/discharging power to/from the battery | δmin | Minimum voltage angle constraints for each bus |
| Loss in capacity of the batteries | δmax | Maximum voltage angle constraints for each bus | |
| Rated energy of the battery | F | Multi-objective function | |
| Maximum energy of the battery | fi | Single objective function | |
| Minimum allowable energy | x | Set of decision variables. | |
| Rated energy of the battery | n | Number of SO functions | |
| CB | Total cost of the batteries | Hourly power from the SEVCS | |
| σ | Self-discharge rate | PEV | Power consumed by EV |
| . | Charging efficiency of the batteries | PEVA. | Average load of the EV during the year |
| Discharging efficiency of the batteries | PED | Price elasticity of demand | |
| PEZ(t) | Power transferred to the electrolyzer | PL | Load power |
| Amount of hydrogen generated from electrolyizer | PLA | Average load power during the year | |
| Rated hydrogen flow (kg/h) | ρ | Electricity price | |
| AEZ, & BEZ | Hydrogen consumption coefficients. | ρ0 | Basic tariff |
| PFC | Generated power from the fuel cells | Allowable minimum amount of Hydrogen in Hydrogen tank | |
| QFC | Amount of Hydrogen consumed in fuel cell | Maximum amount of Hydrogen in Hydrogen tank | |
| PNFC | Rated power of the fuel cell | PEZ | Power consumed by the electrolyizer |
| AFC & BFC | Consumption coefficients of the fuel cell | PG | Generated power from the wind and PV systems |
References
- Eltamaly, A.M.; Alotaibi, M.; Alolah, A.; Ahmed, M. A Novel Demand Response Strategy for Sizing of Hybrid Energy System with Smart Grid Concepts. IEEE Access 2021, 9, 20277–20294. [Google Scholar] [CrossRef]
- Kempton, W.; Letendre, S. Electric vehicles as a new power source for electric utilities. Transp. Res. Part D Transp. Environ. 1997, 2, 157–175. [Google Scholar] [CrossRef]
- Gao, S.; Chau, K.; Liu, C.; Wu, D.; Chan, C. Integrated energy management of plug-in electric vehicles in power grid with renewables. IEEE Trans. Veh. Technol. 2014, 63, 3019–3027. [Google Scholar] [CrossRef]
- Lam, A.; Leung, K.; Li, V. Capacity estimation for vehicle-to-grid frequency regulation services with smart charging mechanism. IEEE Trans. Smart Grid 2015, 7, 156–166. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Longo, M. The exploitation of vehicle-to-grid function for power quality improvement in a smart grid. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2169–2177. [Google Scholar] [CrossRef]
- Falahi, M.; Chou, H.; Ehsani, M.; Xie, L.; Butler-Purry, K. Potential power quality benefits of electric vehicles. IEEE Trans. Sustain. Energy 2013, 4, 1016–1023. [Google Scholar]
- Sadeghian, O.; Nazari-Heris, M.; Abapour, M.; Taheri, S.; Zare, K. Improving reliability of distribution networks using plug-in electric vehicles and demand response. J. Mod. Power Syst. Clean Energy 2019, 7, 1189–1199. [Google Scholar] [CrossRef]
- Jannati, J.; Nazarpour, D. Optimal performance of electric vehicles parking lot considering environmental issue. J. Clean. Prod. 2019, 206, 1073–1088. [Google Scholar] [CrossRef]
- Qu, D.; Liu, Q.; Fan, J.; Yang, J.; Yao, L. Analysis on Peak Clipping Effect of Distribution Network Based on Incentive Demand Response Participated by Electric Vehicles. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC); IEEE: Piscataway, NJ, USA, 2020; pp. 2179–2186. [Google Scholar]
- Lund, H.; Münster, E. Integrated transportation and energy sector CO2 emission control strategies. Transp. Policy 2006, 13, 426–433. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Hou, H.; Zhao, B.; Zhang, L.; Xie, C. Optimization Strategy of Composite Charging Station with Energy Storage for Fast Charging Demand of Electric Vehicles. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 23–25 November 2020; IEEE: Piscataway, NJ, USA, 2022; pp. 213–217. [Google Scholar]
- Hu, J.; Zhou, H.; Li, Y.; Hou, P.; Yang, G. Multi-time scale energy management strategy of aggregator characterized by photovoltaic generation and electric vehicles. J. Mod. Power Syst. Clean Energy 2020, 8, 727–736. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, Y.; Wang, J.; Wu, L.; Zhao, P.; Jiang, Z. Decentralized Demand Management Based on Alternating Direction Method of Multipliers Algorithm for Industrial Park with CHP Units and Thermal Storage. J. Mod. Power Syst. Clean Energy 2022, 10, 120–130. [Google Scholar] [CrossRef]
- Zeng, B.; Wu, G.; Wang, J.; Zhang, J.; Zeng, M. Impact of behavior-driven demand response on supply adequacy in smart distribution systems. Appl. Energy 2017, 202, 125–137. [Google Scholar] [CrossRef]
- Goel, L.; Wu, Q.; Wang, P. Reliability enhancement and nodal price volatility reduction of restructured power systems with stochastic demand side load shift. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Ghahramani, M.; Nazari-Heris, M.; Zare, K.; Mohammadi-ivatloo, B. Optimal energy and reserve management of the electric vehicles aggregator in electrical energy networks considering distributed energy sources and demand side management. In Electric Vehicles in Energy Systems; Springer: Cham, Switzerland, 2020; pp. 211–231. [Google Scholar]
- Deng, Y.; Zhang, Y.; Luo, F.; Mu, Y. Operational planning of centralized charging stations utilizing second-life battery energy storage systems. IEEE Trans. Sustain. Energy 2020, 12, 387–399. [Google Scholar] [CrossRef]
- Domínguez-Navarro, J.; Dufo-López, R.; Yusta-Loyo, J.; Artal-Sevil, J.; Bernal-Agustín, J. Design of an electric vehicle fast-charging station with integration of renewable energy and storage systems. Int. J. Electr. Power Energy Syst. 2019, 105, 46–58. [Google Scholar] [CrossRef]
- Pantoš, M. Stochastic optimal charging of electric-drive vehicles with renewable energy. Energy 2011, 36, 6567–6576. [Google Scholar] [CrossRef]
- Liu, N.; Chen, Q.; Liu, J.; Lu, X.; Li, P.; Lei, J.; Zhang, J. A heuristic operation strategy for commercial building microgrids containing EVs and PV system. IEEE Trans. Ind. Electron. 2014, 62, 2560–2570. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, F.; Hodge, B.; Zhang, J.; Li, Z.; Shafie-Khah, M.; Catalão, J. Dynamic price vector formation model-based automatic demand response strategy for PV-assisted EV charging stations. IEEE Trans. Smart Grid 2017, 8, 2903–2915. [Google Scholar] [CrossRef]
- Wang, R.; Wang, P.; Xiao, G. Two-stage mechanism for massive electric vehicle charging involving renewable energy. IEEE Trans. Veh. Technol. 2016, 65, 4159–4171. [Google Scholar] [CrossRef]
- Yang, H.; Pan, H.; Luo, F.; Qiu, J.; Deng, Y.; Lai, M.; Dong, Z. Operational planning of electric vehicles for balancing wind power and load fluctuations in a microgrid. IEEE Trans. Sustain. Energy 2016, 8, 592–604. [Google Scholar] [CrossRef]
- Erdogan, N.; Erden, F.; Kisacikoglu, M. A fast and efficient coordinated vehicle-to-grid discharging control scheme for peak shaving in power distribution system. J. Mod. Power Syst. Clean Energy 2018, 6, 555–566. [Google Scholar] [CrossRef]
- Jin, C.; Tang, J.; Ghosh, P. Optimizing electric vehicle charging: A customer’s perspective. IEEE Trans. Veh. Technol. 2013, 62, 2919–2927. [Google Scholar] [CrossRef]
- Pirouzi, S.; Aghaei, J.; Vahidinasab, V.; Niknam, T.; Khodaei, A. Robust linear archi-tecture for active/reactive power scheduling of EV integrated smart distribution networks. Electr. Power Syst. Res. 2018, 155, 8–20. [Google Scholar] [CrossRef]
- Soares, J.; Vale, Z.; Borges, N.; Lezama, F.; Kagan, N. Multi-objective robust optimization to solve energy scheduling in buildings under uncertainty. In Proceedings of the 2017 19th International Conference on Intelligent System Application to Power Systems (ISAP), San Antonio, TX, USA, 17–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Singh, M.; Kumar, P.; Kar, I. A multi charging station for electric vehicles and its utilization for load management and the grid support. IEEE Trans. Smart Grid 2013, 4, 1026–1037. [Google Scholar] [CrossRef]
- Jahangir, H.; Tayarani, H.; Ahmadian, A.; Golkar, M.; Miret, J.; Tayarani, M.; Gao, H. Charging demand of plug-in electric vehicles: Forecasting travel behavior based on a novel rough artificial neural network approach. J. Clean. Prod. 2019, 229, 1029–1044. [Google Scholar] [CrossRef]
- Leou, R.; Su, C.; Lu, C. Stochastic analyses of electric vehicle charging impacts on distribution network. IEEE Trans. Power Syst. 2013, 29, 1055–1063. [Google Scholar] [CrossRef]
- Haghi, H.; Qu, Z. A Kernel-based predictive model of EV capacity for distributed voltage control and demand response. IEEE Trans. Smart Grid 2016, 9, 3180–3190. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Integrating EV charging stations as smart loads for demand response provisions in distribution systems. IEEE Trans. Smart Grid 2016, 9, 1096–1106. [Google Scholar] [CrossRef]
- Zhao, H.; Yan, X.; Ren, H. Quantifying flexibility of residential electric vehicle charging loads using non-intrusive load extracting algorithm in demand response. Sustain. Cities Soc. 2019, 50, 101664. [Google Scholar] [CrossRef]
- Lee, Y.; Hur, J. A simultaneous approach implementing wind-powered electric vehicle charging stations for charging demand dispersion. Renew. Energy 2019, 144, 172–179. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Alotaibi, M.; Elsheikh, W.; Alolah, A.; Ahmed, M. Novel Demand Side-Management Strategy for Smart Grid Concepts Applications in Hybrid Renewable Energy Systems. In Proceedings of the 2022 4th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 17–19 March 2022; IEEE: Piscataway, NJ, USA; pp. 1–7. [Google Scholar]
- Rafique, M.M.; Rehman, S.; Alam, M.M.; Alhems, L.M. Feasibility of a 100 MW installed capacity wind farm for different climatic conditions. Energies 2018, 11, 2147. [Google Scholar] [CrossRef]
- Eltamaly, A. Design and implementation of wind energy system in Saudi Arabia. Renew. Energy 2013, 60, 42–52. [Google Scholar] [CrossRef]
- Rajesh, P.; Muthubalaji, S.; Srinivasan, S.; Shajin, F.H. Leveraging a Dynamic Differential Annealed Optimization and Recalling Enhanced Recurrent Neural Network for Maximum Power Point Tracking in Wind Energy Conversion System. Technol. Econ. Smart Grids Sustain. Energy 2022, 7, 1–15. [Google Scholar] [CrossRef]
- Mohamed, M.; Eltamaly, A.M.; Alolah, A.; Hatata, A. A novel framework-based cuckoo search algorithm for sizing and optimization of grid-independent hybrid renewable energy systems. Int. J. Green Energy 2019, 16, 86–100. [Google Scholar] [CrossRef]
- Khan, M.W.; Wang, J.; Ma, M.; Xiong, L.; Li, P.; Wu, F. Optimal energy management and control aspects of distributed microgrid using multi-agent systems. Sustain. Cities Soc. 2019, 44, 855–870. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Musical chairs algorithm for parameters estimation of PV cells. Sol. Energy 2022, 241, 601–620. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Performance of smart maximum power point tracker under partial shading conditions of PV systems. In Proceedings of the IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 17–19 August 2015; pp. 1–8. [Google Scholar]
- Pervez, I.; Antoniadis, C.; Massoud, Y. A Reduced Search Space Exploration Metaheuristic Algorithm for MPPT. IEEE Access 2022, 10, 26090–26100. [Google Scholar] [CrossRef]
- Farh, H.M.; Eltamaly, A.M.; Ibrahim, A.B.; Othman, M.F.; Al-Saud, M.S. Dynamic global power extraction from partially shaded photovoltaic using deep recurrent neural network and improved PSO techniques. Int. Trans. Electr. Energy Syst. 2019, 29, e12061. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, J.; Xu, J.; Fang, X.; Zhang, H. Real-time energy management of a microgrid using deep reinforcement learning. Energies 2019, 12, 2291. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, B.; Tan, Y.; Kirschen, D.; Zhang, B. Optimal battery control under cycle aging mechanisms in pay for performance settings. IEEE Trans. Autom. Control 2018, 64, 2324–2339. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.-S.; Hesse, H.; Truong, N.; Jossen, A.; Liu, Y.-H. Charging strategy for a residential battery storage system using fuzzy logic controller. In Proceedings of the NEIS Conference; Springer: Wiesbaden, Germany, 2016; pp. 182–189. [Google Scholar]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Optimal sizing method for stand-alone hybrid PV/wind power generation system. SMEE 2010, 1, 205–213. [Google Scholar]
- Smaoui, M.; Abdelkafi, A.; Krichen, L. Optimal sizing of stand-alone photovoltaic/wind/hydrogen hybrid system supplying a desalination unit. Sol. Energy 2015, 120, 263–276. [Google Scholar] [CrossRef]
- Alotaibi, M.; Eltamaly, A. A Smart Strategy for Sizing of Hybrid Renewable Energy System to Supply Remote Loads in Saudi Arabia. Energies 2021, 14, 7069. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J. Multi-objective design of PV–wind–diesel–hydrogen–battery systems. Renew. Energy 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
- Liu, X.; Tan, Q.; Niu, Y.; Babaei, R. Techno-economic analysis of solar tracker-based hybrid energy systems in a rural residential building: A case study in South Africa. Int. J. Green Energy 2022, 1–20. [Google Scholar] [CrossRef]
- Lan, T.; Jermsittiparsert, K.; Alrashood, S.T.; Rezaei, M.; Al-Ghussain, L.; Mohamed, M.A. An advanced machine learning based energy management of renewable microgrids considering hybrid electric vehicles’ charging demand. Energies 2021, 14, 569. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y. An innovative Fast-Converging speed MPPT approach without oscillation for temperature varying in photovoltaic systems applications. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 2674–2696. [Google Scholar] [CrossRef]
- AlHashmi, M.; Chhipi-Shrestha, G.; Nahiduzzaman, K.M.; Hewage, K.; Sadiq, R. Framework for Developing a Low-Carbon Energy Demand in Residential Buildings Using Community-Government Partnership: An Application in Saudi Arabia. Energies 2021, 14, 4954. [Google Scholar] [CrossRef]
- Eltamaly, A.; Al-Saud, M. Nested multi-objective PSO for optimal allocation and sizing of renewable energy distributed generation. J. Renew. Sustain. Energy 2018, 10, 035302. [Google Scholar] [CrossRef]
- Soliman, S.A.-H.; Mantawy, A.-A.H. Modern Optimization Techniques with Applications in Electric Power Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Maleki, A.; Pourfayaz, F.; Ahmadi, M.H. Design of a cost-effective wind/photovoltaic/hydrogen energy system for supplying a desalination unit by a heuristic approach. Sol. Energy 2016, 139, 2016. [Google Scholar] [CrossRef]










| SES | VL | L | M | H | VH | |
|---|---|---|---|---|---|---|
| ODA | ||||||
| NB | PB | PB | PM | PS | Z | |
| N | PB | PM | PS | Z | NS | |
| Z | PM | PS | Z | NS | NM | |
| P | PM | Z | NS | NM | NB | |
| PB | PS | NS | NM | NM | NB | |
| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wind speed | 5.6 | 5.5 | 6.5 | 6.1 | 5.9 | 6.3 | 6.6 | 5.7 | 5.5 | 5.5 | 5.4 | 5.5 | 5.84 |
| Solar Irradiance Wh/m2/h | 162 | 202 | 254 | 296 | 319 | 347 | 346 | 317 | 281 | 222 | 173 | 151 | 256 |
| Ta (°C) | 9.3 | 13.5 | 17.4 | 23.3 | 28.2 | 33.0 | 34.8 | 36 | 30.4 | 25.3 | 15.7 | 8.8 | 26.5 |
| Component | Specifications |
|---|---|
| WT (AE-Italia) [54] | Pr = 60 kW, hwt = 30 m, UC = 2.5 m/s, UR = 8 m/s, and UF = 25 m/s, TWT = 20 years, cost of wind turbines = $1500/kW, OMC of wind turbines = $100/kW/year [60] |
| PV parameters [54] | Cost of PV system = $200/m2 [60], OMC of PV=0.01* Cost of PV system, PVA = 1.67 m2, ηpv = 17%, lifetime = 30 year, βt = 0.005 per °C, Tcr = 25 °C |
| Inverter [54] | = 0.95 |
| Battery [54] | = 0.95, σ = 0.01%, DoD = 75% |
| Green Hydrogen | GHSS cost = $10,000/kW, GHSS OMC = $500/kW/year, GHSS lifetime = 10 years AEZ = 40 kW/kg/h and BEZ = 20 kW/kg/h, respectively [53]. AFC = 0.05 and BFC = 0.004 [53] |
| Without V2G | With V2G | |||||
|---|---|---|---|---|---|---|
| Item | PED = 0 | PED = −0.5 | PED = −1 | PED = 0 | PED = −0.5 | PED = −1 |
| NWT | 16 | 12 | 12 | 15 | 12 | 11 |
| PVA (m2) | 3463 | 2363 | 2172 | 3117 | 2,187 | 2154 |
| EGH (kWh) | 1763 | 1125 | 1073 | 1618 | 1014 | 972 |
| Eb (kWh) | 634 | 452 | 412 | 578 | 416 | 384 |
| TPC ($) | 4,954,725 | 3,691,234 | 3,482,671 | 4,541,561 | 3,383,914 | 3,168,145 |
| LCE ($/kWh) | 0.052374 | 0.039018248 | 0.03681363 | 0.048006643 | 0.033769717 | 0.032488927 |
| Max (VWI) | 21 | 5.3 | 3.1 | 12.6 | 3.2 | 1.8 |
| TL Losses (%) | 13.7 | 8.6 | 7.1 | 10.2 | 7.3 | 6.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, M.A.; Eltamaly, A.M. Upgrading Conventional Power System for Accommodating Electric Vehicle through Demand Side Management and V2G Concepts. Energies 2022, 15, 6541. https://doi.org/10.3390/en15186541
Alotaibi MA, Eltamaly AM. Upgrading Conventional Power System for Accommodating Electric Vehicle through Demand Side Management and V2G Concepts. Energies. 2022; 15(18):6541. https://doi.org/10.3390/en15186541
Chicago/Turabian StyleAlotaibi, Majed A., and Ali M. Eltamaly. 2022. "Upgrading Conventional Power System for Accommodating Electric Vehicle through Demand Side Management and V2G Concepts" Energies 15, no. 18: 6541. https://doi.org/10.3390/en15186541
APA StyleAlotaibi, M. A., & Eltamaly, A. M. (2022). Upgrading Conventional Power System for Accommodating Electric Vehicle through Demand Side Management and V2G Concepts. Energies, 15(18), 6541. https://doi.org/10.3390/en15186541







